Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 5 Application of Definite Integration Miscellaneous Exercise 5 Questions and Answers.
12th Maths Part 2 Application of Definite Integration Miscellaneous Exercise 5 Questions And Answers Maharashtra Board
I. Choose the correct option from the given alternatives:
Question 1.
The area bounded by the region 1 ≤ x ≤ 5 and 2 ≤ y ≤ 5 is given by
(a) 12 sq units
(b) 8 sq units
(c) 25 sq units
(d) 32 sq units
Answer:
(a) 12 sq units
Question 2.
The area of the region enclosed by the curve y = \(\frac{1}{x}\), and the lines x = e, x = e2 is given by
(a) 1 sq unit
(b) \(\frac{1}{2}\) sq units
(c) \(\frac{3}{2}\) sq units
(d) \(\frac{5}{2}\) sq units
Answer:
(a) 1 sq unit
![]()
Question 3.
The area bounded by the curve y = x3, the X-axis and the lines x = -2 and x = 1 is
(a) -9 sq units
(b) \(-\frac{15}{4}\) sq units
(c) \(\frac{15}{4}\) sq units
(d) \(\frac{17}{4}\) sq units
Answer:
(c) \(\frac{15}{4}\) sq units
Question 4.
The area enclosed between the parabola y2 = 4x and line y = 2x is
(a) \(\frac{2}{3}\) sq units
(b) \(\frac{1}{3}\) sq units
(c) \(\frac{1}{4}\) sq units
(d) \(\frac{3}{4}\) sq units
Answer:
(b) \(\frac{1}{3}\) sq units
Question 5.
The area of the region bounded between the line x = 4 and the parabola y2 = 16x is
(a) \(\frac{128}{3}\) sq units
(b) \(\frac{108}{3}\) sq units
(c) \(\frac{118}{3}\) sq units
(d) \(\frac{218}{3}\) sq units
Answer:
(a) \(\frac{128}{3}\) sq units
Question 6.
The area of the region bounded by y = cos x, Y-axis and the lines x = 0, x = 2π is
(a) 1 sq unit
(b) 2 sq units
(c) 3 sq units
(d) 4 sq units
Answer:
(d) 4 sq units
![]()
Question 7.
The area bounded by the parabola y2 = 8x, the X-axis and the latus rectum is
(a) \(\frac{31}{3}\) sq units
(b) \(\frac{32}{3}\) sq units
(c) \(\frac{32 \sqrt{2}}{3}\) sq units
(d) \(\frac{16}{3}\) sq units
Answer:
(b) \(\frac{32}{3}\) sq units
Question 8.
The area under the curve y = 2√x, enclosed between the lines x = 0 and x = 1 is
(a) 4 sq units
(b) \(\frac{3}{4}\) sq units
(c) \(\frac{2}{3}\) sq units
(d) \(\frac{4}{3}\) sq units
Answer:
(d) \(\frac{4}{3}\) sq units
Question 9.
The area of the circle x2 + y2 = 25 in first quadrant is
(a) \(\frac{25 \pi}{3}\) sq units
(b) 5π sq units
(c) 5 sq units
(d) 3 sq units
Answer:
(a) \(\frac{25 \pi}{3}\) sq units
Question 10.
The area of the region bounded by the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) is
(a) ab sq units
(b) πab sq units
(c) \(\frac{\pi}{a b}\) sq units ab
(d) πa2 sq units
Answer:
(b) πab sq units
![]()
Question 11.
The area bounded by the parabola y2 = x and the line 2y = x is
(a) \(\frac{4}{3}\) sq units
(b) 1 sq unit
(c) \(\frac{2}{3}\) sq unit
(d) \(\frac{1}{3}\) sq unit
Answer:
(a) \(\frac{4}{3}\) sq units
Question 12.
The area enclosed between the curve y = cos 3x, 0 ≤ x ≤ \(\frac{\pi}{6}\) and the X-axis is
(a) \(\frac{1}{2}\) sq unit
(b) 1 sq unit
(c) \(\frac{2}{3}\) sq unit
(d) \(\frac{1}{3}\) sq unit
Answer:
(d) \(\frac{1}{3}\) sq unit
Question 13.
The area bounded by y = √x and line x = 2y + 3, X-axis in first quadrant is
(a) 2√3 sq units
(b) 9 sq units
(c) \(\frac{34}{3}\) sq units
(d) 18 sq units
Answer:
(b) 9 sq units
Question 14.
The area bounded by the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) and the line \(\frac{x}{a}+\frac{y}{b}=1\) is
(a) (πab – 2ab) sq units
(b) \(\frac{\pi a b}{4}-\frac{a b}{2}\) sq units
(c) (πab – ab) sq units
(d) πab sq units
Answer:
(b) \(\frac{\pi a b}{4}-\frac{a b}{2}\) sq units
Question 15.
The area bounded by the parabola y = x2 and the line y = x is
(a) \(\frac{1}{2}\) sq unit
(b) \(\frac{1}{3}\) sq unit
(c) \(\frac{1}{6}\) sq unit
(d) \(\frac{1}{12}\) sq unit
Answer:
(c) \(\frac{1}{6}\) sq unit
![]()
Question 16.
The area enclosed between the two parabolas y2 = 4x and y = x is
(a) \(\frac{8}{3}\) sq units
(b) \(\frac{32}{3}\) sq units
(c) \(\frac{16}{3}\) sq units
(d) \(\frac{4}{3}\) sq units
Answer:
(c) \(\frac{16}{3}\) sq units
Question 17.
The area bounded by the curve y = tan x, X-axis and the line x = \(\frac{\pi}{4}\) is
(a) \(\frac{1}{3}\) log 2 sq units
(b) log 2 sq units
(c) 2 log 2 sq units
(d) 3 log 2 sq units
Answer:
(a) \(\frac{1}{3}\) log 2 sq units
Question 18.
The area of the region bounded by x2 = 16y, y = 1, y = 4 and x = 0 in the first quadrant, is
(a) \(\frac{7}{3}\) sq units
(b) \(\frac{8}{3}\) sq units
(c) \(\frac{64}{3}\) sq units
(d) \(\frac{56}{3}\) sq units
Answer:
(d) \(\frac{56}{3}\) sq units
Question 19.
The area of the region included between the parabolas y2 = 4ax and x2 = 4ay, (a > 0) is given by
(a) \(\frac{16 a^{2}}{3}\) sq units
(b) \(\frac{8 a^{2}}{3}\) sq units
(c) \(\frac{4 a^{2}}{3}\) sq units
(d) \(\frac{32 a^{2}}{3}\) sq units
Answer:
(a) \(\frac{16 a^{2}}{3}\) sq units
![]()
Question 20.
The area of the region included between the line x + y = 1 and the circle x2 + y2 = 1 is
(a) \(\frac{\pi}{2}-1\) sq units
(b) π – 2 sq units
(c) \(\frac{\pi}{4}-\frac{1}{2}\) sq units
(d) π – \(\frac{1}{2}\) sq units
Answer:
(c) \(\frac{\pi}{4}-\frac{1}{2}\) sq units
(II) Solve the following:
Question 1.
Find the area of the region bounded by the following curve, the X-axis and the given lines:
(i) 0 ≤ x ≤ 5, 0 ≤ y ≤ 2
(ii) y = sin x, x = 0, x = π
(iii) y = sin x, x = 0, x = \(\frac{\pi}{3}\)
Solution:
(i) Required area = \(\int_{0}^{5} y d x\), where y = 2
= \(\int_{0}^{5} 2 d x\)
= \([2 x]_{0}^{5}\)
= 2 × 5 – 0
= 10 sq units.
(ii) The curve y = sin x intersects the X-axis at x = 0 and x = π between x = 0 and x = π.
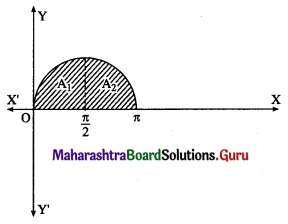
Two bounded regions A1 and A2 are obtained. Both the regions have equal areas.
∴ required area = A1 + A2 = 2A1
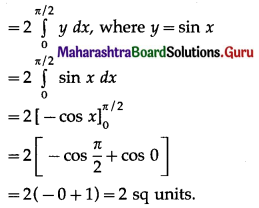
(iii) Required area = \(\int_{0}^{\pi / 3} y d x\), where y = sin x

![]()
Question 2.
Find the area of the circle x2 + y2 = 9, using integration.
Solution:
By the symmetry of the circle, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 3.
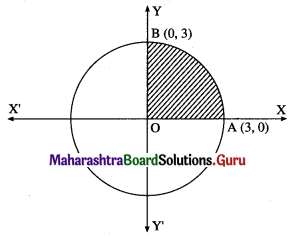
From the equation of the circle, y2 = 9 – x2.
In the first quadrant, y > 0
∴ y = \(\sqrt{9-x^{2}}\)
∴ area of the circle = 4 (area of the region OABO)

Question 3.
Find the area of the ellipse \(\frac{x^{2}}{25}+\frac{y^{2}}{16}=1\) using integration.
Solution:
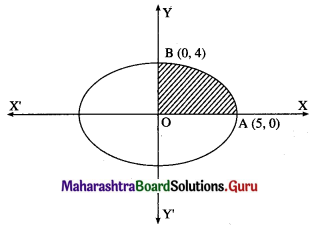
By the symmetry of the ellipse, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 5.
From the equation of the ellipse
\(\frac{y^{2}}{16}=1-\frac{x^{2}}{25}=\frac{25-x^{2}}{25}\)
∴ y2 = \(\frac{16}{25}\) (25 – x2)
In the first quadrant y > 0
∴ y = \(\frac{4}{5} \sqrt{25-x^{2}}\)
∴ area of the ellipse = 4(area of the region OABO)

Question 4.
Find the area of the region lying between the parabolas:
(i) y2 = 4x and x2 = 4y
(ii) 4y2 = 9x and 3x2 = 16y
(iii) y2 = x and x2 = y.
Solution:
(i)
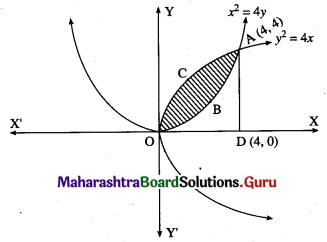
For finding the points of intersection of the two parabolas, we equate the values of y2 from their equations.
From the equation x2 = 4y, y = \(\frac{x^{2}}{4}\)
y = \(\frac{x^{4}}{16}\)
\(\frac{x^{4}}{16}\) = 4x
∴ x4 – 64x = 0
∴ x(x3 – 64) = 0
∴ x = 0 or x3 = 64 i.e. x = 0 or x = 4
When x = 0, y = 0
When x = 4, y = \(\frac{4^{2}}{4}\) = 4
∴ the points of intersection are 0(0, 0) and A(4, 4).
Required area = area of the region OBACO = [area of the region ODACO] – [area of the region ODABO]
Now, area of the region ODACO = area under the parabola y2 = 4x, i.e. y = 2√x between x = 0 and x = 4

(ii)
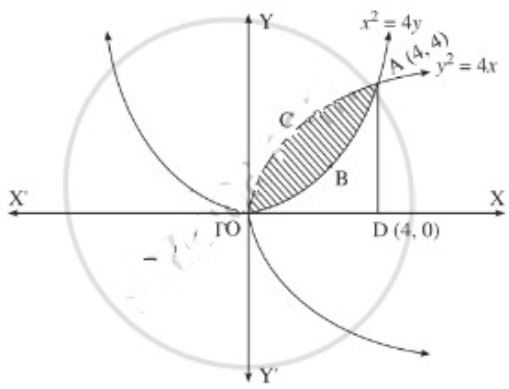
For finding the points of intersection of the two parabolas, we equate the values of 4y2 from their equations.
From the equation 3x2 = 16y, y = \(\frac{3 x^{2}}{16}\)
∴ y = \(\frac{3 x^{4}}{256}\)
∴ \(\frac{3 x^{4}}{256}\) = 9x
∴ 3x4 – 2304x = 0
∴ x(x3 – 2304) = 0
∴ x = 0 or x3 = 2304 i.e. x = 0 or x = 4
When x = 0, y = 0
When x = 4, y = \(\frac{4^{2}}{4}\)
∴ the points of intersection are O(0, 0) and A(4, 4).
Required area = area of the region OBACO = [area of the region ODACO] – [area of the region ODABO]
Now, area of the region ODACO = area under the parabola y2 = 4x,
i.e. y = 2√x between x = 0 and x = 4
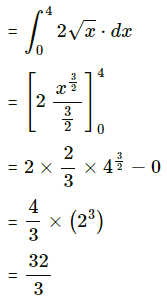
Area of the region ODABO = area under the rabola x2 = 4y,
i.e. y = \(\frac{x^{2}}{4}\) between x = 0 and x = 4
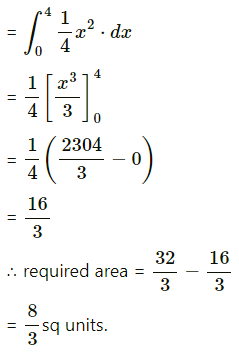
![]()
(iii)
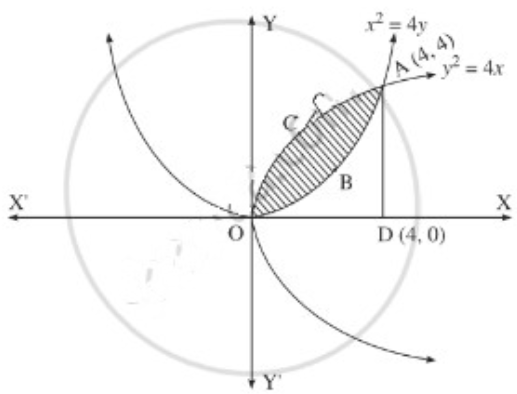
For finding the points of intersection of the two parabolas, we equate the values of y2 from their equations.
From the equation x2 = y, y = \(\frac{x^{2}}{y}\)
∴ y = \(\frac{x^{2}}{y}\)
∴ \(\frac{x^{2}}{y}\) = x
∴ x2 – y = 0
∴ x(x3 – y) = 0
∴ x = 0 or x3 = y
i.e. x = 0 or x = 4
When x = 0, y = 0
When x = 4, y = \(\frac{4^{2}}{4}\) = 4
∴ the points of intersection are O(0, 0) and A(4, 4).
Required area = area of the region OBACO = [area of the region ODACO] – [area of the region ODABO]
Now, area of the region ODACO = area under the parabola y2 = 4x,
i.e. y = 2√x between x = 0 and x = 4
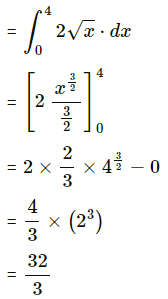
Area ofthe region ODABO = area under the rabola x2 = 4y,
i.e. y = \(\frac{x^{2}}{3}\) between x = 0 and x = 4
Question 5.
Find the area of the region in the first quadrant bounded by the circle x2 + y2 = 4 and the X-axis and the line x = y√3.
Solution:
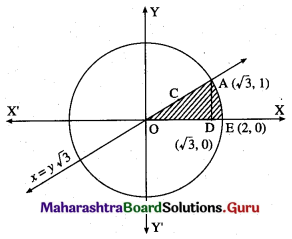
For finding the points of intersection of the circle and the line, we solve
x2 + y2 = 4 ………(1)
and x = y√3 ……..(2)
From (2), x2 = 3y2
From (1), x2 = 4 – y2
3y2 = 4 – y2
4y2 = 4
y2 = 1
y = 1 in the first quadrant.
When y = 1, r = 1 × √3 = √3
∴ the circle and the line intersect at A(√3, 1) in the first quadrant
Required area = area of the region OCAEDO = area of the region OCADO + area of the region DAED
Now, area of the region OCADO = area under the line x = y√3, i.e. y = \(\frac{x}{\sqrt{3}}\) between x = 0
and x = √3

Question 6.
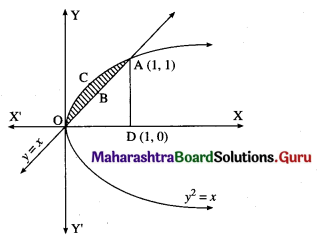
Find the area of the region bounded by the parabola y2 = x and the line y = x in the first quadrant.
Solution:
To obtain the points of intersection of the line and the parabola, we equate the values of x from both equations.
∴ y2 = y
∴ y2 – y = 0
∴ y(y – 1) = 0
∴ y = 0 or y = 1
When y = 0, x = 0
When y = 1, x = 1
∴ the points of intersection are O(0, 0) and A(1, 1).
Required area = area of the region OCABO = area of the region OCADO – area of the region OBADO
Now, area of the region OCADO = area under the parabola y2 = x i.e. y = +√x (in the first quadrant) between x = 0 and x = 1
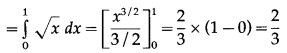
Area of the region OBADO = area under the line y = x between x = 0 and x = 1

![]()
Question 7.
Find the area enclosed between the circle x2 + y2 = 1 and the line x + y = 1, lying in the first quadrant.
Solution:
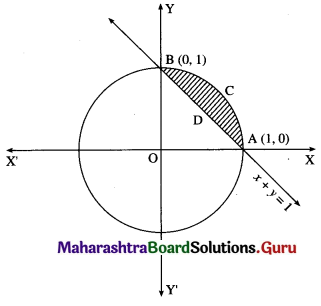
Required area = area of the region ACBPA = (area of the region OACBO) – (area of the region OADBO)
Now, area of the region OACBO = area under the circle x2 + y2 = 1 between x = 0 and x = 1

Area of the region OADBO = area under the line x + y = 1 between x = 0 and x = 1
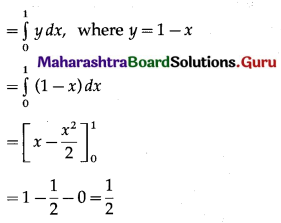
∴ required area = \(\left(\frac{\pi}{4}-\frac{1}{2}\right)\) sq units.
Question 8.
Find the area of the region bounded by the curve (y – 1)2 = 4(x + 1) and the line y = (x – 1).
Solution:
The equation of the curve is (y – 1)2 = 4(x + 1)
This is a parabola with vertex at A (-1, 1).
To find the points of intersection of the line y = x – 1 and the parabola.
Put y = x – 1 in the equation of the parabola, we get
(x – 1 – 1)2 = 4(x + 1)
∴ x2 – 4x + 4 = 4x + 4
∴ x2 – 8x = 0
∴ x(x – 8) = 0
∴ x = 0, x = 8
When x = 0, y = 0 – 1 = -1
When x = 8, y = 8 – 1 = 7
∴ the points of intersection are B (0, -1) and C (8, 7).
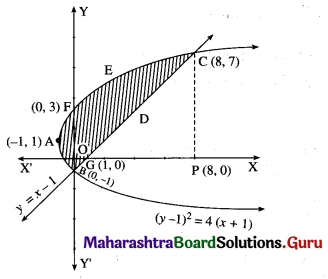
To find the points where the parabola (y – 1)2 = 4(x + 1) cuts the Y-axis.
Put x = 0 in the equation of the parabola, we get
(y – 1)2 = 4(0 + 1) = 4
∴ y – 1 = ±2
∴ y – 1 = 2 or y – 1 = -2
∴ y = 3 or y = -1
∴ the parabola cuts the Y-axis at the points B(0, -1) and F(0, 3).
To find the point where the line y = x – 1 cuts the X-axis.
Put y = 0 in the equation of the line, we get
x – 1 = 0
∴ x = 1
∴ the line cuts the X-axis at the point G (1, 0).
Required area = area of the region BFAB + area of the region OGDCEFO + area of the region OBGO
Now, area of the region BFAB = area under the parabola (y – 1)2 = 4(x + 1), Y-axis from y = -1 to y = 3

Since, the area cannot be negative,
Area of the region BFAB = \(\left|-\frac{8}{3}\right|=\frac{8}{3}\) sq units.
Area of the region OGDCEFO = area of the region OPCEFO – area of the region GPCDG

Since, area cannot be negative,
area of the region = \(\left|-\frac{1}{2}\right|=\frac{1}{2}\) sq units.
∴ required area = \(\frac{8}{3}+\frac{109}{6}+\frac{1}{2}\)
= \(\frac{16+109+3}{6}\)
= \(\frac{128}{6}\)
= \(\frac{64}{3}\) sq units.
![]()
Question 9.
Find the area of the region bounded by the straight line 2y = 5x + 7, X-axis and x = 2, x = 5.
Solution:
The equation of the line is
2y = 5x + 7, i.e., y = \(\frac{5}{2} x+\frac{7}{2}\)
Required area = area of the region ABCDA = area under the line y = \(\frac{5}{2} x+\frac{7}{2}\) between x = 2 and x = 5
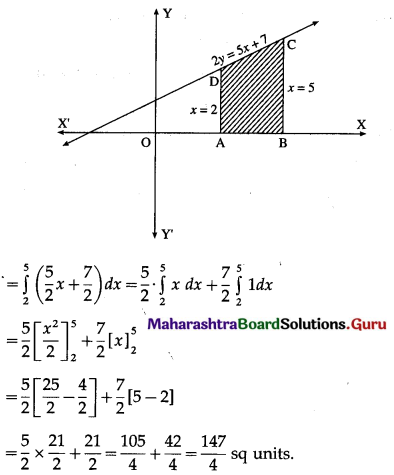
![]()
Question 10.
Find the area of the region bounded by the curve y = 4x2, Y-axis and the lines y = 1, y = 4.
Solution:
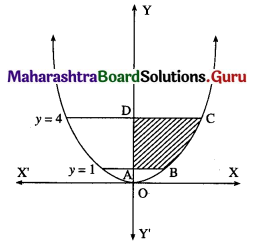
By symmetry of the parabola, the required area is 2 times the area of the region ABCD.
From the equation of the parabola, x2 = \(\frac{y}{4}\)
In the first quadrant, x > 0
∴ x = \(\frac{1}{2} \sqrt{y}\)
∴ required area = \(\int_{1}^{4} x d y\)
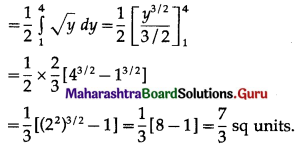
Class 12 Maharashtra State Board Maths Solution