Class 9 English Chapter 1.3 Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 9 English Solutions My English Coursebook Chapter 1.3 ‘Hope’ is the Thing with Feathers Notes, Textbook Exercise Important Questions and Answers.
‘Hope’ is the Thing with Feathers Poem 9th Std Question Answer
My English Coursebook Std 9 Digest Chapter 1.3 ‘Hope’ is the Thing with Feathers Textbook Questions and Answers
Warming up!
Chit-chat:
- Do you ever feel nervous?
- Do you ever feel really depressed?
- What makes you nervous or depressed?
- What do you hope for on these occasions?
- Have you hoped for something that you knew was difficult?
- What do you have to do to fulfil ‘your opes?
![]()
The Only Ray of Hope
1. Divide the class into groups of 4-6. Each group selects for itself, one of the difficult situations listed below. They imagine themselves to be in that situation and carry on with the rest of the activity.
(a) A group of passengers are marooned on an island in the middle of the ocean
(b) A group of pilgrims travelling on foot have lost their way in a thick jungle.
(c) A team of players from an office have got down at the wrong place on a highway at night. It is a lonely spot.
Answer:
Situation: (a)
(a) A group of passengers are marooned on an island in the middle of the ocean
Question 1.
Describe your surroundings in 4-5 sentences:
Answer:
We are trapped on a small island in the middle of the ocean. It is a desolate, uninhabited island. We are all alone on this island. There are thick forests around us and frightening pythons and other poisonous snakes are slithering around us. Nothing can be seen except the thick forests, marshy land and vast waters of the ocean.
![]()
Question 2.
Write the reactions of your companions using exclamations :
Answer:
- “What a horrifying experience!”
- “Look, oh God! Our ship has left the shore without us on this desolate island!”
- “What shall we do now?”
- “How can we escape from this dangerous situation!”
- “Nothing on earth would save us !”
Question 3.
Using your imagination, write what is the only ray of hope for you.
Answer:
Let us hope that the people on our ship find us missing and return back to this island or some other ship, helicopter or a plane notices our movements and save us from this horrible situation that would be our only ray of hope.
Question 4.
Two members of your group are going out to try to get help. They can take any five things with them. Write what they choose, and why they choose it.
Answer:
They will take a piece of white cloth to show their presence on the island to ships, helicopters, planes, etc. They will take mobile phones for contact, food packs, a water bottle, a matchbox and a stick for protection.
![]()
English Workshop:
1. Match the following
Question 1.
Match the following
| ‘A’ | ‘B’ |
| 1. Hope | (a) difficulties and problems |
| 2. Gale/storm | (b) toughest times in life |
| 3. keep warm | (c) a very small bit |
| 4. chillest land | (d) a nest in the tree |
| 5. a crumb | (e) provide comfort |
| (f) Bird |
Answer:
| ‘A’ | ‘B’ |
| 1. Hope | (f) Bird |
| 2. Gale/storm | (b) toughest times in life |
| 3. keep warm | (e) provide comfort |
| 4. chillest land | (a) difficulties and problems |
| 5. a crumb | (c) a very small bit |
![]()
2. Use the proper form of the verb in each line:
‘Hope’ is the thing with feathers –
Question a.
That (perch) in the soul
Answer:
That perches in the soul
Question b.
And (sing) the tune without the words
Answer:
And sings the tune without the words
Question c.
And never (stop) at all
Answer:
And never stops at all
![]()
3. Read the examples and fill in the blanks in the same pattern.
Question 1.
Read the examples and fill in the blanks in the same pattern.
Answer:
(a) Examples of degrees: sweet – sweeter – sweetest
- fast – faster – fastest
- slow – slower – slowest
- high – higher – highest
- low – lower – lowest
- great – greater – greatest
- bright – brighter – brightest
- warm – warmer – warmest
- cold – colder – coldest
(b) Examples: strange – stranger – strangest
- brave – braver – bravest
- fine – finer – finest
- simple – simpler – simplest
- large – larger – largest
- close – closer – closest
- wise – wiser – wisest
(c) Examples: pretty – prettier – prettiest
(Note the changes in the last letter.)
- nasty – nastier – nastiest
- hungry – hungrier – hungriest
- angry – angrier – angriest
- naughty – naughtier – naughtiest
![]()
4. Find the phrases/lines in the poem that mean the following :
Question 1.
(a) Hope is a light, delicate thing: …………………………
(b) Hope offers comfort to your soul: …………………….
(c) Hope is not a wordy thought, it is more like a feeling, an emotion: ………………….
(d) In the most difficult times, hope offers the greatest comfort: …………………………
(e) Hope is not easily defeated: …………………..
(f) Hope has given comfort to many people: ………………….
(g) Hope lives on in very hard times, even when it gets nothing from you: ……………….
Answer:
(a) Hope is a light, delicate: Hope is the thing with thing feathers.
(b) Hope offers comfort to that perches in the your soul soul and sings.
(c) Hope is not wordy: And sings the tune thought, it is more like a without words. feeling, an emotion
(d) In the most difficult: Second stanza – And times, hope offers the sweetest… so many greatest comfort warm
(e) Hope is not easily defeated: And never stops at all
(f) Hope has given comfort: That kept so many to many people warm
(g) Hope lives on in very hard: Yet – never – in times, even when it gets extremity, It asked a nothing from you. crumb – of me.
![]()
5. We can relate many of our feelings and experiences to events or things in nature. Which of our feelings or experiences can we relate to the following?
Question 1.
We can relate many of our feelings and experiences to events or things in nature. Which of our feelings or experiences can we relate to the following?
Answer:
- darkness: evil sign
- a storm: difficulties
- sunrise: beginning, progress, growth
- a light shower: pleasure
- sunshine: happiness
- earthquake: a sudden violent damage
- a rainbow: unexpected joy
- dawn: the beginning of something
- dark clouds: sad or difficult situation
- dusk (evening): almost the end of something
- a peacock: pleasant feeling
- flood: a lot of difficulties, damages
![]()
6. Write in a few lines, about an experience of your own where you scored in your exams much more than you hoped for. What did that experience teach you?
Question 1.
Write in a few lines, about an experience of your own where you scored in your exams much more than you hoped for. What did that experience teach you?
Answer:
I could get much more marks in exams than I hoped for and I was on the cloud nine. Really very happy! Everyone admired me for my effort. It was a great experience. It taught me that if you hope for something heartily and work accordingly, you can achieve anything according to your hope and expectation. Hoping is achieving!
Language study:
7. This poem is an example of personification. When we refer to inanimate objects, ideas, emotions as living things, it is an example of personification. Here, ‘hope’ is portrayed as a little bird. Describe it in your own words. Find other examples of personification.
Question 1.
Describe it in your own words.
Answer:
‘Hope’ in this poem is described as a bird sitting in our soul. Here ‘Hope’ is a non-living thing, but it is described as a living thing, bird. Hope is represented here as a living thing. So it is the example of personification.
![]()
Question 2.
Find other examples of personification.
Answer:
Some examples of personification
- The grass was dancing with the wind. Here dancing is the quality/action of a person. Grass is personified as a person.
- Trees were shivering with fear when they saw the woodcutter. Trees are given the human quality of ‘shivering with fear’
- The moon was laughing in the sky. Here the moon is given the human quality of laughing.
My English Coursebook 9th Class Solutions Chapter 1.3 ‘Hope’ is the Thing with Feathers Additional Important Questions and Answers
Simple Factual Activity:
Question 1.
Complete the following lines from the poem :
(Answers are directly given.)
Answer:
- The hope-bird is sitting in the soul.
- Singing of the bird never stops.
- Its song is the sweetest at the time of storm.
- The poetess has heard the bird’s song in most difficult circumstances.
![]()
Appreciation of Poem:
1. Title: ‘Hope is the thing with feathers -’
2. Poet: The poetess of the poem is Emily Dickinson.
3. Theme/Central Idea: The central idea of the poem is the role played by hope in our lives. According to the poetess, hope – the little bird that nests in our soul – keeps us going even in the most difficult of times and demands nothing in return.
4. Rhyme Scheme: The rhyme scheme of the first 2 stanzas is ‘abab’ whereas in the 3rd stanza it is ‘abbb’.
5. Figure of Speech: ‘Personification’.
6. Special Features: This poem is full of implied meanings. It tells you the importance of hope and helps you to survive in any difficult days or occasions.
7. Favourite Lines: My favourite lines from the poem are :
- “And Sweetest – in the Gale – is heard
- Yet – never – in Extremity, It asked a crumb – of me.
8. Why I like the poem: I like the poem for its positive message. According to the poet, hope is not easily defeated. It sustains us. Hope also encourages us to move forward. This message, I think, is very important for a young person.
My English Coursebook Std 9 Digest Pdf Unit 1
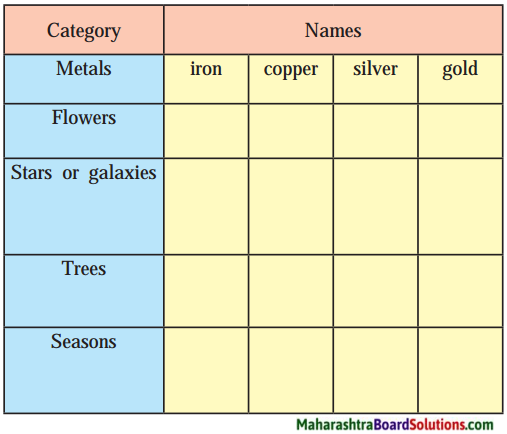
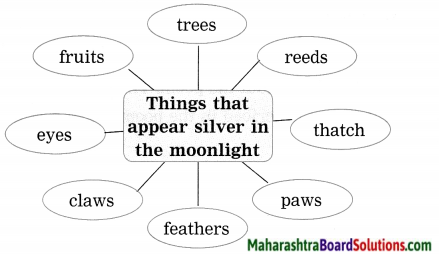





 उत्तर:
उत्तर: