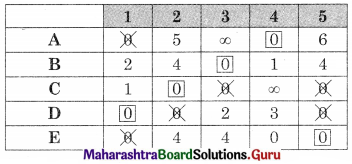
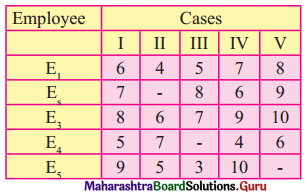
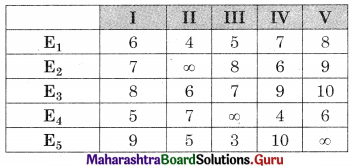
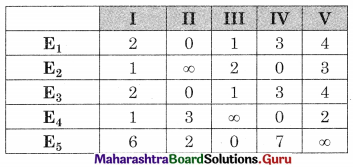
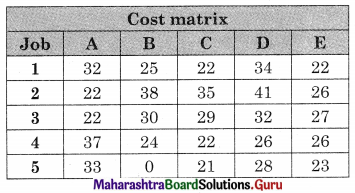
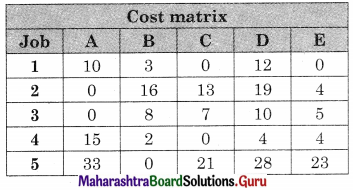
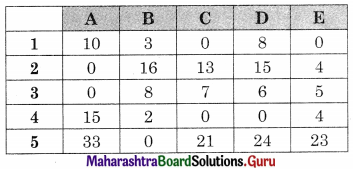
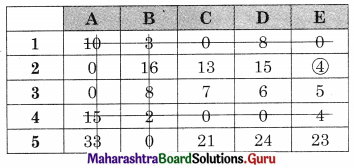
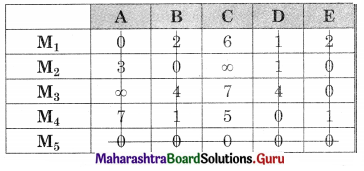
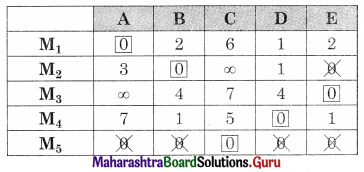
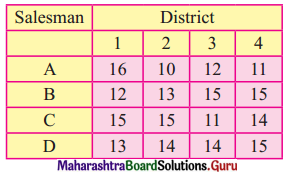
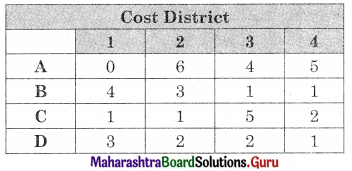
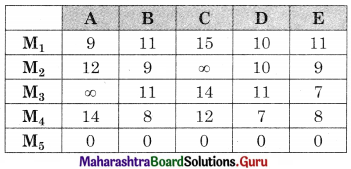
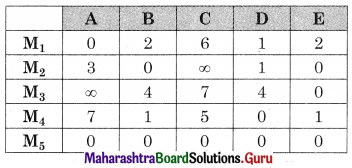
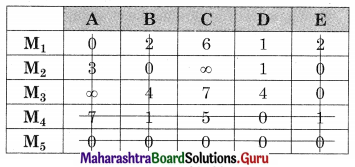
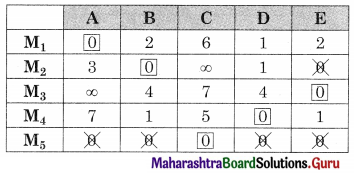
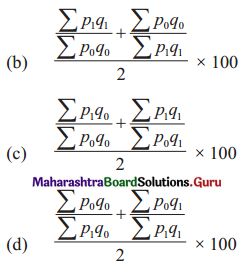
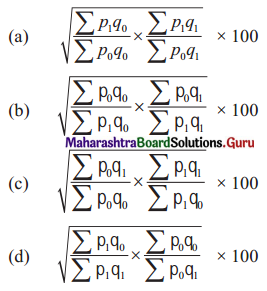
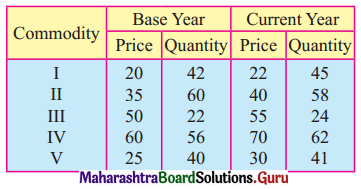
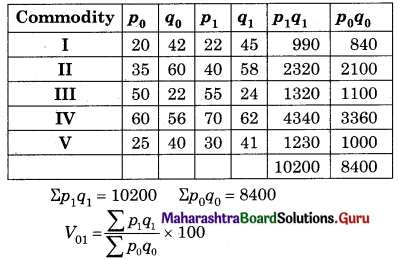
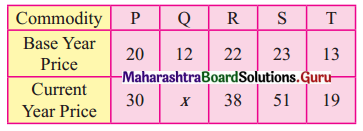
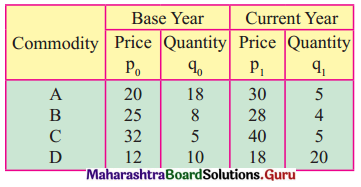
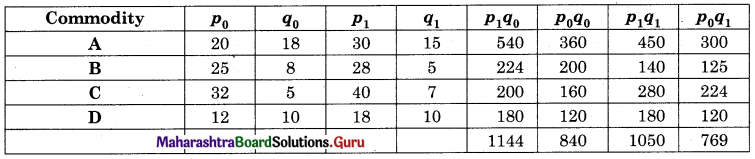
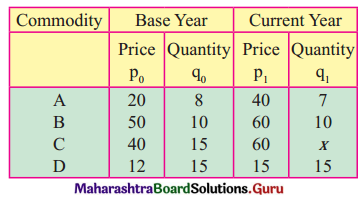
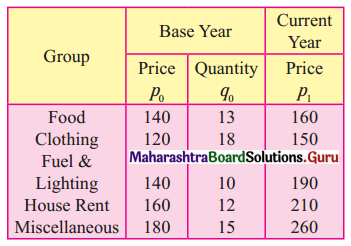
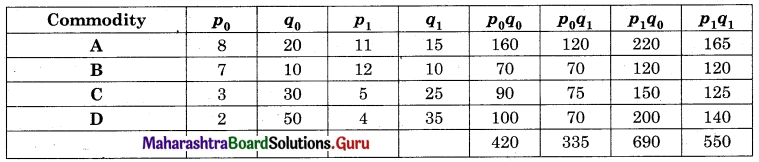
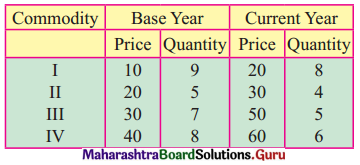
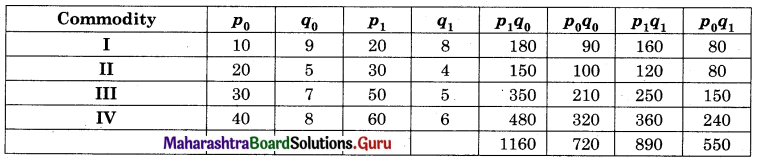
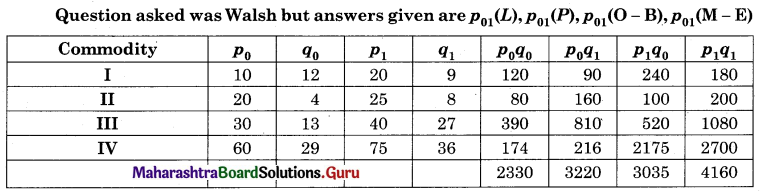
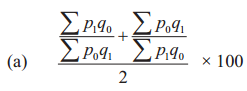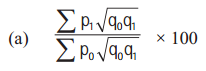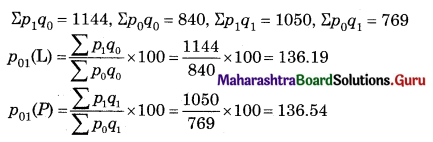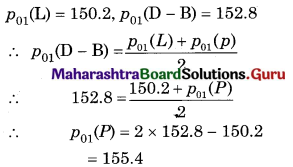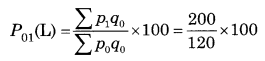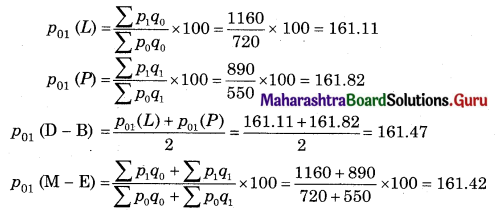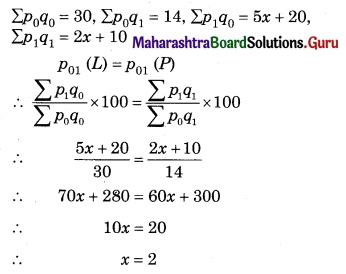Linear Programming Class 12 Commerce Maths 2 Chapter 6 Miscellaneous Exercise 6 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 6 Linear Programming Miscellaneous Exercise 6 Questions and Answers.
Std 12 Maths 2 Miscellaneous Exercise 6 Solutions Commerce Maths
(I) Choose the correct alternative.
Question 1.
The value of the objective function is maximized under linear constraints.
(a) at the centre of feasible region
(b) at (0, 0)
(c) at any vertex of feasible region.
(d) The vertex which is at maximum distance from (0, 0).
Answer:
(a) at the centre of feasible region
Question 2.
Which of the following is correct?
(a) Every LPP has on optional solution
(b) Every LPP has unique optional solution
(c) If LPP has two optional solutions then it has infinitely many solutions
(d) The set of all feasible solutions LPP may not be a convex set.
Answer:
(c) If LPP has two optional solutions then it has infinitely many solutions

Question 3.
Objective function of LPP is
(a) a constraint
(b) a function to be maximized or minimized
(c) a relation between the decision variables
(d) a feasible region.
Answer:
(b) a function to be maximized or minimized
Question 4.
The maximum value of z = 5x + 3y. subject to the constraints 3x + 5y = 15; 5x + 2y ≤ 10, x, y ≥ 0 is
(a) 235
(b) \(\frac{235}{9}\)
(c) \(\frac{235}{19}\)
(d) \(\frac{235}{3}\)
Answer:
(c) \(\frac{235}{19}\)
Question 5.
The maximum value of z = 10x + 6y. subject to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, y ≥ 0 is.
(a) 56
(b) 65
(c) 55
(d) 66
Answer:
(a) 56
Question 6.
The point at which the maximum value of z = x + y subject to the constraint x + 2y ≤ 70, 2x + y ≤ 15, x ≥ 0, y ≥ 0 is
(a) (36, 25)
(b) (20, 35)
(c) (35, 20)
(d) (40, 15)
Answer:
(d) (40, 15)
Question 7.
Of all the points of the feasible region the optimal value of z is obtained at a point
(a) Inside the feasible region
(b) at the boundary of the feasible region
(c) at vertex of feasible region
(d) on x -axis
Answer:
(c) at vertex of feasible region

Question 8.
Feasible region; the set of points which satisfy
(a) The objective function
(b) All of the given function
(c) Some of the given constraints
(d) Only non-negative constraints
Answer:
(b) All of the given function
Question 9.
Solution of LPP to minimize z = 2x + 3y subjected to x ≥ 0, y ≥ 0, 1 ≤ x + 2y ≤ 10 is
(a) x = 0, y = \(\frac{1}{2}\)
(b) x = \(\frac{1}{2}\), y = 0
(c) x = 1, y = -2
(d) x = y = \(\frac{1}{2}\)
Answer:
(a) x = 0, y = \(\frac{1}{2}\)
Question 10.
The corner points of the feasible region given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
(a) (0, 0), (4, 0), (3, 1), (0, 4)
(b) (0, 0), (\(\frac{7}{2}\), 0), (3, 1), (0, 4)
(c) (0, 0), (\(\frac{7}{2}\), 0), (3, 1), (5, 7)
(d) (6, 0), (4, 0), (3, 1), (0, 7)
Answer:
(b) (0, 0), (\(\frac{7}{2}\), 0), (3, 1), (0, 4)
Question 11.
The corner point of the feasible region are (0, 0), (2, 0), (\(\frac{12}{7}\), \(\frac{3}{7}\)) and (0, 1) then the point of maximum z = 6.5x + y = 13
(a) (0, 0)
(b) (2, 0)
(c) (\(\frac{11}{7}\), \(\frac{3}{7}\))
(d) (0, 1)
Answer:
(b) (2, 0)
Question 12.
If the corner points of the feasible region are (0, 0), (3, 0), (2, 1) and (0, \(\frac{7}{3}\)) the maximum value of z = 4x + 5y is
(a) 12
(b) 13
(c) \(\frac{35}{2}\)
(d) 0
Answer:
(b) 13

Question 13.
If the comer points of the feasible region are (0, 10), (2, 2), and (4, 0) then the point of minimum z = 3x + 2y is.
(a) (2, 2)
(b) (0, 10)
(c) (4, 0)
(d) (2, 4)
Answer:
(a) (2, 2)
Question 14.
The half plane represented by 3x + 2y ≤ 0 contains the point.
(a) (1, \(\frac{5}{2}\))
(b) (2, 1)
(c) (0, 0)
(d) (5, 1)
Answer:
(c) (0, 0)
Question 15.
The half plane represented by 4x + 3y ≥ 14 contains the point
(a) (0, 0)
(b) (2, 2)
(c) (3, 4)
(d) (1, 1)
Answer:
(c) (3, 4)
(II) Fill in the blanks.
Question 1.
Graphical solution set of the in equations x ≥ 0, y ≥ 0 is in _________ quadrant.
Answer:
First
Question 2.
The region represented by the in equations x ≥ 0, y ≥ 0 lines in _________ quadrants.
Answer:
First
Question 3.
The optimal value of the objective function is attained at the _________ points of feasible region.
Answer:
End
Question 4.
The region represented by the inequality y ≤ 0 lies in _________ quadrants
Answer:
Third and Fourth

Question 5.
The constraint that a factory has to employ more women (y) than men (x) is given by _________
Answer:
y > x
Question 6.
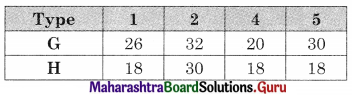
A garage employs eight men to work in its showroom and repair shop. The constants that there must be not least 3 men in showroom and repair shop. The constrains that there must be at least 3 men in showroom and at least 2 men in repair shop are _________ and _________ respectively.
Answer:
x ≥ 3 and y ≥ 2
Question 7.
A train carries at least twice as many first class passengers (y) as second class passangers (x). The constraint is given by _________
Answer:
x ≥ 2y
Question 8.
A dishwashing machine hold up to 40 pieces of large crockery (x) this constraint is given by _________
Answer:
x ≤ 40
(III) State whether each of the following is True or False.
Question 1.
The region represented by the inequalities x ≥ 0, y ≥ 0 lies in first quadrant.
Answer:
True
Question 2.
The region represented by the inqualities x ≤ 0, y ≤ 0 lies in first quadrant.
Answer:
False

Question 3.
The optimum value of the objective function of LPP occurs at the center of the feasible region.
Answer:
False
Question 4.
Graphical solution set of x ≤ 0, y ≥ 0 in xy system lies in second quadrant.
Answer:
True
Question 5.
Saina wants to invest at most ₹ 24000 in bonds and fixed deposits. Mathematically this constraints is written as x + y ≤ 24000 where x is investment in bond and y is in fixed deposits.
Answer:
True
Question 6.
The point (1, 2) is not a vertex of the feasible region bounded by 2x + 3y ≤ 6, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0.
Answer:
True
Question 7.
The feasible solution of LPP belongs to only quadrant I. The Feasible region of graph x + y ≤ 1 and 2x + 2y ≥ 6 exists.
Answer:
True
(IV) Solve the following problems.
Question 1.
Maximize z = 5x1 + 6x2, Subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x ≥ 0, y ≥ 0
Solution:
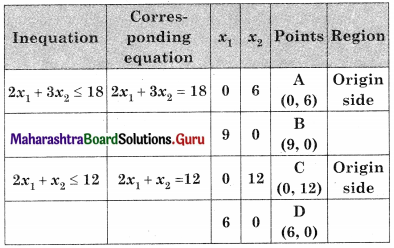
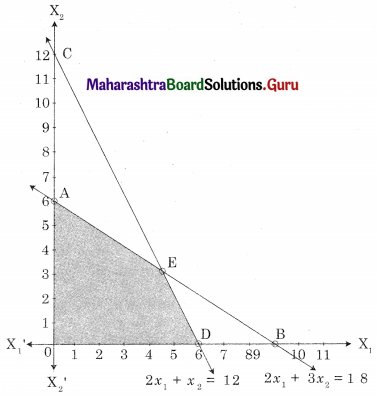
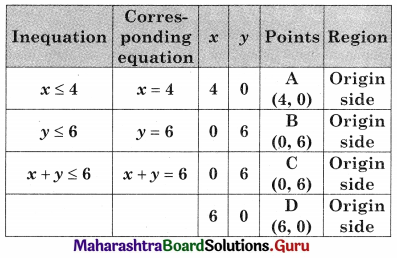
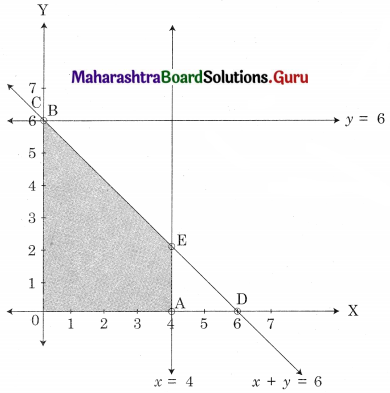
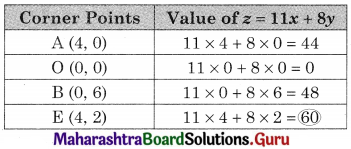
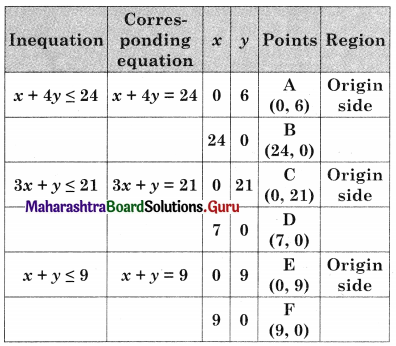
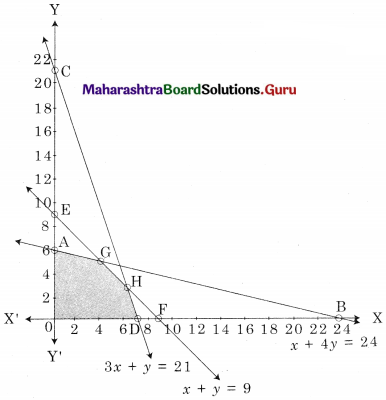
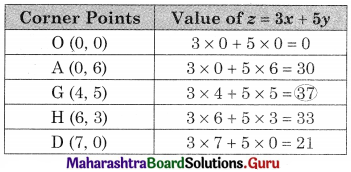
OAED is the feasible region O(0, 0) A(0, 6) D (6, 0)
and E is the intersection of 2x1 + 3x2 = 18 and 2x1 + x2 = 12
For E, Solving, 2x1 + 3x2 = 18 …….(i)
2x1 + x2 = 12 ……(ii)
We get x1 = 4.5, x2 = 3
∴ E = (4.5, 3)
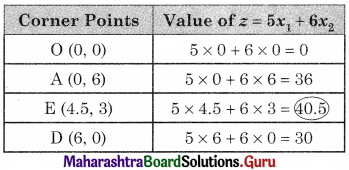
∴ Maximum value of z = 40.5 at E(4.5, 3)
Question 2.
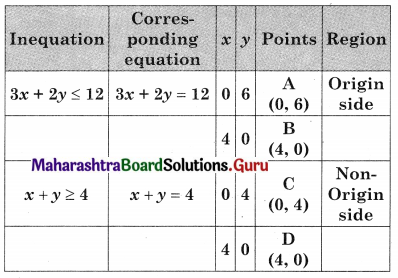
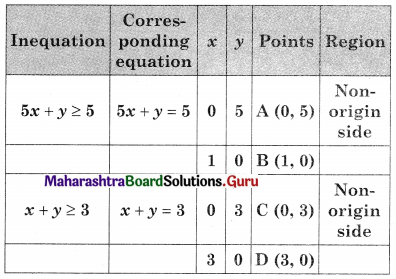
Minimize z = 4x + 2y, Subject to 3x + y ≥ 27, x + y ≥ 21, x ≥ 0, y ≥ 0
Solution:
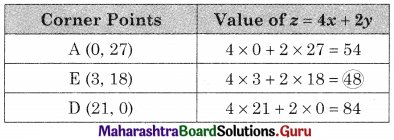
AED is the feasible region A(0, 27), D(21, 0)
and E is the point of intersection of 3x + y = 27 and x + y = 21
For E, Solving 3x + y = 27 ………(i)
x + y = 21 …….(ii)
We get x = 3, y = 18
∴ E(3, 18)
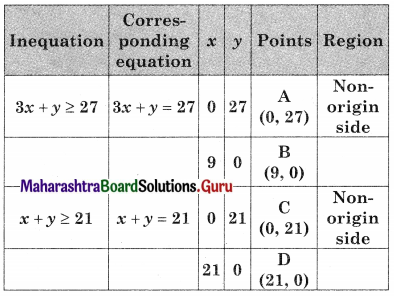
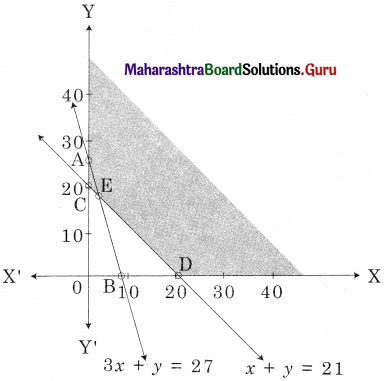
∴ Minimum value of z = 48 at (3, 18)

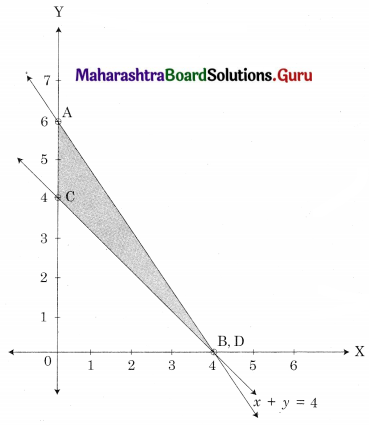
Question 3.
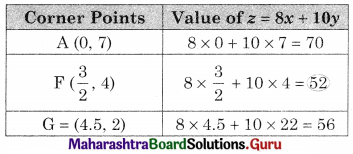
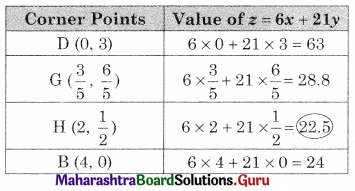
Maximize z = 6x + 10y, subject to 3x + 5y ≤ 10, 5x + 3y ≤ 15, x ≥ 0, y ≥ 0
Solution:
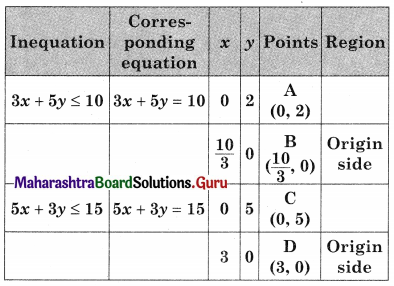
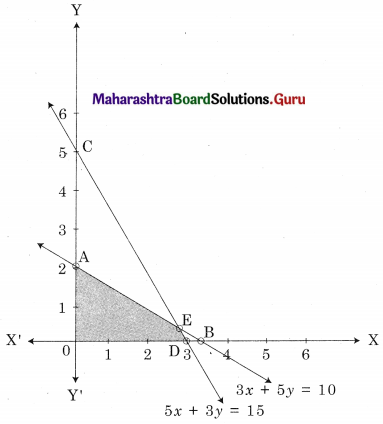
OAED is the feasible region;
O(0, 0), A (0, 2) D (3, 0) and E is the point of intersection of 3x + 5y = 10 and 5x + 3y = 15
For E, Solving 3x + 5y = 10
5x + 3y = 15
We get, x = \(\frac{45}{16}\), y = \(\frac{5}{16}\)
∴ E(\(\frac{45}{16}\), \(\frac{5}{16}\))
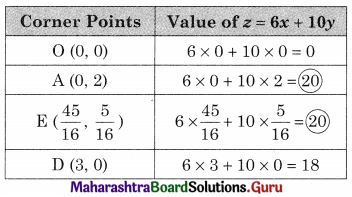
Since the maximum value of z = 20 at two points i.e, at A(0, 2) and E(\(\frac{45}{16}\), \(\frac{5}{16}\)).
z is maximum at all points on segment AE.
Hence it has infinite number of solutions.
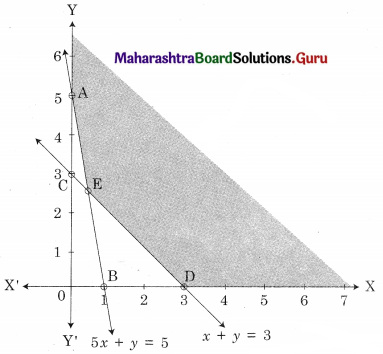
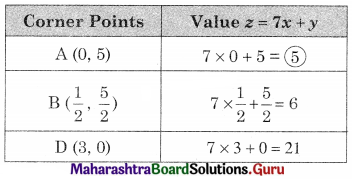
Question 4.
Minimize z = 2x + 3y, Subject to x – y ≤ 1, x + y ≥ 3, x ≥ 0, y ≥ 0
Solution:
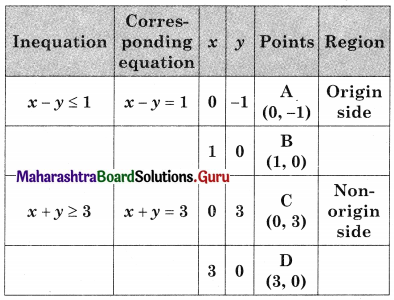
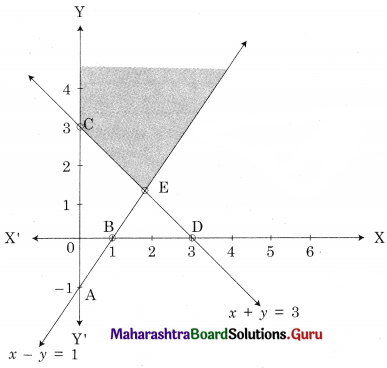
Shaded portion CE is the feasible region
Where C = (0, 3) and E is the point of intersection of x – y = 1 and x + y = 3
For E, Solving x – y = 1 …….(i)
x + y = 3 ………(ii)
We get, x = 2, y = 1
∴ E(2, 1)
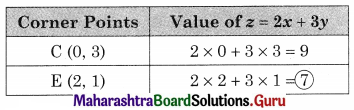
∴ Minimum value z = 7 at E(2, 1)
Question 5.
Maximize z = 4x1 + 3x2, Subject to 3x1 + x2 ≤ 15, 3x1 + 4x2 ≤ 24, x ≥ 0, y ≥ 0
Solution:
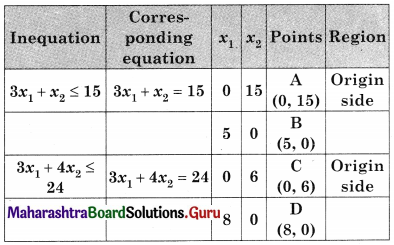
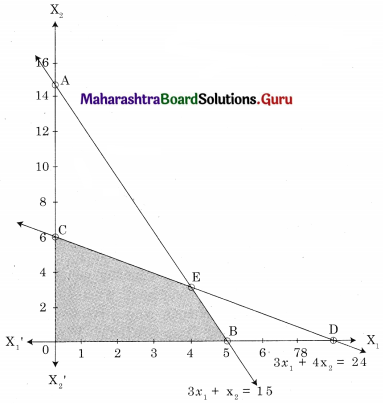
OCEB is the feasible region where O(0, 0), C(0, 6), B(5, 0)
E is the point of intersection of 3x1 + x2 = 15 and 3x1 + 4x2 = 24
For E, Solving 3x1 + x2 = 15 ……..(i)
3x1 + 4x2 = 24 …….(ii)
We get, x1 = 4, x2 = 3
∴ E(4, 3)
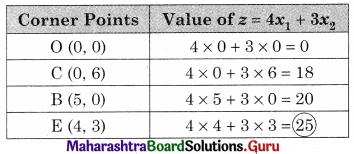
∴ Maximum value of z = 25 at (4, 3)

Question 6.
Maximize z = 60x + 50y, Subject to x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0
Solution:
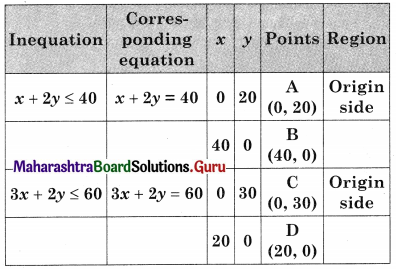
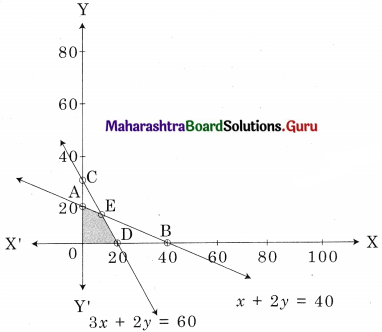
OAED is the feasible region O(0, 0), A(0, 20), D(20, 0)
E is x + 2y = 40 and 3x + 2y = 60
For E, Solving x + 2y = 40
3x + 2y = 60
We get, x = 10, y = 15
∴ E = (10, 15)
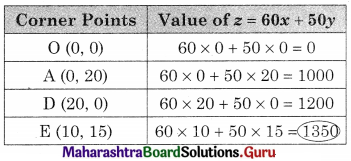
∴ Maximum value of z = 1350 at E(10, 15).
Question 7.
Minimize z = 4x + 2y, Subject to 3x + y ≥ 27, x + y ≥ 21, x + 2y ≥ 30, x ≥ 0, y ≥ 0
Solution:
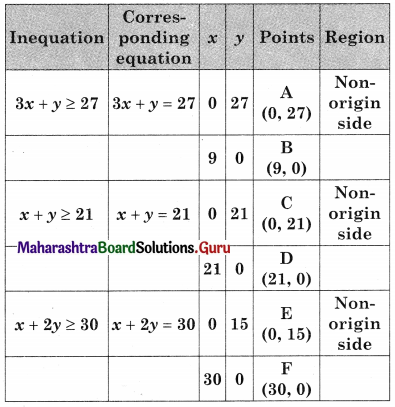
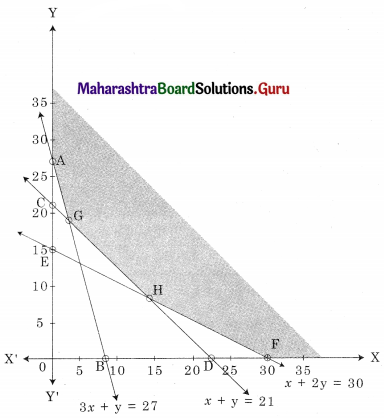
AGHF is the feasible region where A(0, 27) F(30, 0)
G is the point of intersection of 3x + y = 27 and x + y = 21
H is the point of intersection of x + y = 21 and x + 2y = 30
For G, Solving 3x + y = 27 …….(i)
x + y = 21 ………(ii)
We get, x = 3, y = 18
∴ G(3, 8)
For H, Solving x + y = 21 …….(i)
x + 2y = 30 ……..(ii)
We get, x = 12, y = 9
∴ G = (12, 9)
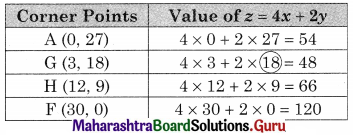
∴ Maximum value of z = 48 at G(3, 18)
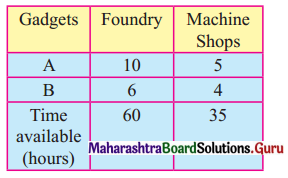
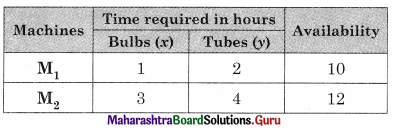
Question 8.
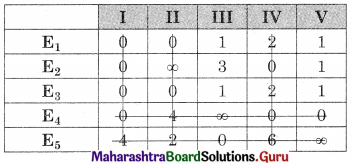
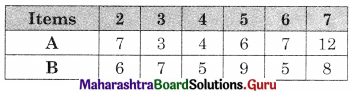
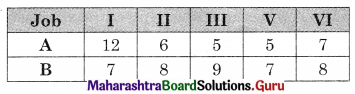
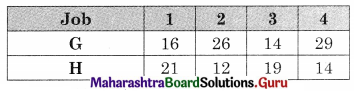
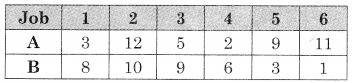
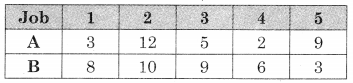
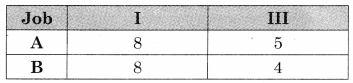
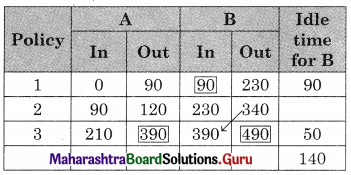
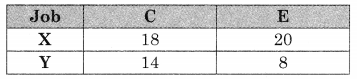
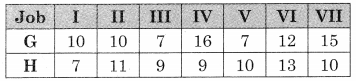
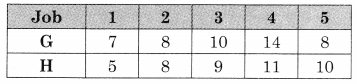
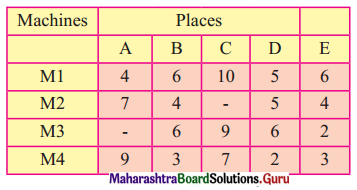
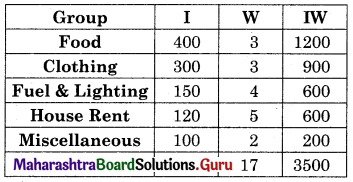
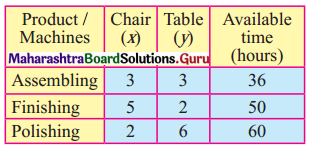
A carpenter makes chairs and table profit are ₹ 140 per chair and ₹ 210 per table Both products are processed on three machines, Assembling, Finishing and Polishing the time required for each product in hours and availability of each machine is given by the following table.
Formulate and solve the following Linear programming problem using graphical method.
Solution:
Let z be the profit which can be made by selling x chair and y table.
∴ x ≥ 0, y ≥ 0
Total profit = 140x + 210y
According to the table, the constraints can be written as
3x + 3y ≤ 36
5x + 2y ≤ 50
2x + 6y ≤ 60
∴ The given LPP can be formulated as.
Maximize z = 140x + 210y
Subject to 3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0.
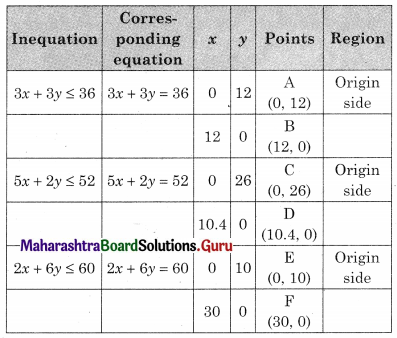
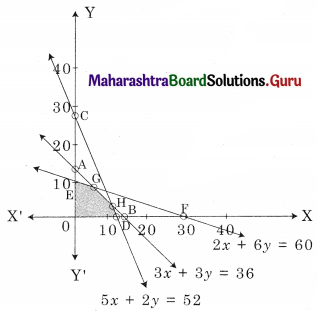
OEGH is the feasible region
O(0, 0), D(10.4, 0), E(0, 10)
For G, Solving 3x + 3y = 36 ……..(i)
2x + 6y = 60 …….(ii)
∴ G = (3, 9)
For H, Solving 5x + 2y = 52 ………(i)
3x + 3y = 36 ……..(ii)
We get, x = \(\frac{28}{3}\), y = \(\frac{8}{3}\)
∴ H(\(\frac{28}{3}\), \(\frac{8}{3}\))
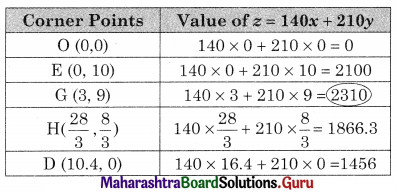
∴ z in maximum at (3, 9) and maximum profit = ₹ 2310.

Question 9.
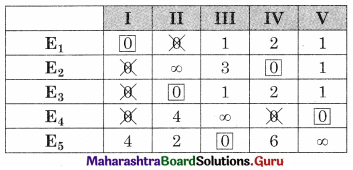
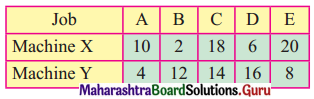
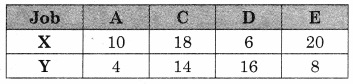
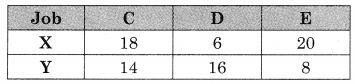
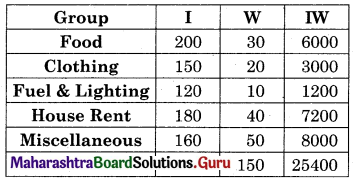
A company manufactures bicycles and tricycles, each of which must be processed through two machines A and B Maximum availability of machines A and B are respectively 120 and 180 hours. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B. If profits are ₹ 180 for a bicycle and ₹ 220 on a tricycle, determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Solution:
Let x number of bicycle and y number of tricycle has to be manufactured and to be sold to get the profit (z)
∴ x ≥ 0, y ≥ 0
Total profit = 180x + 220y.
The given LPP can be tabulated as follows:
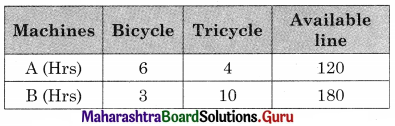
∴ The given LPP can be formulated as
Maximize z = 180x + 220y
Subject to 6x + 4y ≤ 120, 3x + 10y ≤ 180, x ≥ 0, y ≥ 0
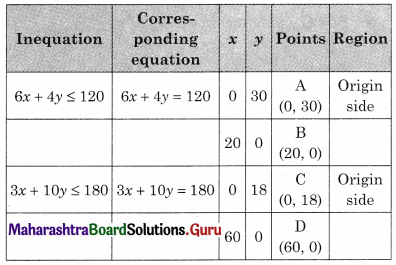
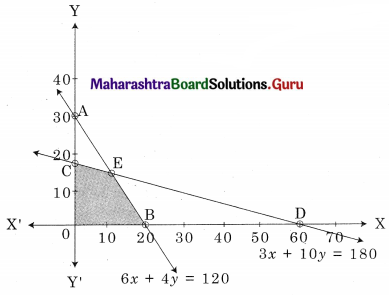
OCEB is the feasible region where O(0, 0) C(0, 18) B(20, 0)
E is the point of intersection of 6x + 4y = 120 and 3x + 10y = 180
For E, Solving 6x + 4y = 120 ……..(i)
3x + 10y = 180 …….(ii)
We get, x = 10, y = 15
∴ E(10, 15)
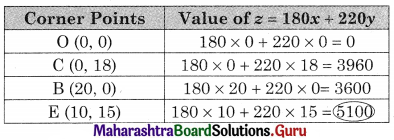
∴ Maximum value of z is 5100 at E(10, 15)
Hence 10 bicycles and 15 tricycles should be produced to get maximum profit.
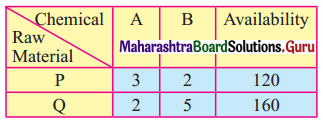
Question 10.
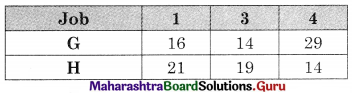
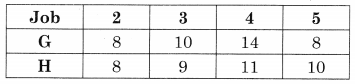
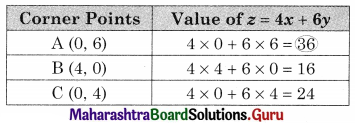
A factory produced two types of chemicals A and B. The following table gives the units of ingredients P and Q (per kg) of chemicals A and B as well as minimum requirements of P and Q and also cost per kg. Chemicals A and B:
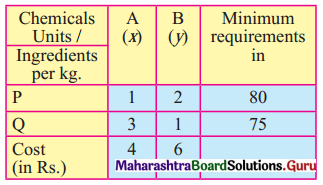
Find the number of units of chemicals A and B should be produced sp as to minimize the cost.
Solution:
Let x be the no. of units of chemicals, A produced and y be the no. of units of chemical B produced.
Total cost is 4x + 6y
The LPP is. Minimise z = 4x + 6y
Subject to x + 2y ≥ 80, 3x + y ≥ 75, x ≥ 0, y ≥ 0.
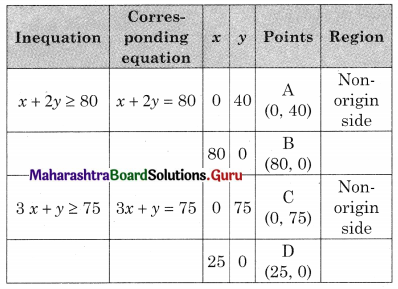
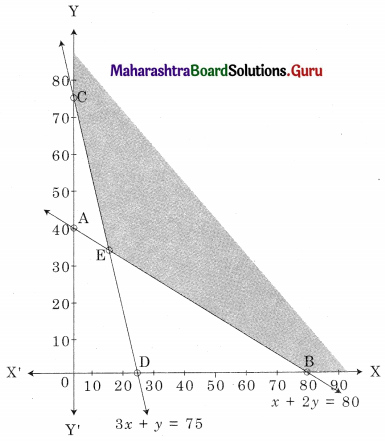
The shaded region BEC in the feasible region B(80, 0) C(0, 75)
and E is the point of intersection of x + 2y = 80 and 3x + y = 75
For E, Solving x + 2y = 80 …….(i)
3x + y = 75 …….(ii)
We get, x = 14, y = 33
∴ E(14, 33)
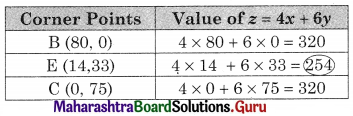
∴ z is minimum at E(14, 33) and the minimum value of z = 254.
Hence 14 units of chemical A and 33 units of chemical B are produced to get a minimum cost of ₹ 254.
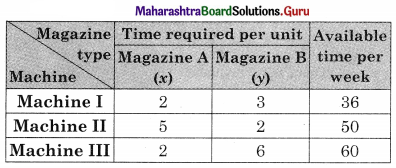
Question 11.
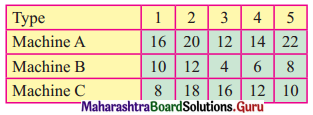
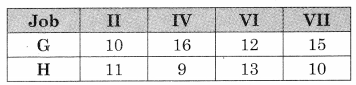
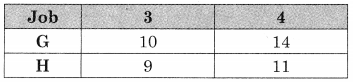
A company produces mixers and food processors. Profit on selling one mixer and one food processor is ₹ 2,000/- and ₹ 3,000/- respectively. Both the products are processed through three Machines A, B, C. The time required in hours by each product and total time available in hours per week on each machine are as follows:
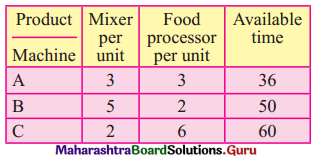
How many mixes and food processors should be produced to maximize profit?
Solution:
Let x be the no. of mixers produced and y be the no.of food processors produced.
The profit is 2000x + 3000y
The LPP is Maximize 2 = 2000x + 3000y
Subject to 3x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60 x, y ≥ 0.
Let 3x + 3y = 36,
i.e. x + y = 12
x = 0, y = 12, (0, 12)
y = 0, x = 12, (12, 0)
5x + 2y = 50
x = 0, y = 25, (0, 25)
y = 0, x = 10, (10, 0)
Let 2x + 6y = 60, x + 3y = 30
x = 0, y = 10 (0, 10)
y = 0, x = 30 (30, 0)
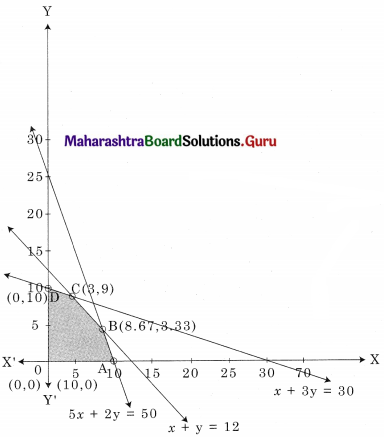
The Shaded region OABCD is the feasible region.
O(0, 0) A (10, 0) D(0, 10)
B is the intersection of x + y = 12 and 5x + 2y = 50
Solving we get x = 8.67, y = 3.33
∴ B(8.67, 3.33)
C is the intersection of x + y = 12 and x + 3y = 30
Solving we get x = 3, y = 9
∴ C(3, 9)
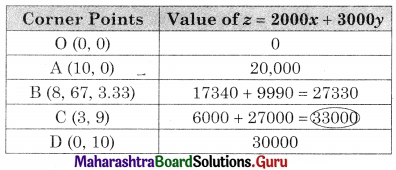
∴ Maximum value of z is 330000 at C(3, 9)
Hence 3 mixers and 9 food processors should be produced to get a maximum profit of ₹ 33,000.

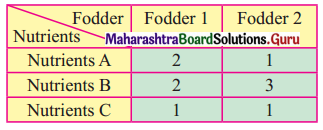
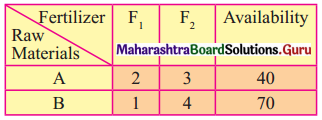
Question 12.
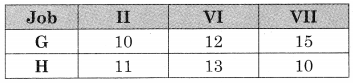
A chemical company produces a chemical containing three basic elements A, B, C so that it has at least 16 liters of A, 24 liters of B, and 18 liters of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 liters of A, 12 liters of B, 2 liters of C. Each unit of compound II has 2 liters of A, 2 liters of B and 6 liters of C. The cost per unit of compound is ₹ 800/- and that of compound II is ₹ 640/- Formulate the problem as L.P.P and solve it to minimize the cost.
Solution:
Let x be the no. of units of compound I used and y be the no of units of compound II used.
The data can be tabulated as
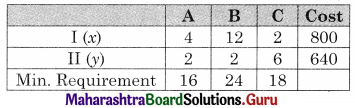
The LPP is minimize z = 800x + 640y
Subject to 4x + 2y ≥ 16, 12x + 2y ≥ 24, 2x + 6y ≥ 18, x, y ≥ 0.
Let 4x + 2 y = 16,
2x + y = 8
x = 0, y = 8, (0, 8)
y = 0, x = 4, (4, 0)
12x + 2y = 24,
6x + y = 12
x = 0, y = 12, (0, 12)
y = 0, x = 2, (2, 0)
2x + 6y = 18
x + 3y = 9
x = 0, y = 3, (0, 3)
y = 0, x = 9, (9, 0)
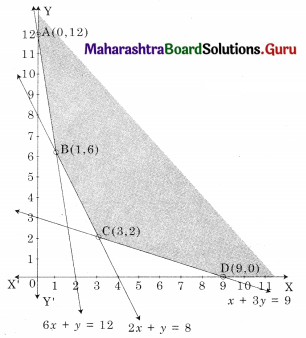
The Shaded region ABCD is the feasible region.
A(0, 12) D(9, 0)
B is the intersection of 6x + y = 12 and 2x + y = 8
Solving we get x = 1, y = 6
∴ B(1, 6)
C is the intersection of 2x + y = 8 and x + 3y = 9
Solving we get x = 3, y = 2
∴ C(3, 2)
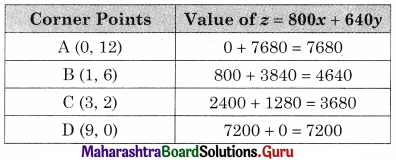
∴ The minimum value of z = 3680 at (3, 2)
Hence 3 unit of compound I and 2 units of compound II should be used to get the minimum cost of ₹ 3680.
Question 13.
A person who makes two types of gift items A and B requires the services of a cutter and a finisher. Gift item A requires 4 hours of the cutter’s time and 2 hours of the finisher’s time. B required 2 hours of the cutter’s time and 4 hours of finisher‘s time. The cutter and finisher have 208 hours and 152 hours available times respectively every month. The profit of one gift item of type A is ₹ 75/- and on gift item B is ₹ 125/-. Assuming that the person can sell all the gift items produced, determine how many gift items of each type should he make every month to obtain the best returns?
Solution:
Let x be the no. of gift A produced and y be the no. of gift B produced.
The data can be tabulated as
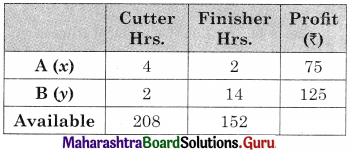
The LLP is maximize z = 75x + 125y
Subject to 4x + 2y ≤ 208, 2x + 4y ≤ 152, x, y ≥ 0
Let 4x + 2y = 208, 2x + 4y = 152,
2x + y = 104, x + 2y = 76,
x = 0, y = 104; (0, 104), x = 0, y = 38; (0, 38)
y = 0, x = 52; (52, 0), y = 0, x = 76; (76, 0)
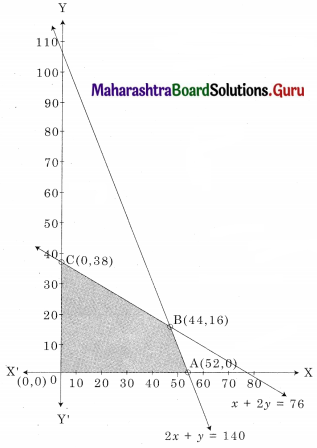
The shaded region OABC is the feasible region.
O(0,0) A (52, 0) C(0, 38)
B is the intersection of 2x + y = 104 and x + 2y = 76
Solving we get x = 44, y = 16
∴ B(44, 16)
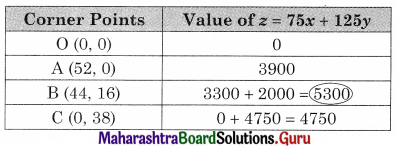
∴ Maximum value of z = 5300 at B(44, 16)
Hence he should produce 44 gifts of type A & 16 of type B to get a maximum profit of ₹ 5300.
Question 14.
A firm manufactures two products A and B on which profit is earned per unit ₹ 3/- and ₹ 4/- respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on Mx and two minutes of processing time on M2. B requires one minute of processing time on M1 and one minute processing time on M2 Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Final the number of units of products A and B to be manufactured to get the maximum profit.
Solution:
Let x denote the number of units of product A and y denote the number of units of product B.
The total profit in ₹ 3x + 4y,
The given statements can be tabulated as
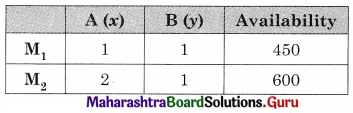
The constraints are x + y ≤ 450, 2x + y ≤ 600, x ≥ 0, y ≥ 0
∴ The LPP can be formulated as
Maximize z = 3x + 4y
Subject to x + y ≤ 450, 2x + y ≤ 600, x ≥ 0, y ≥ 0.
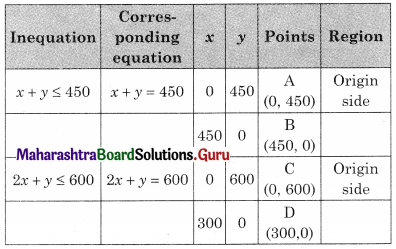
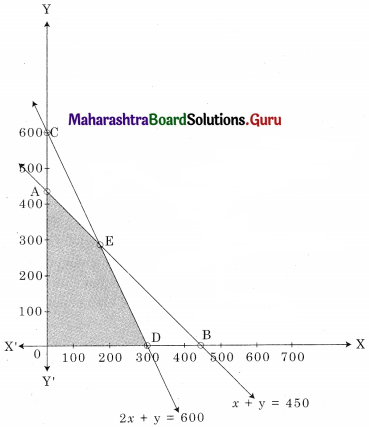
OAED in the feasible region O(0, 0) A(0, 450) D(300, 0)
E is the intersection of x + y = 450 and 2x + y = 600
For E, Solving x + y = 450 ……..(i)
2x + y = 600 ……..(ii)
Solving x = 150, y = 300
∴ E(150, 300)
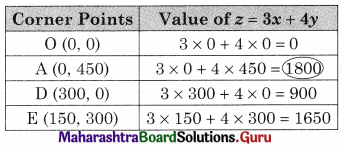
∴ Maximum value of z = 1800 at (0, 450)

Question 15.
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20/- per unit of A and ₹ 30/- per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each unit of B required 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should they manufacture per month to maximize profit? How much is the maximum profit?
Solution:
Let x be the no. of electrical item A and y be the no. of electrical items to be manufactured per month to maximize the profit.
Total profit is ₹ 20x + 30y
The given condition can be tabulated as.
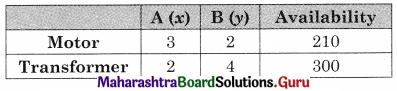
The given LPP can be formulated as
Maximize z = 20x + 30y
Subject of 3x + 2y ≤ 210, 2x + 4y ≤ 300, x ≥ 0, y ≥ 0.
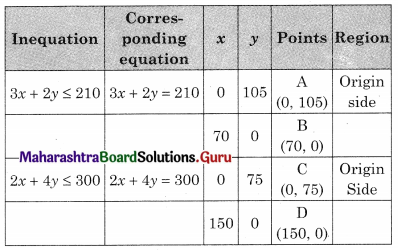
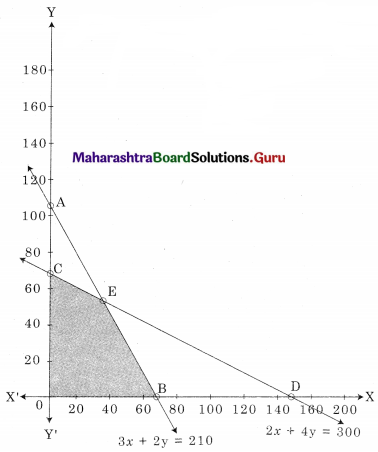
BOCE is the feasible region
B(70, 0) O(0, 0) C(0, 75)
E is the intersection of 3x + 2y = 210 and 2x + 4y = 300
For E, Solving 3x + 2y = 210 ……….(i)
2x + 4y = 300 …….(ii)
We get x = 30, y = 60
∴ E(30, 60)
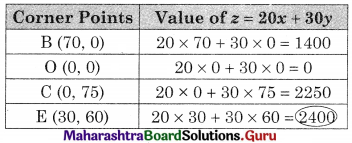
∴ Maximum value of z = ₹ 2400 at (30, 60)
Hence 30 units of A and 60 units of B should be manufactured per month to get the maximum profit of ₹ 2400
12th Commerce Maths Digest Pdf
![]()
![]()



![]()


![]()

![]()