Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 7 Assignment Problem and Sequencing Ex 7.1 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 7 Assignment Problem and Sequencing Ex 7.1
Question 1.
A job production unit has four jobs A, B, C, D which can be manufactured on each of the four machines P, Q, R, and S. The processing cost of each job for each machine is given in the following table:
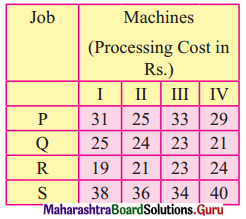
Find the optimal assignment to minimize the total processing cost.
Solution:
The cost matrix is given by
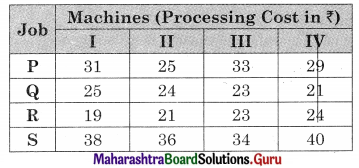
Subtracting row minimum from all the elements in that row we get
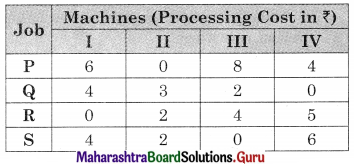
Subtracting column minimum from all the elements in that column we get the same matrix.
As all the rows and columns have single zeros the allotment can be done as follows.
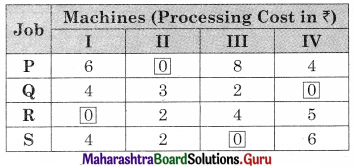
As per the table, the job allotments are
P → II, Q → IV, R → I, S → III
The total minimum cost = 25 + 21 + 19 + 34 = ₹ 99
![]()
Question 2.
Five wagons are available at stations 1, 2, 3, 4, and 5. These are required at 5 stations I, II, III, IV, and V. The mileage between various stations are given in the table below. How should the wagons be transported so as to minimize the mileage covered?
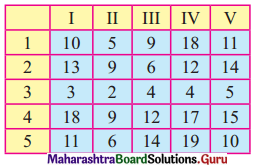
Solution:
The mileage matrix is given by
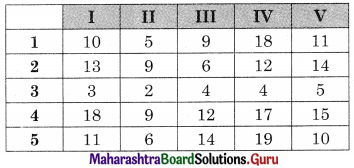
Subtracting row minimum from all elements in that row we get
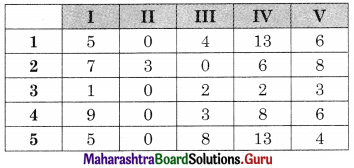
Subtracting column minimum from all elements in that column we get
Draw minimum lines covering all the zeros
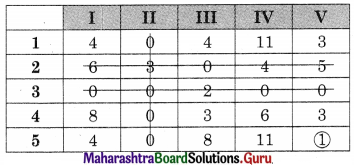
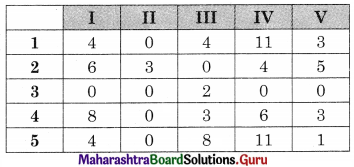
The number of lines covering all the zeros (3) is less than the order of the matrix (5). Hence an assignment is not possible. The modification is required. The minimum uncovered value 1 is subtracted from uncovered values and added to the values at the intersection. The numbers on the lines remain the same we get
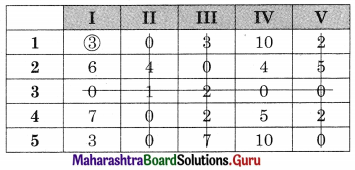
Drawing a minimum number of lines covering all the zeros.
No. of lines covering all the zeros (4) is less than the order of the matrix (5).
Hence assignment is not possible.
Again modification is required. The minimum uncovered value 3 is subtracted from the uncovered values and added to the values at the intersection.
The numbers on the lines remain the same we get
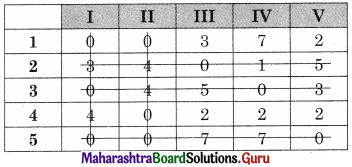
No. of lines covering all the zeros (5) are equal to the order of the matrix so the assignment is possible.
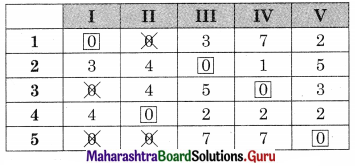
According to the table the assignment is
1 → I, 2 → II, 3 → IV, 4 → II, 5 → V
Total minimum mileage = 10 + 6 + 4 + 9 + 10 = 39 units
![]()
Question 3.
Five different machines can do any of the five required jobs, with different profits five required jobs, with different profits resulting from each assignment as shown below:
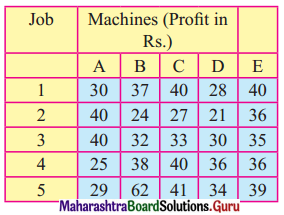
Find the optimal assignment schedule.
Solution:
This profit matrix has to be reduced to cost matrix by subtracting all the values of the matrix from the largest value (62) we get
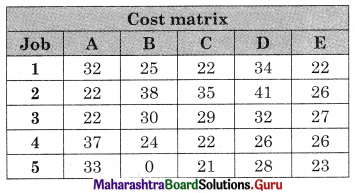
Subtracting row minimum value from all the elements in that column we get
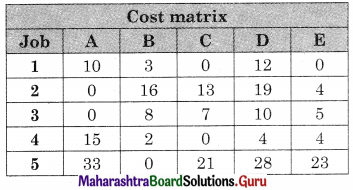
Subtracting column minimum from all the elements in that column we get
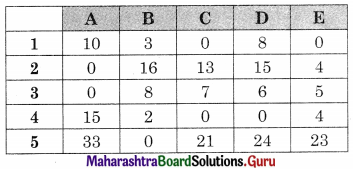
Drawing minimum lines covering all zeros we get
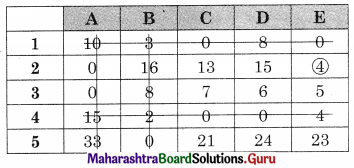
No. of lines (4) is less than the order of the matrix (5). Hence assignment is not possible. The modification is required. The minimum uncovered value (4) is subtracted from the uncovered value and added to the values at the intersection. The values on the lines remain the same, we get
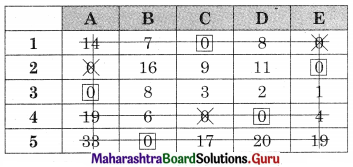
No. of lines (5) are equal to the order of the matrix (5). So assignments are possible
1 → C, 2 → E, 3 → A, 4 → D, 5 → B
For the minimum profit look at the corresponding in the profit matrix given.
Maximum profit = 40 + 36 + 40 + 36 + 62 = 214 units
![]()
Question 4.
Four new machines M1, M2, M3, and M4 are to be installed in a machine shop. There are five vacant places A, B, C, D, and E available. Because of limited space, machine M2 cannot be placed at C and M1 cannot be placed at A. The cost matrix is given below.
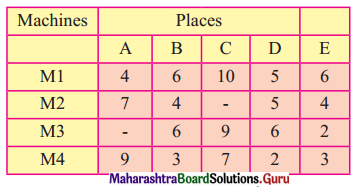
Find the optimal assignment schedule.
Solution:
This is a restricted assignment so we assign a very high cost ‘∞’ to the prohibited all.
Also as it is an unbalanced problem we add a dummy row M5 with all values as ‘0’, we get
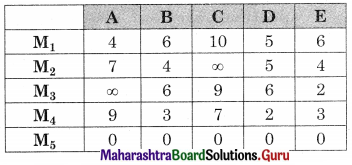
Subtracting row minimum from all the elements in that row, we get
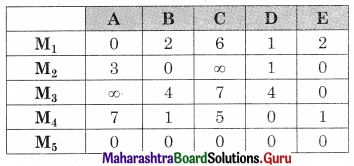
Subtracting column minimum from all the elements in that column we get the same matrix.
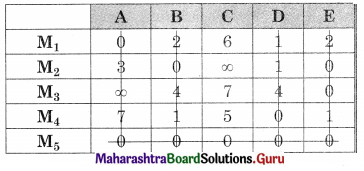
As minimum no. of lines covering all zeros (5) is equal to the order of the matrix, Assignment is possible
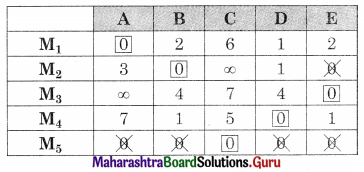
The assignments are given by
M1 → A, M2 → B, M3 → E, M4 → D, M5 → C
As M5 is dummy no machine is installed at C
For minimum cost taking the corresponding values in the cost matrix we get
Minimum cost = 4 + 4 + 2 + 2 = 12 units
![]()
Question 5.
A company has a team of four salesmen and there is four districts where the company wants to start its business. After taking into account the capabilities of salesmen and the nature of districts, the company estimates that the profit per day in rupees for each salesman in each district is as below:
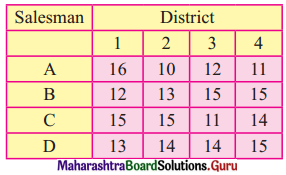
Find the assignments of a salesman to various districts which will yield maximum profit.
Solution:
The profit matrix has to be reduced to the cost matrix. Subtracting all the values from the maximum value (16) we get
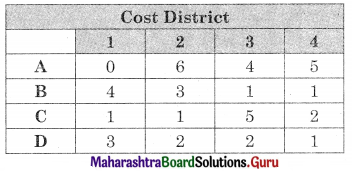
Subtracting row minimum from all values in that row we get
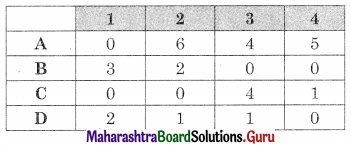
Subtracting column minimum from each column we get the same matrix
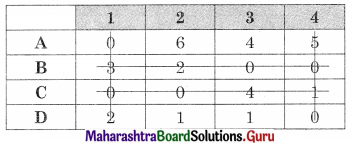
As minimum no. of lines covering all zeros (4) is equal to the order of the matrix (4) Assignment is possible
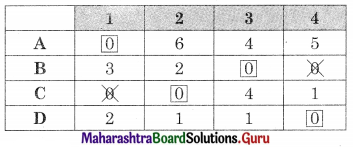
∴ A → 1, B → 3, C → 2, D → 4
For maximum profit, we take the corresponding values in the profit matrix. We get
Maximum profit = 16 + 15 + 15 + 15 = ₹ 61
![]()
Question 6.
In the modification of a plant layout of a factory four new machines M1, M2, M3, and M4 are to be installed in a machine shop. There are five vacant places A, B, C, D, and E available. Because of limited space, machine M2 can not be placed at C and M3 can not be placed at A the cost of locating a machine at a place (in hundred rupees) is as follows.
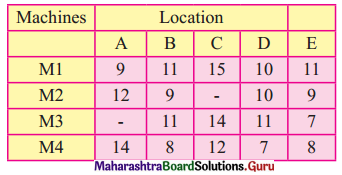
Find the optimal assignment schedule.
Solution:
This is an unbalanced problem so we add a dummy row M5 with all values as ‘0’.
Also, this is on restricted assignment problem. So we assign a very high-cost W to the prohibited cells we have
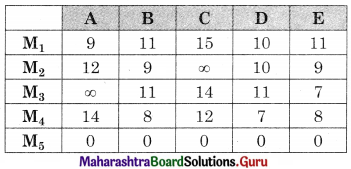
Subtracting row minimum from all values in that row we get
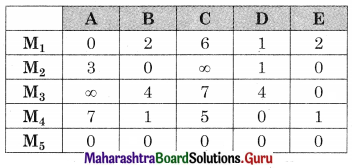
Subtracting column minimum from all values in that column we get the same matrix
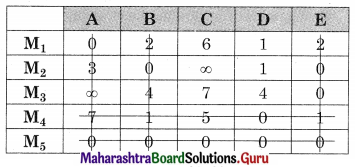
As minimum no. of lines covering all zeros (5) is equal to the order of the matrix (5) assignment is possible.
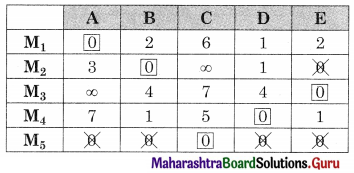
The assignment is
M1 → A, M2 → B, M3 → E, M4 → D, M5 → C
As M5 is dummy, no machine is installed at C.
The minimum cost is found by taking the corresponding values in the cost matrix
Minimum cost = 9 + 9 + 7 + 7 + 0 = 32 (in hundred ₹)