Bhagya

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 4 Supply Analysis Important Questions and Answers.

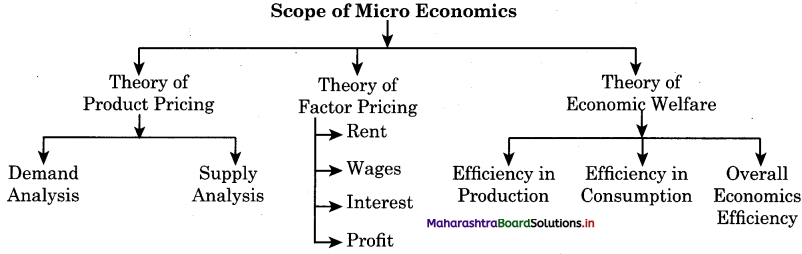
Maharashtra State Board 12th Economics Important Questions Chapter 4 Supply Analysis

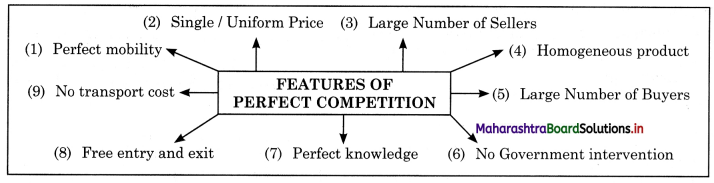
1.[A] Choose the correct option.

Question 1.
Net addition made to the total revenue by selling an extra unit of a commodity is
(a) total revenue
(b) marginal revenue
(c) average revenue
(d) marginal cost
Answer:
(b) marginal revenue

Question 2.
Determinants of supply are …………………..
(a) cost of production
(b) short period
(c) constant price
(d) local market
Answer:
(a) cost of production

Question 3.
Statement related to reservation price are
(a) maximum price
(b) constant price
(c) same for all seller
(d) differ from seller to seller
Answer:
(d) differ from seller to seller

Question 4.
Exceptions to the law of supply are
(a) need for cash
(b) upward sloping supply curve
(c) factory products
(d) future expectation of high price
Answer:
(a) need for cash

Question 5.
Average Revenue is obtained when .
(a) price is multiplied with quantity
(b) last unit is sold
(c) total revenue is divided by quantity sold
(d) all of these
Answer:
(c) total revenue is divided by quantity sold

Question 6.
Increase in supply is shown by
(a) price change only
(b) movement on the same supply curve
(c) shift of supply curve to the left
(d) shift of supply curve to the right
Answer:
(d) shift of supply curve to the right

(B) Complete Correlation

1. Rare goods : Exception to Law of Supply :: Assumption of Law of Supply : ……………….
2. ………………. : Individual supply :: Macro concept: Total supply
3. Marginal Revenue : TR_n – TR_n-1 :: ……………….: TR/TQ
4. Single seller : Individual Supply :: All sellers : ……………….
5. Movement on same supply curve : ……………….:: Shift of supply curve: Change in supply.

Answers:

1. No change in Government Policy
2. Micro concept
3. Average Revenue
4. Market Supply
5. Variation in supply

(C) Give economic terms.

1. Creation of utility.
2. Outcome of the process of production.
3. Total quantity available with the producer for sale at time.
4. Sum total of individual supply.
5. Cost incurred on fixed factors like land, machinery etc.
6. Minimum price below which a seller will not sell a single unit.
7. Expansion and contraction of supply due to change in price.
8. Rise in supply due to fall in taxes.
9. Fall in supply due to fall in taxes.
10. Cost incurred on variable factor like raw material.
11. Net revenue earned by selling an additional unit.

Answer:

1. Production
2. Output
3. Stock
4. Market Supply
5. Fixed Cost
6. Reservation Price
7. Variation in Supply
8. Increase in Supply
9. Decrease in Supply
10. Variable Cost
11. Marginal Revenue

(D) Find the odd word out:

(1) Land, Labour, Capital, Rent.
(2) Rent, Wages, Profit, Capital.
(3) AC, TC, TFC, AR.
(4) Samuelson, Marshall, Robbins, Abdul Kalam.
(5) [ncrease in supply, Decrease in supply, Extension in supply, Market supply.
Answer:

1. Rent
2. Capital
3. AR
4. Abdul Kalam
5. Market supply

(E) Complete the following statements.

1. Production consists of various processes through which ………………
2. Stock determines ………………
3. Stock and supply are same in case of ………………
4. Sum total of individual supply is called ………………
5. Graphical representation of market supply schedule is called ………………
6. When quantity supplied rises due to an increase in price of a commodity, it is called ………………
7. When more quantity is supplied at the same price of a commodity, it is called ………………
8. Per unit cost of production is called ………………
9. Total expenditure incurred by a firm on factors of production for the production of goods and services is called ………………
10. An addition made to TR by selling one additional unit of a commodity is called ………………

Answer:

1. utility is created
2. potential supply
3. perishable goods
4. market supply
5. market supply curve
6. extension or expansion in supply
7. increases in supply
8. Average Cost
9. Total Cost
10. Marginal Revenue

(F) Choose the wrong pair:

I.

Group ‘A’	Group ‘B’
1. Total Output	Sum of quantity produced
2. Stock	Reservation Price
3. Supply	Quantity offered for sale

Answer:
Wrong pair : Stock – Reservation price

II.

Group ‘A’	Group ‘B’
1. Extension in supply	More supply at higher price
2. Contraction in supply	Less supply at lower price
3. Increases in supply	Part of variation in supply

Answer:
Wrong pair : Increase in supply – Part of variation in supply

III.

Group ‘A’	Group ‘B’
1. Total Revenue	Price x Quantity
2. Total Cost	TFC + TVC
3. Average Cost	TR x TQ

Wrong pair : Average Cost – TR x TQ

(G) Choose the correct pair:

I.

Group ‘A’	Group ‘B’
1. Increase in supply	Technology up gradation
2. Exception to law of supply	More supply at higher price
3. Determination of law of supply	Perishable Goods

Answer:
Correct pair : Increases in supply – Technology up gradation

II.

Group ‘A’	Group ‘B’
1. Individual supply	Potential supply
2. Determinants of law of supply	Infrastructural facilities
3. Assumption of the law of supply	Change in government policy

Answer:
Correct pair : Determinations of the law of supply – Infrastructural facility

III.

Group ‘A’	Group ‘B’
1. MCn	TCn – TCn-1
2. TR	Q/P
3. AR	TR x TQ

Answer:
Correct pair : MC_n – TC_n – TC_n-1

2.[A] Identify and explain the concept from given illustration.

Question 1.
All the seller of a similar product are willing to sell their product at a particular price in a given time.
Answer:
Concept: Market Supply
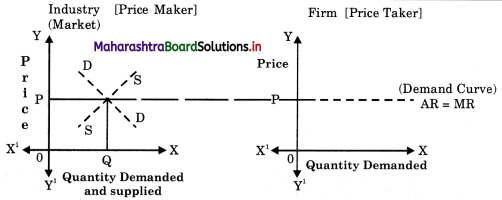
Explanation : Market supply refer to the quantity that all the producers are willing to produce and offer for sale at a particular price in a given time.
As all sellers are ready to sell their product at a particular price, each seller is price taker.
Thus, this concept is of market supply.

Question 2.
Price of old coins, antiques increases as demand increases, but supply cannot be increased.
Answer:
Concept: Exception to the law of supply
Explanation : As per the law of supply, when the price of a product rises, supply increases, but in this case supply cannot be increased.
So, this is an exception to the law and its supply curve is a vertical straight line instead of upward sloping. Thus, this is an exception to the law.

Question 3.
A seller is in urgent need for cash. Therefore, he sell more at lower price.
Answer:
Concept: Exception to the law of supply
Explanation : As per the law of supply, at higher price more is offered for sale.
In this case a seller is selling more at lower price because he is an urgent need for cash.

Question 4.
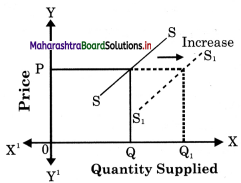
Due to the improvement in technology, supply of cell phones have increased even though price remains same.
Answer:
Concept: Increase in supply Explanation : Increase in supply is a situation when producers are willing to supply a larger quantity of a commodity at the same price.
Due to improvement in the technology of cell phone, producers cost of production falls and they can sell more in the market at the same price.
This is shown with graph.

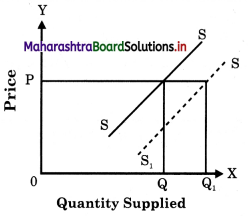
At the same price OP, quantity supplied increases from 0Q to 0Q₁
Thus, this is a case of increase in supply.

Question 5.
Mr. Kriplani produced 2000 bales of cloth during the year 2018-19.
Answer:
Concept: Total Output.
Explanation : Total Output is the sum total of the commodity produced at a given period of time.
So, total output of Mr. Kriplani is taken as total output for the year 2918-19.

Question 6.
Mr. Kriplani had 200 apples in hand. He bought 500 apples from wholesaler.
Answer:
Concept: Stock
Explanation : Stock is the total quantity of commodity available for sale with a seller at a particular point of time.
Now in our case, Mr. Kriplani has total stock of 700 apples (200+500) which he can offer for sale at particular price.

Question 7.
Mr. Chaturvedi has 5000 kg rice at his disposal. He offered 2000 kg rice in market at Rs. 25 per kg.
Answer:
Concept: Stock and Supply
Explanation : Supply means the various quantities of a commodity offered for sale by
producer during a given period of time at a particular price.
In above case, total stock is 5000 kg rice and total supply is 2000 kg rice.

Question 8.
At price Rs. 30 per kg Rameshbhai ( supplied 100 kg of wheat, Bhaveshbhai i supplied 150 kg of wheat and Dharmesh bhai supplied 200 kg of rice. ;
Answer:
Concept : Individual Supply and Market Supply.
Explanation : Individual supply means quantity offer by a single seller at a given price while market supply means total quantity supplied by all the seller in the market a given price.
In above case, 100kg, 150kg and 200 kg is called as individual supply while 450kg is called as market supply.

Question 9.
A seller has go to village urgently. So, he sells his product at low price even if other seller are selling similar product at higher price. Given economic reason in what way it is related to the law of supply.
Answer:
This is an exception to the law of supply. As per the law, more is sold at higher price and less at lower price. In this case an individual seller is in need of cash, as he has to go to village urgently, so he has to sell his product at lower price.

(B) Distinguish between:

Question 1.
Output and Supply
Answer:

Output	Supply
1. Output refers to the total quantity of a commodity that a producer produces with the help of factors of production using a particular technology during a given period of time.	(a) Supply refers to the quantity of a commodity which producers are willing to offer for sale at a given price during a given period of time.
2. Output is a function of input. So, O = f (Inputs)	(b) Supply is a function of stock. So, S =f (Stock)
3. Output depends upon the level of investment, technique of production, cost of production, availability of factors and natural resources, etc.	(c) Supply depends on the stock and price.
4. Output forms the basis of stock.	(d) Stock forms the basis of supply.

Question 2.
Individual Supply and Market Supply
Answer:
Individual Supply:
(a) Individual Supply schedule refers to various quantities of a commodity that an individual seller is willing to sell in the market at different prices during given period of time.
(b) Individual Supply is a narrow concept. It is a part of market_supply.
(c) Schedule:

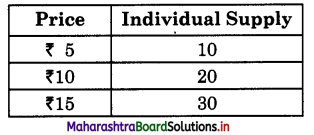
(d) As price rises, a seller likes to sell more.

Market Supply:
(a) Market Supply schedule refers to various quantities of a commodity that all sellers are willing to sell in the market at different prices during given period of time.
(b) Market Supply is a broader concept. It is sum total of individual supply.
(c) Schedule:

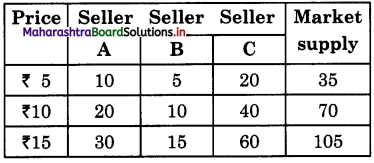
(d) As price rises total quantity supplied in the market increases.

Question 3.
Individual Supply Curve and Market Supply Curve
Answer:
Individual Supply Curve:

1. Individual Supply Curve An individual supply curve is a graphical representation of various quantities of a commodity offered for sale by an individual seller at different prices during a given period of time.
2. It is a narrow concept, as it is a part of market supply.
   
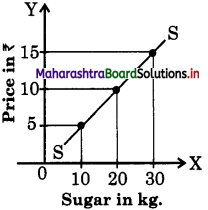
3. The above supply curve shows that as price rises quantity supplied increases to 10, 20, 30 kg.

Market Supply Curve:

1. Market supply curve is the graphical representation of the various quantities of a commodity offered for sale by all the sellers at different prices during a given period of time.
2. It is a broader concept, as it sum total of individual supply.
   
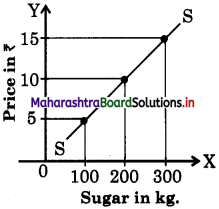
3. The above supply curve shows that as price rises, total supply in the market rises to a greater extent to 100, 200, 300 kg.

Question 4.
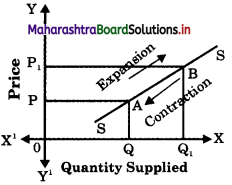
Extension of Supply and Contraction of Supply.
Answer:
Extension of Supply:

1. When the supply of a commodity rises only due to increase in the price of that commodity, then it is said to be extension of supply.
2. Extension in supply is shown by an upward movement to right on the same supply curve.
   
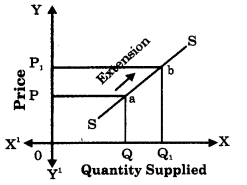
3. When price rises from OP to 0P1, Supply extends from 0Q to 0Q₁.

Contraction of Supply :

1. When supply of a commodity falls only due to fall in the price of that commodity, then it is said to be contraction of supply.
2. Contraction is shown by the downward movement to left on the same supply curve.
   
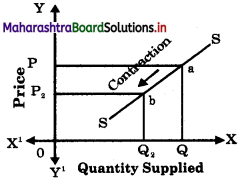
3. When prices falls from 0P to 0P₂, Supply contracts from 0Q to 0Q₂.

Question 5.
Variation in supply and Changes in Supply.
Answer:
Variation in Supply:

1. Variation in supply refers to expansion and contraction of supply which takes place due to change in price.
2. Expansion means more quantity is supplied at a high price while contraction means less quantity is supplied at a lower price.
3. Variation in supply is caused by change in price.
4. Variation is shown by a upward or downward movement on the same supply curve.

Changes in Supply:

1. Changes in supply refers to increase and decrease in supply which takes place due to changes in factors other than price.
2. Increase in supply means more quantity is supplied at same price and decrease means less quantity supplied at the same price.
3. Changes in supply occurs due to change in factors like.
   (1) change in cost of production
   (2) change in techniques of production
   (3) change in government policy.
   (4) change in goal of producer.
   (5) change in climatic condition etc.
4. Changes in supply is shown by a shift in supply curve to the right or left of the original supply curve.
   

Question 6.
Total Cost (TC) and Total Revenue (TR).
Answer:
Total Cost (TC) :

1. TC is the total expenditure incurred by a firm on the factors of production required for production of goods and services.
2. TC is sum total of Total Fixed Cost (TFC) and Total Variable Cost (TVC). TC=TFC+TVC
3. TC increases with the increase in output.
4. TC depends on factors like cost of raw material, cost of factors like labour, land, capital, technology, cost of advertisement, management, etc.
5. When TC > TR firm faces loss.

Total Revenue (TR) :

1. TR refers to the amount received (income earned) by a firm from the sale of given quantity of a commodity at different price.
2. TR is calculated by multiplying price with the quantity sold. TR = Price X Total Quantity
3. TR increases with increase in sale.
4. Total Revenue (TR) depends on the price of product, demand for the product, etc.
5. When TR > TC firm earns profit.

Question 7.
Demand Curve and Supply Curve.
Answer:
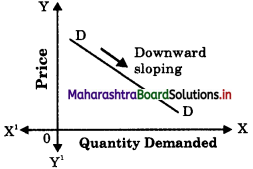
Demand Curve:

1. Demand curve is the graphical representation of a given demand schedule.
2. The demand curve slopes downward from left to right.
3. The demand curve has a negative slope as price and demand are inversely related.
4. The demand curve indicates the consumer’s behaviour in response to change in its price.

Supply Curve:

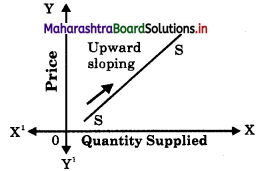
1. Supply curve is a graphical representation of a given supply schedule.
2. The supply curve slopes upward from left to right.
3. The supply curve has a positive slope as price and supply are directly related.
4. The supply curve indicates the seller’s behaviour in response to change in its price.

Question 8.
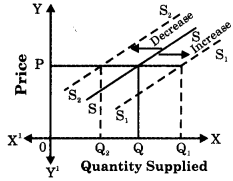
Increase in Supply and Decrease in Supply.
Answer:
Increase in Supply :

1. The supply is said to increase if at the same price more is supplied.
2. Increase in supply is a case of changes in supply.
3. Supply increases due to
   (1) fall in cost of production
   (2) improvement in transport facility
   (3) introduction of modern technology
   (4) government subsidies
   (5) more imports etc.
4. When there is an increase in supply, the supply curve shifts to the right of original supply curve.

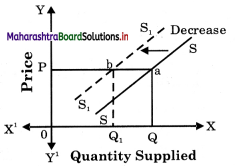
Decrease in Supply

1. Decrease in supply occurs when less quantity is supplied at the same price.
2. It is a case of changes in supply.
3. Supply decreases due to –
   (1) increase in cost of production
   (2) transport strike
   (3) outdated technique
   (4) heavy taxes imposed by government.
   (5) more exports etc.
4. When there is curve shifts to curve.
   

Question 9.
Demand and Supply.
Answer:
Demand:

1. Demand is a desire backed by ability and willingness to pay.
2. Demand is inversely related to price.
3. Demand curve has negative slope.

Supply:

1. Supply means the various quantities offered for sale by a producer at a given price and at a given period of time.
2. Supply is directly related to price.
3. Supply curve has positive slope.

3. Answer the following questions.

Question 1.
What are the exceptions of the law of supply?
Answer:
There are some exceptions to the law of s supply. Following are such cases when supply may fall with the rises in price or rise with the fall in price.

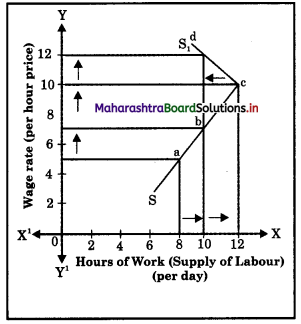
(1) Labour supply : Supply of labour in the terms of hours of work is an important exception pointed out by economists. Generally when wages rise, workers work more, but after a certain point if wages continue to rise, supply of labour falls i.e. workers wish to earn more by work in for less hours and supply curve of labour would bend backwards as shown below :

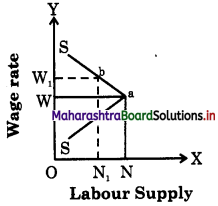
In this figure as wage rate rises up to 0W, ;i supply of labor also rises up to ON, but when wage rate rises to 0W₁, labour supply falls from ON to 0N₁ Hence an exception.

(2) Saving : In case of savings generally it is observed that as the rate of interest rises, savings also rises but some people want to have a fixed regular income by way of interest. They may save less at a higher rate ( of interest and save more at a lower rate of interest. For example : suppose a person is interested in earning a fixed income of ? 800 p.a. then he saves ₹ 10,000/- at 8% rate of interest but when rate of interest increases to 10%, he will save only ₹ 8,000/-.

(3) Future Expectations: If the seller expects a fall in price in future, then he will supply more today even at a low price. But if he expects the prices to rise further in future he will withhold the supply today to supply more in future at a high price.

(4) Need for Cash : When the sellers are in urgent need of liquid cash, then even at a lower price they will offer more goods for sale.

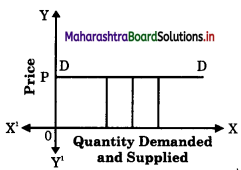
(5) Rare Goods : In case of rare collections such as rare painting, old coins, antique, the law is not applicable as the supply remains fixed. The supply curve is a vertical straight line parallel to Y axis.

(6) Agricultural Goods: Supply of agricultural product is influenced by natural factors like climatic conditions, rainfall etc., which cannot be controlled by man. So in bad weather condition, even at a higher price the supply of agricultural commodities will not increase.

Question 2.
Explain in detail labour supply as an exception to the law of supply.
Answer:
Labour Supply : An interesting exception to the law of supply is provided by the supply curve of labour. In case of supply of labour we come across an unusual phenomenon of the backward bending supply curve. In the beginning, the supply curve of labour slopes upwards as usual from left to right because at higher wage, the units of labour are tempted to offer more hours of work. This continues till the time wage rates have risen sufficiently. When wage rate goes beyond a particular level the worker prefers to substitute work by leisure and cut short the supply of labour. Hence, beyond a certain wage rate the supply curve of labour slopes backwards. This is called the backward bending supply curve of labour and is an exception to the law of supply as shown in the diagram.

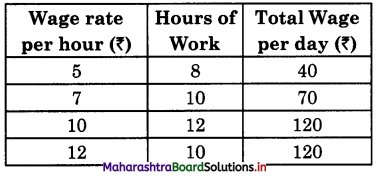
In the above schedule, the supply of labour rises from 8 hours to 10 to 12 hours as the wage rate rises from ₹5 per hour to ₹7 to ₹10 per hours. But thereafter when wage rate – becomes ₹12 per hour the supply of labour ; falls to 10 hours. So the supply curve has a backward bend from point ‘A’. Initially, it slopes upwards i.e., SA then A to S₁ upto it has a backward slope.

Question 3.
Explain variation in supply with the help of diagram.
Answer:
When quantity supplied of a commodity changes due to change in its price, other factors remaining constant, it is known as variation in supply. Variation in supply can be of two types :
(A) Expansion (or Extension) of Supply
(B) Contraction of Supply

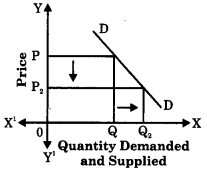
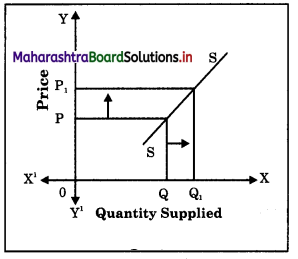
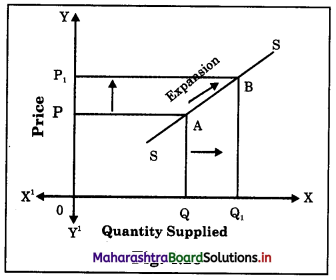
(A) Expansion (or Extension) of Supply : It refers to a rise in the quantity supplied due to an increase in price of a commodity, other factors remaining constant. Extension of supply leads to an upward movement on the same supply curve due to a rise in price as shown in the diagram :

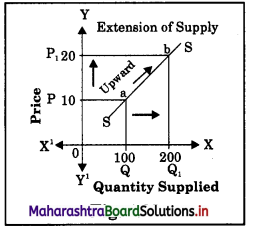
In the above diagram, when price increases from P to P₁, the quantity supplied rises or expands from Q to Q₁ resulting in an upward movement from point A to point B along the same supply curve. It is known as extension of supply.

(B) Contraction of Supply : It refers to fall in quantity supplied due to fall in price, other things remaining constant. Contraction of supply leads to a downward movement on the same supply curve due to a fall in price as shown in the diagram.

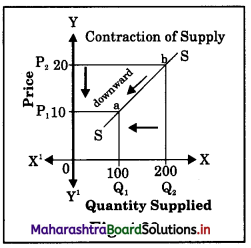
In the diagram when price falls from P₂ to P₁, the quantity supplied falls or contracts from Q₂ to Q₁ resulting in a downward movement from point B to A along the same supply curve. It is known as contraction of supply.

Question 4.
Explain change in supply with the help of diagram.
OR
Explain increase in supply and decrease in supply.
Changes in supply occurs when the quantity supplied changes due to changes in factors other than price.
Changes in Supply are of two types :
(A) Increase in Supply
(B) Decrease in Supply

(A) Increase in Supply : It means when more quantity is supplied at the same price. Increase in supply occurs due to changes in factors other than change in price. It takes place when –

1. There is decrease in price of inputs
2. There is technological upgradation
3. Imports are more
4. There is decrease in tax, etc.

Increase in supply is shown by a shift in i the supply curve to the right of the original; supply curve.

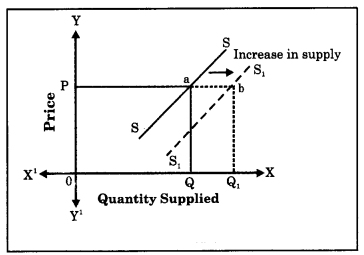
In the diagram, at OP price when quantity supplied rises from OQ to OQ₁ it indicates) an increase in supply. This is shown by a c shift in supply curve from SS to S₁S₁ to the right.

(B) Decrease in Supply : It means when less quantity is supplied at the same price.
Decrease in supply occurs due to change in factors other than change in price. It takes place when –

1. there is increase in price of inputs,
2. technological degradation or out dated technology used.
3. exports are more.
4. there is increase in taxes etc.

Decrease in supply is shown by a shift in the supply curve to the left of the original supply curve.

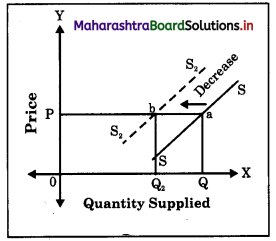
At OP price when quantity supplied falls from OQ to OQ₂, it indicates a decrease in supply. This is shown by a shift in supply curve from SS to S2S2 to the left.

Question 5.
Explain concept of TC, AC and MC.
Answer:
Cost of production is an important factor in governing the supply of a product. Following are the three main types of costs :

(A) Total Cost (TC): It is the total expenditure incurred by a fir m on the factors of production required for the production of goods and services. Total cost is the sum of Total Fixed Cost (TFC) and Total Variable Cost (TVC). Total Fixed Cost is the cost incurred on fixed factors of production like land, factory, building, capital, etc. These factors cannot be changed in the short period. They remain constant. Total Variable Cost is the cost incurred on variable factors such as raw – materials, labour, etc. These factors can be varied or changed according to the change in output level. So the variable cost varies. Total Cost = Total Fixed Cost + Total Variable Cost i.e., TC = TFC + TVC
TC increases as the level of output increases.

(B) Average Cost (AC) : Refers to per unit total cost of production. The average cost is obtained by dividing Total Cost of production by the number of units of that commodity produced
i.e. AC = \(\frac{\mathrm{TC}}{\text { Total Output }}\)
Suppose the total cost of producing 100 units of commodity X is ₹ 1000. Then the average cost is
AC = \(\frac{\mathrm{TC}}{\text { Total Output }}=\frac{1000}{100}\) = 10
∴ AC = ₹ 10

(C) Marginal Cost (MC) : It is net addition made to the total cost (TC) by producing one ( more unit of output.
Suppose the total cost of producing 2 units is ₹ 200 and TC of producing 3 unit is ₹ 240.
MC_n = TC_n – TC_n-1 = ₹ 240 – ₹ 200 = ₹ 40
Where,
n = Number of unit produced ?
MC_n = Marginal Cost of the nth unit ?
TC_n = Total Cost of n unit

Question 6.
Explain the concepts of TR, AR, and MR.
Answer:
Revenue refers to the income earned by a firm from the sale of given quantity of a commodity in the market at different prices. Following are the three main types.

(A) Total Revenue (TR) : Total Revenue (Income) refers to total receipts of the firm from its sales of commodity. It is obtained i by multiplying the price per unit of the commodity with the total number of units!; of commodity sold to the consumers. Thus, Total Revenue = Price per unit x Total Number of units of commodity sold.
TR = Price x Quantity Sold

Example : If the firm sells 10 units of) a commodity at ₹100 per unit then total?
revenue will be TR = 100 x 10. TR = ₹1000

(B) Average Revenue (AR): Average Revenue refers to the revenue (income) per unit of the commodity sold. It can be easily calculated by dividing Total Revenue (TR) by the number of units sold to the consumers. Thus, Average Revenue = Total Revenue + Number of units sold.
i.e., AR = \(\frac{\mathrm{TC}}{\text { Total Quantity Sold }}\)

For example : If the Total Revenue from? the sale of 10 units of commodity is ₹ 1000; then Average Revenue will be
AR = \(\frac{\mathrm{TR}}{\mathrm{Q}}=\frac{1000}{10}\) = ₹100

(C) Marginal Revenue (MR) : Marginal Revenue is the net addition made to TR by selling an additional unit of the commodity. In other words, marginal revenue is the addition made to the total revenue by selling one more unit of a commodity.

Example : If the total revenue from the sale of 10 units is ?1000 and that from the sale of 11th unit the total revenue is 1020 then the MR of 11th unit will be
MR_n = TR_n – TR_n-1 = 1020 – 1000 = 20
Or we can also calculate Marginal Revenue as –
MR = \(\frac{\text { Change in Total Revenue }}{\text { Change in total number of units sold }}\)
MR = \(\frac{\Delta \mathrm{TR}}{\Delta \mathrm{T} Q}=\frac{20}{1}\) = 20
MR = 20

Question 7.
What are the assumptions to the law of supply?
Answer:
Assumptions of the Law of Supply : The law of supply is conditional. It is based on certain assumptions. They are as follows:

1. No change in Cost of Production: The law will hold true only if the cost of production remains constant.
2. No change in Technique of Production : It is assumed that there is no change in the method of production. If there is any improvement in the technique of production then supply will increase at the same price.
3. 3. No change in Weather condition : Changes in weather and climatic condition would affect supply especially of agricultural products, so it is assumed to remain constant.
4. No change in Government Policies : Any change in government policies will affect the supply, so it is assumed that there is no change in government tax policies, subsidies or industrial policy.
5. No Speculations about Future Prices : It is assumed that the producers do not speculate about future changes in price.
6. No change in Transport Cost : It is assumed that there is no change in transport facility and transport cost.
7. Prices of Other Goods : It is assumed that the prices of competitive goods remain constant. If the price of competitive goods rises then it is quite likely that producer may transfer his resource to the production of those goods, whose price has arisen.
8. No change in the quantity of goods kept for Self – consumption : If sellers keep more goods for their personal use then supply cannot be increased even at a high price.
9. Constant Scale of Production : It is assumed that the scale of production remains constant during the given period of time.

4. State with resons whether you agree or disagree with the following statements.

Question 1.
Supply is directly related to price.
Answer:
Yes, I agree with this statement.

• According to the Law of Supply, other things being equal, the supply varies directly with its price.
• More quantity is offered for sale at a higher price and less is offered for sale at a lower price.
• So supply is directly related to its price.
• In order to earn a reasonable profit, the sellers tries to sells more at a higher price and less at a lower price.
  So the supply curve slopes upwards. It has a positive slope.
• Thus, the supply is directly related to price.

Question 2.
Stock can exceed supply.
OR
Supply cannot exceed stock.
Answer:
Yes, I agree with this statement.

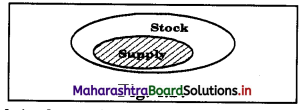
• Stock is the entire quantity of a commodity, which is in the custody of the seller.
• Supply refers to that part of stock of a commodity which is offered for sale at prevailing market price during a period of time.
• Thus supply is a part of stock. c
• Stock is the potential supply. It is a fund or reservoir from which supply flows.
• Stock determines the ability of seller to supply.
  Thus, stock exceeds supply.

Question 3.
When price rises supply expands.
Answer:
Yes, I agree with this statement.

• According to the Law of Supply “Other things remaining constant more is supplied < at a higher price and less at a lower price.”
• The rise in price causes an expansion in supply because (i) the existing sellers will supply more than before in order to get larger profit and (ii) new suppliers with high reservation price will also now enter S the market.
• So supply expands when price rises.

Question 4.
The supply curve has a positive slope..
OR
The supply curve slopes upwards from left to right.
OR
The relationship between price and supply is positive.
OR
There is direct relation between price and quantity supplied.
Answer:
Yes, I agree with this statement.
OR The supply curve slopes downward from left to right.
Answer:
No, I do not agree with this statement.

• According to the Law of Supply “Other things remaining constant supply varies directly with price i.e., more quantity will be offered for sale at a higher price and less at a lower price. So there is a positive relationship between price and supply.”
  S = f(P)
• The supply curve which is a graphical representation of supply schedule slopes upward from left to right indicating a positive slope.
• In order to earn reasonable profit, the sellers try to sell more at higher prices and less at lower prices.
• The sellers earn more profit when market price is greater than their reservation price.
• Thus, the above statement is true.

Question 5.
Agricultural products are exceptions to the law of supply.
Answer:
Yes, I agree with this statement.

• The law of supply states that the supply of a commodity varies directly with its price.
• But in case of agricultural goods supply does not vary directly with price.
• Agricultural product being perishable in nature cannot be stored for long time. The sellers cannot wait for price to rise. They have to sell off the whole stock even at a low price. Here supply coincides with stock.
• Also agricultural production depends on unforeseen changes in weather. So even at higher price supply cannot be increased during drought or flood situation.
• So, the above statement is true.

Question 6.
Due to speedy transport supply falls.
Answer:
No, I do not agree with this statement.

• Transport facilities are one of the important determinants of supply.
• Modern speedy transport facilities in widening r the market.
• It increases the mobility of goods and helps in creating place utility for goods and services.
• Speedy transport helps in domestic as well; as international trade of goods and services.
• Thus, the above statement is false.

Question 7.
Reservation price is very low in respect of perishable commodities.
Answer:
Yes, I agree with this statement. ;

• Reservation price is sellers minimum price, below which the seller will not supply any unit of the commodity.
• Whether the sellers reservation price will be high or low depends upon number of factors. One of them is the durability of the commodity.
• If the commodity is durable like TV set, car etc., then sellers reservation price will be high.
• But if the commodity is perishable like fish, flowers, vegetables, milk etc., then reservation price will be low.
• As perishable commodities cannot be stored for long, it can become stale and useless.
  Therefore, sellers are forced to clear stock as early as possible.
  So the reservation price is low.

Question 8.
Supply depends on many factors.
OR
Market Supply depends on many factors.
Answer:
Yes, I agree with this statement.
OR
Price is the only determinant of Supply.
Answer:
No, I do not agree with this statement.
Supply depends on many factors. Price is the main factor. There is a direct relationship between price and supply. Besides price there are many other factors such as

• Cost of production and supply are indirectly related. Higher the cost, lesser will be the supply.
• State of technology i.e., advanced technology increases supply.
• Government policy like subsidies encourage production and increases supply, whereas heavy taxation decreases supply.
• Natural conditions like favourable weather condition increases supply.
• Exports decreases supply and imports increases supply.
  Better infrastructure facility increases supply.
• Nature of market like competitive market increases supply.
  Thus, the above statement is true.

Question 9.
Total cost includes Total Fixed Cost and Total Variable Cost.
Answer:
Yes, I agree with this statement.

• Total cost is the total cost incurred by a firm on the factors of production required for production of goods and services. Total cost is the sum total of fixed cost and variable cost.
• Total fixed cost includes cost incurred on fixed factors like factory building, plant size, machinery etc. Fixed cost remains fixed in the short run but changes in the long period. Total variable cost includes cost on variable factors like raw materials, fuel, labour etc., which changes according to the output in the short period also. So while calculating Total Cost we include Total Fixed Cost (TFC) and Total Variable Cost (TVC). So, TC = TFC + TVC. Thus, the above statement is true.

Question 10.
Supply of perishable goods is equal to its production.
OR
There is no difference between stock and supply of perishable goods.
Answer:
Yes, I agree with this statement.

• The stock of perishable goods like vegetables, flowers, fruits, milk, etc., is equal to supply.
• This is because perishable goods cannot be stored for long time. They become stale.
• They need to be sold within a short period of time irrespective of the price.
• Also the cost of storage is high.
• So, the above statement is true.

Question 11.
The supply curve of labour is backward bending.
Answer:
Yes, I agree with this statement.

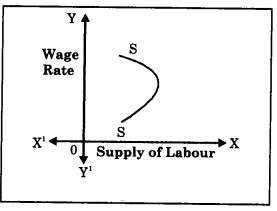
• When the wage rate in the industry rises, the supply of labour (i.e., hours of work) rises upto a certain limit.
• Beyond certain limit with further rise in wages, supply of labour tends to fall.
• This is because the labour prefers leisure to work i.e., he substitutes work with leisure,
• With the increased wage rate he is able to satisfy his needs.
• So the supply curve instead of rising upwards
  starts sloping backward as he reduces the hours of work.

Question 12.
AR is always more than TR.
Answer:
No, I do not agree with this statement.

• TR or Total Revenue refers to total income earned by a firm from the sale of a given quantity of a commodity in the market of different price. It is derived by Price x l Quantity sold.
• AR or Average Revenue refers to the income earned per unit of a commodity sold. It is derived by TR Quantity sold.
• Hence, TR will always be greater than AR.
  Hence, the above statement is false.

Question 13.
Demand and Supply are opposite forces.
Answer:
Yes, I agree with this statement.
Both demand and supply are opposite forces.

• Demand explains the consumer’s behaviour with respect to change in price of a commodity. Supply explains the producer’s behaviour with respect to change in price of a commodity.
• Demand is inversely related to price of a commodity i.e., when price of a commodity rises the demand for it falls and when price falls the demand rises. Supply is directly related to the price i.e., when price rises, supply expands and when price falls, supply falls or contracts.
• The demand curve slopes downwards. It has a negative slope. The supply curve slopes upwards from left to right. It has a positive slope. Both opposite forces together determine the equilibrium price.
• A consumer aims at maximum satisfaction with his limited income. So he demands more at a lower price and less at a higher price. Whereas a producer aims at maximum profit so he supplies more at a higher price and less at a lower price.
• Thus, the above statement is true.

Question 14.
There is difference between stock and supply.
Answer:
Yes, I agree with this statement.
OR
There is no difference between stock and supply.
Answer:
No, I do not agree with this statement.

Stock	Supply
(a) Stock refers to the total quantity of commodity available with producer for sale.	(a)Supply is that part of stock which the seller is willing to offer for sale at a given price.
(b) It is outcome of production. If production increases, stock will also increase.	(b) It is outcome of stock. Stock is the basis of supply.
(c) It is a fund or reservoir and a static concept (inelastic).	(c) It is a flow concept. It changes according to change in price (elastic).
(d) It can exceed supply.	(d) It cannot exceed stock.

Question 15.
There are no exceptions to law of supply.
Answer:
No, I do not agree with this statement.
There are some exceptions to the law of s supply. Following are such cases when supply may fall with the rises in price or rise with the fall in price.

(1) Labour supply : Supply of labour in the terms of hours of work is an important exception pointed out by economists. Generally when wages rise, workers work more, but after a certain point if wages continue to rise, supply of labour falls i.e. workers wish to earn more by work in for less hours and supply curve of labour would bend backwards as shown below :

In this figure as wage rate rises up to 0W, ;i supply of labor also rises up to ON, but when wage rate rises to 0W₁, labour supply falls from ON to 0N₁ Hence an exception.

(2) Saving : In case of savings generally it is observed that as the rate of interest rises, savings also rises but some people want to have a fixed regular income by way of interest. They may save less at a higher rate ( of interest and save more at a lower rate of interest. For example : suppose a person is interested in earning a fixed income of ? 800 p.a. then he saves ₹ 10,000/- at 8% rate of interest but when rate of interest increases to 10%, he will save only ₹ 8,000/-.

(3) Future Expectations: If the seller expects a fall in price in future, then he will supply more today even at a low price. But if he expects the prices to rise further in future he will withhold the supply today to supply more in future at a high price.

(4) Need for Cash : When the sellers are in urgent need of liquid cash, then even at a lower price they will offer more goods for sale.

(5) Rare Goods : In case of rare collections such as rare painting, old coins, antique, the law is not applicable as the supply remains fixed. The supply curve is a vertical straight line parallel to Y axis.

(6) Agricultural Goods: Supply of agricultural product is influenced by natural factors like climatic conditions, rainfall etc., which cannot be controlled by man. So in bad weather condition, even at a higher price the supply of agricultural commodities will not increase.

Question 16.
Price is the only determinant of supply.
Answer:
No, I do not agree with this statement.

1. Cost of Production : Changes in the price of factors of production like rent, wages, interest affects the cost of production. When cost of production increases, supply decreases.
2. Price of Other Goods : The supply of a given commodity depends on the price of other commodity. E.g. if the price of wheat rises and that of rice remains the constant, then the producer will think of producing more of wheat. This will affect the supply of rice.
3. price of the Commodity : Price is an important factor influencing the supply. More is supplied at a higher price and less at a lower price. So price and supply are 5 directly related.
4. Climatic Conditions : The supply of commodity is also influenced by the forces
5. Government Policy : Government policies like taxation, subsidies, industrial policies etc., may encourage or discourage production and supply. A tax on the commodity will raise the cost of production and reduce the supply while a subsidy on the other hand will provide an incentive to increase production and supply.
6. Exports and Imports : When the
   government resort to imports, supply expands, at the same time heavy exports would reduce the supply in the domestic market.
7. Nature of Market : In a competitive market, the supply would be more but in a monopoly market the seller may create artificial scarcity to raise the price.
8. Future Expectation : If future trends indicate a rise in price, the supply decreases at present. On the other hand if the sellers expect the future price to fall, supply would increase in the current period.
9. Technique of Production : Improvement in the technique of production will lead to increase in supply. Application of advanced technology enables the producer to produce goods on large scale at a lower cost and lesser price.
10. Infrastructure Facility : If means of transport and communication are well developed, the extent of market would be wide. i.e. supply will increase.
11. Natural and Man-made Calamities : Natural calamities like earthquake, cyclone, flood etc., will affect the supply in the market. Even man-made calamities like a bomb-blast, affects supply. Even a strike call can affect supply in the market.

5. Study the following table / figures and answer the questions :

Question 1.
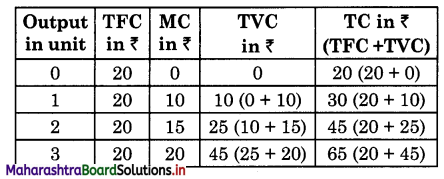
TFC (Total Fixed Cost) of a commodity ‘x’ of a firm is ₹ 20 Calculate (a) TVC and (b) TC from the following data.

Answer:

Question 2.
Find TR of a firm if it sells 500 units of £ commodity ‘X? at 25 ₹ per unit.
Answer:
TR is the revenue derived by a firm by multiplying total units sold by its price.
Hence, TR = P x Q
= 25 x 500
= 12, 500₹

Question 3.
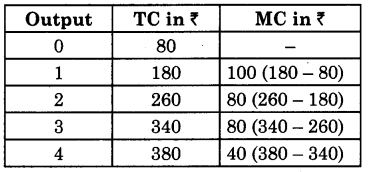
Calculate MC at each level of output of the following data.

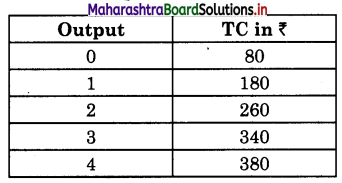
Answer:

Question 4.
Workout : Price of oranges is ₹ 200 per dozen. During festival time at the same price 2 dozen, oranges are offered for sale. On the basis of this answer the following

1. Draw the figure for this.
Answer:

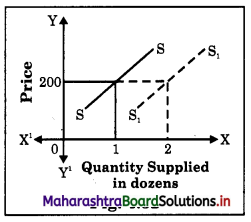
2. Is it the case of variation or change in supply. Give reason.
Answer:
It is a case of change in supply, as here the price remains the same at ? 200, while quantity increases from 1 dozen to 2 dozen. So, here supply changes due to festival season and due to change in price.

Question 5.
Demand in world market for Indian antique goods have increased but supply of these are fixed even though buyers are ready to pay high price for it. On the basis of this answer the following :

1. Draw figure for this.
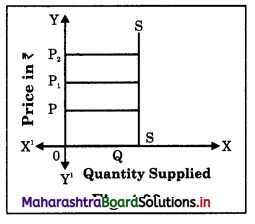
Answer:

Question 6.
Does this justify the law of supply? Give reason for your answer.
Answer:
No, it does not justify the law of supply. As per law of supply, as the price increases, supply of a commodity should increase. But in above case even though the price is increasing supply remains the same. So it is an exception to the law of supply.

6. Answer in detail:

Question 1.
State and explain the law of supply. What are its assumptions?
Answer:
Law of Supply :
(A) Introduction : The law of supply was introduced by Dr. Alfred Marshall in his book “Principles of Economics” published in 1890. The law establishes a functional relationship between the price of a commodity and quantity supplied of that commodity. It explains the general tendency of the sellers in offering more goods for sale at a higher price than at a lower price.

(B) Statement of the Law : According to Prof. Alfred Marshall “Other things remaining constant, the higher the price of the commodity, greater is the quantity supplied and lower the price of the commodity, smaller is the quantity supplied.”In other words, quantity supplied of a commodity varies directly with price i.e., with a fall in price supply contract and with a rise in price supply expands.
S = f (P) [S = Supply, P = Price, f = Function of
The law can be better understood with the help of a market supply schedule and market supply curve.

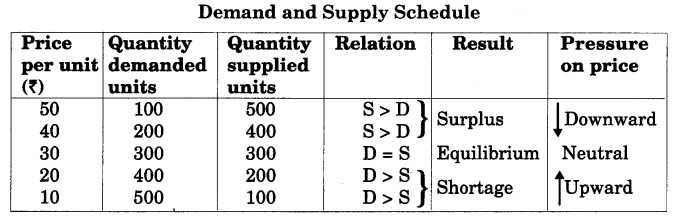
(C) Market Supply Schedule : Market supply schedule is a tabular representation of various quantities of a commodity offered for sale by all the sellers in the market at different prices during a given period of time. The schedule is a hypothetical one except one price rest are imaginary prices.

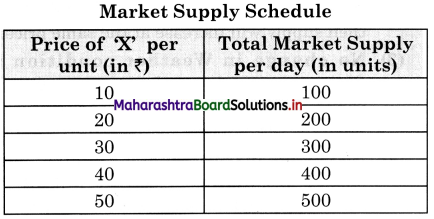
The above schedule clearly shows that sellers in general want to sell more at high prices and less at low price. E.g., at a low price of ₹10 per unit the seller supplies only 100 units per day and at high price of ₹ 50 the supply rises to 500 units of ‘X’ per day.

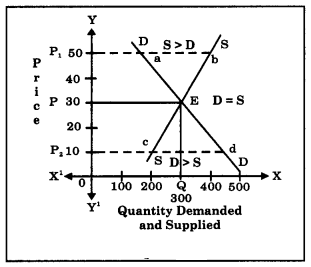
(D) Market Supply Curve : It is graphical representation of the above market supply schedule. Price is measured on ‘Y’ axis and quantity supplied on ‘X’ axis and above schedule is plotted. We derive a supply curve SS. ’

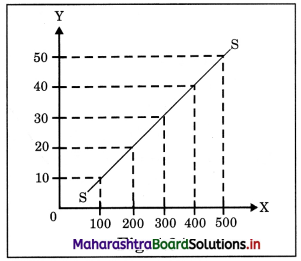
In the diagram, supply curve SS is a linear supply curve (straight – line). It slopes upwards from left to right. It has a positive slope indicating direct relationship between price and quantity supplied.

(E) Assumptions of the Law of Supply : The law of supply is conditional. It is based on certain assumptions. They are as follows:

• No change in Cost of Production: The law will hold true only if the cost of production remains constant.
• No change in Technique of Production : It is assumed that there is no change in the method of production. If there is any improvement in the technique of production then supply will increase at the same price.
• No change in Weather condition : Changes in weather and climatic condition would affect supply especially of agricultural products, so it is assumed to remain constant.
• No change in Government Policies : Any change in government policies will affect the supply, so it is assumed that there is no change in government tax policies, subsidies or industrial policy.
• No Speculations about Future Prices : It is assumed that the producers do not speculate about future changes in price.
• No change in Transport Cost : It is assumed that there is no change in transport facility and transport cost.
• Prices of Other Goods : It is assumed that the prices of competitive goods remain constant. If the price of competitive goods rises then it is quite likely that producer may transfer his resource to the production of those goods, whose price has arisen.
• change in the quantity of goods kept for Self – consumption : If sellers keep more goods for their personal use then supply cannot be increased even at a high price.
• Constant Scale of Production : It is assumed that the scale of production remains constant during the given period of time.

Question 2.
State and explain the law of supply with exceptions.
Answer:
Law of Supply :
(A) Introduction : The law of supply was introduced by Dr. Alfred Marshall in his book “Principles of Economics” published in 1890. The law establishes a functional relationship between the price of a commodity and quantity supplied of that commodity. It explains the general tendency of the sellers in offering more goods for sale at a higher price than at a lower price.

(B) Statement of the Law : According to Prof. Alfred Marshall “Other things remaining constant, the higher the price of the commodity, greater is the quantity supplied and lower the price of the commodity, smaller is the quantity supplied.”In other words, quantity supplied of a commodity varies directly with price i.e., with a fall in price supply contract and with a rise in price supply expands.
S = f (P) [S = Supply, P = Price, f = Function of]
The law can be better understood with the help of a market supply schedule and market supply curve.

(C) Market Supply Schedule : Market supply schedule is a tabular representation of various quantities of a commodity offered for sale by all the sellers in the market at different prices during a given period of time. The schedule is a hypothetical one except one price rest are imaginary prices.

The above schedule clearly shows that sellers in general want to sell more at high prices and less at low price. E.g., at a low price of Rs. 10 per unit the seller supplies only 100 units per day and at high price of Rs. 50 the supply rises to 500 units of ‘X’ per day.

(D) Market Supply Curve : It is graphical representation of the above market supply schedule. Price is measured on ‘Y’ axis and quantity supplied on ‘X’ axis and above schedule is plotted. We derive a supply curve SS. ’

In the diagram, supply curve SS is a linear supply curve (straight – line). It slopes upwards from left to right. It has a positive slope indicating direct relationship between price and quantity supplied.

There are some exceptions to the law of s supply. Following are such cases when supply may fall with the rises in price or rise with the fall in price.

(1) Labour supply : Supply of labour in the terms of hours of work is an important exception pointed out by economists. Generally when wages rise, workers work more, but after a certain point if wages continue to rise, supply of labour falls i.e. workers wish to earn more by work in for less hours and supply curve of labour would bend backwards as shown below :

In this figure as wage rate rises up to 0W, ;i supply of labor also rises up to ON, but when wage rate rises to 0W₁, labour supply falls from ON to 0N₁ Hence an exception.

(2) Saving : In case of savings generally it is observed that as the rate of interest rises, savings also rises but some people want to have a fixed regular income by way of interest. They may save less at a higher rate ( of interest and save more at a lower rate of interest. For example : suppose a person is interested in earning a fixed income of ? 800 p.a. then he saves ₹ 10,000/- at 8% rate of interest but when rate of interest increases to 10%, he will save only ₹ 8,000/-.

(3) Future Expectations: If the seller expects a fall in price in future, then he will supply more today even at a low price. But if he expects the prices to rise further in future he will withhold the supply today to supply more in future at a high price.

(4) Need for Cash : When the sellers are in urgent need of liquid cash, then even at a lower price they will offer more goods for sale.

(5) Rare Goods : In case of rare collections such as rare painting, old coins, antique, the law is not applicable as the supply remains fixed. The supply curve is a vertical straight line parallel to Y axis.

(6) Agricultural Goods: Supply of agricultural product is influenced by natural factors like climatic conditions, rainfall etc., which cannot be controlled by man. So in bad weather condition, even at a higher price the supply of agricultural commodities will not increase.

Question 3.
What is meant by Supply? State its determinants.
Answer:
Law of Supply :
(A) Introduction : The law of supply was introduced by Dr. Alfred Marshall in his book “Principles of Economics” published in 1890. The law establishes a functional relationship between the price of a commodity and quantity supplied of that commodity. It explains the general tendency of the sellers in offering more goods for sale at a higher price than at a lower price.

(B) Statement of the Law : According to Prof. Alfred Marshall “Other things remaining constant, the higher the price of the commodity, greater is the quantity supplied and lower the price of the commodity, smaller is the quantity supplied.”In other words, quantity supplied of a commodity varies directly with price i.e., with a fall in price supply contract and with a rise in price supply expands.
S = f (P) [S = Supply, P = Price, f = Function of]
The law can be better understood with the help of a market supply schedule and market supply curve.

(C) Market Supply Schedule : Market supply schedule is a tabular representation of various quantities of a commodity offered for sale by all the sellers in the market at different prices during a given period of time. The schedule is a hypothetical one except one price rest are imaginary prices.

The above schedule clearly shows that sellers in general want to sell more at high prices and less at low price. E.g., at a low price of Rs. 10 per unit the seller supplies only 100 units per day and at high price of Rs. 50 the supply rises to 500 units of ‘X’ per day.

(D) Market Supply Curve : It is graphical representation of the above market supply schedule. Price is measured on ‘Y’ axis and quantity supplied on ‘X’ axis and above schedule is plotted. We derive a supply curve SS. ’

In the diagram, supply curve SS is a linear supply curve (straight – line). It slopes upwards from left to right. It has a positive slope indicating direct relationship between price and quantity supplied.

1. Cost of Production : Changes in the price of factors of production like rent, wages, interest affects the cost of production. When cost of production increases, supply decreases.
2. Price of Other Goods : The supply of a given commodity depends on the price of other commodity. E.g. if the price of wheat rises and that of rice remains the constant, then the producer will think of producing J more of wheat. This will affect the supply of rice.
3. price of the Commodity : Price is an important factor influencing the supply. More is supplied at a higher price and less at a lower price. So price and supply are 5 directly related.
4. Climatic Conditions : The supply of commodity is also influenced by the forces
5. Government Policy : Government policies like taxation, subsidies, industrial policies etc., may encourage or discourage production and supply. A tax on the commodity will raise the cost of production and reduce the supply while a subsidy on the other hand will provide an incentive to increase production and supply.
6. Exports and Imports : When the
   government resort to imports, supply expands, at the same time heavy exports would reduce the supply in the domestic market.
7. Nature of Market : In a competitive market, the supply would be more but in a monopoly market the seller may create artificial scarcity to raise the price.
8. Future Expectation : If future trends indicate a rise in price, the supply decreases at present. On the other hand if the sellers expect the future price to fall, supply would increase in the current period.
9. Technique of Production : Improvement in the technique of production will lead to increase in supply. Application of advanced technology enables the producer to produce goods on large scale at a lower cost and lesser price.
10. Infrastructure Facility : If means of transport and communication are well developed, the extent of market would be wide. i.e. supply will increase.
11. Natural and Man-made Calamities : Natural calamities like earthquake, cyclone, flood etc., will affect the supply in the market. Even man-made calamities like a bomb-blast, affects supply. Even a strike call can affect supply in the market.

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 9 World: Decolonisation Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 9 World: Decolonisation

1A. Choose the correct alternative and rewrite the statement.

Question 1.
___________ was largely responsible for facilitating the process of decolonisation after Second
World War.
(a) League of Nations
(b) World Health Organisation
(c) United Nations
(d) World Trade Organisation
Answer:
(c) United Nations

Question 2.
The British developed ___________ in Sri Lanka as international port city.
(a) Colombo
(b) Madurai
(c) Kandy
(d) Galle
Answer:
(a) Colombo

Question 3.
The British appointed ___________ as Vice President of Myanmar.
(a) Mahatma Gandhi
(b) Pandit Nehru
(c) Aung San
(d) Mao Tse Tung
Answer:
(c) Aung San

Question 4.
The first conference of Asian and African countries held in 1955 was known as ___________ conference.
(a) Paris
(b) Versailles
(c) Myanmar
(d) Bandung
Answer:
(d) Bandung

Question 5.
H.S. Williams formed ___________ organisation in London for African unity.
(a) Asian Unity
(b) Free State
(c) Pan-African Association
(d) Nationalist Association
Answer:
(c) Pan-African Association

Question 6.
The end of the Second World War created an environment in which the process of ___________ gained momentum.
(a) Industrialisation
(b) decolonisation
(c) mechanisation
(d) urbanisation
Answer:
(b) decolonisation

Question 7.
In 1964 Tanganyika and Zanzibar were amalgamated and the independent state of ___________ came into existence.
(a) South Africa
(b) Ethiopia
(c) The United Republic of Tanzania
(d) Soviet Russia
Answer:
(c) The United Republic of Tanzania

Question 8.
The process of decolonisation is supposed to have received momentum mainly because of the document known as ___________
(a) Paris Peace Conference
(b) Atlantic Charter
(c) Treaty of Versailles
(d) Queen’s Proclamation
Answer:
(b) Atlantic Charter

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) the Maldives	26th July 1965
(b) Sri Lanka	1948
(c) Myanmar (Brahmadesh)	4th January 1948
(d) India	2nd October 1945

Answer:
India – 15th August 1947

2A. Write the names of historical places/persons/events.

Question 1.
The leader of the Indian National Movement –
Answer:
Mahatma Gandhi

Question 2.
An organisation responsible for facilitating the process of decolonisation after World War II –
Answer:
United Nations

Question 3.
The Sultan who ended Portuguese rule from the Maldives –
Answer:
Muhammad Thakuruphanu Al Azam

Question 4.
An organisation created by the people of Myanmar under the leadership of Aung San in 1937 –
Answer:
‘Burma Independence Army’

Question 5.
The country that called the first conference of Asian countries –
Answer:
India

Question 6.
The place where the fifth Pan-African Congress was held in 1945 –
Answer:
Manchester

Question 7.
An American sociologist of African origin was present at the first conference of ‘Pan-American Association’. –
Answer:
W.E.B.Du Bois

Question 8.
The name of the German General who attacked the British empire in Africa –
Answer:
General Erwin Rommel

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The ‘League of Nations’ introduced the system of trustees ___________
(a) to manage the administration of the colonies which were under the control of Germany and Turkey
(b) to introduce western education in French colonies
(c) to give the compensation to axis powers
(d) to conduct a plebiscite in the defeated countries
Answer:
(a) to manage the administration of the colonies which were under the control of Germany and Turkey

Question 2.
The British empire in Africa was in danger because ___________
(a) people participated in the election process
(b) people decided to take part in the war
(c) of the aggression of Italy and the German
(d) of the calamity of 1920
Answer:
(c) of the aggression of Italy and the German

3. Complete the following concept map.

Question 1.

Name of the country	Continent	Colony	Year of Decolonisation (independence)
1. Ivory Coast	……………..	French	7th August 1960
2. South Africa	Africa	……………..	1920
3. Sri Lanka	……………..	British	……………..
4. India	Asia	……………..	……………..

Answer:

Name of the country	Continent	Colony	Year of Decolonisation (independence)
1. Ivory Coast	Africa	French	7th August 1960
2. South Africa	Africa	British	1920
3. Sri Lanka	Asia	British	1948
4. India	Asia	British	15th August 1947

4A. Write short notes.

Question 1.
Atlantic Charter.
Answer:
The Atlantic Charter was a pivotal policy statement issued on August 14, 1941, that defined goals for the post-war world. The Atlantic Charter was drafted by British Prime Minister Winston Churchill and U.S. President F.D. Roosevelt at the Atlantic Conference in Newfoundland. All the allies of World War II later confirmed it.

4B. Explain the following statements with reasons.

Question 1.
After the Second World War independence movements strengthened in the African countries.
OR
How western education created the spirit of Nationalism among the African people.
Answer:

• During the 15 year period of 1950-1965 people in the European colonies in Africa freed themselves from the foreign rule.
• The education system imposed by the Europeans was alien to them. Ironically, African leaders were trained in this alien educational system.
• Their education had introduced them to American Independence Struggle, French Revolution, and Nationalism.
• The African people became aware of nationalism and national pride.
• After Second World War England and France gradually began to grant more rights to the Africans in their colonies.
• This strengthened the independence movements in African nations.

5. State your opinion.

Question 1.
Italy and Germany had to lose their colonies in Africa at the end of the Second World War in 1945.
Answer:

• The African battlefield in the Second World War had spread from Morocco and Libya in the north to Ethiopia and Somali Land on the eastern border of Africa.
• The British empire in Africa was in danger because of the aggressions of Italy and the German General Erwin Rommel.
• Indian soldiers in the British army fought with great resilience. With their help, the British could compel the combined armies of Italy and Germany and they had to lose their colonies in Africa at the end of the Second World War in 1945.

6. Answer the following questions in detail.

Question 1.
Explain the decolonisation of the African continent.
Answer:

• An introduction of western education created awareness and feelings of nationalism among the African people.
• European colonies in Africa were involved in First World War. After the defeat of Germany in the war, allied nations began to compete with each other for occupying German colonies in Africa.
• On the advice of American President Woodrow Wilson, the ‘League of Nations decided with the mutual understanding that England, France, and Belgium should divide the colonies among themselves.
• The four British colonies namely Cape Colony, Natal, Orange Free State, and Transvaal were amalgamated and the state of South Africa was created in 1920.
• Egypt got its independence before the end of the Second World War. Following it Libya, Tunisia, Morocco, Algeria, and Ghana became independent one after another.
• In the middle of the 20th century in all the 12 French colonies, such as Ivory Coast, Madagascar, Mali in central Africa became independent. Somalia, Cameroon, and other European colonies under the care of ‘League of Nations became independent one by one.
• Algeria became independent by conducting a plebiscite in 1962. In 1964 Tanganyika and Zanzibar were amalgamated and ‘The United Republic of Tanzania’ came into existence.
• At the end of the Second World War Italy and Germany had to lose their colonies in Africa.

7. Answer the following question with the help of the given points.

Question 1.
Explain decolonisation of Asian continents.
(a) the Maldives
(b) Sri Lanka
(c) Myanmar
Answer:
By the end of the 20th-century colonialism came to an end and the process of decolonisation was completed.
(a) Maldives:

• Portuguese entered the Maldives in 1529. Since then Maldives began to pay tribute to the Portuguese in Goa.
• Sultan Muhammad Thakuruphanu A1 Azam from Malabar ended the Portuguese rule and signed a treaty with the Dutch and gave them administrative responsibility of Maldives.
• the Later Maldives was taken over by the British. They built naval bases and radio transmission centers in the Maldives. They also took Indian labourers to work in the paddy fields in the Maldives.
• the Maldives became independent on 26th July 1965, by a treaty signed at Colombo.

(b) Sri Lanka:

• The British ruled Sri Lanka (Ceylon) from 1798 to 1948. They defeated the Portuguese and Dutch.
• There were uprisings in Sri Lanka against British rule. The British plantation owners had taken many labourers from Tamil Nadu to work in coffee plantations.
• In Sri Lanka, the British dominated the production of coffee, tea, rubber, and coconut. They developed Colombo as an international port city.
• They established colleges and universities in Sri Lanka and encouraged Buddhist studies. Sri Lanka became independent in 1948.

(c) Myanmar:

• In 1599, the Portuguese annexed Myanmar, however, in 1611 Portuguese were defeated and United Myanmar was formed. Now Myanmar followed expansionist policy and attacked the British territories of Assam and Manipur in India.
• This situation caused three wars between Myanmar and the British also known as Anglo- Burmese war. The British won the third war and got the control of entire Myanmar.
• Till 1935 it was a part of province of British India. In 1935 it was separated from India and granted autonomy. After 1937 the people of Myanmar formed an organization called ‘Burma Independence Army’ under the leadership of Aung San.
• The British granted independence to Myanmar on 4th January 1948 and appointed Aung San as Vice President.

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 12 India Transformed Part 2 Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 12 India Transformed Part 2

1A. Choose the correct alternative and rewrite the statement.

Question 1.
Sundarlal Bahuguna started ___________ movement.
(a) Civil Disobedience
(b) Right to Information
(c) Chipko
(d) Water conservation
Answer:
(c) Chipko

Question 2.
Rahibai Popere is popularly known as ___________
(a) Beejmata (seed mother)
(b) Adimata
(c) Narishakti
(d) Strishakti
Answer:
(a) Beejmata (seed mother)

Question 3.
As a result of work of ‘Sahyadri Nisarga Mitra’ ___________ were included in schedule I of the ‘Wildlife Protection Act – 1972.’
(a) Indian Blackege
(b) Sherpalite
(c) Indian Turtlelets
(d) Indian Swiftlets
Answer:
(d) Indian swiftlets

Question 4.
“Lets’s all learn, Let’s all progress” was the motto of ___________ programme.
(a) Khelo India
(b) Sarva Shiksha Abhiyan – SSA
(c) Padhega India
(d) Mid-day Meal
Answer:
(b) Sarva Shiksha Abhiyan – SSA

Question 5.
Indian wrestler ___________ earned fame in international wrestling.
(a) Kling Chang
(b) Muhammad Ali
(c) Bruce Lee
(d) Khashaba Jadhav
Answer:
(d) Khashaba Jadhav

Question 6.
Sachin Tendulkar was awarded the highest award of ___________
(a) Paramveer Chakra
(b) Bharat Ratna
(c) Dronacharya
(d) Padmacharya
Answer:
(b) Bharat Ratna

Question 7.
In 2011, Government of India announced a scheme named as ___________
(a) Play and music
(b) Play and chat
(c) Come and play
(d) run for India
Answer:
(c) Come and play

Question 8.
The Government of India established National Sports University at ___________ in 2018.
(a) Delhi
(b) Manipur
(c) Pune
(d) Kolkata
Answer:
(b) Manipur

Question 9.
___________ was an advertisement campaign designed to boost tourism.
(a) Mahan Bharat
(b) Atulya Bharat
(c) Enriched India
(d) The Indian Charisma
Answer:
(b) Atulya Bharat

Question 10.
On 6th July 2019, ___________ city in Rajasthan was inscribed as ‘World Heritage’ by UNESCO.
(a) Bikaner
(b) Jaipur
(c) Aajamghad
(d) Kotta
Answer:
(b) Jaipur

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Sahyadri Nisarg Mitra	Institute for conservation of turtles
(b) Department of Ayurveda, Yoga and Naturopathy, Unani Medicine, Siddha and Homeopathy	AYUR
(c) Federation of Association in Indian Tourism and Hospitality (FAITH)	Organised Indian Tourism Mart – 2018
(d) National Education Policy (NEP)	Emphasised on universalisation of education

Answer:
Department of Ayurveda, Yoga, and Naturopathy, Unani Medicine, Siddha, and Homeopathy – AYUSH

Question 2.

Group ‘A’	Group ‘B’
(a) Medha Patkar	Narmada Bachao Movement
(b) Sundarlal Bahuguna	Chipko Movement
(c) Dr. Rajendra Singh	Soil conservation
(d) Premsagar Mestri	SEESCAP

Answer:
Dr. Rajendra Singh – Water Conservation

Question 3.

Group ‘A’	Group ‘B’
(a) (DPEP) District Primary Education Programme	Providing access to Primary Education
(b) Mid-day Meal	to provide mid-day meals to children in Primary Schools
(c) Sarva Shiksha Abhiyan – SSA	The right to free education was granted to children
(d) Sakharshala	Night Schools

Answer:
Sakharshala – Schools for the seasonal workers harvesting sugarcane

2A. Write the names of historical places/persons/events.

Question 1.
This programme was launched by the State Government of Maharashtra to save girl child –
Answer:
Lek Ladki

Question 2.
The fuel which is used for vehicles to overcome pollution problem –
Answer:
CNG – Compressed Natural Gas

Question 3.
Rahibai Popere was felicitated by the President of India by this award on 8th March 2018 –
Answer:
Nari Shakti Award

Question 4.
The annual event celebrated by ‘Sahyadri Nisarg Mitra’ every year –
Answer:
Turtle Festival

Question 5.
To achieve universalisation of education in India, this satellite was launched in 2004 –
Answer:
EDUSAT (GSAT-3)

Question 6.
The travel show was released on the discovery channel to boost tourism to places of unique nature and culture in the northeastern states of India –
Answer:
GO NORTHEAST

Question 7.
The founder of ‘Muslim Satyashodhak Samaj’ –
Answer:
Hamid Dalwai

Question 8.
The act which was formed to provide protection to women from domestic violence in 2005 –
Answer:
Domestic Violence Act

Question 9.
The movement started by Sunadarlal Bahuguna for the protection of the environment –
Answer:
Chipko Movement

Question 10.
The person who started first night school in Maharashtra –
Answer:
Mahatma Jotiba Phule

Question 11.
The schools started by the government for the children of seasonal workers harvesting sugarcane –
Answer:
Sakharshala

Question 12.
The programme is specially meant to benefit the students who work in the daytime –
Answer:
Ratrashala

Question 13.
The motto of Sarva Shiksha Abhiyan – SSA –
Answer:
“Let’s all learn, Let’s all progress”

Question 14.
The satellite launched in 2004 to achieve universalisation of education –
Answer:
EDUSAT (GSAT-3)

Question 15.
An institution established in Delhi, in 1984 which is working for heritage conservation –
Answer:
INTACH – Indian National Trust for Art and Cultural Heritage

Question 16.
The fund which was established for the development of sports in India –
Answer:
The ‘National Sports Development Fund’

Question 17.
The scheme launched by the Ministry of Tourism of the Indian government to chalk out tours to the pilgrim and spiritual centers –
Answer:
‘Swadesh Darshan’ or ‘Prasad’

Question 18.
The Samiti in which Rahibai Popere worked for the conservation of seeds –
Answer:
Kalasubai Parisar Biyanee Samvardhan Samiti

Question 19.
Bhau Katdare and his associates work for the conservation of nature through this institute –
Answer:
Sahyadri Nisarg Mitra

Question 20.
A non-governmental organisation in which Premsagar Mestri and his associates work for the conservation of vultures –
Answer:
SEESCAP ‘Society for Eco Endangered Species Conservation and Protection’.

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The main objective of National Human Rights Commission is ___________
(a) to protect the girl child
(b) to protect fundamental human rights
(c) to provide shelter to all middle-class people
(d) to establish committee far environment conservation
Answer:
(b) to protect fundamental human rights

Question 2.
The pollution of water and food is increasing because ___________
(a) of artificial and non-biodegradable materials like plastic and pesticides
(b) increasing air pollution
(c) using oil for making food
(d) use of natural ingredients for the preparation of food
Answer:
(a) of artificial and non-biodegradable materials like plastic and pesticides

3. Complete the following concept map.

Question 1.

Plan	Year of	Objective
1. (DPEP) District Primary Education Programme	……………………….	To provide access to primary education to all.
2. ………………………….	13th August 1995	To provide mid-day meals to children in primary school
3. Sarva Shiksha Abhiyan (SSA)	………………………..	The right to free education was granted to children in the age group of 6 – 14 years.

Answer:

Plan	Year of	Objective
1. (DPEP) District Primary Education Programme	1994	To provide access to primary education to all.
2. Mid-day Meal (Shaley Poshan Ahar)	13th August 1995	To provide mid-day meals to children in primary school
3. Sarva Shiksha Abhiyan (SSA)	2001	The right to free education was granted to children in the age group of 6 – 14 years.

4A. Write short notes.

Question 1.
AYUSH
Answer:

• For developing alternate medicine a new department was established by the ‘Ministry of Health and Family Welfare of the Government of India.
• In 2009, this department was renamed as ‘Department of Ayurveda, Yoga, and Naturopathy, Unani Medicine, Siddha and Homeopathy (AYUSH).
• This department is also working for the development of syllabi and education of these branches of medicine, advanced research, standardisation of medicine, etc.

Question 2.
Hamid Dalwai.
Answer:

• Hamid Dalwai was a social reformer inspired by the work and thoughts of Mahatma Jotiba Phule.
• He founded ‘Muslim Satyashodhak Samaj’ in 1970. His main concern was the rights of Muslim women.
• He opposed the custom of ‘Triple Talaq’. The law passed by the Indian Parliament in 2019, has declared this custom illegal.
• He was of the opinion that in Secular India uniform civil code should be applicable to all.

4B. Explain the following statements with reasons.

Question 1.
The Indian government launched a new scheme named ‘Khelo India’.
Answer:

• The Indian government launched a new scheme named ‘Khelo India’ by combining some old schemes with some new objectives.
• The main objective of this scheme was to establish excellence in sports by creating a larger popular platform.
• The scheme also aimed at creating interest among the students about sports from early days in schools and to increase girl’s participation in sports.
• For the development of sports, the ‘National Development Fund’ was established and donation to this fund is eligible for 100% exemption of income tax.
• The Indian Government gives various awards for different sports each year. Some of them are the ‘Arjun Award’, ‘Rajiv Gandhi Khel Ratna award, Lifetime Achievement Award, Dronacharya’, etc.
• ₹ 75,00,000 was given to the player who wins the gold medal in Olympics. Similarly visually impaired are given a good amount of rewards and jobs.
• There is a provision of pension for a retired sportsperson. A winner of the Olympics is given a pension of ₹ 20,000 since 2018 and the winner of the Asian games gets ₹ 12,000 per month.
• In this way, the Indian government launched various schemes for making the youth aware of sports as a life career.

Question 2.
The Government of Maharashtra decided to teach English from the 1st standard.
Answer:

• The Government of Maharashtra decided to teach English from 1st standard so that the children could master the English language along with their mother tongue.
• Emphasis was given on listening, speaking, reading, and writing skills with the emphasis on children enjoying the learning of English as a language.
• Following the syllabus, the Maharashtra State Textbook Bureau (Balbharati) took up the responsibility of preparing best-illustrated textbooks. The initiative was appreciated by the national knowledge commission.

5. Answer the following question with the help of the given points.

Question 1.
Explain different policies implemented by the Indian Government in the field of education.
(a) Primary Education
(b) Mid-day Meal
(c) Sarva Shiksha Abhiyan
Answer:
The transformation of India is seen in the field of education as well. 1990 was declared as the ‘International Year of Literacy.’ During this year Kerala became the first state in India to achieve a 100% literacy rate. The government of India has started different innovative programmes to educate people:
(a) Primary Education:

• District Primary Education Programme (DPEP) was started in 1994 aiming at providing access to primary education to all.
• This programme was financially supported by the world bank and started in seven states including Maharashtra, Madhya Pradesh, Karnataka, Tamil Nadu, Kerala, Haryana, and Assam.
• The main objective of this programme was to achieve 100% registration and attendance of children in primary schools and bringing down the number of drop-outs.

(b) Mid-day Meal (Shaley Poshan Ahar):

• A programme was implemented by the government on 15th August 1995, to provide mid-day meals to children in primary schools.
• If the facility to cook the food in schools was not available then food grains were distributed to each child to ensure his/her attendance in school.

(c) Sarva Shiksha Abhiyan:

• This programme was launched in 2001. The motto of this programme was “Let’s all learn, Let’s all progress”.
• By the 86th Amendment in the Constitution of India, the right to free education was granted to children in the age group of 6-14.
• This programme was launched by combining the earlier programme of ‘Khadu-Phala Yojana’ and ‘Mid-day Meal’.
• The programme gives special attention to the education of girl children and children with special needs (Divyang).

Question 2.
Explain the contribution of the following environment activists in the context of conservation and preservation of the environment with special reference to Maharashtra:
(a) Rahibai Popere
(b) Bhau Katdare
(c) Premsagar Mestri
Answer:
Efforts of a number of environmental activists have contributed to environmental conservation and preservation. In Maharashtra, the following three people worked tirelessly to further the goal of environmental conservation and to protect endangered animal species.
(a) Rahibai Popere:

• She was facilitated by the ‘Nari Shakti Award’ by the President of India on 8th March 2018.
• She is popularly known as ‘Beejmata’ (seed mother) for her work in ‘Kalasubai Parisar Biyanee Samvardhan Samiti.’
• She has worked relentlessly to preserve seeds of native cultivars for the future generation.
• The food made with hybrid varieties of food grains and vegetables caused many problems in the human body so thought to preserve native varieties of food grains to overcome the problems.
• She began to cultivate native varieties of food grains and store the seeds of those landraces. She did not confine her efforts to only to her family, but through micro banking groups (bachat gat) she spread this movement into other villages.
• This movement was supported by ‘Bharatiya Agro Industries Foundation (BAIF)’.
• She preserves these seeds in an earthen pot which is covered by the plaster of soil and cow dung in order to save the seeds from ants and insects.
• She has a collection of more than 50 landraces of food grains and 30 landraces of vegetables.
• She is one of the three Indian women selected as ‘Women of the year 2018’ by BBC among 100 women from various countries.

(b) Bhau Katdare:

• Bhau Katdare and his associates worked to save an endangered species of ‘White-breasted Sea Eagle’ through an institute called ‘Sahyadri Nisarg Mitra’.
• He created public awareness to save and conserve this bird by trekking the sea coast of Ratnagiri district.
• The nests of this bird were smuggled out and sold in foreign countries. Due to the efforts of Bhau Katdare and his associate’s Indian swiftlets were included in schedule ‘I’ of the ‘Wildlife Protection Act’ – 1972, which was a remarkable contribution of ‘Sahyadri Nisarg Mitra’.
• Through his institution, he also worked to save Olive Ridley turtles. In the first year, they successfully protected 50 nests and 2734 baby turtles. From these 50 nests were released back into the sea. Hundreds of tourists come every year to watch the ‘Turtle festival’ to watch the occasion of baby turtles returning to sea.
• To accommodate them, facilities of ‘Home Stay’ were developed and the peasants were trained in this.
• Now, they started the protection of the endangered ‘Pangolin’ (anteater / Khavalya Manjar)

(c) Premsagar Mestri:

• Prem Sagar Mestri and his associates are working for the protection of two species of vultures, ‘Long-billed vultures’ and ‘White back vultures’ which are observed in the region around Raigad.
• They are also working for increasing the number of these species of vultures and to make available safe food for them through ‘Society for Eco Endangered Species Conservation and Protection – SEESCAP a non-governmental organisation.
• The number of vultures is decreasing because of the painkillers given to animals which have proved to be toxic for these scavengers. Besides the dearth of trees with adequate height, scarcity of food, etc., are the causes responsible for the decrease in the vulture population. People working for SEESCAP are successful in saving the vultures of this vicinity.

Question 3.
Explain in detail India’s transformation in the social domain.
(a) Human Rights Protection Act-1993
(b) Establishment of Human Rights Commission
(c) The ‘Domestic Violence Act of 2005
(d) Low sex ratio of girls
(e) Government schemes to overcome this problem
Answer:
A lot of changes have been taken place in the field of the social domain. These changes are as follows:
(a) Human Rights Protection Act 1993: The government is trying hard to reduce the social disparity and to bring all the classes of people in the society into the mainstream of economic development. Human Rights Protection Act was passed in 1993.

(b) Establishment of Human Rights Commission: National Human Rights Commission was established under this act. The main objective of this act is to protect fundamental human rights like the right to life, equality, etc., and to see that nobody is deprived of these rights. According to this act, the commission can act on the basis of a report of a case of deprivation of fundamental rights, published in a newspaper or other media (‘Sui Moto cognizance’). A complaint can be lodged by a social activist or a social institute on behalf of the victim.

(c) The ‘Domestic Violence Act of 2005: The domestic violence act was passed in 2005 to provide protection to women from domestic violence. The most important provision of this act is the right of a woman to the house where she has been residing even if she doesn’t own the house.

(d) Low sex ratio of girls: According to the 2011 census, the sex ratio of girls in India is very low. In the age group of 0-6 years, the number of girls is 914 against 1000 boys. This is really an alarming situation and several women organizations raised a voice expressing their concern over this matter.

(e) Government schemes to overcome this problem: The state government of Maharashtra implemented different schemes to overcome the problem of the low sex ratio of girls. The Maharashtra state government banned sex/gender prediction tests of a fetus and launched a programme called ‘Lek Ladki’. After all these programmes, awareness has been created among the people and the social loathing for the birth of a girl is diminishing.

Question 4.
Explain the changes that took place in the field of education with special reference to Maharashtra.
(a) Need for modification in the school syllabi
(b) The guidelines for the new syllabi
(c) Recommendation of ‘Acharya Ram Murti committee
(d) Objectives of ‘Sarva Shiksha Abhiyan’
(e) Establishment of central schools with uniform syllabi
(f) The programs of ‘Ratrashala’ and ‘Sakharshala’
Answer:
Different positive changes that took place in the education field are as follows:
(a) Need for modification in the school syllabi: The National Council of Educational Research and Training, Delhi suggested some modifications in the school syllabi and the structure of school textbooks.

(b) The guidelines for the new syllabi: The guidelines in the new syllabi were based on democratic principles, social justice, awareness of duties and responsibilities, gender equality, protection of the environment, eradication of superstition, population education as also norms of individual behaviour. The syllabi were also formed for creating awareness among the students regarding unity in diversity. Several training programs are arranged for teachers all over Maharashtra for intensifying the effects to fulfill the objectives of the new syllabi. It helped to create awareness regarding the state-level training and school textbooks, comparable to the awareness created at the time of the ‘National Literacy Mission’.

(c) Recommendation of‘Acharya Ram Murti Committee: In 1990, the report of‘Acharya Ram Murti Committee was received by the Government of India. The committee examined the National Educational Policy (NEP). This committee emphasised on universalisation of education, education for women and backward classes, and educational democracy. The most important recommendation of this committee was to include education in fundamental rights and to raise the government funds allotted to education. The directives were issued related to the weight of school bags of children which leads to a reduction in the weight of a school bag. The practices of interviewing children before school admission were banned.

(d) Objectives of ‘Sarva Shiksha Abhiyan’:

• To enroll every child in school to raise the standard of education.
• To eliminate gender discrimination in education.
• To achieve 100% attendance in school by 2010.

(e) Establishment of Central Schools with uniform syllabi: Central schools with uniform syllabi were created throughout the country so that the wards of Central Government’s and Armed forces employee may not have to suffer. The central schools focus on sports and extracurricular activities along with the academic syllabi.

(f) The programmes of ‘Ratrashala’ and ‘Sakharshala’: The Government started the programmes like ‘Ratrashala’ and ‘Sakharshala’. Mahatma Jotirao Phule started first night school in Maharashtra in the 19th century. A number of night schools are opened in Maharashtra inspired by Mahatma Phule’s work. This programme is specially meant to benefit the students who work in the daytime. In the season of sugarcane harvesting, many labourers migrate temporarily to the sites of various sugar factories. To facilitate the education of their children special schools known as ‘Sakharshala’ were started. The State Government also take help of voluntary organization to increase literacy rate. This has helped in increasing the literacy rate. The districts of Sindhudurg and Wardha achieved a 100% literacy rate. It provided an impetus to adult education. The government provided books to school children for supplementary reading.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 5 Forms of Market Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 5 Forms of Market

1. A. Choose the correct option:

Question 1.
Features of Perfect Competition are –
(a) Large number of buyers
(b) Large number of sellers
(c) Different prices
(d) Perfect mobility
Options :
(1) a, b and c
(2) a, b and d
(3) b, c and d
(4) c and d
Answer:
(2) a, b and d

Question 2.
Features of monopoly are –
(a) Single seller
(b) No close substitutes
(c) Control over supply
(d) Price taker
Options :
(1) a, b and d
(2) a, b, c and d
(3) c and d
(4) a, b and c
Answer:
(4) a, b and c

Question 3.
Features of Monopolistic Competition are –
(a) Homogeneous product
(b) Selling cost
(c) Downward sloping demand curve
(d) Few buyers
Options :
(1) b and c
(2) a, b and d
(3) c and d
(4) a, b and c
Answer:
(1) b and c

Question 4.
Legal monopoly is recognized by –
(a) Legal provision
(b) Trade Mark
(c) License
(d) Copyright
Options :
(1) a, b, c and d
(2) a, b and d
(3) a, b and c
(4) a and c
Answer:
(1) a, b, c and d

Question 5.
Examples of discriminating monopoly are –
(a) Doctors
(b) Lawyers
(c) Consultants
(d) All of the above
Options :
(1) a and d
(2) a, b and d
(3) a, b and c
(4) a, b, c and d
Answer:
(4) a, b, c and d

Question 6.
Types of imperfect market are –
(a) Monopoly
(b) Oligopoly
(c) Monopolistic Competition
(d) Perfect Competition
Options :
(1) b and c
(2) a, b and c
(3) only d
(4) all of these
Answer:
(2) a, b and c

(B) Complete the Correlation.

(1) Tata group : Private monopoly :: Indian Railways : ………………..
(2) Few sellers : Oligopoly :: Many sellers : ………………..
(3) Less than one year : Short period :: More than five years : ………………..
(4) Perfect competition : No selling cost :: Monopolistic competition : ………………..
(5) Natural monopoly : Wheat from Punjab :: ……………….. : Copy right
(6) Perfect competition : Homogeneous :: ……………….. : Differentiated products
(7). Theory of Monopolistic competition : Prof. Chamberlin :: Perfect competition : ………………..
(8) Perishable goods : Local market :: Non-perishable goods : ……………….
(9) OPEC : Group Monopoly :: RIL : ………………..
(10) Petroleum : ……………….. :: Scooter : National market.
Answers:

1. Public monopoly
2. Perfect competition
3. Very long period
4. Selling cost
5. Legal monopoly
6. Imperfect competition
7. Mrs. Joan Robinson
8. National Market
9. Private monopoly
10. International market

(C) Give economic terms.

1. A monopoly recognised by law.
2. The cost that can add to the price of the product in a distant market.
3. A market in which laissez faire policy is adopted by the government.
4. A network of dealings between buyers and sellers.
5. A market in which a firm and industry are same.
6. A monopoly that arises when a particular type of natural resources are located in a particular region.
7. A price that is determined by intersection of demand and supply.
8. Welfare oriented monopoly. Railways, Courier services, Water supply,
9. A practice of charging different prices for the same product.
10. A monopoly formed by an organisation of Petroleum Exporting countries.
11. When there is no difference between the firm and industry.

Answer:

1. Legal monopoly
2. Transport cost
3. Perfect competition
4. Market
5. Monopoly
6. Natural monopoly
7. Equilibrium price
8. Public monopoly
9. Price discrimination
10. Voluntary monopoly
11. Monopsony

(D) Find the odd word out

(1) Market structure on the basis of place :
Local, National, Oligopoly, International.
(2) Peculiarities of Perfect competition :
Many buyers, Few sellers, Price taker, No transport cost.
(3) Examples of Public Monopoly :
Railways, Courier services, Water supply, Electricity.
(4) Features of Monopoly :
Many sellers, Many buyers, Entry barriers to sellers, Firm coincides with industry.
(5) Natural Monopoly depends upon :
Climate, Rainfall, Specific location, Many sellers.
(6) Private monopoly :
Tata group, OPEC, Adani power, Post office.
(7) Imperfect competition :
Price discrimination, Uniform price, Barriers to entry, Price maker.
Answer:

1. Oligopoly
2. Few sellers
3. Courier services
4. Many sellers
5. Many sellers
6. Post office
7. Uniform price

(E) Complete the following statements.

(1) Equilibrium price is that level of price where ………………
(2) A seller is price maker in ………………
(3) A welfare oriented monopoly is called ………………
(4) A Market in which sellers sell and buyers buy the product in the region in which it is produced is called ………………
(5) A market in which buyers and sellers trade in goods and services across the national borders is called ………………
(6) A classification of market on the basis of place are local, national and ………………
(7) A market on the basis of competition which is ideal and imaginary concept is called………………
(8) A market showing some but not all the features of a competitive market is called………………
(9) When a private body controls a monopoly firm, it is called ………………
(10) When the production is totally controlled and operated by the government it is known as………………
(11) Tea cultivation in Assam is an example of………………
(12) A firm which charges different prices to different buyers for the same product, it is called………………
(13) When some monopolists come together voluntarily to form a group of monopolists, it is called ………………
(14) Different brands of washing powders, liquid cleaners are examples of………………
(15) Selling cost is an important feature of………………
(16) Mobile service providers and cement companies are examples of ………………
(17) A period of production is so long that all inputs are variable is called ………………
(18) A market in which supply is fixed is called ………………
(19) A book “Theory of Monopolistic Competition is written by ………………
(20) The objective of the seller in monopoly market is ………………
(21) Under monopoly there is existence of ………………
Answer:

1. market demand is equal to market supply
2. monopoly .
3. public monopoly
4. local market
5. international market
6. international
7. perfect competition
8. imperfect market
9. private monopoly
10. public monopoly
11. natural monopoly
12. discriminating monopoly
13. voluntary monopoly
14. monopolistic competition
15. monopolistic competition
16. oligopoly market
17. very long period market
18. very short period market
19. Prof. E. H. Chamberlin
20. profit maximisation
21. single seller

[F] Choose the wrong pair ;

I.

Group ‘A’	Group ‘B’
1. Perfect competition	Many buyers and sellers
2. Oligopoly	Many buyers and few sellers
3. Imperfect market	Monopoly, International market

Answer:
3.

II.

Group ‘A’	Group ‘B’
1. Market on the basis of place	Local, National, International
2. Market on the basis of competition	Perfect competition, International
3. Market on the basis of time	Very short, short, long, Very long

Answer:
2

III.

Group ‘A’	Group ‘B’
1. Public Monopoly	Wheat from Punjab
2. Natural Monopoly	Tea from Assam
3. Private Monopoly	Reliance Group

Answer:
1

(G) Choose the correct pair

I.

Group ‘A’	Group ‘B’
1. Very short period	(a) More than 5 years
2. Short period	(b) Less than 1 year
3. Long period	(c)Few days or weeks
4. Very long period	(d) Upto 5 years

Answer:
(1)-(c), (2)-(b), (3)-(d), (4)-(a).

II.

Group A	Group B
1. Perfect Competition	(a) Product Differentiation
2. Monopoly	(b) Uniform Price
3. Monopolistic Competition	(c) Few Sellers
4. Oligopoly	(d) Single Seller

Answer:
(1)-(b), (2)-(d), (3)-(a), (4)-(c).

2.[A] Identify and explain the concept from given illustrations.

Question 1.

Output sold in units	Price of ‘X’ in ₹	Price of ‘Y‘ in ₹
100	50	50
200	50	40
300	50	30

Identify the type of market of two goods X’ and ‘Y’ Give reason for your answer.
Answer:
Concept : Market for good ‘X’ is perfect competition.
Explanation : At the same price ? 50 sellers are ready to sell more and more in the market.
Concept : Market for good ‘Y’ is
monopolistic competition.
Explanation : As price of ‘Y’ falls, more and more sellers enter the market to sell their product.

Question 2.

Client	Elec, per unit by Government	Lawyer fee in ₹
A	10	1000
B	10	2000
C	10	3000

(1) Identify the type of monopoly by the government and Lawyer. Give reason for your answer.

Answer:
Concept: Electricity charges by government – Public Monopoly.
Explanation : Public monopoly is welfare oriented monopoly and is owned by the government. Therefore, their price per unit remains uniform.
Answer:
Concept : Lawyer fee – Discriminating Monopoly.
Explanation : In case of lawyer, being a private practitioner, he can charge different fee from different customers. Hence, it is called discriminating monopoly.

Question 3.
A washing powder seller incurs extra cost in order to give free samples to the customers as a sales strategy.
Answre:
Concept : Monopolistic Competition (Selling Cost).
Explanation : In this type of market, there are many sellers who sell the product which are close substitutes of each other.
As there are many variety of washing powders available in the market, he distributes free samples to attract the customers to buy his product.

Question 4.
“A monopoly firm can exercise considerable influence on the supply of his commodity and thereby its price.”
Answre:
Concept : Price Maker (Feature of Monopoly).
Explanation : A monopolist is a single seller in the market for his product and has control over the supply and can determine the price for his product.
There are no close substitutes available for his product in the market.
So, he is a price maker.

[B] Distinguish between :

(1) Perfect Competition and Monopoly.
Answer:
Perfect Competition:

1. Perfect competition is a type of market where there are large number of firms producing homogeneous product.
2. The product sold are homogeneous and so they are perfect substitutes.
3. The firm is a price taker so the demand curve is a horizontal demand curve.
4. There is free entry and free exit.
5. Single price prevails in the whole market.
6. 

Monopoly:

1. Monopoly is a type of market where there is only one firm producing a product which has no substitute.
2. The product has no substitute.
3. The firm is a price maker. Thus firm has a downward sloping demand curve.
4. There are strong entry barriers.
5. Price discrimination is possible because seller has complete hold in the market.
6. 

Question 2.
Perfect Competition and Monopolistic Competition.
Answer:
Perfect Competition:

1. It is a market situation in which there are large number of buyers and large number of sellers selling homogeneous product.
2. Products are perfect substitute for another as they are identical.
3. Uniform price prevails in the whole market. There is no selling cost.
4. Firms are price takers. Thus the firm has a horizontal demand curve.
5. It is an unrealistic market.

Monopolistic Competition:

1. It is a market situation in which there are many buyers and many sellers selling differentiated products.
2. Products are similar but not identical. They are close substitutes.
3. Individual price policy is followed and huge selling cost is incurred on sales promotions.
4. The firms are price makers. Thus the firms have a downward sloping demand curve.
5. It is a realistic market.

Question 3.
Natural Monopoly and Social Monopoly.
Answer:
Natural Monopoly:

1. The monopoly power is acquired by a firm due to natural advantages such as good location, control over scarce resources, natural skill, talent, etc.
2. Natural monopoly is determined by the availability of natural resources or natural talents and skills.
3. Normally the monopolist would charge higher prices for the goods.
4. Main objective is to maximise profit.
5. Gulf countries monopolies in production of oil. India’s monopoly in production of jute and cotton. Lata Mangeshkar monopolised as a professional singer once upon a time.

Social Monopoly / Public Monopoly:

1. When government nationalises an industry and acquires complete control over its market that monopoly is called as social monopoly.
2. Social monopoly is determined by economic aims and objectives of the government.
3. Government may not charge higher prices keeping in mind the welfare aspect.
4. The main objective is to provide social welfare.
5. Public utility services like water supply, railway services etc., are examples of public monopoly.

Question 4.
Natural Monopoly and Legal Monopoly.
Answer:
Natural Monopoly:

1. The monopoly power acquired by a firm due to natural advantages such as good location, control over scarce resources or natural skill, etc.
2. The main objective of a natural monopolist is to maximise profits.
3. Monopoly due to location or may be old establishment like the TATA products or Godrej Locks, Cupboards etc., or an actor like Amir Khan.

Legal Monopoly:

1. It arises due to legal protection given to the producers by the government authorities.
2. The objective is to prevent the competitors from producing identical products.
3. Monopoly due to legal rights, conferred by the government such as patent right, copy right, trade marks etc.

Question 5.
Monopoly and Monopolistic Competition.
Answer:
Monopoly:

1. Monopoly is a market structure in which there is a single seller of a product which has no close substitute.
2. There is no competition.
3. There are strong barriers to entry.
4. The demand for the product is less elastic as there are no close substitute.
5. There is no selling cost incurred.
6. Firm and industry are identical.
7. Pure monopoly is an inelastic market.

Monopolistic Competition:

1. It is a market structure in which large number of firms produce and sell products that are differentiated but close substitutes.
2. There is competition among the firms producing very close substitutes.
3. There is free entry and exit for the firms.
4. Demand of the product is elastic as there are close substitutes for the product.
5. Selling cost has an important role in Monopolistic Market.
6. Under monopolistic competition firm and industry are not identical. They are a group.
7. It is a realistic market.

Question 6.
Perfect Competition and Imperfect Competition.
Answer:
Perfect Competition:

1. Perfect competition is a type of market where there are large number of firms producing homogeneous product.
2. Each seller is price taker.
3. Each individual firm controls only a small portion of the total supply.
4. Each seller and buyer has perfect knowledge about the market situation.
5. There are no types in perfect competitive market.

Imperfect Competition:

1. Imperfect competition is a type of market where the product produced by the sellers may be similar or differentiated.
2. Each seller is price maker.
3. Each seller may control more or less portion of the total supply.
4. Each seller and buyer may not have perfect knowledge about the market situation.
5. Examples of imperfect market are monopoly, oligopoly, monopolistic competition, etc.

Question 7.
Local Market and National Market.
Answer:
Local Market:

1. Local market is one in which goods are produced and sold mostly in local areas.
2. Generally, perishable goods like milk, vegetables and bulky goods like sand have local market.
3. Demand is limited in local market.
4. Less variety is available in this market.

National Market:

1. National Market is a domestic market in which goods are produced and sold within the country.
2. Generally goods demanded by common man like wheat, rice, soaps have national market.
3. Demand is very high in national market.
4. Huge variety is available in this market.

Question 8.
Short Period and Long Period.
Answer:
Short Period:

1. A short period is one during which the stock of a commodity can be changed to some extent.
2. This is done by changing the quantity of variable factors like labour and raw material.
3. Supply can be slightly adjusted to the change in demand.
4. Demand plays more important role in determining the price.
5. This period is usually upto 8-10 months.

Long Period:

1. A long period is one during which the stock of a commodity can be fully changed.
2. This is done by changing the size of the plant because all factors are variable.
3. Supply can be fully adjusted to the change in demand.
4. Supply plays more important role in determining the price.
5. This period is usually form 1 year to 4-5 years.

3. Answer the following questions;

Question 1.
Define market.
Answer:
In economics, ‘Market’ refers to an arrangement through which buyers and sellers come in close contact with each other directly or indirectly for exchange of goods at a particular price. Thus, market is a network of dealings between buyers and sellers.
According to Augustin Cournot, “Economist understand by the term market, not any particular market place in which things are bought and sold, but the whole of any region in which buyers and sellers are in such close contact with one another that prices of the same goods tend to equality, easily and quickly.”

Thus, market is said to exist when –

1. there are many buyers and sellers.
2. they may be spread either to a place, region, country or world.
3. goods are bought and sold at a price.
4. people have the knowledge about market price.
5. there is freedom of entry and exit of firms.

Question 2.
Classify the market on basis of place and explain.
Answer:
On the basis of place, market can be classified as follows :

1. Local Market : When the goods are produced and sold in the local area mainly due to the high transport cost are called local markets. For example bricks, stone, etc. Also perishable goods like fish, milk, etc. have local market.

2. National Market : Market confined to a domestic market in a country is called national market. E.g. cars, scooters, TV sets. These goods can be easily transported within the country.

3. International Market : Goods which can be sold in any part of the world have international market. E.g. Tea, cotton, petroleum. Such goods can be exported and imported at a low transport cost.

Question 3.
Classify the market on the basis of time and explain.
Answer:
On the basis of time market can be classified into following four types :

1. Very short period market: A very short period market is one during which supply of a commodity is fixed as it is already produced. This market is for a few days or maximum a week. So the price of the product is determined by demand. Eg. During festival time supply of fruits can be increased, so price rises.

2. Short period market : A short period market is said be a market upto one year. In this market supply of goods can be increased by increasing the variable factors like labour and raw material with the given fixed factors like machinery.

3. Long period market : A long period market is a market upto five years. In this J supply of a commodity can fully increased on demand as all factors of production can j be changed.

4. Very long period market : A very long period market is for more than five years. In this period there can be full adjustment of supply to demand.

Question 4.
Classify the market on the basis of competition and explain.
On the basis of competition, market can be { classified into two main types :
1. Perfect competition
2. Imperfect competition : It is further classified into.
(A) Monopoly
(B) Oligopoly
(C) Monopolistic Competition

According to Mrs. Joan Robinson, “Perfect competition prevails when the demand for the output of each producer is perfectly elastic. ” Hence, it is a market where there are large number of buyers and sellers engaged in buying and selling a homogeneous product at a single price in the market.
Imperfect competition:

(A) Monopoly: According to E. H. Chamberlin, “A monopoly refers to a single firm which has control over the supply of a product which has no close substitutes.” Hence, he can charge different prices from different buyers on the basis of demand.

(B) Oligopoly : An oligopoly is a market situation in which there are few sellers and a large number of buyers. Sellers may sell similar or different products which are close substitutes of each other.

(C) Monopolistic Competition : According to E. H. Chamberlin, “Monopolistic competition refers to competition among a large number of sellers producing close but not perfect substitutes.” Hence, this is a market which has features of both monopoly and perfect competition. E.g. for soaps, washing powders, etc.

Question 5.
What are the main features of Monopoly?
Answer:
Features of Monopoly:

1. Single Seller and Many Buyers : In
Monopoly market, there is only one seller or producer and many buyers. Monopoly firm does not have a rival in the market. So there is no competition.

2. No Close Substitute : The commodity produced by the monopolist does not have close substitutes. Hence they do not face any competition.

3. Entry Barriers : The fact that there is only one firm under monopoly means that other firms are restricted from entering the market. The entry barriers may be natural, legal or financial in nature.

4. Firm Coincides with Industry : In monopoly market, the firm and industry are one and the same. In other words, there is no distinction between firm and industry.

5. Price Maker : In monopoly the seller is a Trice Maker’. Since the monopolist has control over the supply he can determine the price of his product.

6. Profit Maximisation (super normal profit) : A monopolist earns super normal profit. His decision regarding the price and the level of output are guided by profit maximisation motive.

7. Control Over Supply : The monopolisthas a complete hold over market supply as he is the sole producer.
Price discrimination : This implies charging different prices for the same l product to different buyers.

Question 6.
What are the different types of monopoly?
Answer:
There are different types of monopoly as analysed below:

1. Natural Monopoly : A natural monopoly arises when a particular type of natural resource is located in a particular region like petrol or crude oil in Gulf countries. Also natural advantages such as good location, business reputation, age – old establishment s etc., confer natural monopoly. Similarly, many professional skills, natural talents give monopoly power. E.g. A singer or actor has monopoly of his skill, talent.

2. Legal Monopoly : Legal monopolies are those monopolies which are recognised by law. Legal protection granted by the Government in the form of trade mark, copy rights, license etc., give monopoly power to the firms. Here the potential competitors are not allowed to copy the product registered under the given brand names, patents or trade marks according to the law.

3. Joint Monopoly or Voluntary
Monopoly : This monopoly arises through mutual agreement and business combinations like the formation of cartels, syndicate, trust etc. For e.g. Oil producing nations have come together and formed a Cartel OPEC (Organisation of Petroleum Exporting Countries).

4. Simple Monopoly : A simple monopoly firm charges a uniform price for its product to all the buyers.

5. Discriminating Monopoly : A discriminating monopoly firm charges different prices for the same product to different buyers. E.g. a doctor, a teacher, a lawyer, etc., charges different fees from the people. The practice of charging different prices from different buyers is called “Price discrimination.”

6. Private Monopoly : When an individual or a private firm enjoys the monopoly of manufacturing and supplying a particular product, it is called private monopoly. The main aim of private monopolist is profit maximisation.

7. Public Monopoly : When a field of production is solely owned, controlled and operated by the government, it is regarded as public monopoly. Eg. Public utility service like Railways, Electricity, Water Supply etc. Since these monopolies are service motivated and welfare oriented they are also called welfare monopolies.

Question 7.
What are the features of Oligopoly?
Answer:
The term Oligopoly is derived from the Greek words ‘Oligo’ which means few and ‘Poly’ which means sellers. Hence, following are its features –

1. Many buyers and few sellers : There are many buyers and a few sellers or firms (may be five or six) who dominate the market and have major control over the price of a product.

2. Interdependence : Since the number of firms are less, any change in price, output, product etc. by one firm will affect the rival firms and will force them to change their price, output, etc. E.g. In case of Coke and Pepsi in soft drink market.

3. Selling cost or advertising : Each firm in order to sell more of its product takes aggressive steps to advertise or through free samples. This helps them to capture larger sales.

4. Barrier to entry : The firm can easily exit from the industry whenever it wants, but to enter a new industry it has certain entry barriers like government license, patent right, etc.

5. Uncertainty : There is a great uncertainty in this market if the rival firms join hands and may try to fight each other.

6. Lack of Uniformity : The firms may produce either homogeneous or differentiated products. Eg. In automobile industry, Maruti, Indica are examples of differentiated product but cooking gas of Bharat Petroleum and Hindustan Petroleum are examples of homogeneous product or pure oligopoly.

4. State with reasons whether you agree or disagree with the following statements:

Question 1.
Single price prevails in perfect competition.
Answer:
Yes, I agree with this statement.
Single price prevails under perfect competition because.

1. In perfect competition there are large number of buyers and sellers. A single seller nor a single buyer can influence the supply nor the demand and the price.
2. In perfect competitive market price is determined by the interaction of the forces of demand and supply.
3. Hence sellers and buyers are ‘Price takers’ only.
4. Products sold in perfectly competitive market are homogeneous, and hence uniform or single price rules throughout the market for that product and also there is no selling cost incurred.
5. There is perfect knowledge on the part of buyers and sellers about market conditions, which prevents price – discrimination, so single price prevails.
6. Transport costs are ignored under perfect competition. If transport costs are involved then the prices of homogeneous goods would tend to differ.

Question 2.
Price discrimination is possible under monopoly.
Answer:
Yes, I agree with this statement.
Price discrimination is possible under Monopoly because :

1. Monopoly is a market situation where there is only one seller who has complete control over the supply of commodity.
2. So he is the price maker and also there is no close substitute for his product.
3. Therefore, the buyer has no alternative but to buy the product from the monopolist or go without it.
4. So a monopolist can charge different prices from different buyers for the same product.
5. Generally he charges higher price from rich and lower price frpm poor.
6. E.g. a doctor in a village may charge less fees from poor and high fees from rich.

Question 3.
Selling cost is incurred by a firm in Monopolistic Competition.
OR
In Monopolistic market, the selling cost is must.
Answer:
Yes, I agree with this statement.
Selling cost is incurred by a firm in Monopolistic Competition because –

1. Monopolistic competition is a market where there are many sellers selling differentiated products which are substitutes for each other.
2. So there is an element of ‘Monopoly’ and ‘Competition.’
3. There is keen competition among group of monopolists producing same, though not identical product. So selling costs are incurred to increase the demand for the product.
4. Selling costs are those costs which are incurred by the firms to create demand and increase the demand for its product through advertisements, publicity, salesmanship, etc.
5. The main purpose of selling cost is to push up the sales of the product.
6. The buyers in this market buy the product not by chance but by choice and preference. The advertisements, salesmanship etc can change the preference of the consumer towards their product.

Question 4.
A monopolist cannot control the supply of goods.
OR
Monopolist is price maker.
Answer:
No, I do not agree with this statement. A monopolist can control the supply of goods because –

1. Monopoly is a market situation in which there is a single producer or seller of a product, which has no substitute.
2. It means the entire production and supply of a particular product is in the hands of a single firm. Thus monopoly firm does not have a rival in the market. So he controls the supply.
3. There is no distinction between a firm and an industry under monopoly.
4. He is a price maker and normally fixes a higher price for profit maximisation.

Question 5.
Sellers and buyers are the price takers j in Perfect Competition.
Answer:
Yes, I agree with this statement.

1. In perfect competition, there are large number of sellers.
2. Individual seller contributes only a fraction of the total market supply.
3. Similarly, there are large number of buyers.
4. The individual buyers contribute only a fraction of the total market demand.
5. Thus, a single seller or single buyer cannot influence the market price.
6. The market price is determined by an interaction of market demand and market supply, which has to be accepted by the buyers and sellers.
7. Therefore, a large number of sellers and buyers in a perfect competition are the price – takers.

Question 6.
The existence of Perfect Competition is an unrealistic concept. (Oct.’05)
Answer:
Yes, I agree with this statement.

1. Perfect competition is based on certain fundamental assumptions, which are hard to realise because such ideal conditions are not found in real life.
2. In real economic world, products are not homogeneous. Products are differentiated due to influence of advertisement, difference in quality, design, packing etc.
3. Due to ignorance the buyers and sellers do not possess perfect knowledge of market conditions.
4. This leads to imperfect competition and discriminatory price for identical product.
5. Customs and sentiments, also curtail the freedom of buyers and sellers.
6. Also due to social and moral constraints factors of production particularly labour is imperfectly mobile.
7. For all these reasons perfect competition is a myth. It is an unrealistic market.

Question 7.
Monopolistic Competition is not found in real life.
OR
Monopolistic Competition does not enjoys practical existence. (Mar., ’09)
Answer:
No, I do not agree with this statement.
OR In reality, there is monopolistic competition.
Answer:
Yes, I agree with this statement.

1. In real world we find a market in which the characteristics of both Monopoly and Competition are interwoven.
2. For instance we find in the market many producers producing same product ‘Soap’ but it is not homogeneous.
3. The soap for example produced by Hindustan Lever and ITC and Proctor & Gamble is slightly different in shape, size, fragrance etc., like Lux is different from Dove and Vivel.
4. Each producer is the monopolist in a way of his own brand value but has to face competition from his rival.
5. All these producers compete with each other in selling soaps.
6. Thus monopolistic competition is found in real life.

Question 8.
A seller is a price maker in monopoly.
Answer:
Yes, I agree with this statement.

1. In monopoly market there is a single seller of a product. The aim of the monopolist is to earn maximum profit.
2. Being a single seller, the monopolist has complete control over the market supply.
3. The monopolist can thus have control over the price. He is, thus, a price maker.

Question 9.
Public Monopoly is welfare oriented.
Answer:
Yes, I agree with this statement.

• Public Monopoly is solely owned, operated and controlled by the Government.
• Government owned firm provide utility service. It does not aim at profit but welfare maximisation.
• Utility services like the Railways, banks, water supply etc., if left to the private firms will lead to exploitation.
• This is because such services have inelastic demand, so if it is left to private firm they will charge high prices.

Question 10.
Perishable goods have local market.
Answer:
Yes, I agree with this statement.
Perishable goods have local market because:

• Market confined to a particular area or locality like a village or town is called local market.
• Perishable goods are those goods which last for 2-3 days e.g. Goods like fish, milk, fruits, vegetables, flowers, etc. usually have local market.
• Since, such goods are get destroyed soon and if transported to far off markets places, transport cost would also be high, increasing the cost of goods.
  Hence, perishable goods usually have local market.

Question 11.
Market in Economic is a place where goods are bought and sold.
Answre:
No, I do not agree with this statement.

1. In common language, the term market is generally understood as a place buyers and sellers meet to buy and sell the commodities.
2. For market to exist, there should be arrangement through which buyers and sellers come in close contact with each other directly or indirectly for exchange of goods and services.
3. This exchange may be by way of telephone, tele-marketing, internet all over the world.

5. Answer in detail:

Question 1.
What are the features / characteristics / conditions / assumptions / peculiarities of perfect competition?
Answer:

(1) Perfect Mobility of Factors of Production : Factors of production that is land, labour, capital are perfectly free to move from one firm to another or from one industry to another from one region to another or from one occupation to another. This ensures freedom of entry and exit for individuals and firms.

(2) Single / Uniform Price : There exists a single price for homogeneous product in the entire market at a given point of time. The price is determined by forces of demand and supply.

(3) Large Numbers of ellers : There are many sellers in this market. The number of sellers (firms) are so large that a single seller cannot influence the market price nor the total output in the market (Industry). The contribution of one seller is insignificant and microscopic. The price in the market is determined by the forces of market demand and market supply. Hence, a firm or seller is a ‘price taker’ and not a ‘price maker.’

(4) Homogeneous Product : The products produced by all the firms in the industry are identical and are perfect substitute to each other. The products are identical in shape, size, colour, etc. and hence uniform price rules the market for the product.

(5) Large Number of Buyers : There are large number of buyers in the market. One individual buyer’s demand is only a small fraction of total market demand so he is not in a position to influence the price. He is a price taker.

(6) No Government Intervention : It is assumed that the government does not interfere with the working of market economy. There are no tariffs, subsidies, licensing policy or other government interventions. This non – intervention of government is necessary to permit free entry of firms and automatic adjustment of demand and supply. In short, laissez faire policy prevails under perfect

(7) Perfect Knowledge : There is perfect knowledge on the part of buyers and sellers regarding the market conditions especially regarding market price. As a result no buyer will pay a higher price than the market price and no seller will charge a lower price than the market price. So a single price would prevail for a commodity in the entire market.

(8) Free Entry and Free Exit : There is freedom for new firms or sellers to enter the industry or market. There are no legal, j economic or any other type of restrictions or; barriers for new firms to enter the industry or an existing firms to quit the industry, Entry of new firm usually takes place j when existing firms enjoy abnormal profit. Similarly, existing firms quit the industry when they face losses.

(9) No Transport Cost: It is assumed that all firms are close to the market and hence there  is no transport cost. If the transport cost are added to the price of product then the homogeneous commodity will have different prices depending upon the distance from the place of supply to the market

Question 2.
How is the equilibrium price determined under perfect competition?
Answre:
Under perfect competition price is determined by the two forces of Demand and Supply. The interaction of demand and supply determines the equilibrium price of a commodity in the market. Equilibrium price is that price at which quantity demanded is equal to the quantity supplied. According to Marshall, demand and supply are like two blades of a pair of scissors. Just as the cutting of cloth is not possible without the use of both the blades, the equilibrium price of a commodity cannot be determined either by the force of demand or supply alone. Both together determine the price. This can be explained with the help of a table and a graph.

From the above table, we see that at price of ₹50 and ₹40 per unit, the supply is more than demand. This is because more sellers want to supply at higher prices due to greater profit margin but buyer’s demand is less at a higher price, so there is excess supply (i.e. S >D). Here the number of sellers are more than buyers, the competition among sellers will put a downward pressure on price. The price will fall to ₹30 as a result supply will contract and demand will expand. Now at ?30, the demand becomes equal to supply (D = S). So ₹30 is called the equilibrium price.

Now suppose the market price is ₹10, or ₹20 per unit, which is less than the equilibrium price, the demand is greater i.e. 500 and 400 units than supply which is 100 and 200 units (D > S). There is excess of demand because buyers want to buy more at a lower price but sellers want to sell less as the profit margin is less. Hence there will be shortage of supply. Now, since the buyers are more the competition among buyers will put a upward pressure on the price, so the price rises to ₹30.

Here, some of the sellers will exit the market due to the high cost of production and low market price, which lowers the profit margin. But there will be entry of new buyers with low marginal utility. So demand rises and becomes equal to supply. ₹30 will prevail in the market as long as demand and supply conditions remain the same. It is a stable price where quantity demanded and supplied is 300 units.

When the above demand and supply) schedule is represented graphically, we get S demand curve DD sloping downward and supply curve SS sloping upward.

The demand curve DD intersects the; supply curve SS at point E at which the c equilibrium price determined is OP and OQ is equilibrium quantity demanded and supplied.

If the price is OP₁ which is higher than the equilibrium price OP there is excess s supply i.e. ab. This will force the prices to ( fall downward from seller side. If the price ) falls to OP₂ below the equilibrium price OP there is excess demand i.e. cd. This willforce the price to rise upward. In this way the equilibrium price OP is determined by forces of demand and supply. At equilibrium price quantity demanded is equal to quantity supplied i.e. OQ.

Question 3.
What are features of monopolistic competition?
Answer:
Features of Monopolistic Competition

(1) Fairly large number of Sellers : There are large number of sellers selling closely related, but not identical products. There is tough competition among sellers. An individual seller supply is just a small part of the total supply, so he has limited degree l of control over market supply and price. Each firm (seller) can formulate its own price and output policy independently.

(2) Fairly large number of Buyers: There are large numbers of buyers in a monopolistic competition market. Each buyer enjoys his preference over a particular brand and chooses to buy a specific brand of product. Hence, the buying is by choice and not by chance.

(3) Product Differentiation : The most distinguishing feature of monopolistic competition is that the product produced by different firms are not identical, they are slightly different from each other but they are close substitutes. The product differentiation can be done in different ways like may be in the form of brand names say Raymonds. It can be differentiated in terms of colour, size, design, etc., say soap, mobiles etc., or through sales technique. For e.g. cars, two wheelers, air conditioners, etc.

(4) Free Entry of Firms: A firm is free to enter the market as there are no entry barriers. Similarly there are no restrictions if the firm wants to quit the market. Freedom of entry leads to occurrence of only normal profit in the long run.

(5) Selling Cost : One of the special features of monopolistic competition is the selling cost. Selling costs are those costs, which are incurred by firms to create more and more demand for its products through advertisement, salesmanship, free samples, exhibitions, etc.

(6) Downward Sloping Elastic Demand Curve : The demand curve faced by each firm is downward sloping and comparatively more elastic. It implies that an individual firm can sell more only by reducing the price.

(7) Concept of Group : Under monopolistic competition, Prof. E. H. Chamberlin introduced the concept of group in place of Marshallian concept of industry. Industry means a number of firms producing identical products. A group means a number of firms producing differentiated product, which are close substitutes.

Question 4.
What is monopoly? Explain the features of monopoly.
Answer:
Monopoly: According to E. H. Chamberlin, “A monopoly refers to a single firm which has control over the supply of a product which has no close substitutes.” Hence, he can charge different prices from different buyers on the basis of demand.

Features of Monopoly:

1. Single Seller and Many Buyers : In
Monopoly market, there is only one seller or producer and many buyers. Monopoly firm does not have a rival in the market. So there is no competition.

2. No Close Substitute : The commodity produced by the monopolist does not have close substitutes. Hence they do not face any competition.

3. Entry Barriers : The fact that there is only one firm under monopoly means that other firms are restricted from entering the market. The entry barriers may be natural, legal or financial in nature.

4. Firm Coincides with Industry : In monopoly market, the firm and industry are one and the same. In other words, there is no distinction between firm and industry.

5. Price Maker : In monopoly the seller is a Trice Maker’. Since the monopolist has control over the supply he can determine the price of his product.

6. Profit Maximisation (super normal profit) : A monopolist earns super normal profit. His decision regarding the price and the level of output are guided by profit maximisation motive.

7. Control Over Supply : The monopolisthas a complete hold over market supply as he is the sole producer.
Price discrimination : This implies charging different prices for the same l product to different buyers.

Question 5.
Define perfect competition and explain price determination under perfect competition.
Answer:
According to Mrs. Joan Robinson, “Perfect competition prevails when the demand for the output of each producer is perfectly elastic. ” Hence, it is a market where there are large number of buyers and sellers engaged in buying and selling a homogeneous product at a single price in the market.
Imperfect competition:

Under perfect competition price is determined by the two forces of Demand and Supply. The interaction of demand and supply determines the equilibrium price of a commodity in the market. Equilibrium price is that price at which quantity demanded is equal to the quantity supplied. According to Marshall, demand and supply are like two blades of a pair of scissors. Just as the cutting of cloth is not possible without the use of both the blades, the equilibrium price of a commodity cannot be determined either by the force of demand or supply alone. Both together determine the price. This can be explained with the help of a table and a graph.

From the above table, we see that at price of ₹50 and ₹40 per unit, the supply is more than demand. This is because more sellers want to supply at higher prices due to greater profit margin but buyer’s demand is less at a higher price, so there is excess supply (i.e. S >D). Here the number of sellers are more than buyers, the competition among sellers will put a downward pressure on price. The price will fall to ₹30 as a result supply will contract and demand will expand. Now at ?30, the demand becomes equal to supply (D = S). So ₹30 is called the equilibrium price.

Now suppose the market price is ₹10, or ₹20 per unit, which is less than the equilibrium price, the demand is greater i.e. 500 and 400 units than supply which is 100 and 200 units (D > S). There is excess of demand because buyers want to buy more at a lower price but sellers want to sell less as the profit margin is less. Hence there will be shortage of supply. Now, since the buyers are more the competition among buyers will put a upward pressure on the price, so the price rises to ₹30.

Here, some of the sellers will exit the market due to the high cost of production and low market price, which lowers the profit margin. But there will be entry of new buyers with low marginal utility. So demand rises and becomes equal to supply. ₹30 will prevail in the market as long as demand and supply conditions remain the same. It is a stable price where quantity demanded and supplied is 300 units.

When the above demand and supply) schedule is represented graphically, we get S demand curve DD sloping downward and supply curve SS sloping upward.

The demand curve DD intersects the; supply curve SS at point E at which the c equilibrium price determined is OP and OQ is equilibrium quantity demanded and supplied.

If the price is OP₁ which is higher than the equilibrium price OP there is excess s supply i.e. ab. This will force the prices to ( fall downward from seller side. If the price ) falls to OP₂ below the equilibrium price OP there is excess demand i.e. cd. This willforce the price to rise upward. In this way the equilibrium price OP is determined by forces of demand and supply. At equilibrium price quantity demanded is equal to quantity supplied i.e. OQ.

Balbharti Maharashtra State Board Class 12 Sociology Important Questions Chapter 6 Social Problems in India Important Questions and Answers.

Maharashtra State Board 12th Sociology Important Questions Chapter 6 Social Problems in India

1A. Complete the following statements by choosing the correct alternative given in the brackets and rewrite it.

Question 1.
Several social movements emerged to solve __________ problems. (social, legal, political)
Answer:
social

Question 2.
The problems are a __________ process. (singular, mono, two-way)
Answer:
two-way

Question 3.
An individual problem __________ may rest with the individual. (cause, solution, depth)
Answer:
cause

Question 4.
Lack of education or skills is __________ problem. (group, individual, normal)
Answer:
individual

Question 5.
A social problem is __________ than an individual problem. (same, old, different,)
Answer:
different

Question 6.
People feel the need for collection action to solve the __________ problem. (individual, social, legal)
Answer:
social

Question 7.
__________ is an inevitable and irreversible biological process of life. (Ageing, Workplace, Family)
Answer:
Ageing

Question 8.
The commonest criterion for measuring the process of ageing in an individual is one’s __________ age. (death, chronological, birth)
Answer:
chronological

Question 9.
In India, the age of __________ has been adopted by the Census of India for classifying and categorising ageing population. (50, 60, 70)
Answer:
60

Question 10.
Many ages persons are fully or partially dependent for __________ support on their families. (government, financial, NGOs)
Answer:
financial

Question 11.
The National Policy on older persons was announced in __________ (Jan 1997, Jan 1998, Jan 1999)
Answer:
Jan 1999

Question 12.
__________ are helping to solve the problem of the aged in India. (NGOs, Family, Society)
Answer:
NGOs

Question 13.
Nowadays there are __________ communities which gives support to older persons. (dance, online, sports)
Answer:
online

Question 14.
Many __________ are lacking basic amenities and are impersonal in their care of the inhabitants. (old age homes, family, NGOs)
Answer:
old age homes

Question 15.
The term __________ means, “People who are jobless, actively seeking work and available to take a job”. (Job, Work, Unemployment)
Answer:
Unemployment

Question 16.
According to NSSO, an unemployed person is one who puts in less than __________ hours of paid work in a week. (14, 16, 20)
Answer:
14

Question 17.
Advances in technology have rendered numerous workers unemployed as their __________ has become redundant today. (skill sets, habits, experience)
Answer:
skillsets

Question 18.
When individuals are __________ jobs, there is a period of no employment between one job and the next. (joining, switching, enjoying)
Answer:
switching

Question 19.
During the __________ periods, there are greater chances of workers to lose theirs in the construction sector. (important, boom, lull)
Answer:
lull

Question 20.
__________ of people to urban areas has an effect on urban unemployment. (Demand, Poverty, Seasonal migration)
Answer:
Seasonal migration

Question 21.
As per the Census of India definition, the productive category refers to people within the ages of __________ years. (11-49, 15-59, 20-60)
Answer:
15-59

Question 22.
An unemployed __________ population unable to add value to the economy becomes a burden on the working population. (adult, minor, aged)
Answer:
adult

Question 23.
Lack of __________ may drive people to engage in anti-social activities. (obstacles, jobs, opportunities)
Answer:
opportunities

Question 24.
__________ need to develop mindsets that are open to change. (Ageing, Academics, Addiction)
Answer:
Academics

Question 25.
The __________ programmes must be on choice-based, need-based and learner-centred. (educational, occupational, family)
Answer:
educational

Question 26.
The __________ has laid emphasis on vocational training from the secondary stage upwards. (RUSA, New Pension Policy, New Educational Policy)
Answer:
New Educational Policy

Question 27.
__________ is one measure to minimise the extent of unemployment. (Self-employment, Jobs, Shifts)
Answer:
Self-employment

Question 28.
__________ are a significant percentage of the agrarian workforce. (Farmers, Monsoon, Technology)
Answer:
Farmers

Question 29.
Human intervention has led to increased __________ (problem, pollution, solution)
Answer:
pollution

Question 30.
The emission of greenhouse gases has caused depletion of the __________ layer. (Methane, Butane, Ozone)
Answer:
Ozone

Question 31.
Failure of the crops forces impoverished farmers to live a life in __________ (fun, bury, debt)
Answer:
debt

Question 32.
The psychological burden of being indebted passes on the __________ (next generation, neighbours, relatives)
Answer:
next generation

Question 33.
The __________ are farmers with large landholdings. (Zamindars, Deshmukh, Peasants)
Answer:
Zamindars

Question 34.
In rural India, the custom of __________ has wreaked havoc for farmers. (dowry, debt, ageing)
Answer:
dowry

Question 35.
Farmer’s suicide can dampen the spirit of __________ (trading, domestic work, farming)
Answer:
Farming

Question 36.
__________ insurance should be provided to farmers against crop failure. (Crop, Health, Mediclaim)
Answer:
Crop

Question 37.
Water harvesting and water management will help to channelise the use of __________ resources with great discretion. (natural, water, air)
Answer:
water

Question 38.
To stop the exploitation of farmers removal of the system of __________ is necessary. (debt, insurance, middlemen)
Answer:
middlemen

Question 39.
__________ is an alternative to monoculture. (multi-cropping, water harvesting, domestication)
Answer:
multi-cropping

Question 40.
Domestic violence means within the family. (abuse, suicide, policy)
Answer:
abuse

Question 41.
Victims of domestic violence may need __________ (support, intensive counselling, medicines)
Answer:
intensive counselling

Question 42.
__________ plays an effective role to sensitize the public about domestic violence. (family, peers, media)
Answer:
media

Question 43.
NGOs are backed with services of __________ and __________ departments. (social and moral, fun and fair, legal and police)
Answer:
legal and police

Question 44.
__________ is a situation of psychological or physical dependence on alcohol, drugs, the internet, or mobiles. (Addiction, Ageing, Unemployment)
Answer:
Addiction

Question 45.
Addiction can also lead to __________ behaviour. (social and happy, anti-social and depression, moral and value)
Answer:
anti-social and depression

Question 46.
The addictive element in tobacco is __________ which impacts the brain. (amphetamine, nicotine, cocaine)
Answer:
nicotine

Question 47.
The deadly effects of __________ addiction are mouth, throat and lung cancer. (tobacco, alcohol, cocaine)
Answer:
tobacco

Question 48.
__________ are types of drugs that have the potential to be addictive. (Narcotics, hookah, dhumti)
Answer:
Narcotics

Question 49.
__________ is chewing tobacco known as a carcinogen and is highly addictive. (Pan, Gutka, Chaini)
Answer:
Gutka

Question 50.
__________ addiction is on the rise among teenagers in India. (Smoking, Snacks, Whitener,)
Answer:
Whitener

Question 51.
__________ products are abused throughout the country. (Cannabis, Form, International)
Answer:
Cannabis

Question 52.
According to the present __________, smoking in public places is banned. (Friendly Smoking law, Anti-Smoking Law, Peer Smoking law)
Answer:
Anti-Smoking Law

Question 53.
The minimum age of buying tobacco products is __________ years of age. (14, 16, 18)
Answer:
18

1B. Correct the incorrect pair and rewrite it.

Question 1.
(a) Unacceptable behaviour by several persons – Social problem
(b) Degenerative process – Ageing
(c) Single, without a child, isolated people face the problem of – Loneliness
(d) Due to mechanical lifestyle – Weaker section
Answer:
(d) Due to mechanical lifestyle – Lack of empathy

Question 2.
(a) Role of government – Educational stagnation
(b) Old age homes – Lack of basic amenities
(c) Weaker sections – Women, LGBT
(d) Exploitation – If dependent on others
Answer:
(a) Role of government – To care of the aged

Question 3.
(a) Unemployment – Jobless people
(b) Seasonal shift – Family
(c) Rural unemployment – 5.3%
(d) Urban unemployment – 7.8%
Answer:
(b) Seasonal shift – Agriculture

Question 4.
(a) Switching jobs – Influx of people migration in urban areas
(b) Changing economy – Face lull and the boom period
(c) Gap in demand and supply – Unemployment crisis
(d) Productive age group – 12-70 years
Answer:
(d) Productive of age group – 15 to 59 years

Question 5.
(a) Unutilised human resources – Adult employment
(b) Educational stagnation – Educated but skill-deficient
(c) Anti-Social activities – School
(d) Underemployment – Person with Ph.D. degree works as a clerk
Answer:
(c) Anti-social activities – Lack of opportunities

Question 6.
(a) Industry-Education symbiosis – Farmers
(b) Impact on mental health – Disappointed with life
(c) Academics need to change – learner-centered
(d) New educational policy – Vocational training
Answer:
(a) Industry-Education symbiosis – Industry-University

Question 7.
(a) Entrepreneurship and self-employment – Start-ups
(b) Depletion of the ozone layer – Flood
(c) Farmers – Agrarian workforce
(d) Exploitation of natural resources – Environmental degradation
Answer:
(b) Depletion of the ozone layer – Greenhouse gases

Question 8.
(a) Impoverished farmers – Indebtedness
(b) Unaware of new technologies and method farming – Ignorance
(c) Landless – Labourers
(d) Indebted – Zamindars
Answer:
(d) Large landholdings – Zamindars

Question 9.
(a) Wreaked havoc in farmers life – Dowry system
(b) Criminal offense – Social evil dowry
(c) Health status – Life and Crop insurance
(d) Vidarbha and Marathwada regions – Farmer’s suicide
Answer:
(c) For distressed farmers and crop failure – Life and Crop insurance

Question 10.
(a) Multi-cropping – Monoculture
(b) Middlemen – Operator between farmer and markets
(c) Water harvesting – Use of water resources
(d) Role of Banks – Set the system as farmer-friendly
Answer:
(a) Multi-cropping – Polyculture

Question 11.
(a) Sensitise the public and create awareness – Role of media
(b) Support women, children – Role of NGOs
(c) Empowering LGBT – Role of law
(d) Enforcing law – Personal empowerment
Answer:
(d) Enforcing law – Role of Police

Question 12.
(a) Dysfunctional relationships – Snide remarks, bickering
(b) Traditional and religious outlook – The supremacy of man over women
(c) Gender binary – Family
(d) Heteronormativity – Heterosexism
Answer:
(c) Gender binary – Female and male

Question 13.
(a) Vulnerability – Lack of power, control, and finance.
(b) Victims of domestic violence – Psychological trauma
(c) Psycho-somatic disorder – Bedwetting, irregular menstrual cycle
(d) Section 377 – Role of NGO
Answer:
(d) Section 377 – Empowering LGBT persons

1C. Identify the appropriate term from the given options in the box and rewrite it against the given statement.

Rashtriya Uchchatar Shiksha Abhiyan, Internet addiction, Unemployment crises, Narcotic drugs, Verbal spats, and physical assault, Switching job, Environmental deterioration, Peer pressure, Mobile phone, Cannabis, heroin, Gender discrimination, Educational change, Mobile addiction, Chronological age, Domestic violence, Multi cropping, Seva Dhan Foundation, Mumbai, Individual Problem, Inadequate Skills, Higher longevity, Substance addiction, 15-59 years, Startup, Nicotine, NGOs, Internet, NPCP, Domestic violence, Unutilised human resources.

Question 1.
One’s own habit is the root cause of the problem.
Answer:
Individual problem

Question 2.
Collective action is required to solve the problem.
Answer:
Social problem

Question 3.
The size of ageing population is continuously increasing.
Answer:
Higher longevity

Question 4.
The commonest criterion for measuring the process of ageing.
Answer:
Chronological age

Question 5.
In January 1999 a policy was announced for the matter of well-being of older persons.
Answer:
NPCP

Question 6.
Advances in technology have rendered many workers unemployed.
Answer:
Inadequate Skills

Question 7.
It leads to an influx of people in urban areas.
Answer:
Switching job

Question 8.
More job applications and fewer vacancies.
Answer:
Unemployment crises

Question 9.
As per the census of India, the productive age group.
Answer:
15-59 years

Question 10.
The adult population is unemployed.
Answer:
Unutilised human resources

Question 11.
A young company founded by one or more entrepreneurs to develop a unique product and bring it to the market.
Answer:
Startup

Question 12.
Academics need to develop mindsets that are open to change.
Answer:
Educational change

Question 13.
The salient feature of which is to enable institutions of higher education for capacity building in different fields of employment.
Answer:
Rashtriya Uchchatar Shiksha Abhiyan

Question 14.
Farmers find it difficult to engage in gainful agricultural activity.
Answer:
Environmental deterioration

Question 15.
The practice of growing two or more crops on the same price of land in the same growing season.
Answer:
Multi cropping

Question 16.
It finds in almost all classes, ages, categories, sexes, and genders.
Answer:
Domestic violence

Question 17.
Dysfunctional relationships between different members within the family can lead to.
Answer:
Verbal spats and physical assault

Question 18.
Not acceptable in the 21st century.
Answer:
Domestic violence

Question 19.
They provide legal and professional support to deal with domestic violence cases.
Answer:
NGOs

Question 20.
It’s an outcome of physical and biological dependence on chemical substances.
Answer:
Substance addiction

Question 21.
The addictive element in tobacco impacts the brain.
Answer:
Nicotine

Question 22.
The most frequently abused drugs in India.
Answer:
Cannabis, heroin

Question 23.
It is a means to an entire virtual world and the world of social media.
Answer:
Internet

Question 24.
A constant need to access sites for gaming, adult sites, social media, entertainment and stimulation.
Answer:
Internet addiction

Question 25.
The need to almost constantly be on call.
Answer:
Mobile addiction

Question 26.
One of the reasons for the habit of smoking or doing weed among friends.
Answer:
Peer pressure

Question 27.
De-addiction centres in Maharashtra.
Answer:
Seva Dhan Foundation, Mumbai

Question 28.
Nowadays, it’s a status symbol in society.
Answer:
Mobile phone

1D. Correct underlined words and complete the statement.

Question 1.
Smoking in public places is permissible.
Answer:
Smoking in public places is banned.

Question 2.
The minimum age of buying tobacco products is 14 years of age.
Answer:
The minimum age of buying tobacco products is 18 years of age.

Question 3.
Alcohol is a drink that contains ozone.
Answer:
Alcohol is a drink that contains ethanol.

Question 4.
An addict will try to access the car or vehicle at any cost to which he/she is addicted.
Answer:
An addict will try to access the substance or object at any cost to which he/she is addicted.

Question 5.
Games can also lead to anti-social behaviour and depression.
Answer:
Addiction can also lead to anti-social behaviour and depression.

Question 6.
Tobacco addiction refers to habituated tobacco drinking or swallowing.
Answer:
Tobacco addiction refers to habituated tobacco chewing or smoking.

Question 7.
The deadly effects of mobile addiction are mouth, throat, and lung cancer.
Answer:
The deadly effects of tobacco addiction are mouth, throat, and lung cancer.

Question 8.
Alcohol is a type of drug that has the potential to be addictive.
Answer:
Narcotics are types of drugs that have the potential to be addictive.

Question 9.
Codeine-based tablets continue to be diverted from the domestic market for drug abuse.
Answer:
Codeine-based cough syrups continue to be diverted from the domestic market for drug abuse.

Question 10.
Excessive use of garments diminishes the value of interpersonal relationships.
Answer:
Excessive use of the internet diminishes the value of interpersonal relationships.

Question 11.
Addiction is open Pandora’s box of possibilities.
Answer:
Internet/mobile phones are open Pandora’s box of possibilities.

Question 12.
Domestic violence refers to cooperation within the family.
Answer:
Domestic violence refers to abuse within the family.

Question 13.
In a matriarchal context; there is the unwritten acceptance of male authority.
Answer:
In a patriarchal context; there is the unwritten acceptance of male authority.

Question 14.
Industrialists are a significant percentage of the agrarian workforce.
Answer:
Farmers are a significant percentage of the agrarian workforce.

Question 15.
Farmer’s rebirth is a serious social problem.
Answer:
Farmer’s suicide is a serious social problem.

Question 16.
Animal intervention has led to an increased population.
Answer:
Human intervention has led to an increased population.

Question 17.
The impoverished farmers live a life steeped in money.
Answer:
The impoverished farmers live a life steeped in debt.

Question 18.
The psychological burden at farmers being indebted passes on to the villagers.
Answer:
The psychological burden of farmers being indebted passes on to the next generation.

Question 19.
Bt cotton seeds are cheaper.
Answer:
Bt cotton seeds are more expensive.

Question 20.
The seeds obtained from corn crops cannot be used for the next sowing.
Answer:
The seeds obtained from BT crops cannot be used for the next sowing.

Question 21.
Dowry is a social wealth.
Answer:
Dowry is a social evil.

Question 22.
Employed means “people who are jobless.”
Answer:
Unemployed means “people who are jobless.”

Question 23.
The periodic industrial boom is one of the causes of unemployment.
Answer:
The periodic industrial recession is one of the causes of unemployment.

Question 24.
Typing skills on the age-old manual printer has very limited use in present times.
Answer:
Typing skills on the age-old manual typewriter have very limited use in present times.

Question 25.
Addiction is intrinsic to the organism.
Answer:
Ageing is intrinsic to the organism.

Question 26.
Higher longevity and lower mortality have resulted in a decrease in the ageing population in India.
Answer:
Higher longevity and lower mortality have resulted in an increase in the ageing population in India.

Question 27.
The loss of a spouse or loved one can cause much crowded.
Answer:
The loss of a spouse or loved one can cause much loneliness.

Question 28.
Anxiety and depression are significant among youngsters.
Answer:
Anxiety and depression are significant among the aged.

Question 29.
MGOs have contributed significantly towards helping the problem of the aged in India.
Answer:
NGOs have contributed significantly towards helping the problem of the aged in India.

Question 30.
Social problem is experienced by an individual.
Answer:
Individual problem is experienced by an individual.

Question 31.
The problems are one-way processes.
Answer:
The problems are a two-way process.

2. Write short notes.

Question 1.
Factors responsible for unemployment
Answer:
Unemployment means people who are jobless and actively seeking work and are available to take a job.
There are various factors responsible for employment they are as follows.
Inadequate skills – Advancement in technology has made many workers unemployed as their skill-sets have become redundant today. In short lack adequate skills many people face unemployment.

The frequent shift in jobs – Frequently switching jobs, creates a period of no employment between one job and the next. For example, a farmer may remain unemployed after the harvest season and may have to search for other odd jobs in urban areas.

Changing economy – The world economy has ups and downs that affect the opportunities for employment. For example, the construction and real estate sector is well-known for periods of huge economic activity and lull periods In the lull periods there are greater chances of workers losing their jobs.

Seasonal shift – especially in agricultural fields, banking and shipping industry has an effect on urban unemployment.

The gap in demand and supply – Job aspirants are more but job opportunities are less, which creates unemployment crises. The number of individuals who fit a job is far higher than the openings available.
Above are the factors which are responsible for unemployment.

Question 2.
Effects of unemployment
Answer:
Unemployment means “people who are jobless and actively seeking work and available to take a job.”
The effects of unemployment are as follows:
Unutilised human resources – All individuals are valuable human resources whether they are skilled or unskilled but unutilized human resources become a burden on the working population.

Educational stagnation – Educational stagnation means their training has failed to equip them adequately for the world of work. The government spends crores of rupees on education and yet the educated output is largely skill-deficient or unemployable.

Underemployment – There are many examples of persons who are trained in one field but who work in a totally unrelated area are cases of unemployment. A person with a professional degree or Ph.D. may work as a clerk in absence of suitable employment.

Anti-social activities – Increase in anti-social activities due to lack of opportunities.

Impact on mental health – Those who end up being disappointed with life, studies or trapped in boredom. May become frustrated, develop a negative outlook on life; and even fee-lonely, depressed and suicidal.

Question 3.
Causes of Farmers’ suicide
Answer:
Impact of environmental deterioration – Due to environmental deterioration, farmers face many problems such as crops get completely destroyed and it creates adverse conditions wherein farmers find it difficult to engage in gainful agricultural activity. In India, we have in recent times seen instances of flooding and drought.

Impact of globalization – Dumping of agricultural products in India due to globalization’s free trade policy has adversely affected the pricing of local products.

Indebtedness – Farmers who take loans from government agencies, private individuals or organisations, are often unable to repay loans and their interest if the crops fail for one or more seasons. The impoverished farmers live a life in debt.

The disparity of land holdings – Landless agricultural are the largest section of farmers who depend on others’ land for survival. Hence most farmers in India have small and marginal landholding. Their economic resources are inadequate which compel them to suicide. Most farmers in India have small and marginal landholding. Their economic resources are inadequate.

Dowry system – Farmers take money from institutions or money lenders on the pretext of agricultural needs, but end up utilizing the loans for personal purposes such as giving into dowry demands. This has been seen in the case of suicides in the Vidarbha and Marathwada regions of Maharashtra.

Thus, inability to repay the loans to avoid humiliation and out of depression, a large number of Indian farmers are committing suicide.

Question 4.
Causes of domestic violence
Answer:
Patriarchal system – Patriarchal family is the root cause of domestic violence. There is a huge imbalance of power between men and others in our society. There is the unwritten acceptance of male authority.

Insecurity – Insecurity of one partner, especially of men can lead to feelings of suspicion, the threat to one’s ego, one’s authority, notions of infidelity, etc. which are reasons enough to cause violence and abuse.

Heteronormativity – It refers to the social expectation that human behavior must fit into the gender binary. There are numerous instances of gender discrimination not merely against women, but also transgender persons, and gender non-conforming family members.

Dysfunctional relationships – There are various factors responsible for strains in relationships between different members within the family, which can trigger snide remarks, bickering, labelling, verbal spats, and physical assault.

Question 5.
Measures to tackle addiction problems
Answer:
Creating awareness – The very first measure is to create awareness about various kinds of addiction, via educational programs and camps.

Counselling – It is necessary to recommend people with addiction problems to professionals such as counsellors or psychologists for professional intervention.

De-addiction Clinics – Are professional clinics that work as centres to help addicts through de-addiction which works as a support system for the addicts.

Laws – Legislative provisions for those drug peddlers who upload messages or data which are anti-social, dangerous, life-threatening, and so forth.

Mass media – Mass media is an effective tool to do societal awareness about awareness can be created. Through the World Wide Web.

The above listed are the few measures that we can utilize to tackle the addiction problems.

Question 6.
Social problem
Answer:
A social problem is a condition affecting a significant number of people in ways considered undesirable, able which it is felt that something can be done through collective social action.

Social problems are types of behavior seen as unacceptable by several persons and groups. Such behavior is problematic as it goes against existing social norms or the aspirations of people. People feel the need for collective action to solve the problem.

For example, some of the specific social problems which are widespread in 21st century India are ageing, domestic violence, addiction, gender inequality.

The social problem means a violation of the established norm. It gives rise to stress, strain, tension, and conflicts. The social problem is a universal phenomenon. Although social problems are universal their nature differs from society to society.

3. Write differences.

Question 1.
Mobile/smartphones addiction and Internet addiction
Answer:

Mobile addiction	Internet addiction
(i) Nature: It refers to obsession to mobile phone for various reasons ,and a desire to constantly upgrade one’s mobile phone.	(i) Nature: It refers to a compelling need on the part of an individual to have to continuously access to specific internet sites for personal needs orobsessions.
(ii) Impact: Mobile addiction may cause injuries and deaths due to careless behaviours like speaking on the phone while driving, dangerously posing for selfies, anxiety caused by loss of one’s phone and contacts.	(ii) Impact: Internet addiction increases stress or anxiety in the individual. It affects one’s physical health, interpersonal relationships, personal neglect and access to inaccurate, prejudiced, and exploitative data.
(iii) Nature of problem: Mobile addiction is a problem as it leads to the need to almost constantly be on call, taking selfies or photos, the need to post all images of oneself, forwarding messages etc.	(iii) Nature of problem: Internet addiction is a problem because one constantly needs to access sites for gaming, adult sites, social media, entertainment and stimulation.
(iv) Solution: Self-assessment and social involvement in hobby, sports, games can help overcome mobile addiction.	(iv) Solution: Laws to prevent cyber bullying, counselling, group activity can help overcome the problem of internet addiction.
(v) Effects: Smart phone addiction is often fueled by an overuse of internet.	(v) Effects: Internet addiction results to mobile addiction as it give access to Connectivity, social media networking, gaming, web world etc.

4. Explain the following concepts with examples.

Question 1.
Dowry System
Answer:

• Dowry is any property or valuable security given directly or indirectly to a man by his bride or brides family at the time of her marriage is the exploitation of the women by her in laws. Not only the women (bride) but also her family is held to ransom by demanding dowry.
• The ill-treatment makes the life of the women so miserable that she may take recourse to suicide.
• No consideration is paid to the economic conditions of the bride’s parents who may become bankrupt under the burden of the Dowry Prohibition Act-1961 abolishes practice of dowry.
• Examples: Evil system deeply rooted in people give or take dowry for improving their social prestige.

Question 2.
Substance addiction
Answer:

• Substance Addiction: refers to a physical and biological dependence on chemical substances which leads to unpleasant symptoms when the person stops using the substance.
• Most common addictions involve the use of alcohol, tobacco, other legal and illegal drugs and other mood-altering substances. The use of these may be physically, biologically and psychologically harmful to the user and others. It can also lead to anti-social behaviour and depression.
• The epidemic of substance abuse in the younger generations has assumed alarming dimensions in India. Causes for this are changing values, increasing economic stress and dwindling supportive bonds.
• Example: Abuse of substances such as alcohol, marijuana, cocaine, tobacco, gutka, etc. can cause serious problems with family, friends, the workplace and the law.

Question 3.
Mass Media
Answer:

• Mass media communication is an effective tool to raise societal awareness about addiction.
• The mass media has played a significant role in formulating and influencing public opinion on social issues by disseminating information.
• The world wide web has numerous platforms such as FAQs answered, help lines, help groups etc., through which social awareness can be related.
• Examples: Newspaper, T.V., Radio, Internet

Question 4.
Heteronormativity
Answer:

• Heteronormativity refers to the social expectations of human behaviour; that it must necessarily fit into the ‘gender binary’.
• The ‘gender binary’ is the division of gender into boy/man and girl/woman. Heteronormativity implies that boys/men and girls/women are expected to behave differently, according to the sex as male or female. Thus, their behaviour is understood to fall into two categories:
  • behaviour expected from boys and men
  • behaviour expected from girls and women.
• Those who do not follow these expectations are criticized, made fun of, teased, harassed or even punished. However, today, heteronormativity and its related gender stereotypes are questioned or challenged.
• Example: Examples of heteronormative expectations that are found in society are:
  • boys are strong and courageous
  • Teaching or nursing is a girl’s profession, they can be good caretakers.

Question 5.
Ageing
Answer:
According to Hess ageing is “An inevitable and irreversible biological process of life.”

Ageing is universal, it occurs in all members of the population, unlike disease. Ageing is progressive; it is a continuous process. Ageing is intrinsic to the organism. Ageing is degenerative. In India the size of ageing population is continuously increasing. Higher longevity andl ower mortality have resulted in the increase in the number of ageing population in India.

As one ages, there is a tendency for various parts of the physical body to begin deteriorating. There is a sense of being neglected by others in the family, or even in the neighbourhood leading to loneliness.Many aged are fully or partially dependent for financial support on their families.they may not have access to health care of any kind – for physical or psychological ailments.

Example: The youth, younger adults and care givers may also fail to understand the problems of the aged give rise to the problem of ageing

Question 6.
Start-ups
Answer:

• A Start-up is a young company founded by one or more entrepreneurs to develop a unique product or service and bring it to the market.
• It can get its funding from incubators, they help start-ups get started and running.
• The IT field has given a significant boost to start-ups in India.
• Examples: OLA, Flipkart, Makemy Trip, Shop Clues, Trazoo

Question 7.
Patriarchy
Answer:

• A family wherein the authority rests within the eldest male or in his absence, with the eldest son is called patriarchal family.
• Descent is traced to paternal line. After marriage the woman lives in her husband’s house.
• Property is transferred through the father and only the sons inherit it.
• Patriarchal family is universal.
• Examples: In India majority of families are patriarchal based.

5A. Complete the concept map.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

Question 7.

Answer:

Question 8.

Answer:

Question 9.

Answer:

Question 10.

Answer:

Question 11.

Answer:

Question 12.

Answer:

Question 13.

Answer:

Question 14.

Answer:

5B. State whether the following statements are True or False with reasons.

Question 1.
Problems are a two-way process.
Answer:
This statement is True.

• Problems are of two types individual problem and social problem.
• Individual problem are interconnected with social problem.
• Individuals don’t live in isolation but are part of a larger group, e.g., an individual may have a personal of loneliness. This could be rooted in the fact that the people around her/him have’ isolated her/him due to some reason.
• On the other hand, this same individual may feel lonely because of one’s own peculiar personality traits which the larger group disapproves of. e.g., having excess pride due to one’s self-image.
• Hence problems are a two way process.

Question 2.
Ageing is an artificial and reversible process.
Answer:
This statement is False.

• Ageing is an inevitable and irreversible biological process of life.lt is regular changes that occur in mature genetically representative organisms living under representative environmental conditions as they advance in chronological age.
• Ageing is universal, it occurs in all members of the population, unlike disease. It is progressive; and a continuous process.
• Ageing implies changes in the body and mind of a person along with it’s gradual impact on social life and life style.
• Ageing is intrinsic to the organism and degenerative.

Question 3.
The problems of the ageing leads to social, physical and mental health issues.
Answer:
This statement is True.

• Health concerns – Health includes physical, mental and emotional wellness. As one ages, there is a tendency for various parts of the physical body to begin deteriorating Problems can relate to any physiological/biological problem, such as dental, bones, stomach, heart, hearing, vision etc.
• In addition to physical problems, there are mental health issues revolving around feelings of alienation, conflict, dissatisfaction, disappointment, anxiety, loneliness.
• Psychological problems – Loss of a spouse or loved one can cause loneliness. Inability to do things which one was capable of previously can add to the sense of loneliness. Which is a psychological problem, ageing may also lead to Anxiety and depression accompanied by a sense of guilt; a tendency to feel that one is a burden to one’s family, friends and relatives.
• Social concerns – The aged are forced to do all kinds of work and also subjected to cruelty, abuse, mockery, harassment – from within the family as well as from outside. Elderly/Aged persons may become victims of exploitation especially when they become increasingly dependent on others for all kinds of services.
• Thus, the problems of the ageing leads to social, physical and mental health issues.

Question 4.
Changes made in the content of educational courses will help overcome the problem of unemployment.
Answer:
This statement is True.

• If educational programmes are relevant to community needs, local needs, industrial needs, they will help to develop useful human resources for needs in a changing world.
• There is a need to cultivate skills through education especially those which are employment worthy or those which can promote self-employment, and develop entrepreneurial potential of the learners.
• Vocationalisation will provide options for learner to branch into vocational programmes of study and industry.
• Education symbiosis is encouraged in several institutions in areas of science, engineering, pharmacy, medicine, technology, media studies, fashion designing and management it provides employment opportunities.

Question 5.
Training of many individuals has failed to equip them adequately for the world of work.
Answer:
This statement is True.

• There are many individuals who receive formal training and who continue to remain unemployed. Perhaps their training has failed to equip them adequately for the world of work.
• It is true that many educational are out of touch with the needs of the outside world. Much of what is learnt is knowledge-centric. While the role of knowledge is invaluable, there is a desperate need to also cultivate skills, especially those which can promote self-employment, and develop entrepreneurial potential of the learners.
• The government spends crores of rupees on education and yet the educated output is largely skill-deficient or unemployable.

Question 6.
Lack of employment opportunities may drive people to engage in social activities and a negative impact on national development.
Answer:
This statement is False.

• Lack of employment opportunities may drive people to engage in anti-social activities.
• Several children every year drop out from school system and find themselves engaged in anti-social activities. They do this to make quick and easy money.
• An adult population which is unemployed are unable to add value to the economy but become dependent on others for satisfaction of their needs. They become a burden on the working population.
• Youth and young adults make up the future of our society. Unemployment among them can have a negative effect on national development.

Question 7.
In 21st century a mobile phone is a status symbol.
Answer:
This statement is True.

• It is a fact that sale of mobile phones are even increasing.
• The market is flooded with all kinds of advance mobile phones.
• Advertisements have trapping/encouraging the masses to purchase more sophisticated models, with large memories, battery life, camera and many more.
• Above all proves that now mobile phones is not just a communication gadget but status quo.

Question 8.
Internet and mobile addiction is not a serious problem.
Answer:
This statement is False.

• The impact of mobile addiction is similar to the consequences of internet addiction, both have adverse impact on individuals overusing it.
• A teenager or young adult may spend hours on gaming; an older adult could be obsessed with sex sites.
• Internet addiction becomes a problem when it increases stress or anxiety in the individual affects one’s physical health, diminishes the value of interpersonal relationships, leads to personal neglect, leads individuals to data that is inaccurate, prejudiced, titillating, unreliable and exploitative.
• Similarly, mobile addiction is a problem again, like in the case of internet addiction, it leads to a certain type of behaviour. It may create a need to almost constantly be on call, to almost continuously take selfies or photos of any and everything, an urge to post all images of oneself immediately on social media, the need to keep forwarding messages mindlessly to numerous people and so on.
• Mobile phones and internet can be used for destructive, negative and vested purposes.
• There are many accounts of injuries and deaths due to careless behaviours like speaking on the phone while driving, dangerously posing for selfies, being overemotional in a public space; checking one’s messages during sleep. The consequences take a toll on mental and physical well-being.
• Hence, we can conclude mobile and internet have created serious problems.

6. Give your personal response.

Question 1.
Do you think de-addiction centres play a vital role in the life of addicts. Explain it.
Answer:

• Yes, de-addiction centres play a vital rule in the life of addicts.
• De-addiction centres treats the addicts carefully and monitoring their health. As per the requirement of addicts they give them moderate dosages of drugs for to recovery and to face withdrawal syndrome.
• De-addiction centres make a support system for it to help addicts.

Question 2.
A farmer named Lahanu Tatya Khabale and his joint family have been living in Vidharbha region, Marathwada, Maharashtra for almost five generations. But last year all of a sudden, his grandfather committed suicide. Give possible reasons behind his suicide.
Answer:
As per the latest study of Vidharbha regions many farmers suicide focuses majorly on:

• Crop failure, due to this, many farmers in Vidharbha region are switching to use BT cotton seeds.
• BT cotton seeds provide higher yield but are expensive and require good irrigational facilities, which are not available in
• Lahanu Khabale’s land and on top of that irregular monsoons leads to crop failure.
• Besides this, BT seeds obtained from BT crops cannot be used for the next sowing.
• Due to that Lahanu Khabale was deeply rooted in debt.
• He was also in further debt to private money lenders because he had borrowed money for his daughters dowry.
• Above mentioned economic burdens and social stigma provoked Lahanu Khabale’s grandfather to commit suicide.

Question 3.
Youngsters nowadays pick up various forms of addictions even though they were not exposed to these addictions in their family. Explain how this happens.
Answer:

• Today’s youth have access to a vast array of knowledge i.e., internet.
• Many youngsters get exposed to different forms of addiction on the internet.
• Due to a lack of reliable information they become vulnerable to various forms of addiction i.e., drugs.
• Mostly youngsters aren’t introduced to these addictions through their families, but rather through they’re peers with whom they are closer due to the internet.
• It is mostly these peers who provoke them towards addiction.
• Peer pressure and social acceptance are the main driving forces behind addiction in the youth of today.

7. Answer the following question in detail. (About 150-200 words)

Question 1.
Discuss why domestic violence occur suggest remedial measures to prevent domestic violence.
Answer:
Domestic violence happen across all classes, age, categories, sexes and gender. Domestic violence means abuse within the family. Violence means abuse within the family. Violence implies psychological, emotional, verbal and physical torture.

Domestic violence occur because of various reasons such as

• Patriarchy which demands unwritten acceptance of male authority.
• Insecurity of one partner, can lead to feelings of suspicion causing domestic violence.
• Dysfunctional relationships : strains a relationship .
• Traditional and religious outlook.

Following are some of the measures to prevent domestic violence:

• Creating awareness: It is necessary to create awareness that domestic violence is not acceptable in 21st century society.
• Personal empowerment: Especially weaker section like women, child, transgender who are most vulnerable for abuse. It is necessary for them to empower themselves through Self-Help Groups (SHGs), NGOs, age-mates, social workers and so on.
• Role of media: Various types of media can help for creating awareness and can help to dispel ignorance about domestic violence.
• Role of NGOs: Non-governmental organisations play a vital role for dealing with domestic violence cases. NGOs are backed up with police department, legal professionals all together they can help victims to get justice.
• Role of law: Only laws cannot make changes in the society but legal and constitutional provisions make remarkable changes for empowering individuals.
• Role of police: It is very important that police staff become sensitive and serious about the cases of domestic violence. Today there are women police staff specially assigned to handle issues regarding violence towards women.

Question 2.
“Social problem is universal”, discuss this statement with regards to factors responsible for ‘unemployment’.
Answer:
Social problem is when a society traditional or modern, faces some problems. When people feel the need for collective action to solve the problem, that problem is refer as social problem.
Now we will discuss about unemployment a social problem and factors affecting to it:

• Lack of skills or inadequate skills: Due to technology advancement in industry the workers are lacking with required skills. So, such people face unemployment.
• Switching of jobs: When individual switch the job that time, there is a period of no employment between one job and the next e.g., a farmer who is able to work during the monsoons, may remain unemployed after the harvest season.
• Changing economy: The world economy has its up and downs e.g., real estate sector. Due to global economy industry face lull period and boom period and during lull period there are chances of workers to losing their jobs.
• Seasonal shift: Like the season cycle, in certain sectors employment are facing seasonal period. This is seen in agriculture, banking sectors and shipping industry.
• Gap in demand and supply: India is facing unemployment crisis means number of job vacancies are very less as compare to number of applicants.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 8 Public Finance in India Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 8 Public Finance in India

1. A. Choose the correct option:

Question 1.
Optional functions of Government.
(a) Protection from external attack.
(b) Provision of education and health services.
(c) Provision of social security measures.
(d) Collection of tax.
Options :
(1) b and c
(2) a, b and c
(3) b,c and d
(4) All of the above
Answer:
(1) b and c

Question 2.
Public finance is……………..
(a) one of the old branches of economics, which highlights the role of government
(b) a study of the principles of income and expenditure of the government
(c) also a part of the study of political science
(d) less elastic in supply
Options :
(1) a and b
(2) a, b and c
(3) a and d
(4) b, c and d
Answer:
(2) a, b and c

Question 3.
Non tax revenue includes
(a) Prices of public goods and services
(b) Gifts, Grants and Donations
(c) Goods and Service Tax (GST)
(d) Fines and penalties
Options :
(1) a, b and d
(2) a, b and c
(3) b and d
(4) a and c
Answer:
(1) a, b and d

Question 4.
The examples of revenue expenditure …………..
(a) administration cost of the government
(b) huge investments in different developmental projects
(c) salaries, allowances and pensions of government employees
(d) medical and public health services
Options :
(1) a, b and c
(2) a and b
(3) c and d
(4) a, c and d
Answer:
(4) a, c and d

Question 5.
Reasons for growth in public expenditure.
(a) increase in the activities of the government
(b) rapid increase in population
(c) spread of democracy
(d) industrial development
Options :
(1) a, b and c
(2) b, c and d
(3) a, c and d
(4) a, b, c and d
Answer:
(4) a, b, c and d

(B) Complete the Correlation .

(1) Direct Tax : Wealth Tax :: …………….. : Excise Duty
(2) High degree of credit: Public finance:: Limited Credit: ……………..
(3) Expenditure on education : Developmental expenditure :: War expenditure :……………..
(4) Internal debt : Government borrows from its citizens :: …………….. : Government borrows from World Bank
(5) Surplus budget : Government Receipts Government Expenditure:: ……………..: Government Receipts Government Expenditure
(6) Optional function : Provision of social security :: ……………..: Protection from external attacks
(7) Progressive Tax : Tax rate increases with . increase in income :: ………………. : Tax rate decreases with rise in income :
(8) Old age pension : Revenue expenditure :: Investment in machines : ……………….
Answers:

1. indirect tax
2. Private finance
3. Non-developmental expenditure
4. External debt
5. Deficit budget
6. Obligatory function
7. Regressive Tax
8. Capital expenditure

(C) Give economic terms.

(1) The expenditure which is incurred by the public authority for promoting social and economic welfare.
Answer:
Public Expenditure

(2) A financial statement showing the expected receipts and proposed expenditure of the government in a financial year.
Answer:
Budget

(3) A compulsory contribution to the government by a person without receiving any direct or proportionate benefit in return.
Answer:
Tax

(4) Borrowings of the government from financial institutions within the country.
Answer:
Internal Debt

(5) The financial policy implemented by the government which deals with public expenditure, public revenue and public debt.
Answer:
Fiscal Policy

(6) The type of budget where estimated revenue and expenditure of the government are equal.
Answer:
Balanced Budget

(7) The aggregate collection of income with the government through various sources.
Answer:
Public revenue

(8) It is paid by the tax payer on his income and property.
Answer:
Direct Tax

(9) It is a category of tax which is levied at the same and constant rate on all income.
Answer:
Proportionate tax

(10) Revenue received by the government administration, other than taxes.
Answer:
Non Tax Revenue

(D) Find the odd word out.

(1) Fees, Fines and penalties, Excise duty, Special levy.
Answer:
Excise duty

(2) Revenue expenditure, Capital expenditure, Labour expenditure, Developmental expenditure
Answer:
Labour expenditure

(3) Public expenditure, Public park, Public revenue, Public debt.
Answer:
Public park

(4) Service tax, Entry tax, Entertainment tax, Wealth tax
Answer:
Wealth tax

(5) R.B.I, Foreign Banks, IMF, World Bank
Answer:
R.B.I.

(6) Deficit budget, Zero budget, Balanced budget, Surplus budget
Answer:
Zero budget

(7) Inflation, Depression, Rising prices, Reduce purchasing power
Answer:
Depression

(8) Earthquakes, Floods, Cyclones, Social unrest
Answer:
Social unrest

(9) Public health, Social welfare, Spread of education, Donations
Answer:
Donations

(10) Defence, Infrastructure, Registration fees, Health care
Answer:
Registration fees

(E) Complete the sentences .

Question 1.
Obligatory function of the government includes …………..
(a) provision of education and health services ?
(b) maintaining internal law and order
(c) provision of social security
(d) construction of public park and garden
Answer:
(b) maintaining internal law and order

Question 2.
There is a continuous growth in public expenditure
(a) only because of growing population
(b) only because of increase in defence expenditure
(c) only due to inflation
(d) due to all the above mentioned factors
Answer:
(d) due to all the above mentioned factors

Question 3.
Capital expenditure of the government is ……………
(a) pensions of government employees
(b) administration cost of the government
(c) investment in different developmental projects
(d) war expenditure
Answer:
(c) investment in different developmental projects

Question 4.
The expenditure which results in generation of employment is
(a) development expenditure
(b) non-development expenditure
(c) revenue expenditure
(d) capital expenditure
Answer:
(a) development expenditure

Question 5.
Tax is paid by a tax payer because .
(a) he gets good benefits of it
(b) it is owner’s pride and neighbour’s envy
(c) it is a compulsory contribution to the government
(d) he gets good publicity
Answer:
(c) it is a compulsory contribution to the government

Question 6.
Direct tax is paid by the tax-payer .
(a) on sale and purchase of a commodity
(b) on his income and property
(c) which is levied on goods and services
(d) and shifted to other person
Answer:
(b) on his income and property

Question 7.
In case of regressive tax, the larger the income of a tax-payer.
(a) smaller is the proportion of tax levied
(b) tax is levied at the constant rate
(c) greater is the proportion of tax levied
(d) zero tax is levied
Answer:
(a) smaller is the proportion of tax levied

Question 8.
Special assessment, fines and penalties are examples of
(a) direct tax
(b) indirect tax
(c) non-tax revenue
(d) tax revenue
Answer:
(c) non-tax revenue

Question 9.
External debt of the government means
(a) loans from IMF, World bank, etc.
(b) borrowings from the citizens of a country
(c) borrowings from financial institutions in a country
(d) borrowings from Reserve Bank of India
Answer:
(a) loans from IMF, World bank, etc.

Question 10.
The capital budget consists of
(a) capital receipts and revenue receipts
(b) tax revenue and non-tax revenue
(c) revenue receipts and revenue expenditure
(d) capital receipts and capital payments
Answer:
(d) capital receipts and capital payments

(F) Choose the wrong pair :

I.

Group ‘A’	Group ‘B’
1. Direct Tax	(a) Wealth tax
2. Hugh Dalton	(b) Definition of public finance
3. GST	(c) Non-tax revenue
4. External Debt	(d) Foreign Government

Answer:
(3) – c

II.

Group ‘A’	Group ‘B’
1. Revenue expenditure	(a) Administration cost of Government
2. Capital expenditure	(b) Repayment of Government loan
3. Development expenditure	(c) Expenditure on education
4. Non- developmental expenditure	(d) Expenditure on social welfare

Answer:
(4) – d

III.

Group ‘A’	Group ‘B’
1. Balanced budget	(a) Advocated by Adam Smith
2. Public revenue	(b) expenditure of the government
3. A deficit budget	(c) useful in depression period
4. Surplus budget	(d) Receipts  > Expenditure

Answer:
(2) – b

(F) Choose the right group of pairs :

I.

Group ‘A’	Group ‘B’
1. Budget	(a) Simplifying tax system
2. Financial administration	(b) Use of foreign currency
3. External debt	(c) Annual financial statement
4. GST	(d) Implementation of revenue

Options :
(a) (1) – d, (2) – c, (3) – b, (4) – a
(b) (1) – c, (2) – d, (3) – a, (4) – b
(c) (1) – d, (2) – c, (3) – a, (4) – b
(d) (1) – d, (2) – b, (3) – c, (4)-a
Answer:
(c) (1) – d, (2) – c, (3) – a, (4) – b

II.

Group ‘A’	Group ‘B’
1. Fines and Penalties	(a) Use of domestic currency
2. Tax	(b) Violation of the law
3. internal debt	(c) French word
4. Bougette	(d) Major source of government revenue

Options : (a) (1) – c, (2) – b, (3) – d, (4) – a
(b) (1) – b, (2) – d, (3) – a, (4) – c
(c) (1) – b, (2) – c, (3) – d, (4) – a
(d) (1) – d, (2) – c, (3) – a, (4) – b
Answer:
(b) (1) – b, (2) – d, (3) – a, (4) – c

III.

Group ‘A’	Group ‘B’
(1) Budget	(a) Simplifying tax system
(2) Financial administration	(b) Use of foreign currency
(3) External debt	(c) Annual financial statement
(4) GST	(d) Implementation of revenue

Options :
(a) (1) – c, (2) – d, (3) – b, (4) – a
(b) (1) – c, (2) – b, (3) – a, (4) – d
(c) (1) – b, (2) – c, (3) – d, (4) – a
(d) (1) – d, (2) – c, (3) – b, (4)-a
Answer:
(a) (1) – c, (2) – d, (3) – b, (4) – a

2.[A] Identify and explain the concept from given illustrations.

Question 1.
internal law and order to avoid social unrest.
Answer:
Concept: Obligatory Function.
Explanation : Obligatory functions are those functions which must be performed by government for socio-economic welfare and to avoid social unrest and to establish social justice in a country.

Question 2.
Sanjay paid charges to traffic police for jumping signal.
Answer:
Concept: Fine and penalty
Explanation : The government imposes fines and penalties on those who violate the laws of a country.
Traffic police charges fine and collects money for violating traffic rule.
The objective of taking fine is to discourage the citizens from violating the laws framed by government.

Question 3.
Government of India takes loan from World Bank for Mumbai Metro Train.
Answer:
Concept: External Debt
Explanation : When the government borrows from foreign government or international organisations like IMF, World Bank, etc., it is known as external debt.
Government needs to raise loan for investing in developmental project of a country.
Mumbai Metro Train is a project which require huge investment.
So, Government of India takes loan from World Bank.

Question 4.
Prachi can spend only ₹ 80,000/- though her income is one lakh per month.
Answer:
Concept: Disposable Income
Explanation : Disposable income refers to income which remains with a person after deducting income tax from total personal income.
So, Disposable Income = Total Personal Income – Direct Taxes (income tax)
It indicates actual spending capacity of a person.
Every person is legally bound to pay income tax because it is compulsory to the government.

Question 5.
Government of India borrowed from nationalized bank for construction of bridge.
Answer:
Concept: Internal debt
Explanation : When the government borrows from its citizens or nationalized banks, it is called internal debt.
It means borrowing within a country, for development of infrastructure facilities in a country.
Provision of infrastructure like roads, bridge energy supply, etc., require huge investment.
So, government borrows money in form of internal debt from RBI, nationalized banks or citizens of a country.

Question 6.
Jyoti purchased furniture from mall and paid tax on it.
Answer:
Concept: GST (Goods and Service Tax)
Explanation : GST is a comprehensive tax base with nationwide coverage of goods and services.
It came into effect in India from 1st July, 2017.
It is a tax on goods and services. GST simplified the tax system in a country.

(B) Distinguish between

Question 1.
Deficit Budget and Balanced Budget.
Answer:
Deficit Budget:

1. When the government revenue is less than government expenditure, it is called a Deficit Budget.
2. Deficit Budget would lead to increase in aggregate demand.
3. Deficit Budget leads to flow of money from the government to the economy.
4. It is suitable for government when the economy suffers from depression.
5. The policy of deficit budget would lead to increase in employment, investment, etc.

Balanced Budget:

1. When the government revenue is equal to government expenditure, it is called a Balanced Budget.
2. Balanced Budget would not affect the aggregate demand in the economy.
3. The flow revenue of the government is equal to meet the expenditure of the government.
4. It is not possible to introduce a balanced budget under present circumstances.
5. The balanced budget policy is called “Sound Finance” where the government performs only minimum functions.

Question 2.
Government Revenue (income) and Government Expenditure.
Answer:
Government Revenue (income):

1. Government income refers to the revenue of the government from different sources including tax revenue, non-tax revenue, administrative revenue etc.
2. E.g. Tax revenue including Direct and Indirect Tax.
3. Non-tax revenue include profit from government enterprise administrative revenue like fees, fines, penalties.
4. Generally government income results in transfer of purchasing power from people to government.
5. Surplus income with government indicates sound financial background.

Government Expenditure:

1. Government expenditure refers to the expenditure by government to perform various functions and duties.
2. E.g. Revenue expenditure on health, education, defence and administration.
3. Capital expenditure on roads, railways, dams, machinery and public enterprise.
4. Government expenditure leads to transfer of purchasing power from government to people.
5. Massive expenditure indicates more welfare to people.

Question 3.
Revenue Budget and Capital Budget.
Answer:
Revenue Budget:

1. Revenue Budget consists of
   (1) Revenue Receipts
   (2) Revenue Expenditure
2. It explains how revenue is generated by government and how it is allocated among various expenditure heads.
3. Revenue receipts consists of
   (1) Tax Revenue
   (2) Non-Tax Revenue
4. Revenue expenditure includes developmental and non – developmental expenditure of Central Government.
5. Revenue Receipts do not create any liability of the government.
6. Revenue expenditure does not lead to the creation of assets.

Capital Budget:

1. Capital Budget consists of
   (1) Capital Receipts
   (2) Capital Expenditure
2. It deals with the capital aspect.
3. Capital receipts consists of
   (1) Borrowing
   (2) Recovery of loans
   (3) Disinvestment, small savings
4. Capital expenditure includes expenditure on land and building machinery, investment in shares, loans granted by Central Government to State.
5. Capital receipt create a liability of the government.
6. Capital expenditure leads to the creation of assets.

Question 4.
Surplus Budget and Balanced Budget.
Answer:
Surplus Budget:

1. A Surplus Budget is that type of budget in which the estimated revenue is greater than the estimated expenditure.
2. Government raises tax revenue which is more than what is required for meeting the expenditure.
3. Surplus budget would lead to reduction in aggregate demand.
4. It is suitable for families and not favoured for government.
5. The policy of Surplus Budget would lead to unemployment and recession in the economy. ‘

Balanced Budget:

1. Balanced Budget is a type of budget in which the estimated revenue of the government is equal to estimated expenditure of the government.
2. Government raises revenue to such an extent which is just sufficient to meet the expenditure.
3. Balanced budget would not affect the aggregate demand in the economy.
4. It is not possible to introduce a balanced budget under present circumstances.
5. The balanced budget policy is called ‘Sound Finance’ where the government performs only minimum function.

Question 5.
Deficit Budget and Surplus Budget.
Answer:
Deficit Budget:

1. A deficit budget is one in which estimated expenditure exceeds estimated revenue.
2. It leads to flow of money from government to the economy and increases aggregate demand.
3. It is suitable for governments especially when the economy suffers from depression.
4. The policy of deficit budget would lead to employment and revival of economic activities.
5. Deficit budget is not desirable during inflation.

Surplus Budget:

1. A surplus budget is a budget in which estimated revenue are greater than estimated expenditures.
2. It leads to flow of money from economy to government and lead to decrease in aggregate demand.
3. It is suitable for individuals and families but not favoured for government.
4. The policy of surplus budget would lead to unemployment and recession due to low investment.
5. Surplus budget is advocated during inflation to reduce demand and prices by imposing high taxes.

Question 6.
Revenue Expenditure (Budget) and Capital Expenditure (Budget).
Answer:
Revenue Expenditure (Budget):

1. Revenue expenditure of the government refers to expenses incurred on day-to-day functioning of the government.
2. It is recurring in nature as it is incurred regularly.
3. E.g. administration cost, salary, allowances, pensions of the government employees, etc.
4. It does not create any asset to government.

Capital Expenditure (Budget):

1. Capital expense of the government refers to expenses incurred for the development of a country.
2. It is not recurring in nature as it does not incur regularly.
3. E.g. investment in different developmental projects, loans granted to state government, repayment of loan, etc.
4. It makes addition to the assets of the economy.

Question 7.
Obligatory functions of Government and Optional functions of Government.
Answer:
Obligatory functions of Government

1. Obligatory functions are those functions which must be performed by government, by making adequate provision of resources.
2. Obligatory functions are given first priority, as they are compulsory functions.
3. Obligatory functions are mainly performed by public authority for the protection of their citizen.

Optional functions of Government:

1. Optional functions of government are those functions which may be undertaken by government if funds permit.
2. Optional functions are given second priority, as they are called discretionary functions.
3. Optional functions are performed by central, state and local government for promoting economic activities and social welfare.

Question 8.
Tax revenue and Non-tax revenue.
Answer:
Tax revenue:

1. Tax revenue refers to revenue received by the government through various taxes.
2. Tax revenue comes from direct tax, i,e. income tax, wealth tax and indirect tax, i.e,, G.S.T.
3. Tax is a major source of revenue to the government.
4. Tax revenue particularly direct tax is collected to reduce economic inequality.

Non-tax revenue:

1. Non-tax revenue refers to revenue received by the government from various sources, other than taxes.
2. Non-tax revenue comes from fines and penalties, fees, gifts, grants, donations, borrowings, special levy, etc.
3. Non- tax revenue is not a major source of revenue to the government.
4. Non-tax revenue, particularly special levy, fines and penalties, etc. are collected to discourage the citizens from violating the law.

3. Answer the following questions:

Question 1.
Explain non-tax sources of revenue of the government.
Answer:
Non-tax revenue refers to the revenue received by the government from various , sources other than taxes.
The sources of non-tax revenue are as follows:

1. Fees : It refers to charges paid, in return for certain specific services rendered by the government. E.g. fees paid for registration of house, car, education fees, etc.

2. Prices of Public Goods and Services : Various types of goods and services are produced, supplied and sold by modern government to the citizens. It; is added to public revenue when people s purchase them and pay their prices.

3. Special Assessment : It is special kind of tax, which is levied by local government on the residents of a particular area. In exchange of it, government provides some special facilities to them.

4. Fines and Penalties : It is imposed by government on those who violate the laws of the country.

E.g. a traffic police charges fine and collects money if someone violates traffic rule. The objective behind collection of fines and penalties is not to earn money but to discourage the people from violating the laws framed by the government It is small source of income.

5. Gifts, Grants and Donations : The government receives gifts from its citizens and others. It is included in public revenue. The government may also get grants from foreign government and institutions for general and specific purposes.
Foreign aid is also an important form of public revenue for developing country like India. However, this source of revenue is uncertain in nature.

6. Special Levies : It refers to the charges levied by government on those commodities, whose consumption is harmful to human health.
Special levies are paid for using commodities like wine, opium and other intoxicants. Special levy is imposed, not to earn income, but to discourage the people from using harmful products.

7. Borrowings: Government borrows to raise fund because government expenditure generally exceeds government revenue, in a welfare state.
When government borrows from foreign government or international organisations, it is known as external debt. It is more popular source of public revenue for investment in development of projects. Thus, public revenue in form of non-tax sources play very important role in socio economic development of a country.

Question 2.
Explain the classification of public expenditure.
OR
Explain the budget expenditure of the government.
Answer:
Public expenditure is an important aspect which is incurred by the public authority (central, state and local government). Public expenditure is required for the protection of the citizens of a country, for satisfying social needs or collective needs and for promoting social and economic welfare of the people in a country.

Classification of public expenditure is as under:
(1) Revenue expenditure : It is the expenditure of the government to carry out day-to-day functions. It is recurring in nature. It does not create any assets to government It consists of administrative expenditure, interest payment, pensions and salaries to government employees, etc.

(2) Capital expenditure : It refers to the expenditure of the government for the development of a country.
It consists of huge investment in different developmental projects, repayment of government loans, investment on land, building, machines, etc.
It is non-recurring in nature

(3) Developmental expenditure : The expenditure which results in generation of employment and price stability, it is known as developmental expenditure.

It consists of expenditure on education, social welfare, industrial development, etc. It leads to an increase in production. It is s productive in nature.

(4) Non-developmental expenditure : It is that government expenditure which does not yield any direct productive impact on the economy. It is mainly in form of expenses on administration costs, war expenses, etc. It is unproductive in nature. It is observed that, since last 30 years, there is a tremendous growth in the total public expenditure of a country because modern government performs many functions for the social and economic development of a country.

Question 3.
Explain the structure of Tax-revenue of the government.
Answer:

Tax is a major source of revenue to the Government
According to Prof. Taussig, “The essence of a tax as distinguished from other charges by government is the absence of a direct ‘quid pro quo’ (benefit) between the tax payer and the public authority. ”
Prof. Seligman states that, “a tax is a compulsory contribution from a person to the government, without reference to special benefits confessed. ”
Thus, every citizen of a country is legally bound to pay tax.
Tax is imposed on income, property or commodities and services.

Types of Taxes :

(1) Direct Tax : It is paid by the tax payer on his income and property. A tax-payer cannot transfer the burden of direct tax to others.
Impact and incidence of direct tax falls on the same person. E.g. Income tax, wealth tax, etc.
Direct taxes are further classified into three categories.
(i) Proportionate tax (ii) Progressive tax (iii) Regressive tax

(2) Indirect Tax : It is levied on goods and services. It is paid at the time of production or sale and purchase of a commodity or a service.
The burden of indirect tax can be shifted by the tax-payer (producers) to other persons. Hence, impact and incidence of tax are on others. E.g. GST.
Thus, major share of public revenue is the contribution by tax revenue in India.

Question 4.
Explain GST (Goods and Service Tax) in detail.
Answer:
The GST (Goods and Service Tax) came into effect in India on 1st July, 2017.
It was proposed by the Kelkar Task Force on Implementation of the Fiscal Responsibility and Budget Management (FRBM) Act in July, 2004.
GST is an indirect tax used in India on the supply of goods and services.
GST is comprehensive because it has replaced almost all indirect taxes like excise duty, entertainment tax, entry tax, etc.

GST is classified as follows :

• Central Goods and Service Tax (CGST) : It is a tax levied on interstate supplies of both goods and services by the central government which will be governed l by CGST Act.
• State Goods and Service Tax (SGST): It is received by the state in which the goods and services are consumed and not by the state where they are manufactured.
• Integrated Goods and Service Tax (IGST) : It is a tax levied on all interstate supplies of goods and services which will be governed by the IGST Act.

Benefits of GST :

• Comprehensive tax base with nation wide coverage of goods and services.
• Boost to foreign investments and export.
• Encouragement to manufacturing ‘Make in India’ campaign.
• Improvement in investment atmosphere in a country.
• Tax system in a country simplified.
• Generating more employment and poverty eradication.

Question 5.
Explain the term public debt with its types.
Answer:
Public debt policy of the government plays an important role in public finance.
Public debt refers to borrowings of the government Raising debt loan is the most common activity of a government because in a welfare state, government expenditure generally exceeds government revenue.

Public debt is classified into two types : –
(1) Internal debt : It refers to borrowings of  the government to raise fund within the economy. In case of internal debt, domestic currency is used. It is less complex to manage internal debt. E.g. borrowings from RBI, nationalized banks and business organisations within a country.

(2) External debt : It refers to borrowings of the government to raise fund outside the economy. In case of external debt, foreign currency is used. It is more complex to manage external debt. E.g. borrowings from foreign government and international organisation like IMF, World Bank, etc. Government requires fund for investing in production as well as for making provision of infrastructure facilities.

Thus, public debt is more popular source of revenue for the government in the modern times.

Question 6.
Explain the developmental and non-developmental expenditures of the government.
Answer:
Developmental expenditure : The expenditure which results in generation of employment and price stability, it is known as developmental expenditure.

It consists of expenditure on education, social welfare, industrial development, etc. It leads to an increase in production. It is s productive in nature.

Non-developmental expenditure : It is that government expenditure which does not yield any direct productive impact on the economy. It is mainly in form of expenses on administration costs, war expenses, etc. It is unproductive in nature. It is observed that, since last 30 years, there is a tremendous growth in the total public expenditure of a country because modern government performs many functions for the social and economic development of a country.

Question 7.
Explain the importance of budget.
Answer:
Importance of Budget:
Budget is important in number of ways.

• Tax rates presented in the budget indicates disposable income of the tax payer. It also determines the development of business and individuals.
• Government expenditure is also a part of budget. This public expenditure on defence, administration, infrastructure, education, health care, etc. affects the lives of the citizens and overall economy.
• Government uses budget as a medium for implementing economy policies in the country.
• Budgetary actions of the government affect production size and distribution of income, utilization of human and material resources of the country.
  Thus, implementing suitable budgetary policy is very important for overall development of the economy.

4. State with reasons whether you agree or disagree with the following statements:

Question 1.
Tax is a major source of government revenue.
Ans. Yes, I agree with this statement.
One of the important and major source of public revenue is the tax revenue. A tax is a compulsory payment made by the citizens of the country to the government without any direct quid pro-quo. It implies that a tax has to be paid by all people and it does not involve any corresponding obligation on the part of the government i.e., government need not repay anything. Taxes are of two types (1) Direct Tax (2) Indirect Tax.

Question 2.
In Surplus budget, government revenue is greater than government expense.
Ans. Yes, I agree with this statement.
Surplus budget implies that government’s expected revenue is greater than government’s proposed expenditure.
When there is too much inflation, the government can adopt the policy of surplus budget.
In order to curb inflation, government increases revenue by levying taxes on people.
This reduces the disposable income of people and also consumption.
Since governments spending will be less than its income, aggregate demand will decrease and which will help to reduce the price and control inflation.

Question 3.
For the period of depression, deficit budget is prepared.
Answer:
Yes, I agree with this statement.
Deficit budget is one where the estimated government expenditure is more than the l expected revenue.
Normally developing countries have deficit budget.
During depression, it is used as a stabilizing tool to control economic fluctuation.
Recession occurs mainly due to lack of effective demand.
So increase in government expenditure tends to increase the income of people.
As a result, the aggregate demand increases, which will help in reducing unemployment and expanding the economic activities in the economy.
Therefore, for the period of depression deficit budget is prepared. s

Question 4.
The surplus budget creates inflationary pressure in the economy.
Answer:
No, I do not agree with this statement.
The deficit budget creates inflationary pressure in the economy.
Deficit Budget is one where the estimated government expenditure is more than expected revenue.
In order to meet the deficit, the government generally resorts to (a) borrowings from Central Bank (b) borrowings from
Commercial Banks (c) issue of new currency of the government.
This leads to increased supply of money.
As the government spend this money, there is excess supply of money without corresponding increase in the production of goods and services in short period.
As a result the prices of goods and services begin to rise.
Thus, the deficit budget creates inflationary pressure in the economy.

Question 5.
Revenue receipts and revenue expenses are known as revenue budget.
Answer:
Yes, I agree with this statement.
Revenue Budget explains how revenue is generated by the government and how it is allocated among various expenditure heads. Revenue receipts of government refers to income, which is received by government from all sources i.e., tax and non-tax revenue. These receipts do not create a liability. Revenue expenditure is the expenditure incurred for the normal running of government departments and various services.
They neither create any asset nor cause reduction in any liability of the government. E.g. expenditure on defence, police, medical public health, education, transport, etc.

Question 6.
Public finance and Private finance are same.
No, I do not agree with this statement.
There is a difference between public finance and private finance.
Public Finance : Public finance refers to income an expenditure of public authorities. The objective of public finance is to offer maximum social advantage. More credit is available in the market to increase public finance. The supply of public finance is more elastic. In case of public finance, government first determines the volume and different ways of it’s expenditure.

Private Finance : Private finance refers to income and expenditure of individual and private sector organisations. The objective of private finance is to fulfil private interest. Credit availability is limited to increase private finance. The supply of private finance is less elastic. In case of private finance, an individual considers income first and then determines the volume of expenditure.

Question 7.
There is a continuous growth in public expense in India.
Answer:
Yes, I agree with this statement.
In a developing country like India, public expense is continuously increasing.
The modern government has to perform many obligatory as well as optional functions for the social and economy development of a country.

These functions include spread of education, public health, public works, infrastructure facilities, public recreation, social welfare schemes, protection of a country, industrial development, etc.
Old functions are being performed more efficiently and new functions are added i continuously.
In addition to this, many natural and man made calamities occur frequently. So, government has to spend a huge amount for ; disaster management.
So, there is a continuous growth in the public expense in India.

Question 8.
During the period of inflation, surplus budget is advisable.
Answer:
Yes, I agree with this statement.
During inflationary period, price of commodities rises rapidly.
This rise in price can be controlled by lowering the level of effective demand in the economy.
This can be done by increasing taxes which will automatically reduce the purchasing power of the people, which will result in fall of aggregate demand.
The fall in aggregate demand will lead producers and sellers to reduce the price of l their products to increase their sale.
Thus, inflationary pressure is controlled by adopting surplus budget.

5. Study the following table figures passages and answer the following :

1.

Trends in Public Expense
Sr. No.	Year	Total Expense (Rs. in crores)
1	1991-92	72,317
2	2001-02	3,62,450
3	2005-06	5,06,123
4	2009-10	10,24,487
5	2015-16	11,95,025
6	2016-17	13,74,203
7	2017-18	14,35,233
8	2018-19	17,29,682

Question 1.
What was the total public expense in the year 2009-10?
Answer:
In the year 2009-10, the total public expense was ? 10,24,487 crores.

Question 2.
Calculate the difference between public expense of 1991-92 to 2001-02.
Ans. The difference between public expense of 1991-92 and 2001-02 is ? 2,90,133 crore (3,62,450 – 72,317).

Question 3.
Observe the trends in public expense from 2015 to 2019.
Ans. The year 2018-19 shows greater trend in public expense.

Question 4.
What is the tendency of trends in public expense, shown in the given table?
Ans. The given table shows that, there is a tremendous growth in the total public expense of the country over the period of time.

(2) Read the given passage and answer the questions :

“The conventional notion of social security is that the government would make periodic payments to look after people in their old age, ill-health, disability and poverty. This idea should itself change from writing a cheque for the beneficiary to institutional arrangements to care for beneficiaries, including by enabling them to look after themselves, to a large extent.
The write-a-cheque model of social security is a legacy from the rich world at the optimal phase of its demographic transition, when the working population was numerals enough and earning enough to generate the taxes to pay for the care of those not working. This model is ill-suited for less, well-off India with growing life expectancy, increasing urbanization and resultant migration. Social security under urbanization will be different from social security in a static society.

Question 1.
State the conventional notion of social security.
Answer:
The conventional notion of social security is that the government would make periodic payments to look after people in their old age, ill-health, disability and poverty.

Question 2.
What kind of conceptual change is suggested in the given paragraph?
Answer:
The given paragraph suggests that, the idea should change from writing a cheque for the beneficiary to institutional arrangement to care for beneficiaries.
It will enable them to look after themselves to a large extent.

Question 3.
WTiat is a legacy of social security from the rich world?
Answer:
The write-a-cheque model of social security i is a legacy from the rich world.

Question 4.
Which features of India make the traditional model of social security illsuited for the economy?
Answer:
Growing life expectancy, increasing urbanization and resultant migration are the features of India that make the traditional model of social security ill suited for the economy.

6. Answer in detail:

Question 1.
Explain the various types of Government budget (Union budget).
Answer:
There are three types of government budget:
(1) Balanced Budget, (2) Surplus Budget and (3) Deficit Budget.
(1) Balanced Budget : Balanced budget is a situation in which estimated revenue of the government during the year is equal to its anticipated expenditure.

For individuals and families, it is always advisable to have a balanced budget, s Classical economist advocated Balanced
Budget, which was based on the policy of “live-with-in means”. According to them i government’s revenue should not fall short of expenditure.

They favoured balanced budget because they believed that government should not interfere in economic activities and should just concentrate on the maintenance of internal and external security and provision of basic economic and social overheads.

Till 1930 generally accepted norm was that of ‘Sound Finance’ which implied that public authority should balance its budget. But the great depression of 1930’s proved that Balanced Budget was not a guarantee of stability and full employment. It was then realised that the government can play an effective role in recovery of the economy. This is because if governments expenditure exceeds its revenue, it will generate additional demand which will accelerate the pace of economic growth. It was Keynes who gave a new approach to the budgetary policy, he replaced the norm of Balanced Budget with the norm of functional finance.

(2) Surplus Budget: A surplus budget implies when the expected government revenue is greater than proposed government expenditure.
Surplus budget shows the financial soundness of the government. When there is too much inflation, the government can adopt the policy of surplus budget as it reduces aggregate demand by spending less than its income.
In periods of inflation, although there is greater employment, there is also a tendency for prices to rise rapidly. This can be checked. The inflationary gap can be corrected by lowering the level of effective demand in the economy. It can be corrected by increasing taxes. This will reduce the purchasing power of the people but increase the revenue of the government. Thus aggregate demand will fall. The inflationary gap can be corrected by lowering the level of public expenditure.

When Government reduces its expenditure the revenue with government is in excess of its expenditure.
In modern times, governments responsibilities have increased. Surplus budget will mean that the government instead of spending for the welfare of the people is busy earning and accumulating wealth. Hence, surplus budget practically is non-existing.

3. Deficit Budget: Deficit budget is one where the estimated government expenditure is more than expected revenue. Today almost all the countries of the world follow deficit budget instead of surplus or balanced budget.
Deficit Budget solves the problem of recession and depression which occurs mainly due to lack of effective demand. Increase in total expenditure of the government, increases employment and income of the people. As a result, the aggregate demand for consumer goods increases. Increase in total expenditure tends to expand aggregate economic activity in the economy.

Question 2.
Explain components or scope of public finance in India.
OR
Explain the main components of budget.
Answer:
Public finance is one of the most important branches of economy. It highlights the role and functions of the government Government has to perform various functions like protection from external attack, generation of employment, protection of property, maintaining law and order, provision of collective needs, etc.

To perform these functions efficiently, any government needs finance which can be received from various sources.
Public finance deals with the study of principles of income and expense of the government.
The structure of public finance can be explained as follows:

The Components or Scope of Public Finance

(A) Public Expenditure : It refers to that expenditure which is incurred by the public authority (Central, State and Local Government) for promoting economic and social welfare of a country.
Public expenditure is classified as follows:

(a) Public Expenditure : It refers to expenditure on day-to-day functioning of the government. E.g. administration cost, salary allowances and pensions of government employees, etc.
It is incurred regularly but it does not create any assets to government.

(b) Capital Expenditure : It refers to the expenditure for the development of a country. E.g. investment by government in projects, provision of infrastructure, repayment of loan, etc. It does not incur regularly but it makes addition to the assets of the economy.

(c) Developmental Expenditure : It refers to that expenditure of the government, which gives productive impact to the economy.
It results into generation of employment, increase in production, etc.

(d) Non-developmental Expenditure : It refers to that government expenditure which does not yield any direct productive impact on the economy. E.g. war expenditure.
It is unproductive in nature.

(B) Public Revenue : It refers to aggregate collection of income with the government through various sources. They are classified as:
(a) Tax Revenue
(b) Non-tax Revenue

(a) Tax Revenue : There are two types of taxes collected by the government. They are as follows:

Direct tax : Direct tax is that tax which is paid by a person on whom it is legally s imposed. E.g. income tax, wealth tax, etc.
Direct tax can be proportionate – (constant rate of tax on all incomes), progressive (rate of tax increases with an increase in income) or regressive (rate of tax declines ) with rise in income. In India, we have progressive tax rate system.

Indirect tax : Indirect tax is that tax which ( is imposed on one person but can be paid by the other, e.g. GST.

A taxpayer cannot shift the burden of direct tax to others, however, in case of indirect tax, tax burden can be shifted to others.

(b) Non-tax Revenue : Non-tax revenue refers to the revenue received by the government from various sources other than taxes.

Public expenditure is an important aspect which is incurred by the public authority (central, state and local government). Public expenditure is required for the protection of the citizens of a country, for satisfying social needs or collective needs and for promoting social and economic welfare of the people in a country.

Classification of public expenditure is as under:
(1) Revenue expenditure : It is the expenditure of the government to carry out day-to-day functions. It is recurring in nature. It does not create any assets to government It consists of administrative expenditure, interest payment, pensions and salaries to government employees, etc.

(2) Capital expenditure : It refers to the expenditure of the government for the) development of a country.
It consists of huge investment in different developmental projects, repayment of government loans, investment on land, building, machines, etc.
It is non-recurring in nature

(3) Developmental expenditure : The expenditure which results in generation of employment and price stability, it is known as developmental expenditure.

It consists of expenditure on education, social welfare, industrial development, etc. It leads to an increase in production. It is s productive in nature.

(4) Non-developmental expenditure : It is that government expenditure which does not yield any direct productive impact on the economy. It is mainly in form of expenses on administration costs, war expenses, etc. It is unproductive in nature. It is observed that, since last 30 years, there is a tremendous growth in the total public expenditure of a country because modern government performs many functions for the social and economic development of a country.

(C) Public Debt:

Tax is a major source of revenue to the Government
According to Prof. Taussig, “The essence of a tax as distinguished from other charges by government is the absence of a direct ‘quid pro quo’ (benefit) between the tax payer and the public authority. ”
Prof. Seligman states that, “a tax is a compulsory contribution from a person to the government, without reference to special benefits confessed. ”
Thus, every citizen of a country is legally bound to pay tax.
Tax is imposed on income, property or commodities and services.

Types of Taxes :

(1) Direct Tax : It is paid by the tax payer on his income and property. A tax-payer cannot transfer the burden of direct tax to others.
Impact and incidence of direct tax falls on the same person. E.g. Income tax, wealth tax, etc.
Direct taxes are further classified into three categories.
(i) Proportionate tax (ii) Progressive tax (iii) Regressive tax

(2) Indirect Tax : It is levied on goods and services. It is paid at the time of production or sale and purchase of a commodity or a service.
The burden of indirect tax can be shifted by the tax-payer (producers) to other persons. Hence, impact and incidence of tax are on others. E.g. GST.
Thus, major share of public revenue is the contribution by tax revenue in India.

(D) Fiscal Policy : It is the means through s which government adjusts its spending’s c and tax rates. It helps to monitor and influence nation’s economy. It deals with public expenditure, public revenue and l public debt.
Thus, it is the financial policy implemented by the government.

(E) Financial Administration : It implies I an efficient implementation of revenue, external and debt policy of the government. It includes preparation and implementation of the government budget along with overall economic growth of a country.

 

Budgetary actions of the government affect production, size and distribution of income and utilization of material and human resources of a country. Thus, the scope of public finance is important in a modern economy.

Balbharti Maharashtra State Board Class 12 History Important Questions Chapter 1 Renaissance in Europe and Development of Science Important Questions and Answers.

Maharashtra State Board 12th History Important Questions Chapter 1 Renaissance in Europe and Development of Science

1A. Choose the correct alternative and rewrite the statement.

Question 1.
__________ means ‘Rebirth’.
(a) Reformation
(b) Renaissance
(c) Revival
(d) Rejuvenation
Answer:
(b) Renaissance

Question 2.
The first crusade began in the year __________
(a) 1096
(b) 1097
(c) 1098
(d) 1099
Answer:
(a) 1096

Question 3.
__________ is said to have mentioned the sunspots (Tamas Kilakas) in his treatise ‘Brihatsamhita’.
(a) Ibn Batuta
(b) Varahamihir
(c) Alberuni
(d) Arya Bhatt
Answer:
(b) Varahamihir

Question 4.
Edmund Cartwright invented the __________
(a) telescope
(b) printing press
(c) steam engine
(d) power loom
Answer:
(d) power loom

Question 5.
__________ invented the steam engine.
(a) James Watt
(b) Thomas Bell
(c) Robert Fulton
(d) George Stephenson
Answer:
(a) James Watt

Question 6.
__________ landed at the port of Calicut in 1498.
(a) Ferdinand Magellan
(b) Vasco da Gama
(c) Capt. James Cook
(d) Mungo Park
Answer:
(b) Vasco da Gama

Question 7.
__________ is considered to be the father of ‘Hydraulics’.
(a) Ibn Batuta
(b) Amir Khushrow
(c) Alberuni
(d) Abul Fazl
Answer:
(c) Alberuni

1B. Find the incorrect pair from group ‘B’ and write the corrected one.

Question 1.

Group ‘A’	Group ‘B’
(a) Galileo	Telephone
(b) Thomas Bell	Cylinder for printing
(c) Robert Fulton	Steamboat
(d) George Stephenson	Steam engine for transport

Answer:
Galileo – Telescope

Question 2.

Group ‘A’	Group ‘B’
(a) Marco Polo	India
(b) Amerigo Vespucci	Venezuela
(c) Samuel de Champlain	Quebec
(d) Mungo Park	Western Africa expedition

Answer:
Marco Polo – China

2A. Write the names of historical places/persons/events.

Question 1.
Two cities considered holy by Jews, Christians, and Muslims
Answer:
Jerusalem and Bethlehem

Question 2.
Sultan of Egypt who defeated the crusaders by conquering Jerusalem
Answer:
Sultan Saladin

Question 3.
The highest authority of the Catholic Church
Answer:
The Pope

Question 4.
The first printing press was started by
Answer:
Johannes Gutenberg

Question 5.
Author of the epics ‘Iliad’ and ‘Odyssey’
Answer:
Homer

Question 6.
The King who gave trading permission to Vasco da Gama
Answer:
Zamorin

Question 7.
The book written by Louis Antony da Bougainvillea
Answer:
Voyages Around the World

Question 8.
The methodology used in Zoology to classify animals is called
Answer:
Taxonomy

2B. Choose the correct reason from those given below and complete the sentence.

Question 1.
The ‘Medieval’ Period is called ‘Renaissance’ because __________
(a) it saw advances in various fields of life
(b) people wanted change
(c) the rulers imposed restrictions on their thinking
(d) people were tired of fighting wars
Answer:
(a) it saw advances in various fields of life

Question 2.
The ‘Crusades’ was a failure because __________
(a) the Pope and the rulers initiated the wars for their own vested interests
(b) common people losing faith
(c) there was a rift between the Pope and the European rulers
(d) of all of the above reasons
Answer:
(d) of all of the above reasons

Question 3.
The European colonies in the African continent increased because __________
(a) Europeans wanted to settle in Africa
(b) it was rich in diamonds, gold, and copper
(c) the cold climate of Europe made them migrate to Africa
(d) Human labour was very expensive in Europe
Answer:
(b) it was rich in diamonds, gold, and copper

Question 4.
Industrial revolution took place in England because __________
(a) the atmosphere was suitable for the industrial revolution in England
(b) the other nations were weak to compete with England
(c) mechanized production did not take place in the other nations
(d) England wanted to prove her superiority
Answer:
(a) the atmosphere was suitable for the industrial revolution in England

3A. Observe the map on textbook page 05 and answer the questions based on it.

Question 1. Name the ocean that lies in the northern hemisphere.
Answer:
The Arctic

Question 2.
Name the ocean that lies in the southern hemisphere.
Answer:
The Antarctic

Question 3.
Who circumnavigated the earth?
Answer:
Ferdinand Magellan

Question 4.
In which continent lies the Cape of Good Hope?
Answer:
Africa

Question 5.
Where did Vasco da Gama land in India in 1498?
Answer:
Calicut (Kozhikode)

Question 6.
After whom is ‘America’ named?
Answer:
Amerigo Vespucci

3B. Complete the following concept map.

Question 1.

Inventors	Inventions
Galileo	…………………………….
……………………….	Power Loom
James Watt	……………………………
……………………….	Spinning Mule

Answer:

Inventors	Inventions
Galileo	Telescope
Edmund Cartwright	Power Loom
James Watt	Steam Engine
Samuel Crompton	Spinning Mule

Question 2.

Answer:

4. Write Short Notes.

Question 1.
Inventions and Discoveries during the Renaissance period.
Answer:

• In 1543 C.E., Nicolaus Copernicus told the world that the centre of our planetary system is the ‘Sun’ and not the ‘Earth’.
• In 1609, Galileo prepared a sophisticated telescope that supported the theories propounded by Copernicus and Kepler.
• This facilitated research in physical sciences.
• Inventions of gunpowder and printing brought about changes in the techniques of warfare and dissemination of knowledge.
• In the world of printing, the first printing press was started by Johannes Gutenberg in 1440 and the first printing press started in Italy in 1451.

Question 2.
Roman Church.
Answer:

1. In the pre-renaissance period, the Roman church not only controlled the religious life of the people but also the individual life.
2. It exploited the common people in the following ways-
   • By issuing mandates for payments of fees.
   • Put restrictions on free-thinking and its circulation.
   • Anyone who dared to interpret Bible was sentenced to death.
3. The humanist philosophy was instrumental in making a ground for resistance against the powerful church.

Question 3.
Ibn Batuta.
Answer:

• He was a sailor and a famous medieval traveler.
• Ibn Batuta visited several countries like India, Maldives, Sumatra, China, Spain, Sardinia, East, and West Africa.

Question 4.
Alberuni.
Answer:

• accompanied Sultan Mahmud of Ghazni during his visit to India.
• tried to estimate the diameter of the earth.
• determined the latitudes and longitudes accurately.
• prepared a map of the earth indicating its round shape.
• considered as the father of ‘Hydraulics’.

5. Explain the following statements with reasons.

Question 1.
The rise of ‘Economic Nationalism’ was an outcome of the industrial revolution.
Answer:

• Arresting the growth of rival nations along with pursuing the growth of one’s own nation became important.
• Putting economic restrictions on rival nations by devising ways.
• For e.g. Prohibiting the import-export transactions of other countries, levying heavy toll duties on their goods, establishing colonies mainly in Asia and Africa, and fighting with the natives were part of the economic nationalism.
• Thus, economic nationalism led to imperialism.

Question 2.
The number of European colonies in the African continent increased.
Answer:

• The continent was rich in diamonds, gold, and copper.
• It was also rich in fertile land, timber, and forests.
• Later the Portuguese captured them and sold them as slaves.
• Cheap human labour was the need of the Europeans.
• This increased the demand for African slaves and helped them to expand the slave trade.

Question 3.
Galileo is known as the ‘Father of Empirical Sciences’.
Answer:

• Galileo established the rational method of empirical observation and forming a theory based on those observations.
• He proved that the speed of objects of different weights falling down is equal by carrying out actual demonstrations from the heights of the tower of Pisa in Italy.
• He triggered a revolution with his modified telescope which benefited the seafarers to a large extent.
• With his telescope, he discovered four major satellites of the planet Jupiter.
• He proved that there are mountains and valleys on the moon and the light emitted from it are actually the rays of the sun.
• He also calculated that the sun takes 27 days to complete one cycle around itself.
• He was also the first scientist to observe spots on the sun.
• Hence, Galileo is known as the ‘Father of Empirical Sciences’.

6. State your opinion.

Question 1.
Scientific inventions in various fields.
Answer:

• The compass, the barometer, telescope, and the thermometer were invented during this period.
• Microscopes were invented to observe various types of micro-organisms.
• Robert Boyle, an alchemist discovered that that the absolute pressure and the volume of a gas are inversely proportional.
• The research in physics was more focused on heat and sound.
• In zoology, a methodology known as ‘Taxonomy’ was developed to classify animals.
• Benjamin Franklin’s research was on lightning and electricity. He coined many technical terms which are used in science even today.

Question 2.
Galileo is known as the ‘Father of Empirical Sciences’.
Answer:

• Galileo established the rational method of empirical observation and forming a theory based on those observations.
• He proved that the speed of objects of different weights falling down is equal by carrying out actual demonstrations from the heights of the tower of Pisa in Italy.
• He triggered a revolution with his modified telescope which benefited the seafarers to a large extent.
• With his telescope, he discovered four major satellites of the planet Jupiter.
• He proved that there are mountains and valleys on the moon and the light emitted from it are actually the rays of the sun.
• He also calculated that the sun takes 27 days to complete one cycle around itself.
• He was also the first scientist to observe spots on the sun.
• Hence, Galileo is known as the ‘Father of Empirical Sciences’.

Question 3.
In the pre-renaissance period, the Roman Church controlled both the religious as well as the individual life of the people.
Answer:

1. In the pre-renaissance period, the Roman church not only controlled the religious life of the people but also the individual life.
2. It exploited the common people in the following ways-
   • By issuing mandates for payments of fees.
   • Put restrictions on free-thinking and its circulation.
   • Anyone who dared to interpret Bible was sentenced to death.
3. The humanist philosophy was instrumental in making a ground for resistance against the powerful church.

7. Answer the following questions in detail.

Question 1.
Write a detailed note on the industrial revolution in England.
Answer:
‘Industrial Revolution’ indicates the transition from manual production to mechanized production.

• In England, the atmosphere was suitable for the industrial revolution.
• Large amounts of iron ore and coal were available.
• The humid climate of England was suitable for producing yarn.
• These conditions proved to be favourable for the textile industry in England.
• England had also established a large number of colonies by then so England could obtain raw material at cheap rates from these colonies.
• England could also export the processed goods and sell them in their colonies with large profit margins using their navy.
• The availability of cheap labour made it possible for them to maintain an optimum level of costs.
• These factors prepared the ground for the industrial revolution in England thus giving a boost to its economy.
• Because of the above reasons Industrial revolution first began in England.

8. Answer the following questions with the help of given points.

Question 1.
Discuss the scientific inventions that took place in the following fields.
(a) Textile Industry
(b) Metallurgy
Answer:
(a) Textile industry:

• In the year 1738, John Kay made and patented the ‘flying shuttle’ which increased the speed of weaving.
• The ‘spinning jenny’, a spinning frame with multiple spindles were made by James Hargreaves in England. It reduced the amount of labour and time of production.
• In the year 1769, Richard Arkwright made a more advanced spinning frame. It could produce yarns much faster.
• Samuel Crompton invented the ‘spinning mule’ in 1779 C. E..This machine increased the speed of producing cloth two hundred times.
• In 1785, Edmund Cartwright invented the power loom.
• In 1793, a machine called the ‘cotton gin’ was introduced. This machine separated cotton seeds from cotton fibres at a greater speed.

(b) Metallurgy:

• England had a number of iron mines.
• Therefore, it was necessary to advance the technique of smelting iron to acquire purified iron from it.
• The fuel for iron furnaces was replaced from wood to coal.
• Special machines were made to keep the furnaces at a set temperature and to maintain their aeration.
• In 1865, the process of producing steel from molten iron was invented and the nature of the iron industry underwent a major transformation.
• At about the same time, a method was adopted to pour the molten metal into casts for making iron bars (e.g. rails).

Question 2.
Give an account of the geographical discoveries made by the following explorers
(a) Marco Polo
(b) Henry the Navigator
(c) Bartholomew Dias
(d) Christopher Columbus
Answer:
(a) Marco Polo: An Italian traveller who introduced China and other Asian countries to Europe. He stayed at the royal court of Kublai Khan where he studied Mongolian and Chinese languages.

(b) Henry the Navigator: He was the prince of Portugal in the 15th century. He encouraged people to carry out expeditions which resulted in the discovery of ‘Madeira’ and ‘Azores’, two archipelagos near Africa. These are the autonomous regions of Portugal. The Portuguese transported the African people to Portugal and sold them as slaves. The Portuguese also brought African gold with them.

(c) Bartholomew Dias: Dias began his expeditions on the orders of the king of Portugal, John II. He reached the southern tip of Africa which he named the Cape of Storms. Later on, the name was changed to ‘Cape of Good Hope. He was the first to circumnavigate the African continent.

(d) Christopher Columbus: The eastern sea route was closed to the Europeans and it became necessary to search for an alternative trade route to reach Asia. With the help of King Ferdinand and Queen Isabel of Spain, Christopher Columbus, an Italian explorer set sail in search of India. He, however, reached the islands near America instead of India.

Balbharti Maharashtra State Board Class 12 Sociology Important Questions Chapter 1 Introduction to Indian Society Important Questions and Answers.

Maharashtra State Board 12th Sociology Important Questions Chapter 1 Introduction to Indian Society

1A. Complete the following statements by choosing the correct alternative given in the brackets and rewrite it.

Question 1.
Law of _________ is also known as the law of cause and effect. (artha, dharma, karma)
Answer:
karma

Question 2.
_________ is the ultimate goal of salvation according to Hinduism. (Moksha, Artha, karma)
Answer:
Moksha

Question 3.
_________ refers to the acquisition of wealth through the path of righteousness through hard work. (Moksha, Artha, karma)
Answer:
Artha

Question 4.
Ahimsa and tapas are integral components of the _________ way of life. (Jain, Hindu, Buddhist)
Answer:
Jain

Question 5.
The society in the _________ Vedic period was less rigid with respect to occupation-based divisions. (Later, Early, Medieval)
Answer:
Early

Question 6.
_________ advocated an austere and strict lifestyle based on penance. (Jainism, Buddhism, Hinduism)
Answer:
Jainism

Question 7.
_________ is the sacred literature of Buddhism. (Puranas, Tripitkas, Vedas)
Answer:
Tripitkas

Question 8.
_________ promoted the spread of Buddhism across ancient Asia. (Akbar, Harshvardhan, Ashoka)
Answer:
Ashoka

Question 9.
The _________ period is the period of history of ancient peninsular India. (Ancient, Sangham, Vedic)
Answer:
Sangham

Question 10.
_________ do not permit proselytisation. (Zoroastrianism, Judaism, Islam)
Answer:
Zoroastrianism

Question 11.
The _________ movement brought religious reform in Hinduism during the medieval period. (Peasant, Tribal, Bhakti)
Answer:
Bhakti

Question 12.
Some important exponents of _________ are Kabir, Rahim and Guru Nanak. (Jainism, Sufism, Buddhism)
Answer:
Sufism

Question 13.
During the early Vedic period, those women who pursued their education until they were married were known as _________ (Sadyavadhu, Brahmavadinis, Sola Sati)
Answer:
Sadyavadhu

Question 14.
In the _________ Vedic period, the caste system became entrenched. (Early, Later, Medieval)
Answer:
Later

Question 15.
The _________ Vedic period witnessed a decline in the status of women in society. (Early, Later, Medieval)
Answer:
Later

Question 16.
_________ Jains believe that the principle of nudity is an essential element in the path of liberation. (Digambara, Swetambara, Hinayana)
Answer:
Digambara

Question 17.
The _________ learnt the art of warfare and administration. (Shudras, Kshatriyas, Brahmins)
Answer:
Kshatriyas

Question 18.
Education during the medieval period is centred on the _________ (Vedas, Bible, Quran)
Answer:
Quran

Question 19.
_________ included comprehensive study of the Quran. (Maktabs, Madrasas, Khanqahs)
Answer:
Madrasas

Question 20.
_________ literature makes reference to tribes and traditional castes. (Sangham, Vedic, Puranic)
Answer:
Sangham

Question 21.
_________ referred to the four stages in the life of a Hindu. (Purusharthas, Ashramvyavastha, Varna)
Answer:
Ashramvyavastha

Question 22.
Path of knowledge is _________ marg. (Bhatki, Jnana, Raja)
Answer:
Juana

Question 23.
Sadhus are people who choose the path of _________ (Bhatki, Jnana, Asceticism)
Answer:
Asceticism

Question 24.
The _________ Dynasty believed to be the “Golden Age”. (Maurya, Gupta, Kushan)
Answer:
Gupta

Question 25.
_________ wrote on astronomy and astrology during the classical period. (Aryabhatta, Varahamihira, Dhanvantri)
Answer:
Varahamihira

Question 26.
_________ wrote on medicine during the classical period. (Aryabhatta, Varahamihira, Dhanvantri)
Answer:
Dhanvantri

Question 27.
_________ wrote on geometry and cosmology. (Aryabhatta, Varahamihira, Dhanvantri)
Answer:
Aryabhatta

Question 28.
During the _________ society experienced a synthesis of Indian and Islamic culture. (Maurya dynasty, Gupta dynasty, Delhi Sultanate)
Answer:
Delhi Sultanate

Question 29.
_________ gave India a strong and stable political administration. (Akbar, Ashoka, Chandragupta Maurya)
Answer:
Akbar

Question 30.
_________ is referred to as first urbanisation. (Harappa, Mesopotamia, Malwa)
Answer:
Harappa

Question 31.
The small Indo-Aryan chieftaincies are called _________ (Mahajanpadas, Janapadas, Republics)
Answer:
Janapadas

Question 32.
In the year _________ the Suez Canal was opened to promote trade interests. (1869, 1969, 1828)
Answer:
1869

Question 33.
The _________ century saw the emergence of the Indian National Congress. (18th, 19th, 20th)
Answer:
19th

Question 34.
The abrogation of Article _________ in August 2019 gave special status to Jammu and Kashmir. (371, 370, 374)
Answer:
370

Question 35.
The Juvenile Justice Act was passed in the year _________ (2019, 2015, 2005)
Answer:
2015

Question 36.
The Transgender Persons Act was passed in the year _________ (2019, 2015, 2005)
Answer:
2019

1B. Correct the incorrect pair and rewrite it.

Question 1.
(a) Doing one’s duties – Dharma
(b) Sensuous pleasure – Kama
(c) Acquisition of wealth – Dharma
(d) Ultimate goal of salvation – Moksha
Answer:
(c) Acquisition of wealth – Artha

Question 2.
(a) Priests, teachers, intellectuals – Brahmin
(b) Rulers and warriors – Jajman
(c) Menial work – Shudra
(d) Traders, farmers – Vaishya
Answer:
(b) Rulers and warriors – Kshatriya

Question 3.
(a) Studenthood and celibacy – Brahmacharyaashram
(b) Householder – Grihasthashram
(c) Hermithood and retirement – Dharmashastras
(d) Renunciation – Sanyasashram
Answer:
(c) Hermithood and retirement – Vanaprasthashram

Question 4.
(a) Path of Knowledge – Moksha Marg
(b) Path of Devotion – Bhakti Marg
(c) Path of Meditation – Raja Marg
(d) Path of Action – Karma
Answer:
(a) Path of Knowledge – Jnana Marg

Question 5.
(a) Skyclad – Digambaras
(b) White clad – Shvetambaras
(c) Lesser vehicle – Hinayana
(d) Greater vehicle – Vajarayan
Answer:
(d) Greater vehicle – Mahayana

Question 6.
(a) Advisory and supervisory powers – Sangham priests
(b) Nomadic ballad singers – Khema
(c) Hunter and highway robbers – Vedars
(d) Warrior section – Marrakudi
Answer:
(b) Nomadic ballad singers – The Bards

Question 7.
(a) Sultans and their relatives – Aristocrats and nobles
(b) Ulemas and Brahmin – Peasants
(c) Urban wealthy merchants, traders – Townspeople
(d) Rural agriculturalists – Peasants
Answer:
(b) Ulemas and Brahmin – Priests

Question 8.
(a) Brahmo Samaj – Raja Rammohan Roy
(b) Arya Samaj – Swami Dayanand Saraswati
(c) Prathana Samaj – Mahatma Jyotirao Phule
(d) Harijan Sevak Sangh – Mahatma Gandhi
Answer:
(c) Prathana Samaj – Aatmaram Pandurang

Question 9.
(a) The Sati Prohibition Act – 1829
(b) The Indian Slavery Act – 1843
(c) The Caste Disabilities Removal Act – 1850
(d) The Hindu Widow Remarriage Act – 1870
Answer:
(c) The Hindu Widow Remarriage Act – 1856

1C. Identify the appropriate term from the given options in the box and rewrite it against the given statement.

Puranas, Purusharthas, Jati System, Vardhaman Mahavir, Sola Sati, Ardhamagadhi, Jainism, Holy Sabbath, Din-i-Ilahi, Langar, Brahmo Samaj, Social Legislations, Dr. B. R. Ambedkar, Viharas, Buddhism, Animism, Guru Granth Sahib, Lopamudra

Question 1.
Tribal belief system.
Answer:
Animism

Question 2.
Code of Conduct based on the Law of Karma.
Answer:
Puranas

Question 3.
The four aims of Hindu life.
Answer:
Purusharthas

Question 4.
It is based on the principle of “purity and pollution”.
Answer:
Jati system

Question 5.
24th Tirthankar of Jainism.
Answer:
Vardhaman Mahavir

Question 6.
The language of teachings of Mahavir.
Answer:
Ardhamagadhi

Question 7.
It advocated an austere and strict lifestyle based on penance.
Answer:
Jainism

Question 8.
It spread because of the patronage of the Mauryan emperor, Ashoka.
Answer:
Buddhism

Question 9.
A sacred observance of Jews.
Answer:
Holy Sabbath

Question 10.
A religion started by Akbar.
Answer:
Din-i-Ilahi

Question 11.
The sacred literature of Sikhs.
Answer:
Guru Granth Sahib

Question 12.
The Punjabi term for a community kitchen.
Answer:
Langar

Question 13.
One of the notable Vedic and Upanishadic woman scholars.
Answer:
Lopamudra

Question 14.
It highlights exemplary religious qualities which are emulated as role models by Jain women.
Answer:
‘Sola Sati’

Question 15.
Buddhist monasteries.
Answer:
Viharas

Question 16.
It refers to laws passed to promote social justice.
Answer:
Social Legislation

1D. Correct underlined words and complete the statement.

Question 1.
Widow remarriage was permitted in the Later Vedic period.
Answer:
Widow remarriage was permitted in the Early Vedic period.

Question 2.
The Yajur Veda states that “all classes have an equal right to study the Veda”.
Answer:
The Atharva Veda states that “all classes have an equal right to study the Veda”.

Question 3.
Those who never married and continued studying and imparting education throughout their lives were known as Sadyavadhu.
Answer:
Those who never married and continued studying and imparting education throughout their lives were known as Brahmavadinis.

Question 4.
Puducherry had gained prominence and formed the base of the Mauryan Empire.
Answer:
Magadha had gained prominence and formed the base of the Mauryan Empire.

Question 5.
The drainage system is one indicator of the collective life of the Harrapan people.
Answer:
The Great Bath is one indicator of the collective life of the Harrapan people.

Question 6.
Great Traditions include folk art, folklore, and the religious traditions of the local people.
Answer:
Little Traditions include folk art, folklore, and the religious traditions of the local people.

Question 7.
The period c.500 BCE to c.200 BCE is considered the period of First urbanization’.
Answer:
The period c.500 BCE to c.200 BCE is considered the period of Second urbanization’.

Question 8.
The Portuguese entered India for trade in the 17th century CE.
Answer:
The Portuguese entered India for trade in the 16th century CE.

Question 9.
The implementation of the Judiciary system during the time of the British was carried out on a traditional basis.
Answer:
The implementation of the Judiciary system during the time of the British was carried out on a secular basis.

Question 10.
The Wahabi Movement was the Initiative of Behramji Malabari.
Answer:
The Wahabi Movement was the Initiative of Syed Waliullah.

Question 11.
The Constituent Assembly of India was founded on 6th December 1947.
Answer:
The Constituent Assembly of India was founded on 6th December 1946.

Question 12.
The Female Infanticide Prevention Act was passed in the year 1870.
Answer:
The Female Infanticide Prevention Act was passed in the year 1872.

Question 13.
The Narcotic Drugs and Psychotropic Substances Act was enacted in the year 1920.
Answer:
The Narcotic Drugs and Psychotropic Substances Act was enacted in the year 1985.

Question 14.
The economic growth of India until recently was guided by Planned Development, through ten Five-Year Plans till 2017.
Answer:
The economic growth of India until recently was guided by Planned Development, through twelve Five-Year Plans till 2017.

2. Write short notes.

Question 1.
Education during the Later Vedic period.
Answer:
During the Later Vedic period, women were denied access to the Upanayana ceremony, which then denied them access to learning. There was an emphasis on the institution of sacrifice and this led to the growth of large amounts of literature related to sacrifice. The first millennium CE saw the disintegration of tribal units and chieftains were overthrown. In this situation of hopelessness emerges asceticism as a means for salvation from worldly life which was now preached by the Upanishads.

In eastern parts of India, there was the rise of free speculation and the emergence of humanitarian and theistic movements, which in turn led to new centers of spiritual leadership – the ascetics and wanderers (Sramanas or Parivrayakas) who rejected the authority of the Vedas and of Vedic priests. They criticized blood sacrifices which became a part of Brahminic ritual and gave importance to the practice of ahimsa or non-injury of living beings.

After Mahavir became a Kevalin (omniscient), a Jina (conqueror), and Mahavir (a great hero), he now became part of the sect called Nirgranthas, which came to be referred to as Jainas (following of Jina). Mahavir was a religious teacher for three decades.

Buddha borrowed and adapted from the popular beliefs of the region. The Buddhist system of education was conducted through Buddhist monasteries (viharas). The center of the Buddhist system of learning revolved around the Order (Sangh) of monks (bhikkus); later Buddha permitted the entry of women as nuns (bhikkhunis). Religious instruction was imparted in the viharas and like the Brahmanical system of education, there was a special relationship between the learner and teacher; the student had to live with the teacher (Upajjhaya or Acharya) and serve him.

Just as Vedic culture centred on sacrifices, Buddhist education and learning revolved around monasteries. Education in the Sangham period was a widespread social activity. It was a secular factor and not the privilege of any one community. Works on grammar, poetry, mathematics, astronomy, and fine arts (music, dance, drama, painting, sculpture), and architecture were the specializations.

The decline of Buddhist Viharas resulted in the decline of an organized system of education.

Question 2.
Nature of education during Medieval Period.
Answer:
Education during the Medieval Period is centred on the Quran. Without the ability to read and write, it would have been impossible to study the Quran, the Hadith, and other sciences. The Prophet Mohammed exhorts all people of faith to acquire knowledge.

However, unlike the previous systems of learning, there was no requirement for the strictness associated with Vedic schools nor renunciation (rejection) of the world. The Islamic system of education is open to all followers of the faith irrespective of one’s status.

Education was imparted in three ways:

• Maktab (for elementary education)
• Madrasa (for higher learning and generally attached to a mosque)
• Khanqah (theological training)

Maktabs had an age of admission around four years, which was marked by a religious ceremony. Early training focused on the R’s of learning – reading, recitation, writing, and arithmetic. The study of the Quran would start from around age seven.

Madrasas included a comprehensive study of the Quran and its commentary by established theologians alongside practical subjects like agriculture, accountancy, astrology, astronomy history, geography, mathematics, Islamic law and jurisprudence and statecraft i.e., the art of administration) and languages such as Arabic and Persian. Akbar enabled the study of Sanskrit and Upanishads for Hindu students who wished to learn at the Madrasa. The education was based upon the political, social and economic needs of the community at large. Students had the freedom to choose subjects according to one’s interests and their aims in life.

Post-madrasa training could be followed up by engaging the services of a learned teacher (for example, Abdul Qadir Badaoni, Abul Fazl, Faizi). Madrasas provided facilities for residence for both, students and teachers. In this regard, they were similar to Buddhist Viharas and temple colleges of South India from after the 7th century CE. Khanqahs can be linked to monasteries of Medieval Europe and they were often linked to the tombs of celebrated, much loved, and respected saints. These came to be regarded as Dargahs.

In the course of time, the arts themselves came to be influenced by the tast.es, ideas, and interests of the patrons, namely, Muslim rulers in Medieval India.

During the Medieval Period, education suffered a setback due to changed political circumstances. Educational work was carried out in the villages and towns by private individuals and institutions. The mediums of instruction were Sanskrit, Arabic, and Persian. Education, however, was made available to only a small section of people e.g., the elite and the ulema, the Brahmins, and a few upper caste groups. The education of girls was perceived as being a personal matter to be decided by their fathers or guardians. Women from the Muslim nobility were permitted to receive education in their homes at the hands of teachers who were presented with expensive gifts. Since, only a relatively small number of people belonging to the upper strata of society, it is reasonable to assume that the education of girls and women during the Medieval period was bleak.

Question 3.
Urbanisation during the ancient and medieval periods.
Answer:
The archaeological evidence from the Harappan civilization suggests that Harappa was indeed a well-planned town with a ‘way of life that can be referred to as ‘first urbanisation’. The city had a covered drainage system and a well-developed drainage system underground. The social conditions were well-advanced like other contemporary civilizations.

Towards the end of the Later Vedic period, after the pastoral and nomadic Indo-Aryans spread from Punjab to the Gangetic Plain; they deforested large areas of land to pave way for agriculture.

The period c.500 BCE to c.200 BCE is considered the period of ‘second urbanisation’ which brought a large-scale beginning of town life in the middle Gangetic basin. Magadha had gained prominence and formed the base of the Mauryan Empire.

Sixteen monarchies and “republics” known as Mahajanpadas, stretched across the Indo- Gangetic Plain from modern-day Afghanistan to Bengal and Maharashtra.

This period saw the second major rise of urbanism in India after the Harappan civilisation. Evidence for it comes through archaeological excavations, especially those of the Northern Black Polished Ware (NBPW) culture. Jain, Buddhist, and Sutra literature are among the important sources of information about cities and socio-political life of this period.

The beginning of coinage (metallic coins) started in this period. These cities became the centres of administration as well as of trade and commerce. This led to the emergence of city-based artisan and merchant guilds. A network of routes for internal and distant trade developed in both eastern and western regions. The position of ‘king’ gained much strength and respect the king was assisted by ministers and officials, who often came from the Brahmin and Kshatriya caste.

Question 4.
Religious beliefs and practices during the ancient and medieval periods.
Answer:
The impact of three ancient indigenous religions – Hinduism, Jainism, and Buddhism are significant especially up to the end of the Later Vedic period. The Vedic period is usually divided into – Early Vedic Period (c.1500 BCE to c.1000 BCE) and the Later Vedic Period (c.1000 BCE to c.500 BCE).

For Hindus, the Puranas and Dharmashastras laid out a Code of Conduct based on the Law of Karma (Action) rebirth, until it can attain moksha (salvation). The four aims of Hindu life (Purusharthas) are:

• Dharma
• Kama
• Artha
• Moksha

Jainism is said to have been revealed by 24 Tirthankaras of which Vardhaman Mahavir was the last. Similar to the Hindu Doctrine of Karma, Jain teachings are also based on the Theory of Karma. However, ahimsa (non-harming) and tapas (penance) are important and integral components of the Jain way of life. Buddha, with his teachings, advocated the middle path based on the Four Noble Truths and the Eightfold Path.

The Medieval Period (c. 650 CE – c. 1500 CE), saw several religions come to India from outside. These include Judaism, Christianity, Islam, and much later Zoroastrianism. The Sangham Period (6th century BCE to 3rd century CE) is the period of the history of ancient peninsular India.

The roots of Zoroastrianism are found in the Middle East region. People of the Jewish faith are believed to be one of the early foreign religions to come to India. It is in the 1st century CE that Saint Thomas, an Apostle of Jesus Christ, brought Christianity to the shores of Malabar in South India the essential foundation of the Christian faith is the principle of love and all Christians believe in the Death and Resurrection of Jesus Christ, their Saviour.

Islam first came to India in the 8th century CE, the impact and influence of the religion is seen only much later. Like Judaism and Christianity, Islam also preaches monotheism, and the faith centers on the Holy Quran. Muslims believe in the Five Pillars of Faith.

Sikhism emerged in the late 15th century CE and was founded by Guru Nanak (1469 CE – 1539 CE). Like Hinduism, Jainism, and Buddhism, Sikhism too preached the Karma theory.

The Bhakti Movement emerged with the need to bring religious reform in Hinduism during the medieval period.

Question 5.
The Islamic system of education.
Answer:
The Islamic system of education is open to all followers of the faith irrespective of one’s status.

Education was imparted in three ways:

• Maktab (for elementary education)
• Madrasa (for higher learning and generally attached to a mosque), and
• Khanqah (theological training)

Maktabs had an age of admission around four years, which was marked by a rite of entry. Early training focused on the R’s of learning – reading, recitation, writing, and arithmetic.

Several hours were spent on developing the art of writing. The study of the Quran would start from around age seven.

Madrasas included a comprehensive study of the Quran and its commentary by established theologians alongside practical subjects like agriculture, accountancy, astrology, astronomy, history, geography, mathematics, Islamic law and jurisprudence and statecraft (i.e., the art of administration) and languages such as Arabic and Persian (which were languages also taught elsewhere in the contemporary Islamic world). Noted scholar Abul Fazl informs us that Akbar enabled the study of Sanskrit and Upanishads for Hindu students who wished to learn at the Madrasa. The education was based upon the political, social and economic needs of the community at large students had the freedom to choose subjects according to one’s interests and their aims in life.

Khanqahs can be likened to monasteries of Medieval Europe and they were often linked to the tombs of celebrated, much loved, and respected saints. These came to be regarded as Dargahs.

Education of women: Muslim rulers at the imperial capitals at Delhi and Agra did not do anything remarkable for the promotion of the education of women.

The education of girls was perceived as being a personal matter to be decided by their fathers or guardians. Women from the Muslim nobility were permitted to receive education in their homes at the hands of teachers who were presented with expensive gifts.

Art: In the course of time, the arts themselves came to be influenced by the tastes, ideas, and interests of the patrons, namely, Muslim rulers in Medieval India. The mediums of instruction were Sanskrit, Arabic, and Persian. Education, however, was made available to only a small section of people e.g., the elite and the ulema, the Brahmins, and a few upper caste groups.

Question 6.
Zoroastrianism.
Answer:
The roots of Zoroastrianism are found in the Middle East region. Persecution of the people of this faith brought them to the Western coast of India, near present-day Gujarat, into which they culturally assimilated.

Zoroastrianism is the only outside religious community that still practices endogamy; it did not permit proselytization i.e., conversions into their faith. Fire temples are their place of worship and entry into their Fire temples is restricted to members of the community.

It is one of the world’s oldest and continuously practiced religions. It is centered on a dualistic cosmology of good and evil (Heaven and Hell).

Their sacred scripture is Avesta in which it is stated that the supreme creator is Ahura Mazda, from whom Asha (cosmic order) originates. Fire and clean water are agents of ritual purity. The Holy Flame was brought by priests from Persia to Navsari in Gujarat (c. 9th century CE).

While maintaining their strong sense of identity and culture, despite their diminishing numerical strength, Parsis has contributed in all walks of life.

Question 7.
Social life during the ancient and medieval periods.
Answer:
Harappan civilisation was known for its well-planned towns covered drainage system, its granary which was used for storing and trading surplus grain. The Great Bath is one indicator of the collective life of the people. Thus, there were peasants, artisans, traders, fishermen, priests, administrators, artists, weavers, etc.

Sangham literature makes reference to tribes and traditional castes. This indicates their coexistence. Though the Brahmins constituted a numerical minority, they played an important role in the development of Tamilian culture. Sangham priests though not dominating were in the process of assuming advisory and supervisory powers. The Bards (nomadic ballad singers) were a special class. Vedars (hunter and highway robbers) were much feared. The Marrakudi was a separate warrior section that had its own traditions and beliefs. Then, there were the fishermen, salt manufacturers, weavers, agriculturalists, shepherds, and cowherds who were also important.

The Varna System during the Vedic period referred to the social order or class of people. There was flexibility and fluidity with respect to occupation. It was only towards the end of the Vedic period that Varna turned into a rigid jati (caste) hierarchy based on the ideology of purity and pollution.

• Brahmin – priests, teachers, intellectuals
• Kshatriya – rulers, and warriors
• Vaishya – merchants, traders, farmers
• Shudra – menial work

The first three varnas began to call themselves the upper varnas. They became the ‘twice-born (dvija) because they were entitled to the initiation ceremony (upanayana).

Ashramvyavastha was prescribed for the so-called twice-born castes. This referred to the four stages in the life of a Hindu.

• Brahmacharyashram – Student hood, single status, and celibacy
• Grihasthashram – Householder
• Vanaprasthashram – hermithood and retirement.
• Sanyasashram – renunciation

The Classical Period (i.e. the period of the Gupta Dynasty) believed to be the ‘Golden Age, is when Indian society grew and thrived, setting the foundations in arts, science, politics, religion, philosophy, and economics that define Indian culture to this day. It became a global trade center arid an epicenter of artistic and intellectual achievement. Eventually, the smaller kingdoms broke away. This allowed the Huns of Central Asia to invade and defeat the Gupta dynasty around 550 CE and finally, the classical period declined by 650 CE.

Many texts (Nitishastras and Dharmashastras) were written during a period of ‘second urbanisation’, which elaborated on socio-political laws.

The Medieval Period of India witnessed the Muslim invasion of India’s material resources. During the Delhi Sultanate, society experienced a synthesis of Indian and Islamic culture Amir Khusro, used a form of Hindustani, which he called Hindavi. At the same time, the Delhi Sultanate was also responsible for the large-scale destruction and desecration of temples.

During this period also, a rigid caste system was followed. Efforts of Emperor Akbar gave India a strong and stable political administration.

The Medieval Period is often stated to be the darkest period in the history of India however, there emerged several changes that transformed Indian society also. Performing arts, architecture and sculpture flourished alongside internal and foreign trade and commerce. The establishment of Din-I-Ilahi by Akbar was a new religion based on ethical rationalism. Towards the 19th century CE there emerged a widening gap between liberals and orthodox groups from various faiths.

3. Write differences.

Question 1.
Status of women in the Early Vedic period and medieval period.
Answer:

Status of women in the Early Vedic period	Status of women in the Medieval period
(i) Status: Indian women enjoyed a high status during the early Vedic period.	(i) Status: The status of women deteriorated in Medieval India.
(ii) Education: Women during the Early Vedic period had access to Vedic education.	(ii) Education: Only women from upper castes and aristocracy were given education in private.
(iii) Access of Knowledge: There were qualified women and some notable Vedic and Upanishadic women scholars during the early Vedic period.	(iii) Access of Knowledge: Knowledge of the scriptures and literacy was denied to Women and her status was reduced to being dependent on men.
(iv) Widow Remarriage: Widow remarriage was permitted in the Vedic period.	(iv) Widow Remarriage: Widow remarriage was considered taboo.
(v) Marriage: The main form of marriage was Monogamy and women in early Vedic marriage could marry late or decide not to marry.	(v) Marriage: Practices of child marriage, sati, and devadasi system, the customs of polygamy, and early marriage made women the objects of exploitation.
(vi) Freedom: Women were considered as useful and productive members of society and they were given the freedom to choose their life partners for marriage.	(vi) Freedom: Freedom of women was curtailed and was reduced to being dependent on men throughout her lifetime.

Question 2.
Buddhism and Jainism.
Answer:

Buddhism	Jainism
(i) Founder: The founder of Buddhism is Gautama Buddha.	(i) Founder: The founder of Jainism is Vardhaman Mahavir.
(ii) Teaching: The teachings of Gautam Buddha were in the language of the common people, Pali.	(ii) Teaching: The teachings of Mahavira were in the language of the common people, Ardhamagadhi.
(iii) Sacred books: The Sacred book of Buddhists is Tipitaka.	(iii) Sacred books: The Sacred books of Jains is Agamas.
(iv) Principles: Buddhism advocated the middle path based on the Four Noble Truths and the Eightfold Path.	(iv) Principles: Jainism preached (1) Ahimsa (2) Satya (3) Asteya (4) Aparigraha.

4. Explain the following concepts with examples.

Question 1.
Social Reform Movements
Answer:
It was the educated Indians, often from the upper social strata, who campaigned the agenda for change at the micro-socio levels. The 19th century is witness to the emergence of many social and religious reform movements.

All these groups struggled to bring about changes at the local level in which they operated. They aimed in solving social problems which were socio-religious-cultural in nature.

They worked towards reforming obsolete, repressive, and regressive religious practices. The urge for reform was generated largely as a result of their interaction with the West.

Many groups worked to promote education among the ‘weaker sections – especially women and so-called lower castes. Organisations like the Arya Samaj aimed at restoring Vedic traditions and integrating Vedic knowledge with the modern curriculum.

Examples of some movements of social reforms:

• Brahmo Samaj – Raja Rammohan Roy
• Arya Samaj – Swami Dayanand Saraswati
• Prathana Samaj – Aatmaram Pandurang
• Harijan Sevak Sangh – Mahatma Gandhi
• Theosophical Society – Annie Besant

Question 2.
Westernisation
Answer:
Many of the educated elite took to the lifestyle of the British with respect to food habits, dressing, customs, mannerisms, attitudes, beliefs, language, sports, and entertainment, etc. Eminent Indian sociologist, M. N. Srinivas referred to this process of imitation of the British, as ‘Westerisation’.

The impact of Western culture has been classified into four types by Alatas. They are :

• eliminative changes (i.e., fading out of cultural elements)
• additive changes (i.e., new cultural additions)
• supportive changes (i.e., changes that support existing cultural traits)
• synthetic changes (i.e., the synthesis of old and new culture)

Examples: Drinking tea and coffee, changes in eating habits, using the dining table, crockery, and cutlery, hugging and kissing as a form was adopted universally, western sports like cricket, became popular.

5A. Complete the concept map.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

5B. State whether the following statements are True or False with reasons.

Question 1.
The Bhakti Movement brought religious reform to Hinduism during the medieval period.
Answer:
This statement is True.

The Bhakti Movement rejected the caste system. It criticized excessive ritualism and advocated simplicity in worship. It professed that all human beings were equal in the eyes of God. The focus was on devotional singing and the repetition of his name.

Sufism also preached the unity of humanity and believed in the equality of all human beings in the eyes of God. Some important exponents of this are Kabir, Rahim, and Guru Nanak. Kabir and Rahim denounced external observances of religion such as rituals, superstitious practices, idolatry. Guru Nanak decried the caste system, ritualism, and idol worship.

Bhakti Movement in Maharashtra began in the 13th century CE with Dnyaneshwar. Namdev was his contemporary who criticized fasts, pilgrimages, and all other external forms of religious practices.

Question 2.
After Independence, the goals and programmes of the country have not seen many changes.
Answer:
This statement is False.

After Independence, the goals and programmes of the country have seen numerous changes. Some significant factors that have affected India after 1947.

Constitution of India:

• The Constitution of India was framed by the Constituent Assembly which was founded on 6th December 1946 to write the Constitution of India.
• The head of the Drafting Committee of the Constitution was Dr. B. R. Ambedkar.
• It is a document based on the strengths of the diversity of Indian society. It cherishes the goals of liberty, equality, and fraternity. It supports secularism.
• There have been numerous amendments to the Indian Constitution. A recent change has been the abrogation of Article 370 in August 2019 which gave special status to Jammu and Kashmir.

Economy: The economic growth of India recently was guided by Planned Development, through twelve Five-Year Plans till 2017. Each plan period has had its own objectives. It was in 1991, globalisation was introduced in India which has its share of positives and negative sides.

Since 2014, changes such as demonetization, single taxation policy under GST, welfare schemes, borderless trade practices, Swachh Bharat drives, promoting entrepreneurship, etc. have been key points.

Education: There has been a significant expansion of the number of anganwadis, schools, universities, deemed universities, autonomous institutions, IITs (Indian Institute of Technology), IIMs (Indian Institute of Management), IIITs (Indian Institute of Information Technology), NITs (National Institute of Technology), vocational programmes, open learning, online education, self-learning opportunities and so on.

• Enrolment numbers have been swelling beyond control in several cases.
• The number of teachers has also risen.
• The Draft New Education Policy has been formulated in 2019.

Question 3.
India is the most populous democracy in the world. –
Answer:
This statement is True.

In Post-Independent India, we have taken on a system of governance based on the principle of democracy. The three arms of government are the Executive, Assembly Legislature as well as Judiciary. We have the principle of democratic decentralization where power percolates down to the grassroots level.

The Indian political system no longer recognizes the former statuses of prince, nawab, raja or rani. All citizens are equal in the eyes of law. Modern India has embraced the principles and practice of free and fair elections. Voting rights are given to all citizens of India, on the attainment of age 18. India also has a multi-party system – and parties may be national, state or regional in character. Individuals also have the right to contest in elections. We also have a federal system of governance – Centre, and State/Union Territory.

The goals, policies, and agenda of each government are guided by its own principles or ideologies. There are differences and multiple views (for example, Left, Right, and Centre). The role of the opposition is the responsibility of keeping a check on the government in power. Consensus is an important value in a democratic society. Thus, India is the most populous democracy in the world.

6. Give your personal response.

Question 1.
India is a melting pot of culture.
Answer:

• India is a melting pot of many cultures and traditions, It is endowed with rich traditions of art, craft, culture, and cuisine, We have assimilated cultures of all civilizations that have come to our shores.
• Indian society is formed by the incorporation of culture followed by Indians since ancient times.
• Undoubtedly, Indian culture is one of the oldest existing cultures in the world. With each passing decade, it’s evolving.
• Western culture has also influenced Indian society. It has led to a few advancements, but at the same time, has caused Indians to disconnect from their roots rapidly.

7. Answer the following question in detail in about 150-200 words.

Question 1.
Discuss with relevant examples, consequences of Colonialism in India with respect to the following factors.
(i) Introduction of the new education system
(ii) Introduction of new administration system
(iii) Introduction of new7 economic system
(iv) Introduction of Transport and Communication
(v) Nationalist Movement
Answer:
(i) Introduction of the new education system: The British set up a system of education that had a far-reaching impact on Indian society. The medium of instruction in high school now became English. It became the common language of communication among the learned people. Schools and colleges were open to all individuals, irrespective of caste, creed, gender, etc.

The Indian Universities Act, 1856, enabled the establishment of the first universities in Calcutta, Bombay, and Madras. The content of education was secular – which included subjects like Mathematics, Science, Philosophy, Sociology, History, etc. This led to the rise of a new class of intelligentsia, who were of Indian origin but trained in ‘Western’ values customs, and practices. Some of them played a significant role in the reform movements. New values like rationality, equality, social justice, secular approach, and individualism gained firmer ground.

(ii) Introduction of new administration system: The British set in place new systems of administration. They started the system of services like the Economic Service, Education Service, Revenue Service, and Administrative Service. A new judiciary system was created, which took into consideration the earlier legal traditions of the Indian communities.

However, its implementation was carried out on a secular basis; each individual was judged on an equal basis, irrespective of one’s caste and creed. The authority of feudal lords and zamindars was abolished.
The Indian Councils Act, The Indian High Court Act, and The Indian Civil Service Act of 1861 all led to major changes in the Executive, Legislative and Judicial administration of India.

(iii) Introduction of new economic system: The economic system got transformed by industrial growth and its twin process of urbanization. Caste-based skills and occupations and, social relationships were gradually changing due to the impact of a changing economy and the rise of factories. The emergence of economic and educated classes was on the rise. New Revenue systems were started by the British in different parts of India which affected the peasants adversely.

(iv) Introduction of Transport and Communication: Systems of railways and roadways, and, Post and Telegraph offices were set up through the length and breadth of the country. These were ways in which it became possible to reach people in all parts of the country and access resources. In 1869, the Suez Canal was opened to promote trade interests. Development of transportation and communication led to an increase in market outlets for Indian raw materials.

(v) Nationalist Movement: Use of English as a common language of communication among. the educated elite played a significant role in networking, the nationalist movement received momentum. The awakening among the Indian masses against alien rule resulted in the call for the expulsion of the British from India and to fight for independence. The 19th century saw the emergence of the Indian National Congress and Mahatma Gandhi as the key figure in the call for independence.

Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 1 Introduction to Micro and Macro Economics Important Questions and Answers.

Maharashtra State Board 12th Economics Important Questions Chapter 1 Introduction to Micro and Macro Economics

1. A. Choose the correct option:

Question 1.
The term ‘Micro’ is derived from the Greek word.
(a) Makros
(b) Maikros
(c) Mikros
(d) Mikrosoft
Options:
(1) a
(2) b
(3) c
(4) d
Answer:
(3) c

Question 2.
The term ‘micro’ and ‘macro’ economics were first coined and used by Norwegian Economist.
(a) Adam Smith
(b) Ragnar Frisch
(c) Dr. Marshall
(d) Prof. Ricardo
Options :
(1) a
(2) b
(3) d
(4) c
Answer:
(2) b

Question 3.
Statements related to features of Micro economics.
(a) The study of individual unit
(b) It deals with income theory
(c) It splits the whole economy
(d) It suggests suitable economic policies to promote economic growth
Options :
(1) a, b, c and d
(2) a and b
(3) a, c and d
(4) b and d
Answer:
(3) a, c and d

Question 4.
Scope of Micro economics.
(a) Theory of factor pricing
(b) Theory of general price level
(c) Theory of product pricing
(d) Theory of economic welfare
Options :
(1) a, b, c and d
(2) a and b
(3) a, c and d
(4) b and d
Answer:
(3) a, c and d

Question 5.
Theory of Economic Welfare.
(a) Efficiency in production
(b) Efficiency in consumption
(c) Overall economic efficiency
(d) Efficiency in social activities
Options :
(1) c and d
(2) a, b and d
(3) a, b and c
(4) b, c and d
Answer:
(3) a, b and c

Question 6.
Main features of macro economics.
(a) Income theory
(b) Lumping method
(c) Price theory
(d) Study of aggregates
Options :
(1) a, b and c
(2) b, c and d
(3) a, b and d
(4) Only b
Answer:
(3) a, b and d

Question 7.
Importance of Micro Economics.
(a) Free market economy
(b) Functioning of an economy
(c) Basis of welfare economy
(d) Foreign Trade
Options :
(1) a, b, c and d
(2) a, b and c
(3) a, b and d
(4) a, c and d
Answer:
(4) a, c and d

Question 8.
Micro Economic is based on certain assumption.
(a) Perfect competition
(b) Pure capitalism
(c) Full employment
(d) Fluctuations in the national income
Options :
(1) b, c and d
(2) c and d
(3) a, b and c
(4) a, c and d
Answer:
(3) a, b and c

Question 9.
Importance of Macro-economics.
(a) National Income
(b) Economic development
(c) Price determination
(d) General level of employment
Options :
(1) b, c and d
(2) a, b and d
(3) a, b, c and d
(4) None of these
Answer:
(2) a, b and d

Question 10.
Scope of Macro economics.
(a) Theory of Income and employment
(b) Theory of General Price level and inflation
(c) Theory of Economic growth and development
(d) Theory of Factor Pricing
Options :
(1) a and b
(2) a, b and c
(3) a, c and d
(4) a, b, c and d
Answer:
(2) a, b and c

Question 11.
Factors of Production which make contribution in production process.
(a) Land
(b) Profit
(c) Labour
(d) Transport
Options :
(1) a, b and c
(2) a and c
(3) b, c and d
(4) All of above
Answer:
(2) a and c

B. Complete the correlation:

1. Macro economic theory : Income and employment:: Micro economics : ………………
2. General equilibrium : Macro economics :: ……………… : Micro economic
3. Macro Economics : Large :: Micro Economics : ………………
4. Classical Economist: ……………… :: Neo-classical Economist: Prof. Alfred Marshall J
5. Prof. Alfred Marshall : Principles of Economics :: ……………… : General theory of Employment, Interest and Money
6. Study of Individual unit: ……………… :: Study of aggregates : Macro economics
7. Theory of Economic welfare : Scope of Micro economics :: ……………… : Scope of Macro economics
8. Land: Rent:: ……………… : Wages
9. Capital: ……………… :: Entrepreneur : Profit
10. ……………… : Demand and Supply Analysis :: Theory of Income and employment : Consumption and Investment function
11. Macro economics : Entire economy :: Micro economics: ………………
12. Study of the whole economy : Lumping ’ method :: Study of small individual unit : ………………
Answers:

1. Price theory
2. Partial equilibrium
3. Small
4. Adam Smith
5. Maynard Keynes
6. Micro economics
7. Theory of Economic growth and development
8. Labour
9. Interest
10. Theory of Product Pricing
11. Small part of economy
12. Slicing method

(C) Give economic terms.

(1) Micro economics derived from the Greek word.
(2) Macro economics derived from the Greek word.
(3) Study of large economic unit.
(4) Study of small or millionth part of economic unit.
(5) Price determination of individual commodity by forces of demand and supply.
(6) Price determination of factor of production for contributing to the production process.
(7) Maximum satisfaction of people due to efficiency in the allocation of resources.
(8) Determination of the prices of goods and services as well as factors of production.
(9) Equal distribution of produce goods and services to the society for consumption.
(10) Production of most desired goods and services.
(11) Equilibrium position of an individual economic unit.
(12) Assumption of Micro economics i.e. other things remaining constant.
(13) Micro economics does not deal with macro problems.
(14) Economic decisions are taken at individual levels without intervention of government.
(15) Explanation of effects of tariffs, exchange rate, etc.
(16) Micro economics explain various complex economic situation with the help of economic models.
(17) Equilibrium position of whole economy.
Answer:
(1) Mikros
(2) Makros
(3) Macro economics
(4) Micro economics
(5) Theory of Product Pricing
(6) Theory of Factor Pricing
(7) Theory of Economic Welfare
(8) Price Theory
(9) Efficiency in Consumption
(10) Overall Economic Efficiency
(11) Partial equilibrium
(12) Ceteris Paribus
(13) Limited scope
(14) Free Market economy
(15) Foreign Trade
(16) Economic Model building
(17) General Equilibrium Analysis

(D) Find the odd word out:

(1) Prof. Pigou, Prof. Samuelson, Adam Smith, J. R. Hicks.
(2) Individual consumer, Individual producer, Particular commodity, Total savings.
(3) Product pricing, Investment function, Factor pricing, Economic welfare.
(4) Efficiency in social activities, Efficiency in production, Efficiency in consumption, Overall economic efficiency.
(5) Price theory, Slicing method, Limited scope, Lumping method.
(6) Aggregate demand, Aggregate supply, Personal income, National income.
(7) National income, National output, National employment, National anthem.
(8) Keynes, Malthus, Fisher, Marshall.
(9) Theory of Economic welfare, Theory of income and employment, Theory of General price level, Theory of Economic growth.
(10) National Income, National Product, Per Capita Income, Gross Salary.
(11) Big, Large, Vast, Tiny.
(12) Microscopic, Massive, Small, Minimum.
(13) Rent, Wages, Capital, Profit.
(14) Land, Labour, Interest, Entrepreneur.
(15) Railways, Reliance, K.E.M. Hospital,
Answer:
(1) Adam Smith
(2) Total savings
(3) Investment
(4) Efficiency in
function social activities
(5) Lumping
(6) Personal income method
(7) National
(8) Marshall anthem
(9) Theory of Economic Income
Welfare
(10) Per Capita
(11) Tiny
(12) Massive
(13) Capital
(14) Interest
(15) Reliance

(E) Complete the following statements.

(1) The term Macro Economics is derived from the Greek word ‘Makros’ which means …………….
(2) The terms ‘Micro economics’ and ‘Macro economics’ were coined by Norwegian Economist …………….
(3) According to Maurice Dobb, Micro economics is in fact a ……………..
(4) The price of all commodity is determined by the forces of …………….
(5) Four main factors contributing to the production process, are …………….
(6) Micro economics deals with the study of behaviour of …………….
(7) Micro economics is based on ‘Ceteris Paribus’ assumptions which means …………….
(8) Micro economics is useful to government in framing …………….
(9) According to Keynes, macro economics is a …………….
(10) Macro economics is known as theory of Income …………….
(11) Macro economics examines the forest …………….
Answer:
(i) study of large unit
(2) Ragnar Frisch
(3) microscopic study of the economy
(4) demand and supply
(5) land, labour, capital and entrepreneur
(6) small individual unit
(7) other things remaining constant
(8) economic policies
(9) policy oriented science
(10) and employment
(11) not a single tree

[F] Choose the wrong pair :

Group ‘A’	Group ‘B’
(1)Macro	Individual unit
(2) Factor pricing	Rent, wages, interest and profit
(3) Ceteris paribus	Other things being constant
(4) Micro	Price theory

Answer:
Wrong pair : Macro – Individual unit

II.

Group ‘A’	Group ‘B’
(1) Slicing method	Micro economics
(2) Economic welfare	Overall economic efficiency
(3)Macro economics	Income theory
(4) Maynard Keynes	Microscopic study of economy

Answer:
Wrong pair : Maynard Keynes Microscopic study of economy

III.

Group ‘A’	Group ‘B’
(1) Lumping method	Macro economics
(2) Product Pricing	Forces of demand and supply
(3) Micro economics	General equilibrium
(4) National income	Study of aggregate

Answer:
Wrong pair : Micro economics – General equilibrium

IV.

Group ‘A’	Group ‘B’
(1) Maynard Keynes	Macro economic approach
(2) Micro	Mikros
(3) Adam Smith	Classical economist
(4) Census	Limited scope

Answer:
Wrong pair : Census – Limited scope

V.

Group ‘A’	Group ‘B’
(1) Macro	(a) Makros
(2) Prof. Alfred Marshall	(b) Neo-classical economist
(3) Lumping method	(c) Splits the whole economy
(4) Partial equilibrium	(d) Micro economics

Answer:
Wrong pair : Lumping method – Splits the whole economy

(G) Assertion and Reasoning

Question 1.
Assertion (A) – Micro of a small part of the national economy.
Reasoning (R) – Micro economics divides the economy into small units.
(1) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 2.
Assertion (A) – Micro economics is known as Price theory.
Reasoning (R) – Macro economics is known as Income theory.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).

Question 3.
Assertion (A) – Macro economics studies overall conditions in the economy.
Reasoning (R) – Micro economics deals with National income and employment.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(i) (A) is true but (R) is false.

Question 4.
Assertion (A) – General equilibrium deals with the behaviour of individual price of commodity.
Reasoning (R) – Lumping method is the study of aggregates.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(ii) (A) is false but (R) is true.

Question 5.
Assertion (A) – Macro economic analyses shows how the general price level is determined.
Reasoning (R) – The study of general price level is important on account of the problems created by inflation and deflation.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).

Question 6.
Assertion (A) – In Micro economics decision regarding production of goods can be taken by individual.
Reasoning (R) – Study of macro economics help to understand the problems of developing countries and suggest important steps to achieve economic development.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).

Question 7.
Assertion (A) – Micro economics is based on assumption of ‘Ceteris paribus’.
Reasoning (R) – Macro economics consists of the story of economic growth and development.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).

Question 8.
Assertion (A) – Micro economics help to analyse the general level of employment of out put in an economy.
Reasoning (R) – Macro economics helps us to analyse the performance of an economy.
(i) (A) is true but (R) is false.
(ii) (A) is false but (R) is true.
(iii) Both (A) and (R) are true and (R) is the correct explanation of (A).
(iv) Both (A) and (R) are true and (R) is not the correct explanation of (A).
Answer:
(ii) (A) is false but (R) is true.

(H) Choose the correct pair :

Group ‘A’	Group ‘B’
(1)Macro	(a) Slicing method
(2) Micro	(b) Classical economist
(3) Adam Smith	(c) Neo-classical economist
(4) Prof. Marshall	(d) Inflation
	(e)Lumping method

Answer:
(1)-(e), (2)-(a), (3)-(b), (4) – (c).

II.

Group ‘A’	Group ‘B’
(1) Factor of Production	(a) Other things being equal
(2) Ceteris Paribus	(b) Land
(3) Price theory	(c) Micro economics
(4) Lumping method	(d) Profit
	(e)Whole economy

Answer:
(1)-(b), (2) – (a), (3) -(c), (4) -(e).

III.

Group ‘A’	Group ‘B’
(1) National Income	(a) Rent, wages, interest, etc.
(2) Factor Pricing	(b) Mikros
(3) Micro	(c) Study of aggregate
(4) Slicing method	(d) Makros
	(e)Splits the whole economy

Answer:
(1)-(c), (2)-(a), (3)-(b), (4)-(e).

IV.

Group ‘A’	Group ‘B’
(1) Micro economics	(a) Theory of investment
(2) Macro economics	(b) Key tool of micro economics
(3) Marginalism	(c) Price theory
(4) Aggregate study	(d) Forest
	Income and employment theory

Answer:
(1) – (c), (2) – (e). (3) – (b). (4) – (d).

V.

Group ‘A’	Group ‘B’
(1) Maurice Dobb	(a) Principles of Economics
(2) Ragnar Frisch	(b) Policy oriented science
(3) Alfred Marshall	(c) Microscopic study
(4) Adam Smith	(d) Oslo University
	(e) Classical economist

Answer:
(1)-(c), (2)-(d), (3)-(a), (4)-(e).

2.[A] Identify and explain the concept from given illustrations.

Question 1.
Through public distribution system rationing shops distribute goods to poor people.
Answer:
Concept: Efficiency in consumption.
Explanation : Efficiency in consumption means distribution of produced goods and services to the people for consumption for having maximum satisfaction.
Public distribution system is developed specially to help economically weaker section of society to satisfy their consumption.
Rationing shops provide subsidized food and non food items to below poverty line people.

Question 2.
Mukesh divided his departmental J store into two separate divisions i.e. S food grains and garments to find actual profitability separately.
Answer:
Concept: Slicing method.
Explanation : Micro economics splits or divides the whole economy into small individual units and then studies each unit separately in detail.
Mukesh has divided its business into two separate divisions to understand thedetail cost of operations and profitability separately for food business as well as garment business.
Government collect whole information about population through census.
Concept : Lumping method / Macro economics.
Explanation : Macro economics use lumping method to study the whole economy rather than its part.

Question 6.
Government collect whole information about population through census.
Answer:
Concept : Lumping method / Macro economics.
Explanation : Macro economics use lumping method to study the whole economy rather than its part.
Govern ment collects data through census which gives them details about population such as sex ratio, literacy rate, unemployment rate, age composition, etc.

Question 7.
Reliance industries has created more employment opportunities through its biggest oil refinery in Jamnagar and improved the standard of living of its employee.
Answer:
Concept: Economic development. Explanation : Macro economics help to understand the problems of developing countries and suggest important steps to achieve economic development.
Economic development is a growth of the standard of living of people from low income to high income.
Through developing oil refinery Reliance has created numbers of job opportunities and hence improved the standard of living. Amul has fixed price of ₹ 44 per litre of milk after considering the cost such as machinery cost, labour cost, transportation cost, etc.
Concept: Price determination.
Explanation : Micro economics is known as price theory because it deals with determination of the prices of goods and services as well as factors of production. After considering cost of operations such as machinery cost, raw material cost, labour cost, transportation cost, etc. Amul has fixed price of its product (milk).

B. Distinhbish between

Question 1.
Micro Economics and Macro Economics.
Answer:

Micro Economics	Macro Economics
(a) Micro economics deals with the economic behaviour of small units like particular firm, particular household, individual prices, wages, etc.	(a) Macro economics deals with the economic behaviour of large units or entire economy such as National Income, aggregate demand, aggregate supply, etc.
(b) It studies each unit in depth by using slicing method.	(b) It studies the economy as a whole using lumping method.
(c) It is based on partial equilibrium analysis based on assumptions.	(c) It is based on a general equilibrium analysis.
(d) Micro economic analysis is also called as ‘Price theory.’	(d) Macro economic analysis is also called as ‘Income theory.’
(e) Most of the theories are given by Dr. Alfred Marshall.	(e) Theories are profounded by Lord J. M. Keynes.

Question 2.
Micro Variables and Macro Variables.
Answer:

Micro Variables	Macro Variables
(a) Micro variables refer to individual demand, market demand, individual supply, price of a commodity, etc.	(a) Macro variables refer to inflation rate, aggregate demand, aggregate supply, employment.
(b) Micro variables are mostly independent. It does not affect the whole economy, as they are based on assumptions.	(b) Macro Variables are inter related and inter dependent. It affects the working of the economy as a whole.
(c) E.g., Price and Quantity demanded are universally related. This will hold true only if the income of the consumer, taste, fashion, etc., remain constant.	(c) Change in aggregate demand, aggregate supply will affect income, employment, etc. in the economy.

Question 3.
Partial Equilibrium and General Equilibrium.
Answer:

Partial Equilibrium	General Equilibrium
(a) Micro economics uses Partial Equilibrium analysis based on the assumption, other things remaining constant.	(a) Macro economics uses general equilibrium. It is not based on assumption.
(b) Partial Equilibrium studies the equilibrium of a consumer, a firm, an industry or a market.	(b) It deals with the Equilibrium position of the economy as a whole.
(c) It deals with one or two variables at a time. So it is a simple method. It is independent.	(c) It deals with all the variables of the Economic System simultaneously. So it is sophisticated. There is inter dependence.
(d) Partial Equilibrium is regarded as a worm’s eye-view.	(d) General Equilibrium is a bird’s eye-view.

Question 4.
Micro Theory of Distribution and Macro Theory of Distribution.
Answer:

Micro Theory of Distribution	Macro Theory of Distribution.
(a) Micro Theory of distribution refers to distribution of Factor Income to individual factor owners for their contribution to the production of a commodity or service.	(a) Macro theory of distribution refers to distribution of National Income to factors like wages to the labourers, rent to landlords and interest to capitalist.
(b) It is determined by the market forces of demand and supply.	(b) It is determined by the Aggregate demand and Aggregate supply and Employment level in the country.

Question 5.
Slicing Method and Lumping Method.
Answer:

Slicing Method	Lumping Method
(a) In slicing method the entire economy is cut into individual slices and each unit is studied in depth.	(a) In lumping method, we study the economy as a whole without slicing it.
(b) Micro Economics uses the slicing method.	(b) Macro Economics uses the Lumping Method.
(c) In slicing method, in depth study of the behaviour of an individual unit like a household, a firm, a product, a factor is done.	(c) In lumping method, it deals with the behaviour of large aggregates like National Income, aggregate demand, aggregate supply, employment and their functional relationship is studied.
(d) It relates to the in-depth study of a tree and not the study of forest as a whole.	(d) It relates to the study of the forest as a whole and not a particular tree.
(e) Here we achieve a worm’s eye view.	(e) It gives a bird’s eye view of the whole economy.

3. State with reasons whether you agree or disagree with the following statements:

Question 1.
Micro economics is the study of aggregate.
Answer:
No, I do not agree with this statement.
OR Micro economics studies individual economic units.
Yes, I agree with this statement.

• Micro economics is the microscopic study of individual economic units in great detail.
• It deals with individual firms, individual demand and supply, prices of individual, firms, etc.
• But macro-economics deals with economic behaviour of the whole economy with respect to national income, aggregate demand and supply, general price level, etc.
• Hence, micro economics is the study of individual economic units whereas macro economics is the study of aggregates.

Question 2.
Macro economics is a partial equilibrium analysis.
Answer:
No, I do not agree with this statement.
OR
Macro Economics deals with the whole s economy.
Yes, I agree with this statement.

• Macro economics deals with entire economy.
• Macro economics follow general equilibrium analysis. On the other hand, micro economics follow partial equilibrium analysis.
• Macro economics studies the behaviour of number of aggregate economic variables.
• Macro economics follows general equilibrium. It assumes “everything depends on every thing else.”
• General equilibrium deals with the behaviour of demand, supply and prices in the whole economy.
• Therefore, macro economics is not a partial equilibrium analysis but it is a general equilibrium analysis.

Question 8.
Micro economics is useful to the Government.
Answer:
Yes, I agree with this statement.
Useful to Government : It is useful in formulating and evaluating economic policies including pricing and distribution policies that promote economic welfare. It is useful in determining tax policy, public, expenditure policy, etc.

Question 9.
The scope of macro economics is wide.
Answer:
Yes, I agree with this statement.
(A) Theory of Income and Employment : It ?
explains which factors determine the level of National Income and employment and what causes fluctuations in the level of income, output and employment.
To understand how the level of employment is determined, we have to study the consumption function. It includes theory of business cycles.

(B) Theory of General Price Level and Inflation: Macro economics analyses shows how the general price level is determined and the causes for fluctuations in it. This study is important for understanding the problems created by inflation and deflation.

(C) Theory of Economic Growth and Development : Macro economics studies the causes of under development and poverty in poor countries and suggests strategies for accelerating growth and development in the country.

(D) Macro theory of Distribution : Macro theory of distribution deals with the relative share of rent, wages, interest and profit in the total national income of various classes.

Question 10.
Theories of micro economics are based on certain assumptions.
Answer:
Yes, I agree with this statement.
Based on certain ssumption : Micro economics is based on ‘ceteris paribus’ assumption i.e., other things remaining constant like full employment, laissez faire policy, perfect competition, pure capitalism, etc.

Question 11.
Macro economics is also known as income and employment theory.
Answer:
Yes, I agree with this statement.
Theory of Income and Employment : It ?
explains which factors determine the level of National Income and employment and what causes fluctuations in the level of income, output and employment.
To understand how the level of employment is determined, we have to study the consumption function. It includes theory of business cycles.

4. Study the following table / figures / passages and answer :

Question 1.
Read the passage and answer the following questions.
The census of 1991 was the fifth census of independent India and conducted as usual from 9th to 28th February, 2001 to present census data as on sunrise of 1st March 2001, the reference date. The two phases were continued in the same way like previous two censuses.

In the first phase a house list was canvassed to collect the information on housing data and also amenities available to the households. The scope of house list was enlarged and for the first time a question regarding type of fuel used for cooking was canvassed. In 1981 the question on availability of toilet facility was canvassed for urban areas only. However, in 1991, it was canvassed for rural area also.
During 2nd phase following two schedules were canvassed, (a) Household schedule and (b) Individual slip

1. Between which dates the census for 2001 was conducted.
Answer:
The census for 2001 was conducted between 9th to 28th February 2001.

2. What information was collected in the first phase of census?
Answer:
In the first phase of census a house list was canvassed for collecting information about housing data and amenities available.

3. Which question was canvassed in 1991?
Answer:
In 1991 question on availability of toilet were canvassed – (a) household schedule and facility was canvassed for rural area. I 03) Individual slip.

4. Which two schedule were canvassed in IInd phase?
Answer:
During IInd phase below two schedules were canvassed –
(a) household schedule and
(b) Individual slip.

Question 2.
Go through the following chart and answer the questions.
Answer:

1. Which are the two main sectors in Indian education system?
Answer:
The two main sectors in Indian education system are (a) Public sector (b) Private sector.

2. What does public sector education system includes?
Answer:
Public sector education system includes public schools, central government funded institutions, state government funded institutions and higher education institutions.

3. Where are multimedia schools positioned in Indian education system?
Answer:
Multimedia school comes under non-formal setup of private sector in Indian education system.

4. What are the setups in private sector educational system?
Answer:
There are two setups in private sector educational system i.e. formal setup and non-formal setup.

Question 3.
Study the below table and answer the given questions.

(1) Which state has the highest literacy [ rate?
Answer:
Kerala has the highest literacy rate of 90.92%.

(2) What is the male literacy rate for1 Maharashtra?
Answer:
For Maharashtra the male literacy rate is 86.27%.

(3) What is difference of female literacy rate between Delhi and Rajasthan?
Answer:
There is a difference of 30-66% as a whole in female literacy rate between Delhi and Rajasthan.

(4) Which states has highest male literacy and lowest female literacy rate?
Answer:
Kerala has the highest male literacy rate of 94.20% and Uttar Pradesh has the lowest female literacy rate of 42.98%.

5. Answer in detail:

Question 1.
Explain the scope of Micro economics.
OR
Explain the subject matter of micro economics.
Answer:

(a) Theory of Product Pricing : The price of each commodity is determined by the forces of demand and supply. Micro economics is a study of demand analysis i.e. individual consumer behaviour and supply analysis i.e. individual producer behaviour.
(b) Theory of Factor Pricing : There are four main factors contributing to the production process which are land, labour, capital and entrepreneur. Micro economics helps in determining the factor rewards like land gets rent, labour gets wages, capital gets interest and entrepreneur gets profit.
(c) Theory of Economic Welfare : This theory deals with efficiency in allocation of resources which aim at maximum satisfaction of people. Three economic efficiencies are as follows :

• Efficiency in production: It mean producing the maximum amount of goods and services from a given amount of goods and j services from a given amount of resources.
• Efficiency in consumption: It means distribution of produce goods and services to the society for consumption in such a way to have maximum total satisfaction of people.
• Overall economics efficiency: It means to produce those goods and services which are most desired by the people.