Bhagya

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 7 India and Iran (Persia) Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 7 India and Iran (Persia)

1A. Choose the correct alternative and write the complete sentences.

Question 1.
The Ashoka edicts are written in ____________ script.
(a) Sinhala
(b) Aramaic
(c) Kharoshthi
(d) Modi
Answer:
(b) Aramaic

Question 2.
The capital of the empire of Elam was ____________
(a) Athens
(b) Pars
(c) Eretria
(d) Susa
Answer:
(d) Susa

Question 3.
The Iranian empire was established by ____________ of the Achaemenid dynasty.
(a) Cyrus the Great
(b) Alexander the Great
(c) Daryush I
(d) Xerxes
Answer:
(a) Cyrus the Great of Scylax

Question 4.
____________ is the Latin name of Iran.
(a) Pars
(b) Ariana
(c) Susa
(d) Persepolis
Answer:
(b) Ariana

Question 5.
The logbook of the journey of Scylax is known as ____________
(a) Periplus of the Erythrean sea
(b) Periplus of the Mediterranean Sea
(c) Periplus of Scylax
(d) Periplus of the Dead sea
Answer:
(c) Periplus of Scylax

Question 6.
The Mahabharata mentions King ____________ as the king of ‘Naga people’.
(a) Porus
(b) Ambhi
(c) Chandragupta Maurya
(d) Takshaka
Answer:
(d) Takshaka

Question 7.
The gold coins issued by Daryush-I were known as ____________
(a) Darik
(b) Siglos
(c) Tarik
(d) Stater
Answer:
(a) Darik

Question 8.
____________ became the king of Macedonia.
(a) Daryush-I
(b) Xerxes
(c) Cyrus the Great
(d) Alexander
Answer:
(d) Alexander

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Anabasis	To spur into action
(b) Talent	A natural skill or ability
(c) Darik	Gold coins
(d) Sigloi	Silver coins

Answer:
(b) Talent – Unit of weight

Question 2.

Set ‘A’	Set ‘B’
(a) Sisikottas	Shashi Gupta
(b) River Vitasta	Jhelum
(c) Behistun	World Cultural Heritage
(d) Daryush-I	Pasargadae

Answer:
(d) Emperor Cyrus II – Pasargade

Question 3.

Set ‘A’	Set ‘B’
(a) Anatolia	Asia Minor
(b) Eretria	Egypt
(c) Kabul basin	Gandhara
(d) Scythian	Saka

Answer:
(b) Eretria – Greece

1C. Find the odd one out.

Question 1.
Daryush-I, Xerxes, Cyrus-II, Alexander.
Answer:
Alexander

Question 2.
Herodotus, Arrian, Scylax, Pliny
Answer:
Pliny

Question 3.
Susa, Pasargade, Persepolis, Alexandros
Answer:
Alexandros

Question 4.
Alexandras, Ariane, Alexin, Alexander
Answer:
Ariane

Question 5.
Herodotus, Arrian, Curtis, Justin
Answer:
Herodotus

Question 6.
Mathematics, Machinery, Music, Medicine
Answer:
Machinery

2A. Write the names of historical places, persons, and events.

Question 1.
The Greek name of Iran
Answer:
Ariane

Question 2.
Successor of Daryush-I
Answer:
Xerxes

Question 3.
Author of Anabasis of Alexander
Answer:
Arrian

Question 4.
The first historian to collect information and put it in a chronological order
Answer:
Herodotus

Question 5.
Greek sailor from Ionia
Answer:
Scylax of Karyanda

Question 6.
Sanskrit term for the Greeks
Answer:
Yavana

Question 7.
Highway linking the regions from Bihar to Afghanistan
Answer:
Grand Trunk Road

Question 8.
Greek settlement
Answer:
Nysa

Question 9.
The route beginning from Susa and reaching the Mediterranean Sea.
Answer:
Royal Road

Question 10.
The battle between Daryush I and Athens was fought on the grounds of Marathon near Athens
Answer:
Battle of Marathon

2B. Choose the correct reason and complete the sentence.

Question 1.
Alexander was influenced by Porus because ____________
(a) Porus was handsome
(b) Porus was stronger than Alexander
(c) of Porus great valour
(d) Porus surrendered easily
Answer:
(c) of Porus great valour

Question 2.
Taxila was the capital of ____________
(a) Greece
(b) Gandhara mahajanapada
(c) Egyptus
(d) Jhelum
Answer:
(b) Gandhara Mahajanapada

Question 3.
Emperor Cyrus II had begun to build a new capital at ____________
(a) Islamabad
(b) Dhaka
(c) Pasargade
(d) Mahajanapada
Answer:
(c) Pasargadae

Question 4.
Taxila is situated on the Grand Trunk Road, ____________ away from Islamabad, the capital of Pakistan.
(a) 20 kilometres
(b) 35 kilometres
(c) 40 kilometres
(d) 30 kilometres
Answer:
(d) 30 kilometers

2C. Write the correct chronological order.

Question 1.
(a) There was a fierce battle between Alexander and Porus.
(b) Alexander appointed satrapies before starting on the return journey.
(c) Alexander died at Babylon in 325 B.C.E.
(d) Alexander conquered Kabul and Sindh.
Answer:
(a) Alexander conquered Kabul and Sindh.
(b) There was a fierce battle between Alexander and Porus
(c) Alexander appointed satrapies before starting on the return journey.
(d) Alexander died at Babylon in 325 B.C.E.

Question 2.
(a) Cambyses II
(b) Daryush I
(c) Cyrus II
(d) Xerxes
Answer:
(a) Daryush I
(b) Cambyses II
(c) Cyrus II
(d) Xerxes

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

4. Write short notes.

Question 1.
Coins of Daryush – I
Answer:

• Daryush-I issued coins with his own portrait on it. The gold coins issued by him were known as ‘Darik’ and silver coins were known as ‘siglos’.
• A portrait of Daryush-I holding a bow and arrow can be seen on these coins.
• One ‘Darik’ was equivalent to 12 ‘sigloi’ in value.

Question 2.
Cyrus-II
Answer:

• The Iranian empire was established by Cyrus – II (also known as Cyrus the Great) of the Achaemenid dynasty.
• He was from the tribe of Tars’. The region where the tribe dwelt was known by the tribe’s name ‘Pars’.
• The main city of the region was also known by the same name.
• Emperor Cyrus – II had begun to build a new capital at ‘Pasargade’. However, it did not get completed in his lifetime.

Question 3.
Daryush-I
Answer:

• Daryush – I succeeded Cambyses – II. He reinforced the fortification walls of Susa.
• He also built a massive palace and hypostyle (many columned) halls known as ‘Apadana’.
• Daryush also built the city of Persepolis in a style similar to Susa.
• He also built a palace and apadana in Persepolis also.

5. Explain the following statements with reasons.

Question 1.
Herodotus has described the Indian soldiers in the Achaemenid army.
Answer:

• According to Herodotus, Xerxes’ army had soldiers from Gandhara, Sindh, and Punjab when he invaded Greece in 480 B.C.E.
• The soldiers from Gandhara were equipped with bows made of cane and spears with short shafts.
• They also had horses and chariots drawn by horses. The Indian soldiers from Sindh and Punjab used cotton clothes and used bows and arrows made of cane. They were expert archers.

6. State your opinion.

Question 1.
Alexander was impressed by the valour of Porus.
Answer:

• Alexander conquered almost all kingdoms in Kabul, Sindh, and Punjab. However, not all Indian Kings surrendered to Alexander easily.
• Many fought with great valour. One of them was King Porus. On the bank of Jhelum, Alexander and King Porus confronted each other and there was a fierce battle between them.
• Porus was defeated but Alexander and his army were greatly influenced by his valour. The Greeks were influenced by the use of elephants in warfare.
• To penetrate the file of elephants was a great challenge for them.
• The Greek historians have unanimously praised the skill of Porus in warfare and also his courage.

7. Answers the following questions in detail.

Question 1.
Write in detail about Herodotus, the first historian.
Answer:

• Herodotus was born in 484 B.C.E. in Halicarnassus, a Greek city-state.
• He began to write with the intention of tracing the history and causes of the battles between Greek city-states and the
• Achaemenid Empire during 500-449 B.C.E.
• The book he wrote was named ‘Historia’ (The Histories).
• Herodotus was the first historian who collected information-seeking answers to a particular question and then put it in chronological order.
• He did not bring in notions like God, human destiny, etc.
• Putting historical events in a chronological sequence became an essential theme of history writing.
• This theme proved to be fundamental in the development. Therefore, Herodotus is said to be the father of historiography.

Question 2.
Importance of Taxila as a center for learning.
Answer:

• Taxila was the capital of Gandhara Mahajanapadas.
• Some information about Taxila can be gathered from the writings of Greek historians.
• There were several learned individuals (Acharyas) staying in Taxila.
• Many students from various regions of the Indian subcontinent were attracted to Taxila because of the fame of the acharyas.
• It had assumed the magnitude of a natural university.
• An individual acharya had to decide the nature of his method of teaching, the subjects to be taught by him, or the nature of the syllabi.
• There was no formal system of examinations.
• Among the subjects taught at Taxila included Rigveda, Yajurveda, Samaveda, ancillary branches of the Vedas. Ancient Traditions and Ethics, Philosophy, Mathematics, Music, Medicine, Puran Texts, History, Weaponry, Poetry, etc.
• Acharya Chanakya is believed to have taken Chandragupta Maurya to Taxila for education.
• Chandragupta established a regional capital at Taxila.
• Among the subjects taught at Taxila included Rigveda, Yajurveda, Samaveda, ancillary branches of the Vedas. Ancient Traditions and Ethics, Philosophy, Mathematics, Music, Medicine, Puran Texts, History, Weaponry, Poetry, etc.
• Acharya Chanakya is believed to have taken Chandragupta Maurya to Taxila for education.
• Chanakya himself hailed from Taxila.
• During the reign of Ashoka, Maurya Taxila became an important center for learning Buddhist tradition.
• Then Taxila had become a center for learning.

8. Answer the following with the help of the given points.

Question 1.
Write a note on the contribution of the following in establishing the Iranian empire.
(a) Cyrus – II
(b) Cambyses – II
(c) Daryush – I
(d) Xerxes.
Answer:
(a) Cyrus – II (Cyrus the Great): Cyrus – II belonged to the tribe of ‘Pars’. He had begun to build a new capital at ‘Pasargade’. However, it did not get completed in his lifetime. Cyrus – II conquered Lydia, a Greek state to the north of the Mediterranean Sea around the mid of the 6th C.B. C. E. As a result, the Ionian Greek city-states.

(b) Cambyses – II: Cambyses – II was the son of Cyrus – II. He moved back to Susa and re¬established his capital there. Cambyses -II had conquered Egypt.

(c) Daryush – I: He succeeded Cambyses – II reinforced the fortification walls of Susa. He also v built a massive palace and a hypostyle (many columned) halls known as ‘Apadana’. Daryush – I also built the city of ‘Persepolis’ in a style similar to Susa. He also built a palace and apadana in Persepolis also. During the rule of Daryush -I all Ionian city-states got together and rebelled against the Achaemenid rule.

(d) Xerxes: Xerxes, the successor of Daryush -1 tried once again to invade Greece. However, he was also defeated. Thereafter the conflict between the Achaemenids and the Greeks continued over a prolonged time.

Question 2.
The conflict between the Iranian Empire and Greece.
(a) Cyrus – II
(b) Arrian
Answer:
(a) Cyrus – II:

• Cyrus II conquered Lydia, a Greek state to the north of the Mediterranean Sea, around the mid of 6th-century B.C.E.
• As a result, the Ionian Greek city-states under the Lydian rule inevitably became part of the Achaemenid empire.
• The Greeks in Ionia had migrated to Anatolia, that is, the Asian part of Turkey. It is also known as ‘Asia Minor’.
• During the reign of Daryush I all Ionian city-states got together and rebelled against the Achaemenid rule.
• The rebellion was subdued completely after a struggle of five years by the Achaemenid army.
• The effects of this unsuccessful rebellion are important for understanding the interrelationship between Greece and Persia in the ensuing period.

(b) Arrian:

• Arrian was a Greek historian of the 1st-century C.E.
• He wrote a book called ‘Anabasis of Alexander. He has referred to the correspondence between Daryush III, the last Achaemenid emperor, and Alexander.
• Daryush had written to Alexander about the release of his mother, wife, and children.
• Alexander responded by reminding Daryush of the sorrow inflicted on the Greeks by the earlier invasions of the Achaemenid emperors.
• Alexander wrote that he had arrived in Russia by crossing the ocean, with the intention of punishing the aggressive Persians.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 6 Second Urbanisation in India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 6 Second Urbanisation in India

1A. Choose the correct alternative and write complete sentences.

Question 1.
___________ is identified with Nadura in Buldhana district.
(a) Potana
(b) Vidarbha
(c) Bhoja
(d) Dandaka
Answer:
(a) Potana

Question 2.
___________ was the son of Rishabhnath, the first Jain Tirthankara.
(a) Mahavir
(b) Bahubali
(c) Gautama Buddha
(d) Andhakraja
Answer:
(b) Bahubali

Question 3.
The Jataka story known as ___________ Jataka gives us the list of kings who ruled the State of Videha.
(a) Assaka
(b) Chulla Kalinga
(c) Nimi
(d) Mahaparinibbansutta
Answer:
(c) Nimi

Question 4.
The city of ___________ was the capital of Anga.
(a) Varanasi
(b) Shravasti
(c) Rajagriha
(d) Champa
Answer:
(d) Champa

Question 5.
___________ was the 24th Tirthankara.
(a) Vardhaman Mahavir
(b) Parshavanath
(c) Rishabha
(d) Bahubali
Answer:
(a) Vardhaman Mahavir

Question 6.
___________ was known as Tathagatha or Shakyamuni.
(a) Vardhaman Mahavir
(b) Gautam Buddha
(c) Andhakraja
(d) Emperor Ashoka
Answer:
(b) Gautama Buddha

Question 7.
___________ was the capital of Asmaka.
(a) Potali
(b) Varanasi
(c) Vaishali
(d) Mathura
Answer:
(a) Potali

Question 8.
The city of Champa was the capital of ___________
(a) Kasi
(b) Anga
(c) Kosala
(d) Magadha
Answer:
(b) Anga

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Jataka story giving a list of kings who ruled Videha	Nimi Jataka
(b) Jataka story giving the name of the king who ruled Kasi	Assaka Jataka
(c) Jataka story describing the battle between king Assaka and the Kalinga king	Chulla Kalinga Jataka
(d) Buddhist text that mentions that the king of Kasi had defeated Kosala	Mahaparinibbansutta

Answer:
Buddhist text that mentions that the king of Kasi had defeated Kosala – Mahavagga

Question 2.

Set ‘A’	Set ‘B’
(a) Anga	Champa
(b) Magadha	Viratnagar
(c) Vrujji/Vajji	Vaishali
(d) Malla/Malava	Kushinara/Kushinagara

Answer:
Magadha – Girivraja/Rajgriha

Question 3.

Set ‘A’	Set ‘B’
(a) Kuru	Indraprastha/Indrapattan
(b) Uttar Panchala	Ahichchhatra
(c) Dakshina Panchala	Taxila
(d) Matsya	Viratnagar

Answer:
Dakshina Panchala – Kampilya

1C. Find the odd one out.

Question 1.
Buddha, Tathagatha, Shakyamuni, Vardhamana Mahavira
Answer:
Vardhamana Mahavira

Question 2.
Nimi Jataka, Assaka Jataka, Chulla Kalinga Jataka, Mahavagga
Answer:
Mahavagga

Question 3.
Swarajya, Bhaujya, Vairajya, Rajasuya
Answer:
Rajasuya

Question 4.
Aspasioi, Assakenoi, Astakenoi, Andhakraja.
Answer:
Andhakraja

Question 5.
Vidarbha, Paudanya, Bhoja, Dandaka.
Answer:
Paudanya

Question 6.
Purohita, Senani, Rajya, Amatya.
Answer:
Rajya

Question 7.
Svaarajya, Bhaujya, Vairajya, Gramani.
Answer:
Gramani

Question 8.
Ashvamedha, Maharajya, Saamrajya, Parmeshthya.
Answer:
Ashvamedha

2A. Write the names of historical places, persons, and events.

Question 1.
Term mentioned in Panini’s Ashtadhyayi meaning Avanti and Ashmak.
Answer:
Avantyashmak

Question 2.
Region on the bank of the Godavari
Answer:
Andhakratta

Question 3.
Capital of Kosala
Answer:
Shravasti

Question 4.
Statue of Bahubali in the Hassan district of Karnataka
Answer:
Shravanabelagola

Question 5.
Disciple of Gautama Buddha
Answer:
King Prasenjit

Question 6.
The play was written by Bhasa
Answer:
Swapnavasavadatta

Question 7.
Contemporary of Gautama Buddha
Answer:
Bimbisara

Question 8.
Capital of Gandhara
Answer:
Taxila

Question 9.
Chief of a guild of artisans
Answer:
Jyeshthaka

Question 10.
Founder of Buddhism
Answer:
Gautam Buddha

2B. Choose the correct reason and complete the sentence.

Question 1.
The core principle of Vardhamana Mahavir’s philosophy is ___________
(a) Vedanta
(b) Mimamsa
(c) Charavaka
(d) Pluralism (Anekantavada)
Answer:
(d) Pluralism (Anekantavada)

Question 2.
Kamboja mahajanapada is mentioned in the ancient literature along with ___________
(a) Kosala
(b) Magadha
(c) Anga
(d) Gandhara
Answer:
(d) Gandhara

Question 3.
It seems that the king of Assaka was known as ‘Andhakraja’ during ___________
(a) Gautama Buddha’s times
(b) Vardhaman Mahavir’s times
(c) Second Urbanisation
(d) Mahajanpada
Answer:
(a) Gautama Buddha’s times

3. Observe the map on page 39 of your textbook and answer the following questions based on it.

Question 1.
Name the sixteen Mahajanapadas shown on the map.
Answer:
The sixteen Mahajanapadas shown on the map are Kamboja, Ghnadhara, Kuru, Surasena, Pachala, Kosala, Malla, Vrujji, Anga, Magadha, Kasi, Vatsa, Chedi, Avanti, Shoorasena, and Ashmaka.

Question 2.
Name the islands in the Bay of Bengal.
Answer:
The islands in the Bay of Bengal are Andaman and Nicobar Islands.

Question 3.
Name the ocean found at the tip of India.
Answer:
The Ocean found at the tip of India is the Indian Ocean.

Question 4.
Name the sea at the west of India.
Answer:
The Sea at the west of India is the Arabian Sea.

Question 5.
Name the modern city shown on a map.
Answer:
The modern city shown on the map is Delhi.

4. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

5. Explain the following concepts.

Question 1.
Guilds (Shrenis)
Answer:

• Along with agriculture and animal husbandry, trade and systematic management, and organisation of the trade are also essential factors for the prosperity of a state.
• The guilds of the merchants and the artisans played a great role in the growth of the mahajanapadas into wealthy states.
• These guilds had their own way of organisation and functioning.
• Guilds had their own, strict rules. Hence, they had a stringent structure.
• This stringent structure is perceived as one of the main reasons for the rise of the caste system.

6. State your opinion.

Question 1.
The Charavaka/Lokayat school denies the existence of ‘God’.
Answer:

• One of the ancient Indian schools of thought was the Charavaka or the Lokayat school of thought.
• This school denies the existence of God.
• It opposes the authority of Vedas (Vedapramanya) and the notions of the existence of God and life after death.
• It also discarded all rituals arising out of this kind of belief system.
• It is the only materialistic school of philosophy that was developed in ancient India.

Question 2.
The names occurring in the Buddhist texts are accepted as more reliable.
Answer:

• The names of sixteen Mahajanpadas are found in the Jaina and Buddhist literature and also in the Pur ana texts.
• Buddhist texts were written in a period, which was closer to the period of the Mahajanpadas.
• Hence, the names occurring in the Buddhist texts are accepted as more reliable.

Question 3.
The name Assaka in Pali is equivalent to Sanskrit Ashmaka.
Answer:

• It seems that the king of Assaka was known as ‘Andhakraja’ during Gautama Buddha’s times.
• The region on the bank of the Godavari was known as ‘Andhakratta’.
• Sage Bavari, a contemporary of Gautama Buddha, had his ashram in this region, but originally he was from the state of Kosala.
• According to ‘Suttanipata’, a Buddhist text, he came from Shrvasti, the capital of Kosala to Assaka.
• It was situated on the Godavari and in the region of ‘Dakshinapatha’.
• This evidence confirms that the name Assaka in Pali is equivalent to Sanskrit Ashmaka.

7. Answers the following questions in detail.

Question 1.
Explain the Eight Fold Path (Ashtangika Marga) of Gautama Buddha.
Answer:
Gautama Buddha explained the Eight Fold Path by including:

• Samyak Drishti (To understand and accept that nothing happens against the rules of nature)
• Samyak Sankalp (Right determination)
• Samyak Vacha (Right speech)
• Samyak Karmanta (Right behaviour)
• Samyak Ajiva (Livelihood by right means)
• Samyak Vyayam (Conscious avoidance of offensive things)
• Samyak Smriti (watchfulness and memory of right things)
• Samyak Samadhi (Establishing the mind firmly in equanimity; a state beyond pleasure and sorrow)

Question 2.
Discuss in detail the functioning of guilds or shrenis.
Answer:

• The guilds of the merchants and the artisans played a great role in the growth of Mahajanapadas into wealthy states.
• The guilds had their own way of organisation and functioning.
• Guilds had their own strict rules. Hence, they had a stringent structure.
• This stringent structure is perceived as one of the main reasons for the rise of the caste system.
• The paid outsiders who worked in the guilds were known as ‘Karmakara’ and unpaid workers as ‘Dasa’.
• During the Mauryan period, the king’s control of the transactions of guilds was very important.
• Structurally the shrenis had a great potential of channeling the central power.
• The functioning of the guilds was controlled by the state. Detailed records were kept of the production by the guilds.
• Each guild had its own rules based on its traditions. The state did not interfere in the functioning of the guilds.
• The chief of a guild of artisans was known as ‘Jyesthaka’ or ‘Jyetthaka’.
• The chief of a guild of merchants was known as ‘Shreshthi’ or ‘Setthi’.

8. Answers the following questions with the help of given points.

Question 1.
The Contemporary cities of Mahajanapadas, with the help of:
(a) Kasi
(b) Kosala
(c) Anga
(d) Magadha
(e) Vrujji/Vajji
(f) Malla
(g) Chedi
Answer:
(a) Kasi: This Mahajanapada was a powerful one at the beginning of the Mahajanapada period. Varanasi was its capital. The kings of Kasi were ambitious. According to the jataka stories they aspired for the highest position among all contemporary kings (Sabbarajunam aggaraja).

(b) Kosala: Ancient Kosala encompassed the regions of Uttar Pradesh in India and Lumbini in Nepal. Sharavasti was its capital city. King Prasenjit (Pasenadi) was a disciple of the Gautama Buddha. Kosala was destroyed and annexed permanently to Magadha by King Ajatashatru.

(c) Anga: The city of Champa was the capital of Anga. It was the center of the marine trade. It was permanently annexed to Magadha by King Bimbisara.

(d) Magadha: Magadha had its first capital in the city of Girivraja, also known as Rajagriha. Girivraja was surrounded by five hills making it formidable for the enemies. King Bimbisara was a contemporary of Gautama Buddha. The policy of territorial annexation of other kingdoms was started during the reign of Kind Bimbisara.

(e) Vrujji/Vajji: This was a confederation of eight clans, known as ‘Maha Aththkula’. It included clans like Videha, Lichchhavi, Vajji, Shakya, Dnyatruk, etc. The ‘Ekapanna Jataka’ mentions that Vaishali, the capital of this Mahajanapada was fortified with three surrounding walls. It had three entrance gates and bastions.

(f) Malla: The city of Kushinara or Kushinagara (Kasia) in the Gorakhpur district was the capital of this Mahajanapada. Gautama Buddha attained Mahaparinirvana in this city. A copper plate inscription (5th century C.E.) was found at the ‘Parinirvana Stupa’ in this city. It read, “Parinirvana chaitye tamrapattaiti”. By the 3rd century B.C.E. the Malla Mahajanapada was merged into the Maurya Empire.

(g) Chedi: This Mahajanapada had occupied Bundelkhand and the region around it. The city of Shuktimati or Sotthivati was its capital. It is supposed to have been situated near ‘Banda’ in Uttar Pradesh.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 5 Janapadas and Republics Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 5 Janapadas and Republics

1A. Choose the correct alternative and write the complete sentences.

Question 1.
__________ means the ruling class.
(a) Rashtra
(b) Rajya
(c) Gana
(d) Khanda
Answer:
(c) Gana

Question 2.
__________ was the highest decision making authority concerning all matters of the Ganasangha.
(a) Mantriparishad
(b) Sabha
(c) Samiti
(d) Ganaparisha
Answer:
(d) Ganaparishad

Question 3.
Regional Zones were called __________
(a) Sabha
(b) Sangharajya
(c) Khanda
(d) Mahajanpada
Answer:
(c) Khanda

1B. Find the incorrect pairs from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Magadh	Atharvaveda
(b) Kikata	Rigveda and Atharvaveda
(c) Pundra	Mahabharata
(d) Yadu	Samaveda

Answer:
Yadu – Rigveda

Question 2.

Set ‘A’	Set ‘B’
(a) Shalva	Mahabharata
(b) Balhik	Atharvaveda
(c) Pulinda	Emperor Ashoka’s edits
(d) Ghandhara	Yajurveda

Answer:
Ghandhara – Rigveda and Atharvaveda

Question 3.

Set ‘A’	Set ‘B’
(a) ‘Praatichya’	of the west
(b) ‘Udichya’	of the north
(c) ‘Dakshina’	of the south
(d) ‘Madhyadesha’	of the east

Answer:
‘Madhyadesha’ – The central region

1C. Find the odd one out.

Question 1.
Praachya:
(a) Anga
(b) Magadha
(c) Kikat
(d) Shalva
Answer:
(d) Shalva

Question 2.
Madhyadesha:
(a) Aja
(b) Bharata
(c) Vaikarna
(d) Matsya
Answer:
(c) Vaikarna

Question 3.
Praatichya:
(a) Anu
(b) Pundra
(c) Bhalan
(d) Parashu
Answer:
(b) Pundra

Question 4.
Terms of ancient states:
(a) Rajya
(b) Savaarajya
(c) Bhaujya
(d) Mahajanapad
Answer:
(d) Mahajanapad

2A. Write the names of historical places, persons, and events.

Question 1.
The region occupied by Janas
Answer:
Janapada

Question 2.
Settlement
Answer:
Grama

Question 3.
Extended family
Answer:
Kula

Question 4.
Two assemblies
Answer:
Sabha and Samiti

Question 5.
Chief of Janapada
Answer:
Raja

Question 6.
Ruling class
Answer:
Gana

Question 7.
Regional Zones
Answer:
Khanda

Question 8.
Elective representative of the respective regional zone.
Answer:
Ganamukhya

Question 9.
Trade and commerce
Answer:
Varta

Question 10.
Highest decision-making authority
Answer:
Ganaparishada

2B. Choose the correct reason and complete the sentence.

Question 1.
The Ganasangha of Kamboj and Saurashtra are mentioned in Varta-Shastropajivi. Because __________
(a) they were skilled in trade and commerce.
(b) they were created by more than one kula coming together.
(c) some of them were divided into regional zones.
(d) they were oligarchies
Answer:
(a) they were skilled in trade and commerce.

Question 2.
Sense of territoriality and the ensuing awareness of autonomy were the main factors responsible for the __________
(a) geographic boundaries among the Janas.
(b) administrative structures among the Janas.
(c) migration and spread from the Saptasindhu region to the delta region of the Ganga.
(d) formation of ancient janapadas in India.
Answer:
(d) formation of ancient janapadas in India.

Question 3.
The Later Vedic literature, Jaina, and Buddhist literature indicate that __________
(a) some of the janapadas were of oligarchic type.
(b) most of the janapadas were monarchic states.
(c) the state was not ruled by a monarch but the members of the janapada run the state collectively.
(d) more than one ganrajyas coming together to create a sangharajya.
Answer:
(b) most of the janapadas were monarchic states.

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4. Explain the statement with reasons.

Question 1.
The geographic boundaries of a Jana were not defined.
Answer:

• Vedic people used the term Jana to designate a group of people, united under a common bond of singular kinship structure.
• Their settlement was known as ‘Grama’. A cluster of gramas consisting of the same Jana was known by the name of that particular Jana.
• In the beginning, however, the concept of Jana included only an extended family (kul), its settlement (grama), and the cattle pen (goshtha-gotra-gaulivada).
• The concept of Jana was not yet inclusive of the concept of territoriality.
• Hence, the geographic boundaries of a Jana were not defined.

Question 2.
Independent Janapada came into existence.
Answer:

• Vedic Janas gradually began to settle in the new region.
• The concept of Jana increasingly acquired a sense of territoriality.
• The sense of territoriality instilled the sense of geographic boundaries among the Janas.
• It resulted in the emergence of informal local administrative structures among the Janas.
• Thus, independent Janapada came into existence.

5. State your opinion.

Question 1.
Some of the Ganasanghas were divided into regional zones called ‘Khanda’.
Answer:

• The regional zones were known as Khandas.
• They functioned through a group of elected individuals who were found capable.
• Each of the elected members represented his respective Khanda.
• These elected members were installed with collective authority for the smooth running of the Ganasangha.
• This was a democratic system.
• Such Ganasanghas existed in Punjab and Sindh at the time of Alexander’s invasion.

Question 2.
The period of Janapadas saw the rise of the warrior class.
Answer:

• The warrior class people were well-trained in warfare.
• This class of warriors played a major role in the shift of the primary organisation of the janapadas to a more complex state organisation.
• Janapadin is a term mentioned in Panini’s Ashtadhyayi, used to indicate the warrior class.
• Thus, the period of Janapadas saw the rise of the warrior class.

Question 3.
Uttara Kuru and Uttara Madra were of‘Vairajya’ type.
Answer:

• This means that the state was not ruled by a monarch but the members of the Janapada run the state collectively.
• The ancient literature mentions types of states such as ‘Ganasangha’ or ‘Sangharajya’ (oligarchy/republic).
• Thus, Uttar Kuru and Uttar Madra were of the ‘Vairajya’ type.

6. Answer the following questions in detail.

Question 1.
Write in detail about the expansion and development of the Janapadas.
Answer:
The expansion and development of the Janapadas seem to have occurred in three different ways:

• Expansion and development of a society formed into a Jana by uniting of a number of generations of a singular kula (family). For example, the Janapadas namely, Matsya, Chedi, Gandhara, Kashi, Kosala, etc.
• Janapadas rising out of the union of more than one kula. For example, the Panchala janapada. Who were the five Janas united under the name of Panchalas, is not exactly known? According to the renowned historian, Hemchandra Raychaudhuri the following were the Janas who merged together as Panchalas: Krivi, Turvasha, Keshi, Shrinajaya, and Somaka.
• The more powerful Janapadas conquered the less powerful ones.

7. Answer the following questions with help of given points.

Question 1.
Write about:
(a) Janapada
(b) Territoriality and Autonomous Functioning
Answer:
(a) Janapada:

• The term ‘Janapada’ occurs in the Brahmana texts for the first time.
• Thereafter, it is frequently used in the Vedic literature and the epics – Mahabharata and Ramayana, as also in the Jain and the Buddhist literature.
• Considering the ancient Indian geographic perception with reference to the Janapadas, the said literature seems to divide the Indian subcontinent into five sections:
  • ‘Praachya’ – of the east
  • ‘Praatichya’ – of the west
  • ‘Udichya’ – of the north
  • ‘Dakshina’ – of the south
  • ‘Madhyadesha’ – The central region

(b) Territoriality and Autonomous Functioning:

• It may be noted, that the sense of territoriality and the ensuing awareness of autonomy were the main factors responsible for the formation of ancient Janapadas in India.
• However, their administrative system was not much different from that of the Janas in Rigveda.
• The chief of the Janapada was known as ‘Raj an’.
• Two assemblies are known as ‘Sabha’ and ‘Samiti’ were at the apex of all administrative decision-making processes, since the very beginning of the Vedic period.

Question 2.
Write about some of the ancient Janapadas and the literary texts that mention their names.
Answer:
Some of the ancient Janapadas and the literary texts that mention their names are as follows:

• Praachya: Anga, Magadh (Atharvaveda): Kikata (Rigveda and Atharvaveda) Pundra (Mahabharata)
• Praatichya: Anu, Alin, Bhalan, Druhyu, Parashu, Pakhta, Puru, Turvasha, Yadu (Rigveda), Gandhara (Rigveda and Athrvaveda), Shalva (Mahabharata)
• Udichya: Krivi, Vaikarna (Rigveda) Balhik (Atharvaveda)
• Dakshina: Andhra (Mahabharata) Pulinda (Emperor Ashoka’s edicts)
• Madhyadesha: Aja, Chedi, Bharata, Matsya, Shigru, Trutsu, Ushinara, Yakshu (Rigveda), Kuru, Shrinjaya (Rigveda and Atharvaveda).

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 4 Vedic Period Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 4 Vedic Period

1A. Choose the correct alternative and write the complete sentences.

Question 1.
____________ was composed in India around 1500 B.C.E.
(a) Atharvaveda
(b) Samaveda
(c) Yajurveda
(d) Rigveda
Answer:
(d) Rigveda

Question 2.
In the year 1583, an Italian merchant ____________ came to Kochi, Kerala.
(a) Vasco da Gama
(b) Filippo Sassetti
(c) Albuquerque
(d) Ferdinand
Answer:
(b) Fillippo Sassetti

Question 3.
The texts of the four Vedas are known as the ____________
(a) Aranyaka
(b) Brahmanas
(c) Samhitas
(d) Upanishads
Answer:
(c) Samhitas

Question 4.
The verses in the Rigveda are known as ____________
(a) Ruchas
(b) Suktas
(c) Mandala
(d) Mantras
Answer:
(a) Ruchas

Question 5.
The Vedic society was organised into four classes known as ____________
(a) Ashramas
(b) Varnas
(c) Javas
(d) Mahajanapadas
Answer:
(b) Varnas

Question 6.
____________ mentioned as the Lord of Urvara.
(a) Agni
(b) Varun
(c) Indra
(d) Pushan
Answer:
(b) Varun

Question 7.
The chariot makers in the Vedic Period were known as ____________
(a) Rathakara
(b) Taksham
(c) Kulal
(d) Vaya
Answer:
(a) Rathakara

Question 8.
The verses in ____________ is known on ‘Rueha’.
(a) Samaveda
(b) Rigveda
(c) Atharvaveda
(d) Yajurveda
Answer:
(b) Rigveda

Question 9.
The ____________ is regarded as the text that is fundamental in development of Indian music.
(a) Rigveda
(b) Samaveda
(c) Yajurveda
(d) Atharvaveda
Answer:
(b) Samaveda

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Rigveda	Suktas (hymns)
(b) Yajurveda	Explanation of the sacrificial rituals
(c) Samaveda	Rules of reciting mantras
(d) Atharvaveda	Rules of grammar

Answer:
(d) Atharvaveda – Charms and medicines for various problems and diseases

Question 2.

Set ‘A’	Set ‘B’
(a) Shatdru	Sutlej
(b) Asikni	Chinab
(c) Parushi	Bias
(d) Vitasta	Jhelum

Answer:
(c) Parushi – Ravi

Question 3.

Set ‘A’	Set ‘B’
(a) Kubha	Kabul
(b) Gomati	Gomal
(c) Suvastu	Swat
(d) ‘God’s Country	Devraya Desh

Answer:
(d) ‘God’s Country’ – Devnirmit Desh

1C. Find the odd one out.

Question 1.
Deities of the Vedic period:
(a) Indra
(b) Varun
(c) Ashwins
(d) Rathakara
Answer:
(d) Rathakara

Question 2.
Rivers of the Saptasindhu:
(a) Shatdru
(b) Vipas
(c) Asikni
(d) Cauvery
Answer:
(d) Cauvery

Question 3.
The Vedas:
(a) Rigveda
(b)Yajurveda
(c) Upanishad
(d) Atharvaveda
Answer:
(c) Upanishad

Question 4.
Terms associated with the textile industry:
(a) Tantum
(b) Otum
(c) Shuttle
(d) Uran
Answer:
(d) Uran

2A. Write the names of historical places, persons, and events.

Question 1.
Asiatic Society of Bengal in 1784.
Answer:
Sir William Jones

Question 2.
Tribal Settlements.
Answer:
Krishtya

Question 3.
Earthen Jars in Marathi.
Answer:
Rahatgadage

Question 4.
Vedic name for carpenters.
Answer:
Takshan

Question 5.
Vedic name for the weaver.
Answer:
Vaya

Question 6.
Two well-known epics.
Answer:
Ramayana and Mahabharata

Question 7.
River transport.
Answer:
Navya

2B. Choose the correct reason and complete the sentence.

Question 1.
The Rigvedic culture is the culture of the ____________
(a) Early Vedic period
(b) Late Vedic Period
(c) Post Vedic Period
(d) Pre Vedic period
Answer:
(a) Early Vedic period

Question 2.
The Atharvaveda contains information about ____________
(a) Science, Technology and Inventions.
(b) Charms and medicines for various problems and diseases.
(c) Day-to-day life.
(d) The norms of statesmanship.
Answer:
(b) Charms and medicines for various problems and diseases.

Question 3.
The ____________ also mentions trade by exchange, negotiations, and traders travelling far and wide to earn profits.
(a) Atharvaveda
(b) Samaveda
(c) Yajurveda
(d) Rigveda
Answer:
(d) Rigveda

2C. Write the correct chronological order.

Question 1.
(a) Brahmanas
(b) Aryamka
(c) Vedas
(d) Upanishada
Answer:
(a) Vedas
(b) Brahmanas
(c) Aryamka
(d) Upanishads

Question 2.
(a) Grihasthashram
(b) Vanaprasthashram
(c) Brahmacharyashram
(d) Sanyasashram
Answer:
(a) Brahmacharyashram
(b) Grihasthashram
(c) Vanaprasthashram
(d) Sanyasashram

Question 3.
(a) Vedic Literature and Social organisation of Vedic Times
(b) Vedic literature, Linguistics, and Archaeology
(c) Later Vedic Period
(d) The Early Vedic Culture
Answer:
(a) Vedic literature, Linguistics, and Archaeology
(b) Vedic Literature and Social organisation of Vedic Times
(c) The Early Vedic Culture
(d) Later Vedic Period

3. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

4. Explain the following concepts.

Question 1.
Varna System.
Answer:

• The Vedic society was organized into four classes known as ‘Varna’, namely, Brahmana, Kshatriya, Vaishya, and Shudra.
• The varna system is first mentioned in the tenth mandala (chapter) of the Rigveda.
• In the later Vedic period, the varna system lost its flexibility.
• Also, the caste system got rooted firmly by this period.
• In the beginning, the varna or the caste was decided by one’s occupation.
• Later it came to be determined on the basis of birth.

5. Explain the statement with reasons.

Question 1.
It became impossible to change one’s Varna and caste in which he/she was born.
Answer:

• The varna system is first mentioned in the tenth mandala (chapter) of the Rigveda.
• In the later Vedic period, the varna system lost its flexibility.
• Also, the caste system got rooted firmly by this period.
• In the beginning, the varna or the caste was decided by one’s occupation.
• Later it came to be determined on the basis of birth.
• Hence it became impossible to change one’s varna and caste, in which he/she was born.

Question 2.
Vedic literature is supposed to be the earliest literature of India.
Answer:

• The language of Vedic Literature in Sanskrit and it is one of the oldest languages.
• Vid’ in Sanskrit means to know and ‘Ved’ means knowledge.
• The four Vedas namely, Rigveda, Yajurveda, Samaveda, and Atharvaveda form the core of the Vedic literature.
• The texts of these four Vedas are known as the ‘Samhitas’.
• Thus, the Vedic literature is supposed to be the earliest literature of India.

Question 3.
Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.
Answer:

• The Yajurveda offers an explanation of the sacrificial rituals.
• It explains when and how the mantras should be used.
• A Rigvedic Richa, when recited in sacrificial rituals, is regarded as Mantra.
• Thus, the Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.

6. State your opinion.

Question 1.
Later Vedic Period saw the spread of Later Vedic culture from the foothills of the Himalayas in the north to the Vindhya Mountains in the south.
Answer:

• Later Vedic Period is dated to around 1000-600 B.C.E. The information about this period is gathered from the treatises written in that period.
• The material culture as reflected in the epics, Ramayana and Mahabharata was studied with the help of archaeological evidence.
• A picture of the migration in the Later Vedic period can be gathered from the Saptasindhu region toward the east and its geographic markers from the literature of that period.
• Thus, this period saw the spread of Later Vedic culture from the foothills of the Himalayas in the north to the Vindhya Mountains in the south.

7. Answer the following questions in detail.

Question 1.
Write a note on Vedic literature in detail.
Answer:

• Vedic literature is supposed to be the earliest literature of India. Its language is Sanskrit.
• The four Vedas form the core of Vedic literature, i.e., Rigveda, Yajurveda, Samaveda and Atharvaveda.
• The texts of these four Vedas are known as ‘Samhitas’ vid in Sanskrit means ‘to know’ and Veda means ‘knowledge.
• The Rigveda contains Suktas (hymns) composed to eulogize the deities.
• The verses in the Rigveda are known as ‘Rucha’. A number of Ruchas strung together to make a Sukta (hymn).
• Many Suktas make one Mandala. The Yajurveda offers explanations of rituals.
• It explains how and when mantras are to be used. The Samaveda is a text that gives the rules of reciting mantras in a musical form.
• The Atharvaveda is about day-to-day life. It contains information about charms and medicines.

Question 2.
Write a note on the Later Vedic period in detail.
Answer:

• The Later Vedic period is dated around 1000-600 B.C.E. The treatises of the period give information about this period.
• This period saw the spread of Later Vedic from the foothills of the Himalayas in the north to the Vindhyas in the south.
• A story in the Satapatha Brahmana bears evidence of the Later Vedic period settling and bringing land under cultivation from west to east.
• The Later Vedic period saw a gradual formation of the confederacies of the Vedic villages. They were known as ‘Janapadas’.
• Generally, the seniors and the elites in a Janapada collectively took social decisions.
• They functioned like oligarchic states. These slowly expanded into Mahajanapadas.

Question 3.
Write about the following:
(a) Varna System
(b) Ashrama System
Answer:
(a) Varna System:

• The Vedic society was organised into four classes known as “Varna’ namely Brahmana Kshatriya, Vaishya, and Shudra.
• The Varna system is mentioned in the 10th Mandala (chapter) of the Rigveda.
• In the Later Vedic period, the varna system became rigid. Also, the caste system got firmly rooted.
• In the beginning, the varna or the caste was decided by one’s occupation later it came to be determined on the basis of birth.

(b) Ashrama System: The Ashrama System of the Vedic period was divided into four stages namely Brahmacharya Ashram, Grihastha Ashram, Vanaprastha Ashrama, and Sanyasa Ashrama.

• In the first stage, one was expected to spend an austere life and earn knowledge and necessary occupational skills.
• In the second stage, one was expected to fulfill one’s prescribed duties with one’s wife by his side.
• In the third stage, one was expected to retire from the active life of a householder.
• It was also desirable that one should stay away from human settlement, renounce all family bonds, accept a wandering life, etc.
• A Sanyasi was to give up all worldly attachments and not be permitted to settle at one place for a longer time.

8. Answer the following questions with the help of given points.

Question 1.
Write a note on Ashrama System with the help of stages involved in it.
Answer:
The Ashrama System of the Vedic culture lays down the norms of living an ideal life by dividing the span of human life into four successive stages, namely Brahmacharyashram, Grihasthashram, Vanaprasthashram, and Sanyasashram.

• In the first stage, one was expected to spend an austere life and earn knowledge and necessary occupational skills.
• In the second stage, one was expected to fulfill one’s prescribed duties with one’s wife by his side.
• In the third stage, one was expected to retire from the active life of the householder and if the need is to give advice to the younger people. It was also desirable that one should stay away from human settlement.
• In the fourth and the last stage one was expected to renounce all the family bonds, accept a wandering life, and go away. A Sanyasi was not permitted to settle at one place for a longer time.

Question 2.
Write a note on Vedic Literature:
(a) Rigveda
(b) Yajurveda
(c) Samaveda
(d) Atharvaveda
Answer:
Vedic literature is supposed to be the earliest literature of India. Its language is Sanskrit. The four Vedas namely, Rigveda, Yajurveda, Samaveda, and Atharvaveda form the core of the Vedic literature.

(a) Rigveda: The Rigveda contains Suktas (hymns) composed to eulogize the deities. The verses in Rigveda are known as ‘Rucha’. A number of Ruchas strung together makes a Sukta (hymn). Many Suktas make one Mandala.

(b) Yajurveda: The Yajurveda offers an explanation of the sacrificial rituals. It explains when and how the mantras should be used. A Rigvedic Richa, when recited in sacrificial rituals, is regarded as Mantra. The Yajurveda is a combined composition of the Rigvedic richa in verse and the explanation of its use as a mantra in prose.

(c) Samaveda: The Samaveda is a text that gives the rules of reciting mantras in a musical form. The Samaveda is regarded as the text that is fundamental in the development of Indian music.

(d) Atharvaveda: The Atharvaveda is about day-to-day life. It contains information about charms and medicines for various problems and diseases. It also talks about the norms of statesmanship.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 3 Chalcolithic Villages in India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 3 Chalcolithic Villages in India

1A. Choose the correct alternative and write the complete sentences.

Question 1.
___________ culture at Balathal is dated to 4000 B.C.E.
(a) Ahar
(b) Jorwe
(c) Ganeshwar-Jodhpura
(d) Malwa
Answer:
(a) Ahar

Question 2.
Ahar culture is also known as ___________ culture.
(a) Jorwe
(b) Kayatha
(c) Banas
(d) Savalda
Answer:
(c) Banas

Question 3.
___________ is a site situated on the bank of the river known as Chhoti Kali Sindh.
(a) Savalda
(b) Navadatoli
(c) Malwa
(d) Kayatha
Answer:
(d) Kayatha

Question 4.
___________ was known as ‘Rangpur’.
(a) Maharashtra
(b) Gujarat
(c) Madhya Pradesh
(d) Rajasthan
Answer:
(b) Gujarat

Question 5.
Savalda is in ___________ district.
(a) Satara
(b) Ratnagiri
(c) Dhule
(d) Pune
Answer:
(c) Dhule

Question 6.
The culture in south Gujarat is known as ___________ culture.
(a) Pravhas
(b) Nevase
(c) Malwa
(d) Rangpur
Answer:
(a) Pravhas

Question 7.
The age when huge stone slabs were used is known as ___________ age.
(a) Palaeolithic
(b) Mesolithic
(c) Neolithic
(d) Megalithic
Answer:
(d) Megalithic

Question 8.
The archaeological evidence shows that ___________ was a centre of mass production of pottery.
(a) Gilund
(b) Khethri
(c) Balathal
(d) Baras
Answer:
(c) Balathal

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Malwa Culture	1600-1400 B.C.E.
(b) Megalithic circles in India	1500-500 B.C.E
(c) Early Jorwe Culture	1400-1000 B.C.E.
(d) Late Jorwe Culture	1000-800 B.C.E.

Answer:
(d) Late Jorwe Culture – 1000-700 B.C.E.

Question 2.

Set ‘A’	Set ‘B’
(a) Early Harappan phase	3950-2600 B.C.E.
(b) Mature (urban) phase	2500-1800 B.C.E.
(c) Savalda culture	2000-1800 B.C.E.
(d) Post-Harappan phase	1900-900 B.C.E.

Answer:
(b) Mature (urban) phase – 2600-1900 B.C.E.

1C. Find the odd one out.

Question 1.
Ahar, Kayatha, Malwa, Mohenjodaro.
Answer:
Mohenjodaro

Question 2.
Early Harappan phase, Mature (Urban) phase, Pre Harappan Phase, Post-Harappan phase.
Answer:
Pre Harappan Phase

Question 3.
Malwa Culture, Early Jorwe Culture, Late Jorwe Culture, Post Late Jorwe Culture.
Answer:
Post-Late Jorwe Culture

Question 4.
Odisha, Todas, Kurumbas, Nagas.
Answer:
Nagas

Question 5.
Takalghat, Mahuzari, Khasis, Khapa.
Answer:
Khasis

Question 6.
Godavari, Inamgaon, Tapi, Bhima.
Answer:
Inamgaon

2A. Write the names of historical places, persons, and events.

Question 1.
A tributary of the river Banas
Answer:
Ahar

Question 2.
The culture found at Khetri
Answer:
Ganeshwar-Jodhpura

Question 3.
Pottery found in river beds
Answer:
Ochre coloured pottery

Question 4.
An important site of Malwa culture on the banks of Narmada
Answer:
Navadatoli

Question 5.
Tribes in Odisha
Answer:
Bodos

Question 6.
Furnace discovered near Nagpur
Answer:
Naikund

2B. Choose the correct reason and complete the sentence.

Question 1.
Ochre Coloured Pottery (OCP) and copper hoards are supposed to belong ___________
(a) one and the same culture
(b) one and the another culture
(c) similar culture
(d) different culture
Answer:
(a) one and the same culture

Question 2.
People of the Mature Harappan and the Late Harappan culture had the knowledge of ___________
(a) designs include motifs like sun, moon, fish, deer, and peacock
(b) wheel-made pottery
(c) the technology of making copper objects
(d) excavations of copper artifacts
Answer:
(b) wheel-made pottery

Question 3.
Kayatha culture was contemporary to the ___________
(a) Dholavira region
(b) Mohenjodaro
(c) Banas culture
(d) Harappan Civilisation
Answer:
(d) Harappan Civilisation

Question 4.
Ahar culture at Balathal is dated to ___________
(a) 400 B.C.E
(b) 40 B.C.E
(c) 4000 B.C.E
(d) 40000 B.C.E
Answer:
(c) 4000 B.C.E

2C. Write the correct chronological order.

Question 1.
(a) Malwa culture – 1800 B.C.
(b) Early Jorwe culture – 1400 B.C.
(c) Ahar culture – 4000 B.C.E.
(d) Savalda culture – 2000 B.C.E.
Answer:
(a) Ahar culture – 4000 B.C.E.
(b) Savalda culture – 2000 B.C.E.
(c) Malwa culture – 1800 B.C.E.
(d) Early Jorwe culture – 1400 B.C.E.

Question 2.
(a) Late Jorwe Culture – 1000-700 B.C.E.
(b) Kutch – Saurashtra was abandoned by 1900 B.C.E.
(c) Early Jorwe Culture – 1400-1000 B.C.E.
(d) Malwa Culture – 1600-1400 B.C.E.
Answer:
(a) Kutch – Saurashtra were abandoned by 1900 B.C.E.
(b) Malwa Culture – 1600-1400 BCE
(c) Early Jorwe Culture – 1400-1000 B.C.E.
(d) Late Jorwe Culture – 1000-700 B.C.E.

Question 3.
(a) Mature (urban) phase – 2600-1900 B.C.E.
(b) ‘Ahar’ culture at Balathal – 4000 B.C.E.
(c) Post-Harappan phase – 1900-900 B.C.E.
(d) Early Harappan phase – 3950-2600 B.C.E.
Answer:
(a) ‘Ahar’ culture at Balathal – 4000 B.C.E.
(b) Early Harappan phase – 3950-2600 B.C.E.
(c) Mature (urban) phase – 2600-1900 B.C.E.
(d) Post-Harappan phase – 1900-900 B.C.E.

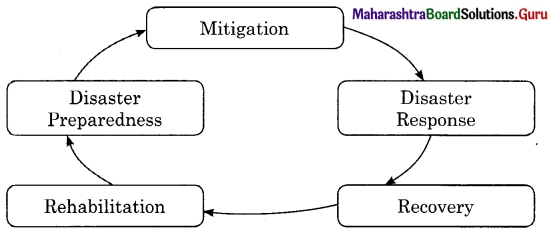
3. Complete the concept maps.

Question 1.

Answer:

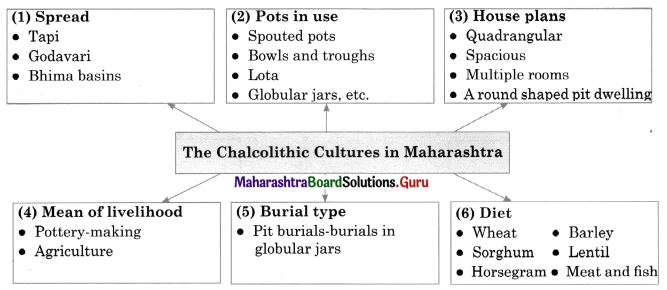
Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

4. Write short notes.

Question 1.
Ochre coloured pottery
Answer:

• Initially, the Ochre Coloured Pottery (OCP) was mostly found in river beds.
• Generally, the potsherds of OCP are found in worn-out, rounded, and brittle conditions as they remained in flowing water for a long time.
• A number of sites of the OCP are found in Punjab, Haryana, Rajasthan, and the western region of Uttar Pradesh.
• The OCP culture in Rajasthan is dated about 3000 B.C.E.

Question 2.
Jorwe Pottery
Answer:

• Jorwe pots are well baked giving a metallic sound and designs on these pots are painted in brown.
• They are red in colour with designs painted in black.
• Jorwe pottery includes shapes like spouted pots, carinated bowls, and troughs (carination is the central ridge on the pot), lota, globular jars, etc.
• The Late Jorwe people made pots of the same shapes, but without any decoration.

5. Explain the statements with reasons.

Question 1.
There were two chalcolithic cultures in Gujarat, in the post-Harappan period.
Answer:

• In the post-Harappan period, there were two chalcolithic cultures in Gujarat.
• The culture in south Gujarat was known as ‘Prabhas’ culture and the one in northeastern Gujarat was known as ‘Rangpur’ culture.
• The pottery of these chalcolithic cultures was akin to Late Harappan pottery with regards to the colour, shapes, and designs.
• These cultures existed till 1800-1200 B.C.E.

Question 2.
Savalda people and The Harappans in Saurashtra had trade relations.
Answer:

• There was a cultural contact between the Savalda people and the Harappans in Saurashtra.
• Its evidence has been found at the site of Kaothe in Dhule district.
• The artifacts made of chank shells found at Kaothe confirm that the Savalda people and The Harappans in Saurashtra had trade relations.

6. State your opinion.

Question 1.
Kayatha culture was contemporary to the Harappan civilisation.
Answer:

• The people of Kayatha culture subsisted on agriculture and animal husbandry.
• They mainly used handmade pots and microliths.
• Artifacts like copper axes and bangles, necklaces made of beads of steatite were found in the Kayatha houses.
• People of Kayatha culture and Harappan culture seem to have been in contact much before the rise of the Harappan cities.

Question 2.
Ochre Coloured Pottery (OCP) and copper hoards are supposed to belong to one and the same culture.
Answer:

• The Copper Hoards found in India come from various regions, such as Uttar Pradesh, Bihar, Bengal, Odisha, and Madhya Pradesh.
• The copper objects found in these hoards indicate that the artisans who fashioned them were very highly skilled.
• The archaeological sites of OCP and the find-spots of the copper hoards often seem to be situated in the same vicinity, not very distant from each other.
• Hence, OCP and copper hoards are supposed to belong to one and the same culture.

7. Answers the following questions in detail.

Question 1.
Write a note on ‘Jorwe’ pottery.
Answer:

• Jorwe pots are well baked giving a metallic sound. They are red in colour with designs painted in black.
• Jorwe pottery includes shapes like spouted pots, carinated bowls, and troughs, lota, globular jars, etc.
• The late Jorwe people made pots of the same shapes but without any decoration.
• Potters kilns were found in both Malwa and Early Jorwe periods.
• They were round in shape. The kiln of the early Jowre period was larger and of greater capacity.
• In the late Jorwe period potters did not have a specially built kiln. They baked their pots directly on the ground.
• Inamgaon was the centre of pottery production which supplied pottery to the surrounding villages.

Question 2.
Discuss the Megalithic period in India.
Answer:

• A nomadic people around 700 B.C.E. erected stone circles by using huge slabs of rock.
• The space within these circles was used to bury dead people.
• These circles are known as Megaliths. The period of these Megaliths is known as the ‘Megalithic Age’.
• They were used for various purposes, but mainly they contain the remains of the dead.
• They were the memorials of the dead. Such megalithic circles have been found in many parts of the world.
• A few tribes in India practice it even today. For instance; the Bodos in Odisha, Todas, and Kurumbas in South India.
• Nagas and Khasis in Northeast India. Most of these circles in India are dated to 1500-500 B.C.E.
• Perhaps these people were from South India. The Megalithic circles in Maharashtra belong to the Iron Age. They are dated to 1000-400 B.C.E.
• In Maharashtra, Megalithic burials have been found in the Vidarbha region especially in the districts of Nagpur, Chandrapur, and Bhandara.
• Megalithic people used horses for transport and travel. They were instrumental in introducing the ‘Iron Age’ in ancient India.

8. Answer the following questions with the help of given points.

Question 1.
Write a note with the help of the following points:
(a) ‘Ahar’ or ‘Banas’ Culture
(b) Ganeshwar – Jodhpur Culture
(c) Kayatha Culture
(d) Malwa Culture
Answer:
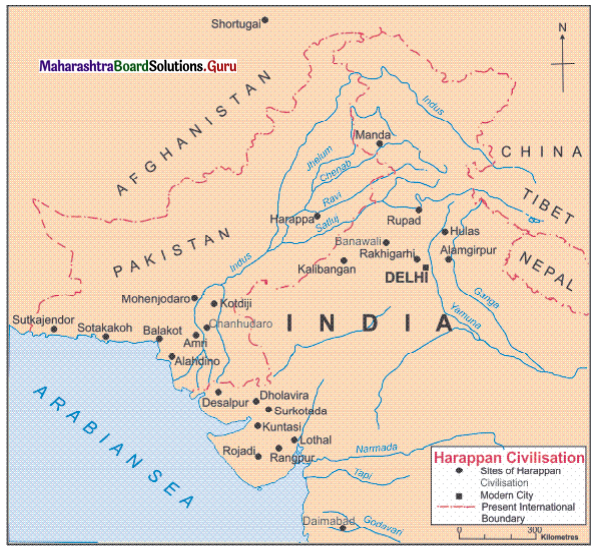
(a) ‘Ahar’ or ‘Banas’ Culture: The chalcolithic cultures in India generally belong to the post- Harappan period. However, the ‘Ahar’ or ‘Banas’ culture in the Mewad region of Rajasthan was contemporary to the Harappan civilisation. Balathal and Gilund near Udaipur are the important sites of Ahar culture. ‘Ahar’ culture at Balathal is dated to 4000 B.C.E and was first discovered at Ahar near Udaipur, so it was named as ‘Ahar’ culture.

(b) Ganeshwar-Jodhpura Culture: Many sites of the culture known as ‘Ganeshwar-Jodhpura’ culture have been found in the vicinity of the copper mines at Khetri. The settlements there are earlier than the Harappan civilisation. During the excavations at Ganeshwar copper artifacts like arrowheads, spearheads, harpoons, bangles, chisels, and also pottery was found. The people of Ganeshwar-Jodhpura culture supplied copper objects to the Harappans.

(c) Kayatha Culture: Kayatha is a site situated on the banks of the river known as Chhoti Kali Sindh, at a distance of 25 kilometers from Ujjain in Madhya Pradesh. Kayatha culture was contemporary to the Harappan civilisation. The people of Kayatha culture subsisted on agriculture and animal husbandry.

(d) Malwa Culture: The name ‘Malwa’ obviously tells us that this culture originated and spread first in the Malwa region. It existed in Madhya Pradesh during 1800-1200 B.C.E. ‘Navadatoli’ situated on the river Narmada, on the opposite bank of Maheshwar, is an important site of Malwa culture. The other important sites are Eran (District Sagar) and Nagda (District Ujjain). They were surrounded by protective walls.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 2 First Cities of India Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 2 First Cities of India

1A. Choose the correct alternative and write the complete sentences.

Question 1.
The __________ empire was founded in 2334 B.C.E. by Emperor Sargon I.
(a) Egyptian
(b) Akkadian
(c) Meluhhan
(d) Mesopotamian
Answer:
(b) Akkadian

Question 2.
__________ is the largest Harappan site among all the sites from India and Pakistan.
(a) Lothal
(b) Dholavira
(c) Gulf of Kutch
(d) Rakhigarhi
Answer:
(d) Rakhigarhi

Question 3.
__________ was a small city compared to Harappa and Mohenjodaro.
(a) Kalibangan
(b) Lothal
(c) Dholavira
(d) Chahanudaro
Answer:
(a) Kalibangan

Question 4.
Lothal was excavated by __________
(a) J. P. Joshi
(b) S. R. Rao
(c) R. D. Banerjee
(d) Madho Swarup
Answer:
(b) S. R. Rao

Question 5.
__________ is described as Purandara.
(a) Agni
(b) Varuna
(c) Indra
(d) Vayu
Answer:
(c) Indra

1B. Find the incorrect pair from set B and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Kalibangan	Bikaner
(b) Mohenjodaro	Lothal
(c) Dholavira	Gujarat
(d) Rakhigarhi	Haryana

Answer:
(b) Mohenjodaro – Pakistan

Question 2.

Set ‘A’	Set ‘B’
(a) Vedic Aryans arrived in India	1500 B.C.E
(b) Discovery of Harappa	1931
(c) Discovery of Mohenjodaro	1922
(d) Total Area covered	1500000

Answer:
(b) Discovery of Harappa – 1921

Question 3.

Set ‘A’	Set ‘B’
(a) Pre-Harappan Cultures	Cultures of the period preceding the Harappan civilisation
(b) Early Harappan period	Late Harappan phase
(c) Mature (Urban) Harappan period	The fully developed phase of Harappan civilisation
(d) Late Harappan period	The period after the decline of the mature (Urban) phase

Answer:
(b) Early Harappan period – Early (beginning) Harappan phase

1C. Find the odd one out.

Question 1.
History of Harappan cities:
(a) Early Harappan
(b) Mature Harappan
(c) Vedic Period
(d) Late Harappan
Answer:
(c) Vedic Period

Question 2.
An archaeologist who excavated Harappan culture:
(a) Sir Alexander Cunningham
(b) Charles Masson
(c) R.K. Banerjee
(d) Sir John Marshall
Answer:
(b) Charles Masson

Question 3.
Harappan Period Sea trade route.
(a) Dilmun
(b) Makan
(c) Meluhha
(d) Lothal
Answer:
(d) Lothal

Question 4.
Religious centers of Harappa:
(a) Mohenjodaro
(b) Lotha
(c) Dholavira
(d) Kalibangan
Answer:
(c) Dholavira

2A. Write the names of historical places, persons, and events.

Question 1.
The city is situated on the banks of the river Ravi in Punjab, Pakistan.
Answer:
Harappa

Question 2.
British traveler who visited and wrote about archaeological remains at Harappa.
Answer:
Charles Masson

Question 3.
First Director-General of the Archaeological Survey of India.
Answer:
Sir Alexander Cunningham

Question 4.
Discovery of Harappa.
Answer:
1921

Question 5.
Excavations at Mohenjodaro.
Answer:
Rakhaldas Banerjee

Question 6.
Remains of Harappan dock in Gujarat.
Answer:
Lothal

Question 7.
Harappan settlement of Shortugai.
Answer:
Badakshan, Afghanistan

Question 8.
Mesopotamian temples.
Answer:
Ziggurats

2B. Choose the correct reason and complete the sentence.

Question 1.
The ancient civilisations of Mesopotamia and Harappa had cultural ties with each other because of __________
(a) fortifications
(b) the similarity between seals and artifacts
(c) public monuments were found
(d) impressive town planning
Answer:
(b) the similarity between seals and artifacts

Question 2.
The evidence of the first excavations at Harappa had indicated __________
(a) the first settlement of the Early Harappan period was established around 3300 B.C.E
(b) the city of Harappa was divided into two parts – the ‘Citadel’ and the ‘Lower Town’.
(c) internal changes begin to appear in Harappan cities.
(d) the decline of Harappan civilisation.
Answer:
(b) the city of Harappa was divided into two parts – the ‘Citadel’ and the ‘Lower Town’

Question 3.
The first settlement of the Early Harappan period was established __________
(a) around 2500 B.C.E
(b) around 2500 – 2800 B.C.E
(c) around 2600 B.C.E
(d) around 3300 B.C.E
Answer:
(d) around 3300 B.C.E

2C. Write the correct chronological order.

Question 1.
(a) Vedic Aryans
(b) Late Harappan period
(c) Mature Harappan period
(d) Early Harappan period
Answer:
(a) Early Harappan period
(b) Mature Harappan period
(c) Late Harappan period
(d) Vedic Aryans

Question 2.
(a) Mature (Urban) Harappan period
(b) Early Harappan period
(c) Post Harappan cultures
(d) Late Harappan period
Answer:
(a) Early Harappan period
(b) Mature (Urban) Harappan period
(c) Late Harappan period
(d) Post Harappan cultures

Question 3.
(a) Discovery of Harappa
(b) Excavation of Dholavira
(c) Excavation of Lothal
(d) Discovery of Mohenjodaro
Answer:
(a) Discovery of Harappa (1921)
(b) Discovery of Mohenjodaro (1922)
(c) Excavation of Lothal (1995 – 1960)
(d) Excavation of Dholavira (1990)
[Note: Years in a bracket are only given for understanding]

3. Observe the map on page 13 of your textbook and answer the following questions based on it.

Question 1.
Point out some of the Harappan sites in India.
Answer:
Some of the Harappan sites in India are Kalibangan, Dholavira, Surkotda, Lothal, Rangpur.

Question 2.
Point out the Harappan sites in modern-day Pakistan.
Answer:
Harappan sites in modern day Pakistan are Mohenjodaro, Harappa, Chahnudaro, Balakot.

Question 3.
Point out the only Harappan site in Afghanistan.
Answer:
The only Harappan site in Afghanistan is Shortugai.

Question 4.
Point out the modern city of India.
Answer:
The modern city of India – Delhi.

Question 5.
Near which river Daimabad is located?
Answer:
Daimabad is located near Godavari River.

4. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

5. Write short notes.

Question 1.
Lothal
Answer:

• Lothal was excavated from 1955 to 1960 under the supervision of S.R. Rao.
• It is situated near the Gulf of Kutch in Gujarat, 80 km away from Ahmedabad.
• It is known for the remains of the Harappan dock.
• The ‘Citadel’ and the ‘Lower Town’ at Lothal are surrounded by a single fortification wall.
• Lothal was established on the banks of the river Bhogao.
• The presence of platforms built for stalls, a warehouse, and the dock confirm that Lothal was an important port and trading center. Lothal is an example of the engineering excellence of ancient people.

Question 2.
Lapis Lazuli Stone
Answer:

• Lapis Lazuli a semi-precious stone was found in the region of Badakshan province of Afghanistan, ‘Shortugai’.
• This region is rich with mines of lapis lazuli.
• There was a great demand for this stone in Mesopotamia.
• The Mesopotamian epics describe Goddess Inanna’s palace, the walls of which were embedded with this stone.
• This Stone was a very important commodity in the Harappan trade with Mesopotamia.

Question 3.
Ziggurats
Answer:

• Mesopotamian temples are known as ‘ziggurats’.
• The administrative system of the Mesopotamian Cities revolved around the administration of these temples.
• The high priest of the temple used to be the ruler of the city.
• The social life, cultural events, Power and hierarchy of officials, etc were organized in accordance with the rituals and festivals of the presiding deity of the temple.

Question 4.
Rakhigarhi
Answer:

• The Hissar district of Haryana has situated the site of Rakhigarhi, a Harappan city.
• It is at a distance of 150 kilometers from Delhi.
• It is located on the banks of Chautang (ancient Drishdvati river).
• Rakhigarhi is the largest Harappan site, among all the sites from India and Pakistan.
• Its total area was more than 350 Hectares. The excavations at Rakhigarhi started in 1963.
• It continued in 1997-2000. Later, Dr. Vasant Shinde of the Deccan College, Pune also conducted excavations at the site.

Question 5.
Harappan Sites
Answer:

• Many sites of the Early Harappan and Mature Harappan (Urban) phases have been found in the basin of the river Ghaggar.
• The latest research based on the evidence from sites like Kunal, Bhirrana, Farman, Girwad, and Mitathal, etc. indicates a possibility of the rise of the Mature Harappan more than 5000 years ago.
• The Harappan sites of Mohenjodaro, Harappa, Ganweriwala in Pakistan, and Rakhigarhi and Dholavira in India have been declared as World Heritage sites.

6. State your opinion.

Question 1.
The river known as ‘Ghaggar Hakra’ flows only during the monsoon.
Answer:

• River Gjaggar Hakra originates in the Siwalik Hills in Himachal Pradesh and flows to Rajasthan through Punjab and Haryana.
• From there it enters the Desert of Cholistan in Pakistan. Ultimately it enters the Rann of Kutch.
• It is known as Ghaggar in India and as Hakra in Pakistan. Its bed remains dry through the year except during the monsoon.
• Thus, a river known as ‘Ghaggar Hakra’ flows only during the monsoon.

7. Answer the following questions in detail.

Question 1.
Explain the interrelationship between cities and villages in the Harappan Civilisation.
Answer:

• The Harappan people depended on natural resources and villages in the vicinity in order to meet the needs of the urban way of life and urban administration.
• The raw material needed for industrial production included clay, various siliceous and semi¬precious stones, metals, etc.
• The interrelationship between Harappan cities and villages was dependent on the mechanism of making available things like food grains and raw materials.
• There was a network of small towns, small and big villages and campsites of semi-nomadic people which functioned to cater to the needs of major urban centers of the Harappan civilization.
• The best example of it is the Harappan Settlement of Shortugai.

Question 2.
Write in detail on Mesopotamian temples, ‘Ziggurats’.
Answer:

• Mesopotamia is known for its grand temples.
• The administrative system of Mesopotamian cities revolved around the administration of these temples.
• Mesopotamian temples are known as ‘ziggurats’.
• The high priest of the temple used to be the ruler of the city.
• The social life, cultural events, power and hierarchy of officials, etc were organized in accordance with the ritual and festival of the presiding deity of the temple.
• The notion of a ‘priest king’ of the Harappan civilisation was formulated by presuming its close similarity with the Mesopotamian culture.

Question 3.
Reasons for the decline of cities.
Answer:
The reasons for the decline of cities are as follows:

• It is known that the Harappan civilisation began to decline around 2000 – 1900 B.C.E.
• People had to regret elsewhere with the beginning of the later Harappan Period.
• The Harappan trade with Mesopotamia was on the decline in the late Harappan Period because the Mesopotamia economy had weakened.
• A deteriorating environment was the main reason for the decline of Mesopotamia.
• Similarly, climatic changes and deteriorating environment were the main reason for the decline of the Harappan civilisation too.
• The late Harappan people were forced to migrate became of natural calamities.
• New villages were settled by the Nature Harappan and Late Harappan people wherever they went.
• The Harappan civilization deteriorated as the cumulative effect of various factors such as a decline in trade, climatic changes, weakening of two economies.

8. Answer the following questions with the help of given points.

Question 1.
Write about some cities of Harappa with the help of the following points:
(a) Harappa
(b) Mohenjodaro
(c) Kalibangan
(d) Lothal
(e) Dholavira
(f) Rakhigarhi
Answer:
(a) Harappa:

• Harappa is situated on the banks of the river Ravi (District Sahiwal in Punjab, Pakistan).
• The ancient site of Harappa had spread on 150 Hectares.
• The first excavation at Harappa began in 1921. The first settlement of the Early Harappan Period was established around 3300 B.C.E.
• It evolved to the Mature Harappan (urban) phase around 2600 B.C.E. It reached its peak during 2450-1900 B.C.E.

(b) Mohenjodaro:

• Mohenjodaro was built on the banks of the river Sindhu (Indus) in Pakistan (District Larkana, Sindh).
• Area-wise, Mohenjodaro is the biggest city, among those discovered in Pakistan so far.
• It was thought that the city was divided into two fortified sections, namely the ‘Citadel’ and the ‘Lower Town’.
• The excavations at Mohenjodaro by Rakhaldas Banerjee began in 1921-22.
• In 1923- 24 to gather more information about Mohenjodaro Madho Sarup Vats, Kashinath Narayan Dikshit, Ernest Mackay, and others conducted further excavations under Sir John Marshall’s direction.
• He was the Director-General of the Archaeological Survey of India at that time.
• During these excavations, various artifacts, houses, and public monuments were unearthed.

(b) Kalibangan:

• The site of Kalibangan is 205 kilometers away from Bikaner. It is located in the Hanumangarh district of Rajasthan.
• It was one of the important urban centers of the Harappan civilisation, situated on the banks of the river Ghaggar.
• L. P. Tessitore, an Italian linguist had visited Kalibangan during his study tour of the region. It was conducted under the direction of Brijabasi Lai, the then Director-General of the Archaeological Survey of India, and Balkrishna Thapar.
• At Kalibangan two settlements, one of the Mature Harappan period and the other of the Early Harappan period, were found. Kalibangan was a small city compared to Harappa and Mohenjodaro.

(c) Lothal:

• Lothal was established on the bank of the river Bhogao.
• The center of the Harappan civilisation at Lothal was situated near the Gulf of Kutch, in Gujarat, 80 kilometers away from Ahmedabad.
• It is known for the remains of Harappan dock.
• Lothal was excavated from 1955 to 1960 under the supervision of S.R. Rao. The ‘Citadel’ and the ‘Lower Town’ at Lothal do not have separate fortification walls.
• Rather, they are surrounded by a single fortification wall.

(d) Dholavira:

• Dholavira was discovered by J.P. Joshi, the Director-General of Archaeological Survey of India. The site is in ‘Khadirbet’ in Gujarat (Dist. Kutch).
• Excavations at the site were started by R.S. Bisht in 1990.
• Among the excavated Harappan sites, extent wise Dholavira is the fifth-largest city.
• An Early Harappan settlement was discovered at Dholavira.
• There was a protective wall built around it by using mud bricks (unbaked bricks) and dressed stones. It was surrounded by an outer fortification wall.
• The settlement within the outer fortification was divided into four sections.
  • Citadel
  • The adjacent section reserved for high officials
  • Lower Town – These three sections had walls, which separated them from each other.
  • The fourth section inside the outer fortification did not have any additional separating walls.

(e) Rakhigarhi:

• The Hissar district of Haryana has situated at the site of Rakhigarhi, a Harappan city.
• It is at a distance of 150 kilometers from Delhi.
• It is located on the banks of Chautang (ancient Drishdvati river).
• Rakhigarhi is the largest Harappan site, among all the sites from India and Pakistan.
• Its total area was more than 350 Hectares.
• The excavations at Rakhigarhi started in 1963. It continued in 1997-2000.
• Later, Dr. Vasant Shinde of the Deccan College, Pune also conducted excavations at the site.

Balbharti Maharashtra State Board Class 11 History Important Questions Chapter 1 First Farmers Important Questions and Answers.

Maharashtra State Board 11th History Important Questions Chapter 1 First Farmers

1A. Choose the correct alternative and write the complete sentences.

Question 1.
____________ made the first stone tools.
(a) Homo erectus
(b) Home sapiens
(c) Homo habilis
(d) Homo phones
Answer:
(c) Homo habilis

Question 2.
Microliths were found in ____________ age.
(a) Neolithic
(b) Chalcolithic
(c) Mesolithic
(d) Palaeolithic
Answer:
(c) Mesolithic

Question 3.
Pasting wet clay ribbons and making patterns on them is known as ____________ work.
(a) application
(b) applique
(c) apply
(d) amalgamation
Answer:
(b) applique

Question 4.
In ____________ mesolithic man existed during 10000-4000 B.C.E.
(a) Uttar Pradesh
(b) Maharashtra
(c) Bihar
(d) Northeast India
Answer:
(b) Maharashtra

Question 5.
A ____________ site was found at Lahuradeva in Sant Kabirnagar district of Uttar Pradesh.
(a) Palaeolithic
(b) Mesolithic
(c) Neolithic
(d) Chalcolithic
Answer:
(c) Neolithic

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Egypt	Misra
(b) China	Sorrow
(c) Mesopotamia	First One
(d) Sindhu	Indus

Answer:
(c) Mesopotamia – Middle One

Question 2.

Set ‘A’	Set ‘B’
(a) First Neolithic villages	6000 B.C.E
(b) Agriculture in Neolithic villages in China	7000 B.C.E
(c) Existence of Mesolithic man	3000 B.C.E
(d) Neolithic settlements in Bihar	2000 B.C.E

Answer:
(c) Existence of Mesolithic man – 10000-4000

Question 3.

Set ‘A’	Set ‘B’
(a) Original name of Egypt	Kemet
(b) Arabic name of Egypt	Misra
(c) Greek name of Egypt	Egyptus
(d) English translation of Huang He	Hwat-ka-Pta

Answer:
(d) English translation of Huang He – Yellow River

1C. Find the odd one out.

Question 1.
Countries with ancient civilizations:
(a) Egypt
(b) China
(c) India
(d) England
Answer:
(d) England

Question 2.
Mesolithic tools:
(a) Fluted Core
(b) Screwdriver
(c) Blades
(d) Arrowheads
Answer:
(b) Screwdriver

Question 3.
Archaeological sites:
(a) Gilgal
(b) Inamgaon
(c) Aurangabad
(d) Lahuradeva
Answer:
(c) Aurangabad

Question 4.
Egypt originally known as:
(a) Kemet
(b) Huang He
(c) Hwat-ka-Pta
(d) Egyptus
Answer:
(a) Kemet

2A. Write the names of historical places, persons, and events.

Question 1.
Species who made the first stone tools.
Answer:
Homo Habilis

Question 2.
Palaeolithic Campsite near the Sea of Galilee.
Answer:
Ohalo

Question 3.
The region between the Tigris and Euphrates.
Answer:
Mesopotamia

Question 4.
The valley of the Nile.
Answer:
Egypt

Question 5.
The original name of Egypt.
Answer:
Kemet

Question 6.
The Arabic name of Egypt.
Answer:
Misra

Question 7.
The valley of the Huang He.
Answer:
China

Question 8.
The English translation of the Huang He.
Answer:
Yellow River

Question 9.
Palestinian city on the banks of the river Jordan.
Answer:
Jericho

Question 10.
Mesolithic culture of Japan
Answer:
Jomon

2B. Choose the correct reason and complete the sentence.

Question 1.
Huang He earned the name ‘Sorrow’ or ‘River of Tears’ ____________
(a) of the yellow silt
(b) Mother of Chinese culture
(c) the torrential floods caused great loss to life and assets.
(d) it flows from the Himalayas
Answer:
(c) the torrential floods caused great loss to life and assets.

Question 2.
Egypt got the name ‘Kemet’ ____________
(a) of the black soil that was deposited by the Nile floods
(b) it means Temple of God
(c) it was the beginning of agriculture
(d) because of the decipherment of the Rosetta stone
Answer:
(a) of the black soil that was deposited by the Nile floods.

Question 3.
The site of Mehrgarh is of great importance among ____________
(a) Neolithic villages in Indian Subcontinents established by farmers
(b) Mesolithic man that existed during 10000 – 4000 B.C.E.
(c) The farmers that cultivate the barley and wheat
(d) Chalcolithic people of Maharashtra
Answer:
(a) Neolithic villages in Indian Subcontinents established by farmers.

Question 4.
The first neolithic villages in Egypt came into ____________
(a) about 5000 B.C.E
(b) about 6000 B.C.E
(c) about 7000 B.C.E
(d) about 8000 B.C.E
Answer:
(b) about 6000 B.C.E

2C. Write correct chronological order.

Question 1.
(a) Making of microliths
(b) Beginning of the Neolithic age
(c) Beginning of the ‘Holocene’ epoch
(d) Beginning of agriculture and domestication of animals
Answer:
(a) Beginning of the ‘Holocene’ epoch.
(b) Making of microliths
(c) Beginning of the Neolithic age
(d) Beginning of agriculture and domestication of animals

Question 2.
(a) Increase in water bodies
(b) Availability of animals and vegetation for food increased
(c) Beginning of Holocene glaciers
(d) Glaciers began to melt
Answer:
(a) Beginning of Holocene glaciers
(b) Glaciers began to melt
(c) Increase in water bodies
(d) Availability of animals and vegetation for food increased

Question 3.
(a) Neolithic settlements in Jammu and Kashmir
(b) Neolithic settlements in Uttar Pradesh
(c) Neolithic settlements in Bihar
(d) Neolithic settlements in Northeast India
Answer:
(a) Neolithic settlements in Bihar
(b) Neolithic settlements in Jammu and Kashmir
(c) Neolithic settlements in Northeast India
(d) Neolithic settlements in Uttar Pradesh

Question 4.
Stages of Bead Making:
(a) To know the sources of siliceous stones and chank shells
(b) To manufacture finished beads from the stones of irregular shape and the core of chank shells
(c) To transport the raw material to the manufacturing site
(d) To obtain the raw material
Answer:
(a) To know the sources of siliceous stones and chank shells
(b) To obtain the raw material
(c) To transport the raw material to the manufacturing site
(d) To manufacture finished beads from the stones of irregular shape and the core of chank shells

3. Observe the map on page 2 of your textbook and answer the following questions based on it.

Question 1.
Name the different continents seen on the map.
Answer:
Asia, Africa, Europe, and Australia are the continents seen on the map.

Question 2.
Name the ocean in the north of Asia.
Answer:
The Arctic Ocean is in the north of Asia.

4. Complete the concept maps.

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

5. Write short notes.

Question 1.
Paleolithic camp ‘Ohalo’
Answer:

• ‘Ohalo’ is a Palaeolithic campsite near the Sea of Galilee.
• At Ohalo the evidence of barley, other cereals, and seeds of fruits have been found, along with traces of human occupation.
• Various weeds, in the form of seeds, have been found with cultivated crops.
• Cereals found at Ohalo were remains of cultivated crops and not of the wild variety.
• Grinding stones found from Ohalo, reveal that cereals were first ground (grinding) and then cooked.

6. Explain the statements with reasons.

Question 1.
Ancient pottery throws light on various aspects of ancient cultures.
Answer:

• In all stages of pottery-making, we can understand the class of skilled potters, who were equipped with essential knowledge of pottery making.
• Ancient pottery throws light on various aspects of ancient cultures.
• We get to know about the cultural history, the material richness of the place, from where it was found.
• We can also know the contacts of the residents of a place with other cultures.

7. State your opinion.

Question 1.
The process of urbanisation began in the Neolithic age.
Answer:

• Settling down at one place for a long time, a feeling of ownership arose among the neolithic people.
• Gradually villages expanded, creating awareness of collective land holdings, making village boundaries prominent.
• Awareness of the natural right over a particular region, known as ‘territoriality’ arose.
• Rules and social norms were created to manage the collective resources, water resources, crafts, dependent on it, trade, and community life, resulting in rituals gaining importance.
• Administrative centers rose to manage and keep records of trade, rituals, and writing systems.
• With the increase in population, officials, and occupations, the periphery of the original settlement kept expanding, cities came into existence and the process of urbanisation began in the Neolithic age.

8. Answer the following questions with the help of given points.

Question 1.
Write a short note on River Valley civilisations.
(a) The valley of Euphrates and Tigris – Mesopotamia.
(b) The valley of Nile – Egypt
(c) The valley of Huang He – China
(d) The valleys of Sindhu (Indus) and Saraswati – India
Answer:
The progress in the techniques of systematic cultivation resulted in the rise of the most ancient river valley civilisations of the Neolithic age. The river valley civilisations grew in four regions of the world. Those regions were Mesopotamia, Egypt, the Indian Subcontinent, and China.

(a) The valley of Euphrates and Tigris – Mesopotamia: Mesopotamia is the Greek name of the region between the two rivers, Tigris and Euphrates. Mesos means the ‘middle one’. Potamos means ‘river’. The region between the two rivers is ‘Mesopotamia’. The Mesolithic people began to stay in this region for longer times because of the availability of ample water. Ancient Mesopotamia included modern Iraq, Syria as well as the western regions of Iran and south-eastern regions of Turkey. The camps of Mesolithic people developed into the first settled neolithic villages. These .first villages are dated to 10000 years B.C.E.

(b) The valley of Nile – Egypt: Napoleon Bonaparte had taken along many scholars from various fields during his invasion of Egypt in 1798. They studied the ancient remains in Egypt and published it. These studies received momentum because of the decipherment of the Rosetta inscriptions. The first neolithic villages in Egypt came into being at about 6000 B.C.E. The beginning of agriculture in Egypt coincides with the same time.

(c) The valley of Huang He – China: The valley of Huang He River is considered to be the v region of origin of the Chinese culture. The Chinese culture evolved here. Agriculture in the neolithic villages of China began at about 7000 B.C.E. Wheat, foxtail millet, and rice was grown by the farmers in these villages.

(d) The valleys of Sindhu (Indus) and Saraswati – Indian subcontinent: The region of the valleys of Sindhu and Saraswati is now divided between India and Pakistan. The archaeological excavations at Harappa on the banks of Ravi in Punjab and Mohenjo Daro on the banks of Sindhu in Sindh indicate the existence of a fully developed civilisation in the Indian subcontinent which was dated to circa 3000 B.C.E. It proves that there were well-settled villages in the Indian subcontinent as early as 8000 B.C.E. There is a general consensus among the scholars that the Harappan cities evolved from these early villages.

Question 2.
Explain the concept with the help of the following points:
(a) Origin of Egypt
(b) Yellow River
(c) Fluted core technique
Answer:
(a) Origin of Egypt: Egypt was originally known as ‘Kemet’. Egypt got this name because of ‘ the black soil that was deposited by the Nile floods. Later Egypt came to be known as ‘Hewat-ka- Pta’. It means the temple of God. The Greeks changed it to ‘Egyptus’. In the course of time, it was changed to ‘Egypt’. The Arabic name of Egypt is ‘Misra’.

(b) Yellow River: Yellow River’ is the English translation of the Chinese name ‘Huang He’. The yellow silt brought by her has earned her this name. ‘River’ and ‘Mother’ are her other names. These names indicate her extraordinary place in Chinese culture. The name ‘River’ indicates that she is considered to be the only river of importance. The fact that she is considered to be the mother of the Chinese culture is obvious in the name, ‘Mother’.

(c) Fluted core technique: The blades used for Mesolithic tools were removed from Siliceous stones by the technique known as ‘Fluted Core Technique’. These blades are as tiny as our fingernails. So they are called ‘Microliths’. The Mesolithic people used wooden arrows fixed with microlithic arrowheads.

Question 3.
Explain some Neolithic Sites in India.
Answer:
Some important Neolithic sites in India are as follows:
(a) The northwest region of the Indian continent: Phase I (7000- 6000 B.C.E.) No evidence of pottery (earthen pots). Phase II (6000-4000 B.C.E.) Beginning of pottery making, e.g. Mehrgarh.

(b) Jammu and Kashmir: In Jammu and Kashmir, around 2500 B.C.E. neolithic settlements were established at the sites of Burzhom and Gufkral.

(c) Uttar Pradesh: In Uttar Pradesh, around 6000 B.C.E. neolithic settlements were established at the sites of Chopani Mando, Koldihwa, and Mahagara.

(d) Bihar: In Bihar, around 2000 B.C.E. Neolithic settlements were established. It includes the sites like Chirand, Senuwar, etc.

(e) Northeast India: The evidence of neolithic settlement was first discovered at the site of Daojali Hading in Assam. The village was established around 2700 B.C.E. The neolithic tools found here show more affinity to neolithic tools found in China.

(f) South India: The neolithic settlements in Karnataka, Andhra Pradesh, and Tamil Nadu first came into being around 4th – 3rd century B.C.E. Karnatak sites – Sangankallu, Maski, Brahmagiri, Tekkalkota, Piklihal, Hallur, etc. Andhra Pradesh site – Nagarjunikonda. Tamilnadu – Payyampalli.

Balbharti Maharashtra State Board Class 11 Geography Important Questions Chapter 9 Disaster Management Important Questions and Answers.

Maharashtra State Board 11th Geography Important Questions Chapter 9 Disaster Management

Complete the chain.

Question 1.

Type of disaster	Name of Disaster	Place
(1) Tectonic	(1) Flood	(1) Malin
(2) Geological	(2) Plague	(2) Kerala
(3) Metrological	(3) Tsunami	(3) Surat
(4) Biological	(4) Mudslide	(4) Indonesia

Answer:

Type of disaster	Name of Disaster	Place
(1) Tectonic	(1) Tsunami	(1) Indonesia
(2) Geological	(2) Mudslide	(2) Malin
(3) Metrological	(3) Flood	(3) Kerala
(4) Biological	(4) Plague	(4) Surat

Question 2.

Measures	Pre-disaster/ Post-disaster	Structural or Non-Structural
(1) Public awareness	(1) Post-disaster	(1) Structural
(2) Preparedness of hospital	(2) Post-disaster	(2) Non-structural
(3) Providing food and shelter to people	(3) Pre-disaster	(3) Structural
(4) Construction of river embankments	(4) Post-disaster	(4) Non-structural

Answer:

Measures	Pre-disaster/ Post-disaster	Structural or Non-Structural
(1) Public awareness	(1) Pre-disaster	(1) Non-structural
(2) Preparedness of hospital	(2) Pre-disaster	(2) Structural
(3) Providing food and shelter to people	(3) Post-disaster	(3) Non-structural
(4) Construction of river embankments	(4) Pre-disaster	(4) Structural

Question 3.

Measures	Pre-disaster/ Post-disaster	Structural or Non-Structural
(1) Community level disaster planning	(1) Post-disaster	(1) Structural
(2) Providing financial support	(2) Post-disaster	(2) Structural
(3) Rebuilding of roads and bridges	(3) Pre-disaster	(3) Non-structural
(4) Providing houses to affected people	(4) Pre-disaster	(4) Non-structural

Answer:

Measures	Pre-disaster/ Post-disaster	Structural or Non-Structural
(1) Community level disaster planning	(1) Pre-disaster	(1) Non-structural
(2) Providing financial support	(2) Post-disaster	(2) Non-structural
(3) Rebuilding of roads and bridges	(3) Post-disaster	(3) Structural
(4) Providing houses to affected people	(4) Post-disaster	(4) Structural

Choose the correct option by identifying the correct correlation in the sentences.

Question 1.
Loss of homes, permanent changes in the position of river channel and adverse effects on tourism in an affected area due to an earthquake etc., are ……………..
(a) tertiary effects of a disaster
(b) quaternary effects of a disaster, me
(c) primary effects of a disaster
(d) secondary effects of a disaster
Answer:
(a) tertiary effects of a disaster

Question 2.
Bhopal gas tragedy of 1984 was a ……………….
(a) Geological disaster
(b) Biological disaster
(c) Anthropogenic disaster
(d) Tectonic disaster
Answer:
(c) Anthropogenic disaster

Question 3.
People living in ………………….. areas are more likely to be affected by Tsunamis.
(a) mountainous
(b) coastal
(c) plateau
(d) plain
Answer:
(b) coastal

Question 4.
The geographical conditions and circumstances of people or region that make them susceptible to a disaster is known as ………………..
(a) ability
(b) society
(c) vulnerability
(d) capacity
Answer:
(c) vulnerability

Question 5.
…………………. is the process of preparing in advance, to face disasters in future.
(a) Pre-disaster planning
(b) Strengthening
(c) Recovery
(d) Rehabilitation
Answer:
(a) Pre-disaster planning

Question 6.
The last phase of disaster management is ………………..
(a) recovery
(b) disaster preparedness
(c) rehabilitation
(d) mitigation
Answer:
(c) rehabilitation

Question 7.
The measure taken to bring life back to normal in affected areas is ………………
(a) recovery
(b) disaster preparedness
(c) rehabilitation
(d) mitigation
Answer:
(c) rehabilitation

Question 8.
Any measure taken to minimize the impact of a disaster before it occurs is ………………..
(a) recovery
(b) disaster preparedness
(c) rehabilitation
(d) mitigation
Answer:
(d) mitigation

Question 9.
Action taken to reduce or avoid disasters and their effects is ………………..
(a) recovery
(b) disaster preparedness
(c) rehabilitation
(d) mitigation
Answer:
(b) disaster preparedness

Question 10.
The Indonesian Tsunami of 2004 is …………………
(a) meteorological disaster
(b) biological disaster
(c) geological disaster
(d) tectonic disaster
Answer:
(d) tectonic disaster

Question 11.
The Malin mudslide of 2014 is …………………
(a) meteorological disaster
(b) biological disaster
(c) geological disaster
(d) tectonic disaster
Answer:
(c) geological disaster

Question 12.
The floods of Kerala of 2018 is ……………………
(a) meteorological disaster
(b) biological disaster
(c) geological disaster
(d) tectonic disaster
Answer:
(a) meteorological disaster

Question 13.
The Surat plague of 1992 is ………………….
(a) meteorological disaster
(b) biological disaster
(c) geological disaster
(d) tectonic disaster
Answer:
(b) biological disaster

Identify the correct correlation.

A : Assertion
R : Reasoning

Question 1.
A – Disasters can be natural or man-made.
R – Disasters may affect human population.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Question 2.
A – Generally man-made disasters can be prevented.
R – Man-made disasters happen due to mistakes or carelessness by human,
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 3.
A – Disaster is more of an anthropocentric concept.
R – A hazard is a result of natural process.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Question 4.
A – Events like earthquake, volcanic eruption, tsunamis etc., cannot be prevented but their effects can be reduced.
R – Events like earthquake, cyclones, tsunami etc can now be forecasted and people can be evacuated.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 5.
A – Recovery and rehabilitation are included in post disaster management.
R – Evacuation, search and rescue are included in pre-disaster management.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(a) Only A is correct.

Question 6.
A – Structural measures include any physical construction to reduce or avoid possible impacts of hazard.
R – Non- structural measures include the use of technology, practice to reduce disaster risks and impacts.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(a) Only A is correct.

Question 7.
A – Remote sensing is very effective in mapping disaster prone area.
R – Remote sensing satellite monitor the path of cyclone.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 8.
A – Epidemics is an example of meteorological type of disaster.
R – Corona pandemic is an example of biological type of disaster.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(b) Only R is correct.

Question 9.
A – The Malin mudslide of Maharashtra in 2014 is geological type of disaster.
R – Tsunami is tectonic type of disaster.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Question 10.
A – The last phase of disaster management is rehabilitation.
R – The first stage of disaster management is mitigation.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(a) Only A is correct.

Identify the incorrect factor.

Question 1.
Tectonic disasters are-
(a) Tsunami
(b) Earthquake
(c) Volcanic eruptions
(d) Flood
Answer:
(d) Flood

Question 2.
Geological disasters are-
(a) Mudslides
(b) Cyclone
(c) Landslides
(d) Avalanches
Answer:
(b) Cyclone

Question 3.
Meteorological disasters are-
(a) Cyclone
(b) Heat wave
(c) Flood
(d) Cholera
Answer:
(d) Cholera

Question 4.
Biological disasters are-
(a) Storm
(b) Dengue
(c) Flu
(d) Cholera
Answer:
(a) Storm

Question 5.
Anthropogenic or Man-made disasters are-
(a) Industrial accidents
(b) Avalanches
(c) Nuclear accidents
(d) Transportation accidents
Answer:
(b) Avalanches

Question 6.
Effects of disaster are-
(a) Primary effects
(b) Secondary effects
(c) Quaternary effects
(d) Tertiary effects
Answer:
(c) Quaternary effects

Question 7.
Disaster response include-
(a) Preparedness of hospitals
(b) Providing food and shelter
(c) Providing financial support
(d) Restoring normal conditions
Answer:
(a) Preparedness of hospitals

Question 8.
Recovery includes-
(a) Cleaning of debris
(b) Giving financial assistance
(c) Rebuilding of roads and bridges
(d) Public awareness
Answer:
(d) Public awareness

Question 9.
Mitigation includes-
(a) Community level disaster planning
(b) Preparedness of hospitals
(c) Information campaign
(d) Providing housing
Answer:
(d) Providing housing

Question 10.
Disaster preparedness include-
(a) Cleaning of debris
(b) Preparing plans for households
(c) Strengthening the weak structures
(d) Awareness campaigns
Answer:
(a) Cleaning of debris

Give geographical reasons.

Question 1.
People living in certain areas are exposed to particular disasters.
Answer:

1. People in the coastal areas of India are more likely to be affected by a cyclone than those in the interior.
2. People living in seismically active areas are prone to earthquakes, volcanic eruption, tsunami, etc.
3. People living in geologically weak areas are prone to landslide, mudslides, avalanches, etc.
4. The social, economic and political conditions may make people more likely to be affected by disasters in the same region.
5. Example, the poor, the old people and the children can easily become victims of disasters.
6. Densely populated areas are more likely to be affected than sparsely populated areas.

Question 2.
Disaster management seeks to reduce risk to damages or losses.
Answer:

1. Many disasters like earthquakes, tsunamis, volcanic eruption, etc., cannot be prevented but their effect can be reduced due to disaster management.
2. Disaster management focuses on the hazard that causes the disaster and attempts to minimize the adverse impact of the same on communities.
3. Now forecast of disasters like cyclone, flooding can be forecasted and people can be evacuated from vulnerable areas.
4. It involves co-ordination from governments, local self-governments, police, military and para¬military forces, NGOs, doctors, scientists, planners, volunteers and groups or communities.

Question 3.
Effects of many disasters can be reduced these days.
Answer:

1. Disasters like gas leakage and rail accidents can be prevented.
2. Disasters like volcanic eruption, tsunamis, earthquakes, etc., cannot be prevented but their effect can be reduced.
3. Cyclones and floods can now be forecasted and people can be evacuated from vulnerable areas.
4. Due to awareness created about disasters, steps can be taken to reduce its effects, evaluate the damage caused by the disasters, provide relief, food and medical aid in affected areas.

Differentiate between.

Question 1.
Structural Measures and Non-structural Measures.
Answer:

Structural Measures	Non-structural Measures
(i) They include any physical construction to reduce or avoid possible impacts of hazards.	(i) They do not include physical construction.
(ii) It is achieved by the application of engineering or technology.	(ii) It includes mainly the use of knowledge, practice or agreement to reduce disaster risks and impacts. It is achieved through policies and laws, public awareness, training and education.

Question 2.
Hazards and Disasters.
Answer:

Hazards	Disasters
(i) Hazards are phenomena that pose a threat to people, structural or economic assets.	(i) A hazard becomes disaster when it affects human population, settlement and their activities.
(ii) High rainfall is a hazard.	(ii) When high rainfall causes floods, it is a disaster.
(iii) Hazard is defined as a potentially damaging physical event, social and economic disruption or environmental widespread human, material or environmental	(iii) A disaster is a serious disruption of the functioning degradation of a society, causing or threatening to cause losses which render the affected community unable to cope using its own resources.
(iv) Hazard is result of natural process.	(iv) Disaster is an anthropocentric concept.

Write short notes on.

Question 1.
Remote Sensing
Answer:

1. Remote sensing is a very effective tool in mapping disaster prone areas particularly flood- affected areas.
2. Micro-wave data can provide information on flood-inundated areas.
3. Remote sensing satellites monitor the path of cyclone and it can provide ample time with warning for evacuation and preparedness in advance.
4. The data obtained from meteorological satellites is used for cyclone-tracking, intensity and land-fall predictions and forecasting of extreme weather events.
5. The data obtained from earth observation satellites is used for monitoring disaster events and assessing the damages.
6. The communication satellites help to establish communication in remote and inaccessible areas.
7. The Navigation satellites are used for providing location-based services.

Question 2.
Disaster Response
Answer:

1. ‘Disaster Response’ is the way the community responds to the disaster.
2. It is a post-disaster process but it reflects the preparedness of the community.
3. It includes the immediate period after the disaster strikes.
4. It is concerned with providing food and shelter to the disaster victims, restoring normal conditions and providing financial support.
5. Under this stage, initiatives are taken to ensure that the needs and provisions of victims are met and suffering is minimised.
6. The main focus in this phase is making people safe till further measures are taken.

Question 3.
Capacity to Cope
Answer:

1. The ability of people, organisation and systems, using available skills and resources to face and manage disasters is known as their capacity to cope.
2. Vulnerability is reduced if the capacity to cope with the disaster is high.
3. The capacity to cope has improved over the years. Example, the cyclone in 1999 had caused 10,000 deaths while cyclone in 2019 had caused only 89 deaths.

Question 4.
Tasks in Disaster Management
Answer:
Disaster Management is a multi-disciplinary task which includes the following tasks:

1. Preparedness.
2. Monitoring, early warning and mitigation.
3. Evacuation, search and rescue.
4. Providing relief in terms of medical help, basic needs such as food, clothes and shelter.
5. Reconstruction and Rehabilitation.

Draw a neat and labelled diagram for

Disaster Management Cycle
Answer:

Answer in Detail

Question 1.
What is meant by Disaster Preparedness?
Answer:

1. Disaster preparedness involves measures taken to prepare for and reduce effect of disasters.
2. This includes carrying out awareness campaigns, strengthening the weak structures, preparing plans for households and community level, etc.
3. Example, if a building catches fire, its residents should know how to escape. For this to occur, they should be trained beforehand.
4. People living in the flood-prone areas should be prepared with items such as medicine, food, water, etc.
5. It is the action taken to reduce or avoid disasters and their effects.
6. It should be included in development policy and planning at regional, national and international levels.
7. It is a continuous process.

Question 2.
Explain what is meant by mitigation and how is it implemented?
Answer:

1. Mitigation means any measure taken to minimize the impact of a disaster before it occurs. In other words, it is an action taken against the potential disasters.
2. It is carried out for those disasters which cannot be prevented.
3. Mitigation is helpful to the people because it creates safer communities and reduces loss of life and property of people.
4. Remote sensing satellites can forecast floods or cyclones so people know about their timings. People can be evacuated from vulnerable areas. Example, when cyclone Fani occurred in India, mitigation efforts helped to reduce loss of life and property.
5. Thus, mitigation helps to reduce the financial impact of disaster on Government agencies.

Some mitigation measures can be as per the following:

1. Community level disaster planning.
2. Public awareness and information campaigns.
3. Preparedness of hospitals.
4. Construction of houses away from hazardous areas.
5. Mitigation efforts can be categorized as structural and non-structural mitigations.
6. Structural mitigation efforts include construction of river embankments or strengthening of the existing buildings.
7. Non-structural mitigation efforts include area training in disaster management, regulating land use, public education, etc.

Question 3.
Explain what is disaster management and how is it carried?
Answer:

1. After every disaster there is a great loss to life and property of people, therefore disaster management is necessary.
2. Some disasters like earthquakes, volcanic eruptions, tsunamis, etc., cannot be prevented but their effects can be reduced by disaster management.
3. Disaster management focuses on the hazard that causes the disaster and attempts are made to minimize the adverse effects on communities in the following ways:
4. With the help of remote sensing now we can forecast disasters like cyclones, earthquakes, or volcanoes and disaster management can be done.
5. Disaster management includes creating awareness about the disaster, taking steps to reduce its effects, providing relief, food, and medical aid in affected areas, and evaluating the damage caused by the disaster.
6. It is a joint effort of government, local self-government, police, doctors, military, and paramilitary forces, scientists, planners, NGOs, volunteers, and communities. Their perfect coordination is necessary.

Disaster management is a multi-disciplinary task that includes the following tasks:

1. Preparedness.
2. Monitoring, early warning, and mitigation.
3. Evacuation, search and rescue.
4. Providing relief in terms of medical help, basic needs such as food, clothes and shelter.
5. Reconstruction and Rehabilitation

Balbharti Maharashtra State Board Class 11 Geography Important Questions Chapter 8 Biomes Important Questions and Answers.

Maharashtra State Board 11th Geography Important Questions Chapter 8 Biomes

Complete the chain.

Question 1.

A	B	C
(1) Tropical Rainforest	(1) 10° to 20° N and S	(1) Khejari, acacia, century plant, cactus
(2) Tropical Deciduous	(2) 20° to 30° N and S	(2) Elephant grass, few shrubs, trees
(3) Savannah Grassland	(3) 0° to 10° N and S	(3) Teak, sal, sandalwood, bamboos
(4) Tropical Desert	(4) 5° to 30° N and S	(4) Mahogany, ebony, rosewood

Answer:

A	B	C
(1) Tropical Rainforest	(1) 0° to 10° N and S	(1) Mahogany, ebony, rosewood
(2) Tropical Deciduous	(2) 5° to 30° N and S	(2) Teak, sal, sandalwood, bamboos
(3) Savannah Grassland	(3) 10° to 20° N and S	(3) Elephant grass, few shrubs, trees
(4) Tropical Desert	(4) 20° to 30s N and S	(4) Khejari, acacia, century plant, cactus

Question 2.

A	B	C
(1) the Mediterranean	(1) 40° to 50° N and S	(1) Maple, elm, walnut, deodar
(2) Temperate Deciduous	(2) 40° to 55° N and S	(2) Willow, alder, poplar, various species of grasses
(3) Temperate Grassland	(3) 30° to 40° N and S	(3) Pine, oak, cedar, rosemary

Answer:

A	B	C
(1) Mediterranean	(1) 30° to 40° N and S	(1) Pine, oak, cedar, rosemary
(2) Temperate Deciduous	(2) 40° to 50° N and S	(2) Maple, elm, walnut, deodar
(3) Temperate Grassland	(3) 40° to 55° N and S	(3) Willow, elder, poplar, various species of grasses

Choose the correct option by identifying the correct correlation in the sentences.

Question 1.
Teak is the main tree in …………….. Biome.
(a) Tropical Rainforest
(b) Tropical Deciduous
(c) Savannah Grassland
(d) Tropical Desert
Answer:
(b) Tropical Deciduous

Question 2.
The ………………. Biome was known as ‘The Heaven for Hunting’.
(a) Savannah Grassland
(b) Tropical Desert
(c) Mediterranean
(d) Tropical Deciduous
Answer:
(a) Savannah Grassland

Question 3.
The ………………… Biome has been ideal for the development of cinema industry.
(a) Temperate Deciduous
(b) Temperate Grassland
(c) Taiga
(c) Mediterranean
Answer:
(c) Mediterranean

Question 4.
One type of tree species is the characteristic of ……………….. Biome.
(a) Taiga
(b) Tundra
(c) Mountain
(d) Tropical Rainforest
Answer:
(a) Taiga

Question 5.
The ……………… Biome is the coldest of the Biomes.
(a) Mediterranean
(b) Temperate Deciduous
(c) Temperate Grasslands
(d) Tundra
Answer:
(d) Tundra

Question 6.
In the grassland areas of Africa, ………………..
(a) various tribal communities inhabit
(b) Masais live along with their cattle
(c) Bedouin tribe lives by trade
(d) human life has flourished very well
Answer:
(b) Masais live along with their cattle

Question 7.
The Sherpas, Bakarwals, Lepchas, Bhutiyas, etc., are communities living in the …………………. mountain biome.
(a) Rockies
(b) Himalayan
(c) Alps
(d) Andes
Answer:
(b) Himalayan

Question 8.
The layer of the marine biome where the animals are adapted to survive on detritus under even greater pressure is ………………..
(a) the darkest and deepest layer
(b) the Euphotic layer
(c) the Disphotic layer
(d) the Aphotic layer
Answer:
(a) the darkest and deepest layer

Question 9.
The various species of grass that include purple needle grass, blue grama, buffalo grass, and galleta are found in ………………….
(a) Savannah Grassland Biome
(b) Temperate Grasslands Biome
(c) Tundra Biome
(d) Highland Biome
Answer:
(b) Temperate Grasslands Biome

Identify the correct correlation.

A : Assertion
R : Reasoning

Question 1.
A – The climate includes conditions like rainfall, temperature, humidity, soil conditions etc.
R – The boundaries of different biomes land are determined mainly by climate.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
Both A and R are correct and R is the correct explanation of A.

Question 2.
A – Different biomes have different animals and plants on the same trophic levels.
R – There can be many ecosystems within a biome.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Question 3.
A – There is degradation in the biome of tropical rainforest biome.
R – There is increasing industrialization and agriculture in the biome of tropical rainforest.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 4.
A – The elephant grass grows in Savanah Grassland biome.
R – There are many grass eating animals therefore carnivores are large in number in Savannah Grassland biome.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 5.
A – The animals in tropical desert region are small and tend to burrow.
R – There are mainly herbivores in tropical desert region.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(a) Only A is correct.

Question 6.
A – In the aquatic biome top layer is called aphotic layer.
R – In the aquatic biome the middle layer is called disphotic layer.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(b) Only R is correct.

Question 7.
A – The subdivision of aquatic biome is based on salt content of water and the aquatic plants live there.
R – In marine biome there are three layers in water.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Question 8.
A – Tourism has developed in mountain or highland biome.
R – People come here for paragliding, trekking and to get relief from heat.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 9.
A – Tundra is the coldest of the biome.
R – Animal life is very scarce here.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 10.
A – Many fruits and flowers are grown in the Mediterranean region.
R – Many heavy industries are developed in the Mediterranean region.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(a) Only A is correct.

Identify the incorrect factor.

Question 1.
The abiotic factors are-
(a) Soil
(b) Bacteria
(c) Water
(d) Sunlight
Answer:
(b) Bacteria

Question 2.
Herbivores found in the Tundra biome are-
(a) Reindeer
(b) Caribou
(c) Bears
(d) Wild horse
Answer:
(d) Wild horse

Question 3.
Tropical rainforest biome is in-
(a) Congo basin
(b) Amazon basin
(c) Andaman and Nicobar Islands
(d) Thailand
Answer:
(d) Thailand

Question 4.
Following birds are observed in the tropical desert biome-
(a) Vulture
(b) Bustard
(c) Barn owls
(d) Desert eagle owls
Answer:
(a) Vulture

Question 5.
The abiotic factors in an ecosystem include …………………
(a) air
(b) sunlight
(c) temperature
(d) animals
Answer:
(d) animals

Question 6.
The climatic conditions that determine the boundaries of different biomes on the land are ……………….
(a) rainfall
(b) temperature
(c) humidity
(d) relief
Answer:
(d) relief

Identify the correct correlations.

Question 1.

Tribes	Locations
(i) Pygmies	(a) Grassland areas of Africa
(ii) Masais	(b) Andaman and Nicobar Islands
(iii) Sentinels	(c) Himalayan Mountain biome
(iv) Sherpa	(d) Congo
	(e) Alaska

Answer:

Tribes	Locations
(i) Pygmies	(d) Congo
(ii) Masais	(a) Grassland areas of Africa
(iii) Sentinels	(b) Andaman and Nicobar Islands
(iv) Sherpa	(c) Himalayan Mountain biome

Question 2.

Trees	Biomes
(i) Ebony	(a) Tropical Deciduous
(ii) Sandalwood	(b) Tropical Desert
(iii) Khejari	(c) Tropical Rain forest
(iv) Willow	(d) Tropical Desert
	(e) Temperate Deciduous

Answer:

Trees	Biomes
(i) Ebony	(c) Tropical Rain forest
(ii) Sandalwood	(a) Tropical Deciduous
(iii) Khejari	(b) Tropical Desert
(iv) Willow	(e) Temperate Deciduous

Question 3.

Birds	Locations
(i) Pale crag martin	(a) Savannah Grassland Biome
(ii) Ostriches	(b) Temperate Deciduous Biome
(iii) Peregrine	(c) Tundra Biome
(iv) Ptarmigan	(d) Tropical Deciduous Biome
	(e) Tropical Desert Biome

Answer:

Birds	Locations
(i) Pale crag martin	(e) Tropical Desert Biome
(ii) Ostriches	(a) Savannah Grassland Biome
(iii) Peregrine	(b) Temperate Deciduous Biome
(iv) Ptarmigan	(c) Tundra Biome

Arrange the given statements as per given instructions.

Question 1.
Arrange the following Marine Biomes from the lowest to the uppermost level.
(a) Aphotic layer
(b) Darkest layer
(c) Euphotic layer
(d) Disphotic layer
Answer:
(c). (d), (a), (b)

Give geographical reasons.

Question 1.
Human life is not very easy in the Tropical Rainforest biome.
Answer:
Human life is not very easy in the tropical rainforest biome because-

1. Tropical Rainforest is present between 0° to 10° N and S.
2. There is no dry season – all months have an average precipitation of at least 60 cm.
3. The ground is marshy and covered with thick undergrowth.
4. The forest is very dense and impenetrable and inaccessible.
5. The rivers are infested with crocodiles, snakes and insects like mosquitoes and flies.
6. The conditions in the Tropical Rainforest are not favourable for human habitation. The indigenous humans in these parts are still in their primitive stage. They are engaged in primary occupations, such as gathering forest products, hunting, etc.

Question 2.
There is a degradation in the Tropical Rainforest biome.
Answer:

1. There is an increase in agriculture and industrialisation in this biome. Therefore, deforestation is on a large scale.
2. The biodiversity found in this biome is getting destroyed.
3. Golden lion tamarin, gorilla, orangutan, harpy – eagle, chimpanzee, poison dart frogs are threatened.
   Hence, there is a degradation in the tropical rainforest biome.

Question 3.
In Tropical and Sub-Tropical biomes, a large diversity exists in fauna.
Answer:

1. The biodiversity found in Tropical and Sub-Tropical biomes ranks second in the world,
2. In tropical region trees have a three-tier system, therefore every bird and animal have its own niche in the areas from the ground to the top of the tree.
3. Therefore, from microscopic organisms to large elephants, hippopotamus, rhinos, tiger, lion, gaur, monkeys, reptiles, etc., are found in huge numbers.
4. Birds like greater coucal, hornbills, Asian koel, peacock, vultures, falcon, pigeons, sparrows, etc., are found here.
5. Similarly, ants, butterflies, insects and worms are also found in plenty.
6. In grassland region, grass eating animals are more, therefore carnivores who are dependent on them are also high.
7. Thus, in Tropical and suh-tropical biomes, a large diversity exists in fauna.

Question 4.
The forests in Tropical Deciduous biomes are in danger.
Answer:

1. There is large scale deforestation and also wildfires.
2. Extensive use of fertilizers by humans and spray of insecticides has threatened many wild species.
3. Due to increasing population there is encroachment on forest areas for human settlements. Hence, the forests in Tropical Deciduous biomes are in danger.
4. The Temperate Grasslands biome is getting degraded.
5. The extent of commercial agriculture is increasing in this biome.
6. Industries are also increasing.
7. Meadows and pastures are reducing because of overgrazing.
8. Hence, the Temperate Grasslands biome is being degraded.
9. Life of Eskimos has changed In the Tundra biome.
10. In the Tundra biome, human settlements are very sparse.
11. Lapps, Samoyeds and Eskimos live in adverse climate.
12. Life of Eskimos has changed after they have come in contact with westernizers.
13. As they have started getting advanced instruments, their life and fishing methods have changed.
14. Thus, they have started exploitation of fish with the help of modern methods at a higher speed in this biome.
15. This biome is seeing development due to increased transportation and means of communication.
16. The standard of life has improved and this has affected the protected factors of this biome.

Differentiate between

Question 1.
Vegetation in Tundra and Mountain Biome.
Answer:

Vegetation in the Tundra Biome	Vegetation in the Mountain Biome
(i) The tundra is the coldest of the biomes.	(i) The temperatures are low and it decreases with increase in height.
(ii) The ground is frozen for 8 months of the year. There is a layer of permanently frozen ground below the surface, called permafrost.	(ii) Climate depends on altitude, location on leeward or windward side, orographic rainfall and snowfall on upper slopes of mountains.
(iii) Vegetation has adapted to the cold and the short growing season.	(iii) The vegetation has range from deciduous to tundra varj-ing according to altitude.
(iv) Mosses and lichens are common, while few trees grow here.	(iv) Rhododendron plants grow on most mountains. Oak, laurel and chestnut trees are also found up to 2000 m above sea-level. Pine trees are found up to 4000 m.
(v) The trees that do manage to grow stay close to the ground so they are insulated by snow during the cold winters.	(v) Above 4000 m altitude only lichens, grass and moss can be found.

Question 2.
Vegetation in Mediterranean and Temperate Deciduous Biome.
Answer:

Vegetation in the Mediterranean Biome	Vegetation in the Temperate Deciduous Biome
(i) The height of the trees is less.	(i) The vegetation has adapted to the cold climate.
(ii) The vegetation is mixed type, evergreen and deciduous.	(ii) They are found in three layers. Tall growing trees (18 m to 30 m), short trees and shrubs such as laurel and berries grows
(iii) The leaves of the trees are waxy and thick.	(iii) The trees have broad leaves.
(iv) The evaporation is less and they can sustain longer in tough conditions.	(iv) In this biome, hardwood and deciduous trees are found.
(v) Rosemary, cork, oak, olive, eucalyptus, peach, pine, sweet chestnut, cedar, Cyprus, etc., are found.	(v) Beech, elm, chestnut, oak, willow, cherry, maple, pine, walnut, deodar, etc., are found.

Answer the following question by using the given map.

Question 1.
Name the biome in Africa and Saudi Arabia.
Answer:
Tropical Desert biome

Question 2.
The continuous belt of which biome do you see in Russia?
Answer:
Taiga biome

Question 3.
Name the biome shown in Brazil in South America.
Answer:
Tropical Rainforest biome

Question 4.
Which biome is marked in the countries bordering the Mediterranean Sea?
Answer:
Mediterranean biome

Question 5.
Name the biome shown in India and its neighboring countries of SE Asia.
Answer:
Tropical Deciduous biome

Answer in detail.

Question 1.
Describe the Aquatic Biomes.
Answer:

1. Approximately, 70% of the earth’s surface is covered by oceans. Besides oceans, there are rivers, lakes, etc., which are freshwater sources.
2. Biomes are found in water, too. Here, the plants and animals have adapted themselves to the existing climatic conditions.
3. The aquatic biomes consist of any part of the earth that is covered with water, including fresh water and saltwater.
4. The aquatic biome can be further divided into freshwater biomes, marine biomes, wetland biomes, coral reef biomes, estuaries, etc., based on the salt content of the water and the aquatic plants that live there.

In the marine biomes, there are three layers:
(i) Euphotic Layer: It is found till a depth of 200 m and sunlight can reach here. It houses many fishes, sea turtles, jellyfish, seals, corals, zooplankton, and mangroves.

(ii) Disphotic Layer: It is the middle layer. Here, some light penetrates to the bottom part. It is around 1000 m deep from the mean sea level. Except for a few phytoplankton that has sunk from the upper layer, plants are not found here. Squid, cuttlefish, wolfish, swordfish, eels, sea dragons, etc., are found. These creatures are adapted to darkness, cold water, and high pressure.

(iii) Aphotic Layer: It is the third and the deepest layer that ranges from 1000 m to 4000 m depth. No light penetrates here. There is no living plant life. Inhabitants of this cold dark environment include elusive giant squid, bioluminescent jellyfish, angler fish, hatchet fish, etc. Sperm whales enter this zone to hunt but return to the upper layers.

Beyond this layer, lies the darkest and deepest zone extending up to the seafloor. Here, the animals are adapted to survive on detritus under even greater pressure.

Balbharti Maharashtra State Board Class 11 Geography Important Questions Chapter 7 Indian Ocean – Relief and Strategic Importance Important Questions and Answers.

Maharashtra State Board 11th Geography Important Questions Chapter 7 Indian Ocean – Relief and Strategic Importance

Complete the chain.

Question 1.

A	B	C
(1) Continental shelf	(1) Archipelagos formed by coral atolls	(1) Very wide on the western side of India
(2) Mid-Oceanic Ridges	(2) Portion of continent submerged underwater	(2) Ashmore
(3) Oceanic Plateaus	(3) Submerged mountain ranges that separate deep portions of the ocean floor	(3) the Ninety East Ridge
(4) Islands	(4) Deep flat areas on the ocean bottom	(4) Chagos

Answer:

A	B	C
(1) Continental shelf	(1) Portion of continents submerged underwater	(1) Very wide on the western side of India
(2) Mid-Oceanic Ridges	(2) Submerged mountain ranges that separate deep portions of the ocean floor	(2) Ninety East Ridge
(3) Oceanic Plateaus	(3) Deep flat areas on the ocean bottom	(3) Chagos
(4) Islands	(4) Archipelagos formed by coral atolls	(4) Ashmore

Complete the table.

Question 1.
The Indian Ocean bordered by

Sr. No	Direction	Continents / Oceans
(1)	West	—–
(2)	North and East	—–
(3)	East	—–
(4)	South	—–

Answer:

Sr. No	Direction	Continents / Oceans
(1)	West	Africa
(2)	North and East	Asia
(3)	East	Australia
(4)	South	Southern Ocean

Question 2.
Bottom Relief of the Indian Ocean

Sr. No	Features	Comprise of
(1)	Continental Shelf	—–
(2)	Mid-oceanic Ridges	—–
(3)	Ocean Basins	—–
(4)	Oceanic Deeps	—–
(5)	Islands	—–

Answer:

Sr. No	Features	Comprise of
(1)	Continental Shelf	Gulf, seas, bays and straits
(2)	Mid-oceanic Ridges	Submerged mountain ranges and plateaus
(3)	Ocean Basins	Terminal destinations for the sediments brought from the continents and from the oceanic part itself.
(4)	Oceanic Deeps	Deep, narrow and steeply sloping depressions found on the ocean floor
(5)	Islands	Coral atolls and volcanic islands

Question 3.
Islands of Indian Ocean

Sr. No	Islands of Indian Ocean:
(1)	Islands in the Arabian Sea	———
(2)	Islands of Bay of Bengal	———
(3)	Islands along Australian Coast	———

Answer:

Sr. No	Islands of Indian Ocean:
(1)	Islands in the Arabian Sea	Madagascar, Comoros, Bassas de India, Europa Island, Reunion, Maldives, Chagos, Mauritius, Seychelles, Island of Socotra, Lakshadweep, Bundle Island, Kish, Hendorabi, Lavan, Siri, etc.
(2)	Islands of Bay of Bengal	Sri Lanka, Andaman and Nicobar, Sumatra Island
(3)	Islands along Australian Coast	Ashmore, Christmas and Cocos (or Keeling) Island.

Choose the correct option by identifying the correct correlation in the sentences.

Question 1.
Most of the trenches of the Indian Ocean are located towards its ………………… boundary.
(a) northern
(b) southern
(c) eastern
(d) western
Answer:
(c) eastern

Question 2.
The Bundle Island is located near the coast of …………………….
(a) Sri Lanka
(b) Pakistan
(c) Bangladesh
(d) Myanmar
Answer:
(b) Pakistan

Question 3.
To the east of …………………. lie the islands like Reunion, Mauritius, Seychelles, Socotra.
(a) Madagascar
(b) Australia
(c) Indonesia
(d) Sri Lanka
Answer:
(a) Madagascar

Question 4.
Diego Garcia is an atoll which was first discovered by the Europeans and named by the ……………………
(a) Portuguese
(b) French
(c) Dutch
(d) Germans
Answer:
(a) Portuguese

Question 5.
The salinity of the oceans is generally …………………. around the Somali Peninsula and closer to the Saudi Arabian Coast.
(a) high
(b) low
(c) moderate
(d) very high
Answer:
(a) high

Question 6.
The South Equatorial current flows from / in the ……………………
(a) west to east
(b) east to west
(c) clockwise direction
(d) anticlockwise direction
Answer:
(b) east to west

Identify the correct correlation.

A : Assertion
R : Reasoning

Question 1.
A – There is a complete blockage of the Indian Ocean towards its north.
R – Unlike the Pacific Ocean and the Atlantic Ocean the Indian Ocean does not extend northwards to the Arctic Ocean.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 2.
A – It is believed by most of the geologists that Madagascar was a part of African Continent in the geological past.
R – It has undergone two separations such as first separation from Africa and later from the Indo-Australian Plate.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(c) Both A and R are correct and R is the correct explanation of A.

Question 3.
A – In the case of Bay of Bengal, the Peninsular rivers lead to the lowering of salinity in this area.
R – The salinity is less during the period of South West Monsoon.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Question 4.
A – The Indian market has emerged as one of the largest importers of South East Asian goods.
R – The recently concluded Free Trade Agreements with countries like Thailand and Singapore are set to contribute to this trend.
(a) Only A is correct.
(b) Only R is correct.
(c) Both A and R are correct and R is the correct explanation of A.
(d) Both A and R are correct but R is not the correct explanation of A.
Answer:
(d) Both A and R are correct but R is not the correct explanation of A.

Identify the incorrect factor.

Question 1.
The islands in Bay of Bengal are-
(a) Andaman and Nicobar
(b) Sri Lanka
(c) Sumatra
(d) Madagascar
Answer:
(d) Madagascar

Question 2.
The islands in the Arabian Sea are-
(a) Sumatra
(b) Mauritius
(c) Seychelles
(d) Chagos
Answer:
(a) Sumatra

Question 3.
The islands along the Australian coast are-
(a) Maldives
(b) Ashmore
(c) Christmas
(d) Cocos
Answer:
(a) Maldives

Question 4.
Islands in the Arabian Sea along the Persian Gulf-
(a) Kish
(b) Siri
(c) Lavan
(d) Bundle
Answer:
(d) Bundle

Question 5.
Ocean basins in the Indian Ocean are-
(a) Andaman basin
(b) Somali basin
(c) Oman basin
(d) Mauritius basin
Answer:
(a) Andaman basin

Question 6.
The Ocean currents in southern part of the Indian Ocean are-
(a) South equatorial current
(b) West wind drift
(c) Northeast current
(d) Mozambique-Agulhas currents
Answer:
(c) Northeast current

Question 7.
Islands to the east of Madagascar island are-
(a) Mauritius
(b) Lavan
(c) Reunion
(d) Seychelles
Answer:
(b) Lavan

Question 8.
The islands in the Arabian Sea are-
(a) Comoros
(b) Bassas de India
(c) Europa island
(d) Sri Lanka
Answer:
(d) Sri Lanka

Question 9.
The busiest straits in the Indian Ocean are-
(a) Hormuz
(b) Malacca
(c) Bab-el-Mandeb
(d) Palk
Answer:
(d) Palk

Give geographical reasons.

Question 1.
Monsoon climate has developed in the Indian sub-continent.
Answer:
Monsoon climate has developed in the Indian sub-continent because-

1. The Indian Ocean spreads between Africa in the west, Asia in the north and east, Australia in the east and Southern Ocean in the south.
2. The Indian Ocean does not extend northwards to the Arctic Ocean like the Atlantic Ocean and the Pacific Ocean.
3. This has resulted in complete blockage of the Indian Ocean towards its north.
4. This peculiar arrangement of the ocean and the continental portion contributes a lot to the development of the monsoon climate of the Indian sub-continent.
5. During summer solstice, sun shines vertically on tropic of cancer, so there is summer season over the Indian sub-continent.
6. Due to continuous heating, low pressure area is created, moisture laden south west monsoon winds give rainfall on the Indian sub-continent, that is rainy season.
7. During winter solstice, due to slanting sunrays, the temperature goes down, that is winter season.
8. Thus, there is monsoon climate with three distinctive seasons.

Question 2.
The study of temperature of the ocean is essential.
Answer:
The study of temperature of the ocean is essential because-

1. The temperature of the ocean provides information on the global climate system.
2. It is also important for the study of marine ecosystems.
3. The temperature of the ocean water is responsible for the movement in the oceanic water.
4. Rising temperatures cause coral bleaching and loss of breeding grounds for marine fishes and mammals.
5. The study of temperature of the ocean can help in establishing marine protected areas and forming precautionary limits to prevent overfishing, protecting ocean ecosystems and shield humans from the effects of ocean warming.

Answer the following question by using the given map.

Question 1.
Name the plateau in South Indian Ocean.
Answer:
Kerguelen Plateau

Question 2.
Name the ocean basin in North Arabian Sea.
Answer:
Oman Basin

Question 3.
Name the ocean current near the equator in the Indian Ocean.
Answer:
Counter Equator Current

Question 4.
Name the ocean current in Western Indian Ocean.
Answer:
Agulhas Current

Question 5.
Name the ocean current in Eastern Indian Ocean.
Answer:
Australian Current

Write short notes on.

Question 1.
Challenges in the Indian Ocean
Answer:

1. India occupies a central and strategic location in the Indian Ocean.
2. Keeping the Indian Ocean as a Zone of Peace free from superpower rivalry is a major challenge in the Indian Ocean.
3. Most of the conflicts since the end of the Cold War have taken place in or around the Indian Ocean region. As a result, almost all the world’s major powers have deployed substantial military forces in the Indian Ocean region.
4. Expanding markets and larger import flows imply vulnerability at sea. Hence, the incidence of piracy, armed robbery and maritime terrorism are on the rise and has placed a premium on the complexity of Sea lane defence.

Question 2.
Islands in Indian Ocean
Answer:

1. There are 39 islands in the Indian Ocean. Most of them are away from the coastline. They are deep sea islands.
2. The islands of the Indian Ocean are a varied collection, including many smallest territories and some large islands like Sri Lanka, Australia and Madagascar.

The islands in the Indian Ocean are grouped into-

1. Islands of Arabian sea
2. Islands along Bay of Bengal
3. Islands along the Australian coast

Islands in Indian Ocean-

1. Islands of the Arabian Sea can be sub grouped such as islands close to the African coast and islands along the Lakshadweep – Chagos Ridge.
2. The largest island close to the African coast is Madagascar island. It is separated from Africa, and later from the Indo-Australian plate. It is one of the seismologically active provinces.
3. There are many islands between the eastern coast of Africa and Madagascar island, such as Comoros, Europa and Bassas de India, etc. To the east of Madagascar are Mauritius, Reunion and Seychelles, etc.
4. The group of islands along Lakshadweep-Chagos Ridge are Maldives, Chagos and Lakshadweep.
5. Apart from these islands, other islands are the Bundle island near the coast of Pakistan and Siri, Lavan, Kish, Hendorabi, etc., along the Persian Gulf part of Iran.
6. The islands in Bay of Bengal are associated with the converging plate boundary. These islands are the peaks of submerged mountains. The islands of Bay of Bengal are Sri Lanka, Andaman and Nicobar group, and chain of islands along the western coast of Sumatra island of Indonesia.
7. Most of these islands are volcanic islands. Sri Lanka is the largest island of this group.
8. There are very few islands along the coastline of Australia such as Cacos, Christmas, Ashmore, etc.

Answer in detail.

Question 1.
Describe the continental shelf of the Indian Ocean.
Answer:

1. The continental shelf is the portion of continents submerged under oceanic water.
2. It is normally occupied by different gulfs, seas, bays and straits.
3. There is a wide range of variation in the continental shelves of the Indian Ocean.
4. There are quite extensive shelves along the Indian coasts.
5. The eastern coast of Africa and Madagascar record relatively narrow width of continental shelves, and along the Indonesian coast, it is very narrow (160 km).
6. The continental shelves are very wide in the west of India whereas these are narrow along the eastern coast.
7. Continental shelves are veneered with deposits brought down by terrestrial agents of erosion.
8. Some of the sedimentary deposits are received from over thousand years.
9. As they remain deposited for a long time, sedimentary rocks are formed.
10. Some of them are a potential source of fossil fuel.

Question 2.
Describe the Mid-Oceanic Ridges of the Indian Ocean.
Answer:

1. Mid-oceanic ridges are submerged mountain ranges that separate deep portion of the sea (Ocean) floor.
2. The Indian Ocean has a Mid Ocean ridge called as a Mid Indian Oceanic Ridge.
3. It originates from the Gulf of Eden near the Peninsula of Somalia.
4. It further extends toward the south and on the eastern side of Madagascar, it divides into two branches.
5. One branch diverts towards southwest and extends up to Prince Edward Island. It is known as Southwest Indian Ocean Ridge.
6. The second branch extends south eastwards up to Amsterdam and St. Paul Island. It is known as Mid Indian Ocean Ridge.
7. Mid Indian Oceanic Ridge has many parallel ridges. This ridge is not continuous due to many fracture Zones in it. e.g. Owen Fracture Zone. Amsterdam Fracture Zone, etc.

Question 3.
Explain in detail the importance of Indian Ocean to India.
Answer:
India has the control and strategic location in the Indian Ocean. Therefore, India’s economic and national interests are linked with the Indian Ocean.

From economic point of view, India’s trade with neighbouring countries is dependent on the Indian Ocean. Indian Ocean provides major sea route connecting Middle East, Africa and East Asia with Europe and America. India’s import of mineral oil mainly comes from Gulf countries.

The sand on the beaches along the Arabian Sea is rich in valuable minerals like uranium. India has offshore deposits of mineral oil at Bombay High in the Arabian Sea. Abyssal plains of the Indian Ocean have deposit of polymetallic nodules. These nodules are source of nickel, copper, manganese and cobalt.

India has developed very good trade relations with countries of east due to its location along the Arabian Sea. Trade volumes with ASEAN countries are increasing every year. The Indian market has emerged as one of the largest importers of South East Asian goods. India also has Free Trade Agreements with Singapore and Thailand.

The northern area of the Indian Ocean is the area of great significance in economic and strategic terms. With expansion of India’s export and import, India is forecasted to become one of the three fastest growing economics in the world.

Due to heavy trade, through Indian Ocean, the incidences of piracy, armed robbery and maritime terrorism are on the rise and therefore, defence work in the Indian Ocean have increased.

To keep the Indian Ocean as a zone of peace, free from superpower rivalry and increasing cooperation among littoral countries in the region has always been India’s foreign policy goal. For example, Indian Ocean Rim Association for Regional Cooperation, Ganga-Mekong Cooperation, etc.