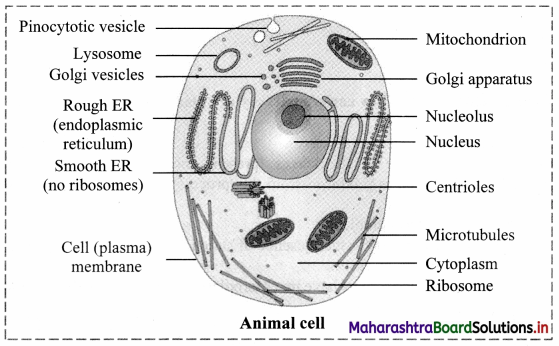
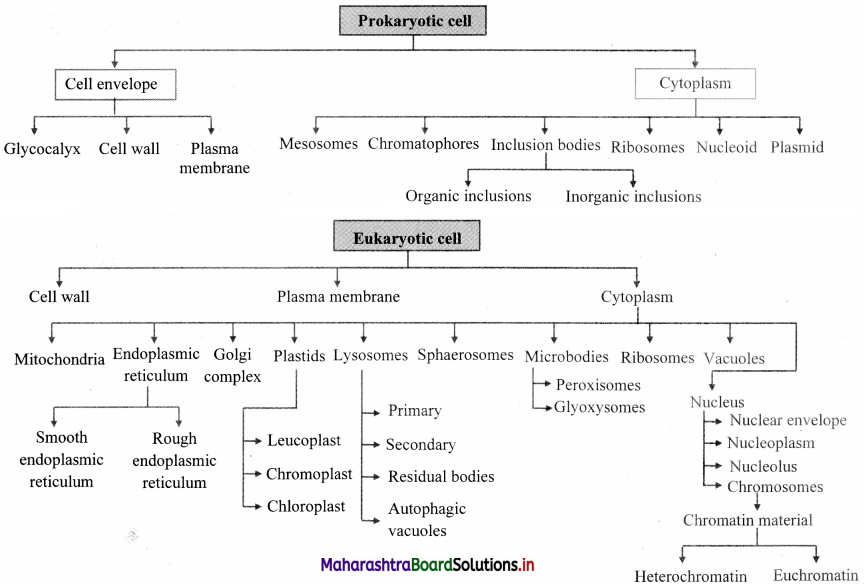
Balbharti Maharashtra State Board 12th Chemistry Important Questions Chapter 4 Chemical Thermodynamics Important Questions and Answers.
Maharashtra State Board 12th Chemistry Important Questions Chapter 4 Chemical Thermodynamics
Question 1.
Define the term energy.
Answer:
The energy of a system is defined as its capacity to perform the work. A system with higher energy can perform more work.
Question 2.
What are different forms of energy ?
Answer:
The energy of a system has many different forms as follows :
- Kinetic energy which arises due to motion, like rotational, vibrational and translational.
- Potential energy which arises due to position and state of a matter. If depends upon the temperature of the system.
- Heat energy (or thermal energy) which is transferred from the hotter body to the colder body.
- Radiant energy which is associated with electro-magnetic or light radiation.
- Electrical energy produced in the galvanic cells.
- Chemical energy stored in chemical substances.
All these various forms of energy can be converted from one form to another without any loss.
Question 3.
Explain the concept of interconversion of different forms of energy.
Answer:
There are various forms of energy like kinetic energy, potential energy, heat or thermal energy, radiant energy, electrical energy and chemical energy.
All these forms of energy are interconvertible. For example, a body at very high level possesses higher potential energy. When it falls down, potential energy is converted into kinetic energy. Falling of water from high level is used to drive turbines converting potential energy into kinetic energy which is further converted into electrical energy.
In galvanic cells, chemical energy is converted into electrical energy.
In electrolytic cells, chemical energy is converted into electrical energy. But during interconversion, the energy can neither be created nor destroyed, and there is a conservation of energy.
Question 4.
What is thermodynamics ? What are its drawbacks?
Answer:
Thermodynamics : It is concerned with the energy changes in physical and chemical changes.
Drawbacks :
- It does not give information on the rates of physical or chemical changes.
- It does not explain mechanisms involved in physical and chemical processes.

Question 5.
Define and explain :
(1) System (2) Surroundings (3) Boundary.
Answer:
(1) System : The portion of the universe under thermo-dynamic consideration to study thermodynamic properties is called a system.
Explanation :
- As such any portion of the universe under thermodynamic consideration is a system. The thermodynamic consideration involves the study of thermodynamic parameters like pressure, volume, temperature, energy, etc.
- The system may be very small or very large.
- The system is confined by a real or an imaginary boundary.
(2) Surroundings : The remaining portion of the universe other than under thermodynamics study i.e„ the system is called the surroundings.
Explanation :
- Surroundings represent a large stock of mass and energy and can be exchanged with the system when allowed.
- For a liquid in an open vessel, the surrounding atmosphere around it represents the surroundings.
(3) Boundary : The wall or interface separating the system from its surrounding is called a boundary.
Explanation :
- This boundary may be either real or imaginary.
- Through this boundary, exchange of heat and matter between the system and surroundings can take place, e.g. when a liquid is placed in a beaker the walls of beaker represent real boundaries while open portion of the beaker is imaginary boundary.
- Everything outside the boundary represents surroundings.
Question 6.
What are the types of systems ?
Answer:
Following are the types of systems :
- Open system
- Closed system
- Isolated system
- Homogeneous system
- Heterogeneous system.
Question 7.
Define and explain the following :
(1) Open system
(2) Closed system
(3) Isolated system.
Answer:
(1) Open system :it is defined as a system which can exchange both matter and energy with its surroundings, e.g. a beaker containing water. The water continuously absorbs energy from the surroundings and forms vapour which diffuse in the surroundings. So that this system exchanges energy and matter (or mass), with the surroundings.
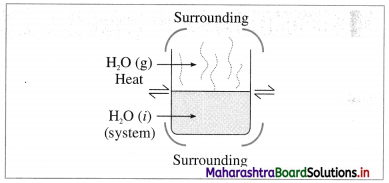
Fig. 4.1 : Open system
(2) Closed system : it is defined as a system which can exchange only energy but not the matter with its surroundings, e.g. A closed vessel containing hot water so that only heat is lost to the surroundings and not the matter.
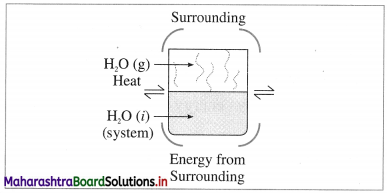
Fig. 4.2 : Closed system
(3) Isolated system : it is defined as a system which can neither exchange energy nor matter with its surroundings, e.g. hot water filled in a thermally insulated closed vessel like thermos flask.
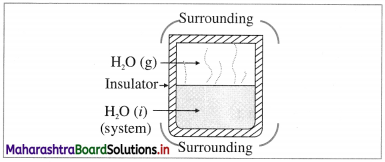
In actual practice, perfectly isolated system is not possible.
Universe represents an isolated system.

Question 8.
‘Universe is an isolated system’. Explain.
Answer:
Universe represents an isolated system due to the following reasons :
- The total mass and energy of the universe remain constant.
- The universe has no boundary.
- The universe has no surroundings.
Question 9.
Define and explain :
(1) Homogeneous system
(2) Heterogeneous system.
Answer:
(1) Homogeneous system : A system consisting of only one uniform phase is called a homogeneous system.
Explanation :
(1) The properties of homogeneous system are uniform throughout the phase or system.
(2) The homogeneous systems are :
- Solutions of miscible liquids (water and alcohol) or soluble solids in liquids, (NaCl in water), etc.
- Mixture of gases. H2 and N2, NH3 and H2, etc.
(2) Heterogeneous system : A system consisting of two or more phases separated by interfacial boundaries is called a heterogeneous system.
Explanation : These systems are :
- Mixture of two or more immiscible liquids. E.g. Water and benzene.
- Solid in equilibrium with liquid.
E.g. Ice ⇌ water.
- Liquid in equilibrium with vapour.
E.g. Water ⇌ vapour.
Question 10.
Explain : (A) Extensive property (B) Intensive property of a system.
OR
What is the difference between extensive and intensive properties?
Answer:
The properties of a system are classified as (A) Extensive property and (B) Intesive property.
(A) Extensive property : It is defined as a property of a system whose magnitude depends on the amount of matter present in the system.
Explanation :
- More the quantity (or amount) of the matter of the system, more is the magnitude of extensive property, e.g., mass, volume, heat, energy, enthalpy, etc.
- The extensive properties are additive.
(B) Intensive property : It is defined as a property of a system whose magnitude is independent of the amount of matter present in the system.
Explanation :
- Intensive property is characteristic of the system, e.g., refractive index, density, viscosity, temperature, pressure, boiling point, melting point, freezing point of a pure liquid, surface tension, etc.
- The intensive properties are not additive.
Question 11.
Select extensive and intensive properties in the following :
Moles, molar heat capacity, entropy, heat capacity.
Answer:
Extensive property : Moles, entropy, heat capacity.
Intensive property : Molar heat capacity.
Question 12.
What is a state function ? Give examples.
Answer:
State function : The property which depends on the state of the system and independent of the path followed by the system to attain the final state is called a state function.
For example, pressure, volume, temperature, etc.

Question 13.
Classify the following properties as intensive or extensive :
(i) Temperature (ii) Density (iii) Enthalpy (iv) Mass (v) Energy (vi) Refractive index (vii) Pressure (viii) Viscosity (ix) Volume (x) Weight.
Answer:
(1) Intensive properties : Temperature, Density, Refractive index. Pressure, Viscosity.
(2) Extensive properties : Enthalpy, Mass, Energy, Volume, Weight.
Question 14.
What are path functions?
Answer:
Path functions : The properties which depend on the path of the process are called path functions. For example, work (W) and heat (Q).
Question 15.
Define thermodynamic equilibrium. Mention different types of thermodynamic equilibria.
Answer:
Thermodynamic equilibrium : A system is said to have attained a state of thermodynamic equilibrium if there is no change in any thermodynamic functions or state functions like energy, pressure, volume, etc. with time.
For a system to be in thermodynamic equilibrium, it has to attain following three types of equilibrium :
- Thermal equilibrium
- Chemical equilibrium
- Mechanical equilibrium
Question 16.
Distinguish between :
(1) Open system and Closed system :
Open system:
- An open system can exchange both matter and energy with the surroundings.
- In this, the total amount of matter does not remain constant.
- Example : Hot water kept in an open beaker.
Closed system:
- A closed system can exchange only energy, but not matter with the surroundings.
- In this, the total amount of matter remains constant.
- Example : Hot water kept in a closed glass flask.
(2) Closed system and Isolated system :
Closed system:
- A closed system can exchange only energy, but not matter with the surroundings.
- In this, the total amount of energy does not remain constant.
- Example : Hot water kept in a sealed glass flask.
Isolated system:
- An isolated system can exchange neither matter nor energy with the surroundings.
- In this, the total amount of energy remains constant.
- Example : Hot water kept in a thermos flask.
(3) Open system and Isolated system :
Open system:
- An open system can exchange matter with the surroundings.
- It can exchange energy with the surroundings.
- In this, the total amount of energy does not remain constant.
- Example : Hot water kept in an open beaker.
Isolated system
- An isolated system cannot exchange matter with the surroundings.
- It cannot exchange energy with the surroundings.
- In this, the total amount of energy remains constant.
- Example : Hot water kept in a thermos flask.

Question 17.
What is a thermodynamic process ? What are different types of processes ?
Answer:
(i) Thermodynamic process : It is defined as a transition by which a state of a system changes from initial equilibrium state to final equilibrium state.
The process is carried out by changing the state functions or thermodynamic variables like pressure, volume and temperature. During the process one or more properties of the system change.
(ii) Types of processes :
- Isothermal process
- Isobaric process
- Isochoric process
- Adiabatic process
- Reversible process
- Irreversible (spontaneous) process.
Question 18.
Define and explain different types of processes.
Answer:
There are following types of processes :
(1) Isothermal process : It is defined as a process in which the temperature of the system remains constant throughout the change of a state of the system.
In this, ΔT = 0.
Features :
- In this process, the temperature at initial state, final state and throughout the process remains constant.
- In this process, system exchanges heat energy with its surroundings to maintain constant temperature. E.g., in case of exothermic process liberated heat is given to the surroundings and in case of endothermic process heat is absorbed from the surroundings so that temperature of the system remains constant and ΔT = 0.
- Isothermal process is carried out with a closed system.
- Internal energy (U) of the system remains constant, hence, Δ U = 0.
- In this process, pressure and volume of a gaseous system change.
(2) Isobaric process : It is defined as a process which is carried out at constant pressure. Hence, Δ P = 0.
Features :
- In this process, the volume (of gaseous system) changes against a constant pressure.
- Since the external atmospheric pressure remains always constant, all the processes carried out in open vessels, or in the laboratory are isobaric processes.
- In this volume and temperature change.
- Internal energy of a system changes, hence, ΔU ≠ 0.
(3) Isochoric process : It is defined as a process which is carried out at constant volume of the system.
Features :
- In this process, temperature and pressure of the system change but volume remains constant.
- Since ΔV = 0, no mechanical work is performed.
- In this internal energy (U) of the system changes. The example of this process in cooking takes place in a pressure cooker.
(4) Adiabatic process : It is defined as a process in which there is no exchange of heat energy between the system and its surroundings. Hence, Q = 0.
Features :
- An adiabatic process is carried out in an isolated system.
- In this process, temperature and internal energy of a system change, ΔT ≠ 0, Δ U ≠ 0.
- During expansion, temperature and energy decrease and during compression, temperature and energy increase.
- If the process is exothermic, the temperature rises and if the process is endothermic the temperature decreases in the adiabatic process.
(5) Reversible process : A process carried out in such a manner that at every stage, the driving force is only infinitesimally greater than the opposing force and it can be reversed by an infinitesimal increase in force and the system exists in equilibrium with its surroundings throughout, is called a reversible process.
Features :
- This is a hypothetical process.
- Driving force is infinitesimally greater than the opposing force throughout the change.
- The process can be reversed at any point by making infinitesimal changes in the conditions.
- The process takes place infinitesimally slowly involving infinite number of steps.
- At the end of every step of the process, the system attains mechanical equilibrium, hence, throughout the process, the system exists in temperature-pressure equilibrium with its surroundings.
- In this process, maximum work is obtained.
- Temperature remains constant throughout the isothermal reversible process.
(6) Irreversible process : it is defined as the unidirectional process which proceeds in a definite direction and cannot be reversed at any stage and in which driving force and opposing force differ in a large magnitude. It is also called a spontaneous process.
Features :
- It takes place without the aid of external agency.
- All irreversible processes are spontaneous.
- All natural processes are irreversible processes.
- Equilibrium is attained at the end of process.
- They are real processes and are not hypothetical.
Examples :
- Flow of heat from a matter at higher temperature to a matter at lower temperature.
- Flow of a gas from higher to lower pressure.
- Flow of water from higher level to lower level.
- Flow of a solvent into a solution through a semipermeable membrane due to osmosis.
- Flow of electricity from higher potential terminal to lower potential terminal.
Question 19.
Distinguish between :
(1) Isothermal process and Adiabatic process.
(2) Reversible and irreversible processes.
Answer:
Isothermal process:
- In an isothermal process, the temperature of the system remains constant. ΔT = 0
- In this process, the system exchanges heat with the surroundings. Q ≠ 0 (Closed system)
- The total internal energy of the system remains constant.
- In this process, the system is not thermally isolated.
- In this process, Q = -W as ΔU = 0.
- ΔH = 0.
Adiabatic process:
- In an adiabatic process, the temperature of the system changes. ΔT ≠ 0
- In this process, the system does not exchange heat with the surroundings. Q = 0 (Isolated system)
- The total internal energy of the system changes. ΔU ≠ 0
- In this process, the system is thermally isolated.
- In this process, W = ΔU.
- ΔH ≠ 0.
(2) Reversible and irreversible processes.
Reversible process:
- The process whose direction can be reversed at any stage by an infinitesimal increase in the opposing force is called a reversible process.
- Such a process is not spontaneous and takes place infinitesimally slowly and takes infinite time for completion.
- In this process, the thermodynamic equilibrium is always maintained between the system and the surroundings at every step.
- The opposing force is infinitesimally less than the driving force.
- It is an ideal or hypothetical process.
- Maximum work can be derived from such a process.
Irreversible process:
- The process whose direction cannot be reversed by an infinitesimal increase in the opposing force is called an irreversible process.
- Such a process is spontaneous and takes finite time for completion.
- The thermodynamic equilibrium is attained only at the end of the process.
- The opposing force is significantly less than the driving force.
- It is a practical or real and spontaneous process.
- Work derived from such a process is always less than the maximum work.

Question 20.
Show that pressure times volume (PV) is equal to work.
Answer:
The work is defined as the energy by which a body is displaced through a distance d by applying a force f.
∴ W = f × d
If area is A = d2 and volume V = d3 then,
PV = \(\frac{f}{A}\) × d3 = \(\frac{f}{d^{2}}\) × d3 = f × d = W
∴ The term PV represents the pressure-volume work.
Question 21.
Explain the process of (A) expansion and (B) compression with suitable examples.
Answer:
(A ) Expansion : Consider an ideal cylinder fitted with a piston and filled with H2O2(l).
2H2O2(l) → 2H2O(l) + O2(l)
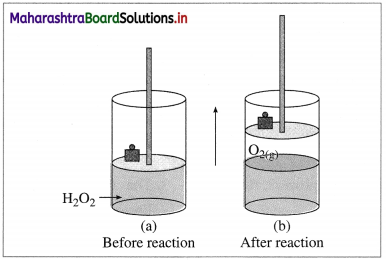
Fig. 4.5 : Decomposition of H2O2
The oxygen gas produced pushes the piston upwards lifting the mass. Thus, the system performs the work on the surroundings and loses energy by expansion. In this work is done by the system.
(B) Compression : Consider an ideal cylinder fitted with a piston and containing gaseous NH3(g) and HCl(g).
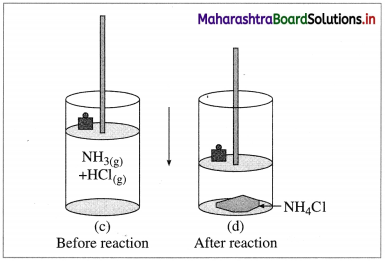
Fig. 4.6 : Reaction between NH3(g) and HCl(g)
NH3(g) + HCl(g) → NH4Cl(s)
As the reaction proceeds, due to consumption of gases, the volume decreases and there is work due to compression. In this work is done on the system by surroundings and the system gains energy.
Question 22.
What are the sign conventions for Q and W in (A) expansion, (B) compression?
Answer:
(A) For expansion, work is done by the system hence,
Q = -ve and W = -ve
(B) For compression, work is done on the system hence,
Q = -ve and W = +ve
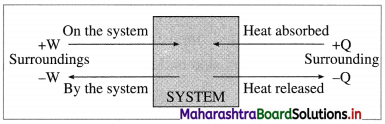
Fig. 4.7 : Sign conventions
Question 23.
Explain sign convention of work during expansion and compression.
OR
Explain +W and -W.
Answer:
(A) Expansion of a gas :
(1) When a gas expands against a constant pressure, Pex changing the volume from initial volume V1 to final volume V2,
Change in volume, Δ V = V2 – V1
The mechanical work = W = -Pex × Δ V
= -Pex (V2 – V1)
(2) During expansion V2 > V1. The work is said to be performed by the system on the surroundings. This results in the decrease in the (work) energy of the system. Hence the work is negative, i.e. W is -ve.
(B) Compression of a gas : During compression, V2 < V1. The work is said to be performed on the system by the surroundings. This results in the increase in the (work) energy of the system. Hence the work is positive, i.e. W is + ve.
Question 24.
What are different units of energy and work ?
Answer:

Question 25.
What are the characteristics of maximum work?
Answer:
(1) The process is carried out at constant temperature.
(2) During the complete process, driving force is infinitesimally greater than opposing force.
(3) Throughout the process, the system exists in equilibrium with its surroundings.
(4) The work obtained is maximum. This is given by,
Wmax = -2.303 nRT log10 \(\frac{V_{2}}{V_{1}}\)
OR
Wmax = -2.303 nRT log10 \(\frac{P_{1}}{P_{2}}\)
where n, P, V and T represent number of moles, pressure, volume and temperature respectively.
(5) ΔU = 0, ΔH = 0.
(6) The heat absorbed in reversible manner
Qrev, is completely converted into work.
Qrev = -Wmax.
Hence work obtained is maximum.

Solved Examples 4.3
Question 26.
Solve the following :
(1) 2.5 moles of an ideal gas are expanded isothermally from 12 dm3 to 25 dm3 against a pressure of 3.0 bar. Calculate the work obtained.
Solution :
Given : n = 2.5 mol; V1 = 12 dm3;
V2 = 25 dm3
Pext = 3.0 bar; W = ?
W = -Pext × (V2 – V1)
= – 3 × (25 – 12)
= -39 dm3 bar
∵ V1 dm3 = 100 J
∴ W = -39 × 100 = -3900 J = -3.9kJ
Ans. W= -3.9 kJ
(2) When 2.2 moles of an ideal gas are expanded from 3.5 dm3 to 12 dm3 against a constant pressure, the work obtained is 3910 J. Estimate the external pressure.
Solution :
Given : n = 2.2 mol; V1 = 3.5 dm3; V2 = 12 dm3
W= -3910 J = \(\frac{-3910}{100}\)dm3 bar
W = -Pex (V2 – V1)
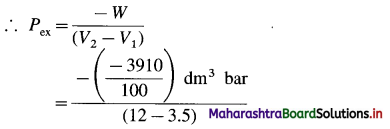
= 4.6 bar
Ans. Pex = 4.6 bar
(3) Three moles of an ideal gas are expanded isothermally from a volume of 300 cm3 to 2.5 dm3 at 300 K against a pressure of 1.9 bar. Calculate the work done in L atm and joules.
Solution :
Given : Number of moles of a gas = n = 3 mol
Initial volume = V1 = 300 cm3
= 0.3 dm3
Final volume = V2 = 2.5 dm3
External pressure = Pex =1.9 bar
Temperature = T = 300 K
∵ W = -Pex (V2 – V1)
= -1.9 (2.5 – 0.3)
= -4.18 dm3 bar
Now, 1 dm3 bar = 100 J
∴ W = -4.18 × 100
= -4180 J
Ans. Work of expansion = W = -4180 J
(4) Calculate the constant external pressure needed to compress an ideal gas from 25 dm3 to 15 dm3. The amount of work done in the compression process is 3500 joules.
Solution :
As the compression of the gas takes place against a constant pressure, the work done is given by
W = -Pex(V2 – V1)
W = Work done by the gas against the external pressure = 3500 J
∴ W = \(\frac{3500}{100}\) = 35 dm3 bar
P = Constant external pressure = ?
V2 = Final volume = 15 dm3
V1 = Initial volume = 25 dm3
∴ 35= -P × (15 – 25)
∴ 35 = 10 × P
∴ P = \(\frac{35}{10}\) = 3.5 bar
Ans. External pressure = 3.5 bar

(5) Three moles of an ideal gas are compressed isothermally and reversibly to a volume of 2 dm3. The work done is 2.983 kJ at 22°C. Calculate the initial volume of the gas.
Solution :
Given : Number of moles of a gas = n = 3 mol
Final volume = V2 = 2 dm3
Initial volume = V1 = ?
For compression,
Wmax = +2.983 kJ = 2983 J
Temperature = T = (273 + 22) K = 295 K
Wmax= -2.303 nRT log10\(\frac{V_{2}}{V_{1}}\)
∴ \(\frac{2983}{2.303 \times 3 \times 8.314 \times 295}\)
= -[log102 – log10V1]
0.1760 = -log102 + log10 V1
= -0.3010 + log10V1
∴ log10 V1 = 0.1760 + 0.3010 = 0.4770
∴ V1 = Antilog 0.4770
= 3.0 dm3
Ans. Initial volume of the gas = 3.0 dm3
(6) A chemical reaction takes place in a container of cross sectional area 100 cm2. As a result of the reaction, a piston is pushed out through 10 cm against an external pressure of 1.0 bar. Calculate the work done by the system.
Solution :
Given : Cross sectional area = A = 100 cm2
Displacement of a piston = 1 = 10 cm
External pressure = P = 1.0 bar
Work = W = ?
Volume change = A × l
∴ ΔV = 100 × 10
= 1000 cm3
= 1 dm3
Work = W = -P × ΔV
= -1 × 1
= -1 dm3 bar
= – 1 × 100 J
= -100 J
Ans. Work = W = -100 J
(7) 5 moles of helium expand isothermally and reversibly from a pressure 4 atm to 0.4 at 300 K. Calculate the work done, change in internal energy and heat absorbed during the expansion. (R = 8.314 J k-1 mol-1)
Solution :
Given : n = 5 mol
P1 = 4 atm
P2 = 0.4 atm
T = 300 K
Wmax = ?, ΔU = ?, Q = ?
Wmax = -2.303 nRT log10 (\(\frac{P_{1}}{P_{2}}\))
= -2.303 × 5 × 8.314 × 300 log10 \(\frac{4}{0.4}\)
= -2.303 × 5 × 8.314 × 300 × 1
= -28720 J
= -28.72 kJ
For an isothermal process, ΔU = 0
By first law, ΔU = Q + Wmax
∴ Q = -Wmax
= – (-28.72) = 28.72 kJ
Ans. Wmax = – 28.72 kJ; ΔU = 0;
Q = 28.72 kJ
(8) 2.8 × 10-2 kg of nitrogen is expanded isothermally and reversibly at 300 K from 15.15 × 105 Pa when the work done is found to be -17.33 kJ. Find the final pressure.
Solution :
Given : Mass of nitrogen = m = 2.8 × 10-2 kg
Temperature = T = 300 K
Work obtained in expansion = Wmax = -17.33 kJ
= – 17330 J
Initial pressure = P1 = 15.15 × 105 Pa
= 1.515 × 106 Pa
Molar mass of nitrogen (N2) = MN2
= 28 × 10-3 kg mol-1
Final pressure = P2 = ?
Number of moles of N2 = n = \(\frac{m}{M_{\mathrm{N}_{2}}}\)
= \(\frac{2.8 \times 10^{-2}}{28 \times 10^{-3}}=1 \mathrm{~mol}\)
Wmax = -2.303 × nRT log10 \(\frac{P_{1}}{P_{2}}\)
17330 = 2.303 × 1 × 8.314 × 300 × \(\log _{10} \frac{1.515 \times 10^{6}}{P_{2}}\)
∴ \(\frac{17330}{2.303 \times 1 \times 8.314 \times 300}\)
= [log10 1.515 × 106 – log10P2]
3.017 = 6.1804 – log10P2
∴ log10P2 = 6.1804 – 3.017 = 3.1634
∴ P2 = Antilog 3.1634
= 1456.8 Pa
Ans. Final pressure = 1456.8 Pa

(9) Carbon monoxide expands isothermally and reversibly at 300 K doing 4.754 kJ of work. If the initial volume changes from 10 dm3 to 20 dm3, calculate the number of moles of carbon monoxide. (R = 8.314 JK-1 mol-1)
Solution :
Wmax = -2.303 nRT log10 \(\frac{V_{2}}{V_{1}}\)
Wmax = Maximum work done = -4.754 kJ
= -4754 J, n = Number of moles = ?,
= 8.314 JK-1 mol-1
T = 300 K, V1 = Initial volume of carbon monoxide = 10 dm3
V2 = Final volume of carbon monoxide = 20 dm3
∴ -4754 = 22.303 × n × 8.314 × 300 log10 \(\frac {20}{10}\)
∴ -4754 = – 2.303 × n × 8.314 × 300 × log102
∴ – 4754 = – 2.303 × n × 8.314 × 300 × 0.3010
∴ n = \(\frac{-4754}{-2.303 \times 8.314 \times 300 \times 0.3010}\)
= 2.75 mol
Ans. Number of mol = 2.75 mol
(10) Given that the work done in isothermal and reversible expansion is 6.4 kJ when 2 moles of an ideal gas expanded to double its volume. Calculate the temperature at which expansion takes place.
Solution :
Given : Work = Wmax = -6.4 kJ (For expansion)
= – 6400 J
Number of moles = 2
If 1 = x L
V2 = 2 L
Temperature = T = ?
For isothermal reversible expansion,

(11) 300 mmol of perfect gas occupies 13 dm3 at 320 K. Calculate the work done in joules when the gas expands :
(a) Isothermally against a constant external pressure of 0.20 bar,
(b) Isothermal and reversible process,
(c) Into vacuum until the volume of gas is increased by 3 dm3. (R = 8.314 J mol-1K-1)
Solution :
Given : Number of moles of a gas = n
= 300 mmol = 0.3 mol
Initial volume = V1 = 13 dm3
Increase in volume = ΔV = 3 dm3
Pressure = Pex = 0.2 atm
Temperature = 320 K
(a) Expansion against constant pressure is an irreversible process.
∴ W = -Pex × ΔV
= -0.2 × 3
= -0.6 dm3 bar
= -0.6 × 100 J
= -60 J
(b) For isothermal reversible process,
Wmax = 2.303 nRT log10 \(\frac{V_{2}}{V_{1}}\)
Now, V2 = V1 + ΔV = 13 + 3 = 16 dm3
Wmax = – 2.303 × 0.3 × 8.314 × 320 log10 \(\frac {16}{13}\)
= -165.4 J
(c) In vacuum, Pex = 0
∴ W = -Pex × ΔV
= -0 × 3
= 0
Ans. (a) W= -60.78 J
(b) Wmax = -165.4 J
(c) W = 0.

Question 27.
Define and explain the term internal energy.
Answer:
Internal energy : It is defined as the total energy constituting potential energy and kinetic energy of the molecules present in the system.
Explanation :
- The internal energy of a system is a state function and thermodynamic function. It is denoted by U.
- Its value depends on the state of a system.
- The change in internal energy (Δ U) depends only on the initial state and the final state of the system.
Δ U = U2 – U1
- It is an extensive property of the system.
- It has same unit as heat and work.
- Total internal energy U of the system is,
Total energy = Potential energy + Kinetic energy
Question 28.
Explain the formulation of first law of thermodynamics.
OR
Deduce mathematical equation for the first law of thermodynamics. Justify its expression.
Answer:
(1) The first law of thermodynamics is based on the principle of conservation of energy.
(2) If Q is the heat absorbed by the system and if W is the work done by surroundings on the system then the internal energy of the system will increase by Δ U.
(3) From the conservation of energy we can write,
Increase in internal energy of the system = Quantity of heat absorbed by the system + Work done on the system
∴ ΔU = Q + W
(4) For an infinitesimal change,
dU = dQ + dW
Question 29.
Deduce the mathematical expression of first law of thermodynamics for the following processes :
(1) Isothermal process
(2) Isobaric process
(3) Isochoric process
(4) Adiabatic process.
Answer:
(1) Isothermal process :This is a process which is carried out at constant temperature. Since internal energy, U of the system depends on temperature there is no change in the internal energy U of the system. Hence ΔU = 0.
By first law of thermodynamics,
ΔU = Q +W
∴ 0 = Q + W
∴ Q = -W or W = -Q.
- Hence in expansion, the heat absorbed by the system is entirely converted into work on the surroundings.
- In compression, the work done on the system is converted into heat which is transferred to the surroundings by the system, keeping temperature constant.
(2) Isobaric process : In this, throughout the process pressure remains constant. Hence the system performs the work of expansion due to volume change ΔV.
W= -Pext × ΔV
Let QP be the heat absorbed by the system at constant pressure.
By first law of thermodynamics,
ΔU = QP + W.
∴ ΔU = QP – PexΔV
or QP = ΔU + PexΔV
In this process, the heat absorbed QP is used to increase the internal energy (ΔU) of the system.
(3) Isochoric process : In this process the volume of the system remains constant. Hence ΔV = 0. Therefore, the system does not perform mechanical work.
∴ W = -PΔV = -P × (0) = 0
Let QV be the heat absorbed at constant volume.
By first law of thermodynamics,
ΔU = Q + W
∴ ΔU = QV.
(4) Adiabatic process : In this process, the system does not exchange heat, Q with its surroundings.
∴ Q = 0.
Since by first law of thermodynamics,
ΔU = Q + W
∴ ΔU = Wad.
Hence,
(i) the increase in internal energy ΔU is due to the work done on the system by surroundings. This results in increase in energy and temperature of the system.
(ii) if the work is done by the system on surroundings, like expansion, then there is a decrease in internal energy (-ΔU) and temperature of the system decreases.
Question 30.
What are the IUPAC sign conventions of Q, U and W?
Answer:
In thermodynamics, the sign conventions are adopted according to IUPAC convention, based on acquisition of energy.
(i) Heat absorbed = +Q
Heat evolved = -Q
(ii) Internal energy change :
Increase in energy = + Δ U
Decrease in energy = – Δ U
(iii) Work done by the system = – W
Work done on the system = + W

Question 31.
Define and explain the term enthalpy.
OR
What is meant by enthalpy of a system ?
Answer:
Enthalpy (H) : It is defined as the total energy of a system consisting of internal energy (U) and pressure – volume (P × V) type of energy, i.e. enthalpy represents the sum of internal energy U and product PV energy. It is denoted by H and is represented as
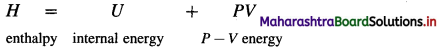
Explanation :
- Enthalpy represents total heat content of the system.
- Enthalpy is a thermodynamic state function.
- Enthalpy is an extensive property.
- The absorption of heat by a system increases its enthalpy. Hence enthalpy is called heat content of the system.
Question 32.
Derive the expression, ΔH = ΔU + PΔV.
Answer:
Enthalpy (H) of a system is defined as
H = U + PV
where U is internal energy
P is pressure and V is volume.
Consider a process in which a state of a system changes from an initial state A to a final state B. Let H1, U1, P1, V1 and H2, U2, P2, V2 be the state functions of the system in initial and final states.
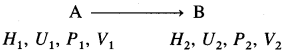
Then,
H1 = U1 + P2V2 and H2 = U2 + P2V2
The enthalpy change ΔH is given by,
ΔH = H2 – H1
= (U2 + P2V2) – (U1 + P1V1)
= (U2 – U1) + (P2V2 – P1V1)
= ΔU + ΔPV
where ΔU = U2 – U1
At constant pressure, P1 = P2 = P
∴ P2V2 – P1V1 = PV2 – PV1
= P(V2 – V1)
= P × ΔV
Hence, ΔH = ΔU + PΔV
This is a relation for enthalpy change.
Question 33.
Show that the heat absorbed at constant pressure is equal to the change in enthalpy of the system.
OR
Why is enthalpy called heat content of the system?
Answer:
By the first law of thermodynamics,
ΔU = Q + W
where ΔU is the change in internal energy
Q is heat supplied to the system
W is the work obtained.
∴ Q = ΔU – W
If QP is the heat absorbed at constant pressure by the system, so that the volume changes by Δ V against constant pressure P then,
W = -PΔV
∴ QP = ΔU – (-PΔV)
∴ QP = ΔU + PΔV ……… (1)
If ΔH is the enthalpy change for the system, then
ΔH = ΔU + PΔV ……….. (2)
By comparing above equations, (1) and (2), we can write, QP = ΔH
Hence heat absorbed at constant pressure is equal to the enthalpy change for the system.
Since by increase in enthalpy heat content of the system increases, enthalpy is also called as the heat content of the system.
Question 34.
What are the conditions under which ΔH = ΔU?
Answer:
- For any thermodynamic process or a chemical reaction at constant volume, Δ V = 0.
- Since ΔH = ΔU + PΔV, at constant volume ΔH = ΔU.
- In the reactions, involving only solids and liquids, Δ V is negligibly small, hence ΔH = ΔH.
- In a chemical reaction, in which number of moles of gaseous reactants and gaseous products are equal, then change in number of moles, Δ n = n2 – n1 = 0. Since ΔH = ΔU + ΔnRT, as Δn = 0, ΔH = ΔU.

Solved Examples 4.6 – 4.8
Question 35.
Solve the following :
(1) Calculate the change in internal energy when a gas is expanded by supplying 1500 J of heat energy. Work done in expansion is 850 J.
Solution :
Given : Q = 1500 J
W = -850 J (For expansion work is negative)
ΔU = ?
By first law of thermodynamics,
ΔU = Q + W
= 1500 + (- 850)
= 650 J
Ans. Change in internal energy = Δ U = 650 J
(2) A system absorbs 520 J of heat and performs work of 210 J. Calculate the change in internal energy.
Solution :
Given : Since the heat is absorbed by the system, the work is of expansion.
Q = 520 J
W= -210 J
ΔV = ?
ΔU = Q + W
= 520 + (- 210)
= 310 J
Ans. Internal energy change = Δ U = 310 J
(3) A gas expands from 6 litres to 20 dm3 at constant pressure 2.5 atmosphere. If the system is supplied with 5000 J of heat, calculate W and ΔU.
Solution :
Given : V1 = 6 dm3
V2 = 20 dm3
P = 2.5 atm
Q = 5000 J
W = ?; ΔU = ?
For expansion,
W = -Pex(V2 – V1)
= -2.5 (20 – 6)
= – 35
= – 35 × 100 J
= – 3500 J
ΔU = Q + W
= 5000 + (-3500)
= -1500 J
Ans. W= -3500 J; ΔU = – 1500 J
(4) An ideal gas expands against a constant pressure of 2.026 × 105 Pa from 5 dm3 to 15 dm3. If the change in the internal energy is 418 J, calculate the change in enthalpy.
Solution :
As the expansion takes place at a constant pressure, the change in enthalpy is given by
ΔH = ΔU + P(V2 – V1)
ΔH = Change in enthalpy = ?
ΔU = Change in internal energy = 418 J
P = Constant pressure = 2.026 × 105 Pa
V2 = 15 dm3 = 15 × 10-3 m3
V1 = 5 dm3 = 5 × 10-3 m3
∴ ΔH = 418 + 2.026 × 105 × (15 × 10-3 – 5 × 10-3)
= 418 + 2026
∴ ΔH = 2.444 × 103 J = 2.444 kJ
Ans. Change in enthalpy = 2.444 × 103 J
= 2.444 kJ

(5) In a reaction, 2.5 kJ of heat is released from the system and 5.5 kJ of work is done on the system. Find ΔU.
Solution :
Given : Q = -2.5 kJ (since heat is released)
W= + 5.5 kJ (since the work will be of compression)
ΔU = ?
ΔU = Q + W
= -2.5 + 5.5
= +3 kJ
Internal energy of the system will increase by 3 kJ.
Ans. Δ U = 3 kJ
(6) A chemical reaction is carried out by supplying 8 kJ of heat. The system performs the work of 2.7 kJ. Calculate ΔH and ΔU.
Solution :
Given : Q = + 8 kJ (since heat is absorbed by the system)
W = -2.7 kJ (It will be a work of expansion)
ΔH = ?, ΔU = ?
ΔU = Q + W = 8 + (-2.7) = 5.3 kJ
Internal energy of the system will increase by 5.3 kJ.
Due to expansion, Δ V > 0,
∴ PΔV = +2.7 kJ
ΔH = ΔU + PΔV = 5.3 + 2.7 = 8 kJ
Enthalpy of the system will increase by 8 kJ
Ans. ΔU = 5.3 kJ, ΔH = 8 kJ
(7) A sample of gas absorbs 4000 kJ of heat, (a) if volume remains constant. What is ΔU? (b) Suppose that in addition to absorption of heat by the sample, the surroundings does 2000 kJ of work on the sample. What is Δ U ? (c) Suppose that as the original sample absorbs heat, it expands against atmospheric pressure and does 600 kJ of work on its surroundings. What is ΔU ?
Solution :
Given : Q = + 4000 kJ (since heat is absorbed)
(a) Since volume remains constant, Δ V = 0.
W = -Pex (V2 – V1)
= -PexΔV = -Pex(0) = 0
∴ ΔU = Q + W = 4000 + 0 = 4000 kJ
(b) Q = + 4000 kJ
W = + 2000 kJ (Work done on the system)
ΔU = Q + W = 4000 + 2000 = 6000 kJ
(c) W = -600 kJ (Work of expansion)
ΔU = Q + W
ΔU = 4000 + (-600) = 3400 kJ
Ans. (a) Δ U = 4000 kJ
(b) Δ U = 6000 kJ
(c) Δ U = 3400 kJ
(8) Calculate the internal energy change at 298 K for the following reaction :
\(\frac{1}{2} \mathbf{N}_{2(\mathrm{~g})}+\frac{3}{2} \mathbf{H}_{2(\mathrm{~g})} \rightarrow \mathbf{N H}_{3(\mathrm{~g})}\)
The enthalpy change at constant pressure is -46.0 kJ mol-1. (R = 8.314 JK-1 mol-1)
Solution :
Given : \(\frac{1}{2} \mathbf{N}_{2(\mathrm{~g})}+\frac{3}{2} \mathbf{H}_{2(\mathrm{~g})} \rightarrow \mathbf{N H}_{3(\mathrm{~g})}\)
ΔH= -46.0 kJ mol-1
ΔH = Heat of formation of NH3 at constant pressure
= -46.0 kJ mol-1 = -4600 J mol-1
Δ U = Change in internal energy = ?
Δn = (Number of moles of ammonia) – (Number of moles of hydrogen + Number of moles of nitrogen)
= [1 – (\(\frac {1}{2}\) + \(\frac {3}{2}\))]= -1 mol
R= 8.314 JK-1 mol-1
T = Temperature in kelvin = 298 K
ΔH = Δ U + ΔnRT
∴ -46000 = ΔU + (-1 × 8.314 × 298)
∴ -46000 = ΔU – 2477.0
∴ ΔU = -46000 + 2477.0
= -43523 J
= -43.523 kJ
Ans. Change in internal energy = -43.523 kJ

(9) 5 moles of helium expand isothermally and reversibly from a pressure 40 × 10-5 Nm-2 to 4 × 10-5 Nm-2 at 300 K. Calculate the work done, change in internal energy and heat absorbed during the expansion. (R = 8.314 JK-1 mol-1)
Solution :
As the expansion takes place isothermally and reversibly, the work done is given by
Wmax = -2.203 nRT log\(\frac{P_{1}}{P_{2}}\)
Wmax = Maximum work done
n = Number of moles of helium = 5 moles
R = Gas constant = 8.314 JK-1 mol-1
T = 300 K
P1 = Initial pressure = 40 × 10-5 Nm-2
P2 = Final pressure = 4 × 10-5 Nm-2
∴ Wmax = -2.303 × 5 × 8.314 × 300 × log \(\frac {40}{4}\)
= – 2.303 × 5 × 8.314 × 300 × log 10
= -2.303 × 5 × 8.314 × 300 × 1
= – 28720J
As the expansion takes place isothermally, i.e., at the same temperature, there is no change in the internal energy of the system.
Q = ΔU + W
∴ Q = – W= + 28720 J as ΔU = 0
Ans. Work done = -28720 J, Heat absorbed = 28720 J, Change in internal energy = 0
(10) Calculate the work done in each of the following reactions. State whether work is done on or by the system.
(a) The oxidation of one mole of SO2 at 50°C.
2SO2(g) + O2(g) → 2SO3(g)
(b) Decomposition of 2 moles of NH4NO3 at 100°C
NH4NO3(s) → N2O(g) + 2H2O(g)
Solution :
(a) Given reaction :
2SO2(g) + O2(g) → 2SO3(g)
For 1 mole of SO2,
SO2(g) + \(\frac {1}{2}\)O2(g) → SO2(g)
∴ Δn = (n2)gaseous products – (n1)gaseous reactants
= 1 – (1 + \(\frac {1}{2}\))
= -0.5 mol
Since there is decrease in number of moles of gases, there will be compression, hence, the work will be done on the system by the surroundings.
Work is given by,
∴ W = – ΔnRT
= – (- 0.5) × 8.314 × (273 + 50)
= + 1342.7 J
(b) Given reaction :
NH4NO3(s) → N2O(g) + 2H2O(g)
For 2 moles of NH4NO3,
2NH4NO3(s) → 2N2O(g) + 4H2O(g)
∴ Change in number of moles,
Δn = (n2)gaseous products – (n1)gaseous reactants
= (2 + 4) – 0
= 6 mol
Since there is an increase in number of moles of gases, work of expansion is done by the system on the surroundings.
∴ W = -ΔnRT
= – 6 × 8.314 × (273+ 100)
= – 18606 J
= – 18.606 kJ
Ans. (a) W = 1342.7 J (b) W= -18.606 kJ
(11) The amount of heat evolved for the combustion of ethane is -900kJ mol-1 at 300K and 1 atm.
C2H6(g) + \(\frac {7}{2}\)O2(g) → 2CO2(g) + 3H2O(l)
Calculate W, ΔH and ΔU for the combustion of 12 × 10-3 kg ethane.
Solution :
Given : ΔH = -900 kJ mol-1
Temperature = T = 300 K
Pressure = P = 1 atm
Mass of ethane = m = 12 × 10-3 kg
Molar mass of ethane (C2H6) = 30 × 10-3 kg mol-1
ΔH = ? Δ U = ? for given ethane.
Number of moles of C2H6 = n = \(\frac{m \mathrm{~kg}}{M \mathrm{~kg} \mathrm{~mol}^{-1}}\)
= \(\frac{12 \times 10^{-3}}{30 \times 10^{-3}}\)
= 0.4 mol
For the given reaction,
C2H6(g) + \(\frac {7}{2}\)O2(g) → 2CO2(g) + 3H2O(l)
Δn = (n2)gaseous products – (n1)gaseous reactants
= 2 – (1 + \(\frac {7}{2}\)) = -2.5 mol
For 1 mol of C2H6, Δn = -2.5 mol
∴ For 0.4 mol of C2H6, Δn = -2.5 × 0.4
= -1 mol
Since there is a decrease in number of moles, the work is of compression on the system.
W = -ΔnRT
= – (-1) × 8.314 × 300
= + 2494 J
= + 2.494 kJ
For 1 mol of C2H6 ΔH = -900 kJ
∴ For 0.4 mol of C2H6, ΔH= – 900 × 0.4
= – 360 kJ
ΔH = ΔU + ΔnRT
ΔU = ΔH – ΔnRT
= -360 – (-1) × 8.314 × 300× 10-3
= – 360 + 2.494
= – 357.506 kJ
Ans. W = + 2.494 kJ, ΔH = -360 kJ;
ΔU= – 357.506 kJ
(12) The latent heat of evaporation of water is 80 kJ mol-1. If 100 g water are evaporated at 100 °C and 1 atm, calculate W, ΔH, ΔU and Q.
Solution :
Given : Latent heat of evaporation = ΔH
= 80 kJ mol-1 of water
Temperature = T = 273 + 100 = 373 K
Pressure = P = 1 atm
Mass of water = m = 100 g
Molar mass of water = 18 g mol-1
W = ?, ΔH = 1, U = ?, Q = ?
Number of moles of water = \(\frac{m}{M}=\frac{100}{18}\) = 5.556 mol
H2O(l) → H2O(g)
5.556 mol 5.556 mol
Change in number of moles = Δn = 5.556 – 0
= 5.556 mol
For evaporation of 1 mol H2O, ΔH = 80 kJ
For 5.556 mol H2O, ΔH= 80 × 5.556 = 444.5 kJ
In this reaction, the work will be of expansion.
W= -ΔnRT
= -5.556 × 8.314 × 373
= – 17230 J
= -17.23 kJ
Now,
ΔH = ΔU + ΔnRT
ΔU = ΔH – ΔnRT
= 444.5 – 5.556 × 8.314 × 373 × 10-3
= 444.5 – 17.23
= 427.27 kJ
In this, Q = QP = ΔH = 444.5 kJ
Ans. W= -17.23 kJ; ΔH = 444.5 kJ
ΔU= 427.21 kJ, Q = 444.5 kJ

(13) Oxidation of propane is represented as
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(g), ΔH0 = -2043 kJ
How much pressure volume work is done and what is the value of AU at constant pressure of 1 bar when the volume change is + 22.4 dm3.
Solution :
Given :
ΔH0 = – 2043 kJ
Change in volume = ΔV = +22.4 L
ΔU = ?
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(g)
Δn = (n2)gaseous products – (n1)gaseous reactants
= (3 + 4) – (1 + 5)
= 1 mol
Since there is an increase in number of moles, the work will be of expansion.
W = -P × ΔV dm3 bar
= – 1 × 22.4
= – 1 × 22.4 × 100 J
= – 2240 J
= -2.240
ΔH = ΔU + PΔV
ΔU = ΔH – PΔV
= – 2043 – (2.24)
= – 2040.7 kJ
Ans. W = -2.27 kJ, ΔU = -2040.7 kJ
(14) How much heat is evolved when 12 g of CO reacts with NO2 ? The reaction is :
4CO(g) + 2NO2(g) → 4CO2(g) + N2(g),
ΔrH0 = -1200 kJ
Solution :
Given : 4CO(g) + 2NO2(g) → 4CO2(g) + N2(g)
Molar mass of CO = 28 g mol-1
ΔrH0 = – 1200 kJ;
Molar mass of CO = 28 g mol-1
mco = 12 g, ΔH = ?
From the reaction,
∵ For 4 × 28 g CO, ΔH0 = – 1200 kJ
∵ For 12g CO ΔH0 = \(\frac{(-1200) \times 12}{4 \times 28}\)
= -128.6 kJ
Ans. Heat evolved = 128.6 kJ
Question 36.
What is phase transformation?
Answer:
Phase transformation (or transition) :
- The transition of one phase (physical state) of a matter to another phase at constant temperature and pressure without change in chemical composition is called phase transformation.
- During phase transformation, both the phases exist at equilibrium.
Solids ⇌ Liquid; Liquid ⇌ Vapour.

Question 37.
Mention different types of phase transitions.
Answer:
The following are the types of phase changes :
(1) Fusion : This involves the change of a matter from solid state to liquid state. In this heat is absorbed, hence it is endothermic (ΔH > 0).
H2O(s) → H2O(l)
(2) Vaporisation or evaporation : This involves the change of a matter from liquid state to gaseous state. In this heat is absorbed, hence it is endothermic (ΔH > 0).
H2O(l) → H2O(g)
(3) Sublimation : This involves the change of matter from solid state directly into gaseous state. In this heat is absorbed, hence it is endothermic (ΔH > 0).
Camphor(s) → Camphor(g)
Question 38.
Define and explain enthalpy of freezing.
Answer:
Enthalpy of freezing (ΔfreezH) : The enthalpy change that accompanies the solidification of one mole of a liquid into solid at constant temperature and pressure is called enthalpy of freezing.
For example,
\(\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \stackrel{1 \mathrm{~atm}, 273 \mathrm{~K}}{\longrightarrow} \mathrm{H}_{2} \mathrm{O}_{(\mathrm{s})}\)
ΔfreezH = -6.01 kJ mol-1
This equation describes that when one mole of water freezes (solidifies) at 0 °C (273 K) and 1 atmosphere, 6.01 kJ of heat will be released to the surroundings.
Question 39.
Define and explain the following :
(A) Enthalpy of vaporisation.
(B) Enthalpy of sublimation.
Answer:
(A) Enthalpy of vaporisation (ΔvapH) : The enthalpy change that accompanies the vaporisation of one mole of a liquid at constant temperature and pressure is called heat of vaporisation or evaporation. For example,
\(\mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})} \stackrel{1 \mathrm{~atm}, 373 \mathrm{~K}}{\longrightarrow} \mathrm{H}_{2} \mathrm{O}_{(\mathrm{g})}\)
ΔvapH = +40.7 kJ mol-1
This equation describes that when one mole of water is evaporated at 100 °C (373 K) and 1 atmosphere, 40.7 kJ of heat will be absorbed.
(B) Enthalpy of sublimation (ΔsubH) : The enthalpy change or the amount of heat absorbed that accompanies the sublimation of one mole of a solid directly into its vapour at constant temperature and pressure is called enthalpy of sublimation.
For example,
\(\mathrm{CO}_{2(\mathrm{~s})} \stackrel{1 \mathrm{~atm}, 195 \mathrm{~K}}{\longrightarrow} \mathrm{CO}_{2(\mathrm{~g})}\)
ΔsubH = 25.2 kJ mol-1
This equation describes that when 1 mole of dry solid carbon dioxide, CO2(s) sublimes forming gaseous CO2(g), 25.2 kJ of heat will be absorbed.
Question 40.
Explain process of sublimation and enthalpy of sublimation ?
OR
How is enthalpy of sublimation related to enthalpy of fusion and enthalpy of vaporisation ?
Answer:
(1) The sublimation involves the conversion of a solid into vapour at constant temperature and pressure. For example,
H2O(s) → H2O(g), ΔsubH = 51.08 kJ mol-1 at 0°C.
(2) This conversion takes place in two steps, first melting of solid into liquid and second vaporisation of the liquid.
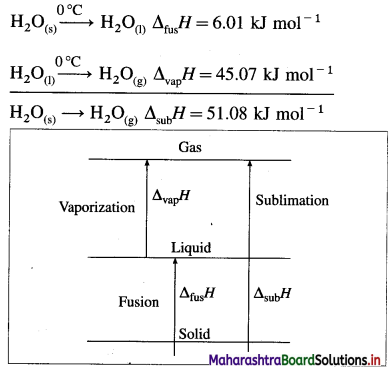
Hence we can write,
ΔsubH = ΔfusH + ΔvapH
Question 41.
Arrange the following in order of increasing enthalpy :
H2O(s), H2O(g), H2O(l)
Answer:
The increasing order of enthalpy of the given substance will be,
HH2O(g), < HH2O(l), < HH2O(s)
This is because the conversion of H2O(s) to H2O(l) and further to H2O(g) involves absorption of heat.

Question 42.
Define and explain :
(A) Enthalpy of atomisation
(B) Enthalpy of ionisation.
Answer:
(A) Enthalpy of atomisation (ΔatoH) : The enthalpy change or amount of heat absorbed accompanying the dissociation of the molecules in one mole of a gaseous substance into free gaseous atoms at constant temperature and pressure is called enthalpy of atomisation.
For example,
Cl2(g) → 2Cl(g), ΔatoH = 242 kJ mol-1
CH4(g) → C(g) + 4H(g), ΔatoH = 1660 kJ mol-1.
(B) Enthalpy of ionisation (ΔionH) : The enthalpy change or amount of heat absorbed accompanying the removal of one electron from each atom or ion in one mole of gaseous atoms or ions is called enthalpy of ionisation.
For example,
Na(g) → Na+(g) + e– ΔionH = 494 kJ mol-1
This equation describes that when one mole of gaseous sodium atoms, Na(g) are ionised forming gaseous ions, Na+(g), the energy required is 494 kJ.
Question 43.
Define and explain electron gain enthalpy.
Answer:
Electron gain enthalpy (ΔegH) : It is defined as the enthalpy change, when mole of gaseous atoms of an element accept electrons to form gaseous ion.
E.g. Cl(g) + e– → Cl– (g) ΔegH = – 349 kJ mol-1.
It is the reverse of ionisation process.
Question 44.
Define enthalpy of solution.
Answer:
Enthalpy of solution : It is defined as the enthalpy change in a process when one mole of a substance is dissolved in specified amount of a solvent.
NaCl(s) + aq ⇌ NaCl(aq) ΔsolnH = 4 kJ mol-1
Question 45.
Define enthalpy of solution at infinite dilution.
Answer:
Enthalpy of solution (ΔsolnH) : It is defined as the enthalpy change when one mole of a substance is dissolved in a large excess of a solvent, so that further dilution will not change the enthalpy at constant temperature and pressure.
For example,
HCl(g) + aq → HCl(aq) ΔsolnH
= -75.14 kJ mol-1
Question 46.
Explain the enthalpy of solution of an ionic compound.
Answer:
An ionic compound dissolves in a polar solvent like water in two steps as follows :
Step-I : The ions are separated from the molecule involving crystal lattice enthalpy ΔLH.
\(\mathrm{MX}_{(\mathrm{s})} \rightarrow \mathrm{M}_{(\mathrm{g})}^{+}+\mathrm{X}_{(\mathrm{g})}^{-} \quad \Delta_{\mathrm{L}} H\)
ΔLH is always positive.
Step-II : The gaseous ions are hydrated with water molecules involving hydration energy, ΔhydH.
\(\mathbf{M}_{(\mathrm{g})}^{+}\) + xH2O(l) → [M(H2O)x]+
\(\mathrm{X}_{(\mathrm{g})}^{-}\) + yH2O(l) → [X(H2O)y]–
ΔhydH is always negative.
The enthalpy change ΔsolnH of solution is given by,
ΔsolnH = ΔLH + ΔhydH
For example, consider enthalpy of solution of NaCl(s).
ΔLHNaCl = 790 kJ mol-1
ΔhydHNaCl = -786 kJ mol-1
Hence enthalpy change for solution of NaCl(s) is,
ΔsolnH = ΔLHNaCl + ΔhydHNaCl
= 790 + (-786)
= + 4 kJ mol-1
Therefore dissolution of NaCl in water is an endothermic process.

Solved Examples 4.9
Question 47.
Solve the following :
(1) Heat of fusion of ice at 0 °C and 1 atmosphere is 6.1 kJ mol-1 and heat of evaporation of water at 100 °C is 40.7 kJ mol-1. Calculate the enthalpy change for the conversion of 1 mole of ice at 0 °C into vapour at 100 °C. Heat capacity of water is 4.184 JK-1 mol-1.
Solution :
Given : Heat of fusion of ice = ΔfusH = 6.01 kJ mol-1
Heat of evaporation of water = ΔvapH = 40.7 kJ mol-1
Temperature of ice = 273 K
Temperature of vapour = (273 + 100) K = 373 K
Heat capacity of water = 4.184 JK-1 g-1
Heat capacity of 1 mole of water
= CH2O = 4.184 × 18
= 75.312 JK-1 mol-1
The conversion of ice at 0 °C to water at 100°C takes place in three steps as follows:
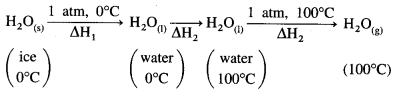
ΔH1 = nice × ΔfusH = 1mol × 6.01kJ mol-1 = 6.01 kJ
ΔH2 is the enthalpy change for raising the temperature from 273 K to 373 K.
ΔH2 = nwater × CH2O × (T2 – T1)
= 1mol × 75.312JK-1 mol-1 × (373 – 273)K
= 7531 J
= 7.531 kJ
ΔH3 = nwater × ΔvapH
= 1 × 40.7
= 40.7 kJ
Hence total enthalpy change will be ΔH = ΔH1 + ΔH2 + ΔH3
= 6.01 + 7.531 + 40.7
= 54.241 kJ
Ans. ΔH = 54.241 kJ
(2) Heat of sublimation of ice at 0°C and 1 atmosphere is 6.01 kJ mol-1 and heat of evaporation of water at 0 °C and 1 atmosphere is 45.07 kJ mol-1. Calculate the heat of sublimation of one mole of ice at 0 °C and 1 atmosphere. Write the equation for the same.
Solution :
The sublimation of ice can be represented by following equation,
\(\mathrm{H}_{2} \mathrm{O}_{(\mathrm{s})} \stackrel{1 \mathrm{~atm}, 0^{\circ} \mathrm{C}}{\longrightarrow} \mathrm{H}_{2} \mathrm{O}_{(\mathrm{g})}\)
This is a process of two steps.
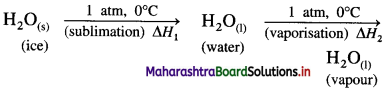
ΔH1 = nH2O × ΔfusH
= 1 × 6.01 =6.01 kJ
ΔH2 = nH2O × ΔvapH
= 1 × 45.07 = 45.07
Heat of sublimation = ΔH = ΔH1 + ΔH2
= 6.01 + 45.07
= 51.08 kJ
Ans. Heat of sublimation of ice = 51.08 kJ
(3) Heat of evaporation of ethyl alcohol at 78.5 °C and 1 atmosphere is 38.6 kJ mol-1. If 100 g ethyl alcohol vapour is condensed, what will be ΔH ?
Solution :
Given : ΔvapHC2H5OH = 38.6 kJ mol-1
Mass of C2H5OH = m = 100 g
Molar mass of C2H5OH = M = 46 g mol-1
ΔcondHC2H5OH = ?
Number of moles of C2H5OH = \(\frac{m}{M}=\frac{100}{46}\)
= 2.174 mol
Heat of condensation = ΔcondH = -38.6 kJ mol-1
∴ ΔcondH = n × ΔcondH
= 2.174mol × (-38.6)kJ mol-1 kJ = – 83.9 kJ
Ans. Heat of condensation = ΔcondH = -83.9 kJ

(4) The hydration enthalpies of Li+(g), and Br–(g) are -500 kJ mol-1 and -350 kJ mol-1 respectively and the lattice energy of LiBr(s) is 807 kJmol-1. Write the thermochemical equations for enthalpy of solution of LiBr(s) and calculate its value.
Solution :
Given : Enthalpy of hydration of Li+(g)
= ΔhydH1
= -500 kJmol-1
Enthalpy of hydration of Br–(g) = ΔhydH2
= -350 kJ mol-1
Lattice energy of LiBr(s) = ΔLH3 = 807 kJ mol-1
Enthalpy of solution of LiBr(s) = ΔsolnΔH = ?
The thermochemical equation for the dissolution of LiBr(s) forming a solution is,
LiBr(s) + aq → Li+(aq) + Br–(aq) (I) ΔsolH = ?
This takes place in two steps as follows :
(i) LiBr(s) → Li+(g) + Br–(g) ΔLH3
(ii) (a) Li+(g) + aq → Li+(aq) ΔhydH1
(b) Br–(g) + aq → Br–(aq) ΔhydH2
Hence by adding equations (i) and (ii) (a) and (b) we get equation I.
∴ ΔsolH = ΔLH3 + ΔhydH1 + ΔhydH2
= 807 + (-500) + (-350)
= -43 kJ mol-1
Ans. Heat of solution of LiBr(s) = ΔsolH = -43 kJ mol-1
(5) Heat of solution of NaCl is 3.9 kJ mol-1. If the lattice energy of NaCl is 787 kJ mol-1, calculate the hydration energies of ions of the salt.
Solution :
Given : Heat of solution of NaCl
= ΔsolnH0
= ΔH1 = 3.9 kJmol-1
Lattice energy of NaCl = ΔLH
= ΔH2 = 787 kJ mol-1
Hydration energy of Na+(g) and Cl–(g)
= ΔhydH(Na+ + Cl–)
= ΔH3 = ?
Thermochemical equation for dissolution of NaCl(s) is;
NaCl(s) + aq → Na+(aq) + Cl–(aq)…ΔH1
NaCl(s) → Na+(g) + Cl–(g)… ΔH2
Na+(g) + Cl–(g) + aq → Na+(aq) + Cl–(aq) ΔH3
∴ ΔH1 = ΔH2 + AH3
3.9 = 787 + AH3
∴ ΔH3 = -787 + 3.9= -783.1 kJmol-1
Ans. Hydration energy of Na+(g) and Cl–(g)
= -783.1 kJmol-1
(6) Enthalpies of solution are given as follows :
CuSO4(s) + 10H2O → CUSO4(10H2O)
ΔH1 = -54.5 kJ mol-1
CuSO4(s) + 100 H2O → CUSO4(100H2O)
ΔH2 = -68.4 kJ mol-1
A solution contains 1 mol of CuSO4 in 180 g water at 25 °C. If it is diluted by adding 1620 g water, calculate the enthalpy of dilution.
Solution :
Given : Enthalpy of solution of CuSO4 in 10 mol H2O
= ΔsolnH = ΔH1 = -54.5 kJ mol-1
Enthalpy of solution of CuSO4 in 100 mol
H2O = ΔH2
= -68.4 kJmol-1
Mass of water = 1620 g
For dilution, ΔdilH = ?
Now 180 g H2O = \(\frac {180}{18}\) = 10 mol H2O
And, 1620 g H2O = \(\frac {1620}{18}\) = 90 mol H2O
Hence for heat of dilution,
CUSO4(10H2O) + 90H2O(l) → CUSO4(100H2O) ΔdilH = ?
∴ ΔdilH = ΔH2 -ΔH1
= -68.4 – (54.5)
= -13.9 kJmol-1
Ans. Heat of dilution = ΔdilH = -13.9 kJ mol-1
(7) Heat of solution and heat of hydration of AgF are -20.5kJmol-1 and -930kJmol-1 respectively. Calculate lattice energy of AgF.
Solution :
Given : Heat of solution of AgF = ΔsolnH
= -ΔH1 = -20.5 kJmol-1
Heat of hydration of AgF = ΔhydH = ΔH2
= -930 kJ mol-1
Lattice energy of AgF = ΔLH = ΔH3 = ?
For heat of solution, AgF(s) + aq → AgF(aq) ΔH1
For heat of hydration,
Ag+(g) + F–(g) + aq → Ag+(aq) + F–(aq) ΔH2
For Lattice energy, Ag+(g) + F–(g) → AgF(s)
ΔLH = ?
From above equations,
∴ ΔH3 = ΔH2 – ΔH1
= -930 – (-20.5)
= -909.5 kJmol-1
Ans. Lattice energy of AgF(s) = -909.5 kJ mol-1

(8) Bond enthalpy of H2 is 436kJmol-1 while hydration energy of hydrogen ion is -1075 kJ mol-1. Calculate the enthalpy of formation of H+(aq). (Ionisation energy of hydrogen is 1312 kJ mol-1
Solution :
Given : Bond enthalpy of H2(g) = ΔH0H2(g)
= 436 kJ mol-1
Hydration energy of H+(g) = ΔH2 = -1075 kJmol-1
Ionisation energy of H(g) = ΔH3 = 1312 kJ mol-1
Enthalpy of formation of H+(aq) = ΔfH = ?
Thermochemical equation for the formation of H+(aq)
\(\frac {1}{2}\)H2(g) + aq → H+(aq)ΔfH
This takes place in three steps as follows :
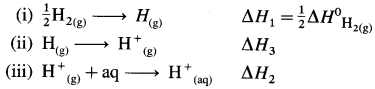
Hence heat of formation of H+(aq) is
ΔfH = ΔH1 + ΔH2 + ΔH3
= \(\frac {1}{2}\) × 436 + (-1075) + 1312
= 218 – 1075 + 1312.
= 455 kJ mol-1
Ans. Enthalpy of formation of H+(aq) = 455 kJmol-1
(9) Calculate lattice energy of crystalline sodium chloride from the following data :

Solution :
Given : Bond enthalpy of Cl2 = ΔH0 = 244 kJmol-1
Thermochemical equation for the formation of 1 mole of NaCl(s),
\(\mathrm{Na}_{(\mathrm{s})}+\frac{1}{2} \mathrm{Cl}_{2} \longrightarrow \mathrm{NaCl}_{(s)} \quad \Delta_{\mathrm{f}} H_{\mathrm{NaCl}}^{0}=-411 \mathrm{~kJ}\)
Lattice energy, ΔLH = ?
Since enthalpy is a state function, this reaction can be written in various steps as follows :
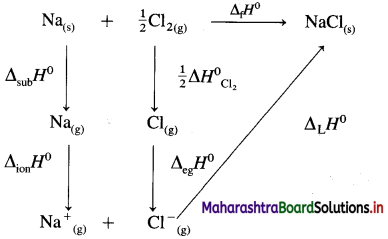
By Hess’s law,
ΔLH0 = ΔsubH0+ ΔionH0 + \(\frac {1}{2}\)ΔH0cl2 + ΔegH0 + ΔLH0
-411 = 109 + 496 + \(\frac {1}{2}\) × 244 + (-348) + ΔLH
= 109 + 496 + 122 – 348 + ΔLH
∴ ΔLH= -790 kJ mol-1.
Ans. Lattice energy of NaCl(s) = -790 kJ mol–
(10) Calculate the internal energy at 298 K for the formation of one mole of ammonia, if the enthalpy change at constant pressure is -42.0 kJ mol-1.
(Given : R = 8.314 J K-1 mol-1)
Solution :
Given : ΔH = -42.0 kJ mol-1, T = 298 K, ΔU = ?
\(\frac{1}{2} \mathrm{~N}_{2(\mathrm{~g})}+\frac{3}{2} \mathrm{H}_{2(\mathrm{~g})} \longrightarrow \mathrm{NH}_{3(\mathrm{~g})}\)
Δn = 1 – (\(\frac {1}{2}\) + \(\frac {3}{2}\)) = -1 mol
ΔH = ΔU + ΔnRT
∴ ΔU = ΔH – ΔnRT
= -42 – (- 1) × 8.314 × 298 × 10-3
= -42 + 2.477
= -39.523 kJ
Ans. ΔU = -39.523 kJ

Question 48.
What is thermochemistry ? Explain.
Answer:
Thermochemistry : Thermodynamic study of heat changes or enthalpy changes during the chemical reactions is called thermochemistry.
Consider a reaction, Reactants → Products
The heat changes ΔH for the reaction may be represented as,
ΔHreaction = Σ Hproducts – Σ Hreactants
where H represents enthalpy.
The energy released or absorbed during a chemical change appears in the form of heat energy.
Question 49.
Define and explain the term, enthalpy or heat of reaction.
Answer:
Enthalpy or heat of reaction : The enthalpy of a chemical reaction is the difference between the sum of the enthalpies of products and that of the reactants with every substance in a definite physical state and in the amounts (moles) represented by the coefficients in the balanced equation.
Explanation : Consider the following general reaction,
aA + bB → cC + dD
The heat of the reaction ΔH is the difference in sum of enthalpies of products and sum of enthalpies of reactants.
∴ ΔH = Σ Hproducts – Σ Hreactants
= [cHC + dHD] – [aHA + bHB]
= ΣPH – ΣRZ
where H represents enthalpy of the substance.
For endothermic reaction, ΔH is positive, (ΔH > 0).
For exothermic reaction, ΔH is negative, (ΔH < 0).
Question 50.
Explain the sign convention used for ΔH.
Answer:
The change in enthalpy or heat of reaction ΔH is given by,
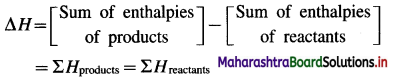
(i) If the sum of enthalpies of products, ΣH and reactants, ΣRH are equal then ΔH for the reaction is zero, (ΔH = 0).
i. e. ΣPH = ΣRH
∴ ΔH = ΣPH – ΣRH = 0
(ii) If the sum of enthalpies of products ΣPH is greater than the sum of enthalpies of reactants ΣRH, then ΔH is positive, (ΔH > 0). Since such reactions take place with the absorption of heat from surroundings, they are called endothermic reactions.
∴ ΣHproducts > ΣHreactants
∴ ΔH > 0
(iii) If the sum of enthalpies of products ΣPH is less than the sum of enthalpies of reactants, ΣRH then ΔH is negative, (ΔH < 0). Since in such reactions heat is given out to the surroundings, they are called exothermic reactions.
∴ ΣPH < ΣRH
∴ ΔH < 0
Question 51.
Define : (i) Exothermic process (ii) Endothermic process.
Answer:
(i) Exothermic process : A process taking place with the evolution of heat is called exothermic process.
For this process, Q is -ve, ΔH is -ve.
(ii) Endothermic process : A process taking place with the absorption of heat (from the surroundings) is called endothermic process.
For this process, Q is +ve, ΔH is +ve.
Question 52.
Distinguish between Endothermic reaction and Exothermic reaction.
Answer:
Endothermic reaction:
- In endothermic reaction heat is absorbed from suroundings.
- Sum of enthalpies of products is greater than sum of enthalpies of reactants i.e. ΣPH > ΣRH
- Heat of reaction, ΔH is positive.
- Products are less stable than reactants.
- C(s) + O2(g) → CO2(g)
ΔH = -394 kJ
- This reaction requires supply of thermal energy.
Exothermic reaction:
- In exothermic reaction heat is given out to surroundings.
- Sum of enthalpies of products is less than sum of enthalpies of reactants.
i.e. ΣPH < ΣRH
- Heat of reaction, ΔH is negative.
- Products are more stable than reactants.
- N2(g) + O2(g) → 2NO
ΔH = + 180 kJ
- This reaction does not require supply of thermal energy.

Question 53.
Explain the standard state of an element.
Answer:
Standard state of an element : It is defined as the most stable state of an element at 298 K and 1 atmosphere (or 1 bar).
In this state, the enthalpy of the element is assumed to be zero.
∴ H0element or in general Helement = 0
∴ H0graphite = HH2(g) = 0; HNa(s) = 0; HHg(l) = 0
Question 54.
What is a thermochemical equation? Explain with an example.
Answer:
Thermochemical equation : It is defined as a balanced chemical equation along with the corresponding heat of reaction (ΔH) and physical states and number of moles of all reactants and all products appropriately mentioned.
E.g. C6H12O6(s) + 6O2(g) = 6CO2(g) + 6H2O(l)
ΔH = -2808 kJ mol-1
Question 55.
What are the guidelines followed for writing thermochemical equations?
Answer:
According to IUPAC conventions, while writing thermochemical equations, following rules must be followed :
(1) Reaction is represented by balanced chemical equation for the number of moles of the reactants and the products. E.g.
CH4(g) + 2O2(g) = CO2(g) + 2H2O(l)
ΔrH°= -890 kJ mol-1
(2) The physical states of all the substances in the reaction must be mentioned. E.g. (s) for solid, (l) for liquid and (g) for gas.
(3) Heat or enthalpy changes are measured at 298 K and 1 atmosphere (or 1 bar).
(4) ΔH0 is written at right hand side of thermochemical equation.
(5) Proper sign must be indicated for ΔH0. For endothermic reaction ΔH0 is positive, (+ΔH0) and for exothermic reaction ΔH is negative, (-ΔH0).
(6) The enthalpy of the elements in their standard states is taken as zero. (H0Element = 0; H0C(s) = 0, H0H2(g) = 0)
(7) When all the substances taking part in the reaction are in their standard states, the enthalpy change is written as ΔH0.
(8) The enthalpy of any compound is equal to its heat of formation.
(9) In case of elements, the allotropic form must be mentioned. E.g. C(graphite), S(rhombic), Sn(white)
(10) For the reverse reaction, ΔH0 value has equal magnitude but opposite sign.

Question 56.
Define the following terms giving examples :
(1) Standard enthalpy of reaction.
(2) Standard enthalpy of formation or standard heat of formation
(3) Standard enthalpy of combustion or standard heat of combustion.
Answer:
(1) Standard enthalpy of reaction : it is defined as the difference between the sum of enthalpies of products and that of the reactants with every substance in its standard state at constant temperature (298 K) and pressure (1 atm).
Reactants → Products
ΔH0reaction = ΣH0products – ΣH0reactants
(2) Standard enthalpy of formation or standard heat of formation (ΔfH0) : It is defined as the enthalpy change ΔH0 when one mole of a pure compound is formed in its standard state from its constituent elements in their standard states at constant temperature (298 K) and pressure (1 atmosphere or 1 bar). It is denoted by ΔfH0. E.g.
C(s) + O2(g) = CO2(g) ΔfH0= -394 kJ mol-1
(ΔfH0 may be positive or negative.)
(3) Standard enthalpy of combustion or standard heat of combustion : it is defined as the enthalpy change when one mole of a substance in the standard state undergoes complete combustion in a sufficient amount of oxygen at constant temperature (298 K) and pressure (1 atmosphere or 1 bar). It is denoted by ΔcH0.
E.g. CH3OH(l) + \(\frac {3}{2}\)O2(g) = CO2(g) + 2H2O
ΔCH0 = -726 kJ mol-1
(ΔcH0 is always negative.)
[Note : Calorific value : It is the enthalpy change or amount of heat liberated when one gram of a substance undergoes combustion.
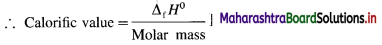
Question 57.
Show that the standard heat of formation of a compound is equal to its enthalpy.
Answer:
Consider the formation of one mole of gaseous CO2 in the standard state at 298 K and 1 atmosphere. The thermochemical equation for formation can be represented as,
C(s) + O2(g) = CO2(g) ΔfH0 = -394 kJ mol-1
Now heat of this reaction, ΔH0 is,
ΔH0reaction = ΣPH0 – ΣRH0
∴ ΔfH0co2(g) = H0co2(g) – [H0c(s) + H0O2(g)]
Since the enthalpies of elements in their standard states are zero,
i.e.
H0c(s) = o, H0O2(g) = 0
∴ ΔfH0co2(g) = H0co2(g) – [0 + 0]
∴ ΔfH0co2 = Hco2(g)
Therefore standard heat of formation of a compound is equal to its enthalpy.
Question 58.
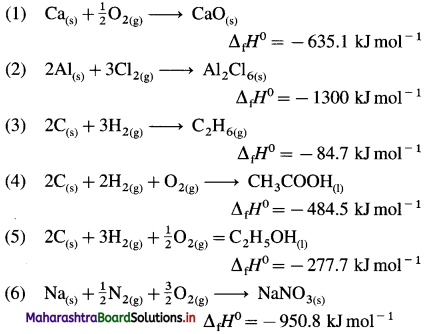
Standard enthalpy of formation of various following compounds are given. Write thermochemical equation for each :
| Compound |
ΔfH0 KJ mol-1 |
| Cao(s) |
-635.1 |
| Al2Cl6(s) |
-1300 |
| C2H6(g) |
-84.7 |
| CH3COOH(l) |
-484.7 |
| C2H5OH(l) |
-277.7 |
| NaNO3(s) |
-950.8 |
Answer:
(Hint: Write one mole of the compound on right hand side and corresponding constituent elements along with their standard physical states on left hand side.)
Question 59.
Standard enthalpy of combustion of different substances are given. Write thermochemical equation for each.
| Substance |
ΔCH0 KJ mol-1 |
| C(graphite) |
-393.5 |
| C6H6(l) |
-3268 |
| C2H5OH(l) |
-1409 |
| CH3CHO |
-1166 |
Answer:
In the combustion reaction, C forms CO2(g),
H forms H2O(l), etc.
(1) C(graphite) + O2(g) → CO2(g)
ΔCH0 = -393.5 kJ mol-1
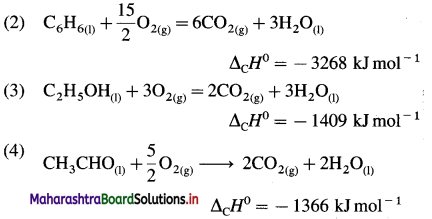
Question 60.
Write the thermochemical equations for enthalpy of solution of :
(1) Glucose (C6H12O6)
(2) NaCl(s)
(3) CaBr2(s)
Answer:
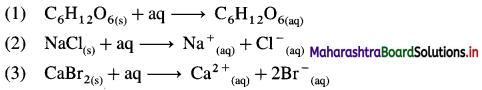

Question 61.
How is standard enthalpy of formation useful to calculate standard enthalpy of reaction ?
Answer:
(1) The standard enthalpies of formation, ΔfH0 of the compounds can be used to determine the standard enthalpy of reaction (ΔrH0).
(2) ΔrH0 of a reaction can be obtained by subtracting the sum of ΔfH0 values of all the reactants from the sum of ΔfH0 values of all the products with each ΔfH0 value multiplied by the appropriate coefficient of that substance in the balanced thermochemical equation.
(3) Consider following reaction :
aA + bB → cC + dD
The standard enthalpy of the reaction is given by,
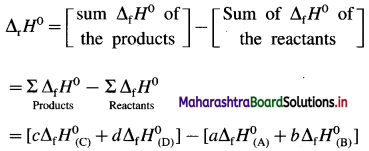
where a, b, c and d are the coefficients (moles) of the substances A, B, C and D respectively.
Question 62.
Write the balanced chemical equation that have ΔH0 value equal to ΔfH0 for each of the following substances :
(1) C2H2(g)
(2) KCIO3(s)
(3) C12H22O11(s) (4) CH3-CH2-OH(1)
Answer:
ΔfH0 represents the standard enthalpy of formation of each given substance. Hence it is necessary to write thermochemical equation for the formation of each substance. ΔH0 of this formation reaction is equal to standard heat of formation, ΔfH0.
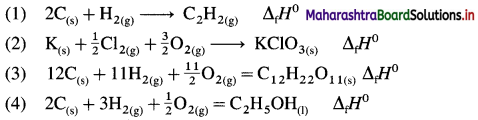
Question 63.
Consider the chemical reaction,
OF2(g) + H2O(g) → O2(g) + 2HF(g) ΔH0 = -323 kJ
What is ΔH0 of the reaction if (a) the equation is multiplied by 3, (b) direction of reaction is reversed?
Answer:
(a) If the given thermochemical equation is multiplied by 3 then,
ΔrH0 = 3ΔH0 = 3 × (-323) = -969 kJ
(b) If the direction of equation is reversed, then the reaction will be,
O2(g) + 2HF(g) → OF2(g) + H2O(g)
∴ ΔrH0 = – ΔH0 = – (- 323) = + 323 kJ
Question 64.
Define bond enthalpy (or bond energy).
Answer:
Bond enthalpy (or Bond energy) : The enthalpy change or amount of heat energy required to break one mole of particular covalent bonds of gaseous molecules forming free gaseous atoms or radicals at constant temperature (298 K) and pressure (1 atmosphere) is called bond enthalpy or bond energy. For example, bond enthalpy of H2 is 436.4 kJ mol-1.

Question 65.
Explain bond enthalpy of diatomic molecules.
Answer:
In case of diatomic molecules, since there is only one bond, the bond enthalpy is equal to heat of atomisation. For example, heat of atomisation of
HCl(g) is 431.9 kJ mol-1.

(Bond enthalpy is generally denoted by D).
Question 66.
Explain bond enthalpy in polyatomic molecules.
Answer:
Consider bond enthalpy in H2O. The thermochemical equation for dissociation of H2O(g) is,
H2O(g) → 2H(g) + O(g), ΔrH0 = 927 kJ mol-1
In this, two O – H bonds are broken. It can be represented in stepwise as follows :
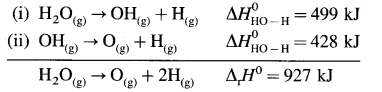
In above, even if two identical O – H bonds are borken, the energies required to break each bond are different.
The average bond enthalpy of O – H bond is,
ΔrH0 = \(\frac {927}{2}\) = 463.5 kJ mol-1
Solved Examples 4.10
Question 67.
Solve the following :
(1) Standard enthalpy of formation of ethane, C2H6(g) is -84.7 kJ mol-1. Calculate the enthalpy change for the formation of 0.1 kg ethane.
Solution :
Given : Enthalpy of formation of C2H6(g)
= ΔfH0 = ΔH1 = -84.7 kJ mol-1
Mass of C2H6(g) = 0.1 kg = 100 g
Molar mass ofC2H6 = 30 g mol-1
ΔH0 for the formation of 0.1 kg C2H6 = 100 g
C2H6 = ΔH2 = ?

Ans. Heat of formation = -282.3 kJ
(2) When 10 g C2H5OH(l) are formed, 51 kJ heat is liberated. Calculate standard enthalpy of formation of C2H5OH(l).
Solution :
Given : Mass of C2H5OH(l) = m = 10 g
Heat liberated = ΔH1 = -51 kJ
Molar mass of C2H5OH = 46 gmol-1
Standard enthalpy of formation of C2H5OH(l)
= ΔfH = ?
Standard enthalpy of formation is the enthalpy change for the formation of 1 mole C2H5OH(l) i.e., 46 g C2H5OH(l).
Now,
∵ For the formation of 10 g C2H5OH(l)
ΔH1 = -51 kJ
∴ For the formation of 46 g C2H5OH,
ΔfH0 = \(\frac{-51 \times 46}{10}\) = – 234.6 kJ mol-1
Ans. Standard enthalpy of formation of C2H5OH = ΔfH0 = – 234.6 kJ mol-1

(3) Standard enthalpy of combustion of CH3OH is -726kJ mol-1. Calculate enthalpy change for the combustion of 0.5 kg CH3OH.
Solution :
Given : Standard enthalpy of combustion of
CH3OH = ΔCH0 = ΔH1 = -726 kJ mol-1
Mass of CH3OH = m = 0.5 kg = 500 g
Molar mass of CH3OH = 32 g mol-1
Enthalpy of combustion = ΔCH = ΔH2 = ?
Now,
Enthalpy of combustion is ΔH for the combustion of 1 mole CH3OH = 32 g CH3OH.
∵ For 1 mole CH3OH = 32g CH3OH
ΔH1 = – 726 kJ
∴ For 500 g CH3OH, ΔH2 = \(\frac{-726 \times 500}{32}\)
= -11344 kJ
Ans. Enthalpy change for combustion of 0.5 kg CH3OH = – 11344 kJ
(4) The heat evolved in a reaction of 7.5 g of Fe2O3 with enough CO is 1.164 kJ.
Calculate ΔH0 for the reaction,
Fe2O3(s) + 3CO(g) → 2Fe(s) + 3CO2(g)
Solution :
Fe2O3(s) + 3CO(g) → 2Fe(s) + 3CO2(g)
ΔH = -1.164 kJ
Atomic mass of Fe = 56 g mol-1
Atomic mass of O = 16 g mol-1
Mass of Fe2O3 = 7.5 g
ΔH = -1.164 kJ
ΔH0 for reaction = ?
Molar mass of Fe2O3 = 2 × 56 + 3 × 16
= 160 g mol-1
∵ For 7.5 g Fe2O3 ΔH= – 1.164 kJ
∴ For 160 g Fe2O3
ΔH0 = \(\frac{-1.164 \times 160}{7.5}\) = -24.86 kJ mol-1
Ans. ΔH0 for the reaction = -24.83 kJ mol-1
(5) Calculate the standard enthalpy of the reaction,
2C (graphite) + 3H2(g) → C2H6(g), ΔH0 = ? from the following ΔH0 values :
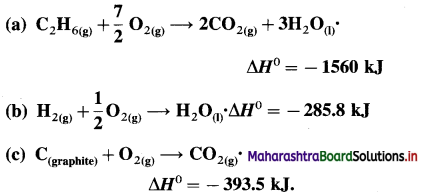
Solution :

Ans. Standard enthalpy of formation of C2H6 = -84.4 kJ mol-1
(6) The enthalpy of combustion of ethane is -1300 kJ. How much heat will be evolved by combustion of 1.3 × 10-3 kg of ethane?
Solution :
Given : ΔCHC2H6(g) = -1300 kJ mol-1
ΔH = ?
Amount of C2H6(g) = 1.3 × 10-3 kg
Molar mass of C2H6 = 30 × 10-3 kg mol-1
Number of moles of C2H6
= nC2H6 = \(\frac{1.3 \times 10^{-3}}{30 \times 10^{-3}}\) = 4,333 × 10-2 mol
For, combustion of 1 mol C2H6 ΔH = -1300 kJ
∴ For combustion of 4.333 × 10-2 mol C2H6,
ΔH = 4.333 × 10-2 × ( -1300) = – 56.33 kJ
Ans. Heat evolved is -56.33 kJ

(7) Calculate heat of formation of pentane from the following data :
(i) C(s) + O2(g) = CO2(g) ΔH0 = -393.51 kJ
(ii) H2(g) + \(\frac {1}{2}\)O2(g) = H2O(l) ΔH0 = -285.80 kJ
(iii) C5H12 + 😯2(g) = 5CO2(g) + 6H2O1 ΔH0 = -3537 kJ
Solution :
Given :
(i) CO(s) + O2(g) = CO2(g) ….. (1)
\(\Delta H_{1}^{0}\) = -393.51 kJ mol-1
(ii) H2(g) + \(\frac {1}{2}\)O2(g) = H2O(l) … (2)
\(\Delta H_{2}^{0}\) = – 285.80 kJ mol-1
(iii) C5H12(g) + 😯2(g) = 5CO2(g) + 6H2O(l) ….. (3)
\(\Delta H_{3}^{0}\) = -3537 kJ mol-1
Required thermochemical equation :
5C(s) + 6H2(g) → C5H12(g) – ΔH = ?
Add 5 × equation (1) and 6 × equation (2) and subtract equation (3), then we get the required equation.
∴ ΔH0 = 5 \(\Delta H_{1}^{0}\) + 6 \(\Delta H_{2}^{0}\) – \(\Delta H_{3}^{0}\)
= 5( -393.52) + 6( -285.8) – (-3537)
= -1967.6 – 1714.8 + 3537
= -145.4 kJ mol-1
Ans. ΔfH0C5H12 = -145.4 kJ mol-1
(8) How much heat is evolved when 12 g of CO react with NO2 according to the following reaction,
4CO(g) + 2NO2(g) → 4CO2(g) + N2(g), ΔH0 = -1198 kJ ?
Solution :
Given : Mass of CO(g) = m = 12 g
Molar mass of CO = 28 g mol-1
4CO(g) + 2NO2(g) → 4CO2(g) + N2(g)
ΔrH0 = -1198 kJ
Mass of 4 moles of CO = 4 × 28 g CO = 112 g CO

Ans. Heat evolved during combustion of 12 g CO = 128.4 kJ, or ΔCH = -128.4 kJ
(9) The heats of formation of C12H22O11(S), CO2(g) and H2O(l) are -2271.82, – 393.50 and 285.76 kJ respectively. Calculate the amount of cane sugar (C12H22O11(S)) which will supply 11296.8 kJ of energy.
Solution :
Given : ΔfHC12H22O11(S) = -2271.82 J mol-1
ΔfHCO2(g) = – 393.5 kJ mol-1
ΔfHH2O(l) = – 285.76 kJ mol-1
Energy required = 11296.8 kJ
Thermochemical equation for combustion of C12H22O11(S) is represented as,
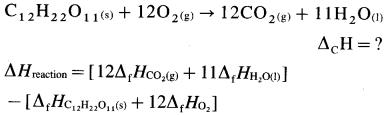
= [ 12(-393.5) + 11 (-285.76] – [-2271.82 + 12(0)]
= [ -4722 – 3143.36] + 2271.82
= -5593.54 kJ mol-1
Molar mass of C12H22O11(S) = 342
To obtain 5593.5 kJ energy, C12H22O11(S) required is 342 gram.
Hence for 11296.8 energy, the amount of C12H22O11(S) required as = \(\frac{11296.8 \times 342}{5593.54}\)
= 690.7 g
Ans. Amount of sugar required = 690.7 g

(10) 6.24 g of ethanol are vaporized by supplying 5.89 kJ of heat energy. What is enthalpy of vaporization of ethanol?
Solution :
Given : Mass of ethanol (C2H5OH) = m = 6.24 g
Heat energy supplied = ΔH = 5.89 kJ
Heat of vaporisation of ethanol = ΔvapH = ?
Molar mass of ethanol, C2H5OH = 46 g mol-1
∵ For 6.24 g C2H5OH ΔH = 5.89kJ
∴ For 1 mole C2H5OH = 46 g C2H5OH
ΔH = \(\frac{5.89 \times 46}{6.24}\)
= 43.42 kJ mol-1
∴ Enthalpy of vaporisation of C2H5OH(l)
= 43.42 kJ
Ans. Enthalpy of vaporisation of C2H5OH(l)
= 43.42 kJ
(11) Given the following equations calculate the standard enthalpy of the reaction :
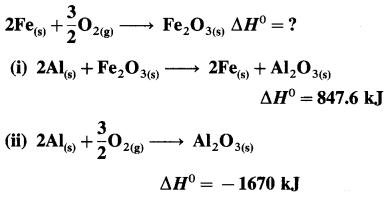
Solution :

By subtracting eq. (ii) from eq. (iii), we get eq. (i)
∴ eq. (i) = eq. (iii) – eq. (ii)
\(\Delta H_{1}^{0}=\Delta H_{3}^{0}-\Delta H_{2}^{0}\)
= -1670 – (-847.6)
= – 822.4 kJ
∴ ΔrH0 = ΔH01 = -822.4 kJ
Ans. Standrad enthalpy of the reaction = ΔrH0 = -822.4 kJ
(12) Calculate the standard enthalpy of combustion of CH2COOH(l) from the following data : ΔfH0(CO2) = -393.3 kJ mol-1
ΔfH0(H2O) = -285.8 kJ mol-1
ΔfH0(CH3COOH) = -483.2 kJ mol-1
Solution :

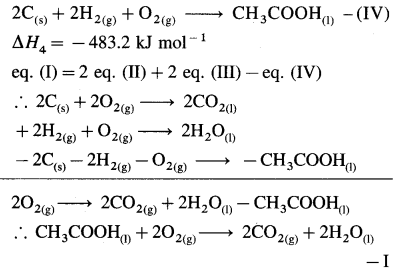
∴ ΔH1 = 2ΔH2 + 2ΔH3 – ΔH4
= 2(-393.3) + 2(-285.8) – (-483.2)
= -786.6 – 571.6 + 483.2
= -875 kJ mol-1
Ans. Standard enthalpy of combustion of CH3COOH = -875 kJ mol-1.
(13) The bond enthalpies of H2(g), Br2(g) and HBr(g) are 436 kJ mol-1, 193 kJ mol-1 and 366 kJ mol-1 respectively. Calculate the enthalpy change for the following reaction,
H2(g) + Br2(g) → 2HBr(g).
Solution :
Given : Bond enthalpy of H2(g) = ΔH0H2(g)
= 436 kJ mol-1
Bond enthalpy of Br2(g) = ΔH0Br2(g) = 193 kJ mol-1
Bond enthalpy of HBr(g) = ΔH0HBr(g) = 366 kJ mol-1
Given reaction,
H2(g) + Br2(g) → 2HBr(g)
OR
H-H(g) + Br-Br(g) → 2H-Br(g)
The enthalpy change of the reaction is,

= [436 + 193] – 2[366]
= 629 – 732
= -103 kJ
Ans. Enthalpy change for the reaction = ΔrH0
= -103 kJ

(14) Calculate ΔrH0 of the reaction
CH4(g) + O2(g) → CH2O(g) + H2O(g)
From the following data:
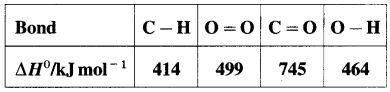
Solution:
Given:
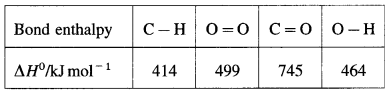
Standard enthalpy change for the reaction = ΔrH0 = ?
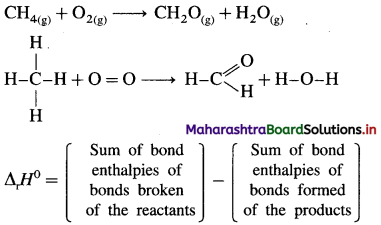
= [ 2ΔH0C-H + ΔH0o=o ] – [ΔH0C=o + 2ΔH0o-H]
= [2 × 414 + 499] – [745 + 2 × 464]
= [828 + 499] – [745 + 928]
= -346 kJ
Ans. Standard enthalpy change for the reaction = ΔrH0 = -346 kJ
(15) Calculate C-Cl bond enthalpy from the following data :
CH3Cl(g) + Cl2(g) → CH2Cl2(g) + HCl(g) ΔH0 = – 104 kJ
| Bond |
C–H |
Cl–Cl |
H–Cl |
| ΔH0/KJ mol-1 |
414 |
243 |
431 |
(330 kJ mol-1)
Solution :
Given :
| Bond |
C–H |
Cl–Cl |
H–Cl |
| ΔH0/KJ mol-1 |
414 |
243 |
431 |
For the given reaction, ΔrH0 = -104 kJ
Bond enthalpy of C-Cl = ΔH0C–Cl] = ?
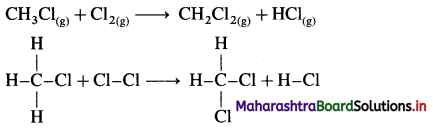
In this reaction, 1 C–H, 1 Cl–Cl bonds of the reactants are broken while 1C–Cl and 1H–Cl bonds of the products are formed.
Sum of bond enthalpies of bonds formed of the products

Ans. Bond enthalpy of C–Cl = ΔH0C–Cl
= 330 kJ mol-1
(16) The enthalpy change for the atomisation of 1010 molecules of ammonia is 1.94 × 10-11 kJ. Calculate the bond enthalpy of N-H bond.
Solution :
Given : Enthalpy change for atomisation of 1010 molecules = 1.94 × 10-11 kJ
Number of NH3 molecules dissociate = 1010
Bond enthalpy of N-H = ΔH = ?
1 mole of NH3 contains 6.022 × 1023 NH3 molecules.
∵ For atomisation of 1010 molecules of NH3
ΔH = 1.94 × 10-11 kJ
∴ For atomisation of 6.022 × 1023 molecules of NH3,
ΔH = \(\frac{1.94 \times 10^{-11} \times 6.022 \times 10^{23}}{10^{10}}\)
= 1168 kJ mol-1
In NH3 three N-H bonds are broken on atomisation.
NH3(g) → N(g) + 3H(g) ΔH = 1168 kJ mol-1
∴ Average bond enthalpy of N-H bond is,
ΔH = \(\frac{1168}{3}\) = 389.3 kJ mol-1
Ans. Bond enthalpy of N-H bond
= 389.3 kJ mol-1
(17) Calculate the enthalpy of atomisation (or dissociation) of CH2Br2(g) at 25°C from the following data :
| Bond enthalpies |
C-H |
C-Br |
| ΔH0 kJ mol-1 |
414 |
352 |
Solution :
Given : Bond enthalpies : ΔH0C-H
= 414 kJ mol-1;
ΔH0C-Br = 352 kJ mol-1
Enthalpy of atomisation of CH2Br2(g) = ?
Thermochemical equation for atomisation (or dissociation) of CH2Br2 is,
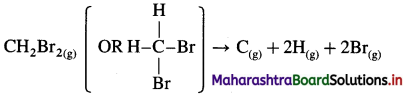
ΔatomH° = sum of bond enthalpies of all bonds broken
= 2ΔH0C-H + 2ΔH0C-Br
= 2 × 414 + 2 × 352
= 828 + 704
= 1532 kJ mol-1
Ans. Enthalpy of atomisation of CH2Br2(g)
= 1532 kJ mol-1

(18) Enthalpy of sublimation of graphite is 716 kJ mol-1.
| Bond enthalpy |
H-H |
C-H |
| ΔH0 kJ mol-1 |
436.4 |
414 |
Calculate standard enthalpy of formation of CH4.
Solution :
Given : ΔsubH0graphite = 716 kJ mol-1
| Bond enthalpy |
H-H |
C-H |
| ΔH0 kJ mol-1 |
436.4 |
414 |
Thermochemical equation for the formation of CH4,
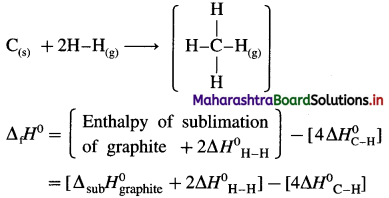
= [716 + 2 × 436.4] – [4 × 414]
= [716+ 872.8] – [1656]
= 1588.8 – 1656
= -67.2 kJ mol-1
Ans. Standard enthalpy of formation of CH4 = ΔfH0CH4(g) = -67.2 kJ mol-1
(19) Calculate enthalpy of formation of propane from the following data :
Heat of sublimation of graphite is 716 kJ mo-1.
| Bond enthalpy |
H-H |
C-H |
C-C |
| ΔH0 kJ mol-1 |
436.4 |
414 |
350 |
Solution :
Given: Enthalpy of sublimation of graphite = ΔsubH0C
= 716 kJmol-1
| Bond enthalpy |
H-H |
C-H |
C-C |
| ΔH0 kJ mol-1 |
436.4 |
414 |
350 |
Enthalpy of formation of propane = ΔfH0 = ?
Thermochemical equation of the formation of propane, CH3-CH2-CH3,
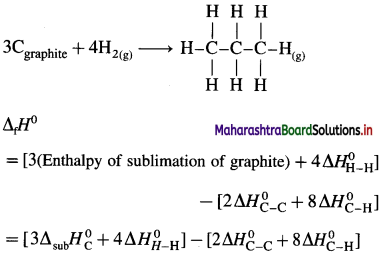
= [3 × 716 + 4 × 436.4] – [2 × 350 + 8 × 414]
= [2148 + 1745.6] – [700 + 3312]
= -118.4 kJmol-1
Ans. Enthalpy of formation of propane (C3H8)
= -118.4 kJmol-1
(20) The standard enthalpy of formation of propene, CH3-CH = CH2 is -13.2 kJ mol-1. Enthalpy of sublimation (atomisation) of graphite is 716 kJmol-1.
| Bond enthalpy |
H-H |
C-H |
C-C |
| ΔH0 kJ mol-1 |
436.4 |
414 |
350 |
Calculate bond enthalpy of C = C
Solution :
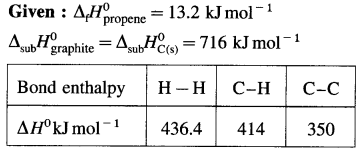
Bond enthalpy of C = C = ΔH0C=C = ?
For the formation of propene, (CH3 – CH = CH2),
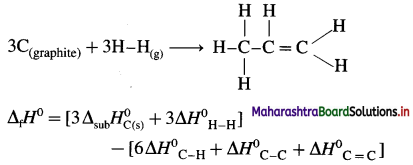
13.2 = [3 × 716 + 3 × 436.4] – [6 × 414 + 350 + \(\Delta H_{\mathrm{C}=\mathrm{C}}^{0}\) ]
= [2148 + 1309.2] – [2484 + 350 + \(\Delta H_{\mathrm{C}=\mathrm{C}}^{0}\) ]
= [3457.2] – [2834 + \(\Delta H_{\mathrm{C}=\mathrm{C}}^{0}\) ]
= 3457.2 – 2834 – \(\Delta H_{\mathrm{C}=\mathrm{C}}^{0}\)
\(\Delta H_{\mathrm{C}=\mathrm{C}}^{0}\) = 3457.2 – 2834 – 13.2
= 610 kJmol-1
Ans. Bond enthalpy of C = C = \(\Delta H_{\mathrm{C}=\mathrm{C}}^{0}\)
= 610 kJ mol-1

(21) Calculate the enthalpy of the reaction,
CH3COOH(g) + CH3CH2OH(g) → CH3COOCH2CH3(g) + H2O(g)
Bond enthalpies of O-H, C-O, in kJmol-1 are 464, 351 respectively.
Solution :
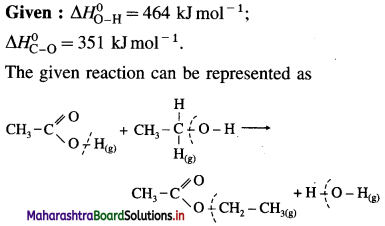
In this reaction 1O-H and 1C-0 bond of the reactants are broken while 1C-0 and 1O-H bonds of the products are formed. Enthalpy of reaction,

Ans. Hence Enthalpy change for the reaction = ΔrH0 = 0.
Question 68.
(1) What is a spontaneous process?
(2) What are its characteristics?
Answer:
(1) Spontaneous process : It is defined as a process that takes place on its own or without the intervention of the external agency or influence. For example, expansion of a gas or flow of a gas from higher pressure to low pressure or a flow of heat from higher temperature to lower temperature.
(2) Characteristics :
- It occurs on its own and doesn’t require external agency.
- It proceeds in one direction and can’t be completely reversed by external stimulant.
- These processes may be fast or slow.
- These processes proceed until an equilibrium is reached.
Question 69.
Give the examples of spontaneous processes.
Answer:
The examples of the spontaneous processes are as follows :
- All natural processes are spontaneous.
- A flow of gas from higher pressure to lower pressure.
- Flow of water on its own from higher level to lower level.
- Flow of heat from hotter body to colder body.
- Acid-base neutralisation is a spontaneous reaction.
Question 70.
What is relation between spontaneity and energy of a system ?
Answer:
(1) The spontaneous process takes place in a direction in which energy of the system decreases. For example, neutralisation reaction between NaOH and HCl solution is exothermic with release of energy.
(2) The spontaneous process also takes place with the increase in energy by absorbing heat. For example,
(a) Melting of ice at 0 °C by absorption of heat
(b) Dissolution of NaCl,
NaCl(s) + aq → NaCl(aq) → Na+(aq) + Cl–(aq)
ΔH0 = + 3.9 kJ mol-1
Question 71.
Which of the following are spontaneous ?
(a) Dissolving sugar in hot coffee.
(b) Separation of Ar and Kr from their mixture.
(c) Spreading of fragrance when a bottle of perfume is opened.
(d) Flow of heat from cold object to hot object.
(e) Heat transfer from ice to room temperature at 25 °C.
Answer:
The spontaneous processes are :
(a) Dissolving sugar in hot coffee.
(b) Separation of Ar and Kr from their mixture.
(c) Spreading of fragrance when a bottle of perfume is opened.
The non-spontaneous processes are :
(d) Flow of heat from cold object to hot object.
(e) Heat transfer from ice to room temperature at 25 °C.
Question 72.
Explain : (a) Order in a system.
(b) Disorder in a system.
Answer:
(a) (i) When the atoms, molecules or ions constituting the system are arranged in a perfect order then the system is said to be in order. For example, in the solid state, the constituent atoms, molecules or ions are tightly placed at lattice points in the crystal lattice.
(ii) When solid melts forming a liquid or when a liquid vaporises, the constituents are separated and are in random motion imparting maximum disorder.
(iii) As energy of the system decreases order increases.
(b) Increase in entropy is a measure of disorder in the system. Consider following process :
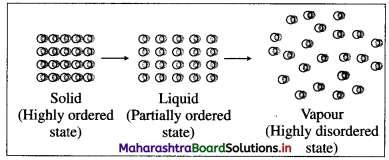
Fig. 4.11 : Order decreases and disorder increases, Entropy increases
Question 73.
What is the change in order and entropy in the following :
(i) Dissolution of solid I2 in water.
(ii) Dissociation of H2(g) into atoms ?
Answer:
(i) For dissolution of solid I2,
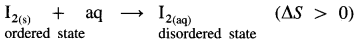
In the solid I2, there is ordered arrangement which collapses in solution increasing disorder and entropy, hence ΔS is positive.
(ii) In the dissociation of H2(g)
H2(g) → 2H(g) (ΔS > 0)
In the molecular state, two H atoms in every molecule are together but in atomic state the disorder is increased with the increase in entropy and hence ΔS > 0.

Question 74.
How does addition of heat to a system at different temperatures changes disorder or ΔS ?
Answer:
- The amount of heat added to a system at higher temperature causes less disorder than when the heat is added at lower temperature.
- Since disorder depends on the temperature at which heat is added, ΔS relates reciprocally to temperature.
- This can also be explained from equation,
ΔS = \(\frac{Q_{\text {rev }}}{T}\)
Question 75.
Explain the change in entropy for the following processes :
(i) 2H2O2(l) → 2H2O(l) + O2(g)
(ii) 2H2(g) + O2(g) → 2H2O(l)
(iii) When ice melts at 0 °C and water vaporises at 100 °C.
Answer:
(i) In the following reaction,
2H2O2(l) → 2H2O(l) + O2(g) ΔS = + 126 JK
Due to formation of O2 gas from liquid, entropy increases.
(ii) In the reaction, entropy decreases due to formation of liquid H2O from gaseous H2 and O2.
(iii) \(\text { Ice } \stackrel{0^{\circ} \mathrm{C}}{\longrightarrow} \text { water } \stackrel{100^{\circ} \mathrm{C}}{\longrightarrow} \text { vapour }\)
In these two steps, entropy increases due to increase in disorder from solid ice to liquid water and further to gaseous state.
Question 76.
How does entropy change in the following processes ? Explain.
(a) freezing of a liquid
(b) sublimation of a solid
(c) dissolving sugar in water
(d) condensation of vapour.
Answer:
(a) Freezing of a liquid results in decrease in randomness and disorder, hence entropy decreases, ΔS < 0.
(b) Sublimation of a solid converts it into vapour where the molecules or atoms are free to move randomly. Hence disorder increases accompanying increase in entropy, ΔS > 0.
(c) Dissolving sugar in water separates the molecules of sugar in the solution increasing disorder and entropy, ΔS > 0.
(d) Condensation of vapour decreases the disorder and randomness, hence entropy, ΔS < 0.
Question 77.
Predict the sign of ΔS in the following processes. Give reasons for your answer :
OR
Explain with reason sign conventions of ΔS in the following reactions.
Answer:
(a) N2O4(g) → 2NO2(g)
Since 1 mole N2O4 on dissociation gives two moles of NO2, the number of molecules increase, disorder increases hence entropy increases, ΔS > 0.
(b) Fe2O3(s) + 3H2(g) → 2Fe(s) + 3H2O(g)
In the reaction number of moles of gaseous reactants and products are same, hence ΔS = 0.
(c) N2(g) + 3H2(g) → 2NH3(g)
In the reaction, 4 moles of gaseous reactants form 2 moles of gaseous products (Δn < 0). Therefore disorder decreases and hence entropy decreases, ΔS < 0.
(d) MgCO3(s) → MgO(s) + CO2(g)
In this 1 mole of orderly solid MgCO3 gives 1 mole of solid MgO and 1 mole of gaseous CO2 (Δn > 0) with more disorder. Hence entropy increases, ΔS > 0.
(e) CO2(g) → CO2(s)
In this system from higher disorder in gaseous state changes to less disorder in the solid state, hence entropy decreases, ΔS < 0.
(f) Cl2(g) → 2Cl(g)
Since the dissociation of Cl2 gas gives double Cl atoms, the number of atoms increases (Δn >0) increasing the disorder of the system. Hence ΔS > 0.

Question 78.
Identify which of the following pairs has larger entropy ? Why ?
(a) He(g) in a volume of 1 L or He(g) in a volume of 5 L both at 25 °C.
(b) O2(g) at 1 atm or O2(g) at 10 atm both at the same temperature.
(c) C2H5OH(l) or C2H5OH(g)
(d) 5 mol of Ne or 2 mol of Ne.
Answer:
(a) Atoms of He in 5 L at 25 °C occupy more volume than in 1 L. Hence, the randomness and disorder is more in 5 L. Expansion of a gas always increases its entropy. Therefore He(g) in 5L will have larger entropy.
(b) O2(g) at 1 atm will occupy more volume than O2(g) at 10 atm at the same temperature. Hence at 1 atm O2(g) will have higher disorder and hence higher entropy.
(c) The molecules of gaseous C2H5OH(g) will have more disorder and randomness due to free motion of molecules than C2H5OH(l). Hence entropy of C2H5OH(g) will be larger.
(d) 5 mol Ne will contain more Ne atoms than 2 mol Ne. Hence disorder in 5 mol will be more. Therefore 5 mol Ne will have larger entropy.
Question 79.
Mention entropy change (ΔS) for :
(i) spontaneous process
(ii) nonspontaneous process
(iii) at equilibrium.
Answer:
(a) ΔStotal > 0, the process is spontaneous
(b) ΔStotal < 0, the process is non-spontaneous
(c) ΔStotal = 0, the process is at equilibrium.
Question 80.
Define Gibbs free energy and change in free energy. What are the units of Gibbs free energy ?
OR
Derive the relation between ΔG and ΔS Total.
Answer:
(i) Gibbs free energy, G is defined as,
G = H – TS
where H is the enthalpy, S is the entropy of the system at absolute temperature T.
Since H, T and S are state functions, G is a state function and a thermodynamic function.
(ii) At constant temperature and pressure, change in free energy ΔG for the system is represented as, ΔG = ΔH – TΔS
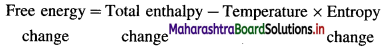
This is called Gibbs free energy equation for ΔG. In this ΔS is total entropy change, i.e., ΔSTotal.
(iii) The SI units of ΔG are J or kJ (or Jmol-1 or kJmol-1).
The c.g.s. units of ΔG are cal or kcal (or cal mol-1 or kcal mol-1.)
Question 81.
Explain Gibbs free energy and spontaneity of the process.
Answer:
The total entropy change for a system and its surroundings accompanying a process is given by,
ΔSTotal = ΔSsystem + ΔSsurr
By second law, for a spontaneous process,
ΔSTotal > 0. If + ΔH is the enthalpy change (or enthalpy increase) for the process, or a reaction at constant temperature (T) and pressure, then enthalpy change (or enthalpy decrease) for the surroundings will be -ΔH.

By Gibbs equation,
ΔG = ΔH – TΔS
By comparing above two equations,
∴ ΔG = -TΔSTotal
As ΔSTotal increases, ΔG decreases.
For a spontaneous process, ΔSTotal > 0
which is according to second law of thermodynamics.
∴ ΔG < 0.
Hence in a spontaneous process, Gibbs free energy decreases (ΔG < 0) while entropy increases (ΔS > 0).
Therefore for a non-spontaneous process Gibbs free energy increases (Δ G > 0).
It can be concluded that for a process at equilibrium, ΔG=0.
Hence,
- For the spontaneous process, Δ G < 0
- For the non-spontaneous process, Δ G > 0
- For the process at equilibrium, Δ G = 0.

Question 82.
How does second law of thermodynamics explain the conditions of spontaneity ?
Answer:
The second law explains the conditions of spontaneity as below :
(i) ΔStotal > 0 and ΔG < 0, the process is spontaneous.
(ii) ΔStotal < 0 and ΔG > 0, the process is nonspontaneous.
(iii) ΔStotal = 0 and ΔG = 0, the process is at equilibrium.
Question 83.
Discuss the factors, ΔH, ΔS and ΔG for spontaneous and non-spontaneous processes.
OR
What can be said about the spontaneity of reactions when (1) ΔH and ΔS are both positive (2) ΔH and ΔS are both negative (3) ΔH is positive and ΔS is negative (4) ΔH is negative and ΔS is positive.
Answer:
For a spontaneous or a non-spontaneous process, ΔH and ΔS may be positive or negative (ΔH < 0 or ΔH > 0; ΔS < 0 or ΔS > 0). But ΔG must decrease, i.e., ΔG < 0. If ΔG > 0, the process or a reaction will definitely be non-spontaneous. This can be explained by Gibbs equation, ΔG = ΔH – TΔS.
(1) If ΔH and ΔS are both negative, then ΔG will be negative only when TΔS < ΔH or when temperature T is low. Such reactions must be carried out at low temperatures.
(2) If ΔH and ΔS are both positive then ΔG will be negative if, TΔS > ΔH; such reactions must be carried out at high temperature.
(3) If ΔH is negative (ΔH < 0) and ΔS is positive (ΔS > 0) then for all temperatures ΔG will be negative and the reaction will be spontaneous. But as temperature increase, ΔG will be more negative, hence the reaction will be more spontaneous at higher temperature.
(4) If ΔH is positive, (ΔH > 0) and ΔS is negative (ΔS < 0), ΔG will be always positive (ΔG > 0) and hence the reaction will be non-spontaneous at all temperatures.
This can be summarised in the following table :
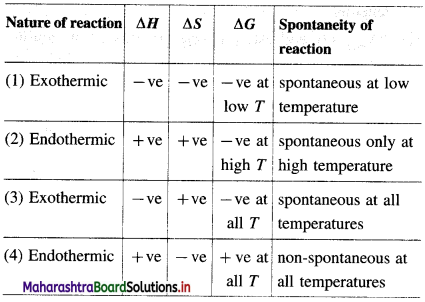
Question 84.
Obtain a temperature condition for equilibrium.
Answer:
For a system at equilibrium, free energy change ΔG is,
ΔG = ΔH – TΔS
where ΔH is enthalpy change, ΔS is entropy change at temperature, T. Since ΔG = 0 at equilibrium,
O = ΔH – TΔS
∴ TΔS = ΔH
OR T = \(\frac{\Delta H}{\Delta S}\)
Hence at temperature T, changeover between forward spontaneous step and backward non-spontaneous step occurs and the system attains an equilibrium.
Here ΔH and ΔS are assumed to be independent of temperature.
Question 85.
Predict the signs of ΔH, ΔS and ΔG of the system when a solid melts at 1 atmosphere and at (a) -55 °C (b) -95 °C (c) -77 °C, if the normal melting point of the solid is -77 °C.
Answer:
Since the normal melting point of the solid is -77°C, to melt the solid at any temperature other than at -77 °C, the pressure is required to be changed. During the phase change, the system will be at equilibrium, hence Δ G = 0.
(a) In case a solid at -55 °C, the temperature should be decreased (ΔH < 0, ΔS < 0) to -77 °C and then it will melt, so ΔH > 0, ΔS > 0, ΔG = 0.
(b) In case of a solid at -95 °C, it represents supercooled system and the temperature should be raised to -77 °C (ΔH > 0, ΔS > 0) and then it will melt so ΔH > 0, ΔS > 0, ΔG = 0.
(c) At -77 °C, solid will melt, solid and liquid will be at equilibrium. Melting involves absorption of heat,
ΔH >0, ΔS > 0, ΔG = 0.

Solved Examples 4.11
Question 86.
Solve the following :
(1) In an isothermal reversible process, 6 kJ heat is absorbed at 27 °C. Calculate the entropy change.
Solution :
Given : Temperature = T = 273 + 21 = 300 K
Heat absorbed = Qrev = 6 kJ = 6000 J
Entropy change = ΔS = ?
ΔS = \(\frac{Q_{\text {rev }}}{T}=\frac{6000}{300}\) = 20 JK-1
Ans. Entropy change = ΔS = 20 JK-1
(2) The latent heat of evaporation of water is 2.26 kJ g-1 at 1 atm and 100 °C. Calculate the entropy change for evaporation of 1 mole of water at 100 °C.
Solution :
Given : Latent heat of evaporation = ΔvapH0
= 2.26 kJ g-1
Temperature = T = 273 + 100 = 373 K
Molar mass of water = 18 g mol-1
ΔS = ?
For 1g H2O(l) ΔvapH0 = 2.26 KJ
∴ For 1 mol H2O(l) = 18 g H2O(l)
ΔvapH0 = 2.26 × 18
= 40.68 kJ
= 40680 J
Entropy change, ΔS is given by,
ΔS = \(\frac{\Delta_{\mathrm{vap}} H^{0}}{T}=\frac{40680}{373}\) = 109.06 JK-1 mol-1
Ans. Entropy change = ΔS = 109.06 JK-1 mol-1
(3) Calculate the standard (absolute) entropy change for the formation of CO2(g).
| Substance |
C(graphite) |
O2(g) |
CO2(g) |
| Standard molar enthalpy JK-1 mol-1 |
5.74 |
205 |
213.7 |
Solution:
Given:
| Substance |
C(graphite) |
O2(g) |
CO2(g) |
| Standard molar enthalpy S0 JK-1 mol-1 |
5.74 |
205 |
213.7 |
For the formation of CO2(g),
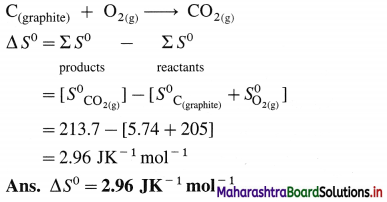
(4) The standard entropies of H2(g), O2(g) and H2O(g) in JK-1 mol-1 are 130, 205 and 189 respectively. The heat of formation of H2O(g) is -242 kJ mol-1. Calculate ΔS for formation of H2O(g), for the surroundings and the universe at 298 K. Mention whether the reaction is spontaneous or non-spontaneous.
Solution :
Given :
| Substance |
H2(g) |
O2(g) |
H2O(g) |
| Standard entropy S0 JK-1 mol-1 |
130 |
205 |
189 |
ΔfH0 = -242 kJ mol-1
ΔSuniverse = ?, ΔSsurr = ?
Thermochemical equation for the formation of H2O(g)
H2(g) + \(\frac {1}{2}\)O2(g) → H2O(g)
ΔS0 = [S0H2O] – [H0H2 + \(\frac {1}{2}\) H0O2]
= 189 – [130 + \(\frac {1}{2}\)(205)]
= 189 – [232.5]
= -43.5 JK-1 mol-1
Hence, ΔSsystem = -43.5 JK-1 mol-1
Since for the formation of H2O(g)
ΔfH0 = -242 kJmol-1 = -242 × 103 Jmol-1, the reaction is exothermic. Hence the surroundings gains heat energy 242 × 103J. Therefore entropy of the system decreases while entropy of surroundings increases.

Hence, ΔSsys < 0 but ΔSuniverse > 0, hence the reaction is spontaneous.
Ans. ΔSH2O(g) = -43.5 JK-1 mol-1
ΔSsurr = 813 JK-1 mol-1
ΔSuniverse = 769.5 JK-1.

(5) Calculate ΔSTotal and hence show whether the following reaction is spontaneous at 25 °C.
Hg(s) + O2(g) → Hg(l) + SO2(g) ΔH0 = – 238.6 kJ
ΔS0 = +36.7 JK-1
Solution :
Given : Hg(s) + O2(g) → Hg(l) + SO2(g)
ΔrH0 = – 238.6 kJ
ΔS0 = +36.7 JK-1
T = 273 + 25 = 298 K
ΔSTotal = ?
ΔSTotal = ΔSsys + Δ Ssurr
Now, ΔSsys = 36.7 JK-1
Since the reaction is exothermic, system loses heat to surroundings. Hence the entropy of the surroundings increases.
ΔHsurr = + 238.6 kJ = 238600 J

∵ ΔSTotal > 0, the reaction is spontaneous.
Ans. ΔSTotal = 837.4 JK-1
The reaction is spontaneous.
(6) What is the value of ASsurr for the following reaction at 298 K ?
6CO2(g) + 6H2O(l) → C6H12O6(s) + 6O2(g),
ΔG0 = 2879 kJ mol-1, ΔS0 = -210 JK-1 mol-1.
Solution :
Given :
6CO2(g) + 6H2O(l) → C6H12O6(s) + 6O2(g),
ΔG0 = 2879 kJmol-1;
ΔS0 = -210 JK-1mol-1 = -0.210 kJ K-1 mol-1
T = 298 K ΔH0 = ?
ΔG0 = ΔH0 – TΔS0
∴ ΔH0 = ΔG0 + TΔS0
= 2879 + 298(-0.210)
= 2879 – 62.58
= 2816.42 kJ mol-1
Since ΔH0 > 0, the reaction is endothermic, and system absorbs heat from surroundings. Hence surroundings loses heat,
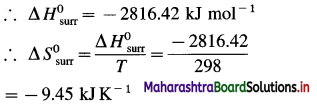
Ans. ΔS0surr = -9.45 kJ K-1
(7) Calculate ΔSsurr when on mole of methanol (CH3OH) is formed from its elements under standard conditions if ΔfH0(CH3OH) = -238.9 J mol-1.
Solution :
Given : Number of moles of ethanol,
(C2H5OH) = n = 1 mol
ΔfH0(CH3OH) = -238.9 kJ mol-1
= -238.9 × 103J mol-1
Temperature = T = 298 K
ΔS = ?
ΔSsurr = ?
Since ΔfH0 is negative, the reaction for the formation of one mole of C2H5OH is exothermic.
As heat is released to the surroundings,
ΔH0surr = + 238.9 kJ mol-1
∴ ΔSsurr = \(\frac{\Delta H_{\text {surr }}^{0}}{T}=\frac{+238.9 \times 10^{3}}{298}\)
= +801.7 JK-1
Thus entropy of the surroundings increases.
Ans. ΔSsurr = +801.7 JK-1
(8) What is the value of ΔSsurr for the following reaction at 298 K –
6CO2(g) + 6H2O(l) → C6H12O6(s) + 6O2(g)
Given that: ΔG° = 2879 KJ mol-1
ΔS0 = -210 J K-1 mol-1
Solution :
Given : ΔG0 = 2879 KJ mol-1 = 2879 × 103 J mol-1
ΔS0 = -210 JK-1 mol-1
ΔSsurr = ?
ΔG0 = ΔH0 – TΔS0
∴ ΔH0 = ΔG0 + TΔS0
= 2879 × 103 + 298 × (- 210)
= 2879 × 103 – 62580
= 2816420 J
Since, for a system, ΔH0 is +2816420 J, the surrounding loses heat to system,
∴ ΔH0surr = – 2816420 J
∴ ΔS0surr = \(\frac{\Delta H_{\text {surr }}^{0}}{T}\)
= \(\frac{-2816420}{298}\)
= -9451 JK-1
= -9.451 kJ K-1
Ans. ΔSsurr = -9.451 kJ K-1

(9) Determine whether the reactions with the following ΔH and ΔS values are spontaneous or non-spontaneous. State whether they are exothermic or endothermic.
(a) ΔH = -110 kJ and ΔS = +40 JK-1 at 400 K
(b) ΔH = +50 kJ and ΔS = -130 JK-1 at 250 K.
Solution :
(a) Given : ΔH= -110 kJ ΔS = 40 JK-1 = 0.04 kJK-1
Temperature = T = 400 K ΔG = ?
Since ΔH is negative, the reaction is exothermic
ΔG = ΔH – TΔS
= -110 – 400 × 0.04
= -110 – 16
= -126 kJ
Since ΔG is negative, the reaction is spontaneous.
(b) Given : ΔH=50 kJ,
ΔS= -130 JK-1 = -0.13 kJ K-1
Temperature = T = 250 K
ΔG = ?
Since ΔH is positive, the reaction is endothermic.
ΔG = ΔH – TΔS
= 50 – 250 × (-0.13)
= 50 + 32.5
= 82.5 kJ
Since ΔG > 0, the reaction is non-spontaneous.
Ans. (a) ΔG = -126 kJ; The reaction is exothermic and spontaneous.
(b) ΔG = 82.5 kJ; The reaction is endothermic and non-spontaneous.
(10) For a certain reaction, ΔH0 = -224 kJ and ΔS0 = -153 JK-1. At what temperature will it change from spontaneous to non-spontaneous ?
Solution :
Given : ΔH0 = – 224 kJ = – 224000 J
ΔS0 = – 153 JK-1
Temperature (T) at which, reaction changes from spontaneous to non-spontaneous = ?
Find the temperature at equilibrium, where ΔG0 = 0
ΔG0 = ΔH0 – TΔS0
0 = ΔH0 – TΔS0
∴ TΔS0 = ΔH0
∴ T = \(\frac{\Delta H^{0}}{\Delta S^{0}}\)
= \(\frac{224000}{153}\)
= 1464 K.
Hence reaction will be spontaneous below 1464 K. It will be at equilibrium at 1464 K and non-spontaneous above 1464 K.
Ans. Change over temperature from spontaneous to non-spontaneous = 1464 K.
(11) Determine whether the reactions with the following ΔH and ΔS values are spontaneous or non-spontaneous. State whether the reactions are exothermic or endothermic.
(a) ΔH = -110 kJ, ΔS = +40 JK-1 at 400 K
(b) ΔH = + 40 kJ, ΔS = – 120 JK-1 at 250 K
Solution :
(a) Given : ΔH = -110 kJ, ΔS = +40 JK-1 at T = 400K
ΔG = ΔH – TΔS
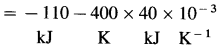
= -110 – 16
= -126 kJ
Since ΔG is negative, the reaction is spontaneous.
Since ΔH is negative, the reaction is exothermic.
(b) Given : ΔH = + 40 kJ, ΔS = -120 JK-1 at T = 250 K
ΔG = ΔH – TΔS
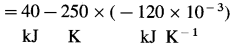
= 40 + 30
= 70 kJ
Since ΔG is negative, the reaction is spontaneous.
Since ΔH is negative, the reaction is exothermic.

(12) Determine whether the following reaction will be spontaneous or non-spontaneous under standard conditions.
Zn(s) + Cu2+ → Zn2+ +Cu(s) ΔH0 = -219 kJ, ΔS0 = -21 JK-1
Solution :
Given : ΔH0 = -219 kJ;
ΔS0 = -21 JK-1= 0.021 kJ K-1
ΔG0 = ?
For standard conditions : Pressure = 1 atm
Temperature = T = 298 K
ΔG0 = ΔH0 – TΔS0
= -219 – 298 × (-0.021)
= -219 + 6.258
= -212.742 kJ
Since ΔG < 0, the reaction is spontaneous.
Ans. The reaction is spontaneous.
(13) The equilibrium constant for a gaseous reversible reaction at 200 °C is 1.64 × 103 atm2. Calculate ΔG° for the reaction.
Solution :
Given : Equilibrium constant = KP = 1.64 × 103 atm2
Temperature = T = 273 + 200 = 473 K
ΔG0 = ?
ΔG0 = -2.303 RTlog10 Kp
= – 2.303 × 8.314 × 473 × log10 1.64 × 103
= – 2.303 × 8.314 × 473 × (3.2148)
= -29115 J
= -29.115 kJ
Ans. ΔG0 = -29.115 kJ
(14) Calculate ΔG for the reaction at 25°C
CO(g) + 2H2(g) ⇌ CH3OH(g)
ΔG0 = -24.8 kJ mol-1.
if Pco = 4 atm, PH2 = 2 atm, PCH3OH = 2 atm.
Solution :
Given : Partial pressures : pco = 4 atm,
PH2 = 2 atm,
PCH3OH = 2 atm
Temperature = T = 273 + 25 = 298 K
ΔG0 = -24.8 kJ mol-1
CO(g) + 2H2(g) ⇌ CH3OH(g)
The reaction quotient, Q is,
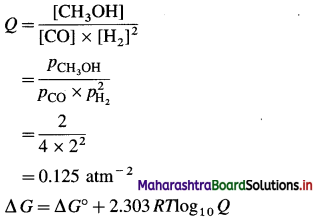
= – 24.8 + 2.303 × 8.314 × 298 × log10 0.125
= – 24.8 + 2.303 × 8.314 × 298 × (\(\overline{1} \cdot 09691\))
= – 24.8 + 2.303 × 8.314 × 298 × (- 0.90709)
= – 24.8 – 2.303 × 8.314 × 298 × 0.90709 × 10-3
= -24.8 – 5.176
= -29.976 kJ mol-1.
Ans. ΔG = – 29.976 kJ mol-1

(15) Calculate KP for the reaction,
C2H4(g) + H2(g) ⇌ C2H6(g),
ΔG0 = -100 kJ mol-1, at 25°C.
Solution :
Given : ΔG0 = – 100 kJ mol-1 = – 100 × 103 J mol-1
= -1 × 105 Jmol-1
Temperature = T = 273 + 25 = 298 K
Equilibrium constant = KP = ?

(16) KP for the reaction,
MgCO3(s) → MgO(s) + CO2(g) is 9 × 10-10.
Calculate ΔG0 for the reaction at 25 °C.
Solution :
Given : KP = 9 Δ 10-10
Temperature = T = 273 + 25 = 298 K
ΔG0 = ?
ΔG0 = -2.303 RTlog10KP
= -2.303 × 8.314 × 298 × log109 × 10-10
= -2.303 × 8.314 × 298 × \([\overline{10} \cdot 9542]\)
= – 2.303 × 8.314 × 298 × [ – 9.0458]
= 51683 Jmol-1
= 51.683 kJmol-1
Ans. ΔG0 = 51.653 kJ mol-1
(17) Calculate ΔH, ΔS and ΔG for melting of 10 g ice at 0 °C and 1 atm. (ΔfusH0 = 6.02 kJ mol-1 for ice)
Solution :
Given : ΔfusH0 = 6.02 kJ mol-1 = 6.02 × 103 Jmol-1
Temperature = T = 273 + 0 = 273 K
Mass of ice = 10 g
Molar mass of H2O = 18 g mol-1
ΔH= ?, ΔS = ?, ΔG = ?
For melting of ice,
H2O(s) ⇌ H2O(l)
For 1 mol ice = 18 g ice ΔfusionH = 6.05 kJ
∴ For 10 g ice
ΔH = \(\frac{6.02 \times 10}{18}\)
= 3.344 kJ
ΔH = 3.344 kJ = 3.344 × 103 J
∴ ΔS = \(\frac{\Delta H}{T}=\frac{3.344 \times 10^{3}}{273}\) = 12.25 JK-1
ΔG = ΔH – TΔS
= 3.344 – 273 × 12.25 ×10-3 kJ
= 3.344 – 3.344
= 0
Since ΔG = 0, the system is at equilibrium.
Ans. ΔH = 3.344 kJ; ΔS = 12.25 JK-1; ΔG = 0
(18) Calculate Kp, ΔG0 for the reaction,
C(s) + H2O(g) ⇌ CO(g) + H2(g)
at 990 K if the equilibrium concentrations are as follows :
[H2O] = 1.10 mol dm--3,
[CO] = [H2] = 0.2 mol dm-3,
R = 0.08206 L atm K-1 mol-1.
Solution :
Given : [H2O] = 1.1 mol dm-3,
[CO] = 0.2 mol dm-3,
[H2] = 0.2 mol dm-3, T = 990 K,
R = 0.08206 L atm K-1 mol-1
KP = ? ΔG0 = ?
C(s) + H2O(g) ⇌ CO(g) + H2(g)

KP = KC × (RT)Δn
= 0.03636 × (0.08206 × 990)
= 2.954 atm
ΔG0 = -2.303 RTlog10KP
= -2.303 × 8.314 × 990 × log10 2.954
= -2.303 × 8.314 × 990 × 0.4704
= -8917 J
= -8.917 kJ
Ans. KP = 2.954 atm; ΔG0 = -8.917 kJ

Multiple Choice Questions
Question 87.
Select and write the most appropriate answer from the given alternatives for each subquestion :
1. For an isochoric process, the change in
(a) pressure is zero
(b) volume is negative
(c) volume is zero
(d) temperature is zero
Answer:
(c) volume is zero
2. Which of the following is an extensive property ?
(a) Surface tension
(b) Refractive index
(c) Energy
(d) Temperature
Answer:
(c) Energy
3. Which of the following is an intensive property ?
(a) Enthalpy
(b) Weight
(c) Refractive index
(d) Volume
Answer:
(c) Refractive index
4. Which of the following pairs is an intensive property ?
(a) Density, viscosity
(b) Surface tension, mass
(c) Viscosity, internal energy
(d) Heat capacity, volume
Answer:
(a) Density, viscosity
5. The property which is not intensive is
(a) freezing point
(b) viscosity
(c) temperature
(d) free energy
Answer:
(d) free energy

6. Which of the following is not an extensive property ?
(a) molarity
(b) molar heat capacity
(c) mass
(d) volume
Answer:
(b) molar heat capacity
7. Which of the following is NOT a state function ?
(a) Work
(b) Enthalpy
(c) Temperature
(d) Pressure
Answer:
(a) Work
8. In an adiabatic process
(a) ΔT ≠ 0
(b) ΔU ≠ 0
(c) Q = 0
(d) All of these
Answer:
(d) All of these
9. For an isothermal and reversible process
(a) P1V1 = P2V2
(b) P1V1 ≠ P2V2
(c) ΔV ≠ 0
(d) ΔH ≠ 0
Answer:
(a) P1V1 = P2V2
10. For the process to occur under adiabatic conditions, the correct condition is :
(a) ΔT = 0
(b) Δp = 0
(c) Q = 0
(d) W = 0
Answer:
(c) Q = 0

11. What is true for an adiabatic process ?
(a) ΔT = 0
(b) ΔU
(c) ΔH = ΔU
(d) Q = 0
Answer:
(d) Q = 0
12. ΔU = 0 is true for
(a) Adiabatic process
(b) Isothermal process
(c) Isobaric process
(d) Isochoric process
Answer:
(b) Isothermal process
13. When a gas expands in vacuum, the work done by the gas is
(a) maximum
(b) zero
(c) less than zero
(d) greater than zero
Answer:
(b) zero
14. When a sample of an ideal gas is allowed to expand at constant temperature against an atomospheric pressure,
(a) surroundings does work on the system
(b) ΔU = 0
(c) no heat exchange takes place between the system and surroundings
(d) internal energy of the system increases
Answer:
(b) ΔU = 0
15. In what reaction of the following work is done by the system on the surroundings ?
(a) Hg(l) → Hg(g)
(b) 3O2(g) → 2O3(g)
(c) H2(g) + Cl2(g) → 2HCl(g)
(d) N2(g) + 3H2(g) → 2NH3(g)
Answer:
(a) Hg(l) → Hg(g)

16. A gas does 0.320 kJ of work on its surroundings and absorbs 120 J of heat from the surroundings. Hence, ΔU is
(a) 440 kJ
(b) 200 J
(c) 120.32 J
(d) -200J
Answer:
(d) -200J
17. For an isothermal and reversible expansion of 0.5 mol of an ideal gas, Wmax is -3.918 kJ. The value of ΔU is
(a) 3.918 kJ
(b) zero
(c) 1.959 kJ
(d) 3918 J
Answer:
(b) zero
18. The mathematical expression of the first law of thermodynamics for an adiabatic process is
(a) W = Q
(b) W = -ΔU
(c) W = +ΔU
(d ) W = -Q
Answer:
(c) W = +ΔU
19. A gaseous system absorbs 600 kJ of heat and performs the work of expansion equal to 130 kJ. The internal energy change is
(a) 730 kJ
(b) -470 kJ
(c) -730 kJ
(d) 470 kJ
Answer:
(d) 470 kJ
20. When a gas is compressed, the work obtained is 360 J while the heat transferred is 190 J. Hence the change in internal energy is
(a) -170 J
(b) 170 J
(c) 550 J
(d) -550 J
Answer:
(b) 170 J

21. For the reaction N2(g) + 3H2(g) = 2NH3(g); Which of the following is valid ?
(a) ΔH = ΔU
(b) ΔH < ΔU
(c) ΔH > ΔU
(d) ΔH = 2ΔH
Answer:
(b) ΔH < ΔU
22. For which reaction ΔH = ΔU ?
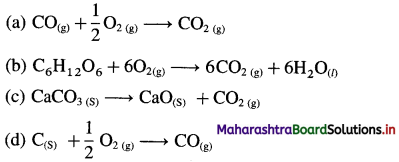
Answer:
(b) \(\mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6(\mathrm{~s})}+6 \mathrm{O}_{2(\mathrm{~g})} \rightarrow 6 \mathrm{CO}_{2(\mathrm{~g})}+6 \mathrm{H}_{2} \mathrm{O}_{(\mathrm{l})}\)
23. For the following reaction at 298 K
H2(g) + \(\frac {1}{8}\)O2(g) = H2O(l)
Which of the following alternative is correct ?
(a) ΔH = ΔU
(b) ΔH > ΔU
(c) ΔH < ΔU
(d) ΔH = 1.5 ΔU
Answer:
(c) ΔH < ΔU
24. The heat of combustion of carbon is 394 kJ mol-1. The heat evolved in combustion of 6.023 × 1021 atoms of carbon is
(a) 3940 kJ
(b) 3940.0 kJ
(c) 3.94 kJ
(d) 0.394 kJ
Answer:
(c) 3.94 kJ
25. Which of the reactions defines the heat of formation ?
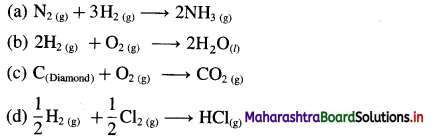
Answer:
(d) \(\frac{1}{2} \mathrm{H}_{2(\mathrm{~g})}+\frac{1}{2} \mathrm{Cl}_{2(\mathrm{~g})} \rightarrow \mathrm{HCl}_{(\mathrm{g})}\)

26. ΔUo of combustion of methane is -X kJ mol-1. The value of ΔH0 is
(a) = ΔUo
(b) > ΔUo
(c) < ΔUo
(d) =0
Answer:
(c) < ΔUo
27. The enthalpy of combustion of 5(rhomic)is -297.4 kJ mol-1. The amount of sulphur required to produce 29.74 kJ of heat is
(a) 32 × 10-2 kg
(b) 3.2 × 10-3 kg
(c) 3.2 × 10-2 kg
(d) 6.4 × 10-3 kg
Answer:
(b) 3.2 × 10-3 kg
28. The heat of formation of SO2(g) and SO3(g) are -269 kJ mol-1 and -395 kJ mol-1 respectively the value of ΔH for the reaction
SO2(g) + \(\frac {1}{2}\)O2(g) → SO3(g) is
(a) -664 kJ mol-1
(b) -126 kJ mol-1
(c) 63 kJ mol-1
(d) 126 kJ mol-1
Answer:
(b) -126 kJ mol-1
29. The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are, -890.3 kJ mol-1, -393.5 kJ mol-1 and -285.8 kJ mol-1 respectively. Enthalpy of formation of CH4(g) will be
(a) – 74.8 kJ mol-1
(b) – 52.27 kJ mol-1
(c) + 74.8 kJ mol-1
(d) + 52.26 kJ mol-1
Answer:
(a) – 74.8 kJ mol-1
30. The enthalpies of formation of N2O(g) and NO(g) are 82 kJ mol-1 and 90 kJ mol-1 respectively. Then enthalpy of a reaction 2N2O(g) + O2(g) → 4NO(g) is …………
(a) 8 kJ
(b) -16 kJ
(c) 88 kJ
(d) 196 kJ
Answer:
(d) 196 kJ

31. The heat of combustion of naphthalene (C10H8) to CO2 gas and water vapour at 298 K and at constant pressure is -5.1567 × 106 J. The heat of combustion at constant volume at 298 K is (R = 8.314 JK-1 mol-1)
(a) -5.1567 × 106 J
(b) -5.6161 × 106 J
(c) -5.1616 × 106 J
(d) -5.7161 × 106 J
Answer:
(c) -5.1616 × 106 J
32. Given the reaction,
2NH3(g) → N2(g) + 3H2(g) ΔH = 92.6 kJ
The enthalpy of formation of NH3 is
(a) -92.6 kJ
(b) 92.6 kJ mol-1
(c) -46.3 kJmol-1
(d) -185.2 kJmol-1
Answer:
(c) -46.3 kJmol-1
33. Calculate the heat of reaction at 298 K for the reaction C2H4(g) + H2(g) = C2H6(g)
Given that the heats of combustion of ethylene, hydrogen and ethane are 337.0, 68.4 and 373.0 kcal respectively.
(a) 23.4 kcal
(b) 62.2 kcal
(c) 32.4 kcal
(d) 34.2 kcal
Answer:
(c) 32.4 kcal
34. Entropy change for a process is given by,
(a) Qrev × T
(b) Qrev/T
(c) \(\frac{T}{Q_{\text {rev }}}\)
(d) ΔHrev × T
Answer:
(b) Qrev/T
35. For a spontaneous process, total entropy change for a system and its surroundings is
(a) ΔStotal < 0
(b) ΔStotal = 0
(c) ΔStotal > 0
(d) ΔStotal ≤ 0
Answer:
(c) ΔStotal > 0

36. For a system at equilibrium,
(a) ΔStotal = 0
(b) ΔStotal > 0
(c) ΔStotal < 0
(d) ΔStotal ≥ 0
Answer:
(a) ΔStotal = 0
37. If the enthalpy of vaporisation of water at 100°C is 186.5 J·mol-1, the entropy of vaporization will be-
(a) 4.0 J·K-1 mol-1
(b) 3.0 J·K-1 mol-1
(c) 1.5 J·K-1 mol-1
(d) 0.5 J·K-1 mol-1
Answer:
(d) 0.5 J·K-1 mol-1
38. Heat of fusion of ice is 6.02kJmol-1 at 0 °C. If 100 g water is frozen at 0 °C, entropy change will be
(a) -0.1225 JK-1
(b) 310.6 JK-1
(c) -122.6 JK-1
(d) 92.8 JK-1
Answer:
(c) -122.6 JK-1
39. If for a reaction ΔH is negative and ΔS is positive then the reaction is
(a) spontaneous at all temperatures
(b) non-spontaneous at all temperatures
(c) spontaneous only at high temperatures
(d) spontaneous only at low temperature
Answer:
(a) spontaneous at all temperatures
40. The relationship between ΔGo of a reaction and its equilibrium constant is
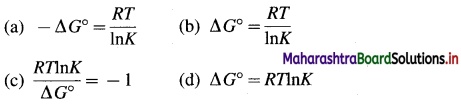
Answer:
(c) \(\frac{R T \ln K}{\Delta G^{0}}=-1\)

41. Which of the following has highest entropy?
(a) Al(s)
(b) CaCO3(s)
(c) H2O(l)
(d) CO2(g)
Answer:
(d) CO2(g)
42. The entropy change for the formation of 3.5 mol NO(g) from the following data will be,

Answer:
(b) 42.875 JK-1
43. Gibbs free energy change at equilibrium is
(a) ΔG = 0
(b) ΔG > 0
(c) ΔG < 0
(d) ΔG ≤ 0
Answer:
(a) ΔG = 0
44. For spontaneous process,
(a) ΔG = 0
(b) ΔG > 0
(c) ΔG < 0
(d) ΔG ≤ 0
Answer:
(c) ΔG < 0
45. A substance which shows highest entropy is
(a) SrCO3(S)
(b) Cu(S)
(c) NaC(aq)
(d) Cl2(g)
Answer:
(d) Cl2(g)

46. For which of the following reactions ΔS is negative ?
Answer:
(a) \(\mathrm{Mg}_{(s)}+\mathrm{Cl}_{2(\mathrm{~g})} \rightarrow \mathrm{MgCl}_{2(s)}\)
47. For a reaction, at 300K enthalpy is 138 kJ and entropy change is 115 JK-1. Hence the free energy change of the reaction is
(a) 130.5 kJ
(b) 103.5 kJ
(c) 82.8 kJ
(d) – 60.5 kJ
Answer:
(b) 103.5 kJ
48. Bond enthalpies of H2-1, I2(g) and HI are 436, 151 and 298 kJ mol-1 respectively. Hence enthalpy of formation of HI(g) is
(a) -9 kJmol-1
(b) -4.5kJmol-1
(c) 4.5 kJ mol-1
(d) 9 kJ mol-1
Answer:
(b) -4.5kJmol-1
49. The average bond energy of C-H bond is 410 kJmol-1. The enthalpy change of atomisation of 3.2 g CH4(g) is
(a) 1312 kJ
(b) 29.8 kJ
(c) 328 kJ
(d) 120 kJ
Answer:
(c) 328 kJ

50. For a chemical reaction ΔS = -0.035 kJ/K and ΔH = -20 kJ. At what temperature does the reaction turn non-spontaneous ?
(a) 5.14 K
(b) 57.14 K
(c) 571.4 K
(d) 5714.0 K
Answer:
(c) 571.4 K
51. For a certain reaction, ΔH = -50 kJ and ΔS = -80 JK-1, at what temperature does the reaction turn from spontaneous to non-spontaneous.
(a) 6.25 K
(b) 62.5 K
(c) 625 K
(d) 6250 K
Answer:
(c) 625 K
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()




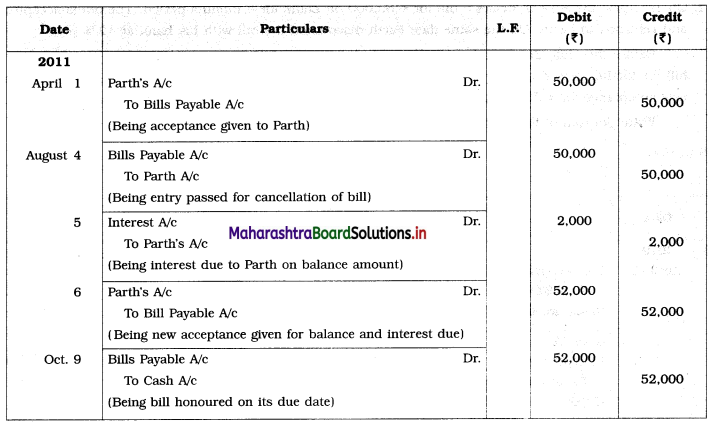

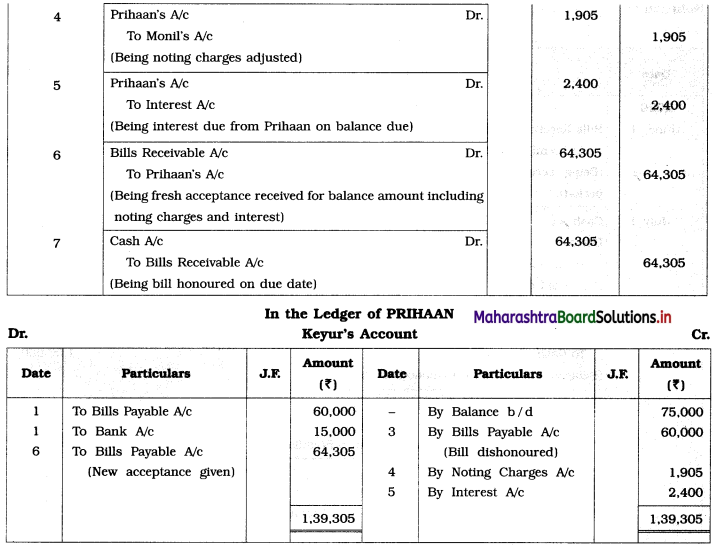
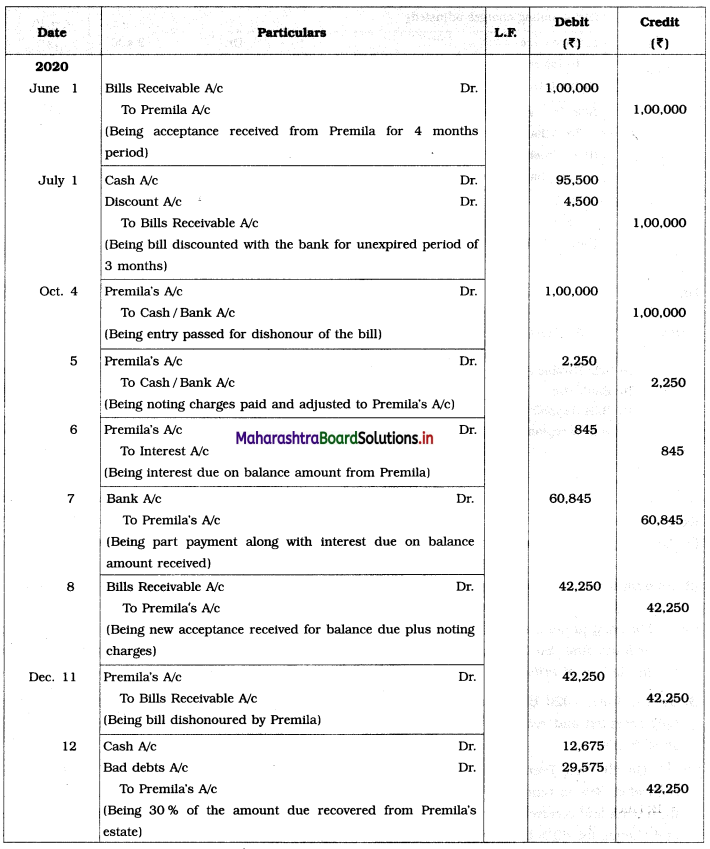
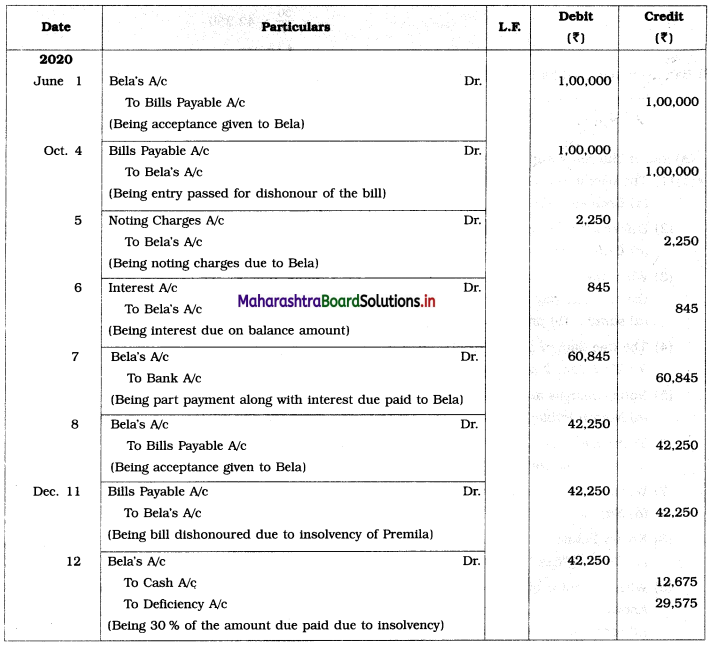









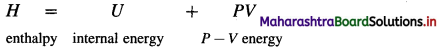
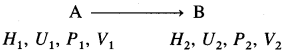

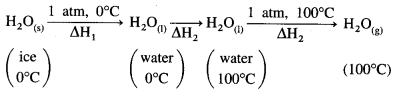
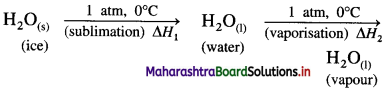
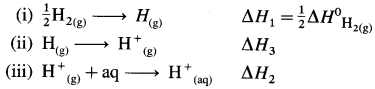


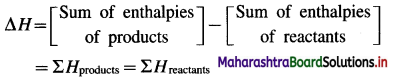

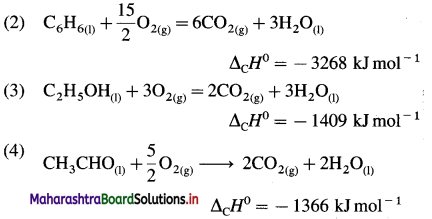
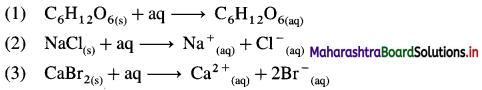
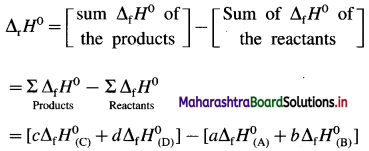
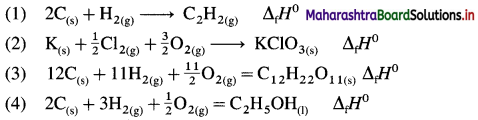

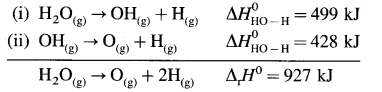

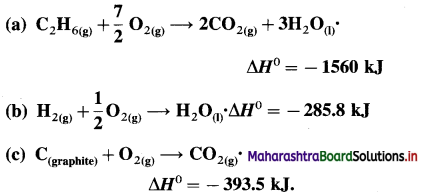


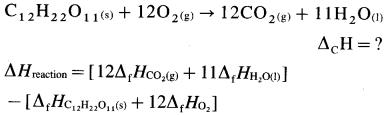
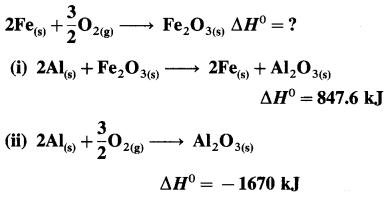


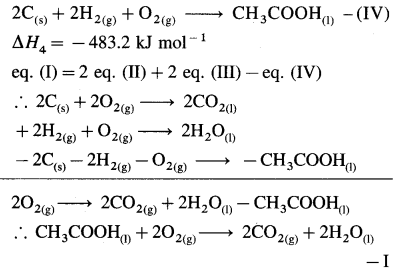















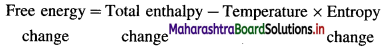











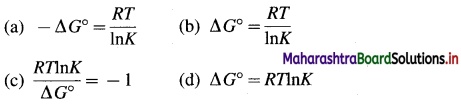




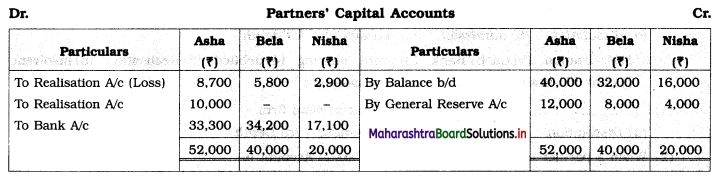
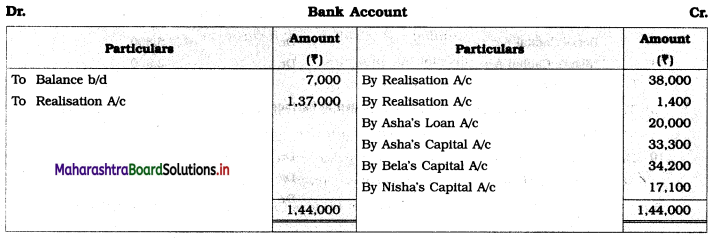



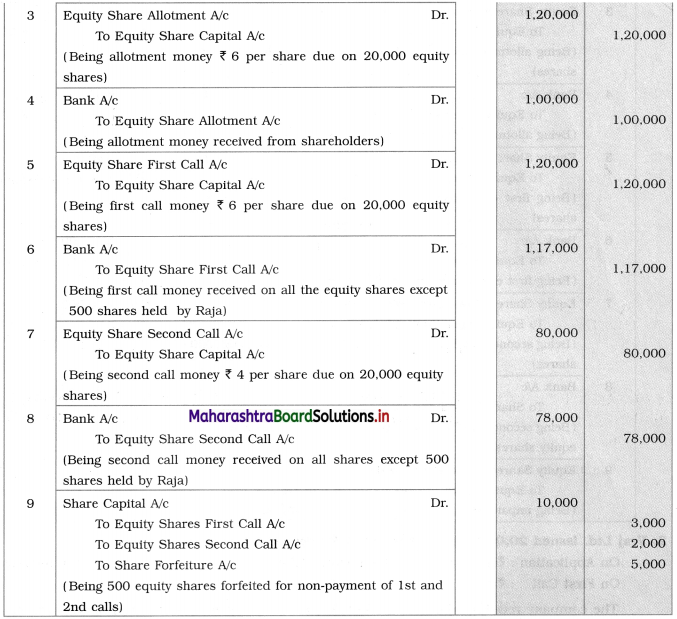
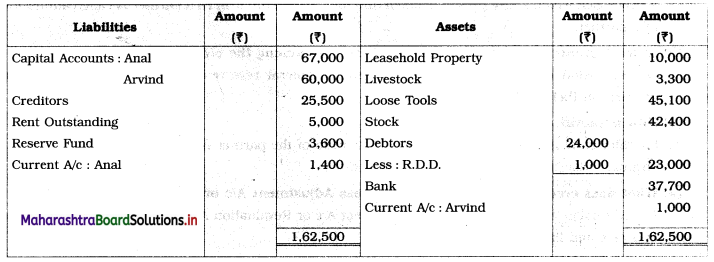
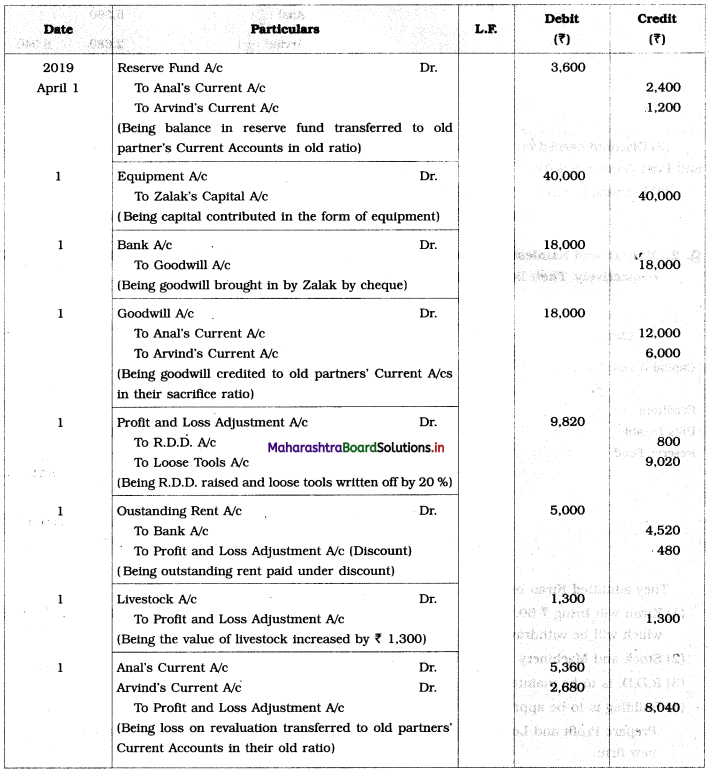
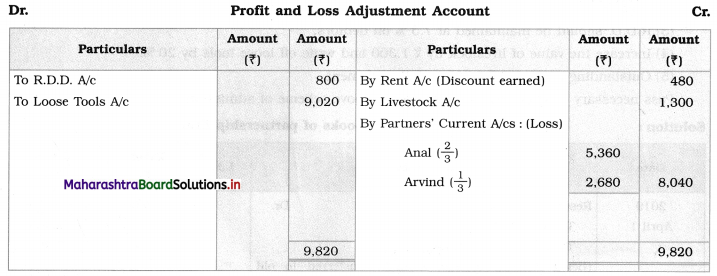
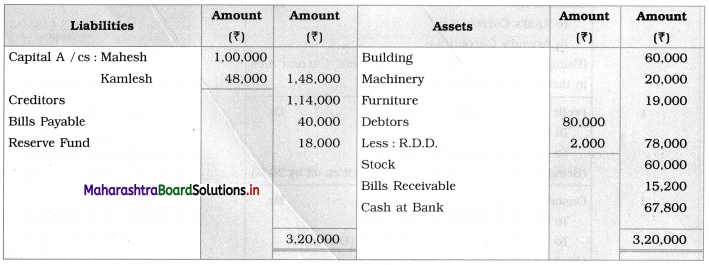
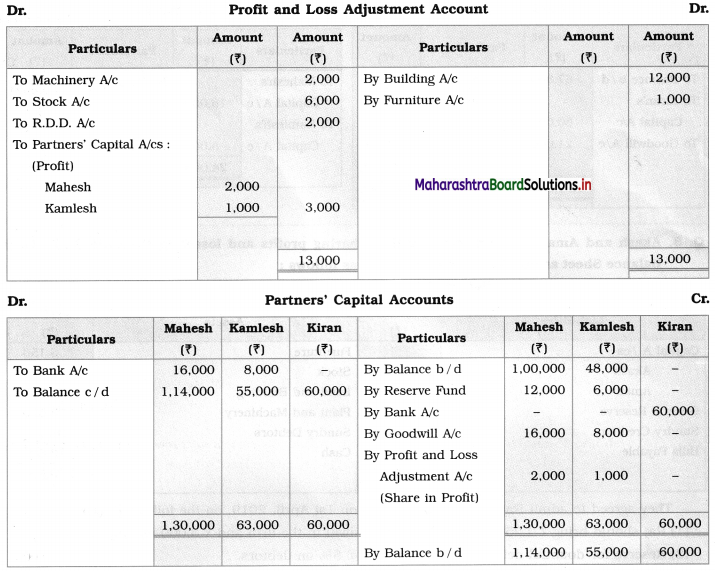
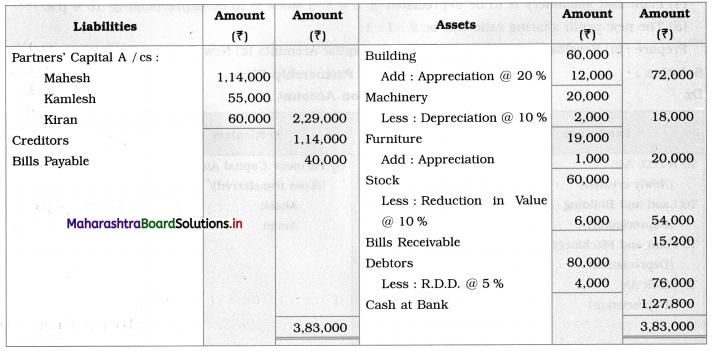
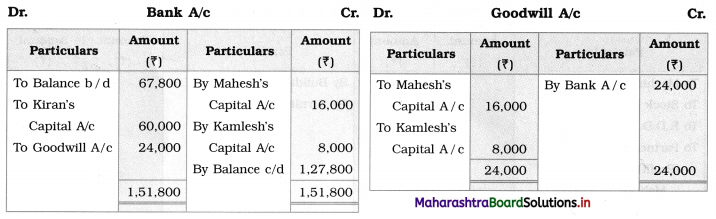
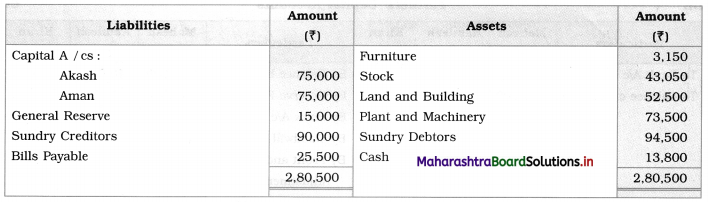
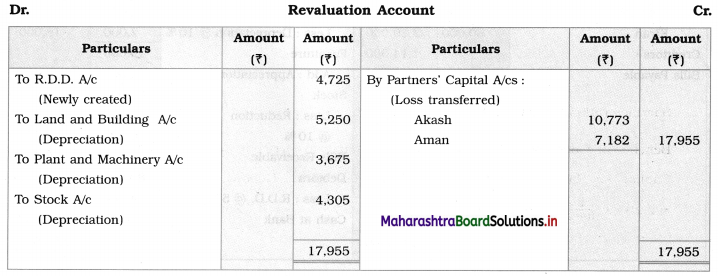
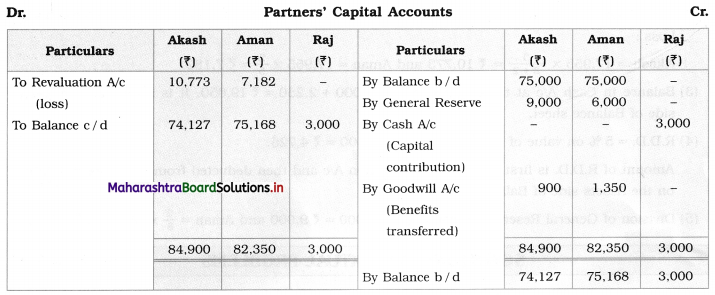
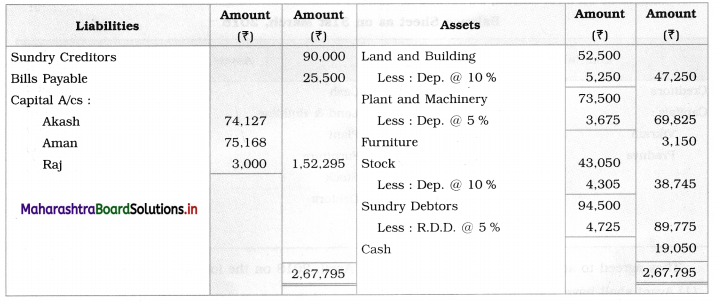
























 Answer:
Answer: