Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 14 Dual Nature of Radiation and Matter Textbook Exercise Questions and Answers.
Maharashtra State Board 12th Physics Solutions Chapter 14 Dual Nature of Radiation and Matter
1. Choose the correct answer.
i) A photocell is used to automatically switch on the street lights in the evening when the sunlight is low in intensity. Thus it has to work with visible light. The material of the cathode of the photocell is
(A) zinc
(B) aluminum
(C) nickel
(D) potassium
Answer:
(D) potassium
ii) Polychromatic (containing many different frequencies) radiation is used in an experiment on the photoelectric effect. The stopping potential
(A) will depend on the average wavelength
(B) will depend on the longest wavelength
(C) will depend on the shortest wavelength
(D) does not depend on the wavelength
Answer:
(C) will depend on the shortest wavelength
iii) An electron, a proton, an α-particle and a hydrogen atom are moving with the same kinetic energy. The associated de Broglie wavelength will be longest for
(A) electron
(B) proton
(C) α-particle
(D) hydrogen atom
Answer:
(A) electron
iv) If NRed and NBlue are the number of photons emitted by the respective sources of equal power and equal dimensions in unit time, then
(A) NRed < NBlue
(B) NRed = NBlue
(C) NRed > NBlue
(D) NRed ≈ NBlue
Answer:
(C) NRed > NBlue
v) The equation E = pc is valid
(A) for all sub-atomic particles
(B) is valid for an electron but not for a photon
(C) is valid for a photon but not for an electron
(D) is valid for both an electron and a photon
Answer:
(C) is valid for a photon but not for an electron
2. Answer in brief.
i) What is photoelectric effect?
Answer:
The phenomenon of emission of electrons from a metal surface when electromagnetic radiation of appropriate frequency is incident on it is known as photoelectric effect.
ii) Can microwaves be used in the experiment on photoelectric effect?
Answer:
No
iii) Is it always possible to see photoelectric effect with red light?
Answer:
No
iv) Using the values of work function given in Table 14.1, tell which metal will require the highest frequency of incident radiation to generate photocurrent.
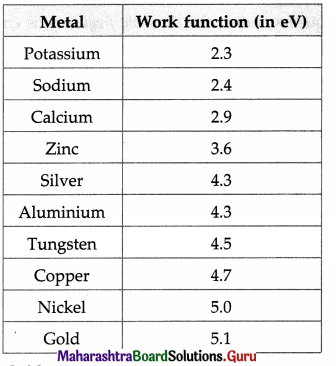
Answer:
Gold.
[ Note : W0 = hv0, where h is Planck’s constant. The larger the work function (W0), the higher is the threshold frequency (v0). ]
v) What do you understand by the term wave-particle duality? Where does it apply?
Answer:
Depending upon experimental conditions or structure of matter, electromagnetic radiation and material particles exhibit wave nature or particle nature. This is known as wave-particle duality.
It applies to all phenomena. The wave nature and particle nature are liked by the de Broglie relation λ = h/p, where λ is the wavelength of matter waves, also called de Broglie waves / Schrodinger waves, p is the magnitude of the momentum of a particle or quantum of radiation and h is the universal constant called Planck’s constant.
[Note : It is the smallness of h (= 6.63 × 10-34 J∙s) that is very significant in wave-particle duality.]
Question 3.
Explain the inverse linear dependence of stopping potential on the incident wavelength in a photoelectric effect experiment.
Answer:
We have V0e = \(\frac{h c}{\lambda}\) – Φ, where V0 is the stopping potential, e is the magnitude of the charge on the electron, h is Planck’s constant, c is the speed of light in free space, λ is the wavelength of the electromagnetic radiation incident on a metal surface and Φ is the work function for the metal, h, c and e are constants. Φ is constant for a particular metal.
Hence, it follows that as \(\frac{1}{\lambda}\) increases, V0 increases.
The plot of V0 verses \(\frac{1}{\lambda}\) is linear. This is because the energy associated with a quantum of radiation (photon) is directly proportional to the frequency of radiation and hence inversely proportional to the wavelength of radiation.
Question 4.
It is observed in an experiment on photoelectric effect that an increase in the intensity of the incident radiation does not change the maximum kinetic energy of the electrons. Where does the extra energy of the incident radiation go? Is it lost? State your answer with explanatory reasoning.
Answer:
When electromagnetic radiation with frequency greater than the threshold frequency is incident on a metal surface, there is emission of electrons. It is observed that not every incident photon is effective in liberating an electron. In fact, the number of electrons emitted per second is far less than the number of photons incident per second. The photons that are not effective in liberation of electrons are reflected (or scattered) or absorbed resulting in rise in the temperature of the metal surface. The maximum kinetic energy of a photoelectron depends on the frequency of the incident radiation and the threshold frequency for the metal. It has nothing to do with the intensity of the incident radiation. The increase in intensity results in increase in the number of electrons emitted per second.
Question 5.
Explain what do you understand by the de Broglie wavelength of an electron. Will an electron at rest have an associated de Broglie wavelength? Justify your answer.
Answer:
Under certain conditions an electron exhibits wave nature. Waves associated with a moving electron are called matter waves or de Broglie waves or- Schrodinger waves. The de Broglie wavelength of these matter waves is given by X = h/p, where h is Planck’s constant and p is the magnitude of the momentum of the electron.
If an electron is at rest, its momentum would be zero, and hence the corresponding de Broglie wavelength would be infinite indicating absence of a matter wave. However, according to quantum mechanics/wave mechanics, this is not possible.
Question 6.
State the importance of Davisson and Germer experiment.
Answer:
The Davisson and Germer experiment directly indicated the wave nature of material particles and quantitatively verified the de Broglie hypothesis for the existence of matter waves.
[Note : The aim of the experiment was not to verify wave like properties of electrons. The realisation came only later, an example of serendipity.]
[Note : Like X-rays, electrons exhibit wave nature under suitable conditions. When the wavelength of matter waves associated with moving electrons is comparable to the inter-atomic spacing in a crystal, electrons show diffraction effects. In 1927, Sir George Thomson (1892 – 1975), British physicist, with his student Alex Reid, observed electron diffraction with a metal foil. It is found that neutrons, atoms, molecules, Œ-particles, etc. show wave nature under suitable conditions.]
Question 7.
What will be the energy of each photon in monochromatic light of frequency 5 × 1014 Hz?
Answer:
Data: y = 5 × 1014 Hz, h = 6.63 × 10-34 Js,
1eV=1.6 × 10-19 J
The energy of each photon,
E = hv = (6.63 × 10-34 J.s)(5 × 1014 Hz)
= 3.315 × 10-19 J
= \(\frac{3.315 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) = 2.072 eV
Question 8.
Observations from an experiment on photoelectric effect for the stopping potential by varying the incident frequency were plotted. The slope of the linear curve was found to be approximately 4.1 × 10-15 V s. Given that the charge of an electron is 1.6 × 10-19 C, find the value of the Planck’s constant h.
Answer:
Data : Slope=4.1 × 10-15 V∙s, e = 1.6 ×10-19 C
V0e = hv – hv0
∴ V0 =\(\left(\frac{h}{e}\right) v-\left(\frac{h v_{0}}{e}\right)\)
∴ Slope = \(\frac{h}{e}\) ∴ Planck’s constant,
h = (slope) (e)=(4.1 × 10-15 V∙s)(1.6 × 10-19 C)
= 6.56 × 10 34J. (as 1 V = \(\frac{1 \mathrm{~J}}{1 \mathrm{C}}\))
Question 9.
The threshold wavelength of tungsten is 2.76 × 10-5 cm. (a) Explain why no photoelectrons are emitted when the wavelength is more than 2.76 × 10-5 cm.(b) What will be the maximum kinetic energy of electrons ejected in each of the following cases
(i) if ultraviolet radiation of wavelength λ = 1.80 × 10-5 cm and
(ii) radiation of frequency 4 × 1015 Hz is made incident on the tungsten surface.
Answer:
Data: λ0 = 2.76 × 10-5 cm = 2.76 × 10-7 m,
λ =1.80 × 10-5 cm = 1.80 × 10-7 m,
v = 4 × 1015 Hz, h = 6.63 × 10-34 J∙s,c = 3 × 108 m/s
(a) For λ > λ0, v < v0 (threshold frequency).
∴ hv < hv0. Hence, no photoelectrons are emitted.
(b) Maximum kinetic energy of electrons ejected
= hc\(\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)\)
=(6.63 × 10-34)(3 × 108)\(\left(\frac{10^{7}}{1.8}-\frac{10^{7}}{2.76}\right)\)J
= (6.63 × 10-19)(0.5555 – 0.3623)
= (6.63)(0.1932 × 10-19)J = 1.281 × 10-19 J
= \(\frac{1.281 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) = 0.8006 eV
(c) Maximum kinetic energy of electrons ejected
= hv – \(\frac{h c}{\lambda_{0}}\)
=(6.63 × 10-34(4 × 1015) – \(\frac{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{2.76 \times 10^{-7}}\)
= 26.52 × 10-19 – 7.207 × 10-19
= 19.313 × 10-19 J
= \(\frac{19.313 \times 10^{-19} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) = 12.07eV
Question 10.
Photocurrent recorded in the micro ammeter in an experimental set-up of photoelectric effect vanishes when the retarding potential is more than 0.8 V if the wavelength of incident radiation is 4950 Å. If the source of incident radiation is changed, the stopping potential turns out to be 1.2 V. Find the work function of the cathode material and the wavelength of the second source.
Answer:
Data: V0 = 0.8 V, λ = 4950 Å = 4.950 × 10-7 m,
V0‘ = 1.2V, h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s.
(i) V0e = hv – Φ = \(\frac{h c}{\lambda}\) – Φ
∴ The work function of the cathode material,
Question 11.
Radiation of wavelength 4500 Å is incident on a metal having work function 2.0 eV. Due to the presence of a magnetic field B, the most energetic photoelectrons emitted in a direction perpendicular to the field move along a circular path of radius 20 cm. What is the value of the magnetic field B?
Answer:
Data: λ = 4500Å = 4.5 × 10-7 m,
Φ = 2.0eV = 2 × 1.6 × 10-19 J = 3.2 × 10-19 J,
h = 6.63 × 10-34 J∙s, c = 3 × 108 m/s,
r = 20 cm = 0.2 m, e= 1.6 × 10-19 C,
m = 9.1 × 10-31kg
This is the value of the magnetic field.
Question 12.
Given the following data for incident wavelength and the stopping potential obtained from an experiment on photoelectric effect, estimate the value of Planck’s constant and the work function of the cathode material. What is the threshold frequency and corresponding wavelength? What is the most likely metal used for emitter?
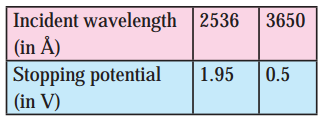
Answer:
Data: λ = 2536Å = 2.536 × 10-7 m,
λ’ = 3650Å = 3.650 ×10-7 m, V0 = 1.95V, V0‘ = 0.5V,
c = 3 × 108 mIs, e = 1.6 × 10-19 C
(i) V0e = \(\frac{h c}{\lambda}\) – Φ and V0‘e =\(\frac{h c}{\lambda^{\prime}}\) – Φ
∴ (V0 – V0‘)e = hc\(\left(\frac{1}{\lambda}-\frac{1}{\lambda^{\prime}}\right)\)
∴ (1.95 – 0.5(1.6 × 10-19)
= h (3 × 108\(\left(\frac{10^{7}}{2.536}-\frac{10^{7}}{3.650}\right)\)
∴ 2.32 × 10-19 = h(3 × 1015)(0.3943 – 0.2740)
∴ h = \(\frac{2.32 \times 10^{-34}}{0.3609}\) = 6.428 × 10-34 J∙s
This is the value of Planck’s constant.
(ii) Φ = \(\frac{h c}{\lambda}\) – V0e
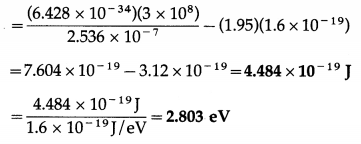
This is the work function of the cathode material.
(iii) Φ = hv0
∴ The threshold frequency, v0 = \(\frac{\phi}{h}\)
= \(\frac{4.484 \times 10^{-19} \mathrm{~J}}{6.428 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}\) = 6.976 × 1014 Hz
(iv) v0 = \(\frac{c}{\lambda_{\mathrm{o}}}\) ∴ The threshold frequency, λ0 = \(\frac{c}{v_{\mathrm{o}}}\)
= \(\frac{3 \times 10^{8}}{6.976 \times 10^{14}}\) = 4.300 × 10-7 m = 4300 Å
(v) The most likely metal used for emitter : calcium
Question 13.
Calculate the wavelength associated with an electron, its momentum and speed
(a) when it is accelerated through a potential of 54 V
Answer:
Data : V = 54 V, m = 9.1 × 10-31 kg, e
e = 1.6 × 10-19 C, h = 6.63 × 10-34 J.s, KE = 150 eV
(a) We assume that the electron is initially at rest.
∴ Ve = \(\frac{1}{2}\)mv2
∴ v = \(\sqrt{\frac{2 V e}{m}}=\sqrt{\frac{2(54)\left(1.6 \times 10^{-19}\right)}{9.1 \times 10^{-31}}}\)
= \(\sqrt{19 \times 10^{12}}\) = 4.359 × 106 m/5
This is the speed of the electron.
p = mv = (9.1× 10-31)(4.359 × 106)
= 3.967 × 10-24 kg∙m/s
This is the momentum of the electron. The wavelength associated with the electron,
λ = \(\frac{h}{p}=\frac{6.63 \times 10^{-34}}{3.967 \times 10^{-24}}\) = 1.671 × 10-10 m
= 1.671 Å = 0.1671 nm
(b) when it is moving with kinetic energy of 150 eV.
Answer:
As KE ∝ \(\sqrt{V}\), we get
\(\frac{v^{\prime}}{v}=\sqrt{\frac{150}{54}}\) = 1.666
∴ v’ = 1.666v = (1.666)(4.356 × 106)
= 7.262 × 106 m/s
This is the speed of the electron.
p’ = mv’’=(9.1 × 10-31)(7.262 × 106)
= 6.608 × 10-24 kg∙m/s
This is the momentum of the electron. The
wavelength associated with the electron,
λ = \(\frac{h}{p^{\prime}}=\frac{6.63 \times 10^{-34}}{6.608 \times 10^{-24}} \) = 1.003 × 10-10 m
= 1.003 Å = 0.1003 nm
Question 14.
The de Broglie wavelengths associated with an electron and a proton are same. What will be the ratio of
(i) their momenta
(ii) their kinetic energies?
Answer:
Data : λ (electron) = λ (proton)
m (proton) = 1836 m (electron)
(i) λ = \(\frac{h}{p}\) As λ (electron) = λ (proton),
\(\frac{p(\text { electron })}{p \text { (proton) }}\) = 1, where p denotes the magnitude of momentum.
(ii) Assuming v «c,
KE = \(\frac{1}{2}\)mv2 = \(\frac{1}{2} \frac{m^{2} v^{2}}{m}=\frac{p^{2}}{2 m}\)
∴ \(\frac{\mathrm{KE} \text { (electron) }}{\mathrm{KE} \text { (proton) }}=\frac{m \text { (proton) }}{m \text { (electron) }}\) = 1836 as p is the same for the electron and the proton.
Question 15.
Two particles have the same de Broglie wavelength and one is moving four times as fast as the other. If the slower particle
is an α-particle, what are the possibilities for the other particle?
Answer:
Data : λ1 = λ2, v1 = 4v2
λ = \(\frac{h}{p}=\frac{h}{m v}\) ∴ λ1 = \(\frac{h}{m_{1} v_{1}}\), λ2 = \(\frac{h}{m_{2} v_{2}}\)
∴ m1 = m2 \(\frac{v_{2}}{v_{1}}\) = m2\(\left(\frac{1}{4}\right)=\frac{m_{2}}{4}\)
As particle 2 is the a-particle, particle 1 (having the mass \(\frac{1}{4}\) times that of the a-particle) may be a proton or neutron.
Question 16.
What is the speed of a proton having de Broglie wavelength of 0.08 Å?
Answer:
Data : λ = 0.08 Å = 8 × 10-12m, h = 6.63 × 10-34 J∙s, m = 1.672 × 10-27 kg
λ = \(\frac{h}{m v}\) ∴ v = \(\frac{h}{\lambda m}=\frac{6.63 \times 10^{-34}}{\left(8 \times 10^{-12}\right)\left(1.672 \times 10^{-27}\right)}\)
∴ v = 4.957 × 104 m/s
This is the speed of the proton.
Question 17.
In nuclear reactors, neutrons travel with energies of 5 × 10-21 J. Find their speed and wavelength.
Answer:
Data : KE = 5 × 10-21 J, m = 1.675 × 10-27 kg, h = 6.63 × 10-34 J∙s
KE = \(\frac{1}{2}\) mv2 = 5 × 10-21 J
∴ v = \(\sqrt{\frac{2 \mathrm{KE}}{m}}=\sqrt{\frac{(2)\left(5 \times 10^{-21}\right)}{1.675 \times 10^{-27}}}\)
= 2.443 × 103 m/s
This is the speed of the neutrons. The de Broglie wavelength associated with the neutron,
λ = \(\frac{h}{m v}=\frac{6.63 \times 10^{-34}}{\left(1.675 \times 10^{-27}\right)\left(2.443 \times 10^{3}\right)}\)
= 1.620 × 10-10 m = 1.620 Å
Question 18.
Find the ratio of the de Broglie wavelengths of an electron and a proton when both are moving with the (a) same speed, (b) same energy and (c) same momentum? State which of the two will have the longer wavelength in each case?
Answer:
Data: mp = 1836 me
12th Physics Digest Chapter 14 Dual Nature of Radiation and Matter Intext Questions and Answers
Remember This (Textbook Page No. 316)
Question 1.
Is a solar cell a photocell?
Answer:
Yes
Remember This (Textbook Page No. 317)
Question 1.
Can you estimate the de Broglie wavelength of the Earth?
Answer:
Taking the mass of the Earth as (about) 6 × 1024 kg, and the linear speed of the earth around the Sun as (about) 3 × 104 m/s, we have, the de Brogue wave length of the Earth as
λ = \(\frac{h}{p}=\frac{h}{M v}=\frac{6.63 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(6 \times 10^{24} \mathrm{~kg}\right)\left(3 \times 10^{4} \mathrm{~m} / \mathrm{s}\right)}\)
= 3.683 × 10-63 m (extremely small)
Question 2.
The expression p = E/c defines the momentum of a photon. Can this expression be used for the momentum of an electron or proton?
Answer:
No
Remember This (Textbook Page No. 319)
Diffraction results described above can be produced in the laboratory using an electron diffraction tube as shown in the figure. It has a filament which on heating produces electrons. This filament acts as a cathode. Electrons are accelerated to quite high speeds by creating large potential difference between the cathode and a positive electrode. On its way, the beam of electrons comes across a thin sheet of
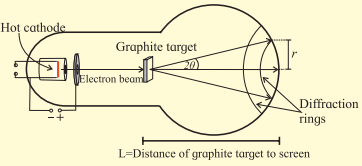
graphite. The electrons are diffracted by the atomic layers in the graphite and form diffraction rings on the phosphor screen. By changing the voltage between the cathode and anode, the energy, and therefore the speed, of the electrons can be changed. This will change the wavelength of the electrons and a change will be seen in the diffraction pattern. By increasing the voltage, the radius of the diffraction rings will decrease. Try to explain why?
Answer:
When the accelerating voltage is increased, the kinetic energy and hence the momentum of the electron increases. This decreases the de Brogue wavelength of the electron. Hence, the radius of the diffraction ring decreases.
Remember This (Textbook Page No. 320)
Question 1.
On what scale or under which circumstances are the wave nature of matter apparent?
Answer:
When the de Brogue wavelength of a particle such as an electron, atom, or molecule is comparable to the interatomic spacing in a crystal, the wave nature of matter is revealed in diffraction/interference.