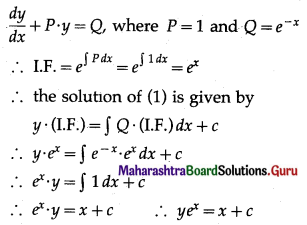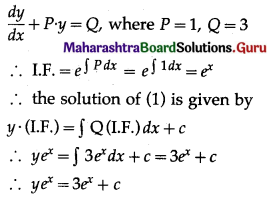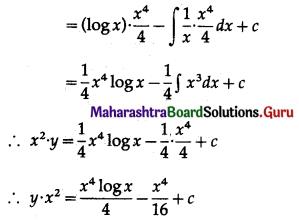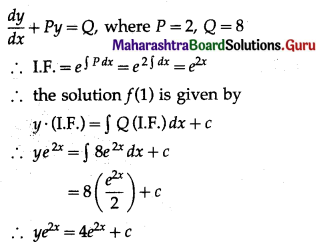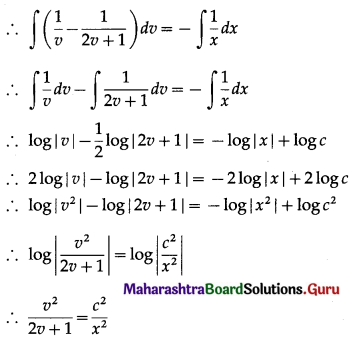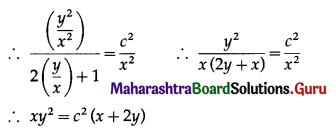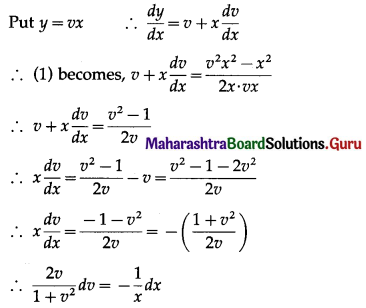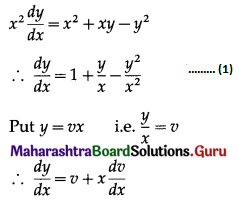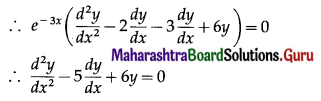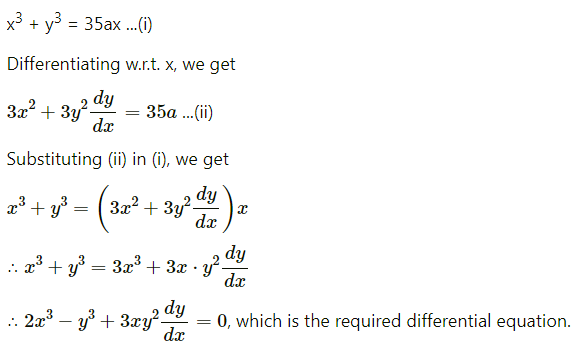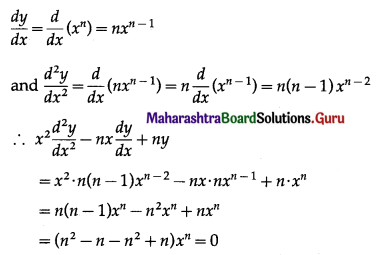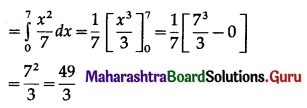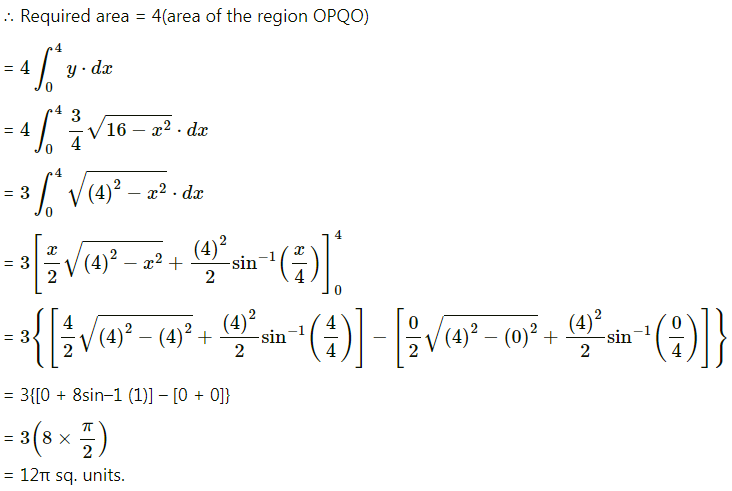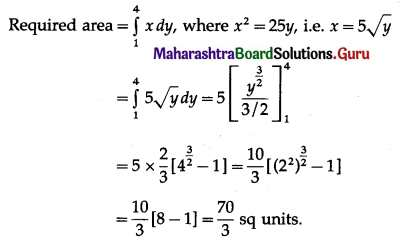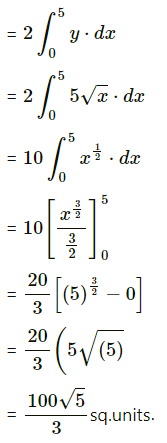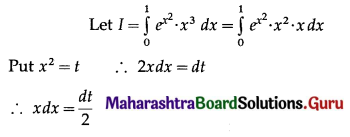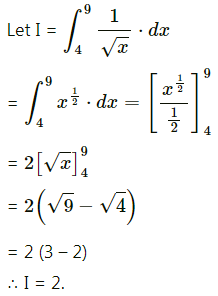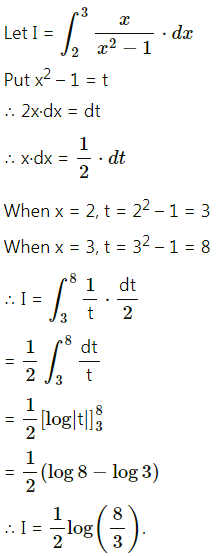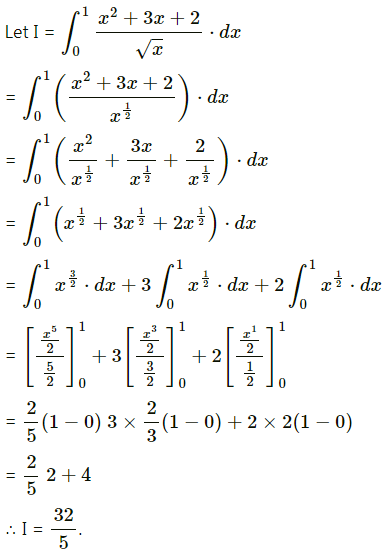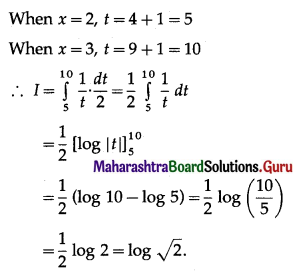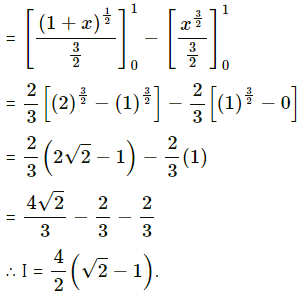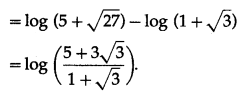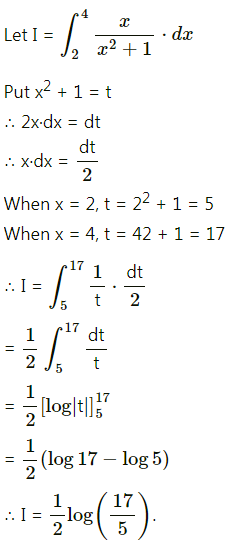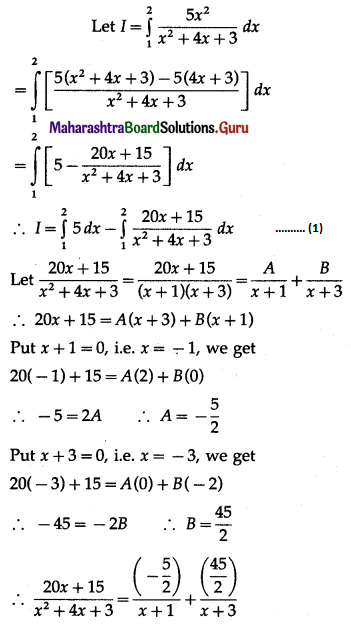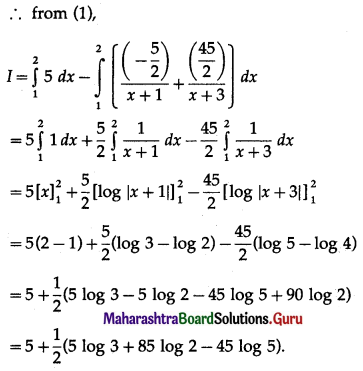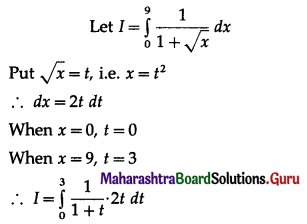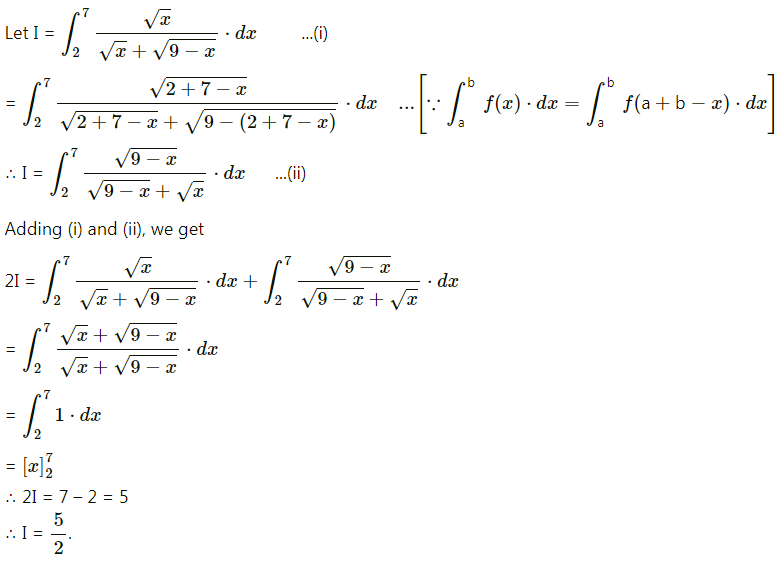Class 12

Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.6 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.6 Questions and Answers.

Std 12 Maths 1 Exercise 8.6 Solutions Commerce Maths

Question 1.
In a certain culture of bacteria, the rate of increase is proportional to the number present. If it is found that the number doubles in 4 hours, find the number of times the bacteria are increased in 12 hours.
Solution:
Let x be the number of bacteria in the culture at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
∫\(\frac{d x}{x}\) = k∫dt
∴ log x = kt + c
Initially, i.e. when t = 0, let x = x₀
∴ log x₀ = k × 0 + c
∴ c = log x₀
∴ log x = kt + log x₀
∴ log x – log x₀ = kt
∴ log(\(\frac{x}{x_{0}}\)) = kt ……(1)
Since the number doubles in 4 hours, i.e. when t = 4, x = 2x₀

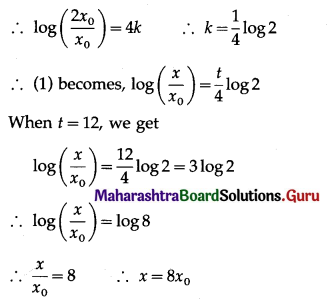
∴ the number of bacteria will be 8 times the original number in 12 hours.

Question 2.
If the population of a town increases at a rate proportional to the population at that time. If the population increases from 40 thousand to 60 thousand in 40 years, what will be the population in another 20 years? (Given: \(\sqrt{\frac{3}{2}}\) = 1.2247)
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population, is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, k is a constant
∴ \(\frac{d P}{P}\) = k dt
Integrating, we get
∫\(\frac{d P}{P}\) = k∫dt
∴ log P = kt + c
Initially, i.e. when t = 0, P = 40000
∴ log 40000 = 0 + c
∴ c = log 40000
∴ log P = kt + log 40000
∴ log P – log 40000 = kt
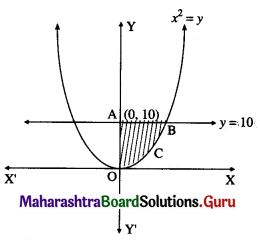
∴ log(\(\frac{P}{40000}\)) = kt ………(1)
When t = 40, P = 60000

∴ population after 60 years will be 73482.

Question 3.
The rate of growth of bacteria is proportional to the number present. If initially, there were 1000 bacteria and the number doubles in 1 hour, find the number of bacteria after \(\frac{5}{2}\) hours. [Given: √2 = 1.414]
Solution:
Let x be the number of bacteria at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
∫\(\frac{d x}{x}\) = k∫dt
∴ log x = kt + c
Initially, i.e. when t = 0, x = 1000
∴ log 1000 = k × 0 + c
∴ c = log 1000
∴ log x = kt + log 1000
∴ log x – log 1000 = kt
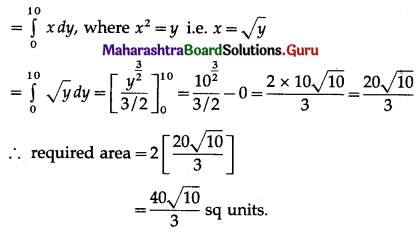
∴ log(\(\frac{x}{1000}\)) = kt …….(1)
Now, when t = 1, x = 2 × 1000 = 2000

∴ number of bacteria after \(\frac{5}{2}\) hours = 5656.

Question 4.
Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years, the population increased from 30,000 to 40,000.
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population, is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant.
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
∫\(\frac{1}{P}\)dP = k∫dt
∴ log P = kt + c
Initially, i.e. when t = 0, P = 30000
∴ log 30000 = k x 0 + c
∴ c = log 30000
∴ log P = kt + log 30000
∴ log P – log 30000 = kt

∴ the population of the city at time t = 30000\(\left(\frac{4}{3}\right)^{\frac{t}{40}}\).

Question 5.
The rate of depreciation \(\frac{d V}{d t}\) of a machine is inversely proportional to the square of t + 1, where V is the value of the machine t years after it was purchased. The initial value of the machine was ₹ 8,00,000 and its value decreased ₹ 1,00,000 in the first year. Find the value after 6 years.
Solution:
Let V be the value of the machine at the end of t years.
Then \(\frac{d V}{d t}\), the rate of depreciation, is inversly proportional to (t + 1)².

Initially, i.e. when t = 0, V = 800000
∴ 800000 = \(\frac{k}{1}\) + c = k + c ………(1)
Now, when t = 1, V = 800000 – 100000 = 700000
∴ 700000 = \(\frac{k}{1+1}\) + c = \(\frac{k}{2}\) + c ……(2)
Subtracting (2) from (1), we get
100000 = \(\frac{1k}{2}\)
∴ k = 200000
∴ from (1), 800000 = 200000 + c
∴ c = 600000 200000
∴ V = \(\frac{200000}{t+1}\) + 600000
When t = 6,
V = \(\frac{200000}{7}\) + 600000
= 28571.43 + 600000
= 628571.43 ~ 628571
Hence, the value of the machine after 6 years will be ₹ 6,28,571.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 8.1 Solutions
• 12th Commerce Maths Exercise 8.2 Solutions
• 12th Commerce Maths Exercise 8.3 Solutions
• 12th Commerce Maths Exercise 8.4 Solutions
• 12th Commerce Maths Exercise 8.5 Solutions
• 12th Commerce Maths Exercise 8.6 Solutions
• 12th Commerce Maths Miscellaneous Exercise 8 Solutions

Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.5 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.5 Questions and Answers.

Std 12 Maths 1 Exercise 8.5 Solutions Commerce Maths

Solve the following differential equations.

Question 1.
\(\frac{d y}{d x}+y=e^{-x}\)
Solution:
\(\frac{d y}{d x}+y=e^{-x}\) …….(1)
This is the linear differential equation of the form

This is the general solution.

Question 2.
\(\frac{d y}{d x}\) + y = 3
Solution:
\(\frac{d y}{d x}\) + y = 3
This is the linear differential equation of the form

This is the general solution.

Question 3.
x\(\frac{d y}{d x}\) + 2y = x² . log x.
Solution:
x\(\frac{d y}{d x}\) + 2y = x² . log x
∴ \(\frac{d y}{d x}+\left(\frac{2}{x}\right) \cdot y=x \cdot \log x\) …….(1)
This is the linear differential equation of the form


This is the general solution.

Question 4.
(x + y)\(\frac{d y}{d x}\) = 1
Solution:
(x + y) \(\frac{d y}{d x}\) = 1
∴ \(\frac{d x}{d y}\) = x + y
∴ \(\frac{d x}{d y}\) – x = y
∴ \(\frac{d x}{d y}\) + (-1) x = y ……(1)
This is the linear differential equation of the form

This is the general solution.

Question 5.
y dx + (x – y²) dy = 0
Solution:
y dx + (x – y²) dy = 0
∴ y dx = -(x – y²) dy
∴ \(\frac{d x}{d y}=-\frac{\left(x-y^{2}\right)}{y}=-\frac{x}{y}+y\)
∴ \(\frac{d x}{d y}+\left(\frac{1}{y}\right) \cdot x=y\) ……(1)
This is the linear differential equation of the form

This is the general solution.

Question 6.
\(\frac{d y}{d x}\) + 2xy = x
Solution:
\(\frac{d y}{d x}\) + 2xy = x ………(1)
This is the linear differential equation of the form

This is the general solution.

Question 7.
(x + a) \(\frac{d y}{d x}\) = -y + a
Solution:
(x + a) \(\frac{d y}{d x}\) + y = a
∴ \(\frac{d y}{d x}+\left(\frac{1}{x+a}\right) y=\frac{a}{x+a}\) ……..(1)
This is the linear differential equation of the form

This is the general solution.

Question 8.
dy + (2y) dx = 8 dx
Solution:
dy + (2y) dx = 8 dx
∴ \(\frac{d y}{d x}\) + 2y = 8 …….(1)
This is the linear differential equation of the form

This is the general solution.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 8.1 Solutions
• 12th Commerce Maths Exercise 8.2 Solutions
• 12th Commerce Maths Exercise 8.3 Solutions
• 12th Commerce Maths Exercise 8.4 Solutions
• 12th Commerce Maths Exercise 8.5 Solutions
• 12th Commerce Maths Exercise 8.6 Solutions
• 12th Commerce Maths Miscellaneous Exercise 8 Solutions

Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.4 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.4 Questions and Answers.

Std 12 Maths 1 Exercise 8.4 Solutions Commerce Maths

Solve the following differential equations:

Question 1.
x dx + 2y dy = 0
Solution:
x dx + 2y dy = 0
Integrating, we get
∫x dx + 2 ∫y dy = c₁
∴ \(\frac{x^{2}}{2}+2\left(\frac{y^{2}}{2}\right)=c_{1}\)
∴ x² + 2y² = c, where c = 2c₁
This is the general solution.

Question 2.
y² dx + (xy + x²) dy = 0
Solution:
y² dx + (xy + x²) dy = 0
∴ (xy + x²) dy = -y² dx
∴ \(\frac{d y}{d x}=\frac{-y^{2}}{x y+x^{2}}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substituting these values in (1), we get



This is the general solution.

Question 3.
x²y dx – (x³ + y³) dy = 0
Solution:
x²y dx – (x³ + y³) dy = 0
∴ (x³ + y³) dy = x²y dx
∴ \(\frac{d y}{d x}=\frac{x^{2} y}{x^{3}+y^{3}}\) ……(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)


This is the general solution.

Question 4.
\(\frac{d y}{d x}+\frac{x-2 y}{2 x-y}=0\)
Solution:



This is the general solution.

Question 5.
(x² – y²) dx + 2xy dy = 0
Solution:
(x² – y²) dx + 2xy dy = 0
∴ 2xy dy = -(x² – y²) dx = (y² – x²) dx
∴ \(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\) ………(1)

Question 6.
xy\(\frac{d y}{d x}\) = x² + 2y²
Solution:

Question 7.
x²\(\frac{d y}{d x}\) = x² + xy – y²
Solution:

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 8.1 Solutions
• 12th Commerce Maths Exercise 8.2 Solutions
• 12th Commerce Maths Exercise 8.3 Solutions
• 12th Commerce Maths Exercise 8.4 Solutions
• 12th Commerce Maths Exercise 8.5 Solutions
• 12th Commerce Maths Exercise 8.6 Solutions
• 12th Commerce Maths Miscellaneous Exercise 8 Solutions

Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.3 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.3 Questions and Answers.

Std 12 Maths 1 Exercise 8.3 Solutions Commerce Maths

Question 1.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = x²y + y
Solution:
\(\frac{d y}{d x}\) = x²y + y
∴ \(\frac{d y}{d x}\) = y(x² + 1)
∴ \(\frac{1}{y}\) dy = (x² + 1) dx
Integrating, we get
∫\(\frac{1}{y}\) dy = ∫(x² + 1) dx
∴ log |y|= \(\frac{x^{3}}{3}\) + x + c
This is the general solution.

(ii) \(\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)\)
Solution:
\(\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)\)

This is the general solution.

(iii) (x² – yx²) dy + (y² + xy²) dx = 0
Solution:
(x² – yx²) dy + (y² + xy²) dx = 0
∴ x²(1 – y) dy + y²(1 + x) dx = 0
∴ \(\frac{1-y}{y^{2}} d y+\frac{1+x}{x^{2}} d x=0\)
Integrating, we get


This is the general solution.

(iv) \(y^{3}-\frac{d y}{d x}=x \frac{d y}{d x}\)
Solution:
\(y^{3}-\frac{d y}{d x}=x \frac{d y}{d x}\)

∴ 2y² log |x + 1| = 2cy² – 1 is the required solution.

Question 2.
For each of the following differential equations find the particular solution:
(i) (x – y²x) dx – (y + x²y) dy = 0, when x = 2, y = 0.
Solution:
(x – y²x) dx – (y + x²y) dy = 0
∴ x(1 – y²) dx – y(1 + x²) dy = 0

∴ the general solution is
log |1 + x²| + log |1 – y²| = log c, where c₁ = log c
∴ log |(1 + x²)(1 – y²) | = log c
∴ (1 + x²)(1 – y²) = c
When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5
∴ the particular solution is (1 + x²)(1 – y²) = 5.

(ii) (x + 1) \(\frac{d y}{d x}\) -1 = 2e^-y, when y = 0, x = 1.
Solution:

∴ log |2 + e^y| = log |c(x + 1)|
∴ 2 + e^y = c(x + 1)
This is the general solution.
Now, y = 0, when x = 1
∴ 2 + e⁰ = c(1 + 1)
∴ 3 = 2c
∴ c = \(\frac{3}{2}\)
∴ the particular solution is
2 + e^y = \(\frac{3}{2}\)(x + 1)
∴ 4 + 2e^y = 3x + 3
∴ 3x – 2e^y – 1 = 0

(iii) y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0, when x = e, y = e².
Solution:

∴ from (1), the general solution is
log |x log x| – log |y| = log c, where c₁ = log c
∴ log |\(\frac{x \log x}{y}\)| = log c
∴ \(\frac{x \log x}{y}\) = c
∴ x log x = cy
This is the general solution.
Now, y = e², when x = e
e log e = ce²
1 = ce ……[∵ log e = 1]
c = \(\frac{1}{e}\)
∴ the particular solution is x log x = (\(\frac{1}{e}\)) y
∴ y = e^x log x

(iv) \(\frac{d y}{d x}\) = 4x + y + 1, when y = 1, x = 0.
Solution:
\(\frac{d y}{d x}\) = 4x + y + 1
Put 4x + y + 1 = v

∴ log |v + 4| = x + c
∴ log |4x + y + 1 + 4| = x + c
i.e. log |4x + y + 5| = x + c
This is the general solution.
Now, y = 1 when x = 0
∴ log|0 + 1 + 5| = 0 + c,
i.e. c = log 6
∴ the particular solution is
log |4x + y + 5| = x + log 6
∴ \(\log \left|\frac{4 x+y+5}{6}\right|\) = x

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 8.1 Solutions
• 12th Commerce Maths Exercise 8.2 Solutions
• 12th Commerce Maths Exercise 8.3 Solutions
• 12th Commerce Maths Exercise 8.4 Solutions
• 12th Commerce Maths Exercise 8.5 Solutions
• 12th Commerce Maths Exercise 8.6 Solutions
• 12th Commerce Maths Miscellaneous Exercise 8 Solutions

Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.2 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.2 Questions and Answers.

Std 12 Maths 1 Exercise 8.2 Solutions Commerce Maths

Question 1.
Obtain the differential equation by eliminating arbitrary constants from the following equations:
(i) y = Ae^3x + Be^-3x
Solution:
y = Ae^3x + Be^-3x ……(1)
Differentiating twice w.r.t. x, we get

This is the required D.E.

(ii) y = \(c_{2}+\frac{c_{1}}{x}\)
Solution:
y = \(c_{2}+\frac{c_{1}}{x}\)
∴ xy = c₂x + c₁
Differentiating w.r.t. x, we get

(iii) y = (c₁ + c₂x) e^x
Solution:
y = (c₁ + c₂x) e^x


This is the required D.E.

(iv) y = c₁ e^3x+ c₂ e^2x
Solution:



This is the required D.E.

(v) y² = (x + c)³
Solution:
y² = (x + c)³
Differentiating w.r.t. x, we get

This is the required D.E.

Question 2.
Find the differential equation by eliminating arbitrary constant from the relation x² + y² = 2ax.
Solution:
x² + y² = 2ax
Differentiating both sides w.r.t. x, we get
2x + 2y\(\frac{d y}{d x}\) = 2a
Substituting value of 2a in equation (1), we get
x² + y² = [2x + 2y \(\frac{d y}{d x}\)]x = 2x² + 2xy \(\frac{d y}{d x}\)
∴ 2xy \(\frac{d y}{d x}\) = y² – x² is the required D.E.

Question 3.
Form the differential equation by eliminating arbitrary constants from the relation bx + ay = ab.
Solution:
bx + ay = ab
∴ ay = -bx + ab
∴ y = \(-\frac{b}{a} x+b\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=-\frac{b}{a} \times 1+0=-\frac{b}{a}\)
Differentiating again w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = 0 is the required D.E.

Question 4.
Find the differential equation whose general solution is x³ + y³ = 35ax.
Solution:

Question 5.
Form the differential equation from the relation x² + 4y² = 4b².
Sol ution:
x² + 4y² = 4b²
Differentiating w.r.t. x, we get
2x + 4(2y\(\frac{d y}{d x}\)) = 0
i.e. x + 4y\(\frac{d y}{d x}\) = 0 is the required D.E.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 8.1 Solutions
• 12th Commerce Maths Exercise 8.2 Solutions
• 12th Commerce Maths Exercise 8.3 Solutions
• 12th Commerce Maths Exercise 8.4 Solutions
• 12th Commerce Maths Exercise 8.5 Solutions
• 12th Commerce Maths Exercise 8.6 Solutions
• 12th Commerce Maths Miscellaneous Exercise 8 Solutions

Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.1 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.1 Questions and Answers.

Std 12 Maths 1 Exercise 8.1 Solutions Commerce Maths

Question 1.
Determine the order and degree of each of the following differential equations:
(i) \(\frac{d^{2} x}{d t^{2}}+\left(\frac{d x}{d t}\right)^{2}+8=0\)
Solution:
The given D.E. is \(\frac{d^{2} x}{d t^{2}}+\left(\frac{d x}{d t}\right)^{2}+8=0\)
This D.E. has highest order derivative \(\frac{d^{2} x}{d t^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.

(ii) \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\left(\frac{d y}{d x}\right)^{2}=a^{x}\)
Solution:
The given D.E. is \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\left(\frac{d y}{d x}\right)^{2}=a^{x}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 2.
∴ the given D.E. is of order 2 and degree 2.

(iii) \(\frac{d^{4} y}{d x^{4}}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3}\)
Solution:
The given D.E. is \(\frac{d^{4} y}{d x^{4}}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3}\)
This D.E. has highest order derivative \(\frac{d^{4} y}{d x^{4}}\) with power 1.
∴ the given D.E. is of order 4 and degree 1.

(iv) (y'”)² + 2(y”)² + 6y’ + 7y = 0
Solution:
The given D.E. is (y”‘)² + 2(y”)² + 6y’ + 7y = 0
This can be written as \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}+2\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+6 \frac{d y}{d x}+7 y=0\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 2.
∴ the given D.E. is of order 3 and degree 2.

(v) \(\sqrt{1+\frac{1}{\left(\frac{d y}{d x}\right)^{2}}}=\left(\frac{d y}{d x}\right)^{3 / 2}\)
Solution:
The given D.E. is \(\sqrt{1+\frac{1}{\left(\frac{d y}{d x}\right)^{2}}}=\left(\frac{d y}{d x}\right)^{3 / 2}\)
On squaring both sides, we get
\(1+\frac{1}{\left(\frac{d y}{d x}\right)^{2}}=\left(\frac{d y}{d x}\right)^{3}\)
∴ \(\left(\frac{d y}{d x}\right)^{2}+1=\left(\frac{d y}{d x}\right)^{5}\)
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 5.
∴ the given D.E. is of order 1 and degree 5.

(vi) \(\frac{d y}{d x}=7 \frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\frac{d y}{d x}=7 \frac{d^{2} y}{d x^{2}}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.

(vii) \(\left(\frac{d^{3} y}{d x^{3}}\right)^{1 / 6}=9\)
Solution:
The given D.E. is \(\left(\frac{d^{3} y}{d x^{3}}\right)^{1 / 6}=9\)
i.e., \(\frac{d^{3} y}{d x^{3}}=9^{6}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 1.
∴ the given D.E. is of order 3 and degree 1.

Question 2.
In each of the following examples, verify that the given function is a solution of the corresponding differential equation:

Solution:
(i) xy = log y + k
Differentiating w.r.t. x, we get

Hence, xy = log y + k is a solution of the D.E. y'(1 – xy) = y².

(ii) y = xⁿ
Differentiating twice w.r.t. x, we get

This shows that y = xⁿ is a solution of the D.E.
\(x^{2} \frac{d^{2} y}{d x^{2}}-n x \frac{d y}{d x}+n y=0\)

(iii) y = e^x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = e^x = y
Hence, y = ex is a solution of the D.E. \(\frac{d y}{d x}\) = y.

(iv) y = 1 – log x
Differentiating w.r.t. x, we get

Hence, y = 1 – log x is a solution of the D.E.
\(x^{2} \frac{d^{2} y}{d x^{2}}=1\)

(v) y = ae^x + be^-x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = a(e^x) + b(-e^-x) = ae^x – be^-x
Differentiating again w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = a(e^x) – b(-e^-x)
= ae^x + be^-x
= y
Hence, y = ae^x + be^-x is a solution of the D.E. \(\frac{d^{2} y}{d x^{2}}\) = y.

(vi) ax² + by² = 5
Differentiating w.r.t. x, we get

Hence, ax² + by² = 5 is a solution of the D.E.
\(x y \frac{d^{2} y}{d x^{2}}+x\left(\frac{d y}{d x}\right)^{2}=y\left(\frac{d y}{d x}\right)\)

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 8.1 Solutions
• 12th Commerce Maths Exercise 8.2 Solutions
• 12th Commerce Maths Exercise 8.3 Solutions
• 12th Commerce Maths Exercise 8.4 Solutions
• 12th Commerce Maths Exercise 8.5 Solutions
• 12th Commerce Maths Exercise 8.6 Solutions
• 12th Commerce Maths Miscellaneous Exercise 8 Solutions

Definite Integration Class 12 Commerce Maths 1 Chapter 7 Miscellaneous Exercise 7 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 7 Application of Definite Integration Miscellaneous Exercise 7 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 7 Solutions Commerce Maths

(I) Choose the correct alternatives:

Question 1.
Area of the region bounded by the curve x² = y, the X-axis and the lines x = 1 and x = 3 is
(a) \(\frac{26}{3}\) sq units
(b) \(\frac{3}{26}\) sq units
(c) 26 sq units
(d) 3 sq units
Answer:
(a) \(\frac{26}{3}\) sq units

Question 2.
The area of the region bounded by y² = 4x, the X-axis and the lines x = 1 and x = 4 is
(a) 28 sq units
(b) 3 sq unit
(c) \(\frac{28}{3}\) sq units
(d) \(\frac{3}{28}\) sq units
Answer:
(c) \(\frac{28}{3}\) sq units

Question 3.
Area of the region bounded by x² = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is
(a) 63 sq units
(b) \(\frac{3}{56}\) sq units
(c) \(\frac{56}{3}\) sq units
(d) \(\frac{63}{7}\) sq units
Answer:
(c) \(\frac{56}{3}\) sq units

Question 4.
Area of the region bounded by y = x⁴, x = 1, x = 5 and the X-axis is
(a) \(\frac{3142}{5}\) sq units
(b) \(\frac{3124}{5}\) sq units
(c) \(\frac{3142}{3}\) sq units
(d) \(\frac{3124}{3}\) sq units
Answer:
(b) \(\frac{3124}{5}\) sq units

Question 5.
Using definite integration area of circle x² + y² = 25 is
(a) 5π sq units
(b) 4π sq units
(c) 25π sq units
(d) 25 sq units
Answer:
(c) 25π sq units

(II) Fill in the blanks:

Question 1.
Area of the region bounded by y = x⁴, x = 1, x = 5 and the X-axis is _________
Answer:
\(\frac{3124}{5}\) sq units

Question 2.
Using definite integration area of the circle x² + y² = 49 is ___________
Answer:
49π sq units

Question 3.
Area of the region bounded by x² = 16y, y = 1, y = 4 and the Y-axis lying in the first quadrant is _________
Answer:
\(\frac{56}{3}\) sq units

Question 4.
The area of the region bounded by the curve x² = y, the X-axis and the lines x = 3 and x = 9 is _________
Answer:
234 sq units

Question 5.
The area of the region bounded by y² = 4x, the X-axis and the lines x = 1 and x = 4 is __________
Answer:
\(\frac{28}{3}\) sq units

(III) State whether each of the following is True or False.

Question 1.
The area bounded by the curve x = g(y), Y-axis and bounded between the lines y = c and y = d is given by \(\int_{c}^{d} x d y=\int_{y=c}^{y=d} g(y) d y\)
Answer:
True

Question 2.
The area bounded by two curves y = f(x), y = g(x) and X-axis is \(\left|\int_{a}^{b} f(x) d x-\int_{b}^{a} g(x) d x\right|\)
Answer:
False

Question 3.
The area bounded by the curve y = f(x), X-axis and lines x = a and x = b is \(\left|\int_{a}^{b} f(x) d x\right|\)
Answer:
True

Question 4.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis, and lines x = a, x = b is positive.
Answer:
False

Question 5.
The area of the portion lying above the X-axis is positive.
Answer:
True

(IV) Solve the following:

Question 1.
Find the area of the region bounded by the curve xy = c², the X-axis, and the lines x = c, x = 2c.
Solution:

= c² log(\(\frac{2 c}{c}\))
= c² . log 2 sq units.

Question 2.
Find the area between the parabolas y² = 7x and x² = 7y.
Solution:

For finding the points of intersection of the two parabolas,
we equate the values of y² from their equations.
From the equation x² = 7y, y² = \(\frac{x^{4}}{49}\)
∴ \(\frac{x^{4}}{49}\) = 7x
∴ x⁴ = 343x
∴ x⁴ – 343x = 0
∴ x(x³ – 343) = 0
∴ x = 0 or x³ = 343, i.e. x = 7
When x = 0, y = 0
When x = 7, 7y = 49
∴ y = 7
∴ the points of intersection are O(0, 0) and A(7, 7)
Required area = area of the region OBACO
= (area of the region ODACO) – (area of the region ODABO)
Now, area of the region ODACO = area under the parabola y² = 7x
i.e. y = √7 √x

Area of the region ODABO = Area under the parabola
x² = 7y
i.e. y = \(\frac{x^{2}}{7}\)

∴ required area = \(\frac{98}{3}-\frac{49}{3}=\frac{49}{3}\) sq units.

Question 3.
Find the area of the region bounded by the curve y = x² and the line y = 10.
Solution:

By the symmetry of the parabola,
the required area is twice the area of the region OABCO
Now, the area of the region OABCO

Question 4.
Find the area of the ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1.
Solution:
By the symmetry of the ellipse, the required area of the ellipse is 4 times the area of the region OPQO.
For the region OPQO, the limits of integration are x = 0 and x = 4.

Question 5.
Find the area of the region bounded by y = x², the X-axis and x = 1, x = 4.
Solution:
Required area = \(\int_{1}^{4} y d x\), where y = x²
= \(\int_{1}^{4} x^{2} d x\)
= \(\left[\frac{x^{3}}{3}\right]_{1}^{4}=\frac{4^{3}}{3}-\frac{1}{3}=\frac{64-1}{3}\)
= 21 sq units.

Question 6.
Find the area of the region bounded by the curve x² = 25y, y = 1, y = 4, and the Y-axis.
Solution:

Question 7.
Find the area of the region bounded by the parabola y² = 25x and the line x = 5.
Solution:

Given the equation of the parabola is y² = 25x
∴ y = 5√x …… [∵ IIn first quadrant, y > 0]
Required area = area of the region OQRPO
= 2(area of the region ORPO)

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 7.1 Solutions
• 12th Commerce Maths Miscellaneous Exercise 7 Solutions

Application of Definite Integration Class 12 Commerce Maths 1 Chapter 7 Exercise 7.1 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 7 Application of Definite Integration Ex 7.1 Questions and Answers.

Std 12 Maths 1 Exercise 7.1 Solutions Commerce Maths

Question 1.
Find the area of the region bounded by the following curves, the X-axis, and the given lines:
(i) y = x⁴, x = 1, x = 5
Solution:

(ii) y = \(\sqrt{6 x+4}\), x = 0, x = 2
Solution:

(iii) \(\sqrt{16-x^{2}}\), x = 0, x = 4
Solution:

(iv) 2y = 5x + 7, x = 2, x = 8
Solution:

(v) 2y + x = 8, x = 2, x = 4
Solution:

(vi) y = x² + 1, x = 0, x = 3
Solution:

(vii) y = 2 – x², x = -1, x = 1
Solution:

Question 2.
Find the area of the region bounded by the parabola y² = 4x and the line x = 3.
Solution:

Required area = area of the region OABO
= 2(area of the region OACO)

Question 3.
Find the area of the circle x² + y² = 25.
Solution:

By the symmetry of the circle, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 5.
From the equation of the circle, y² = 25 – x².
In the first quadrant y > 0
∴ y = \(\sqrt{25-x^{2}}\)
∴ area of the circle = 4(area of region OABO)

Question 4.
Find the area of the ellipse \(\frac{x^{2}}{4}+\frac{y^{2}}{25}\) = 1
Solution:

By the symmetry of the ellipse, its area is equal to 4 times the area of the region OABO.
Clearly, for this region, the limits of integration are 0 and 2.
From the equation of the ellipse,

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 7.1 Solutions
• 12th Commerce Maths Miscellaneous Exercise 7 Solutions

Definite Integration Class 12 Commerce Maths 1 Chapter 6 Miscellaneous Exercise 6 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Miscellaneous Exercise 6 Questions and Answers.

Std 12 Maths 1 Miscellaneous Exercise 6 Solutions Commerce Maths

(I) Choose the correct alternative:

Question 1.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\) = ________
(a) 0
(b) 3
(c) 9
(d) -9
Answer:
(a) 0

Question 2.
\(\int_{-2}^{3} \frac{d x}{x+5}\) = _________
(a) -log(\(\frac{8}{3}\))
(b) log(\(\frac{8}{3}\))
(c) log(\(\frac{3}{8}\))
(d) -log(\(\frac{3}{8}\))
Answer:
(b) log(\(\frac{8}{3}\))

Question 3.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\) = _________
(a) log(\(\frac{8}{3}\))
(b) -log(\(\frac{8}{3}\))
(c) \(\frac{1}{2}\) log(\(\frac{8}{3}\))
(d) \(\frac{-1}{2}\) log(\(\frac{8}{3}\))
Answer:
(c) \(\frac{1}{2}\) log(\(\frac{8}{3}\))

Question 4.
\(\int_{4}^{9} \frac{d x}{\sqrt{x}}\) = ___________
(a) 9
(b) 4
(c) 2
(d) 0
Answer:
(c) 2

Question 5.
If \(\int_{0}^{a} 3 x^{2} d x=8\), then a = __________
(a) 2
(b) 0
(c) \(\frac{8}{3}\)
(d) a
Answer:
(a) 2

Question 6.
\(\int_{2}^{3} x^{4}\) dx = ________
(a) \(\frac{1}{2}\)
(b) \(\frac{5}{2}\)
(c) \(\frac{5}{211}\)
(d) \(\frac{211}{5}\)
Answer:
(d) \(\frac{211}{5}\)

Question 7.
\(\int_{0}^{2} e^{x}\) dx = _______
(a) e – 1
(b) 1 – e
(c) 1 – e²
(d) e² – 1
Answer:
(d) e² – 1

Question 8.
\(\int_{a}^{b} f(x) d x\) = ________
(a) \(\int_{b}^{a} f(x) d x\)
(b) –\(\int_{a}^{b} f(x) d x\)
(c) –\(\int_{b}^{a} f(x) d x\)
(d) \(\int_{0}^{a} f(x) d x\)
Answer:
(c) –\(\int_{b}^{a} f(x) d x\)

Question 9.
\(\int_{-7}^{7} \frac{x^{3}}{x^{2}+7} d x\) = _________
(a) 7
(b) 49
(c) 0
(d) \(\frac{7}{2}\)
Answer:
(c) 0

Question 10.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x\) = _________
(a) \(\frac{7}{2}\)
(b) \(\frac{5}{2}\)
(c) 7
(d) 2
Answer:
(b) \(\frac{5}{2}\)

(II) Fill in the blanks:

Question 1.
\(\int_{0}^{2} e^{x} d x\) = ________
Answer:
e² – 1

Question 2.
\(\int_{2}^{3} x^{4} d x\) = __________
Answer:
\(\frac{211}{5}\)

Question 3.
\(\int_{0}^{1} \frac{d x}{2 x+5}\) = ____________
Answer:
\(\frac{1}{2} \log \left(\frac{7}{5}\right)\)

Question 4.
If \(\int_{0}^{a} 3 x^{2} d x\) = 8, then a = _________
Answer:
2

Question 5.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\) = _________
Answer:
2

Question 6.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\) = _________
Answer:
\(\frac{1}{2} \log \left(\frac{8}{3}\right)\)

Question 7.
\(\int_{-2}^{3} \frac{d x}{x+5}\) = _________
Answer:
\(\log \left(\frac{8}{3}\right)\)

Question 8.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\) = _____________
Answer:
o

(III) State whether each of the following is True or False:

Question 1.
\(\int_{a}^{b} f(x) d x=\int_{-b}^{-a} f(x) d x\)
Answer:
True

Question 2.
\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(t) d t\)
Answer:
True

Question 3.
\(\int_{0}^{a} f(x) d x=\int_{a}^{0} f(a-x) d x\)
Answer:
False

Question 4.
\(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(x-a-b) d x\)
Answer:
False

Question 5.
\(\int_{-5}^{5} \frac{x^{3}}{x^{2}+7} d x=0\)
Answer:
True

Question 6.
\(\int_{1}^{2} \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}} d x=\frac{1}{2}\)
Answer:
True

Question 7.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x=\frac{9}{2}\)
Answer:
False

Question 8.
\(\int_{4}^{7} \frac{(11-x)^{2}}{(11-x)^{2}+x^{2}} d x=\frac{3}{2}\)
Answer:
True

(IV) Solve the following:

Question 1.
\(\int_{2}^{3} \frac{x}{(x+2)(x+3)} d x\)
Solution:

Question 2.
\(\int_{1}^{2} \frac{x+3}{x(x+2)} d x\)
Solution:
Let I = \(\int_{1}^{2} \frac{x+3}{x(x+2)} d x\)
Let \(\frac{x+3}{x(x+2)}=\frac{A}{x}+\frac{B}{x+2}\)
∴ x + 3 = A(x + 2) + Bx
Put x = 0, we get
3 = A(2) + B(0)
∴ A = \(\frac{3}{2}\)
Put x + 2 = 0, i.e. x = -2, we get
-2 + 3 = A(0) + B(-2)
∴ 1 = -2B
∴ B = \(-\frac{1}{2}\)

Question 3.
\(\int_{1}^{3} x^{2} \log x d x\)
Solution:

Question 4.
\(\int_{0}^{1} e^{x^{2}} \cdot x^{3} d x\)
Solution:

Question 5.
\(\int_{1}^{2} e^{2 x}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) d x\)
Solution:

Question 6.
\(\int_{4}^{9} \frac{1}{\sqrt{x}} d x\)
Solution:

Question 7.
\(\int_{-2}^{3} \frac{1}{x+5} d x\)
Solution:

Question 8.
\(\int_{2}^{3} \frac{x}{x^{2}-1} d x\)
Solution:

Question 9.
\(\int_{0}^{1} \frac{x^{2}+3 x+2}{\sqrt{x}} d x\)
Solution:

Question 10.
\(\int_{3}^{5} \frac{d x}{\sqrt{x+4}+\sqrt{x-2}}\)
Solution:

Question 11.
\(\int_{2}^{3} \frac{x}{x^{2}+1} d x\)
Solution:

Question 12.
\(\int_{1}^{2} x^{2} d x\)
Solution:

Question 13.
\(\int_{-4}^{-1} \frac{1}{x} d x\)
Solution:

Question 14.
\(\int_{0}^{1} \frac{1}{\sqrt{1+x}+\sqrt{x}} d x\)
Solution:

Question 15.
\(\int_{0}^{4} \frac{1}{\sqrt{x^{2}+2 x+3}} d x\)
Solution:

Question 16.
\(\int_{2}^{4} \frac{x}{x^{2}+1} d x\)
Solution:

Question 17.
\(\int_{0}^{1} \frac{1}{2 x-3} d x\)
Solution:

Question 18.
\(\int_{1}^{2} \frac{5 x^{2}}{x^{2}+4 x+3} d x\)
Solution:

Question 19.
\(\int_{1}^{2} \frac{d x}{x(1+\log x)^{2}}\)
Solution:

Question 20.
\(\int_{0}^{9} \frac{1}{1+\sqrt{x}} d x\)
Solution:

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 6.1 Solutions
• 12th Commerce Maths Exercise 6.2 Solutions
• 12th Commerce Maths Miscellaneous Exercise 6 Solutions

Definite Integration Class 12 Commerce Maths 1 Chapter 6 Exercise 6.2 Answers Maharashtra Board

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 6 Definite Integration Ex 6.2 Questions and Answers.

Std 12 Maths 1 Exercise 6.2 Solutions Commerce Maths

Evaluate the following integrals:

Question 1.
\(\int_{-9}^{9} \frac{x^{3}}{4-x^{2}} d x\)
Solution:

Question 2.
\(\int_{0}^{a} x^{2}(a-x)^{3 / 2} d x\)
Solution:
We use the property

Question 3.
\(\int_{1}^{3} \frac{\sqrt[3]{x+5}}{\sqrt[3]{x+5}+\sqrt[3]{9-x}} d x\)
Solution:

Question 4.
\(\int_{2}^{5} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{7-x}} d x\)
Solution:

Question 5.
\(\int_{1}^{2} \frac{\sqrt{x}}{\sqrt{3-x}+\sqrt{x}} d x\)
Solution:

Question 6.
\(\int_{2}^{7} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{9-x}} d x\)
Solution:

Question 7.
\(\int_{0}^{1} \log \left(\frac{1}{x}-1\right) d x\)
Solution:

Question 8.
\(\int_{0}^{1} x(1-x)^{5} d x\)
Solution:
We use the property

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 6.1 Solutions
• 12th Commerce Maths Exercise 6.2 Solutions
• 12th Commerce Maths Miscellaneous Exercise 6 Solutions