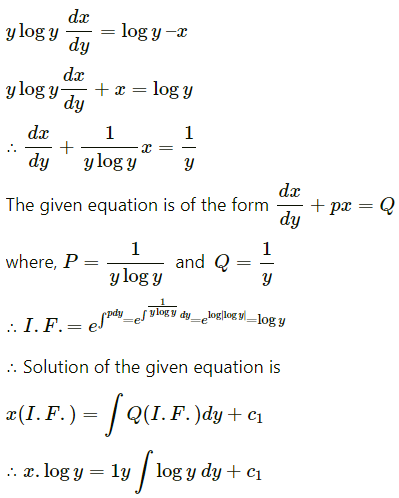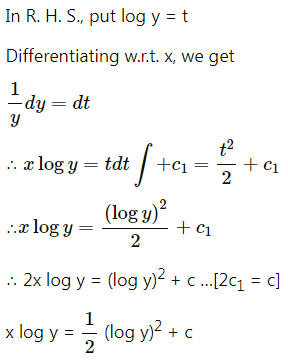Maharashtra Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8

(I) Choose the correct option from the given alternatives:

Question 1.
The order and degree of \(\left(\frac{d y}{d x}\right)^{3}-\frac{d^{3} y}{d x^{3}}+y e^{x}=0\) are respectively.
(a) 3, 1
(b) 1, 3
(c) 3, 3
(d) 1, 1
Answer:
(a) 3, 1

Question 2.
The order and degree of \(\left[1+\left(\frac{d y}{d x}\right)^{3}\right]^{\frac{2}{3}}=8 \frac{d^{3} y}{d x^{3}}\) are respectively
(a) 3, 1
(c) 3, 3
(b) 1, 3
(d) 1, 1
Answer:
(c) 3, 3

Question 3.
The differential equation of y = k₁ + \(\frac{k_{2}}{x}\) is
(a) \(\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
(d) \(x \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=0\)
Answer:
(b) \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0\)

Question 4.
The differential equation of y = k₁ e^x + k₂ e^-x is
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
(b) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}+y \frac{d y}{d x}=0\)
(d) \(\frac{d^{2} y}{d x^{2}}+y=0\)
Answer:
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)

Question 5.
The solution of \(\frac{d y}{d x}\) = 1 is
(a) x + y = c
(b) xy = c
(c) x² + y² = c
(d) y – x = c
Answer:
(d) y – x = c

Question 6.
The solution of \(\frac{d y}{d x}+\frac{x^{2}}{y^{2}}=0\) is
(a) x³ + y³ = 7
(b) x² + y² = c
(c) x³ + y³ = c
(d) x + y = c
Answer:
(c) x³ + y³ = c

Question 7.
The solution of x \(\frac{d y}{d x}\) = y log y is
(a) y = ae^x
(b) y = be^2x
(c) y = be^-2x
(d) y = e^ax
Answer:
(d) y = e^ax

Question 8.
Bacterial increases at a rate proportional to the number present. If the original number M doubles in 3 hours, then the number of bacteria will be 4M in
(a) 4 hours
(b) 6 hours
(c) 8 hours
(d) 10 hours
Answer:
(b) 6 hours

Question 9.
The integrating factor of \(\frac{d y}{d x}\) – y = e^x is
(a) x
(b) -x
(c) e^x
(d) e^-x
Answer:
(c) e^x

Question 10.
The integrating factor of \(\frac{d y}{d x}\) – y = e^x is e^-x, then its solution is
(a) ye^-x = x + c
(b) ye^x = x + c
(c) ye^x = 2x + c
(d) ye^-x = 2x + c
Answer:
(a) ye^-x = x + c

(II) Fill in the blanks:

Question 1.
The order of highest derivative occurring in the differential equation is called ________ of the differential equation.
Answer:
order

Question 2.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called ________ of the differential equation.
Answer:
degree

Question 3.
A solution of differential equation that can be obtained from the general solution by giving particular values to the arbitrary constants is called _________ solution.
Answer:
particular

Question 4.
Order and degree of a differential equation are always _________ integers.
Answer:
positive

Question 5.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is _________
Answer:
e^-x

Question 6.
The differential equation by eliminating arbitrary constants from bx + ay = ab is _________
Answer:
\(\frac{d^{2} y}{d x^{2}}=0\)

(III) State whether each of the following is True or False:

Question 1.
The integrating factor of the differential equation \(\frac{d y}{d x}\) – y = x is e^-x.
Answer:
True

Question 2.
The order and degree of a differential equation are always positive integers.
Answer:
True

Question 3.
The degree of a differential equation is the power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any.
Answer:
True

Question 4.
The order of highest derivative occurring in the differential equation is called the degree of the differential equation.
Answer:
False

Question 5.
The power of the highest ordered derivative when all the derivatives are made free from negative and/or fractional indices if any is called the order of the differential equation.
Answer:
False

Question 6.
The degree of the differential equation \(e^{\frac{d y}{d x}}=\frac{d y}{d x}+c\) is not defined.
Answer:
True

(IV) Solve the following:

Question 1.
Find the order and degree of the following differential equations:
(i) \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given differential equation is \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3 / 2}=\frac{d^{2} y}{d x^{2}}\)
∴ \(\left[\frac{d^{3} y}{d x^{3}}+x\right]^{3}=\left(\frac{d^{2} y}{d x^{2}}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 3
∴ order = 3 and degree = 3

(ii) \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
Solution:
The given differential equation is \(x+\frac{d y}{d x}=1+\left(\frac{d y}{d x}\right)^{2}\)
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 2.
∴ order = 1, degree = 2.

Question 2.
Verify that y = log x + c is a solution of the differential equation \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\).
Solution:
y = log x + c
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{1}{x}+0=\frac{1}{x}\)
∴ x\(\frac{d y}{d x}\) = 1
Differentiating again w.r.t. x, we get
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \times 1=0\)
∴ \(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)
This shows that y = log x + c is a solution of the D.E.
\(x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}=0\)

Question 3.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = 1 + x + y + xy
Solution:
\(\frac{d y}{d x}\) = 1 + x + y + xy
∴ \(\frac{d y}{d x}\) = (1 + x) + y(1 + x) = (1 + x)(1 + y)
∴ \(\frac{1}{1+y}\) dy = (1 + x) dx
Integrating, we get
∫\(\frac{1}{1+y}\) dy = ∫(1 + x) dx
∴ log|1 + y| = x + \(\frac{x^{2}}{2}\) + c
This is the general solution.

(ii) \(e^{d y / d x}=x\)
Solution:

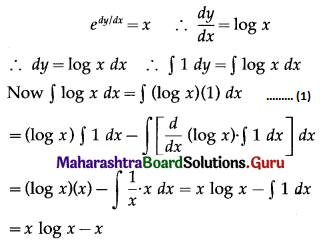
∴ from (1), the general solution is
y = x log x – x + c, i.e. y = x(log x – 1) + c.

(iii) dr = ar dθ – θ dr
Solution:
dr = ar dθ – θ dr
∴ dr + θ dr = ar dθ
∴ (1 + θ) dr = ar dθ
∴ \(\frac{d r}{r}=\frac{a d \theta}{1+\theta}\)
On integrating, we get
\(\int \frac{d r}{r}=a \int \frac{d \theta}{1+\theta}\)
∴ log |r| = a log |1 + θ| + c
This is the general solution.

(iv) Find the differential equation of the family of curves y = e^x (ax + bx²), where a and b are arbitrary constants.
Solution:
y = e^x (ax + bx²)
ax + bx² = ye^-x …….(1)
Differentiating (1) w.r.t. x twice and writing \(\frac{d y}{d x}\) as y₁ and \(\frac{d^{2} y}{d x^{2}}\) as y₂, we get


This is the required differential equation.

Question 4.
Solve \(\frac{d y}{d x}=\frac{x+y+1}{x+y-1}\) when x = \(\frac{2}{3}\) and y = \(\frac{1}{3}\).
Solution:

Question 5.
Solve y dx – x dy = -log x dx.
Solution:
y dx – x dy = -log x dx
∴ y dx – x dy + log x dx = 0
∴ x dy = (y + log x) dx
∴ \(\frac{d y}{d x}=\frac{y+\log x}{x}=\frac{y}{x}+\frac{\log x}{x}\)
∴ \(\frac{d y}{d x}-\frac{1}{x} \cdot y=\frac{\log x}{x}\) …….(1)
This is the linear differential equation of the form


This is the general solution.

Question 6.
Solve y log y \(\frac{d x}{d y}\) + x – log y = 0.
Solution:

Question 7.
Solve (x + y) dy = a² dx
Solution:

Question 8.
Solve \(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\)
Solution:
\(\frac{d y}{d x}+\frac{2}{x} y=x^{2}\) ……..(1)
This is a linear differential equation of the form

This is the general solution.

Question 9.
The rate of growth of the population is proportional to the number present. If the population doubled in the last 25 years and the present population is 1 lakh, when will the city have a population of 400000?
Solution:
Let P be the population at time t years.
Then the rate of growth of the population is \(\frac{d P}{d t}\) which is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant
∴ \(\frac{d P}{P}\)= k dt
On integrating, we get
\(\int \frac{d P}{P}=k \int d t\)
∴ log P = kt + c
The population doubled in 25 years and present population is 1,00,000.
∴ initial population was 50,000
i.e. when t = 0, P = 50000
∴ log 50000 = k × 0 + c
∴ c = log 50000
∴ log P = kt + log 50000
When t = 25, P = 100000
∴ log 100000 = k × 25 + log 50000
∴ 25k = log 100000 – log 50000 = log(\(\frac{100000}{50000}\))
∴ k = \(\frac{1}{25}\) log 2
∴ log P = \(\frac{t}{25}\) log 2 + log 50000
If P = 400000, then
log 400000 = \(\frac{t}{25}\) log 2 + log 50000
∴ log 400000 – log 50000 = \(\frac{t}{25}\) log 2
∴ log(\(\frac{400000}{50000}\)) = \(\log (2)^{t / 25}\)
∴ log 8 = \(\log (2)^{t / 25}\)
∴ 8 = \((2)^{t / 25}\)
∴ \((2)^{t / 25}\) = (2)³
∴ \(\frac{t}{25}\) = 3
∴ t = 75
∴ the population will be 400000 in (75 – 25) = 50 years.

Question 10.
The resale value of a machine decreases over a 10 years period at a rate that depends on the age of the machine. When the machine is x years old, the rate at which its value is changing is ₹ 2200(x – 10) per year. Express the value of the machine as a function of its age and initial value. If the machine was originally worth ₹ 1,20,000 how much will it be worth when it is 10 years old?
Solution:
Let V be the value of the machine after x years.
Then rate of change of the value is \(\frac{d V}{d x}\) which is 2200(x – 10)
∴ \(\frac{d V}{d x}\) = 2200(x – 10)
∴ dV = 2200(x – 10) dx
On integrating, we get
∫dV = 2200∫(x – 10) dx
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + c
Initially, i.e. at x = 0, V = 120000
∴ 120000 = 2200 × 0 + c = c
∴ c = 120000
∴ V = 2200[\(\frac{x^{2}}{2}\) – 10x] + 120000 …….(1)
This gives value of the machine in terms of initial value and age x.
We have to find V when x = 10.
When x = 10, from (1)
V = 2200[\(\frac{100}{2}\) – 100] + 120000
= 2200 [-50] + 120000
= -110000 + 120000
= 10000
Hence, the value of the machine after 10 years will be ₹ 10000.

Question 11.
Solve y² dx + (xy + x²) dy = 0
Solution:

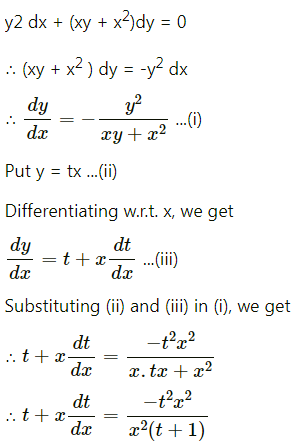
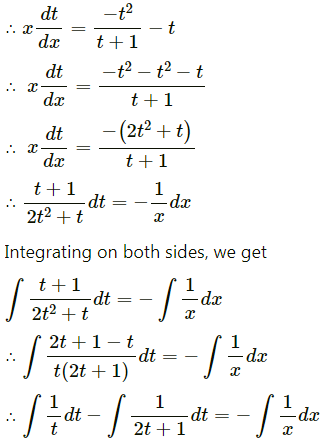
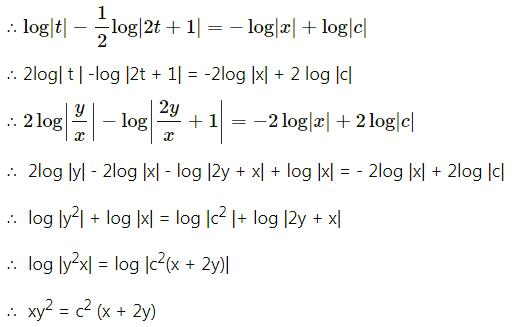
Question 12.
Solve x²y dx – (x³ + y³) dy = 0
Solution:

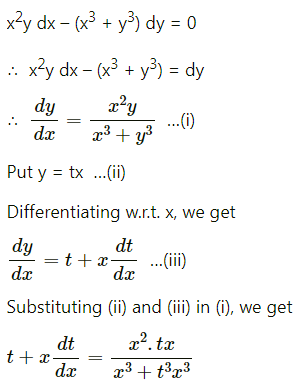
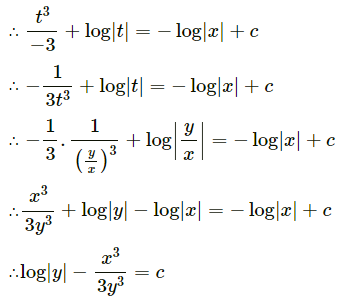
Question 13.
Solve yx \(\frac{d y}{d x}\) = x² + 2y²
Solution:

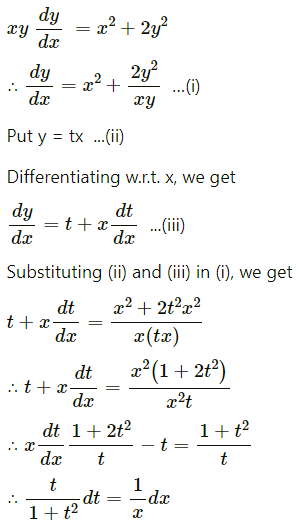
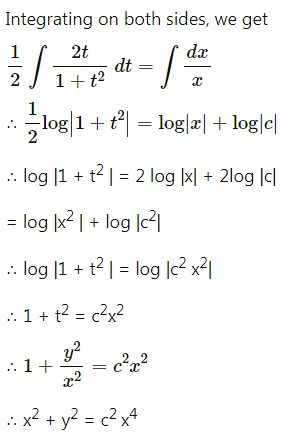
Question 14.
Solve (x + 2y³) \(\frac{d y}{d x}\) = y
Solution:
(x + 2y³) \(\frac{d y}{d x}\) = y
∴ x + 2y³ = y \(\frac{d x}{d y}\)

This is the general solution.

Question 15.
Solve y dx – x dy + log x dx = 0
Solution:
y dx – x dy + log x dx = 0
∴ (y + log x) dx = x dy


This is the general solution.

Question 16.
Solve \(\frac{d y}{d x}\) = log x dx
Solution:
\(\frac{d y}{d x}\) = log x dx
∴ dy = log x dx
On integrating, we get
∫dy = ∫log x . 1 dx
∴ y = (log x) ∫1 dx – \(\int\left[\left\{\frac{d}{d x}(\log x)\right\} \cdot \int 1 d x\right] d x\)
∴ y = (log x) . x – \(\int \frac{1}{x} \cdot x d x\)
∴ y = x log x – ∫1 dx
∴ y = x log x – x + c
This is the general solution.

Question 17.
y log y \(\frac{d x}{d y}\) = log y – x
Solution: