Differential Equation and Applications Class 12 Commerce Maths 1 Chapter 8 Exercise 8.1 Answers Maharashtra Board
Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.1 Questions and Answers.
Std 12 Maths 1 Exercise 8.1 Solutions Commerce Maths
Question 1.
Determine the order and degree of each of the following differential equations:
(i) \(\frac{d^{2} x}{d t^{2}}+\left(\frac{d x}{d t}\right)^{2}+8=0\)
Solution:
The given D.E. is \(\frac{d^{2} x}{d t^{2}}+\left(\frac{d x}{d t}\right)^{2}+8=0\)
This D.E. has highest order derivative \(\frac{d^{2} x}{d t^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.
(ii) \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\left(\frac{d y}{d x}\right)^{2}=a^{x}\)
Solution:
The given D.E. is \(\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+\left(\frac{d y}{d x}\right)^{2}=a^{x}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 2.
∴ the given D.E. is of order 2 and degree 2.
(iii) \(\frac{d^{4} y}{d x^{4}}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3}\)
Solution:
The given D.E. is \(\frac{d^{4} y}{d x^{4}}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{3}\)
This D.E. has highest order derivative \(\frac{d^{4} y}{d x^{4}}\) with power 1.
∴ the given D.E. is of order 4 and degree 1.
![]()
(iv) (y'”)2 + 2(y”)2 + 6y’ + 7y = 0
Solution:
The given D.E. is (y”‘)2 + 2(y”)2 + 6y’ + 7y = 0
This can be written as \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}+2\left(\frac{d^{2} y}{d x^{2}}\right)^{2}+6 \frac{d y}{d x}+7 y=0\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 2.
∴ the given D.E. is of order 3 and degree 2.
(v) \(\sqrt{1+\frac{1}{\left(\frac{d y}{d x}\right)^{2}}}=\left(\frac{d y}{d x}\right)^{3 / 2}\)
Solution:
The given D.E. is \(\sqrt{1+\frac{1}{\left(\frac{d y}{d x}\right)^{2}}}=\left(\frac{d y}{d x}\right)^{3 / 2}\)
On squaring both sides, we get
\(1+\frac{1}{\left(\frac{d y}{d x}\right)^{2}}=\left(\frac{d y}{d x}\right)^{3}\)
∴ \(\left(\frac{d y}{d x}\right)^{2}+1=\left(\frac{d y}{d x}\right)^{5}\)
This D.E. has highest order derivative \(\frac{d y}{d x}\) with power 5.
∴ the given D.E. is of order 1 and degree 5.
(vi) \(\frac{d y}{d x}=7 \frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\frac{d y}{d x}=7 \frac{d^{2} y}{d x^{2}}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.
(vii) \(\left(\frac{d^{3} y}{d x^{3}}\right)^{1 / 6}=9\)
Solution:
The given D.E. is \(\left(\frac{d^{3} y}{d x^{3}}\right)^{1 / 6}=9\)
i.e., \(\frac{d^{3} y}{d x^{3}}=9^{6}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 1.
∴ the given D.E. is of order 3 and degree 1.
![]()
Question 2.
In each of the following examples, verify that the given function is a solution of the corresponding differential equation:

Solution:
(i) xy = log y + k
Differentiating w.r.t. x, we get

Hence, xy = log y + k is a solution of the D.E. y'(1 – xy) = y2.
(ii) y = xn
Differentiating twice w.r.t. x, we get
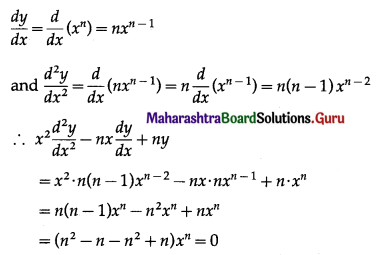
This shows that y = xn is a solution of the D.E.
\(x^{2} \frac{d^{2} y}{d x^{2}}-n x \frac{d y}{d x}+n y=0\)
(iii) y = ex
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = ex = y
Hence, y = ex is a solution of the D.E. \(\frac{d y}{d x}\) = y.
![]()
(iv) y = 1 – log x
Differentiating w.r.t. x, we get

Hence, y = 1 – log x is a solution of the D.E.
\(x^{2} \frac{d^{2} y}{d x^{2}}=1\)
(v) y = aex + be-x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = a(ex) + b(-e-x) = aex – be-x
Differentiating again w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = a(ex) – b(-e-x)
= aex + be-x
= y
Hence, y = aex + be-x is a solution of the D.E. \(\frac{d^{2} y}{d x^{2}}\) = y.
![]()
(vi) ax2 + by2 = 5
Differentiating w.r.t. x, we get

Hence, ax2 + by2 = 5 is a solution of the D.E.
\(x y \frac{d^{2} y}{d x^{2}}+x\left(\frac{d y}{d x}\right)^{2}=y\left(\frac{d y}{d x}\right)\)
12th Commerce Maths Digest Pdf
- 12th Commerce Maths Exercise 8.1 Solutions
- 12th Commerce Maths Exercise 8.2 Solutions
- 12th Commerce Maths Exercise 8.3 Solutions
- 12th Commerce Maths Exercise 8.4 Solutions
- 12th Commerce Maths Exercise 8.5 Solutions
- 12th Commerce Maths Exercise 8.6 Solutions
- 12th Commerce Maths Miscellaneous Exercise 8 Solutions