Class 10

Std 10 Hindi Chapter 4 Chapa Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 4 छापा Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 4 छापा Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 4 छापा Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए सूचना के अनुसार कृतियाँ कीजिए: प्रश्न 1. कृति पूर्ण कीजिए: उत्तर: (ii) प्रश्न 2. संजाल पूर्ण कीजिए: उत्तर: प्रश्न 2. कृति पूर्ण कीजिए: उत्तर: प्रश्न 3. कविता के आधार पर जोड़ियाँ मिलाइए: अ – आ अर्थ – बालों में सुवर्ण – चेहरे पर चाँदी – नई कविता में मुद्रा – काव्य कृतियों में उत्तर: (i) अर्थ – नई कविता में (ii) सुवर्ण – काव्य कृतियों में (iii) चाँदी – बालों में (iv) मुद्रा – चेहरे पर। प्रश्न 4. प्रवाह तालिका पूर्ण कीजिए: उत्तर: प्रश्न 5. ऐसे प्रश्न बनाइए जिनके उत्तर निम्न शब्द हों a. अरण्यकांड b. तख्त c. असफलता d. अनधिकृत उत्तर: a. कवि के घर में क्या देखकर छापा मारने वालों का खिला चेहरा मुरझा गया? b. कवि छापा मारने वालों से अपने घर में क्या डलवाने के लिए कहते हैं? c. कवि के घर छापा मारने पर छापा मारने वालों को क्या मिली? d. छापा मारने वालों को लेखक से किस प्रकार का अर्थ चाहिए था? प्रश्न 6. सोना, चाँदी, अर्थ और मुद्रा इन शब्दों के विभिन्न अर्थ बताते हुए कविता के आधार पर इनके अर्थ लिखिए। उत्तर: प्रश्न 7. कर जमा करना, देश के विकास को गति देना हैं’ विषय पर अपने विचार लिखिए। उत्तर: समाज में दो तरह के लोग होते हैं। एक वे, जो कर अदा करने लायक आय होने पर स्वेच्छा से ईमानदारी के साथ सरकार को कर अदा | कर देते हैं और दूसरे वे, जो कमाई तो जायज-नाजायज अंधाधुंध करते हैं, पर नियम के तहत कर अदा करने से कतराते हैं। यह मनोवृत्ति उचित नहीं है। देश के विकास का कार्य जनता द्वारा प्राप्त कर से ही पूरा होता है। चिकित्सा, परिवहन तथा जनता की सहायतार्थ शुरू किए जाने वाले सारे कार्य जनता से प्राप्त कर से ही पूरे होते हैं। जिस देश में आय करने वाले सभी लोग ईमानदारी और स्वेच्छा से उचित मात्रा में कर अदा करते हैं, उस देश के विकास के सारे कार्य सुचारू रूप से पूरे होते हैं और सामान्य जनता को उसका पूरा-पूरा लाभ मिलता है। यदि कोई व्यक्ति यह सोचता हो कि सभी लोग तो कर अदा करते हैं, उसके अकेले कर अदा न करने या कम कर का भुगतान करने से क्या फर्क पड़ेगा, ‘तो ऐसा सोचने वालों की संख्या अनगिनत हो सकती है। इस तरह कर की कितनी रकम सरकारी खजाने में जमा होने से रह जाती है। इस कारण पैसे के अभाव में सरकार की अनेक योजनाएँ अटकी रह जाती हैं। इसलिए कर योग्य आय पर ईमानदारी से कर जमा करना प्रत्येक नागरिक का कर्तव्य है। कर अदा कर हम अपनी ही सहायता करते हैं। कर जमा करने से ही विकास को गति मिलती है। उपयोजित लेखन निम्न मुद्दों के आधार पर विज्ञापन तैयार कीजिए: उत्तर: Hindi Lokbharti 10th Textbook Solutions Chapter 4 छापा Additional Important Questions and Answers पद्यांश क्र. 1 प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए: कृति 1: (आकलन) प्रश्न 1. संजाल पूर्ण कीजिए: उत्तर: प्रश्न 2. निम्नलिखित प्रश्नों के उत्तर लिखिए: (i) वे (छापा मारने वाले) रोष से बोले तो कवि किस प्रकार बोले? (ii) वे (छापा मारने वाले) कड़ककर बोले तो कवि किस प्रकार बोले? उत्तर: (i) वे रोष से बोले तो कवि जोश से बोले। (ii) वे कड़ककर बोले तो कवि भड़ककर बोले। प्रश्न 3. संजाल पूर्ण कीजिए: उत्तर: प्रश्न 4. कविता के आधार पर जोड़ियाँ मिलाइए: अ – आ अर्थ – बालों में सुवर्ण – चेहरे पर चाँदी – नई कविता में मुद्रा – काव्य कृतियों में कृति 2: (शब्द संपदा) प्रश्न 1. निम्नलिखित शब्दों के दो-दो अर्थ लिखिए: (i) सोना – (1) ……………………. (2) ……………………. (ii) अर्थ – (1) ……………………. (2) ……………………. (iii) नोट – (1) ……………………. (2) ……………………. (iv) चाँदी – (1) ……………………. (2) ……………………. उत्तर: (i) सोना – (1) (धातु) सोना (2) नींद लेना। (ii) अर्थ – (1) संपत्ति (पैसा) (2) (साहित्य में) मतलब। (iii) नोर्ट – (1) (रुपया) नोट (2) (परीक्षा के) टिप्पणी। . (iv) चाँदी – (1) (धातु) चाँदी (2) (बालों में सफेदी) चाँदी। प्रश्न 2. निम्नलिखित शब्दों के विलोम शब्द लिखिए: (i) रात × ……………………….. (ii) अनधिकृत × ……………………….. (iii) नई × ……………………….. (iv) धीरे-धीरे × ……………………….. उत्तर: (i) रात × दिन (ii) अनधिकृत × अधिकृत (iii) नई × पुरानी (iv) धीरे-धीरे × जल्दी जल्दी कृति 3: (सरल अर्थ) प्रश्न. पद्यांश की अंतिम पाँच पंक्तियों – का सरल अर्थ 25 से 30 शब्दों में लिखिए। उत्तर: अधिकारी कवि से छुपाकर रखी गई चाँदी निकालने के लिए कहते हैं। कवि चाँदी का अर्थ चाँदी जैसे सफेद हो गए अपने बालों से जोड़कर कहते हैं, “चाँदी तो मेरे सिर के बालों में आ रही है।” अधिकारी जब कड़ककर पूछते हैं कि उनके नोट (रुपये) कहाँ हैं, तो वे नोट का संबंध विद्यालय की परीक्षा के नोटों से जोड़कर जवाब देते हैं कि परीक्षा के नोट तो वे परीक्षा से एक महीने पहले तैयार करेंगे। पद्यांश क्र. 2 प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए: कृति 1: (आकलन) प्रश्न 1. संजाल पूर्ण कीजिए: प्रश्न 2. आकृति पूर्ण कीजिए: उत्तर: प्रश्न 3. ऐसे प्रश्न बनाइए जिनके उत्तर निम्नलिखित शब्द हों: (i) मुद्रा (ii) शयन कक्ष। उत्तर: (i) कवि ने छापा मारने वालों से अपने मुँह पर क्या देखने के लिए कहा? (ii) छापा मारने वाले कहाँ घुस गए? प्रश्न 4. आकृति पूर्ण कीजिए: उत्तर: कृति 2: (शब्द संपदा) प्रश्न 1. निम्नलिखित शब्दों के वचन बदलकर लिखिए: (i) मुद्राएँ – ………………………. (ii) अलमारी – ………………………. (iii) चेहरा – ………………………. (iv) सूचना – ………………………. उत्तर: (i) मुद्राएँ – मुद्रा (ii) अलमारी – अलमारियाँ (iii) चेहरा -चेहरे (iv) सूचना -सूचनाएँ प्रश्न 2. निम्नलिखित शब्द-समूहों के लिए एक-एक शब्द लिखिए: (i) किसी व्यक्ति या वस्तु को खोजना – ………………………. (ii) मिट्टी का बर्तन जिसमें घन संग्रह किया जाए – ………………………. उत्तर: (i) ढूँढ़ना (ii) गुल्लक। कृति 3: (सरल अर्थ) प्रश्न. पद्यांश की प्रथम छह पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए। उत्तर: अधिकारियों ने गरजते हुए कहा, ‘हमारा कहने का मतलब आपकी मुद्रा (पैसों-सिक्कों) से है।” कवि ने इसका अर्थ मुख मुद्रा से जोड़कर जवाब दिया, “मुद्राएँ तो आप मेरे मुख पर देख लें।” अधिकारी यह उत्तर सुनकर कुछ सोचने लगे। फिर वे उनके सोने के कमरे में घुस गए और उनके फटे तकिए की रुई नोचने लगे (कि शायद पैसे इसमें छुपाकर रखे हों)। पद्यांश क्र. 3 प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए: कृति 1: (आकलन) प्रश्न 1. आकृति पूर्ण कीजिए: उत्तर: प्रश्न 2. संजाल पूर्ण कीजिए: उत्तर: प्रश्न 3. ऐसे प्रश्न तैयार कीजिए, जिनके अर्थ निम्नलिखित शब्द हों: (i) पलंग (ii) धन। उत्तर: (i) परिच्छेद में सोफे के अलावा सोने-चाँदी से बनी और किस वस्तु का उल्लेख हुआ है? (ii) कवि के घर में क्या बिलकुल नहीं है? कृति 2: (शब्द संपदा) निम्नलिखित शब्दों में उचित उपसर्ग चुनकर शब्द लिखिए: (उप, अप, अ, अभि) (i) यश – ………………………………. (ii) ज्ञान – ………………………………. (iii) मान – ………………………………. (iv) वन – ………………………………. उत्तर (i) यश – अपयश (iii) मान – अभिमान (ii) ज्ञान – अज्ञान (iv) वन – उपवन कृति 3: (सरल अर्थ) प्रश्न 1. उपर्युक्त पद्यांश की अंतिम छह पंक्तियों-‘जिनके घर में ….. डलवा दीजिए’ का सरल अर्थ 25 से 30 शब्दों में लिखिए। उत्तर: जिन लोगों के घरों में सोने-चाँदी के पलंग और सोफे होते हैं, उन्हें आप लोग निकलवाकर ले लेते हैं। ठीक है निकलवा लीजिए (आपका काम ही निकलवा लेना है), पर जिनके घर में (टूटी) कुर्सी भी बैठने के लिए नहीं है, उनके घर में बैठने-सोने के लिए एक तखत की व्यवस्था तो करते जाइए। भाषा अध्ययन (व्याकरण) प्रश्न, सूचनाओं के अनुसार कृतियाँ कीजिए: 1. शब्द भेद: अधोरेखांकित शब्दों के शब्दभेद पहचानकर लिखिए: (i) वे कड़ककर बोले-चाँदी कहाँ है। (ii) यह शोर कौन मचा रहा है? (iii) छापा बहुत बड़ा था। उत्तर: (i) चाँदी – द्रव्यवाचक संज्ञा। (ii) कौन – प्रश्नवाचक सर्वनाम। (iii) बड़ा – गुणवाचक विशेषण। 2. अव्यय: निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए: (i) अंदर (ii) आजकल (iii) अब। उत्तर: (i) वे घर के अंदर चले आए। (ii) आजकल उनके अच्छे दिन नहीं हैं। (iii) यह काम अब उनके वश का नहीं है। 3. संधि: कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
……………….	भोजन + आलय	……………….
अथवा
निश्चय	……………….	……………….

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
भोजनालय	भोजन + आलय	स्वर संधि
अथवा
निश्चय	निः + चय	विसर्ग संधि

4. सहायक क्रिया: निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए: (i) आप हमारे घर में कुछ न पा सकेंगे। (ii) वे निराश होकर चले गए। उत्तर: सहायक क्रिया – मूल रूप सकेंगे – सकना गए – जाना 5. प्रेरणार्थक क्रिया: निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए: (i) देना (ii) सोना। उत्तर: क्रिया – प्रथम प्रेरणार्थक रूप – दुवितीय प्रेरणार्थक रूप (i) देना – दिलाना – दिलवाना (ii) सोना – सुलाना – सुलवाना 6. मुहावरे: (1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए: (i) आँखें खुल जाना (ii) ठहाका लगाना। उत्तर: (i) आँखें खुल जाना। अर्थ: सच्चाई का पता लग जाना। वाक्य: कवि के घर की हालत देखकर छापा मारने वालों की आँखें खुल गई। (ii) ठहाका लगाना। अर्थ: जोर से हँसना। वाक्य: बात-बात पर ठहाका लगाना किसी को अच्छा नहीं लगता। (2) अधोरेखांकित वाक्यांश के लिए उचित मुहावरे का चयन कर वाक्य फिर से लिखिए: (खटका लगा रहना, ताँता लगा रहना) जर्जर बिल्डिंग में रहने वाले लोगों को रात-दिन भय बना रहता है। उत्तर: जर्जर बिल्डिंग में रहने वाले लोगों को रात-दिन खटका लगा रहता है। 7. कारक: निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए: (i) छापा मारने वालों ने घर का कोना-कोना छान मारा। (ii) तकिए से रुई नीचे गिर रही थी। उत्तर: (i) वालों ने – कर्ता कारक। (ii) तकिए से – अपादान कारक। 8. विरामचिह्न: निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए: (a) जिनके घर सोने चाँदी के पलंग और सोफे हैं उन्हें आप निकलवा लेते हैं (ii) वे बोले, क्षमा कीजिए हमें किसी ने गलत सूचना दे दी उत्तर: (i) जिनके घर सोने-चाँदी के पलंग और सोफे हैं उन्हें आप निकलवा लेते हैं। (ii) वे बोले, “क्षमा कीजिए, हमें किसी ने गलत सूचना दे दी।” 9. काल परिवर्तन: निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए: (i) अधिकारियों को गुस्सा आता है। (सामान्य भविष्यकाल) (ii) उन्होंने रसोई में खाली पड़े डिब्बे टटोले। (अपूर्ण वर्तमानकाल) (iii) उनके हृदय में करुण रस समा गया था। (सामान्य वर्तमानकाल) उत्तर: (i) अधिकारियों को गुस्सा आएगा। (ii) वे रसोई में खाली पड़े डिब्बे टटोल रहे हैं। (iii) उनके हृदय में करुण रस समा जाता है। 10. वाक्य भेद: (1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए: (i) उनका खिला हुआ चेहरा मुरझा गया। (ii) उन्होंने रसोईघर की पीपियाँ टटोली, जो खाली थीं। (iii) कनस्तरों को ढूँढा, मटकों को ढूँढा, परंतु कहीं कुछ नहीं मिला। उत्तर: (i) सरल वाक्य (ii) मिश्र वाक्य (iii) संयुक्त वाक्य। (2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए: (i) हाय ! मेरे घर पर छापा पड़ा। (विधानवाचक वाक्य) (ii) तुम हमारी बात नहीं समझे। (प्रश्नवाचक वाक्य) (iii) अर्थ तो मेरी कविताओं में आपको मिल सकता है। (संदेहवाचक वाक्य) उत्तर: (i) मेरे घर पर छापा पड़ा। (ii) क्या तुम हमारी बात समझे? (iii) अर्थ तो शायद मेरी कविताओं में आपको मिल सकता है। 11. वाक्य शुद्धिकरण: निम्नलिखित वाक्यों को शुद्ध करके वाक्य फिर से लिखिए: (i) वे बोले, मैं मेरा काम कर रहे हैं। (ii) इस घर में अनेकों खाली पीपी हैं। उत्तर: (i) वे बोले, मैं अपना काम कर रहा हूँ। (ii) इस घर में अनेक खाली पीपियाँ हैं।

छापा Summary in Hindi

विषय-प्रवेश : आयकर विभाग के अधिकारी प्रामाणिक सूचनाओं के आधार पर अनधिकृत रूप से अर्जित धन का पता लगाने और उसे अधिकार में लेने के लिए छापा मारते हैं। प्रस्तुत कविता में कवि ने अपने घर पर छापा मारने वालों द्वारा छापा मारने के बाद की स्थिति का व्यंग्यात्मक एवं रोचक चित्रण किया है। छापे के दौरान अधिकारियों को वहाँ सोना-चाँदी तो दूर रसोईघर की पीपियों में पेट भरने के लिए जरूरी सामान भी नहीं मिलता। कवि ने कविता के माध्यम से छापा मारने वालों की कार्य-प्रणाली और आम आदमी की आर्थिक स्थिति का वास्तविक चित्रण किया है। इसके साथ ही कवि ने व्यवस्था से एक ज्वलंत प्रश्न भी पूछा है कि जब वह अनधिकृत रूप से अर्जित घन अपने अधिकार में कर लेती है, तो अधिकृत रूप से अर्जित आय से जिनके पेट नहीं भरते, वह उनकी सहायता करने की कुछ व्यवस्था क्यों नहीं करती? छापा कविता का सरल अर्थ [आयकर विभाग वाले कर चोरी करने वालों और नाजायज ढंग से संपत्ति अर्जित करने वाले लोगों के घर और कार्यालय पर छापा मारते हैं। कवि के घर पर छापा पड़ा, तो कवि माँगी गई वस्तुओं को साहित्य में इस्तेमाल किए जाने वाले शब्दों से जोड़कर व्यंग्योक्ति में जबाब देते हैं।] 1. मेरे घर ………………………….उन्हें कैसे दे दूँ। कवि कहते हैं कि मेरे घर पर आयकर विभाग का छापा पड़ा। वह भी कोई छोटा-मोटा नहीं, बहुत बड़ा छापा पड़ा। अधिकारी मेरे घर पर पूछताछ करने के लिए आए। वे सीधे घर में घुस गए और पूछने लगे, “सोना कहाँ रखा है?” कवि उन्हें जबाब देते हैं-सोना! वह तो मेरी आँखों में है, मैं कई रात से सोया नहीं हूँ। अधिकारियों को इस पर गुस्सा आता है। वे प्रश्न को और स्पष्ट करते हैं, “स्वर्ण दो।” लेखक स्वर्ण को सुवर्ण से जोड़ते हैं और जबाब देते हैं कि सुवर्ण तो उन्होंने अपने काव्य में बिखेरे हैं। उसे वे उन्हें कैसे सौंप दें। 2. वे झुंझलाकर …………………………. पहले करूंगा तैयार। अधिकारी कवि का जवाब सुनकर झुंझलाकर कहते हैं, ‘तुम हमारी बात समझे नहीं। हमें तुम्हारा वह अर्थ चाहिए, जिसे तुमने अनधिकृत रूप से अर्जित किया है। कवि अधिकारियों के अर्थ (धन) शब्द को कविता के अर्थ से जोड़कर मुसकराकर जवाब देते हैं कि अर्थ तो मेरी नई कविताओं में आपको मिल सकता है। फिर अधिकारी कवि से छुपाकर रखी गई चाँदी निकालने के लिए कहते हैं। कवि चाँदी का अर्थ चाँदी जैसे सफेद हो गए अपने बालों से जोड़कर कहते हैं, “चाँदी तो मेरे सिर के बालों में आ रही है।” अधिकारी जब कड़ककर पूछते हैं कि उनके नोट (रुपये) कहाँ हैं, तो वे नोट का संबंध विद्यालय की परीक्षा के नोटों से जोड़कर जवाब देते हैं कि परीक्षा के नोट तो वे परीक्षा से एक महीने पहले तैयार करेंगे। 3. वे गरजकर बोले, …………………………. एक ही तत्त्व खाली। अधिकारियों ने गरजते हुए कहा, “हमारा कहने का मतलब आपकी मुद्रा (पैसों-सिक्कों) से है।” कवि ने इसका अर्थ मुख मुद्रा से जोड़कर जवाब दिया, “मुद्राएँ तो आप मेरे मुख पर देख लें।’ अधिकारी यह उत्तर सुनकर कुछ सोचने लगे। फिर वे उनके सोने के कमरे में घुस गए और उनके फटे तकिए की रुई नोचने लगे (कि शायद पैसे इसमें छुपाकर रखे हों)। कवि कहते हैं कि अधिकारियों ने उनकी टूटी हुई अलमारी खोली, उनकी रसोई में खाली पड़े पीपों को टटोला, बच्चों का गुल्लक खोल-खोलकर देखा, पर उन्हें कहीं कुछ भी नहीं मिला। सब कुछ खाली था। 4. कनस्तरों को, …………………………. सूचना दे दी। कवि कहते हैं कि अधिकारियों ने उनके घर में पड़े कनस्तरों और पानी रखने के लिए मटकों तक को टटोला, देखा, पर उन्हें सब खाली मिले। वे कहते हैं कि अधिकारियों ने मेरे घर में ऐसा निर्जन दृश्य देखा तो उनका खिला हुआ चेहरा मुरझा गया। (क्योंकि, उन्होंने सोचा था कि छापे में काफी धन मिलेगा, पर यहाँ तो कहीं कुछ भी नहीं था।) अब अधिकारियों का गुस्सा शांत हो गया था। उनके मन में दया के भाव आ गए थे। कवि से उन्होंने क्षमा माँगी और बताया कि किसी की गलत सूचना पर वे उसके यहाँ आ गए थे। 5. अपनी असफलता …………………………. तो डलवा दीजिए। अधिकारियों को कवि के घर में कुछ न मिला, तो वे पछताने लगे। उनके सिर शर्म से झुक गए। वे वापस जाने लगे, तो कवि ने उन्हें रोककर कहा, “आप मेरी एक बात सुन लीजिए। यदि छापे के दौरान मेरे घर में आपको अधिक धन मिलता, तो आप उसे ले लेते। अब आपने देख लिया कि मेरे घर में कोई धन नहीं है। ऐसी हालत में (मेरी यह स्थिति देखकर) आप मुझे कुछ (धन) देकर तो जाइए। जिन लोगों के घरों में सोने-चाँदी के पलंग और सोफे होते हैं, उन्हें आप लोग निकलवाकर ले लेते हैं। ठीक है निकलवा लीजिए (आपका काम ही निकलवा लेना है), पर जिनके घर में (टूटी) कुर्सी भी बैठने के लिए नहीं है, उनके घर में बैठने-सोने के लिए एक तखत की व्यवस्था तो करते जाइए।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 5 अनोखे राष्ट्रपति Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 5 Anokhe Rashtrapati Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 5 अनोखे राष्ट्रपति Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 5 अनोखे राष्ट्रपति Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए:

(१) संजाल पूर्ण कीजिए:

Answer:

(२) कृति में जानकारी लिखिए:

Answer:

(३) उत्तर लिखिए:

Answer:

(४) निम्नलिखित शब्दों के प्रत्यय और मूलशब्द अलग करके लिखिए:

Answer:

(५) उपसर्ग तथा प्रत्यययुक्त शब्द बनाकर लिखिए:

Answer:

अभिव्यक्ति

‘सादा जीवन, उच्च विचार’ विषय पर अपने विचार लिखिए।
Answer:
सादा जीवन यानी सादगी से भरा जीवन। सादे जीवन में सौंदर्य होता है। ऐसा जीवन तन को ही नहीं मन को भी सुंदर बना देता है। सुंदर शरीर और शांत मन ही उच्च विचार को प्रेरित करता है। यदि व्यक्ति को अपने जीवन में सफल होना है, तो उसे ‘सादा जीवन उच्च विचार’ इस सिद्धांत का पालन करना चाहिए। जीवन का सच्चा लाभ आराम का जीवन बिताने में नहीं, बल्कि महान बनने में है।

सफल महापुरुषों के जीवन में प्रकाश डालने से हमें पता चलता है कि उन्होंने ‘सादा जीवन व उच्च विचार’ को अपने जीवन में उतारा है। जीवन में सादगी लाना बहुत ही बड़ा महान गुण है। इसे स्वीकार करने से व्यक्ति तुच्छ विचारों को अपने हृदय से दूर कर देता है। सादगी से भरा जीवन व्यतीत करने वाले व्यक्ति के पास गहरी संवेदना होती हैं जो व्यक्तित्व को गरिमा प्रदान करती है। इसलिए व्यक्ति को ‘सादा जीवन व उच्च विचार’ इस सिद्धांत को अपने जीवन में उतारना चाहिए।

भाषा बिंदु

(१) निम्नलिखित संधि विच्छेद की संधि कीजिए और भेद लिखिए:

Answer:

(२) निम्नलिखित शब्दों का संधि विच्छेद कीजिए और भेद लिखिए:

Answer:

(३) निम्नलिखित शब्दों का विच्छेद कीजिए और संधि भेद लिखिए:

Answer:

(४) पाठों में आए संधि शब्द छाँटकर उनका विच्छेद कीजिए और संधि का भेद लिखिए।

Answer:

उपयोजित लेखन

‘यदि मैं शिक्षा मंत्री होता —–‘ विषय पर लगभग सौ शब्दों में निबंध उपयोजित लेखन लिखिए।
Answer:
यदि मैं शिक्षा मंत्री होता….. जीवन में शिक्षा का अत्यधिक महत्त्व है। शिक्षा के द्वारा व्यक्ति का मानसिक, सामाजिक, बौद्धिक व आर्थिक विकास होता है। शिक्षा मंत्रालय द्वारा देश के पाठ्यक्रम एवं शिक्षा प्रणाली पर ध्यान रखा जाता है। शिक्षा मंत्री शिक्षा मंत्रालय के प्रमुख होते हैं। देश में शिक्षा प्रणाली सुचारू रूप से कार्यान्वित हो रही है या नहीं, इस पर ध्यान एवं नियंत्रण रखने का कार्य शिक्षा मंत्री करते हैं। सचमुच शिक्षा मंत्री एक बहुत बड़ा महत्त्वपूर्ण पद है। मैं भी भविष्य में बड़ा होकर देश का शिक्षा मंत्री बनना चाहता हूँ।

जब मैं शिक्षा मंत्री बनूँगा; तब मैं संपूर्ण देश में शिक्षा का कार्य सुचारू रूप से हो रहा है या नहीं इस पर ध्यान रखूगा। देश की संपूर्ण शिक्षा प्रणाली में एकरूपता लाने हेतु में सभी शिक्षा मंडलों का एकीकरण करूँगा; जिससे देश में एक ही प्रकार की शिक्षा प्रणाली सभी के लिए उपलब्ध हो सके। आज कई स्कूल एवं महाविद्यालयों की हालत बहुत ही दयनीय है। कई स्कूलों में संसाधनों की कमी है। कई स्कूलों में छात्रों को बैठने के लिए कुर्सियाँ तथा पर्याप्त शैक्षणिक साधन भी नहीं है। कई स्कूलों में पर्याप्त मात्रा में शिक्षक उपलब्ध नहीं हैं। इन सारी समस्याओं को तुरंत सुलझाने के लिए मैं शिक्षा मंत्री होने के नाते एक समिति की स्थापना करूँगा। इससे किसी भी नगर या गाँव का छात्र शिक्षा के मूलभूत अधिकारों से वंचित नहीं रह पाएगा।

संपूर्ण देश के पाठ्यक्रम में मैं समयानुसार परिवर्तन करने हेतु विद्वान सदस्यों की एक समिति गठित करूँगा; ताकि भूमंडलीकरण एवं विज्ञान-तकनीकी के इस युग में भारतीय छात्र आगे ही आगे बढ़ सकें। आज हमारे देश में शिक्षकों को दिया जाने वाला वेतन बहुत ही कम है। इसके लिए मैं शिक्षकों के लिए एक नए वेतनमान प्रणाली की शुरुआत करूँगा, जिससे अच्छे से अच्छे उम्मीदवार शिक्षा क्षेत्र से जुड़कर ज्ञान के प्रचार-प्रसार का पवित्र कार्य करने के लिए आगे आ सकें। अब तो बस, यही मेरा ध्येय है। इसे साकार करने के लिए सर्वप्रथम मुझे मन लगाकर पढ़ना होगा। फिर मैं अपने विचारों को वास्तविक रूप में परिवर्तित कर सकता हूँ।

Hindi Lokvani 10th Std Textbook Solutions Chapter 5 अनोखे राष्ट्रपति Additional Important Questions and Answers

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (१): आकलन कृति

कृति पूर्ण कीजिए।

Answer:

समझकर लिखिए।

Question 1.
सच्चे व्यक्तित्व की विशेषता
Answer:
सच्चे व्यक्तित्व में कुछ जोड़ना घटाना संभव नहीं है।

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
लेखिका ने राजेंद्र बाबू को सर्वप्रथम गद्यात्मक वातावरण में देखा।
Answer:
सत्य

Question 2.
सत्य में से जोड़ना या घटाना असंभव नहीं रहता।
Answer:
असत्य

कृति अ (२) : शब्द संपदा

निम्नलिखित शब्दों के अर्थ गद्यांश में से ढूँढ़कर लिखिए।

1. नजर
2. प्रणाम
3. पक्षी
4. याद

Answer:

1. दृष्टि
2. अभिवादन
3. विहंगम
4. स्मृति

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
व्यक्ति की विशेषता या गुण
Answer:
व्यक्तित्व

Question 2.
शीत ऋतु में होनेवाली छुट्टियाँ
Answer:
शीतावकाश

निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
विहंगम
Answer:
पक्षी, नभ यात्री, सम्यक

Question 2.
गद्यांश में प्रयुक्त एक विलोम शब्द की जोड़ी लिखिए।
Answer:
जोड़ना x घटाना

निम्नलिखित शब्द के उपसर्गयुक्त व प्रत्यययुक्त शब्द बनाइए।

Question 1.
सत्य
Answer:
उपसर्गयुक्त शब्द – असत्य, प्रत्यययुक्त शब्द – सत्यवादी

Question 2.
संभव
Answer:
उपसर्गयुक्त शब्द – असंभव, प्रत्यययुक्त शब्द – संभावित

लिंग बदलिए।

1. बाबू
2. भाई

Answer:

1. बबुआइन
2. बहन

कृति अ (३) : स्वमत अभिव्यक्ति

Question 1.
सच्चे व्यक्तित्व की पहचान का आधार बताइए।
Answer:
सच्चा व्यक्तित्व हर समय वास्तविक होता है। सच्चे व्यक्ति का चरित्र प्रकाश की तरह दिव्य व पावन होता है। उसके चरित्र बल के आलोक से लोगों को प्रेरणा मिलती है। उसके विचार आदर्शवादी होते हैं। वह अपने विचारों से ही स्वयं के चरित्र का निर्माण करता है। वह दूसरों की भावनाओं को समझता है। उसके पास दया, प्रेम, करुणा, क्षमा आदि मानवीय गुण होते हैं। वह सदैव दूसरों के हित के बारे में ही सोचता रहता है।

वह कभी भी स्वयं के स्वार्थ का विचार नहीं करता है। उसका जीवन सादा होता है। ‘सादा जीवन व उच्च विचार’ ही उसके जीवन का मूलमंत्र होता है। सच्चे व्यक्तित्व वाला व्यक्ति दूसरों की परेशानियों को अपने हृदय के भीतर महसूस करता है और दूसरों को पीड़ा से मुक्ति दिलाने हेतु प्रयास करता है। वह स्वयं तकलीफों में रहकर दूसरों के जीवन में खुशियाँ निर्माण करता है। प्रश्न २ (आ) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति पूर्ण कीजिए।

Question 1.

Answer:

कृति आ (२): शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. रोमिल
2. भृकुटी
3. ठुड्डी
4. वेशभूषा

Answer:

1. रोयेंदार
2. भौंह
3. ठोढ़ी
4. पहनावा

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
स्वच्छंद रहने के भाव
Answer:
स्वच्छंदतावाद

विलोम शब्द लिखिए।

1. ग्रामीण x ….
2. आवरण x …..

Answer:

1. ग्रामीण x शहरी
2. आवरण x अनावरण

Question 1.
गद्यांश में प्रयुक्त विलोम शब्द की जोड़ी ढूँढ़कर लिखिए।
Answer:

• दाहिना x बाँया
• ऊपर x नीचे

निम्नलिखित शब्दों के वचन बदलिए।

1. फेंटा
2. धोती
3. टोपी
4. भृकुटी

Answer:

1. फेंटे
2. धोतियाँ
3. टोपियाँ
4. भृकुटियाँ

निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।

1. शरीर
2. दृष्टी

Answer:

1. शारीरिक
2. दृष्टिहीन

निम्नलिखित वाक्यों में विराम चिह्न का उचित प्रयोग कीजिए।

Question 1.
क्या गांधी टोपी की स्थिति और भी विचित्र नहीं थी
Answer:
क्या गांधी टोपी की स्थिति और भी विचित्र नहीं थी?

कृति आ (३) : स्वमत अभिव्यक्ति

Question 1.
‘व्यक्तित्व का आईना होती है वेशभूषा।’ विषय पर अपने विचार लिखिए।
Answer:
व्यक्ति का पहनावा या उसकी वेशभूषा उसके व्यक्तित्व का आईना होती है। वह मानव के संपूर्ण जीवन को प्रभावित करती है। यदि आप किसी औपचारिक मीटिंग या कार्यालय में जा रहे हैं तो आप रंग-बिरंगी टी-शर्ट और शॉर्टस् पहनकर जाते हैं तो आप हँसी के पात्र बन सकते हैं या आपके व्यक्तित्व पर इसका गलत असर पड़ सकता है।

यदि आप अनौपचारिक समारोह या पार्टी में सुट पहन कर जाएंगे, तो भी आप बचकाने लगेंगे। यदि व्यक्ति पदवी या पद में बड़ा है; तो उसकी वेशभूषा उसके अनुसार या उससे अधिक फॉर्मल होनी चाहिए। व्यक्ति को स्वच्छ एवं साफ-सुथरे कपड़े पहनने चाहिए। कपड़े अच्छी तरह से प्रेस होने चाहिए। वेशभूषा सादगी से युक्त होनी चाहिए। स्वामी विवेकानंद धोती, कुर्ता व पगड़ी पहनकर विदेश में गए थे। व्यक्ति को अपनी संस्कृति की वेशभूषा में रहना अधिक उचित और श्रेयस्कर है।

निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति इ (१): आकलन

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हो

Question 1.
भारतीय कृषक
Answer:
राजेंद्र बाबू अपने स्वभाव एवं रहन-सहन में किसका प्रतिनिधित्व करते थे ?

Question 2.
राजेंद्र बाबू
Answer:
लेखिका को किसकी मुखाकृति देखकर ऐसा लगता था मानो उन्हें पहले कहीं देखा है?

सही विकल्प चुनकर वाक्य पूर्ण कीजिए।

Question 1.
राजेंद्र बाबू को देखने वालों को कोई-न-कोई आकृति या व्यक्ति स्मरण हो आता था क्योंकि …..
(अ) उनके शरीर के संपूर्ण गठन में एक असामान्य भारतीय जन की आकृति और गठन की छाया थी।
(आ) उनके शरीर के संपूर्ण गठन में एक सामान्य भारतीय जन की आकृति और गठन की छाया थी।
(इ) उनके शरीर के संपूर्ण गठन में एक महापुरुष की आकृति और गठन की छाया थी।
Answer:
राजेंद्र बाबू को देखने वालों को कोई-न-कोई आकृति या व्यक्ति स्मरण हो आता था क्योंकि उनके शरीर के संपूर्ण गठन में एक सामान्य भारतीय जन की आकृति और गठन की छाया थी।

समझकर लिखिए।

Answer:

कृति इ (२) : शब्द संपदा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:

• साथ – साथ
• रहन – सहन

वचन बदलिए।

1. आकृति
2. अनुभूति
3. संवेदना

Answer:

1. आकृतियाँ
2. अनुभूतियाँ
3. संवेदनाएँ

Question 1.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढकर लिखिए।
Answer:
प्रत्यययुक्त शब्द : व्यापकता, सामान्यता, विशिष्टता प्रत्यययुक्त शब्द : गहराई

Question 2.
‘अनुभव’ इस शब्द में निहित उपसर्ग से अन्य दो शब्द बनाकर लिखिए।
Answer:
अनुभव – उपसर्ग : अनु ।
नए शब्द –
अनुकरण
अनुसरण

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. समान x ……..
2. सामान्य x ….

Answer:

1. समान x असमान
2. सामान्य x असामान्य

नीचे दिए शब्द के लिए श्रुतिसम भिन्नार्थक शब्द लिखिए।

1. समान
2. प्रतिभा
3. उपरांत

Answer:

1. सामान
2. प्रतिमा
3. अपरांत

कृति इ (३) : स्वमत अभिव्यक्ति

Question 1.
‘सादा जीवन उच्च विचार’ विषय पर अपने विचार लिखिए।
Answer:
सादा जीवन यानी सादगी से भरा जीवन। सादे जीवन में सौंदर्य होता है। ऐसा जीवन तन को ही नहीं मन को भी सुंदर बना देता है। सुंदर शरीर और शांत मन ही उच्च विचार को प्रेरित करता है। यदि व्यक्ति को अपने जीवन में सफल होना है, तो उसे ‘सादा जीवन उच्च विचार’ इस सिद्धांत का पालन करना चाहिए। जीवन का सच्चा लाभ आराम का जीवन बिताने में नहीं, बल्कि महान बनने में है।

सफल महापुरुषों के जीवन में प्रकाश डालने से हमें पता चलता है कि उन्होंने ‘सादा जीवन व उच्च विचार’ को अपने जीवन में उतारा है। जीवन में सादगी लाना बहुत ही बड़ा महान गुण है। इसे स्वीकार करने से व्यक्ति तुच्छ विचारों को अपने हृदय से दूर कर देता है। सादगी से भरा जीवन व्यतीत करने वाले व्यक्ति के पास गहरी संवेदना होती हैं जो व्यक्तित्व को गरिमा प्रदान करती है। इसलिए व्यक्ति को ‘सादा जीवन व उच्च विचार’ इस सिद्धांत को अपने जीवन में उतारना चाहिए।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति ई (१) : आकलन कृति
कृति पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित गलत विधान सही करके लिखिए।

Question 1.
राजेंद्र बाबू चक्रधर जी के निजी सचिव थे।
Answer:
चक्रधर जी राजेंद्र बाबू के निजी सचिव थे।

Question 2.
राष्ट्रपति के रूप में राजेंद्र बाबू महिला विद्यापीठ का शिलान्यास करने प्रयाग आए।
Answer:
काँग्रेस के अध्यक्ष के रूप में राजेंद्र बाबू महिला विद्यापीठ का शिलान्यास करने प्रयाग आए।

गद्यांश पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हाँ

Question 1.
सन १९३७
Answer:
महिला विद्यापीठ का शिलान्यास करने राजेंद्र बाबू प्रयाग कब आए थे?

Question 2.
पंद्रह-सोलह
Answer:
राजेंद्र बाबू के संयुक्त परिवार में कितनी पौत्रियाँ थी?

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
राजेंद्र बाबू की पत्नी प्रयाग आती थीं।
Answer:
उनकी पौत्रियाँ प्रयाग में महिला विद्यापीठ के छात्रावास में रहकर पढ़ाई करती थीं। अत: उन्हें मिलने के लिए राजेंद्र बाबू की पत्नी प्रयाग आती थीं।

कृति ई (२) : शब्द संपदा
निम्नलिखित वाक्य में विरामचिह्नों का उचित प्रयोग कीजिए।

Question 1.
राजेंद्र बाबू के पुराने परिधान से अपने आपको प्रसाधित कर कितना कृतार्थता का अनुभव किया था चक्रधर जी ने
Answer:
राजेंद्र बाबू के पुराने परिधान से अपने आपको प्रसाधित कर कितना कृतार्थता का अनुभव किया था चक्रधर जी ने !

लिंग बदलिए।

1. अध्यक्ष
2. पौत्री
3. स्वामी
4. दादा

Answer:

1. अध्यक्षा
2. पौत्र
3. स्वामिनी
4. दादी

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:

• ताने – बाने
• पंद्रह – सोलह
• अस्त – व्यस्तता
• गुरु – शिष्य
• स्वामी – सेवक
• कभी – कभी

निम्नलिखित शब्द के लिए समश्रुतभिन्नार्थक शब्द लिखिए।

1. सज्जा
2. सहेज

Answer:

1. सजा
2. सहज

Question 1.
‘ममतालु’ इस शब्द में से प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द बनाइए।
Answer:
ममतालु : शब्द : ममता प्रत्यय : आलु ।
अन्य शब्द :

• कृपालु
• श्रद्धालु

कृति ई (३) : अभिव्यक्ति

Question 1.
‘नारी जीवन में शिक्षा का अनन्यसाधारण महत्त्व है।’ इस विषय पर अपने विचार लिखिए।
Answer:
जिस प्रकार पुरुष समाज का अहम् हिस्सा है ठीक उसी प्रकार नारी भी समाज का महत्त्वपूर्ण अंग है। समाज की उन्नति के लिए स्वी का महत्त्वपूर्ण योगदान होता है। अत: समाज में नारी शिक्षा को महत्त्व दिया जाता है। स्वतंत्रता के समय हमारे देश में स्त्रियों की शिक्षा की उचित व्यवस्था नहीं थी। धीरे-धीरे स्थिति में बदलाव होना शुरू हुआ।

आज भारत में लड़कियों के लिए अलग स्कूल, महाविद्यालय एवं विश्व विद्यालय खोले जा रहे हैं ताकि ज्यादा से ज्यादा संख्या में वे शिक्षा ग्रहण कर सकें। शिक्षा के कारण नारी अपने अधिकार एवं कर्तव्यों के प्रति सजग हो गई है। वह धीरे-धीरे आत्मनिर्भर बन रहीं हैं। एक पढ़ी-लिखी स्त्री अपने परिवार को ठीक से चला सकती है। वह नौकरी करके अपने परिवार को आर्थिक सहयोग देती है। इस प्रकार अनेक दृष्टियों से नारी जीवन में शिक्षा का अनन्यसाधारण महत्व है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (१): आकलन कृति

कारण लिखिए।

Question 1.
राजेंद्र बाबू की पत्नी की रीढ़ की हड्डी झुक गई थी।
Answer:
क्योंकि उन्हें जमींदार परिवार की परंपरा के अनुसार घंटों तक सिर नीचा करके एकासन बैठना पड़ता था।

कृति पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
कर्तव्य विलास नहीं कर्मनिष्ठा है।
Answer:
सत्य

Question 2.
राजेंद्र बाबू अपनी पौत्रियों को अहंकार से दूर नही रखना चाहते थे।
Answer:
असत्य

उचित जोड़ियाँ मिलाइए।

Question 1.

Answer:
i – ग
ii – घ
iii – ख
iv – क

किसने, किससे कहा?

Question 1.
“महादेवी बहन दिल्ली मेरी नहीं है।”
Answer:
राजेंद्र बाबू ने महादेवी वर्मा से कहा।

कृति उ (२) : शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. निर्देश
2. अहंकार
3. स्वतंत्र

Answer:

1. सूचना
2. घमंड
3. आजाद

निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
स्कूल या कॉलेज के विद्यार्थियों के रहने की जगह
Answer:
छात्रावास

Question 2.
वह स्थान जहाँ छात्र पढ़ाई करते हैं
Answer:
विद्यालय

Question 3.
जहाँ पहुँचना हो
Answer:
गंतव्य

नीचे दिए हुए शब्द के विलोम शब्द लिखिए।

1. अहंकार x ……..
2. स्वतंत्र x ……

Answer:

1. अहंकार x नम्रता
2. स्वतंत्र x परतंत्र

Question 1.
गद्यांश में से प्रत्यययुक्त शब्द ढूंढकर लिखिए।
Answer:
योग्यता
कर्मनिष्ठा

नीचे दिए शब्द के लिए श्रुतिसमभिन्नार्थक लिखिए।

1. चिंता
2. जेल

Answer:

1. चिता
2. जल

कृति उ (३) : स्वमत अभिव्यक्ति

Question 1.
‘कर्तव्य विलास नहीं कर्मनिष्ठा है।’ इस विषय पर अपने विचार लिखिए।
Answer:
कर्तव्य शब्द का अभिप्राय उन कार्यों से होता है जिन्हें करने के लिए व्यक्ति नैतिक रूप से प्रतिबद्ध होता है। व्यक्ति को अपने कर्तव्य के प्रति सदैव जाग्रत रहना चाहिए। अंत:करण की प्रेरणा या उचित कार्य की प्रवृत्ति से कर्तव्य का संबंध होता है। यदि व्यक्ति अपने कर्तव्यों का पालन ठीक से नहीं करता है तो उसका अंत:करण उसे धिक्कारता है। कर्तव्य को प्राथमिकता देकर व्यक्ति को अपना कार्य करते रहना चाहिए। उसे अपने कर्म में लीन होना चाहिए। व्यक्ति को हर काम को पूरे मन से करने पर ही आनंद का अनुभव होता है। प्रश्न ६ (क) निम्नलिखित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऊ (१): आकलन कृति

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –

Question 1.
रसोईघर
Answer:
राजेंद्र बाबू की पत्नी के कमरे से संलग्न क्या बन गया था?

Question 2.
दिल्ली
Answer:
बालिकाओं की दादी ने लेखिका को कहाँ आने का विशेष निमंत्रण दिया था?

कृति पूर्ण कीजिए।

Question 1.

Answer:

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कारण लिखिए।

Question 1.
राष्ट्रपति भवन के हर द्वार पर सलाम ठोंकने वाले सिपाहियों की आँखें विस्मय से खुली रह गई। .
Answer:
क्योंकि लेखिका राष्ट्रपति भवन में एक दरजन सूप लेकर गई थीं। ऐसी भेंट लेकर कोई अतिथि न कभी वहाँ पहुँचा था, न पहुँचेगा।

कृति ऊ (२) : शब्द संपदा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:
फटकने-पछोरने

नीचे दिए हुए शब्द के विलोम लिखिए।

1. विशेष x ………
2. आदेश x …….

Answer:

1. विशेष x साधारण
2. आदेश x प्रार्थना

Question 1.
गद्यांश में से ऐसे दो शब्द ढूँढ़कर लिखिए जिनके वचन परिवर्तित नहीं होते।
Answer:
सूप
आदेश

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
वह भवन जिसमें राष्ट्रपति रहते हैं
Answer:
राष्ट्रपति भवन

Question 2.
अतिथि का सत्कार व उनकी देखभाल
Answer:
आतिथ्य

निम्नलिखित शब्दों के अनेकार्थी शब्द लिखिए।

1. ग्रहण
2. अंक

Answer:

1. पकड़ने की क्रिया, लेने की क्रिया, खाने की क्रिया, मुसीबत
2. संख्या, गोद

कृति ऊ (३): स्वमत अभिव्यक्ति

Question 1.
‘सहधर्मिणी अपने पति के आदर्श एवं सिद्धांत का पालन करती है।’ विषय पर अपने विचार लिखिए।
Answer:
सहधर्मिणी वही कहलाती है जो अपने पति का जीवन के प्रत्येक मोड़ पर साथ देती है। वह अपने पति के आदर्श एवं सिद्धांतों का पालन करती है। यदि उसका पति सादा जीवन उच्च विचार रखता है, तो वह भी उसका अनुसरण करती है। भारत के प्रथम राष्ट्रपति डॉ. राजेंद्र प्रसाद जी का जीवन सादगी से भरा हुआ था। उसीप्रकार उनकी पत्नी ने भी उनके इस सिद्धांत को अपने जीवन में उतारा।

उनके पति कितने भी बड़े पद पर क्यों न हों, फिर भी वे घर के काम-काज को संभालने से पीछे नहीं हटीं। सबके लिए भोजन बनाना एवं सभी के खाने के उपरांत स्वयं खाना खाना, आदि संस्कारों का उन्होंने भलीभांति निर्वाह किया। घर के सभी सदस्य एवं घर पर आने वाले अतिथियों के स्वागत में कोई कमी नहीं छोड़ी। इस प्रकार वह अपने पति के पचिह्नों पर चलकर सभी का दिल जीत लेती है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ए (१): आकलन कृति

गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

Question 1.
लेखिका राष्ट्रपति भवन उस दिन पहुँची जिस दिन ….
Answer:
राजेंद्र बाबू और उनकी सहधर्मिणी का उपवास था।

कारण लिखिए।

Question 1.
लेखिका ने निरन्न भोजन की इच्छा प्रकट की।
Answer:
क्योंकि उपवास के दिन वह अतिथेय का साथ देना उचित समझती थीं।

निम्नलिखित गलत विधान सही करके लिखिए।

Question 1.
जीवन मूल्यों की परख करने वाली दृष्टि के कारण राजेंद्र बाबू को पद्मश्री की उपाधि मिली।
Answer:
जीवन मूल्यों की परख करने वाली दृष्टि के कारण राजेंद्र बाबू को देशरल की उपाधि मिली।

Question 2.
राष्ट्रपति भवन में लेखिका ने मेवे व मिष्ठान्न खाया।
Answer:
राष्ट्रपति भवन में लेखिका ने उबले आलू खाए।

गद्यांश: ७ पाठ्यपुस्तक पृष्ठ क्र. १९ . राजेंद्र बाबू तथा उनकी चरित्र ढलते थे?

कृति ए (२) : शब्द संपदा

निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।

Question 1.
लेखिका ने कहा आज वह साँचा टूट गया है जिसमें कठिन कोमल चरित्र ढलते थे
Answer:
लेखिका ने कहा, “आज वह साँचा टूट गया है, जिसमें कठिन कोमल चरित्र बलते थे।”

Question 2.
दिए गए गद्यांश में से देशज शब्द ढूँढकर लिखिए।
Answer:

• उबले
• आलू
• छलक
• ढलते

निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।

Question 1.
संतोष
Answer:
उपसर्गयुक्त शब्द : असंतोष, प्रत्यय युक्त शब्द : संतोषप्रद

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
जिसका कोई शत्रु ही न हो
Answer:
अजातशत्रु

Question 2.
भोजन ग्रहण न करने का निश्चय
Answer:
उपवास

पर्यायवाची शब्द लिखिए।

1. निरन्न
2. अजातशत्रु

Answer:

1. अन्नरहित
2. शत्रुहीन

कृति ए (३) : स्वमत अभिव्यक्ति

Question 1.
‘व्यक्ति के जीवन-मूल्यों का बड़ा महत्व होता है।’ विषय पर अपने विचार लिखिए।
Answer:
जीवन-मूल्य मनुष्य के जीवन में बहुत आवश्यक होते हैं। जीवन मूल्यों का व्यक्ति के जीवन में महत्त्वपूर्ण योगदान रहता है। व्यक्ति इन्हीं के आधार पर अच्छा-बुरा या सही-गलत की परखा करता है। हमेशा नम्र रहना, सबका आदर करना, सादगी से जीवन बिताना आदि जीवन-मूल्य हैं। सुखद व सफल जीवन व्यतीत करने के लिए व्यक्ति को जीवन-मूल्यों को स्वीकार करना पड़ता है। जीवन-मूल्यों के बिनी व्यक्ति अपने जीवन को अनुशासित नहीं कर सकता और न ही अपने मन को स्वयं के नियंत्रण में रख सकता है। जीवन में अपने व्यक्तित्व को निखारने और सफल बनाने के लिए जीवन-मूल्य अनिवार्य है।

अनोखे राष्ट्रपति Summary in Hindi

अनोखे राष्ट्रपति लेखिका – परिचय
जीवन – परिचय : महादेवी वर्मा जी का जन्म सन १९०७ में उत्तर प्रदेश के फर्रुखाबाद में हुआ। ये एक उच्चकोटि की लेखिका एवं प्रतिभावान कवयित्री थीं। छायावाद के चार प्रमुख स्तंभों में से एक हैं। इनके साहित्य में पीड़ा, करुणा, वेदना आदि पाई जाती है। इन्हें हिंदी साहित्य में आधुनिक युग की मीरा’ कहा जाता है। इनका साहित्य समाज के विभिन्न पहलुओं को दर्शाता है तथा प्रत्येक वर्ग को प्रभावित और प्रेरित करता है।

प्रमुख कृतियाँ : ‘नीहार’, ‘रश्मि’, ‘सांध्यगीत’ (कविता संग्रह), ‘संकल्पिता’, ‘श्रृंखला की कड़ियाँ’, (निबंध), ‘पथ के साथी’, ‘मेरा परिवार’, ‘अतीत के चलचित्र’। (रेखाचित्र)

अनोखे राष्ट्रपति गद्य – परिचय
संस्मरण : संस्मरण साहित्य की एक महत्त्वपूर्ण विधा है। स्मृति के आधार पर किसी विषय पर या किसी व्यक्ति पर लिखित आलेख संस्मरण कहलाता है। यह केवल अतीत की घटनाओं पर आधारित होता है। संस्मरण में चारित्रिक गुणों से युक्त किसी व्यक्ति को याद करते हुए उसके परिवेश के साथ उसका प्रभावशाली वर्णन किया जाता है।

प्रस्तावना : ‘अनोखे राष्ट्रपति’ इस संस्मरण में लेखिका महादेवी वर्मा जी ने भारत के पहले राष्ट्रपति डॉ. राजेंद्र प्रसाद जी के ‘सादा जीवन–उच्च विचार’ गुण से परिचित कराया है। जीवन में सादगी, सहजता व सरल स्वभाव अपनाने से व्यक्ति का व्यक्तित्व ऊँचा उठ सकता है, लेखिका ने इस विचार से सभी को अवगत कराया है।

अनोखे राष्ट्रपति सारांश

‘अनोखे राष्ट्रपति’ यह एक संस्मरण है। इस संस्मरण में लेखिका महादेवी वर्मा जी ने डॉ. राजेंद्र प्रसाद जी के जीवन मूल्यों से पाठकों को परिचित कराया है। डॉ. राजेंद्र प्रसाद जी की वेशभूषा में अत्यंत सादगी थी। स्वतंत्रता पूर्व से ही लेखिका डॉ. राजेंद्र प्रसाद जी को अच्छी तरह से जानती थीं। सन १९३७ में प्रयाग में महिला विद्यापीठ का शिलान्यास डॉ. राजेंद्र प्रसाद जी के करकमलों द्वारा हुआ था। तब उन्होंने लेखिका से निवेदन करते हुए कहा था कि वे अपनी पंद्रह–सोलह पौत्रियों की शिक्षा को लेकर चिंतित हैं। इसलिए उन्हें वे प्रयाग के महिला विद्यापीठ में भर्ती करवाना चाहते हैं।

लेखिका ने भी उनकी पौत्रियों को अपने संरक्षण में ले लिया। इस प्रकार उनकी पौत्रियाँ विद्यापीठ के छात्रावास में रहने लगीं। कभी–कभी डॉ. राजेंद्र प्रसाद और उनकी पत्नी सामान्य भारतीय गृहिणी के समान पति, परिवार तथा परिजनों को खिलाने के उपरांत स्वयं अन्न ग्रहण करती थीं। राष्ट्रपति बनने के पश्चात भी डॉ. राजेंद्र प्रसाद जी को अहंकार ने कभी नहीं छुआ। वे अपनी पौत्रियों को अहंकार से दूर रखना चाहते थे। इसलिए साफ शब्दों में उन्होंने लेखिका से कहा था दिल्ली व राष्ट्रपति भवन उनका नहीं है। उनकी पौत्रियाँ जैसी रहती आई हैं; वैसी ही रहेंगी।

एक बार उनकी पत्नी के द्वारा निमंत्रण मिलने पर लेखिका स्वयं राष्ट्रपति भवन जाती हैं। वहाँ पर भारत के पहले राष्ट्रपति डॉ. राजेंद्र प्रसाद जी को उपवास के उपरांत उबले हुए आलू खाते हुए देखती हैं। उनके सादगी एवं संयम से भरे जीवन को देखकर लेखिका नतमस्तक हो जाती हैं। जीवन–मूल्यों की परख करने वाली दृष्टि राजेंद्र बाबू जी के पास थी। उनके पास मन की स्वच्छता थी। उनका कोई शत्रु नहीं था। इसी कारण उन्हें भारतरल की उपाधि मिली थी। ऐसे अनोखे राष्ट्रपति की संगति में लेखिका स्वयं को धन्य समझती हैं।

अनोखे राष्ट्रपति शब्दार्थ

• भृकुटी – भौंह
• ठुड्डी – ठोढ़ी
• रोमिल – रोयेंदार
• निर्देश – सूचना
• सिरकी – सरकंडे या सरई
• पछोरना – अनाज सूप में रखकर फटककर साफ करना
• निरन्न – निराहार, अन्नरहित
• दृष्टि – नजर
• अभिवादन – प्रणाम
• विहंगम – पक्षी
• स्मृति – याद
• वेशभूषा – पहनावा
• निर्देश – सूचना
• अहंकार – घमंड
• कर्तव्य – कार्य
• स्वतंत्र – आजाद
• अजातशत्रु – शत्रुहीन
• भेंट – उपहार

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 3 Vah Re Hamdard Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 3 वाह रे! हमदर्द Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 3 वाह रे! हमदर्द Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 3 वाह रे! हमदर्द Textbook Questions and Answers

कृति

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
अंतर स्पष्ट कीजिए:
प्राइवेट अस्पताल – सार्वजनिक अस्पताल
१. …………………….. – १. ……………………..
प्राइवेट वार्ड – जनरल वार्ड
१. …………………….. – १. ……………………..
उत्तर:

प्राइवेट अस्पताल	सार्वजनिक अस्पताल
प्राइवेट अस्पताल में अच्छी सुविधाएँ होती हैं।	सार्वजनिक अस्पताल में कई बार सुविधाओं का अभाव होता है।

प्राइवेट वॉर्ड	जनरल वॉर्ड
मिलने का कोई निश्चित समय नहीं होता।	मिलने का निश्चित समय होता है।

प्रश्न 3.
आकृति में लिखिए:

उत्तर:

प्रश्न 4.
कारण लिखिए
a. लेखक को अधिक गुस्सा अपनी पत्नी पर आया ……………………..
b. लेखक कहते हैं कि मेरी दूसरी टाँग उस जगह तोड़ना जहाँ कोई परिचित न हो ……………………..
उत्तर:
a. आगंतुक को रोते देखकर लेखक की पत्नी ने उसे कोई रिश्तेदार या करीबी मित्र समझकर टैक्सीवाले को किराये के पैसे दे दिए थे।
b. उस जगह लेखक के परिचित होंगे तो लेखक से समय-असमय मिलने आकर तंग करेंगे।

प्रश्न 5.
शब्दसमूह के लिए एक शब्द लिखिए:
a. वह स्थान जहाँ अनेक प्रकार के पशु-पक्षी रखे जाते हैं – ……………………..
b. जहाँ मुफ्त में भोजन मिलता है – ……………………..
उत्तर:
(i) चिड़ियाघर
(ii) लंगर (भंडारा)।

प्रश्न 6.
शब्द बनाइए:

उत्तर:

प्रश्न 7.
अभिव्यक्ति- मरीज से मिलने जाते समय कौन-कौन-सी सावधानियां बरतनी चाहिए, लिखिए।
उत्तर:
प्राय: सभी को कभी-न-कभी मरीजों से मिलने अस्पताल में जाना पड़ता है। मरीज से मिलने जाते समय कुछ सावधानियाँ बरतना अत्यंत आवश्यक है। मरीज से मिलने जाते समय हमें इस बात का ध्यान रखना चाहिए कि हमारी वजह से उसे कोई कष्ट न पहुँचे। बच्चे चुलबुले होते हैं। इसलिए मरीज के पास बच्चों को नहीं लेकर जाना चाहिए। बीमारी में दवा और पथ्य के साथ मरीज को आराम व अच्छी नींद आवश्यक है।

अत: मरीज के पास ज्यादा देर तक बैठना, जोर-जोर से बोलना, मरीज की बीमारी के बारे में नकारात्मक बातें करना आदि उचित नहीं है। जहाँ तक हो सके, मरीज का उत्साह बढ़ाना चाहिए। अस्पताल में डॉक्टर मरीज को उसकी आवश्यकता के अनुसार दवाएँ देते हैं। इसलिए मरीज से देसी नुस्खे आजमाने की बातें नहीं करनी चाहिए और न ही डॉक्टर की दवा के बारे में रोगी के मन में किसी तरह का भ्रम पैदा करना चाहिए।

भाषा बिंदु
प्रश्न 1.
निम्नलिखित वाक्यों में आए हुए संज्ञा शब्दों को रेखांकित करके उनके भेद लिखिए:
1. सोनाबाई अपने चार बच्चों के साथ आई। ……………………..
2. गाय बहुत दूध देती है। ……………………..
3. मैं रोज ईश्वर से प्रार्थना करता हैं। ……………………..
4. सैनिकों की टुकड़ी आगे बढ़ी। ……………………..
5. सोना-चाँदी और भी महँगे होते जा रहे हैं। ……………………..
6. गोवा देख मैं तरंगायित हो उठा। ……………………..
7. युवकों का दल बचाव कार्य में लगा था। ……………………..
8. आपने विदेश में भ्रमण तो कर लिया है। ……………………..
9. इस कहानी में भारतीय समाज का चित्रण मिलता है। ……………………..
10. सागर का जल खारा होता है। ……………………..
उत्तर:
1. सोनाबाई – व्यक्तिवाचक बच्चों – जातिवाचक।
2. गाय – जातिवाचक दूध – द्रव्यवाचक।
3. ईश्वर – जातिवाचक प्रार्थना- भाववाचक।
4. सैनिकों – जातिवाचक टुकड़ी – समूहवाचक।
5. सोना-चाँदी – द्रव्यवाचक।
6. गोवा – व्यक्तिवाचक।
7. युवकों – जातिवाचक दल – समूहवाचक। कार्य – भाववाचकी
8. विदेश – जातिवाचक भ्रमण – भाववाचका
9. कहानी – जातिवाचक समाज- समूहवाचक। चित्रण- भाववाचक।
10. सागर – जातिवाचक जल – द्रव्यवाचक।

प्रश्न 2.
पाठ में प्रयुक्त किन्हीं पाँच संज्ञाओं को ढूँढकर उनका वाक्यों में प्रयोग कीजिए।
उत्तर:

• साइकिल – मुझे साइकिल चलाना नहीं आता।
• जोश – कई लोग जोश में होश खो बैठते हैं।
• रेत – आन्या को सागर तट पर रेत का घर बनाना बहुत पसंद है।
• आत्मा – प्रत्येक आत्मा परमात्मा का अंश होती है।
• बंदर – बंदर और बच्चे एक जैसे शरारती होते हैं।

प्रश्न 3.
निम्नलिखित वाक्यों के रिक्त स्थानों में उचित सर्वनामों का प्रयोग कीजिए:
1. …………………….. सार्वजनिक अस्पताल के प्राइवेट वार्ड में हैं।
2. …………………….. बाजार जाओ।
3. …………………….. कारखाने में एक ही विभाग में काम करते थे।
4. इसे लेकर …………………….. क्या करोगे?
5. हृदय …………………….. है; …………………….. उदार हो।
6. लोग …………………….. कमरा स्वच्छ कर रहे हैं।
7. …………………….. रिसॉर्ट हमने पहले से बुक कर लिया है।
8. इसके बाद …………………….. लोग दिन भर पणजी देखते रहे।
9. …………………….. इसके पहले उसे मना करता।
10. काम करने के लिए कहा है …………………….. करो।
उत्तर:
1. वे सार्वजनिक अस्पताल के प्राइवेट वार्ड में हैं।
2. तुम बाजार जाओ।
3. हम कारखाने में एक ही विभाग में काम करते थे।
4. इसे लेकर तुम क्या करोगे।
5. हृदय वही है; तुम उदार हो।
6. लोग स्वयं कमरा साफ कर रहे हैं।
7. मैं रिसॉर्ट हमने पहले से बुक कर लिया है।
8. इसके बाद हम लोग दिन भर पणजी देखते रहे।
9. मैं इसके पहले उसे मना करता।
10. काम करने के लिए कहा है वही करो।

प्रश्न 4.
पाठ में प्रयुक्त सर्वनाम ढूँढ़कर उनका स्वतंत्र वाक्यों में प्रयोग कीजिए।
उत्तर:

• मैंने
  वाक्य: मैंने रेत का घर बनाया।
• तुझे
  वाक्य: शिक्षिका ने तुझे बुलाया है, मनन।
• वे
  वाक्य: वे मेरे चाचा हैं।
• कोई
  वाक्य: बाहर कोई है।
• आप
  वाक्य: कल आप कहाँ थे?
• मुझसे
  वाक्य: माँ ने गुस्से में कहा, मुझसे बात मत करो।
• उन्होंने
  वाक्य: उन्होंने मुझे घर तक पहुँचाया।
• मुझे।
  वाक्य: मुझे नींद आ रही है।

उपयोजित लेखन

प्रश्न.
निम्नलिखित मुद्दों के आधार पर किसी समारोह का वृत्तांत लेखन कीजिए:

• स्थान
• तिथि और समय
• प्रमुख अतिथि
• समारोह
• अतिथि संदेश
• समापन

उत्तर:
गांधी जयंती पर गांधी जी का स्मरण
अकोला, 3 अक्तूबर। अकोला के सरदार पटेल विद्यालय में कल 2 अक्तूबर को गांधी जयंती समारोह का आयोजन किया गया। विद्यालय में समारोह सुबह 10 बजे आयोजित किया जाना था। विद्यालय के विद्यार्थी 9 बजे से ही अपने-अपने स्थान पर बैठ गए थे।

विद्यालय के सभी अध्यापक मंच पर खादी का कुर्ता-पाजामा और खादी टोपी पहनकर विराजमान थे। प्रमुख अतिथि के रूप में शहर के वयोवृद्ध गांधीवादी जनार्दन पाटील उपस्थित थे। मंच पर गांधी जी की तस्वीर सुशोभित हो रही थी।

समारोह की शुरुआत ‘वंदे मातरम्’ गीत से हुई। विद्यालय के प्रधानाचार्य राम रतन जोशी ने उपस्थित लोगों का परिचय दिया और देश के लिए गांधी जी के योगदान की चर्चा की।

प्रमुख अतिथि जनार्दन पाटील ने गांधी जी के जीवन की कई घटनाओं के बारे में बताया। उन्होंने गांधी जी के हमेशा सत्य बोलने के आग्रह के बारे में बताया और कहा कि हमें सत्य के मार्ग पर चलना चाहिए। अपने लाभ के लिए कभी झूठ का सहारा नहीं लेना चाहिए।

विद्यालय के उपमुख्याध्यापक सुधीर देशपांडे ने प्रमुख अतिथि के प्रति आभार व्यक्त किया।

राष्ट्रगान के साथ समारोह का समापन हुआ।

Hindi Lokbharti 10th Textbook Solutions Chapter 3 वाह रे! हमदर्द Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 1 (अ) तथा 1(आ) के लिए

गद्यांश क्र.1

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
जोड़ियाँ मिलाइए:

‘अ’	‘आ’
(i) ऐक्सिडेंट	खुला निमंत्रण
(ii) टाँग	दुर्घटना
(iii) प्राइवेट वार्ड	रेत की थैली
(iv) सार्वजनिक अस्पताल में भरती होना	फ्रैक्चर

उत्तर:

‘अ’	‘आ’
(i) ऐक्सिडेंट	फ्रैक्चर
(ii) टाँग	रेत की थैली
(iii) प्राइवेट वॉर्ड	खुला निमंत्रण
(iv) सार्वजनिक अस्पताल में भरती होना	दुर्घटना

कृति 3: (शब्द संपंदा)

प्रश्न 1.
सूचना के अनुसार लिखिए:

उत्तर:

प्रश्न 2.
गद्यांश में प्रयुक्त उर्दू शब्द ढूँढकर लिखिए।
(i) ………………….
(ii) ………………….
(iii) ………………….
(iv) ………………….
उत्तर:
(i) जवाब
(ii) फिक्र
(ii) तकलीफ
(iv) मरीज।

प्रश्न 3.
गद्यांश में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए।
(i) ………………….
(ii) ………………….
(ii) ………………….
(iv) ………………….
उत्तर:
(ii) मिलने-जुलने
(iii) सही-सलामत
(iv) परिचित-अपरिचित।

प्रश्न 4.
गद्यांश में प्रयुक्त उपसर्गयुक्त शब्द ढूँढ़कर उनके मूल शब्द और उपसर्ग अलग करके लिखिए।
(i) ………………….
(ii) ………………….
(iii) ………………….
उत्तर:
(i) अपरिचित = अ + परिचित।
(ii) दुर्घटना = दुर् + घटना।
(iii) हमदर्दी = हम + दर्दी।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
सार्वजनिक अस्पतालों में मरीजों को होने वाली परेशानियों के विषय में अपने विचार लिखिए।
उत्तर:
देश में अनगिनत निजी अस्पताल हैं, परंतु देश की आधी से अधिक गरीब जनता सार्वजनिक अस्पतालों पर ही निर्भर है। इन अस्पतालों की हालत बहुत दयनीय है। इन अस्पतालों की एक्स-रे आदि मशीनों का कोई ठिकाना नहीं होता। गरीबों को वहाँ इलाज के स्थान पर तकलीफ ही मिलती है। सार्वजनिक अस्पतालों में समय पर डॉक्टर नहीं मिलते। डॉक्टर यदि मिल भी जाता है, तो दवाइयाँ नहीं मिलती।

इसलिए मरीजों को महँगे दामों पर बाहर से दवाएँ खरीदने को बाध्य होना पड़ता है। इसके अलावा डॉक्टर के साथ-साथ अस्पताल के कर्मचारियों का व्यवहार भी रोगियों के प्रति बहुत खराब होता है। ऐसे में इन अस्पतालों में मरीज का ढंग से इलाज नहीं हो पाता। इसलिए लोग इन अस्पतालों में जाने से कतराते हैं।

गद्यांश क्र.2
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
वाक्य पूर्ण कीजिए:
(i) इनकी हमदर्दी में यह बात खास छिपी रहती है ………………………..।
(ii) उस दिन सोनाबाई अपने चार बच्चों के साथ आई तो ………………………..।
उत्तर:
(1) इनकी हमदर्दी में यह बात खास छिपी रहती है कि देख बेटा, वक्त सब पर आता है।
(ii) उस दिन सोनाबाई अपने चार बच्चों के साथ आई तो मुझे लगा कि आज फिर कोई दुर्घटना होगी।

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i) दर्द के मारे एक तो मरीज को वैसे ही यह नहीं आती – [ ]
(ii) कुछ लोग सिर्फ यह निभाने आते हैं – [ ]
(iii) इन लोगों को मरीज से यह नहीं होती – [ ]
(iv) कब मेरी टाँग टूटे, कब वे अपना यह चुकाएँ – [ ]
उत्तर:
(i) दर्द के मारे एक तो मरीज को वैसे ही यह नहीं आती [नींद]
(ii) कुछ लोग सिर्फ यह निभाने आते हैं – [औपचारिकता]
(iii) इन लोगों को मरीज से यह नहीं होती – [हमदर्दी]
(iv) कब मेरी टाँग टूटे, कब वे अपना यह चुकाएँ – [एहसान]

प्रश्न 2.
विधानों के सामने सत्य /असत्य लिखिए:
(i) मैंने तय किया कि आज मैं आँख ही नहीं खोलूँगा।
(ii) ऑफिस के बड़े साहब आए।
(iii) उन्होंने मेरी टाँग के टूटे हिस्से को जोर से दबाया।
(iv) कहिए, अब सिरदर्द कैसा है?
उत्तर:
(i) सत्य
(ii) असत्य
(iii) सत्य
(iv) असत्य।

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का वचन बदलकर लिखिए:
(i) बेटा
(ii) टाँग
(iii) दुर्घटनाएँ
(iv) हिस्सा।
उत्तर:
(i) बेटा – बेटे
(ii) नींद – स्त्रीलिंग
(iii) दुर्घटनाएँ – दुर्घटना
(iv) वक्त – पुल्लिग।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) दिन
(ii) नींद
(ii) फुरसत
(iv) वक्त।
उत्तर:
(i) दिन – पुल्लिग
(ii) आँख = नयन
(iii) फुरसत – स्त्रीलिंग
(iv) वक्त = समय।

प्रश्न 3.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) नींद
(ii) आँख
(iii) दर्द
(iv) वक्त।
उत्तर:
(i) नींद = निद्रा
(iii) दर्द = पीड़ा
(ii) टाँग – टाँगें
(iv) हिस्सा – हिस्से।

गद्यांश क्र. 3

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
कारण लिखिए:

(i) आगंतुक ने जब लेखक से आँख मिलाई तो एकदम चुप हो गया …………………………
उत्तर:
(i) आगंतुक किसी अन्य मरीज से मिलने आया था।

प्रश्न 2.
ऐसे दो प्रश्न बनाइए, जिनके उत्तर: निम्नलिखित हों:

(i) दवा की शीशी
(ii) औपचारिकता।
उत्तर:
(i) सोनाबाई की लड़की ने क्या पटक दी?
(ii) कुछ लोग क्या निभाने की हद कर देते हैं?

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
गद्यांश में उल्लिखित शरीर के अंगों के नाम:

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) सिर
(ii) रोना
(iii) गलत
(iv) गुस्सा।
उत्तर:
(i) सिर x पैर
(ii) रोना x हँसना
(iii) गलत x सही
(iv) गुस्सा x प्यार।

प्रश्न 2.
गद्यांश में प्रयुक्त अंग्रेजी शब्द ढूँढकर लिखिए।
(i) …………………………
(ii) …………………………
(iii) …………………………
(iv) …………………………
उत्तर:
(i) टेबल
(ii) डांस
(iii) टैक्सी
(iv) प्रैक्टिस।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘शकुन-अपशकुन’ के बारे में अपने विचार लिखिए।
उत्तर:
शकुन-अपशकुन समाज में प्रचलित एक अवधारणा है। इसमें यह माना जाता है कि कुछ विशेष प्रकार की परिघटनाएँ हमारे भविष्य का संकेत देती हैं। अनुकूल भविष्यवाणी करने वाले संकेतों को शुभ शकुन और प्रतिकूल भविष्यवाणी करने वाले संकेतों को अपशकुन कहा जाता है। हमारे देश में ही नहीं, अपितु संसार भर में लोग शकुन-अपशकुन पर विश्वास करते हैं। भारतीय संस्कृति में शकुन-अपशकुन का वर्णन वेदों, पुराणों और धार्मिक ग्रंथों में भी मिलता है।

काली बिल्ली द्वारा रास्ता काट जाना, किसी कार्य को आरंभ करते समय किसी का छींक देना, घर से बाहर जाते हुए व्यक्ति को किसी के द्वारा टोका जाना आदि समाज में बहुप्रचलित अपशकुन हैं। इन अपशकुनों को मानने वालों की संख्या कम नहीं है। इन अपशकुनों के चक्कर में आकर कभी-कभी लोगों को हानि भी उठानी पड़ती है, फिर भी वे इन्हें मानने से नहीं चूकते। ये मान्यताएँ मनुष्य को कमजोर बनाती हैं। वैज्ञानिक दृष्टि से इन शकुन-अपशकुनों को अंधविश्वास ही माना जाता है।

गद्यांश क्र.4

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
कारण लिखिए:

(i) लेखक ने बड़ी मुश्किल से कवि लपकानंद को विदा किया …………………………
उत्तर:
(i) कवि लपकानंद जब कविता सुनाना शुरू करते, तो रुकने का नाम नहीं लेते थे।

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
ऐसे दो प्रश्न बनाइए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) डायरी
(ii) बड़े बेवफा।
उत्तर:
(i) कवि ने झोले से क्या निकाली?
(ii) हमदर्दी जताने वाले कैसे होते हैं?

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त शब्द-युग्म ढूंढकर उनको वाक्यों में प्रयोग कीजिए।
(i) …………………………
(ii) …………………………
उत्तर:
(i) दस-बीस – गोदाम में दस-बीस किलो गेहूँ पड़ा है।
(ii) चार-पाँच – चार-पाँच लड़कों को भेजो, कक्षा का फर्नीचर बाहर निकलवाना है।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
कवियों की कविता सुनाने की आदत के बारे में अपने विचार लिखिए।
उत्तर:
कवि दो प्रकार के होते हैं। एक वे, जो सचमुच कवि होते हैं और अपने विचारों को मथकर उन्हें सुंदर और सुरुचिपूर्ण शब्दों के माध्यम से कागज पर उतारते हैं। उनकी कविता सुनकर श्रोता को आनंद के साथ-साथ एक दिशा भी मिलती है। दूसरे प्रकार के कवि वे होते हैं, जो अंत:करण से कवि नहीं होते। वे जबरन कवि बनकर कविता लिखना चाहते हैं। इनकी कविता कविता न होकर शब्दों का बेतरतीब समूह होती है।

जोड़-तोड़कर कविता तैयार करते ही ये श्रोता की तलाश करने लगते हैं और जो भी सामने मिल जाता है, उसे अपनी कविता सुनाए बिना नहीं छोड़ते। इनकी कविता सुनने के लिए कोई आसानी से तैयार नहीं होता। पर विद्वान कवि कभी अपनी कविता सुनाने की कोशिश नहीं करते। उनकी कविता सारगर्मित होती है और वे हर किसी को कविता सुनाते नहीं फिरते।

भाषा अध्ययन (व्याकरण)

प्रश्न.
सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
निम्नलिखित वाक्यों में अधोरेखांकित शब्दों के शब्दभेद पहचानकर लिखिए:
(i) मैं अपनी टाँगों की ओर देखता हूँ।
(ii) मेरे दिमाग में एक नये मुहावरे का जन्म हुआ।
(iii) सोनाबाई के बच्चे खेलने लगे।
उत्तर:
(i) मैं – पुरुषवाचक सर्वनाम।
(ii) नये – गुणवाचक विशेषण।
(iii) सोनाबाई – व्यक्तिवाचक संज्ञा।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) अकसर
(ii) इर्द-गिर्द
(iii) धीरे-धीरे।
उत्तर:
(i) मैं लपकानंद को देखकर अकसर भाग खड़ा होता हूँ।
(ii) मेरे इर्द-गिर्द अनेक लोग खड़े थे।
(iii) बड़े बाबू धीरे-धीरे मुझे हिलाने लगे।

3. संधि:
कृति पूर्ण कीजिए:।

संधि शब्द	संधि विच्छेद	संधि भेद
………………..	नै + इका	………………..
अथवा
दुर्बल	………………..	………………..

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
नायिका	नै + इका	स्वर संधि
अथवा
दुर्बल	दुः + बल	विसर्ग संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) अस्पताल का खयाल आते ही में काँप उठा।
(ii) कोई भी आए मैं चुपचाप पड़ा रहूँगा।
(iii) बच्चे खेलने लगे।
उत्तर:
सहायक क्रिया – मूल रूप
(i) उठा – उठना
(ii) रहूँगा – रहना
(iii) लगे – लगना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय ‘ प्रेरणार्थक रूप लिखिए:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) मानना
(ii) लिखना
(ii) जलना

उत्तर:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) मानना	मनाना	मनवाना
(ii) लिखना	लिखाना	लिखवाना
(ii) जलना	जलाना	जलवाना

6. मुहावरे:
(1) निम्नलिखित कहावत का अर्थ लिखिए और वाक्य में प्रयोग कीजिए:
ढाक के तीन पात।
अर्थ: सदा एक-सी स्थिति।
वाक्य: छगनलाल ने सालभर में कई व्यवसाय बदले, पर हालत आज भी वही है ढाक के तीन पात।

(2) अधोरेखांकित वाक्यांश के लिए उचित मुहावरे का चयन कर वाक्य फिर से लिखिए:
सुमधुर गायन सुनकर श्रोताओं ने गायक की प्रशंसा की। (सराहना करना, बोलबाला होना)
उत्तर:
अर्थ: सराहना करना।
वाक्य: सुमधुर गायन सुनकर श्रोताओं ने गायक की सराहना की।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उनका भेद लिखिए:
(i) मैंने उन्हें जल्दी से चाय पिलाई।
(ii) आप अस्पताल में हैं।
उत्तर:
(i) मैंने – कर्ता कारक
(ii) अस्पताल में – अधिकरण कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) वे मुझे ऐसे देख रहे थे मानो उनकी एक आँख पूछ रही हो कहो कविता कैसी रही और दूसरी आँख पूछ रही हो बोल बेटा अब भी मुझसे भागेगा
(ii) सोनाबाई ने लड़की को घूरा फिर हँसते हुए बोली भैया पेड़े खिलाओ दवा गिरना शुभ होता है
(iii) मैंने कराहते हुए पूछा मैं कहाँ हूँ
उत्तर:
(i) वे मुझे ऐसे देख रहे थे, मानो उनकी एक आँख पूछ रही हो, ‘कहो, कविता कैसी रही?’ और दूसरी आँख पूछ रही हो, बोल, बेटा! अब भी मुझसे भागेगा?’
(ii) सोनाबाई ने लड़की को घूरा, फिर हँसते हुए बोली, “भैया, पेड़े खिलाओ, दवा गिरना शुभ होता है।”
(iii) मैंने कराहते हुए पूछा, “मैं कहाँ हूँ?”

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) एक चेहरा बड़ी तेजी से जवाब देता है। (पूर्ण वर्तमानकाल)
(ii) मेरी आँख खुलते ही सबके चेहरों पर प्रसन्नता की लहर दौड़ जाती है। (सामान्य भूतकाल)
(iii) सोनाबाई फिर आती है। (सामान्य भविष्यकाल)
उत्तर:
(i) एक चेहरे ने बड़ी तेजी से जवाब दिया है।
(ii) मेरी आँख खुलते ही सबके चेहरों पर प्रसन्नता की लहर दौड़ गई।
(iii) सोनाबाई फिर आएगी।

10. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) जब आँख खुली तो मैंने स्वयं को बिस्तर पर पाया।
(ii) मैंने उसे जल्दी से चाय पिलाई और विदा किया।
उत्तर:
(i) मिश्र वाक्य
(ii) संयुक्त वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) मेरी टाँग टूटना एक दुर्घटना थी। (प्रश्नवाचक)
(ii) आज फिर कोई दुर्घटना होगी। (इच्छावाचक)
उत्तर:
(i) क्या मेरी टाँग टूटना एक दुर्घटना थी?
(ii) आज फिर कोई दुर्घटना न हो।

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) अब मैं अपने टाँगों की ओर देखता है।
(ii) सोनाबाई से एक पल लड़की को घूरी।
(iii) गुप्ता जी की कमरा शायद बगल में हैं।
उत्तर:
(i) अब मैं अपनी टाँगों की ओर देखता हूँ।
(ii) सोनाबाई ने एक पल लड़की को घूरा।
(iii) गुप्ता जी का कमरा शायद बगल में है।

उपक्रम/कृति/परियोजना

किसी सार्वजनिक या ग्राम पंचायत की सभा में अंगदान’ के बारे में अपने विचार प्रस्तुत कीजिए।
उत्तर:
आदरणीय सरपंच महोदय, पंच परमेश्वर तथा अन्य सभी उपस्थित सज्जनो, आज मैं आप सभी के समक्ष अंगदान के विषय में अपने विचार प्रस्तुत करना चाहता हूँ। अंगदान वह प्रक्रिया है, जिसमें किसी व्यक्ति के शरीर का कोई अंग उसकी व उसके परिवार की सहमति से हटाकर किसी अन्य व्यक्ति को दे दिया जाता है। इस प्रक्रिया द्वारा एक व्यक्ति को नया जीवन मिल जाता है।

प्रत्यारोपण के लिए गुर्दे, लिवर, फेफड़े, हृदय, हड्डियाँ, अस्थि मज्जा, त्वचा, अग्न्याशय, कॉर्निया, आँत आदि का दान दिया जाता है। अंगदान की प्रक्रिया को दुनिया भर में प्रोत्साहित किया जाता है। भारत में यह कानूनन वैध है। अंगदान समाज के लिए एक चमत्कार साबित हुआ है। हालाँकि माँग की तुलना में आपूर्ति बहुत कम है।

वाह रे! हमदर्द Summary in Hindi

वाह रे! हमदर्द विषय-प्रवेश :

अस्पताल में इलाज के लिए भर्ती हुए मरीज को देखने जाने की परंपरा समाज में पुरानी है। इससे मरीज को खुशी होती है और कुछ समय के लिए उसका ध्यान अपने कष्ट से हट जाता है। पर कुछ मिलने वाले ऐसे होते हैं, जो मरीज के लिए परेशानी का कारण बन जाते हैं। प्रस्तुत हास्य-व्यंग्यात्मक निबंध में लेखक ने दुर्घटना के माध्यम से एक ऐसी ही स्थिति का चित्रण किया है। निबंध में जहाँ एक ओर समाज में विद्यमान परोपकार की भावना पर प्रकाश डाला गया है, वहीं दूसरी ओर बड़े ही रोचक ढंग से हमदर्द लोगों की मानसिकता को भी चित्रित किया गया है। कभी-कभी हमदर्दी भी रोगी की मानसिक पीड़ा का कारण बन जाती है।

वाह रे! हमदर्द मुहावरे – अर्थ

• ड़ाना – बाधा डालना।
• काँप उठना – भयभीत होना।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 2 Do Laghu Kathayen Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 2 दो लघुकथाएँ Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 2 दो लघुकथाएँ Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 2 दो लघुकथाएँ Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 3 (अ) के लिए

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
उत्तर लिखिए:

उत्तर:

प्रश्न 3.
कारण लिखिए:
१. युवक को पहले नौकरी न मिल सकी …………………….. .
२. आखिरकार अधिकारियों द्वारा युवक का चयन कर लिया गया …………………….. .
उत्तर:
(i) युवक को पहले नौकरी न मिल सकी, क्योंकि हर जगह भ्रष्टाचार, रिश्वत का बोलबाला था।
(ii) आखिरकार अधिकारियों द्वारा युवक का चयन कर लिया गया, क्योंकि भीतर बैठे अधिकारियों ने गंभीरता से विचार विमर्श करने के बाद युवक के सही उत्तर की दाद दी थी।

प्रश्न 4.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 5.
प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

(अभिव्यक्ति)
‘भ्रष्टाचार एक कलंक’ विषय पर अपने विचार लिखिए।
उत्तर:
भ्रष्टाचार का अर्थ है दूषित आचार या जो आचार बिगड़ गया हो। आज हमारे जीवन के हर क्षेत्र में भ्रष्टाचार व्याप्त है। आए दिन नेताओं के भ्रष्टाचार के समाचार आते रहते हैं। प्रष्टाचार के आरोप में कितने नेता जेल काट रहे हैं। ये जनता के पैसे हड़प कर गए, पर इन्हें शर्म तक नहीं आती। आज हमारे देश में तेजी से भोगवादी संस्कृति फैल रही है। लोगों में रातोरात धनवान बनने की लालसा जोर पकड़ रही है।

चारों ओर घन बटोरने के लिए धोखाधड़ी, छल-कपट, किए जा रहे हैं। अपनी भौतिक समृद्धि बढ़ाने के लिए लोगों ने भ्रष्टाचार को शिष्टाचार बना लिया है। छोटे से छोटे काम के लिए लोगों को रिश्वत का सहारा लेना पड़ता है। शिक्षा का पवित्र क्षेत्र भी इससे अछूता नहीं रह गया है। लोगों में देशभक्ति और कर्तव्यनिष्ठा की भावना घटती जा रही है। भ्रष्टाचार राष्ट्रीय जीवन के लिए अभिशाप बन गया है। हमें आत्मनिरीक्षण करने की आवश्यकता है। भ्रष्टाचार एक कलंक है। इस कलंक को मिटाना जरूरी है। हम सबको इसके लिए निष्ठापूर्वक कार्य करने की जरूरत है।

भाषा बिंदु

प्रश्न 1.
अर्थ के आधार पर निम्न वाक्यों के भेद लिखिए:
1. क्या पैसा कमाने के लिए गलत रास्ता चुनना उचित है? – [ ]
2. इस वर्ष भीषण गरमी पड़ रही थी। – [ ]
3. आप उन गहनों की चिंता न करें। – [ ]
4. सुनील, जरा ड्राइवर को बुलाओ। – [ ]
5. अपने समय के लेखकों में आप किन्हें पसंद करते हैं? – [ ]
6. सैकड़ों मनुष्यों ने भोजन किया। – [ ]
7. हाय ! कितनी निर्दयी हूँ मैं। – [ ]
8. काकी उठो, भोजन कर लो। – [ ]
9. वाह ! कैसी सुगंध है। – [ ]
10. तुम्हारी बात मुझे अच्छी नहीं लगी। – [ ]
उत्तर:
1. क्या पैसा कमाने के लिए गलत रास्ता चुनना उचित है? – [प्रश्नवाचक वाक्य]
2. इस वर्ष भीषण गरमी पड़ रही थी। – [विधानवाचक वाक्य]
3. आप उन गहनों की चिंता न करें। – [निषेधवाचक वाक्य]
4. सुनील, जरा ड्राइवर को बुलाओ। – [आज्ञावाचक वाक्य]
5. अपने समय के लेखकों में आप किन्हें पसंद करते हैं? – [प्रश्नवाचक वाक्य]
6. सैकड़ों मनुष्यों ने भोजन किया। – [विधानवाचक वाक्य]
7. हाय! कितनी निर्दयी हूँ मैं – [विस्मयादिबोधक वाक्य]
8. काकी उठो, भोजन कर लो। – [आज्ञावाचक वाक्य]
9. वाह! कैसी सुगंध है। [विस्मयादिबोधक वाक्य]
10. तुम्हारी बात मुझे अच्छी नहीं लगी। – [निषेधवाचक वाक्य]

प्रश्न 2.
कोष्ठक की सूचना के अनुसार निम्न वाक्यों में अर्थ के आधार पर परिवर्तन कीजिए:
a. थोड़ी बातें हुईं। (निषेधार्थक वाक्य)
b. मानू इतना ही बोल सकी। (प्रश्नार्थक वाक्य)
c. मैं आज रात का खाना नहीं खाऊँगा। (विधानार्थक वाक्य)
d. गाय ने दूध देना बंद कर दिया। (विस्मयार्थक वाक्य)
e. तुम्हें अपना ख्याल रखना चाहिए। (आज्ञार्थक वाक्य)
उत्तर:
a. थोड़ी भी बातें नहीं हुई।
b. क्या मानू इतना ही बोल सकी?
c. मैं आज रात का खाना खाऊँगा।
d. अरे! गाय ने दूध देना बंद कर दिया।
e. तुम अपना ख्याल रखो।

प्रश्न 3.
प्रथम इकाई के पाठों में से अर्थ के आधार पर विभिन्न प्रकार के पाँच वाक्य ढूँढ़कर लिखिए।
उत्तर:
(1) करामत अली इधर दो-चार दिनों से अस्वस्थ था। (विधानवाचक वाक्य)
(2) इन्हें मरीज से हमदर्दी नहीं होती। (निषेधवाचक वाक्य)
(3) तो उसकी सजा इसे लाठियों से दी गई? (प्रश्नवाचक वाक्य)
(4) “जाओ, लक्ष्मी का राशन ले आओ। (आज्ञावाचक वाक्य)
(5) हे ईश्वर, अगर मेरी दूसरी टाँग भी तोड़नी हो तो जरूर तोड़ें, मगर इस जगह जहाँ मेरा कोई न हो। (इच्छावाचक वाक्य)

प्रश्न 4.
रचना के आधार पर वाक्यों के भेद पहचानकर कोष्ठक में लिखिए:
a. अधिकारियों के चेहरे पर हलकी-सी मुस्कान और उत्सुकता छा गई। [………………….]
b. हर ओर से अब वह निराश हो गया था। [………………….]
c. उसे देख-देख बड़ा जी करता कि मौका मिलते ही उसे चलाऊँ। [………………….]
d. वह बूढ़ी काकी पर झपटी और उन्हें दोनों हाथों से झटककर बोली। [………………….]
e. मोटे तौर पर दो वर्ग किए जा सकते हैं। [………………….]
f. अभी समाज में यह चल रहा है क्योंकि लोग अपनी आजीविका शरीर श्रम से चलाते हैं [………………….]
उत्तर:
a. सरल वाक्य।
b. सरल वाक्य।
c. मिश्र वाक्य।
d. संयुक्त वाक्य।
e. सरल वाक्या
f. संयुक्त वाक्य।

प्रश्न 5.
रचना के आधार पर विभिन्न प्रकार के तीन-तीन वाक्य पाठों से ढूँढकर लिखिए।
उत्तर:
(i) सरल वाक्य:
(1) आज उसे साक्षात्कार के लिए जाना है।
(2) अब तक उसके हिस्से में सिर्फ असफलता ही आई थी।
(3) रिश्वत भ्रष्टाचार की बहन है।

(ii) संयुक्त वाक्य:
(1) अधिकारियों के चेहरे पर हल्की-सी मुस्कान आई और उत्सुकता छा गई।
(2) व्यक्ति समाज को कम-से-कम देने की इच्छा रखता है लेकिन समाज से अधिक-से-अधिक लेने की इच्छा रखता है।
(3) विषमता दूर करने में कानून भी कुछ मदद देता है, परंतु कानून से मानवोचित गुणों का विकास नहीं हो सकता।

(iii) मिश्र वाक्य:
(1) भ्रष्टाचार एक ऐसा कीड़ा है, जो देश को घुन की तरह खा रहा है।
(2) वह जानता था कि यहाँ भी उसका चयन नहीं होगा।
(3) संपत्ति तो वे ही चीजें हो सकती हैं, जो किसी-न-किसी रूप में मनुष्य के उपयोग में आती हैं।

उपयोजित लेखन

‘जल है तो कल हैं’ विषय पर अस्सी से सौ शब्दों में निबंध लिखिए।
उत्तर:
हवा के पश्चात प्राणियों को जीवित रहने के लिए जिस चीज की आवश्यकता होती है वह है जल। जल के बिना प्राणी अधिक दिनों तक नहीं जी सकता। इसीलिए कहा जाता है कि जल ही जीवन है।

जल हमें कुओं, तालाबों और नदियों से मिलता है। वर्षा का जंल तालाबों, झीलों आदि में जमा होता है। कुछ पानी भूगर्भ में चला जाता है। शेष पानी नदियों में होता हुआ समुद्र में चला जाता हैं। भूगर्भ का पानी कुओं के माध्यम से पीने के काम में लाया जाता हैं। नदियों और झीलों का पानी शुद्ध किया जाता है। इसके बाद वह पीने लायक होता है। गाँवों में अधिकतर कुओं के पानी से ही काम चलाया जाता है। बड़े-बड़े शहरों में नदियों और झीलों के पानी को शुद्ध करके पीने के काम में लाया जाता है।

हर व्यक्ति को पानी की आवश्यकता होती है। बिना पानी के किसी का काम नहीं चल सकता। निरंतर बढ़ती हुई जनसंख्या के कारण आज पानी की समस्या विकट हो गई है। इसका कारण है पानी का अंधाधुंध उपयोग। गाँवों में सिंचाई के लिए अंधाधुंध तरीके से भू-जल का दोहन किया जा रहा है। इस कारण पानी का स्तर निरंतर नीचे-ही-नीचे जा रहा है। कहीं-कहीं तो कुओं में पानी ही नहीं रहा।

पीने का पानी कम होने का कारण वर्षा का निरंतर कम होते जाना है। पेड़ों और जंगलों की अंधाधुंध कटाई इसका प्रमुख कारण है। आए दिन पानी के लिए झगड़े होते रहते हैं। देश के अंदर एक राज्य दूसरे राज्य से पानी के लिए झगड़ता है। एक देश दूसरे देश से जल के लिए लड़ता है। पानी की समस्या सारी दुनिया में है। कुछ लोग तो यहाँ तक कहते हैं कि भविष्य में पानी के लिए महायुद्ध होगा।

पानी का अशुद्ध होना भी पानी की कमी का एक कारण है। अशुद्ध पानी से तरह-तरह की जानलेवा बीमारियाँ होती हैं। शहरों के किनारे बहने वाली नदियों में शहर की सारी गंदगी डाली जा रही है। कल-कारखानों का विषैला पानी नदियों में प्रवाहित होता है। वही पानी पीने के लिए दिया जाता है। इससे लोगों को तरह-तरह की बीमारियाँ होती है। _सरकार की ओर से हर व्यक्ति तक पर्याप्त शुद्ध पेय जल पहुँचाने का अथक प्रयास किया जा रहा है। फिर भी अभी इस दिशा में और प्रयास करने की जरूरत है। हर व्यक्ति इस उम्मीद में है कि उसे पर्याप्त शुद्ध जल उपलब्ध हो। आखिर जल है, तो कल है।

Hindi Lokbharti 10th Textbook Solutions Chapter 2 दो लघुकथाएँ Additional Important Questions and Answers

गद्यांश क्र. 1
प्रश्न. निम्नलितिर पठित गट्यांश पढ़कर दी गई सूचनाओं के कवियों कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
निम्नलिखित के लिए परिच्छेद में प्रयुक्त शब्द लिखिए:
(i) आराम –
(ii) गरीब
(iii) शांति –
(iv) बेढंगा
उत्तर:
(i) आराम – राहत
(ii) गरीब – कंगाल
(iii) शांति – सुकून
(iv) बेढंगा – लिजलिजा।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘छोटे दुकानदारों और बड़े दुकानदारों से चीजें खरीदते समय हमारा व्यवहार’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
हम अधिकतर दिखावे में विश्वास करते हैं। जब हम बड़ेबड़े शॉपिंग सेंटरों और मॉल में जाते हैं, तो वस्तुओं की कीमतों को लेकर हम कभी मोल-भाव नहीं करते। वहाँ सैकड़ों लोग सामान खरीदते हैं और कीमतों को लेकर कोई मोल-भाव नहीं करता। वहाँ भाव ज्यादा होते हुए भी उसके बारे में पूछने की हिम्मत नहीं होती। क्योंकि वहाँ इज्जत का सवाल होता है। कभी-कभी तो वहाँ ठगाकर लोग चले आते हैं, पर शर्म के मारे कुछ नहीं बोलते। मगर वही लोग बाजार में छोटे दुकानदारों या खोमचेवालों से दो-चार रुपए के लिए झिक-झिक करते देखे जाते हैं। यहाँ उनको.अपनी इज्जत की परवाह नहीं रहती। क्योंकि यहाँ बड़े ग्राहकों के सामने उनको अपने इस व्यवहार पर झंपने का डर नहीं रहता। यहाँ वे अपने को बड़ा दिखाते हैं। क्योंकि सामने गरीब आदमी होता है।

हमें अपनी सोच में बदलाव लाने की जरूरत है। छोटे व्यापारियों या गरीब खोमचेवालों से खरीदे जाने वाले सामान में मोल-भाव करने में झिक-झिक करना उचित नहीं है।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश को पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

*(iii) प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

प्रश्न 4.
आकृति पूर्ण कीजिए:
(i) उसके प्रमाणपत्र उसे सफलता दिलाने में ये रहे – [ ]
(ii) वह भ्रष्ट सामाजिक व्यवस्था को यह करता था – [ ]
(iii) उसके तर्क में अधिकारियों को यह महसूस होने लगी – [ ]
(iv) उसके अनुसार रिश्वत का भ्रष्टाचार से यह रिश्ता है – [ ]
उत्तर:
(i) उसके प्रमाणपत्र उसे सफलता दिलाने में ये रहे – [नाकामयाब]
(ii) वह भ्रष्ट सामाजिक व्यवस्था को यह करता था – [कोसता था]
(iii) उसके तर्क में अधिकारियों को यह महसूस होने लगी – [रुचि]
(iv) उसके अनुसार रिश्वत का भ्रष्टाचार से यह रिश्ता है। – [रिश्वत भ्रष्टाचार की बहन]

उपक्रम/कृति/परियोजना

श्रवणीय
बालक/बालिकाओं से संबंधित कोई ऐतिहासिक कहानी सुनकर उसका रूपांतरण संवाद में करके कक्षा में सुनाइए।

पठनीय
अपनी पसंद की कोई सामाजिक ई-बुक पढ़िए।

संभाषणीय
‘शहर और महानगर का यांत्रिक जीवन’ विषय पर बातचीत कीजिए।

लेखनीय
पहाड़ों पर रहने वाले लोगों की जीवन शैली की जानकारी प्राप्त करके अपनी जीवन शैली से उसकी तुलना करते हुए लिखिए।

मुद्दे:
(i) घर-द्वार
(ii) रहन-सहन
(iii) खान-पान
(iv) रीति-रिवाज
(v) जीवन यापन के साधन
(vi) यातायात व्यवस्था।

दो लघुकथाएँ Summary in Hindi

विषय-प्रवेश : प्रस्तुत पाठ में दो लघुकथाएँ दी गई हैं। प्रथम लघुकथा में हमारी मानसिक प्रवृत्ति के बारे में बताया गया है। लेखक ने इसके माध्यम से यह दर्शाया है कि जब लोग बड़ी-बड़ी दुकानों, मॉल या बड़े होटलों में जाते हैं, तो वहाँ वे सामानों के निश्चित मूल्यों के बारे में कोई मोल-भाव नहीं करते। मांगे गए पैसे शौक से अदा करके चले आते हैं। पर छोटे दुकानदारों या खोमचे वालों से सामान खरीदते समय लोगों का व्यवहार बिलकुल बदल जाता है। लोग उनसे दो-एक रुपये कम करने के बारे में बहस पर उतर आते हैं। हमें यह मानसिकता बदलनी चाहिए।

दूसरी लघुकथा में रिश्वतखोरी और भ्रष्टाचार के शिकार एक युवक के बारे में बताया गया है। उसके सामने भ्रष्ट सामाजिक व्यवस्था को कोसने के अलावा कोई चारा नहीं रहता। पर सत्य का पालन करना उसे एक दिन अपने लक्ष्य तक पहुँचा देता है।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 6 Giridhar Nagar Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 6 गिरिधर नागर Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 6 गिरिधर नागर Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 6 गिरिधर नागर Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए)
सूचनानुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
इस अर्थ में आए शब्द लिखिए:

	अर्थ	शब्द
i.	दासी	………….
ii.	साजन	………….
iii.	बार-बार	………….
iv.	आकाश	………….

उत्तर:

	अर्थ	शब्द
i.	दासी	चेरी
ii.	साजन	पति
iii.	बार-बार	बेर-बेर
iv.	आकाश	अंबर

प्रश्न 4.
कन्हैया के नाम

उत्तर:

प्रश्न 5.
दूसरे पद का सरल अर्थ लिखिए।
उत्तर:
(i) निकट – ढिग
(ii) साजन – पति।

उपयोजित लेखन

निम्नलिखित शब्दों के आधार पर कहानी लेखन कीजिए तथा उचित शीर्षक दीजिए:
अलमारी, गिलहरी, चावल के पापड़, छोटा बच्चा
उत्तर:
जीव दया
एक गाँव में एक छोटा बच्चा रहता था। उसका नाम चिंटू था। एक दिन चिंटू अपने घर के बाहर खेल रहा था। उसने देखा कि सामने एक पेड़ के नीचे दो-तीन कौए किसी चीज पर चोंच मार रहे हैं और वहाँ से हल्की-हल्की चर्ची-चीं की आवाज आ रही है। चिंटू दौड़कर वहाँ पहुँचा और उसने उन कौओं को वहाँ से उड़ाया। उसने देखा कि एक छोटी-सी गिलहरी वहाँ ची-चीं कर रही थी। उसका शरीर कौओं की चोंच से घायल हो गया था। चिंटू ने अपनी जेब से रूमाल निकाला और डरे बिना धीरे से गिलहरी को उठा लिया। उसने घर के अंदर लाकर उसे पानी पिलाया, उसके घावों को साफ करके उन पर सोफामाइसिन लगाई और उसे मेज पर बैठा दिया।

गिलहरी कुछ देर बाद धीरे-धीरे मेज पर घूमने लगी। मेज पर एक प्लेट में चावल के पापड़ रखे थे। गिलहरी ने एक पापड़ उठाया और अपने अगले दोनों पंजों में पकड़कर धीरे-धीरे उसे खाने लगी। चिंटू को बहुत अच्छा लगा। उसने माँ से पूछा कि जब तक गिलहरी बिलकुल ठीक नहीं हो जाती क्या मैं उसे अपने पास रख सकता हूँ। अभी अगर वह बाहर जाएगी तो कौए उसे अपना आहार बना लेंगे। माँ को चिंटू की ऐसी सोच पर गर्व हुआ और उन्होंने खुशी-खुशी उसकी बात मान ली। चिंटू ने अपनी किताबों की खुली आलमारी के एक खाने में एक तौलिया बिछाकर गिलहरी को बैठा दिया। उसके पास चावल के कुछ पापड़ तथा अमरूद के कुछ टुकड़े रख दिए। तीन-चार दिन बाद जब गिलहरी अच्छी तरह दौड़ने लगी तो चिंटू ने उसे बाहर पेड़ पर छोड़ दिया।

सीख: हमें पशु-पक्षियों के प्रति दया भाव रखना चाहिए।

अपठित पद्यांश

सूचना के अनुसार कृतियाँ कीजिए:-

काम जरा लेकर देखो, सख्त बात से नहीं स्नेह से
अपने अंतर का नेह अरे, तुम उसे जरा देकर देखो।
कितने भी गहरे रहें गर्त, हर जगह प्यार जा सकता है,
कितना भी भ्रष्ट जमाना हो, हर समय प्यार भा सकता है।
जो गिरे हुए को उठा सके, इससे प्यारा कुछ जतन नहीं,
दे प्यार उठा पाए न जिसे, इतना गहरा कुछ पतन नहीं ।।

– (भवानी प्रसाद मिश्र)

प्रश्न 1.
उत्तर लिखिए:
a. किसी से काम करवाने के लिए उपयुक्त – ………….
b. हर समय अच्छी लगने वाली बात – ………….
उत्तर:

प्रश्न 2.
उत्तर लिखिए:
a. अच्छा प्रयत्न यही है – ………….
b. यही अधोगति है – ………….
उत्तर:

प्रश्न 3.
पद्यांश की तीसरी और चौथी पंक्ति का संदेश लिखिए।
उत्तर:

भाषा बिंदु

कोष्ठक में दिए गए प्रत्येक/कारक चिह्न से अलग-अलग वाक्य बनाइए और उनके कारक लिखिए:
[ने, को, से, का, की, के, में, पर, हे, अरे, के लिए]
………………………………………………………..
………………………………………………………..
………………………………………………………..
………………………………………………………..
………………………………………………………..
उत्तर:
(1) ने – ऋतु ने खाना बनाया।
(2) को – विपिन ने प्रगति को खाना खिलाया।
(3) से – हिमानी साइकिल से ऑफिस जाती है।
(4) का – शुभम हर्षित का भाई है।
(5) की – पूर्वी आयुष की बहन है।
(6) के – नीरज के तीन चाचा हैं।
(7) में – नीनू घर में है।
(8) पर – पेड़ पर बंदर कूद रहे हैं।
(9) हे – हे भगवान, कितना शोर है यहाँ।
(10) अरे – अरे! सलिल तुम कहाँ हो?
(11) के लिए – अंशु वारिजा के लिए फ्रॉक लाई।

Hindi Lokbharti 10th Textbook Solutions Chapter 6 गिरिधर नागर Additional Important Questions and Answers

पद्यांश क्र. 1

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i)

उत्तर:

(ii) a. श्रीकृष्ण के सिर पर है
b. मीरा इन्हें अपना पति मानती हैं –
उत्तर:
a. श्रीकृष्ण के सिर पर है – मोर मुकट
b. मीरा इन्हें अपना पति मानती हैं – गिरधर गोपाल

प्रश्न 2.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
उचित जोड़ियाँ मिलाइए:

अ	आ
आँसुओं के जल से कुल की मर्यादा प्रेम बेल संत संगति के कारण	छोड़ दी आनंद फल लोक लाज खोई प्रेम की बेल सींची प्रेम से बिलोई।

उत्तर:

अ	आ
आँसुओं के जल से कुल की मर्यादा प्रेम बेल संत संगति के कारण	प्रेम की बेल सींचा। छोड़ दी। आनंद फल। लोक लाज खोई।

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों को शुद्ध रूप में लिखिए:
(i) भगत – …………………….
(ii) माखन – …………………….
(iii) आणंद – …………………….
(iv) जाके – …………………….
उत्तर:
(i) भगत – भक्त
(ii) माखन – मक्खन
(iii) आणंद – आनंद
(iv) जाके – जिसके।

प्रश्न 2.
निम्नालाखत शब्दा क समानाथा शब्दालाखए:
(i) मोर = …………………….
(ii) जगत = …………………….
(iii) दूध = …………………….
(iv) प्रेम = …………………….
उत्तर:
(i) मोर = मयूर
(ii) जगत = संसार
(iii) दूध = दुग्ध
(iv) प्रेम = प्यार।

प्रश्न 3.
निम्नलिखित अर्थवाले शब्द पद्यांश से चुनकर लिखिए:
(i) उद्घार करो – …………………….
(ii) मुझे – …………………….
उत्तर:
(i) उद्घार करो – तारो
(ii) मुझे – मोही।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की अंतिम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
मैंने दूध जमाने के पात्र में जमे दही को मथानी से बड़े प्रेम से बिलोया और उसमें से कृष्ण-प्रेम रूपी मक्खन को निकाल लिया। शेष छाछ रूपी निस्सार जगत को छोड़ दिया। कृष्ण-भक्तों को देखकर मैं प्रसन्न होती हूँ, परंतु संसार का व्यवहार देख मुझे दुख होता है और मैं रो पड़ती हूँ। हे गिरधरलाल, मीरा तो आपकी दासी है, उसे इस संसार रूप भव-सागर से पार लगाओ।

पद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

(i) ये मीरा के प्रतिपालक हैं
(ii) कृष्ण के बिना इनको कहीं आश्रय नहीं है –
(iii) मीरा को प्रभु से मिलने की तीव्र यह है –
(iv) मीरा की यह संसार सागर में डूबने वाली है
उत्तर:
(i) ये मीरा के प्रतिपालक हैं – कृष्ण
(ii) कृष्ण के बिना इनको कहीं आश्रय नहीं है – मीरा
(iii) मीरा को प्रभु से मिलने की तीव्र यह है – लालसा
(iv) मीरा की यह संसार सागर में डूबने वाली है – नौका

प्रश्न 2.
पद्यांश में आए इस अर्थ के शब्द लिखिए:

(i) दासी
(ii) आश्रय
(iii) बार-बार
(iv) नौका।
उत्तर:
(i) दासी – चेरी
(ii) आश्रय – गती
(iii) बार-बार – बेर-बेर
(iv) नौका – बेरी।

प्रश्न 3.
विधानों के सामने सत्य / असत्य लिखिए:

(i) हरि बिना मीरा को कहीं आश्रय नहीं है।
(ii) कृष्ण मीरा के पति हैं और वे उनकी पत्नी।
(iii) मीरा बार-बार प्रभु की आरती करती हैं।
(iv) मीरा की जीवन नौका संसार सागर में डूबने वाली है।
उत्तर:
(i) सत्य
(i) असत्य
(iii) असत्य
(iv) सत्य।

प्रश्न 4.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए:

(i) कूण – …………………..
(ii) रावरी – …………………..
(iii) बेरी – …………………..
(iv) नेरी – …………………..
उत्तर:
(i) कूण – कहाँ
(ii) रावरी – आपकी
(iii) बेरी – बेड़ा
(iv) नेरी – पास, निकट।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचान कर लिखिए:
(i) पखावज …………………..
(ii) पिचकारी …………………..
(iii) गुलाल …………………..
(iv) चरण …………………..
उत्तर:
(i) पखावज – स्त्रीलिंग
(ii) पिचकारी – स्त्रीलिंग
(iii) गुलाल – पुल्लिंग
(iv) चरण – पुल्लिंग।

कृति 3: (सरल अर्थ)

प्रश्न.
उपयुक्त पद्यांश की ‘हरि बिन कूण आरति है तेरी।।’ पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
हे हरि, आपके बिना मेरा कौन है? अर्थात आपके सिवा मेरा कोई ठिकाना नहीं है। आप ही मेरा पालन करने वाले हैं और मैं आपकी दासी हूँ। मैं रात-दिन, हर समय आपका ही नाम जपती रहती हूँ। में बार-बार आपको पुकारती हूँ, क्योंकि मुझे आपके दर्शनों की तीव्र लालसा है।

पद्यांश क्र. 3

कृति 1: (आकलन)

प्रश्न 1.
पद्यांश में आए इस अर्थ के शब्द लिखिए:
बोर्ड की नमूना कृतिपत्रिका

(i) कमल
(ii) आकाश
(iii) श्रेष्ठ
(iv) संतोष।
उत्तर:
(i) कमल – कँवल
(ii) आकाश – अंबर
(iii) श्रेष्ठ – छतीयूँ
(iv) संतोष – संतोख।

प्रश्न 2.
जोड़ियाँ बनाइए:

उत्तर:
(i) सुर – राग
(ii) करताल – झनकार
(iii) घट – पट
(iv) प्रेम – पिचकार।

प्रश्न 3.
आकृति पूर्ण कीजिए:
(i) आकाश लाल हो गया है इससे –
(ii) गिरिधर नागर हैं मीरा के ये –
उत्तर:
(i) आकाश लाल हो गया है इससे – गुलाल से।
(ii) गिरिधर नागर हैं मीरा के ये – प्रभु।

प्रश्न 4.
उत्तर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)

उत्तर:

कृति 2: (शब्द संपदा) (बोर्ड की नमूना कृतिपत्रिका)

पद्यांश से ढूँढ़कर लिखिए:
ऐसे दो शब्द जिनका वचन परिवर्तन से रूप नहीं बदलता –
(i) ……………………..
(ii) ……………………..
उत्तर:
(i) दिन
(ii) चरण।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
हे मेरे मन, फागुन मास में होली खेलने का समय अति अल्प होता है। अतः तू जी भरकर होली खेल। अर्थात मानव जीनव अस्थायी है, इसलिए भगवान कृष्ण से पूर्ण रूप से प्रेम कर ले। जिस प्रकार होली के उत्सव में नाच आदि का आयोजन होता है, उसी प्रकार कृष्ण-प्रेम में मुझे ऐसा प्रतीत होता है मानो करताल, पखावज आदि बाजे बज रहे हैं और अनहद नाद का स्वर सुनाई दे रहा है, जिससे मेरा हृदय बिना स्वर और राग के अनेक रागों का आलाप करता रहता है। मेरा रोम-रोम भगवान कृष्ण के प्रेम के रंग में डूबा रहता है। मैंने अपने प्रिय से होली खेलने के लिए शील और संतोष रूपी केसर का रंग घोला है। मेरा प्रिय-प्रेम ही होली खेलने की पिचकारी है।

भाषा अध्ययन (व्याकरण)

प्रश्न.
सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) बाहर कोई नहीं है।
(ii) माँ को हंसी आ गई।
(iii) चतुर वैद्य विष से भी दवा का काम ले सकता है।
उत्तर:
(i) कोई – अनिश्चयवाचक सर्वनाम।
(ii) हँसी – भाववाचक संज्ञा।
(iii) चतुर – गुणवाचक विशेषण।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) भी
(ii) इसलिए।
उत्तर:
(i) भी – हमारी बेटी गाय से भी अधिक सीधी है।
(ii) इसलिए – नीरज बीमार था, इसलिए दफ्तर नहीं गया।

3. संधि:
कृति पूर्ण कीजिए:
संधि शब्द – संधि विच्छेद – संधि भेद
…………. – उत् + लेख। – ……………
अथवा
तपोबल – …………… – ……………
उत्तर:
संधि शब्द – संधि विच्छेद – संधि भेद
उल्लेख – उत् + लेख – व्यंजन संधि
अथवा
तपोबल – तपः + बल – विसर्ग संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) यह कुरसी दीवार की तरफ खिसका दो।
(ii) हम समय पर स्टेशन पहुंच गए।
उत्तर:
सहायक क्रिया – मूल रूप
(i) दो – देना
(ii) गए – जाना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) पढ़ना
(ii) जीतना
(ii) करना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वितीय प्रेरणार्थक रूप
(i) पढ़ना – पढ़ाना – पढ़वाना
(ii) जीतना – जिताना – जितवाना
(iii) करना – कराना – करवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) चैन न मिल पाना
(ii) झेंप जाना।
उत्तर:
(i) चैन न मिल पाना।

अर्थ: बेचैनी अनुभव करना। वाक्य: मालिक की कड़ी बातें सुनकर मुनीम को चैन न मिल पाया।

(ii) झेंप जाना।
अर्थ: लज्जित होना, शरमाना। वाक्य: नकल करने पर मित्र की फटकार सुनकर अभिनव झेंप गया।

(2) अधोरेखांकित वाक्यांशों के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए:
(नाक-भौं सिकोड़ना, गुदगुदा देना, सिर झुका देना)
(i) अप्रिय बात सुनकर सभी तिरस्कार प्रकट करेंगे।
(ii) जीवन में आनंददायी क्षण बहुत कम होते हैं।
उत्तर:
(i) अप्रिय बात सुनकर सभी नाक-भौं सिकोड़ेंगे।
(ii) जीवन में गुदगुदाने वाले क्षण बहुत कम होते हैं।

7. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) मैं कहाँ से पैसे , पहले तो दूध की बिक्री के पैसे मेरे पास जमा रहते थे
(ii) सहसा कानों में आवाज आई काकी उठो मैं पूड़ियाँ लाई हूँ
उत्तर:
(i) “मैं कहाँ से पैसे दूँ? पहले तो दूध की बिक्री के पैसे मेरे पास जमा रहते थे।”
(ii) सहसा कानों में आवाज आई – “काकी, उठो मैं पूड़ियाँ लाई हूँ।”

8. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) विदा का क्षण आ गया। (सामान्य भविष्यकाल)
(ii) आप छत पर क्या करते हैं? (अपूर्ण भूतकाल)
(iii) मेरी गाड़ी तो बिक जाती है। (पूर्ण वर्तमानकाल)
उत्तर:
(i) विदा का क्षण आ जाएगा।
(ii) आप छत पर क्या कर रहे थे?
(iii) मेरी गाड़ी तो बिक गई है।

9. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचान कर लिखिए:
(i) संसार का व्यवहार देखकर मुझे दुःख होता है और मैं रो पड़ती हूँ।
(ii) मीराबाई कहती हैं कि अब उन्हें लोकलाज का कोई डर नहीं हैं।
उत्तर:
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) संतो के साथ बैठकर मैंने लोकलाज त्याग दी है। (विस्मयादिबोधक वाक्य)
(ii) हे हरि, आप ही मेरा पालन करने वाले हैं। (आज्ञावाचक वाक्य)
उत्तर:
(i) हाय! संतों के साथ बैठकर मैंने लोकलाज त्याग दी है।
(ii) हे हरि, आप ही मेरा पालन करें।।

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) लेखक ने अभिनेता की घमंड तोड़ी।
(ii) हमने क्रिकेट की मैच देखी।
उत्तर:
(i) लेखक ने अभिनेता का घमंड तोड़ा।
(ii) हमने क्रिकेट का मैच देखा।

गिरिधर नागर Summary in Hindi

गिरिधर नागर कविता का सरल अर्थ

1. मेरे तो गिरधर गोपाल …………………………….. तारो अब मोही।।

गिरि को धारण करने वाले, गायों के पालक कृष्ण के सिवा मेरा और कोई नहीं है। जिनके मस्तक पर मोर का मुकुट शोभित है, वे ही मेरे पति हैं। उनके लिए मैंने कुल की मर्यादा छोड़ दी है। चाहे कोई मुझे कुछ भी कहे। संतों के साथ बैठ-बैठकर मैंने लोकलाज त्याग दी है। मैंने अपने प्रेम रूपी बेल को अपने अश्रु रूपी जल से सींच-सींचकर बड़ा किया है। अब तो यह प्रेम-बेल फैल गई है और इसमें आनंद रूपी फल लगने लगा है। मैंने दूध जमाने के पात्र में जमे दही को मथानी से बड़े प्रेम से बिलोया और उसमें से कृष्ण-प्रेम रूपी मक्खन को निकाल लिया। शेष छाछ रूपी निस्सार जगत को छोड़ दिया। कृष्ण-भक्तों को देखकर मैं प्रसन्न होती हूँ, परंतु संसार का व्यवहार देख मुझे दुख होता है और मैं रो पड़ती हूँ। हे गिरधरलाल, मीरा तो आपकी दासी है, उसे इस संसार रूपी भव-सागर से पार लगाओ।

2. हरि बिन कूण गती मेरी …………………………….. मैं सरण हूँ तेरी।।

हे हरि, आपके बिना मेरा कौन है? अर्थात आपके सिवा मेरा कोई ठिकाना नहीं है। आप ही मेरा पालन करने वाले हैं और मैं आपकी दासी हूँ। मैं रात-दिन, हर समय आपका ही नाम जपती रहती हूँ। मैं बार-बार आपको पुकारती हूँ, क्योंकि मुझे आपके दर्शनों की तीव्र लालसा है। यह संसार विभिन्न प्रकार के दोषों और विकारों से भरा हुआ सागर है, जिसके बीच में घिर गई हैं। इस संसार रूपी सागर में मेरी नाव टूट गई है। हे प्रभु, आप शीघ्र इस नाव का पाल बाँधिए, अन्यथा यह जीवन-नौका इस संसार-सागर में डूब जाएगी। हे प्रियतम, आपकी यह विरहिणी निरंतर आपकी बाट जोहती रहती है। आपके आगमन की प्रतीक्षा करती रहती है। आपकी यह दासी मीरा सदा आपके नाम का स्मरण करती रहती है और आपकी शरण में आई है।

3. फागुन के दिन चार …………………………….. चरण कँवल बलिहार रे।।

हे मेरे मन, फागुन मास में होली खेलने का समय अति अल्प होता है। अतः तू जी भरकर होली खेल। अर्थात मानव जीनव अस्थायी है, : इसलिए भगवान कृष्ण से पूर्ण रूप से प्रेम कर ले। जिस प्रकार होली के : उत्सव में नाच आदि का आयोजन होता है, उसी प्रकार कृष्ण-प्रेम में मुझे ऐसा प्रतीत होता है मानो करताल, पखावज आदि बाजे बज रहे हैं और अनहद नाद का स्वर सुनाई दे रहा है, जिससे मेरा हृदय बिना स्वर और राग के अनेक रागों का आलाप करता रहता है। मेरा रोम-रोम भगवान कृष्ण के प्रेम के रंग में डूबा रहता है। मैंने अपने प्रिय से होली खेलने के लिए शील और संतोष रूपी केसर का रंग घोला है। मेरा प्रिय-प्रेम ही होली खेलने की पिचकारी है। उड़ते हुए गुलाल से सारा आकाश लाल हो गया है। अब मुझे लोक-लज्जा का कोई डर नहीं है, इसलिए मैंने हृदय रूपी घर के दरवाजे खोल दिए हैं। अंत में मीरा कहती हैं कि मेरे स्वामी गोवर्धन पर्वत को धारण करने वाले कृष्ण भगवान हैं। मैंने उनके चरण-कमलों में अपना सर्वस्व न्योछावर कर दिया है।

गिरिधर नागर विषय-प्रवेश :

प्रस्तुत काव्य में रसिक शिरोमणि श्रीकृष्ण की अनन्य उपासिका मीराबाई अपना प्रेम प्रकट कर रही हैं। सभी पदों में | श्रीकृष्ण के प्रति मीराबाई के प्रेम, उनकी भक्ति, उत्सुकता, प्रिय-मिलन की आशा, प्रतीक्षा आदि का मार्मिक चित्रण है।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 1 Bharat Mahima Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 1 भारत महिमा Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 1 भारत महिमा Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 1 भारत महिमा Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
निम्नलिखित पंक्तियों का तात्पर्य लिखिए:
a. कहीं से हम आए थे नहीं → …………………….
b. वही हम दिव्य आर्य संतान → …………………….
उत्तर:
(a) हम भारतवासी किसी अन्य देश से आकर यहाँ नहीं बसे। हम यहीं के निवासी हैं। सभ्यता के प्रारंभ से हम यहीं रहते आए हैं।
(b) भारतवासी आर्य थे और हम उन्हीं आर्यों की दिव्य संतानें हैं।

प्रश्न 2.
उचित जोड़ियाँ मिलाइए:
संचय
सत्य
अतिथि
रत्न
वचन
दान
हृदय
तेज
देव
उत्तर:
(i) संचय – दान
(ii) सत्य – वचन
(iii) अतिथि – देव
(iv) रत्न – तेज।

प्रश्न 3.
लिखिए.
a. कविता में प्रयुक्त दो धातुओं के नाम:

उत्तर:

b. भारतीय संस्कृति की दो विशेषताएँ:

उत्तर:

प्रश्न 4.
प्रस्तुत कविता की अपनी पसंदीदा किन्हीं दो पंक्तियों का भावार्थ लिखिए।
उत्तर:
हमारे संचय में था दान, अतिथि थे सदा हमारे देव वचन में सत्य, हृदय में तेज, प्रतिज्ञा में रहती थी टेव। हम भारतीय दीन-दुखियों की सेवा करने के लिए सदैव तत्पर रहते हैं। हम यदि धन और संपत्ति का संग्रह करते भी थे तो दान के लिए करते थे। दानवीरता भारतीयों का गुण रहा है। महर्षि दधीचि और कर्ण जैसे दानवीर इसी भूमि पर हुए हैं। हमारे देश में अतिथियों को देवता के समान माना जाता था। भारतीय सत्यवादी हरिश्चंद्र की संतानें हैं। हमारे हृदय में तेज था, गौरव था। हम सदा अपनी प्रतिज्ञा पर अटल रहते थे। भारतीयों का मानना था- प्राण जाएँ,: पर वचन न जाएँ।

प्रश्न 5.
निम्नलिखित मुद्दों के आधार पर पद्य विश्लेषण कीजिए:
a. रचनाकार का नाम
b. रचना का प्रकार
c. पसंदीदा पंक्ति
d. पसंदीदा होने का कारण
e. रचना से प्राप्त संदेश
उत्तर:
a. रचनाकार का नाम → जयशंकर प्रसाद।
b. रचना की विधा → कविता।
c. पसंद की पंक्तियाँ → व्योमतम पुंज हुआ तब नष्ट, अखिल संसृति हो उठी अशोक। (सूचना: विद्यार्थी अपनी पसंद की पंक्ति लिखेंगे।)
d. पंक्तियाँ पसंद होने का कारण → हम भारतीयों ने पूरे विश्व में ज्ञान का प्रसार किया, जिसके कारण समग्र संसार आलोकित हो गया। अज्ञान रूपी अंधकार का विनाश हुआ और संपूर्ण सृष्टि के सभी दुख-शोक दूर हो गए।
e. रचना से प्राप्त संदेश/प्रेरणा → हमें सदैव अपने देश और इसकी संस्कृति पर गर्व करना चाहिए। जब भी आवश्यकता पड़े, देश के लिए अपना सर्वस्व न्योछावर कर देने के लिए तत्पर रहना चाहिए।

Hindi Lokbharti 10th Textbook Solutions Chapter 1 भारत महिमा Additional Important Questions and Answers

पद्यांश क्र. 1
प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
पद्यांश से ऐसे दो प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) अभिनंदन
(ii) आलोक।
उत्तर:
(i) उषा ने हँसकर क्या किया?
(ii) जब भारतीयों ने ज्ञान का प्रचार किया तो संसार में क्या फैला?

प्रश्न 2.
पद्यांश में प्रयुक्त इन शब्दों से सहसंबंध दर्शाने वाले शब्द लिखिए:
(i) हिमालय – ……………………..
(ii) किरण – ……………………..
(iii) विमल – ……………………..
(iv) कोमल – ……………………..
उत्तर:
(i) हिमालय -आँगन
(ii) किरण – उपहार
(iii) विमल -वाणी
(iv) कोमल -कर

प्रश्न 3.
विधानों के सामने सत्य/असत्य लिखिए:
(i) जब पूरा विश्व जगा तो भारतवासी भी जग गए।
(ii) वीणापाणि ने अपने हाथ में वीणा ली।
(iii) हिमालय के आँगन में किरणों का उपहास मिला।
(iv) सप्तसिंधु में सातों स्वर गूंजने लगे।
उत्तर:
(i) असत्य
(ii) सत्य
(iii) असत्य
(iv) सत्य।

प्रश्न 4.
उचित जोड़ियाँ मिलाइए:
(i) उषा – आलोक
(ii) हीरक – संगीत
(iii) विश्व – अभिनंदन
(iv) वीणा – हार
उत्तर:
(i) उषा – अभिनंदन।
(ii) हीरक – हार
(iii) विश्व – आलोक
(iv) वीणा -संगीत।

कृति 2: (शब्द संपदा)

प्रश्न 1.
पद्यांश में से ढूँढ़कर उपसर्गयुक्त शब्द लिखिए:
(i) ………………. (ii) ……………….
उत्तर:
(i) अभिनंदन
(ii) उपहार।

प्रश्न 2.
अनेक शब्दों के लिए एक-एक शब्द लिखिए:
(i) गले में पहनने की मूल्यवान माला
(ii) सितार जैसा वह वाद्य जो सब वाद्यों में श्रेष्ठ माना जाता है, ……………….
उत्तर:
(i) हार
(ii) वीणा।

प्रश्न 3.
निम्नलिखित शब्दों के लिए पद्यांश में प्रयुक्त शब्द ढूँढ़कर लिखिए:
(i) संपूर्ण
(ii) शोकरहित
(iii) संसार
(iv) आकाश।
उत्तर:
(i) संपूर्ण – अखिल
(ii) शोकरहित – अशोक
(iii) संसार – संसृति
(iv) आकाश – व्योम।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
भारत देश हिमालय के आँगन के समान है। प्रतिदिन उषा भारत को सूर्य की किरणों का उपहार देती है, मानो हँसकर भारत-भूमि का अभिनंदन कर रही हो। ओस की बूंदों पर जब प्रातःकालीन सूर्य की रश्मियाँ पड़ती हैं, तो ओस की बूंदें चमकने लगती हैं और ऐसा लगता है मानो, उषा ने भारत को हीरों का हार पहना दिया हो।

सबसे पहले ज्ञान का उदय भारत में ही हुआ। अर्थात सबसे पहले हम जाग्रत हुए। फिर हमने पूरे विश्व में ज्ञान का प्रसार किया। इसके कारण समग्र संसार आलोकित हो गया। अज्ञानरूपी अंधकार का विनाश हुआ और संपूर्ण सृष्टि के सभी दुख-शोक दूर हो गए।

पद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) भारत में केवल …………………………. की ही विजय नहीं रही। (चाँदी/लोहे/सोने)
(ii) यहाँ …………………………. भिक्षु की तरह रहते थे। (लोग/लड़के/सम्राट)
(iii) हमसे चीन को …………………………. की दृष्टि मिली। (धर्म/कर्म/धन)
(iv) हमारा देश सदा प्रकृति का …………………………. रहा। (खिलौना/आँगन /पालना)
उत्तर:
(i) भारत में केवल लोहे की ही विजय नहीं रही।
(ii) यहाँ सम्राट भिक्षु की तरह रहते थे।
(iii) हमसे चीन को धर्म की दृष्टि मिली।
(iv) हमारा देश सदा प्रकृति का पालना रहा।

प्रश्न 3.
उपर्युक्त पद्यांश पर आधारित ऐसे दो प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) सम्राट
(ii) धर्म।
उत्तर:
(i) कौन भिक्षु होकर रहते?
(ii) चीन को कौन-सी दृष्टि मिली?

प्रश्न 4.
निम्नलिखित पंक्तियों का तात्पर्य लिखिए:
(ii) प्रकृति का रहा पालना यहीं।
उत्तर:
(ii) हमें प्रकृति ने प्रत्येक वस्तु मुक्तहस्त से प्रदान की। यहाँ की शस्य श्यामला भूमि, हिमाच्छादित गिरि शिखर, घाटियाँ, वादियाँ, सदानीरा नदियाँ, झरने, फल-फूल, संसाधनों से भरपूर जंगल सभी अनुपम हैं।

प्रश्न 5.
आकृति पूर्ण कीजिए:
(i) हमने गोरी को इसका दान दिया – [ ]
(ii) भारत की धरती पर इसकी धूम रही – [ ]
उत्तर:
(i) हमने गोरी को इसका दान दिया – [दया का]
(ii) भारत की धरती पर इसकी धूम रही – [धर्म की]

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्द-समूहों के लिए शब्द लिखिए:
(i) बहुमूल्य चमकीले प्रसिद्ध खनिज पदार्थ, जो आभूषणों आदि में जड़े जाते हैं –
(ii) छोटे बच्चों के लिए एक प्रकार का झूला या हिंडोला –
(iii) वह स्थान जहाँ किसी का जन्म हुआ हो –
(iv) बौद्ध संन्यासियों के लिए प्रयोग किया जाने वाला शब्द –
उत्तर:
(i) रत्न
(ii) पालना
(iii) जन्मस्थान
(iv) भिक्षु।

प्रश्न 2.
निम्नलिखित शब्दों के विलोम शब्द लिखिए:
(i) विजय x ………………….
(ii) धर्म x ………………….
(iii) भूमि x ………………….
(iv) जन्म x ………………….
उत्तर:
(i) विजय x पराजय
(ii) धर्म x अधर्म
(iii) भूमि x आकाश
(iv) जन्म – मरण।

कृति 3: (सरल अर्थ)

प्रश्न.
उपर्युक्त पद्यांश की अपनी पसंदीदा किन्हीं दो पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
विजय केवल लोहे की नहीं, धर्म की रही धरा पर धूम भिक्षु होकर रहते सम्राट, दया दिखलाते घर-घर घूम। भारतीयों ने शस्त्रों के बल पर दूसरे देशों को नहीं जीता, बल्कि उन्होंने प्रेमभाव से लोगों के हृदय जीते हैं। भारत में प्राचीन काल से ही लोगों के मन में धर्म की भावना रही है। यहाँ वर्धमान महावीर और गौतम बुद्ध जैसे त्यागी धर्मपुरुष हुए हैं, जिन्होंने अपना विशाल साम्राज्य छोड़कर भिक्षु का स्वरूप धारण किया और घर-घर घूमकर लोगों का कष्ट दूर करने का प्रयास किया, धर्म का प्रचार किया।

पद्यांश क्र. 3

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
निम्नलिखित पंक्तियों का तात्पर्य लिखिए:
(i) किसी को देख न सके विपन्न।
उत्तर:
(i) भारतीय कभी किसी को दुखी नहीं देख सके। दीन-दुखियों की सेवा करने के लिए हम भारतीय सदैव तत्पर रहते हैं।

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i) हम चरित्र के ऐसे थे – [ ]
(ii) हम दान के लिए यह करते थे – [ ]
(iii) हमारे लिए ये देवता के समान थे – [ ]
(iv) हमें अपने गौरव पर यह था – [ ]
उत्तर:
(i) हम चरित्र के ऐसे थे [पवित्र]
(ii) हम दान के लिए यह करते थे [संचय]
(iii) हमारे लिए ये देवता के समान थे [अतिथि]
(iv) हमें अपने गौरव पर यह था [गर्व]

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 4.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (शब्द संपदा)

प्रश्न 1.
पद्यांश से उपसर्ग वाले दो शब्द ढूँढकर लिखिए:
(i) ……………………. (ii) …………………….
उत्तर:
(i) अतिथि
(ii) अभिमान।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) पूत = …………………….
(ii) गर्व = …………………….
(iii) प्रतिज्ञा = …………………….
(iv) प्यारा = …………………….
उत्तर:
(i) पूत – पावन
(ii) गर्व = घमंड
(iii) प्रतिज्ञा = प्रण
(iv) प्रिय = प्यारा।

प्रश्न 3.
पद्यांश से शब्द ढूँढकर लिखिए:
(i) पवित्र शब्द के लिए प्रयुक्त शब्द – …………………….
(ii) गरीब शब्द के लिए प्रयुक्त शब्द – …………………….
उत्तर:
(i) पवित्र शब्द के लिए प्रयुक्त शब्द – पूत
(ii) गरीब शब्द के लिए प्रयुक्त शब्द – विपन्न।

कृति 3: (सरल अर्थ)

पदय विश्लेषण
सूचना: यह प्रश्नप्रकार कृतिपत्रिका के प्रारूप से हटा दिया गया है। लेकिन यह प्रश्न पाठ्यपुस्तक में होने के कारण विद्यार्थियों के अधिक अभ्यास के लिए इसे उत्तर-सहित यहाँ समाविष्ट किया गया है।

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) राजा दशरथ वृद्ध दंपति के सामने बैठ गए।
(ii) सड़क कदाचित कच्ची थी।
उत्तर:
(i) दशरथ – व्यक्तिवाचक संज्ञा।
(ii) सड़क – जातिवाचक संज्ञा।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) बहुत
(ii) सामने
(iii) किंतु।
उत्तर:
(i) प्रयाग बहुत थक गया था।
(ii) स्कूल के सामने एक बगीचा है।
(iii) घर में दीपक तो था, किंतु उसमें तेल न था।

3. संधि:
कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
उज्ज्व	………………	………………
अथवा
प्रश्न + उत्तर	………………	………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
उज्ज्वल	उत् + ज्वल	व्यंजन संधि
अथवा
प्रश्नोत्तर	प्रश्न + उत्तर	स्वर संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका ‘मूल रूप लिखिए:
(i) इस पद ने मोहिनी मंत्र का जाल बिछा दिया।
(ii) बालक भूमि पर लेट गया।
उत्तर:

सहायक क्रिया	मूल रूप
(i) दिया	देना
(ii) गया।	जाना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) दौड़ना
(ii) बोलना
(iii) रोना।
उत्तर:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) दौड़ना।	दौड़ाना	दौड़वाना
(ii) बोलना	बुलाना	बुलवाना
(iii) रोना	रुलाना	रुलवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) दृष्टि फेरना
(ii) राह देखना।
उत्तर:
(i) दृष्टि फेरना।
अर्थ: नजर डालना।
वाक्य: नेताजी ने श्रोताओं पर दृष्टि फेरी।

(ii) राह देखना।
अर्थ: प्रतीक्षा करना।
वाक्य: विद्यार्थी कई दिनों से छुट्टियों की राह देख रहे थे।

(2) अधोरेखांकित वाक्यांश के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (सपने की संपत्ति होना, चल बसना, भनक पड़ना)
(i) हफ्ते भर की बीमारी में मरीज चला गया।
(ii) दारोगाजी ने उड़ती हुई खबर सुनी कि कल दंगा होने वाला है।
(ii) ऐसा भूकंप आया कि क्षण भर में सारी चहल-पहल विलुप्त हो गई।
उत्तर:
(i) हफ्ते भर की बीमारी में मरीज चल बसा।
(ii) दारोगाजी के कान में भनक पड़ी कि कल दंगा होने वाला है।
(iii) ऐसा भूकंप आया कि क्षण भर में सारी चहल-पहल सपने की संपत्ति हो गई।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) नारी महान है।
(ii) वह किसी को किसी प्रकार की कमी नहीं होने देती।
(iii) प्रेरणा का सूक्ष्म प्रभाव होता है।
उत्तर:
(i) नारी – कर्ता कारक
(ii) किसी को – कर्म कारक
(iii) प्रेरणा का – संबंध कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) क्या बताऊँ गाय ने दूध देना बंद कर दिया है बूढ़ी हो गई है इस जमाने में गाय भैंस पालने का खर्चा
(ii) हे मेरे मित्रो परिचितो आओ अपने सारे बदले लेने का यही वक्त है
उत्तर:
(i) “क्या बताऊँ। गाय ने दूध देना बंद कर दिया है, बूढ़ी हो गई है। इस जमाने में गाय-भैंस पालने का खर्चा …।”
(ii) “हे मेरे मित्रो, परिचितो! आओ, अपने सारे बदले लेने का यही वक्त है।”

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) मनु पीछे की ओर मुड़ता है। (सामान्य भूतकाल)
(ii) तुम्हारा मुख लाल होता है। (अपूर्ण वर्तमानकाल)
(iii) रोगी की अवस्था बदल जाती है। (पूर्ण भूतकाल)
उत्तर:
(i) मनु पीछे की ओर मुड़ा।
(ii) तुम्हारा मुख लाल हो रहा है।
(iii) रोगी की अवस्था बदल गई थी।

10. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) भारतीय चरित्र के पवित्र होते हैं।
(ii) बादल आए किंतु पानी नहीं बरसा।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए:
(i) तुम्हें अपना ख्याल रखना चाहिए। (आज्ञावाचक)
(ii) मास्टर जी ने पुस्तकें लाने के लिए पैसे दिए। (प्रश्नवाचक)
उत्तर:
(i) तुम अपना ख्याल रखो।
(ii) क्या मास्टर जी ने पुस्तकें लाने के लिए पैसे दिए?

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) क्रोध से उसकी नेत्र लाल हो गए।
(ii) राम ने हिरण का शिकार की।
(iii) मैं मेरा काम करता है।
उत्तर:
(i) क्रोध से उसके नेत्र लाल हो गए।
(ii) राम ने हिरन का शिकार किया।
(iii) में अपना काम करता हूँ।

भारत महिमा Summary in Hindi

भारत महिमा कविता का सरल अर्थ

1. हिमालय के आँगन …………………………………… मधुर साम संगीत।. . .

हमारा यह प्यारा भारत देश हिमालय के आँगन के समान है। प्रतिदिन उषा भारत को सूर्य की किरणों का उपहार देती है। तब ऐसा लगता है मानो हँसकर वह भारत-भूमि का अभिनंदन कर रही हो। ओस की बूंदों पर जब प्रातःकालीन सूर्य की रश्मियाँ पड़ती हैं तो ऐसा लगता है जैसे उषा ने भारत को हीरों का हार पहना दिया हो।

सबसे पहले ज्ञान का उदय भारत में ही हुआ अर्थात सबसे पहले हम जाग्रत हुए। फिर हमने पूरे विश्व में ज्ञान का प्रसार किया। इसके कारण समग्र संसार आलोकित हो गया। अज्ञान रूपी अंधकार का विनाश हुआ और संपूर्ण सृष्टि के सभी दुख-शोक दूर हो गए।

वाणी की देवी वीणापाणि (सरस्वती) ने इसी पवित्र भूमि पर प्रेम के साथ अपने कमल के समान कोमल करों में वीणा उठाई, उसकी झंकार से सप्तसिंधुओं में सातों स्वरों का मोहक सरगम गूंजने लगा, मधुर संगीत का जन्म हुआ। इसी महान देश में संगीत के वेद सामवेद की रचना हुई।

2. विजय केवल …………………………………… आए थे नहीं।. . .

भारत के लोगों ने शस्त्रों के बल पर देशों को नहीं जीता। यहाँ प्राचीन काल से ही लोगों के मन में धर्म की प्रखर भावना रही है और उन्होंने संसार में धर्म का प्रचार किया। यहाँ गौतम बुद्ध और वर्धमान महावीर जैसे धर्मपुरुष हुए हैं, जिन्होंने विशाल साम्राज्य छोड़कर भिक्षु का स्वरूप धारण किया और घर-घर घूमकर लोगों का कष्ट दूर करने का प्रयास किया, धर्म का प्रचार किया। हमने मोहम्मद गोरी को पराजित करने के बाद भी दयापूर्वक क्षमा कर दिया। हमारे देश से ही चीन को धर्म की दृष्टि मिली। (भारत के महान सम्राट अशोक ने अपने पुत्र महेंद्र और पुत्री संघमित्रा को बौद्ध धर्म के प्रचार के लिए चीन, स्वर्ण भूमि अर्थात जावा और श्रीलंका भेजा) जावा और श्रीलंका के लोगों को पंचशील (अहिंसा, अस्तेय, अपरिग्रह, सत्य, ब्रह्मचर्य आदि) के सिद्धांत मिले।

भारतवासियों ने कभी किसी की संपत्ति या किसी का राज्य छीनने का प्रयास नहीं किया। हमें प्रकृति ने प्रत्येक वस्तु मुक्तहस्त से प्रदान की। प्रकृति की हमारे देश पर महान कृपा रही है। (यहाँ की शस्य श्यामला भूमि, हिमाच्छादित गिरि शिखर, घाटियाँ, वादियाँ, सदानीरा नदियाँ, झरने, फल-फूल, संसाधनों से भरपूर जंगल सभी अनुपम हैं) भारत सदा से हमारी जन्मभूमि है। हम इसी देश की संतानें हैं। हम बाहर के किसी स्थान से आकर यहाँ नहीं बसे हैं। (जैसा कि कुछ विदेशियों का कहना है।)

3. चरित थे पूत …………………………………… प्यारा भारतवर्ष।. . .

भारत के लोग सदा से चरित्रवान रहे हैं। हमारी भुजाओं में भरपूर शक्ति रही है। भारतीयों में वीरता की कभी कमी नहीं रही। साथ ही नम्रता सदा हमारा गुण रहा है। हमने कभी अपनी उपलब्धियों पर घमंड नहीं किया। हमें अपनी सभ्यता और संस्कृति पर गर्व रहा है। हम कभी किसी को दुखी नहीं देख सके। दीन-दुखियों की सेवा करने के लिए हम भारतीय सदैव तत्पर रहते हैं। ‘हम यदि धन और संपत्ति का संग्रह करते भी थे, तो दान के लिए करते थे। दानवीरता भारतीयों का गुण रहा है। हमारे देश में अतिथियों को सदा देवता के समान माना जाता था। भारत के लोग सत्य बोलना अपना धर्म मानते थे। (भारतीय सत्यवादी हरिश्चंद्र की संतानें हैं।) हमारे हृदय में तेज था, गौरव था। हम सदा अपनी प्रतिज्ञा पर अटल रहते थे। प्राण जाए, पर वचन न जाए हमारा जीवनमूल्य रहा है।

आज भी हम भारतीयों की धमनियों में उन्हीं पूर्वजों का रक्त प्रवाहित हो रहा है। आज भी हमारा देश वैसा ही है। आज भी भारतीयों में वैसा ही साहस है। भारतीय आज भी ज्ञान के क्षेत्र में सबसे आगे हैं। आज भी हम पहले के समान शांति के पुजारी हैं। देशवासियों में वैसी ही शक्ति है। हम उन्हीं आर्यों की दिव्य संतानें हैं।

हम जब तक जिएँ, इसी देश के लिए जिएँ। हमें इसकी सभ्यता और संस्कृति पर अभिमान है और हर्ष है कि हमने इस भूमि पर जन्म लिया है। यह हमारा प्यारा भारतवर्ष है। यदि कभी आवश्यकता पड़े, तो इसके लिए अपना सर्वस्व भी न्योछावर कर दें।

भारत महिमा विषय-प्रवेश :

प्रकृति ने हमारे देश भारत की रचना बड़े प्यार से की है। हमारा देश हिमालय की गोद में बसा हुआ है। हमारा देश सबसे पहले जाग्रत हुआ था और इसकी संस्कृति सबसे पुरानी है। प्रस्तुत कविता में छायावाद के प्रवर्तक जयशंकर प्रसाद जी ने हमारे प्यारे देश भारत के इसी महिमामंडित अतीत का मनोरम चित्रण किया है। कवि की आकांक्षा है कि हमें सदैव अपने देश पर, इसकी सभ्यता और संस्कृति पर गर्व करना चाहिए। आवश्यकता पड़ने पर, हमें देश के लिए अपना सर्वस्व न्योछावर कर देने के लिए तत्पर रहना चाहिए।

भारत महिमा मुहावरा –

• अर्थ निछावर करना – अर्पण करना, समर्पित करना।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 7 Khula Aakash Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 7 खुला आकाश Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 7 खुला आकाश Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 7 गिरिधर नागर Textbook Questions and Answers

सूचना के अनुसार कृवियाँ कीविए:
(1) प्रहवलका पूण् कीविए:

उतर:

(2) कृवि पूण् कीविए:

उतर:

(3) आकृवि मे वलखिए:

उतर:

(4)

उतर:

(5) लखिए:
a.

उतर:

b.

उतर:

भाषा हबंदु
(1) हनम्हलखखत संहध हिचछेद की संहध कीहजए और भेद हलखखए:

उतर:

संधि शब्द	संधि विच्छेद	संधि भेद
(i) सज्जन	सत् + जन	व्यंजन संधि
(ii) नमस्ते	नमः+ ते	विसर्ग संधि
(iii) स्वागत	सु + आगत	स्वर संधि
(iv) दिग्दर्शक	दिक् + दर्शक	व्यंजन संधि
(v) यद्यपि	यदि + यपि	स्वर संधि
(vi) दुस्साहस	दुः + साहस	विसर्ग संधि

(2) हनम्हलखखत शब् का संहध हिचछेद कीहजए और भेद हलखखए:

उतर:

संधि विच्छेद	संधि शब्द	संधि भेद
(i) दुः +  लभ	दुर्लभ	विसर्ग संधि
(ii) महा +  आत्मा	महात्मा	स्वर संधि
(iii) अन् +  आसक्त	अनासक्त	स्वर संधि
(iv) अंतः +  चेतना	अंतश्चेतना	विसर्ग संधि
(v) सम् +  तोष	संतोष	व्यंजन संधि
(vi) सदा + एव	सदैव	स्वर संधि

(3) हनम्हलखखत आकृहत मे हदए गए शब् का हिचछेद कीहजए और संहध का भेद हलखखए:

उतर:

संधि शब्द	संधि विच्छेद	संधि भेद
(i) दिग्गज’	दिक् + गज	व्यंजन संधि
(ii) सप्ताह	सप्त + अह	स्वर संधि
(iii) निश्चल	निः + चल	विसर्ग संधि
(iv) भानूदय	भानु + उदय	स्वर संधि
(v) निस्संदेह	निः + संदेह	विसर्ग संधि
(vi) सूर्यास्त	सूर्य + अस्त	स्वर संधि

(4) पाठो मे आए संहध शब् छाँटकर उनका हिचछेद कीहजए और संहध का भेद हलखखए।

संधि शब्द	संधि विच्छेद	संधि भेद
(i) निर्जीव	निः + जीव	विसर्ग संधि
(ii) संभव	सम् + भव	व्यंजन संधि
(iii) उज्ज्व	लउत् + ज्वल	व्यंजन संधि

Hindi Lokbharti 10th Textbook Solutions Chapter 7 खुला आकाश Additional Important Questions and Answers

गद्यांश क्र.1
कृति 1: (आकलन)
(1) आकृति पूर्ण कीजिए:

उत्तर:

(2) उत्तर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)

उत्तर:

कृति 2: (स्वमत अभिव्यक्ति)

‘बढ़ती हुई जनसंख्या का मनुष्य जीवन पर प्रभाव’ के बारे में आपके विचार 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
आज लगभग सभी देशों की जनसंख्या में बढ़ोत्तरी हो रही है। यह जनसंख्या वृद्धि आज संसार के समक्ष एक समस्या बन गई है। सभी देशों के संसाधन सीमित हैं और बढ़ी हुई जनसंख्या की माँग विशाल है, जिसकी पूर्ति करना संभव नहीं है। इसी का परिणाम है कि आज लोगों के सामने बेकारी की समस्या उत्पन्न हो गई है। जनसंख्या वृद्धि के कारण कृषि पर आधारित लोग परेशान हैं। खेती योग्य जमीन बँटती जा रही है।

अब वह इतने लोगों को रोटी देने में असमर्थ हो गई है। गाँवों की आबादी का बोझ शहरों पर आ पड़ा है। यहाँ शहरों में बेकारी की समस्या है। यहाँ भी लोग रोटी, कपड़ा, मकान की समस्याओं से जूझ रहे हैं। लोग गंदी बस्तियों में रहने के लिए मजबूर हैं। न इतने लोगों के लिए ढंग की शिक्षा व्यवस्था उपलब्ध हो पा रही है और न ही चिकित्सा व्यवस्था।

बढ़ती जनसंख्या ने देश की अर्थव्यवस्था बिगाड़ दी है। इस पर अंकुश लगाकर ही इस समस्या से छुटकारा पाया जा सकता है। तभी मनुष्य के जीवन स्तर में भी सुधार हो पाएगा।

गद्यांश क्र.2
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(2) सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) बिलकुल चुपचाप बैठकर सिर्फ ………………………… बारे में सोचें। (मेरे/अपने/सबके)
(ii) दूसरों की सोच-समझ पर ………………………… रखें। (भरोसा/प्रेम/संदेह)
(iii) ………………………… अन्य नहीं, अंतमय है, हमारे ही प्रतिरूप, हमसे अलग या भिन्न नहीं। (दूसरा /सब/वह)
(iv) ………………………… तरह सारे मनुष्य केवल मनुष्य होते और कुछ नहीं। (इसी/उसी/किसी)
उत्तर:
(2) (i) बिलकुल चुपचाप बैठकर सिर्फ अपने बारे में सोचें।
(ii) दूसरों की सोच-समझ पर भरोसा रखें।
(iii) दूसरा अन्य नहीं, अंतमय है, हमारे ही प्रतिरूप, हमसे अलग या भिन्न नहीं।
(iv) उसी तरह सारे मनुष्य केवल मनुष्य होते और कुछ नहीं।

कृति 2: (स्वमत अभिव्यक्ति)

‘आत्मचिंतन के लाभ’ विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
आत्मचिंतन यानी स्वयं के विषय में चिंतन करना। आत्मचिंतन का अर्थ है किसी कार्य को करने या होने के बाद उसे करने के लिए अपनाई. गई क्रिया और विचार पद्धति का विश्लेषण। आत्मचिंतन के द्वारा हमें अपनी गलतियों से सीखने, साथ ही अपने किए गए कार्य को और बेहतर ढंग से करने का मौका मिलता है। किसी भी व्यक्ति को कोई दूसरा जितना सिखा सकता है, उससे कहीं अधिक वह अपने स्वाध्याय एवं आत्मचिंतन के द्वारा सीख सकता है। इस प्रक्रिया में हम शांत भाव से बैठकर किसी समस्या या मुद्दे के बारे में चिंतन कर सकते हैं।

छात्र जीवन में तो इसकी और भी अधिक आवश्यकता है। अपनी क्षमताओं के विषय में अच्छी तरह जाने-समझे बिना हम लक्ष्य निर्धारित कर लेते हैं। शीघ्रातिशीघ्र उसे प्राप्त कर लेना चाहते हैं और बाद में भटक जाते हैं। इसलिए पहले आत्मचिंतन करें, स्वयं को जानें, फिर लक्ष्य प्राप्ति का प्रयास करें।

गद्यांश क्र. 3
प्रश्न.
निम्नलिखित पठित गद्यांश पढकर दी गई ‘सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) उत्तर लिखिए:

उत्तर:

कृति 2: (स्वमत अभिव्यक्ति)

‘जीवन की सार्थकता के विषय में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
ईश्वर ने हमें सर्वश्रेष्ठ योनि अर्थात मानव योनि में जन्म दिया है। हमारा कर्तव्य है कि हम मानव जाति के लिए कुछ अच्छा कार्य करें। हमें जितनी आयु मिली है, वह समय हम अच्छे कार्यों को करने में लगाएँ। कुछ ऐसा काम करें जिससे समाज और देश का हित हो।

कुछ लोग समय की कमी की बात करते हैं। लेकिन यदि कुछ करने की लगन हो तो समय आड़े नहीं आता। स्वामी विवेकानंद 40 वर्ष की आयु से भी पहले इस संसार से चले गए। ईसा मसीह का 30 वर्ष की आयु में ही प्राणांत हो गया। रामानुजम, रानी लक्ष्मीबाई, नेपोलियन, सिकंदर और अन्य अनेक अल्पायु में ही इस असार संसार को छोड़ गए, फिर भी मानव इतिहास में, ये महापुरुष अपनी छाप छोड़ गए।

सीमित समय में भी जितना अधिक-से-अधिक अच्छा हो सके, हमें देश व समाज के कल्याण के लिए कुछ सकारात्मक अवश्य करना चाहिए।

गद्यांश क्र. 4
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) आकृति पूर्ण कीजिए:

उत्तर:

(2) जोड़ियाँ मिलाइए:

अ	आ
(i) शौक	भविष्य
(ii) एकनिष्ठ	गुलाम
(ii) उज्ज्वल	रास्ते
(iv) दरजनों	सेवा

उत्तर:

अ	आ
(i) शौक	रास्ते
(ii) एकनिष्ठ	सेवा
(iii) उज्ज्वल	भविष्य
(iv) दरजनों	गुलाम

कृति 2: (स्वमत अभिव्यक्ति)

→ ‘जो हम शौक से करना चाहते हैं, उसके लिए रास्ते निकाल लेते हैं, इसका सोदाहरण अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
जिन कामों या चीजों का हमें शौक होता है, जिसमें हमारी रुचि होती है, उसके लिए हम समय, विधा सब निकाल लेते हैं। रुचि सफलता की वाहक है। हम सभी अपनी रुचि के कामों को करते समय उसमें डूब जाते हैं। उसी का परिणाम होता है सफलता। शिक्षा काल में जिस विषय में हमारी रुचि होती है, उसे पढ़ने में हम सारी रात भी जग लेते हैं, जबकि किसी ऐसे विषय की पुस्तक खोलते ही आँखें नींद से भर आती हैं, जो हमें पसंद न हो।

व्यायाम, तैराकी, बागवानी, चित्रकला, गायन, वादन आदि ऐसे अनेक कार्य हैं, जिनका यदि शौक हो तो मनुष्य घंटों बिताने पर भी उनसे ऊब अनुभव नहीं करता। किसी भी काम में सफलता प्राप्त करने के लिए उसमें रुचि होना परम आवश्यक है। बिना रुचि के आगे बढ़ने की संभावना बहुत कम होती है। जिस काम में हमारी रुचि होती है, उसे करने के लिए हम अपनी सारी ऊर्जा लगा देते हैं। न दिन देखते हैं, न ही रात। थकान शब्द तो मानो हमारे शब्दकोश में कभी था ही नहीं।

→ ‘कंप्यूटर ज्ञान का महासागर’ विषय पर तर्कपूर्ण चर्चा कीजिए।
उत्तर:
कंप्यूटर इस पृथ्वी पर कल्पवृक्ष के समान है। जीवन का कोई भी ऐसा क्षेत्र नहीं है, जहाँ इसका महत्व न हो। सूचना के क्षेत्र में कंप्यूटर के कारण अद्भुत क्रांति आ गई है। इंटरनेट इसकी अनुपम देन है। दुनियाभर की जानकारी हम मिनटों में प्राप्त कर सकते हैं। यह एक सेकंड में दस हजार करोड़ गणितीय गणना कर सकता है।

चाहे मौसम का पूर्वानुमान हो या प्राकृतिक गैस और खनिज भंडारों का पता लगाना हो, रेलगाड़ियों और हवाईजहाजों का आरक्षण कराना हो या संसारभर की जानकारी प्राप्त करनी हो, कंप्यूटर के द्वारा घर बैठे हम मिनटों में कर सकते हैं। यह समय-समय पर भौगोलिक सूचनाओं से संबंधित जानकारी भी देता है। मुद्रण व प्रसारण के क्षेत्र में इसका योगदान असीमित है।

कंप्यूटर एक चालक की भाँति वायुयान का संचालन करता है। चालक के बटन दबाते ही कंप्यूटर स्वयं गति और दिशा का निर्धारण कर लेता है। शिक्षा के क्षेत्र में तो आज कंप्यूटर एक अनिवार्यता बन गया है।

→ महानगरीय/ग्रामीण दिनचर्या के लाभ तथा हानि के बारे में अपने अनुभव के आधार पर लिखिए।
उत्तर:
गाँवों में आज भी खुला आसमान है। वहाँ का वातावरण शुद्ध, प्रकृति की गोद में है, जबकि महानगरों में आसमान दिखाई नहीं पड़ता। बड़े पैमाने पर वाहनों से होने वाला प्रदूषण, लगातार होने वाला शोर, भीड़ और धुआँ असहज महसूस कराता है। भीड़भाड़, ट्रैफिक जाम, और अपराध महानगरों में रोज की बात है। गाँवों में एक प्रकार का ठहराव है। शाम ढलते ही चारों ओर एक प्रकार का सन्नाटा पसर जाता है।

जबकि, महानगरों में जीवन हर समय गतिमान रहता है। देर रात तक ऑफिस, दुकानें खुली रहती हैं। बस, ट्रेन, टैक्सियाँ, स्कूटर्स सड़कों पर दौड़ते रहते हैं। गाँवों में धूप, हरियाली और शांति का आनंद प्राप्त कर सकते हैं। लोग आज भी गर्मजोशी से मिलते हैं। एक-दूसरे के दुख-तकलीफ में काम आते हैं। महानगरों में बहुत-से लोग पड़ोसी तक को नहीं पहचानते। दोस्तों, रिश्तेदारों के लिए समय नहीं निकाल पाते।

यहाँ लोगों के पास पैसा है, सुविधाएँ हैं, पर शांति कोसों दूर है। ग्रामीण लोगों का जीवन महानगरों की भागदौड़ से दूर एवं प्रकृति के करीब होता है। दूसरी ओर महानगरों में लोग हमेशा समय को पकड़ने के लिए दौड़ते रहते हैं। अति व्यस्तता के कारण तनाव, फिर स्वास्थ्य। संबंधी विभिन्न परेशानियाँ उन्हें घेर लेती हैं।

अपवठि ग‍दयांश

नम्वलखिि पररचछे‍ पढ़कर सूचना के अनुसार कृवियाँ कीविए:

हर फकसी को आतमरक् करनी होगी, हर फकसी को अपना कत्यय करना होगा। मै फकसी की सहायता की प्राशा नही करता। मै फकसी का भी प्राह नही करता। इस दुफनया से मदद की प्र्या करने का मुझे कोई अफधकार नही है। अतीत मे फिन लोगो ने मेरी मदद की है या भफ‍व् मे भी लोग मेरी मदद करें, मेरे प्र उन सबकी करुण मौिूद है, इसका दा‍व कभी नही फकया सकता। इसीफलए मै सभी लोगो के प्र फचर कक तज ञँ।

तुमहारी पररफस्फत इतनी बुरी देखकर मै बेहद फचंफतत हँ। लेफकन यह लो फक-‘तुमसे भी जयादा दुखी लोग इस संसार मे है। मै तुमसे भी जयादा बुरी पररफस्फत मे हँ। इंग् मे सब कुछ के फलए मुझे अपनी ही िेब से खच् करना पड़ता है। आमदनी कुछ भी नही है। लंदन मे एक कमरे का फकराया हर सप्ह के फलए तीन पाउंड होता है। ऊपर से अनय कई खच् है। अपनी तकलीिो के फलए मै फकससे फशकायत करू? यह मेरा अपना कम्यल है, मुझे ही भुगतना होगा।’

(फ‍ववकानंद की आतमकथा से)

(1) कृवि पूण् कीविए:
1.

2.

(2) उतिर वलखिए:
1. पररचछेद मे उखलिखत देश – [ ]
2. हर फकसी को करना होगा – [ ]
3. लेखक की तकलीिे – [ ]
4. हर फकसी को करनी होगी – [ ]

(3) वन‍देानुसार हल कीविए:
(अ) वनम्वलखिि अर् से मेलनेला शब् उपयु्थ् पररचछे‍ से ढूँढ़कर वलखिए ः
1. स्वं की रक् करना – …………………………….
2. दूसरो के उपकारो को मानने ‍वला – …………………………….

(4) लंग पहचानकर वलखिए:
1. जेब [ ]
2. साहित्य [ ]
3. दावा [ ]
4. सेवा [ ]

खुला आकाश Summary in Hindi

विषय-प्रवेश : प्रस्तुत पाठ डायरी विधा का एक उदाहरण है। कुँवर नारायण जी ने इस पाठ के माध्यम से नगरों की भीड़, वहाँ की जीवन-शैली, जीवन के संघर्ष, आत्मचिंतन आदि पर प्रकाश डाला है। लेखक मानते हैं कि व्यक्ति के विकास में आत्मचिंतन का बड़ा महत्त्व है। इसके द्वारा हम अपनी क्षमताओं के बारे में और अधिक जान सकेंगे। साथ ही अपनी गलतियों से सीख ले सकेंगे।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 4 Do Gazal Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 4 दो गजलें Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 4 दो गजलें Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 4 दो गजलें Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

2. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

3. कृति में दिए गज़ल में प्रयुक्त शब्दों की उचित जोड़ियाँ क्रमशः अ और आ तालिका में लिखिए।

प्रश्न 1.
कृति में दिए गज़ल में प्रयुक्त शब्दों की उचित जोड़ियाँ क्रमशः अ और आ तालिका में लिखिए।

उत्तर:

अ	आ
छाँव	उम्मीद
अनुभव	ज्ञान
पर	उड़ान
जान	जिंदगानी

4. उचित शब्द का चयन करते हुए वाक्य पूर्ण कीजिए।
(मिट्टी, कैद, बंदी, रिहा, छूटना)

प्रश्न 1.
उचित शब्द का चयन करते हुए वाक्य पूर्ण कीजिए।
(मिट्टी, कैद, बंदी, रिहा, छूटना)
i. अजब ये जिंदगी की ……….. है।
ii. रिहाई माँगता है और ……….. होने से डरता है।
उत्तर:
i. कैद
ii. रिहा

5. सूचना के अनुसार शब्द में परिवर्तन कीजिए।

प्रश्न 1.
सूचना के अनुसार शब्द में परिवर्तन कीजिए।

उत्तर:

6. ‘जीवन में डर की जगह सावधानी एवं साहस चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए। 

प्रश्न 1.
‘जीवन में डर की जगह सावधानी एवं साहस चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए।
उत्तर:
डर वह भावना है; जो इंसान को कमजोर बना देती है और साहस वह भावना होती है; जो इंसान के हौसलों में उड़ान पैदा करती है। व्यक्ति को अपने जीवन में डर का त्याग कर साहस और सावधानी को अपनाना चाहिए। उसे प्रत्येक काम साहस के साथ सावधानीपूर्वक करना चाहिए। सावधानी बरतने से व्यक्ति के सारे काम सुचारू रूप से पूर्ण होते हैं। साहस असंभव कार्य को भी संभव बनाने की शक्ति रखता है। जो व्यक्ति अपने जीवन में साहस को नहीं अपनाता है: वह व्यक्ति कभी भी सफल नहीं होता। जीवन में कई सफल व्यक्ति हैं, जिन्होंने डर की जगह सावधानी एवं साहस को अपनाकर संसार में अद्भुत कार्य करके सभी को अपने प्रभावी व्यक्तित्व से प्रेरित किया।

भाषा बिंदु :

प्रश्न 1.
निम्नलिखित वाक्यों के रचना के अनुसार भेद लिखिए।

1. वह आदमी भी उस गाँव में रहने के लिए तैयार हो गया। [ ]
2. स्टेशन मास्टर ने सिग्नल नहीं दिया और गाड़ी आउटर पर खड़ी रही। [ ]
3. मजे की बात यह है कि एक समाचारपत्र के कितने उपयोग हो सकते हैं। [ ]
4. वह पशु-पक्षियों के बीच बातें करता दिखाई देता। [ ]
5. आप उस गाँव में जाएंगे तो आपको उस खोए हुए आदमी की वहाँ स्थापित मूर्ति दिख जाएगी। [ ]
6. नींद आती रहती है, जाती रहती है और रह-रहकर टूटने के बावजूद उसमें लय बनी होती है। [ ]

उत्तर:

1. सरल वाक्य
2. संयुक्त वाक्य
3. मिश्र वाक्य
4. सरल वाक्य
5. मित्र वाक्य
6. संयुक्त वाक्य

प्रश्न 2.
पाठों में आए रचना के अनुसार वाक्यों के दो-दो उदाहरण लिखिए।
उत्तरः
1. सरल वाक्य :
i. इससे मेरा भी मन बड़ा दुखी होता है।
ii. मैंने सबकी बात सुनी है।

2. मिश्र वाक्य :
i. जैसी करनी वैसी भरनी।
ii. हमें चाहिए कि हम हवा और पानी को अपना दोस्त बनाकर उन्हें नुकसान न पहुँचाएँ।

3. संयुक्त वाक्य :
i. सोना तो मिट्टी है और मिट्टी का मोह पालकर आज तक किसी ने शांति नहीं पाई।
ii. लोग उसके दर्शन को आने लगे और धीरे-धीरे चारोंतरफ साधु का यश फैल गया।

प्रश्न 3.
निम्नलिखित वाक्यों के अर्थ के अनुसार भेद लिखिए।

1. सुबह उठता हूँ तो थोड़ी ताजगी महसूस होती है। [ ]
2. अरे, वहीं अटके रहोगे, मुझसे बात नहीं करोगे? [ ]
3. कई दिनों तक मैं तुम्हारे चौके में नहीं गई। [ ]
4. ठीक है, मुकदमें की कार्यवाही शुरू करें। [ ]
5. अरे! हवा रानी, नाराज मत हो। [ ]
6. इस बात के लिए ये गाँववाले ही जिम्मेदार हैं। [ ]
7. अधिक वर्षा के लिए कौन जिम्मेदार है? [ ]
8. अच्छा! निकलती हूँ बस पाँच मिनट चाहिए मुझे तैयार होने के लिए। [ ]
9. हौं राजीव, आओ बैठो।
10. यह एक भोले इंसान का विश्वास नहीं था।

उत्तर:

1. विधानार्थक वाक्य
2. प्रश्नार्थक वाक्य
3. निषेधार्थक वाक्य
4. आज्ञार्थक वाक्य
5. आज्ञार्थक वाक्य
6. विधानार्थक वाक्य
7. प्रश्नार्थक वाक्य
8. विस्मयादिबोधक वाक्य
9. आज्ञार्थक वाक्य
10. निषेधार्थक वाक्य

प्रश्न 4.
पाठों में आए अर्थ के अनुसार वाक्यों के दो-दो उदाहरण लिखिए।
उत्तरः
1. विधानार्थक वाक्य :
i. मैं तेजी से वहाँ जाती हूँ।
ii. महाराज यह आरोप झूठा है।

2. आज्ञार्थक वाक्य :
i. पहले पानी को बुलाया जाए।
ii. सेठ मेरा इनाम दें।

3. निषेधार्थक वाक्य :
i. कहीं भी कोई नहीं था।
ii. उसमें भी मेरा कुछ नहीं है।

4. प्रश्नार्थक वाक्य :
i. तू कौन है?
ii. उसकी माया में मुझे क्यों फँसाता है?

5. विस्मयादिबोधक वाक्य :
i. काश, अपने गाँव-शहर में हमें भी ऐसा ‘खोया हुआ आदमी’ मिल जाता!
ii. हाँ महाराज! आज सब शिकायतें हवा और पानी के बारे में हैं।

6. संदेहसूचक वाक्य :
i. शायद मैं खो गया हूँ।
ii. संभव है कि पानी दूषित होने से बच जाए।

उपयोजित लेखन :

प्रश्न 1.
अपने विद्यालय में आयोजित की जानेवाली क्रीड़ा प्रतियोगिताओं का आयोजक के नाते विज्ञापन तैयार कीजिए।

उत्तरः

Hindi Lokvani 10th Std Textbook Solutions Chapter 4 दो गजलें Additional Important Questions and Answers

(अ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तरः

प्रश्न 2.
पद्यांश में प्रयुक्त प्राकृतिक घटकों के नाम
उत्तरः

कृति अ (2) : शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. आसमान
2. पर
3. इतमीनान
4. सोच

उत्तरः

1. अंबर
2. पंख
3. तसल्ली
4. विचार

प्रश्न 2.
पद्यांश में प्रयुक्त ऐसे दो शब्द लिखिए जिनके वचन परिवर्तित नहीं होते हैं।
उत्तर:
i. पेड़
ii. पर

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. हवा में उड़ने की क्रिया
उत्तरः
i. उड़ान

प्रश्न 4.
निम्नलिखित शब्द के अनेक अर्थ लिखिए।
i. फल
ii. पर
उत्तर:
i. फल : खाने का फल, परिणाम
ii. पर : परंतु, पंख

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘अनुभव सबसे बड़ा शिक्षक होता है।’ अपने विचार लिखिए।
उत्तरः
जीवन-रूपी यात्रा में सीखने के लिए कोई किताब साथ नहीं होती। व्यक्ति अपने अनुभवों से ही सीखता है। व्यक्ति जीवन में कार्य करते समय कई गलतियाँ करता रहता है। उन गलतियों से उसका अनुभव समृद्ध हो जाता है। वह फिर से उन गलतियों को नहीं दोहराता। वह अपनी गलतियों से बहत सारी बातें सीखता है और स्वयं के अनुभव को समृद्ध बनाता है। अनुभव सोने के समान होता है।

जिस प्रकार सोना तप-तप कर तैयार हो जाता है उसी प्रकार अनुभव दिन-रात की मेहनत एवं लगन से प्राप्त किया जाता है। व्यक्ति के जीवन में आने वाले अच्छे-बुरे अनुभव उसके मार्गदर्शक बनते हैं। अनुभव से मिलने वाला ज्ञान व्यक्ति को सफलता के शिखर पर पहुँचा देता है। अनुभवहीन ज्ञान जीवन की सच्चाई के सामने टिक नहीं पाते। अत: अनुभव ही सबसे बड़ा शिक्षक होता है।

(आ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
समझकर लिखिए।
उत्तरः

प्रश्न 3.
निम्नलिखित गलत विधान सही करके लिखिए।
i. प्रकृति ने हमें जिंदगी बख्शी है।
उत्तरः
ईश्वर ने हमें जिंदगी बख्शी है।

ii. ईश्वर सायबान निर्माण करेगा।
उत्तर:
इंसान सायबान निर्माण करेगा।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए।

1. संसार
2. स्वयं
3. आशा
4. ईश्वर

उत्तर:

1. दुनिया
2. खुद
3. उम्मीद
4. खुदा

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. छाया
उत्तर:
i. छाँव

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. घर के आगे छाया हेतु बनाया गया छप्पर
उत्तर:
i. सायबान

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘व्यक्ति को जीवन में आत्मनिर्भर होना चाहिए। उसे दूसरों से मदद की अपेक्षा नहीं रखनी चाहिए।’ अपने विचार लिखिए।
उत्तर:
आत्मनिर्भर यानी स्वावलंबी। व्यक्ति को अपने जीवन में आत्मनिर्भर होना चाहिए। उसे दूसरों पर आश्रित नहीं होना चाहिए। यदि व्यक्ति अपने जीवन में दूसरों पर आश्रित रहता है, तो वह तरक्की नहीं कर सकता है। आत्मनिर्भर बनने के लिए व्यक्ति में दृढ़ इच्छा शक्ति का होना जरूरी होता है। आत्मनिर्भर व्यक्ति सदैव कोशिश करते रहता है। इसलिए वह सफलता की मंजिल हासिल करने में सफल हो जाता है। वह भाग्य के भरोसे नहीं बैठता है। आत्मनिर्भर बनकर वह अपनी क्षमताओं का विकास कर लेता है। अब्राहम लिंकन व नेपोलियन जैसे महापुरुषों का जन्म निर्धन परिवार में हुआ था। उन्होंने जीवन में आत्मनिर्भर बनकर सफलता की सीढ़ी हासिल की। इसलिए प्रत्येक व्यक्ति को अपने जीवन में आत्मनिर्भर होना चाहिए।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. अजब
ii. रिहाई
उत्तर:
i. जिंदगी की कैद कैसी है?
ii. दुनिया का हर इंसान क्या माँगता है?

प्रश्न 2.
पद्यांश के आधार पर समझकर लिखिए।
i. इंसान के बस और काबू में ये नहीं है –
ii. हर शख्स इसका बना खिलौना है –
उत्तर:
i. इंसान के बस में जिंदगी नहीं है और काबू में मौत नहीं है।
ii. मिट्टी का

कृति इ (2) : शब्द संपदा

प्रश्न 1.
निम्न शब्दों में उचित उपसर्ग का प्रयोग कीजिए।

1. मौत
2. पल
3. काबू

उत्तर:

1. बेमौत
2. हरपल
3. बेकाबू

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. मृदा
उत्तर:
i. मिट्टी

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. फना
2. मौत
3. रिहाई
4. काबू

उत्तर:

1. नष्ट
2. मृत्यु
3. मुक्ति
4. नियंत्रण

प्रश्न 4.
विलोम शब्द लिखिए।
i. बड़ा × ……….
i. जिंदगी × ………….
उत्तर:
i. छोटा
ii. मौत

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
बचपन की दुनिया और बड़ों की दुनिया में क्या अंतर है? अपने विचार लिखिए।
उत्तर:
बचपन की दुनिया में मासूमियत होती है और बड़ों की दुनिया मुश्किलों और परेशानियों से भरी होती है। बचपन जीवन की एक ऐसी अवस्था होती है; जहाँ पर जीवन का मस्ती से आनंद लिया जाता है और बड़ों की दुनिया जिम्मेदारियों से भरी होती है। कई लोगों को इस कारण जिंदगी कैद के समान लगती है।

लेकिन बच्चों के लिए जिंदगी खुशियाँ एवं प्यार लेकर आती है। मुस्कुराना, शरारत करना, रूठना और फिर सब भुलाकर एक हो जाना; ये बच्चों की पहचान होती है। वहीं बड़ों के जीवन में ईर्ष्या, द्वेष एवं कलह होता है। बच्चे दुनियादारी के झमेलों से दूर होते हैं, तो बड़ों की दुनिया कई प्रकार के झमेले में उलझती रहती है।

दो गजलें Summary in Hindi

कवि-परिचय :

जीवन-परिचय : राजेश रेड्डी जी का जन्म सन १९५२ में महाराष्ट्र के नागपुर में हुआ था। राजेश जी हिंदी, अंग्रेजी व उर्दू भाषा के ज्ञाता हैं। जगबीती को आपबीती में परिवर्तित कर गज़ल लिखने में रेड्डी जी कुशल माने जाते हैं। ये विविध भारती, मुंबई से भी जुड़े हैं। इन्होंने अपनी प्रतिभा से गज़ल एवं नाटक विधा को समृद्ध किया है।
प्रमुख कृतियाँ : ‘उड़ान’, ‘आसमान से आगे’, ‘वजूद’ (गज़ल संग्रह) आदि।

पद्य-परिचय :

गज़ल : ‘गज़ल’ यह अरबी साहित्य की प्रसिद्ध काव्य-विधा है। गज़ल एक ही बहर और वज़न के अनुसार लिखे गए शेरों का समूह है। इसके पहले शेर को मतला कहते हैं। गज़ल के अंतिम शेर को मक़्ता कहते हैं।
प्रस्तावना : ‘दो गज़लें’ इस गज़ल में दो गज़लें सम्मिलित की गई हैं। पहले गज़ल से हमें यह संदेश मिलता है कि व्यक्ति के पास कोई भी कार्य करने से पहले जोश, उत्साह, ज्ञान, आत्मविश्वास आदि का होना जरूरी होता है। दूसरी गज़ल में कवि ने बताया है कि बचपन मासूमियत से भरा होता है। बड़े होने पर परेशानियाँ आती हैं, जिस कारण इंसान अनेक प्रकार की परेशानियों से घिर जाता है।

सारांश :

‘दो गज़लें’ यह एक गज़ल है। इस गज़ल के द्वारा कवि कहता है कि व्यक्ति को कोई भी कार्य करने से पहले अपने आप में जोश, उत्साह, आत्मविश्वास आदि का निर्माण करना चाहिए। व्यक्ति को कोई भी कार्य करने से पहले अपनी आँखों से जिंदगी को पढ़ लेना चाहिए। खुद के अनुभवों से प्राप्त ज्ञान के बिना कार्य की पूर्ति नहीं होती। जीवन में संयम व धैर्य का बहुत बड़ा महत्त्व होता है। कवि मानवतावादी है। अत: वह मानव की भलाई की कामना रखता है।

व्यक्ति को दूसरों से अपेक्षा रखने के बजाय स्वयं आत्मनिर्भर होना चाहिए। प्रत्येक व्यक्ति को ऐसी वाणी में सबके साथ वार्तालाप करना चाहिए कि उसके विचार दूसरों के हृदय में सदा के लिए बस जाए। कवि इस गज़ल के माध्यम से कहता है कि आज का व्यक्ति दुख, तकलीफों और परेशानियों से चारों ओर से घिर चुका है। दुनिया-समाज में पड़कर व्यक्ति की बचपन जैसी मासूमियत खोने लगी है। वह नश्वर है। फिर भी उसकी महत्वाकांक्षा पूरी होती नहीं दिखती। वह अपनी ही जिंदगी में कैद हो गया है। वह मुक्ति भी पाना चाहता है. और इच्छाओं को भी नष्ट करना नहीं चाहता।

भावार्थ :

पहले इक आसमान …………………… उड़ान पैदा कर।
व्यक्ति को कोई भी कार्य करने से पहले अपने आप में जोश, उत्साह व आत्मविश्वास उत्पन्न करना चाहिए। इसलिए कवि कहते हैं कि व्यक्ति को अपने परों में यानी मन में हौसला भरने से पहले आसमान यानी सकारात्मक परिस्थिति उत्पन्न कर लेनी चाहिए। सकारात्मक परिस्थिति व आत्मविश्वास के बिना व्यक्ति सफलता की ऊंची मंजिल हासिल नहीं कर सकता।

अपनी आँखों से ………………. पैदा कर।
व्यक्ति को कोई भी कार्य करने से पहले अपनी आँखों से जिंदगी को पढ़ लेना चाहिए। स्वयं के अनुभवों से प्राप्त ज्ञान के बिना कार्य की पूर्ति नहीं होती। व्यक्ति का अनुभव समृद्ध होना बेहद जरूरी है। अनुभव समृद्ध व्यक्ति के पास ज्ञान का भंडार होता है। अनुभवों के द्वारा ही व्यक्ति को ज्ञान की प्राप्ति होती है।

सब के पेड़ ………………… पैदा कर।
जीवन में संयम व धैर्य का बहुत ही महत्त्व होता है। संयम व धैर्य के बिना मनुष्य को मनचाहे फल की प्राप्ति नहीं हो सकती। कहा भी । गया है कि सब्र का फल मीठा होता है। धैर्य और संयम से आज नहीं तो कल सब का फल जरूर मिलता है। इसलिए व्यक्ति की सोच में भी इतमीनान यानी तसल्ली होनी चाहिए। उसे कोई भी कार्य करने से पहले तसल्ली से सोचना चाहिए।

ऐ खुदा! ………………………… पैदा कर।
कवि इंसान का भला चाहता है। वह नहीं चाहता कि इंसान दुख-दर्द में अपना जीवन व्यतीत करे। इंसान के जीवन में खुशहाली आए । इसलिए कवि ईश्वर से ऐसे सुंदर संसार की कामना करता है; जहाँ पर व्यक्ति सुख-चैन के साथ अपना जीवन जी सके।

तूने बख्शी है …………………….. पैदा कर।
कवि मानवतावादी है। अत: वह मानव की भलाई की कामना रखता है। वह ईश्वर से कहता है, “हे ईश्वर, तूने सभी को जिंदगी का । अनमोल उपहार दिया है। अत: तू ही इस जिंदगी में जान भरने का कार्य कर । तू ही लोगों में जिंदादिली निर्माण कर; ताकि लोग इस जिंदगी के सफर का आनंद ले सकें।

छोड़ दुनिया से ………………….. पैदा कर।
व्यक्ति को जीवन में किसी से भी, कोई भी उम्मीद नहीं रखनी चाहिए। व्यक्ति को दूसरों से उम्मीद रखने के बजाय स्वयं आत्मनिर्भर होना चाहिए। व्यक्ति को दूसरों से सहायता की अपेक्षा नहीं रखनी चाहिए; बल्कि स्वयं ही प्रकाशित होकर स्वयं की जिंदगी को उज्ज्वल बनाना चाहिए। दूसरों से छाँव की अपेक्षा रखने के बजाय स्वयं ही सायबान बनकर खुद को और दूसरों के जीवन में भी छाँव उत्पन्न करनी चाहिए।

दिल से निकले ………………… पैदा कर।
व्यक्ति की वाणी सरल, सहज और मीठी होनी चाहिए। उसके बोलने वाले शब्द दिल से निकले होने चाहिए। यदि वह इस प्रकार वाणी : का प्रयोग करेगा, तो निश्चित ही वह दूसरों की निगाहों में और दिलों में आसानी से जगह प्राप्त कर लेगा।

यहाँ हर शख्स …………………. डरता है।
कवि कहते हैं कि हर इंसान अपनी मृत्यु से सदा भयभीत रहता है। वह अपने ऊपर होनेवाले हादसों और आपदाओं से डरता रहता है। । 5. आखिर इंसान मिट्टी से बना हुआ एक खिलौना ही तो है। उसे एक दिन टूटना ही है। फिर भी वह न जाने क्यों नष्ट होने से डरता रहता है।

मेरे दिल के किसी ……………………… डरता है।
बचपन की मासूमियत सभी को प्यारी और अच्छी लगती है। उसे कोई भी भूलना नहीं चाहता। हर व्यक्ति के दिल में कहीं न कहीं बचपना छिपा रहता है। लेकिन बड़ों की दुनिया जो दुख और तकलीफों से भरी है, उसे देखकर वह अपने बचपन को कहीं न कहीं बचाए रखना चाहता । है। वह बड़ों की दुनिया के साथ बड़ा होना नहीं चाहता क्योंकि बड़ों की दुनिया में मासूमियत नहीं होती।

शब्दार्थ :

1. आसमान – अंबर
2. पर – पंख
3. सोच – विचार
4. इतमीनान – तसल्ली , ढाढ़स
5. जहान – संसार, जगत
6. खुदा – ईश्वर
7. उम्मीद – आशा, भरोसा
8. खुद – स्वयं
9. हादिसा – आपदा
10. फना – नष्ट
11. मौत – मृत्यु
12. रिहाई – मुक्ति
13. काबू – नियंत्रण, वश
14. सायबान – घर के आगे छाया हेतु बनाया हुआ छप्पर
15. जान – प्राण, जीवन
16. सब्र – सबर, संयम, धैर्य

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Std 10 Hindi Chapter 10 Budhi Kaki Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Chapter 10 बूढ़ी काकी Notes, Textbook Exercise Important Questions, and Answers.

Hindi Lokbharti 10th Digest Chapter 10 बूढ़ी काकी Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 10 बूढ़ी काकी Textbook Questions and Answers

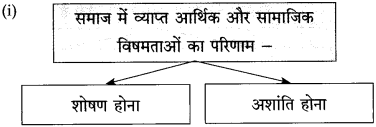
कृति

(कृतिपत्रिका के प्रश्न 3 (अ) के लिए

* सूचना के अनुसार कृतियाँ कीजिए :

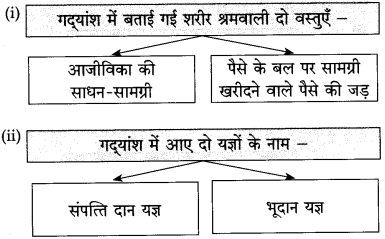
प्रश्न 1.

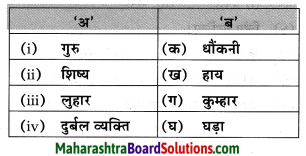
स्वभाव के आधार पर पात्र का नाम
१.	क्रोधी	………………….
२.	लालची	………………….
३.	शरारती	………………….
४.	स्नेहिल	………………….

उत्तर:

स्वभाव के आधार पर पात्र का नाम
१.	क्रोधी	रूपा
२.	लालची	बुद्धिराम
३.	शरारती	दोनों लड़के
४.	स्नेहिल	लाड़ली

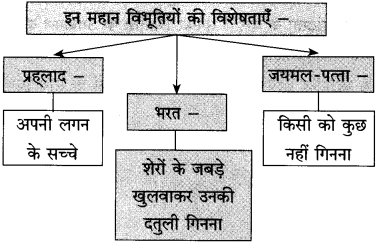
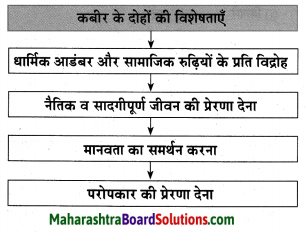
प्रश्न 2.
कृति पूर्ण कीजिए:

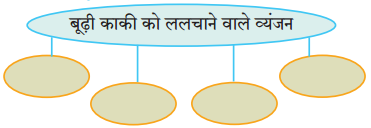
उत्तर:

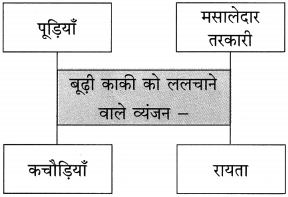
प्रश्न 3.
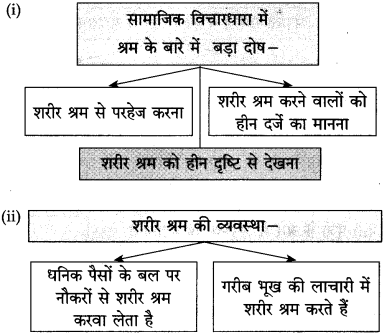
बुद्धिराम का काकी के प्रति दुर्व्यवहार दर्शाने वाली चार बातें :
१) ………………….
४) ………………….
२) ………………….
४) ………………….
उत्तर :
(i) बूढ़ी काकी की संपत्ति अपने नाम लिखाते समय किए गए लंबे-चौड़े वादों को बुद्धिराम द्वारा न निभाना।
(i) बूढ़ी काकी को भरपेट भोजन न देना।
(iii) भोजन कर रहे मेहमानों के बीच रेंगती हुई बूढ़ी काकी के पहुँच जाने पर बुद्धिराम द्वारा निर्दयतापूर्वक पकड़कर उनकी कोठरी में ले जाकर पटक देना।
(iv) बूढ़ी काकी के व्यवहार से रुष्ट होने के कारण तिलक उत्सव में सभी मेहमानों और घरवालों के भोजन कर लेने के बाद भी बुद्धिराम द्वारा उन्हें खाने के लिए न पूछना।

प्रश्न 4.
कारण लिखिए :
a. बूढ़ी काकी ने भतीजे के नाम सारी संपत्ति लिख दी _____________________
b. लाड़ली ने पूड़ियाँ छिपाकर रखीं _____________________
c. बुद्धिराम ने काकी को अँधेरी कोठरी में धम से पटक दिया _____________________
d. अंग्रेजी पढ़े नवयुवक उदासीन थे _____________________
उत्तर:
a. बूढ़ी काकी के परिवार में अब एक भतीजे के सिवाय और कोई नहीं था, इसलिए उन्होंने भतीजे के नाम सारी संपत्ति लिख दी।
b. बुद्धिराम और रूपा दोनों ने ही बूढ़ी काकी को उनकी निर्लज्जता के लिए दंड देने का निश्चय कर लिया था। इसलिए बूढ़ी काकी को किसी ने नहीं पूछा।
c. बूढ़ी काकी रेंगती हुई भोजन कर रहे मेहमान मंडली के बीच पहुँच गई थी। इससे कई लोग चौंककर उठ खड़े हुए थे। बुद्धिराम को इससे गुस्सा आया और उसने काकी को वहाँ से उठाकर कोठरी में ले जाकर धम से पटक दिया।
d. अंग्रेजी पढ़े नवयुवक उदासीन थे, क्योंकि वे गँवार मंडली में बोलना अथवा सम्मिलित होना अपनी प्रतिष्ठा के प्रतिकूल समझते थे।

प्रश्न 5.
सूचना के अनुसार शब्द में परिवर्तन कीजिए :

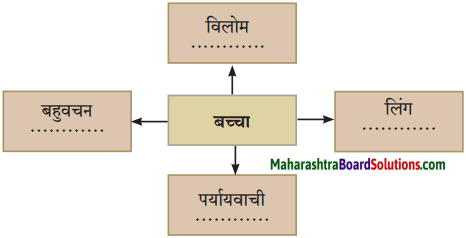
उत्तर :

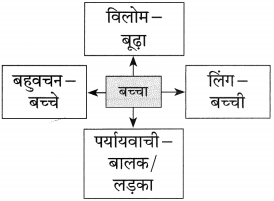
अभिव्यक्ति

‘बुजुर्ग आदर-सम्मान के पात्र होते हैं, दया के नहीं इस सुवचन पर अपने विचार लिखिए।
उत्तर :
हमें यह बात याद रखनी चाहिए कि आज जो व्यक्ति बुजुर्ग है वह हमेशा बूढ़ा और असहाय नहीं था। वह भी पहले युवा था। उसने अपने परिवार का पालन-पोषण और उसकी देखरेख की थी। उसने तरह-तरह की समस्याओं का सामना किया था और उन्हें अपने तरीके से हल किया था। उसे जीवन जीने का अनुभव है। लेकिन वृद्ध हो जाने पर किसी-किसी परिवार में बुजुर्गों को किनारे कर दिया जाता है। उनकी सलाह या सुझाव को कोई महत्त्व नहीं दिया जाता। इस तरह के व्यवहार से बुजुर्गों को अपने सम्मान पर ठेस लगती महसूस होती है।

किसी-किसी परिवार में तो बुजुर्गों के खाने-पीने की भी किसी को चिंता नहीं रहती। घर के लोग अपने में मगन रहते हैं और बुजुर्गों का कोई ख्याल नहीं रखता। बुजुर्गों को खाने-पीने के लिए उनका मुँह ताकना पड़ता है। हमें यह बात नहीं भूलनी चाहिए कि हम इन बुजुर्गों की संतान हैं। उनको पर्याप्त सम्मान देना और उनकी हर प्रकार से देखरेख करना हमारा फर्ज है। बुजुर्गों की प्रसन्नता और उनके आशीर्वाद से ही परिवार फूलता-फलता और खुशहाल रहता है। इसलिए बुजुर्गों को हमें सदा आदर-सम्मान देना चाहिए और उनकी देखरेख करनी चाहिए।

भाषा बिंदु

प्रश्न 1.
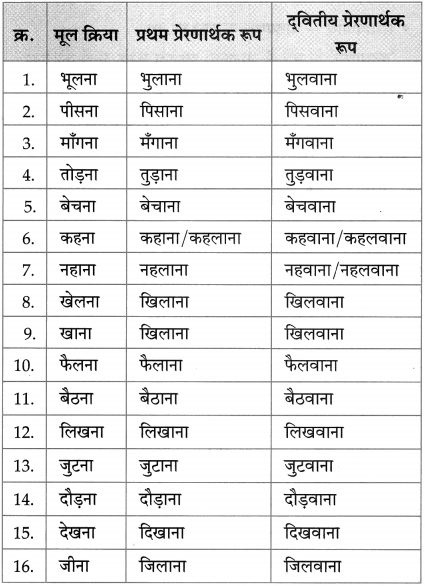
निम्नलिखित क्रियाओं के प्रथम तथा द्वितीय प्रेरणार्थक रूप लिखिए :

मूल क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
भूलना	……………………….	……………………….
पीसना	……………………….	……………………….
माँगना	……………………….	……………………….
तोड़ना	……………………….	……………………….
बेचना	……………………….	……………………….
कहना	……………………….	……………………….
नहाना	……………………….	……………………….
खेलना	……………………….	……………………….
खाना	……………………….	……………………….
फैलना	……………………….	……………………….
बैठना	……………………….	……………………….
लिखना	……………………….	……………………….
जुटना	……………………….	……………………….
दौड़ना	……………………….	……………………….
देखना	……………………….	……………………….
जीना	……………………….	……………………….

उत्तर :

प्रश्न 2.
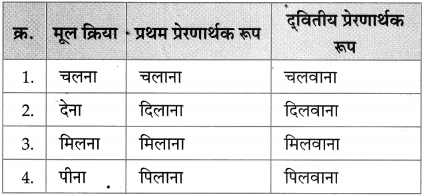
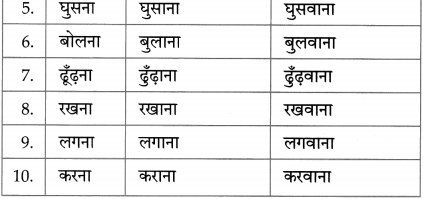
पठित पाठों से किन्हीं दस मूल क्रियाओं का चयन करके उनके प्रथम तथा द्वितीय प्रेरणार्थक रूप निम्न तालिका में लिखिए :

मूल क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….
……………………….	……………………….	……………………….

उत्तर :

उपयोजित लेखन

मेरा प्रिय वैज्ञानिक’ विषय पर निबंध लेखन कीजिए।
उत्तर :
यों तो दुनिया में एक-से-एक बड़े वैज्ञानिक हैं, पर मेरे प्रिय वैज्ञानिक तो सर जगदीशचंद्र बोस ही हैं। सर जगदीशचंद्र बोस की बात ही निराली है। उन्होंने यह सिद्ध करके बता दिया कि पेड़-पौधे भी हमारी तरह साँस लेते हैं और उन्हें पानी और भोजन की आवश्यकता होती है। उनमें भी जान होती है। यदि पेड़-पौधों को सताया या कष्ट दिया जाए, तो वे बीमार हो जाते हैं और उनकी प्रकृति के विरुद्ध उन्हें भोजन दिया जाए अथवा जहरीला रसायन दिया जाए, तो वे मर जाते हैं। वैसे पेड़-पौधों के संपर्क में रहने वाले प्रत्येक व्यक्ति को मालूम होता है कि पेड़-पौधों को नुकसान पहुँचाने या विषैले पदार्थों के संपर्क में आने से वे क्षतिग्रस्त या मृत हो सकते हैं, पर इस बात को सिद्ध किया था सर जगदीशचंद्र बोस ने।

अपने शोध को सिद्ध करने के लिए उन्होंने खुद चुंबकीय क्रेश्कोग्राफ नामक यंत्र तैयार किया। उन्होंने इस यंत्र की सहायता से सब के सामने अपने प्रयोग से यह सिद्ध कर दिया कि पेड़-पौधों में जीवन होता है और प्राणियों की तरह उनमें भी विभिन्न क्रियाएँ होती हैं। इस प्रकार के सूक्ष्म रहस्य का उद्घाटन करने वाले वे पहले वैज्ञानिक थे। वे सच्चे अर्थों में एक महान वैज्ञानिक थे। ऐसे महान वैज्ञानिक पर हमें गर्व है।

Hindi Lokbharti 10th Textbook Solutions Chapter 10 बूढ़ी काकी Additional Important Questions and Answers

गद्यांश क्र.1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
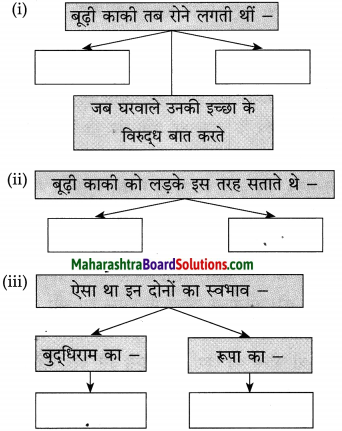
आकृति पूर्ण कीजिए :


उत्तर:

प्रश्न 2.
उत्तर लिखिए :
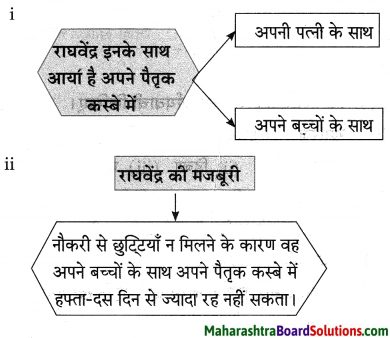
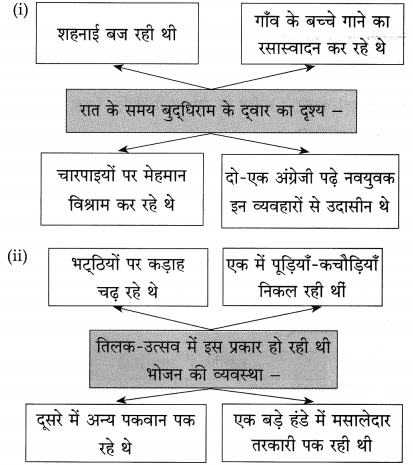
(i) बूढ़ी काकी का शारीरिक स्वास्थ्य –
(ii) बूढ़ी काकी के परिवार में अब बचा एकमात्र सदस्य –
(iii) बुद्धिराम ने इस तरह लिखाई बूढ़ी काकी की संपत्ति –
(iv) बूढ़ी काकी के रोने का ढंग –
उत्तर:
(i) बूढ़ी काकी के नेत्र, हाथ, पैर आदि सभी अंग जवाब दे चुके थे।
(ii) उनका भतीजा बुद्धिराम।
(iii) खूब लंबे-चौड़े वादे करके।
(iv) बूढ़ी काकी गला-फाड़कर रोती थीं।

प्रश्न 3.
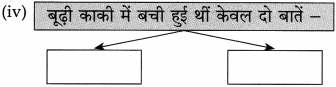
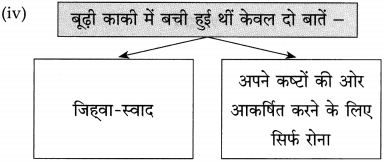
आकृति में दिए गए रिक्त स्थानों में उत्तर लिखकर आकृति पूर्ण कीजिए :

उत्तर:

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
बुढ़ापा बहुधा बचपन का पुनरागमन होता है’ इस विषय पर अपने विचार 25 से 30 शब्दों में व्यक्त कीजिए।
उत्तर :
कहते हैं, बुढ़ापा बचपन का ही एक रूप है। वृद्धावस्था : में मनुष्य की हरकतें बच्चों जैसी हो जाती हैं। इस अवस्था में मनुष्य के अंग-प्रत्यंग कमजोर हो जाते हैं और उन्हें बच्चों की तरह दूसरों का सहारा लेना पड़ता है। दिमाग कमजोर हो जाता है। दाँत गिर जाते हैं और मनुष्य का मुँह बच्चों की तरह पोपला हो जाता है। इतना ही नहीं, बच्चों की तरह ही वृद्धों को भी मान-अपमान की परवाह नहीं होती। जिस तरह लोग बच्चों की बातों पर ध्यान नहीं देते, उसी तरह वृद्धों की बातों पर भी कोई ध्यान नहीं देता। उनकी इच्छा-अनिच्छा का भी कोई महत्त्व नहीं होता। इस तरह वृद्धावस्था और बचपन की अधिकांश बातों में समानता होती है। इसलिए कहा जा सकता है कि बुढ़ापा बहुधा बचपन का पुनरागमन होता है।

गद्यांश क्र.2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए :

उत्तर:

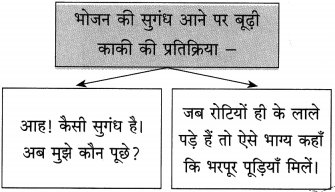
प्रश्न 3.
कारण लिखिए :
(i) उत्सव के दिन बूढ़ी काकी को अपनी स्थिति पर रोना आया, पर वे रो नहीं सकीं।
उत्तर:
(i) उत्सव के दिन बूढ़ी काकी को अपनी स्थिति पर रोना आया, पर वे रो नहीं सकीं, क्योंकि उन्हें रूपा का डर था।

प्रश्न 4.
त्तर लिखिए :
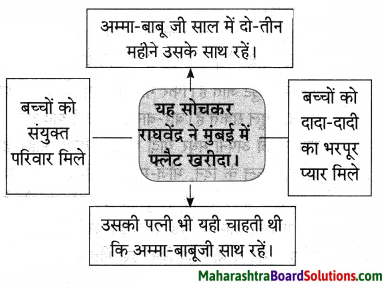
मुखराम के तिलक उत्सव की तैयारियाँ :
उत्तर:
मुखराम के तिलक उत्सव की तैयारियाँ :
(i) पूड़ियाँ-कचौड़ियाँ निकल रही थीं।
(ii) एक बड़े हंडे में मसालेदार तरकारी पक रही थी।

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
‘बुढ़ापा तृष्णा रोग का अंतिम समय है’ इस विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर :
मनुष्य के जीवन की चार अवस्थाएँ होती हैं – बचपन, किशोरावस्था, युवावस्था और बुढ़ापा। अपने जीवन में मनुष्य की तरह-तरह की कामनाएँ होती हैं और उनकी पूर्ति करने का वह भरसक प्रयास करता है। बचपन से लेकर युवावस्था तक मनुष्य को अपनी कामनाओं की जल्द से जल्द पूरी होने की उतनी चिंता नहीं रहती, जितनी बुढ़ापे में। वृद्धावस्था में मनुष्य के जीवन के गिने-चुने वर्ष ही बचे होते हैं। इसलिए उसका प्रयास यह होता है कि अपने बचे-खुचे दिनों में वह अपनी सारी कामनाएं पूरी कर ले। ऐसे में उसे किसी भी तरह अपने उद्देश्य को पूरा कर लेना उचित जान पड़ता है। उसके लिए उसे बुरे-भले, मान-अपमान की परवाह नहीं होती। उसका लक्ष्य येनकेन प्रकारेण अपनी इच्छा पूरी करना होता है। इस प्रकार बुढ़ापा तृष्णा रोग का अंतिम समय है।

गद्यांश क्र.3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1 : (आकलन)

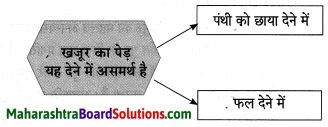
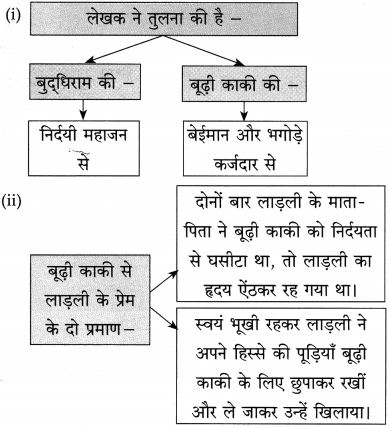
प्रश्न 1.
उत्तर लिखिए :

उत्तर :

प्रश्न 2.
आकृति पूर्ण कीजिए :

उत्तर :

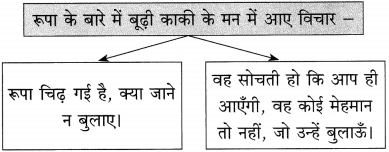
कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
‘लड़कों का बूढों से स्वाभाविक विवेष होता ही है’ इस विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर :
लड़कों और बूढ़ों के बीच पीढ़ियों का अंतर होता है। लड़कों और बूढ़ों में हर बात को लेकर अंतर होना स्वाभाविक है। अधिकांश बूढ़ों की आदत होती है कि वे हर बात को अपने ढंग से सोचते हैं। वे उसमें अपने जमाने की विचारधारा थोपने की कोशिश करते हैं। इसका कारण यह है कि किसी चीज के बारे में उनकी एक धारणा बनी होती हैं। हर बात को वे अपने पैमाने पर कसने की कोशिश करते हैं। जब कि नई पीढ़ी के लड़कों की सोच अलग ढंग की होती हैं। उन्हें पुराने दकियानूसी विचार पसंद नहीं आते। इसलिए बात-बात पर दोनों के विचारों में टकराव होता है। इस तरह लड़कों और बूढ़ों में स्वाभाविक विद्वेष होता है।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई । सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए :

उत्तर:

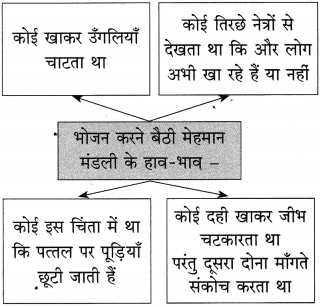
प्रश्न 2.
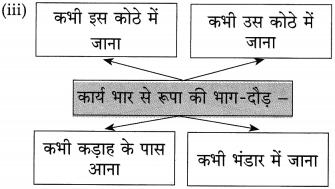
उत्तर लिखिए :

उत्तर:

प्रश्न 3.
कारण लिखिए :
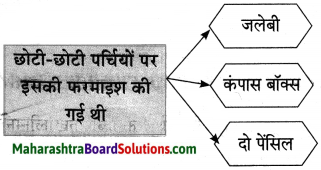
(i) घरवालों ने भोजन किया, परंतु बूढ़ी काकी को किसी ने नहीं पूछा –
(ii) रात के ग्यारह बज गए थे। लाड़ली की आँखों में नींद न थी –
उत्तर:
(i) लाड़ली उन पूड़ियों को बूढ़ी काकी के पास ले जाना चाहती थी, ताकि वे उन्हें खा सके।
(ii) बूढ़ी काकी को पूड़ियाँ खिलाने की खुशी लाड़ली को सोने न देती थी।

गद्यांश क्र.5
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए :

कृति 1 : (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए :


उत्तर :

प्रश्न 2.
कारण लिखिए :
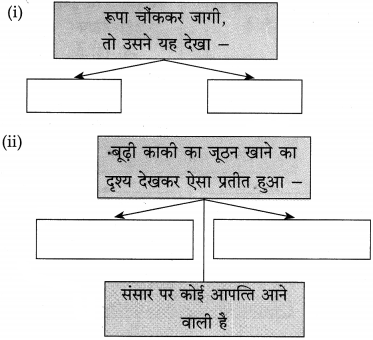
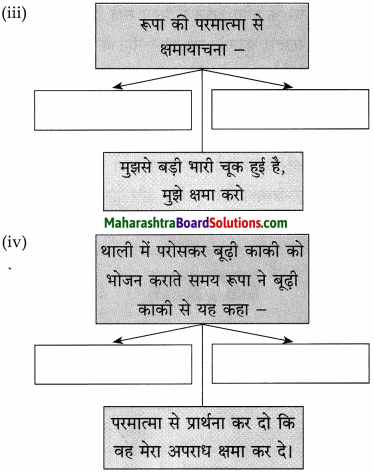
(i) रूपा का हृदय सन्न हो गया –
(ii) रूपा बैठी स्वर्गीय दृश्य का आनंद लेने में निमग्न थी –
उत्तर:
(i) रूपा का हृदय सन्न हो गया, क्योंकि उसने देखा कि बूढ़ी काकी पत्तलों पर से पूड़ियों के टुकड़े उठा-उठाकर खा रही हैं।
(ii) रूपा बैठी स्वर्गीय दृश्य का आनंद लेने में निमग्न थी, क्योंकि बूढ़ी काकी भोले बच्चों की तरह सब कुछ भूलकर बैठी हुई खाना खा रही थीं और उनके एक-एक रोएँ से सच्ची सदिच्छाएँ निकल रही थीं।

प्रश्न 3.
रिश्ता पहचानिए :
(i) बूढ़ी काकी, रूपा की लगती हैं –
(ii) रूपा, बूढ़ी काकी की लगती हैं –
उत्तर:
(i) बूढ़ी काकी, रूपा की लगती हैं – चचेरी सास।
(ii) रूपा, बूढ़ी काकी की लगती है – बहू।

कृति 2 : (स्वमत अभिव्यक्ति)

प्रश्न.
शादी-ब्याह अथवा पारिवारिक समारोहों में प्रीतिभोज में अनाप-शनाप खर्च करना कितना उचित’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर :
हमारे देश में शादी-ब्याह तथा छोटे-मोटे पारिवारिक समारोहों में प्रीतिभोज में लोगों को खिलाने-पिलाने की पुरानी परंपरा चली आ रही है। समर्थ व्यक्तियों को इस तरह का खर्च करना ज्यादा नहीं अखरता, पर आर्थिक दृष्टि से कमजोर लोगों के लिए इस तरह के ३ खर्च का भार उठाना मुश्किल होता है। पर सामाजिक बंधनों तथा अपने ३ नाम के लिए ऐसे समारोह आयोजित करना आज एक फैशन हो गया । हैं। यह फैशन दिनोदिन बढ़ता ही जा रहा है। कुछ लोग तो अपनी प्रतिष्ठा बढ़ाने के लिए कर्ज लेकर लोगों को बुलाकर खिलाते-पिलाते ३ हैं। बाद में यह कर्ज चुकाना उनके लिए समस्या बन जाता है और उन्हें अपनी जायदाद बक बेचनी पड़ जाती है। लोगों को इस तरह के उत्सवों में अनावश्यक रूप से पैसे उड़ाने से बाज आना चाहिए। इस तरह के उत्सवों-समारोहों में अनाप-शनाप खर्च करना अपने ऊपर एक तरह का आर्थिक बोझ लादना है, जिससे कोई लाभ नहीं होता।

उपक्रम/कृति/परियोजना

श्रवणीय
बड़ों से कोई ऐसी कहानी सुनिए जिसके आखिरी हिस्से में कठिन परिस्थितियों से जीतने का संदेश मिल रहा हो।

संभाषणीय
वृद्धाश्रम’ के बारे में जानकारी इकट्ठा करके चर्चा कीजिए।

लेखनीय
‘भारतीय कुटुंब व्यवस्था’ पर भाषण के मुद्दे लिखिए।
उत्तर:
भारतीय कुटुंब व्यवस्था के मुद्दे :

• कुटुंब किसे कहते हैं?
• प्राचीन भारतीय कुटुंब।
• आधुनिक कुटुंब।
• कुटुंब व्यवस्था में बदलाव के कारण।
• कुटुंब व्यवस्था के आधार।
• कुटुंब बनने-टूटने के कारण।
• कुटुंब की आवश्यकता।
• संयुक्त कुटुंब एवं एकल कुटुंब से लाभ-हानि।
• वसुधैव कुटुंबकम्।

पठनीय
‘चलती-फिरती पाठशाला’ उपक्रम के बारे में जानकारी इकट्ठी करके पढ़िए और सुनाइए।

बूढ़ी काकी Summary in Hindi

विषय – प्रवेश : ‘बूढ़ी काकी’ कथा उन दयनीय व्यक्तियों की व्यथा है, जिन्हें परिस्थितिवश मजबूरी में अपनी पूरी संपत्ति किसी अन्य व्यक्ति को सौंपनी पड़ती है और खुद उसकी दया पर जीना पड़ता है। बूढ़ी काकी अपने पति और जवान बेटों की मृत्यु के पश्चात अपने एकमात्र भतीजे बुद्धिराम के वादों पर विश्वास करके अपनी सारी संपत्ति उसके नाम लिख देती हैं। लेकिन थोड़े दिनों के बाद ही ऐसी स्थिति हो जाती है कि उसे पेट भर भोजन मिलना भी मुश्किल हो जाता है। एक बार तो बूढ़ी काकी के जीवन में ऐसी घटना घटती है, जिसके बारे में जानकर दिल दहल उठता है।

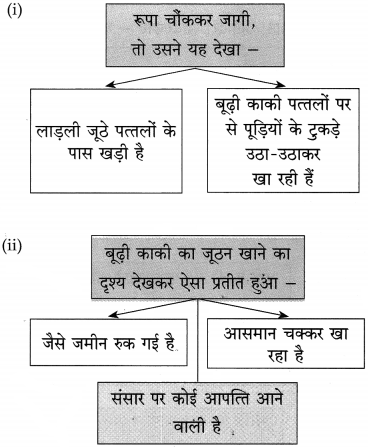
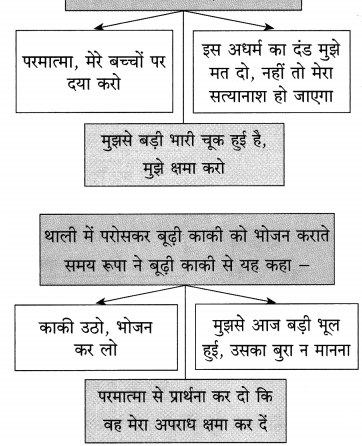
बुद्धिराम के बेटे के तिलक समारोह में सभी मेहमान और घर के सभी लोग भोजन कर सोने चले जाते हैं, पर बूढ़ी काकी को खाने के लिए कोई नहीं पूछता। भूख से व्याकुल बूढ़ी काकी रात के अंधेरे में कूड़े में फेंकी गई पत्तलों पर छूटे जूठन को बीन–बीनकर खाकर अपना पेट भरती हैं। बुद्धिराम की पत्नी रूपा यह दृश्य देखती है, तो उसकी रूह काँप उठती है और वह इस अधर्म के लिए ईश्वर से क्षमा करने की प्रार्थना करती है और बूढ़ी काकी को परोसकर भरपेट भोजन कराती है और उससे अपनी भूल के लिए बुरा न मानने के लिए कहती है।

बूढ़ी काकी मुहावरे – अर्थ

• सब्जबाग दिखाना – बड़े–बड़े झूठे वादे करना।
• गला फाड़ना – शोर करना, चिल्लाना।
• लाले पड़ना – किसी चीज के लिए तरसना।
• उबल पड़ना – क्रोधित होना।
• पानी उतर जाना – बेइज्जत होना।
• होंठ चाटना – कोई स्वादिष्ट पदार्थ अधिक खाने की इच्छा रखना।
• कलेजे में हूक सी उठना – मन में दुख होना।
• कलेजा पसीजना – दया आना।
• हृदय सन्न रह जाना – घोर आश्चर्य में डूब जाना।
• छाती पर सवार होना – सामने अड़े रहना।
• दम घुटना – हवा की कमी के कारण या गर्मी की अधिकता से साँस रुकना।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 8 कर्मवीर Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 8 Karamveer Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 8 कर्मवीर Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 8 कर्मवीर Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

2. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

3. विशेषताएँ लिखिए :

प्रश्न 1.
विशेषताएँ लिखिए :

उत्तर:

4. कविता में इस अर्थ में आए शब्द लिखिए 

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए

1. कर्मभूमि : ………………
2. अकारण : ………………
3. आकाश : ………………
4. विशवास : ………………

उत्तर:

1. कार्यस्थल
2. वृथा
3. गगन
4. विशवास

5. कविता की अपनी पसंदीदा चार पंक्तियों का सरल अर्थ लिखिए। 

प्रश्न 1.
कविता की अपनी पसंदीदा चार पंक्तियों का सरल अर्थ लिखिए।
उत्तर:
जो कभी अपने ……………………..चुराते हैं नहीं।
प्रस्तुत पंक्तियों के माध्यम से कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीरों के लिए समय बहुत महत्त्वपूर्ण होता है। इसलिए वे समय को कभी व्यर्थ नहीं गवाते। जिस काम को जिस समय करना है उसे उसी समय करते हैं। वे काम को कल पर नहीं छोड़ते हैं। जहाँ काम करना हो वहाँ कोई बहानेबाजी और आनाकानी नहीं करते। आज का काम कल पर टालकर वे अपने दिनों को व्यर्थ नहीं गवाते। समय का सदुपयोग करना यही उनका कर्तव्य होता है। कोशिश अथवा मेहनत करने से वे कभी भी पीछे नहीं हटते ।

उपयोजित लेखन :

प्रश्न 1.
मुद्दों के आधार पर कहानी लेखन कीजिए।
एक हंस और एक कौए में मित्रता – हंस का कौए के साथ उड़ते जाना – कौए का दधिपात्र लेकर जाने वाले ग्वाले को देखना – ललचाना – कौए का दही खाने का आग्रह – हंस का इनकार – कौए का घसीटकर ले जाना – कौए का चोंच नचा – नचाकर दही खाना – हंस का बिलकुल न खाना – आहट पाकर कौए का उड़ जाना -हंस का पकड़ा जाना – परिणाम – शीर्षक।
उत्तर:
कुसंगति का फल एक जंगल था। उस जंगल में तरह-तरह के पक्षी एवं जानवर रहते थे। उस जंगल में एक बरगद के पेड़ पर एक हंस व एक कौआ भी रहता था। दोनों में गहरी मित्रता थी। एक दिन वे दोनों खुले आसमान में विचरण कर रहे थे। उस वक्त कौए की नजर सिर पर दधिपात्र लेकर जाने वाले एक ग्वाले पर गई।

दधिपात्र देखकर कौए के मुँह में पानी भर आया। उसने तपाक से हंस से कहा, “क्यों न हम दोनों मिलकर दधिपात्र से थोड़ा-थोड़ा दही खा लें।” हंस ने कहा, “नहीं भाई ! इस प्रकार चोरी या छिपकर खाने से आफत आ सकती है। हम पकड़े जा सकते हैं। फिर भी कौए ने हंस की एक न सुनी।

वह जबरन हंस को घसीटकर दधिपात्र के पास ले आया। वह बड़े मजे से दही को खाने लगा। ढेर सारा दही देखकर वह अपनी चोंच नचा-नचाकर दही खाने लगा। हंस सिर्फ उसके साथ था, लेकिन उसने दही को छुआ तक नहीं। दधिपात्र लेकर जाने वाले ग्वाले को एहसास हुआ कि दधिपात्र में से कौआ या अन्य पक्षी दही खाने की चेष्टा कर रहे हैं।

ग्वाले ने आव देखा न ताव तुरंत अपना दाहिना हाथ ऊपर कर उसने हंस को पकड़ लिया। तब तक आहट पाकर कौआ वहाँ से उड़ गया। बेचारा हंस! उसका बुरा हाल हुआ। ग्वाले ने उसे मार डाला। सीख : बुरे लोगों के साथ रहने से बुरा होता है। इसलिए हमें अच्छे लोगों के साथ रहना चाहिए।

Hindi Lokvani 10th Std Textbook Solutions Chapter 8 कर्मवीर Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
‘कर्मवीर दूसरों का मुँह नहीं ताकते’ इसका तात्पर्य है कि –
उत्तर:
वे स्वावलंबी होते हैं। अत: वे दूसरों पर निर्भर नहीं होते।

कति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. विघ्न
2. बाधा
3. भाग्य
4. चंचल

उत्तर:

1. संकट
2. रुकावट
3. नसीब
4. अस्थिर

प्रश्न 2.
विलोम शब्द लिखिए।
i. कठिन × …….
ii. निर्मल × …….
उत्तर
i. सरल
i. मलीन

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए –
i. अस्थिर स्वभाव का –
उत्तर :
i. चंचल

प्रश्न 4.
निम्नलिखित तद्भव शब्द का तत्सम शब्द लिखिए।
i. मुँह
ii. काम
उत्तर:
i. मुख
ii. कार्य

प्रश्न 5.
निम्नलिखित शब्द के वचन बदलिए।
i. बाधा
ii. काम
उत्तर:
i. बाधाएँ
ii. काम

प्रश्न 6.
निम्नलिखित शब्द के समश्रुतभिन्नार्थक शब्द लिखिए।
i. मान
ii. भाग्य
उत्तर:
i. मन
i. भाग

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘जो विघ्न-बाधाओं का सामना करता है वही सफल होता है।’ अपने विचार लिखिए।
उत्तर:
जीवन में सुख व दुख दोनों हैं। व्यक्ति के जीवन में अनुकूल व प्रतिकूल ये दोनों परिस्थितियाँ आती हैं। व्यक्ति को प्रतिकूल परिस्थिति का डरकर नहीं बल्कि डटकर सामना करना चाहिए। जो व्यक्ति जीवन में आने वाले संघर्षों का सामना करता है वह अंत में सफल हो जाता है। संघर्षों के साथ लड़ते समय उसमें अदम्य शक्ति निर्माण हो जाती है नई ऊर्जा का संचार हो जाता है। परिस्थितियाँ मनुष्य को जीवन अनुभवों से समृद्ध बनाती हैं। जिसके जीवन में संघर्ष नहीं; जो विघ्न-बाधाओं का सामना नहीं करता है, उस व्यक्ति का जीवन नीरस हो जाता है। जो व्यक्ति विघ्न-बाधाओं का सामना करता है वही अंत में अपनी मंजिल पाता है। ऐसा पुरुष ही जीवन का सच्चा कर्मवीर कहलाता है।

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1) : आकलन त

प्रश्न 1.
सही विकल्प चुनकर लिखिए।
i. कार्य कितना भी कठिन हो ………….
(अ) कर्मवीर उसे पूरा करने की ठान नहीं लेते हैं।
(आ) कर्मवीर उसे पूरा करने की ठान लेते हैं।
(इ) उसे पूरा करने की जिम्मेदारी दूसरों पर सौंपते हैं।
उत्तर:
(आ) कर्मवीर उसे पूरा करने की ठान लेते हैं।

ii. कर्मवीर आसमान के फूलों को व्यर्थ बातों से नहीं तोड़ते अर्थात
(अ) वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें नहीं बनाते।
(आ) वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें बनाते हैं।
(इ) वे अपनी प्रशंसा के लिए किसी भी हद तक जा सकते हैं।
उत्तर:
(अ) वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें नहीं बनाते।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए।
i. सहायता : ………………
ii. दिवस : ……………….
उत्तर:
i. मदद
ii. दिन

प्रश्न 2.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर शब्द लिखिए।
i. समय
उत्तरः
उपसर्गयुक्त शब्द : असमय
प्रत्यययुक्त शब्द : सामयिक

प्रश्न 3.
निम्नलिखित शब्दों में उचित उपसर्ग लगाइए।
i. यत्न
ii. मन
उत्तर:
i. प्र + यत्न = प्रयत्न
ii. बे + मन = बेमन

प्रश्न 4.
पद्यांश में प्रयुक्त विलोम शब्द की जोड़ी लिखिए।
उत्तर:
i. आज × कल

प्रश्न 5.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. संपदा
ii. वृथा
उत्तर:
i. संपत्ति
ii. व्यर्थ

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘समय का सदुपयोग करने से व्यक्ति जीवन में ऊँचा उठ सकता है।’ अपने विचार लिखिए।
उत्तरः
मानव जीवन में समय का सदुपयोग अत्यंत महत्त्वपूर्ण है। जो व्यक्ति समय के साथ चलता है वह प्रगति की सीढ़ी हासिल कर लेता है। समय का सदुपयोग करने वाले व्यक्ति को सभी सुखों की प्राप्ति होती है। समय पर कार्य करने वाले व्यक्ति के कारण समाज व राष्ट्र का भी भला होता है। विश्व के सभी महापुरुष समय की कीमत जानते थे।

इसलिए वे जीवन में महान बन सके। समय का सदुपयोग करने वाला व्यक्ति समय का सही विभाजन कर अध्ययन, खेलकूद, समाज सेवा, मनोरंजन आदि जैसे अनेक कार्य सरलतापूर्वक कर सकता है। समय का सदुपयोग करने वाला व्यक्ति समय के साथ कदम से कदम मिला कर चलता है और जीवन में अनेक सफलताओं को प्राप्त करता है।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
सही विकल्प चुनकर वाक्य फिर से लिखिए।
i. कर्मवीरों का नया उत्साह देखने को मिलता है –
(अ) जब उन्हें उलझनें आकर घेर लेती हैं।
(आ) जब वे अपना काम पूरा कर लेते हैं।
(इ) जब वे कार्यस्थल से दूर चले जाते हैं।
उत्तरः
(अ) जब उन्हें उलझनें आकर घेर लेती हैं।

प्रश्न 2.
संजाल पूर्ण कीजिए।
उत्तरः

प्रश्न 3.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. कर्मवीर
ii. कार्यस्थल
उत्तर:
i. असंभव को संभव कौन बनाते हैं?
ii. कर्मवीर किसके बारे में पूछते नहीं है?

कृति इ (3) : शब्द संपदा.

प्रश्न 1.
निम्नलिखित शब्दों में उचित प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. बुद्धि
ii. देश
उत्तर:
i. बुद्धि + मान = बुद्धिमान
ii. देश + ई = देशी

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।

1. सपूत
2. हस्त
3. नव

उत्तरः

1. सुपुत्र
2. हाथ
3. नया

प्रश्न 3.
समानार्थी शब्द लिखिए।
i. उत्साह
ii. बुद्धि
उत्तर:
i. उमंग
ii. मति

प्रश्न 4.
कविता में इस अर्थ में आए शब्द लिखिए।
i. अच्छे पुत्र
उत्तर:
i. सपूत

प्रश्न 5.
पद्यांश में से विलोम शब्द की जोड़ी ढूँढकर लिखिए।
उत्तर:
i. असंभव × संभव
ii. यहाँ × वहाँ

प्रश्न 6.
‘सपूत’ इस शब्द में से उपसर्ग पहचानकर संबंधित उपसर्ग को लगाकर अन्य दो शब्द बनाइए।
उत्तरः
सपूत : उपसर्ग – स
अन्य शब्द : सकारण, सप्रमाण

कृति ग (4) : अभिव्यक्ति

प्रश्न 1.
‘कर्म ही पूजा है, कर्म ही श्रेष्ठ है।’ विषय पर अपने विचार लिखिए।
उत्तर:
गीता में लिखा है कि कर्म ही पूजा है। कर्म से बढ़कर व्यक्ति का अन्य कोई धर्म नहीं है। इसलिए कर्म करना मनुष्य का पहला लक्ष्य होना चाहिए। कर्म करने से व्यक्ति को आनंद मिलता है। सच्चे मन से किया गया कर्म सफल होता है। मनुष्य के कर्म को ही संसार में याद किया जाता है। उसकी मृत्यु के उपरांत वह सिर्फ अपने कर्मों के कारण ही याद किया जाता है। इसलिए सभी को आलस्य त्यागकर कर्म में लीन हो जाना चाहिए। कर्म सफलता का आधार है। कर्म ही श्रेष्ठ है। कर्म करने से ही व्यक्ति के जीवन को सुख की अनुभूति प्राप्त होती है। सबकी भलाई के लिए कर्म करते हुए जीना ही जीवन का मूलमंत्र है।

कर्मवीर Summary in Hindi

जीवन-परिचय :

अयोध्यासिंह उपाध्याय ‘हरिऔध’ जी का जन्म उत्तर प्रदेश राज्य के आजमगढ़ जिले में हुआ था। ये हिंदी साहित्य के एक प्रमुख हस्ताक्षर थे तथा हिंदी साहित्य सम्मेलन के सभापति भी रह चुके हैं। हिंदी साहित्य सम्मेलन समिति के द्वारा इन्हें विद्यावाचस्पति की उपाधि से सम्मानित किया जा चुका है। खड़ी बोली हिंदी साहित्य के विकास में इनका विशेष योगदान रहा है। वियोग तथा वात्सल्य वर्णन, लोक सेवा की भावना व प्रकृति चित्रण इनके काव्य की विशेषता है।
प्रमुख कृतियाँ : ‘वैदेही वनवास’, ‘प्रिय-प्रवास’ (महाकाव्य), ‘ठाठ’, ‘अधखिला फूल’ (उपन्यास), ‘रुक्मणी परिणय’, ‘विजय व्यायोग’ (नाटक) आदि।

पद्य-परिचय :

आधुनिक पद्य : सन 1900 से आधुनिक पद्य की शुरुआत हुई। महावीर प्रसाद द्विवेदी जी के प्रभाव से ब्रज भाषा से हिंदी कविता हटकर खड़ी बोली हिंदी में लिखी जाने लगी। भारत का उज्ज्वल अतीत, देशभक्ति, सामाजिक सुधार, स्वभाषा प्रेम, मानवीय गुण आदि का खड़ी बोली हिंदी में प्रयोग होने लगा। मधुरता एवं सरलता ने हिंदी कविता में प्रवेश कर लिया।
प्रस्तावना : ‘कर्मवीर’ इस कविता के माध्यम से कवि ‘हरिऔध’ जी ने यह बताने का प्रयास किया है कि कर्मवीरों के लिए कर्म ही पूजा होती है, वे कर्म करने के लिए सदैव तत्पर रहते हैं, वे असंभव को संभव बना देते हैं, तथा देश और समाज को उन्नति के मार्ग पर ले जाते हैं।

सारांश :

‘कर्मवीर’ यह एक आधुनिक पद्य है। इस कविता के माध्यम से कवि ने मानवीय गुणों का संचय करने की प्रेरणा दी है। कवि ने कर्मवीरों के पास जो महान गुण होते हैं उनका अनुसरण करने के लिए पाठकों को प्रेरित किया है। कवि कहते हैं, “मनुष्य को विघ्न-बाधाओं का डटकर मुकाबला करना चाहिए। काम के प्रति उकताहट नहीं करनी चाहिए। मनुष्य को स्वावलंबी होना चाहिए। उसे कभी भी किसी पर आश्रित नहीं होना चाहिए।

मनुष्य को समय का सदुपयोग करना चाहिए। कार्य कितना भी कठिन हो फिर भी उसे पूरा करने की ठान लेनी चाहिए। मनुष्य को मुसीबतों का सामना करते हुए असंभव कार्य को संभव कर दिखाना चाहिए। मनुष्य की कर्मनिष्ठा मनुष्य का विकास करेगी पर इसके साथ वह जिस समाज व राष्ट्र में रहता है उसका भी विकास होता है। अत: प्रत्येक मनुष्य का कर्तव्य है कि वह कर्म को श्रेष्ठ मानकर देश और समाज को उन्नति के मार्ग पर ले जाए।

भावार्थ :

देखकर जो ………………………………. वीर दिखलाते नहीं।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर विघ्न बाधाओं को देखकर घबराते नहीं। वे कभी भाग्य के भरोसे नहीं बैठते हैं। इसलिए भाग्य द्वारा दुख मिलने पर उन्हें पछतावा नहीं होता। काम कितना भी कठिन हो फिर भी उन्हें काम के प्रति कोई उकताहट नहीं होती। उनके लिए कर्म ही पूजा होती है। भीड़ अथवा मुश्किलों को देखकर भी उन पर उसका कुछ भी प्रभाव नहीं पड़ता है। वे सच्चे वीर होते हैं। वे किसी भी स्थिति में डरते नहीं हैं।

मानत जी की हैं ………………………….. जिसे सकते नहीं।
‘कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर सबकी बात सुनते हैं लेकिन, कार्य करते समय अपने मन की बात मानते हैं। वे स्वावलंबी होते हैं। वे कभी भी किसी पर आश्रित नहीं होते। वे स्वयं का काम स्वयं पूरा करते हैं। वे कभी भी किसी भी चीज के लिए दूसरों का मुँह नहीं ताकते। अर्थात किसी भी वस्तु के लिए वे दूसरों पर आश्रित नहीं होते हैं। इस दुनिया में भला ऐसा कौन-सा काम है जिसे वे पूरा नहीं कर सकते? अर्थात वे सारे काम करने में सक्षम होते हैं।

जो कभी अपने ………………………………..चुराते हैं नही।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीरों के लिए समय बहुत ही महत्त्वपूर्ण होता है। इसलिए वे समय को कभी व्यर्थ नहीं गँवाते। जिस काम को जिस समय करना है उसे उसी समय करते हैं। उसे कल पर नहीं छोड़ते हैं। जहाँ काम करना हो वहाँ कोई बहानेबाजी और आनाकानी नहीं करते। आज का काम कल पर टालकर वे अपने दिनों को व्यर्थ नहीं गँवाते। समय का सदुपयोग करना यही उनका कर्तव्य होता है। कोशिश या मेहनत से वे कभी भी पीछे नहीं हटते ।

काम को आरंभ ……………………………………. नहीं जो जोड़ते।।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर कार्य को कभी भी बीच में छोड़ते नहीं हैं। कार्य कितना भी कठिन हो फिर भी वे उसे पूरा करने की ठान लेते हैं। काम को पूरा करते समय यदि कोई मुसीबत आ जाए तो भी पीछे नहीं हटते; वे काम से मुँह नहीं मोड़ते। कर्मवीर आसमान के फूलों को व्यर्थ बातों से नहीं तोड़ते अर्थात वे अपनी प्रशंसा के लिए बड़ी-बड़ी बातें नहीं बनाते। जिस कार्य को करना है बस उसी पर अपना : ध्यान केंद्रित करते हैं। वे मन से करोड़ों की संपदा नहीं जोडते।

कार्य थल ……………………………… उतना ही वहाँ।
कवि ‘हरिऔध’ जी कहते हैं कि कर्मवीर कार्यस्थल की तलाश में यहाँ-वहाँ खोजने के लिए भटकते नहीं। वे जहाँ होते हैं वहीं उनका कार्यस्थल होता है। कर्मवीर मुसीबतों का सामना करते हुए असंभव कार्य को भी संभव कर दिखाते हैं। आने वाली उलझनों और मुसीबतों से वे डरते नहीं बल्कि उनका वे उतने ही उत्साह से सामना करते हैं। उलझनों को देखकर उनमें नया जोश और नई चेतना आ जाती है और वे अपना कार्य उत्साह से करते हैं।

सब तरह से ……………………………. सूपतों के पले।
कवि ‘हरिऔध’ जी के अनुसार, आज विश्व में कई ऐसे देश हैं; ‘जो समृद्ध व संपन्न हैं’ प्रगत एवं विकसित हैं। वहाँ पर विद्या, धन, बुद्धि व ऐश्वर्य का भंडार है। इसका कारण है कि वहाँ पर रहने वाले लोगों ने कर्म को ही अपना लक्ष्य मान लिया है। कर्मवीरों के पुरुषार्थ से ही देश संपन्न हुए हैं। कर्मवीरों के कारण ही सबका भला हुआ है। उनके कारण ही चारों ओर प्रगति की लहर छाई हुई है। ऐसे महान सपूतों के कारण ही सभी का जीवन खुशहाल बना है।

शब्दाथ :

1. विघ्न – संकट
2. बाधा – रुकावट
3. भाग्य – नसीब
4. चंचल – अस्थिर
5. वृथा – अकारण, व्यर्थ
6. गगन – आकाश
7. मदद – सहायता
8. दिन – दिवस
9. उत्साह – उमंग
10. संपदा – धन, दौलत
11. बुद्धि – मति
12. वैभव – ऐश्वर्य
13. उकताना – ऊबना
14. यत्न – प्रयत्न

मुहावरे :

1. असंभव को संभव बनाना – कठिन काम को सरल बनाना।
2. मुँह ताकना – दूसरों पर आश्रित होना।
3. जी चुराना – आलस करना।
4. बातें बनाना – बहाने बनाना।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer