Class 10

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokvani Chapter 1 सोंधी सुगंध Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 1 Sondhi Sugandh Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 1 सोंधी सुगंध Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 1 सोंधी सुगंध Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए

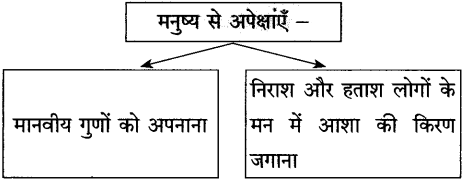
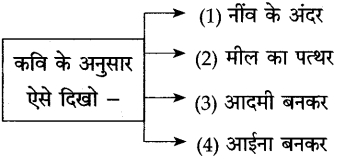
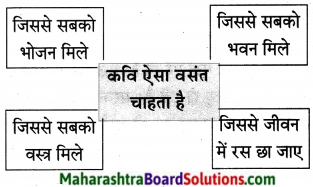
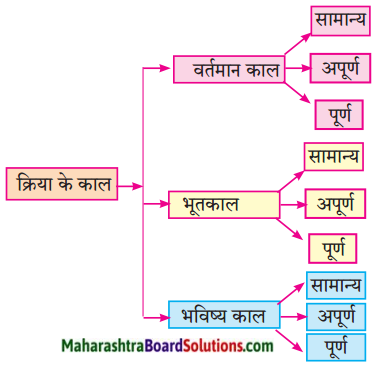
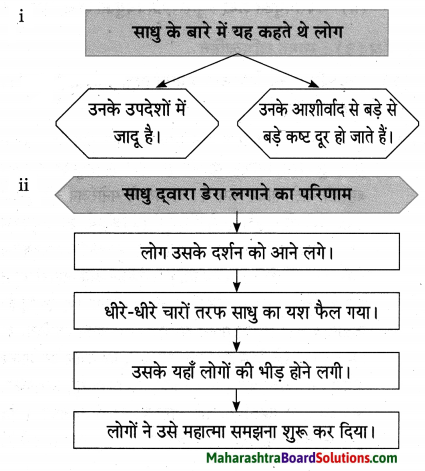
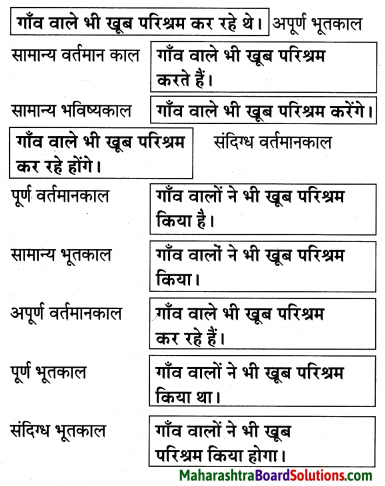
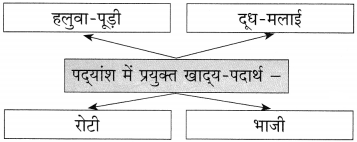
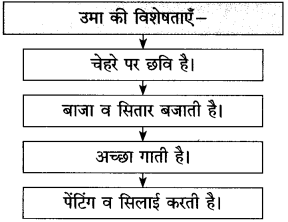
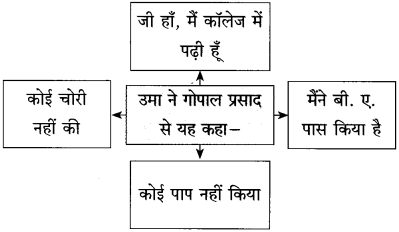
(१) कृति पूर्ण कीजिए:

Answer:

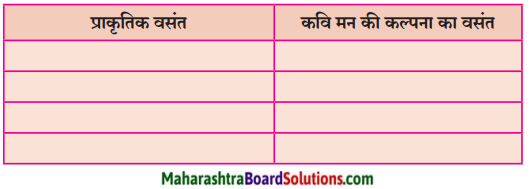
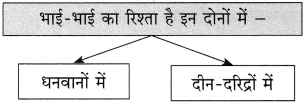
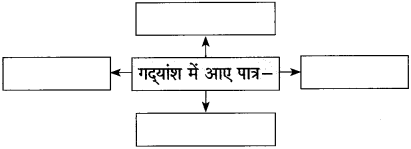
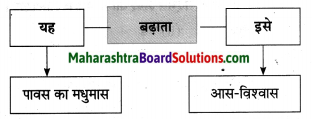
(२) कृति पूर्ण कीजिए:

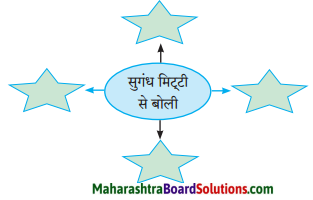
Answer:

(३) गीत में प्रयुक्त क्रियारूप लिखिए:

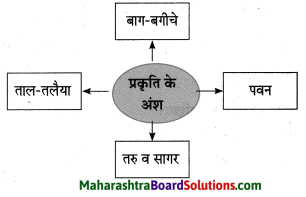
बाग-बगीचे, ताल-तलैया …………
Answer:
मुसकाएँ

झूम-झूमकर मस्ती में तरु गीत ………..
Answer:
सुनाएँ

मधुमास आस-विश्वास ………..
Answer:
किया

धरती ने ………….
Answer:
बढ़ाता

(४) उपसर्ग-प्रत्यय लगाकर शब्द लिखिए :

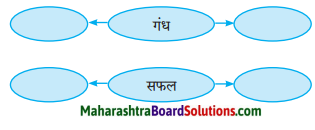
Answer:

अभिव्यक्ति

प्रस्तुत गीत की प्रथम चार पंक्तियों का भावार्थ लिखिए।
Answer:
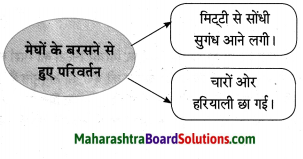
वर्षा ऋतु के आगमन पर धरती पर बारिश की बूंदों का गिरना शुरू हो जाता है। बारिश की बूंदें धरती पर गिरकर मिट्टी को स्पर्श करती हैं, जिस कारण मिट्टी से सोंधी सुगंध आने लगती है। यह सोंधी सुगंध मिट्टी से बातें करने लगती हैं।

बारिश की बूंदों की अनुभूति से धरती प्रफुल्लित हो गई है। इसलिए जैसे ही बारिश थम जाती है; वैसे ही वह अपनी आँखें खोलती हैं। मोर को भी वर्षाऋत अत्यंत प्रिय है। अत: वह भी वर्षाऋत में खश होकर कह रहा है कि चारों ओर हरियाली ही हरियाली छा गई है। भीषण गरमी के कारण धरती बंजर हो गई थी। बादल बरसने के बाद हरियाली-सा हरा वस्त्र धारण करने का धरती का जो सपना था; वह अब वह पूरा हो गया है।

भाषा बिंदु

वर्तनी के अनुसार शुद्ध शब्द छाँटकर लिखिए:

1. विश्वास/विशवास/विसवास ……..
2. मसतक/मस्थक/मस्तक ……….
3. पथ्थर/पथ्तर/पत्थर …………
4. कुरीति/कूरिति/कुरिती …………
5. चिन्ह/चीहन/चिह्न …………..
6. इकठठा/इकट्टा/इकट्ठा ………….
7. खुबसुरत/खूबसुरत/खूबसूरत …………
8. विदयापीठ/विद्यापीठ/विद्यापिठ ………….
9. बुद्धी/बुध्दी/बुद्धि ………….
10. परिक्षार्थि/परीक्षार्थि/परीक्षार्थी ………….

Answer:

1. विश्वास
2. मस्तक
3. पत्थर
4. कुरीति
5. चिह्न
6. इकट्ठा
7. खूबसूरत
8. विद्यापीठ
9. बुद्धि
10. परीक्षार्थी

उपयोजित लेखन

निम्नलिखित सुवचन पर आधारित कहानी लिखिए:

‘स्वास्थ्य ही संपदा है।’
Answer:
श्रीरामपुर गाँव में धनसुखलाल नाम का एक धनी व्यक्ति रहता था। वह बहुत ही कंजूस प्रवृत्ति का था। रईस होने के बावजूद भी वह स्वयं पर कभी भी पैसे खर्च नहीं करता था। वह दिन में सिर्फ एक वक्त का भोजन करता था। इतना ही नहीं वह अपने परिवार वालों पर भी धन खर्च नहीं करता था। उसकी कंजूसी के कारण उसका परिवार प्रतिदिन भूखे पेट ही सोता था। एक दिन धनसुखलाल बीमार पड़ गया।

भरपेट खाना न खाने के कारण उसका शरीर कमजोर हो गया था। उसकी शक्ति कम हो गई थी। परिवार के लोग उसे डॉक्टर के पास ले जाना चाहते थे। लेकिन डॉक्टर के पास जाकर काफी रूपया खर्च हो जाएगा। इसलिए उसने घरेलू औषधियों लेना प्रारंभ कर दिया। आहिस्ता-आहिस्ता उसका शरीर अत्यधिक अस्वस्थ और कमजोर हो गया।

यहाँ तक कि अब उठकर चलने की शक्ति भी उसमें शेष नहीं थी। फिर भी वह डॉक्टर के पास जाने के लिए राजी नहीं हुआ। उसी शाम गाँव में एक महात्मा आए। उन्होंने धनसुखलाल के बारे में सुना और वे स्वयं उसे मिलने गए। महात्मा को देखकर धनसुखलाल ने सोचा कि यह महात्मा उसका इलाज कर देंगे। उसने आशा से महात्मा को प्रणाम किया। महात्मा ने उसे स्पष्ट कहा – ‘मूर्ख धनसुखलाल, मैं तुम्हारा भविष्य जानता हूँ। यदि तुम अभी डॉक्टर के पास नहीं जाओगे; तो कल सुबह तक तुम्हारी मृत्यु निश्चित है।’

महात्मा की भविष्यवाणी सुनकर धनसुखलाल के हाथ-पाँव काँपने लगे और महात्मा को प्रणाम करके वह तुरंत अपने परिवार वालों के साथ डॉक्टर के पास चला गया। डॉक्टर ने पूरी निष्ठा से उसका इलाज किया। कुछ दिनों के बाद वह ठीक हो गया। अब उसकी समझ में आ गया था कि ‘स्वास्थ्य ही संपदा होती है।’ सीख : स्वास्थ्य से बढ़कर दूसरी कोई संपत्ति नहीं होती। व्यक्ति को अपने स्वास्थ्य का सदैव ध्यान रखना चाहिए।

Hindi Lokvani 10th Std Textbook Solutions Chapter 1 सोंधी सुगंध Additional Important Questions and Answers

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।
कृति अ (१): आकलन कृति

कृति पूर्ण कीजिए।

Answer:

समझकर लिखिए।

Answer:

‘सदियों का जो सपना है हो जाए पूरा।’ इससे आप समझते हैं
Answer:
भीषण गरमी के कारण धरती बंजर हो गई थी। अब बारिश के आने से वह फिर से हरी-भरी हो जाएगी।

कृति अ (२) : शब्द संपदा

निम्नलिखित शब्दों के अर्थ पद्यांश में से ढूँढ़कर लिखिए।

1. मेघ
2. मोर
3. मृदा
4. ख्वाब

Answer:

1. बादल
2. मयूरा
3. माटी
4. सपना

विलोम शब्द लिखिए।

1. सुगंध x ……..
2. पूरा x ………

Answer:

1. सुगंध x दुर्गंध
2. पूरा x अधूरा

वचन बदलिए।

1. सदी
2. हरियाली
3. टोली
4. आँखें

Answer:

1. सदियाँ
2. हरियालियाँ
3. टोलियाँ
4. आँख

निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।

1. मयूर
2. हरित

Answer:

1. मोर
2. हरा या हरी

निम्नलिखित शब्द का देशज व तत्सम शब्द लिखिए।

Question 1.
मिट्टी
Answer:
देशज शब्द : माटी, तत्सम शब्द: मृदा

कृति अ (३) : स्वमत अभिव्यक्ति

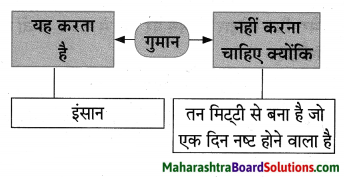
आपने पहली बारिश के बाद चारों और महकने वाली मिट्टी की सुगंध को जरूर महसूस किया होगा। उस वक्त जो अनुभूति हुई थी, उसे अपने शब्दों में लिखिए।
Answer:
बारिश के पहले भीषण गरमी के कारण मिट्टी तपती है। जैसे ही वर्षा की पहली बूंदें धरती पर आती हैं, वैसे ही तपती हुई मिट्टी शीतलता का अनुभव करने लगती है। फिर उसमें से जो गंध उठती है, उसका क्या कहना? मिट्टी की सोंधी सुगंध सभी को आकर्षित करती है। मैं पिछले वर्ष बरसात शुरू होने से पहले अपने गाँव गया था। वहाँ पर मैंने पहली बरसात का अनुभव किया था। बारिश रुकते ही अचानक से सारा वातावरण मिट्टी की भीनी-भीनी सोंधी खुशबू से प्रफुल्लित हो उठा। मानो वह सोंधी महक मुझे बता रही थी कि हम सब उससे जुड़े हैं। हमारा शरीर भी उसी से बना है। आखिर मिट्टी हमें जीवन देती है। सचमुच मिट्टी की उस सोंधी महक ने मेरे चित्त को प्रसन्न कर दिया था। आज भी वह महक मेरे रोम-रोम में समाई हुई है। उस सोंधी महक को महसूस हुए मुझे मनुष्य और मिट्टी के बीच जो गहरा रिश्ता है इसका एहसास भी हुआ था।

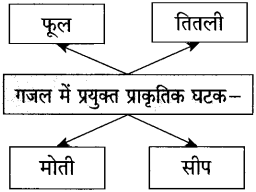
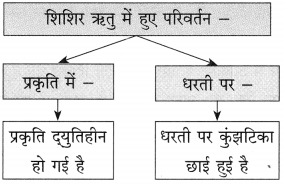
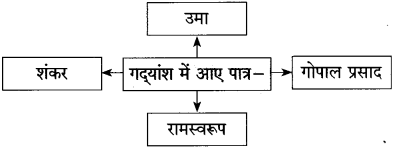
संजाल पूर्ण कीजिए।

Answer:

कृति आ (२) : शब्द संपदा

‘रोली’ शब्द का अनेकार्थी शब्द लिखिए।
Answer:
सिंदूर, प्रसिद्ध भूमि, हल्दी व चूने का चूर्ण

निम्नलिखित तद्भव शब्द का तत्सम रूप लिखिए।

1. माथा
2. पेड़

Answer:

1. मस्तक
2. तरु

वचन बदलिए।

1. बोली
2. रोली
3. झोली
4. बगीचा

Answer:

1. बोलियाँ
2. रोलियाँ
3. झोलियाँ
4. बगीचे

कृति आ (३) : स्वमत अभिव्यक्ति

‘बारिश के बाद प्रकृति में होने वाला परिवर्तन’ विषय पर अपने विचार लिखिए।
Answer:
वर्षा ऋतु समस्त ऋतुओं की रानी है। बारिश होते ही चारों ओर हरियाली छा जाती है। वर्षा होने से तालाबों और नहरों में पानी भर जाता है। सागर अपनी मस्ती में लहरों के साथ नर्तन करता रहता है। वर्षा से सूखे पेड़-पौधों में भी जीवन आ जाता है। संपूर्ण वातावरण खुशनुमा हो जाता है। मिट्टी से सोंधी महक आनी शुरू हो जाती है। यह महक हमारे चित्त को प्रसन्न कर देती है। बारिश के बाद कृषकों में उल्लास बढ़ जाता है और वे अपने खेतों में लगन के साथ जुट जाते हैं। मोर प्रसन्न होकर नाचने लगते हैं और मेंढक टर्र-टर्र की आवाज करते रहते हैं। इस प्रकार बारिश के बाद प्रकृति की शोभा देखने लायक होती है।

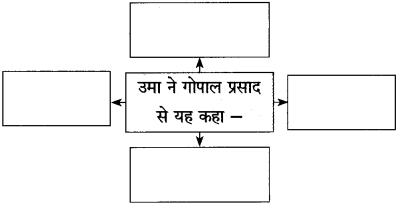
समझकर लिखिए।

Answer:

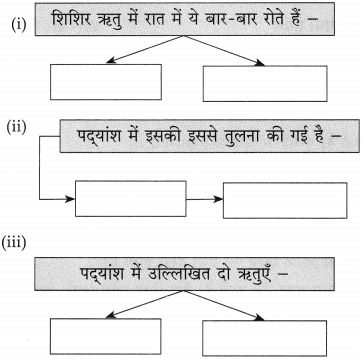
निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (१): आकलन कृति

Question 1.
सदा-सदा से यह चली आई है –
Answer:
हँसी-ठिठोली

Question 2.
यह नतमस्तक हो गए हैं –
Answer:
कवि ‘अचूक’

निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए कि जिनके उत्तर निम्न शब्द हों

Question 1.
माटी
Answer:
सोंधी-सौंधी-सी सुगंध किससे बात कर रही है?

Question 2.
मधुमास
Answer:
कवि ने पावस को किसकी उपमा दी है। (३) कृति पूर्ण कीजिए।

कृति इ (२) : शब्द संपदा

पद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:
आस-विश्वास,
सदा-सदा,
हँसी-ठिठोली,
सोंधी-सौंधी-सी

निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।

1. पद
2. मास

Answer:

1. पाँव या पैर
2. महीना

निम्नलिखित तद्भव शब्द का तत्सम रूप लिखिए।

1. हँसी

Answer:

1. हास्य

निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. मधुमास
2. पुष्प
3. आस
4. नत

Answer:

1. वसंत ऋतु
2. फूल
3. आशा
4. विनीत

कृति इ (३) : स्वमत अभिव्यक्ति

‘मनुष्य जीवन में वर्षा का महत्त्व’ इस विषय पर अपने विचार लिखिए।
Answer:
हमारा भारत देश कृषिप्रधान देश है। यदि बारिश समय पर न होगी, तो सूखा या दुर्भिक्ष (अकाल) की स्थिति निर्माण होने में देर नहीं लगेगी। वर्ष के बारह महीने में से तीन या चार महीनों तक लगातार बारिश होने के कारण प्रकृति का संतुलन बना रहता है। जल के बिना मनुष्य जीवन संभव नहीं। इसलिए हमारे जीवन में वर्षा का अत्यधिक महत्त्व है। वर्षा का मौसम तपती गरमी से राहत दिलाता है। बारिश की बूंदें धरती के बढ़े हुए तापमान को अपने अंदर समा लेती हैं। वर्षाकाल में लोग वर्षा का आनंद लेने के लिए पिकनिक मनाते हैं। वर्षा में सूखे हए तालाब, कुएँ और नदियाँ फिर से भर जाती हैं। इस कारण पूरे वर्ष तक मनुष्य को पीने के लिए पानी उपलब्ध होता है।

सोंधी सुगंध Summary in Hindi

सोंधी सुगंध कवि-परिचय

जीवन-परिचय : डॉ. कृपाशंकर शर्मा जी का जन्म उत्तर प्रदेश के एटा शहर में हुआ। हिंदी साहित्य में इन्हें ‘अचूक’ इस उपनाम से जाना
जाता है। इन्हें बालगीतकार एवं बालकहानीकार के रूप में अधिक जाना जाता है। इन्होंने कविता के विविध अंगों को सूक्ष्मता से जाना-पहचाना है। गीत, गजल, कविता एवं दोहे इनकी रचना का प्रमुख विषय रहे हैं। समीक्षा के क्षेत्र में भी इनका कार्य उल्लेखनीय हैं। पत्रकारिता के क्षेत्र में भी इनकी सक्रियता रही है।

प्रमुख कृतियाँ : ‘फिर भी कहना शेष रह गया’, ‘नदी उफान भरे’ (गीत संग्रह), ‘गीत खुशी के गाओ तुम’ (बालगीत संग्रह) आदि।

सोंधी सुगंध पद्य-परिचय

गीत : गीत हिंदी साहित्य की एक लोकप्रिय विधा है। स्वर, पद और ताल से युक्त जो गान होता है, वह ‘गीत’ कहलाता है। इसमें एक मुखड़ा तथा कुछ अंतरे होते हैं। प्रत्येक अंतरे के बाद मुखड़े को दोहराया जाता है। इसमें गेयता विद्यमान होती है।

प्रस्तावना : ‘सोंधी सुगंध’ इस गीत में कवि डॉ. कृपाशंकर शर्मा ‘अचूक’ जी ने वर्षा ऋतु का आगमन होने पर प्रकृति में छाई प्रसन्नता एवं खुशहाली का बड़ा ही सजीव एवं मनोहारी वर्णन किया है। वर्षा ऋतु में प्रकृति के विविध रूपों में होनेवाले परिवर्तन का अत्यंत आहलाददायी वर्णन प्रस्तुत कविता में किया गया है।

सोंधी सुगंध सारांश

प्रस्तुत कविता के माध्यम से स्पष्ट किया गया है कि प्रत्येक ऋतु का अपना महत्त्व और अपनी विशेषता है। भीषण गर्मी के कारण तापमान बढ़ता है। सभी भीषण गर्मी से व्याकुल हो जाते हैं। वर्षा तपती गर्मी से राहत दिलाती है। छम-छम करता हुआ पानी देख सबके चेहरे पर रौनक आ जाती है। पहली बारिश की बूंदें धरती को स्पर्श करती हैं, जिस कारण मिट्टी से सोंधी सुगंध आने लगती है। यह सोंधी सुगंध मिट्टी से बातें करने लगती हैं। वह वर्षा के कारण प्रकृति के विविध रूपों, वन्य-जीव, पेड़-पौधों, नदी-तालाबों आदि में होने वाले परिवर्तनों से सभी को रूबरू कराती हैं। वर्षा ऋतु एक प्रेरणादायी ऋतु है। वह प्रत्येक मानव के मन में आस एवं विश्वास भर देती है। इसलिए सदियों से वर्षा का स्वागत होता आ रहा है। सदियों से वर्षा के आगमन पर लोग खुश होते हैं और होते रहेंगे।

सोंधी सुगंध शब्दार्थ

• सोंधी – सुगंधित
• रोली – हल्दी-चूने का चूर्ण
• मंसूबा – विचार, इरादा
• मधुमास – वसंत ऋतु
• माटी – मिट्टी
• धरती – पृथ्वी
• मयूरा – मोर
• टोली – दल
• ताल-तलैया – तालाब-झरने
• पवन – हवा
• तरू – पेड़
• ‘अचूक’ – कवि का उपनाम

सोंधी सुगंध भावार्थ

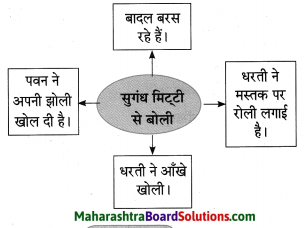
सोंधी-सौंधी-सी …………………………. माटी से बोली।

वर्षा ऋतु के आगमन पर धरती पर बारिश की बूंदों का गिरना शुरू हो जाता है। बारिश की बूंदें धरती पर गिरकर मिट्टी को स्पर्श करती। हैं, जिस कारण मिट्टी से सोंधी सुगंध आने लगती है। यह सोंधी सुगंध मिट्टी से बातें करने लगती है। बारिश की बूंदों की अनुभूति से धरती प्रफुल्लित हो गई है। इसलिए जैसे ही बारिश थम जाती है; वैसे ही वह अपनी आँखें खोलती हैं। मोर को भी वर्षाऋतु अत्यंत प्रिय है।

अत: वह भी वर्षाऋतु में खुश होकर कह रहा है कि चारों ओर हरियाली ही हरियाली छा गई है। भीषण गरमी के कारण धरती बंजर हो गई थी। बादल बरसने के बाद हरियाली-सा हरा वस्त्र धारण करने का धरती का जो सपना था; वह अब पूरा हो गया है। भला वर्षा के आगमन से कौन खुश नहीं होता?

प्रकृति के सभी अपादान अपनी-अपनी टोली में एकत्रित होकर आनंद व्यक्त कर रहे हैं। वर्षाऋतु के इस सुहावने व मनभावन मौसम में कोई भी अकेला रहना नहीं चाहता। सोंधी सुगंध मिट्टी से कह रही है कि इसमें जो इत्र है, उसमें बारिश का जिक्र है अर्थात वर्षा में सर्वत्र मोहक खुशबू छा गई है।

बाग बगीचे …………………………. माटी से बोली।

वर्षा के आगमन से प्रकृति का प्रत्येक अंग हर्षित एवं प्रफुल्लित हो उठा है। बाग-बगीचे, ताल-तलैया आदि सब मुस्करा रहे हैं। पेड़ भी बरसात के मौसम में अपनी मस्ती में झूम रहे हैं। ऐसा प्रतीत होता है कि वे खुशी के गीत गा रहे हैं। वर्षा का साथ पाकर पवन भी आनंदविभोर हो गया है। उसने अपनी ठंड हवा की झोली प्रसन्न होकर खोल दी है। जिससे वातावरण और अधिक खुशनुमा हो गया है। सोंधी सुगंध मिट्टी से कह रही है कि इसमें जो इत्र है, उसमें बारिश का जिक्र है अर्थात वर्षा में सर्वत्र मोहक खुशबू छा गई है।

सागर का जो …………………………. माटी से बोली।

वर्षा के आगमन से सागर की अपनी खुशी का इरादा भी सफल हो गया है। वह खुशी के उफान से भर गया है। सागर वर्षाऋतु में अपनी ही खुशियों की दुनिया में खो गया है। अत: वह अपनी लहरों के साथ नृत्य कर रहा है। वर्षा के आगमन के कारण धरती ने अपने तन पर हरियालीयुक्त हरित वस्त्र का परिधान धारण किया। धरती ने अपने मस्तक पर रोली लगाई है। वर्षा-उत्सव के लिए उसने श्रृंगार किया है।

सोंधी सुगंध मिट्टी से कह रही है कि इसमें जो इत्र है, उसमें बारिश का जिक्र है अर्थात वर्षा में सर्वत्र मोहक खुशबू छा गई है।

पावस का मधुमास …………………………. माटी से बोली।

पावस का मधुमास यानी वर्षाऋतु में वसंत जिस प्रकार वसंत ऋतु में वृक्षों पर नए पत्ते एवं फूल आते हैं। वैसे ही वर्षा ऋतु में प्रकृति सजती-संवरती है। सर्वत्र आनंद व्याप्त होता है। वर्षा ऋतु प्रत्येक मानव के मन में आस एवं विश्वास भर देती है। कवि भी वर्षा के इस आनंद से अछूते नहीं है। वह भी वर्षा ऋतु के सामने नतमस्तक होकर उसके स्वागत में पुष्प अर्पण करते हैं।

यह तो प्रतिवर्ष आने वाला उत्सव है। सदियों से वर्षा का स्वागत होता आ रहा है। सदियों से वर्षा के आगमन पर लोग खुश होते हैं और होते रहेंगे। यह हँसी-ठिठोली सदा से चलती आ रही है। सोंधी सुगंध मिट्टी से कह रही है कि इसमें जो इत्र है, उसमें बारिश का जिक्र है अर्थात वर्षा में सर्वत्र मोहक खुशबू छा गई है।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 8 Gazal Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 8 गजल Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 8 गजल Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 8 गजल Textbook Questions and Answers

सूचना के अनयुार कृहत्‍ँ कीहजए:

(1) गजल की पंक्तियों का तातप्‍:
a. नीं के अंदर हदिाे ————
b. आईना बनकर हदिो ————
उत्तर:
(i) हमें प्रशंसा और वाहवाही का लोभ त्यागकर नींव की ईंटों के समान कुछ अच्छा और सुदृढ़ काम करना चाहिए।
(ii) हमें ऐसी शख्सियत बनना चाहिए कि कैसी भी प्रतिकूल परिस्थिति क्यों न हो, हम विचलित न हों। बिना टूटे, बिना बिखरे हर परिस्थिति का डटकर सामना करें। अपने लक्ष्य को प्राप्त करें।

(2) कृति पूण् कीहजए:

उत्तर:

(3) हजनके उततर हनम् शब् हों ऐसे प्र तै्‍र कीहजए:
1. भीड़
2. जुगनू
3. हततली
4. आसमान
उत्तर:
1. कवि अक्सर किसी शक्ल को कहाँ देखना चाहता है?
2. वक्त की धुंध में साथ रहने को किसने कहा?
3. कवि खिलते फूल के स्थान पर कहाँ दिखने को कहता है?
4. गर्द बनकर कहाँ लिखना चाहिए?

(4) हनम्हलखखत पंक्तियों से प्र तीिनमूल् हलखखए:
१. आपको मिसूस ……………………………………….. भीतर हदिो।
२. कोई ऐसी श्‍ ……………………………………….. मुझे अ्‍र हदिो।.
उत्तर:
(ii) हे ईश्वर, मैं चाहता हूँ कि मैं जिसे भी देखू, मुझे उसी में तुम नजर आओ। अर्थात मानव मात्र ईश्वर का अंश है।

(5) कृहत पूण् कीहजए:
गजल मे प्रयुक्त प्कृहतक घ‍ट

उत्तर:

(6) कहि के अनयुार ऐसे हदखो:

यदि मेरा घर अंतररक में होता,’ हिष् पर अससी से सौ शब्दों मे हनबंध लेखन कीहजए।
उत्तर:
पिछले कई वर्षों में अंतरिक्ष विज्ञान में जो प्रगति हुई है, वह सराहनीय है। पहले अंतरिक्ष यात्रा कल्पना से अधिक कुछ नहीं थी लेकिन आज अंतरिक्ष यात्रा के सपने सच हो गए हैं। रूस ने अंतरिक्ष यान के द्वारा अपने अंतरिक्ष यात्री यूरी गागरिन को पहली बार अंतरिक्ष में भेजा था। फिर तो अमेरिकी अंतरिक्ष यात्री नील आर्मस्ट्रांग और एडविन एल्ड्रिन सबसे पहले चंद्रमा पर पहुचनेवाले अंतरिक्ष यात्री हो गए।

अब तो ऐसा लगता है कि कभी-न-कभी हम को भी अंतरिक्ष में जाने का मौका मिल सकता है। लेकिन यह कब संभव होगा, कहा नहीं जा सकता। काश, मेरा घर अंतरिक्ष में होता…. यदि सच में मेरा घर अंतरिक्ष में होता तो कितना अच्छा होता। जिस आसमान को दूर से देखा करते हैं, हम उसकी खूब सैर करते। चाँद, सितारों को नजदीक से देखते। बादलों के बीच लुका-छिपी खेलते। परियों के देश में जाते।

वे किस तरह रहती हैं, जानने-देखने का अवसर पाते। हम अंतरिक्ष से अपनी सुंदर धरती को देखते। अपने प्यारे भारत को देखते। आकाशगंगा के विभिन्न ग्रहों-उपग्रहों को देखते। सौरमंडल के सबसे सुंदर ग्रह शनि और उसके वलयों को देखते। उनके जितना निकट जा सकते, अवश्य जाते। स्पेस वॉक करते। वहाँ फैली शांति का अनुभव करते। वहाँ के प्रदूषणरहित वातावरण में रहने का मौका मिलता, जिससे हमारा स्वास्थ्य बहुत बढ़िया हो जाता। काश ऐसा हो पाता…

प्रयु गजल की अपनी पसंदीदा हकनिी चार पंक्तियों का केंद्रीय भाव सपष् कीहजए।

Hindi Lokbharti 10th Textbook Solutions Chapter 8 गजल Additional Important Questions and Answers

पद्यांश क्र.1

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) आकृति पूर्ण कीजिए:

उत्तर:

(2) विधानों के सामने सत्य / असत्य लिखिए:
(i) स्वर्णिम शिखर बनकर जीना ही जीना है।
(ii) मील का पत्थर बनकर जीना अच्छा नहीं है।
(iii) मोमबत्ती के धागे जैसा जीवन जियो।
(iv) जिंदगी टूटकर नहीं बिखरनी चाहिए।
उत्तर:
(i) असत्य
(ii) असत्य
(iii) सत्य
(iv) सत्य।

(3) उचित जोड़ियाँ मिलाइए:

अ	आ
(i) शिखर	गर्द
(ii) आस्मान	जिंदगी
(iii) पत्थर	स्वर्णिम
(iv) शक्ल	मील
	नींव

उत्तर:

अ	आ
(i) शिखर	स्वर्णिम
(ii) आस्मान	गर्द
(iii) पत्थर	मील
(iv) शक्ल	जिंदगी

(4) दो ऐसे प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) आईना
उत्तर:
(i) पत्थरों के शहर में क्या बनकर दिखना चाहिए?

(5) एक शब्द में उत्तर लिखिए:
(i) पत्थर के शहर में यह बनकर दिखना है –
(ii) दिखने का शौक है तो यह बनो –
उत्तर:
(i) आईना।
(ii) नींव।

कृति 2: (शब्द संपदा)

(1) निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) शक्ल = ……………………
(ii) शिखर = ……………………
(iii) गर्द = ……………………
(iv) पत्थर = ……………………
उत्तर:
(i) शक्ल = चेहरा
(ii) शिखर = शीर्ष
(ii) गर्द = धूल
(iv) पत्थर = पाषाण।

(2) निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) आदमी x
(ii) शहर x
(ii) आसमान x
(iv) टूटना x
उत्तर:
(i) आदमी x जानवर
(ii) शहर x गाँव
(iii) आसमान x जमीन
(iv) टूटना x जुड़ना।

कृति 3: (सरल अर्थ)

प्रश्न.
उपयुक्त पदयांश की आरंभ की चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
किसी भी अट्टालिका के चमचमाते शिखरों को सभी देखते हैं। उनकी शान की प्रशंसा भी करते हैं। लोग समाज में इन शिखरों के समान ही सम्मान पाना चाहते हैं। परंतु वास्तव में देखा जाए तो इन शिखरों से अधिक महत्व है उन ईंटों और पत्थरों का, जिनके कारण ये शिखर बन सके। यदि नींव की ईंटों ने गुमनामी के अंधेरे में रहना स्वीकार न किया होता, तो इन शिखरों का अस्तित्व ही न होता। यदि हम समाज के लिए कुछ करना चाहते हैं, तो हमें प्रशंसा और जैं सुदृढ़ काम करना चाहिए।

पद्यांश क्र. 2
प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन):

(1) सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) वक्त की इस धुंध में तुम …………………………….. बनकर दिखो। (सितारा/चिराग/रोशनी)
(ii) हम सभी के लिए एक …………………………….. है। (दुनिया/मर्यादा/मंच)
(iii) कोई …………………………….. कली फूल बनने से डर जाए। (छोटी/सुंदर/नाजुक)
(iv) कोई ऐसी शक्ल तो मुझको दिखे इस …………………………….. में। (भीड़/संसार/घर)
उत्तर:
(i) वक्त की इस धुंध में तुम रोशनी बनकर दिखो।
(ii) हम सभी के लिए एक मर्यादा है।
(iii) कोई नाजुक कली फूल बनने से डर जाए।
(iv) कोई ऐसी शक्ल तो मुझको दिखे इस भीड़ में।

(2) निम्नलिखित पंक्तियों से प्राप्त जीवनमूल्य लिखिए:
(i) एक जुगनू ने …………………………….. रोशनी बनकर दिखो।
उत्तर:
(i) जब वक्त साथ न दे रहा हो। हर तरफ असफलता और निराशा का साम्राज्य हो। ऐसे समय में एक छोटी-सी आशा की किरण भी बहुत बड़ा सहारा बन सकती है। हमें निराश, हताश लोगों के मन में आशा की किरण जगाना चाहिए।

(3) ऐसे प्रश्न तैयार कीजिए, जिनके उत्तर निम्नलिखित शब्द हों:
(iv) मोती।
उत्तर:
(iv) मोती को किसके अंदर दिखना चाहिए?

(4) जोड़ियाँ मिलाइए:

‘अ’	‘आ’
(i) धुंध	सीप
(ii) मर्यादा	तितली
(iii) मोती	रोशनी
(iv) फूल	मनुष्य

उत्तर:

‘अ’	‘आ’
(i) धुंध	रोशनी
(ii) मर्यादा	मनुष्य
(iii) मोती	सीप
(iv) फूल	तितली

कृति 2: (शब्द संपदा)

निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) जुगनू – ……………………….
(ii) रोशनी – ……………………….
(iii) मोती – ……………………….
(iv) सीप – ……………………….
उत्तर
(i) जुगनू – पुल्लिंग
(ii) रोशनी – स्त्रीलिंग
(iii) मोती – पुल्लिंग
(iv) सीप – स्त्रीलिंग

कृति 3: (सरल अर्थ):

प्रश्न.
उपर्युक्त पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
जब वक्त हमारा साथ न दे रहा हो। हर तरफ असफलताएँ धुंध के समान छाई हों। निराशा रूपी अंधकार का साम्राज्य हो। ऐसे: समय में एक छोटी-सी आशा की किरण भी बहुत बड़ा सहारा बन सकती है। ठीक उसी प्रकार, जैसे घने अंधकार में चमकता हुआ जुगनू । तुम्हें भी निराश, हताश लोगों के मन में आशा की किरण जगाना चाहिए।

सभी मनुष्यों के लिए समाज में रहने के लिए कुछ सीमाएँ हैं, जिनका हमें पालन करना होता है। तभी समाज हमें और हमारे व्यवहार को स्वीकार करता है। अगर तुम चाहते हो कि लोगों में तुम्हारी कोई पहचान बने तो जिस प्रकार सीप के अंदर मूल्यवान मोती छिपा होता है, उसी प्रकार तुम्हें समाज के कल्याण के लिए श्रेष्ठ कर्म करने चाहिए।

भाषा अध्ययन (व्याकरण)

प्रश्न.
सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों के शब्दभेद पहचानिए:
(i) मैं दिल्ली में अच्छा घर ढूँढ़ रहा हूँ।
(ii) वे तेजी के साथ बगीचे की ओर चल पड़े।
(iii) तुम अब पढ़ने बैठ जाओ।
उत्तर:
(i) अच्छा – गुणवाचक विशेषण।
(ii) बगीचे – जातिवाचक संज्ञा।
(iii) तुम – पुरुषवाचक सर्वनाम।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) के मारे.
(ii) या
(iii) पर।
उत्तर:
(i) के मारे – लड़का डर के मारे काँप रहा था।
(ii) या – वे खेलने या घूमने गए होंगे।
(iii) पर – गाड़ी थी, पर पर्याप्त पेट्रोल नहीं था।

3. संधि:
कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
नरेश	…………………	…………………
अथवा
…………………	दिक् + अंबर	…………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
नरेश	नर + ईश	स्वर संधि
अथवा
दिगंबर	दिक् + अंबर	व्यंजन संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) वे गरीबों को फल बाँटते रहे।
(ii) देरी करने को मेरा मन गवारा नहीं कर पाया।
(iii) उनके शब्द मेरे कानों में गूंजने लगे।
उत्तर:
सहायक क्रिया – मूल रूप
(i) रहे – रहना
(ii) पाया – पाना
(iii) लगे – लगना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) छोड़ना –
(ii) डूबना –
(iii) सूखना। –
उत्तर:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) छोड़ना	छुड़ाना	छुड़वाना
(ii) डूबना	डुबाना	डुबवाना
(iii) सूखना	सुखाना	सुखवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग किजिए:
(i) नाम-निशान न रहना
(ii) रटता जाना।
उत्तर:
(i) नाम-निशान न रहना।
अर्थ: अस्तित्व मिट जाना।
वाक्य: भूकंप के कारण पुराने कार्यालय का नाम-निशान नहीं रहा।

(ii) रटते जाना।
अर्थ: बार-बार कहते जाना।
वाक्य: विजय गाँव जाने की बात रटता जा रहा है।

(2) अधोरेखांकित वाक्यांशों के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (तोलकर बोलना, तीर की तरह निकल जाना, कानों में गूंजना, ठहाका लगाना)
(i) पाकिटमार महिला का बटुआ छीनकर बहुत तेजी से निकल गया।
(ii) माता-पिता द्वारा दी गई सीख जीवनभर ध्वनित होती रहती है।
(iii) सज्जन हमेशा सोच-समझकर बोलता है।
उत्तर:
(i) पाकिटमार महिला का बटुआ छीनकर तीर की तरह निकल गया।
(ii) माता-पिता द्वारा दी गई सीख जीवनभर कानों में गूंजती रहती है।
(iii) सज्जन हमेशा तौलकर बोलते हैं।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उनका भेद लिखिए:
(i) ईश्वर की प्राप्ति आसानी से नहीं होती।
(ii) एक बच्चा कुर्सी पर चढ़ा तो दूसरा नाचने लगा।
(iii) मैंने तय किया कि आज किसी से नहीं मिलूँगा।
उत्तर:
(i) की – संबंध कारक।
(ii) पर – अधिकरण कारक।
(iii) से – करण कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) “गरम गरम भूनकर मसाला लगाकर दूंगा’
(ii) आदमी ने आकर पूछा-अभी भोजन तैयार होने में कितना विलंब है
(iii) हाँ, सूर ने एक जगह लिखा है-मैं दसों दिशाओं में देख लेता हूँ
उत्तर:
(i) “गरम-गरम भूनकर मसाला लगाकर दूंगा।”
(ii) आदमी ने आकर पूछा – “अभी भोजन तैयार होने में कितना विलंब है?”
(iii) हाँ, सूर ने एक जगह लिखा है- ‘मैं दसों दिशाओं में देख लेता हूँ।’

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) ठीक ग्यारह बजे प्रधानमंत्री बाहर आते हैं। (सामान्य भूतकाल)
(ii) मुझे भाई का जला हुआ चेहरा याद आता है। (सामान्य भविष्यकाल)
(iii) गुरुदेव अपने समय पर स्नान करते हैं। (पूर्ण भूतकाल)
उत्तर:
(i) ठीक ग्यारह बजे प्रधानमंत्री बाहर आए।
(ii) मुझे भाई का जला हुआ चेहरा याद आएगा।
(iii) गुरुदेव ने अपने समय पर स्नान किया था।

10. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) ईश्वर ने हमें मनुष्य जीवन दिया है।
(ii) हमारा उद्देश्य, सजना, सँवरना ही नहीं है, बल्कि हमारे द्वारा किए गए कार्य सुंदर होने चाहिए।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य।

(2) निम्नलिखित वाक्यों को अर्थ के आधार दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए:
(i) चाची जली-भुनी रहती थी। (संदेहवाचक वाक्य)
(ii) मन अब सुकून अनुभव कर रहा था। (निषेधवाचक वाक्य)
उत्तर:
(i) शायद चाची जली-भुनी रहती थी।
(ii) मन अब सुकून अनुभव नहीं कर रहा था।

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) इस मंदिर में अनेकों बूध की मूर्तियाँ हैं।
(ii) माँ को यहाँ से गए बस एक मिनेट हुई है।
(iii) मेरा घर तुमसे अच्छा है।
उत्तर:
(i) इस मंदिर में बुद्ध की अनेक मूर्तियाँ हैं।
(ii) माँ को यहाँ से गए बस एक मिनट हुआ है।
(iii) मेरा घर तुम्हारे घर से अच्छा है।

गजल Summary in Hindi

गजल विषय-प्रवेश :
प्रस्तुत गजल में माणिक वर्मा ने हमें निरंतर आगे बढ़ते रहने की प्रेरणा दी है। कवि का मानना है कि बाहरी रंग-रूप तो। अस्थायी होता है। सुंदरता हमारे विचारों में, हमारे कामों में होनी चाहिए।

गजल कविता का सरल अर्थ

1. आपसे किसने ………………………… भीतर देखो।

किसी भी अट्टालिका के चमचमाते शिखरों को सभी देखते हैं। उनकी शान की प्रशंसा भी करते हैं। लोग समाज में इन शिखरों के समान ही सम्मान पाना चाहते हैं। परंतु वास्तव में देखा जाए तो इन शिखरों से अधिक महत्व है उन ईंटों और पत्थरों का, जिनके कारण ये शिखर बन सके। यदि नींव की ईंटों ने गुमनामी के अंधेरे में रहना स्वीकार न किया होता, तो इन शिखरों का अस्तित्व ही न होता। यदि हम समाज के लिए कुछ करना चाहते हैं, तो हमें प्रशंसा और वाहवाही का लोभ त्यागकर नींव की ईंटों के समान कुछ अच्छा और सुदृढ़ काम करना चाहिए।

यदि आप मंजिल की ओर अग्रसर हैं तो अपने अच्छे कर्मों के कारण उसी प्रकार आसमानों तक छा जाइए, जैसे आँधी आने पर पृथ्वी से आकाश तक धूल-ही-धूल दृष्टिगोचर होती है। अर्थात आपके द्वारा किए गए अच्छे कामों का प्रभाव और चर्चा हर तरफ हो। और यदि आप मंजिल की ओर बढ़ते हुए मार्ग में कहीं बैठ जाते हो तो मील के पत्थर के समान बनो। मील का पत्थर जिस प्रकार एक पथिक को अपनी मंजिल की ओर बढ़ते समय सहायता करता है, उसी प्रकार क्रियाशील न होते हुए भी आप दूसरों की मदद करें।

ईश्वर ने हमें मनुष्य जीवन दिया है। हमारा उद्देश्य केवल सजना, सँवरना और सुंदर दिखना ही नहीं होना चाहिए। हमारे द्वारा किए गए काम सुंदर होने चाहिए। ईश्वर द्वारा प्रदत्त इस श्रेष्ठ मानव जीवन में हमें मानवीय गुणों को अपनाना चाहिए। हमारा कोई भी काम ऐसा न हो, जो मानवता के दायरे से बाहर हो। समाज में सभी के प्रति हमारा व्यवहार ऐसा हो कि सारा संसार हमें एक अच्छे मनुष्य के रूप में जाने। हमें ऐसी शख्सियत बनना चाहिए कि कैसी भी प्रतिकूल परिस्थिति क्यों न हों, हम विचलित न हों। बिना टूटे, बिना बिखरे हर परिस्थिति का डटकर सामना करें। अपने लक्ष्य को प्राप्त करें।

हमें प्रत्येक मानव से सहानुभूति रखनी चाहिए। यह तभी संभव हो सकेगा, जब हम उनके हर दुख-तकलीफ को समझें। जैसे मोमबत्ती का धागा सदा उसके साथ रहता है। उसके साथ जलता है। उसी प्रकार जब हम दीन-दुखियों की पीड़ा को समझेंगे, तो उसे दूर करने का यथासंभव प्रयास करेंगे। इस प्रकार हम अपना मानव-धर्म निभा पाएँगे।

2. एक जुगनू ………………………… अक्सर देखो।

जब वक्त हमारा साथ न दे रहा हो; हर तरफ असफलताएँ धुंध के समान छाई हों; निराशा रूपी अंधकार का साम्राज्य हो; ऐसे समय में एक छोटी-सी आशा की किरण भी बहुत बड़ा सहारा बन सकती है। ठीक उसी प्रकार, जैसे घने अंधकार में चमकता हुआ जुगनू। तुम्हें भी निराश, हताश लोगों के मन में आशा की किरण जगाना चाहिए।

सभी मनुष्यों के लिए समाज में रहने के लिए कुछ सीमाएँ हैं, जिनका हमें पालन करना होता है। तभी समाज हमें और हमारे व्यवहार को स्वीकार करता है। अगर तुम चाहते हो कि लोगों में तुम्हारी कोई पहचान बने तो जिस प्रकार सीप के अंदर मूल्यवान मोती छिपा होता है, उसी प्रकार तुम्हें समाज के कल्याण के लिए श्रेष्ठ कर्म करने चाहिए। तुम्हारी यह कल्याण-भावना तुम्हें एक पहचान देगी, सम्मान देगी।

यदि कोई कोमल कली फूल बनने से डर रही हो। कली जानती है कि उसके खिलते ही तितली उसका रस चूसने के लिए आएगी और फूल बनी कली को परेशान करेगी। तुम फूल को तितली से बचाने का प्रयास करो। अर्थात उसके डर को दूर करने में उसकी मदद करो।

यह संसार मनुष्यों का एक सागर है। भीड़ में जाने-अनजाने अनगिनत चेहरे हर तरफ दिखाई देते हैं। हे ईश्वर, मैं चाहता हूँ कि मैं जिसे भी देखू, मुझे उसी में तुम नजर आओ। तुम तो सर्वव्यापक हो।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 11 Krushak Gan Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 11 कृषक गान Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 11 कृषक गान Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 11 कृषक गान Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए
सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
कृतियाँ पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
वाक्य पूर्ण कीजिए:
a. कृषक कमजोर शरीर को ____________
b. कृषक बंजर जमीन को ____________
उत्तर:
(i) कृषक कमजोर शरीर को पत्तियों से पालता है।
(ii) कृषक बंजर जमीन को अपने खून से सींचकर उर्वरा बना देता है।

प्रश्न 4.
निम्नलिखित पंक्तियों में कवि के मन में कृषक के प्रति जागृत होने वाले भाव लिखिए:

पंक्ति	भाव
१. आज उसपर मान कर लूँ
२. आह्वान उसका आज कर लूँ
३. नव सृष्टि का निर्माण कर लूँ
४. आज उसका ध्यान कर लूँ।

उत्तर:

पंक्ति	भाव
१. आज उसपर मान कर लूँ	अभिमान
२. आह्वान उसका आज कर लूँ	मानवता
३. नव सृष्टि का निर्माण कर लूँ	सृजनशीलता
४. आज उसका ध्यान कर लूँ।	आदर

प्रश्न 5.
कविता में आए इन शब्दों के लिए प्रयुक्त शब्द हैं:
१. निर्माता – ____________
२. शरीर – ____________
३. राक्षस – ____________
४. मानव – ____________
उत्तर:
१. निर्माता – सृजक
२. शरीर – तन
३. राक्षस – असुर।
४. मानवता – मनुजता।

प्रश्न 6.
कविता की प्रथम चार पंक्तियों का भावार्थ लिखिए।
उत्तर:
कृषक के अभावों की कोई सीमा नहीं है। परंतु वह संतोष रूपी धन के सहारे अपना जीवन व्यतीत कर रहा है। पूरे संसार में कैसा भी वसंत आए, कृषक के जीवन में सदैव पतझड़ ही बना रहता है। अर्थात ऋतुएँ बदलती हैं, लोगों की परिस्थितियाँ बदलती हैं, परंतु कृषक के भाग्य में अभाव ही अभाव हैं। ऐसी दयनीय स्थिति के बावजूद उसे किसी से कुछ माँगना अच्छा नहीं लगता। वह हाथ फैलाना नहीं जानता। कृषक को अपनी दीन-हीन दशा पर भी नाज है। मैं ऐसे व्यक्ति पर अभिमान करना चाहता हूँ। कृषक के गीत गाना चाहता हूँ।

प्रश्न 7.
निम्न मुद्दों के आधार पर पद्य विश्लेषण कीजिए:
1. रचनाकार कवि का नाम:
2. रचना का प्रकार:
3. पसंदीदा पंक्ति:
4. पसंदीदा होने का कारण:
5. रचना से प्राप्त प्रेरणा:
उत्तर:
(1) रचनाकार का नाम → दिनेश भारद्वाज।
(2) कविता की विधा → गान।
(3) पसंदीदा पंक्ति → हाथ में संतोष की तलवार ले जो उड़ रहा है।
(4) पसंदीदा होने का कारण → अनगिनत अभावों के होते हुए भी कृषक के पास संतोष रूपी धन है।
(5) रचना से प्राप्त संदेश/प्रेरणा → कृषक दिन-रात परिश्रम करके संपूर्ण सृष्टि का पालन करता है। हमें उसके परिश्रम के महत्त्व को समझना चाहिए। उसका सम्मान करना चाहिए।

Hindi Lokbharti 10th Textbook Solutions Chapter 11 कृषक गान Additional Important Questions and Answers

पद्यांश क्र. 1

प्रश्न.
निम्नलिखित पठित पट्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

→ कृति 1: (आकलन)

(1) कविता में आए इन शब्दों के लिए प्रयुक्त शब्द हैं:
(i) वसंत
(ii) पाला हुआ
उत्तर:
(i) वसंत – मधुमास
(ii) पाला हुआ – पालित

(2) सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) कृषक हाथ में _____________ की तलवार लेकर चल रहा है। (श्रम/संतोष/धन)
(ii) सारे संसार में _____________ और उस पर सदा पतझड़ रहता है। (वसंत/वर्षा/फूल)
(iii) कृषक को अपनी _____________ पर अभिमान है। (मेहनत/गरीबी/दीनता)
(iv) उसके लिए _____________ और छाया एक जैसी है। (धूप/रोशनी/कालिमा)
उत्तर:
(i) कृषक हाथ में संतोष की तलवार लेकर चल रहा है।
(ii) सारे संसार में वसंत और उस पर सदा पतझड़ रहता है।
(iii) कृषक को अपनी दीनता पर अभिमान है।
(iv) उसके लिए धूप और छाया एक जैसी है।

→ कृति 2: (शब्दल)

(1) पद्यांश से प्रत्यय जुड़े हुए दो शब्द ढूँढकर लिखिए:
(i) ______________
(ii) ______________
उत्तर:
(i) दीनता (ii) मनुजता।

(2) निम्नलिखित शब्दों के अर्थ लिखिए:
(i) मधुमास – ______________
(ii) आह्वान – ______________
उत्तर:
(i) मधुमास – वसंत ऋतु
(ii) आह्वान – पुकार।

पद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

→ कृति 1: (आकलन)

(1) संजाल पूर्ण कीजिए:

उत्तर:

(2) उत्तर लिखिए:

उत्तर:

(3) आकृति पूर्ण कीजिए:
(i) कृषक विश्व का यह है
(ii) वह अपने क्षीण तन को इनसे पालता है
(iii) कृषक अपने खून से सींचकर ऊसरों को यह बना देता है
(iv) आज यह पीड़ित होकर रो रही है
उत्तर:
(i) कृषक विश्व का यह है – पालक
(ii) वह अपने क्षीण तन को इनसे पालता है – पत्तियों से
(iii) कृषक अपने खून से सींचकर ऊसरों को यह बना देता है – उर्वर
(iv) आज यह पीड़ित होकर रो रही है – मनुजता

(4) कविता की पंक्तियों को उचित क्रमानुसार लिखकर प्रवाह तख्ता पूर्ण कीजिए:
(i) आज उससे कर मिला, नव सृष्टि का निर्माण कर लूँ।
(ii) छोड़ सारे सुर-असुर, मैं आज उसका ध्यान कर लूँ।
(iii) जोड़कर कण-कण उसी के, नीड़ का निर्माण कर लूँ।
(iv) किंतु अपने पालितों के, पद दलित हो मर रहा है।
उत्तर:
(i) किंतु अपने पालितों के, पद दलित हो मर रहा है।
(ii) आज उससे कर मिला, नव सृष्टि का निर्माण कर लूँ।
(iii) छोड़ सारे सुर-असुर, मैं आज उसका ध्यान कर लूँ।
(iv) जोड़कर कण-कण उसी के, नीड़ का निर्माण कर लूँ।

(5) आकृति पूर्ण कीजिए:

उत्तर:

→ कृति 2: (शब्द संपदा)

(1) पद्यांश में प्रयुक्त शब्द-युग्म ढूँढ़कर लिखिए:
(i) …………………
(ii) …………………
उत्तर:
(i) सुर-असुर
(ii) कण-कण।

(2) निम्नलिखित शब्दों में से प्रत्यय अलग करके लिखिए:
(i) पालक = _____________
(ii) मनुजता = _____________
(iii) पीड़ित = _____________
(iv) जोड़कर = _____________
उत्तर:
(i) पालक = पाल + क
(ii) मनुजता = मनुज + ता”
(iii) पीड़ित = पीड़ा + इत
(iv) जोड़कर = जोड़ + कर।

(3) पद्यांश में आए इन शब्दों के लिए प्रयुक्त शब्द हैं:
(i) उपजाऊ
(ii) किसान
उत्तर:
(i) उपजाऊ – उर्वरा
(ii) किसान – कृषक

→ कृति 3: (सरल अर्थ)

प्रश्न.
पद्यांश की अंतिम चार पंक्तियों का सरल अर्थ लिखिए।
उत्तर:
देखिए कविता का सरल अर्थ [5]।

पद्य विश्लेषण

सूचना: यह प्रश्नप्रकार कृतिपत्रिका के प्रारूप से हटा दिया गया है। लेकिन यह प्रश्न पाठ्यपुस्तक में होने के कारण विद्यार्थियों के अधिक अभ्यास के लिए इसे उत्तर-सहित यहाँ समाविष्ट किया गया है।

भाषा अध्ययन (व्याकरण)

1. शब्द भेद:
अधोरेखांकित शब्दों के शब्दभेद पहचानकर लिखिए:
(i) हमें अपने देश पर अभिमान है।
(ii) भूकंप में घंटों मलबे के नीचे दबे रहकर भी बच्चा जीवित रहा।
उत्तर:
(i) अभिमान – भाववाचक संज्ञा।
(ii) जीवित – गुणवाचक विशेषण।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) बल्कि
(ii) तो।
उत्तर:
(i) सिरचन को लोग पूछते ही नहीं थे, बल्कि उसकी खुशामद भी करते थे।
(ii) लहरें बच्चों का रेत का घर गिरा देती तो वे नया घर बनाने लगते।

3. संधि:
कृति पूर्ण कीजिए

संधि शब्द	संधि विच्छेद	संधि भेद
…………..	सम् + सार	…………..
अथवा
निश्चय	…………..	…………..

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
संसार	सम् + सार	व्यंजन संधि
अथवा
निश्चय	निः + चय	विसर्ग संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) सामने शेर को देखते ही सभी यात्री काँपने लगे।
(ii) तुम्हारी भाभी ने कहाँ से सीखी हैं?
उत्तर:
सहायक क्रिया – मूल रूप
(i) लगे – लगना
(ii) हैं – होना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) चलना
(ii) चमकना
(iii) लिखना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वितीय प्रेरणार्थक रूप
(i) चलना – चलाना – चलवाना
(ii) चमकना – चमकाना – चमकवाना
(iii) लिखना – लिखाना – लिखवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों के अर्थ लिखकर वाक्यों में प्रयोग कीजिए:
(i) चंपत होना
(ii) मन न लगना।
उत्तर:
(i) चंपत होना।
अर्थ: गायब हो जाना।
वाक्य: पुलिस के आते ही चोर चंपत हो गया।

(ii) मन न लगना।
अर्थ: इच्छा न होना।
वाक्य: सिरचन का किसी काम में मन नहीं लग रहा था।

(2) अधोरेखांकित वाक्यांशों के लिए उचित मुहावरे का चयन कर वाक्य फिर से लिखिए: (खून का चूंट पीकर रह जाना, पानी फेरना, पिंड छुडाना)
(i) लालची और निर्लज्ज लोगों से छुटकारा पाना आसान नहीं होता।
(ii) शिवाजी आगरे से भाग निकले, इसलिए औरंगजेब को अपना मन मारकर रह जाना पड़ा।
उत्तर:
(i) लालची और निर्लज्ज लोगों से पिंड छुड़ाना आसान नहीं होता।
(ii) शिवाजी आगरे से भाग निकले, इसलिए औरंगजेब को अपना खून का चूंट पीकर रह जाना पड़ा।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कास्क पहचानकर उनका भेद लिखिए:
(i) मानू फूट-फूटकर रो रही थी।
(ii) सिरचन ने जीभ को दाँत से काटकर दोनों हाथ जोड़ दिए।
उत्तर:
(i) मानू-कर्ता कारक
(ii) दाँत से-करण कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) माँ हँसकर कहती जा जा बेचारा मेरे काम में पूजा भोग की बात ही नहीं उठाता कभी
(ii) मानू कुछ नहीं बोली बेचारी किंतु मैं चुप नहीं रह सका चाची और मँझली भाभी की नजर न लग जाए इसमें भी
उत्तर:
(i) माँ हँसकर कहती,“जा-जा बेचारा मेरे काम में पूजा भोग की बात ही नहीं उठाता कभी।”
(ii) मानू कुछ नहीं बोली।…बेचारी! किंतु मैं चुप नहीं रह सका-“चाची और मँझली भाभी की नजर न लग जाए इसमें भी!”

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) सिरचन को एक सप्ताह पहले ही काम पर लगा दिया। (पूर्ण भूतकाल)
(ii) मानू ससुराल जाती है। (सामान्य भविष्यकाल)
(iii) उनके आशीर्वाद आज भी हमें मिले। (सामान्य वर्तमानकाल)
उत्तर:
(i) सिरचन को एक सप्ताह पहले ही काम पर लगा दिया था।
(ii) मानू ससुराल जाएगी।
(iii) उनके आशीर्वाद आज भी हमें मिलते हैं।

10. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद लिखिए:
(i) यह वही लड़का है, जिसे पुरस्कार मिला था।
(ii) मजदूर गड़ढ़ा खोदे और घर चले गए।
उत्तर:
(i) मिश्र वाक्य
(ii) संयुक्त वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) गाँव के किसान सिरचन को मजदूरी के लिए नहीं बुलाते। (इच्छावाचक वाक्य)
(ii) तुम्हें समय पर स्कूल जाना चाहिए। (आज्ञावाचक वाक्य)
उत्तर:
(i) काश! गाँव के किसान सिरचन को मजदूरी के लिए नहीं बुलाते।
(ii) तुम समय पर स्कूल जाओ।

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) लोग गंगा नदी को पवीत्र मानते हैं।
(ii) किसी झमाने में यह शहर बहुत आबाद हैं।
उत्तर:
(i) लोग गंगा नदी को पवित्र मानते हैं।
(ii) किसी जमाने में यह शहर बहुत समृद्ध था।

कृषक गान Summary in Hindi

विषय-प्रवेश : प्रस्तुत गीत में गीतकार दिनेश भारद्वाज एक कृषक का महत्त्व प्रतिपादित कर रहे हैं। कृषक, जो कि संपूर्ण संसार का अन्नदाता है, स्वयं अभावों में जीता है। पर किसी के समक्ष हाथ नहीं फैलाता। कवि समाज में उसका सम्मान पूर्ववत स्थापित करना चाहते हैं।

कविता का सरल अर्थ

1. हाथ में संतोष ………………………… का गान कर लूँ।।

कृषक के अभावों की कोई सीमा नहीं है। परंतु उसके पास संतोष रूपी धन है। वह उसी संतोष के सहारे अपना जीवन व्यतीत कर रहा है। पूरे संसार में कैसा भी वसंत आए, कृषक के जीवन में सदैव पतझड़ ही रहता है। अर्थात ऋतुएँ बदलती हैं, लोगों की परिस्थितियाँ बदलती हैं, परंतु कृषक के भाग्य में अभाव ही अभाव हैं। ऐसी दयनीय स्थिति के बावजूद उसे किसी से कुछ माँगना अच्छा नहीं लगता। कृषक को अपनी दीन-हीन दशा पर भी नाज है। कवि कहते हैं कि में ऐसे व्यक्ति पर अभिमान करना चाहता हूँ। मैं कृषक के गीत गाना चाहता हूँ।

2. चूसकर श्रम रक्त ………………………… का गान कर लूँ।।

कृषक दिन-रात खेतों में काम करता है। अपने रक्त को पसीने के रूप में बहाता है और संपूर्ण जगत को जीवन-रस प्रदान करता है। ईश्वर की बनाई इस सृष्टि में उसके लिए धूप-छाया दोनों एक-सी हैं। मौसम में कैसा भी बदलाव आए, कृषक की स्थिति नहीं बदलती। मैं मानवता के साथ उसका आह्वान करना चाहता हूँ। मैं कृषक के गीत गाना चाहता हूँ।

3. विश्व का पालक  ………………………… का गान कर लूँ।।

कृषक संपूर्ण संसार का अन्नदाता है। वह अन्न उगाकर पूरे विश्व का पालन करता है। लोगों को जीवन देता है। किंतु अफसोस की बात है कि जिन लोगों को वह पालता है, उन्हीं के द्वारा उसे पददलित

किया जाता है। अपमानित किया जाता है। मैं चाहता हूँ कि मैं कृषक का हाथ पकड़कर एक नवीन सृष्टि का निर्माण करूँ, जहाँ लोग उसके महत्त्व को समझें। उसका सम्मान करें। मैं कृषक के गीत गाना चाहता हूँ।

4. क्षीण निज बलहीन ………………………… का गान कर लूँ।।

कृषक को जीवन में पर्याप्त सुविधाएँ नहीं मिल पाती। उसे अपने दुर्बल, क्षीण शरीर को ढकने के लिए कपड़े तक नहीं प्राप्त होते। वह पत्तों से अपना तन ढकने को मजबूर होता है। कृषक ऊसर धरती में जी-तोड़ मेहनत करके, पसीने के रूप में अपने खून को बहाकर उसे उपजाऊ बनाता है। मेरे लिए वह सभी देवी-देवताओं से ऊपर है। मैं चाहता हूँ कि देव-दानवों के स्थान पर कृषक का ही ध्यान करूं, उसी के जीवन को बेहतर बनाने का प्रयास करूं। मैं कृषक के गीत गाना चाहता हूँ।

5. यंत्रवत जीवित बना ………………………… का गान कर लूँ।

कृषक एक जीवित मशीन के समान है। वह बिना अपने अधिकार माँगे मशीन की तरह पूरा जीवन काम करता रहता है। उस अन्नदाता, सृष्टि के पालक की दुर्दशा देखकर आज मानवता रो रही है। मैं कण-कण जोड़कर कृषक के लिए एक ऐसे नीड़ का, ऐसे घर का निर्माण करना चाहता हूँ, जहाँ उसे एक अच्छा जीवन जीने के लिए सभी आवश्यक सुविधाएँ प्राप्त हों। मैं कृषक के गीत गाना चाहता हूँ।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 8 Aisa Vasant Kab Aayega Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 8 ऐसा वसंत कब आएगा? Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 8 ऐसा वसंत कब आएगा? Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 8 ऐसा वसंत कब आएगा? Textbook Questions and Answers

सुचना के अनुसर क्रुतिय कीजिए ।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तरः

प्रश्न 2.
निम्नलिखित शब्द पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
1. अधर
2. आँखें
उत्तर:
1. पद्यांश में इसके खिलने की बात हो रही है?
2. पद्यांश में इनके हँसने की बात हो रही है?

प्रश्न 3.
अंतिम सात पंक्तियों का भावार्थ लिखिए।
सबको दे भोजन …………… कब आएगा?
उत्तर:
कवि की कामना है कि प्रत्येक व्यक्ति को खाने के लिए भरपेट भोजन, शरीर पर पहनने के लिए वस्त्र व रहने के लिए घर उपलब्ध हो, जिससे प्रत्येक व्यक्ति के जीवन में आनंद और खुशहाली का आगमन हो। इस धरती पर ऐसे वास्तविक वसंत का आगमन हो, जिससे प्रत्येक व्यक्ति के चेहरे पर खुशी झलकती रहे; उसके अधर प्रसन्नता से खिलते रहें व उसकी आँखें हँसहँसकर आनंदविभोर हो जाएँ। ऐसा खुशहाल, समृद्ध, संपन्न वसंत; ग्रीष्म-शिशिर में भी वसंत कहलाएगा। सचमुच, जब ऐसा होगा; तब वास्तविक वसंत का आगमन होगा।

स्वाध्याय:

स्वाध्याय विषयक कृतियाँ

1. तुलना कीजिए।

प्रश्न 1.
तुलना कीजिए।

उत्तरः

प्राकृतिक वसंत	कवि मन की कल्पना का वसंत
प्रकृति का सदाबहार होना	मानवता का फूल खिलना
नए पौधों व फूलों का आगमन	सुख-सुविधा के समान अधिकार पाकर नव यौवनमय जीवन
चारों तरफ हरियाली होना	नव संस्कृति व नव विश्व व्यवस्था का युग
हवा तरोताजा करने वाली होती है।	ऐसा वसंत जो सबको भोजन,  वस्त्र और भवन दे सके

2. उत्तर लिखिए।

प्रश्न 1.
उत्तर लिखिए।
(क) वसंत के अलावा पद्य में प्रयुक्त दो ऋतुएँ –
(ख) सबके लिए समान है –
उत्तर:
(क) ग्रीष्म व शिशिर
(ख) भूमि, गगन, पवन, रवि, शशि

3. निम्न शब्दों के लिए कविता में प्रयुक्त समानार्थी शब्द चुनकर लिखिए।

प्रश्न 1.
निम्न शब्दों के लिए कविता में प्रयुक्त समानार्थी शब्द चुनकर लिखिए।

1. कमी
2. हँसी
3. फूल
4. महल
5. मनुष्य
6. चाँद
7. वस्त्र
8. मन

उत्तर:

1. अभाव
2. मुस्कान
3. प्रसून
4. प्रासाद
5. मानव
6. शशि
7. वसन
8. मानस

4. शब्दसमूह के लिए एक शब्द लिखिए।

प्रश्न 1.
शब्दसमूह के लिए एक शब्द लिखिए।

1. जिसकी कोई निश्चित सीमा नहीं है –
2. जिसका शोषण किया जाता है –
3. बिना थके –
4. जिसका अंत नहीं –

उत्तर:

1. असीम
2. शोषित
3. अथक
4. अनंत

भाषा बिंदु:

1. निम्नलिखित मुहावरों का अर्थ लिखकर सार्थक वाक्यों में प्रयोग कीजिए।

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर सार्थक वाक्यों में प्रयोग कीजिए।

1. खाली हाथ लौटना
2. बिना सिर-पैर की बातें करना
3. यादों में जाग उठना
4. भरा-पूरा अनुभव करना

उत्तरः

1. खाली हाथ लौटना: निराश होकर वापस आना।
   वाक्य: लंदन गोलमेज परिषद किसी भी नतीजे पर नहीं पहुँच सका इसलिए गांधीजी को खाली हाथ लौटना पड़ा।
2. बिना सिर-पैर की बातें करना: निरर्थक बातें करना।
   वाक्य: जो कुछ भी बोल रहे हो उसका कुछ प्रमाण होना चाहिए अन्यथा बिना सिर-पैर की बातें करने से कुछ भी हासिल नहीं होगा।
3. यादों में जाग उठना : पुरानी यादें ताजा हो जाना।
   वाक्य: डॉ ए.पी.जे. अब्दुल कलाम स्वर्ग सिधारे हैं; परंतु वे आज भी हमारी यादों में जाग उठते हैं।
4. भरा-पूरा अनुभव करना: संतुष्ट हो जाना।
   वाक्य: यजमान द्वारा किए गए आतिथ्य सत्कार से हमने भरा-पूरा अनुभव किया।

2. निम्नलिखित वाक्यों के अधोरेखांकित शब्दसमूह के लिए कोष्ठक में दिए मुहावरों में से उचित मुहावरे का चयन करके वाक्य फिर से लिखिए। (चौपट हो जाना, निछावर करना, नाक-भौं सिकोड़ना, मन मारना, फूला न समाना, दंग रह जाना)

प्रश्न 1.
सरकस की गुड़ियों के करतब देखकर दर्शक आश्चर्य – चकित हो गए।
उत्तर:
सरकस की गुड़ियों के करतब देखकर दर्शक दंग रह गए।

प्रश्न 2.
अचानक पिता जी द्वारा पर्यटन पर जाने का निर्णय सुनकर बच्चे बहुत आनंदित हुए।
उत्तर:
अचानक पिता जी द्वारा पर्यटन पर जाने का निर्णय सुनकर बच्चे फूले न समाए।

3. पाठों में आए सभी प्रकार के अव्ययों को ढूँढ़कर उनसे प्रत्येक प्रकार के दस-दस वाक्य लिखिए।

प्रश्न 1.
पाठों में आए सभी प्रकार के अव्ययों को ढूँढ़कर उनसे प्रत्येक प्रकार के दस-दस वाक्य लिखिए।
उत्तरः
क्रियाविशेषण अव्यय:

1. आज: आज रविवार है।
2. कल: मैं कल गाँव जाऊँगा।
3. शायद: शायद मैं कल बाज़ार नहीं जाऊँगा।
4. अचानक: अचानक बिजली चली गई।
5. अभी: अभी भी देर नहीं हुई है।
6. चुपचाप: वह चुपचाप चला गया।
7. अब: अब मैं मन लगाकर पढ़ाई करूँगा।
8. वहाँ: वहाँ कोई तो है।
9. धीरे-धीरे: गाड़ी धीरे-धीरे जा रही थी।
10. जगह-जगह: जगह-जगह फूल ही फूल दिखाई दे रहा है।

संबंधसूचक अव्यय:

1. के लिए: मैंने उसके लिए खिलौने लाए।
2. की ओर: राम ने उसकी ओर देखा।
3. की तरफ: नदी की तरफ मत जाओ।
4. के साथ: मुझे उसके साथ जाना बिलकुल अच्छा नहीं लगता।
5. के बाद: परीक्षा खत्म होने के बाद मैं घूमने चला गया।
6. के पास: विजय के पिता जी के पास बहुत धन है।
7. के अनुसार: उसके अनुसार यह गलत है।
8. के प्रति: उसके प्रति मेरे दिल में हमदर्दी है।
9. के बीच: उन दोनों के बीच झगड़ा हुआ है।
10. के पीछे: घर के पीछे एक पेड़ है।

समुच्चयबोधक अव्यय:

1. और: राम और श्याम मित्र हैं।
2. परंतु: मैं तुम्हारे घर आने वाला था; परंतु कुछ कारणवश नहीं आ सका।
3. बल्कि: वे एक धर्मात्मा ही नहीं हैं; बल्कि एक पहुँचे हुए _महापुरुष भी हैं।
4. व: सीता व गीता बाजार जा रही हैं।
5. क्योंकि: वह निराश है; क्योंकि उसे मनचाही चीज नहीं मिली।
6. कारण: रमेश को चोट लगने के कारण वह स्कूल नहीं जा सका।
7. कि: उसने कहा कि तुम अपना काम करो।
8. पर: मैंने उसे बहुत समझाया पर वह नहीं माना।
9. किंतु: मुझे उसके साथ बात करना अच्छा नहीं लगता, किंतु आज मैं उसके साथ बात करूँगा।
10. अपितु: महात्मा गांधी जी सिर्फ युगपुरुष नहीं थे; अपितु वे भारतीय संस्कृति के व्याख्याता भी थे।

विस्मयादिबोधक अव्यय:

1. जी हाँ!: जी हाँ ! मैं सच कह रहा हूँ।
2. अरे!: अरे ! यह तुमने क्या कर डाला?
3. अच्छा!: अच्छा ! तो यह चित्र तुमने बनाया है।
4. क्या!: क्या ! यह क्या कह रहे हो?
5. हे!: हे ! ये कौन है?
6. हाय राम!: हाय राम! अब मैं क्या करूँ?
7. वाह!: वाह ! क्या मूर्ति है।
8. अजी! : अजी ! सुनते हो।
9. अहा! : अहा ! बहुत मजा आया।
10. बाप रे बाप! : बाप रे बाप ! कितना बड़ा हाथी।

उपयोजित लेखन:

प्रश्न 1.
मुद्दों के आधार पर कहानी लेखन कीजिए।

उत्तरः

‘कुसंगति का परिणाम’

प्रयाग में चक्रधर नामक एक युवक रहता था। युवक पढ़ालिखा था; लेकिन गलत संगति में रहने के कारण वह बुरी आदतों का शिकार हो गया था। वह दिन-रात अपने बुरे दोस्तों के साथ रहता, मौज-मस्ती करता और गलत व्यसनों के चक्कर में पड़ा रहता। एक बार की बात है। उस युक्क के बुरे दोस्तों ने एक घर में चोरी की। चोरी में चुराया हुआ सामान लाकर उन्होंने चक्रधर के घर में उसके लाख मना करने पर भी छुपा दिया। चोरी की जाँच करते हुए पुलिस को भनक मिल गई कि चोरी का माल कहाँ छुपाया गया है।

उन्होंने उस युवक के घर में छापा मारा। पुलिस को वहाँ से चोरी के सामान बरामद हुए। साथ-साथ पुलिस ने उस युवक और उसके दोस्तों को भी धर-पकड़ा। दूसरे दिन पुलिस अधिकारी ने युवक से पूछताछ की। पूछताछ के दौरान अधिकारी को पता चला कि इस चोरी में उसका हाथ नहीं है। गलत संगति के कारण वह भी इस जुर्म में फँस गया है। उसकी सच्चाई जानकर पुलिस अधिकारी ने उसका समुपदशन करवाया और उसे उचित सलाह दी; ताकि वह बुरे लोगों की संगति छोड़कर सही मार्ग पर चल सके।

अधिकारी की सलाह का चक्रधर पर सकारात्मक प्रभाव पड़ा। रिहा होने के पश्चात उसने अपने बुरे दोस्तों का साथ छोड़ दिया और छोटा-मोटा व्यवसाय करना शुरू कर दिया। आहिस्ता-आहिस्ता समय बीतता गया और उस युवक का व्यवसाय बढ़ने लगा। उसके कारोबार में वृद्धि होने लगी। उसने अपने जैसे गलत संगति के शिकार हुए युवकों को अपनी कंपनी में नौकरियाँ दीं; ताकि वे बुरी संगति में फँसकर तथा गलत मार्ग पर चलकर स्वयं को बरबाद न करें।

सीख: कुसंगति का फल हमेशा बुरा होता है और सुसंगति का फल सदैव अच्छा ही होता है।

व्याकरण विभाग:

1&2.

3.

4.

5.

6. मुहावरों का प्रयोग/चयन करना

7. शब्दों का शुद्धीकरण

शब्द संपदा – (पाँचवीं से नौवीं तक)

शब्दों के लिंग, वचन, विलोमार्थक, समानार्थी, पर्यायवाची, शब्दयुग्म, अनेक शब्दों के लिए एक शब्द, समोच्चारित मराठी-हिंदी शब्द, भिन्नार्थक शब्द, कठिन शब्दों के अर्थ, उपसर्ग-प्रत्यय पहचानना/अलग करना, कृदंत-तद्धित बनाना, मूल शब्द अलग करना।

उपयोजित लेखन (रचना विभाग)

पत्रलेखन:

अपने विचारों, भावों को शब्दों के द्वारा लिखित रूप में अपेक्षित व्यक्ति तक पहुँचा देने वाला साधन है पत्र ! हम सभी ‘पत्रलेखन’ से परिचित हैं ही । आज-कल हम नई-नई तकनीक को अपना रहे हैं। संगणक, भ्रमण ध्वनि, अंतरजाल, ई-मेल, वीडियो कॉलिंग जैसी तकनीक को अपने दैनिक जीवन से जोड़ने का प्रयास कर रहे हैं। दूरध्वनि, भ्रमणध्वनि के आविष्कार के बाद पत्र लिखने की आवश्यकता कम महसूस होने लगी है फिर भी अपने रिश्तेदार, आत्मीय व्यक्ति, मित्र/सहेली तक अपनी भावनाएँ प्रभावी ढंग से पहुंचाने के लिए पत्र एक सशक्त माध्यम है।

पत्रलेखन की कला को आत्मसात करने के लिए अभ्यास की आवश्यकता होती है । अपना कहना (माँग/शिकायत/अनुमति/विनती/आवेदन) उचित तथा कम-से-कम शब्दों में संबंधित व्यक्ति तक पहुँचाना, अनुरूप भाषा का प्रयोग करना एक कौशल है । अब तक हम जिस पद्धति से पत्रलेखन करते आए हैं, उसमें नई तकनीक के अनुसार अपेक्षित परिवर्तन करना आवश्यक हो गया है।

पत्रलेखन में भी आधुनिक तंत्रज्ञान/तकनीक का उपयोग करना समय की मांग है। आने वाले समय में आपको ई-मेल भेजने के तरीके से भी अवगत होना है। अतः इस वर्ष से पत्र के नये प्रारूप के अनुरूप ई-मेल की पद्धति अपनाना अपेक्षित है। * पत्र लेखन के मुख्य दो प्रकार हैं, अनौपचारिक और औपचारिक । (पृष्ठ क्र. 35, 41)

औपचारिक पत्र:

1. प्रति लिखने के बाद पत्र प्राप्तकर्ता का पद और पता लिखना
2. पत्र के विषय तथा संदर्भ का उल्लेख करना करना चाहिए ।
3. इसमें महोदय/महोदया शब्द द्वारा आदर कुशलक्षेम पूछना चाहिए। लेखन स्नेह सम्मान सहित प्रभावी प्रकट किया जाता है।
4. निश्चित तथा सही शब्दों में आशय शब्दों और विषय विवेचन के साथ होना चाहिए।
5. पत्र का समापन करते समय बायीं ओर पत्र भेजने वाले के हस्ताक्षर, नाम तथा पता लिखना है।
6. ई-मेल आईडी देना आवश्यक है।

अनौपचारिक पत्र:

1. संबोधन तथा अभिवादन रिश्तों के अनुसार आदर के साथ आवश्यक है ।
2. प्रारंभ में जिसको पत्र लिखा है उसका आवश्यक है।
3. रिश्ते के की प्रस्तुति करना अपेक्षित है।
4. इस पत्र में बायीं ओर पत्र भेजने वाले का नाम, पता लिखना चाहिए। विषय उल्लेख आवश्यक नहीं।.
5. पत्र का समापन करते समय अनुसार विषय विवेचन में परिवर्तन अपेक्षित है।

टिप्पणी: पत्रलेखन में अब तक लिफाफे पर पत्र भेजने बाले (प्रेषक) का पता लिखने की प्रथा है । ई-मेल में लिफाफा नहीं होता है। अब पत्र में ही पता लिखना अपेक्षित है।

गद्य आकलन (प्रश्न निर्मिति)

1. भाषा सीखकर प्रश्नों की निर्मिति करना एक महत्त्वपूर्ण भाषाई कौशल है । पाठ्यक्रम में भाषा कौशल को प्राप्त करने के लिए प्रश्ननिर्मिति घटक का समावेश किया गया है। दिए गए परिच्छेद (गट्यांश) को पढ़कर उसी के आधार पर पाँच प्रश्नों की निर्मिति करनी है । प्रश्नों के उत्तर एक वाक्य में हों ऐसे ही प्रश्न बनाए जाएँ।

प्रश्न ऐसे हों:

1. तैयार प्रश्न सार्थक एवं प्रश्न के प्रारूप में हों।
2. प्रश्नों के उत्तर दिए गए निर्मित गद्यांश में हों ।
3. रचित प्रश्न के अंत में प्रश्नचिह्न लगाना आवश्यक है।
4. प्रश्न रचना का कौशल प्राप्त करने के लिए अधिकाधिक अभ्यास की आवश्यकता है।
5. प्रश्न का उत्तर नहीं लिखना है। प्रश्न रचना पूरे गद्यांश पर होनी आवश्यक है।

1. प्रश्न निर्मिति के लिए आवश्यक प्रश्नवाचक शब्द निम्नानुसार हैं :

निबंध लेखन:

निबंध लेखन एक कला है । निबंध का शाब्दिक अर्थ होता है ‘सुगठित अथवा ‘सुव्यवस्थित रूप में बंधा हुआ’ । साधारण गदय रचना की अपेक्षा निबंध में रोचकता और सजीवता पाई जाती है। निबंध गदय में लिखी हई रचना होती है, जिसका आकार सीमित होता है । उसमें किसी विषय का प्रतिपादन अधिक स्वतंत्रतापूर्वक और विशेष अपनेपन और सजीवता के साथ किया जाता है। एकसूत्रता, व्यक्तित्व का प्रतिबिंब, आत्मीयता, कलात्मकता निबंध के तत्त्व माने जाते हैं । इन तत्वों के आधार पर निबंध की रचना की जाती है।

निबंध लिखते समय निम्नलिखित बातों की ओर ध्यान दें:

1. प्रारंभ, विषय विस्तार, समापन इस क्रम से निबंध
2. विषयानुरूप भाषा का प्रयोग करें।
3. भाषा प्रवाही, रोचक और मुहावरेदार हो ।
4. कहावतों, सुवचनों का यथास्थान प्रयोग करें ।
5. शुद्ध, सुवाच्य और मानक वर्तनी के अनुसार निबंध लेखन आवश्यक है ।
6. सहज, स्वाभाविक और स्वतंत्र शैली में निबंध की रचना हो ।
7. विचार स्पष्ट तथा क्रमबद्ध होने आवश्यक हैं।
8. निबंध की रचना करते समय शब्द चयन, वाक्य-विन्यास की ओर ध्यान आवश्यक देना है। निबंध लेखन में विषय को प्रतिपादित करने की पद्धति के साथ ही कम-से-कम चार अनुच्छेदों की रचना हो ।
9. निबंध का प्रारंभ आकर्षक और जिज्ञासावर्धक हो ।
10. निबंध के मध्यभाग में विषय का प्रतिपादन हो । निबंध का मध्यभाग महत्त्वपूर्ण होता है इसलिए उसमें नीरसता न हो ।
11. निबंध का समापन विषय से संबंधित, सुसंगत, उचित, सार्थक विचार तक ले जाने वाला हो।

आत्मकथनात्मक निबंध लिखते समय आवश्यक तथा महत्त्वपूर्ण बातें:

1. आत्मकथन अर्थात एक तरह का परकाया प्रवेश है।
2. किसी वस्तु, प्राणी, पक्षी, व्यक्ति की जगह पर स्वयं को स्थापित/आरोपित करना होता है ।
3. आत्मकथनात्मक लेखन की भाषा प्रथमपुरुष, एकवचन में हो । जैसे – मैं …. बोल रहा/रही हूँ।
4. प्रारंभ में विषय से संबंधित उचित प्रस्तावना, सुवचन, घटना, प्रसंग संक्षेप में लिख सकते हैं सीधे मैं… हूँ से भी प्रारंभ किया जा सकता है।

वैचारिक निबंध लिखते समय आवश्यक बातें:

1. वैचारिक निबंध लेखन में विषय से संबंधित में जो विचार होते हैं, उनको प्रधानता दी जाती है। वर्णन, कथन, कल्पना से बढ़कर विचार महत्त्वपूर्ण होते हैं। विचार के पक्ष-विपक्ष में लिखना आवश्यक होता है।
2. विषय के संबंध में विचार, मुद्दे, मतों की तार्किक प्रस्तुति महत्त्वपूर्ण होती है।
3. पूरक पठन, शब्दसंपदा, विचारों की संपन्नता जितनी अधिक होती है उतना ही वैचारिक निबंध लिखना हमारे लिए सहज होता है। उदा.

कहानी लेखन:

कहानी सुनना-सुनाना आबाल वृद्धों के लिए रुचि और आनंद का विषय होता है । कहानी लेखन विद्यार्थियों की कल्पनाशक्ति, नवनिर्मिति व सृजनशीलता को प्रेरणा देता है । इसके पूर्व की कक्षाओं में आपने कहानी लेखन का अभ्यास किया है। कहानी अपनी कल्पना और सृजनशीलता से रची जाती है । कहानी का मूलकथ्य (कथाबीज) उसके प्राण होते हैं । मूल कथ्य के विस्तार के लिए विषय को पात्र, घटना, तर्कसंगत विचारों से परिपोषित करना लेखन कौशल है। इसी लेखन कौशल का विकास करना कहानी लेखन का उद्देश्य है । कहानी लेखन का मनोरंजन तथा आनंदप्राप्ति भी उद्देश्य है।

कहानी लेखन में निम्न बातों की ओर विशेष ध्यान दें:

1. शीर्षक, कहानी के मुद्दों का विस्तार और कहानी से प्राप्त सीख, प्रेरणा, संदेश ये कहानी लेखन के अंग हैं।
2. कोई भी कहानी घटना घटने के बाद लिखी जाती है, अतः कहानी भूतकाल में लिखी जाए। कहानी के संवाद प्रसंगानुकूल वर्तमान या भविष्यकाल में हो सकते हैं । संवाद अवतरण चिह्न में लिखना अपेक्षित है।
3. कहानी लेखन की शब्दसीमा सौ शब्दों तक हो।
4. कहानी के आरंभ में शीर्षक लिखना आवश्यक होता है । शीर्षक छोटा, आकर्षक, अर्थपूर्ण और सारगर्भित होना चाहिए ।
5. कहानी में कालानुक्रम, घटनाक्रम और प्रवाह होना आवश्यक है । प्रत्येक मुद्दे या शब्द का अपेक्षित विस्तार आवश्यक है। घटनाएँ धाराप्रवाह अर्थात एक दूसरे से शृंखलाबद्ध होनी चाहिए ।
6. कहानी के प्रसंगानुसार वातावरण निर्मिति होनी चाहिए । उदा. यदि जंगल में कहानी घटती है तो जंगल का रोचक, आकर्षक तथा सही वर्णन अपेक्षित है।
7. कहानी के मूलकथ्य/विषय (कथाबीज) के अनुसार पात्र व उनके संवाद, भाषा पात्रानुसार प्रसंगानुकूल होने चाहिए ।
8. प्रत्येक परिसर/क्षेत्र की भाषा एवं भाषा शैली में भिन्नता/विविधता होती है । इसकी जानकारी होनी चाहिए।
9. अन्य भाषाओं के उद्धरण, सुवचनों आदि के प्रयोग से यथासंभव बचे ।
10. कहानी लेखन में आवश्यक विरामचिह्नों का प्रयोग करना न भूलें । कहानी लेखन करते समय अनुच्छेद बनाएँ । जहाँ तक विचार, एक घटना समाप्त हो, वहाँ परिच्छेद समाप्त करें।
11. कहानी का विस्तार करने के लिए उचित मुहावरे, कहावतें, सुवचन, पर्यायवाची शब्द आदि का प्रयोग करें।

कहानी लेखन-[शब्द सीमा अस्सी से सौ तक]

विज्ञापन:

वर्तमान युग स्पर्धा का है और विज्ञापन इस युग का महत्त्वपूर्ण अंग है । उत्कृष्ट विज्ञापन पर उत्पाद की बिक्री का आंकड़ा आज संगणक तथा सूचना प्रौदयोगिकी के युग में, अंतरजाल (इंटरनेट) एवं भ्रमणध्वनि (मोबाइल) क्रांति के काल में विज्ञापन का क्षेत्र विस्तृत होता जा रहा है । विज्ञापनों के कारण किसी वस्तु. समारोह, शिविर आदि के बारे में पूरी जानकारी आसानी से समाज तक पहुंच जाती है। लोगों के मन में रुचि निर्माण करना, ध्यान आकर्षित करना विज्ञापन का मुख्य उद्देश्य होता है। विज्ञापन लेखन करते समय निम्न मुद्दों की ओर ध्यान दें:

1. कम-से-कम शब्दों में अधिकाधिक आशय व्यक्त हो ।
2. विज्ञापन की ओर सभी का ध्यान आकर्षित हो, अतः शब्दरचना, भाषा शुद्ध हो ।
3. जिसका विज्ञापन करना है उसका नाम स्पष्ट और आकर्षक ढंग से अंकित हो ।
4. विषय के अनुरूप रोचक शैली हो । आलंकारिक, काव्यमय, प्रभावी शब्दों का उपयोग करते हुए विज्ञापन अधिक आकर्षक बनाएँ ।
5. ग्राहकों की बदलती रुचि, पसंद, आदत, फैशन एवं आवश्यकताओं का प्रतिबिंब विज्ञापन में परिलक्षित होना चाहिए।
6. विज्ञापन में उत्पाद की गुणवत्ता महत्त्वपूर्ण होती है, अतः छूट का उल्लेख करना हर समय आवश्यक नहीं है।
7. विज्ञापन में संपर्क स्थल का पता, संपर्क (मोबाइल नंबर, ई-मेल आईडी) का स्पष्ट उल्लेख करना आवश्यक है।
8. विज्ञापन केबल पेन से लिखें।
9. पेन्सिल, स्केच पेन का उपयोग न करें।
10. चित्र, डिजाइन बनाने की आवश्यकता नहीं है।
11. विज्ञापन की शब्द मर्यादा पचास से साठ शब्दों तक अपेक्षित है । विज्ञापन में आवश्यक सभी मुद्दों का समावेश हो।

निम्नलिखित जानकारी के आधार पर आकर्षक विज्ञापन तैयार कीजिए:

Hindi Lokvani 10th Std Textbook Solutions Chapter 8 ऐसा वसंत कब आएगा? Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
तुलना कीजिए।
उत्तरः

वसंत में प्रकृति एवं मानव जीवन	पतझड़ में प्रकृति एवं मानव जीवन
वसंत में प्रकृति सदाबहार होती है।	पतझड़ में पेड़ से पत्ते अलग होते हैं।
नए फूल व पौधों का आगमन होता है।	पेड़ पर्ण विहीन होते है।
वसंत सभी के जीवन में खुशियाँ लाता है।	पतझड़ में मानव जीवन उसके समान दुखी एवं करुणामय दिखाई देता है।

प्रश्न 2.
समझकर लिखिए।
मानवता के वन-उपवन का हर प्रसून खिल पाएगा।’ इसका तात्पर्य है –
उत्तरः
जब मानवता के जीवन मूल्य को विश्व भर में सभी लोगों द्वारा अपनाया जाएगा और उसमें सभी लोग खुशीपूर्वक रहेंगे तब वास्तविक वसंत का आगमन होगा।

कृति (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. मानवता
2. उपवन
3. यौवन
4. वितरण

उत्तर:

1. इंसानियत
2. वाटिका
3. जवानी
4. बाँटना

प्रश्न 2.
विलोम शब्द लिखिए।

1. वसंत × ……………….
2. सम × ……………….
3. विजय × …………….
4. जीवन × …………….

उत्तरः

1. पतझड़
2. विषम
3. पराजय
4. मरण

प्रश्न 3.
निम्नलिखित तत्सम शब्द का तद्भव शब्द लिखिए।
नव
उत्तरः
नया

प्रश्न 4.
निम्नलिखित शब्दों में उचित प्रत्ययों का प्रयोग कीजिए।
1. मनुज
2. विजय
उत्तर:
1. मनुजता
2. विजेता

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘मानवता का पालन करने से सभी के जीवन में खुशियाँ छा जाएँगी।’ इस कथन के संदर्भ में अपने विचार लिखिए।
उत्तरः
मानवता का अर्थ है मनुष्य होने का कर्तव्य निभाना, मानव की सेवा करना; मानव के जीवन में खुशी निर्माण करना। मनुष्य होने का यह सबसे बड़ा धर्म है। प्रत्येक व्यक्ति को मानवता के जीवन मूल्यों का पालन करना चाहिए। यदि ऐसा हुआ तो सभी के जीवन में खुशियाँ छा जाएँगी। आज मानव जीवन धीरे-धीरे खतरे की ओर बढ़ रहा है।

अणविक अस्त्रों का निर्माण हो रहा है। संपूर्ण विश्व में अशांति एवं अराजकता फैली रही है। यदि ऐसा ही चलता रहा तो एक दिन इस पृथ्वी से मानव का अस्तित्व नष्ट हो सकता है। अत: सभी की भलाई हेतु एवं सभी के जीवन को खुशहाल बनाने हेतु मानवता का पालन अनिवार्य है। मनुष्य जीवन के विकास के साथ विश्व भर के लोगों के जीवन में सुख-शांति आए, इसलिए हमें मानवता का पालन करना होगा।

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
उत्तर लिखिए।
1. मानव हृदय पर इनका प्रभाव पड़ता है –
2. इनके आँगन का जिक्र पद्यांश में हुआ है –
उत्तरः
1. सुख-दुख का
2. प्रासाद व कुटी के आँगन का

प्रश्न 2.
समझकर लिखिए।
उत्तरः

कृति (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के श्रुतिसम भिन्नार्थक शब्द लिखिए।
1. प्रासाद
2. समान
उत्तरः
1. प्रसाद
2.सामान

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।
1. मानव
2. क्षण
उत्तर:
1. मनुष्य
2. समय

प्रश्न 3.
उपसर्ग व प्रत्यय लगाकर नए शब्द लिखिए।
1. समान
2. प्राण
उत्तरः
1. उपसर्गयुक्त शब्दः असमान, प्रत्यययुक्त शब्द : समानता
2. उपसर्गयुक्त शब्दः निष्प्राण, प्रत्यययुक्त शब्दः प्राणहीन

प्रश्न 4.
वचन बदलिए।
1. कुटी
2. आँगन
उत्तरः
1. कुटियाँ
2. आँगन

प्रश्न 5.
पद्यांश में प्रयुक्त विलोम शब्द की जोड़ियाँ लिखिए।
उत्तरः
1. सुख × दुख
2. प्रासाद × कुटी

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘व्यक्ति के जीवन में सुख और दुख अनिवार्य अंग होते हैं।’ इस विषय पर अपने विचार लिखिए।
उत्तरः
जीवन की प्रतिमा को सुंदर और सुसज्जित बनाने में सुख और दुख आभूषण के समान हैं। मानव जीवन में सुख व दुख, धूप और छाँव की तरह आते-जाते रहते हैं। आखिर व्यक्ति का जीवन सुख-दुख का मेल है। कभी व्यक्ति जीवन में सुख की शीतल सुगंध की फुहारें उड़ती है तो कभी दुख की जलतीबिखरती चिनगारियाँ फैलती हैं। सुख के पल जीवन में कब आए और कब चले गए. इसका व्यक्ति को पता भी नहीं चलता है। लेकिन दुख के पल काटे नहीं कटते। सुख में व्यक्ति इतना प्रफुल्लित हो जाता है कि वह स्वयं को भी भूल जाता है और सातवें आसमान पर पहुँच जाता है। दुख में व्यक्ति इतना डूब जाता है कि वह गहराई के समुंदर से बाहर आने का नाम ही नहीं लेता है। इस प्रकार सुख-दुख आते-जाते रहते हैं।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तरः

प्रश्न 2.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
1. सीमित
2. वंदन
उत्तरः
1. कवि के मन में छाया हुआ वसंत कैसा है?
2. भू पर अभिनव क्या बनेगा?

प्रश्न 3.
निम्नलिखित विधान सत्य है या असत्य लिखिए।
1. कवि को जन-जन की चिंता है।
2. मानव की दुनिया यह धरती का अभिनव नंदन नहीं बन सकती।
उत्तरः
1. सत्य
2. असत्य

कृति (2): शब्द संपदा

प्रश्न 1.
पद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तरः
जन-जन

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
मनुज
उत्तरः
मानव

प्रश्न 3.
निम्नलिखित शब्द से उपसर्ग अलग कीजिए और संबंधित उपसर्ग से अन्य दो शब्द तैयार कीजिए।
अभिनव
उत्तर:
उपसर्ग: अभि, अन्य शब्द: अभिनेता, अभिजीत

प्रश्न 4.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।
1. साकार
2. भू
उत्तरः
1. आकारयुक्त
2. भूमि

प्रश्न 5.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
नंदन
उत्तरः
आनंद देने वाला, पुत्र

प्रश्न 6.
लिंग बदलिए।
1. नंदन
2. कवि
उत्तरः
1. नंदिनी
2. कवयित्री

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘धरती को स्वर्ग-सी सुंदर बनाने के लिए मेरा प्रयास …..।’ इस विषय पर अपने विचार लिखिए।
उत्तरः
धरती पर जीवन का स्पंदन है। यह धरती आने वाली पीढ़ियों के लिए एक सौगात है। इसे सुंदर व स्वच्छ रखना मेरा परम कर्तव्य है। इस धरती को स्वर्ग के जैसा सुंदर बनाने के लिए मैं पेड़-पौधे लगाऊँगा। धरती को सदैव हरित रखूगा। यहाँ-वहाँ कूड़ा-कचरा नहीं फेकूँगा। जल स्रोतों को दूषित होने से बचाऊँगा। पर्यावरण का संतुलन बनाए रखने के लिए वन एवं वन्य जीवों का संरक्षण करूँगा। सर्वत्र शांति का वातावरण बनाए रखूगा।

प्राकृतिक स्रोतों का सोच-समझकर उपयोग करूँगा। पर्यावरण प्रदूषण एवं ग्लोबल वार्मिंग को नियंत्रित करने वाले संभव प्रयासों का कड़ाई से पालन करूँगा। बिजली एवं पानी का जरूरत से ज्यादा उपयोग नहीं करूँगा। मानवीय मूल्यों का प्रचार एवं प्रसार करके सभी के मन में एक-दूसरे के प्रति एवं धरती के प्रति मानवीय संवेदना उत्पन्न करने की कोशिश करूँगा।

(ई) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
उत्तर लिखिए।
1. पद्यांश में पवन की विशेषता बताने वाला शब्द –
2. नवयुग यह लेकर आएगा –
उत्तर:
1. मुक्त
2. नव संस्कृति व नव विश्व व्यवस्था

प्रश्न 2.
समझकर लिखिए।
उत्तर:

कृति (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के श्रृतिसम भिन्नार्थक शब्द लिखिए।
पवन
उत्तरः
पावन

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. मुक्त
2. गगन
3. व्यवस्था

उत्तर:

1. स्वतंत्र
2. आसमान
3. प्रबंध

प्रश्न 3.
पद्यांश में से तत्सम शब्द ढूँढ़कर लिखिए।
उत्तर:

1. रवि
2. शशि
3. पवन
4. नव

प्रश्न 4.
वचन बदलिए।
1. संस्कृति
2. व्यवस्था
उत्तर:
1. संस्कृतियाँ
2. व्यवस्थाएँ

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘नव संस्कृति व नव विश्व व्यवस्था आधुनिकता की देन है।’ इस विषय पर अपने विचार लिखिए।
उत्तरः
पुराने जमाने में हमारे देश में जाति-प्रथा व धार्मिक आडंबरों को अत्याधिक महत्त्व दिया जाता था। स्त्रियों को सामाजिक बंधन में बँधकर रहना पड़ता था। उन्हें शिक्षा का अधिकार नहीं था। समाज में पुरुष-प्रधान व्यवस्था थी। पुराने रीति-रिवाजों को अधिक महत्त्व दिया जाता था। आधुनिक युग में नए मूल्यों एवं नई विचारधारा का प्रचार एवं प्रसार हो जाने से जाति-पाति की भावना समाज से आहिस्ता-आहिस्ता खत्म होती जा रही है।

आज हमारे समाज में स्त्रियों को शिक्षा का अधिकार दिया गया है। आज कई ऐसे परिवार हैं, जो स्त्री-प्रधान हैं। आज हम स्वच्छंद एवं स्वतंत्र हैं। हमें मनचाही शिक्षा या मनचाहा व्यवसाय चुनने का अधिकार है। नव संस्कृति को अपनाने से हमारे विचारों में भारी परिवर्तन हुआ है। आज हम शांति एवं एकता को अपनाने की बात कर रहे हैं। नव संस्कृति ने हमें अध्यात्म व विज्ञान इन दो विषयों से भली-भाँति परिचित कराया है। नव संस्कृति एवं नव विश्व व्यवस्था से आज व्यक्ति, समाज और राष्ट्र प्रगति कर रहा है। ‘वसुधैव कुटुंबकम्’ की भावना धीरे-धीरे प्रबल हो रही है।

प्रश्न (उ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (2): शब्द संपदा

प्रश्न 1.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
वसन
उत्तर:
वस्त्र

प्रश्न 2.
निम्नलिखित शब्द में उचित उपसर्ग लगाइए।
रस
उत्तरः
नी + रस = नीरस

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. अधर
2. आँखें
3. भवन

उत्तरः

1. होंठ
2. नयन
3. मकान

प्रश्न 4.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
रस
उत्तरः
स्वाद, जलीय अंश।

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘रोटी, कपड़ा व मकान मनुष्य जीवन की प्राथमिक आवश्यकता होती है।’ विषय पर अपने विचार लिखिए।
उत्तर:
मानव जीवन अनमोल है। मनुष्य को एक साधारण जीवन जीने के लिए रोटी, कपड़ा व मकान की आवश्यकता होती है। इनमें से किसी एक का भी अभाव होने से उसका जीवन संतुलन सुचारू रूप से नहीं चल सकता। आज हमारे देश की आबादी बढ़ रही है। बढ़ती आबादी को प्राथमिक सुविधाएँ उपलब्ध कराने में सरकार निष्फल हो रही है। आज हमारे देश में कई लोगों को तन ढंकने के लिए कपड़े भी नहीं मिल पाते हैं। कई लोग बेघर हैं और वे रेल्वे स्टेशन या सड़क पर ही अपना बसेरा बना रहे हैं।

कई बच्चे-बड़े भूखे मर रहे हैं। भुखमरी की समस्या से आए दिन लोगों की मृत्यु हो रही है। सरकार अपनी ओर से प्रयास कर रही है परंतु जनता का भी कर्तव्य है कि वे अभावग्रस्त की सहायता के लिए आगे आए। मनुष्य ने इस धरती पर जन्म लिया है, तो उसे रोटी, कपड़ा व मकान जैसी प्राथमिक सुविधाएँ मिलनी ही चाहिए और लोगों को उसे प्राप्त करने के लिए मेहनत भी करनी चाहिए। यदि ऐसा नहीं हो सका, तो इन सुविधाओं के बिना मानव जीवन नीरस व व्यर्थ साबित होगा।

ऐसा वसंत कब आएगा? Summary in Hindi

कवि-परिचय:

जीवन-परिचय: जगन्नाथ प्रसाद ‘मिलिंद’ जी का जन्म सन 1906 में मध्यप्रदेश के ग्वालियर शहर में हुआ। इन्हें हिंदी के अतिरिक्त उर्दू, बांग्ला, मराठी, गुजराती और अंग्रेजी भाषा का भी ज्ञान था। आप हिंदी साहित्य जगत में कवि एवं नाटककार के रूप में प्रसिद्ध हैं। इन्होंने खंड काव्य एवं समीक्षा ग्रंथ लिखकर हिंदी साहित्य की सेवा की है। इनके साहित्य पर गांधीवादी विचारधारा का प्रभाव पड़ा है। इन्होंने अध्यापन के साथ-साथ स्वतंत्रता आंदोलन एवं राजनीति में भी भाग लिया था। इन्हें ‘साहित्य वाचस्पति’ एवं ‘भारत भाषा भूषण’ की उपाधि से सम्मानित किया गया है।

प्रमुख कृतियाँ: ‘अंतिमा’, ‘पूर्णा’, ‘बलिपद के गीत’, ‘नवयुग के गान’, ‘मुक्ति के स्वर’ (काव्य संग्रह) आदि।

पद्य-परिचय:

गीत: गीत साहित्य की एक लोकप्रिय विधा है। स्वर, पद और ताल से युक्त जो गान होता है, वह गीत कहलाता है। इसमें एक मुखड़ा तथा कुछ अंतरे होते हैं। प्रत्येक अंतरे के बाद मुखड़े को दोहराया जाता है। गीत को गाया भी जाता है।

प्रस्तावना: ‘ऐसा वसंत कब आएगा?’ इस गीत में कवि जगन्नाथ प्रसाद ‘मिलिंद’ जी का मानना है कि जिस दिन सुख-सुविधाओं पर अमीर-गरीब का समान अधिकार होगा और राष्ट्र-समाज के सुखों में भी महलों एवं कुटियों का समान अधिकार होगा, उस दिन धरती पर वास्तविक वसंत आ सकेगा।

सारांश:

‘ऐसा वसंत कब आएगा?’ यह एक गीत है। इस गीत के माध्यम से कवि ‘मिलिंद’ जी ने मानवता पर अपने विचार व्यक्त करते हुए सभी के मंगलमय एवं खुशहाल जीवन की कामना की है। कवि के अनुसार सुख-सुविधाओं पर अमीर-गरीब सभी का समान अधिकार होना चाहिए और जिस दिन ऐसा होगा उस दिन सच्चे अर्थ में वसंत अर्थात खुशहाली का आगमन होगा। मानव जीवन अभावरूपी पतझड़ से भरा पड़ा है। अतः मानव को अपने जीवन के अभावों पर विजय प्राप्त करने हेतु संघर्ष करना पड़ता है। सुख-दुख का मानव हृदय पर समान प्रभाव पड़ता है।

कवि के अनुसार जब प्रत्येक व्यक्ति का हृदय प्रेम एवं हर्ष से प्रफुल्लित हो जाएगा, तब वास्तविक वसंत का आगमन होगा। सभी का सूरज, चंद्र व मुक्त विचरण करने वाले पवन पर समान अधिकार होता है। जब नवयुग समानता पर आधारित नवसंस्कृति को अपनाएगा, तब नई विश्व व्यवस्था स्थापित होने में देर नहीं लगेगी। कवि की कामना है कि प्रत्येक व्यक्ति को खाने के लिए भरपेट भोजन, शरीर पर पहनने के लिए वस्त्र व रहने के लिए घर उपलब्ध हो, जिससे प्रत्येक व्यक्ति के जीवन में आनंद और खुशहाली हो।

शब्दार्थ:

1. मानवता – इंसानियत
2. साकार – आकारयुक्त
3. उपवन – वाटिका
4. भू – भूमि
5. यौवन – जवानी
6. मुक्त – स्वतंत्र
7. वितरण – बाँटना
8. गगन – आसमान
9. क्षण – समय, पल
10. रवि – सूर्य
11. शशि – चंद्रमा
12. सम- समान
13. रण – लड़ाई
14. प्रसून – फूल
15. सर्जन – निर्मित, रचना
16. पुलक – प्रेम, हर्ष
17. स्पंदन – धड़कन
18. व्यवस्था – प्रबंध
19. अधर – होंठ
20. भवन – मकान
21. वसन – वस्त्र

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Std 10 Hindi Chapter 2 Kalakar Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 2 कलाकार Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 2 कलाकार Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 2 कलाकार Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

2. परिणाम लिखिए :

प्रश्न 1.
बीमार सेठानी पर धूनी की चुटकी भर राख का…..
उत्तर:
सकारात्मक प्रभाव पड़ा और धीरे-धीरे उसकी तबीयत सुधरने लगी।

प्रश्न 2.
बहुरूपिये की वास्तविकता जानने के उपरांत सेठ जी की स्थिति –
उत्तरः
वह आश्चर्य के मारे आसमान से गिरा।

3. निम्नलिखित विधान सही करके लिखिए।

प्रश्न 1.
बहुरूपिये हू-ब-हू उसी तरह का व्यवहार करके प्राय: लोगों को भ्रम में नहीं डालते थे।
उत्तर:
बहुरूपिये हू-ब-हू उसी तरह का व्यवहार करके प्रायः लोगों को भ्रम में डालते थे।

प्रश्न 2.
एक बार सेठ जी बीमार हो गए।
उत्तर:
एक बार सेठानी बीमार हो गई।

प्रश्न 3.
सेठानी कभी-कभी आने लगी।
उत्तर:
सेठ रोज आने लगा।

प्रश्न 4.
साधु ने झगड़ा करके सेठ को लौटा दिया।
उत्तरः
साधु ने समझा-बुझाकर सेठ को लौटा दिया।

प्रवाह तालिका पूर्ण कीजिए।

प्रश्न 1.
प्रवाह तालिका पूर्ण कीजिए।

उत्तर:

5. निम्नलिखित वाक्यों को घटनाक्रम के अनुसार लिखिए।

प्रश्न 1.
निम्नलिखित वाक्यों को घटनाक्रम के अनुसार लिखिए।

1. सेठजी द्वारा सेठानी को साधु के पास ले जाना।
2. बहुरूपिये का साधु का रूप लेना।
3. सेठानी का बीमार होना।
4. धीरे-धीरे सेठानी की तबीयत सुधरना।

उत्तर:

1. बहुरूपिये का साधु का रूप लेना।
2. सेठानी का बीमार होना
3. सेठजी द्वारा सेठानी को साधु के पास ले जाना।
4. धीरे-धीरे सेठानी की तबीयत सुधरना।

6. इन कृदंत शब्दों की मूल क्रियाएँ लिखिए।

प्रश्न 1.
इन कृदंत शब्दों की मूल क्रियाएँ लिखिए।

1. झुकाव = [ ]
2. सोच = [ ]
3. बनावट = [ ]
4. लगाव = [ ]

उत्तर:

1. झुकाव = [झुकाना या झुकना]
2. सोच = [सोचना]
3. बनावट = [बनवाना]
4. लगाव = [लगना]

7. ‘कला के प्रति ईमानदारी ही सच्चे कलाकार की पहचान है।’ विषय पर अपने विचार लिखिए। 

प्रश्न 1.
‘कला के प्रति ईमानदारी ही सच्चे कलाकार की पहचान है।’ विषय पर अपने विचार लिखिए।
उत्तरः
कलाकार उसे कहते हैं जो कला का ज्ञाता हो, जिसे अपनी कला के सिवा अन्य कुछ नहीं भाता हो। अपनी कला का बेहतर प्रदर्शन करके लोगों का मनोरंजन करना ही उसका मुख्य उद्देश्य होता है। फिर वह कलाकार, अभिनेता हो या फिर कोई बहुरूपिया। उसकी कला ही उसकी पहचान होती है। इसलिए उसे अपनी पहचान एवं अस्तित्व को कभी नहीं खोना चाहिए। चरित्र निर्माण एवं संस्कार करने में कलाकार की भूमिका अनन्यसाधारण होती

है। इसलिए वह अपनी कला के माध्यम से लोगों पर अपनी अमिट छाप छोड़ता है। यदि वह अपनी कला के प्रति ईमानदार नहीं होता अथवा उसका सहारा लेकर गलत कार्य करता है, तो इससे उसकी कला का अपमान होता है। अत: वह हमेशा अपना व्यक्तिगत स्वार्थ त्यागकर, अपने पेशे के प्रति ईमानदारी पर अधिक बल देता है। इसी कारण समाज में उसकी प्रतिष्ठा बढ़ती है और सभी उसका और उसकी कला का सम्मान करते हैं।

अभिव्यक्ति :

प्रश्न 1.
‘सहयोग से कठिन कार्य की पूर्ति होती है।’ विषय पर अपने विचार शब्दांकित कीजिए।
उत्तर:
मनुष्य एक सामाजिक प्राणी है जिसकी उन्नति सहयोग की बुनियाद पर निर्भर है। सहयोग भावना मानवता का प्रतीक है। किसी भी व्यक्ति को सहयोग करना एवं उसे सहायता पहुँचाना सबसे बड़ा धर्म होता है। हमें सबकी समान भाव से मदद करनी चाहिए। सहयोग से बहुत बड़े-बड़े कार्य पूर्ण होते हैं। सहयोग से पुल का निर्माण होता है, बड़ी-बड़ी इमारतें सहयोग के बल पर ही बनती हैं।

सहयोग से व्यक्ति, समाज व राष्ट्र की उन्नति होती है। सहयोग के बल पर ही आधुनिक भारत का नवनिर्माण संभव है। गाँधी जी ने सभी भारतीयों का सहयोग पाकर ही इस देश को अंग्रेजों के शासन से मुक्त कराया तथा हमें आजादी दिला पाने में सफल रहे। सहयोग असंभव को संभव कर देता है। अत: सभी को इसका पालन करना चाहिए।

भाषाबिंदु :

प्रश्न 1.
पाठ में प्रयुक्त तीन-तीन क्रियाविशेषण अव्यय व संबंधसूचक अव्यय बकर उनका स्वतंत्र वाक्य में प्रयोग कीजिए।
उत्तर:
1. क्रियाविशेषण अव्यय :

• धीरे-धीरे : गाड़ी धीरे-धीरे जा रही थी।
• एक बार : एक बार मैं बहुत बीमार हो गया था।
• अब : अब मैं जा रहा हूँ।

2. संबंधसूचक अव्यय :

• के लिए : मैंने उसके लिए खिलौने लाए।
• की तरफ : मैंने तुरंत उसकी तरफ देखा।
• के नीचे : पेड़ के नीचे एक लड़का बैठा था।

उपयोजित लेखन :

प्रश्न 1.
आपके विद्यालय की सैर का वर्णन करने वाला पत्र अपनी सहेली या अपने मित्र को लिखिए। (पत्र निम्न प्रारूप में हों।)

उत्तर:

10 जुलाई, 2018
प्रिय मित्र राहुल,
सप्रेम नमस्ते।
तुम कैसे हो? बहुत दिन हो गए लेकिन तुम्हारा पत्र नहीं मिला। आशा करता हूँ कि तुम ठीक होगे। मैं भी कुशल हूँ। मेरी चिंता मत करना राहुल, हमारे विद्यालय ने महाबलेश्वर की सैर आयोजित की थी। सैर तीन दिन की थी। दिनांक 25 जून को हम सुबह 7 बजे महाबलेश्वर की ओर निकले। करीबन शाम के 4 बजे तक हम महाबलेश्वर पहुंच गए थे। महाबलेश्वर के बारे में तुम्हें क्या बताऊँ? बहुत ही रम्य प्राकृतिक स्थल है महाबलेश्वर । वहाँ की वादियाँ एवं घाटियाँ देखकर मेरा मनमयूर नाचने लगा था।

सघन वृक्ष देखने लायक थे। चारों ओर का वातावरण बड़ा ही शांत और खुशनुमा था। हवा में ठंडक व ताज़गी थी। पेड़ों पर उछल-कूद करने वाले बंदरों की सेना देखकर मैं आनंदविभोर हो गया। वहाँ का रम्य वातावरण एवं मित्रों के साथ घूमते-घूमते तीन दिन कैसे बीत गए, इस बात का मुझे पता ही नहीं चला।

जैसे ही छुट्टियाँ शुरू हो जाएगी; वैसे ही तुम मेरे घर पर आना। फिर हम मिलकर खूब खेलेंगे। तुम्हारे माता जी एवं पिता जी को मेरा सादर प्रणाम।
तुम्हारा प्रिय मित्र,
विजय मेहता
पता : 201, गीता महल,
कृष्ण नगर,
मुंबई : 400 012
vijay-44@gmail.com

Hindi Lokvani 10th Std Textbook Solutions Chapter 2 कलाकार Additional Important Questions and Answers

(अ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
निम्नलिखित विधान सही करके लिखिए।

i. बहुरूपियों के बारे में सभी नहीं जानते हैं।
उत्तर:
बहुरूपियों के बारे में हम सब जानते हैं।

प्रश्न 3.
समझकर लिखिए।
i. गद्यांश में इस प्रांत की लोक कथाओं का जिक्र हुआ है।
उत्तर:
राजस्थान

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ गद्यांश में से ढूँढ़कर लिखिए।

1. पेशा
2. नगर
3. इनाम
4. धोखा

उत्तर:

1. व्यवसाय
2. शहर
3. उपहार
4. विश्वासघात

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. कपड़े धोने का पेशा करनेवाली एक जाति –
ii. अनेक प्रकार के रूप धारण करने वाला –
उत्तर:
i. धोबी
ii. बहुरूपिया

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. सफलता × ……….
2. व्यवहार × ……….
3. भीतर × ……….

उत्तर:

1. असफलता
2. अव्यवहार
3. बाहर

प्रश्न 4.
निम्नलिखित शब्द से उपसर्ग व प्रत्यययुक्त शब्द बनाइए।
i. व्यवहार
ii. रूप
उत्तर:
i. उपसर्गयुक्त शब्द : अव्यवहार, प्रत्यययुक्त शब्द : व्यावहारिक
ii. उपसर्गयुक्त शब्द : कुरूप, प्रत्यययुक्त शब्द : रूपवान

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘बहुरूपियों का पेशा अब समाप्त होता जा रहा है।’ अपने विचार लिखिए।
उत्तर:
पुराने जमाने में मनोरंजन के साधन सीमित होते थे। सिनेमा हॉल, दूरदर्शन, संगणक या मोबाइल जैसे अत्याधुनिक एवं मन बहलाने वाले साधन कम थे। वास्तव में मनोरंजन की दुनिया बहुत छोटी थी। पहले पुराने संस्कार एवं विधियों का अनुकरण किया जाता था। लोक कथाओं एवं लोक कलाओं का अनुकरण करने में सभी को आनंद मिलता था। लेकिन अब जमाना बदल गया है। लोगों की मनोरंजन को लेकर मानसिकता बदल गई है।

विज्ञान व तकनीकी ने मानव सभ्यता में परिवर्तन ला दिया है। इस कारण पहले जिस प्रकार बहुरूपिया द्वार-द्वार पर जाकर अपनी कलाबाजी एवं हुनर को प्रदर्शित करता था, उस प्रकार अब द्वार पर बुहरूपिया नहीं आता है। उसकी कलाबाजी एवं हुनर को देखने के लिए लोगों के पास पर्याप्त समय भी नहीं है। आपाधापी के इस युग में जहाँ अपनों के लिए वक्त नहीं है, वहाँ बहुरूपिए के करतब देखने के लिए किसी के पास समय नहीं है। इसलिए बहुरूपियों का पेशा अब समाप्त होता जा रहा है।

(आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलंन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तर:

कृति आ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. भस्म
2. साधु
3. उपदेश
4. समाचार

उत्तर:

1. राख
2. सज्जन
3. सलाह
4. खबर

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।

1. तीन आड़ी रेखाओं का तिलक .
2. कमर में बाँधने का एक प्रकार का वस्त्र –
3. जिसने संसार को त्यागा है –

उत्तर:

1. त्रिपुंड
2. लँगोटी
3. संसारत्यागी

प्रश्न 3.
विलोम शब्द लिखिए।

1. कीर्ति × ……….
2. आशीर्वाद × ………….
3. साधु × …………..
4. नगर × ………….

उत्तर:

1. अपकीर्ति
2. शाप
3. गाँव

प्रश्न 4.
गद्यांश में प्रयुक्त पर्यायवाची शब्द को ढूँढ़कर लिखिए।
उत्तर:
i. सिर, माथा

प्रश्न 5.
वचन बदलिए।

1. डेरा
2. झोपड़ी
3. बगीचा
4. सफलता

उत्तर:

1. डेरे
2. झोपड़ियाँ
3. बगीचे
4. सफलताएँ

प्रश्न 6.
निम्नलिखित शब्दों में से उपसर्ग छाँटकर लिखिए।
i. महात्मा
ii. उपदेश
उत्तर:
i. महा
ii. उप

प्रश्न 7.
गद्यांश से प्रयुक्त शब्द-युग्म +डकर लिखिए।
उत्तरः
i. कभी-कभी
ii. धीरे-धीरे

प्रश्न 8.
निम्नलिखित शब्द के लिए अनेकार्थी शब्द लिखिए। –
i. रूप
उत्तरः
सूरत, प्रकृति, खूबसूरत, समान।।

प्रश्न 9.
गद्यांश में से तत्सम शब्द ढूँढ़कर लिखिए।
उत्तरः
संसार, कीर्ति, साधु

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘साधु माला, जटा, त्रिपुंड, कमंडल, तिलक, भस्म क्यों धारण करते हैं? अपने विचार लिखिए।
उत्तर:
भारत में हिंदू साधुओं का एक विशेष पहनावा होता है। भारतीय संस्कृति की परंपरा के अनुसार ये माला, जटा, त्रिपुंड, कमंडल, तिलक, भस्म आदि का प्रयोग करके स्वयं को संसारत्यागी

कहलवाते हैं। हिंदू समाज में तुलसी की माला का विशेष महत्व होता है। अतः साधुओं के हाथ व गले में माला होती है। जटा, भस्म व कमंडल का सीधा संबंध भगवान शिव से होता है। भगवान शिव अपने शरीर पर भस्म लगाते थे। हिंदू संप्रदाय में तिलक का भी अपना विशेष महत्त्व होता है। धार्मिक कार्य एवं ईश्वर की उपासना करने के पश्चात माथे पर तिलक लगाया जाता है। माला, जटा, त्रिपुंड, कमंडल, तिलक, भस्म आदि का आध्यात्मिक महत्त्व भी है। इनके प्रयोग से व्यक्ति शुद्ध आचरण करने लगता है। अत: साधु उपर्युक्त साधनों को धारण करते हैं।

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
गद्यांश पड़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –
i. सेठ
ii. सेठानी
उत्तर:
i. अविश्वास से कौन हँस पड़ा?
ii. कौन बीमार हो गई?

प्रश्न 2.
सही विकल्प चुनकर वाक्य पूर्ण कीजिए।
i. सेठ साधु को मिलने के लिए तैयार हो गया क्योंकि…..
(अ) दुनियाभर के इलाज कराने के बाद भी उसकी माँ ठीक नहीं हुई।
(आ) दुनियाभर के इलाज कराने के बाद भी उसकी बेटी ठीक नहीं हुई।
(इ) दुनियाभर के इलाज कराने के बाद भी उसकी पत्नी ठीक नहीं हुई।
उत्तर:
सेठ साधु को मिलने के लिए तैयार हो गया क्योंकि दुनियाभर के इलाज कराने के बाद भी उसकी पत्नी ठीक नहीं हुई।

प्रश्न 3.
निम्नलिखित विधान सही करके लिखिए।

i. बड़ी प्रसन्नता से सेठ साधु को मिलने गया।
उत्तर:
हारकर सेठ साधु से मिलने गया।

प्रश्न 4.
किसने, किससे कहा?
i. “सेठानी को जीवनदान दीजिए।”
उत्तर:
सेठ ने साधु से कहा।

ii. “ऐसे ढोंगी जाने यहाँ कितने आते रहते हैं।”
उत्तर:
सेठ ने व्यक्ति से कहा।

कृति इ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तर:
i. कभी-कभी
ii. वैद्य-डॉक्टर

प्रश्न 2.
वचन बदलिए।
i. सेठानी
ii. पेशा
उत्तर:
i. सेठानियाँ
i. पेशे

प्रश्न 3.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढकर लिखिए।
उत्तर:

1. जीवनदान : प्रत्यय : दान
2. करोड़पति : प्रत्यय : पति
3. बेईमानी : प्रत्यय : ई

प्रश्न 4.
‘अविश्वास’ इस शब्द में निहित उपसर्ग प्रत्यय को पहचानकर संबंधित उपसर्ग लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तरः
अविश्वास : प्रत्यय : अ, नए शब्द : अकारण, अप्रसन्न

प्रश्न 5.
निम्नलिखित गद्यांश में प्रयुक्त लिंग शब्द की जोड़ी ढूँढकर लिखिए।
उत्तरः
सेठ-सेठानी

प्रश्न 6.
निम्नलिखित गद्यांश में प्रयुक्त पर्यायवाची शब्दों की जोड़ी ढूँढकर लिखिए।
उत्तर:
i. वैद्य-डॉक्टर
ii. चरण-पाँव

प्रश्न 7.
नीचे दिए शब्द के लिए श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. संपत्ति
ii. अब
उत्तर:
i. संप्रति
ii. आब

प्रश्न 8.
निम्नलिखित शब्दों के अनेकार्थी शब्द लिखिए।
i. डोली
ii. जीवन
उत्तर:
i. एक क्रिया जो ‘डोलना’ से संबंधित है, पालकी
ii. पानी, जिंदगी

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘क्या कोई साधु बीमार व्यक्ति को स्वस्थ करने की शक्ति रखता है।’ विधान को वर्तमान समय के संदर्भ में अपने विचार लिखिए।
उत्तर:
आज का युग विज्ञान एवं तकनीकी का युग है। आज हमारे समाज में साधु और तांत्रिक के वेश में कुछ ढोंगी भी देखने को मिलते हैं। वे दूसरे की अज्ञानता और सीधेपन का लाभ उठाकर पैसा कमाते हैं। ऐसे में यदि घर का कोई व्यक्ति बीमार हो जाए, तो उसे साधु या तांत्रिक के पास ले जाना उचित नहीं है। फिर भी लोग अंधविश्वास के कारण बीमार व्यक्ति को साधु महाराज के पास लेकर जाते हैं। साधु के पास कोई भी ऐसी अद्भुत शक्ति नहीं होती है। वह तो सिर्फ उसके पास आने वाले व्यक्ति

को आशीर्वाद दे सकता है और ईश्वर से उनके कष्ट हरने की प्रार्थना कर सकता है। इससे ज्यादा उसके हाथ में कुछ नहीं होता है। फिर भी लोग उस पर विश्वास रखते हैं। हमें समाज में चारों ओर फैले कुछ ढोंगी साधुओं से बचना चाहिए और बीमार व्यक्ति को डॉक्टर के पास लेकर जाना चाहिए तथा डॉक्टर से उसका इलाज करवाना चाहिए।

(ई) गद्यांश को पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1): आकलन कृति

प्रश्न 1.
परिणाम लिखिए।

i. सेठानी की तबीयत ठीक हो जाने पर …..
उत्तरः
सेठ का साधु पर गहरा विश्वास हो गया और वह रोज साधु के पास आने लगा।

प्रश्न 2.
गद्यांश पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. सात-आठ
ii. धन
उत्तर:
i. सेठानी की तबीयत कितने दिनों में ठीक हो गई?
ii. क्या बढ़ने से लोभ भी उतना ही बढ़ता है?

प्रश्न 3.
संजाल पूर्ण कीजिए।
उत्तर:

कृति ई (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. साधु ने सेठ से कहा सच्चा सुख धन का त्याग करने में है अपना ध्यान भगवान के चरणों में लगा दो
उत्तरः
साधु ने सेठ से कहा, “सच्चा सुख धन का त्याग करने में है; अपना ध्यान भगवान के चरणों में लगा दो।”

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. भगवान
2. विश्वास
3. संसार
4. लोभ

उत्तर:

1. ईश्वर
2. भरोसा
3. जग
4. लालच

प्रश्न 3.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तर:
i. सात-आठ
ii. धीरे-धीरे

प्रश्न 4.
नीचे दिए शब्द के लिए श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. सात
ii. समाधी
उत्तर:
i. साथ
ii. समधी

प्रश्न 5.
‘बीमारी’ इस शब्द में से प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द बनाइए।
उत्तरः
बीमारी : शब्द : बीमार प्रत्यय : ई अन्य शब्द : लोभी, संबंधी

प्रश्न 6.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. योगसाधना द्वारा अंतर्ध्यान लगाकर बैठना –
उत्तरः
समाधी

कृति ई (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘जीवन का सच्चा सुख धन का त्याग करने में है।’ विषय पर अपने विचार लिखिए।
उत्तरः
उपर्युक्त बिल्कुल शतप्रतिशत: सही है। जीवन का सच्चा सुख धन का त्याग करने में ही है। जिस व्यक्ति को धन का लोभ नहीं होता है; वह धन का कभी भी संचय नहीं करता है। जैसे-जैसे उसके पास धन आ जाता है; वैसे-वैसे वह धन दीन-दुखियों में बाँट देता है। दीन-दुखियों के चेहरे पर संतोष देखकर उसे अथाह खुशी मिलती है। ऐसा व्यक्ति सच्चे सुख का अनुभव करता है। जीवन में जो भी महान पुरुष हुए हैं, उन्होंने कभी भी धन का संचय नहीं किया था। आजीवन उन्होंने मानवता की भलाई हेतु ही कार्य किया। आखिर यह संसार एक माया है। धन का लोभ आदमी को आदमी नहीं रहने देता। जो व्यक्ति जितना धन का संचय करता है; उतना ही उसका लोभ बढ़ता जाता है।

(उ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (1): आकलन कृति

प्रश्न 1.
कारण लिखिए।
i. सेठ का संसार से मन फिर गया।
उत्तर:
क्योंकि साधु महाराज के उपदेश का उस पर सकारात्मक असर पड़ा।

प्रश्न 3.
उचित जोड़ियाँ लगाइए।

‘अ’	‘ब’
1. बैलगाड़ियों	(क) कपट
2. सच्चा	(ख) झुंड
3. साधु	(ग) ज्ञान
4. झूठ	(घ) उपदेश

उत्तरः

‘अ’	‘ब’
1. बैलगाड़ियों	(ख) झुंड
2. सच्चा	(ग) ज्ञान
3. साधु	(घ) उपदेश
4. झूठ	(क) कपट

कृति उ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. प्रणाम
2. कुटी
3. असलियत
4. मंदिर

उत्तर:

1. नमस्कार
2. झोपड़ी
3. सच्चाई
4. देवालय

प्रश्न 2.
नीचे दिए हुए शब्द के विलोम शब्द लिखिए।
i. शिष्य × ……….
ii. सच्चा × ……….
उत्तर:
i. गुरु
ii. झूठा

प्रश्न 4.
‘असलियत’ शब्द में प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तर:
असलियत : प्रत्यय : इयत, अन्य शब्द: इनसानियत, हैवानियत

प्रश्न 5.
नीचे दिए गए तत्सम शब्दों के तद्भव रूप लिखिए।
i. सुवर्ण
ii. उष्ट्र
उत्तर:
i. सोना
ii. ऊँट

प्रश्न 6.
नीचे दिए गए शब्द का श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. चरण
उत्तर:
चारण

कृति उ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘हृदय परिवर्तन व्यक्ति को सत्मार्ग की ओर अग्रसित करता है।’ विषय पर अपने विचार लिखिए।
उत्तर:
हृदय परिवर्तन एक ऐसी प्रक्रिया है, जिससे व्यक्ति का स्वभाव, उसकी बुराइयाँ आदि सब कुछ अच्छाई में परिवर्तित हो जाती हैं। हृदय परिवर्तन व्यक्ति के व्यक्तित्व को संपूर्णत: नया आयाम देता है। भगवान बौद्ध के उपदेश का अंगुलिमाल के हृदय पर सकारात्मक प्रभाव पड़ा और उसका हृदय परिवर्तन हो गया। मोहनदास गांधी का भी हृदय परिवर्तन हुआ और वे महात्मा गांधी बने। दीन-दुखियों का दुख देखकर मदर टेरेसा का भी हदय परिवर्तन हुआ था।

जिस व्यक्ति का हृदय परिवर्तन हो जाता है वह व्यक्ति सत्मार्ग की ओर अग्रसित हो जाता है और फिर वह अपने जीवन में कभी भी बुराइयों को अपनाता नहीं। वह अपने जीवन में सत्संग कर दूसरों के जीवन में खुशहाली निर्माण करता है। जिसका हृदय परिवर्तन हो जाता है वह दूसरों की सेवा निःस्वार्थ भाव से करता है। हृदय परिवर्तन व्यक्ति के जीवन का सबसे बड़ा परिवर्तन होता है।

(ऊ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऊ (1): आकलन कृति

प्रश्न 1.
गद्यांश पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –
i. धन
ii. सेठ जी
उत्तर:
i. साधु के अनुसार मिट्टी क्या है?
ii. बहुरूपिये के अनुसार चतुर आदमी कौन है?

प्रश्न 2.
परिणाम लिखिए।
i. बहुरूपिये ने सेठ जी से धन नहीं लिया –
उत्तर:
सेठ की आँखों में आँसू आ गए।

प्रश्न 3.
निम्नलिखित विधान सही करके लिखिए।

ii. प्रसन्न भाव से बहुरूपिया सिर ऊँचा करके खड़ा था।
उत्तर:
अपराधी भाव से बहुरूपिया सिर झुकाए खड़ा था।

प्रश्न 4.
कारण लिखिए।
i. बहुरूपिये ने सेठ से अपना इनाम माँगा।
उत्तर:
क्योंकि उसने सेठ जैसे चतुर आदमी को धोखा दे दिया था और अपनी कला का सम्मान चाहता था।

कृति ऊ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:
i. समझा-बुझाकर
ii. इधर-उधर

प्रश्न 2.
विलोम शब्द लिखिए।

1. बड़ा × ………….
2. स्वीकार × ……….
3. इनाम × …………..
4. चतुर × ……………

उत्तर:

1. छोटा
2. अस्वीकार
3. हर्जाना
4. मूर्ख

प्रश्न 3.
पर्यायवाची शब्द लिखिए।
i. कसूर
ii. इनाम
उत्तर :
i. गलती
ii. उपहार

प्रश्न 4.
गोश में से ऐसे दो शब्द ढूँढकर लिखिए जिनके वचन परिवर्तित नहीं होते।
उत्तर:
सिर, इनाम

प्रश्न 5.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. वस्तु पर से अपना स्वत्व हटा लेना –
उत्तर:
त्याग

प्रश्न 6.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. माया
उत्तर:
माया, धन, देवी, लक्ष्मी

(ए) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ए (1) : आकलन कृति

प्रश्न 1.
गद्यांश के आधार पर वाक्य पूर्ण कीजिए।
i. अगर बहुरूपिया सेठ जी की संपत्ति लेकर भाग जाता …..
उत्तर:
अगर बहुरूपिया सेठ जी की संपत्ति लेकर भाग जाता तो उसके रूप में खोट आ सकती थी।

ii. बहुरूपिए ने रूप को सच्चा रखने के लिए
उत्तर:
बहुरूपिए ने रूप को सच्चा रखने के लिए संपत्ति का त्याग कर दिया था।

प्रश्न 2.
कारण लिखिए।
i. बहुरूपिया अब खुशी से इनाम ले सकता है।
उत्तर:
क्योंकि उसने अपने बहुरूपिये का काम पूरा कर लिया था।

प्रश्न 3.
निम्नलिखित गलत विधान सही करके लिखिए।
i. सेठानी बहुरूपिये के आशीर्वाद से ठीक हो गई थी।
उत्तर:
सेठानी और सेठ का विश्वास और संयोग इनके मिलन से सेठानी ठीक हो गई थी।

ii. दुर्जन व्यक्ति की तरह बहुरूपिये ने साधु का रूप त्याग दिया था।
उत्तर:
सच्चे महत्मा की तरह बहुरूपिये ने साधु का रूप त्याग दिया था।

कृति ए (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. बहुरूपिये ने सेठ से कहा अब आप जो इनाम मुझे देंगे खुशी से ले लूँगा
उत्तर:
बहुरूपिये ने सेठ से कहा, “अब आप जो इनाम मुझे देंगे, खुशी से ले लूंगा।”

प्रश्न 2.
दिए गए गद्यांश में से विदेशी शब्द ढूँढकर लिखिए।
उत्तर:
अशर्फी

प्रश्न 3.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. नम
ii. संतुष्ट
उत्तर:
i. उपसर्गयुक्त शब्द: विनम्र, प्रत्यययुक्त शब्द: नम्रता
ii. उपसर्गयुक्त शब्द: असंतुष्ट, प्रत्यययुक्त शब्दः संतुष्टि

प्रश्न 4.
विलोम शब्द लिखिए।
i. विश्वास ×
ii. नम्रता ×
उत्तर:
i. अविश्वास
ii. अशिष्टता

प्रश्न 5.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. सोने का सिक्का –
उत्तर:
अशर्फी

कृति ए (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘हमें अपने व्यवसाय के प्रति ईमानदार होना चाहिए।’ अपने विचार लिखिए।
उत्तर:
‘व्यवसाय’ का अर्थ है काम-धंधा एवं पेशा। व्यवसाय से व्यक्ति को रोजगार प्राप्त होता है। व्यवसाय एक नैतिक उत्तरदायित्व होता है। लाभ कमाने के ध्येय से व्यवसाय किया जाता है। व्यवसाय के कई प्रकार हैं। जैसे कि अध्यापन, डॉक्टरी, चित्रकारी आदि तरह-तरह के व्यवसाय हैं। व्यक्ति किसी भी व्यवसाय का चयन करें, पर उसे अपने व्यवसाय के प्रति ईमानदार होना चाहिए। उसे अपना काम निष्ठा एवं विश्वास से करना चाहिए। उसके मन में अपने व्यवसाय के प्रति अपनत्व की भावना होनी चाहिए तथा प्रतिकूल परिस्थिति में भी वह अपने व्यवसाय की नैतिकता में सतर्क रहे। जो व्यक्ति अपने व्यवसाय के प्रति ईमानदार होता है; वह राष्ट्रीय विकास हेतु अपना योगदान देने में सक्षम होता है। व्यवसाय के प्रति ईमानदार रहने से व्यक्ति का व्यवसाय समाज में प्रतिष्ठित स्थान प्राप्त कर लेता है। अत: हमें व्यवसाय के प्रति ईमानदार होना चाहिए।

कलाकार Summary in Hindi

लेखक – परिचय :

जीवन-परिचय : राजेंद्र यादव जी का जन्म सन 1929 में उत्तर प्रदेश के आगरा शहर में हुआ। आप साठोत्तरी पीढ़ी के जाने-माने उपन्यासकार एवं साहित्यकार हैं। राजेंद्रजी हिंदी के सर्वाधिक लोकप्रिय संपादक भी थे। इन्होंने ‘नई कहानी’ के नाम से हिंदी साहित्य में एक नई विधा का सूत्रपात भी किया था। इन्होंने ‘हम’ पत्रिका का पुनः प्रकाशन किया और यह कार्य अपने जीवन के अंतिम समय तक यानी पूरे 27 वर्ष तक जारी रखा। हिंदी अकादमी दिल्ली द्वारा आपको समग्र लेखन के लिए ‘सर्वोच्च शलाका सम्मान’ प्रदान किया गया।
प्रमुख कृतियाँ : ‘जहाँ लक्ष्मी कैद है. ‘छोटे-छोटे ताजमहल’, ‘किनारे से किनारे तक (कहानी संग्रह), ‘सारा आकाश’, ‘शह और मात’। तथा ‘उखड़े हुए लोग’ (उपन्यास) आदि।

गद्य-परिचय :

कहानी : कहानी साहित्य की एक महत्वपूर्ण विधा है। जीवन की किसी एक घटना के रोचक वर्णन को ‘कहानी’ कहते हैं। कहानी का उद्देश्य उपदेश देना और मनोरंजन करना माना जाता है। कहानी का लक्ष्य मानव जीवन की विभिन्न समस्याओं और ! संवेदनाओं को व्यक्त करना होता है।
प्रस्तावना : ‘कलाकार’ इस कहानी में लेखक राजेंद्र यादव जी ने बहुरूपिए के माध्यम से बताया है कि श्रेष्ठ कलाकार को अपनी कला के प्रति ईमानदार रहना चाहिए अर्थात व्यक्ति का कोई भी पेशा या व्यवसाय हो; उसे उसके प्रति ईमानदार होना चाहिए।

सारांश :

‘कलाकार’ एक कहानी है। यह कहानी हमें अपनी कला और व्यवसाय के प्रति ईमानदार रहने की प्रेरणा देती है। इस कहानी का नायक एक बहुरूपिया है। तरह-तरह के रूप धारण कर लोगों का मनोरंजन करना उसका पेशा है। वह अपनी कला में माहिर है। एक बार वह साधु के जैसा हू-ब-रूप धारण करके नगर के बाहर डेरा लगाकर बैठ जाता है। धीरे-धीरे लोग उसके बारे में जानने लगते हैं और उससे मिलने आने लगते हैं। चारों तरफ उसका नाम फैल जाता है। नगर में रहने वाले एक सेठ की पत्नी बीमार पड़ जाती है।

डॉक्टर एवं वैद्यों द्वारा इलाज करने पर भी वह ठीक नहीं होती है। आखिर सेठ अपनी पत्नी को लेकर साधु महाराज के पास आते हैं। संयोग वश सेठानी की तबीयत सुधरने लगता हा सात-आठ दिना म उसका तबीयत ठीक हो जाती है। अब सेठ पूरी निष्ठा से साधु महाराज का भक्त बन जाता है। साधु महाराज उसे मोह-माया को त्यागने के लिए कहते हैं। साधु के उपदेश का सेठ पर गहरा असर होता है और वह एक दिन अपनी सारी संपत्ति लेकर साधु के पास आता है। वह अपनी संपत्ति साध महाराज को दान करना चाहता है। लेकिन साधु उसे विनम्रता से ठुकरा देता है।

अब साधु को लगता है कि उसने अपनी कला का बेहतर प्रदर्शन करके सेठ जैसे चतुर आदमी को धोखा दे दिया है। अत: वह साधु का वेश त्यागकर सेठ के पास अपना इनाम माँगता है और सेठ को सब कुछ सच बता देता है। उसकी बातों को सुनकर सेठ आश्चर्यचकित हो जाते हैं। वे बहुरूपिए से कहते है कि अगर वह चाहता; तो उनका सारा धन लेकर भाग सकता था। तब बहुरूपिया कहता है कि यदि वह ऐसा करता, तो उसके रूप में खोट आ सकती थी। रूप को सच्चा रखने के लिए उसने धन का त्याग कर दिया था। फिर भी सेठ जी की समझ में कुछ नहीं आ रहा था कि यह कैसा बहुरूपिया है। जो करोड़ों की संपत्ति छोड़कर अशर्फियों के इनाम के लिए इतना प्रसन्न और संतुष्ट है।

शब्दार्थ :

1. बहुरूपिया – तरह-तरह के रूप धारण करने वाला
2. जिक्र – चर्चा
3. पेशा – व्यवसाय, उद्यम
4. नगर – शहर
5. इनाम – उपहार
6. धोखा – फरेब
7. भस्म – राख
8. साधु – सज्जन
9. उपदेश – सलाह
10. समाचार – खबर
11. अशर्फी – मूल्यवान धातु के सिक्के
12. प्रणाम – नमस्कार
13. कुटी – झोपड़ी
14. असलियत – सच्चाई
15. मंदिर – देवालय
16. कमाल – सर्वोत्तम
17. इनाम – उपहार
18. धिक्कारना – झिड़कना
19. शुभचिंतक – किसी कार्य/व्यक्ति के बारे में अच्छा सोचने वाला
20. धूनी – साधुओं द्वारा बनाया गया अग्निकुंड

मुहावरे :

1. डेरा लगाना – निवास के लिए जम जाना।
2. आसमान से गिरना – आश्चर्यचकित होना।

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Std 10 Hindi Chapter 4 Mann Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 4 मन Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 4 मन Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 4 मन Textbook Questions and Answers

कृति

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
लिखिए:

हाइकु द्वारा मिलने वाला संदेश
करते जाओ पाने की मत सोचो जीवन सारा।	भीतरी कुंठा नयनों के द्वार से आई बाहर।

उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
उत्तर लिखिए:
a. मँझधार में डोले —-
b. छिपे हुए ——-
c. धुल गए ——-
d. अमर हुए ——-
उत्तर:
a. मँझधार में डोले – जीवन नैया।
b. छिपे हुए सितारे
c. घुल गए विषाद
d. अमर हुए गीतों के स्वर।

प्रश्न 4.
निम्नलिखित काव्य पंक्तियों का केंद्रीय भाव स्पष्ट कीजिए:
a. चलतीं साथ पटरियाँ रेल की फिर भी मौन।
b. काँटों के बीच खिलखिलाता फूल देता प्रेरणा।
उत्तर:
a. रेल की पटरियाँ अनंत काल से साथ चल रही हैं, परंतु वे सदा मौन रहती हैं। एक-दूसरे से कभी बात नहीं करती।
b. गुलाब का फूल काँटों के बीच भी हँसता है, खिलखिलाता है। वह हमें हर पल प्रेरणा देता है कि हमें परेशानियों से घबराए बिना अपना काम करते जाना है।

उपयोजित लेखन

वक्तृत्व प्रतियोगिता में प्रथम स्थान पाने के उपलक्ष्य में आपके मित्र/सहेली ने आपको बधाई पत्र भेजा है, उसे धन्यवाद देते हुए निम्न प्रारूप में पत्र लिखिए:
दिनांक: ……………………….
संबोधन: ……………………….
अभिवादन: ……………………….

प्रारंभ:
विषय विवेचन:
…………………………………………………………………………
…………………………………………………………………………
…………………………………………………………………………
…………………………………………………………………………
…………………………………………………………………………
…………………………………………………………………………

तुम्हारा/तुम्हारी,
……………………….
नाम: ……………………….
पता: ……………………….
ई-मेल आईडी: ……………………….
उत्तर:
दिनांक: 25/8/20
प्रिय अविनाश,
नमस्ते!
तुम्हारा पत्र अभी-अभी मिला। धन्यवाद।
अंतर विद्यालय वक्तृत्व प्रतियोगिता में प्रथम स्थान पाने के लिए तुम्हारा बधाई-पत्र मिला। पत्र पाकर दिल गदगद हो गया। वास्तव में मेरी इस सफलता में तुम जैसे मित्रों का मुझे सदा उत्साह दिलाते रहने का बड़ा हाथ है। तुम तो जानते हो, मंच पर बोलने में मुझे कितनी झिझक होती थी।

पर तुम जैसे मित्रों और हमारे कक्षा अध्यापक के निरंतर प्रोत्साहन से आज मुझे अंतर विद्यालय वक्तृत्व प्रतियोगिता में प्रथम स्थान प्राप्त करने का अवसर मिला है। में इसके लिए तुम जैसे अपने सभी मित्रों और अपने कक्षा अध्यापक नरेश कौशल जी का तहे दिल से आभारी हूँ।

मेरा, उत्साह बढ़ाने के लिए धन्यवाद!
तुम्हारा मित्र
राजेश शर्मा।
17, विमल मेंशन,
महात्मा गांधी रोड,
औरंगाबाद।
ई-मेल आईडी: rajesh@xyz.com

Hindi Lokbharti 10th Textbook Solutions Chapter 4 मन Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 3 (आ) के लिए)
पद्यांश क्र. 1

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

(1) उत्तर लिखिए:
(i) खिले हुए ……………………….
उत्तर:
(i) खिले हुए – फूल।

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
फागुन के महीने में प्रकृति रंगों से रंग जाती है। इस विषय पर 25 से 30 शब्दों में अपने विचार लिखिए।
उत्तर:
फागुन का महीना बहुत महत्त्वपूर्ण होता है। इस महीने में प्रकृति में चारों ओर नवीनता दिखाई देती है। खेत सरसों के पीले-पीले फूलों से भर जाते हैं। इन्हें देखकर ऐसा लगता है जैसे जमीन पर पीले रंग की विशाल चादरें बिछाई दी गई हों। बीच-बीच में अलसी के नीले-नीले फूल पीले रंग पर छाप जैसे लगते हैं। पलाश के वन लाल रंग के बड़े-बड़े फूलों से लद जाते हैं।

दूर से इन वनों को देखकर ऐसा लगता है, मानो पेड़ों से आग की लपटें निकल रही हों। विभिन्न प्रकार के पेड़ों पर गुलाबी रंग की नई-नई कोंपलें आ जाती हैं। इन्हें देखकर लगता है जैसे ये पेड़ गुलाबी रंग के वस्त्रों से सज गए हैं। इनके अतिरिक्त फागुन के महीने में ही तो होली का त्योहार आता है जब चारों ओर तरह-तरह के रंगों और अबीर-गुलाल की बहार आ जाती है। लोग खुशी से एक-दूसरे को रंगों से सराबोर कर देते हैं। इस तरह फागुन के महीने में प्रकृति तरह-तरह के रंगों से रँग जाती है।

पद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

(1) उचित जोड़ियाँ मिलाइए:

‘अ’	‘आ’
(i) मछली	मौन
(ii) गीतों के स्वर	सूना
(iii) रेल की पटरियाँ	प्यासी
(iv) आकाश	अमर
	पीड़ा

उत्तर:

‘अ’	‘आ’
(i) मछली	प्यासी
(ii) गीतों के स्वर	अमर
(iii) रेल की पटरियाँ	मौन
(iv) आकाश	सूना।

(2) परिणाम लिखिए:
(i) सितारों का छिपना।
(ii) तुम्हारा गीतों को स्वर देना।
उत्तर
(i) सूना आकाश
(ii) गीतों का अमर होना।

(3) मन की ……………………. बरसी आँखें। इस हाइकु का सरल अर्थ लिखिए।
उत्तर
जब मन की पीड़ा बहुत गहरी हो जाती है, तो वह बादल बनकर आँसुओं के रूप में बरसने लगती है।

(4) तालिका पूर्ण कीजिए:

स्थिति	निवास	स्थान
मछली	प्यासी	सागर
सितारे	छिपे हुए	आकाश

कृति 2: (स्वमत अभिव्यक्ति)

प्रश्न.
‘आँखें देखने के अलावा और भी कई तरह के काम करती हैं’, इस विषय पर 25 से 30 शब्दों में अपने विचार स्पष्ट कीजिए।
उत्तर:
मनुष्य के शरीर में विभिन्न अंग होते हैं और वे अपनाअपना निर्धारित काम करते हैं। कुछ अंगों से निर्धारित कामों के अलावा और भी कई तरह के काम लिए जाते हैं। आँखें हमारे शरीर का महत्त्वपूर्ण अंग हैं। इनसे देखने का काम तो लिया ही जाता है, साथ ही साथ और भी कई काम लिए जाते हैं। आँखों से तरह-तरह के इशारे किए जाते हैं, जिन्हें सामनेवाला आदमी आसानी से समझ लेता है। आँखें तरेरकर क्रोध प्रकट किया जाता है।

आँखें झुकाकर शर्म प्रदर्शित की जाती है। मन में छुपी दुख देने वाली भावनाओं को आँखों में आँसू लाकर प्रकट किया जाता है। मन भारी होने पर लोग रोकर अपना मन हल्का करते हैं। कोई अचंभेवाली घटना होने पर वाणी के साथ-साथ आँखों से भी भाव प्रदर्शित होता है। आँखों का एक आवश्यक काम मनुष्य को निद्रावस्था में ले जाकर उसे आराम दिलाना है। इस तरह आँखें देखने के अलावा कई महत्त्वपूर्ण काम करती हैं।

मन Summary in Hindi

मन कविता का सरल अर्थ

1. घना अंधेरा ……………………………. आई बहार।

जब अँधेरा घना होता है, तब प्रकाश और अधिक चमकता है अर्थात जब प्रतिकूल परिस्थितियाँ घने अंधकार के रूप में हमें घेर लेती हैं, तब वहीं से एकाएक प्रकाश की किरणें फूट पड़ती हैं।

हमें पूरा जीवन काम करते रहना चाहिए। यह नहीं सोचना चाहिए कि हमें क्या प्राप्त होगा।

जीवन रूपी नैया यदि संसार रूपी सागर में डगमगा रही है, तो उसे कोई अन्य सँभालने के लिए नहीं आएगा। हमें स्वयं उसे पार लगाने के लिए प्रयास करना होगा।

फागुन का महीना अपने संग बसंत के विविध रंग लेकर आया है। यह समय उल्लास और उमंग का समय है। अतः हम सभी को कुछ समय के लिए चिंताओं और परेशानियों को भूलकर बसंत ऋतु का आनंद लेना चाहिए।

गुलाब का फूल काँटों के बीच भी हंसता है, खिलखिलाता है। वह हमें हर पल प्रेरणा देता है कि परेशानियों से घबराए बिना अपना काम करते जाना है।

जब नेत्रों से अश्रु बहते हैं, तो यह मानना चाहिए कि मन की कुंठा नयन रूपी द्वार से बाहर आ रही है।

2. खारे जल ……………………………. प्यासी ही रही। . . .

जब नेत्रों से अश्रु बहते हैं तो यह समझना चाहिए कि आँसुओं के खारे जल के साथ मन का संपूर्ण विषाद धुल गया है और मन पहले के समान पावन हो गया है।

प्रत्येक मनुष्य के जीवन में अनेक परेशानियाँ हैं, चिंताएँ हैं, और हैं अप्रिय प्रसंग। ऐसे में जीवन रूपी संग्राम में डटे रहना हमारी जिजीविषा का प्रमाण है।

जब आकाश में बादल बहुत घने होते हैं, तभी वर्षा होती है। उसी प्रकार जब मन की पीड़ा बहुत गहरी हो जाती है, तो वह बादल बनकर आँसुओं के रूप में बरसने लगती है।

रेल की पटरियाँ अनंत काल से साथ चल रही हैं, परंतु वे सदा मौन रहती हैं। एक-दूसरे से कभी बात नहीं करती।

सितारे आकाश का शृंगार हैं। वे आकाश की शोभा बढ़ाते हैं। जैसे ही सितारे बादलों की ओट में छिपे, आकाश सूना हो जाता है। ठीक इसी प्रकार कुछ लोग हमारे जीवन में अत्यंत महत्त्वपूर्ण होते हैं। उनके चले जाने पर या विमुख हो जाने पर मानो हमारा जीवन निरर्थक हो जाता है।

कवि के अंदर अनोखी सामर्थ्य होती है। वह जिन गीतों को स्वर देता है, वे अमर हो जाते हैं। इसी प्रकार कवि अपनी रचनाओं के द्वारा समाज में परिवर्तन ला सकता है।

सागर में अथाह जलराशि होती है, परंतु खारा होने के कारण अथाह होने पर भी वह जलराशि पीने योग्य नहीं होती। उसी प्रकार कोई व्यक्ति कितना भी बड़ा या धनवान क्यों न हो, यदि वह किसी जरूरतमंद के काम नहीं आ सकता तो उसका बड़प्पन व्यर्थ है।

मन विषय-प्रवेश:

प्रस्तुत कविता ‘मन’ जापान की लोकप्रिय विधा हाइकु’ पर आधारित है। यह विधा हिंदी साहित्य में स्वीकृति पा चुकी है। इस विधा को विश्व की सबसे छोटी कविता का स्थान प्राप्त है। इस कविता में कवि ने तीन-तीन छोटी पंक्तियों में अलग-अलग घटनाओं को सुंदर ढंग से पिरोया है। प्रस्तुत कविता की यह अपनी विशेषता है।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 6 ऐसा भी होता है Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 6 Aisa Bhi Hota Hai Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 6 ऐसा भी होता है Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 6 ऐसा भी होता है Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए

प्रश्न 1.
कृति पूर्ण कीजिए

उत्तर:

2. उचित शब्द लिखिए। 

प्रश्न 1.
उचित शब्द लिखिए।

1. सहमकर काँपने वाली –
2. घोंसला उजड़ने पर रोने वाला –
3. सुख-दुख बाँटने वाला –
4. वृद्धाश्रम से चिट्ठी भेजने वाली –

उत्तर :

1. कच्ची दीवार
2. पखेरू या पंछी
3. डाकिया
4. बूढी माँ

3. किरण शब्द की विशेषताएँ : 

प्रश्न 1.
किरण शब्द की विशेषताएँ :

उत्तर :

भाषा बिंदु :

प्रश्न 1.
आकृति में दिए गए वाक्य का काल पहचानकर निर्देशानुसार काल परिवर्तन कीजिए।

उत्तरः

उपयोजित लेखन :

प्रश्न 1.
‘मेरा प्रिय त्योहार’ विषय पर 80 से 100 शब्दों में निबंध लिखिए।
उत्तरः
मेरा प्रिय त्योहार हमारा भारत देश त्योहारों का देश है। भारत में दीपावली, होली, नवरात्रि, गणेशचतुर्थी आदि तरह-तरह के त्योहार मनाए जाते हैं। प्रत्येक त्योहार की अपनी सांस्कृतिक एवं आध्यात्मिक विशेषता होती है। इस प्रकार प्रत्येक त्योहार का अपना महत्त्व होता है। सभी को त्योहार अच्छे लगते हैं। मैं भी इसका अपवाद नहीं हूँ। मेरा प्रिय त्योहार दीपावली है। इसे दीवाली भी कहते हैं। दीपावली दीपों का त्योहार है।

यह त्योहार पाँच दिनों तक मनाया जाता है। धन त्रयोदशी, नरक चतुर्दशी, दीपावली, गोवर्धन पूजा और भैयादूज ये पाँच पर्व पाँच दिन मनाए जाते है। अमावस्या की अंधेरी रात जगमग दीपों से जममगाने लगती है। यह दृश्य बहुत ही मनोरम व अद्भुत होता है। इस दिन भगवान श्रीराम, माता सीता व भाई लक्ष्मण के साथ चौदह वर्ष का वनवास पूरा करके अयोध्या वापस पधारे थे। इसी कारण लोगों ने खुश होकर अपने घरों के द्वार पर भगवान के स्वागत हेतु दीप जलाए थे।

तब से यह शुभ दिन दीपावली के रूप में मनाया जाता है। यह त्योहार बुराई पर अच्छाई की जीत का प्रतीक है। दीपावली की शाम को लोग देवी लक्ष्मी और गणेश जी की पूजा करते हैं। बच्चे पटाखे छोड़ते हैं। इस दिन लोग अपने परिवार वालों के पास जाकर उनसे मिलते हैं और खुशियाँ बाँटते हैं, एकदूसरे को मिठाइयाँ बाँटते हैं। यह त्योहार शांति, भाईचारा व एकता का संदेश देता है। हमें एक-दूसरे के साथ प्रेम से रहना और एक-दूसरे के जीवन में खुशियाँ निर्माण करने का संदेश दीपावली से मिलता है। इसलिए हर्षित होकर मैं कहता हूँ –

“त्योहार है दीपावली का
सुख-समृद्धि और खुशहाली का।
बुराई के राक्षस को मन से भगाएँ
हृदय में शांति का दीपक जलाएँ।”

Hindi Lokvani 10th Std Textbook Solutions Chapter 6 ऐसा भी होता है Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1) आकलन कृति

प्रश्न 1.
उचित शब्द लिखिए।
i. थकी हारी
उत्तर :
i. सूरज की किरण

प्रश्न 2.
समझकर लिखिए।
i. कच्ची दीवार सहमी क्योंकि –
उत्तरः
मेघ गरजने लगे।

ii. किरण ने धरती की गोद का सहारा लिया क्योंकि –
उत्तर:
सुबह से शाम तक प्रकाश देने की कार्य करने के बाद शाम को वह थक गई।

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ पद्यांश में से ढूँढ़कर लिखिए।

1. बादल
2. सूर्य
3. पवित्र
4. धरती

उत्तर :

1. मेघ
2. रवि
3. निर्मल
4. धरा

प्रश्न 2.
विलोम शब्द लिखिए।
i. कच्ची × …….
ii. निर्मल × …….
उत्तर:
i. पक्की
i. मलिन

प्रश्न 3.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. गोद
उत्तर:
i. पहलू, आँचल

प्रश्न 4.
निम्नलिखित शब्द के वचन बदलिए।
i. दीवार
ii. किरण
उत्तर:
i. दीवारें
ii. किरणें

प्रश्न 5.
निम्नलिखित शब्द के श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. काँपी
उत्तर:
i. कॉपी

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
समाज के कमजोर वर्गों के उत्थान और उनकी प्रगति हेतु आप क्या कर सकते हैं? अपने विचार लिखिए।
उत्तरः
समाज के कमजोर वर्गों के उत्थान और उनकी प्रगति हेतु हम विशिष्ट अभियान चला सकते हैं। उस अभियान के अंतर्गत हम दुर्बल घटकों में जागरूकता निर्माण करने का प्रयास करेंगे। ग्रामीण क्षेत्रों में इनकी संख्या अधिक होती है। अत: ग्रामीण क्षेत्रों का विकास करने हेतु हम अभियान चलाएंगे; ताकि सरकार ग्रामीण क्षेत्रों का विकास करने हेतु ठोस कदम उठाए। आज हमारे समाज में वंचित वर्गों को अच्छी शिक्षा नहीं मिल पा रही है। अत: उन्हें शिक्षा मिले इसके लिए हम प्रशासन का ध्यान उनकी ओर आकर्षित करने हेतु अभियान चलाएँगे। समाज में सामाजिक न्याय प्रस्थापित हो इसलिए व्यक्तिगत स्वार्थ से ऊपर उठकर हम आपसी प्रेम, भाईचारा, मानवता आदि नौतियों का पालन करेंगे।

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1) : आकलन कृति

प्रश्न 1.
सही विकल्प चुनकर लिखिए।
i. खुली आँखों ने जीवन भर देखे –
(अ) खुले सपने
(आ) बंद सपने
(इ) मनचाहे सपने
उत्तर:
(आ) बंद सपने

ii.बच्चों की जीवनरूपी पतंग माँ-बाप ने थाम ली इसलिए –
(अ) उन्होंने आसमान को छू लिया।
(आ) उन्होंने स्वर्ग को छू लिया।
(इ) उन्होंने अंतरिक्ष को छू लिया।
उत्तर:
(अ) उन्होंने आसमान को छू लिया।

प्रश्न 2.
समझकर लिखिए।
i. वृक्षों के कटने का परिणाम –
उत्तर:
पंछियों का आशियाना उजड़ गया और वे रोने लगे।

प्रश्न 3.
उचित जोड़ियाँ लगाइए।

‘अ’	‘ब’
1. तन	(क) बंद
2. कद	(ख) माटी
3. आशियाना	(ग) काठी
4. सपने	(घ) उजड़ा

उत्तर:

‘अ’	‘ब’
1. तन	(ख) माटी
2. कद	(ग) काठी
3. आशियाना	(घ) उजड़ा
4. सपने	(क) बंद

प्रश्न 4.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 5.
उचित शब्द लिखिए।
i. स्वयं पर गुमान करने वाला –
उत्तर:
i. इंसान

कृति आ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

1. पतंग
2. जीवन
3. गुमान

उत्तर:

1. फतिका, सूर्य
2. पानी, जिंदगी
3. अभिमान, अनुमान

प्रश्न 2.
निम्नलिखित तद्भव शब्द का तत्सम शब्द लिखिए।
i. माटी
ii. सपना
उत्तर:
i. मृदा
ii. स्वप्न

प्रश्न 3.
उपसर्ग व प्रत्यय लगाकर शब्द लिखिए।
i. जीवन
उत्तरः
उपसर्गयुक्त शब्द – आजीवन, प्रत्यय
युक्त शब्द – जीवनभर

प्रश्न 4.
पर्यायवाची शब्द लिखिए।

1. पखेरू
2. तन
3. आशियाना
4. डोर

उत्तर:

1. पक्षी
2. शरीर
3. घोंसला
4. रस्सी

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
वक्षों के कटने के दुष्परिणाम अपने शब्दों बताइए।
उत्तरः
आजकल शहरों को बसाने के लिए बड़े स्तर पर वृक्षों की कटाई हो रही है। इसके कई दुष्परिणाम सामने आ रहे हैं। अंधाधुंध पेड़ काटे जाने के कारण ऑक्सीजन की मात्रा कम हो रही है तथा हवा प्रदूषित होती जा रही है। शहरों में वायु-प्रदूषण की समस्या सबसे ज्यादा बढ़ गई है। लोगों को अस्थमा जैसी साँस लेने की समस्या, हृदय रोग आदि हो रहे हैं। पेड़ों की कटाई करने के कारण वन्यजीवों का अस्तित्व भी खतरे में पड़ गया है। कई प्रजातियाँ विलुप्त हो गई हैं और कुछ विलुप्त होने के कगार पर हैं।

पेड़ों की कटाई का प्राकृतिक जलवायु परिवर्तन पर प्रभाव पड़ रहा है। जिस कारण ग्लोबल वार्मिग जैसी समस्या उत्पन्न हो रही है। तापमान में वृद्धि हो रही है। पेड़ों की कटाई की वजह से भूमि का क्षरण हो रहा है। इंसान हरी-भरी जिंदगी से वंचित हो गया है। उसका जीवन परेशानी से भर रहा है।

(इ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
उचित शब्द लिखिए –
i. ठसा-सा रहने वाला –
ii. आसमान में उड़ने वाला –
उत्तर:
i.तरू
ii. पखेरू

प्रश्न 2.
समझकर लिखिए –
उत्तर:

प्रश्न 3.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. वृद्धाश्रम
ii. संस्कारों
उत्तर:
i. मैया कहाँ रहती है?
ii. तिजोरी किससे भरी थी?

कृति इ (2) : शब्द संपदा

प्रश्न 1.
पद्यांश में से देशज शब्द ढूंढकर लिखिए।
उत्तर:
i. देशज शब्द : मैया, पखेरू, चिट्ठी
ii. तत्सम शब्द : तरू, वृद्ध

प्रश्न 2.
निम्नलिखित तद्भव शब्द का तत्सम रूप लिखिए।
i. दुख
उत्तर:
i. दुःख

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।
i. चिट्ठी
i. झोला
उत्तर:
i. खत
ii. थैला

प्रश्न 4.
पद्यांश में से विलोम शब्द की जोड़ी ढूंढकर लिखिए।
उत्तर:
i. सुख × दुख

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘बढ़ती संस्कारहीनता’ विषय पर अपने विचार लिखिए।
उत्तरः
समाज की सबसे छोटी इकाई परिवार होती है। परिवार में बच्चों को अच्छे संस्कार में डालकर सभ्य मनुष्य बनाया जाता है और इसी से सभ्य समाज का निर्माण होता है; परंतु संस्काररहित व्यक्तियों के कारण समाज में कई दुष्परिणाम देखने को मिल रहे हैं। संस्कारहीनता के प्रभाव से परिवार भी एक-दूसरे से अलग हो रहे है। एकाकी परिवार में बच्चे अपना समय कंप्यूटर या टी. वी. के साथ बिताते हैं।

टेलीविजन व वीडियो गेम ने पाश्चात्य संस्कृति को जन्म दिया है; जो सिर्फ उपभोक्तावाद को बढ़ावा दे रही है। इस कारण आज की पीढ़ी का जीवन मूल्यहीन हो गया है। आज की पीढ़ी धीरे-धीरे स्वार्थ के दलदल में फंसती जा रही है। कुछ लोग बुड़े माता-पिता को बोझ मानकर उन्हें वृद्धाश्रम भेज देते हैं। उन्हें उपेक्षित किया जाता हैं। आज व्यक्तिगत और सामाजिक सरोकार अलग-अलग हो गए है। समाज में चोरी, डकैती, लूटमार, दंगे-फसाद आदि कुरीतियों का बोलबाला है। संस्कारहीनता के कारण समाज की दुर्गति होती जा रही है। समाज में अनुशासनहीनता व अराजकता बढ़ रही है।’

ऐसा भी होता है Summary in Hindi

कवि-परिचय :

जीवन-परिचय : अभिषेक जैन जी आधुनिक साहित्यकार के रूप में हिंदी जगत में प्रसिद्ध हैं। कविता, कहानी, निबंध आदि विधाओं में इन्होंने लेखन किया है। जीवन के अनुभवों पर आधारित इनकी विविध रचनाएँ हिंदी पत्र-पत्रिकाओं में प्रकाशित होती रहती हैं। इन्होंने हाइकु काव्य विधा में भी लेखन किया है। इनकी हाइकु रचनाएँ जीवन के समृद्ध अनुभवों का भंडार है।
प्रमुख कृतियाँ : अभिषेक जैन जी ने कविता, कहानी, निबंध आदि विविध विधाओं में लेखन किया है। अनुभवों पर आधारित इनकी रचनाएँ विविध पत्र-पत्रिकाओं में नियमित प्रकाशित होती हैं।

पद्य-परिचय :

हाइकु काव्य : हाइकु एक जापानी काव्य विधा है। हाइकु यानी तीन पंक्तियों की कविता। यह विश्व की एक सबसे लघु कविता कही जाती है। हाइकु कविता 5 + 7 + 5 = 17 वर्ण के ढाँचे में लिखी जाती है। यह कविता आज भारत में सिर्फ हिंदी में ही नहीं, बल्कि मराठी, गुजराती, बंगाली, मलयालम आदि भाषाओं में भी लिखी जाती है।
प्रस्तावना : ‘ऐस भी होता है’ इस हाइकु में कवि अभिषेक जैन जी ने समाज में सबल घटकों द्वारा दुर्बलों पर होने वाले अत्याचार, गरीबी, थकान, वृक्षों के कटने के दुष्परिणाम, अनावश्यक अहं, वृद्धाश्रम के दर्द, संस्कारहीनता आदि विविध विषयों पर प्रकाश डाला है।

सारांश :

‘ऐसा भी होता है’ यह हाइकु काव्य है। कवि ने इस हाइकु के द्वारा विविध विषयों को अभिव्यक्त करने की कोशिश की है। समाज के सबल वर्ग दुर्बलों पर अपना रोब या अधिकार जमाते रहते हैं। उनके द्वारा किए गए अन्याय एवं शोषण से समाज के दुर्बल घटक सहम जाते हैं। सूरज प्रतिदिन अपने निर्मल किरणों से धरती को प्रकाशित करता रहता है। इसके बदले में वह धरती से किसी भी चीज की अपेक्षा नहीं करता।

ठीक उसी प्रकार सज्जन व्यक्ति दीन-दुखी लोगों के लिए अपना सर्वस्व अर्पण कर देते हैं। दिनभर सभी को रोशनी देने वाली किरण शाम होते ही थक जाती है और वह धरा की गोद में आकर विश्राम करती है। गरीब व्यक्ति की आशा-आकांक्षाएँ कभी भी पूर्ण नहीं होती। वह जीवनभर सपने देखते रहता है; फिर भी उसके सपने पूर्ण नहीं होते। वृक्षों को काटने से पंछियों का आशियाना यानी घोसला उजड़ जाता है। उनके आशियाने उजड़ने पर पक्षी रोने लगते हैं। माँ-बाप के अथक परिश्रम और सुसंस्कारों के कारण ही बच्चे आसमान को छूते हैं। व्यक्ति को अपने जीवन से अभिमान का त्याग कर अपने जीवन को सुंदर बनाना चाहिए।

संस्कारहीनता के कारण कई बच्चे बड़े हो जाने के बाद अपने माता-पिता को छोड़कर दूर जाकर अपने लिए अलग से बसेरा बना लेते हैं। डाकिए की तरह सभी को जीवन में आने वाली सुख-दुख की भावनाओं से प्रभावित न होकर अपना कार्य करते रहना चाहिए। अनेक तिरस्कारों के बावजूद माँ की ममता अपने बच्चों के लिए कम नहीं होती। संस्कारहीनता के कारण सामाजिक पतन हो रहा है। जिस कारण चारों ओर लूटमार और भगदड़ मची हुई है।

भावार्थ :

गरजे मेघ ………………………………………. कच्ची दीवार।
प्रस्तुत हाइकु में कवि ने बताया है कि आसमान में मेघों के गरजने पर एक कच्ची दीवार सहमकर काँपने लगी; वह बहुत डर गई। यहाँ गरजने वाले मेघ समाज के सबल वर्ग का प्रतिनिधित्व करते हैं और कच्ची दीवार समाज के दुर्बल वर्ग का प्रतिनिधित्व करती है। इसका अर्थ यह है कि समाज के सबल वर्ग दुर्बल वर्गों पर अपना रोब या अधिकार जमाते रहते हैं। उनके द्वारा किए गए अन्याय एवं शोषण से समाज के दुर्बल घटक सहम जाते हैं।

रवि चढ़ाए ………………………………………. धरा को अर्ध्व !
प्रस्तुत हाइकु में रवि यानी सूरज एक सज्जन व्यक्ति का प्रतीक है। सूरज प्रतिदिन अपने निर्मल किरणों से धरती को प्रकाशित करता है। बदले में वह धरती से किसी भी चीज की अपेक्षा नहीं करता। उसका कार्य निःस्वार्थ एवं मानवता के लिए होता है। ठीक उसी प्रकार सज्जन व्यक्ति दीन-दुखियों के लिए अपना सर्वस्व अर्पण कर देते हैं। इसके बदले में वे किसी भी प्रकार की चाह नहीं रखते हैं।

आ के पसरी ………………………………………. धरा की गोद।
प्रस्तुत हाइकु में बताया गया है कि दिनभर सभी को रोशनी देने वाली किरण शाम होते ही थक जाती है और वह धरा की गोद में आकर । विश्राम करती है। प्रकृति का यही नियम है। जो श्रम करता है; वह दिन ढलने के उपरांत थक जाता है। व्यक्ति दिनभर मेहनत करता है और फिर शाम होते ही वह थककर अपने घर आकर आराम करने लगता है।

खुली आँखो ने ………………………………………. बंद सपने।
प्रस्तुत हाइकु द्वारा समाज में व्याप्त गरीबों की स्थिति का चित्रण किया गया है। गरीब व्यक्ति की आशा-आकांक्षाएँ कभी भी पूर्ण नहीं । होती। वह जीवनभर सपने देखते रहता है; परंतु उसके सपने कभी भी पूर्ण नहीं होते।

कटते तरु ………………………………………. रोए पखेरू।
प्रस्तुत हाइकु में वृक्षों के कटने के दुष्परिणाम दिखाए गए हैं। वृक्षों को काटने से पंछियों का आशियाना यानी घोंसला उजड़ जाता है। वे । बेघर हो जाते हैं; जिस कारण वे दुखी होकर रोने लगते हैं।

बच्चे पतंग ………………………………………. छ्ते गगन।
बच्चों के जीवनरूपी पतंग की डोर माँ-बाप के हाथ में होती है। वे अपने बच्चों को अच्छी शिक्षा और संस्कार देकर उनका जीवन संवारने की कोशिश करते हैं। माँ-बाप के अथक परिश्रम और सुसंस्कारों के कारण ही बच्चे आसमान को छूते हैं यानी जीवन में ऊँचा उठकर सफलता की मंजिल हासिल करते हैं।

तन माटी का ………………………………………. कद काठी का।
प्रस्तुत हाइकु में कवि अनावश्यक अहं पर अपने विचार व्यक्त करते हैं। व्यक्ति का शरीर मिट्टी से बना है; जो एक दिन नष्ट होने वाला है। फिर भी व्यक्ति को अपनी इस छोटी-सी जिंदगी पर बहुत बड़ा अभिमान होता है। मनुष्य को अपने जीवन से अभिमान का त्याग कर अपने जीवन को सुंदर बनाना चाहिए। उसे अनावश्यक अहं नहीं करना चाहिए।

उड़ा पखेरू ………………………………………. ठगा-सा तम्।
प्रस्तुत हाइकु मनुष्य की कृतघ्नता पर करारा व्यंग्य करती है। पक्षी का बच्चा जब तक छोटा होता है यानी उसके पंखों में जब तक उड़ने की शक्ति नहीं आती है, तब तक वह वृक्ष पर ही रहता है। लेकिन जब उसके पंखों में उड़ने की शक्ति आ जाती है; तब वह उस वृक्ष को छोड़कर अनंत आकाश में विचरण करने के लिए उड़ जाता है। उसे जाते देखकर पेड़ विस्मित, सा रह जाता है। उसी प्रकार संस्कारहीनता के कारण कई बच्चे बड़े हो जाने के बाद अपने माता-पिता को छोड़कर दूर जाकर अपने लिए अलग बसेरा बना लेते हैं। इससे माता-पिता किंकर्तव्यविमूढ हो जाते हैं।

हाकिया चला ………………………………………. भर के झोला।
प्रस्तुत हायक में लोगों के आने वाले खत बाँटने वाला डाकिया के बारे में है। कुछ पत्रों से खशी झलकती है तो कछ पत्र दुखद गहराई का अहसास दिलाते हैं। फिर भी किसी की भी भावना से सरोकार न रखते हुए डाकिया अपनी झोली भरकर पत्र बाँटने का काम करता रहता है। डाकिए की तरह हमें भी जीवन में आने वाले सुख-दुख की भावनाओं से प्रभावित न होकर अपना कार्य करते रहना चाहिए।

मैया की आई ………………………………………. कैसे हो बेटा।
माता-पिता अपनी संतान पर अपना सर्वस्व लुटाकर उसका लालन-पोषण करके उसे कामयाब इंसान बनाते हैं। वही संतान बाद में अपने माता-पिता को वृद्धाश्रम में भेज देते हैं। फिर भी उसकी इस निर्दयता को माँ भूल जाती है और वह उसे वृद्धाश्रम से खत लिखकर उसका हाल जानना चाहती है। माँ आखिर माँ ही होती है। वह अपने बेटे द्वारा किए गए अत्याचारों को भूलकर मन ही मन में याद करती रहती है।

हो गई चोरी ………………………………………. लुट गया मैं।
प्रस्तुत हाइकु में बताया गया है कि आज हमारे समाज में संस्कारों का अभाव है। समाज से जीवन-मूल्यों का पतन हो रहा है। संस्काररूपी तिजोरी का समाज से हनन हो गया है। आज समाज में संस्कारों का धीरे-धीरे लोप होता आ रहा है। इस कारण समाज में समस्याएँ उभरकर सामने आ रही हैं। संस्कारहीनता के कारण सामाजिक पतन हो रहा है। जिस कारण चारों ओर लूटमार और भगदड़ मची हुई है।

शब्दार्थ :

1. डाकिया – चिट्ठी बाँटनेवाला
2. तरू – वृक्ष, पेड़
3. पखेरू – पंछी, पक्षी
4. गुमान – अभिमान, गर्व, घमंड
5. कद – काठी, शरीर की बनावट
6. रवि – सूर्य
7. निर्मल – पवित्र
8. धरा – धरती
9. तन – शरीर
10. आशियाना – घोंसला
11. डोर – रस्सी
12. चिट्ठी – खत
13. झोला – थैला

मुहावरे :

ठगा-सा रह जाना – किंकर्तव्यविमूढ़ हो जाना या विस्मित हो जाना।

ऐसा भी होता है Summary in Hindi

ऐसा भी होता है कवि-परिचय

जीवन-परिचय : अभिषेक जैन जी आधुनिक साहित्यकार के रूप में हिंदी जगत में प्रसिद्ध हैं। कविता, कहानी, निबंध आदि विधाओं में इन्होंने लेखन किया है। जीवन के अनुभवों पर आधारित इनकी विविध रचनाएँ हिंदी पत्र-पत्रिकाओं में प्रकाशित होती रहती हैं। इन्होंने हाइकु काव्य विधा में भी लेखन किया है। इनकी हाइकु रचनाएँ जीवन के समृद्ध अनुभवों का भंडार है।

प्रमुख कृतियाँ : अभिषेक जैन जी ने कविता, कहानी, निबंध आदि विविध विधाओं में लेखन किया है। अनुभवों पर आधारित इनकी रचनाएँ विविध पत्र-पत्रिकाओं में नियमित प्रकाशित होती हैं।

ऐसा भी होता है पद्य-परिचय

हाइकु काव्य : हाइकु एक जापानी काव्य विधा है। हाइकु यानी तीन पंक्तियों की कविता। यह विश्व की एक सबसे लघु कविता कही जाती है। हाइकु कविता ५ + ७ + ५ = १७ वर्ण के ढाँचे में लिखी जाती है। यह कविता आज भारत में सिर्फ हिंदी में ही नहीं, बल्कि मराठी, गुजराती, बंगाली, मलयालम आदि भाषाओं में भी लिखी जाती है।

प्रस्तावना : ‘ऐस भी होता है’ इस हाइकु में कवि अभिषेक जैन जी ने समाज में सबल घटकों द्वारा दुर्बलों पर होने वाले अत्याचार, गरीबी, थकान, वृक्षों के कटने के दुष्परिणाम, अनावश्यक अहं, वृद्धाश्रम के दर्द, संस्कारहीनता आदि विविध विषयों पर प्रकाश डाला है।

ऐसा भी होता है सारांश

‘ऐसा भी होता है’ यह हाइकु काव्य है। कवि ने इस हाइकु के द्वारा विविध विषयों को अभिव्यक्त करने की कोशिश की है। समाज के सबल वर्ग दुर्बलों पर अपना रोब या अधिकार जमाते रहते हैं। उनके द्वारा किए गए अन्याय एवं शोषण से समाज के दुर्बल घटक सहम जाते हैं। सूरज प्रतिदिन अपने निर्मल किरणों से धरती को प्रकाशित करता रहता है। इसके बदले में वह धरती से किसी भी चीज की अपेक्षा नहीं करता।

ठीक उसी प्रकार सज्जन व्यक्ति दीन-दुखी लोगों के लिए अपना सर्वस्व अर्पण कर देते हैं। दिनभर सभी को रोशनी देने वाली किरण शाम होते ही थक जाती है और वह धरा की गोद में आकर विश्राम करती है। गरीब व्यक्ति की आशा-आकांक्षाएँ कभी भी पूर्ण नहीं होती। वह जीवनभर सपने देखते रहता है; फिर भी उसके सपने पूर्ण नहीं होते। वृक्षों को काटने से पंछियों का आशियाना यानी घोसला उजड़ जाता है।

उनके आशियाने उजड़ने पर पक्षी रोने लगते हैं। माँ-बाप के अथक परिश्रम और सुसंस्कारों के कारण ही बच्चे आसमान को छूते हैं। व्यक्ति को अपने जीवन से अभिमान का त्याग कर अपने जीवन को सुंदर बनाना चाहिए। संस्कारहीनता के कारण कई बच्चे बड़े हो जाने के बाद अपने माता-पिता को छोड़कर दूर जाकर अपने लिए अलग से बसेरा बना लेते हैं।

डाकिए की तरह सभी को जीवन में आने वाली सुख-दुख की भावनाओं से प्रभावित न होकर अपना कार्य करते रहना चाहिए। अनेक तिरस्कारों के बावजूद माँ की ममता अपने बच्चों के लिए कम नहीं होती। संस्कारहीनता के कारण सामाजिक पतन हो रहा है। जिस कारण चारों ओर लूटमार और भगदड़ मची हुई है।

ऐसा भी होता है शब्दार्थ

• डाकिया – चिट्ठी बाँटनेवाला
• तरू – वृक्ष, पेड़
• पखेरू – पंछी, पक्षी
• गुमान – अभिमान, गर्व, घमंड
• कद – काठी, शरीर की बनावट
• निर्मल – पवित्र
• धरा – धरती
• तन – शरीर
• आशियाना – घोंसला
• डोर – रस्सी
• चिट्ठी – खत
• झोला – थैला

ऐसा भी होता है मुहावरे

• ठगा-सा रह जाना – किंकर्तव्यविमूढ़ हो जाना या विस्मित हो जाना।

ऐसा भी होता है भावार्थ

गरजे मेघ ……………………. कच्ची दीवार।

प्रस्तुत हाइकु में कवि ने बताया है कि आसमान में मेघों के गरजने पर एक कच्ची दीवार सहमकर काँपने लगीं; वह बहुत डर गई। यहाँ । गरजने वाले मेघ समाज के सबल वर्ग का प्रतिनिधित्व करते हैं और कच्ची दीवार समाज के दुर्बल वर्ग का प्रतिनिधित्व करती है। इसका अर्थ यह है कि समाज के सबल वर्ग दुर्बल वर्गों पर अपना रोब या अधिकार जमाते रहते हैं। उनके द्वारा किए गए अन्याय एवं शोषण से समाज के दुर्बल घटक सहम जाते हैं।

रवि चढ़ाए ……………………. धरा को अर्य।

प्रस्तुत हाइकु में रवि यानी सूरज एक सज्जन व्यक्ति का प्रतीक है। सूरज प्रतिदिन अपने निर्मल किरणों से धरती को प्रकाशित करता है। बदले में वह धरती से किसी भी चीज की अपेक्षा नहीं करता। उसका कार्य निःस्वार्थ एवं मानवता के लिए होता है। ठीक उसी प्रकार सज्जन। व्यक्ति दीन-दुखियों के लिए अपना सर्वस्व अर्पण कर देते हैं। इसके बदले में वे किसी भी प्रकार की चाह नहीं रखते हैं।

आ के पसरी ……………………. धरा की गोद।

प्रस्तुत हाइकु में बताया गया है कि दिनभर सभी को रोशनी देने वाली किरण शाम होते ही थक जाती है और वह धरा की गोद में आकर। विश्राम करती है। प्रकृति का यही नियम है। जो श्रम करता है; वह दिन ढलने के उपरांत थक जाता है। व्यक्ति दिनभर मेहनत करता है और फिर शाम होते ही वह थककर अपने घर आकर आराम करने लगता है।

खुली आँखो ने ……………………. बंद सपने।

प्रस्तुत हाइकु द्वारा समाज में व्याप्त गरीबों की स्थिति का चित्रण किया गया है। गरीब व्यक्ति की आशा-आकांक्षाएँ कभी भी पूर्ण नहीं। होती। वह जीवनभर सपने देखते रहता है; परंतु उसके सपने कभी भी पूर्ण नहीं होते।

कटते तरु ……………………. रोए पखेरू।

प्रस्तुत हाइकु में वृक्षों के कटने के दुष्परिणाम दिखाए गए हैं। वृक्षों को काटने से पंछियों का आशियाना यानी घोंसला उजड़ जाता है। वे बेघर हो जाते हैं; जिस कारण वे दुखी होकर रोने लगते हैं।

बच्चे पतंग ……………………. छूते गगन।

बच्चों के जीवनरूपी पतंग की डोर माँ-बाप के हाथ में होती है। वे अपने बच्चों को अच्छी शिक्षा और संस्कार देकर उनका जीवन सँवारने की कोशिश करते हैं। माँ-बाप के अथक परिश्रम और सुसंस्कारों के कारण ही बच्चे आसमान को छूते हैं यानी जीवन में ऊँचा उठकर सफलता की मंजिल हासिल करते हैं।

तन माटी का ……………………. कद काठी का।

प्रस्तुत हाइकु में कवि अनावश्यक अहं पर अपने विचार व्यक्त करते हैं। व्यक्ति का शरीर मिट्टी से बना है; जो एक दिन नष्ट होने । वाला है। फिर भी व्यक्ति को अपनी इस छोटी-सी जिंदगी पर बहुत बड़ा अभिमान होता है। मनुष्य को अपने जीवन से अभिमान का त्याग कर अपने जीवन को सुंदर बनाना चाहिए। उसे अनावश्यक अहं नहीं करना चाहिए।

उड़ा पखेरू ……………………. ठगा – सा तरू

प्रस्तुत हाइकु मनुष्य की कृतघ्नता पर करारा व्यंग्य करती है। पक्षी का बच्चा जब तक छोटा होता है यानी उसके पंखों में जब तक उड़ने की शक्ति नहीं आती है, तब तक वह वृक्ष पर ही रहता है। लेकिन जब उसके पंखों में उड़ने की शक्ति आ जाती है; तब वह उस वृक्ष को छोड़कर अनंत आकाश में विचरण करने के लिए उड़ जाता है। उसे जाते देखकर पेड़ विस्मित, सा रह जाता है। उसी प्रकार संस्कारहीनता के कारण कई बच्चे बड़े हो जाने के बाद अपने माता-पिता को छोड़कर दूर जाकर अपने लिए अलग बसेरा बना लेते हैं। इससे माता-पिता किंकर्तव्यविमूढ हो जाते हैं।

डाकिया चला ……………………. भर के झोला।

प्रस्तुत हायकु में लोगों के आने वाले खत बाँटने वाला डाकिया के बारे में है। कुछ पत्रों से खुशी झलकती है तो कुछ पत्र दुखद गहराई । का अहसास दिलाते हैं। फिर भी किसी की भी भावना से सरोकार न रखते हुए डाकिया अपनी झोली भरकर पत्र बॉटने का काम करता रहता है। डाकिए की तरह हमें भी जीवन में आने वाले सुख-दुख की भावनाओं से प्रभावित न होकर अपना कार्य करते रहना चाहिए।

मैया की आई ……………………. कैसे हो बेटा।

माता-पिता अपनी संतान पर अपना सर्वस्व लुटाकर उसका लालन-पोषण करके उसे कामयाब इंसान बनाते हैं; वही संतान बाद में अपने माता-पिता को वृद्धाश्रम में भेज देते हैं। फिर भी उसकी इस निर्दयता को माँ भूल जाती है और वह उसे वृद्धाश्रम से खत लिखकर उसका हाल जानना चाहती है। माँ आखिर माँ ही होती है। वह अपने बेटे द्वारा किए गए अत्याचारों को भूलकर मन ही मन में याद करती रहती है।

हो गई चोरी ……………………. लुट गया मैं।

प्रस्तुत हाइकु में बताया गया है कि आज हमारे समाज में संस्कारों का अभाव है। समाज से जीवन-मूल्यों का पतन हो रहा है। संस्काररूपी तिजोरी का समाज से हनन हो गया है। आज समाज में संस्कारों का धीरे-धीरे लोप होता जा रहा है। इस कारण समाज में समस्याएँ उभरकर सामने आ रही हैं। संस्कारहीनता के कारण सामाजिक पतन हो रहा है; जिस कारण चारों ओर लूटमार और भगदड़ मची हुई है।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 11 Samta Ki Aur Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 11 समता की ओर Notes, Textbook Exercise Important Questions, and Answers.

Hindi Lokbharti 10th Digest Chapter 11 समता की ओर Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 11 समता की ओर Textbook Questions and Answers

कृति

(कृतिपत्रिका के प्रश्न 2 (अ) तथा प्रश्न 2 (आ) के लिए)

सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
जीवन शैली में अंतर स्पष्ट कीजिए :

धनी	दीन- दरिद्र
…………………….. …………………….. …………………….. ……………………..	…………………….. …………………….. …………………….. ……………………..

उत्तर:

धनी	दीन- दरिद्र
(i) रात दिन मौज, आनंद ही आनंद (ii) हलुवा-पूड़ी, दूध-मलाई का भोजन	शिशिर ऋतु के सारे दुख. सूखी रोटी और भाजी का भी अभाव।

प्रश्न 3.
तालिका पूर्ण कीजिए:

ऋतुएँ	अंग्रेजी माह	हिंदी माह
१. वसंत	मार्च, अप्रैल	चैत्र, बैसाख
२. ग्रीष्म	…………………..	…………………..
३. वर्ष	…………………..	…………………..
४. शरद	…………………..	…………………..
५. हेमंत	…………………..	…………………..
६. शिशिर	…………………..	…………………..

उत्तर:

ऋतुएँ	अंग्रेजी माह	हिंदी माह
१. वसंत	मार्च, अप्रैल	चैत्र, बैसाख
२. ग्रीष्म	मई–जून	ज्येष्ठ–आषाढ़
३. वर्ष	जुलाई–अगस्त	श्रावण–भाद्रपद
४. शरद	सितंबर–अक्तूबर	आश्विन–कार्तिक
५. हेमंत	नवंबर–दिसंबर	मार्गशीर्ष–पौष
६. शिशिर	जनवरी–फरवरी।	माघ–फाल्गुन

प्रश्न 4.
निम्न मुद्दों के आधार पर पद्य विश्लेषण कीजिए :
1. रचनाकार
2. रचना का प्रकार
3. पसंदीदा पंक्ति
4. पसंदीदा होने का कारण
5. रचना से प्राप्त संदेश
उत्तर:
1. रचनाकार का नाम → मुकुटधर पांडेय।
2. रचना का प्रकार (विधा) → नई कविता।

3. पसंद की पंक्तियाँ →
‘हमको भाई का करना उपकार नहीं क्या होगा,
भाई पर भाई का कुछ अधिकार नहीं क्या होगा’।

4. पसंद होने का कारण → जन्म से सभी मनुष्य एक जैसे होते हैं, ऊँच-नीच, बड़ा-छोटा, धनवान-गरीब तो मनुष्य अपनी-अपनी उपलब्धियों से बनता है। मनुष्य का आपस में भाई-भाई का नाता है। प्रस्तुत पंक्तियों में कहा गया है कि मनुष्य में आपस में एक-दूसरे का उपकार करने की भावना होनी चाहिए।

5. रचना से प्राप्त संदेश → सभी मनुष्य समान होते हैं। कोई अपने को बड़ा या छोटा न समझे। मनुष्य को एक-दूसरे का उपकार करना चाहिए। (विद्यार्थी अपनी पसंद की पंक्ति लिखेंगे।)

प्रश्न 5.
अंतिम दो पंक्तियों से मिलने वाला संदेश लिखिए।
उत्तर:
कवि कहते हैं कि मनुष्य-मनुष्य में कोई अंतर नहीं होता। सभी का आपस में भाई-भाई का नाता है। एक भाई का दूसरे भाई पर कुछ-न-कुछ अधिकार होता है। इसलिए हमारे, मन में एक-दूसरे का उपकार करने की भावना होनी चाहिए।

उपयोजित लेखन

प्रश्न.
विश्वबंधता वर्तमान युग की माँग’ विषय पर अस्सी से सौ शब्दों में निबंध लिखिए।
उत्तर:
वैज्ञानिक प्रगति और उपलब्धियों के बल पर आज विश्व सिमटकर बहुत छोटा हो गया है। विभिन्न देशों के लोग आज एक-दूसरे के बहुत करीब आ गए हैं। किसी भी देश में कोई घटना होती है, तो उससे दूसरे देश भी प्रभावित होते हैं। आज लोगों का एक-दूसरे के देशों में आना-जाना और व्यापारव्यवहार बहुत सुलभ हो चुका है। लोगों में आपसी प्रेम-भाव भी बहुत है। पर कुछ शक्तियाँ ऐसी हैं, जिनके कारण लोगों के बीच वैसा सौमनस्य स्थापित नहीं हो पा रहा है, जैसा होना चाहिए। इसके कारण कई देशों में अशांति का वातावरण है।

आतंकवाद और युद्ध का भय उनमें से एक है। विश्व में लोगों में आपसी भाईचारे के प्रयास पहले भी होते रहे हैं और आज तो बहुत तेजी से जारी हैं। आज के युग में विश्वबंधुता की सबसे अधिक आवश्यकता है। आज विश्व विस्फोटकों के ढेर पर बैठा हुआ है। तरह-तरह के विनाशक अस्त्र-शस्त्रों का भय लोगों को सता रहा है, जिसकी चपेट में सारा विश्व आ सकता है। इसलिए आज सभी देशों के बीच आपसी प्रेम-भाव और सौहाय की अत्यधिक आवश्यकता है। इस बात को अब सभी देश समझने लगे हैं और इस दिशा में प्रयास भी शुरू हो गए हैं। विश्वबंधुता की भावना से ही विश्व में शांति और सौहाय स्थापित हो सकता है।

Hindi Lokbharti 10th Textbook Solutions Chapter 11 समता की ओर Additional Important Questions and Answers

पद्यांश क्र. 1
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
एक शब्द में उत्तर लिखिए:
(i) पद्यांश में आए एक फूल का नाम –
(ii) श्वेत कणों के रूप में पृथ्वी पर गिरने वाली हवा में मिली भाप –
(iii) लंबे-चौड़े प्राकृतिक गड्ढे के लिए प्रयुक्त शब्द जिसमें बरसाती पानी जमा होता है –
(iv) शिशिर ऋतु से पहले आने वाली ऋतु –
उत्तर:
(i) पद्यांश में आए एक फूल का नाम – पद्म (कमल)।
(ii) श्वेत कणों के रूप में पृथ्वी पर गिरने वाली हवा में मिली भाप – तुषार (बर्फ)।
(iii) लंबे-चौड़े प्राकृतिक गड्ढे के लिए प्रयुक्त शब्द जिसमें बरसाती पानी जमा होता है – ताल।
(iv) शिशिर ऋतु से पहले आने वाली ऋतु – हेमंत ऋतु।

प्रश्न 2.
उचित जोड़ियाँ मिलाकर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)
‘अ’ – ‘आ’
(i) प्रकृति – ताल
(ii) अवनि – युतिहीन
(iii) पद्मदल – नृप
(iv) अन्यायी – कुंझटिका लोग
उत्तर:
(i) प्रकृति – युतिहीन
(ii) अवनि – कुंझटिका
(iii) पद्मदल – ताल
(iv) अन्यायी -नृप।

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (शब्द संपदा) (बोर्ड की नमूना कृतिपत्रिका)

प्रश्न 1.
लिंग पहचानकर लिखिए:
(i) नृप –
(ii) प्रकृति –
(iii) अवनि –
(iv) निशा –
उत्तर:
(i) नृप – पुल्लिग
(ii) प्रकृति – स्त्रीलिंग
(iii) अवनि – स्त्रीलिंग
(iv) निशा – स्त्रीलिंग।

प्रश्न 2.
वचन परिवर्तन कीजिए:
(i) ऋतु –
(ii) घर –
उत्तर:
(i) ऋत – ऋतुएँ
(ii) घर – घर।

कृति 3: (सरल अर्थ)

प्रश्न.
प्रस्तुत पद्यांश की प्रथम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
निशा काल में लोग घरों में निज-निज जा सोते हैं। बाहर श्वान, स्यार चिल्लाकर बार-बार रोते हैं। कवि कहते हैं कि शिशिर ऋतु के भाई हेमंत का समय बीत गया है। अब शिशिर ऋतु का आगमन हो गया है। शिशिर ऋतु की कँपा देने वाली ठंड के कार प्रकृति की आभा खत्म हो गई है और वह कांति रहित हो गई है। पृथ्वी पर धुंधलका छां गया है।

ठंड के कारण खूब बर्फ गिर रही है। इससे तालाबों में खिले हुए कमल के फूलों को बहुत कष्ट हो रहा है। कवि कहते हैं यह कष्ट कुछ उसी तरह का है, जैसे किसी निर्दयी और अन्यायी राजा के तरह-तरह के दंडों से उसके राज्य की प्रजा दुखी होती है।

पद्यांश क्र. 2
प्रश्न, निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
एक शब्द में उत्तर लिखिए:
(i) रात के एक हिस्से का नाम –
(ii) घर के भीतर खुला छोड़े गए भाग का नाम –
(iii) देखने के अर्थ में आया हुआ शब्द –
(iv) सौर मंडल के एक उपग्रह का नाम –
उत्तर:
(i) रात के एक हिस्से का नाम – अर्धरात्रि।
(ii) घर के भीतर खुला छोड़े गए भाग का नाम – आँगन।
(iii) देखने के अर्थ में आया हुआ शब्द – ‘लख’।
(iv) सौर मंडल के एक उपग्रह का नाम – चंद्रमा।

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदलकर लिखिए:
(i) रोटी
(ii) दुशाले
उत्तर:
(i) रात-दिन
(ii) दूध-मलाई।

कृति 3: (सरल अर्थ)

प्रश्न.
पद्यांश की अंतिम चार पंक्तियों का सरल अर्थ 25 से 30 शब्दों में लिखिए।
उत्तर:
कवि कहते हैं कि शिशिर ऋतु की कष्टदायी ठंड में धनी वर्ग के व्यक्तियों को आनंद ही आनंद है। वे रात-दिन मौज-मजा करते हैं और प्रसन्न रहते हैं। लेकिन गरीबों और दरिद्रों के लिए शिशिर ऋतु की ठंड में दुख ही दुख है।

धनिक वर्ग के लोग हलुवा-पूड़ी और ताजी दूध-मलाई खाते हैं और ठंडक का आनंद लेते हैं। लेकिन गरीबों और दरिद्रों को सुखी रोटी और सब्जी भी नसीब नहीं होती (यानी उन्हें उपवास करना पड़ता है)।

पयांश क्र. 3
प्रश्न. निम्नलिखित पठित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
जीवन-शैली में अंतर स्पष्ट कीजिए:
घनी – दीन-दरिद्र
(i) …………… – ………………
(ii) ………….. – ……………….
उत्तर:
धनी – दीन-दरिद्रमा
(i) वे रंगीन कीमती शाल – दुशाले ओढ़ते हैं – इनके काँपते हुए शरीर पर रोज पाला गिरता है
(ii) ये सुविधा-संपन्न मकानों में रहते हैं, – ये टूटे-फूटे घरों में रहते हैं जहाँ हमेशा उदासी छाई रहती हैं

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
एक शब्द में उत्तर लिखिए:
(i) पहले इन्हें इसकी चिंता नहीं सताती थी –
(ii) यह इनका माता की तरह भरण-पोषण करती थी –
उत्तर:
(i) पहले इन्हें इसकी चिंता नहीं सताती थी – उदर की।
(ii) यह इनका माता की तरह भरण-पोषण करती थी – प्रकृति।

कृति 2: (शब्द संपदा)

(1) निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) उदर =
(ii) माता =
उत्तर:
(i) उदर = पेट
(ii) माता = माँ

(2) निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) सुख x
(ii) उपकार x
उत्तर:
(i) सुख x दुख
(ii) उपकार x अपकार

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:

अधोरेखांकित शब्दों के शब्दभेद पहचानकर लिखिए:
(i) वे हलुवा-पूड़ी और ताजी दूध-मलाई खाते हैं।
(ii) वे कीमती शाल-दुशाले ओढ़ते हैं।
उत्तर:
(i) ताजी – गुणवाचक विशेषण।
(ii) वे – पुरुषवाचक सर्वनाम।

2. अव्यय:

निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) रात-दिन
(ii) उधर।
उत्तर:
(i) वह रात-दिन गरीबों की सेवा में लगा रहता है।
(ii) विधि उधर मत जाओ।

3. संधि:

कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
सदैव	……………………	……………………
अथवा
……………………	निः + रज	……………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
सदैव	सदा + एव	स्वर संधि
अथवा
नीरज	निः + रज	विसर्ग संधि

4. सहायक क्रिया पहचानना:

निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उसका मूल रूप लिखिए:
(i) अब वह अपने नए मकान में रहने लगा।
(ii) वे शाल-दुशाले ओढ़े रहते हैं।
उत्तर:
सहायक क्रिया – मूल रूप
(i) लगा – लगना
(ii) हैं – होना

5. प्रेरणार्थक क्रिया का रूप लिखना:

निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) गिरना
(ii) खाना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वितीय प्रेरणार्थक रूप
(i) गिरना – गिराना – गिरवाना
(ii) खाना। – खिलाना – खिलवाना

6. मुहावरे:

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) पौ-बारह होना
(i) नाच नचाना।
उत्तर:
(i) पौ-बारह होना।
अर्थ – लाभ का अवसर मिलना।
वाक्य: आई.ए.एस. परीक्षा में यदि वह लड़का पास हो गया, तो उसके पौ-बारह हो जाएंगे।

(ii) नाच नचाना।
अर्थ: खूब परेशान करना।
वाक्य: वह शैतान लड़का अपनी माँ को रात-दिन नाच नचाता रहता है।

प्रश्न 2.
अधोरेखांकित वाक्यांशों के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (जाल बिछाना, राह देखना, भनक पड़ना)
(i) पुलिस ने बदमाश को गिरफ्तार करने के लिए पूरे इलाके की घेराबंदी कर दी।
(ii) बोर्ड की परीक्षा हो जाने पर विद्यार्थी परिणाम की प्रतीक्षा करने लगे।
उत्तर:
(i) पुलिस ने बदमाश को गिरफ्तार करने के लिए पूरे इलाके में जाल बिछा दिया।
(ii) बोर्ड की परीक्षा हो जाने पर विद्यार्थी परिणाम की राह देखने लगे।

7. कारक:

निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) चंद्रमा ने पांडुवर्ण पाया है।
(ii) वे सुख से अपने घरों में रहते हैं।
उत्तर:
(i) चंद्रमा ने – कर्ता कारक।
(ii) सुख से – करण कारक।

8. विरामचिह्न:

निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) वाह आपने तो कमाल कर दिया
(ii) क्रिकेट खिलाड़ी की प्रशंसा करते हुए उन्होंने कहा एक दिन तुम देश का नाम रोशन करोगे।
उत्तर:
(i) वाह! आपने तो कमाल कर दिया।
(ii) क्रिकेट खिलाड़ी की प्रशंसा करते हुए उन्होंने कहा, “एक दिन तुम देश का नाम रोशन करोगे।”

9. काल परिवर्तन:

निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) वे सुंदर मकानों में रहते हैं। (अपूर्ण वर्तमानकाल)
(ii) इनके बदन पर नित पाले गिरते हैं। (सामान्य भविष्यकाल)
उत्तर:
(i) वे सुंदर मकानों में रह रहे हैं।
(ii) इनके बदन पर नित पाले गिरेंगे।

10. वाक्य भेद:

प्रश्न 1.
निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचान कर लिखिए:
(i) रात के समय लोग अपने-अपने घरों में सो जाते हैं।
(ii) हेमंत ऋतु बीत गई और शिशिर ऋतु आ गई।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य।

प्रश्न 2.
निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए:
(i) उन्हें काँपते हुए रात काटनी पड़ती है। (निषेधवाचक वाक्य)
(ii) ठंड भरे मौसम में आकाश के तारे धुंधले से दिखाई देते हैं। (प्रश्नवाचक वाक्य)
उत्तर:
(i) उन्हें काँपते हुए रात नहीं काटनी पड़ती है।
(ii) क्या ठंड भरे मौसम में आकाश के तारे धुंधले दिखाई देते हैं?

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए:
(i) पहले प्रक्रिति हमारे माता के समान थी।
(ii) इनकी बदन पर पाला गिरती है।
उत्तर:
(i) पहले प्रकृति हमारी माता के समान थी।
(ii) इनके बदन पर पाला गिरता है।

समता की ओर Summary in Hindi

विषय-प्रवेश : शिशिर ऋतु की ठंडक समूचे वातावरण को प्रभावित कर देती है। उसका प्रभाव प्रकृति, पृथ्वी, वनस्पतियों, जीवजंतुओं, मनुष्यों तथा आकाश में स्थित चाँद-तारों पर भी पड़ता है।
यह ऋतु धनिक वर्ग जैसे सुविधा-संपन्न लोगों के लिए जहाँ आनंददायी होती है, वहीं दीन-दरिद्र जैसे सुविधा-विहीन लोगों के लिए कष्टदायी होती है।

प्रस्तुत कविता में कवि ने शिशिर ऋतु में पड़ने वाली अत्यधिक ठंड से परेशान प्राणियों तथा साधन-संपन्न एवं अभावग्रस्त व्यक्तियों के जीवनयापन का सजीव वर्णन किया है। अंत में कवि कहता है कि धनवान और निर्धन दोनों भाई-भाई हैं। इसलिए धनी वर्ग के लोगों को अपने दीन-दरिद्र भाइयों की भलाई के लिए प्रयास करना चाहिए।

समता की ओर कविता का सरल अर्थ

1. बीत गया हेमंत ………………………….. बार-बार रोते हैं।

कवि कहते हैं कि शिशिर ऋतु के भाई हेमंत का समय बीत गया है। अब शिशिर ऋतु का आगमन हो गया है। शिशिर ऋतु की कँपा देने वाली ठंड के कारण प्रकृति की आभा खत्म हो गई है और वह कांति रहित हो गई है। पृथ्वी पर धुंधलका छा गया है।

ठंड के कारण खूब बर्फ गिर रही है। इससे तालाबों में खिले हुए कमल के फूलों को बहुत कष्ट हो रहा है। कवि कहते हैं कि यह कष्ट कुछ उसी तरह का है, जैसे किसी निर्दयी और अन्यायी राजा के तरहतरह के दंडों से उसके राज्य की प्रजा दुखी होती है।

रात्रि के समय बहुत ठंड होती है। ऐसे समय लोग अपने-अपने घरों में जाकर सो जाते हैं। पर ठंड के मारे बाहर कुत्तों और सियार जैसे जानवरों का बुरा हाल है। ये असहाय प्राणी चिल्ला-चिल्लाकर सारी रात रोते रहते हैं।

2. अर्धरात्रि को घर से ………………………….. और न भाजी।

आधी रात को यदि कोई व्यक्ति घर के आँगन में आकर निर्जन आकाश-मंडल की ओर देखता है, तो वहाँ का दृश्य देखकर उसे डर लगने लगता है।

ठंड भरे इस मौसम में आकाश के तारे भी धुंधले दिखाई देते हैं और चंद्रमा का रंग पीलापन लिए हुए सफेद हो गया है। इन्हें देखकर ऐसा लगता है, जैसे किसी राज्य पर कोई राष्ट्रीय संकट आ गया हो।

कवि कहते हैं कि शिशिर ऋतु की कष्टदायी ठंड में धनी वर्ग के व्यक्तियों को आनंद ही आनंद है। वे रात-दिन मौज-मजा करते हैं और प्रसन्न रहते हैं। लेकिन गरीबों और दरिद्रों के लिए शिशिर ऋतु की ठंड में दुख ही दुख है।

धनिक वर्ग के लोग हलवा-पूड़ी और ताजी दूध-मलाई खाते हैं और ठंडक का आनंद लेते हैं। लेकिन गरीबों और दरिद्रों को सूखी रोटी और सब्जी भी नसीब नहीं होती (यानी उन्हें उपवास करना पड़ता है)।

3. वे सुख से रंगीन ………………………….. नहीं क्या होगा।

घनिक वर्ग के लोगों पर ठंड का कोई असर नहीं होता। वे रंगीन और मूल्यवान शाल-दुशाले ओढ़ते हैं इससे उन पर जाड़े का तनिक भी असर नहीं होता। मगर ऐसे समय गरीबों की बुरी हालत होती है। उन्हें काँपते हुए दिन-रात काटनी पड़ती है और ऊपर से उन्हें ओस और पाले का भी सामना करना पड़ता है। धनिक वर्ग के पास सुख के तरह-तरह के साधन होते हैं और वे सुंदर-सुंदर घरों में रहते हैं। दूसरी ओर गरीबों और दरिद्रों के घर टूटे फूटे, झुग्गी-झोपड़ियोंवाले होते हैं और उनमें किसी तरह की कोई सुविधा नहीं होती। वहाँ सदा उदासी का माहौल होता है।

कवि कहते हैं कि पहले सब लोग प्रकृति पर निर्भर करते थे। किसी को पेट भरने यानी क्षुधा-पूर्ति की कोई चिंता करने की आवश्यकता नहीं थी। प्रकृति से ही सारी आवश्यकताएं पूरी हो जाती थीं। वह माता की तरह हमारा पालन-पोषण किया करती थी।

कवि कहते हैं कि मनुष्य-मनुष्य में कोई अंतर नहीं होता। सभी का आपस में भाई-भाई का नाता है। एक भाई का दूसरे भाई पर कुछ-नकुछ अधिकार होता है। इसलिए हमारे मन में एक-दूसरे का उपकार करने की भावना होनी चाहिए।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 5 Char Hath Chandna Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 5 चार हाथ चाँदना Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokvani 10th Digest Chapter 5 चार हाथ चाँदना Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 5 चार हाथ चाँदना Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. विधानों के सामने सही अथवा गलत लिखिए :

प्रश्न 1.
विधानों के सामने सही अथवा गलत लिखिए :

1. शोभा सिंह ने ‘सत्यम्, शिवम्, सुंदरम्’ का क्रम बदला है। [ ]
2. प्रश्नकर्ता के अनुसार हमारी धरती का यथार्थ बहुत भयानक नहीं है। [ ]
3. कलाकार की शक्ति उसके चिंतन में है। [ ]
4. शोभा सिंह कलाकार का कर्म एक छोटी-सी जलती हुई मोमबत्ती नहीं समझते । [ ]

उत्तर:

1. सत्य
2. असत्य
3. सत्य
4. असत्य

2. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

3. उचित जोड़ियाँ मिलाइए।

प्रश्न 1.
उचित जोड़ियाँ मिलाइए।

‘अ’	‘ब’
1. चित्रकार	(क) अमृता प्रीतम
2. लेखिका	(ख) शोभा सिंह
3. जीनियस	(ग) कलाकार
4. ईश्वर	(घ) माँ

उत्तर:

‘अ’	‘ब’
1. चित्रकार	(ख) शोभा सिंह
2. लेखिका	(क) अमृता प्रीतम
3. जीनियस	(घ) माँ
4. ईश्वर	(ग) कलाकार

4. उचित विकल्प चुनकर रिक्त स्थानों की पूर्ति कीजिए।

प्रश्न 1.
उचित विकल्प चुनकर रिक्त स्थानों की पूर्ति कीजिए।

1. सुंदरता के लिए ………………….. सबसे पहली अवस्था है। (नजर, दृष्टि, नजरिया)
2. हमारी धरती का ……………… बहुत भयानक है। (सत्य, यथार्थ, वास्तव)
3. कलाकार की शक्ति उसके …………….. में है। (चिंतन, मनन, साधना)
4. मैं रचनात्मक ……………. के संबंध में कह रहा हूँ। (युक्ति, कृति, शक्ति)

उत्तर:

1. नजरिया
2. यथार्थ
3. चिंतन
4. शक्ति

5. पाठ में प्रयुक्त ऐसे शब्द ढूँढकर लिखिए जिनका वचन परिवर्तन नहीं होता।
जैसे : वृक्ष – वक्ष

प्रश्न 1.
पाठ में प्रयुक्त ऐसे शब्द ढूँढकर लिखिए जिनका वचन परिवर्तन नहीं होता।
जैसे : वृक्ष – वक्ष
उत्तर:

कलाकार	रंग	चित्रकार	घर
दीमक	गुलाब	फूल	दर्शक

अभिव्यक्ति :

प्रश्न 1.
‘कला जीवन को आनंदित करने का साधन है।’ विषय पर अपना मत स्पष्ट कीजिए।
उत्तरः
कला के माध्यम से मनुष्य अपने भावों की अभिव्यक्ति करता है। कला जीवन की अनुकृति है। कला जीवन को आनंदित करने का साधन है। कला में ऐसी शक्ति होती है जो कलाकार को संकीर्ण सीमाओं से उठाकर सफलता की मंजिल पर बिठा देता है। कला के कारण मानव मन में संवेदनाएँ एवं अभिरूचि निर्माण होती है। कला जीवन को सत्यम्, शिवम् और सुंदरम् से समन्वित करती है। कला उस क्षितिज की भाँति है जिसका कोई छोर नहीं है।

रसात्मकता कला का प्राण होता है। व्यक्ति को जो कला अच्छी लगती है, उसमें वह मग्न हो जाता है। अपनी मनपसंद कला के साथ एकाकार होने से उसका मन हर्ष से भर जाता है। मनपसंद कला उसके जीवन को प्रभावित करती है और उसे आनंद की अनुभूति दिलाती है। जो व्यक्ति अपने जीवन से निराश एवं उदास हो जाता है, वह यदि कला के सान्निध्य चला जाए तो उसके मन से उदासी की भावना सदा के लिए खत्म हो जाती है और वह चिर-आनंद का अनुभव करने लगता है।

भाषाबिंदु :

प्रश्न 1.
वर्तनी के नियमों के अनुसार शुद्ध शब्द छाँटकर लिखिए। |

1. मुश्कील/मुशकील/मुश्किल/मुष्कील = …………….
2. परसिद्ध/प्रसिद्ध/प्रसीध्द/प्रसिध्ध =…………….
3. मिट्टी/मिट्यी/मिट्टी/मीट्ठी = …………….
4. रूतूएँ/ऋतुएँ/ऋतूए/ऋतू = …………….

उत्तर:

1. मुश्किल
2. प्रसिद्ध
3. मिट्टी
4. ऋतुएँ

उपयोजित लेखन :

प्रश्न 1.
‘पुस्तक मेल में दो घंटे’ विषय पर अस्सी से सौ शब्दों में निबंध लिखिए।
उत्तरः
पुस्तक मेल में दो घंटे पुस्तकों का हमारे जीवन में महत्त्वपूर्ण स्थान होता है। वे एक मित्र के समान हमारी सहायक एवं मार्गदर्शक होती हैं। वे अपना ज्ञानरूपी अमृत कोष सदा हम पर न्योछावर करती रहती हैं। अतः पुस्तकों का वाचन सभी को करना चाहिए। पुस्तकों का भी अपना एक मेला होता है। पुस्तक मेले में तरह-तरह की पुस्तकें होती हैं। वहाँ पर लेखक एवं कवि आते हैं और स्वयं अपनी पुस्तकों के बारे में पाठकों को परिचित कराते हैं। मैं भी सरस्वती भवन द्वारा आयोजित पुस्तक मेले में गया था।

मेरे साथ मेरे मित्र भी थे। जैसे ही हमने पुस्तक मेले में प्रवेश किया वैसे ही पुस्तक मेले के प्रवेशद्वार पर एक व्यक्ति पुस्तक का मुखौटा पहनकर पुस्तकों के महत्त्व से हमें परिचित कराने लगा हमें बहुत ही अच्छा लगा। जैसे ही हम भीतर गए वैसे ही हमने चारों ओर नजर डाली।

तब हमने देखा कि चारों ओर पुस्तक खरीदने के लिए लोगों की भीड़ एकत्रित हुई है। कई दुकानों पर लोगों का तांता लगा हुआ था। भारतीय भाषाओं के सर्वश्रेष्ठ ग्रंथ एवं महापुरूषों की जीवनी सर्वत्र विक्री हेतु उपलब्ध थी। अंग्रेजी किताबें भी थीं। हिंदी साहित्य की पुस्तकों के बारे में क्या कहना? प्रत्येक दुकान में पंत जी, निराला जी, बच्चन जी, गुप्त जी, सुभद्रा जी, महादेवी जी, अज्ञेय जी, मन्नू भंडारी जी, भारती जी आदि पुस्तक रूप में विराजमान थे।

इन श्रेष्ठ साहित्यकारों के अनुपम ग्रंथ देखकर मैं आनंदविभोर हो गया। इतने में मेरे एक मित्र ने तपाक से कहा, “अरे देखो, हिंदी साहित्य के श्रेष्ठ वर्तमान साहित्यकार श्री. राम जी तिवारी बच्चों के साथ वार्तालाप कर रहे हैं।”

हम तुरंत उस स्थान पर पहुंच गए जहाँ पर श्री तिवारी जी बच्चों से तन्मयता और सहदयता से बात कर रहे थे। उनके विचार सुनकर हम सब गद्गद हो गए। उन्होंने ‘कितावें करती हैं बातें…’ इस कविता को हमारे सामने अभिव्यक्त करके पुस्तकों के वाचन हेतु जो संस्कार किया, उसका वर्णन करना मेरे लिए कठिन है।

पुस्तक मेले में घूमते-घूमते हमें कई ऐसी किताबों के बारे में पता चला, जिनके नाम भी हमने पहले कभी सुने नहीं थे। पुस्तक मेले में भ्रमण करते समय दो घंटे कब खत्म हुए, इसका पता भी नहीं चला। मनचाही पुस्तकें खरीद कर एवं प्राप्त ज्ञान को मस्तिष्क में संग्रहित कर हम खुशी-खुशी घर की ओर लौट पड़े।

Hindi Lokvani 10th Std Textbook Solutions Chapter 5 चार हाथ चाँदना Additional Important Questions and Answers

(अ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
निम्नलिखित विधान सत्य है या असत्य लिखिए। –
i. श्री शोभा सिंह प्रसिद्ध साहित्यकार हैं।
उत्तर:
i. असत्य

प्रश्न 3.
समझकर लिखिए।
उत्तर:

प्रश्न 4.
उचित विकल्प चुनकर रिक्त स्थानों की पूर्ति कीजिए।
i. सुंदरता की …………………………. अवस्था सत्य है। (पहली, दूसरी, तीसरी)
उत्तर:
i. पहली

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. रूहानी
2. तकनीकी
3. अवस्था
4. गहराई

उत्तर:

1. आत्मिक
2. प्रविधिक
3. हालत
4. गहनता

प्रश्न 2.
निम्नलिखित शब्दों के वचन बदलिए।
i. कल्पना
ii. लकीर
उत्तर:
i. कल्पनाएँ
ii. लकीरें

प्रश्न 3.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. अवस्था
ii. कल्पना
उत्तर:
i. हालत, देहादि की कालकृत स्थिति जैसे बचपन, जवानी, बुढ़ापा, उम्र, स्थिति
ii. नई बात, सोचना, मन की उपज

प्रश्न 4.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. सत्य
उत्तर:
i. सच

प्रश्न 5.
गद्यांश में प्रयुक्त अन्य भाषाओं के शब्द ढूँडकर लिखिए।
उत्तर:
i. रूहानी
ii. कैनवस

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘रंगों का जीवन में बड़ा महत्व है।’ इस विषय पर अपने विचार लिखिए।
उत्तर:
रंगों का व्यक्ति के जीवन में महत्त्वपूर्ण स्थान होता है। रंग चेतन जीव पर गहराई तक असर डालते हैं। रंग व्यक्ति को सिर्फ खुशी ही नहीं देते बल्कि उसके शारीरिक एवं मानसिक विकारों को भी दूर भगाते हैं। रंग व्यक्ति के जीवन में दोहरी भूमिका निभाते हैं। उदाहरण के तौर पर रंग हमें उत्तेजित करते हैं और हमें शांत भी करते हैं। इसलिए जीवन में रंगों का ज्योतिषीय महत्त्व है। रंगों के बिना व्यक्ति का जीवन नीरस होता है।

इंद्रधनुष के सात रंगों को रंगों का रचयिता माना जाता है। हरा रंग संपन्नता का प्रतीक माना जाता है। श्वेत रंग शांति का प्रतीक माना जाता है। पीला रंग प्रकाश का प्रतीक माना जाता है, तो गुलाबी रंग कोमलता व सुंदरता का प्रतीक माना जाता है। नीला रंग एकता व ठंडक का प्रतीक माना जाता है। रंग हमारे विचारों को प्रभावित करते हैं। इसलिए हमारे जीवन में रंगों का विशेष महत्त्व है।

(आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:
i.

ii.

प्रश्न 2.
प्रस्तुत गद्यांश को पढ़कर ऐसे दो प्रश्न तैयार कीजिए कि जिनके उत्तर निम्न शब्द हों –
i. परछत्ती
ii. तस्वीरें
उत्तर:
i. आँगन में क्या बनी हुई थी?
ii. बचपन में शोभा सिंह जी घर की दीवारें सजाने के लिए क्या बनाने लगे?

कृति आ (3) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।
i. जन्म × ……………
ii. निचली × ……………
उत्तर:
i. मरण
ii. ऊपरी

प्रश्न 2.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

1. घास-फूस का बना छप्पर –
2. कागज़, चमड़े आदि से मड़ी हुई दफ़्ती या पुस्तक की प्रति –
3. लकड़ी और किताबों को खानेवाला कीट –

उत्तर:

1. परछत्ती
2. जिल्द
3. दीमक

प्रश्न 3.
नीचे लिखे शब्दों में से उपसर्ग छाँटिए और संबंधित उपसर्ग से दो अन्य शब्द बनाइए।
i. परछत्ती
उत्तर:
i. परछत्ती : उपसर्ग : पर अन्य शब्द : परदादा, परदादी

प्रश्न 4.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:
i. धो-पोंछकर
ii. इर्द-गिर्द

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों
i. रचनात्मक
ii. चाँदना
उत्तर:
i. गद्यांश में किस शक्ति की बात हो रही है?
ii. जलती हुई मोमबत्ती धरती को क्या दे सकती है?

प्रश्न 2.
निम्नलिखित विधान सत्य है या असत्य लिखिए।
i. औरत सब कुछ छोड़कर एक नई और ऊपरी धरती पर चली जाती है।
ii. दो-दो, चार-चार हाथ चाँदना पूरी संस्कृति को प्रभावित कर सकता है।
उत्तर:
i. सत्य
ii. असत्य

कृति इ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:

1. माँ-बाप
2. भाई-बहन
3. दो-दो, चार-चार
4. ईद-गिर्द

प्रश्न 2.
वचन बदलिए।
i. शक्ति
ii. मोमबत्ती
उत्तर:
i. शक्तियाँ
ii. मोमबत्तियाँ

प्रश्न 3.
‘कलाकार’ इस शब्द में निहित प्रत्यय को पहचानकर संबंधित उपसर्ग लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तरः
कलाकारः प्रत्यय : कार नए शब्द : शिल्पकार, चित्रकार

प्रश्न 4.
अनेक शब्दों के लिए एक शब्द लिखिए।

1. किसी लक्ष्य को पाने के लिए किया गया अभ्यास –
2. रचना से संबंधित –
3. सभ्य होने का भाव –

उत्तर :

1. साधना
2. रचनात्मक
3. सभ्यता

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘कला अभिव्यक्ति का माध्यम है।’ विषय पर अपने विचार लिखिए।
उत्तरः
मन के अंत:करण की सुंदर प्रस्तुति कला होती है। कला में मानसिक व शारीरिक कौशलों का प्रयोग होता है। कला का अर्थ है – रचना करना। चित्रकला, संगीत, काव्य, नृत्य, स्थापत्यकला, रंगमंच आदि कला के विविध रूप हैं। कला के द्वारा मनुष्य अपने भावों की अभिव्यक्ति करता है। कला मानव, प्राणियों में अमृत भर देती हैं। फिर वह कला संगीत कला हो या चित्रकला। वह अभिव्यक्ति का कुशल साधन बनकर मनुष्य के हृदय पर सकारात्मक प्रभाव निर्माण करती है। कला के द्वारा मनुष्य अपनी संवेदनाएं व अभिरुचि को दिशा देने की अद्भुत क्षमता रखता है। कला मानवीय मन को सम्मोहित करती है।

कला की अभिव्यक्ति जितनी कुशल होती है। उतनी वह मानव मन पर अपनी छाप छोड़ने में सक्षम होती है। ताजमहल देखने के लिए प्रतिवर्ष लाखों लोग आते हैं। लोग चार मिनार की सैर करते हैं। ये सारी कला ही तो हैं जो अपने अभिव्यक्ति के सशक्त पहिए पर खड़ी हैं। अत: कहा जाता है : अभिव्यक्ति की कुशल शक्ति कला होती है। वह अभिव्यक्ति का सशक्त माध्यम होती है।

(ई) गद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1) : आकलन कृति

प्रश्न 1.
समझकर लिखिए।

1. यहाँ पर चित्रित होकर पड़ा है धरती का यथार्थ –
2. धरती के यथार्थ –
3. ये लोप होती जा रही हैं –
4. गद्यांश में इस अंग्रेजी कवि का नाम आया है –
5. कवि ब्लेक का कथन –

उत्तर:

1. जगह-जगह पर व सड़कों की पटरियों पर
2. भयानक गरीबी और अंतहीन दुखों का इतिहास
3. जिंदगी की खूबसूरती व जिंदगी की अच्छाई
4. कवि विलियम ब्लेक
5. सुंदर ईश्वर को एक गुलाब का फूल बनाने में पचास हजार बरस लगे थे।

प्रश्न 2.
गद्यांश के आधार पर वाक्य पूर्ण कीजिए।

1. शोभा सिंह गुरुओं के चित्र बनाते हैं क्योंकि
2. कला का तब तक कोई प्रभाव नहीं होता जब तक
3. चित्रकार जिंदगी की खूबसूरती एवं अच्छाई को चित्रित करना चाहता है क्योंकि

उत्तर:

1. शोभा सिंह गुरुओं के चित्र बनाते हैं क्योंकि उनके ‘स्वयं’ महान थे।
2. कला का तब तक कोई प्रभाव नहीं होता जब तक वह कला के लिए होती है।
3. चित्रकार जिंदगी की खूबसूरती एवं अच्छाई को चित्रित करना चाहता है क्योंकि वह दिनोंदिन लोप होती जा रही है।

कृति ई (3) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. शोभा सिंह ने कहा कलाकार का कर्म भी एक व्यक्तित्व बनना है तभी कला में उसका प्रभाव आ सकता है।
उत्तर:
शोभा सिंह ने कहा, “कलाकार का कर्म भी एक व्यक्तित्व बनना है, तभी कला में उसका प्रभाव आ सकता है।”

प्रश्न 2.
लिंग बदलिए।
i. कलाकार
i. गुरु
उत्तर:
i. कलावती
ii. गुरुआइन

प्रश्न 3.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढ़कर लिखिए।
उत्तर:
i. खूबसूरती : प्रत्यय : ई
ii. अच्छाई : प्रत्यय : ई

प्रश्न 4.
निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।
i. कल्पना
ii. इतिहास
उत्तर:
i. कल्पना + इक = काल्पनिक
ii. इतिहास + इक = ऐतिहासिक

प्रश्न 5.
विलोम शब्द लिखिए।

1. यर्थाथ × ………………..
2. खूबसूरत × ………………..
3. फूल × ………………..
4. महान × …………………

उत्तर:

1. कल्पित
2. बदसूरत
3. काँटा
4. साधारण

कृति ई (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘क्या जिंदगी की खूबसूरती व अच्छाई सचमुच लोप होती जा रही है ?’ विषय पर अपने विचार लिखिए।
उत्तर:
जिंदगी खूबसूरती व अच्छाई का नाम है। जिंदगी में जो कुछ प्राकृतिक है, वह सब ईश्वर निर्मित है। इंसान की जिंदगी में उसके कर्म बहुत ही मायने रखते हैं। वह जो कुछ करता है उसी के आधार पर उसकी जिंदगी भविष्य के रास्ते बनाती है। इंसान का अच्छा कर्म उसे अच्छाई की ओर ले जाता है। इंसान को जो यह अनमोल जीवन मिला है वह बहुत ही खूबसूरत है। इंसान का यह कर्तव्य है कि वह इस सुंदर जीवन को और खूबसूरत बनाए।

लता दीदी अपनी सुमधुर आवाज के लिए विश्व भर में पहचानी जाती हैं। सचिन क्रिकेट खेल जगत का भगवान बन गया है। अमिताभ बच्चन जी अपनी उत्कृष्ट अदाकारी के लिए देश-विदेश में प्रसिद्ध हैं। अत: मुझे ऐसा बिल्कुल नहीं लगता कि आज जिंदगी की खूबसूरती एवं अच्छाई लोप होती जा रही है। अपनी जिंदगी को खूबसूरत एवं अच्छा रखना प्रत्येक मनुष्य के हाथ में ही है।

(ङ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति छ (1): आकलन कृति

प्रश्न 1.
उचित विकल्प चुनकर रिक्त स्थानों पूर्ति किजिए।
i. क्या प्रसाद सिर्फ …….. होता है? (बूंदी, लड्डू, पेड़ा)
उत्तर:
i. बूंदी

प्रश्न 3.
समझकर लिखिए।
उत्तर:

कृति उ (3) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. अमौर
2. प्रसाद
3. दर्शक

उत्तर:

1. रईस
2. अनुग्रह
3. देखनेवाला

प्रश्न 2.
निम्नलिखित शब्द के लिए अनेकार्थी शब्द लिखिए।
i. प्रसाद
उत्तर:
i. कृपा, भगवान को चढ़ाई गई वस्तु, अनुग्रह

प्रश्न 3.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. कला का प्रदर्शन करने वाला –
उत्तरः
कलाकार

प्रश्न 4.
निम्नलिखित शब्दों के श्रुतिसमभिन्नार्थक शब्द लिखिए।
i. दर्शक
ii. अमल
उत्तर:
i. दशक
ii. कमल

कृति ङ (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘कलाकार की शक्ति उसके चिंतन में है।’ विषय पर अपने विचार लिखिए।
उत्तर:
कलाकार वह होता है जो अपनी अद्भुत कला से सभी को मंत्रमुग्ध कर देता है और सभी के हृदय पर छाप छोड़ देता है। फिर वह कलाकार चित्रकार हो या कवि। कलाकार के पास अद्भुत शक्तियाँ होती हैं। नित्य साधना, चिंतन व मनन के जरिए कलाकार को कलात्मक शक्तियों की प्राप्ति होती है। भारत के महान गायक मोहम्मद रफी साहब के स्वरों में जो जादू था, वह उन्हें एक दिन में नहीं प्राप्त हुई। उसके लिए उन्होंने बचपन से रियाज़ करना शुरू कर दिया था।

दिन के दस-दस घंटे तक वे संगीत का अभ्यास करते थे। अपनी कड़ी तपस्या के कारण ही वे महान गायक बने थे। चिंतन के बिना कलाकार की प्रतिभा खिल नहीं सकती। चिंतन-रूपी तपस्या के बाद ही कलाकार की प्रतिभा पर दिव्य फल लगना शुरू होता है। कवि भी कविता लिखने के पहले चिंतन करता है। महर्षि वाल्मीकी की जीवनी से कौन परिचित नहीं है? उन्होंने भी ‘रामायण’ लिखने से पहले कड़ी साधना एवं चिंतन किया था। तब जाकर वे ‘रामायण’ जैसे महाकाव्य की रचना कर सकें। अत: कलाकार के लिए चितन करना बेहद जरूरी होता है।

चार हाथ चाँदना Summary in Hindi

लेखक-परिचय :

जीवन-परिचय : अमृता प्रीतम जी का जन्म सन 1919 में पंजाब के गुजरांवाला में हुआ। ये पंजाबी एवं हिंदी भाषा की प्रतिभाशाली साहित्यकार थीं। इन्होंने अपनी प्रतिभा से साहित्य के सभी विधाओं जैसे उपन्यास, कविता, कहानी, संस्मरण, आत्मकथा आदि को समृद्ध किया है। इन्हें ज्ञानपीठ, साहित्य अकादमी एवं पद्म विभूषण आदि पुरस्कारों से सम्मानित किया जा चुका है। इन्होंने अपने साहित्य के माध्यम से मानवीय संवेदनाओं को झझकोरने का प्रयास किया है।
प्रमुख कृतियाँ : “पिंजर’, ‘कोरे कागज’, ‘सागर और सीपियाँ’ (उपन्यास), ‘रसीदी टिकट’ (आत्मकथा), ‘कच्चा आँगन’, ‘एक थी सारा’ (संस्मरण), ‘हीरे दी कनी’, ‘इक शहर दी मौत’, ‘तीसरी औरत’ (कहानी संग्रह) आदि हिंदी में अनूदित।

गद्य-परिचय :

साक्षात्कार : दो या दो से अधिक व्यक्तियों के बीच किसी विशेष उद्देश्य से प्रत्यक्ष बातचीत एवं विचारों का आदान-प्रदान साक्षात्कार कहलाता है। इसमें एक व्यक्ति दूसरे व्यक्ति से प्रश्न पूछता है और दूसरा व्यक्ति प्रश्नों के उत्तर देता है।
प्रस्तावना : ‘चार हाथ चाँदना’ इस साक्षात्कार में लेखिका अमृता प्रीतम जी ने पंजाब के प्रसिद्ध चित्रकार श्री शोभा सिंह जी से उनके अनुभव एवं चित्रकला विषय से संबंधित प्रश्न पूछे हैं। श्री शोभा सिंह ने भी उनके प्रश्न के उत्तर विस्तारपूर्वक दिए हैं।

सारांश :

‘चार हाथ चाँदना’ यह साक्षात्कार है। पंजाब की सुप्रसिद्ध साहित्यकार अमृता प्रीतम जी ने चित्रकार श्री शोभा सिंह जी का साक्षात्कार लिया है। अमृता जी ने श्री शोभा सिंह से कलाकार के कर्म की व्याख्या, चित्रकला चुनने का कारण, माँ का महत्त्व, धरती का भयानक यथार्थ व कलाकार की चिंतन शक्ति आदि मुद्दों पर प्रश्न पूछे हैं। श्री शोभा सिंह ने भी सभी प्रश्नों के विस्तार के साथ उत्तर दिए हैं। उनके अनुसार ‘सत्यम्, शिवम्, सुंदरम्’ के क्रम में बदलाव की जरूरत है। वह ‘सुंदरम्, शिवम्, सत्यम्’ इस प्रकार होना चाहिए। शोभा जी को चित्रकारी का शौक बचपन से था। वे जब आठ साल के थे तब उन्होंने खयाली घर की दीवारें सजाने के लिए तस्वीरें बनाई थीं।

वे औरत को माँ के तौर पर महत्त्व देते हैं। वे कहते हैं कि माँ के पास रचनात्मक शक्ति होती है। उसके पास साधना, दैवी शक्ति, कला एवं ज्ञान का भंडार होता है। अत: वह ‘जीनियस’ होता है। उनके अनुसार सच्चे कलाकार का कर्म एक छोटी सी जलती हुई मोमबत्ती की भाँति होता है जो अपने आस-पास की धरती को प्रकाशित करता है। श्री शोभा सिंह धरती के यथार्थ को चित्रों में स्थान नहीं देना चाहते।

वे जिंदगी की खूबसूरती एवं अच्छाई को कागज पर चित्रित करते हैं क्योंकि वह दिनोंदिन लोप होती जा रही है। उनका मानना है कि कलाकार का कर्म एक व्यक्तित्व बनना है, तब कला में उसका प्रभाव आ सकता है। कलाकार की शक्ति उसके चिंतन में होती है और कलाकार दर्शक को एक अच्छी सोच व सूझ दे सकने का कार्य करता है।

शब्दार्थ :

1. चाँदना – प्रकाश
2. परछत्ती – घास-फूस का बना छप्पर
3. रूहानी – आत्मिक
4. तकनीकी – प्राविधिक
5. अवस्था – हालत
6. गहराई – गहनता
7. दर्शक – देखनेवाला
8. यर्थाथ – सत्य
9. अंतहीन – कभी न खत्म होनेवाला

मुहावरे :

भुलावा हो जाना – भ्रम हो जाना।

Hindi Lokvani 10th Std Textbook Solutions दूसरी इकाई

• मातृभूमि Question Answer
• कलाकार Question Answer
• मुकदमा Question Answer
• दो गजलें Question Answer
• चार हाथ चाँदना (पठनार्थ) Question Answer
• अति सोहत स्याम जू Question Answer
• प्रकृति संवाद Question Answer
• ऐसा वसंत कब आएगा? Question Answer

Std 10 Hindi Chapter 9 Ridh Ki Haddi Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 9 रीढ़ की हड्डी Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 9 रीढ़ की हड्डी Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 9 रीढ़ की हड्डी Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए।

सूचना के अनयुार कृहत्‍ँ कीहजए:-

प्रश्न 1.
संजाल पूण् कीहजए:

उत्तर:

प्रश्न 2.
कृहत पूण् कीहजए:

उत्तर:

प्रश्न 3.
गोपाल प्रसाद की दृष्टि में बहू ऐसी हो:

उत्तर:

प्रश्न 4.
कारण लिखिए :
a. बाप-बेटे चौंक उठे –
b. उमा को चश्मा लगा –
c. रामस्वरूप ने हारमोनियम उठाकर लाने को कहा –
d. उमा को गुस्सा आया –
उत्तर:
a. उन्होंने उमा के चेहरे पर सुनहरी रिमवाला चश्मा देखा।
b. पिछले महीने उमा की आँखें दुखने लगी थीं।
c. रामस्वरूप, गोपाल प्रसाद और शंकर को दिखाना चाहते थे कि उनकी लड़की हारमोनियम बजाना जानती है।
d. गोपाल प्रसाद उमा के चश्मे, उसके गाने-बजाने, पेंटिंग, सिलाई और उसकी पढ़ाई आदि के बारे में एक के बाद एक प्रश्न करते जा रहे थे।

प्रश्न 5.
सूचनानुसार लिखिए :
१. कृदंत बनाइए :
पढ़ना [ ]
समझना [ ]
सीना [ ]
चाहना [ ]
उत्तर:
(i) पढ़ना – पढ़ाकू
(ii) समझना – समझदार
(iii) सीना – सीनेवाला
(iv) चाहना – चाहत।

२. शब्दयुग्म पूर्ण कीजिए :
a. पढ़े – ……….,
b. सभा – ………
c. पेंटिंग – ……….,
d. सीधा – ……… .
उत्तर:
a. पढ़े – लिखे
b. सभा – सोसायटी
c. पेंटिंग – वेंटिंग
d. सीधा – सादा।

अभिव्यक्ति

सुनी-पढ़ी अंधविश्वास की किसी घटना में निहित आधारहीनता और अवैज्ञानिकता का विश्लेषण करके लिखिए।
उत्तर:
मेरी दादी बड़ी अंधविश्वासी हैं। उनका मानना था कि कोई घर से बाहर जा रहा हो और किसी को छींक आ जाए तो जाने वाले का काम पूरा नहीं होगा। किसी के बाहर जाते समय कोई छींक दे तो दादी बाहर जाने वाले को रोक देती थीं। घर के सभी लोग उनकी इस आदत से परेशान थे। एक बार मेरे भाई को इंटरव्यू के लिए बाहर। जाना था। यह इंटरव्यू हमारे जिले के सर्वश्रेष्ठ स्कूल में वाइस प्रिंसिपल के पद के लिए था। भाई काफी दिनों से इसके लिए तैयारी और प्रतीक्षा कर रहे थे। मुझे बहुत खाँसी-जुकाम हो रहा था। जैसे ही भाई ने बैग उठाकर चलना चाहा; मुझे जोर-जोर से छींकें आने लगी।

दादी ने भाई को जाने नहीं दिया और उनका वह महत्त्वपूर्ण इंटरव्यू छूट गया। घर के सभी लोग इस घटना से बहुत दुखी हुए। मैंने दादी को समझाया कि छींक एक स्वाभाविक क्रिया है। जुकाम होने पर नाक में एक प्रकार की सरसराहट होती है। नाक में मौजूद नर्व सेल इसका संकेत मस्तिष्क को भेजते हैं। मस्तिष्क इसकी प्रतिक्रिया में चेहरे, गले और छाती की मांसपेशियों को सक्रिय कर देता है, जिसके फलस्वरूप ये सब मिलकर तेज हवा निकालकर बाहरी कणों को बाहर फेंक देते हैं। यही क्रिया 8 छींक है। दादी के मन में भी भाई के इंटरव्यू को लेकर अफसोस था।। उन्होंने मेरी बात समझी और धीरे-धीरे अपनी इस आदत को छोड़ दिया।

भाषा बिंदु

प्रश्न 1.
निम्नलिखित वाक्यों में आए हए अव्ययों को रेखांकित कीजिए और उनके भेद दिए गए स्थान पर लिखिए :

वाक्य	अव्यय भेद
गाय को घर के सामने खूटे से बाँधा।	_____________________
वह उठा और घर चला गया।	_____________________
अरे ! गऊशाला यहाँ से दो किलोमीटर दूर है।	_____________________
वह भारी कदमों से आगे बढ़ने लगा।	_____________________
उन्होंने मुझे धीरे-धीरे हिलाना शुरू किया।	_____________________
मुझे लगा कि आज फिर कोई दुर्घटना होगी।	_____________________
वाह-वाह ! खूब सोचा आपने !	_____________________
चाची, माँ के पास चली गई।	_____________________

उत्तर:
(1) गाय को घर के सामने – के सामने – संबंधबोधक खूटे से बाँधा। – अव्यय
(2) वह उठा और घर चला – और – समुच्चयबोधक – अव्यय
(3) अरे! गऊशाला यहाँ से दो – अरे: – विस्मयादिबोधक किलोमीटर दूर है। – अव्यय
(4) वह भारी कदमों से आगे – आगे – क्रियाविशेषण बढ़ने लगा। – अव्यय
(5) उन्होंने मुझे धीरे-धीरे – धीरे-धीरे – क्रियाविशेषण हिलाना शुरू किया। – अव्यय
(6) मुझे लगा कि आज फिर – आज – क्रियाविशेषण कोई दुर्घटना होगी। – अव्यय
(7) वाह-वाह! खूब सोचा – वाह-वाह – विस्मयादिबोधक आपने! – अव्यय
(8) चाची, माँ के पास चली – के पास – संबंधबोधक गई। – अव्यय

प्रश्न 2.
पाठ में प्रयुक्त अव्यय छाँटिए और उनसे वाक्य बनाकर लिखिए :

क्रियाविशेषण अव्यय
1. ———- 2. ———- वाक्य = _______________
उत्तर:
(1) धीरे-धीरे। वाक्य: मुन्ना धीरे-धीरे चलने लगा।
(2) ज्यादा। वाक्य: बीमारी से अभी उठे हो, ज्यादा मत खाओ।

संबंधसूचक अव्यय
1. ———- 2. ———- वाक्य = _______________
उत्तर:
(1) के पास। वाक्य: हमारे स्कूल के पास नदी बहती है।
(2) के साथ। वाक्य: टॉमी गाड़ी के साथ दौड़ रहा है।

समुच्चयबोधक अव्यय
1. ———- 2. ———- वाक्य = _______________
उत्तर:
(1) कि। वाक्य: गांधी जी ने कहा था कि गाय करुणा की कविता है।
(2) और। वाक्य: दुर्योधन और कर्ण की मित्रता अनमोल थी।

विस्मयादिबोधक अव्यय
1. ———- 2. ———- वाक्य = _______________
उत्तर:
(1) ओह! वाक्य: ओह! कितनी गरमी है।
(2) हैं हैं हैं! वाक्य: हैं हैं हैं ! आइए, विराजिए।

प्रश्न 3.
नीचे आकृति में दिए हुए अव्ययों के भेद पहचानकर उनका अर्थपूर्ण स्वतंत्र वाक्यों में प्रयोग कीजिए :

उत्तर:
(1) हाय! – विस्मयादिबोधक अव्यय
वाक्य: हाय! कितनी भयानक रेल-दुर्घटना थी।

(2) काश! – विस्मयादिबोधक अव्यय
वाक्य: काश! समय पर दवा मिल जाती, तो रोगी बच जाता।

(3) प्रायः – क्रियाविशेषण अव्यय
वाक्य: प्रयाग प्रायः स्कूल में अनुपस्थित रहता है।

(4) बाद – क्रियाविशेषण अव्यय
वाक्य: स्कूल से आने के बाद थोड़ा आराम करके पढ़ने बैठो।

(5) और – समुच्चयबोधक अव्यय
वाक्य: शुभम और हर्षित भाई हैं।

(6) बल्कि – समुच्चयबोधक अव्यय
वाक्य: आपको निबंध केवल पढ़ना ही नहीं है, बल्कि उसकी समीक्षा भी करनी है।

(7) के पास – संबंधबोधक अव्यय
वाक्य: हमारे घर के पास एक मंदिर है।

(8) यदि… तो – समुच्चयबोधक अव्यय
वाक्य: यदि इसी तरह समय बरबाद करते रहे, तो पास नहीं हो पाओगे।

(9) इसलिए – समुच्चयबोधक अव्यय
वाक्य: मेहमान आने वाले हैं इसलिए जल्दी से खाना बना लो।

(10) वाह! – विस्मयादिबोधक अव्यय
वाक्य: वाह! कितना सुंदर दृश्य है।

(11) की तरफ – संबंधबोधक अव्यय
वाक्य: नदी की तरफ जाओ।

(12) के अलावा – संबंधबोधक अव्यय
वाक्य: यहाँ मेरे और भगवान के अलावा कोई नहीं है।

(13) कारण – क्रियाविशेषण अव्यय
वाक्य: महिम, किस कारण तुम दस दिन तक स्कूल नहीं आए?

(14) के लिए – संबंधबोधक अव्यय
वाक्य: अंशु ने वारिजा के लिए फ्रॉक खरीदा।

(15) अच्छा – विस्मयादिबोधक अव्यय
वाक्य: अच्छा! स्तुति भी नृत्य में भाग लेगी।

(16) क्योंकि – समुच्चयबोधक अव्यय
वाक्य: अनुज कल स्कूल नहीं आया था, क्योंकि बीमार था।

(17) नहीं… तो – समुच्चयबोधक अव्यय
वाक्य: खेल-कूद छोड़कर पढ़ाई पर ध्यान दो, नहीं तो फेल हो जाओगे।

उपयोजित लेखन

अपने परिसर में विद्यार्थियों के लिए योगसाधना शिविर का आयोजन करने हेतु आयोजक के नाते विज्ञापन तैयार कीजिए।
उत्तर:

Hindi Lokbharti 10th Textbook Solutions Chapter 9 रीढ़ की हड्डी Additional Important Questions and Answers

गद्यांश क्र. 1

प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
कारण लिखिए:
(i) उमा मेहमानों के सामने जरा करीने से आए –
उत्तर:
(i) गोपाल प्रसाद खूबसूरत बहू चाहते थे।

प्रश्न 2.
ये वाक्य किसने, किससे कहे हैं? लिखिए:
(i) अबे! धीरे-धीरे चल।
(ii) बिछा दें साहब?
(iii) लेकिन वह तुम्हारी लाड़ली बेटी उमा तो मुँह फुलाए पड़ी है।
(iv) अरे हाँ, देखो, उमा से कह देना कि जरा करीने से आए।
उत्तर:
(i) अबे! धीरे-धीरे चल। – रामस्वरूप ने रतन से कहा है।
(ii) बिछा दें साहब?- रतन ने रामस्वरूप से कहा है।
(iii) लेकिन वह तुम्हारी लाड़ली बेटी उमा तो मुँह फुलाए पड़ी है। – प्रेमा ने रामस्वरूप से कहा है।
(iv) अरे हाँ, देखो, उमा से कह देना कि जरा करीने से आए। – रामस्वरूप ने प्रेमा से कहा है।

प्रश्न 3.
दो ऐसे प्रश्न बनाइए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) तख्त
(ii) उमा।
उत्तर:
(i) कमरे में रतन क्या बिछाता है?
(ii) मुँह फुलाए कौन पड़ी है?:

कृति 3: (शब्द संपदा)

प्रश्न 1.
म्नलिखित शब्दों का वचन बदलकर लिखिए:
(i) बेटी
(ii) तकलीफ
(iii) रास्ता
(iv) छुट्टी।
उत्तर:
(i) बेटी – बेटियाँ
(ii) तकलीफ – तकलीफें
(iii) रास्ता – रास्ते
(iv) छुट्टी – छुट्टियाँ।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) पसीना
(ii) अक्ल
(iii) मजबूरी
(iv) सितार।
उत्तर:
(i) पसीना – पुल्लिंग
(ii) अक्ल – स्त्रीलिंग
(iii) मजबूरी – स्त्रीलिंग
(iv) सितार – पुल्लिंग।

प्रश्न 3.
गद्यांश में प्रयुक्त शब्द-युग्म पूर्ण कीजिए।
(i) ठीक ………………………………
(ii) धीरे ………………………………
उत्तर:
(i) ठीक-ठाक
(ii) धीरे-धीरे।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘रामस्वरूप अपनी बेटी की उच्च शिक्षा की बात छिपाते हैं,: उसे अपनी मजबूरी बताते हैं’ इस विषय में अपने विचार लिखिए।
उत्तर:
रामस्वरूप एक अच्छे पिता हैं। उमा उनकी इकलौती पुत्री है। वे स्त्री शिक्षा के पक्षधर हैं। इसलिए उमा को बी. ए. तक पढ़ाते हैं। वे उमा का विवाह एक शिक्षित परिवार के सुशिक्षित युवक से करना चाहते हैं। यह नाटक जिस दौर में लिखा गया, उस समय सभी लोग स्त्री शिक्षा को महत्त्व नहीं देते थे, आवश्यक नहीं समझते थे। लोगों की नजरों में बहू की उच्च शिक्षा घरेलू जीवन में व्यवधान थी। परिणामस्वरूप जहाँ कहीं भी वे विवाह-संबंध के लिए बात करते, बेटी की उच्च शिक्षा बाधा बन जाती। कहीं भी विवाह निश्चित न हो पाने के कारण रामस्वरूप परेशान हो जाते हैं और मजबूर होकर उमा के बी. ए. तक पढ़े होने की बात छिपाने का रास्ता चुनते हैं। स्वयं प्रगतिशील विचारों का होते हुए भी विवाह योग्य लड़की का पिता होने के कारण रामस्वरूप जी को विवशतावश रूढ़िग्रस्त लोगों के सामने झुकना पड़ता है। यही उनकी मजबूरी है।

गद्यांश क्र.2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) अच्छा तो साहब, फिर ……………………….. की बातचीत हो जाए। (काम/शादी/बिजनेस)
(ii) जरा ……………………….. तो कर लीजिए। (नाश्ता/आराम/भोजन)
(iii) ब्याह तय करने आए हो, ……………………….. सीधी करके बैठो। (गरदन/कमर/टाँगें)
(iv) वाकई आजकल ……………………….. का सवाल भी बेढब हो गया है। (खूबसूरती/महँगाई/टैक्स)
उत्तर:
(i) अच्छा तो साहब, फिर बिजनेस की बातचीत हो जाए।
(ii) जरा नाश्ता तो कर लीजिए।
(iii) ब्याह तय करने आए हो, कमर सीधी करके बैठो।
(iv) वाकई आजकल खूबसूरती का सवाल भी बेढब हो गया है।

कृति 2: (आकलन)

प्रश्न 1.
गलत वाक्यों को सही करके फिर से लिखिए:
(i) यह तो मेरी बड़ी तकदीर है कि आप मेरे यहाँ ठहरेंगे।
(ii) सुना है, सरकार अब ज्यादा जमीन खरीदने वालों पर टैक्स लगाएगी।
उत्तर:
(i) यह तो मेरी बड़ी तकदीर है कि आप मेरे यहाँ तशरीफ लाए।
(ii) सुना है, सरकार अब ज्यादा चीनी लेने वालों पर टैक्स लगाएगी।

प्रश्न 2.
घटना के अनुसार वाक्यों का उचित क्रम लगाकर लिखिए:
(i) शादी तय करने में खूबसूरती का हिस्सा कितना होना चाहिए?
(ii) ठाकुर जी के चरणों में रख दिया है।
(iii) तुम्हारे दोस्त ठीक कहते हैं कि शंकर की बैकबोन-
(iv) आपको विलायती चाय पसंद है या हिंदुस्तानी?
उत्तर:
(i) तुम्हारे दोस्त ठीक कहते हैं कि शंकर की बैकबोन
(ii) आपको विलायती चाय पसंद है या हिंदुस्तानी?
(iii) शादी तय करने में खूबसूरती का हिस्सा कितना होना चाहिए?
(iv) ठाकुर जी के चरणों में रख दिया है।

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) दोस्त
(ii) आमदनी
(iii) मुश्किल
(iv) खूबसूरती।
उत्तर:
(i) दोस्त x दुश्मन
(ii) आमदनी x खर्च
(iii) मुश्किल x आसान
(iv) खूबसूरती x बदसूरती।

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) नाश्ता
(ii) खयाल
(iii) ब्याह
(iv) जरूरी।
उत्तर:
(i) नाश्ता = जलपान
(ii) खयाल = विचार
(iii) ब्याह = शादी
(iv) जरूरी = आवश्यक।

प्रश्न 3.
गद्यांश में प्रयुक्त उर्दू शब्द ढूँढकर लिखिए।
(i) ……………………………
(ii) ……………………………
(iii) ……………………………
(iv) ……………………………
उत्तर:
(i) तकल्लुफ
(ii) तकदीर
(iii) तशरीफ
(iv) खूबसूरती।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
गोपाल प्रसाद विवाह को बिजनेस मानते हैं इस विषय में अपने विचार लिखिए।
उत्तर:
गोपाल प्रसाद विवाह को एक बिजनेस मानते हैं। जिस प्रकार एक व्यापारी पहले अपने लाभ-हानि का विचार करता है, फिर व्यापार करता है। उसी प्रकार गोपाल प्रसाद अपने डॉक्टर पुत्र का विवाह एक संपन्न परिवार में करना चाहते हैं। हिंदू समाज में विवाह एक ऐसा पवित्र बंधन माना जाता है, जो दो परिवारों को सदा के लिए एक कर देता है। दोनों परिवार एक-दूसरे के सुख-दुख में साथी होते हैं। परंतु गोपाल प्रसाद के लिए विवाह दो परिवारों का मिलन न होकर एक प्रकार का बिजनेस है। वे चाहते हैं कि एक अच्छी हैसियत वाले परिवार की कम पढ़ी-लिखी लड़की से बेटे का विवाह कराया जाए, ताकि बढ़िया-सा दहेज मिले और बहू बिना किसी नाज-नखरे के घर के कामों में लगी रहे।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
उमा की विशेषताएँ लिखिए।

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
वाक्य पूर्ण कीजिए:
(i) जी हाँ सितार भी और बाजा भी। सुनाओ तो उमा ………………….
(ii) सिलाई तो सारे घर की इसी के जिम्मे रहती है, ………………….
उत्तर:
(i) जी हाँ सितार भी और बाजा भी। सुनाओ तो उमा एकाध गीत. सितार के साथ।
(ii) सिलाई तो सारे घर की इसी के जिम्मे रहती है, यहाँ तक कि मेरी कमीजें भी।

प्रश्न 2.
विधानों के सामने सत्य/असत्य लिखिए:
(i) पढ़ाई-वढ़ाई की वजह से तो नहीं है कुछ।
(ii) आपकी लड़की सितार अच्छा बजाती है।
(iii) तो तुमने पेंटिंग-वेंटिंग भी सीखी है?
(iv) हाँ बेटी, तुमने कुछ इनाम-बिनाम भी जीते थे।
उत्तर:
(i) असत्य
(ii) असत्य
(iii) सत्य
(iv) सत्य।

प्रश्न 3.
जोड़ियाँ मिलाइए:
‘अ’ – ‘आ’
(i) सकपकाना – मीरा
(ii) भजन – तख्त
(iii) तस्वीर चश्मा
(iv) बाजा – कुत्तेवाली
उत्तर:
(i) सकपकाना – चश्मा
(ii) भजन – मीरा
(ii) तस्वीर -कुत्तेवाली
(iv) बाजा – तख्त

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का वचन बदलकर लिखिए:
(i) दीवार
(ii) महीना
(iii) कमीज
(iv) आँखें।
उत्तर:
(i) दीवार – दीवारें
(ii) महीना – महीने
(iii) कमीज – कमीजें
(iv) आँखें – आँख।

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) चश्मा
(ii) सिलाई
(iii) तख्त
(iv) दीवार।
उत्तर:
(i) चश्मा – पुल्लिंग
(ii) सिलाई – स्त्रीलिंग
(iii) तख्त – पुल्लिंग
(iv) दीवार – स्त्रीलिंग।

प्रश्न 3.
गद्यांश में प्रयुक्त शब्द-युग्म पूर्ण कीजिए:
(i) गाना ……………………..
(ii) पढ़ाई ……………………..
(iii) इनाम ……………………..
उत्तर:
(i) गाना-बजाना
(ii) पढ़ाई-वढ़ाई
(iii) इनाम-बिनाम।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘गोपाल प्रसाद बहू में गाना-बजाना, सिलाई, पेंटिंग आदि गुण चाहते हैं पर पढ़ाई नहीं, क्या यह उचित है’ इस विषय में अपने विचार लिखिए।
उत्तर:
गोपाल प्रसाद एक वकील हैं। उनका पुत्र डॉक्टर है। वे अपने पुत्र के लिए लड़की देखने आए हैं। वे अपनी पत्रवधू के रूप में एक मैट्रिक पास लड़की चाहते हैं। डॉक्टर पुत्र और मैट्रिक पास पुत्रवधू। कैसा विरोधाभास लगता है। पति और पत्नी गृहस्थी रूपी गाड़ी के दो पहियों की तरह होते हैं। यदि दोनों पहिये समान नहीं होंगे, तो गाड़ी सुचारू रूप से कैसे चलेगी। गोपाल प्रसाद चाहते हैं कि भावी पुत्रवधू सुंदर हो। वह बाजा बजाना जानती हो, उसे अच्छी तरह गाना आता हो। वह न केवल सिलाई-पेंटिंग करना जानती हो, बल्कि उसमें प्रवीण भी हो। घर के सारे काम करती रहे। उसके गुणों की चर्चा करके परिवार के लोग वाहवाही लूटते रहें। गोपाल प्रसाद की सोच किसी भी तरह उचित नहीं कही जा सकती।

गद्यांश क्र. 4
प्रश्न. निम्नलिखित पठित मद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i) दुकानदार इनसे कुछ नहीं पूछता
(ii) जो आप इतनी देर से यह कर रहे हैं –
(iii) क्या हम लड़कियों की यह नहीं होती –
(iv) बाबू रामस्वरूप आपने मेरे साथ यह किया –
उत्तर:
(i) दुकानदार इनसे कुछ नहीं पूछता – कुर्सी-मेज से |
(ii) जो आप इतनी देर से यह कर रहे हैं – नाप-तौल
(ii) क्या हम लड़कियों की यह नहीं होती – बेइज्जती
(iv) बाबू रामस्वरूप आपने मेरे साथ यह किया – दगा

प्रश्न 2.
नीचे दिए गए शब्दों के आधार पर प्रश्न बनाइए:
(i) शंकर
(i) उमा।
उत्तर:
(i) नौकरानी के पैरों में पड़कर मुंह छुपाकर कौन भागा था?
(ii) कौन बी.ए. पास है?

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
कारण लिखिए:
(i) शंकर नौकरानी के पैरों में पड़कर मुंह छिपाकर भागा।
(ii) गोपाल प्रसाद का रामस्वरूप पर गुस्सा होना।
(iii) उमा का तेज आवाज में बोलना।
उत्तर:
(i) शंकर लड़कियों के होस्टल में ताक-झाँक करता पकड़ा गया था।
(ii) क्योंकि रामस्वरूप ने उनके साथ दगा किया है।
(iii) क्योंकि नाप-तोल करके उमा की बेइज्जती की जा रही थी।

कृति 3: (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त अंग्रेजी शब्द ढूँढकर लिखिए।
(i) ……………………..
(ii) ……………………..
(iii) ……………………..
(iv) ……………………..
उत्तर:
(i) पेंटिंग
(ii) बैकबोन
(iii) होस्टल
(iv) मैट्रिक।

प्रश्न 2.
गद्यांश में प्रयुक्त प्रत्यययुक्त शब्दों से मूल शब्द और प्रत्यय अलग करके लिखिए।
(i) ……………………..
(ii) ……………………..
(iii) ……………………..
(iv) ……………………..
उत्तर:
(i) दुकानदार = दुकान + दार
(ii) कायरता = कायर + ता
(iii) नौकरानी = नौकर + आनी
(iv) बेइज्जती = बेइज्जत + ई।

प्रश्न 3.
गद्यांश में आई हुई दो समानार्थी शब्दों की जोड़ियाँ ढूँढ़कर लिखिए:
(i) ……………………………
(ii) ……………………………
उत्तर:
(i) बेटा = पुत्र
(ii) इज्जत = मान।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न 1.
उमा को गोपाल प्रसाद की किन बातों पर गुस्सा आया? क्या वह उचित था? इस विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
गोपाल प्रसाद अपने डॉक्टर लड़के के विवाह के लिए उमा को देखने आते हैं। वे स्वयं वकील हैं परंतु उन्हें पुत्रवधू केवल मैट्रिक पास चाहिए। गोपाल प्रसाद का मानना है कि स्त्रियों का काम केवल घर सँभालना होता है। वे कभी उमा से गाने-बजाने की बात कर रहे थे, कभी यह जानना चाह रहे थे कि उसे सिलाई-पेंटिंग आदि करना आता है या नहीं, कुछ इनाम वगैरह भी जीते हैं या नहीं। उमा को इन सब बातों पर तो गुस्सा आ ही रहा था। परंतु उसे इससे भी अधिक गुस्सा उनके पुत्र को देखकर आ रहा था। वह जानती थी कि शंकर एक चरित्रहीन युवक है।

वह लड़कियों के होस्टल के पास ताक-झाँक करते हुए पकड़ा गया था और उसे बेइज्जत करके वहाँ से निकाला गया था। शंकर के जीवन का कोई आदर्श नहीं था। ऐसे विचारहीन, चरित्रहीन व्यक्ति का उमा के जीवन में कोई स्थान नहीं था। उमा कोई भेड़-बकरी या निर्जीव वस्तु नहीं है कि लोग देख-भालकर अपनी इच्छानुसार खरीद सकें। विवाह में उसे भी पसंद-नापसंद का अधिकार मिलना चाहिए। उसे उचित सम्मान मिलना चाहिए।

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:

अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) बापू की लिखावट अच्छी नहीं थी। –
(ii) कुछ बिजनेस की बातचीत हो जाए।
(iii) मैंने आपसे पहले ही कहा था।
उत्तर:
(i) अच्छी – गुणवाचक विशेषण।
(ii) बातचीत – भाववाचक संज्ञा।
(iii) मैंने – पुरुषवाचक सर्वनाम।

2. अव्यय:

निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) शायद
(ii) या
(iii) ऊपर।
उत्तर:
(i) शायद आज वर्षा होगी।
(ii) बच्चे खेलने या घूमने गए होंगे।
(iii) छत के ऊपर बंदर कूद रहे हैं।

3. संधि:

कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
…………………	मनः + हर	…………………
अथवा
…………………	वागीश	…………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
मनोहर	मनः + हर	विसर्ग संधि
अथवा
वागीश	वागीश	व्यंजन संधि

4. सहायक क्रिया:

निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूलरूप लिखिए:
(i) आपकी लड़की अच्छा गाती है।
(ii) मैं आपको बताना ही भूल गया।
(iii) अब तख्त को उधर मोड़ दें।:
उत्तर:
सहायक क्रिया – मूल रूप
(i) है – होना
(ii) गया – जादेा
(iii) दें – देना

5. प्रेरणार्थक क्रिया:

निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) चढ़ना
(ii) पढ़ना
(iii) उड़ना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वि.प्रेरणार्थक रूप
(i) चढ़ना – चढ़ाना – चढ़वाना
(ii) पढ़ना – पढ़ाना – पढ़वाना
(ii) उड़ना – उड़ाना – उड़वाना

6. मुहावरे:

(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) तिलिस्म टूटना
(ii) बस चलना
(iii) खेल करना।
उत्तर:
(i) तिलिस्म टूटना।
अर्थ: वास्तविकता सामने आना। वाक्य: ढोंगी साधु की सच्चाई प्रकट होते ही उसका तिलिस्म टूट गया।

(ii) बस चलना।
अर्थ: काबू में होना, सामर्थ्य होना।
वाक्य: बेटे का बस चले तो वह अपनी माँ को सारे तीर्थ करा दे।

(iii) खेल करना।
अर्थ: काम को ठीक से न करना, काम को बिगाड़ना।
वाक्य: सड़क बनाने का काम कर रहे मजदूरों में से कुछ तो खेल ही कर रहे थे।

(2) अधोरेखांकित वाक्यांश के लिए उचित मुहावरे का चयन कर वाक्य फिर से लिखिए:
(गिनती में न होना, अंजाम देना, कानों में गूंजना)
(i) काम कैसा भी हो, उसे पूरा करना कर्मचारी का कर्तव्य है।
(ii) माता जी के कहे वचन आज भी राजू को सुनाई देते हैं।
उत्तर:
(i) काम कैसा भी हो, उसे अंजाम देना कर्मचारी का कर्तव्य है।
(ii) माता जी के कहे वचन आज भी राजू के कानों में गूंजते हैं।

7. कारक:

निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उनका भेद लिखिए:
(i) नहीं साहब वह तो मैंने अर्ज किया न।
(ii) आपके लाड़ले बेटे के रीढ़ की हड्डी भी है या नहीं।
(iii) अब तख्त को उधर मोड़ दे।
उत्तर:
(i) मैंने – कर्ता कारक।
(ii) आपके – संबंध कारक।
(iii) तख्त को – कर्म कारक।

8. विरामचिहन:

निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) अरे प्रेमा वे आ भी गए तुम उमा को समझा देना थोड़ा सा गा देगी मेहमानों से हैं हैं हैं आइए आइए
(ii) ठीक लेकिन हाँ बेटी तुमने कुछ इनाम बिनाम भी जीते थे
(iii) बिजनेस समझकर ओह अच्छा अच्छा लेकिन जरा नाश्ता तो कर लीजिए
उत्तर:
(i) अरे प्रेमा, वे आ भी गए। … तुम उमा को समझा देना, थोड़ा-सा गा देगी। (मेहमानों से) हैं-ह-हैं। आइए, आइए!
(ii) ठीक।… लेकिन, हाँ बेटी, तुमने कुछ इनाम-बिनाम भी जीते थे?
(iii) “बिजनेस’ ? – (समझकर) ओह !…अच्छा, अच्छा। लेकिन जरा नाश्ता तो कर लीजिए।

9. काल परिवर्तन:

निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) ठीक समय पर गो. प्रसाद और शंकर आते हैं। (सामान्य भूतकाल)
(ii) मेरी चाय में चीनी ज्यादा डालते हैं। (सामान्य भविष्यकाल)
(iii) आपके पुत्र मुंह छिपाकर भागते हैं। (पूर्ण भूतकाल)
उत्तर:
(i) ठीक समय पर गो. प्रसाद और शंकर आए।
(ii) मेरी चाय में चीनी ज्यादा डालिएगा।
(iii) आपके पुत्र मुँह छिपाकर भागे थे।:

10. वाक्य भेद:

(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानिए:
(i) मैंने कोई पाप नहीं किया और न ही कोई चोरी की है।
(ii) उमा से कह देना कि जरा करीने से आए।
उत्तर:
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) उमा ने सितार पर भजन गाया। (निषेधवाचक)
(ii) गोपाल प्रसाद शंकर का विवाह उमा से करेंगे। (प्रश्नवाचक)
उत्तर:
(i) उमा ने सितार पर भजन नहीं गाया।
(ii) क्या गोपाल प्रसाद शंकर का विवाह उमा से करेंगे?

11. वाक्य शुद्धिकरण:

निम्नलिखित वाक्यों को शुद्ध करके फिर से लिखिए:
(i) वे असली भारत के सपूत थे।
(ii) सोमनाथ को आबादी इतिहास में प्रसिद्ध है।
(iii) जिंदगी हमारी अब नहीं बचेगी।
उत्तर:
(i) वे भारत के असली सपूत थे।
(ii) सोमनाथ की समृद्धि इतिहास में प्रसिद्ध है।
(iii) अब हमारी जिंदगी नहीं बचेगी।

उपक्रम/कृति/परियोजना

पठनीय
उत्तर:

• कॉलेज – महाविद्यालय
• सोसायटी – समाज
• बी. एस्सी – विज्ञान स्नातक
• कोर्स – पाठ्यक्रम
• वीक एंड – सप्ताहांत
• मार्जिन – गुंजाइश
• बिजनेस – व्यापार
• बैकबोन – रीढ़ की हड्डी
• टैक्स – कर
• पेंटिंग – चित्रकारी
• होस्टल – छात्रावास
• मैट्रिक – मैट्रिक

श्रवणीय
विवाह में गाए जाने वाले पारंपरिक मंगल गीत सुनिए और सुनाइए।

संभाषणीय
‘दहेज एक अभिशाप’ विषय पर चर्चा कीजिए।

प्रश्न.
‘दहेज प्रथा’ विषय पर अपने विचार लिखिए।
उत्तर:
दहेज अर्थात पुत्री के विवाह के समय पिता द्वारा उसे प्रेमपूर्वक दिए जाने वाले उपहार। समाज में यह प्राचीन काल से प्रचलित है। महाराज जनक ने भी सीता को दहेज दिया था। परंतु समय के साथ-साथ यह प्रथा कुप्रथा बनती गई। हमारे देश में अधिकतर समाजों में यह कुप्रथा अपना स्थान बना चुकी है। आज विवाह संबंध दो परिवारों का मिलन न होकर धन बटोरने का साधन बन गया है। कन्या पक्ष से बटोरी जाने वाली राशि वर की शिक्षा एवं पद के अनुरूप तय की जाती है। समाज में व्याप्त इस कलंक के कारण न जाने कितनी मासूम बच्चियाँ जन्म लेने से पहले ही मार दी जाती हैं। अनेक वधुएँ ससुराल वालों के अत्याचारों से त्रस्त होकर या तो आत्महत्या कर लेती हैं, या उन्हीं के द्वारा मार डाली जाती हैं। हालाँकि सन 1961 में दहेज प्रतिबंध अधिनियम लागू किया जा | चुका है, पर फिर भी अनगिनत लोग दहेज ले रहे हैं और कन्याओं के माता-पिता को देना पड़ रहा है।

लेखनीय

प्रश्न.
आपके घर की किसी परंपरा के बारे में घर के बुजुर्गों से जानकारी प्राप्त कीजिए। वह परंपरा उचित है या अनुचित, इस पर अपना मत शब्दांकित कीजिए।
उत्तर:
हमारे घर में जिससे कुछ लाभ होता है, उसकी पूजा करने की परंपरा रही है। हम सूर्य और चंद्रमा की पूजा करते हैं। इसके अलावा वृक्षों में नीम, वट और पीपल की भी पूजा की जाती है। इन सबसे हमें कोई न कोई लाभ होता है। तुलसी के पौधे से तो लाभ ही लाभ है। इससे वातावरण शुद्ध रहता है। घर में मच्छर-मक्खी नहीं आते। इसकी पत्तियाँ और मंजरी औषधि के रूप में काम में आती हैं। इसलिए लोग तुलसी को अपने आँगन, बगीचे तथा घर के आसपास लगाते हैं। उसकी श्रद्धापूर्वक सेवा और पूजा करते हैं। इससे इस उपयोगी पौधे का संरक्षण होता है। इसलिए तुलसी की पूजा अवश्य होनी चाहिए।

रीढ़ की हड्डी Summary in Hindi

विषय-प्रवेश : प्रस्तुत अति प्रसिद्ध एकांकी में एकांकीकार जगदीशचंद्र माथुर ने तत्कालीन समाज में स्त्री-शिक्षा के विषय में लोगों की दकियानूसी विचारधारा पर प्रकाश डाला है। उमा के द्वारा स्त्रियों की भावनाओं को महत्त्व दिया गया है। नारी के सम्मान का मुद्दा उठाया गया है।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer