Class 10

Class 10th Sanskrit Anand Chapter 4 स एव परमाणुः Question Answer Maharashtra Board

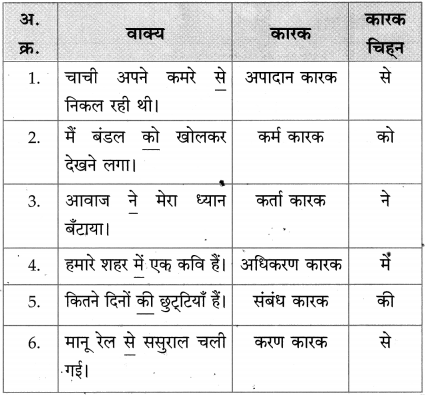
Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 4 स एव परमाणुः Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 4 Question Answer

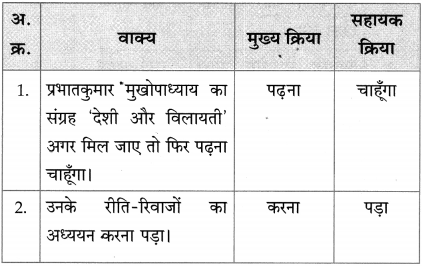
Sanskrit Anand Std 10 Digest Chapter 4 स एव परमाणुः Textbook Questions and Answers

भाषाभ्यास:

1. पूर्णवाक्येन उत्तरं लिखत ।

प्रश्न अ.
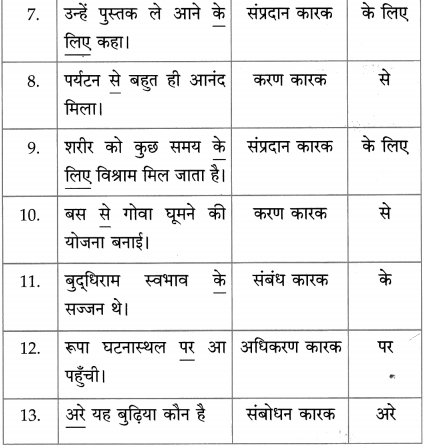
अर्णवः पाकगृहात् किम् आनयति?
उत्तरम्‌ :‌
अर्णवः पाकगृहात् मुष्टिमात्रान् तण्डुलान् आनयति।

प्रश्न आ.
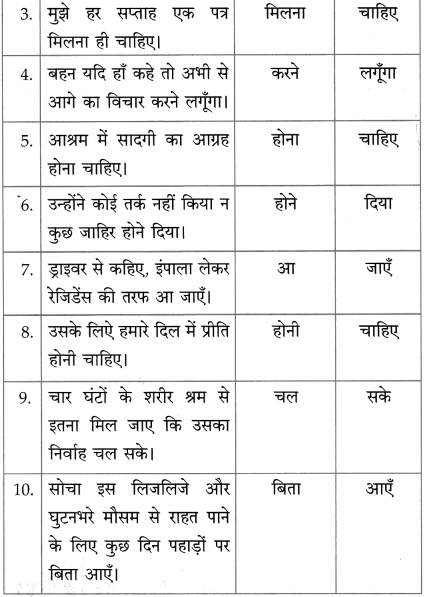
कः परमाणुः?
उत्तरम्‌ :‌
द्रव्यस्य अन्तिम : घटक : मूलं तत्त्वं च परमाणुः ।

प्रश्न इ.
परमाणुसिद्धान्तः केन महर्षिणा कथितः?
उत्तरम्‌ :‌
परमाणुसिद्धान्त: कणादमहर्षिणा कथितः ।

प्रश्न ई.
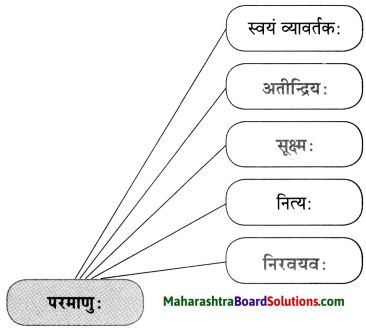
महर्षिणा कणादेन परमाणुविषये किं प्रतिपादितम् ?
उत्तरम्‌ :‌
महर्षिणा कणादेन परमाणुविषये प्रतिपादितं यत् परमाणुः अतीन्द्रियः, सूक्ष्मः, निरवयवः, नित्यः, स्वयं व्यावर्तकः च ।

प्रश्न उ.
महर्षेः कणादस्य मतानुसारं परमाणोः व्याख्या का?
उत्तरम्‌ :‌
जालसूर्यमरीचिस्थं यत् सूक्ष्म रजः दृश्यते तस्य षष्ठतमः भाग: स: परमाणु: उच्यते इति परमाणो: व्याख्या महर्षे: कपादस्य।

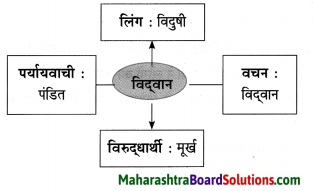
2. समानार्थकशब्दान् लिखत ।
कुसुमम्, विश्वम्, पिता, नामधेयम्, सूर्यः ।

प्रश्न 1.
समानार्थकशब्दान् लिखत ।
कुसुमम्, विश्वम्, पिता, नामधेयम्, सूर्यः ।

3. माध्यमभाषया उत्तरं लिखत ।

प्रश्न अ.
महर्षिः कणादः परमाणुविषये किं प्रतिपादितवान् ?
उत्तरम्‌ :‌

भारतीय ऋषि व तत्वज्ञ कणाद यांनी परमाणूचा सिद्धांत मांडला. त्यानुसार, परमाणू हा द्रव्याचा अंतिम घटक आहे. व त्यामागील मूलतत्त्व आहे. परमाणू हे द्रव्याचे मूळ कारण आहे. परमाणूच्या स्वरूपाविषयी सांगताना कणाद पुढील स्पष्टीकरण देतात – परमाणू हा इंद्रियांना अगोचर, अतिशय सूक्ष्म, अवयवहीन, नित्य व स्वत:भोवती भ्रमणशील असा आहे.

थोडक्यात, कणाद ऋषी परमाणूचा सिद्धांत स्पष्ट करतात व विश्वाचे अस्तित्व टिकवून ठेवणाऱ्या प्रत्येक द्रव्यामागे ‘परमाणू हेच कारण असल्याचे मानतात.

The theory of atoms was formulated by an Indian sage and philosopher कणाद, Sage कणाद considered the last element of a substance and the basic principle as परमाणु, an atom. परमाणु is the chief cause of the substance. Sage कणाद further explained that परमाणु is inaccessible to the senses, very small (microscopic), formless, eternal and self-revolving.

In brief, sage कणाद believed in the theory of परमाणु and accepted it to be the cause of each substance, because of which the world exists.

प्रश्न आ.
‘तण्डुलान् आनय’ इति पिता अर्णवं किमर्थम् आदिष्टवान् ?
उत्तरम्‌ :‌

स एव परमाणु:’ या पाठातील अर्णव व त्याच्या वडिलांच्या संभाषणाद्वारे परमाणूची संकल्पना स्पष्ट होते. एकदा अर्णव त्याच्या बागेतून जास्वंदाचे फूल आणतो. फुलातील परागकण बघत असताना अर्णवचे वडील त्याला सूक्ष्मदर्शिकेमधून ते कण पाहण्याचा सल्ला देतात. परागकणांतील इतर घटकही सूक्ष्मदर्शिकेतून सहज दिसल्यावर अर्णवला आश्चर्य वाटते.

तेव्हा त्याचे वडील ‘स एव त्याला विचारतात की ज्याप्रमाणे आपण सूक्ष्मदर्शिकतून परागकण पाहू शकतो, तसेच परमाणू सुद्धा पाहता येतो का? यानंतर अर्णव त्याच्या वडिलांना परमाणूबद्दल विचारतो. त्याच्या शंकेचे निरसन करण्यासाठी अर्णवचे वडील त्याला मूठभर तांदूळ आणावयास सांगतात.

त्यातील एक तांदळाचा दाणा जितका विभागला जाऊ शकतो, तितके त्याचे विभाजन करण्यास सांगतात. पुढे ‘परमाणू’ बद्दल स्पष्टीकरण देताना ते सांगतात की तांदूळ एका मर्यादपर्यंतच तोडला जाऊ शकतो, त्या विभाजनानंतर जो सूक्ष्म कण राहतो, तो म्हणजे परमाणू. अशा प्रकारे, तांदळाच्या उदाहरणाद्वारे अर्णवचे वडील त्याला परमाणूबद्दल योग्य ते ज्ञान देतात.

‘स एव परमाणुः’ reveals the philosophy behind the concept of परमाणु through the conversation between अर्णव and his father.

Once अर्णव brought a hibiscus-flower from his garden. He was observing its pollengrains, then his father advised him to observe it through microscope. was amazed to see the pollen-grain with its elements. After a while, father asked him, can we see परमाणू like pollen-grains through microscope? अर्णव questioned his father about 40. To answer his question, aura’s father instructed him to bring handful of rice-grains.

Later, father told अर्णव to break it till its last part. Father explained that just as rice. grains will be powdered if divided further likewise an atom is that part of the substance which can’t be obtained by division In this way, with the help of rice-grains example ama’s father aptly explains the concept of परमाणू.

4. विरुद्धार्थकशब्दान् मञ्जूषात: अन्विष्य लिखत |
सत्यम्, अन्तिमः, अनित्यः, लघुः, सूक्ष्मः, (आद्यः, गुरुः, नित्यः, असत्यम्, स्थूल:)

प्रश्न 1.
विरुद्धार्थकशब्दान् मञ्जूषात: अन्विष्य लिखत |
सत्यम्, अन्तिमः, अनित्यः, लघुः, सूक्ष्मः, (आद्यः, गुरुः, नित्यः, असत्यम्, स्थूल:)
उत्तरम्‌ :‌

• सत्यम् × असत्यम्, अनृतम्।
• अन्तिमः × आद्यः।
• अनित्यः × नित्यः।
• लघुः × बृहत्, स्थूलः।
• सूक्ष्मः × स्थूलः।

5. उचितं पर्यायं चित्वा वाक्यं पुनर्लिखत ।

प्रश्न 1.
अ. एतद् विश्वं ………… निर्मितम् । (तण्डुलै:/अणुभिः)
आ. …………… द्रव्यस्य मूलकारणम् । (परमाणुः/विज्ञानं) ।
इ. रजसः ……….. भागः परमाणुः । (षष्ठतमः/शततमः)
उत्तरम्‌ :‌
अ. अणुभिः
आ. परमाणुः
इ. षष्ठतम

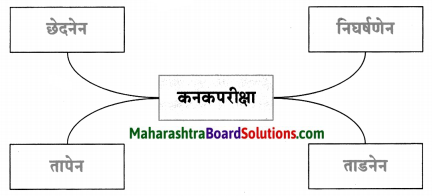
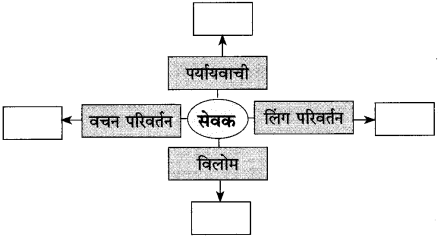
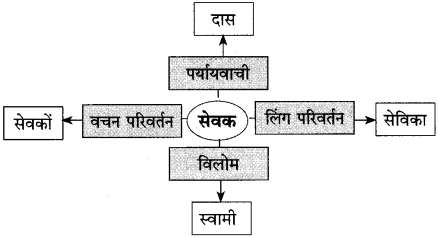
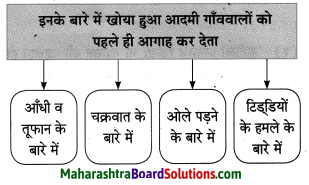
6. जालरेखाचित्रं पूरयत

प्रश्न 1.
जालरेखाचित्रं पूरयत

उत्तरम्‌ :‌

Sanskrit Anand Class 10 Textbook Solutions Chapter 4 स एव परमाणुः Additional Important Questions and Answers

अवबोधनम्

उचितं पर्यायं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.

1. अर्णवः उद्यानात् ……………. गृहीत्वा प्रविशति। (कमलम् / जपाकुसुमम्)
2. जपाकुसुमस्य परागकणाः …………. आसन्। (सूक्ष्माः / स्थूला:)
3. सूक्ष्मकणेषु तस्य …………. दृश्यन्ते। (अङ्गानि/गात्राणि)
4. अर्णव: मुष्टिमात्रान् तण्डुलान् ……….. आनयति। (उद्यानत: / महानसत:)
5. अणुभ्यः …………….. परमाणवः । (सूक्ष्मतराः / स्थूलतराः)

उत्तरम् :

1. जपाकुसुमम्
2. सूक्ष्मा:
3. अगानि
4. महानसतः
5. सूक्ष्मतरा:

प्रश्न 2.
पिता अर्णवाय स्वमहाविद्यालयम् आगन्तुं कथयति यतः …..।
(अ) पितु: महाविद्यालये कणादविषयकानि पुस्तकानि सन्ति।
(ब) पितुः महाविद्यालये स्नेह – सम्मेलनम् अस्ति।
उत्तरम् :
पितुः महाविद्यालये कणादविषयकानि पुस्तकानि सन्ति।

कः कं वदति?

प्रश्न 1.
1. अस्माकम् उद्यानात् जपाकुसुमम् आनीतम् मया।
2. किं दृष्टं त्वया?
उत्तरम् :
1. अर्णवः पितरं वदति।
2. पिता अर्णवं वदति।

प्रश्न 2.
मुष्टिमात्रान् तण्डुलान् महानसतः आनय।
उत्तरम् :
पिता अर्णवं वदति।

प्रश्न 3.
कियान् लघुः अस्ति एषः।
उत्तरम् :
अर्णव : पितरं वदति।

प्रश्न 4.
अयं खलु कणादमहर्षेः सिद्धान्तः।
उत्तरम् :
पिता अर्णवं वदति।

प्रश्न 5.
वयं तु केवलं महाभागस्य नामधेयम् एव जानीमः।
उत्तरम् :
अर्णवः पितरं वदति।

पूर्णवाक्येन उत्तरत।

प्रश्न 1.
सूक्ष्मेक्षिका कुत्र वर्तते?
उत्तरम् :
अर्णवस्य पितु: पार्श्वे उत्पीठिकायां सूक्ष्मेक्षिका वर्तते।

प्रश्न 2.
अर्णवेन कुत: जपाकुसुमम् आनीतम्?
उत्तरम् :
अर्णवेन तस्य उद्यानात् जपाकुसुमम् आनीतम्।

प्रश्न 3.
विश्व केभ्य: निर्मितम्?
उत्तरम् :
विश्वं परमाणुभ्यः निर्मितम्।

प्रश्न 4.
अणवस्य जिज्ञासा कश्वं शाम्येत्?
उत्तरम् :
कणादविषयकस्य नैकानि पुस्तकानि पठित्वा अर्णवस्य जिज्ञासा शाम्येत्।

वाक्यं पुनर्लिखित्वा सत्यम् । असत्यम् इति लिखत।

प्रश्न 1.

1. एतद् विश्वम् अणुभ्यः निर्मितम्।
2. परमाणवः सूक्ष्मेक्षिकया दृश्यन्ते।
3. अर्णवस्य पिता चित्रकलायाः प्राध्यापकः।

उत्तरम् :

1. सत्यम्।
2. असत्यम्।
3. असत्यम्।

प्रश्न 2.
1. अर्णवः क्षेत्रात् तण्डुलान् आनयति।
2. अर्णवेन तण्डुलस्य भागत्रयं कृतम्।
उत्तरम् :
1. असत्यम्।
2. असत्यम्।

प्रश्न 3.
एष: गद्यांश: कस्मात् पाठात् उद्धृतः?
उत्तरम् :
एष: गद्यांशः ‘स एव परमाणुः’ इति पाठात् उद्धतः।

शब्दज्ञानम् :

सन्धिवग्रहः

1. उद्यानाद् जपाकुसुमम् – उद्यानात् + जपाकुसुमम्।
2. एतद् विश्वम् – एतत् + विश्वम्।
3. तदपि  – तत् + अपि।
4. षष्ठतमो भागः – षष्ठतम : + भागः।
5. स उच्यते – सः + उच्यते।
6. एतद्विषये – एतत् + विषये।

त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि।

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ड्वा / इत्वा /अयित्वा	तुमन्त अव्यय  धातु + तुम् / धुम् / टुम् / डुम् / इतुम्/अयितुम्
गृहीत्वा, उक्त्वा	द्रष्टुम, कर्तुम्, पठितुम्

विभक्त्यन्तरूपाणि।.

• तृतीया – मया, त्वया, सूक्ष्मेक्षिकया।
• पज्ञमी – परमाणुभ्यः, उद्यानात्।
• षष्ठी – तस्य, अस्माकम, तेषाम्, विज्ञानस्य, कणानाम्।
• सप्तमी – पुस्तकपठने, उत्पीठिकायाम, सूक्ष्मकणेषु ।
• सम्बोधन – पितः।

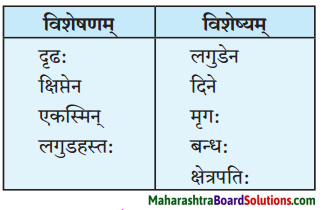
विशेषण – विशेष्य – सम्बन्धः।

विशेषणम्	विशेष्यम्
1. कियन्तः, सूक्ष्माः	परागकणाः
2. मग्नः	पिता
3. मुष्टिमात्रान्	तण्डुलान्
4. लघुतरम्	भागम्
5. सूक्ष्मतराम	भागम्
6. परमः	अणुः
7. अन्तिमः	घटकः
8. मूलम्	तत्वम्
9. पञ्चमे, षष्ठे	शतके
10. महर्षिणा	कणादेन
11. अतीन्द्रियः	परमाणुः
12. सूक्ष्मः	परमाणुः
13. निरवयवः	परमाणुः
14. नित्यः	परमाणुः
15. स्वयं व्यावर्तकः	परमाणुः
16. सूक्ष्मम्	रज:
17. षष्ठतमः	भागः
18. नैकानि	पुस्तकानि

लकारं लिखत।

प्रश्न 1.
1. सूक्ष्मेक्षिकया पश्य।
2. तेषां कणानां रचनाम् अपि द्रष्टुं शक्नोषि।
उत्तरम् :
1. लोट्लकारः
2. लट्लकार:

प्रश्न 2.
1. इमं तण्डुलं विभज।
2. यदि क्रियते तर्हि चूर्णं भवेत्।
उत्तरम् :
1. लोट्लकारः
2. विधिलिङ्लकार:

प्रश्न 3.

1. कणादविषयकाणि नैकानि पुस्तकानि सन्ति।
2. वयं महाभागस्य नामधेयम् एव जानीमः।
3. मम महाविद्यालयम् आगच्छ।

उत्तरम् :

1. लट्लकारः
2. लट्लकारः
3. लोट्लकार:

पृथक्करणम् ।

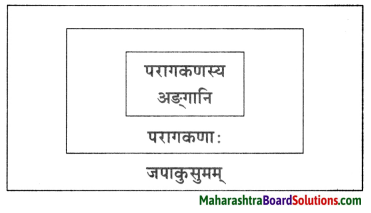
घटकाधारेण शब्दपेटिकां पूरयत।

1.
(सूक्ष्मकणस्य अङ्गानि, परागकणाः, जपाकुसुमम्)

2.

1. तथेति – तथा + इति।
2. यथाकथमपि – यश्चाकश्चम् + अपि ।
3. इतोऽपि – इत: + अपि।
4. सम्यग् उक्तम् – सम्यक् + उक्तम्।
5. एतद् विभाजनम् – एतत् + विभाजनम्।

क्रमेण योजयत।

प्रश्न 1.

1. अणवस्य सूक्ष्मेक्षिकया निरीक्षणम्।
2. पितुः पुस्तकपठनम्।
3. सूक्ष्मकणेषु तेषाम् अङ्गानां दर्शनम्।
4. अर्णवेन जपाकुसुमस्य चयनम्।

उत्तरम् :

1. अर्णवेन जपाकुसुमस्य चयनम्।
2. पितुः पुस्तकपठनम्।
3. अर्णवस्य सूक्ष्मेक्षिकया निरीक्षणम्।
4. सूक्ष्मकणेषु तेषाम् अङ्गानां दर्शनम्।

प्रश्न 2.

1. पितुः परमाणुविषयकं स्पष्टीकरणम्।
2. अर्णवस्य परमाणुविषये पृच्छा।
3. अर्णवेन तण्डुलस्य भागद्वये विभाजनम्।
4. मुष्टिमात्रान् तण्डुलान् आनेतुं पितुः आदेशः।

उत्तरम् :

1. अर्णवस्य परमाणुविषये पृच्छा।
2. मुष्टिमात्रान् तण्डुलान् आनेतुं पितुः आदेशः ।
3. अर्णवेन तण्डुलस्य भागद्वये विभाजनम्।
4. पितुः परमाणुविषयकं स्पष्टीकरणम्।

प्रश्न 3.

1. पितुः स्वस्य महाविद्यालये निमन्त्रणम्।
2. ‘वैशेषिकसूत्राणि’ इति ग्रन्थविषये चर्चा।
3. पित्रा कणादमहर्षेः सिद्धान्तविषये कथनम्।
4. अर्णवस्य विस्तरेण पठनस्य इच्छा।

उत्तरम् :

1. पित्रा कणादमहर्षेः सिद्धान्तविषये कथनम्।
2. ‘वैशेषिकसूत्राणि’ इति ग्रन्थविषये चर्चा ।
3. अर्णवस्य विस्तरेण पठनस्य इच्छा।
4. पितुः स्वस्य महाविद्यालये निमन्त्रणम्।

विभक्त्यन्तरूपाणि।

• तृतीया – मया, त्वया।
• पक्षमी – पाकगृहात, यस्मात्।
• षष्ठी – एतस्य, तस्य।
• तृतीया – तेन, महर्षिणा, मुनिना, निश्चयेन।
• षष्ठी – महर्षेः, द्रव्यस्य, तस्य, महाभागस्य, परमाणोः ।
• सप्तमी – पञ्चमे, षष्ठे, शतके, ग्रन्थे।

विरुद्धार्थकशब्दान् मञ्जूषात: अन्विष्य लिखत |

• अधुना × अनन्तरम्।
• स्मरसि × विस्मरसि।
• बहूनि × अल्पानि।
• समानः × भिन्नः।

वाक्यं पुनर्लिखित्वा सत्यम् । असत्यम् इति लिखत।

प्रश्न 1.

1. द्रव्यस्य आदिम: घटक; परमाणुः अस्ति।
2. परमाणो: सिद्धान्तः प्राय: एकोनविंशतितमे शतके महर्षिकणादेन प्रतिपादितः।
3. अर्णवस्य पितुः महाविद्यालये कणादविषयकाणि नैकानि पुस्तकानि सन्ति।

उत्तरम् :

1. असत्यम्।
2. असत्यम्।
3. सत्यम्।

त्वं स्थाने ‘भवान् / भवती’ अथवा ‘भवान् / भवती’ स्थाने ‘त्वं’ योजयत।

प्रश्न 1.
त्वं द्रष्टुं शक्नोषि।
उत्तरम् :
भवान् द्रष्टुं शक्नोति।

प्रश्न 2.
त्वं श्व: मम महाविद्यालयम् आगच्छ।
उत्तरम् :
भवान् श्व: मम महाविद्यालयम् आगच्छतु ।

प्रश्न 3.
त्वं सूक्ष्मेक्षिकया पश्य।
उत्तरम् :
भवान् सूक्ष्मेक्षिकया पश्यतु ।

प्रश्न 4.
त्वम् इमं तण्डुलं विभज।
उत्तरम् :
भवान् इमं तण्डुल विभजतु ।

प्रश्न 5.
त्वं जानासि किम्?
उत्तरम् :
भवान् जानाति किम्?

वचनं परिवर्तयत।

प्रश्न 1.
ते परमाणवः सूक्ष्मेक्षिकया अपि न दृश्यन्ते। (वाक्यं एकवचने परिवर्तयत।)
उत्तरम् :
सः परमाणुः सूक्ष्मेक्षिकया अपि न दृश्यते ।

प्रश्न 2.
इमं तण्डुल विभज। (वाक्यं बहुवचने परिवर्तयत।)
उत्तरम् :
इमान्/एनान् तण्डुलान् विभज।

प्रश्न 3.
कियन्तः सूक्ष्माः तस्य परागकणाः । (वाक्यं एकवचने परिवर्तयत।)
उत्तरम् :
कियान् सूक्ष्म: तस्य परागकणः।

प्रश्न 4.
अहम् एतद्विषये विस्तरेण पठितुम् इच्छामि। (वाक्यं बहुवचने परिवर्तयत।)
उत्तरम् :
वयम् एतद्विषये विस्तरेण पठितुम् इच्छामः।

लकारं परिवर्तयत।

प्रश्न 1.
अर्णवः तथा करोति। (वाक्यं लङ्लकारे परिवर्तयत।)
उत्तरम् :
अर्णवः तथा अकरोत्।

प्रश्न 2.
तव जिज्ञासा निश्चयेन शाम्येत्। (वाक्यं लोट्लकारे परिवर्तयत।)
उत्तरम् :
तव जिज्ञासा निश्चयेन शाम्यतु।

समासाः

समस्तपदम्	अर्थ:	समासविग्रहः	समासनाम
जपाकुसुमम्	a flower named जपा	जपा नाम कुसुमम्।	कर्मधारयः समासः।
परमाणुः	atom	परम: अणुः।	कर्मधारयः समासः।
सूक्ष्मकणा:	small particles	सूक्ष्माः कणाः।	कर्मधारयः समास:।
कणादमुनिः	sage कणाद	कणाद: नाम मुनिः।	कर्मधारयः समासः।
महर्षिः	great sage	महान् ऋषिः।	कर्मधारयः समासः।
मूलतत्त्वम्	basic principle	मूलं तत्त्वम्।	कर्मधारयः समासः।
पुस्तकपठनम्	reading of books	पुस्तकस्य पठनम्।	षष्ठी-तत्पुरुष: समासः।
परागकणा:	grains of a pollen	परागस्य कणा:।	षष्ठी-तत्पुरुषः समासः।
महाभागः	he who has good fortune	महान् भाग: यस्य सः।	बहुव्रीहिः समासः।

स एव परमाणुः Summary in Marathi and English

प्रस्तावना :

जगाच्या उत्पत्तीबाबत आतापर्यंत अनेक सिद्धांत मांडले गेले आहेत. विश्व हे छोट्या कणांनी बनलेले आहे हा विचार अतिशय प्राचीन आहे. आण्विक सिद्धांताच्या विकासाचे श्रेय जॉन डाल्टन या इंग्रज रसायन व भौतिकशास्त्रज्ञास दिले जाते.

प्राचीन काळात, भारतीय ऋषी व तत्त्वज्ञ, आचार्य कणादांनी अणूचा सिद्धांत मांडला. त्यांच्या अणुविषयक संकल्पना व विश्वाचे स्वरूप याबाबत सखोल माहिती ‘वैशेषिक दर्शन’ या त्यांच्या ग्रंथात दिली आहे ‘स एव परमाणु:’ या पाठामध्ये अर्णवचे वडील सुबोध, सोप्या उदाहरणाने परमाणूची संकल्पना स्पष्ट करतात.

Many propositions regarding world’s evolution have been put forth to date. The world is made of tiny particles is a very ancient insight. John Dalton, an English chemist and physicist is the man credited today with the development of atomic theory.

In the ancient times, theory of atoms was formulated by an Indian sage and philosopher, कणाद. His ideas about the atom and the nature of the universe are written in his trentise ‘वैशेषिक दर्शन’. In the lesson, ‘स एव परमाणु: अर्णव’s father explains the concept of sty (atom) with lucid examples.

परिच्छेदः 1

अर्णव: जपाकुसुम …………………. न दृश्यन्ते।

अनुवादः

(अर्णव जास्वंदाचे फूल घेऊन प्रवेश करतो. त्याचे वडील विज्ञानाचे प्राध्यापक आहेत. ते पुस्तक वाचण्यात तल्लीन झाले आहेत. त्यांच्या जवळच टेबलावर सूक्ष्मदर्शिका आहे.)

• अर्णव – अहो बाबा, मी आपल्या बागेतून जास्वंदाचे फूल आणले आहे. त्याचे परागकण किती सूक्ष्म आहेत ना!
• वडील – सूक्ष्मदर्शिकने पहा. तू त्याच्या कणांची रचनासुद्धा पाहू शकतोस. (अर्णव तसे करतो)
• वडील – तू काय पाहिलेस?
• अर्णव – बाबा, ते (अद्भुत) विलक्षण आहे. सूक्ष्मकणांमध्ये त्यांचे भाग दिसत आहेत.
• बाबा – अर्णव, फुलाचे हे अंश तू सूक्ष्मदर्शिकेने पाहू शकतोस. पण हे जग अणूंनी निर्माण झाले आहे. ते अणू सूक्ष्मदर्शिकने सुद्धा दिसत नाहीत.

(अर्णव enters taking the hibiscus-flower. His father is a professor of science. He is engrossed in reading a book. Near him, there is a microscope on the table.)

• Arnav: Oh father, I have brought a hibiscus flower from our garden. Its pollen-grains are indeed microscopic!
• Father: Observe it through a microscope. You can see even the structure of its particles. (Arnav does accordingly.)
• Father: What did you see (observe)?
• Arnav: O father, it is amazing. The parts of these minute particles are seen.
• Father: Arnav, you can see the parts of this flower through microscope. But this world is created from atoms. Those atoms are not seen even through the microscope.

परिच्छेदः 2

अर्णवः परमाणुः ………….. परमः अणुः ।

अनुवादः

• अर्णव – परमाणू म्हणजे काय?
• बाबा – अच्छा, मी सांगतो. स्वयंपाकघरातून मूठभर तांदूळ आण.
• अर्णव – (हो असे म्हणून, तो स्वयंपाकघरातून तांदूळ आणतो) बाबा, है घ्या.
• बाबा – आता या तांदळाचे भाग कर.
• अर्णव – बाबा, किती लहान (तांदूळ) आहे हा. बघा, मी कसेबसे याचे दोन तुकडे केले.
• बाबा – इथून पुढे (याचे) लहान भाग करणे शक्य आहे का?
• अर्णव – जर केले तर त्याची भुकटी होईल.
• बाबा – तू बरोबर सांगितले. जिथे हे विभाजन संपते व जिथून सर्वात सूक्ष्म भाग मिळविणे (सुद्धा) शक्य नसते, तोच परमाणू होय.
• Arnav: What is an atom?
• Father: Well, I tell you. Bring a handful of rice
• grains from the kitchen.
• Arnav: (Saying yes, brings rice-grains from the kitchen.) O father, please take it.
• Father: Now divide this rice grain.
• Arnav: O father, how small is this! See, somehow I made it into two parts.
• Father: Is it possible to make (even) smaller than this?
• Arnav: If we do it (if it is done), it would be powdered.
• Father: You said it right. Where this division ends from which no smaller part can be obtained, that itself is an atom.

परिच्छेदः 3

अर्णवः परमाणुः ……….. परमः अणुः ।

अनुवादः

• अर्णव – परमाणू हा द्रव्याचा अंतिम घटक व मूळतत्त्व आहे; हे खरे आहे ना?
• बाबा – बरोबर, खरे तर, हा महर्षी कणादांचा सिद्धांत आहे; तुला माहीत आहे का? परमाणू हे द्रव्याचे मूळ कारण आहे असे प्रतिपादन महर्षीनी केले. ते सुद्धा, सुमारे ख्रिस्तपूर्व पाचव्या किंवा सहाव्या शतकात.
• अर्णव – बाबा, परमाणूसंबंधी महर्षी कणादांनी काय काय सांगितले आहे? आम्हांला तर फक्त त्या महान व्यक्तीचे नावच माहीत आहे.
• बाबा – कणाद ऋषींनी स्पष्ट केले (की) – अणू (हा) इंद्रियांच्या पलीकडे, सूक्ष्म, अवयवहीन, नित्य आणि स्वयंपरिभ्रमणशील आहे. ‘वैशेषिकसूत्राणि’ या त्यांच्या ग्रंथात त्यांनी परमाणूची व्याख्या केली आहे.
• अर्णव – ती व्याख्या काय आहे?
• बाबा – जाळीदार खिडकीतून येणाऱ्या सूर्यकिरणांतील सूक्ष्म धूलिकणाच्या साव्या भागाला परमाणू असे म्हटले जाते.
• अर्णव – मला त्याबद्दल सविस्तर जाणून घ्यायची इच्छा आहे.
• बाबा – छान! तू उद्या माझ्या महाविद्यालयात ये. तिथे कणादांविषयी अनेक पुस्तके आहेत. तुझी जिज्ञासा नक्कीच शमेल.
• Arnav: An atom is the last element of a substance and the basic principle, isn’t it?
• Father: Right. This is great sage कणाद’s theory. Do you know? The sage explained that an atom is the basic reason of the substance. That too, probably in the fifth-sixth century BC.
• Arnav: O father, what all is told by sage regarding an atom? We merely know the name of the great one.
• Father: The Sage कणाद explained-An atom is beyond senses, tiny, indivisible, eternal and self-revolving. He has given the definition of परमाणु in his book ‘वैशेषिकसूत्राणि.’
• Arnav: What is that definition?
• Father: An atom is the sixth part of the fine (micro) dust particle that is located in a beam of sun-rays entering through a grilled window
• Arnav: I wish to know about it in detail.
• Father: Good! (Then) You come to my college tomorrow. There are many books regarding US Definitely your curiosity would be pacified.

शब्दार्थाः

1. प्राध्यापक: – professor – महाविद्यालयातील शिक्षक
2. मानः – engrossed – तल्लीन
3. परमाणुः – atom – अणू
4. जपाकुसुमम् – hibiscus-flower – जास्वंदाचे फूल
5. सूक्ष्मेक्षिका – microscope – सूक्ष्मदर्शिका
6. परागकणाः – pollen – grains – परागकण
7. अङ्गानि – parts – भाग
8. उत्पीठिकायाम् – on the table – टेबलावर
9. गृहीत्वा – taking – घेऊन
10. पश्चे – near – जवळ
11. द्रष्टुं शक्नोषि – able to see – तू पाहू शकतोस
12. कियान् – how much – किती
13. चूर्णम् – powder – भुकटी
14. सूक्ष्मतरम् – minuscule – सर्वात सूक्ष्म / लहान
15. तण्डुलान् – rice-grains – तांदूळ
16. मुष्टिमात्रान् – handful of – मूठभर
17. महानसतः/ पाकगृहात् – from kitchen – स्वयंपाकघरातून
18. समाप्यते – ends/stops – संपते / थांबते
19. आनय – bring – आण
20. विभज – split – भाग कर / विभाजन कर
21. यथाकथमपि – somehow – कसेतरी
22. इतोऽपि – than this – यापेक्षा
23. सम्यक् – right – बरोबर
24. सिद्धान्तः – proposition, theory – सिद्धांत
25. निरवयवः – formless – अवयव नसलेला / अवयवहीन
26. स्वयं व्यावर्तक: – self-revolving – स्वयं परिभ्रमणशील
27. अतीन्द्रियः – beyond senses – इंद्रियांच्या पलीकडे
28. षष्ठतमः – sixth – सहावा
29. तत्वम् – basic principle – मूळतत्त्व
30. जालसूर्य – located in a beam – झरोक्यातील
31. मरीचिस्थम् – of the sun-ray from a grill – सूर्यकिरणात
32. प्रतिपादितम् – explained, stated – स्पष्टीकरण दिले, मांडले
33. रजः – dust particle – धूलिकण
34. जिज्ञासा – curiosity – उत्सुकता
35. द्रव्यस्य – of substance – द्रव्याचे
36. शाम्येत् – would pacify – शमविली जाईल
37. प्रायः – approximately – सुमारे
38. श्चः – tomorrow – उद्या

10th Standard Sanskrit Anand Digest Pdf  

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्यस्तबकः Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Aamod Chapter 6 युग्ममाला Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 6 युग्ममाला Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 6 Question Answer

Sanskrit Amod Std 10 Digest Chapter 6 युग्ममाला Textbook Questions and Answers

भाषाभ्यास:

श्लोकः 1

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
कनकपरीक्षा कथं भवति?
उत्तरम् :
निघर्षणच्छेदनतापताडनैः एतै: चतुर्भिः प्रकारैः कनकपरीक्षा भवति।

प्रश्न आ.
पुरुषपरीक्षा कथं भवति?
उत्तरम् :
पुरुषपरीक्षा श्रुतेन शीलेन गुणेन कर्मणा (इति) चतुर्भिः प्रकारैः भवति।

2. जालरेखाचित्रं पूरयत

प्रश्न अ.

उत्तरम् :

प्रश्न आ.

उत्तरम् :

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
‘यथा चतुर्भिः’ इति श्लोकस्य स्पष्टीकरणं लिखत ।
उत्तरम् :

युग्ममाला हा अशा श्लोकांचा संग्रह आहे की जेथे श्लोकाचा अर्थ पूर्ण करण्याकरिता तसेच त्याचे भाषिक सौंदर्य वाढविण्यासाठी शब्दयुग्मांचा वापर केलेला दिसून येतो. ‘यथा चतुर्भिः’ या श्लोकामध्ये यथा-तथा अव्यय वापरुन आदर्श व्यक्तीचे स्पष्टीकरण दिले आहे. गुणी व आदर्श व्यक्ती ज्ञानी तसेच सद्गुणांनी युक्त असते. ती स्वत:ला चांगल्या कार्यामध्ये मग्न ठेवते.

ज्याप्रमाणे चकाकी तपासण्यासाठी सोन्याला घासले जाते, लवचिकता तपासण्यासाठी त्याला कापले जाते, शुद्धता तपासण्यासाठी त्याला तापविले जाते व मऊपणा तपासण्यासाठी त्याला ठोकले जाते, म्हणजे चार प्रकारांनी सोन्याची पारख केली जाते. याचप्रमाणे, माणसाने शुद्ध मनाने संकटातही ज्ञानी गुणी राहून त्याचा चांगुलपणा दाखविल्यास तो परीक्षेत सफल होतो.

युग्ममाला is a collation of those verses wherein शब्दयुग्म is used to complete the meaning of the verse as well as to enhance its linguistic beauty An ideal person should be knowledgeable and virtuous. He should indulge himself in “right deeds.

Just as gold is scratched to check its shine, it is cut to see its elasticity, it is heated to understand its purity and its softness can be examined by hammering on it. Similarly, a man with pure mind, knowledge and virtues overcomes troubles.

4. अमरकोषात् शब्द प्रयुज्य वाक्यं पुनर्लिखत ।

प्रश्न 1.
जनैः कनकं परीक्ष्यते ।
उत्तरम् :
जनैः स्वर्ण/सुवर्ण/हिरण्यं/हेम/हाटकं परीक्ष्यते।

श्लोक: 2.

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
अल्पधी: कुत्र श्लाघ्यः भवति?
उत्तरम् :
यत्र विद्वज्जन: न अस्ति, तत्र अल्पधी: अपि श्लाघ्यः भवति।

प्रश्न आ.
एरण्डः कुत्र द्रुमायते?
उत्तरम् :
निरस्तपादपे देशे एरण्ड: द्रुमायते।

2. सन्धि-विग्रहं कुरुत ।

प्रश्न अ.
श्लाघ्यस्तत्र
उत्तरम् :
श्लाघ्यस्तत्राल्पधीरपि – श्लाघ्य: + तत्र + अल्पवी: + अपि।

प्रश्न आ.
अल्पधीरपि ।
उत्तरम् :
अल्पधी: – मन्दबुद्धिः, मूढमतिः

3. अमरकोषात् शब्द प्रयुज्य वाक्यं पुनर्लिखत ।

प्रश्न 1.
यत्र एकः अपि पादपः नास्ति तत्र एरण्डः द्रुमायते ।
उत्तरम् :
यत्र एकः अपि वृक्ष:/महीरुहः/शाखी/विटपी/तरुः नास्ति तत्र एरण्ड: द्रुमायते।

श्लोक: 3.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
मनुष्यः द्विप इव मदान्धः कदा भवति?
उत्तरम् :
बदा मनुष्य किमिज्ञः आसीत् तदा सः द्विप इव मदान्धः भवति।

प्रश्न आ.
‘मूर्खः अस्मि’ इति मनुष्येण कुतः अवगतम्?
उत्तरम् :
‘मूर्खः अस्मि’ इति मनुष्येण बुधजनसकाशात् अवगतम्।

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
किश्चिज्ज्ञोऽहम्
उत्तरम् :
किचिज्जोऽहम् – किञ्चिज्ज्ञः + अहम्।

प्रश्न आ.
अभवदवलिप्तम् ।
उत्तरम् :
सर्वज्ञोऽस्मीत्यभवदलिप्तम् – सर्वज्ञः + अस्मि + इति + अभवत् + अलिप्तम्।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
कदा मदः व्यपगच्छति?
उत्तरम् :
युग्ममाला हा अशा श्लोकांचा संग्रह आहे की जेथे श्लोकाचा अर्थ पूर्ण करण्याकरिता तसेच त्याचे भाषिक सौंदर्य वाढविण्यासाठी शब्दयुग्मांचा वापर केलेला दिसून येतो. ‘यदा ….. व्यपगतः।’ या श्लोकामध्ये एक मनुष्य त्याचे अज्ञान मान्य करतो व ज्ञानी लोकांची संगत फायदेशीर असते हे सांगतो.

या श्लोकातील माणसाला त्याच्या थोड्याशा ज्ञानाचा खोटा अभिमान असतो व या अभिमानामुळे तो स्वतःला सर्वज्ञ समजत असतो पण जेव्हा त्याला ज्ञानी लोकांची संगत प्राप्त होते तेव्हा त्यांच्या सद्विचारांनी या मनुष्याचा अज्ञपणा दूर होतो व तापासारखा त्याचा मद नाहीसा होतो. त्याला त्याच्या चुकीची जाणीव होते.

युग्ममाला is a collation of those verses wherein शब्दयुग्म is used to complete the meaning of the verse as well as to enhance its linguistic beauty.

In the verse, ‘यदा ….. व्यपगतः। A man admits his ignorance and focuses the benefit of learned people’s company. A man says he had false pride of his little knowledge and he was blinded by it like an elephant with rut who is directionless, thoughtless. But a man terms himself fool as he gets associated with learned people. His pride gets disappeared when he meets learned people.

श्लोक: 4.

1. पूर्णवाक्येन उत्तरत।

प्रश्न अ.
आगतं भयं वीक्ष्य नरः किं कुर्यात् ?
उत्तरम् :
आगतं भयं वीक्ष्य नरः यथोचितं कुर्यात्।

2. सन्धिविग्रहं कुरुत।

प्रश्न 1.
भयाद्धि ।
उत्तरम् :
भयाद्धि – भयात् +हि।

श्लोक: 5.

1. पूर्णवाक्येन उत्तरत

प्रश्न अ.
क: बहु भाषते?
उत्तरम् :
अधम: बहु भाषते।

2. सन्धिविग्रहं कुरुत।

प्रश्न अ.
स्यादधमः ।
उत्तरम् :
स्यादधमो बहु – स्यात् + अथमः + बहु।

श्लोक: 6.

1. पूर्णवाक्येन उत्तरत ।

प्रश्न अ.
कर्षक: कीदृशं फलं लभते?
उत्तरम् :
कर्षक: क्षेत्रम् आसाद्य यादृशं बीजं वपते तादृशं फलं लभते।

2. सन्धिविग्रहं कुरुत ।

प्रश्न अ.
क्षेत्रमासाद्य
उत्तरम् :
क्षेत्रमासाद्य – क्षेत्रम् + आसाद्य।

प्रश्न आ.
वाऽपि ।
उत्तरम् :
वाऽपि . वा + अपि।

3. माध्यमभाषया उत्तरत ।

प्रश्न 1.
मनुष्यः स्वकर्मणः कीदृशं फलं लभते?
उत्तरम् :
युग्ममाला हा अशा श्लोकांचा संग्रह आहे की जेथे श्लोकाचा अर्थ पूर्ण करण्याकरिता तसेच त्याचे भाषिक सौंदर्य वाढविण्यासाठी शब्दयुग्मांचा वापर केलेला दिसून येतो. शेतकऱ्याने चांगले धान्य पेरले असता त्याला त्याचे उत्तम फळ मिळते. तसेच त्याने कमी प्रतीचे / हलक्या दर्जाचे बी पेरले असता त्याला तसेच साधारण फळ प्राप्त होते. याप्रमाणे, मनुष्याने चांगले कर्म केल्यास त्याला त्याची आनंददायी फळे मिळतात अन्यथा त्याला दुष्कर्मामुळे होणाऱ्या दुष्परिणामांना सामोरे जावे लागते.

युग्ममाला is a collation of those verses wherein शब्दयुग्म is used to complete the meaning of the verse as well as to enhance its linguistic beauty. The farmer gets the results if he sows well. He gets poor results if he sows low-quality seeds. Similarly, a man gets pleasurable results of his good deeds and he has to suffer if he is involved in bad deeds.

4. अमरकोषात् शब्दं प्रयुज्य वाक्यं पुनर्लिखत ।

प्रश्न 1.
कर्षक: बीजं वपते ।
उत्तरम् :
क्षेत्राजीव:/कृषिक:/कृषीवल:/कर्षक: बीजं वपते।

1. समानार्थकशब्दान् लिखत ।
कनकम्, विद्वान्, पादपः, अधमः

प्रश्न 1.
समानार्थकशब्दान् लिखत ।
कनकम्, विद्वान्, पादपः, अधमः
उत्तरम् :

1. कनकम् – स्वर्णम्, सुवर्णम्, कनकम्, हिरण्यम, हेम, हाटकम्।
2. विद्वज्जनः – विद्वान, प्राज्ञः।
3. पादपः – वृक्षः, महीरुहः, शाखी, विटपी, तरुः।
4. अधमः – मन्दबुद्धिः, मूढमतिः

2. विरुद्धार्थकशब्दान् लिखत ।
गुणः, विद्वान्, उत्तमः, सुकृतम् ।

प्रश्न 1.
विरुद्धार्थकशब्दान् लिखत ।
गुणः, विद्वान्, उत्तमः, सुकृतम् ।
उत्तरम् :

1. गुणः × दुर्गुणः, अवगुणः, दोषः ।
2. विद्वज्जनः / विद्वान् × मूर्खजनः, अज्ञः।
3. उत्तमः × अनुत्तमः / अधमः।
4. सुकृतम् × दुष्कृतम्।

3. चतुर्थपदं लिखत ।

प्रश्न 1.
अ. मनः – चेतः :: अवगतम् – …………………
आ. बुधजन: – ज्ञानी :: मूर्ख: – ………………….
इ) नरः – मनुष्यः :: उचितम् – …………………
ई) वीक्ष्य – दृष्टा :: भयम् – ………………….
उत्तरम् :
अ. मनः – अन्त: करणम्, चेतः, चित्तम्।
आ. मूर्खः – मूढः
इ. उचितम् – योग्यम, युक्तम्।
ई. भयम् – भीतिः।

4. समानार्थकशब्दानां मेलनं कुरुत।

प्रश्न 1.
समानार्थकशब्दानां मेलनं कुरुत।

उत्तरम् :

सुवर्णम्	हेम
उत्तमः	श्रेष्ठः
अवलिप्तम्	व्याप्तम्
ध्वनिः	शब्दः

5. उचितं शब्दयुग्मं योजयत । (यत्र-तत्र, यदि-तर्हि, यदा-तदा, यथा-तथा)

प्रश्न 1.
अ. ………… अध्यापक: न आगच्छति …………….. छात्रा: स्वाध्यायं कुर्वन्ति ।
आ. …………. धूमः …………. बहिः ।
इ. ……………… आकाशे मेघाः गर्जन्ति मयूरः नृत्यति ।
ई. ……………… विचारः …………… वर्तनम् ।
उ. …………….. सूर्यः उदेति …………….. विश्वं प्रकाशमयं भवति ।
ऊ) ………… शर्करा ……………… पिपीलिकाः ।
ए) सज्जनाः …………. वदन्ति ……………. कुर्वन्ति ।
ऐ. ………………. बालक: व्यायामं करिष्यति …………… स: सुदृढः भविष्यति ।

Sanskrit Amod Class 10 Textbook Solutions Chapter 6 युग्ममाला Additional Important Questions and Answers

अवबोधनम्

(क) पूर्णवाक्येन उत्तरं लिखत।

प्रश्न 1.
मनुष्यस्य मदः कदा व्यपगतः?
उत्तरम् :
बदा मनुष्येण बुधजनसकाशात् किन्नित् किञ्जित् अवगतम् तदा सः आत्मानं मूर्खम् अमन्यत तदनन्तरं तस्य मदः व्यपगतः ।

प्रश्न 2.
मनुष्यस्य मदः कथं व्यपगतः?
उत्तरम् :
मनुष्यस्य मद: ज्वर: इव व्यपगतः।

प्रश्न 3.
कदा पर्यन्तं भयात् भेतव्यम्?
उत्तरम् :
यावत् भयम् अनागतं तावत् भयात् भेतव्यम्।

प्रश्न 4.
उत्तमः कीदृशः न स्यात्?
उत्तरम् :
उत्तम: अतिवक्ता न स्यात्।

प्रश्न 5.
सुवर्णे ध्वनिः प्रजायते वा न?
उत्तरम् :
सुवर्णे ध्वनि: न प्रजायते।

प्रश्न 6.
मनुष्यः स्वकर्मणः कीदृशं फलं लभते ?
उत्तरम् :
मनुष्यः सुकृतस्य इष्ट दुष्कृतस्य अनिष्टं फलं लभते।

पृथक्करणम् :

(ख) विशेषण – विशेष्य सम्बन्धः ।

विशेषणम्	विशेष्यम्
श्लाध्य	अल्पधी:
आगतम्	भयम्
अनागतम्	भयम्

पृथक्करणम्।

(ग) जालरेखाचित्रं पुरयत।

1.

2.

3.

सन्धिविग्रहः

• किशिविजि बुधजनसकाशादवगतम् – किञ्जित् + किञ्जित् + बुधजनसकाशात् + अवगतम्।
• मूखोऽस्मीति – मूर्खः + अस्मि + इति ।
• विद्वज्जनो नास्ति – विद्वज्जनः + न + अस्ति।
• एरण्डोऽपि – एरण्ड:+ अपि।
• भयमनागतम् – भयम् + अनागतम्।
• उत्तमो नातिवक्ता – उत्तम: + न + अतिवक्ता।
• ध्वनिस्तादृग्यादृक्कांस्ये – ध्वनिः + तादृक् + यादृक् + कांस्ये।

समासा:

समस्तपदम्	अर्थ:	समसाविग्रहः	समासनाम
निघर्षणच्छेदनतापताडनैः	by rubbing, cutting, heating and hammering	निघर्षणं च छेदनं च तापं च ताडनं च,तेः।	इतरेतर द्वन्द्व समास
मदान्धः	blind due to pride	मदेन अन्धः।	तृतीया तत्पुरुष समास
किञ्चिज्ज्ञः	knows little	किञ्चित् जानाति इति।	उपपद तत्पुरुष समास
सर्वज्ञः	knows everything	सर्वं जानाति इति।	उपपद तत्पुरुष समास
अनागतम्	not arrived	न आगतम्।	नञ् तत्पुरुष समास
अल्पधी:	one who has dull intellect	अल्पा धी: यस्य सः।	बहुव्रीहि समास
यथोचितम्	according to proper (deed)	उचितम् अनुसत्य।	अव्ययीभाव समास

भाषाभ्यासः

(क) समानार्थकशब्दान् लिखत।

1. पुरुषः – नरः, मानवः, मनुजः, मनुष्यः, मानुष: मर्त्यः ।
2. कर्षक: – कृषकः, क्षेत्राजीवः, कृषिकः, कृषीवलः।
3. श्रुतेन – ज्ञानेन, विद्यया।
4. श्लाघ्यः – प्रशंसनीयः, स्तुत्यः।
5. अल्पधी: – मन्दबुद्धिः, मूढमतिः ।
6. द्विपः – गजः, दन्ती, हस्ती।
7. मदान्धः – मदोन्मत्तः।
8. सकाशात् – समीपम्।
9. मदः – वृथाभिमानः, आटोपः।
10. वीक्ष्य – अवलोक्य, दृष्ट्वा, विलोक्य।
11. बहु – भूरि, विपुलम्।
12. ध्वनिः – रवः, नादः, शब्दः।
13. अवलिप्तम् – व्याप्तम्।
14. उत्तमः – श्रेष्ठः ।
15. अवगतम् – अधीतम् ।

(ख) विरुद्धार्थकशब्दान् लिखत।

1. श्लाघ्यः × निन्दनीयः।
2. अल्पधीः × विचक्षणः।
3. आगतम् × अनागतम्।
4. उचितम् × अनुचितम्।
5. बहु × अल्पम्, स्वल्पम्।

युग्ममाला Summary in Marathi and English

प्रस्तावना :

संस्कृत साहित्यात अनेक शब्दयुग्मे (शब्दांच्या जोड्या). उदाहरणार्थ – यदा – तदा, यावत् – तावत्, यत्र – तत्र, इ. आढळतात. वाक्य व श्लोकांमध्ये अशी शब्दयुग्मे वापरल्यास वाक्यांचे व श्लोकांचे सौंदर्य वाढते. जसे- यथा राजा तथा प्रजा। युग्ममाला हा अशा श्लोकांचा संग्रह आहे की जेथे श्लोकाचा अर्थ पूर्ण करण्याकरिता तसेच त्याचे भाषिक सौंदर्य वाढविण्यासाठी शब्दयुग्मांचा वापर केलेला दिसून येतो.

शब्दयुग्म, pair of words are noticeable in Sanskrit literature. For example : यदा- तदा, यावत् – तावत, यत्र-तत्र,etc. The usage of such pair of words (शब्दयुग्म) in sentences or in verses increases its beauty eg: यथा राजा तथा प्रजा। युग्ममाला is a collation of those verses wherein शब्दयुग्म is used to complete the meaning of the verse as well as to enhance its linguistic beauty.

श्लोकः 1

यथा चतुर्भि: कनक परीक्ष्यते निघर्षणच्छेदनतापताडनैः। (वृत्तम् – वंशस्थम्)
तथा चतुर्भिः पुरुषः परीक्ष्यते श्रुतेन शीलेन गुणेन कर्मणा।।1।। (वद्धचाणक्यशतकात्)

अन्वय:- यथा कनक निघर्षण – छेदन – ताप – ताडनैः (इति) चतुर्भिः परीक्ष्यते, तथा पुरुषः श्रुतेन, शीलेन, गुणेन, कर्मणा (इति) चतुर्भिः परीक्ष्यते।

अनुवाद:

ज्याप्रमाणे सोन्याची परीक्षा (पारख) घासणे, छेदन करणे (तोडणे), तापविणे व (हातोडीने) ठोकणे, (या) चार प्रकारांनी होते. त्याप्रमाणे, ज्ञान, चारित्र्य, सद्गुण व कर्म या चार प्रकारांनी मनुष्याची परीक्षा होते. स्पष्टीकरण – सोन्याची चकाकी तपासण्याकरिता त्याला घासावे लागते, ते काळे पडते का हे पाहण्याकरिता त्याला तापवावे लागते, त्याचा चिवटपणा पाहण्याकरिता त्याला तोडावे लागते व हातोड्याने ठोकून त्याचा मऊपणा हा गुण कसाला लागतो. थोडक्यात, सोन्याची शुद्धता सिद्ध करण्यासाठी त्याला चार कसोट्या लावतात. त्याप्रमाणे मनुष्य ज्ञानी, सदाचरणी व गुणी राहून त्याचा चांगुलपणा सिद्ध करतो.

Just as the gold is tested by four tests – rubbing, cutting, heating, (and) hammering, similarly, a man is tested by four (dimensions) knowledge, character, virtues (and) deeds. Explanation – The gold is scratched to check its shine. It is cut to see elasticity. It is heated to check whether it turns black and its softness can be examined by striking with the hammer. In brief, the gold has to undergo four tests to prove its purity. Likewise, a man proves his goodness by being knowledgeable, (righteous, and virtuous.

श्लोकः 2

यत्र विद्वज्जनो नास्ति श्लाघ्यस्तत्राल्पधीरपि। (वृत्तम् – अनुष्टप)
निरस्तपादपे देशे एरण्डोऽपि द्रुमायते।।2।। (सङ्ग्रहात्।)

अन्वयः- यत्र विद्वज्जनः न अस्ति, तत्र अल्पधी: अपि श्लाघ्यः (भवति)। (यथा) निरस्तपादपे देशे एरण्डः अपि दुमायते।

अनुवादः

जेथे विद्वान नसतो तेथे अल्पबुद्धीचा माणूसही प्रशंसनीय ठरतो. (स्तुतीस पात्र ठरतो.) वृक्षहीन (वैराण) प्रदेशात एरंडही वृक्ष होतो (ठरतो.)

स्पष्टीकरण-दबळया समहावर अंकुश ठवणान्या लाकाना उप्पसून वरील श्लोकाची रचना केली आहे. अल्प क्षमता असलेल्या लोकांच्या समूहामध्ये किचित अधिकतर क्षमता असलेलाही स्तुतीस पात्र ठरतो.।

(In a place) where there is no learned one, even a dull-witted person becomes praiseworthy. In a place where there is no vegetation, even a castor – plant becomes a tree.

Explanation – The poet takes a dig at people that are in power in a weak setup. When everyone around is of mediocre capacity, one with every few accolades becomes the hero.

श्लोकः 3

यदा किजिज्ञोऽहं द्विप इव मदान्धः समभवं
तदा सर्वज्ञोऽस्मीत्यभवदलिप्तं मम ममः।
यदा किजिकिशिद् बुधजनसकाशादवगतं (वृत्तम् – शिखरिणी)
तदा मूर्योऽस्मीति ज्वर इव मदो मे व्यपगतः।।3।। (नीतिशतकात)

अन्वय:- यदा अहं किजिजः (रादा) (अहं) द्विपः इव मदान्धः समभवम् । तदा मम मनः ‘सर्वज्ञ: अस्मि’ इति अवलिप्तम् अभवत्। यदा बुधजनसकाशात् किंचित् किक्षित् अवगतम् तदा (अह) मूर्खः अस्मि (इति ज्ञात्वा) में मद; ज्वर: इव व्यपगतः।

अनुवादः

जेव्हा मला थोडेसे ज्ञान प्राप्त झाले, तेव्हा मदाने आंधळा झालेल्या हत्तीसारखा मी (आंधळा) झालो आणि माझे मन ‘मी सर्वज्ञ आहे’ या कल्पनेने वेढले गेले. (पण) जेव्हा ज्ञानी माणसांकडून मला थोडे थोडे कळू लागले, तेव्हा मी मूर्ख आहे’ असे मला जाणवले व तापाप्रमाणे माझा गर्व नाहीसा झाला (उतरला.)
स्पष्टीकरण – स्वत:च्या ज्ञानाचा कधीही गर्व बाळगू नये कारण ज्ञानी माणसांच्या सहवासाने अल्पज्ञानात भर पडते.

When I had scanty knowledge, I was blinded with pride, like and elephant (in a rut) (and) my mind got conceited thinking that I know everything. (But) When I began to acquire knowledge, little by little, from the learned, I learned that ‘I am a fool and my (false) pride disappeared like fever.

Explanation – Never be proud of little knowledge as it continues to upgrade when one comes into contact with a more knowledgeable person.

श्लोकः 4

तावद् भवाद्धि भेतव्यं यावद्भयमनागतम्। (वृत्तम् – अनुष्टप)
आगतं तु भयं वीक्ष्य नरः कुर्याद् यथोचितम् ।।4।। (पञ्चतन्त्रात्)

अन्वय:- यावत् भयम् अनागतं तावत् हि भयात् भेतव्यम्। (तथापि) आगतं तु भयं वीक्ष्य नरः यथोचितं कुर्यात्।

अनुवादः

जोपर्यंत भयाने (माणसाला) ग्रासले नाही (संकटात पकडले नाही) तोपर्यंत (माणसाने) भयाला घाबरावे. (परंतु) भयाला आलेले पाहून मनुष्याने जे योग्य आहे तेच आचरावे

(योग्य ते करावे.) As long as fear has not arrived (a person is not caught in the calamity) till then one should be scared of fear. (But) Having seen fear approaching, a man should do what is proper/right.

श्लोकः 5

उत्तमो नातिवक्ता स्यादधमो बहु भाषते।
सुवर्णे न ध्वनिस्तादृग्यादृक्कांस्ये प्रजायते।।5।। (वृत्तम् – अनुष्टुप)

अन्वयः- उत्तमः अतिवक्ता न स्यात्, अधम: बहु भाषते। यादृक् कांस्ये (ध्वनिः) प्रजायते तादृक् सुवर्णे ध्वनिः न (प्रजायते)।

अनुवादः

उत्तम व्यक्ती फार बोलत नाही (वायफळ गोष्टींमध्ये सहभाग घेत नाही) (बुद्धीने व ज्ञानाने) सामान्य लोक खूप बडबड करतात. ज्याप्रमाणे, काश्याच्या भांड्याचा आवाज होतो तसा सोन्याचा होत नाही.
स्पष्टीकरण: ज्ञानी माणसे वायफळ बोलत नाहीत; ज्यांचे ज्ञान अल्प आहे, अशी माणसे नेहमी बडबड करत राहतात.

An excellent person does not talk much (does not indulge in loose talks), inferior person talks much (unnecessarily). Just as gold (best and expensive metal) does not produce (loud) sound like bronze (base metal) makes.
Explanation: Knowledgeable people do not indulge in unnecessary and loose talk, whereas those who have less knowledge always chatter.

श्लोकः 6

यादृशं वपते बीज क्षेत्रमासाद्य कर्षकः।
सुकृते दुष्कृते वाऽपि तादृशं लभते फलम्।।6।। (वृत्तम् – अनुष्टुप्)

अन्वय:- कर्षक: क्षेत्रम् आसाद्य यादृशं बीजं वपते (तादृशं फलं लभते)। (तथैव मनुष्यः) सुकृते वा दुष्कृते वा अपि तादृश (इष्टम् अनिष्ट वा) फलं लभते।

अनुवादः

शेतकरी शेतात जाऊन ज्या त-हेचे बीज पेरतो, त्या तमेचे फळ त्याला मिळते. कृती चांगली वा वाईट (जशी असेल) त्यानुसार मनुष्यास त्याचे फळ मिळते. (चांगल्या कृतीचे आनंददायी तर वाईट कृतीचे क्लेशकारक फळ मिळते.) स्पष्टीकरण – पेरावे तसे उगवते.

Just as the farmer obtains the fruit based on what he sows, (similarly, a man) acquires a fruit in good or bad deeds. (through pleasurable and painful experiences.)
Explanation – As you sow, so shall you reap.

शब्दार्थाः

1. निघर्षण – rubbing – घर्षण
2. छेदन – cutting – तोडणे
3. ताप – heating – तापवणे
4. कनकम् – gold – सोने
5. शीलेन – by character – चारित्र्याने
6. गुणेन – by virtues – गुणांनी
7. कर्मणा – by deeds – कर्माने
8. श्रुतेन – by learning/ knowledge – ज्ञानाने
9. ताडनैः – by hammering – ठोकून
10. चतुर्भिः – by four (ways) – चार (प्रकारे)
11. परीक्ष्यते – is tested – तपासले जाते
12. यथा – तथा – just as – similarly – ज्याप्रमाणे – त्याप्रमाणे
13. विद्वज्जनः – learned – विद्वान
14. श्लाघ्यः – praiseworthy – स्तुतीस पात्र/प्रशंसनीय
15. एरण्ड : – castor plant – एरंड
16. अल्पधी: – dull-witted person – अल्पबुद्धी असलेला
17. निरस्तपादपे – no tree – वृक्षहीन
18. दुमायते – becomes a tree – वृक्ष मानला जातो
19. यत्र – तत्र – where-there – जेथे – तेथे
20. किञ्चिज्ञ – having scanty knowledge – अल्पज्ञान असलेला
21. मदान्धः – blinded with pride – मदाने आंधळा
22. व्यपगतः – disappeared – नाहीसा झाला
23. द्विपः इव – like an elephant – हतीसारखा
24. ज्वर: इव – like fever – तापासारखा
25. अवलिप्तम् – conceited – बेडले गेले
26. अवगतम् – learnt – समजले
27. बुधजनसकाशात् from learned – ज्ञानी मानसांकडून
28. समभवम् – I became – मी झालो
29. सर्वज्ञः अस्मि – know everything – मी सर्वज्ञ आहे
30. यदा-तदा – when-then – जेव्हा तेव्हा
31. भेतव्यम् – should frighten – घाबरून रहावे
32. अनागतम् – not arrived – आले नाही
33. वीक्ष्य – seeing carefully – काळजीपूर्वक पाहून
34. यथोचितं – should do what is – योग्य ते करावे
35. कुर्यात् – proper
36. यावद्-तावद् – as long as-till then जोपर्यंत – तोपर्यंत
37. उत्तमः – excellent
38. अधमः – inferior
39. कांस्य – bronze
40. उत्तम – अधम काशे
41. प्रजायते – is produced – निर्माण होतो
42. यादृक् – तादृक् – just as-likewise – जसा – तसा
43. न अतिवक्ता स्यात् – does not talk much – जास्त बोलत नाही
44. कर्षक: – farmer – शेतकरी
45. सुकृते – in good or bad – चांगल्या वा
46. दुष्कृते वा – deed – वाईट कृतीमध्ये
47. बीजं वपते – Sows seeds – धान्य पेरतो
48. फलं लभते – obtains a fruit – फळ मिळते
49. क्षेत्रमासाद्य – going to the fields – शेतात जाऊन
50. यादृशम् – just as – जसे
51. तादृशम् – likewise – तसे

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Anand Chapter 7 वाचनप्रशंसा Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Anand Chapter 7 वाचनप्रशंसा Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 7 Question Answer

Sanskrit Anand Std 10 Digest Chapter 7 वाचनप्रशंसा Textbook Questions and Answers

भाषाभ्यास:

1. पूर्णवाक्येन उत्तरं लिखत ।

प्रश्न अ.
वाचनेन के गुणाः वर्धन्ते ?
उत्तरम् :
वाचनेन शीलं, सद्गुणसम्पत्तिः, ज्ञानं, विज्ञानं उत्साहः च एते गुणा: वर्धन्ते।

प्रश्न आ.
वाचनेन मनुजाः किं बोधन्ते ?
उत्तरम् :
वाचनेन मनुजा: बहून् विषयान् बोधन्ते।

प्रश्न इ.
विद्यार्थिना कथं कालक्षेपः न कर्तव्यः ?
उत्तरम् :
विद्यार्थिना वृथाभ्रमणेन, कुक्रीडया, परपीडया, अपभाषणेन च कालक्षेपः न कर्तव्यः।

2. माध्यमभाषया उत्तरं लिखत ।

प्रश्न अ.
वाचनम् उपकारकं कथम् इति स्पष्टीकुरुत।
प्रश्न आ.
हितं सद्ग्रन्थवाचनम् इति कविः किमर्थं वदति?

3. समानार्थकशब्दान् लिखत ।
शीलम्, दक्षः, रताः, कालक्षेपः, वार्धक्यम्, पण्डितः

प्रश्न 1.
समानार्थकशब्दान् लिखत ।
शीलम्, दक्षः, रताः, कालक्षेपः, वार्धक्यम्, पण्डितः
उत्तरम् :

• शीलम् – चारित्र्यम्।
• दक्षः – सतर्कः, जागरुकः, तत्परः।
• रताः – तल्लीनाः, मग्नाः।
• कालक्षेपः – कालापव्ययः।
• वार्धक्यम् – वार्धकम, वृद्धावस्था, स्थाविरम्।
• पण्डितः – विद्वान्, विदग्धः, प्राज्ञः।

4. जालरेखाचित्रं पूरयत ।

प्रश्न अ.

उत्तरम् :

प्रश्न आ.

उत्तरम् :

प्रश्न इ.

उत्तरम् :

5. विरुद्धार्थकशब्दान् लिखत ।
सद्गुणः, उत्साहः, प्राचीनाः, उपकारकम्

प्रश्न 1.
विरुद्धार्थकशब्दान् लिखत ।
सद्गुणः, उत्साहः, प्राचीनाः, उपकारकम्
उत्तरम् :

1. सद्गुणः × दुर्गुणः।
2. उत्साहः × अनुत्साहः ।
3. प्राचीनाः × अर्वाचीनाः ।
4. उपकारकम् × अपकारकम्।

6. सन्धिविग्रहं कुरुत ।

प्रश्न अ.
वाचनेनैव
उत्तरम् :
वाचनेनैव – वाचनेन + एव।

प्रश्न आ.
अद्ययावद्धि
उत्तरम् :
अद्ययावद्धि – अद्ययावत् + हि।

7. विशेषण-विशेष्याणां मेलनं कुरुत ।

प्रश्न 1.

विशेषणम्	विशेष्यम्
उपकारकम्	मनुजाः
प्राचीनाः	विषयान्
दक्षाः	वाचनम्
बहून्	कविपण्डिताः

उत्तरम् :

विशेषणम्	विशेष्यम्
उपकारकम्	वाचनम्
प्राचीनाः	कविपण्डिताः
दक्षाः	मनुजाः
बहून्	विषयान्

8. अमरकोषात् योग्यं समानार्थशब्दं योजयित्वा वाक्यं पुनर्लिखत ।

प्रश्न अ.
मनुजाः वाचनेन बहून् विषयान् बोधन्ते ।
उत्तरम् :
मनुष्याः / मानुषा: / माः / मानवाः / नरा: वाचनेन बहून् विषयान् बोधन्ते।

वाचनप्रशंसा Summary in Marathi and English

प्रस्तावना :

क्षेपणास्त्रक्षेत्राच्या विकासकार्यातील योगदानामुळे सन्मानननीय डॉ. ए.पी.जे. अब्दुल कलाम यांना ‘इंडियाज मिसाईलमॅन’ असे संबोधित करण्यात आले. तसेच तरुणवर्ग व लोकांना प्रगतीपथावर जाण्यासाठी नेहमी प्रोत्साहित करणाऱ्या या राष्ट्रपतींना ‘पिपल्स प्रेसिडण्ट’ (लोकांचे राष्ट्रपती) हा किताबही देण्यात आला होता.

डॉ. ए.पी.जे. अब्दुल कलाम यांनी पुस्तकांना आजन्म सोबती मानले. त्यांनी म्हटले आहे, “चांगल्या पुस्तकाच्या संपर्कात येणे व त्याला बाळगणे ही चिरस्थायी संपन्नता आहे.” ते पुस्तकांचा आदर करायचे. म्हणूनच, त्यांची जन्मतिथी, 15 ऑक्टोबर हा ‘वाचनप्रेरणा दिवस’ म्हणून पाळला जातो. वाचनप्रशंसा हे पद्य, वैविध्यपूर्ण पुस्तकांच्या वाचनामुळे होणाऱ्या लाभावर प्रकाश टाकते.

Honourable Dr. A.P.J. Abdul Kalam was titled as ‘India’s missile man’ for his work in the development of missiles. Also, he was labelled as ‘People’s president’ as he often spoke and inspired youth for their development.

Dr. A.P.J. Abdul Kalam considered the book as a permanent companion. He said, “Coming into contact with a good book and possessing it is indeed an everlasting enrichment.” He used to respect books. So, his birth date 15 October is celebrated as ‘वाचनप्रेरणादिवस’ that means, a day to promote, reading. वाचनप्रशंसा throws light on the benefits of reading various books.

श्लोकः 1

शीलं सद्गुणसम्पत्तिः ज्ञानं विज्ञानमेव च।
उत्साहो वर्धते येन वाचनं तद् हितावहम् ।।1।।

अनुवादः

ते वाचन हितावह आहे, ज्यामुळे मनुष्याचे चारित्र्य, सद्गुणरूपी संपत्ती, ज्ञान, विशेष आकलन व उत्साह (यांचे) संवर्धन होते.

That reading is beneficial which enhances a man’s character, treasure in a form of good virtues, knowledge, comprehension and enthusiasm (towards learning).

श्लोक: 2

मनुजा वाचनेनैव बोधन्ते विषयान् बहून्।
दक्षा भवन्ति कार्येषु वाचनेन बहुश्रुताः।।2।।

अनुवादः

केवळ वाचनाने लोकांना अनेक विषयांचे आकलन होते. (लोक) वाचनामुळे (त्यांच्या) कार्यात दक्ष व सुविद्य होतात.
People understand many subjects by mere reading. They become prompt/alert in work and well versed/knowledgeable by reading.

श्लोक: 3

वाल्मीकिव्यासबाणाद्याः प्राचीनाः कविपण्डिताः।
तान् शिक्षयन्ति सततं ये सदा वाचने रताः।।3।।
अन्वय:- ये सदा वाचने रताः तान् वाल्मीकि-व्यास-बाणाद्याः प्राचीनाः कविपण्डिताः शिक्षयन्ति।

अनुवादः

जे नेहमी वाचनामध्ये मग्न असतात, त्यांना, वाल्मीकि, व्यास, बाण इ. कवी व विद्वान (त्यांच्या लिखाणातून) नेहमी शिकवितात. (या कवींचे साहित्य वाचल्यास वाचकांचा भ्रम दूर होऊन ते ज्ञानी बनतात.)

Ancient poets and scholars like वाल्मीकि, व्यास, बाण etc. teach those who are always engrossed in reading (The works of these poets enlighten readers and make them knowledgeable.)

श्लोकः 4

अद्ययावद्धि ज्ञानाय वृत्तपत्रं पठेत्सदा।
सर्वविधसुविद्यार्थ वाचनमुपकारकम्।।4।।

अनुवादः

मनुष्याने अद्ययावत ज्ञान (माहिती) मिळण्यासाठी नेहमी वर्तमानपत्र वाचावे. वाचन हे सर्व प्रकारचे ज्ञान मिळविण्यासाठी (अतिशय) उपयुक्त आहे.

Indeed, a man should always read a newspaper for updated knowledge, Reading is helpful (useful) for all sorts of learning

श्लोकः 5

वथाभ्रमणकुक्क्रीडापरपीडापभाषणैः।
कालक्षेपो न कर्तव्यो विद्यार्थी वाचनं श्रयेत्।।5।।

अनुवादः

विद्यार्थ्यांनी दिशाहीन भटकण्यात, अपायकारक क्रीडा खेळण्यात, इतरांना क्लेश (त्रास) देण्यात, (व) (इतरांना) बोल लावण्यात (दोष देण्यात) वेळ वाया घालवू नये. विद्यार्थ्याने वाचनाचा आश्रय घ्यावा. (वाचनात अधिकाधिक मग्न असावे) स्पष्टीकरण – वाचनाने माणसाचे चारित्र्य समृद्ध होते, याउलट, विद्यार्थी श्लोकात उद्धृत केलेल्या वायफळ कृतींमध्ये मग्न असल्यास, त्याचा वेळ तर वाया जातोच व त्याचे मनही कलुषित होते.

A student should not waste time in wandering aimlessly, playing harmful game, troubling/ bothering others (and) by abusive talk. (Infact) A student should resort to reading. Explanation – Reading helps in building up good character, however, if a student is involved in abovementioned futile activities, he wastes his time and corrupts his mind.

श्लोकः 6

वाचनं ज्ञानदं बाल्ये तारुण्ये शीलरक्षकम्।
वार्थक्ये दुःखहरणं हितं सद्ग्रन्थवाचनम्।।6।।
अन्वयः- वाचनं बाल्ये ज्ञानदं, तारुण्ये शीलरक्षकम्, वार्धक्ये दुःखहरणं (भवति) (अत:) सद्ग्रन्थवाचनं हितं (भवति)।

अनुवादः

वाचन लहानपणात ज्ञान देणारे, तरुणपणी चारित्र्याचे संरक्षण करणारे, (व) म्हातारपणात दुःख दूर करणारे आहे. (म्हणून) चांगल्या पुस्तकांचे वाचन हितावह असते.

Reading gives knowledge in the childhood, (it) guards the character in the youth, (it) wards off sorrow in the old age. (Hence) Reading good books (is beneficial.

सन्धिविग्रहः

1. विज्ञानमेव – विज्ञानम् + एव।
2. उत्साहो वर्धते . उत्साहः + वर्धते।
3. दक्षा भवन्ति – दक्षा: + भवन्ति ।
4. पठेत्सदा – पठेत् + सदा।
5. कालक्षेपो न – कालक्षेप: + न ।
6. कर्तव्यो विद्यार्थी – कर्तव्यः + विद्यार्थी।
7. वाचनमुपकारकम् – वाचनम् + उपकारकम्।

शब्दार्थाः

1. उत्साहः – enthusiasm – उत्साह
2. सम्पत्तिः – treasure/wealth – संपन्नता
3. शीलम् – character – चारित्र्य
4. विज्ञानम् – comprehension, wisdom – विशेष आकलन, शहाणपणा
5. हितावहम् – beneficial – हितकारक
6. वर्धते – increases – वाढते
7. पण्डिताः – scholars – विद्वान
8. प्राचीनाः – ancient – प्राचीन
9. रताः – engrossed – मग्न
10. शिकवितात – teach /educate – शिक्षयन्ति
11. सर्वविध – of all sorts – सर्व प्रकारच्या
12. वृत्तपत्रम् – newspaper – वर्तमानपत्र
13. उपकारकम् – useful / helpful – उपयोगी / उपयुक्त
14. अद्ययावत् – updated – अद्ययावत
15. सुविद्यार्थम् – for good learning – ज्ञानासाठी
16. वृथाभ्रमण – aimless wandering – दिशाहीन भटकणे
17. अपभाषण – abusive talk – चुकीचे बोलणे
18. कुक्रीडा – harmful game – अपायकारक खेळ
19. परपीडा – troubling others – इतरांना त्रास देणे
20. कालक्षेप:न – should not waste – वेळ वाया घालवू नये
21. कर्तव्यः – time
22. श्रयेत् – one should resort to – आश्रय घ्यावा (अवलंब करावा)
23. ज्ञानदम् – gives knowledge – ज्ञान देणारे
24. शीलरक्षकम् – guards the character – चारित्र्याचे संरक्षण करणारे
25. बाल्ये – in the childhood – लहानपणी
26. तारुण्ये – in the youth – तरुणपणात
27. वार्धक्ये – in the old age – म्हातारपणी
28. दुःखहरणं भवति – wards off sorrow – दुःख दूर करते
29. दक्षाः – prompt / alert – दक्ष, सावध
30. बोधन्ते – understand – आकलन होते
31. बहुश्रुताः – well-versed/ knowledgeable – सुविद्य

10th Standard Sanskrit Anand Digest Pdf  

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्यस्तबकः Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Aamod Chapter 10 नदीसूक्तम् Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 10 नदीसूक्तम् Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 10 Question Answer

Sanskrit Amod Std 10 Digest Chapter 10 नदीसूक्तम् Textbook Questions and Answers

भाषाभ्यास:

1. माध्यमभाषया उत्तरत ।

प्रश्न अ.
विश्वामित्र: नद्यौ किं प्रार्थयते ?
उत्तरम् :
विश्वामित्र – नदी संवाद, हे संवादसूक्त ऋग्वेदाच्या तिसऱ्या मंडलात आढळते. यामध्ये, विश्वामित्र ऋषी नदीला मातेसमान मानून तिची पूजा करतात आणि तिला जपण्याचे व तिची सेवा करण्याचे वचन देतात.

विश्वामित्र ऋषी बियास व सतलज नद्यांच्या संगमाजवळ पोहोचले. तेव्हा त्यांनी नद्यांना आदरयुक्त शुभेच्छा दिल्या. त्यांनी नद्यांना ‘माता’ असे संबोधून त्यांना उथळ होण्याची विनंती केली. याचप्रमाणे विश्वामित्रांनी नद्यांना त्यांचे प्रवाह कमी करण्यासाठी प्रार्थना केली.

विश्वामित्र – नदी संवाद is one of the dialogue-hymns found in third मण्डल of ऋग्वेद. Herein the sage विश्वामित्र worships river asa mother and pleases her with the assurance to take care of her and serve her.

विश्वामित्र, reached the union of Bias and Sutlej river. Then he greeted the rivers with respect. He termed rivers as mother and requested them to become shallow. He requested them to moderate the flow.

प्रश्न आ.
मानवानां जीवनं नदीनां साहाय्येन कथं समृद्धं जातम् ?
उत्तरम् :
विश्वामित्र – नदी संवाद, हे संवादसूक्त ऋग्वेदाच्या तिसऱ्या मंडलात आढळते. यामध्ये, विश्वामित्र ऋषी नदीला मातेसमान मानून तिची पूजा करतात आणि तिला जपण्याचे व तिची सेवा करण्याचे वचन देतात.

संपूर्ण पृथ्वीवर नदीजल हा पाण्याचा उपयुक्त स्रोत आहे. पुष्कळ वर्षांपासून नद्या या शेतीमध्ये शेतकऱ्यांना उपयुक्त ठरतात. केवल शेतांचीच नव्हे तर संपूर्ण पृथ्वीची पाण्यामुळे भरभराट झाली. पाण्याचा योग्य प्रकारे संचय करुन वीजनिर्मितीकरता जनित्र (जनरेटर) सुद्धा लावले गेले व मानवाचे जीवन पाण्यामुळे प्रकाशमान झाले. या प्रकारे नद्यांच्या साहाय्याने मानवी जीवन समृद्ध झाले.

विश्वामित्र – नदी संवाद is one of the dialogue-hymns found in third मण्डल of ऋग्वेद. Herein the sage विश्वामित्र worships river as a mother and pleases her with the assurance to take care of her and serve her.

River water is a useful source. Since many years, rivers are helpful to the farmers in agriculture. Not only the fields but the earth is prospered due to rivers. River water was well-restored. Even the generator was placed for creating electricity, thus water illuminated lives of.people. In this way human lives were flourished with the assistance of rivers..

नदीसूक्तम् Summary in Marathi and English

प्रस्तावना :

ऋग्वेद संस्कृत साहित्यातील अतिशय प्राचीन वेद मानला जातो. पौराणिक प्रसंग, काव्य, प्रार्थना यांनी युक्त अशा दहा मंडलांनी तो समृद्ध आहे. ऋग्वेदाच्या विविध सूक्तांतून देव, देवता व नैसर्गिक शक्ती यांचे स्तवन केलेले दिसून येते.

विश्वामित्र – नदी संवाद, हे संवादसूक्त ऋग्वेदाच्या तिसऱ्या मंडलात आढळते. यामध्ये, विश्वामित्र ऋषी नदीला मातेसमान मानून तिची पूजा करतात आणि तिला जपण्याचे व तिची सेवा करण्याचे वचन देतात.

पाण्याचा उत्तम स्रोत असलेल्या नद्यांच्या तीरावर मानवी संस्कृती विकसित होत गेली. पाण्याच्या प्राणवाहक तत्त्वामुळे, धार्मिक कार्यातील त्याच्या विनियोगामुळे व स्वच्छतेवर दिला गेलेला भर, यामुळे भारतीय संस्कृतीमध्ये पाण्याला विशेष महत्त्व प्राप्त झाले आहे. यास्तव, आपण सर्वांनी नद्यांचे रक्षण करावयास हवे.

नेमका हाच विचार महोदया डॉ. मंजूषा गोखले यांनी ऋग्वेदातील नदीसूक्तावर आधारित संवादपाठात मांडला आहे.

ऋग्वेद is considered to be the most ancient perhaps the foremost literature in Sanskrit. It is comprised of ten HUSE is filled with liturgical material as well as mythological accounts, poetry and prayers.

Gods, goddesses, natural elements are praised through hymns of in a poetic form. विश्वामित्र – नदी संवाद, is one of the dialogue-hymns found in third मण्डल of ऋग्वेद. Herein the sage विश्वामित्र worships नदी (river) as a mother and pleases her with the assurance to care and serve her.

Human civilisation expanded on the banks of the river. Indeed, water is of special significance in Indian culture for its life-sustaining properties as well as its use in rituals and because of the stress given to cleanliness.

Hence, we should take care of the rivers. This thought is appropriately brought out through the dialogue based on नदीसूक्तम् from ऋग्वेद written by respectable Dr. Manjusha Gokhale.

अनुवादः

व्यासपीठावर – कीर्तनकार कीर्तन करत आहे, श्रोतृगण ऐकण्यात तल्लीन झाला आहे.)

गंगे, यमुने, गोदावरी, सरस्वती, नर्मदे, सिंधु, कावेरी (सर्व नद्यांनो) पृथ्वीवर (तुमचा) संगम होवो. (हिंदू पंचांगाप्रमाणे) ज्येष्ठ महिन्यात, शुक्लपक्षातील दशमीला गंगादशहरा उत्सवाचा प्रारंभ होतो. या उत्सवामध्ये नदीची पूजा करावी.

(टीप : पवित्र असणाऱ्या गंगानदीचे स्वर्गातून पृथ्वीवर याच दिवशी अवतरण झाले, असे मानतात. म्हणून हा दिवस गङ्गादशहरा किंवा गङ्गावतरणम् या नावाने साजरा केला जातो.) श्रोतृगण – नदीचे पूजन? नदीचे पूजन कशासाठी (करायचे)?

कीर्तनकार – खरोखर, नदी जीवन देणारी आहे. म्हणून या प्रसंगी, कृतज्ञता दर्शविण्यासाठी लोक पाण्यामध्ये दीपदान करतात. द्रोणामध्ये दिवे लावून नदीच्या पाण्यामध्ये अर्पण करतात. (पाण्यात सोडतात).

पिण्यासाठी पाणी (उपयोगात येते.) शेतीची वाढ होण्यासाठी (पाण्याचा उपयोग होतो.) वीज निर्माण करण्यासाठी (पाणी वापरले जाते.) (खरोखरच), पाणी जीवन जगण्यासाठी (महत्त्वाचे ठरते.) सजीवांसाठी नदी देवीतुल्य आहे. नदी ही मातृतुल्य आहे. यास्तव, आज सर्व प्रकारे नदीसूक्त ऐकण्याजोगे व स्मरणीय आहे.

श्रोतृगण – अहो पुराणिकवर्य, नदी आपली माता कशी म्हणता येईल? नदीचे (आपल्यावर) उपकार कसे काय?

कीर्तनकार – सज्जनहो ऐका. ही कथा फार जुनी आहे. कुशिकांचे पुत्र विश्वामित्र नावाचे एक श्रेष्ठ मुनी होते. कुटुंबासहित व गोधनासहित ते दूरवरुन आले होते. मार्ग चालत चालत ते बियास व शुतुद्री (सतलज) या नद्यांच्या संगमाजवळ पोहोचले.
(त्यानंतर विश्वामित्र प्रवेश करतो. नदीला प्रणाम करुन / नमस्कार करुन)

विश्वामित्र – मी नदीचा प्रवाह कसा पार करू? गोधनाचे कसे रक्षण करू? (दुसऱ्या तीरापर्यंत) ओलांडून जाण्यासाठी मार्गाची याचना कशी करू? नद्यांकरिता शुभेच्छांची प्रार्थना कशी करू?

नदी (बियास) – हा माणूस कोण आहे? हा कशासाठी आपल्याला वंदन करत आहे व (आपली) प्रशंसा करत आहे? आर्य, (आपले) तुमचे नाव काय आहे? आम्हांला कोवून बोलावत आहेस?

विश्वामित्र – माते, मी विश्वामित्र आहे. मी रथ व गाड्यांसहीत दूरवरून आलो आहे. आम्ही सर्व दुसऱ्या तीरावर जाण्यासाठी उत्सुक आहोत.

नदी (सतजल) – हे ब्राह्मणश्रेष्ठा, तुझी वाणी खरोखर गोड आहे. (ती)
आम्हाला आनंदित करत आहे. (आम्हांला) सांग, आम्ही तुला कसे साहाय्य करू?

विश्वामित्र – माते, माझी विनंती ऐक तू माझ्यासाठी उथळ होशील का? कृपया पाण्याचा ओघ कमी कर. ज्यामुळे आम्ही सर्व दुसऱ्या तीरावर सहज जाऊ शकतो.

नदी (बियास) – खरचं, इंद्रदेवाने मला. हा मार्ग दिला आहे. वृत्रासुराला मारुन इंद्राने(च) नदीचा प्रवाह मोकळा करुन दिला आहे. मी त्याची अवज्ञा करू शकत नाही, (अन्यथा) इंद्रदेव माझ्यावर रुष्ट होतील / रागावतील (म्हणून) हे विश्वामित्रा, मला क्षमा कर. (मी) कधीही विराम घेऊ शकत नाही.

दोन्ही नद्या – हे विश्वमित्रा, आम्ही तुझ्यासाठी थांबू शकत नाही. इंद्रदेवाच्या कार्यात अधिक्षेपही करू शकत नाही.

विश्वामित्र – हे माते, इंद्रदेवाची अवज्ञा (अपमान) नको (च) करू, आम्ही केवळ दुसऱ्या तीरावर जाण्याची इच्छा करतो. माते, कृपा कर, आम्ही सर्व तुझीच मुले आहोत. / तुझेच पुत्र आहोत. तुझे उपकार आम्ही कधीही विसरणार नाही. आम्ही असे काही करणार नाही ज्याने तुझा अवमान होईल. ही माझी प्रतिज्ञा आहे.

नदी (बियास) – काय? हा माणूस मला माते असे संबोधत आहे?

नदी (सतजल) – आई स्वत:च्या पुत्राला मदत कशी नाही करणार? हे मानवश्रेष्ठा, फारच छान. पण, तुझे वंशज जर हे वचन विसरले तर?

विश्वामित्र – नाही माते, हे शक्य नाही. (असे होणार नाही) सगळ्या नद्या सुखाने वाहू देत. सर्व लोक सुखी असू देत. (विश्वामित्र जातात).

कीर्तनकार – अशा रितीने, नद्यांना आनंदित करुन विश्वामित्र दुसऱ्या तीरावर गेला, श्रोत्यांनो, अशा प्रकारे, नद्यांनी व लोकांनी परस्परांना संतुष्ट करुन संस्कृतीचे संवर्धन केले. नदी वाहत आहे.

संस्कृती विकसित झाली आहे (आणि) नदीच्या कृपेने मानव आनंदित झाले आहेत.

शेतकरी आनंदित झाले आहेत, पृथ्वी आनंदली आहे. (ही) पृथ्वी, अन्नदात्री असून समृद्ध झाली आहे. नद्यांचे पाणी नियंत्रित केले आहे. व सेतूंनी (योग्यपणे) रोखले आहे. येथे जनित्र चालविण्यात आले आहे. (एकंदरीतच) आयुष्य प्रकाशित झाले
आहे.

श्रोत्यांनो, या रितीने नद्यांच्या साहाय्याने मानवी जीवन नद्यांच्या काठावर समृद्ध झाले आहे. आता सांगा, विश्वामित्राचे वंशज असलेले आपण सर्व मानव, आजही त्याचे वचन पाळतो का?

(On the stage, कीर्तनकार, a person is singing कीर्तन (spiritual teaching through story telling), audience is engrossed in listening to it.) 0 गङ्गा, यमुना, गोदावरी, सरस्वती, नर्मदा, सिन्धु (Indus), कावेरी. May (you all) unite on the earth.

The festival of TSTARTET commences on the tenth day of the waxing moon, in the month of ज्येष्ठ (according to Hindu calendar).

The river should be worshipped on this festival. (Note: It is believed that the holy river गङ्गा descended from the heaven on the earth on this day. Thus, this day is celebrated as गङ्गावतरणम्)

Audience – Worshipping the river? Why we should worship the river?

कीर्तनकार – Indeed, the river gives (us) life. Therefore, On this occasion, people release lamps in the river to express gratitude. By lighting the small lamp in a leaf-bowl, people offer it to the river -water.

Water (can be used) for drinking. (it is used) to prosper the agriculture (It is used) to create the electricity (Indeed) the water is for (sustaining) life. The river is like goddess for living beings. The river is like mother. Hence, today by all means नदीसूक्त is worth-listening and remembering.

Audience – O great पुराणिक, How the river can be considered as our mother? How has she favoured us?

कीर्तनकार – O noble people, please listen.

Indeed this story is very old. There was a great sage named विश्वामित्र, the son of कुशिक, He had come from afar with his family and cows. Following the way, he reached the union of bias and Sutlej river. (Then enters विश्वामित्र. Saluting the river.)

विश्वामित्र – How to cross the river-flow? How to save cows? How shall I ask them a path for crossing? How shall I pray for well-being of rivers.

River (Bias) – Who is this man? Why does he salute and praise us? O noble one, What is the name of the respected one? From where are you calling us?

विश्वामित्र – Omother, I am विश्वामित्र. I have come from a far along with chariots and carts. We all are eager to go to the other bank.

River (Sutlaj) – O great brahmin, your speech is really sweet. It pleases us. Please tell, how shall we assist you?

विश्वामित्र – O mother, please listen to my request. Will you please become shallow for me? Please attenuate (moderate) the water force by which we can go to the other bank easily.

River (Bias) – Indeed, the Lord इंद्र has given me the path having killed the demon, released the flow of the river. I should not insult it, (or else) the Lord will be displeased / angry with us. (Hence), O विश्वामित्र, forgive me. There can’t be cessation ever.

Both rivers – O विश्वामित्र, We can’t stop for you. We can’t interfere in the Lord’s task.

विश्वामित्र – O mother, please do not disregard the Lord Indra’s words. We just wish to go to the other bank. O mother, please favour me. We all are your sons. We shall never forget your favour. We will not behave (wrong) due to which you will be discredited. This (indeed) is my pledge.

River (Bias) – What? Does this man call me mother?

River (Sutlej) – How would a mother not help her child? O, great man, very good. But what if your descendants forget this promise?

विश्वामित्र – No mother. This is not possible. (This won’t happen) may all rivers flow happily? May all people be happy. (विश्वामित्र exits).

कीर्तनकार – In this way, विश्वामित्र, pleasing both rivers went to the other bank. O listeners, In this way, rivers and people having gratified each other, expanded the culture. The river flows, The culture is developed and People are risen up (advanced) due to favour of the river.

Farmers are happy, The earth is delighted. The earth is independent in terms of food grains (because of fertility) and bountiful. The river water is obstructed and controlled by bridges. The generator is placed here (and) the life is gleaned.

O listeners, In this way, with the help of rivers itself, human life has prospered. Now tell (me), Do we all, the descendants of (विश्वामित्र) keep his promise even today?

शब्दार्थाः

1. श्रोतृवृन्दः – audience – श्रोतृगण
2. सङ्गमः – union – संगम
3. जलौघः – water flow – पाण्याचा ओघ
4. वज्रहस्त: – Lord Indra – इंद्रदेव
5. विराम: – stop/halt – थांबा
6. मर्त्यः – man – मनुष्य
7. लङ्घनीयः – fit to cross – ओलांडण्यायोग्य
8. याचितव्यः – worthy to be asked for – याचना करण्यायोग्य
9. प्रदत्तवान् – has given – दिला आहे
10. विमुक्तवान् – released – मुक्त केला आहे
11. आक्रामन् – crossing – ओलांडून जाणारा
12. अभ्यर्थना – request – विनंती
13. गाधा – shallow – उथळ
14. अवज्ञा – disregard – अपमान
15. प्रफुल्लिता – shines – सुंदर दिसत आहे
16. कृतज्ञता – gratitude – कृतज्ञता
17. जीवनदायिनी – giver of life – जीवन देणारी
18. जनित्रम् – generator – जनित्र
19. श्रवणीयम् – worth listening – ऐकण्याजोगे
20. आर्या: – good people – सृजन
21. वंशजा: – descendants – वंशज
22. अधिक्षेपम् – insult – अवमान
23. शकटैः – with carts – गाड्यांसहित
24. रङ्गमछे – on the stage – रंगमंचावर
25. पर्वणि – on the festival – उत्सवसमयी
26. विप्रवर – O great brahmin – हे ब्राह्मणश्रेष्ठा
27. स्तौति – praises – स्तुती करतो
28. आह्वयति – approaches – बोलावतो
29. रजयति – pleases – आनंदित करतो/ते
30. स्वल्पीभवतु – may attenuate – कमी होवो
31. प्रसीद – please do favour – कृपा करा
32. हत्वा – having killed – मारून
33. प्रीणयित्वा – gratifying – संतुष्ट करुन
34. इत्थम् – in this manner – अशा रितीने
35. प्राशनार्थम् – for drinking – पिण्यासाठी
36. विद्युनिर्माणथम् – for generating electricity – वीज निर्माण करण्यासाठी
37. सन्निधिं कुरु – may unite – संगम होवो
38. अपि वचनम् – do we keep a – आपण वचन
39. अनुसरामः – promise? – पाळतो का?

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Class 10th Sanskrit Aamod Chapter 2 व्यसने मित्रपरीक्षा Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Sanskrit Solutions Amod Chapter 2 व्यसने मित्रपरीक्षा Notes, Textbook Exercise Important Questions and Answers.

Std 10 Sanskrit Chapter 2 Question Answer

Sanskrit Amod Std 10 Digest Chapter 2 व्यसने मित्रपरीक्षा Textbook Questions and Answers

अवबोधनम्‌ :

1. पूर्णवाक्येन उत्तरं लिखत ।

प्रश्न अ.
अरण्ये कौ निवसतः स्म ?
उत्तरम्‌ :‌
अरण्ये मृग: काक:च निवसतः स्म।

प्रश्न आ.
काकः किम् उपादिशत् ?
‌उत्तरम्‌ :‌
काक: उपादिशत्, “अकस्मादागन्तुना सह मित्रता न युक्ता।”

प्रश्न इ.
मृगः प्रत्यहं क्षेत्रं गत्वा किम् अकरोत् ?
‌उत्तरम्‌ :‌
मृगः प्रत्यहं क्षेत्रं गत्वा सस्यम् अखादत् ।

प्रश्न ई.
क्षुद्रबुद्धिः कुत्र निभृतं स्थितः ?
‌उत्तरम्‌ :‌
क्षुद्रबुद्धिः समीपमेव वक्षस्य पृष्ठतः निभृतं स्थितः।

प्रश्न उ.
शृगालः केन हतः ?
‌उत्तरम्‌ :‌
क्षेत्रपतिना क्षिप्तेन लगुडेन शृगालः हतः।

2. कः कं वदति ?

प्रश्न अ.
‘वनेऽस्मिन् एकं सस्यपूर्ण क्षेत्रमस्ति ।’
‌उत्तरम्‌ :‌
जम्बूक; मृगं वदति।

प्रश्न आ.
‘मित्र, छिन्धि तावन्मम बन्धनम् ।’
‌उत्तरम्‌ :‌
मृग: जम्बूकं वदति।

प्रश्न इ.
‘स वञ्चक: क्वास्ते ?’
‌उत्तरम्‌ :‌
काकः मृगं वदति।

3. प्रश्ननिर्माणं कुरुत ।

प्रश्न अ.
शृगालः मृगेण सह मित्रताम् ऐच्छत् ।
‌उत्तरम्‌ :‌
शृगाल: केन सह मित्रताम् ऐच्छत् ?

प्रश्न आ.
प्रदोषकाले मृगमन्विष्यन् काकः क्षेत्रे उपस्थितः।
‌उत्तरम्‌ :‌
कदा मृगमन्विष्यन् काकः क्षेत्रे उपस्थितः?

प्रश्न इ.
स: वृक्षस्य पृष्ठतः निभृतं स्थितः।
‌उत्तरम्‌ :‌
स: वृक्षस्य पृष्ठतः कथं स्थितः?

4. उत्तरपदं लिखत ।

प्रश्न 1.
अ. काकोऽवदत् = काकः + …………… ।
आ. मृगेणोक्तम् = मृगेण + …………… ।
इ. जम्बूकोऽयम् = जम्बूकः + ………….. ।
‌उत्तरम्‌ :‌
अ. काकोऽवदत् – काकः + अवदत्।
आ. मृगेणोक्तम् – मृगेण + उक्तम्।
इ. जम्बूकोऽयम् – जम्बूकः + अयम्।

5. पूर्वपदं लिखत ।

प्रश्न 1.
अ. मृगोऽब्रवीत् = …………….. + अब्रवीत्
आ. वातेनोदरम् = …………… + उदरम्
इ. मृतोऽसि = ………………. + असि
‌उत्तरम्‌ :‌
अ. मृगोऽब्रवीत् – मृगः + अब्रवीत्।
आ. वातेनोदरम् – वातेन + उदरम्।
इ. मृतोऽसि – मृत: + असि।

6. सूचनानुसारं कृती: कुरुत ।

ऊ. त्वं सत्वरं पलायिष्यसे । (‘त्वं’ स्थाने ‘भवान्’ योजयत ।)

प्रश्न अ.
मृगः प्रत्यहं तत्र गत्वा सस्यम् अखादत्। (त्वान्त-अव्ययं निष्कासयत ।)
उत्तरम् :
मृगः प्रत्यहं तत्र अगच्छत् सस्यम् अखादत् च।

प्रश्न आ.
मित्र छिन्धि तावन्मम बन्धनम् । (लकारं लिखत ।)
उत्तरम् :
लोट्लकार:

प्रश्न इ.
वयम् आनन्देन एकत्र निवसामः । (लट्लकारस्थाने लङ्लकारं योजयत ।)
उत्तरम् :
वयम् आनन्देन एकत्र न्यवसाम।

प्रश्न ई.
त्वं पादान्स्तब्धीकृत्य तिष्ठ । (‘त्वं’ स्थाने ‘भवान्’ योजयत ।)
उत्तरम् :
भवान् पादान्स्तब्धीकृत्य तिष्ठतु ।

प्रश्न उ.
भवानपि अपरिचितः एव आसीत् । (‘भवान्’ स्थाने ‘त्वं’ योजयत ।)
उत्तरम् :
भवान् पादास्तब्धीकृत्य पलायिष्यते।

7. स्तम्भमेलनं कुरुत।

प्रश्न 1.
स्तम्भमेलनं कुरुत।

‌उत्तरम्‌ :‌

विशेषणम्	विशेष्यम्
1. दृढः	बन्धः
2. क्षिप्तेन	लगुडेन
3. एकस्मिन्	दिने
4. लगुडहस्तः	क्षेत्रपतिः

8. जालरेखाचित्रं पूरयत ।

प्रश्न 1.
जालरेखाचित्रं पूरयत ।

‌उत्तरम्‌ :‌

9. तालिकां पूरयत ।

प्रश्न 1.

(मञ्जूषा – त्रायस्व माम्, दर्शयामि त्वाम्, दृढोऽयं बन्धः, छिन्धि मम बन्धनम्)
‌उत्तरम्‌ :‌

जम्बूकः	मृगः
दर्शयामि त्वाम्।	त्रायस्व माम्।
दृढोऽयं बन्धः	छिन्धि मम बन्धनम्

प्रश्न 2.

(मञ्जूषा – अलं विवादेन, कोऽयं द्वितीयः?, एवमस्तु, अस्मत्सख्यम् इच्छति ।)
‌उत्तरम्‌ :‌

मृगः	काकः
अलं विवादेन।	कोऽयं द्वितीयः?
अस्मत्सख्यम् इच्छति।	एवमस्तु।

10. माध्यमभाषया उत्तरत ।

प्रश्न अ.
‘स नरः शत्रुनन्दनः’ इति वचनं कथायाः आधारेण स्पष्टीकुरुत ।
‌उत्तरम्‌ :‌
व्यसने मित्रपरीक्षा या कथेच्या संदर्भात ‘स: नरः शत्रुनन्दनः’ ही उक्ती आलेली दिसून येते. हितोपदेश या पुस्तकात मित्रलाभ 1.3. या प्रकरणात ही कथा आवळते. धूर्त कोल्हा हरिणाला त्याच्या शब्दांमध्ये फसवितो व त्याच्याशी मैत्री करतो. कोल्हा हरिणाला धान्यांनी भरलेले एक शेत दाखवितो.

साहजिकच हरिणाच्या मनात धान्याबद्दल हाव निर्माण होते. पण नंतर, शेताच्या मालकाने टाकलेल्या जाळ्यात हरिण अडकते. हरिणाने कोल्ह्याकडे मदत मागताच धूर्त कोल्हा जाळे घट्ट असल्याचे सांगतो. त्यामुळे तो तोडण्यास समर्थ नाही असे दर्शवितो.

हरिणाला कोल्ह्याचा धूर्तपणा हळूहळू लक्षात येतो. कावळ्याचे न ऐकल्याचा त्याला पश्चात्ताप होतो. जेव्हा कावळा हरिणाला शोधत शोधत हरिणाजवळ पोहोचतो, तेव्हा तो ‘स: नर: शत्रुनन्दनः’ हा श्लोक उद्धृत करतो. या श्लोकाचा अर्थ असा, की, “जो आपल्या मित्रांचा, हितचिंतकांचा सल्ला ऐकत नाही, तो संकटात सापडतो व त्याच्या शāना आनंदित करतो, त्यांचे शत्रुत्व ओढून घेतो.

हरिणाने अनोळखी प्राण्यांशी (कोल्ह्याशी) मैत्री न करण्याचा कावळ्याचा सल्ला ऐकला नाही व कोल्ह्याशी मैत्री केल्याने अखेर त्याला जाळ्यात अडकावे लागले. म्हणजे तो संकटात सापडला व हरिणाला शत्रुनन्दन हे विशेषण लागू पडले. ‘स: नरः शत्रुनन्दनः’ इति वचनं कथायाः आधारेण स्पष्टीकुरुत।

‘सः नरः शत्रुनन्दनः’ occurs in the context of the story व्यसने मित्रपरीक्षा. It is found in the chapter 1.3 of मित्रलाभ, in हितोपदेश. The crooked jackal trapped the deer in its words. It intentionally showed the deer a field full of grains. Due to greed for the grains, the deer got caught in the net set by the owner of the field. When the deer asked the jackal for his help, it cleverly answered, the net is tendon, so it can’t break it.

The deer understood the jackal’s plan. It repented for not listening to the crow’s advice. When crow came searching for him, It uttered the verse सुडदा …..स: नर:शत्रुनन्दन: which means, “The one who does not listen to the words of well-wishing friends, calamity becomes his neighbour and he pleases enemies.” The deer disregarded crow’s advice of not making friendship with strangers. It had friendship with a deceitful jackal and was finally trapped in the net. Seeing him caught in the net, the jackal became happy.

In this way, the deer proved himself as शत्रुनन्दन, the one whopleases enemies as the deer also pleased the mind of the crooked jackal.

प्रश्न आ.
काकेन क: उपायः उक्त : ?
‌उत्तरम्‌ :‌

व्यसने मित्रपरीक्षा या कथेच्या संदर्भात ‘स: नरः शत्रुनन्दनः’ ही उक्ती आलेली दिसून येते. हितोपदेश या पुस्तकात मित्रलाभ 1.3. या प्रकरणात ही कथा आढळते. शेताच्या मालकाने हरिणाला जाळ्यात अडकविले. कावळा हरिणाला शोधत तेथे आला. कावळ्याने विचारले असता हरिणाने सर्व हकीकत त्याला सांगितली. कोल्ह्याच्या धूर्तपणामुळे हरिण जाळ्यात अडकले होते.

कावळ्याने हरिणाला मेल्यासारखे दर्शविण्यास सांगितले, तसेच कावळ्याने हरिणाला पोट फुगवायला व पायही स्तब्ध ठेवण्यास सांगितले. कावळ्याच्या म्हणण्यानुसार वागल्यामुळे शेताच्या मालकाला हरिण मृत असल्याचा भास झाला. शेताचा मालक हरिणाजवळ आला व जाळे काढले. ठरल्याप्रमाणे कावळ्याने काव-काव असा आवाज केला. आवाज ऐकताच हरिण उठले व पटकन पळून गेले. कावळ्याने शोधलेल्या या उपायामुळे व त्याच्या चातुर्यामुळे हरिणाचे प्राण वाचले.

‘स: नरः शत्रुनन्दनः’ occurs in the context of the story व्यसने मित्रपरीक्षा. It is found in the chapter 1.3 of मित्रलाभ, in हितोपदेश. The deer was trapped in the net set by the owner of the field. The crow came in search of the deer. The crow saw the trapped deer. The deer narrated the account of a deceitful jackal.

The crow told the deer to pretend to be dead by blowing up its belly with air and told to keep legs stiff. The crow gave the deer an idea of running away. The deer followed likewise. The owner of the field thought the deer is certainly dead. So, he released the deer. At the same time, the crow made alarming sound and the deer ran away quickly. The crow’s wisdom and true friendship with the deer saved the deer’s life.

11. अमरकोषात् समानार्थकं शब्द योजयित्वा वाक्यं पुनर्लिखत ।

प्रश्न अ.
अरण्ये मृगः काकः च स्नेहेन निवसतः ।
‌उत्तरम्‌ :‌
अरण्ये कुरङ्गः / वातायुः / हरिणः / अजिनयोनिः काकः च सेहेन निवसतः।

प्रश्न आ.
जम्बूकः तेन सह मृगस्य निवासस्थानं गतः ।
‌उत्तरम्‌ :‌
शृगालः / वञ्चकः / क्रोष्टा / फेरुः / फेरव: तेन सह मृगस्य निवासस्थानं गतः ।

प्रश्न इ.
मृगमन्विष्यन् काक: तत्र उपस्थितः ।
‌उत्तरम्‌ :‌
मृगमन्विष्यन् करटः / अरिष्टः / बलिपुष्टः / सकृत्प्रज: तत्र उपस्थितः।

12. विरुद्धार्थकशब्द लिखत ।
दृढः, मैत्री, बद्धः, प्रभूतम् ।

प्रश्न 1.
विरुद्धार्थकशब्द लिखत ।
दृढः, मैत्री, बद्धः, प्रभूतम् ।
‌उत्तरम्‌ :‌

1. दृढः × शिथिलः।
2. मैत्री × शत्रुत्वम्, वैरम्।
3. बद्धः × मुक्तः ।
4. प्रभूतम् × अल्पम, स्तोकम, स्वल्पम्, न्यूनम्।

उपक्रम :
1. पाठात् उपपदविभक्तियुक्तानि वाक्यानि चित्वा लिखत ।
2. पाठात् शतृरूपाणि चित्वा लिखत ।

Sanskrit Amod Class 10 Textbook Solutions Chapter 2 व्यसने मित्रपरीक्षा Additional Important Questions and Answers

अवबोधनम्।

(क) उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
शृगालः मृगेण सह सख्यम् इच्छति यतः
(अ) शृगाल: मृगमांसं खादितुम् इच्छति।
(ब) शृगालः मृगे स्निह्यति।
उत्तरम् :
(अ) शृगाल: मृगमांसं खादितुम् इच्छति।

(ख) उचितं पर्यायं चित्वा वाक्यं लिखत।

प्रश्न 1.
शृगालः स्वार्थहतुना ………… सह मैत्रम् ऐच्छत्। (मृगेण / काकेन)
उत्तरम् :
शृगालः स्वार्थहतुना मगेण सह मैत्रम् ऐच्छत्।

(ग) पूर्णवाक्येन उत्तरत।

प्रश्न 1.
क: चित्राङ्गम् अपश्यत्?
उत्तरम् :
गाल: चित्राङ्गम् अपश्यत्।

प्रश्न 2.
शृगालस्य नाम किम् आसीत्?
उत्तरम् :
शृगालस्य नाम क्षुद्रबुद्धिः आसीत्।

प्रश्न 3.
शृगालः किमर्थं मृगेण सह मित्रताम् ऐच्छत्?
उत्तरम् :
शृगालः स्वार्थहेतुं पूरयितुं मृगेण सह मित्रताम् ऐच्छत्।

प्रश्न 4.
कदा क्षुद्रबुद्धिः निवासस्थानं गतः?
उत्तरम् :
अस्तङ्गते सवितरि क्षुद्रबुद्धिः निवासस्थानं गतः।

प्रश्न 5.
जम्बूकः किम् इच्छति?
उत्तरम् :
जम्बूक: मृगशृगालयोः सख्यम् इच्छति।

(घ) वाक्यं पुनर्लिखित्वा सत्यम्/असत्यम् इति लिखत।

प्रश्न 1.

1. अरण्ये एकाक्ष: नाम मृगः चित्राङ्ग नाम काक: निवसतः स्म।
2. शुदबुद्धिः उदिते सवितरि (सूर्योदये) निवासस्थानं गतः।
3. अकस्मात् आगन्तुना सह मैत्री युक्ता।

उत्तरम् :

1. असत्यम्।
2. असत्यम्।
3. असत्यम्।

(च) कः कं वदति।

प्रश्न 1.
“सखे चित्राङ्ग, कोऽयं द्वितीयः?”
उत्तरम् :
काक: मृगं वदति।

प्रश्न 2.
“जम्बूकोऽयम्। अस्मत्सख्यम् इच्छति।”
उत्तरम् :
मृगः काकं वदति।

प्रश्न 3.
“अकस्मादागन्तुना सह मित्रता न युक्ता।”
उत्तरम् :
काक: मृगं वदति।

प्रश्न 4.
मृगस्य प्रथमदर्शने भवानपि अपरिचितः एव आसीत्।
उत्तरम् :
शृगालः काकं वदति।

प्रश्न 5.
यथायं मृगः मम बन्धुः तथा भवानपि।
उत्तरम् :
शृगालः काकं वदति।

प्रश्न 6.
अलं विवादेन।
उत्तरम् :
मृग: काकशृगालौ वदति।

प्रश्न 7.
वयं सर्वे आनन्देन एकत्र निवसामः ।
उत्तरम् :
मृगः काकशृगाली वदति।

प्रश्न 8.
एवमस्तु।
उत्तरम् :
काकः मृगशृगाली वदति।

शब्दज्ञानम्।

(क) सन्धिविग्रहं कुरूत।

1. चित्राङ्गो नाम – चित्राङ्गः + नाम ।
2. एकाक्षो नाम – एकाक्ष: + नाम।
3. काकश्च – काकः + च।
4. केनापि – केन+अपि।
5. कोऽयम् – क + अयम्।
6. अकस्मादागन्तुना – अकस्मात् + आगन्तुना।
7. तदाकर्ण्य – तत् + आकर्य।
8. भवानपि – भवान् + अपि।
9. यथायम् – यथा + अयम्।
10. काकेनोक्तम् – काकेन + उक्तम्।
11. एवमस्तु – एवम् + अस्तु।

(ख) विशेषण – विशेष्य – सम्बन्धः।

विशेषणम्	विशेष्यम्
1. भ्रमन्	चित्राङ्गः
2. अस्त गते	सवितर

(ग) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि।

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा / अयित्वा	ल्यबन्त अव्यय – उपसर्ग + धातु + य / त्य
आकर्य	दृष्ट्वा

(घ) विभक्त्यन्तरूपाणि।

• प्रथमा – मृगः, काकः, भ्रमन्, सः, अयम्, जम्बूकः, भवान्, बन्धुः, वयम्, सर्वे।
• द्वितीया – सख्यम्, मित्रताम्।
• तृतीया – स्नेहेन, केन, शृगालेन, हेतुना, मृगेण, आगन्तुना, विवादेन, आनन्देन, काकेन।
• पञ्चमी – अस्मत्।
• सप्तमी – वने, सवितरि, दर्शन।

(च) लकारं लिखत।

प्रश्न 1.
1. शृगालः मृगेण सह मित्रताम् ऐच्छत्।
2. जम्बूक: सकोपम् आह।
उत्तरम् :
1. लङ्लकारः
2. लङ्लकार:

क्रमेण योजयत।

प्रश्न 1.

1. मृगकाकयोः नेहेन निवासः।
2. काकस्य उपदेशः।
3. मृगकाकशृगालानाम् एकत्र निवासः।
4. शुगालस्य मृगेण सह मित्रता।

उत्तरम् :

1. मृगकाकयोः स्नेहेन निवासः।
2. शृगालस्य मृगेण सह मित्रता।
3. काकस्य उपदेशः।
4. मृगकाकशृगालानाम् एका निवासः।

भाषाभ्यासः

(क) समानार्थकशब्दाः

1. अरण्यम् – काननम्, वनम्, विपिनम्, अटवी।
2. मृगः – हरिणः, कुरङ्गः, वातायुः, अजिनयोनिः ।
3. काकः – वायसः, करटः, ध्वाक्षः, अरिष्टः, बलिपुष्टः, सकृत्प्रजः।
4. शृगालः – जम्बूकः, वाकः, क्रोष्टा, फेरुः, फेरवः।

(क) उचितं कारणं चित्त्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
जम्बूक: मनसि आनन्दितः यतः
(अ) मृगः पाशे बद्धः।
(ब) जम्बूकस्य अन्येन सह मित्रता अभवत्।
उत्तरम् :
(अ) मृग: पाशे बद्धः।

(ख) उचितं पर्यायं चित्त्वा वाक्यं लिखत।

प्रश्न 1.

1. फलितं मे ……………..। (प्रयोजनम् / मनोरथम्)
2. ………………. मम शरणम्। (शत्रवः / सुहद:)
3. बने …………. क्षेत्रम् अस्ति। (सस्यविहीनं / सस्ययुक्त)

उत्तरम् :

1. मनोरथम्
2. सुहृदः
3. सस्ययुक्तं

(ग) पूर्णवाक्येन लिखत।

प्रश्न 1.
केन मृगस्य कृते पाशः योजितः?
उत्तरम् :
क्षेत्रपतिना मृगस्य कृते पाश: योजितः।

प्रश्न 2.
मृगं पाशैर्बद्धं दृष्ट्वा क: मनसि आनन्दितः?
उत्तरम् :
मृगं पाशैर्वद्धं दृष्ट्वा जम्बूक: मनसि आनन्दितः।

प्रश्न 3.
जम्बूक: मनसि किम् अचिन्तयत्?
उत्तरम् :
जम्बूक: मनसि अचिन्तयत्, ‘यत् फलितं मे मनोरथम्। इदानीं प्रभूतं भोजनं प्राप्स्यामि ।’

प्रश्न 4.
मृग: जम्बूकं दृष्ट्वा किम् अब्रवीत्?
उत्तरम् :
मृगः जम्बूकं दृष्ट्वा अब्रवीत्, “मित्र, छिन्धि तावन्मम बन्धनम्। त्रायस्व माम्।” इति ।

(घ) कः कं वदति।

प्रश्न 1.
दर्शयामि त्वाम्।
उत्तरम् :
जम्बूक: मृगं वदति।

प्रश्न 2.
दृढोऽयं बन्धः।
उत्तरम् :
जम्बूक: मृगं वदति।

प्रश्न 3.
स्नायुनिर्मितान् पाशानेतान् कथं वा व्रतदिवसे स्मृशामि।
उत्तरम् :
जम्बूकः मृगं वदति।

(च) वाक्यं पुनलिखित्वा सत्यम् / असत्यम् इति लिखत।

प्रश्न 1.

1. मृगः शृगालं सस्यपूर्ण क्षेत्रम् अदर्शयत्।
2. मृगः प्रतिदिन क्षेत्रे सस्यम् अखादत्।
3. जम्बूकः पाशैर्बद्धः।
4. जम्बूक: मनसि खिन्नः जातः।
5. जम्बूक: मृगं साहाय्यम् अकरोत्।
6. जम्बूक: निभृतं स्थितः।

उत्तरम् :

1. असत्यम्।
2. सत्यम्।
3. असत्यम्।
4. असत्यम्।
5. असत्यम्।
6. सत्यम्।

शब्दज्ञानम् ।

(क) सन्धिविग्रहः।

1. किञ्चित्कालानन्तरम् – किञ्चित् + कालानन्तरम् ।
2. वनेऽस्मिन् – बने + अस्मिन्।
3. क्षेत्रमस्ति – क्षेत्रम् + अस्ति ।
4. तत्रागतः – तत्र + आगतः।
5. पाशैर्बद्धः – पाशैः + बद्धः।
6. मित्राण्येव – मित्राणि + एव।
7. सोऽचिन्तयत् – स: + अचिन्तयत्।
8. मृगस्तम् – मृगः + तम्।
9. तावन्मम – तावत् + मम।
10. जम्बूको दूरादेवावदत् – जम्बूक: + दुरात् + एव + अवदत्।
11. दृढोऽयम् – दृढ : + अयम्।
12. पाशानेतान् – पाशान् + एतान्।
13. इत्युक्त्वा . इति + उक्त्वा ।
14. समीपमेव – समीपम् + एव।

(ख) विशेषाण – विशेष्य – सम्बन्धः।

विशेषणम्	विशेष्यम्
1. सस्यपूर्णम्	क्षेत्रम्
2. मगः	बद्धः
3. प्रभूतम	भोजनम्
4. स्नायुनिर्मितान्	पाशान्

(ग) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि।

त्वान्त अव्यय धातु + त्वा/ध्वा/ट्वा/वा/इत्वा/अयित्वा

दृष्ट्वा, उक्त्वा

(घ) विभक्त्यन्तरूपाणि।

• प्रथमा – शृगालः, पाशः, सः, जम्बूकः, अयम्, बन्धः, मिवाणि।
• द्वितीया – मृगम्, क्षेत्रम्, एकम, त्वाम्, भोजनम्, तम्, माम, पाशान, एतान्।
• तृतीया – क्षेत्रपतिना, पाशैः।
• पशमी – दूरात्। षष्ठी – वृक्षस्य, मम।
• सप्तमी – एकस्मिन्, दिने, मनसि, व्रतदिवसे।
• सम्बोधन – मित्र।

(च) लकारं लिखत।

प्रश्न 1.
1. प्रभूतं भोजनं प्राप्स्यामि।
2. त्रायस्व माम्।
उत्तरम् :
1. लृट्लकार:
2. लोट्लकार:

क्रमेण योजयत।

(क)

प्रश्न 1.

1. क्षेत्रपतिना पाशयोजनम्।
2. शृगालेन मृगाय सस्यपूर्णक्षेत्रस्य दर्शनम्।
3. मृगस्य पाशबन्धनम्।
4. मृगस्य प्रत्यहं क्षेत्रं गमनम्।

उत्तरम् :

1. शृगालेन मृगाय सस्यपूर्णक्षेत्रस्य दर्शनम्।
2. मृगस्य प्रत्यहं क्षेत्रं गमनम्।
3. क्षेत्रपतिना पाशयोजनम्।
4. मृगस्य पाशबन्धनम्।

(ख)

प्रश्न 1.

1. मृगः पाशैर्बद्धः।
2. मृगः सस्यम् अखादत्।
3. जम्बूक; मनसि आनन्दितः।
4. क्षेत्रपतिना पाश: योजितः।

उत्तरम् :

1. मृगः सस्यम् अखादत्।
2. क्षेत्रपतिना पाश: योजितः।
3. मृगः पाशैर्बद्धः।
4. जम्बूक: मनसि आनन्दितः ।

भाषाभ्यासः

(क) समानार्थकशब्दाः

1. कालः – समयम, वेला।
2. प्रत्यहम् – प्रतिदिनम्।
3. सस्यम् – धान्यम्।
4. गत्वा उपगम्य।
5. क्षेत्रपतिः – सस्यपालः।
6. इदानीम् – सम्पति, साम्प्रतम्।
7. मनसि – चित्ते, चेतसि, अन्त:करणे।
8. आनन्दितः – प्रमुदितः, हर्षितः, प्रहृष्टः।
9. मनोरथम् – मनोकामना, मनीषा, ईहा।
10. प्रभूतम् – भूरि, विपुलम्, पुष्कलम्, प्रचुरम्।

(ख) विरुद्धार्थकशब्दाः

1. अनन्तरम् × पूर्वम्, प्राक्।

अवबोधनम् ।

(क) उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
मृगः क्षेत्रपतिना बद्धः यतः ……….
(अ) मृगः क्षेत्रपतेः शत्रुः आसीत्।
(ब) मृगः सुहद्वाक्यस्य अनादरम् अकरोत्।
उत्तरम् :
(ब) मृगः सुहृद्वाक्यस्य अनादरम् अकरोत्।

प्रश्न 2.
शृगालः हत: यत:
(अ) क्षेत्रपतिना लगुडं क्षिप्तम्।
(ब) काकः शृगालम् अमारयत्।
उत्तरम् :
(अ) क्षेत्रपतिना लगुडं क्षिप्तम्।

प्रश्न 3.
क्षेत्रपतिः मृगं बन्धनात् व्यमुशत् यतः
(अ) सः ‘मृगः मृतः’ इति चिन्तितवान् ।
(ब) पाशबद्धं मृगं दृष्ट्वा तस्य हृदयं करुणया अद्रवत्।
उत्तरम् :
(अ) सः ‘मृगः मृतः’ इति चिन्तितवान्।

(ख) पूर्णवाक्येन उत्तरत।

प्रश्न 1.
क्षेत्रपतिः कदा हस्ते लगुडं धृत्वा आगच्छत् ?
उत्तरम् :
क्षेत्रपतिः प्रभाते हस्ते लगुडं धृत्वा आगच्छत्।

प्रश्न 2.
केन क्षेत्रपति: अवलोकित:?
उत्तरम् :
काकेन क्षेत्रपति: अवलोकितः।

प्रश्न 3.
क्षेत्रपतिना मृगं विलोक्य किम् उक्तम्?
उत्तरम् :
क्षेत्रपतिना मृगं विलोक्य उक्तं, “आ ! स्वयं मृतोऽसि।”

प्रश्न 4.
मृगः कदा पलायित:?
उत्तरम् :
काकशब्द श्रुत्वा मृग: पलायितः।

(ग) वाक्यं पुनलिखित्वा सत्यम् / असत्यम् इति लिखत।

प्रश्न 1.

1. काकः सायङ्काले मृगमन्विष्यन् आगतः।
2. मृगः मृतः आसीत्।
3. मृगः मृतवत् संदर्शयत्।
4. मृगः शनैः शनै: पलायितः।
5. क्षेत्रपतिना क्षिप्तेन लगुडेन जम्बूक: हतः।
6. क्षेत्रपति: मृगं बन्धनात् व्यमुञ्चत्।

उत्तरम् :

1. सत्यम्।
2. असत्यम्।
3. सत्यम्।
4. असत्यम्।
5. सत्यम्।
6. सत्यम्।

(घ) कः कं वदति?

प्रश्न 1.
“सखे ! किमेतत् ?”
उत्तरम् :
काक: मृगं वदति।

प्रश्न 2.
सुहद्वाक्यस्य अनादरात् बद्धोऽहम्।
उत्तरम् :
मृग: काकं वदति।

प्रश्न 3.
मन्मांसार्थी तिष्ठति अत्रैव ।
उत्तरम् :
मृग: काकं वदति।

प्रश्न 4.
उपायस्तावत् चिन्तनीयः।
उत्तरम् :
काकः मृगं वदति।

प्रश्न 5.
त्वमात्मानं मृतवत्संदर्शय।
उत्तरम् :
काकः मृगं वदति।

शब्दज्ञानम्

(क) सन्धिविग्रहः।

1. मृगमन्विष्यन् – मृगम् + अन्विष्यन् ।
2. काकस्तत्रोपस्थितः – काक: + तत्र + उपस्थितः।
3. किमेतत् – किम् + एतत्।
4. बद्धोऽहम् – बद्धः + अहम्।
5. स्वास्ते – क्व + आस्ते।
6. तिष्ठत्यत्रैव – तिष्ठति + अत्र + एव।
7. उपायस्तावत् उपाय: + तावत्।
8. क्षेत्रपतिलगुडहस्तः – क्षेत्रपतिः + लगुडहस्तः।
9. काकेनावलोकितः – काकेन + अवलोकितः।
10. तमालोक्य – तम् + आलोक्य।
11. काकेनोक्तम् – काकेन + उक्तम्।
12. त्वमात्मानम् – त्वम् + आत्मानम्।
13. मृतवत्संदर्शय – मृतवत् + संदर्शय।
14. पादास्तब्धीकृत्य – पादान् + स्तब्धीकृत्य ।
15. यदाहम् – यदा + अहम्।
16. त्वमुत्थाय – त्वम् + उत्थाय।
17. मृगस्तथैव – मृग: + तथा + एव।
18. उक्तञ्च – उक्त म् + च।
19. तमुद्दिश्य – तम् + उहिश्य।
20. शृगालस्तावद् हतः – शृगालः + तावत् + हतः।

(ग) त्वान्त-ल्यबन्त-तुमन्त-अव्ययानि ।

त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा / अयित्वा	ल्यबन्त अव्यय उपसर्ग + धातु + या / त्य
दृष्ट्वा, पूरयित्वा, श्रुत्वा	आलोक्य, स्तब्धीकृत्य, उद्दिश्य, उत्थाय

(घ) विभक्त्यन्तरूपाणि ।

• प्रथमा – काकः, सः,अहम, यः, नरः, वञ्चकः, क्षेत्रपतिः, आगच्छन्, त्वम्, मृगः, शृगालः।
• द्वितीया – मृगम्, किम्, एतत्, तम्, आत्मानम्, उदरम्, पादान्, शब्दम्।
• तृतीया – मृगेण, काकेन, वातेन, क्षेत्रपतिना, लगुडेन।
• पञ्चमी – अनादरात्, बन्धनात्।
• षष्ठी – वाक्यस्य, सुहृदाम, हितकामानाम, तस्य।
• सप्तमी – प्रदोषकाले, प्रभाते।
• सम्बोधन – सखे, मृग।

(च) लकारं लिखत।

प्रश्न 1.

1. मृगं तथाविधं दृष्ट्वा स उवाच।
2. स वशक: क्व आस्ते?
3. त्वमात्मानं मृतवत्संदर्शय।
4. सत्वरं पलायिष्यसे।
5. सः मृगं बन्धनात् व्यमुञ्चत्।

उत्तरम् :

1. लिट्लकारः
2. लट्लकारः
3. लोट्लकार:
4. लट्लकारः
5. लङ्लकार:

क्रमेण योजयत।

(क)

प्रश्न 1.

1. मृगः मृतवत् स्थितः ।
2. शृगाल: लगुडेन हतः।
3. काकेन क्षेत्रपति: अवलोकितः।
4. काकेन शब्दः कृतः।

उत्तरम् :

1. काकेन क्षेत्रपति: अवलोकितः।
2. मृगः मृतवत् स्थितः।
3. काकेन शब्दः कृतः।
4. शृगाल: लगुडेन हतः।

भाषाभ्यासः

(क) समानार्थकशब्दाः

1. प्रदोषकालः – सन्ध्याकालः।
2. सुहृद् – सखा, मित्रम्।
3. विपत् – आपत्तिः, सङ्कटम्।
4. आलोक्य – अवलोक्य, विलोक्य, वीक्ष्य।
5. वातेन – पवनेन, वायुना।
6. सत्वरम् – शीघ्रम्, तूर्णम्, झटिति, आशु।

(ख) विरुद्धार्थकशब्दाः

1. सुहद् × शत्रुः, अरिः, वैरी।
2. अनादरात् × आदरात्।
3. मृतः × जीवितः।
4. सत्वरम् × शनैः शनैः।

लेखनकौशलम्

समासाः

समस्तपदम्	अर्थ	समासविग्रहः	समासनाम
मृगशृगालो	deer and jackal	मृगः च शृगाल: च।	इतरेतर द्वन्द्व समास
प्रत्यहम्	every day	अहनि अहनि।	अव्ययीभाव समास
सकोपम्	with anger	कोपेन सह।	अव्ययीभाव समास
अपरिचितः	not known	न परिचितः।	नञ्तत्पुरुष समास
क्षेत्रपतिः	owner of the field(s)	क्षेत्रस्य / क्षेत्राणां पतिः।	षष्ठी तत्पुरुष समास
क्षुदबुद्धिः	he who has mean intellect	क्षुद्रा बुद्धिः यस्य सः।	बहुव्रीहि समास
लगुडहस्तः	he who hasastick in the hand	लगुडं हस्ते यस्य सः।	बहुव्रीहि समास

व्यसने मित्रपरीक्षा Summary in Marathi and English

Introduction:

हितोपदेश is an ancient Indian text in Sanskrit language consisting of fables of animals and human Characters. It incorporates maxims, wordly wisdoms and morals on political affairs in a simple and entertaining manner.

नारायण पंडित is considered to be the author of this book. His purpose behind composing हीतोपदेश is to give knowledge to be wise. This is done through moral stories in which birds, beasts and humans interact. हितोपदेश has four sections – मित्रलाभ, सुहृद्भेद, विग्रह, सन्धि.

The story of the lesson व्यसने मित्रपरीक्षा is found in the chapter 1.3 of “मित्रलाभ’. The repercussion of trusting strangers is well brought out through the story of deer, jackal and crow.

प्रस्तावना :

हितोपदेश हे प्राणी व मानवी पात्रांनी युक्त कथांचे भारतीय पुस्तक आहे. यात नीतिसूत्रे, उपदेशात्मक वचने, तसेच राजकीय संबंधावर आधारित मूल्ये यांचे सहज व रोचक पद्धतीने स्पष्टीकरण केलेले आहे. नारायण पंडित हा या ग्रंथाचा कर्ता मानला जातो. योग्य आचरण शिकवणे हा त्याचा यामागील हेतू आहे. पक्षी, प्राणी व मानव यांच्या परस्पर संभाषणातून हे त्याने व्यक्त केले आहे.

हितोपदेशाचे चार भाग आहेत.

1. मित्रलाभ
2. सुहृद्भेद
3. विग्रह
4. सन्धि

‘व्यसने मित्रपरीक्षा’ या पाठाचा कथाभाग ‘मित्रलाभ’ या भागातील 1.3 या प्रकरणात सापडतो. अनोळखी व्यक्तीवर विश्वास ठेवल्याचे दुष्परिणाम हरिण, कोल्हा व कावळ्याच्या गोष्टीद्वारे उत्तमरीत्या कथन केले आहेत.

परिच्छेदः, शब्दार्थाः, अनुवादः

परिच्छेदः 1

अस्ति कश्चित् ……………. एवमस्तु।.

अनुवादः

चंपक नावाचे एक जंगल होते. जंगलात चित्रांग नावाचे हरिण व एकाक्ष नावाचा कावळा प्रेमाने (एकत्र) राहत होते. एकदा चित्रांग वनात भटकत असताना कोण्या एका कोल्ह्याने त्याला पाहिले. क्षुद्रबुद्धी नावाच्या त्या कोल्ह्याची स्वार्थापोटी हरिणाबरोबर मैत्री करण्याची इच्छा होती. सूर्यास्त झाल्यावर, क्षुद्रबुद्धी हरिणाबरोबर हरिणाच्या घरी गेला.

हरिण व कोल्ह्याला पाहून कावळा म्हणाला, “अरे मित्रा चित्रांग! ह्य दुसरा कोण आहे ?” हरिण म्हणाले, “हा कोल्हा आहे. त्याला आपल्याबरोबर मैत्री करण्याची इच्छा आहे.” (त्यावर) कावळा म्हणाला “अचानक आलेल्या अपरिचितासोबत मैत्री योग्य नव्हे.” ते ऐकून कोल्हा रागाने म्हणाला, “हरिणाच्या प्रथमदर्शनी तू सुद्धा अनोळखी होतास. ज्याप्रमाणे हे हरिण माझ्या मित्रासमान आहे, त्याप्रमाणे तू आहेस.” हरिण म्हणाले, “(हा) वाद पुरे! आपण सर्व आनंदाने एकत्र राहूया.” कावळा म्हणाला, “असेच होवो.”

There was a certain forest named चंपक. A deer named चित्रांग and acrow named एकाक्ष used to live in the forest affectionately. Once, a certain jackal saw fait who was wandering in the forest. That jackal named yoga wished to befriend the deer with a selfish purpose.

At the time of sunset ya went to deer’s place with the deer. The crow said having seen the dear and the jackal, “Ofriend चित्रांग ! Who is this second (another) one?” The deer said, “This is a jackal. He wishes our friendship.”

(He wishes to befriend us.) The crow advised, “Friendship with a stranger, suddenly, is not appropriate.” Having heard it, the jackal angrily said, “At first sight you were stranger as well. Just as this deer is my friend so too are you.” The deer said, “Enough of this arguement. All of us will live together happily.” The crow said, “May it be so.”

परिच्छेदः 2.

किश्चित्कालानन्तरं ……………… स्थितः।

अनुवादः

मराठी थोड्या वेळानंतर, कोल्हा हरिणाला म्हणाला, ‘या अरण्यात धान्याने भरलेले एक शेत आहे. मी तुला दाखवतो.’ तसे केल्यावर, दररोज हरिण तेथे जाऊन धान्य खात असे. ते पाहून, एके दिवशी शेतमालकाने जाळे टाकले. तेथे आलेले हरिण जाळ्यामध्ये अडकले. त्याने विचार केला, “आता फक्त मित्रच माझा आसरा आहेत.” दूरवरून ते पाहणारा कोल्हा मनातून खूष झाला.

त्याने विचार केला, “माझे ईप्सित फळास आले. आता मला पुष्कळ खाद्य मिळेल.” ते पाहून हरिण म्हणाले, “अरे मित्रा, माझे हे बंध तोडून टाक. मला वाचव.” कोल्हा लांबूनच म्हणाला, “अरे मित्रा, हे बंध (फार) घट्ट आहेत, मी स्नायूंनी बनविलेल्या जाळ्याला उपवासाच्या दिवशी कसे तोंड लावू?” असे म्हणून तो जवळ असलेल्या झाडाच्या मागे स्थिर उभा राहिला.

After some time, the jackal said to the deer, “There is a field, full of grains in this forest. I(will) show (it) to you.’ Having done so, the deer ate the grain, going there everyday. Having seen this, one day a trap was set by the owner of the field. The dear, who had come (arrived) there, was trapped in the net.

He thought, “Now, my friends only are my resort.” The jackal, who was seeing it from a far was delighted in the mind. He thought, “My desire is fulfilled. Now I shall get plenty of food.” Having seen it, the deer said, “O friend, cut through my bonds. Please save me.” The jackal replied from a far “Ofriend, this bond is strong. How can I touch the net made of sinews on my fasting day?” Having said this, he stood steady behind the tree that was nearby.

परिच्छेदः 3.

प्रदोषकाले …………………हतः।

अनुवादः

तिन्हीसांजेच्या वेळी (सायंकाळी), हरिणाला शोधत कावळा तेथे हजर झाला. हरिणाला तशा प्रकारे पाहून तो म्हणाला, “अरे मित्रा ! हे काय?” हरिण म्हणाले, “मित्राच्या शब्दांची अवहेलना केल्यामुळे (शब्दांकडे दुर्लक्ष केल्यामुळे) मी अडकलो.

मराठी आणि म्हटलेले आहे – जो हितचिंतक मित्रांचे शब्द (सल्ला) ऐकत नाही, त्याच्याजवळ विपत्ती (निवास करते), अशी व्यक्ती शजूंना आनंदित करते.” (शत्रुत्व ओढवून घेते) कावळा म्हणाला, “तो (कपटी) फसविणारा कोठे आहे?” हरिण म्हणाले, “माझ्या मांसाच्या हावेने इथेच थांबला आहे.”

कावळा म्हणाला, ‘तर मग (यावर) उपाय शोधला पाहिजे.’ नंतर सकाळी, हातामध्ये काठी घेऊन येणाऱ्या शेतमालकाला कावळ्याने पाहिले. त्याला पाहून कावळा म्हणाला, “मित्रा हरिणा, तू स्वत:ला मेल्यासारखा दाखव.” (तुझे) पोट हवेने फुगवून पाय स्थिर ठेव.

जेव्हा मी आवाज करेन / ओरडेन, तेव्हा तू उठून पटकन पळ.” हरिण तसेच थांबले. शेतमालकाने हरिणाला पाहिले व म्हणाला, “बापरे ! तू तर मेलेला आहेस.” त्याने हरिणाला जाळ्यातून मुक्त केले. नंतर, कावळ्याचे ओरडणे ऐकल्यावर हरिण पटकन पळून गेले. शेताच्या मालकाने त्याला (हरिणाला) रोखून फेकलेल्या काठीने कोल्हा मारला गेला.

English At nightfall, the crow arrived there looking for the deer. Seeing the deer so (trapped) he said, “O friend! What is this?” The deer said, “I was caught (trapped) due to disregarding a friend’s words (advice).

and it is said The one who does not listen to words/advice of friends well-wishing, the calamity is placed close to him. That person is the delight of enemies. The crow said, “where is the deceiver ?” The deer said, “(He) is waiting here itself longing for my flesh.” The crow said, ‘We must think of a solution.’ Then in the morning, the crow saw the owner of the field coming with a stick in the hand.

Seeing him, the crow said, “O friend deer, pretend as if you are dead. Blow your belly with air, stiffen your legs and lie still. When I shall make a sound then, having stood up, you run away quickly The deer stayed accordingly. The owner of the field saw the deer and said, “Oh ! You are dead on your own.” He released the deer from the bonds.

Then, listening to the sound of the crow, the deer ran away quickly. Meanwhile, the stick which was thrown towards the deer by the owner of the field, killed the jackal.

शब्दार्थाः

1. मृग – deer – हरिण
2. काकः – crow – कावळा
3. जम्बूकः – jackal – कोल्हा
4. अवलोकितः – was seen – पाहिले
5. अपरिचितः – stranger – अनोळखी
6. कक्षित् – certain – कोणी एक
7. भ्रमन् – roaming, wandering – भटकत असताना
8. सख्यम् – friendship – मैत्री
9. युक्ता – proper – योग्य
10. शृगालेन – by jackal – कोल्ह्याने
11. स्नेहेन – affectionately प्रेमाने
12. स्वाहतुना – with selfish purpose – स्वार्थापोटी
13. प्रथमदर्शने – at the first sight – प्रथमदर्शनी
14. अस्तङ्गते – at the time of sunset – सूर्यास्त
15. सवितरि – झाल्यावर
16. निवसतः स्म – both used to live – दोघे राहत होते
17. अबूत – said – म्हणाला
18. अब्रवीत् – said – म्हणाला
19. उक्तम् – said – म्हणाला
20. आह – said – म्हणाला
21. आकर्ण्य – having heard – ऐकून
22. अकस्मात् – at once – अचानक
23. सकोपम् – angrily – रागाने
24. आगन्तुना सह – with a stranger – अनोळखी माणसासह
25. दृढः – strong – घट्ट
26. बन्धः – bond – बंध
27. पाश: – noose – जाळे
28. योजितः – arranged – व्यवस्था केली
29. बद्धः – got stuck/caught – अडकले
30. सस्यपूर्णम् – full of grains – धान्ययुक्त
31. क्षेत्रम् – field – शेत
32. शरणम् – resort – आश्रयस्थान, आसरा
33. फलितम् – fulfilled – फळास आले
34. मनोरथम् – desire – ईप्सित/इच्छा
35. स्नायुनिर्मितान् – made of sinews – स्नायूंनी बनलेले
36. क्षेत्रपतिना – by the field-owner – शेतमालकाने
37. व्रतदिवसे – on the day of fast – उपवासादिवशी
38. दर्शयामि – I show – मी दाखवतो
39. प्रापयामि – I shall get – मला मिळेल
40. छिन्धि – you break – तू तोड
41. जायस्व – you save – तू वाचव
42. प्रत्यहम् – every day – दररोज
43. इदानीम् – now – आता
44. प्रभूतम् – plenty of – भरपूर
45. निभृतम् – still – निश्चल
46. तथा कृते – having done so – तसे केल्यावर
47. उपस्थितः – arrived – हजर झाला
48. वञ्चक: – crooked / deceitful – फसविणारा
49. लगुडहस्त: – stick in the hand – काठी हातात घेतलेला
50. हतः – killed – मेलेला
51. अन्विष्यन् – searching – शोधत
52. विपत् – calamity – संकट
53. सन्निहिता – placed close by – जवळ
54. मृतवत् – like dead – मेल्यासारखा
55. सुङद्वाक्यम् – friend’s speech – मित्राचे बोलणे
56. वातेन – with air – हवेने
57. क्षिप्तेन – thrown – फेकलेल्या
58. अनादरात् – due to disrespecting – अवहेलना केल्यामुळे
59. हितकामानाम् – of well-wishers – हितचिंतकांचे
60. प्रदोषकाले – at the nightfall – तिन्हीसांजेला
61. शृणोति – listens – ऐकतो
62. पलायिष्यसे – you will run – पळशील
63. व्यमुञ्चत् – released – मुक्त केले
64. अब्रूत – said – म्हणाला
65. संदर्शय – appear – दाखव
66. उद्दिश्य – pointing – रोखून
67. उत्थाय – having got up – उठून
68. आलोक्य – seeing – पाहून
69. स्तब्धीकृत्य – keeping still – स्थिर / स्तब्ध राहून
70. क्व – where – कोठे
71. उदरं पूरयित्वा – blowing the belly – पोट भरून
72. मन्मांसार्थी – longing for my flesh – माझ्या मांसाच्या हावेने

Aamod Sanskrit Book 10th Class Solutions

• आद्यकृषक: पृथुवैन्यः Class 10 Question Answer
• व्यसने मित्रपरीक्षा Class 10 Question Answer
• सूक्तिसुधा Class 10 Question Answer
• अमूल्यं कमलम् Class 10 Question Answer
• स एव परमाणुः Class 10 Question Answer
• युग्ममाला Class 10 Question Answer
• संस्कृतनाट्ययुग्मम् Class 10 Question Answer
• वाचनप्रशंसा Class 10 Question Answer
• धेनोर्व्याघ्रः पलायते Class 10 Question Answer
• नदीसूक्तम् Class 10 Question Answer
• जटायुशौर्यम् Class 10 Question Answer
• आदिशङ्कराचार्यः Class 10 Question Answer
• चित्रकाव्यम् Class 10 Question Answer
• प्रतिपदं संस्कृतम् Class 10 Question Answer
• मानवताधर्मः Class 10 Question Answer

Std 10 Hindi Chapter 2 Lakshmi Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 2 लक्ष्मी Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 2 लक्ष्मी Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 2 लक्ष्मी Textbook Questions and Answers

सूचना के अनयुार कृहत्‍ँ कीहजए:

प्रश्न 1.
संजाल पूण् कीहजए:

उत्तर:

प्रश्न 2.
उचित घटनाक्रम लगाकर वाक्य फिर से लिखिए:
१. उसके गले में रस्सी थी।
२. रहमान बड़ा मूर्ख है।
३. वह लक्ष्मी को सड़क पर ले आया।
४. उसने तुम्हें बड़ी बेदर्दी से पीटा है।
उत्तर:
(i) उसने तुम्हें बेदर्दी से पीटा है।
(ii) रहमान बड़ा मूर्ख है।
(iii) उसके गले में रस्सी थी।
(iv) वह लक्ष्मी को सड़क पर ले आया।

प्रश्न 3.
उततर हलखखए:

उत्तर:

प्रश्न 4.
गलत वाक्य, सही करके लिखिए:
१. करामत अली पिछले चार सालों से गाय की सेवा करता चला आ रहा था।
२. करामत अली को लक्ष्मी की पीठ पर रोगन लगाने के बाद इत्मीनान हुआ।
उत्तर:
(i) करामत अली पिछले एक साल से गाय की सेवा करता चला आ रहा था।
(ii) करामत अली को लक्ष्मी की पीठ पर रोगन लगाने के बाद भी इत्मीनान नहीं हुआ।

प्रश्न 5.
हनम्हलखखत मयु्दो के आधार पर वर्णन कीहजए:

उत्तर:

प्रश्न 6.
कारण हलखखए:
a. करामत अली लक्ष्मी के हलए सानी तैयार करने लगा।
b. रमजानी ने करामत अली को रोगन हदया।
c. रिमान ने लक् को इलाके से भहर तोडा हदया।
d. करामत अली ने लक् को गऊशाला मे भरती हकया।
उत्तर:
a. सुबह से रमजानी या रहमान किसी ने भी लक्ष्मी को चारा, दर्रा कुछ भी नहीं दिया था। लक्ष्मी बहुत भूखी थी।
b. रहमान के मारने के कारण लक्ष्मी की पीठ पर चोट आई थी।
c. रहमान ने सोचा कि लक्ष्मी नाले के पास उगी दूब खाकर पेट भर लेगी।
d. पैसे की तंगी के कारण करामत अली लक्ष्मी के दाने-चारे का प्रबंध नहीं कर पा रहा था। वह लक्ष्मी को भूखों मरता नहीं देख सकता था।

प्रश्न 7.
हिंदी-मराठी मे समोच्ररत शब् के हभन नर् हलखखए:

उत्तर:

	हिंदी	मराठी
(1) खत	पत्र	खाद
(2) पीठ	पीठ (शरीर का अंग)	आटा
(3) खाना	भोजन	दराज
(4) चारा	उपाय	जानवरों को खिलाने की सामग्री
(5) कल	बीता हुआ अथवा आने वाला समय (कल)	रुझान, प्रवृत्ति

प्रश्न.
यदि आप करामत अली की जगि पर होते तो’ इस संदभ् मे अपने हिचार लिखिए।
उत्तर:
करामत अली दोस्त को दिए गए वचन को निभाने वाला और पशु की पीड़ा समझने वाला इन्सान है। यदि करामत अली की जगह मैं होती/होता तो मैं भी वही करती/करता, जो करामत अली ने किया। जब हम किसी पशु को पालते हैं, तो उसकी सुख-सुविधा और खाने-पीने की उचित व्यवस्था करना हमारी जिम्मेदारी होती है। यदि मेरे समक्ष करामत अली जैसी स्थिति (आर्थिक संकट) उत्पन्न होती, तो मैं भी अपने पालतू पशु को भूखा मरते देखने या उसे कसाई के हाथों बेचने के स्थान पर किसी अच्छे पशुघर (गऊशाला) में ही दाखिल कराती/कराता। पशुघर में अपने जैसे अन्य पशुओं के साथ मेरा प्रिय पशु भी सुखपूर्वक अपना शेष जीवन बिता सकता। इससे मुझे बहुत संतोष होता।

भाषा बिंदु
प्रश्न 1.
निम्नलिखित वाक्यों में उचित विरामचिह्नों का प्रयोग कर वाक्य पुनः लिखिए:

१. ओह कंबख्त ने कितनी बेदर्दी से पीटा है
२. मैंने कराहते हुए पूछा मैं कहाँ हूँ
३. मँझली भाभी मुट्ठी भर बँदियाँ सूप में फेंककर चली गई
४. बड़ी बेटी ने ससुराल से संवाद भेजा है उसकी ननद रूठी हुई है मोथी की शीतलपाटी के लिए
५. केवल टीका नथुनी और बिछिया रख लिए थे
६. ठहरो मैं माँ से जाकर कहती हूँ इतनी बड़ी बात
७. टाँग का टूटना यानी सार्वजनिक अस्पताल में कुछ दिन रहना
८. जल्दी-जल्दी पैर बढ़ा
९. लक्ष्मी चल अरे गऊशाला यहाँ से दो किलोमीटर दर है
१०. मानो उनकी एक आँख पूछ रही हो कहो कविता कैसी रही

प्रश्न 2.
निम्नलिखित विरामचिह्नों का उपयोग करते हुए बारह-पंद्रह वाक्यों का परिच्छेद लिखिए:

विरामचिह्न	वाक्य
।
–
?
;
,
!
‘ ’
‘‘ ’’
x x x
— 0 —
……………
( )
[ ]
^
:
-/

उत्तर:

विरामचिह्न	वाक्य
।	लक्ष्मी बड़ी भयभीत और घबराई हुई थी।
–	मालिक आज दर्रा-खली कुछ नहीं।
?	कौन खरीदेगा इस बूढ़ी गाय को?
;	हिंदी साहित्य के विकास; उन्नति में डायरी का भी योगदान है।
,	देखो, मुझे गाय बेचनी ही नहीं है।
!	ये देखो चाचाजी!
‘ ’	गोआ में ‘सी-फूड’ की अधिकता है।
‘‘ ’’	“ऐसी कोई विशेष बात नहीं है।”
x x x	हे ग्रामदेवता नमस्कार xxx
– ० –	इस तरह राजा – ० – रानी सुख से रहने लगे।
……………	तुम इस गाय को लेकर क्या करोगे…..?
( )	रवींद्रनाथ ठाकुर का [(बंगला भाषा) अनुवादित (अनूदित)] साहित्य सभी पढ़ते हैं।
[ ]	रवींद्रनाथ ठाकुर का [(बंगला भाषा) अनुवादित (अनूदित)] साहित्य सभी पढ़ते हैं।
^	मामा जी आगरा से आएँगे।
:	मनु (हँसते हुए): मैंने तो लड्डू का डिब्बा देखा भी नहीं।
-/	परीक्षार्थी उत्तीर्ण/अनुत्तीर्ण में से एक तो अवश्य होगा।

प्रश्न.
हकसी पालतूप्री की आतमकरा हलखखए।
उत्तर:
ऐसे अनेक जानवर हैं, जो या तो संख्या में कम हैं या बदलते पर्यावरण और परभक्षण मानकों के कारण लुप्तप्राय हो रहे हैं। साथ ही वनों की कटाई के कारण भोजन और पानी की कमी हो जाना भी इनकी आबादी कम होने का कारण है। भारतीय वन्थ जीवों में अनूप मृग, चौसिंगा, कस्तूरी मृग, नीलगाय, चीतल, कृष्णमृग, एक सींग वाला गैंडा, सांभर, गोर, जंगली सूअर आदि दुर्लभ प्रजातियाँ हैं।

पर्यावरण संतुलन में इन जीवों की भूमिका अत्यंत महत्त्वपूर्ण है। इन प्रजातियों में बड़ी तेजी से गिरावट आ रही है। भारत में स्तनपायी वन्य जीवों की 81 प्रजातियाँ संकटग्रस्त हैं। इनमें से कुछ हैं-शेर, चीता, बाघ, सफेद तेंदुआ, गैंडा, जंगली भैंसा, जंगली सूअर, लाल पांडा, चिम्पैंजी, नीलगिरि लंगूर, बारहसिंगा, कस्तूरी मृग, नीलगिरि हिरन, चौसिंगा हिरन, कश्मीरी हिरन आदि।

कुत्ते की आत्मकथा
मैं गलियों में मारा-मारा फिरने वाला एक कुत्ता हूँ। मैंने अपने जीवन में बहुत सुख-दुख सहे हैं। मैं आपको अपनी व्यथा-कथा सुनाता हूँ।

मेरी माँ एक किसान-परिवार की पालतू कुतिया थी। उसी के घर में मेरा जन्म हुआ था। मेरा रंग दूध की तरह सफेद था। बच्चे-बूढ़े सभी मुझे प्यार से उठा लेते थे। वे मुझे गोद में लेकर सहलाते। लोग मुझे तरह-तरह की चीजें खाने के लिए देते थे। मैं बहुत खुश था।

एक दिन उस किसान ने मुझे एक अमीर आदमी के हाथों सौंप दिया। मेरा मालिक मुझे पाकर बहुत खुश हुआ। वह मेरा बहुत ख्याल रखता था। वह मुझे ‘टॉमी’ कहकर बुलाता था। जहाँ भी जाता, वह अपने साथ मुझे ले जाता था।

मैं भी अपने मालिक की बहुत सेवा करता था। रात के समय में उसके बँगले की रखवाली करता था। मालिक के बच्चे मुझे बहुत प्यार करते थे। लेकिन सब दिन एक समान नहीं होते। धीरे-धीरे मेरा स्वास्थ्य गिरने लगा। मैं कमजोर होता चला गया। न मैं अब पहले जैसा ताकतवर रहा और न ही सुंदर। इसलिए मेरे प्रति मालिक और उसके परिवार का रुख बदल गया।

मेरे बुढ़ापे ने मुझे कहीं का नहीं रखा। मुझे अब अपना जीवन बोझ-सा लगने लगा है। मैं पेट भरने के लिए मारा-मारा फिरता हूँ। जिसके दरवाजे पर पहुँचता हूँ, वही दो डंडे जमा देता है। (यहाँ पर ‘कुत्ते की आत्मकथा’ नमूने के रूप में दी गई है। विद्यार्थी अपनी पसंद के पालतू प्राणी की आत्मकथा लिखें।)

Hindi Lokbharti 10th Textbook Solutions Chapter 2 लक्ष्मी Additional Important Questions and Answers

गद्यांश क्र. 1
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) कारण लिखिए:
(i) रहमान ने लक्ष्मी की पीठ पर डंडे बरसा दिए।
उत्तर:
(i) लक्ष्मी ने दूध नहीं दिया था।

(2) संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)
• संजाल पूर्ण कीजिए:

उत्तर:

कृति 3: (शब्द संपदा)
(1) गद्यांश में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए।
(i) …………………
(ii) …………………
(iii) …………………
(iv) …………………
उत्तर:
(i) उछलती-कूदती
(ii) दो – चार
(iii) धीरे-धीरे
(iv) इधर-उधर।

(2) निम्नलिखित शब्दों के लिंग बदलकर लिखिए:
(i) गाय
(ii) बेटी
(iii) रस्सी
(iv) खूटा।
उत्तर:
(i) गाय – बैल
(ii) बेटी – बेटा
(iii) रस्सी – रस्सा
(iv) खूटा – खूटी।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
पालतू जानवरों के साथ किए जाने वाले सौहार्दपूर्ण व्यवहारों के बारे में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
जानवरों का मनुष्य के जीवन में बहुत महत्त्व है। इसलिए प्राचीन काल से पशु मनुष्य के साथी रहे हैं। गाय, बैल, भैंस, कुत्ता, घोड़ा आदि जानवर हमारे लिए बहुत उपयोगी हैं। पालतू पशु मनुष्य के परिवार के सदस्य जैसे होते हैं। हमें उन्हें प्रेम से पालना चाहिए। हमें उनके प्रति सौहार्दपूर्ण व्यवहार रखना चाहिए। उन्हें उचित समय पर अच्छी खुराक देनी चाहिए।

उनकी साफ-सफाई का ध्यान रखना चाहिए। पशु मूक प्राणी होते हैं। वे अपना दुख-दर्द बता नहीं सकते। इसलिए मनुष्य को उनके भोजन के साथ-साथ उनकी भावनाओं को भी समझना जरूरी है। ये जानवर हमारे प्रति भी सद्व्यवहार और स्नेह रखते हैं। उनकी अच्छी देखभाल करना हमारा कर्तव्य है।

गद्यांश क्र. 2
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) संजाल पूर्ण कीजिए:
(i)

उत्तर:

(ii)

उत्तर:

(iii)

उत्तर:

(2) आकृति पूर्ण कीजिए:
(i) लक्ष्मी शांत खड़ी जख्मों पर यह लगवाती – [ ]
(ii) लक्ष्मी की पीठ पर रोगन लगाने के बाद भी करामत अली को यह नहीं हुआ – [ ]
उत्तर:
(i) लक्ष्मी शांत खड़ी जख्मों पर यह लगवाती रही – [तेल]
(ii) लक्ष्मी की पीठ पर रोगन लगाने के बाद भी करामत अली को यह नहीं हुआ – [इत्मीनान]

कृति 2: (आकलन)
(1) उत्तर लिखिए:
(i)

उत्तर:

(ii)

उत्तर:

कृति 3: (शब्द संपदा)
(1) निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) बरस
(ii) गाय
(iii) दूध
(iv) जरूरत।
उत्तर:
(i) बरस – साल
(ii) गाय – धेनु
(iii) दूध – दुग्ध
(iv) जरूरत – आवश्यकता।

(2) निम्नलिखित शब्दों का वचन बदलकर लिखिए:
(i) निशानी
(ii) समस्या
(iii) बेटी
(iv) जरूरत।
उत्तर:
(i) निशानी – निशानियाँ
(ii) समस्या – समस्याएँ
(iii) बेटी – बेटियाँ
(iv) जरूरत – जरूरतें।

(3) गद्यांश में प्रयुक्त उर्दू शब्द ढूँढकर लिखिए।
(i) ……………….
(ii) ……………….
(iii) ……………….
(iv) ……………….
उत्तर:
(i) मवेशी
(ii) शौक
(iii) जरूरत
(iv) खुशनसीबी।

(4)

उत्तर:

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
पशुपालन के विषय पर 25 से 30 शब्दों में अपने विचार लिखिए।
उत्तर:
आदि मानव जब से एक स्थान पर समूह बनाकर रहने और खेती करने लगा, तभी से मनुष्यों और पशुओं का साथ रहा है। कृषि कार्य में उसे कई पशुओं को पालतू बनाना पड़ा था। भारतीय समाज में पशुपालन की परंपरा तभी से चली आ रही है। देश के प्रत्येक कृषक की यह इच्छा रहती है कि उसके पास बैलों की एक जोड़ी और एक गाय अवश्य हो।

ये जानवर उसके लिए मात्र खेती में काम आने वाले, दूध देने वाले, सवारी तथा रखवाली के काम आने वाले ही नहीं होते, वरन ये कृषक परिवार का अभिन्न अंग होते हैं। घर के सभी सदस्यों को इनसे अत्यंत प्रेम होता है। ये अपने बच्चों के समान इन पशुओं के खान-पान और इनकी सुख-सुविधा का ध्यान रखते हैं।

गद्यांश क्र. 3

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
कारण लिखिए:
(a) करामत अली लक्ष्मी को बेचना नहीं चाहता था।
उत्तर:
(a) करामत अली जानता था कि बूढ़ी लक्ष्मी को अगर कोई खरीदेगा तो वह उसे काट-काटकर बेचने के लिए ही खरीदेगा।

कृति 2: (आकलन)
(1) आकृति पूर्ण कीजिए:

उत्तर:

(2) उत्तर लिखिए:

उत्तर:

(ii) रमजानी ने संदूकची से यह निकाला – [ ]
उत्तर:
(ii) रमजानी ने संदूकची से यह निकाला – [बीस का एक नोट]

कृति 3: (शब्द संपदा)
(1) निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) विशेष
(ii) बूढ़ी
(iii) आसान
(iv) बेचना।
उत्तर:
(i) विशेष x सामान्य
(ii) बूढ़ी x युवा
(iii) आसान x कठिन
(iv) बेचना x खरीदना।

(2) निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) दूध
(ii) परेशानी
(iii) जमाना
(iv) सानी।
उत्तर:
(i) दूध – पुल्लिंग
(ii) परेशानी – स्त्रीलिंग
(iii) जमाना – पुल्लिग
(iv) सानी – स्त्रीलिंग।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
मानव और पशु के संबंध के विषय में 25 से 30 शब्दों में अपने विचार लिखिए।
उत्तर:
आदि-मानव पशुओं का शिकार पेट भरने के लिए करता था। कालांतर में उसने पशुओं का शिकार छोड़कर कृषि करना सीखा, साथ ही पशुओं को पालकर उनसे काम लेना प्रारंभ किया। गाय, बैल, घोड़ा और कुत्ता आदि हमारे बहुत अच्छे मित्र हैं। उनसे हमारे अनेक कार्य सिद्ध होते हैं। पशु अपनी मित्रता में सदा खरे उतरे हैं। उन्होंने मानव की हर तरह से सेवा की है। कुत्ता एक स्वामिभक्त जानवर है। अपने मालिक के लिए यह अपने प्राण भी न्योछावर कर देता है। सुरक्षा करने, मार्ग दिखाने आदि में कुत्ता अतुलनीय भूमिका निभाता है। संकट में फंसे लोगों को बचाने में भी कुत्ते बहुत कुशल होते हैं। कुत्तों में सूंघने की अद्भुत शक्ति होती है। कुत्ते पुलिस के काम में बहुत सहायता करते हैं।

गद्यांश क्र.4
प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)
(1) (i) आकृति पूर्ण कीजिए:

उत्तर:

(ii)

उत्तर:

(2) संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)
(1) कारण लिखिए:
(i) लक्ष्मी को कांजी हाउस में पहुँचाने की धमकी देना
(ii) माँ-बेटे को आश्चर्य होना
(iii) रहमान ने लक्ष्मी को इलाके से बाहर छोड़ दिया।
उत्तर:
(i) क्योंकि लक्ष्मी दूसरे व्यक्ति की गाय का सब चारा खा गई है।
(ii) क्योंकि लक्ष्मी एक-डेढ घंटे बाद ही घर के सामने खड़ी थी।

(2) केवल एक/दो शब्दों में उत्तर लिखिए:
(i) करामत अली इस समय ड्यूटी से लौटा – ……………………….
(ii) दूसरों की गाय का चारा खाने वाली – ……………………….
(ii) रमजानी इसकी बातें सुनती रही – ……………………….
(iv) लक्ष्मी को देखकर आश्चर्यचकित होने वाले – ……………………….
उत्तर:
(i) दोपहर बाद।
(ii) लक्ष्मी
(iii) आगंतुक की।
(iv) माँ – बेटे।

(3) आकृति पूर्ण कीजिए:

उत्तर:

कृति 3: (शब्द संपदा)
(1) निम्नलिखित शब्दों के समानार्थी शब्द लिखिए: –
(i) दिन
(ii) घर
(iii) माँ
(iv) आश्चर्य।
उत्तर:
(i) दिन = दिवस
(ii) घर = सदन
(iii) माँ = जननी
(iv) आश्चर्य = अचरज।

(2) निम्नलिखित शब्दों का वचन बदलकर लिखिए:
(i) इलाका
(ii) आँखें
(iii) गली
(iv) नाला।
उत्तर:
(i) इलाका – इलाके
(ii) आँखें – आँख
(iii) गली – गलियाँ
(iv) नाला – नाले।

(3) लिंग पहचानकर लिखिए:
(i) रस्सी – ……………………….
(ii) झाड़-झंखाड़ – ……………………….
उत्तर:
(i) रस्सी-स्त्रीलिंग
(ii) झाड़-झंखाड़-पुल्लिग।

(4) गद्यांश में प्रयुक्त निम्नलिखित शब्द के भिन्न-भिन्न अर्थ लिखिए:

उत्तर:

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘कांजी हाउस में पशुओं के रखरखाव’ विषय पर 25 से 30 शब्दों में अपने विचार लिखिए।
उत्तर:
कांजी हाउस सरकार द्वारा संचालित एक केंद्र (पशुधर) होता है। यहाँ उन पशुओं को रखा जाता है, जो लावारिस इधर-उधर घूमते रहते हैं और खेतों में घुसकर लोगों की फसल को नुकसान पहुँचाते हैं। शिकायतकर्ता इन पशुओं को कांजी हाउस में भेज देते हैं। इन पशुओं का नियमपूर्वक रिकॉर्ड रखा जाता है। इनके मालिक जब इन्हें लेने आते हैं तो उनसे जुर्माना वसूल कर पशु उनके हवाले कर दिए जाते हैं। यदि लंबे समय तक किसी पशु की खोज-खबर लेने कोई नहीं आता, तो उसे नीलाम कर दिया जाता है। कांजी हाउस में इन पशुओं के खान-पान का कोई ध्यान नहीं रखा जाता।

गद्यांश क्र. 5
कृति 1: (आकलन)
(1) दो ऐसे प्रश्न बनाकर लिखिए जिनके उत्तर निम्नलिखित शब्द हों:
(i) लक्ष्मी
(ii) गऊशाला में।
उत्तर:
(i) टुकड़े-टुकड़े होकर कौन बिक जाएगी?
(ii) करामत अली लक्ष्मी को कहाँ भरती करा देगा?

(2) संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)
(1) संजाल पूर्ण कीजिए:

उत्तर:

(2) कारण लिखिए:
(a) लक्ष्मी बिना किसी रुकावट के करामत अली के पीछे-पीछे चली आ रही थी।
उत्तर:
(a) लक्ष्मी करामत अली के प्रेम को पहचानती थी। वह जानती थी कि करामत अली उसे किसी भी प्रकार का नुकसान नहीं पहुंचाएगा।

(3) एक-दो शब्दों में उत्तर लिखिए:
(i) रमजानी ने किसके चेहरे के भाव भाँप लिए?
(ii) रमजानी कहाँ खड़ी लक्ष्मी को बाहर ले जाते देखती रही?
उत्तर:
(i) करामत अली
(ii) दरवाजे पर।

कृति 3: (शब्द संपदा)
(1) निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) दोस्त
(ii) रात
(iii) सवेरा
(iv) बाहर।
उत्तर:
(i) दोस्त x दुश्मन
(ii) रात x दिन
(iii) सवेरा x साँझ
(iv) बाहर x भीतर।

(2) गद्यांश में प्रयुक्त उर्दू के शब्द ढूँढकर लिखिए।
(i) ………………..
(ii) ………………..
(ii) ………………..
(iv) ………………..
उत्तर:
(i) किस्मत
(ii) खुद
(iii) हुज्जत
(iv) इत्मीनान।

(3) गद्यांश में प्रयुक्त शब्द-युग्म ढूँढकर लिखिए।
(i) ………………..
(ii) ………………..
(ii) ………………..
(iv) ………………..
उत्तर:
(i) मुँह-हाथ
(ii) पीछे-पीछे
(iii) थके-माँदे
(iv) खाए-पिए।

भाषा अध्ययन (व्याकरण)
प्रश्न, सूचनाओं के अनुसार कृतियाँ कीजिए:
1. शब्द भेद:
• अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) वह लक्ष्मी को किसी भी हालत में बेचना नहीं चाहता था।
(ii) रामू ने देखा कि दूध नदारद!
(iii) राशन के लिए कुछ रुपए रखे थे।
उत्तर:
(i) वह – पुरुषवाचक सर्वनाम ।
(ii) दूध – द्रव्यवाचक संज्ञा।
(iii) कुछ – संख्यावाचक विशेषण।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) और
(ii) जहाँ
(iii) अरे!
(iv) अरे रे!
उत्तर:
(i) लक्ष्मी ने चारे को सूंघा और फिर उसकी ओर निराशा से देखने लगी।
(ii) जहाँ इसकी किस्मत में होगा, वहीं छोड़ आऊँगा।
(iii) अरे। लक्ष्मी जल्दी चल।
(iv) अरे रे! साँप ने उसे काट लिया।

3. संधि:
कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
निराशा	……………………	……………………
अथवा
…………………..	अति + अंत	……………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
निराशा	निः + आशा	विसर्ग संधि
अथवा
अत्यंत	अति + अंत	स्वर संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) रमजानी काम में जुट गई।
(ii) रहमान ने लक्ष्मी को घर से निकालने के लिए कमर कस ली।
(iii) लक्ष्मी ने घास छोड़ दिया।

सहायक क्रिया	मूल रूप
(i) गई	जाना
(ii) ली	लेना
(iii) दिया	देना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) मिलना
(ii) पीना
(iii) बनना।
उत्तर:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) मिलना	मिलाना	मिलवाना
(ii) पीना	पिलाना	पिलवाना
(i) बनना	बनाना	बनवाना

6. मुहावरे:
(1) मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) चंपत होना
(ii) कमर कसना
(iii) ताँता लगना
उत्तर:
(i) चंपत होना।
अर्थ: गायब होना।
वाक्य: पुलिस को देखकर चोर चंपत हो गया।

(ii) कमर कसना।
अर्थ: तैयार होना।
वाक्य: अकाल का मुकाबला करने के लिए लोगों ने कमर कस ली।

(iii) ताँता लगना।
अर्थ: कतार लग जाना, भीड़ लगना।
वाक्य: गांधी जी के दर्शनों के लिए आश्रम में हमेशा लोगों का तांता लगा रहता।

(2) अधोरेखांकित वाक्यांश के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (पैर पकड़ना, जान में जान आना, ताँता बंध जाना)
(i) वर्षा होने पर किसानों को धीरज प्राप्त हुआ।
(ii) रमण ने पिता जी से क्षमा याचना की।
उत्तर:
(i) वर्षा होने पर किसानों की जान में जान आई।
(ii) रमण ने पिता जी के पैर पकड़े।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उनका भेद लिखिए:
(i) कंबख्त ने कितनी बेरहमी से पीटा है।
(ii) लक्ष्मी ने आज भी दूध नहीं दिया।
(iii) उसने लक्ष्मी के माथे पर हाथ फेरा।
उत्तर:
(i) बेरहमी से-करण कारक
(ii) लक्ष्मी ने-कर्ता कारक
(iii) माथे पर-अधिकरण कारक।

8. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) लक्ष्मी उसकी ओर देखती है। (अपूर्ण भूतकाल)
(ii) रहमान लक्ष्मी को मारता है। (पूर्ण वर्तमानकाल)
(iii) लक्ष्मी बड़ी घबराई हुई है। (पूर्ण भूतकाल)
उत्तर:
(i) लक्ष्मी उसकी ओर देख रही थी।
(ii) रहमान ने लक्ष्मी को मारा है।
(iii) लक्ष्मी बड़ी घबराई हुई थी।

9. वाक्य भेद:
(1) निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) रमजानी खड़ी थी और आगंतुक की बातें सुन रही थी।
(ii) जो भी गाय के पास जाता, वह उसे सिर मारने की कोशिश करती।
उत्तर:
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए:
(i) करामत अली ने लक्ष्मी की पीठ सहलाई। (निषेधवाचक वाक्य)
(ii) यह तुम्हारा पुराना धंधा है। (प्रश्नवाचक वाक्य)
उत्तर:
(i) करामत अली ने लक्ष्मी की पीठ नहीं सहलाई।
(i) क्या यह तुम्हारा पुराना धंधा है?

10. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) लक्ष्मी की आँख में आँसू आई।
(ii) नईम का आवाज करामत के कान में पहुंचा।
(iii) मामला लक्ष्मी को गऊशाला ले जाने पर ठिक हो गई।
उत्तर:
(i) लक्ष्मी की आँखों में आँसू आए।
(ii) नईम की आवाज करामत के कान में पहुंची।
(iii) मामला लक्ष्मी को गऊशाला ले जाने पर ठीक हो गया।

लक्ष्मी Summary in Hindi

लक्ष्मी विषय – प्रवेश :

लक्ष्मी मवेशियों के शौकीन ज्ञान सिंह की अधेड़ उम्र की प्रिय गाय थी। नौकरी से अवकाश के बाद ज्ञान सिंह को मकान खाली करने की नौबत आई तो लक्ष्मी को रखने की समस्या आई। उसका हल उन्होंने निकाला अपने पड़ोसी और दोस्त करामत अली को लक्ष्मी को सौंप देने से। करामत अली जी – जान से लक्ष्मी की सेवा करते थे, पर जब लक्ष्मी ने दूध देना बंद कर दिया, तो वह उनके परिवार के लिए समस्या बन गई।

प्रस्तुत कहानी में कहानीकार गुरुबचन सिंह ने एक ओर मित्र को दिए गए वचन के पालन पर बल दिया है, तो दूसरी ओर प्राणिमात्र के प्रति दया – भावना को प्रतिपादित किया है। कहानी में दर्शाया गया है कि अनुपयोगी हो जाने के बाद भी पालतू प्राणियों की उचित देखभाल करना आवश्यक है।

लक्ष्मी मुहावरे – अर्थ

• मुँह मारना – जल्दी – जल्दी खाना।
• गला भर आना – भाव विह्वल होना, आवाज भर आना।
• हाथ थामना – सहारा देना।
• कोरा जवाब देना – साफ मना करना।
• तैश में आना – आवेश (जोश) में आना।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Std 10 Hindi Chapter 5 Imandari Ki Pratimurti Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 5 ईमानदारी की प्रतिमूर्ति Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 5 ईमानदारी की प्रतिमूर्ति Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 5 ईमानदारी की प्रतिमूर्ति Textbook Questions and Answers

कृति

कृतिपत्रिका के प्रश्न 1 (अ) तथा 1 (आ) के लिए

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
परिणाम लिखिए:
a. सुबह साढ़े पाँच-पौने छह बजे दरवाजा खटखटाने का –
२. साठ पैसे प्रति किलोमीटर के हिसाब से पैसे जमा करवाने का-
उत्तर:
a. सुबह साढ़े पाँच-पौने छह बजे दरवाजा खटखटाने का – नींद टूटना और बड़ी तेज आवाज में बोलना।
b. साठ पैसे प्रति किलोमीटर के हिसाब से पैसे जमा करवाने का – पिता की यह बात सुनकर दोनों भाई वहाँ रुक नहीं सके। कमरे में जाकर देर तक फूट-फूटकर रोते रहे।

प्रश्न 3.
पाठ में प्रयुक्त गहनों के नाम:

उत्तर:

प्रश्न 4.
वर्ण पहेली से विलोम शब्दों की जोड़ियाँ ढूँढकर लिखिए:

उत्तर:
(i) दुख x सुख
(ii) बुरा x भला
(iii) प्रसन्न x अप्रसन्न
(iv) सदुपयोग x दुरुपयोग।

प्रश्न 5.
पर जो असल गहना है वह तो है’ इस वाक्य से अभिप्रेत भाव लिखिए।
उत्तर:
स्त्री के सोने-चाँदी, हीरे-मोती के गहने उसके शरीर के बाह्य शृंगारिक गहने होते हैं। ये गहने स्थायी नहीं होते। स्त्री का असली गहना तो उसका पति होता है, जो जीवन भर उसका साथ निभाता है।

प्रश्न 6.
कुरते के प्रसंग से शास्त्री जी के इन गुणों (स्वभाव) का पता चलता है: १. _____________ १. _____________

प्रश्न 7.
पाठ में प्रयुक्त परिमाणों की सूची तैयार कीजिए:
a. _____________ b. _____________
उत्तर:
a. ग्राम, किलोमीटर, पैसे। साढ़े (पाँच), पौने (छह)।
b. पल, मिनट, बजे, सप्ताह, महीना।

प्रश्न 8.
‘पर’ शब्द के दो अर्थ लिखकर उनका स्वतंत्र वाक्य में प्रयोग कीजिए। १. _____________ १. _____________
उत्तर:
a. पर-अर्थ: पक्षी का पंख, डैना।
वाक्य: गिद्ध के पर बहुत बड़े और भारी होते हैं।

b. पर-अर्थ: लेकिन, परंतु।
वाक्य: सरकार ने किसानों के कर्ज माफ करने की घोषणा कर दी, पर उस पर कोई कार्रवाई नहीं हुई।

(अभिव्यक्ति)

प्रश्न.
‘सादा जीवन, उच्च विचार’ विषय पर अपने विचार लिखिए।
उत्तर:
संसार में दो प्रकार के मनुष्य होते हैं। एक वे, जो भौतिक सुखों को ही अपने जीवन का उद्देश्य मानते हैं। इनके लिए किसी भी तरह धन-दौलत तथा सुख-सुविधा की वस्तुएँ प्राप्त करना अनुचित नहीं होता। दूसरे प्रकार के मनुष्य हर स्थिति में अपने आप को संतुष्ट रखते हैं। ये अपने सीमित साधनों से अपना और अपने परिवार का निर्वाह करते हैं और प्रसन्न रहते हैं।

इनका रहन-सहन साधारण ढंग का होता है। विलासितापूर्ण वस्तुएँ इन्हें प्रभावित नहीं कर पातीं। वे केवल जीवनावश्यक वस्तुओं से अपना गुजारा कर लेते हैं, पर ईमानदारी, सच्चरित्रता, सच्चाई, सरलता तथा दूसरों के प्रति सहानुभूति रखना वे अपने जीवन का आदर्श मानते हैं। हमारे देश के संतों, महात्माओं तथा महापुरुषों का जीवन इसी तरह का रहा है। इन महापुरुषों को जनता आज भी याद करती है और उनका गुणगान करती है। सादा जीवन उच्च विचार को हर युग में हमारे यहाँ मान्यता मिली है और इन्हें अपने जीवन का मूलमंत्र मानकर ही मनुष्य सुखी रह सकता है।

भाषा बिंदु

प्रश्न 1.
निम्नलिखित वाक्यों को व्याकरण नियमों के अनुसार शुद्ध करके फिर से लिखिए: [प्रत्येक वाक्य में कम-से-कम दो अशुद्धियाँ हैं]
1. करामत अली गाय अपनी घर लाई।
2. उसने गाय की पीठ पर डंडे बरसाने नहीं चाहिए थी।
3. करामत अली ने रमजानी पर गाय के देखभाल का जिम्मेदारी सौंपी।
4. आचार्य अपनी शिष्यों को मिलना चाहते थे।
5. घर में तख्ते के रखे जाने का आवाज आता है।
6. लड़के के तरफ मुखातिब होकर रामस्वरूप ने कोई कहना चाहा।
7. सिरचन को कोई लड़का-बाला नहीं थे।
8. लक्ष्मी की एक झूब्बेदार पूँछ था।
9. कन्हैयालाल मिश्र जी बिड़ला के पुस्तक को पढ़ने लगे।
10. डॉ. महादेव साहा ने बाजार से नए पुस्तक को खरीदा।
11. लेखक गोवा को गए उनकी साथ साढू साहब भी थे।
12. टिळक जी ने एक सज्जन के साथ की हुई व्यवहार बराबर थी।
13. रंगीन फूल की माला बहोत सुंदर लग रही थी।
14. बूढ़े लोग लड़के और कुछ स्त्रियाँ कुएँ पर पानी भर रहे थे।
15. लड़का, पिता जी और माँ बाजार को गई।
16. बरसों बाद पंडित जी को मित्र का दर्शन हुआ।
17. गोवा के बीच पर घूमने में बड़ी मजा आई।
18. सामने शेर देखकर यात्री का प्राण मानो मुरझा गया।
19. करामत अली के आँखों में आँसू उतर आई।
20. मैं मेरे देश को प्रेम करता हूँ।
उत्तर:
1. करामत अली गाय अपने घर ले आए।
2. उसे गाय की पीठ पर डंडे नहीं बरसाने चाहिए थे।
3. करामत अली ने रमजानी पर गाय की देखभाल की जिम्मेदारी सौंपी।
4. आचार्य अपने शिष्यों से मिलना चाहते थे।
5. घर में तख्ता रखे जाने की आवाज आती है।
6. लड़के की तरफ मुखातिब होकर रामस्वरूप ने कुछ कहना चाहा।
7. सिरचन को कोई बाल-बच्चा नहीं था।
8. लक्ष्मी की एक झब्बेदार पूँछ थी।
9. कन्हैयालाल मिश्र जी बिड़ला की पुस्तक पढ़ने लगे।
10. डॉ. महादेव साहा ने बाजार से नई पुस्तक खरीदी।
11. लेखक गोवा गए और उनके साथ उनके साढू साहब भी थे।
12. टिळक जी द्वारा एक सज्जन के साथ किया हुआ व्यवहार सही था।
13. रंगीन फूलों की माला बहुत सुंदर लग रही थी।
14. बूढ़े, लड़के और कुछ स्त्रियाँ कुएँ से पानी भर रहे थे।
15. लड़का, पिताजी और माँ बाजार गए।
16. बरसों बाद पंडित जी को मित्र के दर्शन हुए।
17. गोवा के बीच पर घूमने में बड़ा मजा आया।
18. सामने शेर देखकर यात्री के प्राण मानो मुरझा गए।
19. करामत अली की आँखों में आँसू उतर आए।
20. मैं अपने देश को प्यार करता हूँ।

उपयोजित लेखन

निम्नलिखित मुद्दों के आधार पर कहानी लिखिए। उसे उचित शीर्षक दीजिए।

गाँव में लड़कियाँ-सभी पढ़ने में होशियार-गाँव में पानी का अभाव-लड़कियों का घर के कामों में सहायता करना-बहुत दूर से पानी लाना-पढ़ाई के लिए कम समय मिलनालड़कियों का समस्या पर चर्चा करना-समस्या सुलझाने का उपाय खोजना-गाँववालों की सहायता से प्रयोग करना-सफलता पाना-शीर्षक।
उत्तर:
राघोपुर आदिवासियों की आबादीवाला काफी बड़ा गाँव था। यह गाँव कस्बे और शहर से बहुत दूर था। इसलिए इस गाँव में विकास के नाम पर एक सेकेंडरी स्कूल चालू करने के अलावा कुछ भी नहीं किया गया था। गाँव के लड़के-लड़कियाँ इसी स्कूल में पढ़ते थे।

राघोपुर में पीने के पानी का भारी संकट था। इसलिए लोगों को एक किलोमीटर दूर किसनपुर से पानी लाना पड़ता था। किसनपुर के सरपंच ने गाँव वालों के सहयोग से एक बड़े कुएँ का निर्माण करवाया था। उस कुएँ में बहुत पानी था। उस कुएँ से दूर-दूर के गाँवों के लोग पीने का पानी ले जाते थे।

राघोपुर की लड़कियाँ घर के काम-काज में तो मदद करती ही थीं, किसनपुर से पीने का पानी लाने का काम भी उन्हींके जिम्मे होता था। इसलिए लड़कियों की पढ़ाई में इससे बाधा पहुँचती श्री।

एक दिन किसनपुर का सरपंच अपने गाँव के कुएँ की सफाई करवा रहा था। इसलिए राघोपुर की लड़कियों को कुएँ से पानी लेने में काफी देर हो गई। इसलिए लड़कियाँ उस दिन स्कूल नहीं जा सकी। सरपंच को इससे बहुत दुख हुआ।

सरपंच ने लड़कियों को प्रोत्साहित करते हुए कहा, “तुम सब अपने गाँव में कुआँ खोदना शुरू करो। मैं तुम्हारी मदद करूँगा।” यह सुनकर लड़कियों को बहुत खुशी हुई। उन्होंने गाँव में आकर यह बात गाँव के लोगों को बताई। लड़कियों ने उसी दिन से कुआँ खोदने की शुरुआत कर दी। वे पढ़ाई और काम-धाम से बचा समय कुआँ खोदने में लगाने लगीं। उनकी देखादेखी गाँव वाले भी इस काम जुटने लगे।

एक दिन कुआँ खुदकर तैयार हो गया और उसके छोटे से गाँव के लोगों के प्रतिदिन के उपयोग करने भर का पर्याप्त पानी निकल आया। अब गाँव की लड़कियों का समय दूसरे गाँव से पानी लाने में बर्बाद नहीं होता था। वे पूरे समय स्कूल में पढ़ाई करने लगी।। गाँव के लोग भी बहुत प्रसन्न थे।

शीर्षक: सूझबूझ का फल

Hindi Lokbharti 10th Textbook Solutions Chapter 5 ईमानदारी की प्रतिमूर्ति Additional Important Questions and Answers

गद्यांश क्र.1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i) पिता के न रहने पर लेखक पर यह बीता –
(ii) लेखक के जन्म के समय उनके पिता यह थे –
(iii) लेखक सदा यह कल्पना किया करते थे –
(iv) लेखक के पिता प्रधानमंत्री हुए तो वहाँ। यह गाड़ी थी –
उत्तर:
(i) पिता के न रहने पर लेखक पर यह बीता – [उन्हें बैंक में नौकरी करनी पड़ी]
(ii) लेखक के जन्म के समय उनके पिता यह थे – [उत्तर प्रदेश के पुलिस मंत्री]
(iii) लेखक सदा यह कल्पना किया। करते थे – [उनके पास बड़ी आलीशान गाड़ी होनी चाहिए]
(iv) लेखक के पिता प्रधानमंत्री हुए तो। वहाँ यह गाड़ी थी – [इंपाला शेवरलेट]

प्रश्न 2.
ऐसे दो प्रश्न बनाइए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) सहाय साहब
(ii) अभाव।
उत्तर:
(i) लेखक के पिता के निजी सचिव का नाम क्या था?
(ii) लेखक ने अपने पिता के रहते जीवन में क्या नहीं देखा?

प्रश्न 3.
किसने, किससे कहा?
(i) मैं तो इसे चलाऊँगा नहीं। तुम्हीं चलाओ।’
(ii) ‘तुम बैठो, आराम करो, हम लोग वापस आते हैं अभी।’
उत्तर:
(i) मैं तो इसे चलाऊँगा नहीं। तुम्हीं चलाओ’
– लेखक के बड़े भाई अनिल भैया ने लेखक से कहा।

(ii) ‘तुम बैठो, आराम करो, हम लोग वापस आते हैं अभी’
– लेखक ने ड्राइवर से कहा।

प्रश्न 4.
उत्तर लिखिए:
(i) शान की सवारी याद आने का परिणाम – …………………..
(ii) बातचीत में समय बिताने का परिणाम – …………………..
उत्तर:
(i) (लेखक कल्पना किया करते थे कि, उनके पास बड़ी आलीशान गाड़ी होनी चाहिए। इस समय वे आलीशान गाड़ी इंपाला शेवरलेट में शान से सवारी कर रहे थे।) वह पुरानी बात याद आने पर उनके शरीर में झुरझुरी आने लगी।
(ii) (लेखक अपने परिचित व्यक्ति के यहाँ इंपाला शेवरलेट में सवार होकर भोजन करने गए थे। वहाँ बातचीत में उन्हें समय का ध्यान नहीं आया) उन्हें देर हो गई।

कृति 2: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
उत्तर लिखिए:
(i) लेखक हमेशा कल्पना किया करते थे –
(ii) लेखक को इस बात का गर्व था –
(iii) लेखक ने संतरी को सैलूट मारने से रोका –
(iv) लेखक घर में यहाँ से घुसे –
उत्तर:
(i) बड़ी आलीशान गाड़ी की।
(ii) प्रधानमंत्री का लड़का होने का।
(iii) ताकि आवाज न हो और लेखक के पिता को उनके लौटने का। अंदाज न हो।
(iv) पीछे किचन के दरवाजे से।

प्रश्न 3.
आकृति पूर्ण कीजिए:
(i) लेखक के पिता पहले इस राज्य के गृहमंत्री थे – [ ]
(ii) पहले गृहमंत्री को यह कहा जाता था – [ ]
उत्तर:
(i) लेखक के पिता पहले इस राज्य के गृहमंत्री थे – [उत्तर प्रदेश]
(ii) पहले गृहमंत्री को यह कहा जाता था – [पुलिस मंत्री]

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) पुलिस
(ii) बदन
(iii) संतरी
(iv) पानी।
उत्तर:
(i) पुलिस – स्त्रीलिंग
(iii) संतरी – पुल्लिग
(ii) बदन – पुल्लिग
(iv) पानी – पुल्लिंग।

प्रश्न 2.
गद्यांश में आए अंग्रेजी शब्द खोजकर लिखिए।
(i) ……………………..
(ii) ……………………..
(iii) ……………………..
(iv) ……………………..
उत्तर:
(i) आर्डर
(ii) रेजिडेंस
(iii) गेट
(iv) सैलूट।

प्रश्न 3.
गद्यांश से ऐसे दो शब्द ढूँढ़कर लिखिए, जिनका वचन परिवर्तन से रूप नहीं बदलता।
(i) ……………………..
(ii) ……………………..
उत्तर:
(i) घर
(ii) समय

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘बच्चों की कल्पनाएँ और माता-पिता का डर’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
बचपन में बच्चों को हर चीज के बारे में उत्सुकता होती है। उनके मन में तरह-तरह की कल्पनाएँ आती हैं। इन कल्पनाओं को साकार रूप देने की वे कोशिश भी करते हैं। पर वे दुनियादारी से अनभिज्ञ होते हैं। इसलिए कभी-कभी उनसे गलतियाँ हो जाया करती हैं। कुछ बच्चे डर के कारण इन गलतियों को अपने माता-पिता से छुपाने का प्रयास करते हैं। मगर ये गलतियाँ जब खुल जाती हैं, तब ये बच्चे लज्जित होते हैं। इस तरह की गलतियों को अपने माता-पिता को न बताकर बच्चे बड़ी भूल करते हैं। अपनी गलतियों को अपने मातापिता से बता देने वाले बच्चे फायदे में रहते हैं।

समझदार माता-पिता बच्चों की गलतियों पर डाँटने-फटकारने के बजाय उन्हें प्यार से समझाते हैं। वे उन्हें स्थिति से निपटने का मार्ग बताकर उनकी सहायता करते हैं। ऐसे बच्चे भविष्य में इस तरह की गलतियों करने से बचे रहते हैं। माता-पिता सदा बच्चों के हित के बारे में सोचते हैं। इसलिए बच्चों को अपने मन में उत्पन्न किसी तरह की कल्पना के बारे में अपने मातापिता को बताना चाहिए और उसके बारे में उनकी सलाह के अनुसार कार्य करना चाहिए। उन्हें उनसे डरना नहीं चाहिए।

गद्यांश क्र.2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
एक शब्द में उत्तर लिखिए:
(i) लेखक ने दरवाजा खटखटाने वाले को यह समझा ………………….
(ii) लेखक के पिता ने लेखक को इसके लिए बुलाया ………………….
उत्तर:
(i) लेखक ने दरवाजा खटखटाने वाले को यह समझा – नौकर।
(ii) लेखक के पिता ने लेखक को इसके लिए बुलाया – चाय के लिए।

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
परिणाम लिखिए:
(i) दरवाजे पर दुबारा दस्तक देने का –
उत्तर:
(i) दरवाजे पर दुबारा दस्तक देने का – झुंझलाना और जोर से बिगड़ने के मूड में बड़बड़ाना।

प्रश्न 3.
ऐसे दो प्रश्न बनाइए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) खाने पर
(ii) इंपाला का।
उत्तर:
(i) लेखक और उनके भाई कहाँ गए थे?
(ii) लेखक के पिताजी किसका बहुत कम उपयोग करते थे?

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदलकर लिखिए:
(i) गाड़ी
(ii) कमरे
(iii) दरवाजा
(iv) हम।
उत्तर:
(i) गाड़ी – गाड़ियाँ
(ii) कमरे – कमरा
(iii) दरवाजा – दरवाजे
(iv) हम – मैं।

गद्यांश क्र. 3

प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
परिणाम लिखिए:
(i) अलमारी और कमरा ठीक करने का –
उत्तर:
(i) अलमारी और कमरा ठीक करने का – फटे कुरतों के बारे में पूछताछ की गई।

प्रश्न 2.
सही विकल्प चुनकर वाक्य फिर से लिखिए:
(i) आपसे यह बात ……………………….. के तहत नहीं कर रहा। (सम्मान/अभिमान/शान)
(ii) मेरे बच्चे कहते हैं कि पापा आप हमें ……………………….. से भेजते हैं। (बाइक/रिक्शा/साइकिल)
(iii) दूसरे दिन मैं ……………………….. जाने के लिए तैयार हो रहा था कि बाबू जी ने मुझे बुलाया। (कार्यालय/बाजार/स्कूल)
(iv) वे छोटे हैं, उन्हें ……………………….. चीरकर नहीं बता सकता। (सीना/कलेजा/हृदय)
उत्तर:
(i) आपसे यह बात शान के तहत नहीं कर रहा।
(ii) मेरे बच्चे कहते हैं कि पापा आप हमें साइकिल से भेजते हैं।
(iii) दूसरे दिन मैं स्कूल जाने के लिए तैयार हो रहा था कि बाबू जी ने मुझे बुलाया।
(iv) वे छोटे हैं, उन्हें कलेजा चीरकर नहीं बता सकता।

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:


उत्तर:

प्रश्न 2.
वाक्य पूर्ण कीजिए:
(i) इतना जो उनका कहना था कि हम ……………………
(ii) याद आते हैं बचपन के वे हसीन दिन, ……………………
उत्तर:
(i) इतना जो उनका कहना था कि हम – और अनिल भैया वहाँ एक नहीं सके।
(ii) याद आते हैं बचपन के वे हसीन दिन, – वे पल, जो मैंने बाबू जी के साथ बिताए।

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) रुलाई
(ii) शान
(iii) रिक्शा
(iv) नींव।
उत्तर:
(i) रुलाई – स्त्रीलिंग
(ii) शान – स्त्रीलिंग
(iii) रिक्शा – पुल्लिंग
(iv) नींव – स्त्रीलिंग

प्रश्न 2.
निम्नलिखित शब्दों के बहुवचन रूप लिखिए:
(i) बात
(ii) कोशिश
(iii) साइकिल
(iv) महीना।
उत्तर:
(i) बात – बातें
(ii) कोशिश – कोशिशें
(iii) साइकिल – साइकिलें
(iv) महीना – महीने।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘जीवन में अनुशासन की आवश्यकता’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
मनुष्य के जीवन में अनुशासन का बहुत महत्त्व है। अनुशासन का पालन करने वाले व्यक्ति के कार्य सुचारु रूप से संपन्न होते हैं और अन्य लोग ऐसे व्यक्ति की प्रशंसा करते हैं और उससे प्रेरणा लेते हैं। अनुशासित व्यक्ति ही समाज को नई दिशा दे सकते हैं। रात और दिन का होना, सूर्य और चंद्रमा का अपने नियत समय पर उदय और अस्त होना, फसलों का उगना, बढ़ना और समय पर पकना आदि अनुशासन का ही नतीजा है।

अनुशासित व्यक्ति अपने सभी काम समय पर और ईमानदारी से करने में विश्वास रखता है। उसे इस मामले में लापरवाही बर्दाश्त नहीं होती। दूसरों से भी वह ऐसी ही अपेक्षा रखता है। प्रत्येक व्यक्ति का कर्तव्य है, कि वह अपने आप को अनुशासित रखे। इसके लिए अपने ऊपर अंकुश लगाना और अपने। आप को नियंत्रण में रखना अनुशासन में रहने का आरंभिक पाठ है। यह प्रक्रिया अपने आप को अनुशासित करने का उत्तम मार्ग है।

गयांश क्र.4
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
उत्तर लिखिए:
(i) इन्हें घाटा लगा था – [ ]
(ii) गद्यांश में आया महापुरुष का नाम – [ ]
(iii) गद्यांश में प्रयुक्त एक शहर का नाम – [ ]
(iv) लेखक की माँ विदा होकर यहाँ आई थी – [ ]
उत्तर:
(i) इन्हें घाटा लगा था – [लेखक के पिता जी के चाचा जी को]
(ii) गद्यांश में आया महापुरुष का नाम – [गाँधी जी]
(iii) गद्यांश में प्रयुक्त एक शहर का नाम – [मिरजापुर]
(iv) लेखक की माँ विदा होकर यहाँ आई थी – [रामनगर]

प्रश्न 4.
दो ऐसे प्रश्न बनाकर लिखिए, जिनके उत्तर निम्नलिखित हों:
(i) सुहाग वाले
(ii) सुख-दुख।
उत्तर:
(i) लेखक की माँ ने किस तरह के गहने रख लिए थे?
(ii) जीवन में क्या सदा ही लगा रहता है?

कृति 3: (शब्द संपदा)

प्रश्न 1.
गद्यांश में आए प्रत्यययुक्त शब्द छाँटकर लिखिए और प्रत्यय तथा शब्द अलग-अलग कीजिए।
(i) ……………………
(ii) ……………………
(iii) ……………………
(iv) ……………………
उत्तर:
(i) व्यक्तित्व = व्यक्ति + त्व।
(ii) रिश्तेवालों = रिश्ते + वालों।
(iii) जिम्मेदारी = जिम्मेदार + ई।:
(iv) हिचकिचाहट = हिचकिच + आहट।:

प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) शादी = ……………………
(ii) जरूरत = ……………………
(iii) गहना = ……………………
(iv) पीड़ा = ……………………
उत्तर:
(i) शादी = विवाह
(ii) जरूरत = आवश्यकता:
(iii) गहना = आभूषण
(iv) पीड़ा = कष्ट।:

प्रश्न 3.
(a) निम्नलिखित शब्दों के बिलोम शब्द लिखिए:
(i) प्यार x ……………………
(ii) घाटा x ……………………
उत्तर:
(i) प्यार x नफरत
(ii) घाटा x मुनाफा।

(b) निम्नलिखित शब्दों के वचन पहचानकर लिखिए:,
(i) गहने
(ii) घर।
उत्तर:
(i) गहने-बहुवचन
(ii) घर-एकवचन/बहुवचन।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
महिलाओं को गहनों का शौक’ विषय पर अपने विचार 25 से 30: शब्दों में लिखिए।
उत्तर:
शृंगार और स्त्रियों का पुराना नाता रहा है। केश-विन्यास, परिधान और मेकअप के साथ-साथ स्त्रियों के श्रृंगार में आभूषणों का महत्त्वपूर्ण योगदान होता है। आभूषण के प्रति स्त्रियों के आकर्षण को ध्यान में रखते हुए आभूषण निर्माता तरह-तरह के सुंदर आभूषणों का निर्माण करते हैं। हमारे देश के अधिकांश हिस्सों में विवाह के समय कन्या को वर पक्ष एवं माता-पिता की ओर से आभूषण देने की प्रथा चली आ रही है। इसके पीछे कन्या को श्रृंगार के साधन के साथ-साथ जीवन में वक्त-जरूरत के समय काम आने वाली छोटी-मोटी पूँजी देने का उद्देश्य होता है। हमारे पुरखों ने इसी उद्देश्य से आभूषणों को चढ़ावे की रस्म से जोड़ दिया था, जो आज भी हमारे समाज में प्रचलित है। आभूषण शृंगार और पूँजी दोनों के काम आते हैं।

भाषा अध्ययन (व्याकरण)

प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:

अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) गाड़ी लेकर हम चल पड़े
(ii) सोना मूल्यवान धातु है।
उत्तर:
(i) पुरुषवाचक सर्वनाम
(ii) द्रव्यवाचक संज्ञा।

2. अव्यय:

निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) अंदर
(ii) कभी-कभी।
उत्तर:
(i) हम दबे पैर पीछे किचन के दरवाजे से अंदर घुसे।
(ii) लेखक बच्चों को कभी-कभी अपनी गाड़ी से स्कूल छोड़ देते थे।

3. संधि:

कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
सूर्यास्त	……………………	……………………
अथवा
……………………	दिक् + अंबर	……………………

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
सूर्यास्त	सूर्य + अस्त	स्वर संधि
अथवा
दिगंबर	दिक् + अंबर	व्यंजन संधि

4. सहायक क्रिया:

निम्नलिखित वाक्यों में से सहायक क्रिया पहचानकर उनका मूल रूप लिखिए:
(i) मैंने तुम्हारे बदन के सारे गहने उतरवा लिए।
(ii) वह सब मैंने अम्मा को दे दिए हैं।
उत्तर:
सहायक क्रिया – मूल रूप
(i) लिए – लेना
(ii) हैं – होना

5. प्रेरणार्थक क्रिया:

निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) देखना
(ii) दौड़ना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – दवितीय प्रेरणार्थक रूप
(i) देखना – दिखाना – दिखवाना
(ii) दौड़ना। – दौड़ाना – दौड़वाना

6. मुहावरे:

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) फूट-फूट कर रोना
(ii) देखते रह जाना।
उत्तर:
(i) फूट-फूट कर रोना।
अर्थ: जोर-जोर से रोना।
वाक्य: माँ की नाजुक हालत देखकर बेटा फूट-फूट कर रोने लगा।

(ii) देखते रह जाना।
अर्थ: आश्चर्यचकित होना।
वाक्य: प्लेटफार्म पर पहुँचते-पहुँचते यात्री की गाड़ी छूट गई और वह देखता रह गया।

प्रश्न 2.
अधोरेखांकित वाक्यांशों के लिए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (बाएँ हाथ का खेल, डौंग मारना, तौलकर बोलना)
(i) रमेश के लिए तैरकर नदी पार कर लेगा बहुत सरल है।
(ii) राघव बहुत समझ-बूझकर बोलता है।
उत्तर:
(i) रमेश के लिए तैरकर नदी पार कर लेना बाएँ हाथ का खेल है।
(ii) राघव बहुत तौलकर बोलता है।

7. कारक:

निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) एक दिन बाबू जी ने कहा, “सुनील मेरी अलमारी बहुत बेतरतीब हो गई है।”
(ii) मैंने बाबू जी के कपड़ों की तरफ ध्यान देना शुरू किया।
उत्तर:
(i) बाबू जी ने – कर्ता कारक।
(ii) बाबू जी के – संबंध कारक।

8. विरामचिह्न:

निम्नलिखित वाक्यों में यथास्थान उचित विरामचिहनों का प्रयोग करके वाक्य फिर से लिखिए:
(i) अजी आप इतनी देर से क्यों घर लौटे
(ii) वाह आपने तो गजब कर दिया
उत्तर:
(i) अजी, आप इतनी देर से क्यों घर लौटे?
(ii) वाह! आपने तो गजब कर दिया।

9. काल परिवर्तन:

निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) अब हम उसका प्रयोग कर सकेंगे। (अपूर्ण वर्तमानकाल)
(ii) हम एक जगह खाने पर चले गए थे। (सामान्य भविष्यकाल)
उत्तर:
(i) अब हम उसका प्रयोग कर रहे हैं।
(ii) हम एक जगह खाने पर चले जाएंगे।

10. वाक्य भेद:

प्रश्न 1.
निम्नलिखित वाक्यों का रचमा के आधार पर भेद पहचानकर लिखिए:
(i) बाबूजी खुद इंपाला का प्रयोग न के बराबर करते थे और वह किसी स्टेट गेस्ट के आने पर ही निकाली जाती थी।
(ii) संतरी को जैसा कहा गया था, उसने वैसा ही किया।
उत्तर:
(i) संयुक्त वाक्य
(ii) मिश्र वाक्य।

प्रश्न 2.
निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) हमने बहाना सोच लिया है। (विस्मयादिबोधक वाक्य)
(ii) यह बात शान के तहत नहीं कर रहा हूँ। (विधानवाचक वाक्य)
(iii) तुम लॉग बुक रखते हो? (आज्ञावाचक वाक्य)
उत्तर:
(i) अहा ! हमने बहाना सोच लिया।
(ii) यह बात शान के तहत कर रहा हूँ।
(ii) तुम लॉग बुक रखो।

11. वाक्य शुद्धिकरण:

निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए:
(i) वह मुसकराया और बोले, “आप चिंता न करें।”
(ii) बचपन के वह दीन याद आता है।
उत्तर:
(i) वे मुसकराए और बोले, “आप चिंता न करें।”
(ii) बचपन का वह दिन याद आता है।

उपक्रम/कृति/परियोजना

लेखनीय
आज के उपभोक्तावादी युग में पनप रही दिखावे की संस्कृति पर अपने विचार लिखिए।

पठनीय
पुलिस द्वारा नागरी सुरक्षा के लिए किए जाने वाले कार्यों की जानकारी पढ़िए एवं उनकी सूची बनाइए।

संभाषणीय
अनुशासन जीवन का एक अंग है, इसके विभिन्न रूप आपको कहाँ-कहाँ देखने को मिलते हैं, बताइए।

ईमानदारी की प्रतिमूर्ति Summary in Hindi

विषय-प्रवेश:
लाल बहादुर शास्त्री भारत के प्रधानमंत्री थे। वे एक सामान्य परिवार में जन्मे ‘सादा जीवन उच्च विचार’ के सिद्धांत | को मानने वाले व्यक्ति थे। वे अपनी ईमानदारी, सादगी, सरलता आदि के लिए प्रसिद्ध थे। प्रस्तुत संस्मरण में उनके पुत्र सुनील शास्त्री ने शास्त्री जी और अपने बीच घटी कई प्रेरक एवं यादगार घटनाओं का बेबाक वर्णन किया है।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer

Std 10 Hindi Chapter 5 Goa Jaisa Maine Dekha Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Lokbharti Chapter 5 गोवा जैसा मैंने देखा Notes, Textbook Exercise Important Questions and Answers.

Hindi Lokbharti 10th Digest Chapter 5 गोवा जैसा मैंने देखा Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 5 गोवा जैसा मैंने देखा Textbook Questions and Answers

कृति

सूचना के अनुसार कृतियाँ कीजिए:

प्रश्न 1.
प्रवाह तालिका पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
लिखिए
a. नीले पानीवाला पथरीला –
b. रेतीला तथा उथला –
c. सबसे लंबा –
d. मछुआरों की पहली पसंद –
उत्तर:
(i) नीले पानीवाला पथरीला – अंजुना बीच
(ii) रेतीला तथा उथला – बेनालियम बीच
(iii) सबसे लंबा – कलिंगवुड बीच
(iv) मछुआरों की पहली पसंद – बेनालियम बीच।

प्रश्न 4.
सूची बनाइए:

गोवा का प्राकृतिक सौंदर्य दर्शाने वाले वाक्य
१.
२.
३.
४.

उत्तर:

गोवा का प्राकृतिक सौंदर्य दर्शाने वाले वाक्य
(i)	हरीतिमा से भरपूर
(ii)	खूबसूरत सफेद रेतीले समुद्र तट
(iii)	चंद्रमा की चाँदनी में नहाया समुद्र
(iv)	गहरा नीला पानी।

प्रश्न 5.
कृति पूर्ण कीजिए:

उत्तर:
(1) नवरात्रि की परंपराएँ –
(i) घरों में, गली-मोहल्लों में माँ दुर्गा की घटस्थापना।
(ii) लड़कियों द्वारा गरबा का पर्व मनाना।

(ii) दशहरा की परंपराएँ –
(1) सुबह लोग अपने वाहनों की सफाई करके उनकी पूजा करते हैं।
(2) शाम को भगवान की एक पालकी मंदिर ले जाई जाती है और लोग एक विशेष पेड़ की पत्तियाँ तोड़कर एक-दूसरे को देकर बधाई देते हैं।

प्रश्न 6.
‘बेनालिया’, ‘अंजुना’ तथा ‘कलिंगवुड’ बीच की विशेषताएँ:

उत्तर:
बेनालियम –
(1) यह बीच उथला और रेतीला है।
(2) यहाँ सुबह-सुबह बड़ी मात्रा में मछलियाँ पकड़ी जाती हैं।
(3) यह बीच मछुआरों की पहली पसंद है।

अंजुना –
(1) यह गहरा और नीले पानीवाला खूबसूरत बीच है।
(2) इस पथरीले बीच के एक ओर लंबी-सी पहाड़ी है।
(3) यह बीच बॉलीवुड की पहली पसंद है। यहाँ कई हिट फिल्मों की शूटिंग हुई है।

कलिंगवुड –
(1) यह काफी रेतीला बीच है।
(2) यह बीच 3 से 4 किमी. तक फैला हुआ है।
(3) यह गोवा का सबसे लंबा बीच है।

प्रश्न 7.
सोचिए और लिखिए:

उत्तर:

अभिव्यक्ति-

प्रकृति को सुंदर बनाए रखने में मेरा योगदान’ विषय पर अपने विचार लिखिए।
उत्तर:
हम इस ब्रह्मांड के सबसे सुंदर, हरियाली से युक्त और बेहद आकर्षक ग्रह धरती पर निवास करते हैं। प्रकृति हम इन्सानों को ईश्वर द्वारा दिया गया सबसे खूबसूरत उपहार है। सुंदर पुष्प, आकर्षक पक्षी, वनस्पति, नीला आकाश, भूमि, समुद्र, जंगल, पर्वत, पठार, सूरज, चाँद इस सुंदर प्रकृति का हिस्सा हैं। स्वस्थ जीवन के लिए प्रकृति बहुत आवश्यक है। मैं इस बात का सदा ध्यान रखता हूँ कि यथासंभव प्रकृति की रक्षा कर सकूँ। मैं जब भी बाहर पार्क या बगीचे में जाता है, अनावश्यक रूप से किसी भी फूल-पत्ते को नहीं तोड़ता।

वहाँ खेलते हुए बच्चों को भी फूल-पत्ते तोड़ने से मना करता हूँ, उन्हें समझाता हूँ। मैं एक स्काउट लीडर हूँ। प्रकृति को बचाने के लिए लोगों में जागरूकता फैलाने का प्रयास करता हूँ। अन्य स्काउट्स के साथ मिलकर रैली निकलवाता हूँ कि घर के बाहर कचरा न फैलाएँ, प्लास्टिक की थैलियों के स्थान पर कपड़े के थैलों का प्रयोग करें।

भाषा बिंद

प्रश्न 1.
कोष्ठक में दी गई संज्ञाओं से विशेषण संलग्न हैं। नीचे दी गई सारिणी में संज्ञा तथा विशेषणों को भेदों सहित लिखिए: [भयभीत गाय, नीला पानी, दस लीटर दूध, चालीस छात्र, कुछ लोग, दो गज जमीन, वही पानी, यह लड़का]

संज्ञा	भेद	विशेषण	भेद
…………………………. …………………………. …………………………. …………………………. ………………………….	…………………………. …………………………. …………………………. …………………………. ………………………….	…………………………. …………………………. …………………………. …………………………. ………………………….	…………………………. …………………………. …………………………. …………………………. ………………………….

उत्तर:

संज्ञा	भेद	विशेषण	भेद
(1) गाय	जातिवाचक	भयभीत	गुणवाचक
(2) पानी	द्रव्यवाचक	नीला	गणवाचक
(3) दूध	द्रव्यवाचक	दस लीटर	परिमाणवाचक
(4) छात्र	जातिवाचक	चालीस	संख्यावाचक
(5) लोग	समूहवाचक	कुछ	सार्वनामिक
(6) जमीन	जातिवाचक	दो गज	परिमाणवाचक
(7) पानी	द्रव्यवाचक	वही	सार्वनामिक
(8) लड़का	जातिवाचक	यह	सार्वनामिक

प्रश्न 2.
उपर्युक्त संज्ञा-विशेषणों की जोड़ियों का स्वतंत्र वाक्यों में प्रयोग कीजिए।
उत्तर:
(i) भयभीत गाय – लाठियों के डर से भयभीत गाय इधर-उधर दौड़ रही थी।
(ii) नीला पानी – झील का नीला पानी चाँद की रोशनी में चमक रहा था।
(iii) दस लीटर दूध – हमारी गाय दोनों समय दस लीटर दूध देती है।
(iv) चालीस छात्र – स्वाति की कक्षा में चालीस छात्र हैं।
(v) कुछ लोग – छत पर कुछ लोग चहलकदमी कर रहे हैं।
(vi) दो गज जमीन – औरंगजेब सारी उम्र युद्ध करता रहा। अंत में उसे अपनी दिल्ली में दो गज जमीन भी नहीं मिली।
(vii) वही पानी – यह वही पानी है, जो कल भरा था।
(viii) यह लड़का – यह लड़का चोर नहीं है।

प्रश्न 3.
पाठ में प्रयुक्त विशेषणों को ढूँढ़कर उनकी सूची बनाइए।
उत्तर:

• समुद्री
• खूबसूरत
• सफेद
• सांस्कृतिक
• शांत
• शीतल
• स्थानीय
• रोमांचक
• सुस्वादु
• शाकाहारी।।

प्रश्न 4.
निम्नलिखित वाक्यों में आई हुईं सहायक क्रियाओं को अधोरेखांकित कीजिए तथा उनका अर्थपूर्ण वाक्यों में प्रयोग कीजिए:
(i). टैक्सी एक पतली-सी सड़क पर दौड़ पड़ी।
वाक्य = ……………………………..

(ii). शरीर को कुछ समय के लिए विश्राम मिल जाता है।
वाक्य = ……………………………..

(iii). हम आराम करने के इरादे से अपने-अपने स्यूट चले गए।
वाक्य = ……………………………..

(iv). फिर भी धूप तीखी ही होती जाती है।
वाक्य = ……………………………..

(v). सबके बावजूद यह अपने में एक सांस्कृतिक विरासत भी समेटे हुए हैं।
वाक्य = ……………………………..

(vi). इधर बच्चे रेत का घर बनाने लगे।
वाक्य = ……………………………..

(vii). अब समुद्र स्याह और भयावह दिखने लगा।
वाक्य = ……………………………..

(viii). यहाँ सुबह-सुबह बड़ी मात्रा में मछलियाँ पकड़ी जाती हैं।
वाक्य = ……………………………..
उत्तर:
(i) टैक्सी एक पतली-सी सड़क पर दौड़ पड़ी।
वाक्य – गोली की आवाज सुनकर उड़ती हुई चिड़िया नीचे गिर पड़ी।

(ii) शरीर को कुछ समय के लिए विश्राम मिल जाता है।
वाक्य – सरदियों में सूरज जल्दी छिप जाता है।

(iii) हम आराम करने के इरादे से अपने-अपने स्यूट में चले गए।
वाक्य – बिटिया के विदा होते ही सारे मेहमान चले गए।

(iv) फिर भी धूप तीखी ही होती है।
वाक्य – प्रातःकाल आकाश की आभा मनोरम होती है।

(v) सबके बावजूद यह अपने में एक सांस्कृतिक विरासत भी समेटे हुए है।
वाक्य – जल्दी कक्षा में पहुँचो, विद्यार्थी खाली बैठे हुए हैं।

(vi) इधर बच्चे रेत का घर बनाने लगे।
वाक्य – पिता जी तेजी से दौड़ने लगे।

(vii) अब समुद्र स्याह और भयावह दिखने लगा।
वाक्य – बेटा, अब उठो। सूरज दिखने लगा।

(viii) यहाँ सुबह-सुबह बड़ी मात्रा में मछलियाँ पकड़ी जाती हैं।
वाक्य – गुजरात में मकर संक्रांति के दिन सुबह से रात तक पतंग उड़ाई जाती हैं।

प्रश्न 5.
पाठ में प्रयुक्त दस सहायक क्रियाएँ छाँटकर लिखिए।
उत्तर:

• हो उठता है।
• चले आते हैं।
• देते हैं।
• जा पहुँचा।
• हो गए।
• रुक गई।
• पकड़े हुए है।
• भाग रहे थे।
• दौड़ पड़ी।
• बटौं हुआ है।

उपयोजित लेखन-

विजय/विजया मोहिते, वरदा सोसाइटी, विजयनगर, कोल्हापुर से व्यवस्थापक, औषधि भंडार, नागपुर को पत्र लिखकर आयुर्वेदिक औषधियों की माँग करता/करती है।
उत्तर:
5/7/2020
सेवा में,
व्यवस्थापक महोदय,
औषधि भंडार,
नागपुर।
विषय: आयुर्वेदिक औषधियाँ मँगाने के लिए पत्र।

महोदय,
मैं कोल्हापुर निवासी विजय/विजया हूँ। मुझे कुछ आयुर्वेदिक औषधियों की आवश्यकता है, जो हमारे यहाँ उपलब्ध नहीं हैं। कृपया आप निम्नलिखित औषधियाँ शीघ्रातिशीघ्र भेजकर अनुगृहीत
करें:
(1) कायम चूर्ण 10 शीशी (50 ग्राम)
(2) सुदर्शन धनवटी 3 शीशी (50 ग्राम)
(3) खदिरादि वटी 2 शीशी (50 ग्राम)
(4) शीतोपलादि चूर्ण 5 शीशी (50 ग्राम)

औषधियाँ मिलने पर आपको बैंक ड्राफ्ट द्वारा राशि भेज दी जाएगी।

धन्यवाद।
भवदीया,
विजय/विजया मोहिते
वरदा सोसाइटी,
कोल्हापुर।
ई-मेल आईडी: vijay@xyz.com

Hindi Lokbharti 10th Textbook Solutions Chapter 5 गोवा जैसा मैंने देखा Additional Important Questions and Answers

कृतिपत्रिका के प्रश्न 1 (अ) तथा प्रश्न 1 (आ) के लिए)

गद्यांश क्र. 1

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
उत्तर:

उत्तर:

प्रश्न 2.
गलत वाक्यों को सही करके लिखिए:
(i) देश के मध्य में स्थित होने के कारण यह छोटा-सा राज्य प्रत्येक पर्यटक के दिल की धड़कन है।
(ii) शीतल हवा के झोंकों से मन प्रसन्न हो गया और यात्रा की चिंता मिट गई।
उत्तर:
(i) देश के एक कोने में स्थित होने के कारण यह छोटा-सा राज्य प्रत्येक पर्यटक के दिल की धड़कन है।
(ii) शीतल हवा के झोंकों से मन प्रसन्न हो गया और यात्रा की सारी थकान मिट गई।

प्रश्न 3.
संजाल पूर्ण कीजिए: (बोर्ड की नमूना कृतिपत्रिका)

उत्तर:

प्रश्न 4.
एक-दो शब्दों में उत्तर: लिखिए: (बोर्ड की नमूना कृतिपत्रिका)
(i) लेखक का ध्यान अपनी ओर खींचने वाला – [ ]
(ii) समस्याओं से निजात पाने का सबसे अच्छा तरीका – [ ]
(iii) लेखक के सफर का साधन – [ ]
(iv) लेखक के मड़गाँव में पहुँचने का दिन – [ ]
उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
उत्तर: लिखिए:

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
गद्यांश में प्रयुक्त २ प्रत्यययुक्त शब्द ढूँढकर लिखिए। – (बोर्ड की नमूना कृतिपत्रिका)
(i) _____________
(ii) _____________
उत्तर:
(i) तरंगायित
(ii) प्रत्येक

प्रश्न 2.
निम्नलिखित शब्दों को वर्तनी के नियमानुसार लिखिए:
(i) त्रंगाइत
(ii) आर्कषन
(iii) ओप्चारिक
(iv) खानपुर्ती।
उत्तर:
(i) गाइत -तरंगायित
(ii) आर्कषन -आकर्षण
(iii) ओप्चारिक -औपचारिक
(iv) खानपुर्ती -खानापूर्ति।

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द गद्यांश से ढूँढ़कर लिखिए: (बोर्ड की नमूना कृतिपत्रिका)
(i) अप्रसन्न x _____________
(ii) बुरा x _____________
उत्तर:
(i) अप्रसन्न x प्रसन्न
(ii) बुरा x अच्छा।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘आनंद प्राप्ति का साधन: पर्यटन’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए। (बोर्ड की नमूना कृतिपत्रिका)
उत्तर:
पर्यटन से हमारे ज्ञान में वृद्धि होती है। किसी स्थान के बारे में पढ़कर जानकारियाँ प्राप्त करने और उसे प्रत्यक्ष देखने में अंतर होता है। यह सुख हमें पर्यटन से प्राप्त होता है। पर्यटन से हमें भिन्नभिन्न प्रदेशों और देशों के प्रसिद्ध स्थलों एवं धरोहरों को देखने का अवसर मिलता है। उनकी संस्कृतियों, उनके रहन-सहन और रीतिरिवाजों को प्रत्यक्ष देखने का मौका मिलता है। इससे हम एक-दूसरे के करीब आते हैं। वहाँ हुए विकास कार्यों से प्रेरणा लेते हैं। इसके अतिरिक्त पर्यटन से अपने रोजमर्रा के कार्यों से कुछ दिन दूर रहने और निश्चित होकर देश-दुनिया को देखने, उससे कुछ सीखने और अपने आप में सुधार करने तथा तनावों से मुक्त रहने का अवसर मिलता है। इस तरह पर्यटन निश्चित रूप से आनंद प्राप्ति का एक सुंदर और मनोरंजक साधन है।

गद्यांश क्र. 2

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

ति 1: (आकलन)

प्रश्न 1.
सही विकल्प चुनकर वाक्य फिर से लिखिए:

(i) गोवा की __________________ बड़ी अच्छी होती है। (सुबह/शाम/रात)
(ii) __________________ सागर देखने का उत्साह बढ़ता जा रहा था। (अरब/हिंद/बंगाल)
(iii) यही __________________ का सत्य भी है। (लोगों/दुनिया/जीवन)
(iv) __________________ सुस्ताने के लिए किनारे पर बैठ जाते हैं। (कुत्ते/पक्षी/लोग)
उत्तर:
(i) गोवा की शाम बड़ी अच्छी होती है।
(ii) अरब सागर देखने का उत्साह बढ़ता जा रहा था।
(iii) यही जीवन का सत्य भी है।
(iv) पक्षी सुस्ताने के लिए किनारे पर बैठ जाते हैं।

प्रश्न 2.
वाक्य पूर्ण कीजिए:

(i) फिर भी धंसे हुए पैरों को __________________
(ii) मानो, लहर कह रही हो कि __________________
उत्तर:
(i) फिर भी धंसे हुए पैरों को पूरी ताकत से उठा-उठाकर भाग रहे थे।
(ii) मानो, लहर कह रही हो कि बनने के बाद मिटना ही नियति है।

प्रश्न 3.
आकृति पूर्ण कीजिए:

(i) (1) लहरों की आवाज – [ ]
(2) बच्चों से मिली सीख – [ ]
(ii)

उत्तर:
(i) (1) लहरों की आवाज – रणभेरी जैसी।
(2) बच्चों से मिली सीख – जीवन में आशावाद हो, तो कोई काम असंभव नहीं

(ii)

ति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

(i) खूबसूरत यह देखते ही मैं उससे जाकर लिपट गया
(ii) बहुत ही खूबसूरत और शांत जगह है यह –
(ii) तभी अचानक इनकी आवाज सुनाई दी
(iv) जल्दी-जल्दी चलने के बाद भी यह तय नहीं हो पा रही थी
उत्तर:
(i) खूबसूरत यह देखते ही मैं उससे जाकर लिपट गया – [समुंदर]
(ii) बहुत ही खूबसूरत और शांत जगह है यह – [बेनालियम]
(iii) तभी अचानक इनकी आवाज सुनाई दी – [लहरों की]
(iv) जल्दी-जल्दी चलने के बाद भी यह तय नहीं हो पा रही थी – [दूरी]

प्रश्न 2.
उत्तर: लिखिए:

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का वचन बदलकर लिखिए:
(i) हवा
(ii) मछली
(ii) लहर
(iv) बच्चे।
उत्तर:
(i) हवा – हवाएँ
(ii) मछली – मछलियाँ
(iii) लहर – लहरें
(iv) बच्चे – बच्चा

प्रश्न 2.
निम्नलिखित शब्दों के लिंग पहचानकर लिखिए:
(i) जगह
(ii) रेत
(iii) जीवन
(iv) सड़क।
उत्तर:
(i) जगह – स्त्रीलिंग
(ii) रेत – पुल्लिग
(iii) जीवन – पुल्लिंग
(iv) सड़क – स्त्रीलिंग।

प्रश्न 3.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) शांत
(ii) मुश्किल
(iii) शाम
(iv) खूबसूरत।
उत्तर:
(i) शांत x अशांत
(ii) मुश्किल x आसान
(iii) शाम x सुबह
(iv) खूबसूरत X बदसूरत।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘गोवा की शाम’ के विषय में अपने विचार लिखिए।
उत्तर:
भारत के पश्चिमी समुद्र तट पर बसे गोवा की खूबसूरती के समान यहाँ की शामें भी अद्भुत होती हैं। जैसे-जैसे शाम होती है, गोवा मस्ती में डूबने लगता है। सागर के तट पर चाँदी जैसी रेत, नीलम जैसा पानी, चर्च, नारियल के पेड़ों का सौंदर्य मन को मोह लेता है। दूर-दूर तक विदेशी सैलानियों की भीड़ दिखाई देती है, कोई उछल रहा है, कोई कूद रहा है, कोई नाच रहा है। बीच पर तरह-तरह के वॉटर स्पोर्ट्स चल रहे हैं।

कहीं मोटरबोट राइडिंग हो रही है, तो कहीं पैराशूट राइडिंग। सैलानियों के लिए क्रूज एक अलग ही आकर्षण होता है। क्रूज अर्थात एक छोटे से स्टीमर में सौ-डेढ़ सौ लोग संगीत की तेज धुन पर थिरकते हुए। यह स्टीमर करीब एक घंटे की घुमावदार परिक्रमा कराता है।

गद्यांश क्र. 3

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
जोड़ियाँ मिलाइए:

‘अ’	‘आ’
(i) मनोरम	फिल्में
(ii) युवा	बाजार
(iii) हिट	दृश्य
(iv) स्थानीय	मस्ती

उत्तर:

‘अ’	‘आ
(i) मनोरम	दृश्य
(ii) युवा	मस्ती
(iii) हिट	फिल्में
(iv) स्थानीय	बाजार

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
विधानों के सामने सत्य/असत्य लिखिए:
(i) पानी नीले पत्थरों पर पछाड़ खाता रहता है।
(ii) पानी ने काट-काटकर पत्थरों में छेद कर दिए हैं।
(iii) गोवा की सारी मछलियाँ निर्यात कर दी जाती हैं।
(iv) हम लोग दिन भर पणजी शहर देखते रहे।
उत्तर:
(i) असत्य
(ii) सत्य
(iii) असत्य
(iv) सत्य।

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) समुद्र
(ii) पानी
(iii) पत्थर
(iv) किनारा।
उत्तर:
(i) समुद्र – जलधि
(ii) पानी – सलिल
(iii) पत्थर – पाषाण
(iv) किनारा – तट।

प्रश्न 2.
गद्यांश में प्रयुक्त अंग्रेजी शब्द ढूँढकर लिखिए।
(i) ____________
(ii) ____________
(iii) ____________
(iv) ____________
उत्तर:
(i) शूटिंग
(ii) फिल्म
(iii) बॉलीवुड
(iv) बीच।

प्रश्न 3.
गद्यांश में प्रयुक्त प्रत्यययुक्त शब्द ढूँढ़कर उनके मूल शब्द और प्रत्यय अलग करके लिखिए।
(i) ____________
(ii) ____________
(iii) ____________
(iv) ____________
उत्तर:
शब्द – मूल शब्द – प्रत्यय
(i) पथरीला – पत्थर – ईला
(ii) पहाड़ी – पहाड़ – ई
(iii) स्थानीय – स्थान – ईय
(iv) व्यावसायिक – व्यवसाय – ई

गद्यांश क्र. 4

प्रश्न.
निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
सही विकल्प चुनकर वाक्य फिर से लिखिए:

(i) आप भी अपनी ______________ के अनुसार हाथ आजमा सकते हैं। (इच्छा/जेब/रुचि)
(ii) हम यानी मैं और मेरी ______________ दोनों डर भी रहे थे। (पत्नी/बिटिया/माँ)
(iii) कोलबा बीच पर हमने ______________ मछलियाँ देखीं। (व्हेल/डॉल्फिन/शार्क)
(iv) शाम को भगवान की एक ______________ मंदिर ले जाई जाती है। (मूर्ति/फोटो/पालकी)
उत्तर:
(i) आप भी अपनी रुचि के अनुसार हाथ आजमा सकते हैं।
(ii) हम यानी मैं और मेरी पत्नी दोनों डर भी रहे थे।
(iii) कोलबा बीच पर हमने डॉल्फिन मछलियाँ देखीं।
(iv) शाम को भगवान की एक पालकी मंदिर ले जाई जाती है।

प्रश्न 2.
कारण लिखिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
सोचिए और लिखिए:

प्रश्न 2.
गद्यांश में प्रयुक्त अंग्रेजी शब्द ढूंढकर लिखिए।

(i) _____________
(ii) _____________
(iii) _____________
(iv) _____________
उत्तर:
(i) बोटिंग
(ii) वॉटर
(iii) स्पोर्ट्स
(iv) पैराग्लाइडिंग।

प्रश्न 3.
गद्यांश में प्रयुक्त शब्द-युग्म ढूँढ़कर लिखिए।
(i) _____________
(ii) _____________
(iii) _____________
(iv) _____________
उत्तर:
(i) रचा-बसा
(ii) अपनी-अपनी
(iii) एक-दूसरे
(iv) घूमना-फिरना।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘गोवा की संस्कृति’ के विषय में 25 से 30 शब्दों में अपने विचार लिखिए।
उत्तर:
सुरम्य सागरतट पर बसा गोवा प्रांत अपनी प्राकृतिक सुंदरता और अनूठी संस्कृति के लिए प्रसिद्ध है। यहाँ की संस्कृति काफी प्राचीन है। आजादी से पहले गोवा पुर्तगाल और फ्रांस का उपनिवेश था। इस वजह से आज भी यहाँ के रहन-सहन, खान-पान पर पश्चिमी संस्कृति का पूरा प्रभाव दिखाई देता है। यहाँ लगभग 80 प्रतिशत लोग ईसाई हैं।

गोवा की एक खास बात यह है कि यहाँ के ईसाई समाज में भी हिंदुओं जैसी जाति व्यवस्था पाई जाती है। दक्षिण गोवा में ईसाई समाज का प्रभाव अधिक है, लेकिन वहाँ के वास्तुशास्त्र में हिंदू प्रभाव दिखाई देता है। गोवा में अत्यंत प्राचीन मंदिर पाए जाते हैं, जबकि उत्तर: गोवा में पुर्तगाली वास्तुकला के नमूने ज्यादा दृष्टिगोचर होते हैं।

भाषा अध्ययन (व्याकरण)

प्रश्न.
सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) मैं उनसे पूछने लगा।
(ii) हम मड़गाँव 23 नवंबर को पहुंचे।
उत्तर:
(i) उनसे – पुरुषवाचक सर्वनाम।
(ii) मड़गाँव – व्यक्तिवाचक संज्ञा।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) वहाँ
(ii) कभी-कभी।
उत्तर:
(i) वहाँ! एक मजेदार दृश्य देखने को मिला।
(ii) कभी-कभी कोई जल-पक्षी कुत्तों का शिकार बन जाता है।

3. संधि:
कृति पूर्ण किजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
स्वच्छ	___________	___________
अथवा
सत् + आचार	___________	___________

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
स्वच्छ	सु + अच्छ	स्वर संधि
अथवा
सदाचार	सत् + आचार	व्यंजन संधि

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उनका मूल रूप लिखिए:
(i) हम सभी समुद्र की ओर दौड़ पड़े।
(ii) हम दिन भर पणजी शहर देखते रहे।
उत्तर:
सहायक क्रिया – मूल रूप
(i) पड़े – पड़ना
(i) रहे – रहना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) सुनना
(ii) बनना
(iii) झुकना।
उत्तर:

क्रिया	प्रथम प्रेरणार्थक रूप	द्वितीय प्रेरणार्थक रूप
(i) सुनना	सुनाना	सुनवाना
(ii) बनना	बनाना	बनवाना
(iii) झुकना	झुकाना	झुकवाना

6. मुहावरे:
(1) निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) शिकार होना
(ii) दीवार टूट जाना।
उत्तर:
(i) शिकार होना।
अर्थ: पीड़ित होना।
वाक्य: पुराने जमाने में न जाने कितने गरीब जींदारों के अत्याचारों के शिकार हो जाते थे।

(ii) दीवार टूट जाना।
अर्थ: अड़चन समाप्त हो जाना।
वाक्य: स्त्रियों को समानता का अधिकार मिल जाने से सभी स्त्री-पुरुष के बीच असमानता की दीवार टूट गई।

(2) अधोरेखांकित वाक्यांश के लिए कोष्ठक में दिए गए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (कान पक जाना, भनक पड़ना, कान पकड़ना) थानेदार ने उड़ती हुई बात सुनी कि गाँव में डाकू आने वाले हैं।
उत्तर:
भनक पड़ना। वाक्य: थानेदार के कान में भनक पड़ी कि गाँव में डाकू आने वाले हैं।

7. कारक:
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उनका भेद ‘लिखिए:
(i) गोवा की मांडवी नदी वर्ष भर पानी से भरी रहती है।
(ii) गोवा राज्य दो भागों में बँटा हुआ है।
उत्तर:
(i) पानी से-करण कारक।
(ii) भागों में-अधिकरण कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का प्रयोग करके वाक्य फिर से लिखिए:
(i) दूर दूर तक पानी ही पानी तेज हवा और रस्सियों से हवा में लटके हम
(ii) गोवा यह नाम सुनते ही सभी का मन तरंगायित हो उठता है और हो भी क्यों न यहाँ की प्रकृति आबोहवा जीवनशैली ही ऐसी है
उत्तर:
(i) दूर-दूर तक पानी-ही-पानी, तेज हवा और रस्सियों से हवा में लटके हम।
(ii) गोवा ! यह नाम सुनते ही सभी का मन तरंगायित हो उठता है और हो भी क्यों न, यहाँ की प्रकृति, आबोहवा जीवनशैली ही ऐसी है।

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन कीजिए:
(i) मंत्री जी ने लोगों को एक मशवरा दिया। (पूर्ण वर्तमानकाल)
(ii) गोवा में मुझे मेरे पुराने अध्यापक मिले थे। (सामान्य भूतकाल)
उत्तर:
(i) मंत्री जी ने लोगों को एक मशवरा दिया है।
(ii) गोवा में मुझे मेरे पुराने अध्यापक मिले।

10. वाक्य भेद:
(1) रचना के आधार पर निम्नलिखित वाक्यों का भेद पहचानकर लिखिए:
(i) सबकी अपनी-अपनी सांस्कृतिक परंपरा है।
(ii) डॉल्फिन मछलियाँ छोटी थीं पर बच्चों को आनंद आया।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य।

(2) निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार परिवर्तन कीजिए:
(i) पर्यटन का अपना ही आनंद है। (विस्मयवाचक)
(ii) आशावाद हो तो हर काम संभव है। (निषेधवाचक)
उत्तर:
(i) वाह! पर्यटन का अपना ही आनंद है।
(ii) आशावाद हो तो कोई काम असंभव नहीं है।

11. वाक्य शुद्धिकरण:
निम्नलिखित वाक्य शुद्ध करके लिखिए:
(i) भाषा ईश्वर का बड़ा देन है।
(ii) पैसेवाली व्यक्ति कटु बोलती है।
उत्तर:
(i) भाषा ईश्वर की बड़ी देन है।
(ii) पैसेवाला व्यक्ति कटु बोलता है।

उपक्रम/कृति/परियोजना

प्रश्न.
गोवा की ऐतिहासिक पृष्ठभूमि की जानकारी पदिए और कालानुक्रम के अनुसार प्रमुख घटनाओं की तालिका बनाइए।
उत्तर:
गोवा की ऐतिहासिक पृष्ठभूमि:

मौर्य वंश	तीसरी सदी ईसा पूर्व से पहली सदी तक
कोल्हापुर के सातवाहन	पहली सदी से 580 ईसवी तक
बादामी के चालुक्य	580 ईसवी से 750 ईसवी तक
विजयनगर	1312 ईसवी सें1468 तक
दिल्ली सल्तनत	1469 ईसवी से 1510 ईसवी तक
पुर्तगाली शासन	1510 ईसवी से 1960 ईसवी तक

प्रश्न.
गोवा की प्राकृतिक सुंदरता पर संवाद प्रस्तुत कीजिए।
उत्तर:
गोवा की प्राकृतिक सुंदरता पर दो सहेलियों के बीच संवाद:
रुचि: नीनू, बहुत दिनों बाद दिखी। कैसी हो? कहीं बाहर गई थी क्या?

नीनू: हाँ रुचि, हम लोग एक सप्ताह के लिए गोवा गए थे।

रुचि: गोवा! नीनू मैंने सुना है कि गोवा बहुत सुंदर है।

नीनू: सच सुना है रुचि। गोवा इतना सुंदर है कि मेरा तो मन करता था कि वहाँ से वापस ही नहीं आऊँ।

रुचि: मुझे भी तो कुछ बताओ।

नीनू: रुचि, गोवा अपने समुद्र तटों के लिए बहुत प्रसिद्ध है। साफ नीला पानी, लंबे समुद्र तट, चमचमाती रेत और नारियल के वृक्ष यहाँ की विशेषता है। गोवा में इतनी अधिक हरियाली है कि ऐसा लगता है मानो घरती ने हरी चादर ओढ़ रखी है।

रुचि: ओह! सुनकर ही कितना अच्छा लग रहा है।

नीनू: गोवा के लोग प्रकृति से बहुत प्रेम करते हैं। छोटे-से छोटे घर के आगे भी सुंदर-सुंदर फूल-पौधे जरूर होते हैं। वहाँ बड़ा शांत और मनोरंजक वातावरण है।

रुचि: गोवा के समुद्र तट के बारे में कुछ और बताओ न।

नीनू: वहाँ सागर से आसमान देखकर लगता है मानो नीला आसमान पानी से मिल रहा है। प्रातःकाल में उगता हुआ सूरज ऐसा लगता है, मानो समुद्र में से ही उग रहा हो। इसी तरह सूर्यास्त के समय सूरज का लाल गोला धीरे-धीरे नीचे जाता हुआ अचानक समुद्र में डूबता-सा लगता है। जैसे-जैसे शाम होती है, समुद्र की लहरों का ऊँचा उठन्य शुरू हो जाता है।

गोवा जैसा मैंने देखा Summary in Hindi

गोवा जैसा मैंने देखा विषय–प्रवेश :

प्रस्तुत यात्रा निबंध में विनय शर्मा ने भारत के पश्चिमी तट पर बसे गोवा की प्राकृतिक सुंदरता, वहाँ के लोगों की जीवन शैली, त्योहारों तथा समुद्र तटों का मनोरम, मनोहारी चित्रण किया है। यहाँ के समुद्र तट पर्यटकों के आकर्षण के केंद्र बिंदु हैं। पश्चिमी फैशन के साथ अपने आप को ढालते हुए भी गोवा अपनी भारतीय परंपरा और सभ्यता को नहीं भूला है।

गोवा जैसा मैंने देखा मुहावरे – अर्थ

• मन तरंगायित होना – मन उमंग से भरना।
• निजात पाना – मुक्ति पाना।
• दो – चार होना – जूझना।
• जेब ढीली होना – जेब खाली होना, बहुत खर्च होना।

Hindi Lokbharti 10th Std Digest पहली इकाई

• भारत महिमा Question Answer
• लक्ष्मी Question Answer
• Chapter 3 वाह रे! हमदर्द Question Answer
• मन Question Answer (पूरक पठन)
• गोवा : जैसा मैंने देखा Question Answer
• गिरिधर नागर Question Answer
• खुला आकाश Question Answer (पूरक पठन)
• गजल Question Answer
• रीढ़ की हड्डी Question Answer
• ठेस Question Answer (पूरक पठन)
• कृषक गान Question Answer

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 2 खोया हुआ आदमी Notes, Textbook Exercise Important Questions and Answers.

Std 10 Hindi Chapter 2 Khoya Hua Aadmi Question Answer Maharashtra Board

Hindi Lokvani 10th Digest Chapter 2 खोया हुआ आदमी Questions And Answers

Hindi Lokvani 10th Std Digest Chapter 2 खोया हुआ आदमी Textbook Questions and Answers

सूचना के अनुसार कृतियाँ कीजिए :

(१) कृति पूर्ण कीजिए :

Answer:

(२) उत्तर लिखिए :

Answer:

(३) ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों :

भविष्यवाणी
Answer:
गाँव वालों को मुसीबत से बचाने के लिए खोया हुआ आदमी क्या बताता था?

झमाझम बारिश
Answer:
बच्चे-बड़े सभी किसमें भीगने का भरपूर आनंद लेने लगे?

खुशहाली
Answer:
खोए हुए आदमी की मदद गाँव वालों के लिए क्या लेकर आई?

गंधक
Answer:
जिस रात मौसम बौराया उस रात किसकी तेज गंध पूरे गाँव में फैल गई?

(४) दिए गए निर्देश के अनुसार परिवर्तन कीजिए

Answer:

अभिव्यक्ति

‘मानवता ही सच्चा धर्म है।’ पर अपने विचार लिखिए।
Answer:
मानवता शब्द का सरल शब्दों में मतलब है – मनुष्यता मानवता
मनुष्य का धर्म होता है। आज मानवीय मूल्यों का पतन हो रहा है। इंसान स्वार्थ की पट्टी के कारण अंधा होता जा रहा है। इंसान को स्वार्थ, लोभ, मोह आदि से परहेज करना चाहिए। प्रत्येक मनुष्य की सहायता करनी चाहिए। मानवता के बदले हम सुख, शांति और समृद्धि प्राप्त कर सकते हैं। मानवता से भरा जीवन जीने से व्यक्ति के अंदर सहज रूप से शक्ति और स्फूर्ति आ जाती है।

एक-दूसरे की मदद करने से हम एक-दूसरे की पीड़ा, व्यथा, वेदना को दूर कर सकते हैं। इससे बढ़कर कोई अन्य धर्म नहीं हो सकता। जीवन में जो महापुरूष हुए हैं, उन्होंने अपने जीवन में मानवता के धर्म को ही अपनाया था। महाकवि गुप्त जी ने ठीक ही लिखा है – ‘वही मनुष्य है जो मनुष्य के लिए मरे।’ मानवता का धर्म मानव जाति को एक-दूसरे से प्रेम करना सिखाता है।

भाषा बिंदु

(१) निम्नलिखित वाक्यों में आए हुए अव्ययों को रेखांकित करते हुए उनके भेद लिखिए :

उसके जहन से उसका नाम और पता पूरी तरह खो चुके थे। —–
Answer:
परंतु

ओह ! दिव्या मैं ठीक हूँ। —–
Answer:
अरेरे!

उसकी भविष्यवाणी के कारण गाँववाले मुसीबतों से बच जाते । —-
Answer:
के समान

वहाँ से तुलसीनगर पास पड़ता है । —–
Answer:
धीरे-धीरे

काश, अपने गाँव-शहर में हमें भी ‘खोया हुआ आदमी’ मिल जाता ! —–
Answer:
इसलिए

कभी-कभी मेरा मन उच्चाकाश में उड़ने वाले पक्षियों के साथ अनंत के ओर-छोर नापना चाहता है। —————
Answer:
छि !

ब्लडप्रेशर भी ज्यादा है पर चिंता की कोई बात नहीं । ——–
Answer:
ऊपर

इतनी जल्दी लौट जाते हैं । —–
Answer:
के अलावा

(२) निम्नलिखित अव्ययों का सार्थक वाक्य में प्रयोग कीजिए।

परंतु :
Answer:
मैं तुम्हें मिलने आने ही वाला था परंतु कुछ कारण वश नहीं आ सका।

अरेरे! :
Answer:
अरेरे! यह क्या हो गया?

के सामान :
Answer:
उसके समान कोई भी बहादुर नहीं है।

धारे-धीरे :
Answer:
गाड़ी धीरे-धीरे जा रही थी।

इसलिए :
Answer:
वह बीमार है इसलिए आज स्कूल नहीं गया।

छि! :
Answer:
छि! कितनी गंदगी है।

ऊपर :
Answer:
उसके ऊपर एक किताब है।

के अलावा :
Answer:
मुझे इसके अलावा और कुछ नहीं अच्छा लगता।

उपयोजित लेखन

‘विश्व बंधुता : वर्तमान युग की माँग’ इस विषय पर अस्सी से सौ शब्दों में निबंध लिखिए।
Answer:
संस्कृत में एक सुभाषित है – सर्वे भवन्तु सुखिन। सर्वे सन्तु निरामयाः । इसका अर्थ यह है कि संसार में सब सुखी रहें, सब निरोग रहें और विश्व में कोई दुखी न हो। इसे ही विश्व बंधुत्व कहते है। ‘वसुधैव कुटुम्बकम्’ ऐसा जो कहा गया है, वह शत-प्रतिशत उचित है। जब तक व्यक्ति विश्व बंधुत्व को नहीं अपनाएगा; तब तक मानवता अधूरी रहेगी, मानव अधूरा रहेगा, राष्ट्र अधूरा रहेगा और विश्व भी अधूरा ही रहेगा। आज हमारे देश में ही नहीं बल्कि विश्व के कई देशों में अशांति, अराजकता, हिंसा आदि प्रवृत्तियाँ दिखाई दे रही हैं। इनके कारण व्यक्ति, समाज और राष्ट्र की हानि हो रही है।

आज हमारे समाज में ईर्ष्या, द्वेष, नफरत की भावनाएँ बढ़ रही हैं। इस कारण समाज में दुश्मनी का भाव पनपने लगा है। ये दशा राष्ट्र की भी है। एक राष्ट्र दूसरे राष्ट्र की सीमा पर आए दिन हमला कर रहा है। इस कारण अशांति निर्माण हो रही है। इसी कारण ‘विश्व-बंधुत्व’ वर्तमान युग की माँग है। विश्व बंधुत्व की भावना मानव अधिकारों की सुरक्षा की कुंजी है। विश्व-बंधुत्व की भावना को अपनाने से सभ्य मानवी समाज विकसित होगा।

गरीबी, जाति, धर्म, ऊंच-नीच आदि समस्याओं का समाज से निर्मूलन होगा। विश्व-बंधुत्व की भावना को अपनाने से विश्व में अहिंसा का प्रचार होगा। विश्व में शांति निर्माण होगी। युद्ध व हिंसा खत्म हो जाएगी। सर्वत्र समानता दिखाई देगी। सर्वत्र भाईचारा निर्माण होगा। मानवीय मूल्यों का संवर्धन होगा। आखिर, प्रत्येक मानव को श्रेष्ठ समाज के निर्माण के लिए विश्व बंधुत्व की भावना को आत्मसात करना ही होगा।

लेखनीय

प्रतिभा जन्मजात होती है; परंतु उसके पल्लवन हेतु उचित वातावरण की आवश्यकता होती है।
Answer:
प्रतिभा ईश्वर से मिलती है। प्रत्येक मानव के पास प्रतिभा होती है। फर्क सिर्फ इतना ही होता है कि वह किसी व्यक्ति में अत्यधिक रूप से विकसित होती है, तो किसी व्यक्ति में वह विकसित नहीं होती। प्रतिभा का पल्लवन एक उचित वातावरण में ही होता है। उदाहरण के तौर पर देखिए – बचपन में इंदिरा गांधी को रवींद्रनाथ टैगोर व महात्मा गांधी का साथ मिला। उनके साथ वह पली-बढ़ीं। उनके विचार एवं सिद्धांतों से प्रभावित हुई। तब जाकर उनकी प्रतिभा रग लाई। प्रतिभा वृद्धि की कोई सीमा नहीं होती।

टाटा और अंबानी जैसे व्यक्ति उद्योगपतियों के रूप में सफल हुए हैं, तो सचिन तेंदुलकर व पी. टी. ऊषा जैसे खिलाड़ी क्रीडा क्षेत्र में सफल हुए हैं। ये सब अद्भुत प्रतिभा के ही उदाहरण हैं। व्यक्ति को अपने भीतर की प्रतिभा को पहचानकर मनचाहे क्षेत्र में आगे बढ़ना चाहिए। किसी ने ठीक ही कहा है – ‘जीवन का आनंद स्वयं को जानने में है।’ अत: हर व्यक्ति को स्वयं का निरीक्षण करके अपनी प्रतिभा का पता लगाना चाहिए और उसके विकास के लिए निरंतर प्रयास करते रहना चाहिए। व्यक्ति को स्वयं की प्रतिभा के पल्लवन हेतु स्वयं ही अग्रसर होकर उचित माहौल या परिस्थिति निर्माण करनी जाहिए। आखिर जहाँ चाह होती है, वहाँ राह भी होती है।

Hindi Lokvani 10th Std Textbook Solutions Chapter 2 खोया हुआ आदमी Additional Important Questions and Answers

निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (१): आकलन कृति

कृति पूर्ण कीजिए।

Question 1.

Answer:

समझकर लिखिए।

Question 1.

Answer:

किसने, किससे कहा?

Question 1.
“शायद मैं खो गया हूँ।”
Answer:
गाँव में आए एक आदमी ने गाँव के एक भले आदमी से कहा।

सही विकल्प चुनकर लिखिए।

Question 1.
गाँव में आया हुआ आदमी कुत्तों को पागल लगा क्योंकि ……….
(क) वह चीथड़ों में लिपटा था।
(ख) उसका शरीर रेशमी कपड़ों में लिपटा था।
(ग) उसका शरीर कंबल में लिपटा था।
Answer:
गाँव में आया हुआ आदमी कुत्तों को पागल लगा क्योंकि वह चीथड़ों में लिपटा था।

कृति अ (२) : शब्द संपदा

निम्नलिखित शब्दों के अर्थ गद्यांश में से ढूँढ़कर लिखिए।

1. प्रतिष्ठा
2. निशान
3. बड़ी तेजी से
4. देहात

Answer:

1. गरिमा
2. चिह्न
3. बेतहाशा
4. गाँव

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
अचानक आ जाने वाला
Answer:
आंगतुक

निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
बेतहाशा
Answer:
अचानक, वेगपूर्वक, बिना सोचे-समझे

Question 2.
‘ग्राम’ तत्सम शब्द का तद्भव रूप लिखिए।
Answer:
गाँव

दिए गए निर्देश के अनुसार परिवर्तन कीजिए।

कृति अ (३) : स्वमत अभिव्यक्ति

Question 1.
‘खोया हुआ आदमी’ इस संकल्पना से आप क्या समझते हैं? अपने विचार लिखिए।
Answer:
‘खोया हुआ आदमी’ वह है जिसके चेहरे पर खोने के भाव मौजूद होते हैं। जिस व्यक्ति को अपनी जाति एवं धर्म के बारे में कुछ भी ज्ञात नहीं होता है, वह खोए हुए आदमी की श्रेणी में आता है। इतना ही नहीं, जो व्यक्ति अपने घर, परिवार एवं रिश्तेदारों को भूल गया हो और अकेले यत्र-तत्र घुमक्कड़ की भाँति भटकता-फिरता हो, वह खोया हुआ आदमी होता है। जीवनकाल में व्यक्ति के हृदय पर भारी आघात हो जाने पर या गहरा सदमा पहुँचने पर व्यक्ति की दशा खोए हुए आदमी के जैसी हो जाती है। जीवन की आपाधापी में जिन लोगों के मन में भावों का ऊहापोह मचना शुरू हो जाता है, ऐसे लोग मेरे मतानुसार खोए हुए आदमी की श्रेणी में आते हैं।

प्रश्न २ (आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (१): आकलन कृति

संजाल पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
गाँव के लोगों को खोया हुआ आदमी बेहद अपना-सा लगा।
Answer:
सत्य

Question 2.
खोया हुआ आदमी गाँव में रहने के लिए राजी नहीं हुआ।
Answer:
असत्य

कृति आ (२) : शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. जहन
2. लिहाजा
3. स्मृति
4. लोप

Answer:

1. दिमाग
2. इसलिए
3. याद
4. अभाव

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
गायब या खत्म हो जाने का भाव
Answer:
लोप

विलोम शब्द लिखिए।

1. परिचित x ………….
2. अपना x …………

Answer:

1. परिचित x अपरिचित
2. अपना x पराया

वचन बदलिए।

1. जाति
2. तैयारी
3. स्मृति
4. फैसला

Answer:

1. जातियाँ
2. तैयारियाँ
3. स्मृतियाँ
4. फैसले

उपसर्ग व प्रत्यय लगाकर शब्द लिखिए।

Question 1.
धर्म
Answer:
उपसर्ग : अधर्म, प्रत्यय : धार्मिक

निम्नलिखित वाक्यों में विरामचिह्न का उचित प्रयोग कीजिए।

Question 1.
गाँव के लोगों ने कहा अरे बह खोया हुआ आदमी तो बेहद अपना-सा लग रहा है।
Answer:
गाँव के लोगों ने कहा, “अरे, यह खोया हुआ आदमी तो बेहद अपना-सा लग रहा है।”

कृति आ (३) : स्वमत अभिव्यक्ति

Question 1.
स्मृति का लोप हो जाने वाले व्यक्ति के साथ आप किस प्रकार का व्यवहार करेंगे? अपने विचार लिखिए।
Answer:
हम स्मृति का लोप हो जाने वाले व्यक्ति के साथ मित्रवत व्यवहार करेंगे। उनके साथ आवश्यकता से अधिक बात नहीं करेंगे। उन्हें ईश्वर के प्रति ध्यान करने के लिए कहेंगे, जिससे उनके मन को परिवर्तित किया जा सके। ऐसे व्यक्ति के साथ हर परिस्थिति में संतोष व सहनशीलता दिखाएँगे। उन्हें दूध, ग्लूकोज, नारियल पानी और तरल पदार्थ पीने के लिए देंगे। हम इस बात की सावधानी बरतेंगे कि ऐसे व्यक्ति अत्यधिक क्रोधित एवं अत्यधिक भावुक न बनें। उन्हें प्रतिदिन बगीचे में सैर के लिए लेकर जाएँगे; ताकि उनका मन सदैव प्रसन्न रहे। उनसे यदि कोई गलती हो जाती है, तो उन्हें बड़े प्यार से समझाएँगे।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (१)आकलन कृति

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हो –

Question 1.
मधुर
Answer:
खोए हुए आदमी की आवाज कैसी थी?

Question 2.
गाय-भैंसें
Answer:
खोए हुए आदमी के गीत से कौन मंत्रमुग्ध होते थे?

कृति इ (२) : शब्द संपदा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
गाय-भैंसें
स्वर-लहरियों
बड़े-बुजुर्गों
कभी-कभी

लिंग बदलिए।

1. गाय
2. कुत्ता
3. भैंस

Answer:

1. बैल
2. कुतिया
3. भैंसा

वचन बदलिए।

1. तितलियाँ
2. भैंसा

Answer:

1. तितली.
2. भैंसें

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. सगा x …..
2. पुराना x ……….
3. सुरीला x …..
4. गाँव x ……..

Answer:

1. सगा x सौतेला
2. पुराना x नया
3. सुरीला x बेसुरा
4. गाँव x शहर

नीचे दिए हुए शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
कमाल
Answer:
चमत्कारिक कार्य, निपुणता, सर्वोत्तम

कृति इ (३) : स्वमत अभिव्यक्ति

Question 1.
‘सुरीली आवाज किसी भी व्यक्ति की पहचान होती है।’ विषय पर अपने विचार लिखिए।
Answer:
सुरीली आवाज किसी भी व्यक्ति की पहचान होती है। वाणी व्यक्ति के व्यक्तित्व की भी पहचान होती है। सुरीली और मधुर आवाज हर किसी को अपनी ओर आकर्षित करती है। सुरीली आवाज लोगों पर अपना प्रभाव निर्माण करती है। लता मंगेशकर, मोहम्मद रफी, किशोर कुमार आदि महान गायकों की आवाज ने आज भी लोगों को अपना दीवाना बनाए रखा है। इसलिए स्वर कोकिला लता दीदी बड़े शान से कहती हैं – ‘मेरी आवाज ही मेरी पहचान है।’ सुरीली आवाज के कारण कई व्यक्तिओं को सफलता मिली है। कई लोगों को यश, नाम, कीर्ति, धन आदि सुरीली आवाज के कारण प्राप्त हुआ है। इसलिए कहा गया है कि व्यक्ति की आवाज उस व्यक्ति की पहचान होती है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (१): आकलन कृति

कृति पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित गलत विधान सही करके लिखिए।

Question 1.
खोए हुए आदमी ने गरीब वृद्धा की बात नहीं मानी।
Answer:
खोए हुए आदमी ने खुशी-खुशी गरीब वृद्धा की बात मान ली।

Question 2.
खोए हुए आदमी ने गरीब वृद्धा की देखभाल नहीं की।
Answer:
खोए हुए आदमी ने गरीब वृद्धा की इतनी सेवा की कि वृद्धा को लगा कि उसका जीवन धन्य हो गया।

संजाल पूर्ण कीजिए।

Question 1.

Answer:

कृति ई (२) : शब्द संपदा

निम्नलिखित वाक्य में विरामचिह्नों का उचित प्रयोग कीजिए।

Question 1.
खोया हुआ आदमी आँधी तूफान चक्रवात व ओले पड़ने से पहले सबको आगाह कर देता था
Answer:
खोया हुआ आदमी आँधी, तूफान, चक्रवात व ओले पड़ने से पहले सबको आगाह कर देता था।

दिए गए निर्देशानुसार परिवर्तन कीजिए।

Question 1.

Answer:

निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।

Question 1.
जीवन
Answer:
उपसर्ग : आजीवन, प्रत्यय : जीवनदीप

गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
धीरे-धीरे
पशु-पक्षियों
पेड़-पौधों
बच्चे-बड़े

कृति ई (३) : स्वंमत अभिव्यक्ति

Question 1.
‘गुणी व्यक्ति के लिए संसार में कोई भी कार्य असाध्य नहीं होते।’ अपने विचार लिखिए।
Answer:
गुणी व्यक्ति के पास अद्भुत गुण होते हैं। वह अपने गुणों के द्वारा समाज में अपना प्रभाव स्थापित करता है। जिसके पास सदबुद्धि होती है वही इंसान गुणी व्यक्ति कहलाता है। महात्मा गांधी, लोकमान्य तिलक, नेल्सन मंडेला आदि महापुरुषों का व्यक्तित्व गुणी था। वे हमेशा समय के अनुसार चलते रहे और दूरदृष्टा भी रहें। उन्होंने सिर्फ अपने मन की आवाज को महत्त्व दिया था और अपनी ऊर्जा सकारात्मक कार्य के लिए ही प्रयोग की थी।

गुणी व्यक्ति जीवन में संकटों को देखकर विचलित नहीं होता; बल्कि आने वाले संकट से स्वयं को बाहर निकालने के लिए और उनका सामना करने के लिए तैयार हो जाता है। गुणी व्यक्ति एक बार कार्य स्वीकार करने पर उसे पूरा करके ही दम लेते हैं। गुणी व्यक्ति के पास प्रतिकूल परिस्थितियों का सामना करते हुए सफल होने की इच्छा शक्ति होती है। उनके लिए कोई भी कार्य असाध्य नहीं होता।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (१): आकलन कृति

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
खोए हुए आदमी के कारण दलितों में परिवर्तन हुआ।
Answer:
सत्य

Question 2.
खोए हुए आदमी के कारण गाँव में सांप्रदायिकता व जातिवाद की भावना पनपने लगी।
Answer:
असत्य

संजाल पूर्ण कीजिए।

Question 1.

Answer:

समझकर लिखिए।

Question 1.

Answer:

कृति पूर्ण कीजिए।

Question 1.

Answer:

गद्यांश से ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
Question 1.
स्त्रियाँ
Answer:
कौन पुरुषों की ज्यादतियों के खिलाफ एकजुट हो गईं?

Question 2.
अधिकार
Answer:
खोए हुए आदमी ने किसके लिए स्त्रियों को लड़ना सिखाया?

कृति उ (२) : शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. मित्रता
2. कर्तव्य
3. दशा
4. विरुद्ध

Answer:

1. दोस्ती
2. कार्य
3. अवस्था
4. खिलाफ

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
दूसरे के श्रम का अनुचित लाभ उठाना
Answer:
शोषण

Question 2.
धर्म को लेकर विवाद या झगड़ा
Answer:
सांप्रदायिकता

Question 3.
आपस में बंधु और भाई होने का भाव
Answer:
भाईचारा

Question 4.
अपनी जाति को सर्वश्रेष्ठ मानने का सिद्धांत
Answer:
जातिवाद

नीचे दिए हुए शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
विरुद्ध
Answer:
बाधित, अवरुद्ध

Question 2.
गद्यांश में प्रयुक्त प्रत्यययुक्त शब्द ढूंडकर लिखिए।
Answer:
मित्रता
भाईचारा
सांप्रदायिकता
जातिवाद

निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।

Question 1.
कर्तव्य
Answer:
कार्य

कृति उ (३) : स्वमत अभिव्यक्ति

Question 1.
‘परिवर्तन संसार का नियम है’ क्या आप इस कथन से सहमत हैं? अपने विचार लिखिए।
Answer:
जी हाँ, मैं इस कथन से सहमत हूँ। छोड़ो कल की बातें, कल की बात पुरानी। नए दौर में लिखेंगे हम, मिलकर नई कहानी। कितनी सच्चाई है इस गीत में। इस संसार में कुछ भी अपरिवर्तनशील नहीं है। व्यक्ति को समय के अनुसार बदलना पड़ता है। समय व परिस्थिति के सामने नतमस्तक होकर व्यक्ति को अपनी पुरानी परंपरा एवं रीति-रिवाजों का त्याग करना ही पड़ता है।

आज विज्ञान व तकनीकी के इस युग में सर्वधर्म समभाव, भाईचारा व स्त्री-पुरुष समानता आदि मूल्यों का प्रचार-प्रसार होता दिखाई दे रहा है। आज शिक्षा का सर्वत्र प्रसार हो गया है। इस कारण लोगों की मानसिकता में सकारात्मक बदलाव होता दिखलाई दे रहा है। आज गाँव में रहने वाली लड़कियाँ एवं स्त्रियाँ भी स्कूल-कॉलेज जाकर आत्मनिर्भर हो रही हैं। सर्वत्र परिवर्तन की धूम मची हुई है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऊ (१): आकलन कृति

गद्यांश से ऐसे प्रश्न तैयार कीजिए कि जिनके उत्तर निम्नलिखित शब्द हों –

Question 1.
खुशहाली
Answer:
खोए हुए आदमी की मदद गाँव वालों के लिए क्या लेकर आई?

Question 2.
मछलियों
Answer:
गाँव का तालाब किससे भर गया?

Question 3.
प्रश्नवाचक
Answer:
शुरू-शुरू में कुछ लोग खोए हुए आदमी को किस निगाहों से देखते थे?

कृति पूर्ण कीजिए।

Question 1.

Answer:

संजाल पूर्ण कीजिए।

Question 1.

Answer:

उचित विकल्प चुनकर उत्तर लिखिए।

Question 1.
खोए हुए आदमी के अनुसार सफलता का मंत्र है –
(क) गाँववालों के विश्वसनीय व्यवहार में हैं।
(ख) गाँववालों के सहज और सरल व्यवहार के परिणाम में है।
(ग) गाँववालों के कठिन परिश्रम के परिणाम में छिपा हैं।
Answer:
खोए हुए आदमी के अनुसार सफलता का मंत्र है गाँववालों के कठिन परिश्रम के परिणाम में।

कृति ऊ (२) : शब्द संपदा

Question 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
शुरू-शुरू
धीरे-धीरे
खेती-बाड़ी

Question 2.
गद्यांश में प्रयुक्त विलोम शब्द की जोड़ी ढूँढ़कर लिखिए।
Answer:
आलोचक x प्रशंसक

वचन बदलिए।

1. सफलता
2. निगाह

Answer:

1. सफलताएँ
2. निगाहें

निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. सगा x ……….
2. पुराना x ………
3. सुरीला x ………
4. गाँव x …………

Answer:

1. सगा x सौतेला
2. पुराना x नया
3. सुरीला x बेसुरा
4. गाँव x शहर

अनेक शब्दों के लिए एक शब्द लिखिए।

1. आलोचना करने वाला –
2. प्रशंसा करने वाला –
3. लोगों में प्रिब

Answer:

1. आलोचक
2. प्रशंसक
3. लोकप्रिय

पर्यायवाची शब्द लिखिए।

1. बरकत
2. मछली

Answer:

1. बढ़ती या लाभ
2. मीन या मत्स्य

निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
निगाह
Answer:
दृष्टि, राय

कृति ऊ (३) : स्वमत अभिव्यक्ति

Question 1.
‘परिश्रम सफलता की कुंजी है।’ विषय पर अपने विचार लिखिए।
Answer:
मनुष्य जीवन में सफलता और परिश्रम एक-दूसरे से सिक्के के दो पहलू की तरह जुड़े हुए हैं। जीवन में सफलता हर व्यक्ति चाहता है। हर व्यक्ति के पास जीतने की इच्छा होती है। लेकिन जीतना इतना आसान नहीं होता। जीतने के लिए व्यक्ति को अपने जीवन में परिश्रम करना पड़ता है। एक चीज को लक्ष्य बनाकर उस दिशा में सतत प्रयास करना होता है।

नियमित रूप से लगातार परिश्रम करने से व्यक्ति में गुणों की वृद्धि होने लगती है और वह अपने मनचाहे लक्ष्य की ओर अग्रसर होना शुरू कर देता है। एकाग्रता से किया हुआ परिश्रम मानव को सफलता दिला सकता है। हमारा इतिहास इस बात का साक्षी है कि मनुष्य ने कठोर परिश्रम द्वारा असंभव को संभव कर दिखाया है। जीवन में कुछ पाना है या सफल होना है, तो व्यक्ति को कठोर परिश्रम करने पड़ेंगे। परिश्रम करने से साधारण व्यक्ति भी बड़ा और महान बन सकता है।

गद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ए (१): आकलन कृति

कृति पूर्ण कीजिए।

Question 1.

Answer:

संजाल पूर्ण कीजिए।

Question 1.


Answer:

निम्नलिखित गलत विधान सही करके लिखिए।

Question 1.
खोए हुए आदमी ने लोगों को गुमराह करने का कार्य किया।
Answer:
खोए हुए आदमी ने विश्वास, नया जोश व नया उत्साह भर दिया।

Question 2.
सारी रात मौसम खुशनुमा रहा।
Answer:
सारी रात मौसम बौराया रहा।

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –

Question 1.
गंधक
Answer:
जिस रात मौसम बौराया उस रात किसकी तेज गंध पूरे गाँव में फैल गई?

Question 2.
बिजली
Answer:
भयावह गड़गड़ाहट के साथ गाँव में क्या गिरी?

कृति ए (२) : शब्द संपदा

निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।

Question 1.
खोए हुए आदमी ने लोगों से कहा आप अपनी ऊर्जा को रचनात्मक और सकारात्मक कामों में लगाओ
Answer:
खोए हुए आदमी ने लोगों से कहा, “आप अपनी ऊर्जा को रचनात्मक और सकारात्मक कामों में लगाओ।”

Question 2.
दिए गए गद्यांश में से देशज शब्द ढूँढ़कर लिखिए।
Answer:
गड़गड़ाहट
धुक-धुकी
झिर्रियों
चौंधिया

निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द बनाइए।

Question 1.
विश्वास
Answer:
उपसर्ग – अविश्वास, प्रत्यय – विश्वासपात्र

Question 2.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
Answer:
खिड़कियों-दरवाजों
अपने-अपने
धुक-धुकी

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
सहसा होने वाला बहुत बड़ा अनिष्ट
Answer:
वज्रपात

कृति ए (३): स्वमत अभिव्यक्ति

Question 1.
प्रेरणादायी व्यक्ति दूसरों के जीवन बदल देने का सामर्थ्य रखता है।’ अपने विचार लिखिए।
Answer:
‘प्रेरणादायी व्यक्ति सच्चे दोस्त की तरह होते हैं। वे दूसरों को जीवन में आगे बढ़ने का रास्ता दिखाते हैं। वे नकारात्मक स्थिति एवं मुश्किल दौर से निकलने में दूसरों की मदद करते हैं। वे हमें सकारात्मकता की ओर ले जाते हैं। ऐसे लोगों के संपर्क में आने के कारण व्यक्ति की सोच बदल जाती है और अंत में उनका जीवन भी पूरी तरह से बदल जाता है। प्रेरणादायी व्यक्ति के व्यक्तित्व में ऊर्जा, लगन, जोश, उमंग व उत्साह होता है। वह अपने परिपूर्ण व्यक्तित्व से दूसरों के जीवन में आशाएँ निर्माण करता है। इस प्रकार प्रेरणादायी व्यक्ति आम लोगों के जीवन में नया विश्वास भर देता है।

गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऐ (१): आकलन कृति

संजाल पूर्ण कीजिए।

Question 1.

Answer:

निम्नलिखित विधान सत्य है या असत्य लिखिए।

Question 1.
खोए हुए आदमी को किसी ने गायब करवाया था।
Answer:
असत्य

Question 2.
खोए हुए आदमी के चले जाने पर लोग दुखी हो गए।
Answer:
सत्य

समझकर लिखिए।

Question 1.


Answer:

ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –

Question 1.
पंचायत
Answer:
किसकी बैठक मूर्ति के नीचे हुआ करती थीं?

Question 2.
सुबह
Answer:
मौसम कब साफ हुआ?

कृति ऐ (२): शब्द संपदा

निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. मूर्ति
2. कुत्ता
3. प्रण
4. गायब

Answer:

1. प्रतिमा
2. श्वान
3. प्रतिज्ञा
4. नदारद

अनेक शब्दों के लिए एक शब्द लिखिए।

Question 1.
जन समूह के बारे में विधिवत रूप से सूचना प्राप्त करना एवं उसे रेकार्ड करना
Answer:
जनगणना

Question 2.
पंचों की सभा
Answer:
पंचायत

नीचे दिए हुए शब्द के अनेकार्थी शब्द लिखिए।

Question 1.
पंचायत
Answer:
पंचों की सभा, निरर्थक पूछताछ

Question 2.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
Answer:
आस-पास
गाँव-शहर

Question 3.
गद्यांश में से कोई भी दो तत्सम शब्द ढूँढकर लिखिए।
Answer:
सदा
धर्म

कृति ऐ (३) : स्वमत अभिव्यक्ति

Question 1.
‘असाधारण प्रतिभा के लोग या असामान्य व्यक्ति हमारे पथ-प्रदर्शक होते हैं।’ उनके चले जाने के बाद भी हम उनका अनुसरण करते रहते हैं। अपने विचार लिखिए।
Answer:
असाधारण प्रतिभा के लोग या असामान्य व्यक्ति हमार पथ-प्रदर्शक होते हैं। उनके चले जाने के बाद भी हम उनका अनुसरण करते रहते हैं। महात्मा गांधी, स्वामी विवेकानंद, मदर टेरेसा, बाबा आमटे आदि असामान्य लोग आज हमारे बीच नहीं हैं; फिर भी उनके विचार एवं सिद्धांत आज भी हमारे साथ हैं। आज भी हम उनके बताए हुए मार्ग पर चल रहे हैं। पूज्य बापूजी को स्वर्ग सिधारे पचहत्तर साल हो गए हैं।

फिर भी आज हमारे देश में सत्य व अहिंसा जैसे विचार कायम हैं। आज हमने जो भी उपलब्धि पाई है; वह सब हमारे महापुरुषों के महान विचारों व कार्यों की ही देन है। हम तो सिर्फ उनके बताए हुए मार्ग पर चलकर उनका अनुसरण कर रहे हैं और करते रहेंगे। इसलिए कहा भी गया है कि पथ प्रदर्शक के बिना जीवन में सफलता मिलना मुश्किल ही; नहीं बल्कि असंभव भी है।

खोया हुआ आदमी Summary in Hindi

खोया हुआ आदमी  लेखक – परिचय
जीवन–परिचय : सुशांत सुप्रिय जी का जन्म २८ मार्च, १९६८ में बिहार राज्य के पटना शहर में हुआ। इन्होंने पंजाब व अमृतसर से शिक्षा ग्रहण की। इनकी रचनाएँ भाषा विभाग (पंजाब) तथा प्रकाशन विभाग (भारत सरकार) द्वारा पुरस्कृत हो चुकी हैं। इनकी रचनाएँ जीवन की सच्चाइयों और विडंबनाओं का सहज रूप से साक्षात्कार करवाती हैं। आप हिंदी, अंग्रेजी व पंजाबी भाषा में लेखन करते आ रहे हैं।

प्रमुख कृतियाँ : ‘एक बूँद यह भी’ (कविता संग्रह), ‘हत्यारे तथा हे राम’ (कथा संग्रह), ‘इन गांधीजीज कंट्री’ (अंग्रेजी कविता संग्रह) आदि।

खोया हुआ आदमी गद्य – परिचय
वर्णनात्मक : साहित्य की सभी विधाओं में कहानी सबसे पुरानी विधा है। जनजीवन में यह सबसे अधिक लोकप्रिय है। कहानी का मुख्य

कहानी : उद्देश्य जीवन की विभिन्न समस्याओं एवं संवेदनाओं को सहज रूप से व्यक्त करना है।

प्रस्तावना : ‘खोया हुआ आदमी’ इस कहानी के माध्यम से लेखक सुशांत सुप्रिय जी ने यह संदेश दिया है कि समाज में व्याप्त सांप्रदायिकता, जातीयता, संकीर्णता आदि कुरीतियों को भुला देने में ही मानव समाज की भलाई है। व्यक्ति की पहचान उसके कार्य से होती है, जो व्यक्ति अपने जीवन में अच्छा कार्य करेगा; वह समाज में पूजनीय बन जाएगा।

खोया हुआ आदमी सारांश

‘खोया हुआ आदमी’ एक वर्णनात्मक कहानी है। इस कहानी को कहानीकार ने निवेदन की शैली में लिखा है। इसलिए कहानी के पात्र आपस में वार्तालाप करते हुए दिखलाई नहीं देते। ‘खोया हुआ आदमी’ कहानी का प्रमुख पात्र है। वह एक गाँव में कहीं से आ जाता है। उसे गाँव का एक भला आदमी देखता है। उस भले आदमी को उसके चेहरे पर गरिमा के चिह्न दिखाई देते हैं। भले आदमी द्वारा पूछने पर वह कहता है कि वह शायद से खो गया है। इस कारण उसका नाम ‘खोया हुआ आदमी’ पड़ जाता है। उसके गाँव में आने से गाँव का कायापलट हो जाता है।

खोया हुआ आदमी प्रतिभा का धनी है। उसकी आवाज मधुर है। सुरीली आवाज के कारण गाँव के जानवर एवं बच्चे उसकी ओर आकर्षित हो जाते हैं। गाँव की एक वृद्धा उसे अपना बचपन में खोया हुआ बेटा मान लेती है। वह भी उस वृद्धा की पूरी निष्ठा से सेवा करता है। वह गाँववालों को परिश्रम का महत्त्व समझाता है। गाँव वाले परिश्रम करना शुरू कर देते हैं। इस प्रकार गाँव के खेतों में फसलें लहलहाने लगती हैं और गाँव का तालाब भी पानी से भर जाता है। धीरे–धीरे गाँव के सभी लोग उसके प्रशंसक बन जाते हैं।

उसके द्वारा गाँव वालों को समझाने के कारण गाँव में आपसी भाईचारा बढ़ने लगा और दलितों का शोषण बंद हो गया। गाँव के सभी जाति–धर्म के लोग एक–दूसरे के साथ मिल–जुलकर रहने लगे और मिलकर त्योहार मनाने लगे। इस कारण गाँव से सांप्रदायिकता एवं जातिवाद की भावना दूर हो गई। गाँव की स्त्रियों की दशा में सुधार आया और उन्हें भी सम्मान मिलने लगा। उन पर होने वाले अत्याचार खत्म हो गए। एक रात गाँव में मौसम खराब हो गया। भीषण गड़गड़ाहट के साथ बिजली गिरी। जब दूसरे दिन सुबह मौसम साफ हुआ तो खोए हुए आदमी का कहीं पता नहीं था।

सभी लोगों ने उसे बहुत ढूँढ़ा; परंतु उसका कोई पता नहीं चला। इससे गाँव के सभी लोग दुखी हुए। गाँववाले उस आदमी की याद में गाँव के बीचोंबीच उसकी मूर्ति स्थापित करते हैं और अब पंचायत की सभी बैठक उसी मूर्ति के पास होने लगती है। वे उसके द्वारा दिखाए मार्ग पर चलने की ठान लेते हैं। कुछ समय बाद जनगणना अधिकारी गाँव में जनगणना के लिए आते हैं तो किसी को भी न अपनी जाति याद होती है और न ही धर्म; जैसे जाति और धर्म के बारे में उनकी स्मृतियाँ खोए हुए आदमी के साथ सदा के लिए खो चुकी थीं। अंत में कहानीकार कहते हैं – ‘काश, हमें भी अपने गाँव और शहर में ऐसा ही ‘खोया हुआ आदमी’ मिल जाता।।

खोया हुआ आदमी शब्दार्थ

• दूर–दराज – दूर तक फैला हुआ
• तंग – परेशान
• जहन – दिमाग, मन
• लिहाजा – इसलिए
• स्मृति – याद, याददाश्त, स्मरण शक्ति
• लोप – अभाव, नाश
• मित्रता – दोस्ती
• कर्तव्य – कार्य
• दशा – अवस्था
• विरुद्ध – खिलाफ
• मूर्ति – प्रतिमा
• कुत्ता – श्वान
• प्रण – प्रतिज्ञा
• गायब – नदारद
• बरकत – लाभ, समृद्धि, संपन्नता
• बेतहाशा – बड़ी तेजी से, बहुत घबराकर और बिना सोचे समझे
• गरिमा – गौरव
• फैसला – निर्णय, निपटारा
• ज्यादतियाँ – अन्याय, परेशान करने की वृत्ति
• चीथड़ा – गंदे और फटे हुए कपड़े
• अतीत – पुरानी, बीती हुई
• तृप्त – संतुष्ट
• कस्बा – छोटा शहर
• प्रण – सौगंध
• वज्रपात – सहसा होनेवाला बहुत बड़ा अनिष्ट, आघात

खोया हुआ आदमी मुहावरे

• आगाह कर देना – सचेत करना।
• खाली हाथ लौटना – कुछ भी न पाना।
• जमीन का निगल जाना – लापता हो जाना।
• आसमान का खा जाना – लापता हो जाना।
• मंत्रमुग्ध होना – आकर्षित होना।

Hindi Lokvani 10th Std Digest पहली इकाई

• सोंधी सुगंध Question Answer
• खोया हुआ आदमी Question Answer
• सफर का साथी और सिरदर्द Question Answer
• जिन ढूँढ़ा Question Answer
• अनोखे राष्ट्रपति Question Answer
• ऐसा भी होता है (पठनार्थ) Question Answer
• दो लघुकथाएँ Question Answer
• कर्मवीर Question Answer

Std 10 Hindi Chapter 9 Jab Tak Jinda Rahun Likhta Rahun Question Answer Maharashtra Board

Balbharti Maharashtra State Board Class 10 Hindi Solutions Chapter 9 जब तक जिंदा रहूँ, लिखता रहूँ Notes, Textbook Exercise Important Questions, and Answers.

Hindi Lokbharti 10th Digest Chapter 9 जब तक जिंदा रहूँ, लिखता रहूँ Questions And Answers

Hindi Lokbharti 10th Std Digest Chapter 9 जब तक जिंदा रहूँ, लिखता रहूँ Textbook Questions and Answers

कृति-स्वाध्याय एवं उत्तर

कृतिपत्रिका के प्रश्न 1(अ) तथा 1(आ) के लिए

सूचना के अनुसार कृतियाँ कीजिए :

प्रश्न 1.
कृति पूर्ण कीजिए:

अमृतलाल नागर जी के साहित्य सृजन में सहायक	लेखक	१. ……………………	१. ……………………
	पत्रिकाएँ	२. ……………………	२. ……………………

उत्तर:

अमृतलाल नागर जी के साहित्य में सहायक सृजन	लेखक	1. सनेही जी	2. अयोध्यासिंह उपाध्याय
	पत्रिकाएँ	1. सरस्वती	2. गृहलक्ष्मी

प्रश्न 2.
उत्तर लिखिए :
(i) नागर जी की पहली कविता को प्रस्फुटित करने वाला अनुभव – – – – – – – – – – – –
(ii) नागर जी अपने पिता जी के इस गुण से प्रभावित थे – – – – – – – – – – – –
उत्तर:
(i) सन 1928 – 1929 में साइमन कमीशन के बहिष्कार के समय किए गए लाठी चार्ज के अनुभव ने नागर जी की पहली कविता को प्रस्फुटित किया।
(ii) किसी के दुख-दर्द में तुरंत पहुँचने का गुण।

प्रश्न 3.
कोष्ठक में दी गई नागर जी की साहित्य कृतियों का वर्गीकरण कीजिए:
[कब लौं कहीं लाठी खाय, खंजन नयन, अपशकुन, नाच्यो बहुत गोपाल, महाकाल, प्रायश्चित, गदर के फूल]

कहानी	उपन्यास	कविता	अन्य
…………	…………	…………	…………

उत्तर:

कहानी	उपन्यास	कविता	अन्य
अपशकुन	नाच्यो बहुत गोपाल	कब लौं कहौं लाठी खाय	गदर के फूल
प्रायश्चित	महाकाल
	खंजन नयन

प्रश्न 4.
कृति पूर्ण कीजिए:

उत्तर:

प्रश्न 5.
लिखिए :

उत्तर:

प्रश्न 6.
एक शब्द में उत्तर लिखिए :
(i) नागर जी के प्रिय लेखक –
(ii) नागर जी के प्रिय आलोचक –
(iii) अपनी इस रचना के लिए नागर जी को बहुत लोगों से मिलना पड़ा –
(iv) नागर जी का पहला उपन्यास –
उत्तर:
(i) नागर जी के समय के लेखकों में उनकी पसंद के लेखक – रामविलास शर्मा।
(ii) नागर जी के प्रिय आलोचक – [पाठकीय – प्रतिक्रियाएँ देने वाले पत्र लेखक]
(iii) अपनी इस रचना के लिए नागर जी को बहुत लोगों से मिलना पड़ा – गदर के फूल’।

प्रश्न 7.
लिखिए:
(अ) तद्धित शब्दों का मूल शब्द :
(i) साहित्यिक = _____________
(ii) विलायती = _____________
उत्तर:
(i) साहित्यिक – साहित्य
(ii) विलायती – विलायत

(ब) कृदंत शब्दों का मूल शब्द :
(i) खिंचाव = _____________
(ii) लिखावट = _____________
उत्तर:
(i) खिंचाव – खिंच + आव
(ii) लिखावट – लिख + आवट

प्रश्न 8.
उचित जोड़ियाँ मिलाइए:

‘अ’ रचना	उत्तर	‘ब’ रचनाकार
१. देसी और विलायती	१. _____________	अमृतलाल नागर
२. अपशकुन	२. _____________	तुलसीदास
३. आनंद मठ	३. _____________	प्रभात कुमार मुखोपाध्याय
४. रामचरितमानस	४. _____________	बंकिमचंद्र चटर्जी सूरदास

उत्तर:

‘अ’ रचना	उत्तर	‘ब’ रचनाकार
१. देसी और विलायती	१. प्रभातकुमार मुखोपाध्याय।	अमृतलाल नागर
२. अपशकुन	२. अमृतलाल नागर	तुलसीदास
३. आनंद मठ	३. बंकिमचंद्र चटर्जी	प्रभात कुमार मुखोपाध्याय
४. रामचरितमानस	४. रामचरितमानस	बंकिमचंद्र चटर्जी सूरदास

अभिव्यक्ति

‘ज्ञान तथा आनंद प्राप्ति का साधन : वाचन’ पर अपने विचार लिखिए।
उत्तर:
कहते हैं, पुस्तक मनुष्य का सबसे बड़ा मित्र होती है। पुस्तकों में ज्ञानभरी बातें होती हैं। किताबों में संचित ज्ञान हमारे लिए सहायक होता है। विभिन्न विचारकों, लेखकों तथा महान व्यक्तियों के विचार पुस्तकों में ही संग्रहित होते हैं। हमारे यहाँ साहित्य, तकनीक, विज्ञान, धर्म, राजनीति आदि सभी विषयों से संबंधित पुस्तकें उपलब्ध हैं। आवश्यकता है इन्हें पढ़ने में रुचि रखने की। पुस्तकें पढ़ने से ज्ञान प्राप्ति के साथ-साथ अद्भुत आनंद की प्राप्ति होती है। कोई भी मनुष्य हर दृष्टि से परिपूर्ण नहीं होता। मनुष्य बहुत सारी बातें देख-सुन और पढ़कर सीखता है।

विद्यार्थी पाठ्यपुस्तकों से ज्ञानार्जन करता है। बड़े होने पर इन पुस्तकों से उसका काम नहीं चलता। उसे ज्ञानार्जन के लिए और खुराक की आवश्यकता होती है। वह अपने पसंद वाले विषयों की पुस्तकें पढ़ता है। आई.सी.एस., आई.पी.एस. तथा आई.ए.एस. जैसी बड़ी-बड़ी परीक्षाओं की तैयारी करने के लिए भी वाचन की आवश्यकता होती है। पुस्तकों में क्या नहीं है? इसमें जो जितने गोते लगाता है, उसे उतना ही ज्ञान प्राप्त होता है।

भाषा बिंदु

प्रश्न 1.
निम्न वाक्यों में आई हुई मुख्य और सहायक क्रियाओं को रेखांकित करके दी हुई तालिका में लिखिए :

	सहायक क्रिया	मुख्य क्रिया
उनके रीति रिवाजों का अध्ययन करना पड़ा।	1. ……………………	……………………
माता पिता का यह रंग देखकर तो वे बूढ़ी काकी को और सताने लगे।।	2. ……………………	……………………
उसकी ननद रूठ गई।	3. ……………………	……………………
वे हड़बड़ा उठे।	4. ……………………	……………………
वे पुस्तक पकड़े न रख सके।	5. ……………………	……………………
उन्होंने पुस्तक लौटा दी।	6. ……………………	……………………
समुद्र स्याह और भयावह दीखने लगा।	7. ……………………	……………………
मैं गोवा को पूरी तरह नहीं समझ पाया।	8. ……………………	……………………
काकी घटनास्थल पर आ पहुँची।	9. ……………………	……………………
अवश्य ही लोग खा पीकर चले गए।	10. ……………………	……………………

उत्तर:

प्रश्न 2.
पाठों में प्रयुक्त सहायक क्रियाओंवाले दस वाक्य ढूँढ़कर मुख्य और सहायक क्रियाएँ चुनकर लिखिए।
उत्तर:

प्रश्न 3.
निम्नलिखित वाक्यों के रिक्त स्थानों की पूर्ति उचित कारक चिह्नों से कीजिए तथा संबंधित कारक और कारक चिहन तालिका में वाक्य के सामने लिखिए :

उत्तर:

प्रश्न 4.
पाठ में प्रयुक्त विभिन्न कारकों का एक-एक वाक्य छाँटकर उनसे कारक और कारक चिह्न चुनकर लिखिए।
उत्तर:

उपयोजित लेखन

प्रश्न 1.
निम्नलिखित परिच्छेद पढ़कर इसपर आधारित ऐसे पाँच प्रश्न तैयार उपयोजित लेखन कीजिए, जिनके उत्तर एक-एक वाक्य में हों :

विख्यात गणितज्ञ सी.वी. रमण ने छात्रावस्था में ही विज्ञान के क्षेत्र में अपनी प्रतिभा का सिक्का देश में ही नहीं विदेशों में भी जमा लिया था।

रमन का एक साथी छात्र ध्वनि के संबंध में कुछ प्रयोग कर रहा था। उसे कुछ कठिनाइयाँ प्रतीत हुईं, संदेह हुए। वह अपने अध्यापक जोन्स साहब के पास गया परंतु वह भी उसका संदेह निवारण न कर सके। रमण को पता चला तो उन्होंने उस समस्या का अध्ययन-मनन किया और इस संबंध में उस समय के प्रसिद्ध लॉर्ड रेले के निबंध पढ़े और उस समस्या का एक नया ही हल खोज निकाला। यह हल पहले हल से सरल और अच्छा था। लॉर्ड रेले को इस बात का पता चला तो उन्होंने रमण की प्रतिभा की भूरि-भूरि प्रशंसा की। अध्यापक जोन्स भी प्रसन्न हुए और उन्होंने रमण से इस प्रयोग के संबंध में लेख लिखने को कहा। रमण ने लेख लिखकर श्री जोन्स को दिया, पर जोन्स उसे जल्दी लौटा न सके। कारण संभवतः यह था कि वह उसे पूरी तरह आत्मसात न कर सके।

प्रश्न :
1. ________________________
2. ________________________
3. ________________________
4. ________________________
उत्तर:
1. विज्ञान के क्षेत्र में देश में ही नहीं, विदेशों में भी बचपन में अपना सिक्का किसने जमा लिया था?
2. रमण का साथी किसके संबंध में प्रयोग कर रहा था?
3. रमण ने समस्या के संबंध में किसका निबंध पढ़ा?
4. रमण की प्रतिभा की प्रशंसा किसने की?

प्रश्न 2.
अंतरजाल’ से ‘मेक इन इंडिया’ योजना संबंधी जानकारी प्राप्त करके इसे बढ़ावा देने हेतु विज्ञापन तैयार कीजिए : – मुद्दे

उत्तर:

Hindi Lokbharti 10th Textbook Solutions Chapter 9 जब तक जिंदा रहूँ, लिखता रहूँ Additional Important Questions and Answers

गद्यांश क्र.1
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
उत्तर लिखिए:
(i) नागर जी का साइमन कमीशन के बहिष्कार की घटना के बाद राजनीति की ओर न जाना –
उत्तर:
(i) नागर जी के पिता सरकारी कर्मचारी थे। सरकारी कर्मचारी के परिवार के किसी सदस्य का सरकार के खिलाफ विद्रोह करने का अर्थ उसका नौकरी से हाथ धोना था। इसलिए नागर जी राजनीति की ओर नहीं गए।

प्रश्न 2.
संजाल पूर्ण कीजिए:

उत्तर:

प्रश्न 3.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i) नागर जी के सामने इनका साहित्य था – [ ]
(ii) नागर जी ने शुरू में इन्हें पढ़ा – [ ]
(iii) नागर जी का पहला मित्र यह था – [ ]
(iv) नागर जी की पहली कविता का शीर्षक यह था – [ ]
उत्तर:
(i) नागर जी के सामने इनका – प्रेमचंद और कौशिक का साहित्य था
(ii) नागर जी ने शुरू में इन्हें पढ़ा – बंकिम के उपन्यास।
(iii) नागर जी का पहला मित्र यह था – छापे का अक्षर
(iv) नागर जी की पहली कविता का शीर्षक यह था – कब लौं कहौं लाठी खाय!

प्रश्न 2.
ऐसे दो प्रश्न बनाकर लिखिए, जिनके उत्तर निम्नलिखित शब्द हों:
(i) 1933 में
(ii) चंडीप्रसाद हृदयेश।
उत्तर:
(i) नागर जी की पहली कहानी ‘अपशकुन’ किस सन में छपी ?
(ii) नागर जी को किसकी लेखन शैली ने बहुत प्रभावित किया?

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों का लिंग परिवर्तन कीजिए:
(i) लेखक – …………………….
(ii) कवि – …………………….
(iii) पितामह – …………………….
(iv) मित्र – …………………….
उत्तर:
(i) लेखक – लेखिका
(ii) कवि – कवयित्री
(iii) पितामह – पितामही
(iv) मित्र – सहेली।

प्रश्न 2.
उचित उपसर्ग जोड़कर सार्थक शब्द बनाइए: (अभि, आ, अनु, उप)
(i) …………………………… शासन
(ii) …………………………… वन
(iii) …………………………… जीवन
(iv) …………………………… मान
उत्तर:
(i) अनु + शासन = अनुशासन
(ii) उप + वन = उपवन
(iii) आ + जीवन = आजीवन
(iv) अभि + मान = अभिमान।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘पत्र-पत्रिकाओं का महत्त्व’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
भाषा के विकास में पत्र-पत्रिकाओं का बहुत योगदान होता है। इनसे तरह-तरह की जानकारियाँ तो मिलती ही हैं, लेखन में होने वाली नई-नई प्रवृत्तियों की भी जानकारी मिलती है। पत्र-पत्रिकाओं में साहित्य, समाज, देश, राजनीति, विज्ञान, शिल्प, फिल्म, कला, मनोरंजन, कार्टून, व्यापार आदि सभी क्षेत्रों की जानकारी मिलती है। हमारे देश में विभिन्न भाषाओं में अनेक पत्र-पत्रिकाएँ प्रकाशित होती हैं और उनका बड़ा बाजार है। पढ़े-लिखे लोगों के घर में पत्र-पत्रिकाएँ आना आवश्यक माना जाता है। इनसे घर बैठे विभिन्न क्षेत्रों के बारे में जानकारी मिलती है। इनमें परिवार के हर आयु के लोगों के लिए . कुछ-न-कुछ होता है।

दूरदर्शन की लोकप्रियता के पहले पत्र-पत्रिकाएँ ही जानकारियों और मनोरंजन का एकमात्र साधन थीं। आज मोबाइल फोन तथा दूरदर्शन के युग में पत्रिकाओं की लोकप्रियता में थोड़ी कमी जरूर आई है, पर अखबारों की लोकप्रियता पहले जैसी ही कायम है। समझदार लोग पत्र-पत्रिकाओं के दीवाने हैं। कुछ लोग तो पत्रिकाओं के पुराने अंकों की जिल्दसाजी करवाकर रखते हैं। पत्र-पत्रिकाओं की हर युग में माँग रहेगी और इनका महत्त्व हमेशा बना रहेगा।

गद्यांश क्र. 2
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
उत्तर लिखिए:
(i) नागर जी के पिता जी ने उन्हें इनमें भाग लेने से रोका –
उत्तर:
(i) क्रांतिकारी आंदोलनों में

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i) गद्यांश में आए दो महान नेताओं के नाम – [ ]
(ii) नागर जी के लेखन की एक विशेषता – [ ]
(iii) नागर जी की पहली कहानी का नाम – [ ]
(iv) परिच्छेद में उल्लिखित स्वतंत्रता आंदोलन से संबंधित एक महत्त्वपूर्ण घटना – [ ]
उत्तर:
(i) परिच्छेद में आए दो महान नेताओं गांधी जी, जवाहरलाल के नाम नेहरू
(ii) नागर जी के लेखन की एक विशेषता – गरीबों के प्रति करुणा का भाव होना
(iii) नागर जी की पहली कहानी का नाम – प्रायश्चित
(iv) परिच्छेद में उल्लिखित स्वतंत्रता आंदोलन से संबंधित एक महत्त्वपूर्ण घटना – काकोरी बमकांड

प्रश्न 3.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

प्रश्न 2.
दो ऐसे प्रश्न बनाकर लिखिए जिनके उत्तर निम्नलिखित शब्द-समूह हों:
(i) 1933 में
(ii) सामाजिक आंदोलनों में।
उत्तर:
(i) जवाहर लाल नेहरू से नागर जी की पहली बार किस सन में भेंट हुई थी?
(ii) नागर जी के पिता जी ने उन्हें किस तरह के आंदोलनों में जाने से कभी नहीं रोका?

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए:
(i) निश्चित x …………………….
(ii) दुख x …………………….
(iii) तेज x …………………….
(iv) पहला x …………………….
उत्तर:
(i) निश्चित x अनिश्चित
(ii) दुख x सुख
(iii) तेज x मद्धिम
(iv) पहला x अंतिम।

प्रश्न 2.
तद्धित शब्दों का मूल शब्द लिखिए:
(i) प्रभावित – …………………….
(ii) सामाजिक – …………………….
उत्तर:
(i) प्रभावित – प्रभाव
(ii) सामाजिक – समाज।

गद्यांश क्र. 3
प्रश्न. निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:

कृति 1: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:

उत्तर:

(ii)

प्रश्न 2.
आकृति पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
आकृति पूर्ण कीजिए:
(i) नागर जी ने अपनी इस कृति में सूरदास के चमत्कारों का वर्णन किया है – [ ]
(ii) नेत्रहीनों के चमत्कार के बारे में नागर जी की धारणा – [ ]
(ii) नागर जी सात साल तक प्रतिवर्ष जिस लेखक से एक शहर में मिलते रहे वे – [ ]
उत्तर:
(i) नागर जी ने अपनी इस कृति में सूरदास के चमत्कारों का वर्णन किया है – [खजन नयन]
(ii) नेत्रहीनों के चमत्कार के बारे में नागर जी की धारणा – [नेत्रहीनों की भविष्यवाणियाँ कभी-कभी सच होती हैं]
(iii) नागर जी सात साल तक प्रतिवर्ष जिस लेखक से एक शहर में मिलते रहे वे – [शरतचंद्र]

प्रश्न 2.
आकृति पूर्ण कीजिए:
(i)
(ii)
उत्तर:

प्रश्न 3.
वाक्य पूर्ण कीजिए:
(i) तुलसीदास को तो …………………….।
(ii) सूरपंचशती के अवसर पर काफी विवाद चला था कि …………………….।
उत्तर:
(i) तुलसीदास को तो मुझे घुट्टी में पिलाया गया है।
(ii) सूरपंचशती के अवसर पर काफी विवाद चला था कि सूर जन्मांध थे या नहीं।

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए:
(i) नयन =
(ii) पुराना =
(iii) सच =
(iv) मौका =
उत्तर:
(i) नयन = नेत्र
(ii) पुराना = प्राचीन
(iii) सच = सत्य
(iv) मौका= अवसर।

प्रश्न 2.
निम्नलिखित कृदंत शब्दों के मूल शब्द लिखिए:
(i) लगाव – …………………….
(ii) मिलावट – …………………….
उत्तर:
(i) लगाव – लग + आव
(ii) मिलावट – मिल + आवट।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘आँख देखने का माध्यम है, देखने वाला मन है’ विषय पर अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
प्रत्येक प्राणी की दो आँखें होती हैं, जिनके द्वारा वह इस पृथ्वी की समस्त चीजें देखने में समर्थ होता है। मनोरंजक दृश्य देखकर वह प्रसन्न होता है और दुखद दृश्य देखकर दुखी और बेचैन होता है। यह आँखों से दिखाई देने वाले प्रत्यक्ष दृश्यों पर मनुष्य की प्रतिक्रिया होती है। पर मनुष्य की एक दृष्टि और होती है – उसके मन की यानी उसकी कल्पना की। वह प्रत्यक्ष दृष्टि से भी तेज होती है। जब वह किसी घटित – अघटित दृश्य की कल्पना करता है तो वह दृश्य उसकी कल्पना में उसके सामने दिखाई देने लगता है।

किसी व्यक्ति की इच्छित घटित अथवा अघटित घटना फिल्म की रील की तरह उसे दिखाई देती है। यह दृश्य उसकी आँखें नहीं देखती हैं। यह दृश्य देखता है उसका मन। मनुष्य को सपने में दिखाई देने वाले दृश्य भी उसकी आँखें नहीं, उसका मन देखता है। इस प्रकार मनुष्य को क्या देखना है और क्या नहीं, इसका आदेश मनुष्य का मन ही उसे देता है। हाँ, देखने-देखने में अंतर अवश्य है। प्रत्यक्ष दृश्य वास्तविक आँखें देखती हैं, जब कि मन के काल्पनिक दृश्य मन की आँखें देखती हैं।

गद्यांश क्र. 4
प्रश्न, निम्नलिखित पठित गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए:
कृति 1: (आकलन)

प्रश्न 1.
उत्तर लिखिए:
(i) नागर जी को इस पुस्तक को फिर से पढ़ने की उत्कंठा है –
(ii) नागर जी के पास संग्रह है इनका –
उत्तर:
(i) नागर जी को इस पुस्तक को फिर से पढ़ने की उत्कंठा है – प्रभातकुमार मुखोपाध्याय का संग्रह ‘देशी और विलायती’।
(ii) नागर जी के पास संग्रह है इनका – पत्रों और प्रत्येक जाति के रीति-रिवाजों का।

प्रश्न 2.
संजाल पूर्ण कीजिए:

उत्तर:

कृति 2: (आकलन)

प्रश्न 1.
लिखिए:

उत्तर:

प्रश्न 2.

उत्तर:

कृति 3: (शब्द संपदा)

प्रश्न 1.
निम्नलिखित शब्दों के वचन बदलकर लिखिए:
(i) बूढ़े – ……………….
(ii) कहानियों – ……………….
(iii) जाति – ……………….
(iv) रचनाएँ – ……………….
उत्तर:
(i) बूढ़े – बूढ़ा
(ii) कहानियों – कहानी
(iii) जाति – जातियाँ
(iv) रचनाएँ – रचना।

प्रश्न 2.
उचित उपसर्ग चुनकर सार्थक शब्द बनाकर लिखिए: (अव, दुर्, अप, दुर्)
(i) ………………. गुण
(ii) ………………. बल
(iii) ………………. मन
(iv) ………………. भाग्य
उत्तर:
(i) गुण – अवगुण
(ii) बल – दुर्बल।
(iii) मान – अपमान
(iv) भाग्य – दुर्भाग्य।

कृति 4: (स्वमत अभिव्यक्ति)

प्रश्न.
‘लेखन में वास्तविकता लाने के लिए विषय की तह में जाना आवश्यक है’ इसके बारे में अपने विचार 25 से 30 शब्दों में लिखिए।
उत्तर:
किसी विषय पर लिखने के लिए उस विषय की पूर्ण जानकारी होना जरूरी होता है। लिखने वाले का विषय के बारे में जितना अच्छा गृहकार्य होगा, लेखन उतना ही अच्छा होगा। उदाहरण के लिए समाज के किसी वर्ग के बारे में कुछ लिखना है, तो सबसे पहले उसके बारे में पूरी जानकारी एकत्र करनी चाहिए। उसके रहन-सहन, रीति-रिवाज तथा मान्यताओं का नजदीकी परिचय प्राप्त करना चाहिए। पूरी जानकारी हो जाने पर ही लिखने की शुरुआत करनी चाहिए। लेखक के पास जितनी अच्छी जानकारी होगी, उतनी ही अच्छी उसकी रचना तैयार होगी। अच्छे लेखक पूरी जानकारी प्राप्त किए बिना किसी कृति की रचना नहीं करते। ऐसे लेखकों की रचनाएँ ही पाठक को बाँधे रखती हैं। उनमें पाठक को वास्तविकता के दर्शन: होते हैं।

भाषा अध्ययन (व्याकरण)
प्रश्न. सूचनाओं के अनुसार कृतियाँ कीजिए:

1. शब्द भेद:
अधोरेखांकित शब्दों का शब्दभेद पहचानकर लिखिए:
(i) उस समय नागर जी के सामने प्रेमचंद का साहित्य था।
(ii) मेरा छोटा भाई भी मेडिकल कालेज में दाखिल था।
उत्तर:
(i) प्रेमचंद – व्यक्तिवाचक संज्ञा।
(ii) छोटा – गुणवाचक विशेषण।

2. अव्यय:
निम्नलिखित अव्ययों का अपने वाक्यों में प्रयोग कीजिए:
(i) भी
(ii) बहुत।
उत्तर:
(i) नागर जी ने पत्रों का भी बहुत संकलन किया है।
(ii) चंडीप्रसाद की लेखन शैली ने नागर जी की लेखन शैली को बहुत प्रभावित किया।

3. संधि:
कृति पूर्ण कीजिए:

संधि शब्द	संधि विच्छेद	संधि भेद
………………….	नदी + ईश	………………….
अथवा
………………….	सत् + मार्ग	………………….

उत्तर:

संधि शब्द	संधि विच्छेद	संधि भेद
नदीश	नदी + ईश	स्वर संधि
अथवा
सन्मार्ग	सत् + मार्ग	व्यंजन संधि।

4. सहायक क्रिया:
निम्नलिखित वाक्यों में से सहायक क्रियाएँ पहचानकर उसका मूल रूप लिखिए:
(i) ‘देशी और विलायती’ संग्रह अगर मिले तो फिर पढ़ना चाहूँगा।
(ii) तुम लोग यह मनाओ कि जब तक जिंदा रहूँ , लिखता रहूँ।
उत्तर:
सहायक क्रिया – मूल रूप
(i) चाहूँगा – चाहना
(ii) रहूँ – रहना

5. प्रेरणार्थक क्रिया:
निम्नलिखित क्रियाओं के प्रथम प्रेरणार्थक और द्वितीय प्रेरणार्थक रूप लिखिए:
(i) चमकना
(ii) लिखना।
उत्तर:
क्रिया – प्रथम प्रेरणार्थक रूप – द्वितीय प्रेरणार्थक रूप
(i) चमकना – चमकाना – चमकवाना
(ii) लिखना – लिखाना – लिखवाना

6. मुहावरे:

प्रश्न 1.
निम्नलिखित मुहावरों का अर्थ लिखकर वाक्य में प्रयोग कीजिए:
(i) फूला न समाना
(i) तिलिस्म टूटना।
उत्तर:
(i) फूला न समाना।
अर्थ – अत्यधिक प्रसन्न होना
वाक्य: परीक्षा में अच्छे अंकों से पास होने पर अशोक फूला न समाया।

(ii) तिलिस्म टूटना।
अर्थ: करामात का भेद खुल जाना
वाक्य: ढोंगी साधु की सच्चाई प्रकट होते ही उसका तिलिस्म टूट गया।

प्रश्न 2.
अधोरेखांकित वाक्यांश के लिए उचित मुहावरे का चयन करके वाक्य फिर से लिखिए: (एकटक देखना, दम भरना, गले मिलना)
(i) दर्शनार्थी मंदिर में देवी जी की मूर्ति को लगातार देख रहे थे।
(ii) किसी काम को करने का दावा करना और उसे कर दिखाना, दोनों में बड़ा अंतर है।
उत्तर:
(i) दर्शनार्थी मंदिर में देवी जी की मूर्ति को एकटक देख रहे थे।
(ii) किसी काम को करने का दम भरना और उसे कर दिखाना, दोनों में बड़ा अंतर है।

7. कारक
निम्नलिखित वाक्यों में प्रयुक्त कारक पहचानकर उसका भेद लिखिए:
(i) नेत्रहीनों के चमत्कार हमने बहुत देखे हैं।
(ii) लिखने से पहले नागर जी ने पढ़ना शुरू किया था।
उत्तर:
(i) नेत्रहीनों के – संबंध कारक।
(ii) नागर जी ने – कर्ता कारक।

8. विरामचिह्न:
निम्नलिखित वाक्यों में यथास्थान उचित विरामचिह्नों का
प्रयोग करके वाक्य फिर से लिखिए:
(i) नहीं कोई आदर्श नहीं
(ii) यहाँ कश्मीरी लोगों को छोड़कर कोई आता जाता नहीं था
उत्तर:
(i) नहीं, कोई आदर्श नहीं।
(ii) यहाँ कश्मीरी लोगों को छोड़कर कोई आता-जाता नहीं था।

9. काल परिवर्तन:
निम्नलिखित वाक्यों का सूचना के अनुसार काल परिवर्तन लिखिए:
(i) नागर जी, आपने भ्रमण तो काफी किया है। (पूर्ण भूतकाल)
(ii) मेरे पास बहुत पत्र आते हैं। (अपूर्ण वर्तमानकाल)
उत्तर:
(i) नागर जी, आपने भ्रमण तो काफी किया था।
(ii) मेरे पास बहुत पत्र आ रहे हैं।

10. वाक्य भेद:

प्रश्न 1.
निम्नलिखित वाक्यों का रचना के आधार पर भेद पहचानकर लिखिए:
(i) लिखने के पहले मैंने पढ़ना शुरू किया था।
(ii) पत्रों का संग्रह बहुत है, लेकिन यह व्यवस्थित नहीं है।
उत्तर:
(i) सरल वाक्य
(ii) संयुक्त वाक्य।

प्रश्न 2.
निम्नलिखित वाक्यों का अर्थ के आधार पर दी गई सूचना के अनुसार वाक्य परिवर्तन कीजिए:
(i) नागर जी के पिता जी सरकारी कर्मचारी थे। (निषेधवाचक वाक्य)
(ii) नागर जी ने नेहरू जी की माता जी के पास रोज जाते थे। (प्रश्नवाचक वाक्य)
उत्तर:
(i) नागर जी के पिता जी सरकारी कर्मचारी नहीं थे।
(ii) क्या नागर जी नेहरू जी की माता जी के पास रोज जाते थे?

11. वाक्य शुद्धिकरण:

निम्नलिखित वाक्य शुद्ध करके फिर से लिखिए:
(i) नेत्रहीनों के भविष्यवाणियाँ कभी-कभी. सच होते हैं।
(ii) आपने कभी आपके लिखने की सार्थकता की परख किया है।
उत्तर:
(i) नेत्रहीनों की भविष्यवाणियाँ कभी-कभी सच होती हैं।
(ii) आपने कभी अपने लिखने की सार्थकता की परख की है।

भाषा बिंदु

(3) निम्नलिखित वाक्यों के रिक्त स्थानों की पूर्ति उचित कारक चिह्नों से कीजिए तथा संबंधित कारक और कारक चिह्न तालिका में वाक्य के सामने लिखिए:

उपक्रम/कृति/परियोजना

श्रवणीय
किसी बुजुर्ग से स्वतंत्रतापूर्व भारत की विस्तृत जानकारी सुनिए और मित्रों को सुनाइए।

पठनीय
प्रसिद्ध व्यक्तियों के भाषण पढ़िए और चर्चा कीजिए।

लेखनीय
किसी खिलाड़ी का साक्षात्कार लेने हेतु प्रश्नों की सूची बनाइए।
उत्तर:

• आपको इस खेल में रुचि कैसे हुई?
• आपने इसे सीखने के लिए क्या-क्या किया?
• क्या आपने इसके लिए विशेष प्रशिक्षण लिया? किससे? इससे आपको क्या लाभ हुआ?
• क्या आपने किसी प्रतियोगिता में भाग लिया है?
• क्या कभी कोई पुरस्कार, प्रशंसा मिला/मिली है?
• आपका लक्ष्य क्या है?
• आप अपना आदर्श किसे मानते हैं?
• आगे चलकर आपकी क्या योजनाएँ है?
• क्या आप अपने इस प्रयास से संतुष्ट हैं?
• आप इस खेल से जुड़े खिलाड़ियों को क्या संदेश देना चाहते हैं?

संभाषणिय
‘आज के समय में पत्र लेखन की सार्थकता’ पर अपने विचार व्यक्त कीजिए।

जब तक जिंदा रहूँ, लिखता रहूँ Summary in Hindi

विषय-प्रवेश : साक्षात्कार साहित्य की एक महत्त्वपूर्ण विधा है। साक्षात्कार में प्रश्न उत्तर के माध्यम से किसी व्यक्ति से साक्षात्कारकर्ता उसके कार्यों एवं जीवन के विविध पक्षों के बारे में समुचित जानकारी प्राप्त करता है। साक्षात्कार में व्यक्ति के बारे में हर प्रकार की जानकारी आईने में दिखाई देने वाली तस्वीर की भाँति झलकने लगती है। __प्रस्तुत साक्षात्कार में विश्वनाथ प्रसाद तिवारी ने प्रसिद्ध लेखक अमृतलाल नागर से उनके साहित्य-सृजन, साहित्य, उनकी लेखन प्रक्रिया, उनके समकालीन साहित्यकारों, तत्कालीन राजनैतिक एवं सामाजिक परिस्थितियों तथा उनकी कुछ प्रमुख कृतियों के बारे में अनेक |. प्रश्न पूछे हैं और उन्होंने उनका बेबाक उत्तर दिया है।

Hindi Lokbharti 10th Textbook Solutions दूसरी इकाई

• बरषहिं जलद Question Answer
• दो लघुकथाएँ Question Answer (पूरक पठन)
• श्रम साधना Question Answer
• छापा Question Answer
• ईमानदारी की प्रतिमूर्ति Question Answer
• हम उस धरती की संतति हैं Question Answer (पूरक पठन)
• महिला आश्रम Question Answer
• अपनी गंध नहीं बेचूँगा Question Answer
• जब तक जिंदा रहूँ, लिखता रहूँ Question Answer
• बूढ़ी काकी Question Answer (पूरक पऊन)
• समता की ओर Question Answer