Class 10

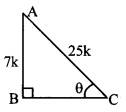
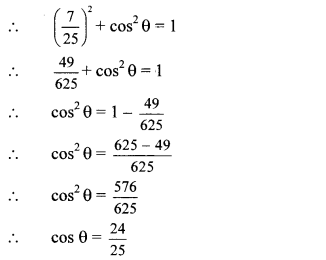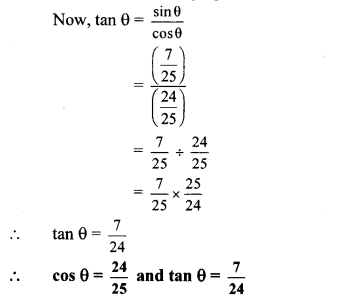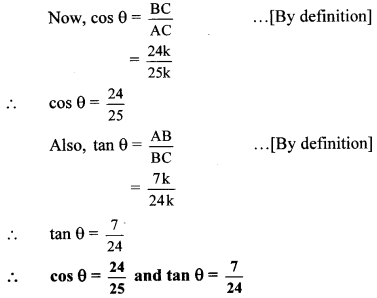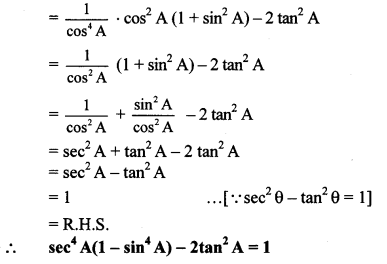Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.4 The Height of the Ridiculous Notes, Textbook Exercise Important Questions and Answers.

Class 10 English Chapter 4.4 Question Answer Maharashtra Board

The Height of the Ridiculous Poem 10th Std Question Answer

The Height Of The Ridiculous Appreciation Question 1.
The teacher writes incomplete sentences on the board. He/She asks the students to complete them in their notebooks.
(a) Today, I am happy because ……………………………… .
(b) Today after the class, I wish ……………………………… .
(c) Tomorrow, I feel that ……………………………… .
(d) I want to laugh because ……………………………… .
(e) Today, the class seems to be cheerful about ……………………………… .
Answer:
(a) my grandparents are coming for a holiday.
(b) to eat an ice cream.
(c) I will go for a movie.
(d) I am very happy.
(e) the forthcoming football match.

The Height Of The Ridiculous Question 2.
The teacher writes an incomplete sentence and asks the students to complete it in a funny way.
Answer:
(1) Mother gave me cheese but the cat ate it.
(2) I went to the market and bought an elephant.

Appreciation Of Poem The Height Of Ridiculous Question 3.
Give the words related to:

Syllable
A syllable is a unit of spoken language made up of a single uninterrupted sound formed by a vowel and consonants. For example, single syllable : ant, two syllables – water, three syllables : Inferno.
Answer:

The Height Of The Ridiculous Theme Question 4.
Pick out the word from the given box and write it in the correct columns below.

jump, narrow, cable, live, queen, butter, tree, kitten, van, yellow, dale, happy, night, printer, star, sober, paper, cloud, pearl, within, bike, began, slender.

Here the focus is not on the spellings but the pronunciation of the words.

Words with one syllable	Words with two syllables

Answer:

Words with one syllable	Words with two syllables
jump, live, queen, tree, van, dale, night, star, cloud, pearl, bike	narrow, cable, butter, kitten, yellow, happy, printer, sober, paper, within, began, slender

The Height Of The Ridiculous Notes Question 5.
Count the syllables and circle the appropriate number in the box.

Answer:

The Height Of The Ridiculous Question 6.
Write the names of any five of your friends and mention the number of syllables in each name.

Name	Number of syllables

Answer:

Name	Number of syllables
Rohan	2
Namrata	3
Poonam	2
Jai	1
Nilima	3

The Height of the Ridiculous Class 10 English Workshop Questions and Answers Maharashtra Board

The Height Of The Ridiculous Question 1.
Find out expressions from the poem that indicate funny moments.
For example, I laughed as I would die.
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………
Answer:
(1) was all upon the grin
(2) the grin grew broad
(3) and shot from ear to ear
(4) He read the third; a chuckling noise
(5) The fourth; he broke into a roar
(6) The fifth; his waistband split;
(7) The sixth; he burst five buttons off;
(8) And tumbled in a fit.

Appreciation Of The Poem The Height Of Ridiculous Question 2.
Order of sequence : Arrange the following reactions in their proper order, as per the poem.
(a) His waistband split
(b) The grin grew broad.
(c) Sleepless eye.
(d) Was all upon the grin.
(e) He broke into a roar.
(f) He burst five buttons off.
Answer:
(d) Was all upon the grin
(b) The grin grew bro^d
(e) He broke into a roar
(a) His waistband split
(f) He burst five buttons
(c) Sleepless eye

Height Of Ridiculous Appreciation Question 3.
Form pairs and find out the various rhyming words in the poem and two of your own. Complete the following table.

Words	Rhyming words from the poem	Rhyming words more of your own
ear
within
man
split
way
him
die
mood

Answer:

Words	Rhyming words from the poem	Rhyming words more of your own
Way	Pay	Say, ray
Him	Limb	Dim, rim
Die	I	Fly, shy
Mood	Good	Food, wood
Ear	Hear	fear, dear
Within	Grin	sin, bin
Man	Can	fan, ran
Split	Fit	knit, lit

The Height Of Ridiculous Appreciation Question 4.
Match the lines with the Figures of Speech.

Lines	Figures of Speech
1.   In wondrous merry mood 2.  They were so queer, so very queer. 3.  And saw him peep within 4.  The grin grew broad. 5.  And shot from ear to ear. 6.  He broke into a roar. 7.  Ten days and nights with sleepless eye	Tautology Alliteration Onomatopoeia Repetition Hyperbole Repetition Transferred Epithet

Answer:

Lines	Figures of Speech
1. In wondrous, merry mood	Tautology
2. They were so queer, so very queer	Repetition
3.  And saw him peep within	Repetition
4. The grin grew broad	Alliteration
5. And shot from ear to ear	Hyperbole
6. He broke into a roar –	Onomatopoeia
7. Ten days and nights with sleepless eye	Transferred Epithet

Appreciation Of The Poem The Height Of The Ridiculous Question 5.
Copy any two stanzas of the poem in the lines below. Using a coloured pen underline the stressed syllables in each line and put a stress-mark ( ) over each.
Answer:
I wrote some lines once on a time
In wondrous merry mood,
And thought, as usual, men would say
They were exceeding good.

The Height Of The Ridiculous Question 6.
Complete the lines of the poem by choosing proper pairs of rhyming words and make it meaningful.
– We returned home late, one ………………………. ,
In the window, there glowed a ………………………. .
Burglars !! was our very first ………………………. ;
For defence, sticks ‘n stones we ………………………. .
”Let’s grab the loot and ………………………. ,”
was uttered soft, by ………………………..
The door we softly ……………………….,
And then we were truly ………………………..
Oops! Before, outside, we’d ……………………….,
The television had been left ………………………..
(run, shocked, gone, night, sought, on, someone, thought, light, unlocked)
Answer:
We returned home late, one night,
In the window there glowed a light.
Burglars! Was our very first thought,
For defence, sticks ‘n stones we sought.
“Let’s grab the loot and run.”
Was uttered soft, by someone.
The door we softly unlocked.
And then we were truly shocked.
Oops! Before outside we’d gone,
The television had been left on!

The Height Of Ridiculous Poem Appreciation Question 7.
Form goups in your class and together compose a short humorous poem. Use jokes, experiences, etc. and convert it to a poetic form. Write and decorate it on chart-paper and put it up in your class, in turns.

Appreciation Of The Height Of The Ridiculous Question 8.
Go through the poem and write an appreciation of the poem in a paragraph format.
Answer:
Point Format
(for understanding)
The title of the poem: ‘The Height of the Ridiculous’
The poet: Oliver Wendell Holmes
Rhyme scheme: abcb.
Figures of speech: Transferred Epithet, Hyperbole, Onomatopoeia, Tautology, Alliteration, etc.
Theme/Central idea: A funny poem to simply entertain the audience; written for Enjoyment.

Paragraph Format
The poem ‘The Height of the Ridiculous’ is written by Oliver Wendell Holmes.

The rhyme scheme of the poem is abcb. There are many figures of speech, like Hyperbole, Tautology, Onomatopoeia, Alliteration, etc. but the one that stands out is Transferred Epithet. In the line ‘Ten days and nights, with sleepless eye’, the adjective ‘sleepless’ should be for the man and not for the eye.

The poem is a humorous one written for enjoyment, with plenty of funny expressions. The main purpose of the poet is to simply entertain the reader.

Appreciation Of Poem The Height Of The Ridiculous Question 9.
Project :
Reading a poem.
Arrange the poetry reading competition. Select the poem of your choice.

• Read the poem silently.
• Repeat the reading of the poem.
• Focus on the pauses, stresses, intonation etc.
• Pay attention to the proper pronunciations.

Poem Appreciation Of The Height Of Ridiculous Question 10.
Choose the correct alternatives: (The answers are given directly and underlined.)
(1) The poet was in a very …………….. mood when he wrote the lines.
(a) tired
(b) happy
(c) bored
(d) wondering
Answer:
(b) happy

(2) The poet was generally a ……………… man.
(a) humorous
(b) wonderful
(c) serious
(d) good
Answer:
(c) serious

Question 11.
Explain:
(a) the contrast between the poet and his servant.
Answer:
The poet was a thin and slender man while his servant was strong and muscular.

(b) the poet’s reaction when he read the lines.
Answer:
The poet laughed heartily when he read the lines. He laughed so hard he thought he would die.

Question 12.
Find out the expression from the extract that indicates funny moments:
Answer:
‘I laughed as I would die’.

Question 13.
Match the lines with the figures of speech:
Lines – Figures of Speech
(a) A sober man am I – (c) Tautology
(b) To mind a slender man like me – (d) Inversion
Answer:
(a) A sober man am I – Inversion
(b) To mind a slender man like me – Alliteration

Question 14.
Complete the following:
(1) There was a grin on the servant’s face when …………………………
(2) The chuckling noise was heard when ……………………..
(3) When he read the fifth line ………………….
(4) The grin grew from ear to ear when the servant ………………….
Answer:
(1) he read the first line.
(2) the servant read the third line.
(3) his waistband split.
(4) read the second line.

Question 15.
Describe the outcome of this experience on the poet.
Answer:
After this experience, the poet has never dared to write any more funny poems.

Question 16.
Which line suggests that the servant was totally out of control?
Answer:
The line ‘And tumbled into a fit’ suggests that the servant was totally out of control.

Read More:

• A Thing of Beauty is a Joy For Ever Question Answers
• The Luncheon Question Answers
• World Heritage Question Answers
• The Height of the Ridiculous Question Answers
• The Old Man and The Sea Book Review Question Answers
• The Gift of the Magi Question Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

10th Standard Maths 2 Practice Set 6.1 Chapter 6 Trigonometry Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 6.1 Chapter 6 Trigonometry Questions With Answers Maharashtra Board

Question 1.
If sin θ = \(\frac { 7 }{ 25 } \), find the values of cos θ and tan θ.
Solution:
sin θ = \(\frac { 7 }{ 25 } \) … [Given]
We know that,
sin² θ + cos² θ = 1

…[Taking square root of both sides] Now, tan θ = \(\frac{\sin \theta}{\cos \theta}\)

Alternate Method:
sin θ = \(\frac { 7 }{ 25 } \) …(i) [Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
sin θ = \(\frac { AB }{ AC } \) … (ii) [By definition]
∴ \(\frac { AB }{ AC } \) = \(\frac { 7 }{ 25 } \) … [From (i) and (ii)]

LetAB = 7k and AC = 25k
In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (7k)² + BC² = (25k)²
∴ 49k² + BC² = 625k²
∴ BC² = 625k² – 49k²
∴ BC² = 576k²
∴ BC = 24k …[Taking square root of both sides]

Question 2.
If tan θ = \(\frac { 3 }{ 4 } \), find the values of sec θ and cos θ.
Solution:

Alternate Method:
tan θ = \(\frac { 3 }{ 4 } \) …(i)[Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
tan θ = \(\frac { AB }{ BC } \) … (ii) [By definition]
∴ \(\frac { AB }{ BC } \) = \(\frac { 3 }{ 4 } \) … [From (i) and (ii)]

Let AB = 3k and BC 4k
In ∆ABC,∠B = 90°
∴ AB² + BC² = AC² …[Pythagoras theorem]
∴ (3k)² + (4k)² = AC²
∴ 9k² + 16k² = AC²
∴ AC² = 25k²
∴ AC = 5k …[Taking square root of both sides]

Question 3.
If cot θ = \(\frac { 40 }{ 9 } \), find the values of cosec θ and sin θ
Solution:

..[Taking square root of both sides]

Alternate Method:
cot θ = \(\frac { 40 }{ 9 } \) ….(i) [Given]
Consider ∆ABC, where ∠ABC = 90° and
∠ACB = θ
cot θ = \(\frac { BC }{ AB } \) …(ii) [By defnition]
∴ \(\frac { BC }{ AB } \) = \(\frac { 40 }{ 9 } \) ….. [From (i) and (ii)]
Let BC = 40k and AB = 9k

In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (9k)² + (40k)² = AC²
∴ 81k² + 1600k² = AC²
∴ AC² = 1681k²
∴ AC = 41k … [Taking square root of both sides]

Question 4.
If 5 sec θ – 12 cosec θ = θ, find the values of sec θ, cos θ and sin θ.
Solution:
5 sec θ – 12 cosec θ = 0 …[Given]
∴ 5 sec θ = 12 cosec θ

Question 5.
If tan θ = 1, then find the value of

Solution:
tan θ = 1 … [Given]
We know that, tan 45° = 1
∴ tan θ = tan 45°
∴ θ = 45°

Question 6.
Prove that:
i. \(\frac{\sin ^{2} \theta}{\cos \theta}+\cos \theta=\sec \theta\)
ii. cos² θ (1+ tan² θ) = 1
iii. \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sec \theta-\tan \theta\)
iv. (sec θ – cos θ) (cot θ + tan θ) tan θ. sec θ
v. cot θ + tan θ cosec θ. sec θ
vi. \(\frac{1}{\sec \theta-\tan \theta}=\sec \theta+\tan \theta\)
vii. sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ
viii. \(\sec \theta+\tan \theta=\frac{\cos \theta}{1-\sin \theta}\)

Proof:
i. L.H.S. = \(\frac{\sin ^{2} \theta}{\cos \theta}+\cos \theta\)

ii. L.H.S. = cos² θ(1 + tan² θ)
= cos² θ sec² θ …[∵ 1 + tan² θ = sec² θ]

= 1
= R.H.S.
∴ cos² θ (1 + tan² θ) = 1

iv. L.H.S. = (sec θ – cos θ) (cot θ + tan θ)

∴ (sec θ – cos θ) (cot θ + tan θ) = tan θ. sec θ

v. L.H.S. = cot θ + tan θ

∴ cot θ + tan θ = cosec θ.sec θ

vii. L.H.S. = sin⁴ θ – cos⁴ θ
= (sin² θ)² – (cos² θ)²
= (sin² θ + cos² θ) (sin² θ – cos² θ)
= (1) (sin² θ – cos² θ) ….[∵ sin² θ + cos² θ = 1]
= sin² θ – cos² θ
= (1 – cos² θ) – cos² θ …[θ sin² θ = 1 – cos² θ]
= 1 – 2 cos² θ
= R.H.S.
∴ sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ

viii. L.H.S. = sec θ + tan θ

xi. L.H.S. = sec⁴ A (1 – sin⁴ A) – 2 tan² A
= sec⁴ A [1² – (sin² A)²] – 2 tan² A
= sec⁴ A (1 – sin²A) (1 + sin² A) – 2 tan² A
= sec⁴ A cos²A (1 + sin² A) – 2 tan²A
[ ∵ sin² θ + cos² θ = 1 ,∵ 1 – sin² θ = cos² θ]

Maharashtra Board Class 10 Maths Chapter 6 Trigonometry Intext Questions and Activities

Question 1.
Fill in the blanks with reference to the figure given below. (Textbook pg. no. 124)

Solution:

Question 2.
Complete the relations in ratios given below. (Textbook pg, no. 124)

Solution:
i. \(\frac{\sin \theta}{\cos \theta}\) = [tan θ]
ii. sin θ = cos (90 – θ)
iii. cos θ = (90 – θ)
iv. tan θ × tan (90 – θ) = 1

Question 3.
Complete the equation. (Textbook pg. no, 124)
sin² θ + cos² θ = [______]
Solution:
sin² θ + cos² θ = [1]

Question 4.
Write the values of the following trigonometric ratios. (Textbook pg. no. 124)

Solution:

Maharashtra Board Class 10 Maths Solutions

Class 10 Maths Digest

• Practice Set 6.1 Class 10 Answers
• Practice Set 6.2 Class 10 Answers
• Problem Set 6 Class 10 Answers
• Practice Set 7.1 Class 10 Answers
• Practice Set 7.2 Class 10 Answers
• Practice Set 7.3 Class 10 Answers
• Practice Set 7.4 Class 10 Answers
• Problem Set 7 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 7 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

10th Standard Maths 2 Problem Set 7 Chapter 7 Mensuration Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Problem Set 7 Chapter 7 Mensuration Questions With Answers Maharashtra Board

Problem Set 7 Question 1. Choose the correct alternative answer for each of the following questions.

i. The ratio of circumference and area of a circle is 2 : 7. Find its circumference.
(A) 14 π
(B) \(\frac{7}{\pi}\)
(C) 7π
(D) \(\frac{14}{\pi}\)
Answer:

(A)

ii. If measure of an arc of a circle is 160° and its length is 44 cm, find the circumference of the circle.
(A) 66 cm
(B) 44 cm
(C) 160 cm
(D) 99 cm
Answer:

(D)

iii. Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
(A) 44 cm
(B) 25 cm
(C) 36 cm
(D) 56 cm
Answer:

(B)

iv. Find the curved surface area of a cone of radius 7 cm and height 24 cm.
(A) 440 cm²
(B) 550 cm²
(C) 330 cm²
(D) 110 cm²
Answer:

(B)

v. The curved surface area of a cylinder is 440 cm² and its radius is 5 cm. Find its height.
(A) \(\frac{44}{\pi}\) cm
(B) 22π cm
(C) 44π cm
(D) \(\frac{22}{\pi}\)
Answer:

(A)

vi. A cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5 cm, find the height of the cone.
(A) 15 cm
(B) 10 cm
(C) 18 cm
(D) 5 cm
Answer:

(A)

vii. Find the volume of a cube of side 0.01 cm.
(A) 1 cm
(B) 0.001 cm³
(C) 0.0001 cm³
(D) 0.000001 cm³
Answer:
Volume of cube = (side)³
= (0.01)³ = 0.000001 cm³
(D)

viii. Find the side of a cube of volume 1 m³
(A) 1 cm
(B) 10 cm
(C) 100 cm
(D) 1000 cm
Answer:
Volume of cube = (side)³
∴ 1 = (side)³
∴ Side = 1 m
= 100 cm
(C)

Problem Set 7 Geometry Class 10 Question 2. A washing tub in the shape of a frustum of a cone has height 21 cm. The radii of the circular top and bottom are 20 cm and 15 cm respectively. What is the capacity of the tub? = (π = \(\frac { 22 }{ 7 } \))
Given: For the frustum shaped tub,
height (h) = 21 cm,
radii (r₁) = 20 cm, and (r₂) = 15 cm
To find: Capacity (volume) of the tub.
Solution:
Volume of frustum = \(\frac { 1 }{ 3 } \) πh (r₁² + r₂² + r₁ × r₂)

∴ The capacity of the tub is 20.35 litres.

10th Geometry Problem Set 7 Question 3. Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm and 30 cm respectively. How many balls were melted to make the tube?
Given: For the cylindrical tube,
height (h) = 90 cm,
outer radius (R) = 30 cm,
thickness = 2 cm
For the plastic spherical ball,
radius (r₁) = 1 cm
To find: Number of balls melted.
Solution:

Inner radius of tube (r)
= outer radius – thickness of tube
= 30 – 2
= 28 cm
Volume of plastic required for the tube = Outer volume of tube – Inner volume of hollow tube
= πR²h – πr²h
= πh(R² – r²)
= π × 90 (30² – 28²)
= π × 90 (30 + 28) (30 – 28) …[∵ a² – b² = (a + b)(a – b)]
= 90 × 58 × 2π cm³

∴ 7830 plastic balls were melted to make the tube.

Problem Set 7 Geometry Question 4.
A metal parallelopiped of measures 16 cm × 11cm × 10cm was melted to make coins. How many coins were made if the thickness and diameter of each coin was 2 mm and 2 cm respectively?
Given: For the parallelopiped.,
length (l) = 16 cm, breadth (b) = 11 cm,
height (h) = 10 cm
For the cylindrical coin,
thickness (H) = 2 mm,
diameter (D) 2 cm
To find: Number of coins made.
Solution:
Volume of parallelopiped = l × b × h
= 16 × 11 × 10
= 1760 cm³
Thickness of coin (H) = 2 mm
= 0.2 cm …[∵ 1 cm = 10 mm]
Diameter of coin (D) = 2 cm

∴ 2800 coins were made by melting the parallelopiped.

Mensuration Problem Question 5.  The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of ₹ 10 per sq.m.
Given: For the cylindrical roller,
diameter (d) =120 cm,
length = height (h) = 84 cm
To find: Expenditure of levelling the ground.
Solution:
Diameter of roller (d) = 120 cm

Now, area of ground levelled in one rotation = curved surface area of roller
= 3.168 m²
∴ Area of ground levelled in 200 rotations
= 3.168 × 200 =
633.6 m²
Rate of levelling = ₹ 10 per m²
∴ Expenditure of levelling the ground
= 633.6 × 10 = ₹ 6336
∴ The expenditure of levelling the ground is ₹ 6336.

Question 6.
The diameter and thickness of a hollow metal sphere are 12 cm and 0.01 m respectively. The density of the metal is 8.88 gm per cm3. Find the outer surface area and mass of the sphere, [π = 3.14]
Given: For the hollow sphere,
diameter (D) =12 cm, thickness = 0.01 m
density of the metal = 8.88 gm per cm³
To find: i. Outer surface area of the sphere
ii. Mass of the sphere.

Solution:
Diameter of the sphere (D)
= 12 cm
∴ Radius of sphere (R)
= \(\frac { d }{ 2 } \) = \(\frac { 12 }{ 2 } \) = 6 cm
∴ Surface area of sphere = 4πR²
= 4 × 3.14 × 6²
= 452.16 cm²
Thickness of sphere = 0.01 m
= 0.01 × 100 cm …[∵ 1 m = 100 cm]
= 1 cm
∴ Inner radius of the sphere (r)
= Outer radius – thickness of sphere
= 6 – 1 = 5 cm
∴ Volume of hollow sphere
= Volume of outer sphere – Volume of inner sphere

∴ The outer surface area and the mass of the sphere are 452.16 cm² and 3383.19 gm respectively.

Question 7.
A cylindrical bucket of diameter 28 cm and height 20 cm was full of sand. When the sand in the bucket was poured on the ground, the sand got converted into a shape of a cone. If the height of the cone was 14 cm, what was the base area of the cone?
Given: For the cylindrical bucket,
diameter (d) = 28 cm, height (h) = 20 cm
For the conical heap of sand,
height (H) = 14 cm
To find: Base area of the cone (πR²).
Solution:
Diameter of the bucket (d) = 28 cm


The base area of the cone is 2640 cm².

Question 8.
The radius of a metallic sphere is 9 cm. It was melted to make a wire of diameter 4 mm. Find the length of the wire.
Given: For metallic sphere,
radius (R) = 9 cm
For the cylindrical wire,
diameter (d) = 4 mm
To find: Length of wire (h).
Solution:

∴ The length of the wire is 243 m.

Question 9.
The area of a sector of a circle of 6 cm radius is 157t sq.cm. Find the measure of the arc and length of the arc corresponding to the sector.
Given: Radius (r) = 6 cm,
area of sector = 15 π cm²
To find: i. Measure of the arc (θ),
ii. Length of the arc (l)
Solution:

∴ The measure of the arc and the length of the arc are 150° and 5π cm respectively.

Question 10.
In the adjoining figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.

(π = 3.14, \(\sqrt { 3 }\) = 1.73)
Given: Radius (r) = PA = 8 cm,
PC = 4 cm
To find: Area of shaded region.
Solution:

Similarly, we can show that, ∠BPC = 60°
∠APB = ∠APC + ∠BPC …[Angle sum property]
∴ θ = 60° + 60° = 120°


Area of shaded region = A(P-ADB) – A(∆APB)
= 66.98 – 27.68
= 39.30 cm²
∴ The area of the shaded region is 39.30 cm².

Question 11.
In the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.

Solution:
Side of square ABCD
= radius of sector C-BXD = [20] cm
Area of square = (side)² = 20² = 400 cm² ….(i)
Area of shaded region inside the square = Area of square ABCD – Area of sector C-BXD

Radius of bigger sector
= Length of diagonal of square ABCD
= \(\sqrt { 2 }\) × side
= 20 \(\sqrt { 2 }\) cm
Area of the shaded regions outside the square
= Area of sector A-PCQ – Area of square ABCD
= A(A – PCQ) – A(꠸ABCD)

Alternate method:

□ABCD is a square. … [Given]
Side of □ABCD = radius of sector (C-BXD)
= 20 cm
Radius of sector (A-PCQ) = Diagonal
= \(\sqrt { 2 }\) × side
= \(\sqrt { 2 }\) × 20
= 20 \(\sqrt { 2 }\) cm

Now, Area of shaded region
= A(A-PCQ) – A(C-BXD)
= 628 – 314
= 314 cm²
∴ The area of the shaded region is 314 cm².

Question 12.
In the adjoining figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles.

Solution:
Let the radius of the bigger circle be R and that of smaller circle be r.
OA, OB, OC and OD are the radii of the bigger circle.
∴ OA = OB = OC = OD = R
PQ = PA = r
OQ + BQ = OB … [B – Q – O]
OQ = OB – BQ = R – 9
OE + DE = OD ….[D – E – O]
OE = OD – DE = [R – 5]
As the chords QA and EF of the circle with centre P intersect in the interior of the circle, so by the property of internal division of two chords of a circle,
OQ × OA = OE × OF
∴ (R – 9) × R = (R – 5) × (R – 5) …[∵ OE = OF]
∴ R² – 9R = R² – 10R + 25
∴ -9R + 10R = 25
∴ R = [25units]
AQ = AB – BQ = 2r ….[B-Q-A]
∴ 2r = 50 – 9 = 41
∴ r = \(\frac { 41 }{ 2 } \) = 20.5 units

Class 10 Maths Digest

• Practice Set 6.1 Class 10 Answers
• Practice Set 6.2 Class 10 Answers
• Problem Set 6 Class 10 Answers
• Practice Set 7.1 Class 10 Answers
• Practice Set 7.2 Class 10 Answers
• Practice Set 7.3 Class 10 Answers
• Practice Set 7.4 Class 10 Answers
• Problem Set 7 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 5 Probability.

10th Standard Maths 1 Practice Set 5.3 Chapter 5 Probability Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Practice Set 5.3 Chapter 5 Probability Questions With Answers Maharashtra Board

Question 1.
Write sample space ‘S’ and number of sample points n(S) for each of the following experiments. Also write events A, B, C in the set form and write n(A), n(B), n(C).

i. One die is rolled,
Event A: Even number on the upper face.
Event B: Odd number on the upper face.
Event C: Prime number on the upper face.

ii. Two dice are rolled simultaneously,
Event A: The sum of the digits on upper faces is a multiple of 6.
Event B: The sum of the digits on the upper faces is minimum 10.
Event C: The same digit on both the upper faces.

iii. Three coins are tossed simultaneously.
Condition for event A: To get at least two heads.
Condition for event B: To get no head.
Condition for event C: To get head on the second coin.

iv. Two digit numbers are formed using digits 0, 1, 2, 3, 4, 5 without repetition of the digits.
Condition for event A: The number formed is even.
Condition for event B: The number is divisible by 3.
Condition for event C: The number formed is greater than 50.

v. From three men and two women, environment committee of two persons is to be formed.
Condition for event A: There must be at least one woman member.
Condition for event B: One man, one woman committee to be formed.
Condition for event C: There should not be a woman member.

vi. One coin and one die are thrown simultaneously.
Condition for event A: To get head and an odd number.
Condition for event B: To get a head or tail and an even number.
Condition for event C: Number on the upper face is greater than 7 and tail on the coin.
Solution:
i. Sample space (S) = {1, 2, 3, 4, 5, 6}
∴ n(S) = 6
Condition for event A: Even number on the upper face.
∴ A = {2,4,6}
∴ n(A) = 3
Condition for event B: Odd number on the upper face.
∴ B = {1, 3, 5}
∴ n(B) = 3
Condition for event C: Prime number on the upper face.
∴ C = {2, 3, 5}
∴ n(C) = 3

ii. Sample space,
S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
∴ n(S) = 36
Condition for event A: The sum of the digits on the upper faces is a multiple of 6.
A = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 6)}
∴ n(A) = 6

Condition for event B: The sum of the digits on the upper faces is minimum 10.
B = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
∴ n(B) = 6

Condition for event C: The same digit on both the upper faces.
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
∴ n(C) = 6

iii. Sample space,
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
∴ n(S) = 8

Condition for event A: To get at least two heads.
∴ A = {HHT, HTH, THH, HHH}
∴ n(A) = 4

Condition for event B: To get no head.
∴ B = {TTT}
∴ n(B) = 1

Condition for event C: To get head on the second coin.
∴ C = {HHH, HHT, THH, THT}
∴ n(C) = 4

iv. Sample space (S) = {10, 12, 13, 14, 15,
20, 21, 23, 24, 25,
30, 31, 32, 34, 35,
40, 41, 42, 43,
45, 50, 51, 52, 53, 54}
∴ n(S) = 25
Condition for event A: The number formed is even
∴ A = {10, 12, 14, 20, 24, 30, 32, 34, 40, 42, 50, 52, 54)
∴ n(A) = 13
Condition for event B: The number formed is divisible by 3.
∴ B = {12, 15, 21, 24, 30, 42, 45, 51, 54}
∴ n(B) = 9
Condition for event C: The number formed is greater than 50.
∴ C = {51,52, 53,54}
∴ n(C) = 4

v. Let the three men be M₁, M₂, M₃ and the two women be W₁, W₂.
Out of these men and women, a environment committee of two persons is to be formed.
∴ Sample space,
S = {M₁M₂, M₁M₃, M₁W₁, M₁W₂, M₂M₃, M₂W₁, M₂W₂, M₃W₁, M₃W₂, W₁W₂}
∴ n(S) = 10
Condition for event A: There must be at least one woman member.
∴ A = {M₁W₁, M₁W₂, M₂W₁, M₂W₂, M₃W₁, M₃W₂, W₁W₂}
∴ n(A) = 7
Condition for event B: One man, one woman committee to be formed.
∴ B = {M₁W₁, M₁W₂, M₂W₁, M₂W₂, M₃W₂, M₃W₂}
∴ n(B) = 6
Condition for event C: There should not be a woman member.
∴ C = {M₁M₂, M₁M₃, M₂M₃}
∴ n(C) = 3

vi. Sample space,
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
∴ n(S) = 12
Condition for event A: To get head and an odd number.
∴ A = {(H, 1), (H, 3), (H, 5)}
∴ n(A) = 3
Condition for event B: To get a head or tail and an even number.
∴ B = {(H, 2), (H, 4), (H, 6), (T, 2), (T, 4), (T, 6)}
∴ n(B) = 6
Condition for event C: Number on the upper face is greater than 7 and tail on the coin.
The greatest number on the upper face of a die is 6.
∴ Event C is an impossible event.
∴ C = { }
∴ n(C) = 0

Class 10 Maths Digest

• Practice Set 5.1 Class 10 Answers
• Practice Set 5.2 Class 10 Answers
• Practice Set 5.3 Class 10 Answers
• Practice Set 5.4 Class 10 Answers
• Problem Set 5 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 5 Probability.

10th Standard Maths 1 Practice Set 5.2 Chapter 5 Probability Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Practice Set 5.2 Chapter 5 Probability Questions With Answers Maharashtra Board

Question 1.
For each of the following experiments write sample space ‘S’ and number of sample Point n(S)
i. One coin and one die are thrown simultaneously.
ii. Two digit numbers are formed using digits 2,3 and 5 without repeating a digit.
Solution:
i. Sample space,
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
∴ n(S) =12
ii. Sample space,
S = {23,25,32, 35, 52, 53}
∴ n(S) = 6

Question 2.
The arrow is rotated and it stops randomly on the disc. Find out on which colour it may stop.

Solution:
There are total six colours on the disc.
Sample space,
S = {Red, Orange, Yellow, Blue, Green, Purple}
∴ n(S) = 6
∴ Arrow may stop on any one of the six colours.

Question 3.
In the month of March 2019, find the days on which the date is a multiple of 5. (see the given page of the calendar).

Solution:
Dates which are multiple of 5:
5,10, 15,20,25,30
∴ S = {Tuesday, Sunday, Friday, Wednesday, Monday, Saturday}
∴ n(S) = 6
∴ The days on which the date will be a multiple of 5 are Tuesday, Sunday, Friday, Wednesday, Monday and Saturday.

Question 4.
Form a ‘Road safety committee’ of two, from 2 boys (B₁ B₂) and 2 girls (G₁, G₂). Complete the following activity to write the sample space.
Solution:

Question 1.
Sample Space

• The set of all possible outcomes of a random experiment is called sample space.
• It is denoted by ‘S’ or ‘Ω’ (omega).
• Each element of a sample space is called a sample point.
• The number of elements in the set S is denoted by n(S).
• If n(S) is finite, then the sample space is called a finite sample space.

Some examples of finite sample space. (Textbook pg. no, 117)
Solution:

Class 10 Maths Digest

• Practice Set 5.1 Class 10 Answers
• Practice Set 5.2 Class 10 Answers
• Practice Set 5.3 Class 10 Answers
• Practice Set 5.4 Class 10 Answers
• Problem Set 5 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 5 Probability.

10th Standard Maths 1 Practice Set 5.1 Chapter 5 Probability Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Practice Set 5.1 Chapter 5 Probability Questions With Answers Maharashtra Board

Question 1.
How many possibilities are there in each of the following?
i. Vanita knows the following sites in Maharashtra. She is planning to visit one of them in her summer vacation. Ajintha, Mahabaleshwar, Lonar Sarovar, Tadoba wild life sanctuary, Amboli, Raigad, Matheran, Anandavan.
ii. Any day of a week is to be selected randomly.
iii. Select one card from the pack of 52 cards.
iv. One number from 10 to 20 is written on each card. Select one card randomly.
Solution:
i. Here, 8 sites of Maharashtra are given.
∴ There are 8 possibilities in a random experiment of visiting a site out of 8 sites in Maharashtra.

ii. There are 7 days in a week.
∴ There are 7 possibilities in a random experiment of selecting a day of the week.

iii. There are 52 cards in a pack of cards.
∴ There are 52 possibilities in a random experiment of selecting one card from the pack of 52 cards.

iv. There are 11 cards numbered from 10 to 20.
∴ There are 11 possibilities in a random experiment of selecting one card from the given set of cards.

Question 1.
In which of the following experiments possibility of expected outcome is more? (Textbook pg, no. 116)
i. Getting 1 on the upper face when a die is thrown.
ii. Getting head by tossing a coin.
Solution:
i. On a die there are 6 numbers.
∴ There are 6 possibilities of getting any one number from 1 to 6 on the upper face i.e. \(\frac { 1 }{ 6 } \) is the possibility.

ii. There are two possibilities (H or T) on tossing a coin i.e. \(\frac { 1 }{ 2 } \) possibility.
∴ In the second experiment, the possibility of expected outcome is more.

Question 2.
Throw a die, once. What are the different possibilities of getting dots on the upper face? (Textbook pg. no. 114)
Answer:
There are six different possibilities of getting dots on the upper face. They are

Class 10 Maths Digest

• Practice Set 5.1 Class 10 Answers
• Practice Set 5.2 Class 10 Answers
• Practice Set 5.3 Class 10 Answers
• Practice Set 5.4 Class 10 Answers
• Problem Set 5 Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 4.4 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 4 Financial Planning.

10th Standard Maths 1 Practice Set 4.4 Chapter 4 Financial Planning Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Practice Set 4.4 Chapter 4 Financial Planning Questions With Answers Maharashtra Board

Question 1.
Market value of a share is ₹ 200. If the brokerage rate is 0.3% then find the purchase value of the share.
Solution:
Here, MV = ₹ 200, Brokerage = 0.3%
Brokerage = 0.3% of MV
= \(\frac { 0.3 }{ 100 } \) × 200
= ₹ 0.6
∴ Purchase value of the share = MV + Brokerage
= 200 + 0.6
= ₹ 200.60
∴ Purchase value of the share is ₹ 200.60.

Question 2.
A share is sold for the market value of ₹ 1000. Brokerage is paid at the rate of 0.1%. What is the amount received after the sale?
Solution:
Here, MV = ₹ 1000, Brokerage = 0.1%
∴ Brokerage = 0.1 % of MV
= \(\frac { 0.1 }{ 100 } \) × 1000
∴ Brokerage = ₹ 1
∴ Selling value of the share = MV – Brokerage
= 1000 – 1
= ₹ 999
∴ Amount received after the sale is ₹ 999.

Question 3.
Fill in the blanks given in the contract note of sale-purchase of shares.
(B – buy S – sell)

Solution:
For buying shares:
Here, Number of shares = 100,
MV of one share = ₹ 45
∴ Total value = 100 × 45
= ₹ 4500
Brokerage= 0.2% of total value 0.2
= \(\frac { 0.2 }{ 100 } \) × 4500
CGST = 9% of brokerage
= \(\frac { 9 }{ 100 } \) × 9 = ₹ 0.81
But, SGST = CGST
∴ SGST = ₹ 0.81
∴ Purchase value of shares
= Total value + Brokerage
= 4500 + 9 + 0.81 + 0.81
= ₹ 4510.62

ii. For selling shares:
Here, Number of shares = 75,
MV of one share = ₹ 200
∴ Total value = 75 × 200
= ₹ 15000
Brokerage = 0.2% of total value
= \(\frac { 0.2 }{ 100 } \) × 15000
= ₹ 30
CGST = 9% of brokerage
= \(\frac { 9 }{ 100 } \) × 30 = ₹ 2.70
But, SGST = CGST
∴ SGST = ₹ 2.70
∴ Selling value of shares = Total value – (Brokerage + CGST + SGST)
= 15000 – (30 + 2.70 + 2.70)
= 15000 – 35.40
= ₹ 14964.60

Question 4.
Smt. Desai sold shares of face value ₹ 100 when the market value was ₹ 50 and received ₹ 4988.20. She paid brokerage 0.2% and GST on brokerage 18%, then how many shares did she sell?
Solution:
Here, face value of share = ₹ 100,
MV = ₹ 50,
Selling price of shares = ₹ 4988.20,
Rate of brokerage = 0.2%, Rate of GST = 18%
Brokerage = 0.2% of MV

Question 5.
Mr. D’souza purchased 200 shares of FV ₹ 50 at a premium of ₹ 100. He received 50% dividend on the shares. After receiving the dividend he sold 100 shares at a discount of ₹ 10 and remaining shares were sold at a premium of ₹ 75. For each trade he paid the brokerage of ₹ 20. Find whether Mr. D’souza gained or incurred a loss? By how much?
Solution:
For purchasing shares:
Here, FV = ₹ 50, Number of shares = 200,
premium = ₹ 100
MV of 1 share = FV + premium
= 50 + 100
= ₹ 150
∴ MV of 200 shares = 200 × 150 = ₹ 30,000
∴ Mr. D’souza invested amount
= MV of 200 shares + brokerage
= 30,000 + 20
= ₹ 30,020
For selling shares:
Rate of dividend = 50 %, FV = ₹ 50,
brokerage = ₹ 20
Number of shares = 200
Dividend per share = 50% of FV
= \(\frac { 50 }{ 100 } \) × 50
= ₹ 25
∴ Dividend of 200 shares = 200 × 25 = ₹ 5,000
Now, 100 shares are sold at a discount of ₹ 10.
∴ Selling price of 1 share = FV – discount
= 50 – 10
= ₹ 40
∴ Selling price of 100 shares = 100 × 40
= ₹ 4000
∴ Amount obtained by selling 100 shares
= selling price – brokerage
= 4000 – 20
= ₹ 3980
Also, remaining 100 shares are sold at premium of ₹ 75.
∴ selling price of 1 share = FV + premium
= 50 + 75
= ₹ 125
∴ selling price of 100 shares = 100 × 125
= ₹ 12,500
∴ Amount obtained by selling 100 shares
= selling price – brokerage
= 12,500 – 20
= ₹ 12,480
∴ Mr D’souza income = 5000 + 3980 + 12480
= ₹ 21460
Now, Mr D’souza invested amount > income
∴ Mr D’souza incurred a loss.
∴ Loss = amount invested – income
= 30020 – 21460
= ₹ 8560
∴ Mr. D’souza incurred a loss of ₹ 8560.

Question 1.
Nalinitai invested ₹ 6024 in the shares of FV ₹ 10 when the Market Value was ₹ 60. She sold all the shares at MV of ₹ 50 after taking 60% dividend. She paid 0.4% brokerage at each stage of transactions. What was the total gain or loss in this transaction? (Textbook pg. no. 106)
Solution:
Rate of GST is not given in the example, so it is not considered.
For Purchased Shares:
FV = ₹ 10, MV = ₹ 60

Question 2.
In the above example if GST was paid at 18% on brokerage, then the loss is ₹ 451.92. Verify whether you get the same answer. (Textbook pg, no. 107)
Solution:
For Purchased Shares:
FV = ₹ 10, MV = ₹ 60, sum invested = ₹ 6024, brokerage = 0.4 %, GST = 18%
Brokerage per share = \(\frac { 0.4 }{ 100 } \) × 60 = ₹ 0.24 100
GST per share = \(\frac { 18 }{ 100 } \) × 0.24 = ₹ 0.0432
∴ Cost of one share = 60 + 0.24 + 0.0432
= ₹ 60.2832
∴ Cost of 100 shares = 100 × 60.2832 = ₹ 6028.32
For sold shares:
FV = ₹ 10, MV = ₹ 50, brokerage = 0.4 %,
GST = 18%, Number of shares = 100
Brokerage per share = \(\frac { 0.4 }{ 100 } \) × 50 = ₹ 0.20
GST per share = \(\frac { 18 }{ 100 } \) × 0.20 = ₹ 0.036
Selling price per share = 50 – 0.2 – 0.036
= ₹ 49.764
Selling price of 100 shares = 100 × 49.764
= ₹ 4976.4
Dividend received 60 %
∴ Dividend per share = \(\frac { 60 }{ 100 } \) × 10 = ₹ 6
Dividend on 100 shares = 6 × 100 = ₹ 600
∴ Nalinitai’s income = 4976.4 + 600 = ₹ 5576.4
∴ Cost of 100 shares = ₹ 6028.32
∴ Loss = 6028.32 – 5576.4 = ₹ 451.92
∴ Nalinitai’s loss is ₹ 451.92.

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Practice Set 4.3 Class 10 Answers
• Practice Set 4.4 Class 10 Answers
• Problem Set 4A Class 10 Answers
• Problem Set 4B Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 4B Algebra 10th Class Maths Part 1 Answers Solutions Chapter 4 Financial Planning.

10th Standard Maths 1 Problem Set 4B Chapter 4 Financial Planning Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Problem Set 4B Chapter 4 Financial Planning Questions With Answers Maharashtra Board

Financial Planning Class 10 Problem Set 4b
Question 1.
Write the correct alternative for the following questions.

i. If the Face Value of a share is ₹ 100 and Market value is ₹ 75, then which of the following statement is correct?
(A) The share is at premium of ₹ 175
(B) The share is at discount of ₹ 25
(C) The share is at premium of ₹ 25
(D) The share is at discount of ₹ 75
Answer:
(B)

ii. What is the amount of dividend received per share of face value ₹ 10 if dividend declared is 50%.
(A) ₹ 50
(B) ₹ 5
(C) ₹ 500
(D) ₹ 100
Answer:
Dividend = 10 × \(\frac { 50 }{ 100 } \) = ₹ 5
(B)

iii. The NAV of a unit in mutual fund scheme is ₹ 10.65, then find the amount required to buy 500 such units.
(A) 5325
(B) 5235
(C) 532500
(D) 53250
Answer:
(A)

iv. Rate of GST on brokerage is _______
(A) 5%
(B) 12%
(C) 18%
(D) 28%
Answer:
(C)

v. To find the cost of one share at the time of buying the amount of Brokerage and GST is to be ______ MV of share.
(A) added to
(B) subtracted from
(C) Multiplied with
(D) divided by
Answer:
(A)

Problem Set 4b Algebra Class 10 Question 2. Find the purchase price of a share of FV ₹ 100 if it is at premium of ₹ 30. The brokerage rate is 0.3%.
Solution:
Here, Face Value of share = ₹ 100,
premium = ₹ 30, brokerage = 0.3%
MV = FV + Premium
= 100 + 30
= ₹ 130
Brokerage = 0.3% of MV
= \(\frac { 0.3 }{ 100 } \) × 130 = ₹ 0.39
Purchase price of a share = MV + Brokerage
= 130 + 0.39
= ₹ 130.39
Purchase price of a share is ₹ 130.39.

Question 3.
Prashant bought 50 shares of FV ₹ 100, having MV ₹ 180. Company gave 40% dividend on the shares. Find the rate of return on investment.
Solution:
Here, Number of shares = 50, FV = ₹ 100,
MV = ₹ 180, rate of dividend = 40%
∴ Sum invested = Number of shares × MV
= 50 × 180
= ₹ 9000
Dividend per share = 40% of FV
= \(\frac { 40 }{ 100 } \) × 100
Dividend = ₹ 40
∴ Total dividend on 50 shares = 50 × 40
= ₹ 2000

∴ Rate of return on investment is 22.2%.

Question 4.
Find the amount received when 300 shares of FV ₹ 100, were sold at a discount of ₹ 30.
Solution:
Here, FV = ₹ 100, number of shares = 300,
discount = ₹ 30
MV of 1 share = FV – Discount
= 100 – 30 = ₹ 70
∴ MV of 300 shares = 300 × 70
= ₹ 21,000
∴ Amount received is ₹ 21,000.

Question 5.
Find the number of shares received when ₹ 60,000 was invested in the shares of FV ₹ 100 and MV ₹ 120.
Solution:
Here, FV = ₹ 100, MV = ₹ 120,
Sum invested = ₹ 60,000

∴ Number of shares received were 500.

Question 6.
Smt. Mita Agrawal invested ₹ 10,200 when MV of the share is ₹ 100. She sold 60 shares when the MV was ₹ 125 and sold remaining shares when the MV was ₹ 90. She paid 0.1% brokerage for each trading. Find whether she made profit or loss? and how much?
Solution:
For purchasing shares:
Here, sum invested = ₹ 10,200, MV = ₹ 100

For selling shares:
60 shares sold at MV of ₹ 125.
∴ MV of 60 shares = 125 × 60
= ₹ 7500
Brokerage = \(\frac { 0.1 }{ 100 } \) × 7500 = ₹ 7.5
∴ Sale value of 60 shares = 7500 – 7.5 = ₹ 7492.5
Now, remaining shares = 102 – 60 = 42
But 42 shares sold at MV of ₹ 90.
∴ MV of 42 shares = 42 × 90 = ₹ 3780
∴ Brokerage = \(\frac { 0.1 }{ 100 } \) × 3780 = ₹ 3.78
∴ Sale value of 42 shares = 3780 – 3.78 = ₹ 3776.22
Total sale value = 7492.5 + 3776.22 = ₹ 11268.72
Since, Purchase value < Sale value
∴ Profit is gained.
∴ Profit = Sale value – Purchase value
= 11268.72 – 10210.2
= ₹ 1058.52
∴ Smt. Mita Agrawal gained a profit of ₹ 1058.52.

Question 7. Market value of shares and dividend declared by the two companies is given below.
Face value is same and it is 7 100 for both the shares. Investment in which company is more profitable?
i. Company A – ₹ 132,12%
ii Company B – ₹ 144,16%
Solution:
For company A:
FV = ₹ 100, MV = ₹ 132,
Rate of dividend = 12%
Dividend = 12% of FV

∴ Rate of return of company B is more.
∴ Investment in company B is more profitable.

Question 8. Shri. Aditya Sanghavi invested ₹ 50,118 in shares of FV ₹ 100, when the market value is ₹ 50. Rate of brokerage is 0.2% and Rate of GST on brokerage is 18%, then How many shares were purchased for ₹ 50,118?
Solution:
Here, FV = ₹ 100, MV = ₹ 50
Purchase value of shares = ₹ 50118,
Rate of brokerage = 0.2%, Rate of GST = 18%
Brokerage = 0.2% of MV


∴ 1000 shares were purchased for ₹ 50,118.

Question 9. Shri. Batliwala sold shares of ₹ 30,350 and purchased shares of ₹ 69,650 in a day. He paid brokerage at the rate of 0.1% on sale and purchase. 18% GST was charged on brokerage. Find his total expenditure on brokerage and tax.
Solution:
Total amount = sale value + Purchase value
= 30350 + 69650
= ₹ 1,00,000
Rate of Brokerage = 0.1 %
Brokerage = 0.1 % of 1,00,000
= \(\frac { 0.1 }{ 100 } \) × 1,00,000
= ₹ 100
Rate of GST = 18%
∴ GST = 18 % of brokerage
= \(\frac { 18 }{ 100 } \) × 100
∴ GST = ₹ 18
Total expenditure on brokerage and tax
= 100 + 18 = ₹ 118
∴ Total expenditure on brokerage and tax is ₹ 118.

Alternate Method:
Brokerage = 0.1 %, GST = 18%
At the time of selling shares:
Total sale amount of shares = ₹ 30,350
Brokerage = 0.1% of 30,350

For purchasing shares:
Total purchase amount of shares = ₹ 69,650
Brokerage = 0.1% of 69,650
= \(\frac { 0.1 }{ 100 } \) × 69650
= ₹ 69.65
GST = 18% of 69.65
= \(\frac { 18 }{ 100 } \) × 69.65
= ₹ 12.537
∴ Total expenditure on brokerage and tax = Brokerage and tax on selling + Brokerage and tax on purchasing
= (30.35 + 5.463) + (69.65 + 12.537)
= ₹ 118
∴ Total expenditure on brokerage and tax is ₹ 118.

Question 10. Sint. Aruna Thakkar purchased 100 shares of FV 100 when the MV is ₹ 1200. She paid brokerage at the rate of 0.3% and 18% GST on brokerage. Find the following –
i. Net amount paid for 100 shares.
ii. Brokerage paid on sum invested.
iii. GST paid on brokerage.
iv. Total amount paid for 100 shares.
Solution:
Here, FV = ₹ 100,
Number of shares = 100, MV = ₹ 1200
Brokerage = 0.3%, GST = 18%
i. Sum invested = Number of shares × MV
= 100 × 1200 = ₹ 1,20,000
∴ Net amount paid for 100 shares is ₹ 1,20,000.

ii. Brokerage = 0.3% of sum invested
= \(\frac { 0.3 }{ 100 } \) × 1,20,000 = ₹ 360
∴ Brokerage paid on sum invested is ₹ 360.

iii. GST = 18% of brokerage
= \(\frac { 18 }{ 100 } \) × 360 = ₹ 64.80
∴ GST paid on brokerage is ₹ 64.80.

iv. Total amount paid for 100 shares
= Sum invested + Brokerage + GST
= 1,20,000 + 360 + 64.80
= ₹ 1,20,424.80
∴ Total amount paid for 100 shares is ₹ 1,20,424.80.

Question 11. Smt. Anagha Doshi purchased 22 shares of FV ₹ 100 for Market Value of ₹ 660. Find the sum invested. After taking 20% dividend, she sold all the shares when market value was ₹ 650. She paid 0.1% brokerage for each trading done. Find the percent of profit or loss in the share trading. (Write your answer to the nearest integer)
Solution:
For purchasing shares:
Here, FV = ₹ 100, MV = ₹ 660, Number of shares = 22, rate of brokerage = 0.1%
Sum invested = MV × Number of shares
= 660 × 22
= ₹ 14,520
Brokerage = 0.1 % of sum invested
= \(\frac { 0.1 }{ 100 } \) × 14520 = ₹ 14.52
∴ Amount invested for 22 shares
= Sum invested + Brokerage
= 14520 + 14.52
= ₹ 14534.52
For dividend:
Rate of dividend = 20%
∴ Dividend per share = 20 % of FV

∴ Percentage of profit in the share trading is 1 % (nearest integer).

Alternate Method:
For purchasing share:
Here, FV = ₹ 100, MV = ₹ 660, Number of shares = 22, rate of brokerage = 0.1%
Sum invested = MV × Number of shares
= 660 × 22
= ₹ 14,520
Brokerage = 0.1 % of MV
= \(\frac { 0.1 }{ 100 } \) × 660 = ₹ 0.66
Amount invested for 1 share = 660 + 0.66
= ₹ 660.66
For dividend:
Rate of dividend = 20%
Dividend = 20% of FV = \(\frac { 20 }{ 100 } \) × 100 = ₹ 20
For selling share:
MV = ₹ 650, rate of brokerage = 0.1%
Brokerage = 0.1 % of MV
= \(\frac { 0.1 }{ 100 } \) × 650 = ₹ 0.65 100
Amount received after selling 1 share
= 650 – 0.65 = 649.35
∴ Amount received including divided
= selling price of 1 share + dividend per share
= 649.35 + 20
= ₹ 669.35
Since, income > Amount invested
∴ Profit is gained.
∴ profit = 669.35 – 660.66 = ₹ 8.69
Profit Percentage = \(\frac { 8.69 }{ 660.66 } \) × 100= 1.31%
∴ Percentage of profit in the share trading is 1 % (nearest integer).

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Practice Set 4.3 Class 10 Answers
• Practice Set 4.4 Class 10 Answers
• Problem Set 4A Class 10 Answers
• Problem Set 4B Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 4A Algebra 10th Class Maths Part 1 Answers Solutions Chapter 4 Financial Planning.

10th Standard Maths 1 Problem Set 4A Chapter 4 Financial Planning Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Problem Set 4A Chapter 4 Financial Planning Questions With Answers Maharashtra Board

Financial Planning Class 10 Problem Set 4a Question 1.
Write the correct alternative for each of the following.

i. Rate of GST on essential commodities is ______
(A) 5%
(B) 12%
(C) 0%
(D) 18%
Answer:
(C)

ii. The tax levied by the central government for trading within state is ______
(A) IGST
(B) CGST
(C) SGST
(D) UTGST
Answer:
(B)

iii. GST system was introduced in our country from ______
(A) 31^st March 2017
(B) 1^st April 2017
(C) 1^st January 2017
(D) 1^st July 2017
Answer:
(D)

iv. The rate of GST on stainless steel utensils is 18%, then the rate of state
GST is ______
(A) 18%
(B) 9%
(C) 36%
(D) 0.9%
Answer:
(B)

v. In the format of GSTIN there are ______ alpha-numerals.
(A) 15
(B) 10
(C) 16
(D) 9
Answer:
(A)

vi. When a registered dealer sells goods to another registered dealer under GST, then this trading is termed as ______
(A) BB
(B) B2B
(C) BC
(D) B2C
Answer:
(B)

10th Class Algebra Problem Set 4a Question 2.
A dealer has given 10% discount on a showpiece of ₹ 25,000. GST of 28% was charged on the discounted price. Find the total amount shown in the tax invoice. What is the amount of CGST and SGST.
Solution:
Printed price of showpiece = ₹ 25,000,
Rate of discount = 10%
∴ Amount of discount = 10% of printed price
= \(\frac { 10 }{ 100 } \) × 25000
= ₹ 2500
∴ Taxable value
= Printed price – discount
= 25,000 – 2500 = ₹ 22,500
Rate of GST = 28%
∴ Rate of CGST = 14% and
Rate of SGST = 14%
CGST = 14% of taxable value
= \(\frac { 14 }{ 100 } \) × 22500
= ₹ 3150
∴ CGST = SGST = ₹ 3150
∴ Total amount of tax invoice
= Taxable value + CGST + SGST
= 22500 + 3150 + 3150
= ₹ 28,800
∴ The total amount shown in the tax invoice is ₹ 28,800, and the amount of CGST and SGST is ₹ 3150 each.

Financial Planning Problem Set 4a Question 3.
A ready-made garment shopkeeper gives 5% discount on the dress of ₹ 1000 and charges 5% GST on the remaining amount, then what is the purchase price of the dress for the customer?
Solution:
Printed price of dress = ₹ 1000
Rate of discount = 5%
∴ Amount of discount = 5% of printed price
= \(\frac { 5 }{ 100 } \) × 1000
= ₹ 50
∴ Taxable value = Printed price – discount
= 1000 – 50
= ₹ 950
Rate of GST = 5%
∴ GST = 5% of taxable value
= \(\frac { 5 }{ 100 } \) × 950
∴ GST = ₹ 47.5
Purchase price of the dress
= Taxable value + GST
= 950 + 47.5 = ₹ 997.50
∴ Purchase price of the dress for the customer is ₹ 997.50.

Question 4.
A trader from Surat, Gujarat sold cotton clothes to a trader in Rajkot, Gujarat. The taxable value of cotton clothes is ₹ 2.5 lacs. What is the amount of GST at 5% paid by the trader in Rajkot?
Solution:
Taxable amount of cotton clothes = ₹ 2.5 lacs,
Rate of GST = 5%
GST = 5% of taxable amount
= \(\frac { 5 }{ 100 } \) × 2,50,000
= ₹ 12500
∴ Trader of Rajkot has to pay GST of ₹ 12,500.

Question 5.
Smt. Malhotra purchased solar panels for the taxable value of ₹ 85,000. She sold them for ₹ 90,000. The rate of GST is 5%. Find the ITC of Smt. Malhotra. What is the amount of GST payable by her?
Solution:
Output tax = 5% of 90000
= \(\frac { 5 }{ 100 } \) × 90000
= ₹ 4500
Input tax = 5% of 85000
= \(\frac { 5 }{ 100 } \) × 85000
= ₹ 4250
ITC = ₹ 4250.
∴ GST payable = Output tax – ITC
= 4500 – 4250
GST payable = ₹ 250
∴ ITC of Smt. Malhotra is ₹ 4250 and amount of GST payable by her is ₹ 250.

Question 6.
A company provided Z-security services for the taxable value of ₹ 64,500. Rate of GST is 18%. Company had paid GST of ₹ 1550 for laundry services and uniforms etc. What is the amount of ITC (input Tax Credit)? Find the amount of CGST and SGST payable by the company.
Solution:
Output tax = 18% of 64500
= \(\frac { 18 }{ 100 } \) × 64500
= ₹ 11610
Input tax = ₹ 1550
GST payable = Output tax – ITC
= 11610 – 1550
∴ GST payable = ₹ 10060

∴ Amount of ITC is ₹ 1550. Amount of CGST and SGST payable by the company is ₹ 5030 each.

Question 7.
A dealer supplied Walky-Talky set of ₹ 84,000 (with GST) to police control room. Rate of GST is 12%. Find the amount of state and central GST charged by the dealer. Also find the taxable value of the set.
Solution:
Let the amount of GST be ₹ x.
Price of walky talky with GST = ₹ 84,000
Taxable value of walky talky = ₹ (84,000 – x)
Now, GST = 12% of taxable value


∴ Amount of state and central GST charged by the dealer is ₹ 4,500 each. Taxable value of the set is ₹ 75,000.

Question 8.
A wholesaler purchased electric goods for the taxable amount of ₹ 1,50,000. He sold it to the retailer for the taxable amount of ₹ 1,80,000. Retailer sold it to the customer for the taxable amount of ₹ 2,20,000. Rate of GST is 18%. Show the computation of GST in tax invoices of sales. Also find the payable CGST and payable SGST for wholesaler and retailer.
Solution:
For Wholesaler:
Output tax = 18% of ₹ 1,80,000

Statement of GST payable at each stage of trading:

Question 9.
Anna Patil (Thane, Maharashtra) supplied vacuum cleaner to a shopkeeper in Vasai (Mumbai) for the taxable value of ₹ 14,000, and GST rate of 28% . Shopkeeper sold it to the customer at the same GST rate for ₹ 16,800 (taxable value). Find the following:
i. Amount of CGST and SGST shown in the tax invoice issued by Anna Patil.
ii. Amount of CGST and SGST charged by the shopkeeper in Vasai.
iii. What is the CGST and SGST payable by shopkeeper in Vasai at the time of filing the return.
Solution:
i. For Anna Patil:
Output tax = 28% of 14,000
= \(\frac { 18 }{ 100 } \) × 14000
= ₹ 3920
∴ CGST = SGST = \(\frac { GST }{ 2 } \)
= \(\frac { 3920 }{ 2 } \)
= ₹ 1960
∴ Amount of CGST and SGST shown in the tax invoice issued by Anna Patil is ₹ 1960 each.

ii. For Shopkeeper in Vasai:
Output tax = 28% of 16,800
= \(\frac { 28 }{ 100 } \) × 16,800
= ₹ 4704
∴ CGST = SGST = \(\frac { GST }{ 2 } \)
= \(\frac { 4704 }{ 2 } \)
= ₹ 2352
∴ Amount of CGST and SGST charged by the shopkeeper in Vasai is ₹ 2352 each.

iii. ITC = ₹ 3920
GST payable by shopkeeper in Vasai
= Output tax – ITC
= 4704 – 3920
= ₹ 784

∴ CGST and SGST payable by shopkeeper in Vasai at the time of filing the return is ₹ 392 each.

Question 10.
For the given trading chain prepare the tax invoice I, II, III. GST at the rate of 12% was charged for the article supplied.

i. Prepare the statement of GST payable under each head by the wholesaler, distributor and retailer at the time of filing the return to the government.
ii. At the end what amount is paid by the consumer?
iii. Write which of the invoices issued are B2B and B2C.
Solution:
i. For wholesaler:
Output tax = 12% of 5000
= \(\frac { 12 }{ 100 } \) × 5000 = ₹ 600
For Distributor:
Output Tax = 12% of 6000
= \(\frac { 12 }{ 100 } \) × 6000 = ₹ 720
ITC = ₹ 600
∴ GST payable = Output tax – ITC
= 720 – 600
= ₹ 120
For Retailer:
Output tax = 12 % of 6500
= \(\frac { 12 }{ 100 } \) × 6500 = ₹ 780
ITC = ₹ 720
∴ GST payable = Output tax – ITC
= 780 – 720 = ₹ 60
Statement of GST payable at each stage of trading:

ii. ITC for consumer = ₹ 780
∴ Amount paid by consumer
= taxable value + ITC
= 6500 + 780
= ₹ 7280
∴ Amount paid by the consumer is ₹ 7280.

iii. B2B = Wholesaler to Distributor
B2B = Distributor to Retailer
B2C = Retailer to Consumer

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Practice Set 4.3 Class 10 Answers
• Practice Set 4.4 Class 10 Answers
• Problem Set 4A Class 10 Answers
• Problem Set 4B Class 10 Answers

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 4.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 4 Financial Planning.

10th Standard Maths 1 Practice Set 4.2 Chapter 4 Financial Planning Textbook Answers Maharashtra Board

Class 10 Maths Part 1 Practice Set 4.2 Chapter 4 Financial Planning Questions With Answers Maharashtra Board

Question 1. ‘Chetana Store’ paid total GST of ₹ 1,00,500 at the time of purchase and collected GST ₹ 1,22,500 at the time of sale during 1^st of July 2017 to 31^st July 2017. Find the GST payable by Chetana Stores.
Answer:
Output tax (Tax collected at the time of sale)
= ₹ 1,22,500
Input tax (Tax paid at the time of purchase)
= ₹ 1,00,500
ITC (Input Tax credit) = ₹ 1,00,500.
GST payable = Output tax – ITC
= 1,22,500 – 1,00,500
= ₹ 22,000
GST payable by Chetana stores is ₹ 22,000.

Question 2. Nazama is a proprietor of a firm, registered under GST. She has paid GST of ₹ 12,500 on purchase and collected ₹ 14,750 on sale. What is the amount of ITC to be claimed? What is the amount of GST payable?
Solution:
Output tax = ₹ 14,750
Input tax = ₹ 12,500
∴ ITC for Nazama = ₹ 12,500.
∴ GST payable = Output tax – ITC
= 14750 – 12500
= ₹ 2250
∴ Amount of ITC to be claimed is ₹ 12,500 and amount of GST payable is ₹ 2250.

Question 3. Amir Enterprise purchased chocolate sauce bottles and paid GST of ₹ 3800. He sold those bottles to Akbari Bros, and collected GST of ₹ 4100. Mayank Food Corner purchased these bottles from Akbari Bros, and paid GST of ₹ 4500. Find the amount of GST payable at every stage of trading and hence find payable CGST and SGST.
Solution:
For Amir Enterprise:
Output tax = ₹ 4100
Input tax = ₹ 3800
ITC for Amir enterprise = ₹ 3800.
∴ GST payable = Output tax – ITC
= 4100 – 3800
= ₹ 300
For Akbari Bros.:
Output tax = ₹ 4500
Input tax = ₹ 4100
ITC for Akbari Bros = ₹ 4100.
GST payable = Output tax – ITC
= 4500 – 4100 = ₹ 400
∴ Statement of GST payable at every stage of trading:

Question 4. Malik Gas Agency (Chandigarh Union Territory) purchased some gas cylinders for industrial use for ₹ 24,500, and sold them to the local customers for ₹ 26,500. Find the GST to be paid at the rate of 5% and hence the CGST and UTGST to be paid for this transaction, (for Union Territories there is UTGST instead of SGST.)
Solution:
For Malik Gas Agency:
Output tax = 5% of 26500
= \(\frac { 5 }{ 100 } \) × 26500
= ₹ 1325
Input tax = 5% of 24500
= \(\frac { 5 }{ 100 } \) × 24500
= ₹ 1225
ITC for Malik Gas Agency = ₹ 1225.
∴ GST payable = Output tax – ITC
= 1325 – 1225
= ₹ 100

∴ CGST = UTGST = ₹ 50
∴ The GST to be paid at the rate of 5% is ₹ 100 and hence, CGST and UTGST paid for the transaction is ₹ 50 each.

Question 5.
M/s Beauty Products paid 18% GST on cosmetics worth ₹ 6000 and sold to a customer for ₹ 10,000. What are the amounts of CGST and SGST shown in the tax invoice issued?
Solution:
Output tax = 18% of 10,000
= \(\frac { 18 }{ 100 } \) × 10,000
= ₹ 1800

∴ Amount of CGST and SGST shown in the tax invoice issued is ₹ 900 each.

Question 6.
Prepare Business to Consumer (B2C) tax invoice using given information. Write the name of the supplier, address, state, Date, Invoice number, GSTIN etc. as per your choice.
Supplier: M/s ______ Address _______ State _______ Date _______ Invoice No. _______ GSTIN _______
Particulars
Rate of Mobile Battery ₹ 200 Rate of GST 12% HSN 8507 1 PC
Rate of Headphone ₹750 Rate of GST 18% HSN 8518 1 Pc
Solution:
Rate of Mobile Battery = ₹200
CGST = 6% of 200
= \(\frac { 6 }{ 100 } \) × 200
= ₹ 12
∴ CGST = SGST = ₹ 12

Rate of Headphone = ₹ 750
COST = 9% of 750
= \(\frac { 9 }{ 100 } \) × 750
= ₹ 67.5
∴ CGST = SGST = ₹ 67.5

Question 7.
Prepare Business to Business (B2B) Tax Invoice as per the details given below, name of the supplier, address, Date etc. as per your choice.
Supplier – Name, Address, State, GSTIN, Invoice No., Date
Recipient – Name, Address, State, GSTIN,
Items:
i. Pencil boxes 100, HSN – 3924, Rate – ₹ 20, GST 12%
ii. Jigsaw Puzzles 50, HSN 9503, Rate – ₹ 100 GST 12%.
Solution:
Cost of 100 Pencil boxes
= 20 × 1oo
= ₹ 2000
CGST = 6% of 2000
= \(\frac { 6 }{ 100 } \) × 2000
= ₹ 120
∴ CGST = SGST = ₹ 120

Cost of 50 Jigsaw Puzzles = 100 × 50
= ₹ 5000
CGST = 6% of 5000
= \(\frac { 6 }{ 100 } \) × 5000
= ₹ 300
CGST – SGST = ₹ 300

Question 1.
Suppose a manufacturer sold a cycle for a taxable value of ₹ 4000 to the wholesaler. Wholesaler sold it to the retailer for ₹ 4800 (taxable value). Retailer sold it to a customer for ₹ 5200 (taxable value). Rate of GST is 12%. Complete the following activity to find the payable CGST and SGST at each stage of trading. (Textbook pg. no. 92)
Solution:

GST payable by manufacturer = ₹ 480
Output tax of wholesaler
= 12% of 4800 = \(\frac { 12 }{ 100 } \) × 4800 = ₹ 576
∴ GST payable by wholesaler
= Output tax – Input tax
= 576 – 480
= ₹ 96
Output tax of retailer = 12% of 5200

Question 2. Suppose in the month of July the output tax of a trader is equal to the input tax, then what is his payable GST?(Textbook pg. no. 93)
Answer:
Here, output tax is same as input tax.
∴ Trader payable GST will be zero.

Question 3.
Suppose in the month of July output tax of a trader is less than the input tax then how to compute his GST? (Textbook pg. no. 93)
Answer:
If output tax of a trader in a particular month is less than his input tax, then he won’t be able to get entire credit for his input tax. In such a case his balance credit will be carried forward and adjusted against the subsequent transactions.

Class 10 Maths Digest

• Practice Set 4.1 Class 10 Answers
• Practice Set 4.2 Class 10 Answers
• Practice Set 4.3 Class 10 Answers
• Practice Set 4.4 Class 10 Answers
• Problem Set 4A Class 10 Answers
• Problem Set 4B Class 10 Answers