Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 5 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 5 Probability.
10th Standard Maths 1 Problem Set 5 Chapter 5 Probability Textbook Answers Maharashtra Board
Class 10 Maths Part 1 Problem Set 5 Chapter 5 Probability Questions With Answers Maharashtra Board
Question 1.
Choose the correct alternative answer for each of the following questions.
i. Which number cannot represent a probability?
(A) \(\frac { 2 }{ 3 } \)
(B) 1.5
(C) 15%
(D) 0.7
Answer:
The probability of any 0 to 1 or 0% to 100%. event is from
(B)
ii. A die is rolled. What is the probability that the number appearing on upper face is less than 3?
(A) \(\frac { 1 }{ 6 } \)
(B) \(\frac { 1 }{ 3 } \)
(C) \(\frac { 1 }{ 2 } \)
(D) 0
Answer:
(B)
iii. What is the probability of the event that a number chosen from 1 to 100 is a prime number?
(A) \(\frac { 1 }{ 5 } \)
(B) \(\frac { 6 }{ 25 } \)
(C) \(\frac { 1 }{ 4 } \)
(D) \(\frac { 13 }{ 50 } \)
Answer:
n(S) = 100
Let A be the event that the number chosen is a prime number.
∴ A = {2, 3, 5. , 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}
∴ n(A) = 25
∴ P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac { 25 }{ 100 } \) = \(\frac { 1 }{ 4 } \)
(C)
iv. There are 40 cards in a bag. Each bears a number from 1 to 40. One card is drawn at random. What is the probability that the card bears a number which is a multiple of 5?
(A) \(\frac { 1 }{ 5 } \)
(B) \(\frac { 3 }{ 5 } \)
(C) \(\frac { 4 }{ 5 } \)
(D) \(\frac { 1 }{ 3 } \)
Answer:
(A)
v. If n(A) = 2, P(A) = \(\frac { 1 }{ 5 } \), then n(S) = ?
(A) 10
(B) \(\frac { 5 }{ 2 } \)
(C) \(\frac { 2 }{ 5 } \)
(D) \(\frac { 1 }{ 3 } \)
Answer:
(A)
Question 2.
Basketball players John, Vasim, Akash were practising the ball drop in the basket. The probabilities of success for John, Vasim and Akash are \(\frac { 4 }{ 5 } \), 0.83 and 58% respectively. Who had the greatest probability of success ?
Solution:
The probability that the ball is dropped in the basket by John = \(\frac { 4 }{ 5 } \) = 0.80
The probability that the ball is dropped in the basket by Vasim = 0.83
The probability that the ball is dropped in the basket by Akash = 58% = \(\frac { 58 }{ 100 } \) = 0.58
0.83 > 0.80 > 0.58
∴ Vasim has the greatest probability of success.
Question 3.
In a hockey team there are 6 defenders , 4 offenders and 1 goalie. Out of these, one player is to be selected randomly as a captain. Find the probability of the selection that:
i. The goalie will be selected.
ii. A defender will be selected.
Solution:
Total number of players in the hockey team
= 6 + 4 + 1 = 11
∴ n(S) = 11
i. Let A be the event that the captain selected will be a goalie.
There is only one goalie in the hockey team.
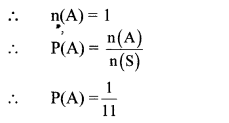
ii. Let B be the event that the captain selected will be a defender.
There are 6 defenders in the hockey team.
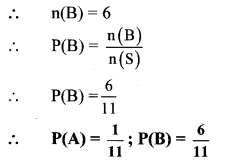
Question 4.
Joseph kept 26 cards in a cap, bearing one English alphabet on each card. One card is drawn at random. What is the probability that the card drawn is a vowel card ?
Solution:
Each card bears an English alphabet.
∴ n(S) = 26
Let A be the event that the card drawn is a vowel card.
There are 5 vowels in English alphabets.
∴ A = {a, e, i, o, u}
∴ n(A) = 5
![]()
∴ The probability that the card drawn is a vowel card is \(\frac { 5 }{ 26 } \).
Question 5.
A balloon vendor has 2 red, 3 blue and 4 green balloons. He wants to choose one of them at random to give it to Pranali. What is the probability of the event that Pranali gets,
i. a red balloon.
ii. a blue balloon,
iii. a green balloon.
Solution:
Let the 2 red balloon be R1, R2,
3 blue balloons be B1, B2, B3, and
4 green balloons be G1, G2, G3, G4.
∴ Sample space
S = {R1, R2, B1, B2, B3, G1, G2, G3, G4}
∴ n(S) = 9
i. Let A be the event that Pranali gets a red balloon.
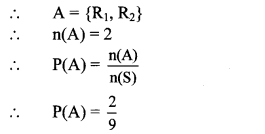
∴ The probability that Pranali gets a red balloon is \(\frac { 2 }{ 9 } \)
ii. Let B be the event that Pranali gets a blue balloon.
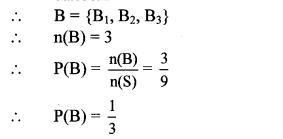
∴ The probability that Pranali gets a blue balloon is \(\frac { 1 }{ 3 } \).
iii. Let C be the event that Pranali gets a green balloon.
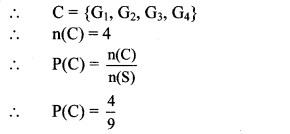
∴ The probability that Pranali gets a green balloon is \(\frac { 4 }{ 9 } \).
Question 6.
A box contains 5 red, 8 blue and 3 green pens. Rutuja wants to pick a pen at random. What is the probability that the pen is blue?
Solution:
Let 5 red pens be R1, R2, R3, R4, R5.
8 blue pens be B1, B2, B3, B4, B5, B6, B7, B8. and
3 green pens be G1, G2, G3.
∴ Sample space
S = {R1, R2, R3, R4, R5, B1, B2, B3, B4, B5, B6, B7, B8, G1, G2, G3}
∴ n(S) = 16
Let A be the event that Rutuja picks a blue pen.
∴ A = {B1, B2, B3, B4, B5, B6, B7, B8}
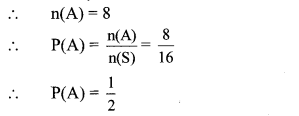
∴ The probability that Rutuja picks a blue pen is \(\frac { 1 }{ 2 } \).
Question 7.
Six faces of a die are as shown below.
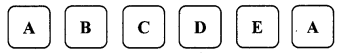
If the die is rolled once, find the probability of
i. ‘A’ appears on upper face.
ii. ‘D’ appears on upper face.
Solution:
Sample space
S = {A, B, C, D, E, A}
∴ n (S) = 6
i. Let R be the event that ‘A’ appears on the upper face.
∴ R = {A, A}
∴ n(R) = 2
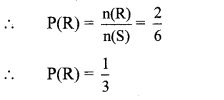
ii. Let Q be the event that ‘D’ appears on the upper face.
Total number of faces having ‘D’ on it = 1
Q = {D}
∴ n(Q) = 1
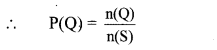
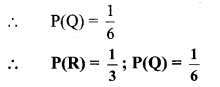
Question 8.
A box contains 30 tickets, bearing only one number from 1 to 30 on each. If one ticket is drawn at random, find the probability of an event that the ticket drawn bears
i. an odd number.
ii. a complete square number.
Solution:
Sample space,
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}
∴ n(S) = 30
i. Let A be the event that the ticket drawn bears an odd number.
∴ A = {1,3,5,7,9,11,13,15,17,19,21, 23,25,27,29}
∴ n(A) =15
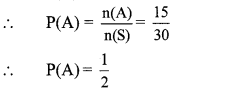
ii. Let B be the event that the ticket drawn bears a complete square number.
∴ B = {1,4,9,16,25}
∴ n(B) = 5

Question 9.
Length and breadth of a rectangular garden are 77 m and 50 m. There is a circular lake in the garden having diameter 14 m. Due to wind, a towel from a terrace on a nearby building fell into the garden. Then find the probability of the event that it fell in the lake.
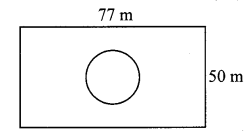
Solution:
Area of the rectangular garden
= length × breadth
= 77 × 50
∴ Area of the rectangular garden = 3850 sq.m
Radius of the lake = \(\frac { 14 }{ 2 } \) = 7 m

∴ The probability of the event that the towel tell in the lake is \(\frac { 1 }{ 25 } \).
Question 10.
In a game of chance, a spinning arrow comes to rest at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8. All these are equally likely outcomes. Find the probability that it will rest at
i. 8.
ii. an odd number.
iii. a number greater than 2.
iv. a number less than 9.
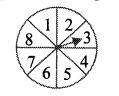
Solution:
Sample space (S) = {1,2, 3, 4, 5, 6, 7, 8}
∴ n(S) = 8
i. Let A be the event that the spinning arrow comes to rest at 8.
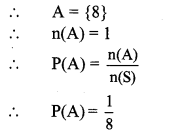
ii. Let B be the event that the spinning arrow comes to rest at an odd number.
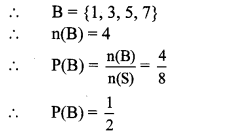
iii. Let C be the event that the spinning arrow comes to rest at a number greater than 2.
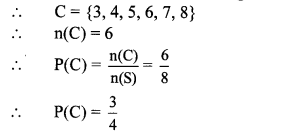
iv. Let D be the event that the spinning arrow comes to rest at a number less than 9.
∴ D = {1,2, 3, 4, 5, 6, 7, 8}
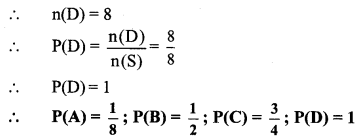
Question 11.
There are six cards in a box, each bearing a number from 0 to 5. Find the probability of each of the following events, that a card drawn shows,
i. a natural number.
ii. a number less than 1.
iii. a whole number.
iv. a number greater than 5.
Solution:
Sample space (S) = {0, 1, 2, 3, 4, 5}
∴ n(S) = 6
i. Let A be the event that the card drawn shows a natural number.
∴ A = {1,2,3,4,5}
∴ n(A) = 5
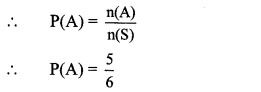
ii. Let B be the event that the card drawn shows a number less than 1.
∴ B = {0}
∴ n(B) = 1
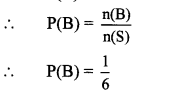
iii. Let C be the event that the card drawn shows a whole number.
∴ C = {0,1, 2, 3, 4, 5}
∴ n(C) = 6
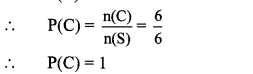
iv. Let D be the event that the card drawn shows a number greater than 5.
Here, the greatest number is 5.
∴ Event D is an impossible event.
∴ D = { }
∴ n(D) = 0
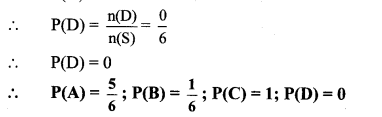
Question 12.
A bag contains 3 red, 3 white and 3 green balls. One ball is taken out of the bag at random. What is the probability that the ball drawn is:
i. red.
ii. not red.
iii. either red or white.
Solution:
Let the three red balls be R1, R2, R3, three white balls be W1, W2, W3 and three green balls be G1, G2, G3.
∴ Sample space,
S = {R1, R2, R3, W1, W2, W3, G1, G2, G3}
∴ n(S) = 9
i. Let A be the event that the ball drawn is red.
∴ A = {R1, R2, R3}
∴ n(A) = 3
![]()
ii. Let B be the event that the ball drawn is not red.
B = {W1,W2,W3,G1,G2,G3}
∴ n(B) = 6
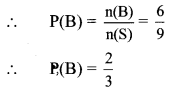
iii. Let C be the event that the ball drawn is red or white.
∴ C = {R1, R2, R3, W1, W2, W3}
∴ n(C) = 6
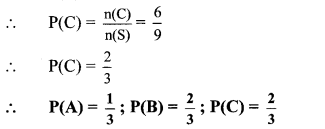
Question 13.
Each card bears one letter from the word ‘mathematics’. The cards are placed on a table upside down. Find the probability that a card drawn bears the letter ‘m’.
Solution:
Sample space
= {m, a, t, h, e, m, a, t, i, c, s}
∴ n(S) = 11
Let A be the event that the card drawn bears the letter ‘m’
∴ A = {m, m}
∴ n(A) = 2
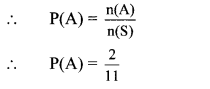
∴ The probability that a card drawn bears letter ‘m’ is \(\frac { 2 }{ 11 } \).
Question 14.
Out of 200 students from a school, 135 like Kabaddi and the remaining students do not like the game. If one student is selected at random from all the students, find the probability that the student selected dosen’t like Kabaddi.
Solution:
Total number of students in the school = 200
∴ n(S) = 200
Number of students who like Kabaddi = 135
∴ Number of students who do not like Kabaddi
= 200 – 135 = 65
Let A be the event that the student selected does not like Kabaddi.
∴ n(A) = 65
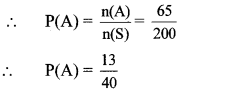
∴ The probability that the student selected doesn’t like kabaddi is \(\frac { 13 }{ 40 } \).
Question 15.
A two digit number is to be formed from the digits 0, 1, 2, 3, 4. Repetition of the digits is allowed. Find the probability that the number so formed is a:
i. prime number.
ii. multiple of 4.
iii multiple of 11.
Solution:
Sample space
(S) = {10, 11, 12, 13, 14,
20, 21, 22, 23, 24,
30, 31, 32, 33, 34,
40, 41, 42, 43, 44}
∴ n(S) = 20
i. Let A be the event that the number so formed is a prime number.
∴ A = {11,13,23,31,41,43}
∴ n(A) = 6
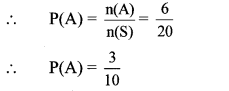
ii. Let B be the event that the number so formed is a multiple of 4.
∴ B = {12,20,24,32,40,44}
∴ n(B) = 6
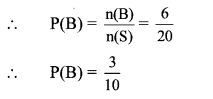
iii. Let C be the event that the number so formed is a multiple of 11.
∴ C = {11,22,33,44}
∴ n(C) = 4
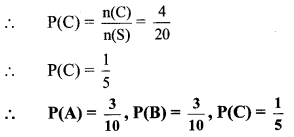
Question 16.
The faces of a die bear numbers 0,1, 2, 3,4, 5. If the die is rolled twice, then find the probability that the product of digits on the upper face is zero.
Solution:
Sample space,
S = {(0, 0), (0,1), (0,2),
(1,0), (1,1), (1,2),
(2,0), (2,1), (2,2),
(3.0), (3,1), (3,2),
(4.0), (4,1), (4,2),
(5.0), (5,1), (5,2),
∴ n(S) = 36
Let A be the event that the product of digits on the upper face is zero.
∴ A = {(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (1,0), (2, 0), (3,0), (4, 0), (5,0)}
∴ n(A) = 11
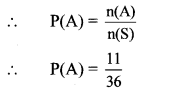
∴ The probability that the product of the digits on the upper face is zero is \(\frac { 11 }{ 36 } \).
Class 10 Maths Digest