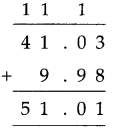
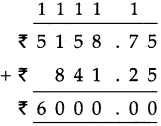
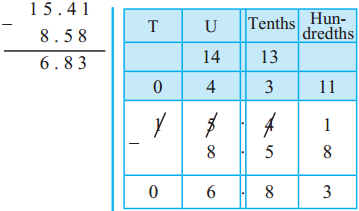
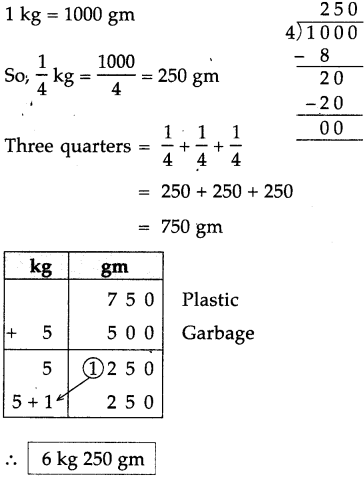
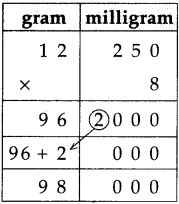
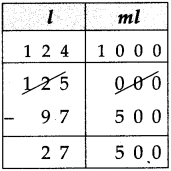
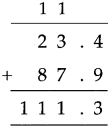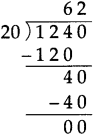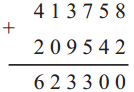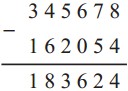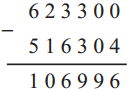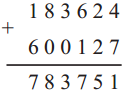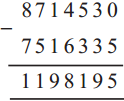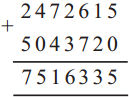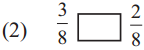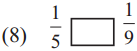Measuring Time Class 5 Problem Set 43 Question Answer Maharashtra Board
Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 10 Measuring Time Problem Set 43 Textbook Exercise Important Questions and Answers.
Std 5 Maths Chapter 10 Measuring Time
Question 1.
Write the time shown in each clock in the box given below it.
(1) 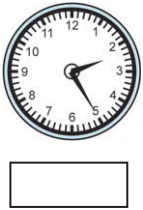
Answer:
25 minutes past 2
![]()
(2) 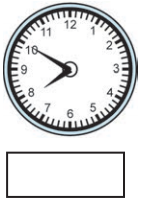
Answer:
50 minutes past 7
(3) 
Answer:
5 minutes past 8
(4) 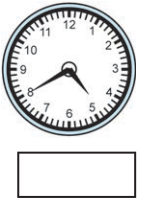
Answer:
40 minutes past 4
![]()
Question 2.
Draw the hands of the clock to show the time given in the box.
(1) 
Four-thirty
Answer:
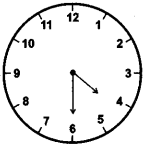
(2) 
Quarter past nine
Answer:
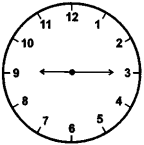
![]()
(3) 
Quarter to five
Answer:
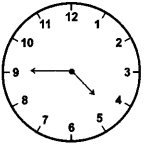
(4) 
20 minutes past 11
Answer:
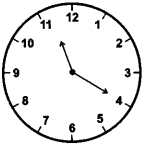
![]()
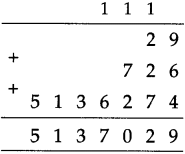
Question 3.
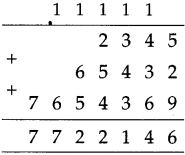
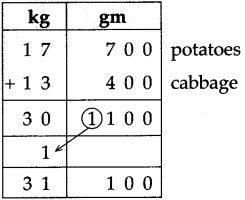
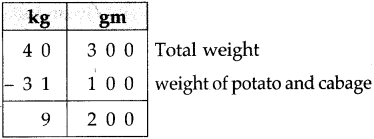
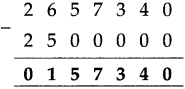
If a bus that leaves Nashik at 5 o’clock in the morning reaches Pune that same day at ten-thirty in the morning, how long does the journey take?
Solution:
| Hrs. | Min. |
| 10 – 5 |
30 00 |
| 5 | 30 |
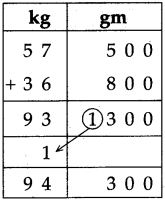
∴ Bus took 5 hrs 30 min
Question 4.
A play that was to start at nine fifteen at night was delayed by half an hour because of a power outage. What time did the play start?
Solution:
| Hrs. | Min. |
| 9 + |
15 30 |
| 9 | 45 |
∴ Play started 9:45 at night
![]()
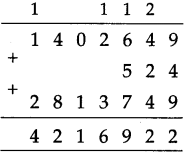
Question 5.
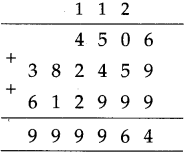
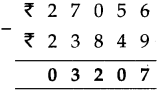
If a train leaves Mumbai at ten-fifteen at night and reaches Nagpur at one forty the next afternoon, how long does the journey take?
Solution:
Ten fifteen at night to 12 mid night is
| Hrs. | Min. |
| 1 2 -10 | 0 0 1 5 |
| 1 | 4 5 |
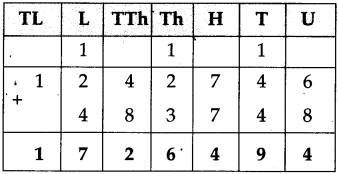
12 mid night to next 1:40 afternoon = 13 hours 40 minutes
Total times
| Hrs. | Min. |
| 1 + 13 |
45 40 |
| 15 | 25 |
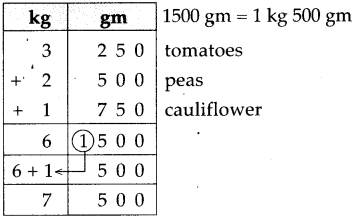
∴ Total time of the journey is 15 hrs. 25 min:
![]()
Learning about seconds
This clock is showing 5 minutes past 3. We know this because of the position of the hour and minute hands. There is another hand in the picture called the second hand. This hand moves swiftly. The second is a very small unit used to measure time less than a minute.
The face of a clock is a circle divided into 60 equal parts. When the second-hand moves one part, it takes one second. When it completes one round of the clock face, it moves across all 60 parts. This takes 60 seconds. In the same time, the minute hand moves one place, which means that one minute is over.
It means that, 1 minute is equal to 60 seconds.
1 minute = 60 seconds
The clock in the picture above shows 5 minutes and 50 seconds past 3.
 20 minutes and 10 seconds past 7
20 minutes and 10 seconds past 7
 15 minutes and 40 seconds past 10
15 minutes and 40 seconds past 10
![]()
Seconds are used on various occasions such as measuring temperature with a thermometer, measuring heartbeats or timing a race.
Ante meridiem and post meridiem
Shripati was sitting at home at night, tired. There were guests at home. They asked, “You must have worked very hard in the fields today. How long were you working?”
Shripati said, “I was in the field from six o’clock to eight o’clock.” Someone asked, “You’re this tired even though you were in the field for only two hours?”
Shripati said, “No, no, I was in the field from 6 in the morning till 8 at night! Now tell me how many hours I spent in the field.”
The guests had not understood what Shripati said at first. To avoid such mistakes, it has been internationally agreed that as the clock strikes 12 midnight, one day ends and the next day begins. From that moment on, the clock shows the time for the next day. When one hour passes after 12 midnight, it is 1’o’clock. After that, it is 2, 3, 4, …, 12 o’clock in serial order. After 12 noon, again it is 1, 2, 3, …, 12 o’clock in serial order. The time before 12 noon is stated as ante meridiem or am. The time after 12 noon is stated as post meridiem or pm.
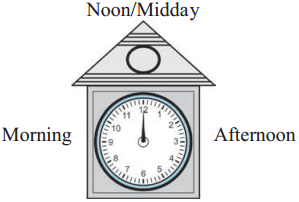
![]()
This method of measuring time is called the 12 hour clock.
Shripati was in the field from 6 am to 8 pm or for 14 hours.
The 24 hour clock
The 24 hour clock is used to avoid this division of the day into ante meridiem and post meridiem. This method is used in timetables for trains, planes, buses and long distance boat journeys. In this method, instead of starting again from 1, 2, 3 after 12 noon, we continue with 13, 14, 15,…,24. In a 24 hour digital watch, time is shown only in the form of numbers. It does not have hands. In such a clock, 20 minutes past 6 in the morning is shown as ‘6:20’ and 20 minutes past 6 in the evening is shown as ‘18:20’.
23:59 means 59 minutes after 23 and one minute later, 24 hours will be complete. The digital clock will show this time as 00:00 at midnight and the day will change. At that time, a 12 hour clock shows 12 midnight.
Study the following table to see how different times of the day are shown in the 12 hour and 24 hour clocks.

![]()
The timetables of some trains going from Badnera to Nagpur are given below. Observe the use of the 24 hour clock in the timetable.
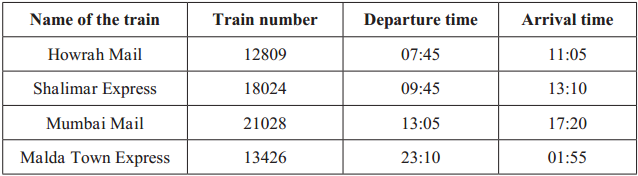
Measuring Time Problem Set 43 Additional Important Questions and Answers
Write the time shown in each clock in the box given below it.
(1) 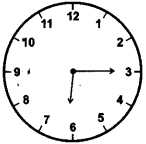
Answer:
15 minutes past 6
(2) 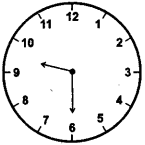
Answer:
30 minutes past 9
![]()
Draw the hands of the clock to sho the time given in the box.
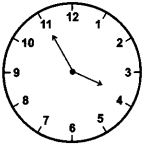
(1) 5 minutes to four
Answer:
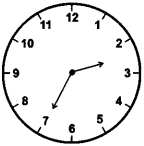
(2) 35 minutes past to 2
Answer:
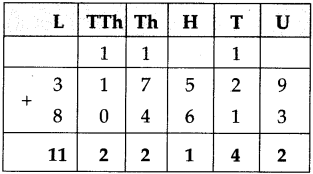
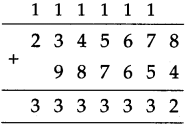
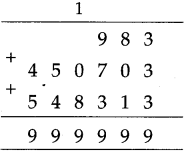
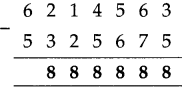
(3) Sujata left home 6:30 and returned at 11. How much time did she spend away from home?
Solution:
| Hrs. | Min* |
| 11 – 6 |
00 30 |
| 4 | 30 |
∴ 4 hrs. 30min. spent away from home.
![]()
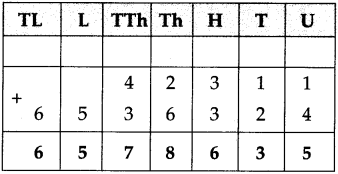
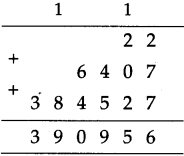
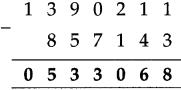
(4) A speech that started at 4:20 in the afternoon ended at 5:45. How long was the speech?
Solution:
| Hrs. | Min. |
| 5 + 4 |
4.5 20 |
| 1 | 25 |
∴ Speech was for 1 hr. 25 min.
Class 5 Maths Solution Maharashtra Board