Prasanna

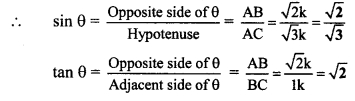
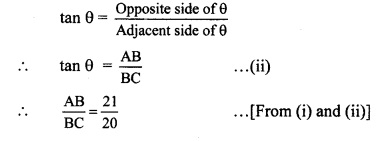
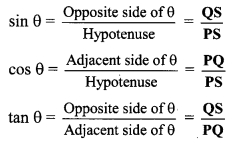
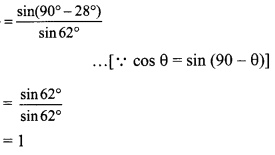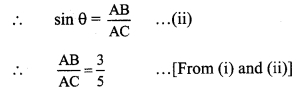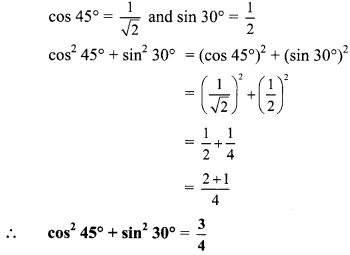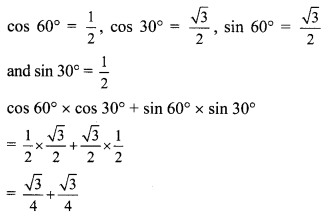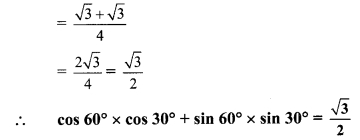Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 17.1 8th Std Maths Answers Solutions Chapter 17 Circle: Chord and Arc.

Circle: Chord and Arc Class 8 Maths Chapter 17 Practice Set 17.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 17.1 Chapter 17 Solutions Answers

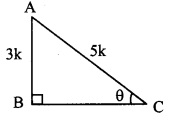
Question 1.
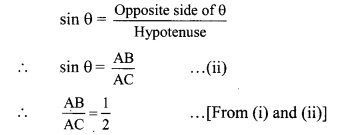
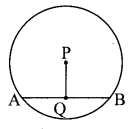
In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⊥ chord AB, then find l(QB)

Solution:
seg PQ ⊥ chord AB … [Given]
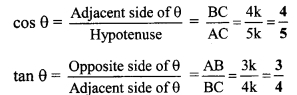
∴l(QB) = \(\frac { 1 }{ 2 }\) l(AB)… [Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(QB) = \(\frac { 1 }{ 2 }\) x 13 …[∵ l(AB) = 13 cm]
∴l(QB) = 6.5 cm

Question 2.
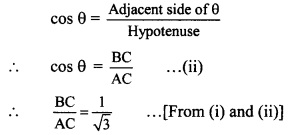
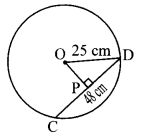
Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if length of the chord is 48 cm.

Solution:
seg OP ⊥ chord CD … [Given]
∴l(PD) = \(\frac { 1 }{ 2 }\) l(CD) … [Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴l(PD) = \(\frac { 1 }{ 2 }\) x 48 …[∵ l(CD) = 48 cm]
∴l(PD) = 24 cm …(i)
In ∆OPD, m∠OPD = 90°
∴[l(OD)]² = [l(OP)]² + [l(PD)]² … [Pythagoras theorem]
∴(25)² = [l(OP)]² + (24)² … [From (i) and l(OD) = 25 cm]
∴(25)² – (24)² = [l(OP)]²
∴(25 + 24) (25 – 24) = [l(OP)]² …[∵ a² – b² = (a + b) (a – b)]
∴49 x 1 = [l(OP)]²
∴[l(OP)]² = 49
∴l(OP) = √49 …[Taking square root of both sides]
∴l(OP) = 7 cm
∴The distance of the chord from the centre of the circle is 7 cm.

Question 3.
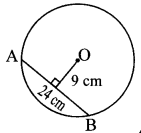
O is centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the

Solution:
Let seg OP ⊥ chord AB
∴ l(AP) = \(\frac { 1 }{ 2 }\) l(AB) … [Perpendicular drawn from the centre of a circle to its chord bisects the chord]

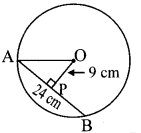
∴l(AP) = \(\frac { 1 }{ 2 }\) x 24 …[∵ l(AB) = 24 cm]
∴l(AP) = 12 cm …(i)
In ∆OPA, m∠OPA = 90°
∴[l(AO)]² = [l(OP)]² + [l(AP)]² … [Pythagoras theorem]
∴[l(AO)]² = (9)² + (12)² … [From (i) and l(OP) = 9 cm]
= 81 + 144
∴[l(AO)]² = 225
∴l(AO) = √225 …[Taking square root of both sides]
∴l(AO) = 15 cm
∴The length of radius of the circle is 15 cm.

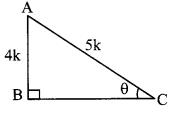
Question 4.
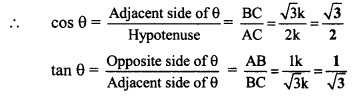
C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.
Solution:
Let seg AB be the chord of the circle with centre C.
Draw seg CD ⊥ chord AB.

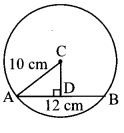
∴l(AD) = \(\frac { 1 }{ 2 }\) l(AB) …[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
= \(\frac { 1 }{ 2 }\) x 12 …[∵ l(AB) = 12 cm]
∴l(AD) = 6 cm …(i)
∴In ∆ACD, m∠ADC = 90°
∴[l(AC)]² = [l(AD)]² + [l(CD)]² … [Pythagoras theorem]
∴(10)² = (6)² + [l(CD)]² … [From (i) and l(AC) = 10 cm]
∴(10)² – (6)² = [l(CD)]²
∴100 – 36 = [l(CD)]²
∴64 = [l(CD)]²
i. e. [l(CD)]² = 64
∴l(CD) = √64 …[Taking square root of both sides]
∴l(CD) = 8 cm
∴The distance of the chord from the centre of the circle is 8 cm.

Maharashtra Board Class 8 Maths Chapter 17 Circle: Chord and Arc Practice Set 17.1 Intext Questions and Activities

Question 1.
In the given figure, O is the centre of the circle. With reference to the figure fill in the blanks. (Textbook pg. No. 114)

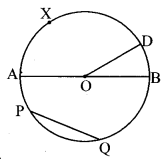
Solution:

1. Seg OD is radius of the circle.
2. Seg AB is diameter of the circle.
3. Seg PQ is chord of the circle.
4. ∠DOB is the central angle.
5. Minor arc : arc AXD, arc BD, arc AP, arc PQ, arc BQ, etc.
6. Major arc : arc PAB, arc PDQ, arc PDB, arc ADQ, etc.
7. Semicircular arc : arc ADB, arc AQB.
8. m (arc DB) = m∠DOB
9. m (arc DAB) = 360° – m∠DOB

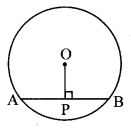
Question 2.
Draw chord AB of a circle with centre O. Draw perpendicular OP to chord AB. Measure seg AP and seg PB. What do you observe. (Textbook pg. no. 114)
Solution:
l(AP) = l(PB) = 0.9 cm
∴the perpendicular drawn from the centre of the circle to its chord bisects the chord.

Question 3.
Draw five circles with different radii. Draw a chord and perpendicular from the centre to each chord in each circle. Verify with a divider that the two parts of the chords are equal. (Textbook pg. no. 114)
Solution:
[Students should attempt the above activities on their own.]

Question 4.
Draw five circles of different radii on a paper. Draw a chord in each circle. Find the midpoint of each chord. Join the centre of the circle and midpoint of the chord as shown in the figure. Name the chord as AB and midpoint of the chord as P. Check with set-square or protractor that ∠APO or ∠BPO are right angles.
Check whether the same result is observed for the chord of each circle. (Textbook pg, no. 115)
Solution:
[Students should attempt the above activities on their own.]

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 8 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 8 Trigonometry.

9th Standard Maths 2 Problem Set 8 Chapter 8 Trigonometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Problem Set 8 Chapter 8 Trigonometry Questions With Answers Maharashtra Board

Question 1.
Choose the correct alternative answer for the following multiple choice questions.

i. Which of the following statements is true?
(A) sin θ = cos (90 – θ)
(B) cos θ = tan (90 – θ)
(C) sin θ = tan (90 – θ)
(D) tan θ = tan (90 – θ)
Answer:
(A) sin θ = cos (90 – θ)

ii. Which of the following is the value of sin 90°?
(A) \( \frac { \sqrt { 3 } }{ 2 }\)
(B) 0
(C) \(\frac { 1 }{ 2 }\)
(D) 1
Answer:
(D) 1

iii. 2 tan 45° + cos 45° – sin 45° = ?
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
2 tan 45° + cos 45° – sin
\( =2(1)+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=2\)
(C) 2

iv. \( \frac{\cos 28^{\circ}}{\sin 62^{\circ}}\) =?
(A) 2
(B) -1
(C) 0
(D) 1
Answer:
\( \frac{\cos 28^{\circ}}{\sin 62^{\circ}}\)

(D) 1

Question 2.
In right angled ∆TSU, TS = 5, ∠S = 90°, SU = 12, then find sin T, cos T, tan T. Similarly find sin U, cos U, tan U.

Solution:
i. TS = 5, SU = 12 …[Given]
In ∆TSU, ∠S = 90° … [Given]
∴ TU² = TS² + SU² …[Pythagoras theorem]
= 5² + 12² = 25 + 144 = 169
∴ TU = \(\sqrt { 169 }\) .. .[Taking square root of both sides]
= 13

Question 3.
In right angled ∆YXZ, ∠X = 90°, XZ = 8 cm, YZ = 17 cm, find sin Y, cos Y, tan Y, sin Z, cos Z, tan Z.

Solution:
i. XZ = 8 cm, YZ = 17 cm …[Given]
In ∆YXZ, ∠X = 90° … [Given]
∴ YZ² = XY² + XZ² .. .[Pythagoras theorem]
∴ 17² = XY² + 8²
∴ 289 = XY² + 64
∴ XY² = 289 – 64
= 225
∴ x = \(\sqrt { 225 }\) .. .[Taking square root of both sides]
= 15

Question 4.
In right angled ∆LMN, if ∠N = θ, ∠M = 90°, cos θ = \(\frac { 24 }{ 25 }\), find sin θ and tan θ. Similarly, find (sin²θ) and (cos²θ).

Solution:
i. cos θ = \(\frac { 24 }{ 25 }\)
In ∆LMN, ∠M = 90°, ∠N = θ

Let the common multiple be k.
∴ MN = 24k and LN = 25k
Now, LN²= LM² + MN² … [Pythagoras theorem]
∴ (25k)² = LM² + (24k)²
∴ 625 k² = LM² + 576k²
∴ LM² = 625k² – 576k²
∴ LM² = 49k²
∴ LM = \(\sqrt { 49{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 7k

Question 5.
Fill in the blanks.
i. sin 20° = cos
ii. tan 30° x tan  = 1
iii. cos 40° = sin
Solution:
i. sin 20° = cos (90° – 20°) …..[∵ sin θ = cos (90 – θ)]
= cos 70°

ii. tan θ x tan (90 – θ) = 1
Substituting θ = 30°,
tan 30° x tan (90 – 30)° = 1
∴ tan 30° x tan 60° = 1

iii. cos 40° = sin (90° – 40°) …[∵ COS θ = sin (90 – θ)]
= sin 50°

Maharashtra Board Class 9 Maths Solutions Chapter 8 Trigonometry Problem Set 8

Question 1.
Measuring height of a tree using trigonometric ratios. (Textbook pg. no. 101)

This experiment can be conducted on a clear sunny day. Look at the figure given above. Height of the tree is QR, height of the stick is BC.
Thrust a stick in the ground as shown in the figure. Measure its height and length of its shadow. Also measure the length of the shadow of the tree. Using these values, how will you determine the height of the tree?
Solution:
Rays of sunlight are parallel.
So, ∆PQR and ∆ABC are equiangular i.e., similar triangles.
Sides of similar triangles are proportional.
∴ \(\frac { QR }{BC }\) = \(\frac { PR }{ AC }\)
∴ Height of the tree (QR) = \(\frac { BC }{ AC }\) x PR
Substituting the values of PR, BC and AC in the above equation, we can get length of QR i.e., the height of the tree.

Question 2.
It is convenient to do the above experiment between 11:30 am and 1:30 pm instead of doing it in the morning at 8’O clock. Can you tell why? (Textbook pg. no. 101)
Solution:
At 8’O clock in the morning, the sunlight is not very bright. At the same time, the sun is on the horizon and the shadow would by very long. It would be extremely difficult to measure shadow in that case.
Between 11:30 am and 1:30 pm, the sun is overhead and it would be easier to measure the length of shadow.

Question 3.
Conduct the above discussed activity and find the height of a tall tree in your surrounding. If there is no tree in the premises, then find the height of a pole. (Textbook pg. no. 101)

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 16.3 8th Std Maths Answers Solutions Chapter 16 Surface Area and Volume.

Surface Area and Volume Class 8 Maths Chapter 16 Practice Set 16.3 Solutions Maharashtra Board

Std 8 Maths Practice Set 16.3 Chapter 16 Solutions Answers

Question 1.
Find the volume of the cylinder if height (h) and radius of the base (r) are as given below.
i. r = 10.5 cm, h = 8 cm
ii. r = 2.5 m, h = 7 m
iii. r = 4.2 cm, h = 5 cm
iv. r = 5.6 cm, h = 5 cm
Solution:
i. Given: r = 10.5 cm and h = 8 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 10.5 x 10.5 x 8
= 22 x 1.5 x 10.5 x 8
= 2772 cc
∴ The volume of the cylinder is 2772 cc.

ii. Given: r = 2.5 m and h = 7 m
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 2.5 x 2.5 x 7
= 22 x 2.5 x 2.5
= 137.5 cu.m
∴ The volume of the cylinder is 137.5 cu.m.

iii. Given: r = 4.2 cm and h = 5 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 4.2 x 4.2 x 5
= 22 x 0.6 x 4.2 x 5
= 277.2 cc
∴ The volume of the cylinder is 277.2 cc.

iv. Given: r = 5.6 cm and h = 5 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 5.6 x 5.6 X 5 7
= 22 x 0.8 x 5.6 x 5
= 492.8 cc
∴ The volume of the cylinder is 492.8 cc.

Question 2.
How much iron is needed to make a rod of length 90 cm and diameter 1.4 cm?
Solution:
Given: For cylindrical rod: length of rod (h) = 90 cm, and
diameter (d) = 1.4 cm
To find: Iron required to make a rod
diameter (d) = 1.4 cm
∴ radius (r) = \(\frac{\mathrm{d}}{2}=\frac{1.4}{2}\) = 0.7 cm
Volume of rod = πr²h
= \(\frac { 22 }{ 7 }\) x 0.7 x 0.7 x 90
= 22 x 0.1 x 0.7 x 90
= 138.60 cc
∴ 138.60 cc of iron is required to make the rod.

Question 3.
How much water will a tank hold if the interior diameter of the tank is 1.6 m and its depth is 0.7 m?
Solution:
Given: interior diameter of the tank (d) = 1.6 m
and depth (h) = 0.7 m
To find: Capacity of the tank
interior diameter of the tank (d) = 1.6 m
∴ Interior radius (r) = \(\frac{\mathrm{d}}{2}=\frac{1.6}{2}\)
= 0.8 m
= 0.8 x 100
…[∵ 1m = 100cm]
= 80cm
h = 0.7 m = 0.7 x 100 = 70 cm
Capacity of the tank = Volume of the tank = πr²h
= \(\frac { 22 }{ 7 }\) x 80 x 80 x 70
= 22 x 80 x 80 x 10
= 1408000 cc
= \(\frac { 1408000 }{ 1000 }\)
…[∵1 litre = 1000 cc]
= 1408 litre
∴The tank can hold 1408 litre of water.

Question 4.
Find the volume of the cylinder if the circumference of the base of cylinder is 132 cm and height is 25 cm.
Solution:
Given: Circumference of the base of cylinder = 132 cm and height (h) = 25 cm
To find: Volume of the cylinder
i. Circumference of base of cylinder = 2πr
∴132 = 2 x \(\frac { 22 }{ 7 }\) x r
∴\(\frac{132 \times 7}{2 \times 22}=r\)
∴\(\frac{6 \times 7}{2}=r\)
∴3 x 7 = r
∴r = 21 cm

ii. Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 21 x 21 x 25
= 22 x 3 x 21 x 25
= 34650 cc
∴ The volume of the cylinder is 34650 cc.

Maharashtra Board Class 8 Maths Chapter 16 Surface Area and Volume Practice Set 16.3 Intext Questions and Activities

Question 1.
Leonard Euler, discovered an interesting formula regarding the faces, vertices and edges of solid figures.
Count and write the faces, vertices and edges of the following figures and complete the table. From the table verify Euler’s formula, F + V = E + 2. (Textbook pg. No. 113)

Solution:

From the above table, F + V = E + 2 i.e. Euler’s formula is verified.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 8.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 8 Trigonometry.

9th Standard Maths 2 Practice Set 8.2 Chapter 8 Trigonometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 8.2 Chapter 8 Trigonometry Questions With Answers Maharashtra Board

Question 1.
In the following table, a ratio is given in each column. Find the remaining two ratios in the column and complete the table.

Solution:
i. cos θ = \(\frac { 35 }{ 37 }\) …(i) )[Given]
In right angled ∆ABC,

∠C = θ.

Let the common multiple be k.
∴ BC = 35k and AC = 37k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (37k)² = AB²+ (35k)²
1369k² = AB² + 1225k²
AB2 = 1369k² – 1225k²
= 144k²
AB = 144k²
AB = \(\sqrt { 2ghK }\)² … [Taking square root of both sides]
= 12k

ii. sin θ = \(\frac { 11 }{ 61 }\) …..(i) [Given]
In right angled ∆ABC, ∠C = θ.


Let the common multiple be k.
AB = 11k and AC = 61k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (61k)² = (11k)² + BC²
∴ 3721k² = 121k² + BC²
∴ BC² = 3721k² – 121k² = 3600k²
BC = \(\sqrt { 3600{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 60k

iii. tan θ = 1 = \(\frac { 1 }{ 1 }\) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 1k and BC = 1k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= K² + K²
= 2K²
∴ AC = \(\sqrt { 2{ k }\)

iv. sin θ = \(\frac { 1 }{ 2 }\) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 1k and BC = 2k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ 2K² = K² + BC²
∴ 4K² = K² + BC²
∴ BC² = 4K² – K² = 3K²
∴ BC = \(\sqrt { 3{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= \(\sqrt { 3{ k }\)

v. cos θ = \(\frac { 1 }{ \sqrt { 3 } } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 1k and BC = √3k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (√3K)² = AB² + K²
∴ 3K² = 3K² – K² = 2K²
∴ AB = \(\sqrt { 2{ k }^{ 2 } }\) .. .[Taking square root of both sides]
AB = √2K

vi. cos θ = \(\frac { 21 }{ \sqrt { 20 } } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 21k and BC = 20k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= (21)K² + (20K)²
= 441K² – 400²
= 841K²
∴ AB = \(\sqrt { 841{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 29K

vii. tan θ = \(\frac { 8 }{ 15 } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 8k and BC = 15k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= (8)K² + (15K)²
= 64K² – 225²
= 289K²
∴ AC = \(\sqrt { 289{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 17K

viii. sin θ = \(\frac { 3 }{ 5 } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.



Let the common multiple be k.
∴ AB = 3k and AC = 5k
Now, AC² = AB² + BC² …[Pythagoras theorem]
∴ (5)K²= (3)K² + BC²
∴ 25K² = 9K² – 225²
∴ BC² = 25K² – 9K²
∴ BC = \(\sqrt { 16{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 4K

ix. tan θ = \(\frac { 1 }{ 2\sqrt { 2 } }\) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 1k and AC = 2√2 k
Now, AC² = AB² + BC² …[Pythagoras theorem]
= K² + (2√2 k )²
= K² – 225²
= 25K² + 8K²
= 9K²
∴ AC = \(\sqrt { 9{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 3K

Question 2.
Find the values of:
i. 5 sin 30° + 3 tan 45°
ii. \(\frac { 4 }{ 5 }\)tan² 60° + 3 sin² 60°
iii. 2 sin 30° + cos 0° + 3 sin 90°
iv. \(\frac{\tan 60^{\circ}}{\sin 60^{\circ}+\cos 60^{\circ}}\)
v. cos² 45° + sin² 30°
vi. cos 60° x cos 30° + sin 60° x sin 30°
Solution:
i. sin 30° = \(\frac { 1 }{ 2 }\) and tan 45° = 1

ii. \(\frac { 4 }{ 5 }\)tan² 60° + 3 sin² 60°

iii. 2 sin 30° + cos 0° + 3 sin 90°
2 sin 30° + cos0° + 3 sin 90° = 2 (\(\frac { 1 }{ 2 }\)) + 1 + 3(1)
= 1 + 1 + 3
∴ 2 sin 30° + cos 0° + 3 sin 90° = 5

iv. \(\frac{\tan 60^{\circ}}{\sin 60^{\circ}+\cos 60^{\circ}}\)

v. cos² 45° + sin² 30°

vi. cos 60° x cos 30° + sin 60° x sin 30°

Question 3.
If sin θ = \(\frac { 4 }{ 5 }\) , then find cos θ.
Solution:
sin θ = \(\frac { 4 }{ 5 }\) .. .(i)[Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 4k and AC = 5k
Now, AC² = AB² + BC² … [Pythagoras theorem]
∴ (5 k)² = (4k)² + BC²
∴ 25k² = 16k² + BC²
∴ BC² = 25k² – 16k² = 9k²
∴ BC = \(\sqrt { 9{ k }^{ 2 } }\) . .[Taking square root of both sides]
= 3k

Question 4.
If cos θ = \(\frac { 15 }{ 17 }\) , then find sin θ.
Solution:
cos θ = \(\frac { 15 }{ 17 }\) .. .(i)[Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ BC = 15k and AC = 17k
Now, AC² = AB² + BC² … [Pythagoras theorem]
∴ (17 k)² = AB² + (15K)²
∴ 289k² = AB² + 225²
∴ AB² = 289k² – 225k²
= 64k²
∴ AB = \(\sqrt { 64{ k }^{ 2 } }\) . .[Taking square root of both sides]
= 8k

Maharashtra Board Class 9 Maths Chapter 8 Trigonometry Practice Set 8.2 Intext Questions and Activities

Question 1.
In right angled ∆PQR, ∠Q = 900. Therefore ∠P and ∠R are complementary angles of each other. Verify the following ratios.
i. sin θ = cos (90 – θ)
ii. cos θ = sin (90 – θ)
iii. sin 30° = cos (90° – 30°) = cos 60°
iv. cos 30° = sin (90° – 30°) = sin 60° (Textbook pg. no. 107)
Solution:
In ∆PQR, ∠Q = 90°, ∠P = θ
∴ ∠R = 90 – θ

i. sin θ = cos (90 – θ)

ii. cos θ = sin (90 – θ)

iii. Let ∠P = θ = 30°
∴ ∠R = 90° – 30°

sin 30° = cos (90° – 30°) … [From (i) and (ii)]
sin 30° = cos 60°

iv. cos 30° = sin (90° – 30°) = sin 60°

∴ cos 30° = sin (90° – 30°) .,.[From (i) and (ii)]
∴ cos 30° = sin 60°

Question 2.
In right angled ∆PQR, ∠Q = 90°, ∠R = θ and if sin θ = \(\frac { 5 }{ 13 }\), then find cos θ and tan θ. (Textbook pg. no. 110)
Solution:
i. Take the given trigonometric ratio as 13k equation (i).
sin θ = \(\frac { 5 }{ 13 }\) .. .(i)[Given]
By using the definition write the trigonometric ratio of sin O and take it as equation (ii).
In right angled ∆PQR, ∠R = θ


Let the common multiple be k.
∴ PQ = 5k and PR = 13k
Find QR by using Pythagoras theorem.
PR² = PQ² + QR² … [Pythagoras theorem]
∴ (13k)² = (5k)² + QR²
∴ 169k² = 25k² + QR²
∴ QR² = 169k² – 25k²
= 144k²
∴ QR = \(\sqrt { 144{ k }^{ 2 } }\) . . . [Taking square root of both sides]
= 12k

Question 3.
While solving the above Illustrative example, why the lengths of PQ and PR are taken 5k and 13k? (Textbook pg. no. 111)
Solution:
\(\frac { PQ }{ PR }\) = \(\frac { 5 }{ 13 }\) … [Given]
Here, the ratio of the lengths of sides PQ and PR is 5 : 13.
The actual lengths of the sides can be any multiple of the ratio. Hence, we consider the multiple k while solving.

Question 4.
While solving the above illustrative example, can we take the lengths of PQ and PR as 5 and 13? If so, then what changes are needed In the writing of the solution. (Tcxtbook pg. no. 111)
Solution:
Yes, we can take lengths of PQ and PR as 5 and 13.
In that case, we will have to take k = 1 and solve the problem accordingly.

Question 5.
Verify that the equation ‘sin² θ + cos² θ = 1’ is true when θ = 0° or θ = 90°.
(Textbook pg. no. 112)
Solution:
sin² θ + cos² θ = 1
i. lf θ = 0°,
LH.S. = sin² θ + cos² θ
= sin² 0° + cos² 0°
= 0 + 1 …[∵ sin 0° = 0, cos 0° = 1]
= R.H.S.
∴ sin² θ + cos² θ = 1

ii. If θ = 90°,
L.H.S.= sin² θ +cos² θ
= sin² 90° + cos² 90°
= 1 + 0 … [ ∵ sin 90° = 1, cos 90° = 0]
= 1
= R.H.S.
∴ sin² θ + cos² θ = 1

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 16.2 8th Std Maths Answers Solutions Chapter 16 Surface Area and Volume.

Surface Area and Volume Class 8 Maths Chapter 16 Practice Set 16.2 Solutions Maharashtra Board

Std 8 Maths Practice Set 16.2 Chapter 16 Solutions Answers

Question 1.
In each example given below, radius of base of a cylinder and its height are given. Then find the curved surface area and total surface area.
i. r = 7 cm, h = 10 cm
ii. r = 1.4 cm, h = 2.1 cm
iii. r = 2.5 cm, h = 7 cm
iv. r = 70 cm, h = 1.4 cm
v. r = 4.2 cm, h = 14 cm
Solution:
i. Given: r = 7 cm and h = 10 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 7 x 10
= 2 x 22 x 10
= 440 sq.cm
Total surface area of the cylinder:
= 2πr(h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 7(10 + 7)
= 2 x \(\frac { 22 }{ 7 }\) x 7 x 17
= 2 x 22 x 17
= 748 sq.cm
The curved surface area of the cylinder is 440 sq.cm and its total surface area is 748 sq.cm.

ii. Given: r = 1.4 cm and h = 2.1 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 1.4 x 2.1
= 2 x 22 x 0.2 x 2.1
= 18.48 sq.cm
Total surface area of the cylinder = 2πr (h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 1.4 (2.1 + 1.4)
= 2 x \(\frac { 22 }{ 7 }\) x 1.4 x 3.5
= 2 x 22 x 0.2 x 3.5
= 30.80 sq.cm
∴ The curved surface area of the cylinder is 18.48 sq.cm and its total surface area is 30.80 sq.cm.

iii. Given: r = 2.5 cm and h = 7 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 2.5 x 7
= 2 x 22 x 2.5
= 110 sq.cm
Total surface area of the cylinder = 2πr(h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 2.5 (7+ 2.5)
= 2 x \(\frac { 22 }{ 7 }\) x 2.5 x 9.5
= \(\frac { 1045 }{ 7 }\)
= 149.29 sq.cm
∴ The curved surface area of the cylinder is 110 sq.cm and its total surface area is 149.29 sq.cm.

iv. Given: r = 70 cm and h = 1.4 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 70 x 1.4
= 2 x 22 x 10 x 1.4
= 616 sq.cm
Total surface area of the cylinder = 2πr(h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 70(1.4 + 70)
= 2 x \(\frac { 22 }{ 7 }\) x 70 x 71.4
= 2 x 22 x 10 x 71.4
= 2 x 22 x 714
= 31416 sq.cm
∴ The curved surface area of the cylinder is 616 sq.cm and its total surface area is 31416 sq.cm.

v. Given: r = 4.2 cm and h = 14 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 4.2 x 14 = 2 x 22 x 4.2 x 2
= 369.60 sq.cm
Total surface area of the cylinder = 2πr (h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 4.2 (14+ 4.2)
= 2 x \(\frac { 22 }{ 7 }\) x 4.2 x 18.2
= 2 x 22 x 0.6 x 18.2
= 480.48 sq.cm
∴ The curved surface area of the cylinder is 369.60 sq.cm and its total surface area is 480.48 sq.cm.

Question 2.
Find the total surface area of a closed cylindrical drum if its diameter is 50 cm and height is 45 cm. (π = 3.14)
Given: For cylindrical drum:
Diameter (d) = 50 cm
and height (h) = 45 cm
To find: Total surface area of the cylindrical drum
Solution:
Diameter (d) = 50 cm
∴ radius (r) = \(\frac{\mathrm{d}}{2}=\frac{50}{2}\) = 25 cm
Total surface area of the cylindrical drum = 2πr (h + r)
= 2 x 3.14 x 25 (45 + 25)
= 2 x 3.14 x 25 x 70
= 10,990 sq.cm
∴ The total surface area of the cylindrical drum is 10,990 sq.cm.

Question 3.
Find the area of base and radius of a cylinder if its curved surface area is 660 sq.cm and height is 21 cm.
Given: Curved surface area = 660 sq.cm, and height = 21 cm
To find: area of base and radius of a cylinder
Solution:
i. Curved surface area of cylinder = 2πrh
∴ 660 = 2 x \(\frac { 22 }{ 7 }\) x r x 21
∴ 660 = 2 x 22 x r x 3
∴ \(\frac{660}{2 \times 22 \times 3}=r\)
∴ \(\frac{660}{2 \times 66}=r\)
∴ 5 = r
i.e., r = 5 cm

ii. Area of a base of the cylinder = πr²
= \(\frac { 22 }{ 7 }\) x 5 x 5
= \(\frac { 550 }{ 7 }\)
= 78.57 sq.cm
∴The radius of the cylinder is 5 cm and the area of its base is 78.57 sq.cm.

Question 4.
Find the area of the sheet required to make a cylindrical container which is open at one side and whose diameter is 28 cm and height is 20 cm. Find the approximate area of the sheet required to make a lid of height 2 cm for this container.
Given: For cylindrical container:
diameter (d) = 28 cm, height (h₁) = 20 cm
For cylindrical lid: height (h₂) = 2 cm
To find: i. Surface area of the cylinder with one side open
ii. Area of sheet required to made a lid
Solution:
diameter (d) = 28 cm
∴ radius (r) = \(\frac{\mathrm{d}}{2}=\frac{28}{2}\) = 14 cm
i. Surface area of the cylinder with one side open = Curved surface area + Area of a base
= 2πrh₁ + πr²
= πr (2h₁ + r)
= \(\frac { 22 }{ 7 }\) x 14 x (2 x 20 + 14)
= 22 x 2 x (40 + 14)
= 22 x 2 x 54
= 2376 sq.cm

ii. Area of sheet required to made a lid = Curved surface area of lid + Area of upper surface
= 2πrh₂ + πr²
= πr (2h₂ + r)
= \(\frac { 22 }{ 7 }\) x 14 x (2 x 2 + 14)
= 22 x 2 x (4 + 14)
= 22 x 2 x 18
= 792 sq cm
∴ The area of the sheet required to make the cylindrical container is 2376 sq. cm and the approximate area of a sheet required to make the lid is 792 sq. cm.

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 16.1 8th Std Maths Answers Solutions Chapter 16 Surface Area and Volume.

Surface Area and Volume Class 8 Maths Chapter 16 Practice Set 16.1 Solutions Maharashtra Board

Std 8 Maths Practice Set 16.1 Chapter 16 Solutions Answers

Question 1.
Find the volume of a box if its length, breadth and height are 20 cm, 10.5 cm and 8 cm respectively.
Given: For cuboid shaped box,
length (l) = 20 cm, breadth (b) = 10.5 cm and height (h) = 8cm
To find: Volume of a box
Solution:
Volume of a box = l x b x h
= 20 x 10.5 x 8
= 1680 cc
∴ The volume of the box is 1680 cc.

Question 2.
A cuboid shaped soap bar has volume 150 cc. Find its thickness if its length is 10 cm and breadth is 5 cm.
Given: For cuboid shaped soap bar,
length (l) = 10 cm, breadth (b) = 5 cm and volume = 150 cc
To find: Thickness of the soap bar (h)
Solution:
Volume of soap bar = l x b x h
∴ 150 = 10 x 5 x h
∴ 150 = 50h
∴ \(\frac { 150 }{ 50 }=h\)
∴ 3 = h
i.e., h = 3 cm
∴ The thickness of the soap bar is 3 cm.

Question 3.
How many bricks of length 25 cm, breadth 15 cm and height 10 cm are required to build a wall of length 6 m, height 2.5 m and breadth 0.5 m?
Given: For the cuboidal shape brick:
length (l₁) = 25 cm,
breadth (b₁) = 15 cm,
height (h₁) = 10 cm
For the cuboidal shape wall:
length (l₂) = 6 m,
height (h₂) = 2.5 m,
breadth (b₂) = 0.5 m
To find: Number of bricks required
Solution:
When all the bricks are arranged to build a wall, the volume of all the bricks is equal to volume of wall.
∴ \(\text { Number of bricks }=\frac{\text { volume of the wall }}{\text { volume of a brick }}\)

i. Volume of a brick = l₁ x b₁ x h₁
= 25 x 15 x 10 cc

ii. l₂ = 6m = 6 x 100 …[∵ 1m = 100cm]
= 600 cm
h₂ = 2.5 m = 2.5 x 100 = 250 cm
b₂ = 0.5 m = 0.5 x 100 = 50 cm
Volume of the wall = l₂ x b₂ x h₂
= 600 x 50 x 250 cc

iii. \(\text { Number of bricks }=\frac{\text { volume of the wall }}{\text { volume of a brick }}\)
= \(\frac{600 \times 50 \times 250}{25 \times 15 \times 10}\)
= 40 x 2 x 25
= 2000 bricks
∴ 2000 bricks are required to build the wall.

Question 4.
For rain water harvesting a tank of length 10 m, breadth 6 m and depth 3 m is built. What is the capacity of the tank? How many litre of water can it hold?
Given: For a cuboidal tank,
Length (l) = 10 m, breadth (b) = 6 m, depth (h) = 3 m
To find: Capacity of the tank and litre of water tank can hold.
Solution:
i. l = 10m = 10 x 100 …[∵ 1m = 100cm]
= 1000 cm,
b = 6 m = 6 x 100 = 600 cm,
h = 3 m = 3 x 100 = 300 cm
Volume of the tank = l x b x h
= 1000 x 600 x 300
= 18,00,00,000 cc

ii. Capacity of the tank = Volume of the tank
= 18,00,00,000 cc
= \(\frac{18,00,00,000}{1000}\)
…[∵ 1 litre =1000 cc]
= 1,80,000 litre
∴ The capacity of the tank is 18,00,00,000 cc and it can hold 1,80,000 litre of water.

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 8.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 8 Trigonometry.

9th Standard Maths 2 Practice Set 8.1 Chapter 8 Trigonometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 8.1 Chapter 8 Trigonometry Questions With Answers Maharashtra Board

Question 1.
In the given figure, ∠R is the right angle of ∆PQR. Write the following ratios.

i. sin P
ii. cos Q
iii. tan P
iv. tan Q
Solution:

Question 2.
In the right angled ∆XYZ, ∠XYZ = 90° and a, b, c are the lengths of the sides as shown in the figure. Write the following ratios.

i. sin x
ii. tan z
iii. cos x
iv. tan x.
Solution:

Question 3.
In right angled ∆LMN, ∠LMN = 90°, ∠L = 50° and ∠N = 40°. Write the following ratios.

i. sin 50°
ii. cos 50°
iii. tan 40°
iv. cos 40°
Solution:

Question 4.
In the given figure, ∠PQR = 90°, ∠PQS = 90°, ∠PRQ = α and ∠QPS = θ. Write the following trigonometric ratios.
i. sin α, cos α , tan α
ii. sin θ, cos θ, tan θ

Solution:
i. In ∆PQR,

ii. In ∆PQS,

Maharashtra Board Class 9 Maths Chapter 8 Trigonometry Practice Set 8.1 Intext Questions and Activities

Question 1.
In the figure gIven below, ∆PQR is a right angled triangle. Write the names of sides opposite and adjacent to ∠P and ∠R. (Textbook pg no. 102)

Solution:
In right angled ∆PQR,
i. side opposite to ∠P = QR
ii. side opposite to ∠R = PQ
iii. side adjacent to ∠P = PQ
iv. side adjacent to ∠R = QR

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 7 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 7 Co-ordinate Geometry.

9th Standard Maths 2 Problem Set 7 Chapter 7 Co-ordinate Geometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Problem Set 7 Chapter 7 Co-ordinate Geometry Questions With Answers Maharashtra Board

Question 1.
Choose the correct alternative answer for the following questions.

i. What is the form of co-ordinates of a point on the X-axis?
(A) (b,b)
(B) (0, b)
(C) (a, 0)
(D) (a, a)
Answer:
(C) (a, 0)

ii. Any point on the line y = x is of the form _____.
(A) (a, a)
(B) (0, a)
(C) (a, 0)
(D) (a, -a)
Answer:
(A) (a, a)

iii. What is the equation of the X-axis ?
(A) x = 0
(B) y = 0
(C) x + y = 0
(D) x = y
Answer:
(B) y = 0

iv. In which quadrant does the point (-4, -3) lie ?
(A) First
(B) Second
(C) Third
(D) Fourth
Answer:
(C) Third

v. What is the nature of the line which includes the points (-5, 5), (6, 5), (-3, 5), (0, 5)?
(A) Passes through the origin
(B) Parallel to Y-axis
(C) Parallel to X-axis
(D) None of these
Answer:
The y co-ordinate of all the points is the same.
∴ The line which passes through the given points is parallel to X-axis.
(C) Parallel to X-axis

vi. Which of the points P(-1, 1), Q(3, -4), R( -1, -1), S(-2, -3), T (-4, 4) lie in the fourth quadrant?
(A) P and T
(B) Q and R
(C) only S
(D) P and R
Answer:
(B) Q and R

Question 2.
Some points are shown in the adjoining figure. With the help of it answer the following questions :

i. Write the co-ordinates of the points Q and R.
ii. Write the co-ordinates of the points T and M.
iii. Which point lies in the third quadrant ?
iv. Which are the points whose x and y co-ordinates are equal ?
Solution:
i. Q(-2, 2) and R(4, -1)
ii. T(0, -1) and M(3, 0)
iii. Point S lies in the third quadrant.
iv. The x and y co-ordinates of point O are equal.

Question 3.
Without plotting the points on a graph, state in which quadrant or on which axis do the following points lie.
i. (5, -3)
ii. (-7, -12)
iii. (-23, 4)
iv. (-9, 5)
v. (0, -3)
vi. (-6, 0)
Solution:

Question 4.
Plot the following points on one and the same co-ordinate system.
A(1, 3), B(-3, -1), C(1, -4), D(-2, 3), E(0, -8), F(1, 0)
Solution:

Question 5.
In the graph alongside, line LM is parallel to the Y-axis.

i. What is the distance of line LM from the Y-axis?
ii. Write the co-ordinates of the points P, Q and R.
iii. What is the difference between the x co-ordinates of the points L and M?
Solution:
i. Distance of line LM from the Y-axis is 3 units.
ii. P(3, 2), Q (3, -1), R(3, 0)
iii. x co-ordinate of point L = 3
x co-ordinate of point M = 3
∴ Difference between the x co-ordinates of the points L and M = 3 – 3
= 0

Question 6.
How many lines are there which are parallel to X-axis and having a distance 5 units?
Solution:
The equation of a line parallel to the X-axis is y = b.
There are 2 lines which are parallel to X-axis and at a distance of 5 units.
Their equations are y = 5 and y = -5.

Question 7.
If ‘a’ is a real number, what is the distance between the Y-axis and the line x = a?
Solution:
Equation of Y-axis is x = 0.
Since, ‘a’ is a real number, there are two possibilities.
Case I: a > 0
Case II: a < 0 ∴ Distance between the Y-axis and the line x = a = a-0 = a Since, |a| = a, a > 0
= – a, a < 0
∴ Distance between the Y-axis and the line x = a is |a|.

Maharashtra Board Class 9 Maths Chapter 7 Co-ordinate Geometry Problem Set 7 Intext Questions and Activities

Question 1.
As shown in the adjoining figure, ask girls to sit in lines so as to form the X-axis and Y-axis.
i. Ask some boys to sit at the positions marked by the coloured dots in the four quadrants.
i. Now, call the students turn by turn using the initial letter of each student’s name. As his or her initial is called, the student stands and gives his or her own co-ordinates. For example Rajendra (2, 2) and Kirti (-1, 0)
iii. Even as they have fun during this field activity, the students will leam how to state the position of a point in a plane. (Textbook pg. no. 92)

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.6 8th Std Maths Answers Solutions Chapter 15 Area.

Area Class 8 Maths Chapter 15 Practice Set 15.6 Solutions Maharashtra Board

Std 8 Maths Practice Set 15.6 Chapter 15 Solutions Answers

Question 1.
Radii of the circles are given below, find their areas.
i. 28 cm
ii. 10.5 cm
iii. 17.5 cm
Solution:
i. Radius of the circle (r) = 28 cm … [Given]
Area of the circle = πr²
= \(\frac { 22 }{ 7 }\) x (28)²
= \(\frac { 22 }{ 7 }\) x 28 x 28
= 22 x 4 x 28
= 2464 sq. cm

ii. Radius of the circle (r) = 10.5 cm … [Given]
Area of the circle = πr²
= \(\frac { 22 }{ 7 }\) x (10.5)²
= \(\frac { 22 }{ 7 }\) x 10.5 x 10.5
= 22 x 1.5 x 10.5
= 346.5 sq. cm

iii. Radius of the circle (r) = 17.5 cm … [Given]
Area of the circle = πr²
= \(\frac { 22 }{ 7 }\) x(17.5)²
= \(\frac { 22 }{ 7 }\) x 17.5 x 17.5
= 22 x 2.5 x 17.5
= 962.5 sq. cm

Question 2.
Areas of some circles are given below, find their diameters.
i. 176 sq.cm
ii. 394.24 sq. cm
iii. 12474 sq. cm
Solution:
i. Area of the circle =176 sq. cm .. .[Given]
Area of the circle = πr²
∴ 176 = \(\frac { 22 }{ 7 }\) x r²
∴ r² = 176 x \(\frac { 7 }{ 22 }\)
∴ r² = 56
∴ r = √56 … [Taking square root of both sides]
Diameter = 2r = 2√56 CM

ii. Area of the circle = 394.24 sq. cm … [Given]
Area of the circle = πr²

∴ Diameter = 2r = 2 x 11.2 = 22.4 cm

iii. Area of the circle = 12474 sq. cm …[Given]
Area of the circle = πr²
∴ 12474 = \(\frac { 22 }{ 7 }\) x r²
∴ r² = 12474 x \(\frac { 7 }{ 22 }\)
∴ r² = 567 x 7
∴ r² = 3969
∴ r = 63 …[Taking square root of both sides]
∴ Diameter = 2r = 2 x 63 = 126cm

Question 3.
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.

Solution:

Diameter of the circular garden is 42 m. … [Given]
∴ Radius of the circular garden (r) = \(\frac { 42 }{ 2 }\) = 21 m
Width of the road = 3.5 m …[Given]
Radius of the outer circle (R)
= radius (r) + width of the road
= 21 + 3.5
= 24.5 m
Area of the road = area of outer circle – area of circular garden
= πR² – πr²
= π (R² – r²)
= \(\frac { 22 }{ 7 }\) [(24.5)² – (21)²]
= \(\frac { 22 }{ 7 }\) (24.5 + 21) (24.5 – 21)
…..[∵ a²-b² = (a+b)(a-b)]
= \(\frac { 22 }{ 7 }\) x 45.5 x 3.5
= 22 x 45.5 x 0.5
= 500.50 sq. m
∴ The area of the road is 500.50 sq. m.

Question 4.
Find the area of the circle if its circumference is 88 cm.
Solution:
Circumference of the circle = 88 cm …[Given]
Circumference of the circle = 2πr
∴ 88 = 2 x \(\frac { 22 }{ 7 }\) x r
∴ \(r=\frac{88 \times 7}{2 \times 22}\) ∴ r = 14cm
Area of the circle = πr² = \(\frac { 22 }{ 7 }\) x (14)²
= \(\frac { 22 }{ 7 }\) x 14 x 14 = 22 x 2 x 14 = 616 sq. cm
∴ The area of circle is 616 Sq cm

Maharashtra Board Class 8 Maths Chapter 15 Area Practice Set 15.6 Intext Questions and Activities

Question 1.
Draw a circle of radius 28mm. Draw any one triangle and draw a trapezium on the graph paper. Find the area of these figures by counting the number of small squares on the graph paper. Verify your answers using formula for area of these figures.
Observe that smaller the squares of graph paper, better is the approximation of area. (Textbook pg. no. 105)
Solution:
(Students should do this activity on their own.)

Std 8 Maths Digest

• Practice Set 15.1 Class 8 Answers
• Practice Set 15.2 Class 8 Answers
• Practice Set 15.3 Class 8 Answers
• Practice Set 15.4 Class 8 Answers
• Practice Set 15.5 Class 8 Answers
• Practice Set 15.6 Class 8 Answers
• Practice Set 16.1 Class 8 Answers
• Practice Set 16.2 Class 8 Answers
• Practice Set 16.3 Class 8 Answers
• Practice Set 17.1 Class 8 Answers
• Practice Set 17.2 Class 8 Answers

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 7 Co-ordinate Geometry.

9th Standard Maths 2 Practice Set 7.2 Chapter 7 Co-ordinate Geometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 7.2 Chapter 7 Co-ordinate Geometry Questions With Answers Maharashtra Board

Question 1.
On a graph paper plot the points A(3, 0), B(3, 3), C(0, 3). Join A, B and B, C. What is the figure formed?
Soiution:

d(O, A) = 3 cm, d(A, B) = 3 cm, d(B, C) = 3 cm, d(O, C) = 3 cm and each angle of □ OABC is 90°
∴ □ OABC is a square.

Question 2.
Write the equation of the line parallel to the Y-axis at a distance of 7 units from it to its left.
Solution:
The equation of a line parallel to the Y-axis is x = a.
Since, the line is at a distance of 7 units to the left of Y-axis,
∴ a = -7
∴ x = -1 is the equation of the required line.

Question 3.
Write the equation of the line parallel to the X-axis at a distance of 5 units from it and below the X-axis.
Solution:
The equation of a line parallel to the X-axis is y = b.
Since, the line is at a distance of 5 units below the X-axis.
∴ b = -5
∴ y = -5 is the equation of the required line.

Question 4.
The point Q( -3, -2) lies on a line parallel to the Y-axis. Write the equation of the line and draw its graph.
Solution:
The equation of a line parallel to the Y-axis is x = a.
Here, a = -3
∴ x = -3 is the equation of the required line.

Question 5.
Y-axis and line x = – 4 are parallel lines. What is the distance between them?
Solution:
Equation of Y-axis is x = 0.
Equation of the line parallel to the Y-axis is x = – 4. … [Given]
∴ Distance between the Y-axis and the line x = – 4 is 0 – (- 4) … [0 > -4]
= 0 + 4 = 4 units
∴ The distance between the Y-axis and the line x = – 4 is 4 units.
[Note: The question is modified as X-axis cannot be parallel to the line x = – 4.]

Question 6.
Which of the equations given below have graphs parallel to the X-axis, and which ones have graphs parallel to the Y-axis? [1 Mark each]
i. x = 3
ii. y – 2 = 0
iii. x + 6 = 0
iv. y = -5
Solution:
i. The equation of a line parallel to the Y-axis is x = a.
∴ The line x = 3 is parallel to the Y-axis.

ii. y – 2 = 0
∴ y = 2
The equation of a line parallel to the X-axis is y = b.
∴ The line y – 2 = 0 is parallel to the X-axis.

iii. x + 6 = 0
∴ x = -6
The equation of a line parallel to the Y-axis is x = a.
∴ The line x + 6 = 0 is parallel to the Y-axis.

iv. The equation of a line parallel to the X-axis is y = b.
∴ The line y = – 5 is parallel to the X-axis.

Question 7.
On a graph paper, plot the points A(2, 3), B(6, -1) and C(0, 5). If these points are collinear, then draw the line which includes them. Write the co-ordinates of the points at which the line intersects the X-axis and the Y-axis.
Solution:

From the graph, the line drawn intersects the X-axis at D(5, 0) and the Y-axis at C(0, 5).

Question 8.
Draw the graphs of the following equations on the same system of co-ordinates. Write the co-ordinates of their points of intersection.
x + 4 = 0,
y – 1 = 0,
2x + 3 = 0,
3y – 15 = 0
Solution:
i. x + 4 = 0
∴ x = – 4

ii. y – 1 = 0
∴ y = 1

iii. 2x + 3 = 0
∴2x = -3
∴ x = \(\frac { -3 }{ 2 }\)
∴ x = -1.5

iv. 3y- 15 = 0
3y = 15
y = \(\frac { 15 }{ 3 }\)
∴ y = 5

The co-ordinates of the point of intersection of x + 4 = 0 and y – 1 = 0 are A(-4, 1).
The co-ordinates of the point of intersection ofy – 1 = 0 and 2x + 3 = 0 are B(-1.5, 1).
The co-ordinates of the point of intersection of 3y – 15 = 0 and 2x + 3 = 0 are C(-1.5, 5).
The co-ordinates of the point of intersection of x + 4 = 0 and 3y – 15 = 0 are D(-4, 5).

Question 9.
Draw the graphs of the equations given below.
i. x + y = 2
ii. 3x – y = 0
iii. 2x + y = 1
Solution:
i. x + y = 2
∴ y = 2 – x
When x = 0,
y = 2 – x
= 2 – 0
= 2
When x = 1,
y = 2 – x
= 2 – 1
= 1
When x = 2,
y = 2 – x
= 0

ii. 3x – y = 0
∴ y = 3x
When x = 0,
y = 3x
= 3(0)
= 0

When x = 1,
y = 3x
= 3(1)
= 3

When x = -1,
y = 3x
= 3(-1)
= -3

iii. 2x + y = 1
∴ y = 1 – 2x
When x = 0,
y = 1 – 2x
= 1 – 2(0)
= 1 – o
When x = 1,
y = 1 – 2x
= 1- 2(1)
= 1 – 2
= -1
When x = -1,
y = 1 – 2x
= 1 – 2(-1)
= 1 + 2
= 3

Maharashtra Board Class 9 Maths Chapter 7 Co-ordinate Geometry Practice Set 7.2 Intext Questions and Activities

Question 1.
i. Can we draw a line parallel to the X-axis at a distance of 6 unIts from It and below the X-axis?
ii. Will all of the points (-3,-6), (10,-6), ( \(\frac { 1 }{ 2 }\), -6) be on that line?
iii. What would be the equation of this line?(Textbook pg. no. 94)
Solution:

i. Yes.
This line will pass through the point (0,-6).

ii. Yes.
Here, y co-ordinate of the points (-3, -6), (10,-6), ( \(\frac { 1 }{ 2 }\), -6) is the same, which is -6.
∴ All the above points lie on the same line.

iii. Since, the line is at a distance of 6 units below the X-axis.
∴ b = -6
∴ Equation of the line is y = -6.

Question 2.
i. Can we draw a line parallel to the Y – axis at a distance of 2 units from ¡t and to its right?
ii. Will all of the points (2, 10), (2, 8), (2, -) be on that line?
iii. What would be the equation of this line? (Textbook pg. no. 95)
Solution:

i. Yes.
(2, 10)
This line will pass through the point (2, 0).
(2,8)
ii. Yes.
Here, x co-ordinate of the points (2, 10), (2, 8), (2,-\(\frac { 1 }{ 2 }\) ) is the same, which is 2.
∴ All the above points lie on the same line.

iii. Since, the line is at a distance of 2 units to the right of Y-axis.
a = 2
∴ Equation of the line is x = 2.

Question 3.
On a graph paper, plot the points (0, 1), (1, 3), (2, 5). Are they collinear? If so, draw the line that passes through them.
i. Through which quadrants does this line pass ?
ii. Write the co-ordinates of the point at which it intersects the Y-axis.
iii. Show any point in the third quadrant which lies on this line. Write the co-ordinates of the point. (Textbook pg. no. 96)
Solution:
i. The line passes through the quadrants I, II and III.
ii. The line intersects the Y-axis at (0, 1).
iii. (-1,-1)

Class 9 Maths Digest

• Practice Set 7.1 Class 9 Answers
• Practice Set 7.2 Class 9 Answers
• Problem Set 7 Class 9 Answers
• Practice Set 8.1 Class 9 Answers
• Practice Set 8.2 Class 9 Answers
• Problem Set 8 Class 9 Answers
• Practice Set 9.1 Class 9 Answers
• Practice Set 9.2 Class 9 Answers
• Practice Set 9.3 Class 9 Answers
• Problem Set 9 Class 9 Answers