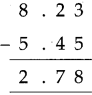Prasanna

Fractions Class 5 Problem Set 22 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 5 Fractions Problem Set 22 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 5 Fractions

Question 1.
Add the following:

\(\text { (1) } \frac{1}{8}+\frac{3}{4}\)
Solution:
The smallest common multiple of 4 and 8 is 8. So making 8 is the common denominator of the given fractions.

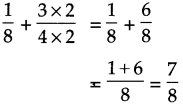
Answer:
\(\frac{7}{8}\)

\(\text { (2) } \frac{2}{21}+\frac{3}{7}\)
Solution:
21 is the multiple of 7. So making 21 as denominator of both the fractions.

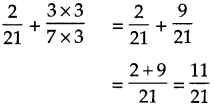
Answer:
\(\frac{11}{21}\)

\(\text { (3) } \frac{2}{5}+\frac{1}{3}\)
Solution:
Least common multiple of 5 and 3 is 15. So making common denominator of both the fractions 15.

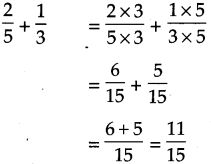
Answer:
\(\frac{11}{15}\)

\(\text { (4) } \frac{2}{7}+\frac{1}{2}\)
Solution:
Smallest common multiple of 2 and 7 is 14. So, making denominator of both the fractions 14.

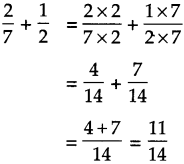
Answer:
\(\frac{11}{14}\)

\(\text { (5) } \frac{3}{9}+\frac{3}{5}\)
Solution:
Smallest common multiple of 9 and 5 is 45.

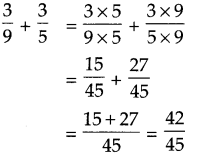
Answer:
\(\frac{42}{45}\)

Question 2.
Subtract the following:

\(\text { (1) } \frac{3}{10}-\frac{1}{20}\)
Solution:
20 is the multiples of 10. So,


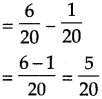
Answer:
\(\frac{5}{20}\)

\(\text { (2) } \frac{3}{4}-\frac{1}{2}\)
Solution:
4 is the multiple of 2. So,

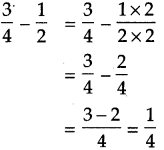
Answer:
\(\frac{1}{4}\)

\(\text { (3) } \frac{6}{14}-\frac{2}{7}\)
Solution:
14 is the multiples of 7. So,

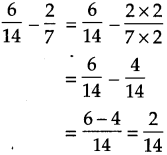
Answer:
\(\frac{2}{14}\)

\(\text { (4) } \frac{4}{6}-\frac{3}{5}\)
Solution:
Smallest common multiple of 6 and 5 is 30. So,

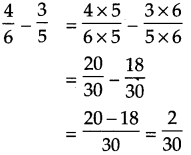
Answer:
\(\frac{2}{30}\)

\(\text { (5) } \frac{2}{7}-\frac{1}{4}\)
Solution:
Smallest common multiple of 7 and 4 is 28.

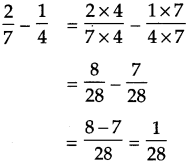
Answer:
\(\frac{1}{28}\)

A fraction of a collection and a multiple of a fraction

\(\frac{1}{4}\) of a collection of 20 dots – \(\frac{1}{2}\) of a collection of 20 dots

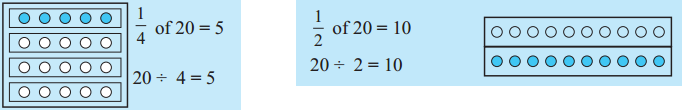
\(\frac{3}{4}\) of a collection of 20 dots

Twice 5 is 10 – \(\frac{1}{2}\) times 10

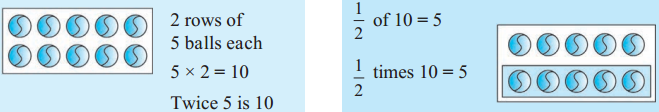
Thrice 5 – \(\frac{1}{3}\) times 15

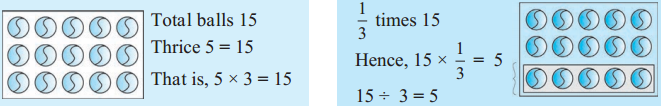
\(\frac{1}{3}\) times 15

Meena has 5 rupees. Tina has twice as many rupees. That is, Tina has 5 × 2 = 10 rupees. Meena has half as many rupees as Tina, that is, \(\frac{1}{2}\) of 10, or, 5 rupees.

Ramu has to travel a distance of 20 km. If he has travelled \(\frac{4}{5}\) of the distance by car, how many kilometres did he travel by car?
\(\frac{4}{5}\) of 20 km is 20 × \(\frac{4}{5}\). So, we take \(\frac{1}{5}\) of 20, 4 times.
\(\frac{1}{5}\) of 20 = 4. 4 times 4 is 4 × 4 = 16.
It means that 20 × \(\frac{4}{5}\) = 16.
Ramu travelled a distance of 16 kilometres by car.

Addition and Subtraction Problem Set 13 Additional Important Questions and Answers

\(\text { (1) } \frac{5}{6}+\frac{1}{12}\)
Solution:
12 is the multiple of 6

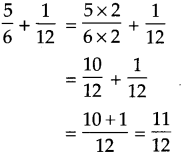
Answer:
\(\frac{11}{12}\)

\(\text { (2) } \frac{1}{9}+\frac{2}{3}\)
Solution:
Here 9 is the multiples of 3. So, making like fractions of denominator 9, we get

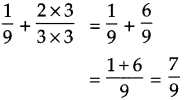
Answer:
\(\frac{7}{9}\)

Subtract the following:

\(\text { (1) } \frac{4}{9}-\frac{2}{5}\)
Solution:
Common multiple of 9 and 5 is 45

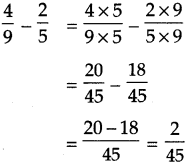
Answer:
\(\frac{2}{45}\)

\(\text { (2) } \frac{1}{2}+\frac{3}{4}-\frac{7}{8}\)

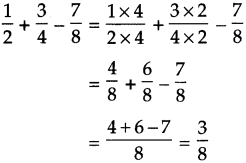
Answer:
\(\frac{3}{8}\)

Class 5 Maths Solution Maharashtra Board

• Fractions Problem Set 17 Class 5 Maths Solutions
• Fractions Problem Set 18 Class 5 Maths Solutions
• Fractions Problem Set 19 Class 5 Maths Solutions
• Fractions Problem Set 20 Class 5 Maths Solutions
• Fractions Problem Set 21 Class 5 Maths Solutions
• Fractions Problem Set 22 Class 5 Maths Solutions
• Fractions Problem Set 23 Class 5 Maths Solutions

Patterns Class 5 Problem Set 53 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 15 Patterns Problem Set 53 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 15 Patterns

Question 1.
Find the square numbers from the list given below.
5, 9, 12, 16, 50, 60, 64, 72, 80, 81
Answer:
9,16, 64, 81, 4, 25, 49 are square numbers.

Question 2.
Which are the triangular numbers in the given list?
3, 6, 8, 9, 12, 15, 16, 20, 21, 42
Answer:
3, 6, 15, 21, 28, 10, 45, 55 are triangular numbers.

Question 3.
Name a number which is square as well as triangular.
Answer:
36 is square as well as triangular number.

Question 4.
If 4 is the first square number, which is the tenth one?
Answer:
121 is the tenth square number.

Question 5.
If 3 is the first triangular number, which is the tenth one?
Answer:
66 is the tenth triangular number.

Think about it.

• How will you decide if a given number is a square number?
• How will you decide if a given number is a triangular number?
• How many square numbers do you think there are?
• How many triangular numbers do you think there are?

Activity

Make a collection of pictures in which you can see square or triangular numbers.

Patterns in floor tiles

The tiles in each picture below form a specific pattern. Observe that there is no gap or open ground between two tiles.

On a large piece of card sheet, draw several shapes like the one shown alongside. Colour half of them. Cut them all out and separate them.

One pattern made of these shapes is shown alongside. Make some other patterns of your own.

Cut out many pieces of each of the shapes shown alongside. Join them in a pattern like floor tiles.

Note the pattern and complete the design.

Make your own shapes and use them to make patterns for sari and shawl borders, etc.

Perimeter and Area Problem Set 49 Additional Important Questions and Answers

Solve the following :

Question 1.
If 4 is the first square number which is the eighth one?
Answer:
81 is the eighth square number.

Question 2.
If 3 is the first triangular number which is the eighth one?
Answer:
45 is the eighth triangular number.

Question 3.
Classify the following into square numbers and triangular numbers.
3, 4, 9,10,15,16; 45, 49, 64, 66, 81, 91
Answer:
Square Numbers : 4, 9,16, 49, 64, 81
Triangular Numbers : 3, 10, 15, 45, 66, 91

Question 4.
Find out the numbers which are neither square nor triangular numbers from the following.
4, 5, 6, 8, 9, 10, 14, 15, 16, 25, 26, 27, 28.
Answer:
5, 8 14, 26 and 27

Question 5.
(1) If 4 is the first square number, which is the fifth one?
(2) If 3 is the first triangular number, which is the sixth one?
(3) Write all the square numbers between 20 and 80.
(4) Write all the triangular numbers between 20 and 80.
(5) Write the greatest two-digit square numbers as well as triangular numbers.
(6) Write the next three square numbers, 36, 49, 64,…….,
(7) Write the next three triangular numbers 36, 45, 55,
Answer:
(1) 36
(2) 28
(3) 25, 36, 49, 64
(4) 21, 28, 36, 45, 55, 66, 78
(5) 81, 91
(6) 81, 100, 121
(7) 66, 78, 91

Question 6.
Match the columns

A	B
(1) Third square number	(a) 15
(2) Fourth triangular number	(b) 36
(3) Number neither square nor triangular	(c) 16
(4) Number is both square as well as triangular number	(d) 35

Answer:
(1 – c),
(2 – a),
(3 – d),
(4 – b).

Class 5 Maths Solution Maharashtra Board

• Three Dimensional Objects and Nets Problem Set 51 Class 5 maths Solutions
• Pictographs Problem Set 52 Class 5 maths Solutions
• Patterns Problem Set 53 Class 5 maths Solutions
• Preparation for Algebra Problem Set 54 Class 5 maths Solutions
• Preparation for Algebra Problem Set 55 Class 5 maths Solutions
• Preparation for Algebra Problem Set 56 Class 5 maths Solutions

Number Work Class 5 Problem Set 5 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 2 Number Work Problem Set 5 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 2 Number Work

Question 1.
Write the place value of the underlined digit.

(1) 78, 95,210
(2) 14, 95,210
(3) 3,52,749
(4) 50,000
(5) 89, 99,988
Answer:
(1) Here, the underlined digit 7 is in ten lakhs place.
So, its place value is 70,00,000 (70 lakhs)

(2) Here, the underlined digit 4 is in lakhs place.
So, its place value is 4,00,000 (4 lakhs)

(3) Here, the underlined digit 5 in ten thousands place.
So, its place value is 50,000 (50 thousands)

(4) Here, the underlined digit ‘0’ is in the unit place.
Hence, its place value is 0 (zero)

(5) Here, the underlined digit 9 is in ten thousands place
So, its place value is 90,000 (90 thousands)

Question 2.
Write the numbers in their expanded form.
(1) 56, 43, 215
(2) 70, 815
(3) 8, 35, 999
(4) 8, 88, 889
(5) 92, 32, 992
Answer:
(1) 56,43,215: 50,00,000 + 6,00,000 + 40,000 + 3,000 + 200 + 10 + 5
(2) 70,815 : 70,000 + 800 + 10 + 5
(3) 8,35,999 : 8,00,000 + 30,000 + 5,000 + 900 + 90 + 9
(4) 8,88,889 : 8,00,000 + 80,000 + 8,000 + 800 + 80 + 9
(5) 92,32,992: 90,00,000 + 2,00,000 + 30,000 + 2,000 + 900 + 90 + 2

Question 3.
Write the place name and place value of each digit in the following numbers.
(1) 35, 705
Answer:
Digit 3 is in ten thousands place, its place value is 30,000
Digit 5 is in thousands place, its place value is 5,000
Digit 7 is in hundreds place, its place value is 700
Digit 0 is in ten place, its place value is 0
Digit 5 is in units place, its place value is 5

(2) 7, 82, 899
Answer:
Digit 7 is in lakhs place, its place value is 7.0. 000
Digit 8 is in ten thousands place, its place value is 80,000
Digit 2 is in thousands place, its place value is 2,000
Digit 8 is in hundreds place, its place value is 800
Digit 9 is- in ten place, its place value is 90 Digit 9 is in units place, its place value is 9

(3) 82, 74, 508
Answer:
Digit 8 is in ten lakhs place, its place value is 80,00,000
Digit 2 is in lakhs place, its place value is 2.0. 000
Digit 7 is in ten thousands place, its place value is 70,000
Digit 4 is in thousands place, its place value is 4,000
Digit 5 is in hundreds place, its place value is 500
Digit 0 is in ten place, its place value is 0
Digit 8 is in units place, its place value is 8

Question 4.
The expanded form of the number is given. Write the number.
(1) 60, 000 + 4000 + 600 + 70 + 9
(2) 9, 00, 000 + 20,000 + 7000 + 800 + 5
(3) 20,00,000 + 3,00,000 + 60,000 + 9000 + 500 + 10 + 7
(4) 7,00,000 + 80,000 + 4000 + 500
(5) 80,00,000 + 50,000 + 1000 + 600 + 9
Answer:
(1) The number is 64,679
(2) The number is 9,27,805
(3) The number is 23,69,517
(4) The number is 7,84,500
(5) The number is 80,51,609

An interesting dice game

Prepare a table with the name of each player, as shown below.
In front of each name, there are boxes to make seven-digit numbers.

Game 1 :
The first player throws the dice and writes that number in any one of the boxes in front of his/her name. You can write only one number in each box and once it is written, you cannot change its place. The other players do the same till all the boxes are filled and each one gets a seven-digit number. The one with the largest number is the winner.

Game 2 :
Use the same table, but you may write the number (you get on throwing the dice) in any box in front of anyone’s name. The one with the largest number is the winner.

Game 3 :
The rules are the same as for game 2, but the one with the smallest number is the winner.

Bigger and smaller numbers

Hamid : How do we determine the smaller or bigger number when we are dealing with six- or seven-digit numbers ?

Teacher : You have learnt how to do that with five-digit numbers. The number with the bigger ten thousands digit is the bigger number. If they are the same, we look at the thousands digits to determine the smaller or bigger number.

Now, can you tell how to compare six- or seven-digit numbers ?

Hamid : Yes, I can. First, we’ll look at the ten lakhs digits. If they are the same, we’ll look at the digits in the lakhs place. If those are equal, we look at the ten thousands place to tell the smaller or bigger number and so on. Besides, we might be able to tell which of the numbers is bigger, just by looking at the number of digits in each number. Right ?

Teacher : Absolutely ! The number with more digits is the bigger number.

Roman Numerals Problem Set 5 Additional Important Questions and Answers

Question 1.
Write the place value of the underlined digit.

(1) 81,67,303
Answer:
Here, the underlined digit 7 is in thousands place.
So, its place value is 7,000 (7 thousands)

(2) 41,35,062
Answer:
Here, the underlined digit 6 is in ten’s place.
So, its place value is 60 (sixty)

(3) 90,31,265
Answer:
Here, the underlined digit 3 is in ten thousands place.
So, its place value is 30,000 (30 thousands)

Question 2.
Write the numbers in their expanded form.
Answer:
(1) 51,03,640: .50,00,000 + 1,00,000 + 3,000 + 600 + 40
(2) 60,60,600: 60,00,000 + 60,000 + 600
(3) 71,45,042 : 70,00,000 + 1,00,000 + 40,000 + 5,000 + 40 + 2

Question 3.
Write the place name and place value of each digit in the following numbers.

(1) 1,88,919
Answer:
Digit 1 is in lakhs place, its place value is 1,00,000
Digit 8 is in ten thousands place, its place value is 80,000
Digit 8 is in thousands place, its place value is 8,000
Digit 9 is in hundreds place, its place value is 900
Digit 1 is in ten place, its place value is 10
Digit 9 is in units place, its place value is 9

Question 4.
The expanded form write the number.

(1) 40,00,000 + 5,00,000 + 10,000 + 3,000 + 200 + 70+8
Answer:
The number is 45,13,278

(2) 80,000 + 300 + 40 + 1
Answer:
The number is 80,341

Class 5 Maths Solution Maharashtra Board

• Roman Numerals Problem Set 1 Class 5 Maths Solutions
• Number Work Problem Set 2 Class 5 Maths Solutions
• Number Work Problem Set 3 Class 5 Maths Solutions
• Number Work Problem Set 4 Class 5 Maths Solutions
• Number Work Problem Set 5 Class 5 Maths Solutions 
• Number Work Problem Set 6 Class 5 Maths Solutions

Measuring Time Class 5 Problem Set 44 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 10 Measuring Time Problem Set 44 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 10 Measuring Time

Question 1.
The time below is given by the 12 hour clock. Write the same by the 24 hour clock.
(1) 30 minutes past 10 in the morning –
(2) 10 minutes past 8 in the morning –
(3) 20 minutes past 1 in the afternoon –
(4) 40 minutes past 5 in the evening –
Answer:
(1) [10:30]
(2) [8:10]
(3) [13:20]
(4) [17:40]

Question 2.
Match the following.
12 hour clock – 24 hour clock
(1) 9:10 am – 23:10
(2) 2:10 pm – 7:25
(3) 5:25 pm – 14:10
(4) 11:10 pm – 9:10
(5) 7:25 am – 17:25
Answer:
(1) – d
(2) – c
(3) – e
(4) – a
(5) – b

Examples of time measurement

Example (1) If Abdul started working on the computer at 11 in the morning and finished his work at 3:30 in the afternoon, how long did he work?

Method 1 :
From 11 in the morning to 12 noon, it is 1 hour. From 12 noon to 3:30 in the afternoon, it is 3 hours and 30 minutes. Therefore, the total time is 4 hours and 30 minutes.

Method 2 :
According to the 24 hour clock, 11’o’clock in the morning is 11:00 and 3:30 in the afternoon is 15:30.

Hr	Min
15 – 11	30 00
4	30

Abdul worked for a total of 4 hours and thirty minutes, or four and a half hours.

Example (2) Add : 4 hours 30 min + 2 hours 45 min

Example (3) Subtract : 5 hr 30 min – 2 hr 45 min

45 minutes cannot be subtracted from 30 minutes. Therefore, we borrow 1 hour and convert it into 60 minutes for the subtraction.

Example (4) Amruta travelled by bus for 3 hours 40 minutes and by motorcycle for 1 hour 45 minutes. How long did she spend travelling?

(60 + 25) minutes are 85 minutes, that is, 1 hour and 25 minutes.
Let us add this 1 hour to 4 hours.

Therefore, Amruta travelled for a total of 5 hours and 25 minutes.

Measuring Time Problem Set 44 Additional Important Questions and Answers

The time is given by the 12-hour clock. Write the same by the 24-hour clock.

(1) 15 minutes past 9 in the evening –
(2) 12 midnight –
Answer:
[21:15]
[0o:00]

The time below is given by the 24-hour clock. Write the same by the 12-hour clock.

(1) 20:20 =
(2) 9:30 =
(3) 23:00 =
(4) 4:00 =
(5) 12:00 =
(6) 00:00 =
Answer:
[8:20 pm]
[9:30 am]
[11 pm]
[4 am]
[12 noon] or [12:00]
[12 midnight]

Class 5 Maths Solution Maharashtra Board

• Measuring Time Problem Set 43 Class 5 Maths Solutions
• Measuring Time Problem Set 44 Class 5 Maths Solutions
• Measuring Time Problem Set 45 Class 5 Maths Solutions

Decimal Fractions Class 5 Problem Set 42 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 42 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 9 Decimal Fractions

Question 1.
Subtract the following :

(1) 25.74 – 13.42
Solution:

(2) 206.35 – 168.22
Solution:

(3) 63.4 – 31.8
Solution:

(4) 63.43 – 31.8
Solution:

(5) 63.4 – 31.83
Solution:

(6) 8.23 – 5.45
Solution:

(7) 18.23 – 9.45
Solution:

(8) 78.03 – 41.65
Solution:

Question 2.
Vrinda was 1.48 m tall. After a year, her height became 1.53 m. How many centimeters did her height increase in a year?
Answer:

∴ 5 cm height has increased in a year.

Something more

Decimals used for measurement

We need to measure distance, mass (weight) and volume every day. We use suitable units for these measurements. Kilometre, metre and centimeter for distance; litre, millilitre for volume and kilogram and gram for mass are the units that are used most of the time.

All these units are decimal units. In this method, gram, metre and litre are taken as the basic units for mass, distance and volume respectively. Units larger than these increase 10 times at every step and smaller units become \(\frac{1}{10}\) of the previous unit at each step.

Look at the table of these units given below.

The origin of the terms kilo, hecto… milli is in the Greek or Latin language. Their English equivalents are given in brackets along with the terms.

Decimal Fractions Problem Set 42 Additional Important Questions and Answers

Subtract the following:

(1) 304.17 – 95.28
Solution:

(2) 72.84 – 36.96
Solution:

(3) 9.17 – 5.88
Solution:

(4) 100 – 49.99
Solution:

(5) Atul has 56.25 and Anup has 65. Whose amount is more? How much?
Solution:

∴ Anup’s amount is more by ₹ 8.75

Class 5 Maths Solution Maharashtra Board

• Decimal Fractions Problem Set 36 Class 5 Maths Solutions
• Decimal Fractions Problem Set 37 Class 5 Maths Solutions
• Decimal Fractions Problem Set 38 Class 5 Maths Solutions
• Decimal Fractions Problem Set 39 Class 5 Maths Solutions
• Decimal Fractions Problem Set 40 Class 5 Maths Solutions
• Decimal Fractions Problem Set 41 Class 5 Maths Solutions
• Decimal Fractions Problem Set 42 Class 5 Maths Solutions

Multiples and Factors Class 5 Problem Set 33 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 8 Multiples and Factors Problem Set 33 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 8 Multiples and Factors

Question 1.
(1) Write five three-digit numbers that are multiples of 2.
Answer:
100, 102, 104, 106, 108.

(2) Write five three-digit numbers that are multiples of 5.
Answer:
100, 105, 110, 115, 120.

(3) Write five three-digit numbers that are multiples of 10.
Answer:
100, 110, 120, 130, 140.

Question 2.
Write 5 numbers that are multiples of 2 as well as of 3.
Answer:
2 as well as of 3 means 2 and 3 that is multiples of 6.
They are 6, 12, 18, 24, 30.

Question 3.
A ribbon is 3 metres long. Can we cut it into 50 cm pieces and have nothing left over? Write the reason why or why not.
Answer:
3 metres = 300 cm.
We can cut it into 50 cm pieces.
Since 300 is exactly divisible 50.
That is 300 is multiples of 50.
300 ÷ 50 = 6
We will get 6 pieces, nothing is left over.

Question 4.
A ribbon is 3 metres long. I need 8 pieces of ribbon each 40 cm long. How many centimetres shorter is the ribbon than the length I need?
Answer:
1 piece of 40 cm, so for 8 pieces ribbon needed is 40 x 8 = 320 cm.
But ribbon is 3 metre = 300 cm long.
So ribbon is shorter by 320 – 300 = 20 cm.

Question 5.
If the number given in the table is divisible by the given divisor, put ✓ in the box. If it is not divisible by the divisor, put ✗ in the box.

Answer:

Prime and composite numbers

Some numbers are given in the tables below. Write all of their factors.

Dada : What do you notice on studying the table?

Ajay : The number 1 is a factor of every number. Some numbers have only 1 and the number itself as factors. For example, the only factors of 3 are 1 and 3. Similarly, the factors of 2 are only 1 and 2 and the factors of 19 are only 1 and 19. Some numbers have more than two factors.

Dada : Numbers like 2, 3, 19 which have only two factors are called prime numbers.

A number which has only two factors, 1 and the number itself, is called a prime number.

Ajay : What do we call numbers like 4, 6 and 16 which have more than two factors?

Dada : Numbers like 4, 6 and 16 are called composite numbers.

A number which has more than two factors is called a composite number.

Dada : Think carefully and tell me whether 1 is a prime or composite number.

Ajay : The number 1 has only one factor, 1 itself, so I can’t answer your question.

Dada : You’re right. 1 is considered neither a prime number nor a composite number.

1 is a number which is neither prime nor composite.

Multiples and Factors Problem Set 33 Additional Important Questions and Answers

Question 1.
Write five three-digit numbers that are multiples of 3.
Answer:
102, 105, 108, 111, 114.

Question 2.
Write five two-digit numbers that are multiples of 7.
Answer:
14, 21, 28, 35, 42

Question 3.
Write five three-digit numbers that are multiples of 4.
Answer:
112, 116, 120, 124, 128.

Question 4.
Write 5 numbers that are multiples of 3 as well as 5.
Answer:
3 as well as 5 means 3 and 5. i.e. multiples of 15.
They are 15, 30, 45, 60, 75.

Question 5.
A string is 4 metres long. Can we cut it into 50 cm pieces and have nothing left over?
Answer:
4 metres = 400 cm.
We can cut it into 50 cm pieces.
Since 400 is exactly divisible by 50.
That is 400 is multiple of 50 400 + 50 = 8
We will get 8 pieces. Nothing is left over.

Question 6.
A paper Is 2 metres long. I need 8 pieces of paper each 30 cm long. How many centimetres shorter is the paper than the length I need?
Answer:
A piece of 30 cm, so for 8 pieces paper needed is 30 x 8 = 240 cm.
But paper is 2 metre = 2 x 100 = 200 cm long.
So paper is shorter by 240 – 200 = 40 cm

Question 7.
If the number given in the table is divisible by the given divisor, put P in the box. If it is not divisible by the divisor, put in the box.
Answer:

Class 5 Maths Solution Maharashtra Board

• Multiples and Factors Problem Set 32 Class 5 Maths Solutions
• Multiples and Factors Problem Set 33 Class 5 Maths Solutions
• Multiples and Factors Problem Set 34 Class 5 Maths Solutions
• Multiples and Factors Problem Set 35 Class 5 Maths Solutions

Circles Class 5 Problem Set 29 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 7 Circles Problem Set 29 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 7 Circles

Question 1.
If the radius of a circle is 5 cm, what will its diameter be?
Solution :
Diameter
= 2 x radius
= 2 x 5 = 10 cm

Question 2.
If the diameter of a circle is 6 cm, what will its radius be?
Solution :
Radius
= diameter ÷ 2
= 6 ÷ 2
= 3 cm

Question 3.
Complete the following table by filling in the blanks.

Answer:

The interior and the exterior of a circle

We play ‘Land and Sea’ inside a circle on the playground. In this game, the children inside the circle are in the ‘sea’, while the children outside the circle are on ‘land’.

In the picture alongside, K, L, M and N are points on a circle with centre T.

The coloured area inside the circle in the picture is the interior of the circle. P, Q, R and T are points in the interior of the circle.

A, B, C and D are points in the exterior of the circle.

Circles Problem Set 29 Additional Important Questions and Answers

Question 1.
If the radius of a circle is 3.5 cm, what will its diameter be?
Solution :
Diameter
= 2 x radius
= 2 x 3.5
= 7 cm

Question 2.
If the diameter of a circle is 5 cm, what will its radius be?
Solution :
Radius
= Diameter ÷ 2
= 5 ÷ 2
= 2.5 cm

Class 5 Maths Solution Maharashtra Board

• Circles Problem Set 28 Class 5 Maths Solutions
• Circles Problem Set 29 Class 5 Maths Solutions
• Circles Problem Set 30 Class 5 Maths Solutions
• Circles Problem Set 31 Class 5 Maths Solutions

Preparation for Algebra Class 5 Problem Set 54 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 16 Preparation for Algebra Problem Set 54 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 16 Preparation for Algebra

Question 1.
Using brackets, write three pairs of numbers whose sum is 13. Use them to write three equalities.
Answer:
(7 + 6), (8 + 5), (9 + 4). since 7 + 6
= 13,8 + 5
= 13, 9 + 4
= 13.

(7 + 6)
= (8 + 5), (7 + 6)
= (9 + 4) or (8 + 5)
= (9 + 4).

Question 2.
Find four pairs of numbers, one for each of addition, subtraction, multiplication and division that make the number 18. Write the equalities for each of them.
Answer:
(9 + 9), (20 – 2), (9 x 2), (36 ÷ 2).
since 9 + 9
= 18, 20 – 2
= 18, 9 x 2
= 18 and 36 + 2
= 18, so (9 + 9)
= (20 – 2)
= (9 x 2)
= (36 ÷ 2).

Inequality
The values of 7 + 5 and 7 × 5 are 12 and 35 respectively. It means that they are not equal. To represent ‘not equal’, the symbol ‘≠’ is used.

To show that (7 + 5) and (7 × 5) are not equal, we write (7 + 5) ≠ (7 × 5) in short.

This kind of representation is called an ‘inequality’.

(9 – 5) ≠ (15 ÷ 3) means that the expressions (9 – 5) and (15 ÷ 3) are not equal.

If two expressions are not equal, one of them is greater or smaller than the other.

To show greater or lesser values, we use the symbols ‘<’ and ‘>’. Therefore, these symbols can also be used to show inequalities.

The value of (9 – 5) is 4 and the value of (15 ÷ 3) is 5. 4 < 5, so the relation between (9 – 5) and (15 ÷ 3) can be shown as (9 – 5) < (15 ÷ 3) or (15 ÷ 3) > (9 – 5).

Fill in the boxes between the expressions with <, = or > as required.

(1) (9 + 8) [ ] (30 ÷ 2)
9 + 8 = 17,
30 ÷ 2 = 15
17 > 15
Therefore (9 + 8) [ > ] (30 ÷ 2)

(2) (16 × 3) (4 × 12)
16 × 3 = 48,
4 × 12 = 48,
48 = 48
Therefore (16 × 3) [ = ] (4 × 12)

(3) (16 – 5) [ ] (2 × 7)
16 – 5 = 11,
2 × 7 = 14,
11 < 14
Therefore (16 – 5) [ < ] (2 × 7)

Write a number in the box that will make this statement correct.
(1) (7 × 2) = ( [ ] – 6)

The value of the expression 7 × 2 is 14, so the number in the box has to be one that gives 14 when 6 is subtracted from it. Subtracting 6 from 20 gives us 14.

Therefore (7 × 2) = ( [ 20 ] – 6 )
(2) (24 ÷ 3) < (5 + [ ] )
The value of the expression 24 ÷ 3 is 8, so the number in the box has to be such that when it is added to 5, the sum is greater than 8.

Now, 5 + 1 = 6, 5 + 2 = 7, 5 + 3 = 8. So the number in the box has to be greater than 3.

Therefore, writing any number like 4, 5, 6 … onwards will do. It means that this problem has several answers. (24 ÷ 3) < (5 + [ 4 ] ) is one among many answers. Even if that is true, writing only one answer will be enough to complete this statement.

Preparation for Algebra Problem Set 54 Additional Important Questions and Answers

Question 1.
Fill in the blanks.
(1) 7 + 3 = …………….. – ……………..
(2) 7 + 3 = …………….. x ……………..
(3) 7 + 3 = …………….. + ……………..
Answer:
(1) 7 + 3 = 10 and 12 – 2 = 10 or 15 – 5 = 10
(2) 7 + 3 = 10 and 10 x 1 = 10 or 5 x 2 = 10
(3) 7 + 3 = 10 and 20 + 2 = 10 or 30 + 3 = 10

Question 2.
Write the proper number in the box.
(1) 7 + 8 = 10 + [ ]
(2) 7 + 8 = 20 – [ ]
(3) 7 + 8 = 30 + [ ]
(4) 7 + 8 = 5 x [ ]
Answer:
(1) 7 + 8 = 15 so, 10 + [ ] = 15.
∴ [ ] = 15 – 10 = 5

(2) 7 + 8 = 15 s0, 20 – [ ] = 15.
∴[ ] = 20 – 15 = 5

(3) 7 + 8 = 15 so, 30 + [ ] = 15.
∴ [ ] = 30 + 15 = 2

(4) 7 + 8 = 15 so, 5 x [ ] = 15.
∴[ ] = 15 + 5 = 3

Class 5 Maths Solution Maharashtra Board

• Three Dimensional Objects and Nets Problem Set 51 Class 5 maths Solutions
• Pictographs Problem Set 52 Class 5 maths Solutions
• Patterns Problem Set 53 Class 5 maths Solutions
• Preparation for Algebra Problem Set 54 Class 5 maths Solutions
• Preparation for Algebra Problem Set 55 Class 5 maths Solutions
• Preparation for Algebra Problem Set 56 Class 5 maths Solutions

Pictographs Class 5 Problem Set 52 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 14 Pictographs Problem Set 52 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 14 Pictographs

Question 1.
Stocks of various types of grains stored in a warehouse are as given below. Make a pictograph based on the information given.

Grain	Sacks
Rice	40
Wheat	56
Bajra	8
Jowar	32

Answer:
Scale :1 picture = 8 sacks

Question 2.
Information about the various types of vehicles in Wadgaon is given below. Make a pictograph for this data.

Types of vehicles	Number
Bicycles	84
Automatic two-wheelers	60
Four-wheelers (cars/jeeps)	24
Heavy vehicles (truck, bus, etc.)	12
Tractors	24

Answer:

Question 3.
The numbers of the various books kept in a cupboard in the school library are given below. Make a pictograph showing the information given.

Type of book	Number
Science	28
Sports	14
Poetry	21
Literature	35
History	7

Answer:

Activity
Collect information based on the points given below and make a pictograph for each.

• Which crops are grown on the farms owned by students in your class? (Vegetables, grains, pulses, fruits, etc.)
• Which storybooks do your classmates like? (fairytales, stories about kings and queens, historical stories, stories about saints, picture stories, etc.)
• What do your classmates want to be when they grow up ? (doctor, teacher, farmer, engineer, officer, etc.)

Perimeter and Area Problem Set 49 Additional Important Questions and Answers

Solve the following

Question 1.
Information regarding the number of pages of novel book read in different days by Rosi are as follows. Make a pictograph showing the information given.

Days	1st day	2nd day	3rd day	4th day
Pages	60	40	30	20

Question 2.
Different types of currency notes had with Shamin are as follows. Make a pictograph showing the information given.

Types of Notes	₹ 500	₹ 100	₹ 50	₹ 10
Number of Notes	8	10	6	4

Question 3.
Different types of colour of scooters sold by a merchant are as follows. Make a pictograph showing the data given.

Colour	White	Red	Black	Yellow
No, of scooters sold	6	9	12	3

Question 4.
Ajhount of sales of goods in rupees for the first four days of a week are as follows. Make a pictograph from the information given below.

Days	Marks
Monday	₹ 150
Tuesday	₹ 200
Wednesday	₹ 250
Thursday	₹ 100

Answer:
(1) All the given numbers can be divided by 2, 5, and 10. 1 picture of 10 pages will be convenient scale so 6 pictures for 60 pages. 4 pictures for 40, 3 for 30 and 2 for 20.
(2) All the given numbers can divided by 2 only, so 1 picture for 2 notes will be the scale. So, 4 pictures for notes of ? 500, 5 for ? 100 notes, 3 for ? 50 and 2 for ? 10.
(3) All given numbers are divisible by 3, so 1 picture for 3 scooters will be the scale. So, 2 pictures for white, 3 for Red, 4 for Black and 1 pictures for Yellow.
(4) All the given numbers can be divided by 2, 5,10, 25 and 50. So, 1 picture for 50 rupees will be convenient scale. So, draw 3 pictures for Monday, 4 for Tuesday, 5 for Wednesday and 2 for Thursday.
(5) Number of books are multiples of 50. Therefore Take number of pictures = 5,4,2, 1, 3 respectively.

Class 5 Maths Solution Maharashtra Board

• Three Dimensional Objects and Nets Problem Set 51 Class 5 maths Solutions
• Pictographs Problem Set 52 Class 5 maths Solutions
• Patterns Problem Set 53 Class 5 maths Solutions
• Preparation for Algebra Problem Set 54 Class 5 maths Solutions
• Preparation for Algebra Problem Set 55 Class 5 maths Solutions
• Preparation for Algebra Problem Set 56 Class 5 maths Solutions

Perimeter and Area Class 5 Problem Set 50 Question Answer Maharashtra Board

Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 12 Perimeter and Area Problem Set 50 Textbook Exercise Important Questions and Answers.

Std 5 Maths Chapter 12 Perimeter and Area

Question 1.
The length of the side of each square is given below. Find its area.

(1) 12 metres
Solution:
Area of a square
= side x side
= 12 x 12

(2) 6 cm
Solution:
Area of a square
= side x side
= 6 x 6
= 36 sq.cm.

(3) 25 metres
Solution:
Area of a square
= side x side
= 25 x 25
= 625 sq.m.

(4) 18 cm
Solution:
Area of a square
= side x side
= 18 x 18
= 324 sq.cm.

Question 2.
If the cost of 1 sq m of a plot of land is 900 rupees, find the total cost of a plot of land that is 25 m long and 20 m broad.
Solution:
Area of the rectangular plot
= length x breadth
= 25 x 20
= 500 sq.m.

Cost of the plot of land
= Area of the plot x rate
= 500 x 900
= 4,50,000 rupees

Question 3.
The side of a square is 4 cm. The length of a rectangle is 8 cm and its width is 2 cm. Find the perimeter and area of both figures.
Solution:
Perimeter of a square = 4 x side
= 4 x 4
= 16 cm

Area of a square = side x side
= 4 x 4
= 16 sq.cm.

Perimeter of a rectangle
= 2 x length + 2 x breadth
= 2 x 8 + 2 x 2
= 16 + 4
= 20 cm

Area of a rectangle
= length x breadth
= 8 x 2
= 16 sq.cm.

Question 4.
What will be the labour cost of laying the floor of an assembly hall that is 16 m long and 12 m wide if the cost of laying 1 sq m is 80 rupees?
Solution:
Area of rectangular floor
= length x breadth
= 16 x 12
= 192 sq.cm.

The cost of laying 1 sq.m, is 80 rupees.
Hence, the cost of laying 192 sq.m.
= 192 x 80
= 15,360 rupees.
∴ ₹ 15,360

Question 5.
The picture alongside shows some squares. Find out how many squares with the same measures will fit in the empty space in the figure.

Solution:
length of the empty space = 4 – 1 = 3 cm
breadth of the empty space = 3 – 1 = 2 cm
square in empty space
= length x breadth
= 3 x 2 = 6 sq.cm.

∴ 6 squares will fit in the empty space in the figure

Question 6.
Divide the figure given alongside into four parts in such a way that the area and shape of each part is the same. Colour the parts with different colours.

Fair and square

As shown in the figure alongside, a square plot of land owned by the government contains four houses and a well right in the centre. The government has to divide the houses and the land between four poor persons according to the following conditions.
(1) Each person must get only one house.
(2) The shape and area of the land must be the same.
(3) Each person must be able to use the well without trespassing on any one else’s land.

Show the appropriate divisions in four different colours.

Activity
Using a graph paper, find out the area of different rectangles and squares.

Perimeter and Area Problem Set 50 Additional Important Questions and Answers

Question 1.
15 cm
Solution:
Area of a square
= side x side
= 15 x 15
= 225 sq.cm.

Question 2.
21 cm
Solution:
Area of a square = side x side
= 21 x 21
= 441 sq.cm.

Solve the following:

Question 1.
The side of a square hall is of length 8 m. If it is tiled with a tile of length 4 m and breadth 2 m., how many tiles will be required?
Solution:
Area of the square hall
= side x side
= 8 x 8
= 64 sq.m.

Area of 1 rectangular tile
= length x breadth
= 4 x 2

∴ 8 sq.m.

For 8 sq.m., 1 tile is required,
but for 64 sq.m = \(\frac{64}{8}\) = 8 tiles required

∴ 8 tiles required

Question 2.
Perimeter of a square is 16 cm. What is the length of each side? What is the area of the square?
Solution:
Perimeter of square = 4 x side
16 = 4 x side

∴ side of a square = \(\frac{16}{4}\) = 4 cm
Area of the square
= side x side
= 4 x 4
= 16 sq.cm

∴ Side of square is 4 cm and area of the sqaure is 16 sq.cm

Question 3.
Write the perimeter of each figure in the box given below it.

Answer:
24 cm

Answer:
18 cm

Answer:
21 cm

Answer:
20 cm

Question 4.
Two squares of side 2 cm is cut out of two corners of a larger square with side 5 cm (see the figure). What will be the perimeter of the remaining shape?

Answer:
20 cm

Question 5.
Match the columns ‘A’ and ‘B’

Answer:
(1- d),
(2- a),
(3 – b),
(4 – c)

Question 6.
Solve the following word problems:
(1) What is the perimeter of a rectangle having length 9 cm and its breadth 6 cm?
(2) The sides of a rectangular field are having length 150 m and breadth 100 m. Find the perimeter of field.
(3) If each side of a square is 8 cm then what is the perimeter of the square?
(4) A rectangular garden of length 650 m and breadth 350 m. Mohan makes four rounds daily. How many kilometres does he walk everyday?
(5) One square field is having one side of it is of 225 m, Soham makes 6 rounds of the square field daily. How much distance is covered by him? Write it in km and m.
(6) A rectangular field whose length is 58 m and breadth is 32 m. Fencing the field by 4 rounds with a wire, what length of wire is required? If the cost of 1 m wire is ? 75, then what is the expenditure of fencing the field?
(7) A length of a rectangular classroom is 8 m and its breadth is 5 m. A wooden strip is to be fitted along the four walls to hang charts and pictures. What is the length of the wooden strip required?
(8) The side of a square table is 1.5 m. To fit a strip of tin sheet around the table, how many metres of strip is required?
(9) What is the perimeter of the triangle whose sides are 13.8 cm, 17.6 cm and 10.6 cm?
(10) The sides of some squares are given below. Find their areas.
(i) 11 cm (ii) 23 cm (iii) 9 cm
(11) Find the perimeter and area of the following:
(i) square of side 6 cm
(ii) Rectangle: length 12 cm and breadth 6 cm
(12) A rectangular land is having its length 25 m and breadth 16 m. If the cost of 1 sq.m, land is ? 1,500, then what will be cost of land?
(13) The side of a square plot is 10 metre. It is tiled at the rate of 50 rupees per sq.m. What will be cost of tiling the floor?
(14) A wall of length 25 m and breadth 12 m. It is painted at the rate of 60 rupees per sq.m. What will be cost of painting the wall?
Answer:
(1) 30 cm
(2) 500 m
(3) 32 cm
(4) 8 km
(5) 5 km 400 m
(6) ₹ 54,000
(7) 26 m
(8) 6 m
(9) 42 cm

(10) (i) 121 sq. cm
(ii) 529 sq.cm
(iii) 81sq.cm.

(11) (i) Perimeter = 24 cm, Area = 36 sq.cm,
(ii) Perimeter = 36 cm, Area = 72 sq. cm

(12) 6,00,000 rupees
(13) 5,000 rupees
(14) t 18,000

Question 7.
Look at the figures on the sheet of graph paper. Measure their sides with the help of the lines on the graph paper. Write the perimeter of each in the right box.

Perimeter of Rectangle
(1) XYZW = [ ] cm
(2) CDEF = [ ] cm
(3) JKLM = [ ] cm
(4) NOPQ = [ ] cm
Answer:
(1) 12 cm
(2) 10 cm
(3) 10 cm
(4) 8 cm

Question 8.
Find the area of the. following figures. (All small squares are having side 1 cm)

Answer:
5 sq.cm

Answer:
4 sq.cm

Answer:
9 sq.cm

Answer:
16 sq.cm.

Question 9.
The pictures below shows some squares. Find out how many squares with the same measures will fit in the empty space in the figures.

Answer:
(1) 9
(2) 9

Question 10.
Fill in the blanks:

Answer:
(1) Area = 24 sq.cm., Perimeter = 22 cm
(2) Breadth = 4 cm, Perimeter = 20 cm
(3) Length = 2 cm, Perimeter = 8 cm

Class 5 Maths Solution Maharashtra Board

• Problems on Measurement Problem Set 46 Class 5 Maths Solutions
• Problems on Measurement Problem Set 47 Class 5 Maths Solutions
• Perimeter and Area Problem Set 48 Class 5 Maths Solutions
• Perimeter and Area Problem Set 49 Class 5 Maths Solutions
• Perimeter and Area Problem Set 50 Class 5 Maths Solutions