Prasanna

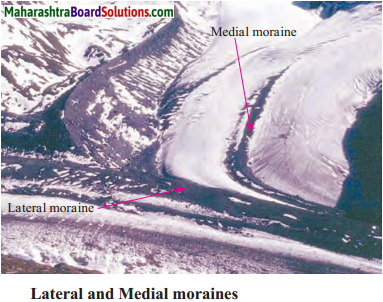
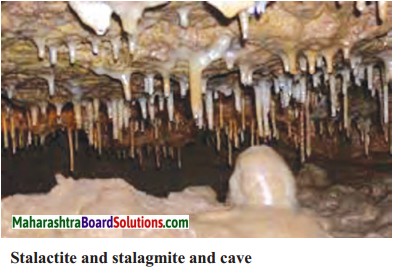
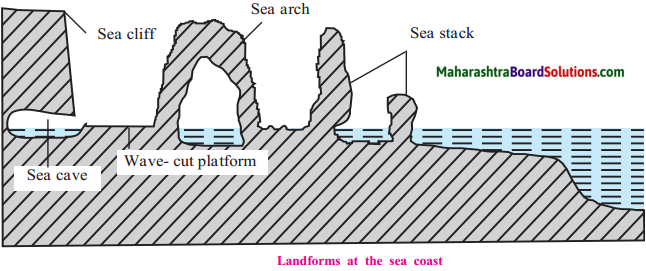
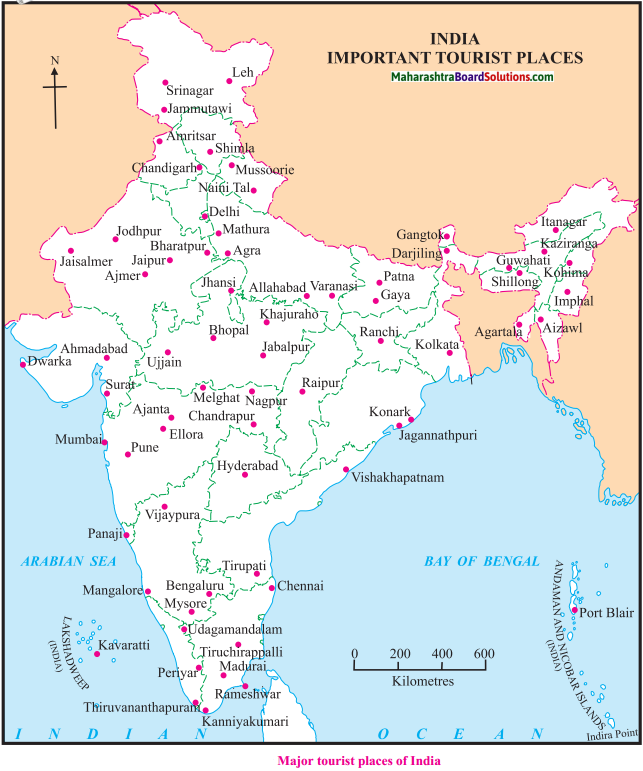
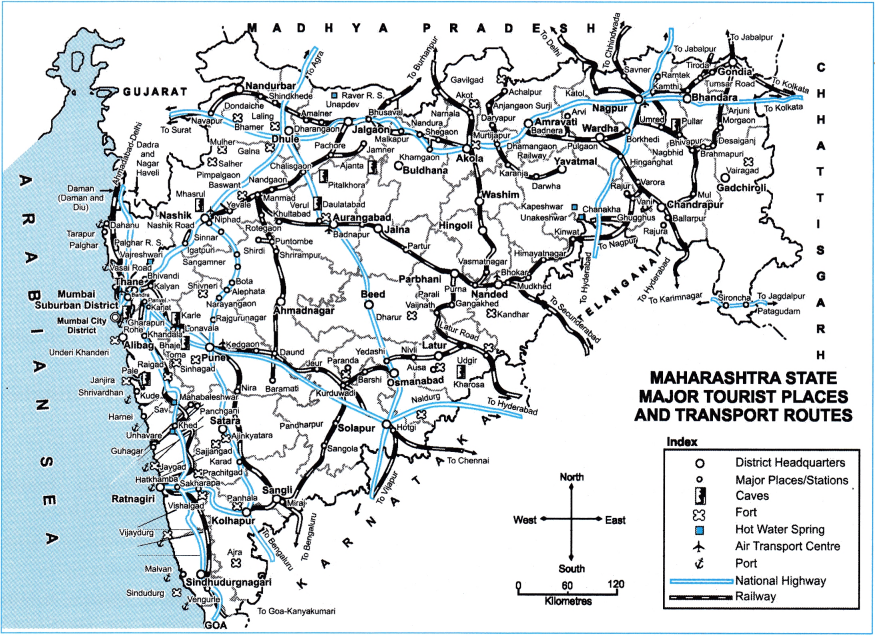
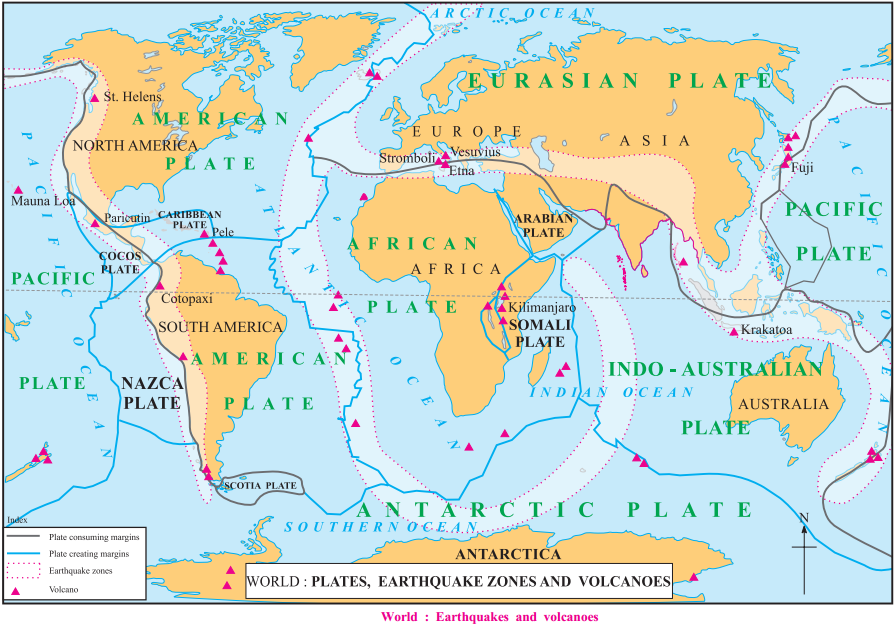
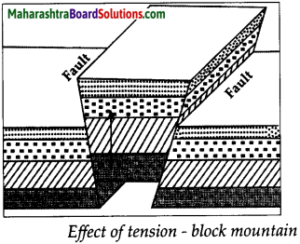
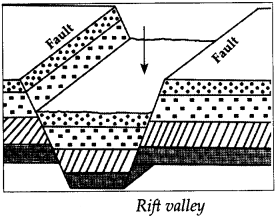
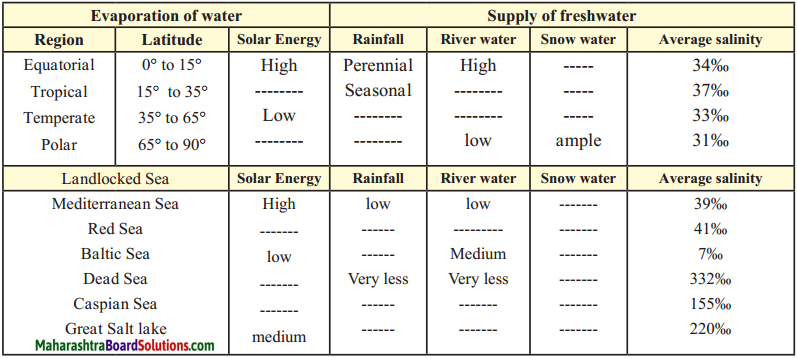
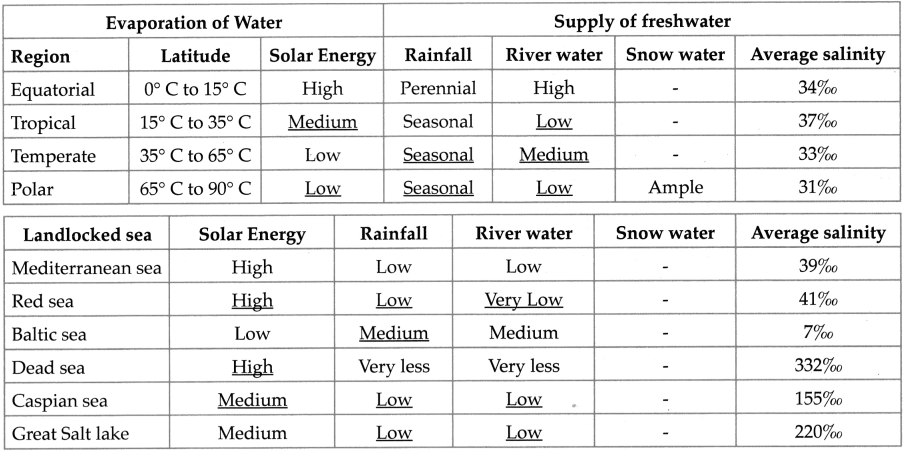
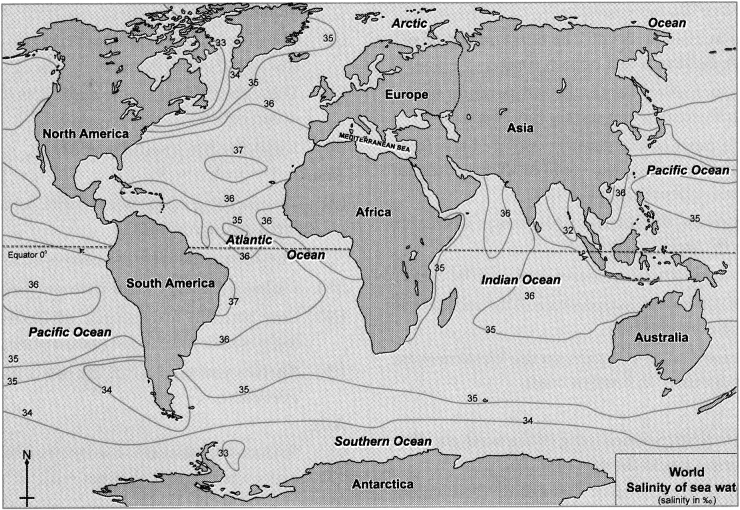
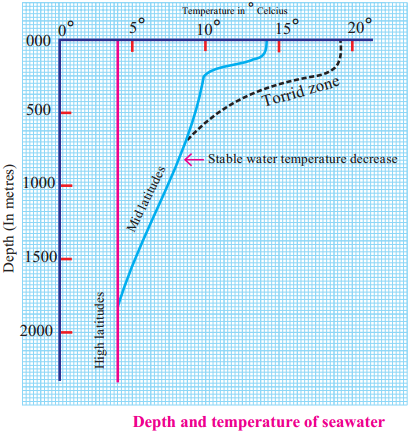
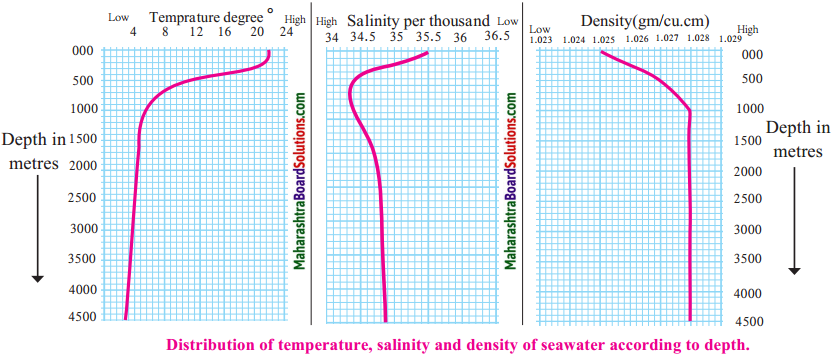
Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 3 Exogenetic Movements Part 1 Notes, Textbook Exercise Important Questions and Answers.

Exogenetic Movements Part 1 Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 3 Exogenetic Movements Part 1 Questions And Answers Maharashtra Board

Geography Class 9 Chapter 3 Question Answer Maharashtra Board

1. Answer in brief.
(a) What is mechanical weathering?
Answer:

1. The disintegration of rocks without any change in their chemical composition is called mechanical weathering.
2. The minerals in the rocks expand because of heat and contract when the temperature decreases. Due to such continuous contracting and expansion, tension develops in the rock particles.
3. Each mineral reacts differently to the temperature; some minerals expand more, while others do not expand as much. Consequently, the tension formed in the rocks also increases and decreases. As a result, cracks develop in the rocks and they break.
4. In areas where the temperatures drop below 0°C for quite some time, the water accumulated in the cracks and crevices in the rocks freezes. Its volume increases which leads to tension in the rocks and they shatter.
5. When the alkaline water of the sea fills in the cracks of the rocks, the soluble minerals in the rock get dissolved leading to the formation of small holes in the rocks.
6. Because of the heat, this water turns into water vapour and only crystals of alkaline materials remain in the rocks. Crystals occupy more space which causes tension in the rock.
7. Sometimes the outer layers of the rocks exert pressure on the inner or lower layers. When this pressure ceases to exist, the lower or inner layers get freed from the pressure. This also leads to weathering.
8. In areas of heavy rainfall soaking of rock water also causes weathering of some rocks like sandstone and conglomerate. When water penetrates such rocks, the particles get loose and separate from the main rock.

(b) What are the main types of chemical weathering?
Answer:
The process of decomposition of rocks due to changes in their chemical composition is called chemical weathering.
Its main types are:
(i) Carbonation

• When the rain water mixes with the carbon dioxide in the atmosphere it leads to the formation of dilute carbonic acid.
• Many rocks like limestone get easily dissolved in such acids.

(ii) Solution

• Some minerals in the rock get dissolved in water.
• Because of this solution, alkalis in the rock dissolve and make them brittle.

(iii) Oxidation

• This process occurs in rocks which have iron present in them. The iron in the rock comes in contact with water and a chemical reaction takes place between iron and oxygen.
• Hence, a reddish coloured layer forms on the rocks. This is called rust.
• It occurs in rocks in areas with high rainfall.

(c) How does biological weathering occur?
Answer:

• It is the process by which rocks are broken into small fragments and fine particles due to the action of plants, animals and human beings.
• The roots of the plants enter the points and ! cracks of the rocks in search of moisture.
• As the roots grow bigger, they create tension in the rocks and start breaking them.
• Animals such as mice, rabbits and rats dig I holes, anthills etc. and weaken the rock, which makes them loose and break into pieces.
• Besides these, algae, moss1, lichen2, other flora grow in the rocks. They also help in weathering.
• Thus, the weathering caused by living organisms is called biological weathering,

(d) Distinguish between weathering and mass wasting.
Answer:

Weathering	Mass Wasting
(i) Breaking or weakening of rocks is called as weathering.	(i) When weathered rock material moves down the slopes due to gravity and accumulate near the foothills or gentle slopes, it is mass wasting.
(ii) Weathering is of three types – Mechanical, Chemical and Biological.	(ii) Mass wasting is of two types – Rapid and Slow.

2. Write whether the statements are true or false. Correct the incorrect ones.

(a) Climate affects earthquakes.
Answer:
False – Internal movements affect (leads to) earthquakes.

(b) Mechanical weathering is less effective in humid climates.
Answer:
True

(c) Mechanical weathering happens on a large scale in dry climates.
Answer:
True

(d) The breaking down of rocks into smaller particles is called weathering.
Answer:
True

(e) Lateritic rocks are formed through exfoliation.
Answer:
False – Lateritic rocks are formed due to oxidation.

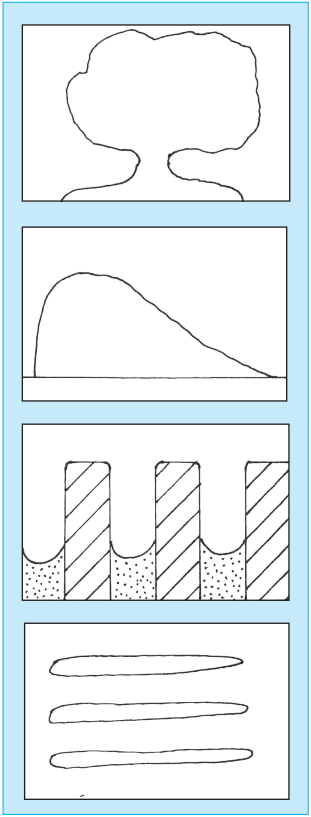
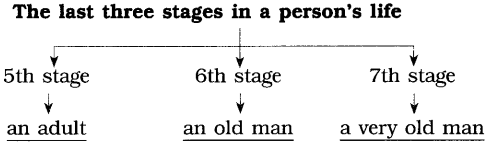
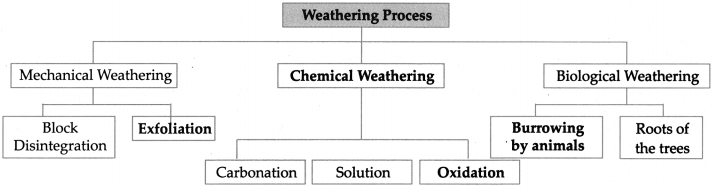
3. Complete the flowchart below.

Answer:

4. Identify the type of weathering from the given description.

(a) Some animals live inside the grounds by making burrows.
(b) The rock rusts.
(c) Water which has accumulated in the crevices of the rocks freezes. Consequently, the rock breaks.
(d) The pipes supplying water in colder regions break.
(e) Sand formation occurs in deserts
Answer:
(a) Biological weathering
(b) Chemical weathering
(c) Mechanical weathering
(d) Mechanical weathering
(e) Mechanical weathering

Class 9 Geography Chapter 3 Exogenetic Movements Part 1 Intext Questions and Answers

Can You Tell?
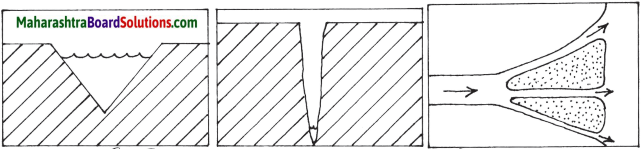
(1) See the given pictures. Observe the physical appearance of the rocks in each picture. You can see that rocks are broken, fractured and have holes in them. In a picture you can also see that the statue has been deformed. Why are the rocks in such a condition? Think about them and briefly tell the reasons you can think of. Discuss the reasons. Check with the teachers if your reasons are relevant.
Answer:

• At some places the day temperatures are very high and the night temperatures are very low. In the given pictures the rocks may have broken due to temperature variation during day time and night time.
• In coastal areas when the sea waves hit the rocks, the rocks fracture and break down.
• Due to the roots of trees, and activities of burrowing animals like ant, rats etc. in the soft rocks, the rocks break down.
• The statues might be deformed due to heat and humidity.

Lets Recall

Question 1.
Have you seen the process of biological weathering3 around you?
Answer:
I have seen process of biological weathering3 around me. Many plants and trees have grown in an old dilapidated building which is located near my house. The roots of the trees have broken the walls and slabs of the building at many places.

Class 9 Geography Chapter 3 Exogenetic Movements Part 1 Additional Important Questions and Answers

Complete the statements choosing the correct option from the bracket:

Question 1.
…………………… is formed due to chemical precipitation between water and alkalis.
(a) Limestone
(b) Sandstone
(c) Coal
(d) Iron
Answer:
(a) Limestone

Question 2.
…………………… process occurs in rocks which have iron present in them.
(a) Shattering
(b) Oxidation
(c) Carbonation
(d) Granular
Answer:
(b) Oxidation

Question 3.
Sometimes the weathered materials do not move downward but sink ‘in situ’. This is called ………………….. .
(a) carbonation
(b) exfoliation
(c) precipitation
(d) slumping
Answer:
(d) slumping

Question 4.
periglacial regions along the slopes, small layers of soil accumulate because of the movement of soil. This is called ………………….. .
(a) soil erosion
(b) solifluction
(c) shattering
(d) block disintegration
Answer:
(b) solifluction

Question 5.
Biological weathering occurs because of ………………….. .
(a) high temperatures
(b) frost
(c) crystal growth
(d) living organisms
Answer:
(d) living organisms

Question 6.
come minerals in the rock get dissolved in the water and undergo chemical weathering. This process is called ………………….. .
(a) solution
(b) carbonation
(c) exfoliation
(d) precipitation
Answer:
(a) solution

Question 7.
When dilute carbonic acids reacts with the minerals in the rocks the process is called as ………………….. .
(a) carbonation
(b) exfoliation
(c) precipitation
(d) slumping
Answer:
(a) carbonation

Question 8.
When the outer layers of the rock fall apart from the main rock due to difference in temperatures, the process is called ………………….. .
(a) shattering
(b) oxidation
(c) exfoliation
(d) carbonation
Answer:
(c) exfoliation

Question 9.
…………………… is a universal solvent¹.
(a) Soil
(b) Water
(c) Carbon
(d) Oxygen
Answer:
(b) Water

Question 10.
Alkalis in the rock dissolve because of the solution and make them ………………….. .
(a) even
(b) sturdy
(c) brittle
(d) crusty
Answer:
(c) brittle

Match the Column:

I.

(I) Column ‘A’	Column ‘B’
(1) Mechanical weathering (2) Chemical weathering (3) Biological weathering	(a) burrowing (b) frost (c) carbonation (d) erosion

Answer:
(1-b),
(2- c),
(3 – a)

II.

Column ‘A’	Column ‘B’
(1) Oxidation (2) Slumping (3) Solifluction	(a) Mass movement occurring slowly (b) Carbon dioxide gets mixed with air (c) Chemical reaction between iron and oxygen (d) Weathered material which sink in situ

Answer:
(1 – c),
(2 – d),
(3 – a)

Answer in one sentence each;

Question 1.
What are the Exogenetic processes?
Answer:
Exogenetic processes are external processes 1 that occur on or above the earth’s surface, E.g. weathering, erosion, transportation, deposition etc.

Question 2.
Explain the Process of weathering
Answer:
Breaking or weakening of rocks is called as weathering.

Question 3.
What is Mechanical Weathering?
Answer:
The disintegration of rocks without any change in their chemical composition is called mechanical weathering.

Question 4.
What is Chemical Weathering (Salt Weathering)?
Answer:
The process of decomposition of rocks due to changes in their chemical composition is called chemical weathering.

Question 5.
What do you mean by Biological Weathering?
Answer:
The weathering process caused by human beings, animals and plants is called biological weathering.

Question 6.
What is Slumping?
Answer:
Sometimes the weathered materials do not move downward but sink ‘in situ’ (where they ! are). This is called slumping. ;

Question 7.
What is Solifluction?
Answer:
In periglacial regions along the slopes, small layers of soil accumulate because of the movement of soil. This is called solifluction.

Question 8.
Explain Granular Weathering.
Answer:
When water penetrates in rocks like sandstones and conglomerates1, the particles get loose and separate from the main rock. This is called granular weathering.

Question 9.
What is Block Disintegration?
Answer:
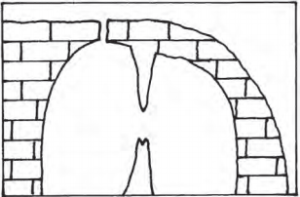
When water accumulates in wide points and big blocks of rocks separate from each other, this is called block disintegration.

Question 10.
What is Exfoliation?
Answer:
When the outer layer of the racks fall apart from the main rock due to temperature, the process is called exfoliation.

Question 11.
What does the term ‘diurnal Range’ mean
Answer:
The difference between the daily maximum and minimum temperature is diurnal Range.

Question 12.
What is Solution?
Answer:
The minerals in rocks which dissolve in water leads to the formation of solutions.

Question 13.
Name the two types of mass movements.
Answer:
The two types of mass movements are:
(a) Rapid Mass Movement and
(b) Show Mass movement.

Question 14.
What are the types of Mechanical weathering?
Answer:
The types of Mechanical weathering are
(a) Temperatures
(b) Frost
(c) Crystal growth
(d) Release of pressure and
(c) water

Question 15.
Types of chemical weathering.
Answer:
The types of chemical weathering are:
(a) Carbonation
(b) Solution and
(c) Oxidation

Question 16.
Where does Mechanical weathering occur?
Answer:
Mechanical weathering occurs mainly in the arid climates.

Question 17.
Chemical weathering can be seen in which climates?
Answer:
In humid conditions, one can see chemical weathering.

Write whether the statements are TRUE or FALSE. Correct the incorrect statements.

Question 1.
Soil creep is uncommon in areas with dry climates and gentle slopes.
Answer:
False – It is a common phenomenon in such areas.

Question 2.
Shattering is a type of mechanical weathering
Answer:
True.

Question 3.
Granular weathering occurs in areas of heavy rainfall.
Answer:
True.

Distinguish between:

Question 1.
Mechanical Weathering and Chemical Weathering.
Answer:

Mechanical Weathering	Chemical Weathering
(i) In this type of weathering, rocks get disintegrated but the chemical composition of the rocks does not change.	(i) It is a process where rocks get disintegrated and the chemical composition of the rocks change.
(ii) It is caused due to differences in the day and night temperature.	(ii) It is caused due to the reaction of oxygen, carbon dioxide and water with certain rock minerals.
(iii) It is more common in an extremely cold climates and hot dry desert climates.	(iii) It is more common in hot and humid climates.

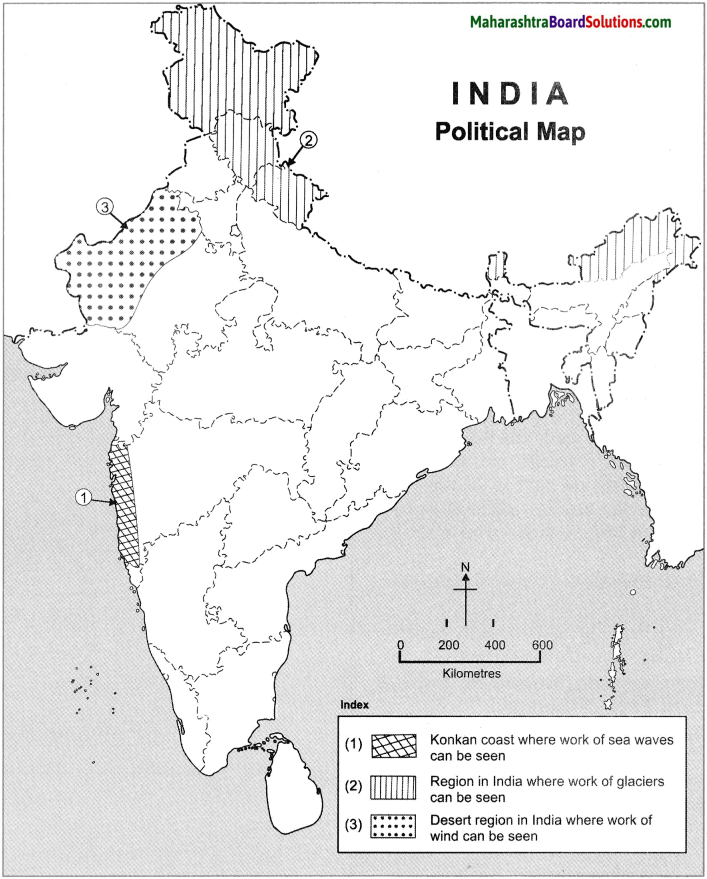
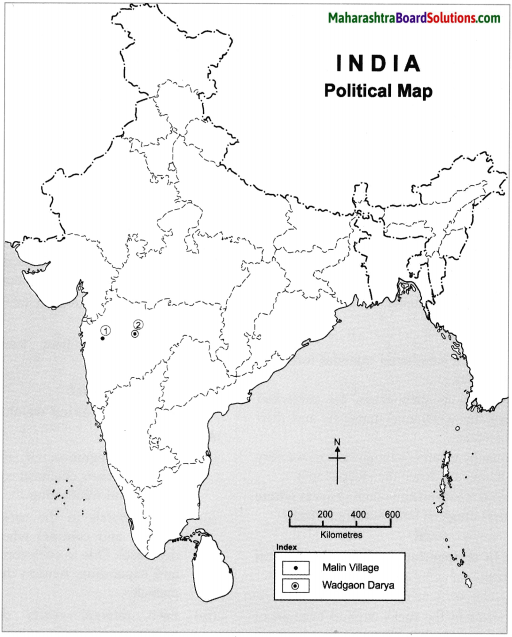
Fill the map with the given information and make a legend.
(1) Area affected by a landslide (mudslide) in Maharashtra.
(2) Wadgaon Darya

Give geographical reasons:

Question 1.
Oxidation process occurs in heavy rainfall areas.
Answer:

• The oxidation process occurs in rocks which have iron present in them.
• The iron in the rock comes in contact with water and a chemical reaction takes place between iron and oxygen.
• A reddish coloured layer forms on the rocks.
• Thus, the oxidation process occurs in heavy rainfall areas.

Question 2.
Chemical weathering occurs in areas of heavy rainfall.
Answer:

• The rain water travels through the atmosphere before reaching the ground. Carbon dioxide in the air gets mixed in the water in this process.
• Dilute carbonic acid gets formed. Materials like limestone get easily dissolved in such acids leading to weathering of rocks.
• Some minerals in the rock gets dissolved in water. Limestone is formed due to chemical precipitation between water and alkalis.
  Similarly, because of the solution, alkalis in the rock dissolves and make them brittle.
• Oxidation process occurs in rocks which have iron present in them. The iron in the rock comes in contact with water and a chemical reaction takes place between iron and oxygen.
• Hence, a reddish coloured layer forms on the rocks. This is called rust.

Question 3.
Mechanical weathering3 takes place in the cold regions.
Answer:

• In the cold regions, the temperature drops below 0°C for a period of time.
• The water that has percolated through the cracks in the rocks freezes and turns into ice.
• Ice requires greater space than water. Tension is developed when the ice tries to acquire greater space.
• The continuous process of freezing and melting finally leads to the breaking of the rock mass.

Question 4.
Rapid mass movements occurs along the steep slopes.
Answer:

• A thick layer of weathered material forms on the steep slopes.
• When it rains in such areas, the rainwater penetrates the weathered materials and their weight increases.
• Due to this the weathered materials move very rapidly and come down the steep slopes.

Question 5.
Mechanical weathering is seen in areas where the diurnal range of temperature is high.
OR
Change in temperature leads to Mechanical weathering.
Answer:

• The minerals in the rocks expand because of heat and contract when the temperature decreases.
• Due to such continuous contracting and expanding, tension develops in the rock particles.
• Each mineral reacts differently to the temperature. Some minerals expand more, while others do not expand as much.
• Consequently, the tension formed in the rocks also increases and decreases. As a result, cracks develop in the rocks and they break.
• Thus in areas, where the diurnal range of temperature is higher, mechanical weathering is seen.

Question 6.
Water plays an important role in chemical weathering.
Answer:

• Rock is a mixture of many minerals.
• Since many things get dissolved easily in water, it is considered a universal solvent.
• The solubility1 of the solution increases because the matter gets dissolved in water.
• Water speeds up the process of carbonation, solution and oxidation. These processes lead to the weathering of rocks.
• Thus water plays an important role in chemical weathering.

Question 7.
Frost leads to mechanical weathering.
Answer:

• In areas where the temperatures drop below 0°C for quite some time, the water accumulated in the cracks and crevices in the rocks freezes.
• The volume of water increases on freezing.
• This leads to tension in the rocks and they shatter.
• In this way frost leads to mechanical weathering.

Answer in brief:

Question 1.
What is a mass movement? What are the types of mass movements?
Answer:
The weathered rock materials move along the slopes due to gravity and accumulate near the foothills or the gentler slopes. When the weathered particles move down due to gravity alone, the process is called mass movements.

Types of Mass movements:
(i) Rapid mass movements:

• A thick layer of weathered material forms on the slope. When it rains in such areas, the rain water penetrates the weathered materials and their weight increases.
• The weathered materials move very rapidly and come down the slope.
• Sometimes the weathered materials sink in situ. (Where they are)
• Rockfalls, landslides, land subsidence are ; termed as rapid mass movements.

(ii) Slower mass movements:

• Soil creep is the most common phenomenon in areas with dry climate and gentler slopes.
• In periglacial regions along the soil. This is called as solifluction.

Question 2.
How does external processes occur?
Answer:

• External processes occur because of the forces working on the earth’s surface.
• They are mainly solar energy, gravitational force and kinetic energy associated with the moving objects on the earth’s surface.

Question 3.
What is exfoliation?
Answer:

• In regions of high temperatures, the exposed part of the rock heats more while the inner part is comparatively cooler.
• As a result, the outer layers of the rocks fall apart from the main rock.
• This is called the exfoliation of the rock.

Question 4.
Explain the process of oxidation.
Answer:

• The oxidation process occurs in rocks which have iron present in them.
• The iron in the rock comes in contact with water and a chemical reaction takes place between iron and oxygen.
• Hence, a reddish coloured layer forms on the rocks. This is called rust.

Explain:

Question 1.
Block Disintegration
Answer:

• Sometimes both temperature and water are responsible for weathering.
• The difference in temperature cause contraction and expansion of minerals in the rocks. This leads to widening theoints or cracks in the rocks.
• Water accumulates in such wideouts and big blocks of rocks separate from each other.
• This is called Block Disintegration.

Question 2.
Carbonation
Answer:

• Carbonation is a type of chemical weathering.
• The rainwater travels through the atmosphere before reaching the ground.
• Carbon dioxide in the air gets mixed in the water in this process and dilute carbonic acid gets formed.
• For e.g Water + Carbon Dioxide = Carbonic Acid (H₂O +CO₂ = H₂CO₃)
• Materials like limestone get easily dissolved in such acids.

Question 3.
Solution
Answer:

• Some minerals in the rock get dissolved in water.
• Limestone is formed due to chemical precipitation between water and alkalis.
• At Wadgaon Darya in Ahmadnagar district, limestone gets precipitated chemically i.e. undergoes chemical weathering again.
• Similarly, because of solution, alkalis in the rock dissolve and make them brittle.

Question 4.
Make a record of few landslides that have occured in India and write about them briefly.
Answer:
Landslide is a rapid mass movement which is caused majorly due to heavy rains, floods, earthquakes etc. The following are some fatal landsides in India.

1. Guwahati landslide, Assam:- The landslide took place in the year 1948 due to heavy rains & over 500 people died in this landslide.
2. Darjeeling landslide, West Negal:- This landslide happened in the year of 1968. It was triggered by floods and thousands of people died due to this landslide.
3. Malpa landslide, Uttarkhand:- Consecutive landslides occured in August 1998 in village of Mapla due to which 380 people died as an entire village was destroyed in the landslide.
4. Kedarnath landslide, Uttarakhand:- This landslide took place onune 16, 2013 & was the result of Uttar Khand floods. Over 5700 people were reported dead and over 4200 villages were affected by floods and post-flood landslide.
5. Malin landslide, Maharashtra:- This landslide occured onuly 30, 2014, in a village in Malin. The landslide occured due to heavy rainfall and around 151 people died and 100 people went missing after the disaster.

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 8 Introduction to Economics Notes, Textbook Exercise Important Questions and Answers.

Introduction to Economics Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 8 Introduction to Economics Questions And Answers Maharashtra Board

Geography Class 9 Chapter 8 Question Answer Maharashtra Board

1. Explain the types of economies by filling correct information in the place of questions in the circle.

Answer:

2. Give an explanation:

Question 1.
The economy begins at home.
Answer:

• Household finance is related to income and expenditure.
• Every household has unlimited expenditure and the income earned is limited.
• The household has to make a choice regarding how it has to spend its limited resources.
• Management of this limited income to meet the unlimited expenses is Economics.
• As we manage the finance of our family, similarly the villages/cities, states, countries and the whole world needs to have economic management. So we say Economy begins at home.

Question 2.
India’s economy is of mixed type.
Answer:

• Mixed economy is a combination of Capitalism and Socialism.
• India is said to be a Mixed economy because there is a co-existence of both public and the private sectors.
• The private sector undertakes production for the profit motive, whereas the state tries to achieve social welfare.
• India, therefore, tries to achieve a balance between maximum social welfare for its citizens on one hand and profit on the other. Therefore, India’s economy is of Mixed type.

Question 3.
On the basis of economies, we can divide countries into three groups.
Answer:
The activities related to the production, distribution and consumption of goods and services in a specific region is called economy. On the basis of economies, countries are divided into three groups. Capitalist Economy, Socialist Economy and Mixed Economy.

1. Capitalistic Economy is a kind of economy in which the means of production is in the hands of the private sector, e.g. Germany, Japan, the U.S.A.
2. Socialist Economy is a kind of economy in which the means of production belongs to the society i.e. the government’s control, e.g. China, Russia.
3. Mixed Economy is a kind of economy in which there is a co-existence of both private and public sectors, e.g. India, Sweden, the U.K.

3. Write the following questions in one line:

Question 1.
To which economic factor is the management of individual or family finances related?
Answer:
Management of individual or family finances is related to the economic factor of ‘income and expenditure.

Question 2.
From which Greek word is the term ‘Economics’ derived?
Answer:
The word ‘Economics’ is derived from the Greek word ‘Oikonomia’ which means family management.

Question 3.
In a capitalistic economy, to whom does the ownership and management of means of production belong?
Answer:
In a Capitalistic Economy, the ownership and management of means of production belong to the private sector.

Question 4.
What do you mean by globalisation?
Answer:
Globalisation means aligning the country’s economy with the world economy.

Class 9 Geography Chapter 8 Introduction to Economics Intext Questions and Answers

Can you tell?
Suppose this is your expenditure this month and your monthly income is? 20,000. To strike a balance between your income and your expenditure, decide that will be your preferences for expenditure.

Rewrite the table according to your preferences and discuss in class.

Sr.No.	—	Estimated Expenditure (₹)
1.	Daily food	6,000
2.	Buying two sets of Uniform	2,000
3.	School Stationery	500
4.	Medical expenditure	450
5.	Recreation	500
6.	Mobile Bill	1,000
7.	Vegetables, Fruits, etc.	1,000
8.	Public transport (bus, railway, rick-shaw, etc.)	2,600
9.	Electricity Bill	1,500
10.	Tourism	4,000
11.	Bank Installment	3,000
	Total Expenditure	22,550

Answer:
Income And Expenditure Statement

• Preferences have been rearranged to their urgency.
• Most urgent wants are placed on the top. Least urgent wants are placed at the bottom.
• Expenses have been cut down wherever possible.
• Money spent on tourism is nil.
• Mobile bill has been reduced to? 500 from? 1000.
• And Savings equals? 3000.

Can you do it?

Question 1.
Suppose you are the finance minister of an agrarian country. Giving priority to the overall development of the country, make a five-point program.
Answer:
As a Finance Minister of an Agrarian country like India, I would focus on transforming India in five areas:

• Modernization of agriculture, encouragement to export-oriented agro-processing industries.
• Education, skill-building, and healthcare.
• Information and communication technology.
• Infrastructure development for rural industrialization.
• Spirit of Entrepreneurship.

Class 9 Geography Chapter 8 Introduction to Economics Additional Important Questions and Answers

Complete the statements choosing the correct option:

Question 1.
The term economics’ is derived from Greek word
(a) oikomonia
(b) oikonomica
(c) oikonomia
(d) oikonomics
Answer:
(c) oikonomia

Question 2.
China and Russia have adopted type of economy.
(a) Socialistic
(b) Capitalistic
(c) Mixed
(d) None of these
Answer:
(a) Socialistic

Question 3.
The main motive of a economy is to earn profit.
(a) Mixed
(b) Capitalistic
(c) Simple
(d) Socialistic
Answer:
(b) Capitalistic

Question 4.
The main aim of Socialistic economy is to achieve
(a) social welfare
(b) profit
(c) injustice
(d) tolerance
Answer:
(a) social welfare

Question 5.
Germany is an example of a country which has adopted economy.
(a) Simple
(b) Socialistic
(c) Mixed
(d) Capitalistic
Answer:
(d) Capitalistic

Question 6.
Adam Smith has defined economics as the
(a) science of knowledge
(b) science of wealth
(c) science of peace
(d) science of needs
Answer:
(b) science of wealth

Question 7.
means making the country’s economy aligned with world economy.
(a) Liberalisation
(b) Privatisation
(c) Globalisation
(d) None of these
Answer:
(c) Globalisation

Question 8.
Economics is an important science.
(a) social
(b) political
(c) physical
(d) alternative
Answer:
(a) social

Question 9.
One of the main functions of the economy is to the production cost
(a) maximize
(b) inflate
(c) increase
(d) minimize
Answer:
(d) minimize

Question 10.
An economy strives to create a balance between resources and needs.
(a) unlimited, limited
(b) limited, unlimited
(c) plentiful, limited
(d) limited, scarce
Answer:
(b) limited, unlimited

Question 11.
is known as the Father of Economics.
(a) Lionel Robbins
(b) Prof. Samuelson
(c) Amartya Sen
(d) Adam Smith
Answer:
(d) Adam Smith

Question 12.
Economics is a science which studies human behaviour as a relationship between and scarce which have alternative uses.
(a) means, ends
(b) people, resources
(c) money, land
(d) ends, means
Answer:
(d) ends, means

Question 13.
We understand from economics, how to use, money, land and effectively.
(a) minerals, factory
(b) time, labour
(c) food grains, machines
(d) people, power
Answer:
(b) time, labour

Question 14.
On a global level, there are types of economies.
(a) four
(b) two
(c) three
(d) five
Answer:
(c) three

Question 15.
economy is a borderless economy.
(a) State
(b) Town
(c) Village
(d) World
Answer:
(d) World

Question 16.
In Globalisation, there is trade and all restrictions on are set aside.
(a) restricted, economy
(b) free, investments
(c) no, activity
(d) zero, labour
Answer:
(b) free, investments

Match the column

Group A	Group B
(1) Capitalist economy	(a) India
(2) Socialist economy	(b) USA
(3) Mixed economy	(c) Russia

Answer:
(1 – b),
(2 – c),
(3 – a)

Answer the following questions in one sentence each:

Question 1.
Define Economics.
Answer:
According to Lionel Robbins, “Economics is a science which studies human behaviour as a relationship between ends and scarce means which have alternative uses”.

Question 2.
What is an Economy?
Answer:
The activities related to the production, distribution and consumption of goods and services in a specific region is called an economy.

Question 3.
What is a Capitalistic Economy?
Answer:
The economy in which the ownership and management of the means of production is in the hands of private individuals is called as a Capitalistic Economy.

Question 4.
What is the main aim of a Capitalistic Economy?
Answer:
The main aim of a Capitalistic Economy is to earn maximum profit.

Question 5.
Which countries have adopted Capitalistic Economy?
Answer:
Germany, Japan and USA are the examples of countries which have adopted Capitalistic economy.

Question 6.
What do you mean by Socialistic economy?
Answer:
The economy in which the means of production belong to the society as a whole i.e. the government’s control is known as a Socialistic economy.

Question 7.
What is the main aim of a Socialistic economy?
Answer:
The main aim of a Socialistic economy is to achieve social welfare.

Question 8.
Name Adam Smith’s book and year of publication.
Answer:
Adam Smith’s book is titled ‘Wealth of Nations/ and was published in 1776.

Question 9.
What are the types of economy at the global level?
Answer:
Capitalist, Socialist and Mixed Economy are the types of economy at the global level

Question 10.
Which economist is known as Father of Economics?
Answer:
Adam Smith is known as Father of Economics.

Question 11.
How does Adam Smith describe Economics in his ‘Wealth of Nations’?
Answer:
In the book ‘Wealth of Nations’ Adam Smith describes Economics as ‘the science of wealth’.

Question 12.
What is the World Economy?
Answer:
World Economy is a borderless economy in which natural resources, profit, services, capital, labour and technology flow freely across the countries.

Distinguish between Capitalist Economy and Socialist Economy.
Answer:

Capitalist Economy	Socialist Economy
(i) Ownership and management of means of production is in the hands of the private individuals. (ii) To earn maximum profit is the main aim of the Capitalist Economy. (iii) The USA, Germany and Japan have Capitalist Economy.	The means of production belong to the society as a whole and are under the control of the government. To achieve social welfare is the main aim of the Socialist Economy. Russia and China have Socialist Economy.

Answer the following in detail.

Question 1.
Explain the functions of an economy.
Answer:
Every country has a different economy. But the main functions of an economy are similar. Some of the main functions of an economy are:

• Deciding the product and quantity of its production.
• Deciding for whom will the goods be produced.
• Minimising the production costs as much as possible.
• Distributing national income1 according to social and economic justice2.
• Making appropriate provisions3 for the economic needs of the future.

Question 2.
Explain the importance of Economics.
Answer:
Economics is an important Social Science Subject.

• We use Economics on a large scale in agriculture, trade, finance, administration, law and in our daily life.
• Economics holds a paramount4 importance in the overall social development of humans.

Question 3.
Name the factors affecting an economy.
Answer:
The factors affecting an economy are:

• Geographical area and natural resources.
• Population
• Occupations
• Political Sovereignty

Question 4.
Write a description of Economics given by Lionel Robbins.
Answer:

• According to Lionel Robbins, “Economics is a science which studies human behaviour as a relationship between ends and scarce means which have alternative uses”.
• Since human wants are unlimited their priority is determined.
• The satisfaction of the basic needs are given priority.
• A scarce resource like land can be used either for agriculture or industries or development of infrastructure.
• In this way, Economics studies human behaviour related to unlimited wants with limited resources that have alternative uses.

Question 5.
Explain the nature of the Capitalist Economy.
Answer:

• The ownership and control of means of production is in the hands of the private individuals in the Capitalist Economy.
• There is no control of the government over economic activities in their ‘Free Market Economy’.
• The objective of economic activities is to earn maximum profit.
• The capitalist economy exists in Germany, Japan and the USA.

Question 6.
Explain the nature of the Socialist Economy.
Answer:

• There is no private ownership of the means of production as these belong to the society as a whole.
• There is total control of the State over the economy.
• The objective of the economic activities is the fulfilment of social needs (social welfare).
• Socialist economy exists in Russia and China.

Question 7.
What are the main features (components) of the economy?
Answer:

1. The economy is a system related to the production, distribution and consumption of goods and services in a specific region.
2. The main features of an economy are :
   • Well defined geographical area.
   • Population, i.e. the people living within that geographical area and undertaking various economic activities.
   • Natural resources to undertake economic activities.
   • Political sovereignty that exercises control over the economy.

Question 8.
Explain the nature of globalisation.
Answer:

• Globalisation means aligning the economy of the country with the world economy.
• There is free trade and all restrictions on (foreign) investments are set aside.
• There is free flow of natural resources, profit, services, capital, labour and technology across the world.
• The aim is to establish a borderless economy.
• The recent economic policies of the government are leading the economy towards globalisation.

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 4 Exogenetic Movements Part 2, Textbook Exercise Important Questions and Answers.

Exogenetic Movements Part 2 Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 4 Exogenetic Movements Part 2 Questions And Answers Maharashtra Board

Geography Class 9 Chapter 4 Question Answer Maharashtra Board

1. Rewrite the correct statement:

Question 1.
The temperature range helps the wind in its work.
Answer:
Correct.

Question 2.
River’s work is more prominent than other agents of erosion in desert regions.
Answer:
Incorrect. Work of wind is more prominent in desert regions than other agents of erosion.

Question 3.
The work of groundwater is effective in the area with soft rocks.
Answer:
Correct.

2. Correct and rewrite the incorrect statements:

Question 1.
The ice on the lateral side of the glacier moves faster than the ice at the base.
Answer:
Incorrect. The ice on the base of the glacier moves faster than the ice on the lateral side.

Question 2.
The depositional work by rivers happens because of gentle slope, reduced speed and transported sediments.
Answer:
Correct.

Question 3.
A river flows at a faster speed than the glacier.
Answer:
Correct.

Question 4.
The speed of the glacier is more on both the banks than in the middle.
Answer:
Correct.

3. Identify the wrong pair

Question 1.
Deposition – V-shaped valley
Answer:
Wrong pair.
Correct pair is – Erosion – V-shaped valley

Question 2.
Transport – Ripple Marks
Answer:
Transport – Ripple Marks

Question 3.
Erosion – Mushroom Rocks
Answer:
Erosion – Mushroom Rocks

4. Identify and name the landforms in the following diagrams :

Answer:
(i) V-shaped valley
(ii) Gorge (Canyon)
(iii) Delta

5. Complete the following table by classifying the landforms according to their agents of erosion.
(waterfall, delta, cirque, arête, barchans, moraine, pothole, mushroom rock, sinkholes, beach, pillars, lagoons)
Rivers Wind Glacier Sea Waves Groundwater
Answer:

Rivers	Wind	Glacier	Sea waves	Ground Water
Waterfall	Barchans	Cirque	Beach	Sinkholes
Delta	Mushroom rock	Aretes	Lagoons	Pillars
Pothole		Moraine

6. Answer the following questions in brief.

Question 1.
List the landforms that are a result of the erosional work of the rivers.
Answer:
Gorges (canyons), V-shaped valleys and waterfalls are the result of the erosional work of the rivers.
(i) ‘V’ Shaped Valley:

• A ‘V shaped valley is formed due to the erosional work of a river.
• Over a period of time, the amount of load in the flow starts increasing.
• More and more energy of the river gets consumed in transporting the material.
• As a result, there is less erosion of the bed. The erosion along the banks and the slopes of the valley increases.
• Hence, the slopes recedes and the valley with near-vertical sides becomes wider, resembling the letter ‘V’.

(ii) Gorge:

• A gorge is found in the upper course of the river.
• It is a deep and narrow valley with steep sides.
• In mountainous areas, the river flows with great speed. Therefore, the bed of the river gets eroded more than its banks, giving rise to a gorge that has a steep banks and a narrow bed.

(iii) Waterfall:

• Waterfalls are formed as a result of the erosional work of a river.
• Water flowing over a hilly region cascades down a cliff, forming a waterfall.
• In the areas, where the hard and soft rocks are next to each other, the soft rocks are eroded faster than the hard ones. A difference in the height along the river bed leads to the formation of a waterfall.

Question 2.
Which agent is responsible for the formation of stalactites and stalagmites and where are they formed?
Answer:

• The work of groundwater is responsible for the formation of stalactites and stalagmites.
• In areas of limestone, the alkaline water seeps through the roof of the limestone caves.
• When this water evaporates, minerals get deposited at the bottom and at the top of the limestone caves.
• This leads to formation of stalactites and stalagmites.

Question 3.
List the landforms that are produced by the depositional work of the sea waves
Answer:
The landforms like beaches, sand bar, lagoons are formed due to depositional work of the sea waves.
(i) Beach:

• Large amount of sediments come from the landward side in areas between two adjoining headlands.
• Moreover, as these areas are shallow, the velocity of the waves decreases.
• As a result, the sediments that come from the land, as well as those coming from the deep sea, get deposited in this area.
• Predominantly fine sand gets settled along the coast.
• Such sandy deposits along the coasts are called beaches.

(ii) Lagoon:

• The brackish water separated from the seawater by sand bars and lying in the areas between the coast and bars is called a lagoon.
• As the waters are separated from the open sea, large waves are not generated.
• These lagoons run parallel to the sea coast.

(iii) Sand bars:

• Sand gets deposited along the sides of the headlands.
• The deposition extends parallel to the coast from one headland to the next.
• Over a period of time, these deposits extend over long distances forming bars that protrude into the water at some distance away from the beach.
• These are known as ‘sand bars’, Sometimes, the eroded material from the’ beach, gives rise to the sand bars.

Question 4.
Name the types of moraines.
Answer:
The glaciers carry sediments with them. These sediments are called moraines. Depending ond the location of the deposits, moraines can be divided into 4 types: ground moraines, lateral moraines, medial moraines and terminal moraines.

• The material deposited at the base of a glacier is called ground moraine.
• The material deposited along the banks of a glacier is called Lateral moraine.
• After the confluence of two glaciers, the moraine deposited in the central part of the glacier is known as medial moraine. It is formed out of . the side moraine of the inner banks of the two glaciers.
• At the end where a glacier turns into a stream, huge quantity of moraine is deposited. The stream of water is unable to carry the moraine further. As the deposited moraine is at the terminal part of a glacier, it is called terminal moraine.

7. Observe the following picture carefully. Identify the landforms formed by different agents of erosion. Number them with a pencil here and write their names in the sequence in your notebook.

(i)

Answer:
Depositional work of river

(ii)

Answer:
Depositional work of river

(iii)

Answer:
Erosional work of river

(iv)

Answer:
Depositional work of river

(2) Some pictures of the landforms formed by glaciers3 are given below. Write the function because of which they have been formed.

(i)

Answer:
Erosional work of glacier

(ii)

Answer:
Erosional work of glacier

(iii)

Answer:
Depositional work of glacier

(iv)

Answer:
Depositional work of glacier

(v)

Answer:
Erosional work of glacier

(vi)

Answer:
Erosional work of glacier

(vii)

Answer:
Depositional work of glacier

(3) Some pictures of the Iandforms produced by the work of the winds are given below. See the pictures and write in the box whether they have been formed by erosion or deposition.

(i)

Answer:
Erosional work of wind

(ii)

Answer:
Depositional work of wind

(iii)

Answer:
Depositional work of wind

(iv)

Answer:
Depositional work of wind

(v)

Answer:
Erosional work of wind

(vi)

Answer:
Erosional work of wind

(4) Some pictures of the landforms produced by the work of the sea waves are given below. See the pictures and write in the box whether they have been formed by erosion or deposition.

With the help of internet, obtain information regarding the places along the Konkan coast where you will find the landforms formed by sea waves.

(i)

Answer:
Erosional work of sea waves.

(ii)

Answer:
Depositional work of sea waves

(iii)

Answer:
Erosional work of sea waves.

(iv)

Answer:
Erosional work of sea waves.

(v)

Answer:
Erosional work of sea waves.

(vi)

Answer:
Depositional work of sea waves.

(vii)

Answer:
Depositional work of sea waves.

(5) See the pictures of the landforms produced by the work of groundwater. Write in the box below them whether they are formed through the work of erosion or deposition.

(i)

Answer:
Erosional work of ground water

(ii)

Answer:
Depositional work of ground water

Class 9 Geography Chapter 4 Exogenetic Movements Part 2 Intext Questions and Answers

Draw a diagram showing landforms at the sea coast:
Answer:

Can You Tell?

Question 1.
How will you differentiate between a rill, gully, stream and a river?
Answer:
The smallest natural flow of rain water is a rill. Many rills come together to form a gully. Many gullies come together and form a stream. Many streams come together and form a river. Thus we can see that rills, gullies, streams nad rivers are the various forms of flowing water in increasing order of their size.

Question 2.
What is a river?
Answer:
Running water flows naturally in a direction according to gravity along the slope, making its own way. This is called a flow of water when many such flows of water come together a river is formed.

Question 3.
Where can you see the work by glaciers in India?
Answer:
Glaciers can be seen in the Himalayan region in India.

Question 4.
In which natural region can you see the work of glaciers at the sea level?
Answer:
We can see the work of glacier at sea level in the Polar regions (Antarctica).

Question 5.
Where will you find the landforms formed by sea waves along the Konkan coast?
Answer:
Along the Konkan coast, landforms formed by sea waves can be found at Harihareshwar, Bhagwatibandar, Shrivardhan, Ratnagiri and Sindhudurg.

Think about it.

Question 1.
There are many creeks found in the coastal areas of Konkan but no delta, why?
Answer:
The Konkan coast has an indented (broken) coastline. Hence many creeks are found here. Many small seasonal rivers originate in the steep western side of the Western Ghats. As the rivers flow through the steep slopes their velocity increases. So, there is very little erosion done by them. Due to the narrow width of the Konkan coast, the rivers cover a short distance and drain in the Arabian sea. Thus they do not form estuaries rather than deltas.

Question 2.
Can you see a glacier moving just as you can observe the movement of river water?
Answer:
No

Question 3.
Ramu has to dig a well in his farm. But he is in a dilemma as to which season should he dig it so that there is water supply for a longer time. What will you suggest to Ramu?
Answer:
Ramu should dig a well during the summer season. A deep well can be dug during the summer season. This will ensure water supply not only during the monsoon and winter season but also during the next summer season.

Question 4.
Which agent has more kinetic energy of all-wind, river or glacier?
Answer:
Glacier is the agent of erosion which has the most kinetic energy of all. The glacier is a mixture of heavy soil and rock particles which are flowing. Thus it has both weight and movement.

Find out.

Question 1.
Is there any lake found near the meanders of the river? Obtain information about them.
Answer:

• Ox-Bow lakes are usually found near the meanders of a river.
• Wherever the river changes its direction, erosion takes place along the outer banks.
• If these conditions occur again and again, the river develops a zigzag path.
• Such a zigzag path is called a meandering path (course) and each loop along the path is called meander.
• When the turns in the course become acute, the limbs of a turn come very close.
• During flood, as the force of water increases, the river skips the meandering path and follows a straight path.
• The abandoned portion of the loop develops into a lake that is called an ‘ox-bow’ lake.

Question 2.
Where will you find mushroom rocks in the Deccan Plateau?
Answer:
Mushroom rocks can be found in the Hyderabad.

Question 3.
Can you find the work of wind near coastal areas? What landforms will be formed there?
Answer:
Yes, Ripple marks and sand mounds can be seen on the sand in the coastal regions.

Question 4.
Where are limestone caves, stalactites and stalagmites found in Maharashtra?
Answer:
Limestone caves, stalactites and stalagmites are found in Kanhur caves in the Ahmednagar district of Maharashtra.

Question 5.
Why are the landforms formed in limestone called Karst?
Answer:
A karst is an area of land formation created by eroding and dissolving portions of limestone or other soluble rock layers above or below the ground. According to the prevalent interpretation, the term is derived from the German name for the Karst region, a limestone plateau above the city of Trieste in the northern Adriatic.

Class 9 Geography Chapter 4 Exogenetic Movements Part 2 Additional Important Questions and Answers

Complete the statements by choosing the correct options.

Question 1.
The sediments are deposited at the foothills of the mountains in a triangular area forming an/a ………….. .
(a) alluvial fan
(b) yardang
(c) delta
(d) V-shaped valley
Answer:
(a) alluvial fan

Question 2.
The sediments carried by the glacier2 are called ………….. .
(a) sediments
(b) silt
(c) moraines
(d) alluvium
Answer:
(c) moraines

Question 3.
The erosional, transportation and depositional work of wind is more prominent in ………….. .
(a) polar regions
(b) deserts
(c) temperate regions
(d) grasslands
Answer:
(b) deserts

Question 4.
When many flows of water come together a …………… is formed.
(a) gorge
(b) river
(c) glacier
(d) canyon
Answer:
(b) river

Question 5.
The water which percolates through the porous rocks on the non-porous layer of rock is termed as ………….. .
(a) glacier
(b) flood leeves
(c) ground water
(d) surface water
Answer:
(c) ground water

Question 6.
…………… is formed due to depositional work of river.
(a) Delta
(b) Gorge
(c) V-shaped valley
(d) Canyon
Answer:
(a) Delta

Question 7.
In regions, where the temperatures are generally below freezing points, precipitation is in the form of ………….. .
(a) rainfall
(b) hail
(c) snowfall
(d) frost
Answer:
(c) snowfall

Question 8.
The erosional work of glacier forms ………….. .
(a) drumlins
(b) eskers
(c) cirques
(d) yardangs
Answer:
(c) cirques

Question 9.
The Jacobshavn Glacier in …………… is one of the fastest moving glaciers in the world.
(a) Finland
(b) Greenland
(c) Antarctica
(d) Himalayas
Answer:
(b) Greenland

Question 10.
The depositional work of ground water forms ………….. .
(a) limestone caves
(b) lagoons
(c) ripple marks
(d) seifs
Answer:
(a) limestone caves

Question 11.
Stalactites grow ………….. .
(a) downwards
(b) upwards
(c) sidewards
(d) fast
Answer:
(a) downwards

Question 12.
The ground water levels sink down in …………… season.
(a) summer
(b) winter
(c) rainy
(d) spring
Answer:
(a) summer

Question 13.
…………… is formed as a result of the depositional work of the sea waves.
(a) Sea cliff
(b) Lagoon
(c) Wave-cut platform
(d) Sea cave
Answer:
(b) Lagoon

Question 14.
The landforms developed in limestone areas are also called as …………… landforms.
(a) lime
(b) sinkhole
(c) krast
(d) coastal
Answer:
(c) krast

Match the Columns:

(1) River

Column A’		Column B’
(1)	Erosion	(a)	Ox-bow lake
(2)	Deposition	(b)	Meanders
		(c)	Yardangs

Answer:
(1 – b),
(2-a)

(2) Glacier

Column ‘A’		Column ‘B’
(1)	Erosion	(a)	Seif
(2)	Deposition	(b)	Eskers
		(c)	Cirque

Answer:
(1 – c),
(2 – b)

(3) Wind

Column ‘A’		Column B’
(1)	Erosion	(a)	Sand dunes
(2)	Deposition	(b)	Mushroom Rock
		(c)	Lagoon

Answer:
(1 – b),
(2 – a)

(4)

Column ‘A’		Column B’
(1)	Ground water	(a)	Delta region
(2)	Sea waves	(b)	Lagoon
		(c)	Sink holes

Answer:
(1 – c),
(2 – b)

(5)

Column ‘A’		Column B’
(1)	Stalactites & stalagmites	(a)	wind
(2)	Sand bar	(b)	ground water
		(c)	sea waves

Answer:
(1 – b),
(2 – c)

Answer in one sentence:

Question 1.
Name the agents of erosion.
Answer:
The agents of erosion are wind, rivers, glaciers, sea waves and ground water.

Question 2.
What factors does the work of a river depend on?
Answer:
The works of river depends on the nature of rock, the slope of land, velocity of the flow and the volume of water.

Question 3.
What are the important phases of a river’s work?
Answer:
The important phases of a river’s work are erosion, transportation and deposition.

Question 4.
What factors does the work of glaciers depend on?
Answer:
The work of glacier depends on the thickness of the accumulated ice, the temperature, and the slope of the land.

Question 5.
Which landforms are created due to the processes of erosion by the river?
Answer:
Landforms like gorges, V-shaped valleys, potholes and waterfalls are created due to the processes of erosion by the river.

Question 6.
Which landforms are formed mainly due to the transportational and depositional work of a river?
Answer:
Due to the transportational and depositional work of a river, meanders, ox-bow lakes, flood levees, flood plains and delta regions are formed.

Question 7.
Which landforms are created as a result of the erosional work of a glacier?
Answer:
The landforms such as a cirque, arete and matterhorn, U-shaped valley, hanging valleys, etc. are created as a result of the erosional work of a glacier.

Question 8.
Name the landforms formed by the depositional work of glaciers.
Answer:
The landforms formed by the depositional work of glaciers are drumlins, eskers etc.

Question 9.
Name the types of moraine.
Answer:
Ground moraine, lateral moraine, medial moraine and terminal moraine are the different types of moraine.

Question 10.
Which landforms are created as a result of the erosional work of the wind?
Answer:
The landforms like mushroom rocks, deflation hollows, yardangs etc. are created as a result of the erosional work of the wind.

Question 11.
Which landforms are created as a result of the transportation and depositional work of the wind?
Answer:
Sand dunes, barchans, seif, ripple marks, and loess plains are created as a result of transportation and depositional work of the wind.

Question 12.
Which landforms are produced as a result of the erosional work of sea waves?
Answer:
The landforms like sea cliffs, sea caves, wave-cut platforms, sea arches and sea stacks are produced as a result of the erosional work of sea waves.

Question 13.
Mention the landforms created due to the transportation and depositional work of sea waves.
Answer:
Beaches, sand bars and lagoons are created due to the transportation and depositional work of sea waves.

Fill the map with the given information and make a legend.

(1) Konkan Coast where work of sea waves can be seen
(2) Region in India where work of glaciers can be seen
(3) Desert region in India where work of wind can be seen
Answer:

Give geographical reasons:

Question 1.
Like the river, a glacier too carries out the work of erosion, transportation and deposition.
Answer:

• In regions, where the temperatures are generally below freezing points, precipitation is in the form of snowfall.
• Layers of snow accumulate on the earth’s surface because of snowfall.
• The heavy weight of these overlying layers makes the snow move along the slope.
• At the base of the layer, the snow starts melting because of the friction and the pressure from above. Glacier starts moving slowly along the slope.
• Thus like the river, a glacier too carries out the work of erosion, transportation and deposition.

Question 2.
Specific landforms are formed due to deposition by wind in arid and semi arid regions.
Answer:

• Sand particles that blow with the winds are of different shapes and sizes.?
• Those particles which are very fine are carried to larger distances while the larger ones get transported to shorter distances only.
• These sand particles get deposited in deserts and semi-arid climates.
• As a result, specific landforms are formed.
• Sand dunes, barchans, seifs, ripple marks, loess plains, etc. are formed by deposition by wind.

Question 3.
The work of sea waves cause different landforms.
Answer:

• In coastal areas, the sea waves carry out erosional, depositional and transportational work.
• Winds and tides cause the movements of sea water. As a result, waves come to the coast.
• Because of their hitting the rocks at the coasts, erosion of the rocks occurs.
• The landforms like wave cut platforms, sea caves, sea arches, sea cliffs, etc. are formed because of the erosional work of the waves.
• The landforms like beaches, sand bar, lagoons are formed due to depositional work of the sea waves.

Question 4.
In the desert, the work of wind is effective.
Answer:

• The work of wind is predominantly found in the hot desert and semi-arid regions.
• Hot deserts are found close to the Tropic of Cancer and Tropic of Capricorn.
• The average annual rainfall in the hot deserts is 250 mm or even less. Therefore, the vegetal cover is negligible.
• As there are no obstacles due to lack of vegetal cover, the work of wind is effective in the desert.

Question 5.
Glaciers have a low velocity.
Answer:

• In the high altitude areas and the areas of high elevation, the ice slides down the slope. Such a sliding mass of ice is called a glacier.
• As the ice moving in a glacier is in the solid state, its velocity is very low.
• The thickness of the accumulated ice, the temperature and the slope of the land are the factors that determine the velocity of the glacier.

Question 6.
The ground water level changes according to seasons.
Answer:

• The upper level of the stored ground water is called ground water level.
• It varies according to the slope of the land, porosity and compactness of the rocks and the rainfall in the region.
• Ground water level also changes according to season.
• In the rainy season, it is closer to the ground surface whereas during summer, it drops down deeper.

Identify the land forms made by waves and write their names in the given picture.

Answer:

• Wave-cut platform
• Lagoon
• Beach
• Sea cave
• Sea arch
• Sea stack
• Sea cliff

Write the name of the landforms with which the following diagrams are associated. Colour the eroded and the remaining part, if any, in the given diagrams.

Answer:
(a) Mushroom Rock
(b) Sand Dune (Barchan)
(c) Yardangs
(d) Seif (Sand Mounds)

Identify the landforms formed by groundwater in the given diagram.

Answer:
Stalactite and Stalagmite cave.

Answer the following questions in brief:

Question 1.
List the agents responsible for new landforms. i
Answer:
The agents – running water (river), glaciers, wind, sea waves and groundwater, – do the work of erosion, transportation and deposition. Because of these agents, the earth’s surface keeps undergoing changes and new landforms are formed.
(i) Running water (river):

• The river beds, as well as the banks of a river, are eroded due to the speedy flowing stream of water. The load that a river carries also erodes the banks and the bed of the river.
• The rocks, stones, sand, etc. collide with one another and break into fragments
• Different landforms like gorge, V-shaped valley, pothole and waterfall are formed due to the erosional work of a river.

(ii) Glaciers:

• As a glacier is nothing but a solid mass of ice, its velocity is very low. Nevertheless, the mass of water in the solid form is quite high. Therefore, glaciers cause a considerable amount of erosion.
• The glaciers erode the ice-clad base of the mountain slopes and the snow-clad sides of the mountains to a large extent.
• The Cirque, Arete and horn, U-Shaped valley and hanging valley are the landforms formed by the erosional work of a glacier.

(iii) Wind:

• The wind carries sand and pebbles.
• When they strike and scratch the rocks, the elevated and basal parts of the rocks get eroded.
• Due to the erosional processes of the wind, deflation hollows, mushroom rocks and yardangs3 are formed.

(iv) Sea waves:

• The basal portions of the headlands get severely eroded due to the continuous attack of sea waves. This leads to the erosion of the rocks on a large scale.
• Rocky coasts are formed where the headlands get severely eroded.
• Landforms such as sea cliffs, sea caves, wave- cut platforms, sea arches and sea stacks are formed due to the erosional work of sea waves.

(v) Groundwater:

• Soluble minerals in the rocks dissolve in water and they move along with the ground water. This process is called erosion by ground water.
• The work of ground water is predominant in the region where rock like limestone is found on a large scale.
• Limestone dissolves in carbonic acid. Carbonic acid is formed due to the presence of carbon? dioxide in ground water. This acid dissolves carbonates like limestone. Thus, chemical weathering takes place.
• The landforms like sinkholes and caves are the result of the erosional work of groundwater.

Question 2.
List the landforms that are produced due to deposition of sediments by rivers.
Answer:
Landforms like flood levees, flood plains, deltas are formed because of deposition of sediments,

1. Flood levees: When in flood, the river deposits ; the coarser material on the banks which in duecourse rises parallel to the banks of the river. These are called ‘flood levees’.
2. Flood plains: The finer silt deposited away from the banks during the flood form plains on ! either side of the river. They are called ‘flood plains’.
3. Delta: The continuous deposition leads to the formation of a plain in the shape of a triangle called delta. Extensive deltas have been formed ! at the mouth of rivers Ganga, Godavari, Kaveri.

Question 3.
Write in detail about the erosional and depositional work of wind.
Answer:
(i) Erosional work of winds:

• Wind carries small sand particles, small pebbles, etc. along with it.
• These particles cause erosion along rocks coming in the way due to friction.
• This leads to formation of mushroom rocks, deflation hollows, yardangs, etc.

(ii) Depositional work of winds:

• Sand particles that blow with the winds are of different shapes and sizes.
• Those particles which are very fine are carried to larger distances while the larger ones get transported to shorter distances only.
• These sand particles get deposited in deserts and semi-arid climates. As a result, specific landforms are formed.
• Sand dunes, barchans, seifs, ripple marks, loessplains, etc. are formed by deposition by wind.

Question 4.
Write in detail about the erosional and depositional work of sea waves.
Answer:
(i) Erosional work of sea waves:

• When the waves break at the coast, they bring with them water, transported stones, pebbles,sand particles, etc. This leads to the erosion of the coast.
• Because of the chemical and hydraulic action of the sea wave too, the erosion occurs. The landforms like wavecut platforms, sea caves, sea arches, sea cliffs, etc. are formed because of the erosional work of the waves.

(ii) Depositional work of sea waves:

• The eroded materials accumulate at the sea bed. Because of tides, they keep on moving towards the coast and away from the coast.
• They become fine because of attrition and hitting towards each other.
• Deposition of such materials occurs at the places where the effect of waves is less. The landforms like beaches, sand bar, lagoons are formed due to the depositional work of the sea waves.

Explain:

Question 1.
Erosional work of rivers
Answer:

• The rivers originate at a much higher altitude from the sea level.
• Here, the river flows at a great speed and therefore, its power to erode is great.
• The riverbed and the river banks get eroded because of the speedy flow of the river, sand particles, pebbles. Also, various tributaries join the main river.
• All these lead to the formation of gorges (canyons), V-shaped valleys and waterfalls.

Question 2.
Transportation and deposition by rivers
Answer:

• A river flows down the slope from a hilly region.
• At the foothills, the change in the slope causes deposition of coarse sediments.
• As these are deposited in a triangular shape, they form an alluvial fan. As the steepness of the slope decreases and the transport capacity of the river reduces, it starts flowing slowly.
• It bends (meanders) often in its way in an effort to cross even small obstacles.
• By the time the river reaches the sea, its riverbed becomes very wide and its speed becomes very slow.
• The sediments of the river get deposited in its bed and on its banks. The factors that determine the deposition of sediments are thelength of the rivers, volume of water, amountof sediments, and the slope of the river and the earth’s surface.
• Thus, landforms like flood levees, flood plains,deltas are formed because of deposition of sediments.

Question 3.
Erosion work by glaciers
Answer:

• Though the velocity of glaciers is less, the mass of the ice is more and hence the glacier erodes its own banks and its bed on a large scale.
• The erosional work of glaciers produces landforms like cirques, aretes, horns, U-shaped valleys, hanging valleys and roche moutonnees (or sheepbacks).

Question 4.
Transportation and deposition by glaciers
Answer:

• The glaciers carry sediments with them. These sediments are called moraines.
• Depending on the location of the deposits, moraines can be divided into 4 types: ground moraines, lateral moraines, medial moraines and terminal moraines.
• The depositional work of glacier produces landforms like drumlins, eskers, etc.

Question 5.
Erosional and depositional work of wind
Answer:

• Erosional work of wind: Wind carries smallsand particles, small pebbles, etc. along with I it. These particles cause erosion along rockscoming in the way due to friction.
• This leads to formation of mushroom rocks, deflation hollows, yardangs, etc.
• Depositional work of winds: Sand particles that blow with the winds are of different shapes and sizes.
• Those particles which are very fine are carried to larger distances while the larger ones get transported to shorter distances only.
• These sand particles get deposited in deserts ; and semi-arid climates. As a result, specific landforms are formed.
• Sand dunes, barchans, seifs, ripple marks, loess plains, etc. are formed by deposition by wind.

Question 6.
Erosional work of sea waves
Answer:

• When the waves break at the coast, they bring with them water, transported stones, pebbles, sand particles, etc.
• This leads to the erosion of the coast. Because of the chemical and hydraulic action of the sea wave too, the erosion occurs.
• The landforms like wave cut platforms, sea caves, sea arches, sea cliffs, etc. are formed because of the erosional work of the waves.

Question 7.
Depositional work of sea waves
Answer:

• The eroded materials accumulate at the sea bed.
• Because of tides, they keep on moving towards the coast and away from the coast.
• They become fine because of attrition and hitting towards each other. Deposition of such materials occurs at the places where the effect of waves is less.
• The landforms like beaches, sand bar, lagoons are formed due to depositional work.

Question 8.
Work of groundwater and landforms
Answer:

• The rainwater seeps below the earth’s surface through porous rocks or the cracks in the rocks.
• This water accumulates at the non-porous layer of the rock. This accumulated water is called groundwater.
• The soluble minerals in the water get dissolved and flow with the groundwater. This is the erosional work of the groundwater.
• When the groundwater evaporates or the volume of soluble minerals is more than the solubility of the groundwater, the deposition of dissolved materials starts.
• Landforms like sinkholes, limestone caves, stalactites and stalagmites are formed.
• Thus, the groundwater carries out the erosion, transportation and depositional work.

Question 9.
Groundwater table
Answer:

• The upper surface of the water accumulated below the ground is called the ground water table.
• Factors like seasons, porosity of rocks, amount of rainfall, etc. affect the level of water table.
• The water table is closer to the ground during rainy seasons while it is deeper in the summers.?

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 12 Tourism Notes, Textbook Exercise Important Questions and Answers.

Tourism Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 12 Tourism Questions And Answers Maharashtra Board

Geography Class 9 Chapter 12 Question Answer Maharashtra Board

1. Identify the type of tourism from the statement.

(A) Hemant Kumar went to Mexico to learn about the architectural skills of the Mayan culture
Answer:
Cultural Tourism

(B) Portuguese tourists had come to Goa to participate in the Goa Carnival.
Answer:
Cultural Tourism

(C) To seek treatment in a naturopathy centre, John and Amar went to Kerala.
Answer:
Medical Tourism.

(D) Pundalikrao accomplished the Char Dham Yatra with his family
Answer:
Religious Tourism.

(E) Rameshwari from Pune went to enjoy Hurda ( Roasted Grain) party and learn about modern and traditional methods of agriculture
Answer:
Agro-tourism.

(F) Sayyed family went to Ajmer Durgah.
Answer:
Religious tourism.

2. Match the columns identifying the correlation. Make a chain.

	Group ‘A’	Group ‘B’	Group ‘C’
(1)	Tadoba	Madhya Pradesh	Lake
(2)	Bird Sanctuary	Agra	Butterflies
(3)	Sanjay Gandhi National Park	Manipur	Kailash caves
(4)	Taj Mahal	Nannaj	Film city
(5)	Ramoji Film City	Ellora	World-famous wonder
(6)	Radhanagari	Mumbai	Ancient cave- paintings
(7)	Bimbetka	Hyderabad	Great Indian Bustard (Maaldhok)
(8)	Ancient Caves	Kolhapur	Kanheri Caves
(9)	Eaglenest Wildlife Sanctuary	Chandrapur	Bison
(10)	Loktak	Arunachal Pradesh	Tiger

Answer:

	Group ‘A’	Group ‘B’	Group ‘C’
(1)	Tadoba	Chandrapur	Tiger
(2)	Bird Sanctuary	Nannaj	Great Indian Bustard (Maaldhok)
(3)	Sanjay Gandhi National Park	Mumbai	Kanheri Caves
(4)	Taj Mahal	Agra	World-famous wonder
(5)	Ramoji Film City	Hyderabad	Film city
(6)	Radhanagari	Kolhapur	Bison
(7)	Bimbetka	Madhya Pradesh	Ancient cave- paintings
(8)	Ancient Caves	Ellora	Kailash caves
(9)	Eaglenest Wildlife Sanctuary	Arunachal Pradesh	Butterflies
(10)	Loktak	Manipur	Lake

3. Answer in brief.

Question 1.
Differentiate between religious and cultural tourism.
Answer:

Religious tourism	Cultural tourism
(i) religious tourism is a type of tourism in which tourists travel for pilgrimage.	Cultural tourism refers to a type of tourism in which tourists travel to cultural attractions away from residence to gather new information and experience.
(ii) In religious tourism various religious places, temples, churches, etc. are visited for performing religious activities and gaining spiritual peace.	In cultural tourism art, architecture, religion, customs, traditions, lifestyle, etc. of a particular region are experienced and studied.
(iii) For example, a visit to Shirdi, Haji Ali, Mount Mary Church, etc.	For example, Portuguese tourists participating in Goa carnival.

Question 2.
What are the objectives of tourism?
Answer:
Following are the objectives of tourism:

• Getting joy
• Getting entertained
• Trading
• Staying
• Availing health facilities
• Getting a glimpse of agricultural life
• Performing religious activities, etc.

Question 3.
Explain the environmental effects of tourism.
Answer:
Following are the environmental effects of tourism:

• Sometimes, tourists damage tourist place and degrade the environment. Some tourists throw litter and pollute the tourist place.
• Therefore, all tourists must follow the concept of eco-tourism. Eco-tourism includes taking precautions of not degrading and polluting the environment as well as not damaging tourist places.
• Tourism is good for environmental development as the government makes economic investment in developing sanctuaries and national parks for the sake of the tourism industry.
• In eco-friendly tourism, factors like designing houses, resorts, traffic routes are designed in an eco-friendly manner in which electricity and water are used judiciously.
• The concept of recycling and reuse is also applied in eco-friendly tourism.

Question 4.
What opportunities develop with the development of tourism?
Answer:

• Tourism and Economic Development: The development of infrastructural facilities generates employment on an large scale. Eg. transportation, banking, restaurants, shops, resorts, medical services etc.
• Tourism and Environmental development: Due to the Eco-friendly tourism concept, tourist places are developed while caring for the environment. Eg. Eco-tourism.
• Tourism and’ Health: Opportunities to avail health facilities develop with tourism. Eg. Indian Ayurveda, Yoga, Pranayam.
• Tourism and Social Developments: Tourism creates social consciousness among tourists which helps in the development of neglected components of the society. For eg. Visit to Anandwan village.

Question 5.
Suggest measures after explaining the problems arising at the tourist places.
Answer:
(i) The problems that may arise at the tourist places:

• Lack of basic facilities.
• Lack of frequency of means of transportation.
• Lack of medical facilities.
• Lack of communication facilities.
• Petty crimes and security issues.

(ii) Measures to minimize the problems arising at the tourist places:

• Government can provide lodges, eateries, clean drinking water and good sanitation facilities.
• All tourist places can be connected by speedy means of transportation.
• Government can open dispensaries and arrange ambulance facilities.
• Communication facilities can be developed at every tourist place.
• Installation of CCTVs in public places and prompt action by the law and order forces can help tourist immensely.

Question 6.
Explain with the reason the places of interest that can be developed as tourist centers in your district.
Answer:

• In the district of Mumbai, there are many tourists destinations which fascinate the tourists.
• But there are few places which can be developed as tourist centres, which are currently neglected.
• To name a few, there are some small forts on the beaches of Mumbai and some caves in the suburbs of Mumbai.
• The Sion fort and the fort of Mahim are currently in a bad state and need urgent restoration.
• The Mahakali caves situated in western suburbs of Mumbai need to be developed in order to preserve cultural heritage which can attract many tourists.

(Disclaimer: The students can write answer of this above question in their own words as per the district they belong to.)

Question 7.
Local people get employment due to tourism. Give reasons.
Answer:

• Tourism is an important tertiary occupation through which many tourists visit places of interest.
• Many job opportunities are created to serve the tourists.
• When basic infrastructure improves, it leads to generation of employment.
• Many local people get job opportunities from various restaurants, transportation systems and recreational places.

5. Make a notice board containing instructions for the tourists at a tourist place.
Answer:

6. Explain how relevant is the concept of “Atithi Devo Bha va” (Guest is our God) with respect to tourism.
Answer:

1. In Sanskrit “Atithi Devo Bhava” means “Guest is our God”. This is a tag line of India’s, Ministry of Tourism’s campaign to improve the treatment of tourists in India.
2. India attracts millions of tourists every year but it still lags far behind compared to other destinations.
3. With an attempt to improve the number of tourists travelling to India, the Tourism Department of India started this social awareness campaign which provides training and orientation to taxi drivers, guides, immigration officers, police and other personnel who interact directly with the tourists.
4. This campaign educates the citizens of our country about the importance of our cultural heritage, benefits of cleanliness, importance of foreign tourists and maintaining our historical monuments.
5. All these efforts will lead to the economic development of our country.

7. The tourism map of Maharashtra is given. Answer the following questions based on the map.

Question 1.
Make a list of places having hot springs. What are the reasons for these being located here?
Answer:
Say, Vajreshwari, Kapeshwar, Unakeshwar, linhavare, Unapdev are the places that have hot springs.
Reason of hot water springs because geothermally heated ground water rises from the Earth’s crust.

Question 2.
At what places do you find the correlation between transportation routes and the development of tourism?
Answer:

• Aurangabad: The national highway and the airport is located in Aurangabad which facilitates the tourists to visit Ajanta and Ellora caves.
• Shirdi: Since Shirdi has got a railway station, more devotees will visit the temple every year.

Class 9 Geography Chapter 12 Tourism Intext Questions and Answers

Can you tell?

(I) Dear Students, imagine that you have to go on a vacation with your family. Make a list of 15 favourite places in Maharashtra.
After the list is prepared, put your places in the relevant classification.

• Places near the sea
• Historical places
• National parks and sanctuaries
• Hill stations
• Religious places

Select one place from each group which you would like to visit.

Discuss the reasons of your choice in the class.
Answer:
(A) A list of 15 favourite places in Maharashtra

• Mumbai
• Pune
• Nashik
• Alibaug
• Guhagar
• Malvan
• Shirdi
• Shegaon
• Chandoli
• Pench
• Kamala
• Matheran
• Mahabaleshwar
• Jawhar
• Parli Vaijanath.

(B) A relevant classification of 15 favourite places is as follows:
(1) Places near the sea :

• Alibaug
• Guhagar
• Malvan.

(2) Historical places :

• Pune
• Mumbai
• Nashik.

(3) National parks and sanctuaries :

• Chandoli
• Pench
• Kamala.

(4) Hill stations:

• Matheran
• Mahabaleshwar
• Jawhar.

(5) Religious places :

• Parli Vaijanath
• Shirdi
• Shegaon.

(C) Name of a place from each group which we would like to visit with reason :
(1) Name of a place near the sea which we would like to visit: Guhagar.
Reason: Guhagar is famous for its clean white sand beach. ‘Shri Vyadeshwar’ an ancient shiv temple is also located at Guhagar.

(2) Name of a historical place which we would like to visit: Pune.
Reason : Many historical forts are located in Pune.

(3) Name of a national park and sanctuary which we would like to visit: Karnala.
Reason : Karnala bird sactuary houses many species of resident birds.

(4) Name of a hill station which we would like.to visit: Matheran.
Reason : One can reach Matheran by a Toy Train. Horse riding is another tourist attraction of Matheran. There are gardens, waterfalls, temples, markets and many scenic points at Matheran.

(5) Name of a religious place which we would like to visit: Shegaon.
Reason : A famous ‘Gajanan Maharaj Temple’ is located at Shegaon. Anand Sagar’, a spiritual and entertainment park centre is also located at Shegaon.

(II) (i) Which new forms of tourism have developed recently? (Textbook Page no. 92)
(ii) Tell the reasons why new forms of tourism emerge. (Textbook Page no. 92)
Answer:
(i) In recent years, following are the new forms of tourism that have developed:

• Eco-Tourism
• Agro-Tourism
• Film Tourism
• Medical Tourism
• Cultural tourism

(ii) Nowadays people are more aware of new tourist destinations and attractions, have the ability to spend and need break from their routine stressful life. They take breaks to refresh and relax or may travel for some psychological and social needs.

Think about it.

We saw the various types of tourism. Just think, can we go into the space for tourism? What will we have to do for that? Where can we go? Present your ideas in the form of picture or paragraphs, etc.
Answer:
Yes, we can go into the space for tourism. We will require a the most powerful rocket built with a spaceship designed to carry atleast 100 people. We can go to the Red Planet-Mars.

Use your brain power!

Some issues related to tourism development are given below. Rewrite the inappropriate ones after correcting them.
Answer:

• The income of a country should be substantially high for development of tourism. Inappropriate: The income of a country is high due to development of tourism.
• Domestic tourism should be given a boost. Inappropriate: Domestic tourism should be given a boost.
• Tourists from other countries should be banned. Inappropriate: Tourists from other countries should be welcomed for economic development of our country.
• Appropriate: Tourists should be assured of a safe journey.
• Appropriate: The cultural heritage of a country should be preserved.
• Appropriate: We should respect other country’s culture.
• Appropriate: Government subsidies1 and incentives should be given for tourism businesses.
• Appropriate: Participation in international sports should be increased.
• Appropriate: Tourism should be encouraged through advertisements.
• Appropriate: It is necessary to preserve the tourist places.
• Appropriate: We should preserve buildings of famous people who have contributed in various sectors for memorials.
• Appropriate: Services and amenities3 should be developed for tourism.
• Tourist agencies should be banned. Inappropriate: Tourists agencies should be encourage for their businesses.
• There is no ample scope in this field. Inappropriate: There is ample scope in the field of tourism.
• Appropriate: Tourism is a type of invisible trade.
• Appropriate: All types of facilities should be developed for tourists.
• The country’s economy does not benefit at all from tourism. Inappropriate: The country’s economy benefits a lot from tourism.
• Appropriate: The hidden potential of other sites should also be developed.
• Appropriate: The forts and castles should be developed.

Class 9 Geography Chapter 12 Tourism Additional Important Questions and Answers

Complete the following statements by choosing the appropriate alternatives from those given in the brackets:

Question 1.
Visiting various places away from our homes for getting joy, entertainment, trading, staying, etc. is called
(a) boarding
(b) lodging
(c) visiting
(d) tourism1
Answer:
(d) tourism

Question 2.
On the basis of political boundaries, tourism can be of two types and
(a) domestic tourism and local tourism
(b) international tourism and foreign tourism
(c) local tourism and holidays
(d) domestic tourism and international tourism
Answer:
(a) domestic tourism and international tourism

Question 3.
Tourism within the limits of a country is called …………………. .
(a) domestic tourism
(b) international tourism
(c) foreign tourism
(d) abroad tourism
Answer:
(a) domestic tourism

Question 4.
A person from Maharashtra going to Kanyakumari in Tamil Nadu for tourism, a person from Nagpur visiting Ellora Caves in Aurangabad are examples of
(a) international tourism
(b) abroad tourism
(c) domestic tourism
(d) foreign tourism
Answer:
(c) domestic tourism

Question 5.
Crossing country’s boundaries and visiting some other country for tourism is called
(a) local tourism
(b) international/ foreign tourism
(c) city tourism
(d) state tourism
Answer:
(b) international foreign tourism

Question 6.
Indian going to Switzerland for tourism, an American coming to India for tourism are examples of
(a) city tourism
(b) state tourism
(c) local tourism
(d) intemational/foreign tourism
Answer:
(d) international/ foreign tourism

Question 7.
………………….. tourism should be promoted as it is necessary to preserve the cultural heritage1 of a country.
(a) Mumbai
(b) Local
(c) Andheri
(d) Domestic
Answer:
(d) Domestic tourism

Question 8.
To go to a foreign country, one needs a ………………, ………………, travel insurance and other documents.
(a) passport, train tickets
(b) visa, bus tickets
(c) movie tickets, bus tickets
(d) passport, visa
Answer:
(d) passport and visa

Question 9.
The ……………… system in our smartphones or the GPS instrument is largely used for tourism. For that we need special applications like the
(a) GPRS and atlas
(b) GPS and radio
(c) GPS and google map
(d) google play store and GPRS
Answer:
(c) GPS and google map

Question 10.
Tourism is an important occupation.
(a) primary
(b) secondary
(c) tertiary
(d) quaternary
Answer:
(c) tertiary

Question 11.
Besides domestic tourists2, foreign tourists also visit various places of interest and therefore, ……………… currency increases in our economy.
(a) domestic
(b) foreign
(c) FOREX
(d) shares
Answer:
(b) foreign

Question 12.
Tourism should be promoted through in various media which will help in its growth.
(a) slogans
(b) word of mouth
(c) references
(d) advertisements
Answer:
(d) advertisements

Question 13.
……………… has implemented many programmes by providing guest houses, water sports, tourist houses near coastal areas, etc.
(a) Maharashtra Tourism Development Corporation (MTDC)
(b) Maharashtra Transportation Development Corporation (MTDC)
(c) Maharashtra Traffic Development Corporation (MTDC)
(d) Maharashtra Training Development Corporation (MTDC)
Answer:
(a) Maharashtra Tourism Development Corporation (MTDC)

Question 14.
……………… is a train started especially for tourism which is operated in coordination with MTDC, Indian Railways and Ministry of Tourism.
(a) Deccan Chronicle
(b) Deccan Express
(c) Mumbai Local
(d) Deccan Odyssey
Answer:
(d) Deccan Odyssey

Question 15.
………………….. train takes the Delhi-Jaipur-Udaipur-Bharatpur-Agra- Delhi route.
(a) Palace of Tiles
(b) Palace on Train
(c) Palace on Wheels
(d) Palace in Rajasthan
Answer:
(c) Palace on Wheels

Question 16.
The Indian railways have started a new train with coaches having transparent ceiling as a special attraction for tourism.
(a) superdome
(b) astrodome
(c) imax dome
(d) vistadome
Answer:
(d) vistadome

Question 17.
………………….. is an eco-friendly type of tourism.
(a) Medical tourism
(b) Eco-tourism
(c) Social tourism
(d) Religious tourism
Answer:
(b) Eco-tourism

Question 18.
A pollution-free location away from the city holding an agricultural activity where the tourist is shown a glimpse of agricultural life is called
(a) agro-tourism
(b) social tourism
(c) cultural tourism
(d) medical tourism
Answer:
(a) agro-tourism

Question 19.
In and districts of Maharashtra number of agro-tourism centres have been developed.
(a) Pune, Mumbai
(b) Mumbai, Nagpur
(c) Pune, Kolhapur
(d) Kolhapur, Amravati
Answer:
(c) Pune, Kolhapur

Question 20.
Places, where film shooting takes place, are and
(a) Mumbai film city, Ramoji city
(b) Pune city and Mahableshwar
(c) Ramoji city and Pune city
(d) Lonavala and Khandala
Answer:
(a) Mumbai film city, Ramoji City

Question 21.
………………….. in Konkan is famous for its seabed and the biodiversity found there.
(a) Juhu Beach
(b) Tarkali
(c) Alibaugh
(d) Sindhudurg
Answer:
(b) Tarkali

Question 22.
The tribal life in of Maharashtra and visit to model villages like project of the social activist Baba Amte, Ralegan Siddhi, Hiwre Bazaar, etc. creates social consciousness.
(a) Phonda Ghat, Vrindavan
(b) Melghat, Sunderbans
(c) Melghat, Anandwan
(d) Bor Ghat, Anandwan
Answer:
(b) Melghat, Anandwan

Answer in one sentence

Question 1.
What is meant by tourism?
Answer:
Visiting various places away from our homes for getting joy, entertainment, trading, staying etc. is called tourism.

Question 2.
By which name is the tourism within one’s own country’s boundaries is known?
Answer:
The tourism within one’s own country’s boundaries is known as ‘domestic tourism’.

Question 3.
What do mean by International tourism?
Answer:
Crossing country’s boundaries and visiting some other country for tourism is called international tourism.

Question 4.
A visit to which places in Maharashtra creates social consciousness?
Answer:
Visit to Melghat to see the tribal life and visit to model villages like Anandwan, Ralegansiddhi, Hiwre Bazaaro of Maharashtra creates social consciousness.

Question 5.
Anandwan’ is a project of which social activist?
Answer:
Anandwan’ is a project of the social activistt Baba Amte.

Question 6.
What is Cultural Tourism?
Answer:
Cultural tourism is a type of tourism in which tourists travel to collect information and to experience traditions, customs, art, lifestyle of people, etc. of a particular region.

Question 7.
What is Health Tourism?
Answer:
Health tourism is a type of tourism in which tourists travel for availing health facilities, achieving mental peace and physical strength.

Question 8.
What do we require when travelling abroad?
Answer:
To go abroad one requires a passport, visa, travel insurance, other documents and currency of the country where we are going.

Question 9.
Name the agro-tourism centres in Maharashtra.
Answer:
Pune and Kolhapur districts of Maharashtra have agro-tourism centres.

Observe fig. 12.1 and answer the following questions: Use an atlas for reference:

Question 1.
Out of these, which tourist places1 do you know? Make a list.
Answer:
A list of known tourist places :

• Leh
• Shimla
• Mussoorie
• Nainital
• Jaisalmer
• Ajanta
• Ellora
• Tirupati
• Udagamandalam
• Rameshwar
• Jagannath puri
• Konark
• Khajuraho
• Panaji.

Question 2.
For what are the selected places famous?
Answer:
The selected places are famous for the following:

• Leh, Shimla, Mussoorie, Naini Tal, etc. – famous for their natural beauty.
• Rameshwaram, Tirupati, Jagannathpuri – religious places.
• Ajanta, Ellora, Konark, Khajuraho – cultural sites.
• Mumbai, Pune, Delhi, Kolkata – historical sites

Question 3.
Make a list of religious and historical sites from the map.
Answer:

Religious sites	Historical sites
Tirupati	Dwarka
Mathura	Agra
Varanasi	Jhansi
Konark	Jaipur

Question 4.
Make a list of hill stations, places having sanctuaries and places along the coasts.
Answer:
(A) Hill stations –

• Shimla
• Massoorie
• Nainital
• Darjiling

(B) Sanctuaries –

• Maharashtra – Koyna, Wild life Sanctuary
• Goa – Bird sanctuary
• Gujarat – Indina wild Ass. sanctuary
• Karnataka – Bhadra wild life sanctuary

(C) Places along coast –

• Mumbai
• Panaji
• Mangalore
• Chennai

Question 5.
Correlate the physiography and tourist places in India.
Answer:

• There is a close relationship between physiography and tourist places in India.
• Many tourist places are developed at various locations having different physiography.
• The hill stations like Jammu, Srinagar, Nainital, Darjiling, Udagamandalam are developed in mountainous region of India.
• The tourist places like Ujjain, Pune, Jabalpur, etc. are located at plateau region of India.
• The tourist places Jodhpur, etc. are developed in desert area of India.
• The tourist places like Mumbai, Panaji, Mangalore, Kanniyakumari, Chennai, etc. are located in the coastal area of India.

The tourism map of Maharashtra is given below. Answer the following questions based on the map:

Question 3.
Name the ports of Konkan coast and is there any connectivity of ports with tourism?
Answer:
Mumbai, Vijaydurg, Sindhudurg, Ratnagiri, Jaygad, Harne, Shrivardhan.
Yes, there is a close connectivity between ports and tourism as tourists can reach such places by sea without wasting much time in travelling.

Question 4.
Name some of the caves in Maharashtra.
Answer:
Karle, Bhaje, Mhasrul, Ajanta, Verul, Kharosa, Pullar are some of the caves in Maharashtra.

Give reason

Question 1.
Social development be accomplished through tourism.
Answer:

1. When facets1 like rural lifestyle, tribal life and culture are included in tourism then tourism gets a social dimension1 and the neglected components can be included in development.
2. The tribal life of Mel ghat of Maharashtra and visit to model villages like ‘Anandwan’, a project of the social activist Baba Amte, Ralegansidhhi, Hiwre Bazaar, etc. creates social consciousness and gives a fillip to development there.
3. There is a great potential2 for development of such a type of tourism in India through which social development can be accomplished.

Question 3.
Tourism is an invisible Trade’.
Answer:

1. Invisible Trade is a trade in which exchange of services occurs. Example of invisible trade. Tourism is a type of invisible trade.
2. Various restaurants, shops, transportation systems and recreational places are developed because of tourism and contribute directly to the economy.
3. Also, basic infrastructure improves and employment is generated which is an advantage to the economy indirectly.
4. Thus, tourism plays an important role in economic development and hence it is said that tourism is an invisible trade.

Question 4.
Tourism is good for environmental development.
Answer:

• Tourism is good for environmental development.
• Because of eco-friendly tourism concept, tourist places can be developed while caring for the environment.
• Factors like housing, resorts, traffic routes, etc. are also designed in an eco-friendly manner.
• In this type of development process, electricity, water are used very judiciously. The concept of recycle and reuse is also applied.
• Natural environment is maintained and tourism is developed too.

Answer in 2-3 Sentences.

Question 1.
What is the speciality of Deccan Odyssey?
Answer:

• Deccan Odyssey is a luxury train operated in co-ordination with MIDC, Indian Railways and Ministry of Tourism.
• Deccan Odyssey is like a moving palace.
• It originates at Mumbai and takes tourists to Nasik, Ellora, Ajanta, Koihapur, Goa and Ratnagiri.

Question 2.
Write about the luxury train for tourists visiting Northern india.
Answer:

• Palace on wheels” is the luxury train that covers the Northern India.
• This train takes the Deihi-Jaipur, Udaypur, Bharatpur, Agra Delhi route.
• Domestic arid foreign tourists enjoy travelling in this train.

Question 3.
Why is Vistadome a special attraction for tourists?
Answer:

• The coaches of Vistadome have a transparent ceiling which is a special attraction for tourists.
• It runs on the Vishakapatnam Kirandul route.
• As the train has a glass roof, the tourists can enjoy the panaromic view of the beautiful Arakuvalley, Anantgiri Ghat and Borra Coves.

Question 4.
What is Tarkarli in Konkan renowned for?
Answer:

• Tarkarli in Konkan is renowned for its seabed and biodiversity.
• Tourists can do snorkelling and scuba diving here.
• MTDC has set up a ‘scuba diving’ training centre of International standards at Tarkarli.

Question 5.
How is the GPS useful for tourists?
Answer:

• The GPS instrument found in applications like Google App location.
• Information regarding all possible routes of travel, distances, time require according to the type of vehicle, amenities on the way like petrol pump, restaurants etc. becomes available through GPS.

Write short note on:

Question 1.
GPS for tourism
Answer:

• The GPS system in our smartphones or the GPS instrument is largely used for tourism.
• For that we need special applications like the Google Map.
• We can know our exact location with the help of the map.
• Once it is decided where we want to head, then information regarding all the possible routes of travel, distances, time required according to type of vehicle, amenities on the way like petrol pump, restaurants, lodges, etc. becomes available in the app.
• We can use this for tourism.

Question 2.
MTDC
Answer:

• Maharashtra Tourism Development Corporation (MTDC) has implemented many programmes.
• It has provided guest houses, water sports, tourist houses near coastal areas, etc.
• “Deccan Odyssey” is a train started especially for tourism which is operated in coordination with MTDC, Indian Railways and Ministry of Tourism.
• The train originates at Mumbai and takes tourists to places like Nashik, Ellora, Ajanta, Kolhapur, Goa and Ratnagiri and back to Mumbai.

Question 3.
Domestic Tourism.
Answer:

• Tourism within the limits of the country is called Domestic Tourism.
• For example, a person from Maharashtra going to Kanyakumari in Tamil Nadu for a vacation, a person from Nagpur visiting Ellora Caves in Aurangabad and so on.

Question 4.
International Tourism.
Answer:

• Crossing the country’s boundaries and visiting some other country for tourism is called International Tourism.
  Glossary
• For example, an Indian going to Switzerland 1 for tourism, an American coming to India for tourism and so on.

Question 5.
Things required to travel to a foreign country.
Answer:
Following are the things required to travel to a foreign country:

• A Passport, visa, travel insurance and other documents.
• Currency of the country you are going to visit.

Question 6.
Eco-friendly tourism (Eco tourism).
Answer:

• The concept of eco-friendly tourism came into light when it was realised that due to increasing population, pollution and urbanization, environment is degrading.
• The nature of ecotourism is eco-friendly.
• In ecotourism, the tourists the place are visited by taking precautions of not damaging or degrading the environment.
• Ecotourism includes avoiding sound pollution, and air pollution, not hurting trees, birds, animals, etc. in the forests, etc.

Question 7.
Agro tourism.
Answer:

• Recently the concept of ‘agro-tourism’ has arisen which is visiting a pollution-free location away from the city holding an agricultural activity.
• In agro-tourism, the tourists are shown a glimpse of agricultural life.
• For a change from the urban life, tourists live on the farm and accept the hospitality of the farmers on payment in agro-tourism.
• In Pune and Kolhapur districts of Maharashtra number of agro-tourism centres have been developed.

Question 8.
Film tourism.
Answer:

• In film tourism, the locations where films are shot are shown to the tourists.
• A number of amenities and facilities are provided at such places to attract tourists.
• Mumbai film city, Ramoji film city are the famous film tourist places in India.

Question 9.
Coastal (sea) tourism
Answer:

• Coastal (sea) tourism is a new type of tourism.
• Tarkarli in Konkan is famous for snorkelling and scuba diving. It is also famous for its seabed and the biodiversity.
• MTDC has started a ‘scuba diving training centre’ of international standards at Tarkarli of Malwan taluka in Sindhudurg district.

Answer in brief:

Question 1.
Which new forms of tourism have developed recently?
Answer:
In recent years, the following are the new forms of tourism that have developed:

• Eco-tourism: While touring a place the environment should not be degraded or damaged by tourists, then it is called Ecotourism.
• Agro-tourism: Concept of ‘agro-tourism’ has arisen where pollution-free location away from the city holding an agricultural activity is visited. There the tourists are shown a glimpse of agricultural life.
• Film Tourism: Film tourism is a new type of tourism. The locations where films are shot are shown to tourists.
• Medical Tourism: The medicinal and surgical treatment in Indian hospitals are cost-effective and therefore, many patients from various developing countries come here for treatment.
• Medical Tourism develops from such facilities required by these tourists.

Question 2.
Explain the importance of tourist development in India.
Answer:

• India is diverse in terms of culture and nature, due to which India has a lot of potential for tourism.
• The richness of natural beauty in India, attractive landscapes and high mountains like Flimalayas exquisite coastal areas attract tourists.
• Also, the diversity of Indian culture, festivals, traditions and customs have resulted in opportunities for tourism in India.

Question 8.
What are the reasons of following medical tourists in India?
Answer:

• Many tourists visit India to avail health facilities, to achieve mental peace and physical strength through Indian Ayurveda, Yoga and Pranayam.
• The medicinal and surgical treatment in Indian hospitals are cost-effective and therefore many patients from various developing countries come here for treatment.
• Hence, medical Tourism develops from the facilities required by these tourists.

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 7 International Date Line Notes, Textbook Exercise Important Questions and Answers.

International Date Line Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 7 International Date Line Questions And Answers Maharashtra Board

Geography Class 9 Chapter 7 Question Answer Maharashtra Board

1. Two boxes in different hemispheres are given in the following diagram. The IDL passes through both the boxes. In one box, the meridian, day and date is given. Find the day and date for the other box.

Answer:

2. Select the correct option :

Class 9 Geography Chapter 7 International Date Line Question 1.
While crossing the IDL, a person will have to add one day when traveling from
(a) East to West
(b) West to East
(c) South to North
(d) North to South
Answer:
(a) East to West

International Date Line Class 9 Question 2.
If it is Wednesday 10 a.m. at 150 E meridian, then what will be the time at IDL?
(a) Wednesday at 6 a.m.
(b) Wednesday 9 p.m.
(c) Thursday 2 p.m.
(d) Thursday at 6 p.m.
Answer:
(b) Wednesday 9 p.m.

International Date Line Questions And Answers Question 3.
According to the international convention, at which meridian does the day and date change occurs?
(a) 0°
(b) 90° E
(c) 90° W
(d) 180°
Answer:
(d) 180°

International Date Line 9th Std Geography Question 4.
At which direction of the IDL does a new day start immediately?
(a) East
(b) West
(c) North
(d) South
Answer:
(b) West

9 Std Geography International Date Line Question 5.
IDL brings coordination in which of the following?
(a) GPS system
(b) Defence departments
(c) Transportation schedules
(d) Determining the hemisphere
Answer:
(c) Transportation schedules

3. Give geographical reasons

Std 9 Geography Chapter 7 International Date Line Question 1.
IDL is proving to be very useful in today’s times
Answer:
IDL is proving to be very useful in today’s times because:

• The IDL brings coordination between international airlines, transportation services, economic and trade activities.
• The IDL has been carved out of the necessity of coordinating time and date.
• It is also important in today’s modern era and rapidly happening global developments.
• We can keep a track of all the calculations of a day and time accurately with the help of IDL in case of global transportation especially, with respect to airways.
• It is only because of the IDL that the schedules of the traffic worldwide are organised properly.

Class 9th Geography Chapter 7 Question Answer Question 2.
The day starts in the Pacific Ocean on the earth
Answer:

• The IDL passes through the Pacific Ocean.
• With reference to the IDL, the day on Earth starts in the West and ends in the East.
• It is one and the same day only at 12 o’clock midnight at the 180° meridian.
• For the countries lying to the east of it i.e. the USA, Chile, etc., it is the end of the day while for the countries lying to the west of it i.e. Japan, Australia, etc. it is the start of a new day.

Thus, a new day starts in the Pacific Ocean on Earth.

4. Write in brief:

International Date Line Std 9 Question 1.
What considerations have been made while deciding the IDL?
Answer:
The following points were taken into consideration while drawing the International Date Line. (IDL):

1. The direction of travel
2. The current day and date

• • Accordingly, while traveling from East to West of IDL, a day is added. For example, while travelling from America to Japan, if it is Thursday 25th December, then it will be Friday 26th December in Japan.
  • While from West to East of IDL, the day remains the same. For example, while travelling from Japan to America, if it is Thursday 25th December, then Thursday 25th December, only should be considered.

Question 2.
While crossing the IDL, what changes will you make?
Answer:

• When you cross the 180° meridian, some precautions need to be taken.
• There is a difference of 12 hours from Prime Meridian, if you go from East or West.
• According to the convention, the start (and end) of a date is considered to be at 180° Meridian.
• Accordingly, an adjustment or change in day and time is made. Thus, while travelling from east to west of IDL , a day is added whereas while travelling from west to east of IDL, the day remains the same.

Question 3.
Why is the IDL not a straight line like the 1800 meridian?
Answer:

• Attempt has been made to make the IDL pass through the Pacific Ocean completely.
• Had it passed through a land or some islands, the people there would have had to follow different dates and timings because dates would have been different on their Eastern and Western parts.
• Also, it would have been difficult to know when one crosses the IDL on land, and when the date changes on the calendar.
• Therefore, the IDL is not a straight line like the 1 180° Meridian. At places, it turns East while at other places, it turns West.

Question 4.
Why doesn’t the IDL pass through land?
Answer:

• If the IDL had passed through a land or some islands, the people there would have had to follow different dates and timings because dates would have been different on their Eastern and Western parts.
• Also, it would have been difficult to know when one crosses the IDL on land and when the date changes on the calendar.
• Hence, the IDL does not pass through land

Question 5.
Why is the IDL considered with respect to the 1800 meridian only?
Answer:

• Our 24-hour day starts at 12 midnight. Because of the earth’s rotation, the midnight occurs at different times, at different places.
• As the Earth is spherical in shape, every place has a place to its East.
• So, it was necessary to determine at what location to the East does the day start on Earth.
• Hence, representatives of many nations got together, under the leadership of an American Professor, Davidson, in the year 1884 and decided the International Date Line.
• The line was drawn opposite to the Greenwich Prime Meridian i.e. with reference to the 180° Meridian.

5. Using an atlas, tell in which of the following routes the IDL will be crossed and show them on the map.

(1) Mumbai- London- New York- Los Angeles- Tokyo
(2) Delhi- Kolkata- Singapore- Melbourne
(3) Kolkata- Hong Kong- Tokyo- San Francisco
(4) Chennai-Singapore- Tokyo- Sydney-Santiago
(5) Delhi-London-New York

Answer:
(1) Mumbai – London – New York – Los Angeles – Tokyo – IDL will be crossed.
(2) Delhi – Kolkata – Singapore – Melbourne – IDL will not be crossed
(3) Kolkata – Hong Kong – Tokyo – San Fransico – IDL will be crossed.
(4) Chennai – Singapore – Tokyo – Sydney – Santiago – IDL will be crossed
(5) Delhi – London – New York – IDL will not be crossed.

Class 9 Geography Chapter 7 International Date Line Intext Questions and Answers

Use your Brain Power:

Question 1.
You are traveling from the Kamchatka Peninsula (in the northern hemisphere) to New Zealand (in the southern hemisphere) along the IDL. It is Monday, 22nd June in the northern hemisphere. What will the day and date in the southern hemisphere?
Answer:
The day will be Monday, 22nd June as we are not crossing the IDL.

Examine a ticket of UA 876 Boeing 787-9 Dreamliner closely and find the answers to the following questions:

Question 1.
From which country will the plane take off and where will it go?
Answer:
The plane will take off from Tokyo (Japan) and will go to San Francisco, California (USA)

Question 2.
What is the duration of the flight?
Answer:
The duration of the flight is 9hrs and 15 min.

Question 3.
What is the day, date and time given at the starting point and destination of the flight?
Answer:
At the starting point of Tokyo (Japan) it is Friday, 1st April 12.30 am and at the destination of San Francisco California (USA) it will arrive on Thursday March 31st at 5.45 pm.

Question 4.
What special note is given on the air ticket?
Answer:
A special note on the ticket states that the flight involves a date change.

Question 5.
What could be the reason behind giving such a note?
Answer:
The reason behind giving such a note is to make us understand that the flight will cross the IDL

Question 6.
During this flight, will the plane cross the IDL? If yes, then from which direction to which direction?
Answer:
During this flight, the plane will cross the IDL from west to east.

Question 7.
What did you understand by reading the ticket?
Answer:
We understand that a day is deducted and the time is fixed backward by 1 day while crossing the IDL from west to east.

Try this:

Question 1.
Complete the following table to understand the time at different meridians: (In this activity we are not taking into consideration the rotation of the earth.)
Answer:

• All places to east of Prime Meridian are ahead of GMT and all places to west of Prime Meridian are behind GMT.
• Earth rotates on its axis and covers 1° longitude in 4 minutes.
• As Sunil is moving 30° east, time will move ahead by 120 min, i.e. 2 hours (30° x 4 min.) and as Minal is moving 30° west, time will move backwards by 120 min. i.e. 2 hours.

Question 1.
What is the day at 00 meridians at Greenwich after completing the table ‘A’?
Answer:
The day at 0° meridian at Greenwich after completing the table ‘A’ is Wednesday.

Question 2.
What is the day at 00 meridians at Greenwich after completing the table ‘B’?
Answer:
The day at 0° meridian at Greenwich after completing the table B is Friday.

Question 3.
Though both were at the same place, why were they experiencing different days? How did this happen?
Answer:
Because Sunil was moving eastward, so time will move ahead whereas Meenal was moving westward, so time is moving backward.

Question 4.
How many days occurred while doing this activity? Name them.
Answer:
While doing this activity, 3 days came in reference as Wednesday, Thurday and Friday.

Question 5.
Which day is correct: Wednesday in Table ‘A’ or Friday in Table ‘B’? Why?
Answer:
None of the given days are correct. The correct day is Thursday after considering IDL.

Explanation:
(i) When Sunil reached 180° meridian i.e. IDL, according to him it is Thursday midnight (24.00). When IDL is crossed from west to east we need to deduct a day (24 hrs.). Thus when 24 hrs are deducted from Thursday 24.00 (midnight) we get Thursday 00.00. So after crossing the IDL the day to be considered is Thursday i.e. the same day.

(ii) When Minal reached 180° meridian i.e. IDL, according to her it is Wednesday midnight (24.00). When IDL is crossed from east to west we need to add a day (24 hrs.). Thus when 24 hrs are added to Wednesday 24.00 (midnight) we get Thursday 24.00 (midnight). So after crossing the IDL the day to be considered is Thursday.

Give it a try:

Your are now aware of the changes required to be made while crossing the ¡DL. Now redo the activity given on Page 59. Tell us the changes that you will have to make while crossing the IDL i.e. 1800 meridian. Your travel will start on Sunday, 21st May 2016 at 10 a.m.

Let’s Recall:

Question 1.
Which meridian is used to determine world standard Time (GMT)?
Answer:
World Standard Time (GMT) is determined using Prime Meridian at 0° longitude.

Question 2.
Which meridian determines Indian Standard Time (1ST)?
Answer:
82°30′ E is the standard meridian of India.

Question 3.
What is the time difference between the GMT and the IST?
Answer:
IST is 5hrs and 30 min ahead of GMT.

Class 9 Geography Chapter 7 International Date Line Additional Important Questions and Answers

Complete the Statements choosing correct option:

Question 1.
Man has studied the rotation speed, direction and shape of the earth and prepared the system.
(a) monometric
(b) chronometric
(c) topographic
(d) GIS
Answer:
(b) Chronometric

Question 2.
Earth rotates from
(a) north to south
(b) south to north
(c) east to west
(d) west to east
Answer:
(d) west to east

Question 3.
In terms of time the part of the earth is ahead of the part.
(a) northern, southern
(b) southern, northern
(c) eastern, western
(d) western, eastern
Answer:
(c) eastern, western

Question 4.
is reached after 12 hours from Prime Meridian
(a) 90° W
(b) 90° E
(c) 180°
(d)120°W
Answer:
(c) 180°

Question 5.
According to IDL, while traveling from east to west
(a) a day is added
(b) a day is deducted
(c) keep the same day
(d) None of these
Answer:
(a) a day is added

Question 6.
Many nations got together under the leadership of in 1884 and decided on International Date Line.
(a) Professor Davidson
(b) Professor Samuelson
(c) Professor Adam Smith
(d) Professor Richardson
Answer:
(a) Professor Davidson

Answer in one sentence:

Question 1.
If it is 12noon at the Prime Meridian then what will be the time at 60°E longitude?
Answer:
If its is 12noon at the Prime Meridian, then it will be 16.00hrs (4pm) at 60°E longitude.

Question 2.
Which part of the earth is ahead in terms of time?
Answer:
In terms of time the eastern part of the earth is ahead of the western part.

Question 3.
When was it decided to draw the International Date line?
Answer:
When representatives of many nations got together under the leadership of American professor Davidson in the year of 1884 they decided on the International Date line.

Question 4.
A new day starts on the earth in which Ocean?
Answer:
A new day starts in the Pacific Ocean on the earth.

The following table shows the days and time to welcome New Year in different countries and cities according to 1ST. Observe the table and answer the questions gives below:

Country-city	Day	Indian Time
England – London	Sunday	05.30
Japan – Tokyo	Saturday	20.30
USA-New York	Sunday	10.30
USA – Baker Island	Sunday	17.30
Australia – Sydney	Saturday	18.30
New Zealand – Auckland	Saturday	16.30
Samoa Island – Apia	Saturday	15.30
Tuvalu – Funafuti Island	Saturday	17.30

Question 1.
Which location was the first to welcome the New Year in the World? What day was it then?
Answer:
Samoa islands in Apia was the first to welcome the New Year in the world on Saturday.

Question 2.
Which location bid farewell to the year 2016, the last of all?
Answer:
Baker islands in USA was last to bid farewell to the year 2016.

Question 3.
On which day did that location welcome 2017?
Answer:
Baker islands in USA welcomed 2017 on Sunday.

Question 4.
What could be the reason behind the change in the day of Sydney and London?
Answer:
According to 1ST, India welcomed the New Year at 12 midnight on Saturday. Sydney being 5 hours and 30 minutes ahead of IST and has already welcomed the New year before India on Saturday itself. But London is 5 hours and 30 minutes behind IST will welcome the New Year the next day i.e. on Sunday.

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 2 Endogenetic Movements Notes, Textbook Exercise Important Questions and Answers.

Endogenetic Movements Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 2 Endogenetic Movements Questions And Answers Maharashtra Board

Geography Class 9 Chapter 2 Question Answer Maharashtra Board

1. Tick in front of the correct option ✓

(a) On which of the following are slow movements in the earth’s interior dependent?
Landforms [ ]
Velocity [ ]
Direction [ ]
Answer:
Velocity

(b) When waves divert from each other, what do they create
Compression [ ]
Tension [ ]
Mountain [ ]
Answer:
Tension

(c) For the formation of a rift valley, which of the following processes should occur in the earth’s crust?
Compression [ ]
Tension [ ]
Weathering [ ]
Answer:
Tension

(d) Which of these is a fold mountain?
The Satpudas [ ]
The Himalayas [ ]
The Western Ghats [ ]
Answer:
The Himalayas

(e) The formation of extensive plateaus is a result of which type of movements?
Mountain-building [ ]
Continent-building [ ]
Horizontal [ ]
Answer:
Continent-building

2. Give geographical reasons.

(a) Buildings collapsed at the foothills of the Himalayas because of an earthquake. Before collapsing they were moving forward and backward.
Answer:

• The seismic waves can be divided into primary, secondary and surface waves.
• The primary waves are the first ones to reach the surface of the earth after the energy is emitted in the Earth’s interior.
• Subjected to a ‘P’ wave, particles in the rock move in the direction of waves to and fro and therefore, these waves are also called forward-backward waves.
• Thus, during an earthquake, the buildings at the foothills of the Himalayas moved forward and backward as they were first subjected to “P” waves.

(b) There is a difference in the formation of the Meghalaya Plateau and the Deccan Plateau.
Answer:

1. The Meghalaya plateau is formed due to slow movements (orogenic movements) whereas the Deccan Plateau is formed due to sudden movements (fissure volcano).
2. During the formation of the Meghalaya plateau, a part of the Earth’s crust in between two parallel faults was lifted forming a plateau whereas, the Deccan plateau was formed due to molten material coming out with the eruption spreading on both sides of the fissure.
3. Thus, there is a difference in the formation of the Meghalaya plateau and the Deccan plateau.

(c) Most of the volcanoes are found on the plate boundaries.
Answer:

• The plate boundaries are directly related to the areas of volcanoes.
• Most of the volcanoes are located on the plate boundaries.
• The part of the plate boundary which slides under the crust, results in the loss of material. Such boundaries are called plate consuming boundaries.
• In areas where new material (magma) is coming up onto the Earth’s crust, they are called plate creating boundaries.
• Both the processes result in earthquakes and volcanoes. Thus, most of the volcanoes are formed in the plate boundaries.

(d) The Barren Island is becoming conical in shape.
Answer:

• Barren island which was considered a dormant volcano has become active since February 2017.
• Mainly dust, smoke and mud are coming out of this eruption along with some lava.
• During eruption, the lava is spread around the mouth of this vent, when it comes out.
• As a result, a cone-shaped mountain starts forming.

Therefore Barren Island is becoming conical in shape.

(e) Volcanic eruptions can cause earthquakes.
Answer:

• Generally, the movements in the Earth’s interior occur in the upper layer of the mantle
• Tremendous energy is released by radioactive materials present here.
• This leads to a sudden movement in form of volcanic eruptions where hot solid, liquid and gaseous materials are forcefully thrown out from the mantle of the Earth, onto the surface of the Earth.
• This causes a lot of instability within the crust of the Earth which would also lead to the release of pressure in the form of seismic waves or tremors causing earthquakes.

3. Identify and name the internal movement.

(a) Tsunamis are generated in coastal areas.
Answer:
Sudden Movement

(b) The Himalayas are an example of fold mountains.
Answer:
Slow movement – Mountain Building Movements.

(c) Molten magma is thrown out of the earth’s mantle.
Answer:
Sudden Movement

(d) Rift valley is formed because of faulting.
Answer:
The slow movement – Upward – Downward Movement.

4. Arrange the following statements in chronological order in which an earthquake occurs.

(a) The earth’s surface vibrates
Answer:
The plates suddenly move.

(b) The plates suddenly move.
Answer:
Due to the movements in the mantle compression goes on increasing.

(c) Due to the movements in the mantle, compression goes on increasing.
Answer:
Along the weak point (faultlines) rocks break apart.

(d) Along the weak points ( faultlines) rocks break apart.
Answer:
Stored energy is released in the form of seismic waves.

(e) Stored energy is released in the form of seismic waves.
Answer:
The earth’s surface vibrates.

5. Distinguish between

(a) Block Mountain and Fold Mountain
Answer:

Block Mountain	Fold Mountain
(i) When a part of the earth’s crust between two parallel faults is lifted a block mountain is formed.	(i) Because of the energy waves and pressure working towards each other, the layers of the soft rocks form folds leading to the formation of fold mountains.
(ii) Block mountains are formed due to tension.	(ii) Fold mountains are formed due to compression.
(iii) e.g. The Black forest mountains of Europe and the Meghalaya Plateau of India.	(iii) e.g. The Himalayas, the Aravalis, the Rockies, the Andes, the Alps

(b) Primary and Secondary Seismic Waves
Answer:

Primary Seismic Waves	Secondary Seismic waves
(i) Primary waves are the first one to reach the surface of the earth after the energy is emitted in the Earth’s interior.	(i) The waves which reach the Earth’s surface after the primary waves are called secondary waves.
(ii) Primary waves can travel through solid, liquid and gaseous medium.	(ii) Secondary waves can travel only through only solid medium.
(iii) While travelling through liquid medium, primary waves change their direction.	(iii) Secondary waves get absorbed as they enter the liquid medium.
(iv) The waves move to and fro in the direction of energy transfer.	(iv) These waves move up and down in the direction of energy transfer.

(c) Earthquakes and volcanoes
Answer:

Earthquakes	Volcanoes
(i) Earthquake is the movement of the Earth’s crust.	A volcano is an opening in the Earth’s crust from which hot solid, liquid and gaseous materials are thrown out from the mantle of.
(ii) Nothing is ejected out during an earthquake.	During a volcanic eruption, ash, water vapor, various types of poisonous and inflammable gases, hot molten magma etc. is ejected from the earth’s interior.

6. Answer in brief
(a) Give reasons why an earthquake occurs.
Answer:

• When the movements occur in the interior of the Earth, tremendous tension is created in the Earth’s crust.
• When the tension goes beyond limits, the energy is released in the form of waves.
• This results in the trembling of the earth’s surface, i.e. an earthquake occurs.

Following are the reasons for the occurrence of an earthquake:

• Moving of the plates
• Colliding of the plates
• Plates sliding one below the other
• Forming of fractures in rock layers, due to tension in the interior of the Earth.
• Occurring of volcanic eruption

(b) Which type of movements have led to the formation of the major fold mountains in the world?
Answer:

• Fold mountains are formed due to mountain-building (erogenic) movements.
• Energy is transferred from the interior of the Earth. Because of these energy waves and pressure working towards each other and in horizontal direction, the layers of the soft rocks form folds.
• If the pressure is very high, large scale folds are formed and their complexity increases.
• As a result, the surface of the Earth gets uplifted and fold mountains are formed.
• The Himalayas, the Aravalis, the Rockies, the Andes, the Alps are the major fold mountains of the world.

(c) How is the magnitude of the earthquake-related to the collapse of houses
Answer:

• Through a seismogram, a graph showing movement of seismic waves (seismograph) can be generated.
• After studying this graph, the magnitude of the earthquake is known.
• The magnitude of the earthquake is measured with the help of a richter scale.
• It is because of the primary waves that the buildings on the Earth’s surface move back and forth.
• The buildings on the Earth’s surface move up and down because of the secondary waves. These are more destructive than the T’ waves leading to collapse of buildings.

(d) What are the effects of earthquakes on the earth’s surface and human life?
Answer:
Following are the effects of earthquakes:

• Cracks/fractures develop on the ground.
• These causes landslides which leads to sliding of rocks.
• Sometimes the groundwater changes its course. For example, wells may get water, or may dry up.
• Some areas get uplifted while some may subside.
• Tsunamis are generated in oceans These waves can cause great loss of life and property in the coastal areas.
• In snow-covered areas, avalanches may occur.
• Buildings collapse and loss of life and property occurs.
• Transportation routes get disrupted.
• The communication system collapses.

(e) Explain the types of seismic waves.
Answer:
When the intension is released at the focus, the released energy travels in all directions. This energy comes towards the Earth’s surface in the form of waves. The seismic waves can be divided into primary, secondary and surface waves.
(i) Primary or ‘P’ waves:

• These waves are first to reach the surface of the Earth, after the energy is emitted in the Earth’s interior. They travel at a very fast speed from the focus of the earthquake in radial direction.
• The waves moves to and fro, therefore these waves are called forward-backward waves.
• These waves can travel through all the three states – liquid, solid and gaseous.
• While travelling through liquid medium, their direction gets changed. It is because of the primary waves that the buildings on the Earth’s surface move back and forth.

(ii) Secondary or ‘S’ waves :

• The waves which reach the Earth’s surface after I the primary waves are called secondary waves. :
• These waves also scatter in all directions from the focus of the earthquake.
• Their velocity is less than ’P’ waves.
• The particles lying in the way of these waves j move up and down in the direction of energy transfer.
• These waves can travel only through the solid medium and they get absorbed as they enter the liquid medium.
• The buildings on the Earth’s surface move up and down because of these waves. These are more destructive than ‘P waves.

(iii) Surface or ‘L’ waves :

• These waves are generated after the main ’P’ and ‘S’ waves reach the epicenter.
• They travel in the direction of the circumference of the Earth, along the crust and are highly destructive.

(f) Explain the types of volcanoes on the basis of the periodicity of eruption with examples.
Answer:
According to the periodicity of the volcanic eruptions, three types of volcanoes can be identified.
(i) Active Volcanoes –

• If the volcanic eruptions are regular even in the present times, then such volcanoes are called active volcanoes.
• E.g., Mt Fujiyama in Japan and Mt. Stromboli in the Mediterranean Sea.

(ii) Dormant Volcanoes –

• When a volcano has not erupted since long, but may become active suddenly is called a dormant volcano.
• E.g., Mt. Vesuvius in Italy, Mt. Katmai in Alaska and Barren Island, India.

(iii) Extinct volcanoes –

• Those volcanoes which have not erupted in the past since long and are not likely to erupt in the future are called extinct volcanoes.
• E.g., Mr. Kilimanjaro in Tanzania.

7. Show the epicenter, focus and the primary, secondary and surface waves of an earthquake with the help of a neat labeled diagram.
Answer:

8. Show the following on a given outline map of the world.

(a) Mt. Kilimanjaro
(b) Mid-Atlantic Earthquake zone
(c) Mt. Fuji
(d) Krakatoa
(e) Mt. Vesuvius
Answer:

Class 9 Geography Chapter 2 Endogenetic Movements Intext Questions and Answers

Can you tell?
Read the following news. Observe the photograph and answer the questions.

Question 1.
What caused large-scale casualties?
Answer:
Calamity of earthquake led to large scale casualties.

Question 2.
What was the magnitude of the earthquake?
Answer:
The magnitude of the earthquake was 7.9 Richter scale.

Question 3.
Which country was the most affected because of this earthquake?
Answer:
Nepal was most affected because of this earthquake.

Question 4.
Where was the epicentre of the earthquake?
Answer:
Lamjung in Nepal was the epicentre of the earthquake.

Question 5.
Which are the other affected areas?
Answer:
Bihar, West Bengal and Uttar Pradesh in India as well as China, Bhutan, Pakistan and Bangladesh were affected by earthquake.

Question 6.
At what depth was the focus located?
Answer:
The focus of the earthquake was located at the depth of 11 km.

Question 7.
What kind of damage is seen because of the earthquake?
Answer:
Nearly 1500 people were killed and over 1000 people were injured in the disaster.

Question 8.
According to you, what could be the reason behind the earthquake?
Answer:
The sudden release of energy from the interior of the earth leads to earthquakes.

Question 9.
Have you ever experienced a similar earthquake? Discuss.
Answer:
Answers may vary.

Class 9 Geography Chapter 2 Endogenetic Movements Additional Important Questions and Answers

Complete the statements choosing the correct option from the bracket:

Question 1.
Richter scale is a unit of measuring the magnitude of a/an
(a) volcano
(b) creation of plate
(c) earthquake
(d) earth movement
Answer:
(c) earthquake

Question 2.
There are in all major plates on the Earth.
(a) five
(b) seven
(c) nine
(d) four
Answer:
(b) seven

Question 3.
Large scale and sudden release of energy in the interior of the Earth gives rise to Earth movements.
(a) slow
(b) sudden
(c) internal
(d) external
Answer:
(b) sudden

Question 4.
Earthquakes occur due to the movement of
(a) plates
(b) earth
(c) oceans
(d) land
Answer:
(a) plates

Question 5.
Earthquake is measured with the help of an instrument called a
(a) seismogram
(b) thermometer
(c) barometer
(d) hygrometer
Answer:
(a) seismogram

Question 6.
If lava is released through a vent, it is called a vent volcano.
(a) fissure
(b) central
(c) upper
(d) below
Answer:
(b) central

Question 7.
Kilimanjaro is a volcano.
(a) central type
(b) fissure type
(c) extinct type
(d) dormant type
Answer:
(a) central type

Question 8.
A tremendous amount of energy is given out by the radioactive elements in the
(a) crust
(b) core
(c) mantle
(d) sial
Answer:
(c) mantle

Question 9.
The movements that give rise to mountains are called movements.
(a) epiorogenic
(b) orogenic
(c) slow
(d) sudden
Answer:
(b) orogenic

Question 10.
When a portion of the crust between two parallel faults2 is raised up, it is called a mountain.
(a) block
(b) fold
(c) residual
(d) ancient
Answer:
(a) block

Question 11.
The area between two adjoining faults subsides, such area of subsidence is called
(a) rift valley
(b) block mountain
(c) fold mountain
(d) faulting
Answer:
(a) rift valley

Question 12.
Black Forest Mountain in Europe is a mountain.
(a) fold
(b) residual
(c) block
(d) ancient
Answer:
(c) block

Question 13.
The movements that give rise to continents are
(a) orogenic
(c) fold
(b) epeirogenic
(d) fault
Answer:
(b) epeirogenic

(Endogenetic Movements Class 9 Geography Chapter 2 )Tick in front of the correct option.

Question 1.
Which of these is a block mountain?
(a) Black forest mountain
(b) Alps
(c) Andes
Answer:
(a) Black forest mountain

Question 2.
Which type of volcano has eruptions regularly even during present times?
(a) Dormant
(b) Extinct
(c) Active
Answer:
(c) Active

Give one word for each of the following:

Question 1.
A volcano, where lava reaches the surface through a vent or a pipe.
Answer:
Central Vent Volcano

Question 2.
An instrument, which is used for recording earthquakes.
Answer:
Seismogram

Question 3.
The surface position immediately above the origin of an earthquake.
Answer:
Epicenter

Question 4.
An example of a volcanic plateau.
Answer:
Deccan Plateau.

Question 5.
An example of Conical volcanic mountains.
Answer:
Mt. Kilimanjaro

(Class 9 Geography Chapter 2 Endogenetic Movements Questions And Answers ) Answer in one sentence each.

Question 1.
What are Endogenetic processes?
Answer:
Endogenetic processes are processes that originate internally in the Earth’s surface. E.g. earthquakes, volcanoes, continent building, mountain building etc.

Question 2.
What is a Richter scale?
Answer:
It is a scale for expressing the magnitude of an earthquake.

Question 3.
What is a Focus or Hypocentre?
Answer:
The point below the Earth’s surface where energy is released during an earthquake is called the focus of the earthquake.

Question 4.
What are Primary Waves?
Answer:
The earthquake waves that reach the surface of the Earth first, immediately after the energy is released in the interior of the Earth, are called Primary waves.

Question 5.
What are Secondary Waves?
Answer:
The earthquake waves reporting at the surface after the primary waves are called the secondary waves.

Question 6.
What are Surface Waves?
Answer:
Primary and secondary waves affect the surface on reaching it. As a result a new set of waves gets generated at the surface. These waves are called surface waves.

Question 7.
What are Plates?
Answer:
The parts of varying sizes of the Earth’s crust floating on the upper portion of the mantle are called plates.

Question 8.
What do you mean by an Epicentre?
Answer:
The point located on the surface of the Earth nearest to the focus is called the epicenter of the earthquake.

Question 9.
Explain Orogenic Movements
Answer:
The slow movements in the interior of the Earth that give rise to mountains are called orogenic movements (mountain building movements).

Question 10.
What is Folding1?
Answer:
As energy moves through the interior of the Earth, soft rocks are subjected to pressure leading to creation of folds called folding.

Question 11.
Define Fault.
Answer:
The fracture line created in a rock due to the energy waves moving away from each other is called a fault.

Question 12.
What is a Block Mountain?
Answer:
A raised portion of the crust between two parallel faults is called a block mountain.

Question 13.
What is a Rift valley?
Answer:
The area of subsidence between two adjoining faults is called a rift valley.

Question 14.
Explain Epeirogenic Movements.
Answer:
The Earth’s slow movements that give rise to continents and extensive plateaus are called epeirogenic movements.

Question 15.
Explain the process of Volcanic Eruption.
Answer:
A process in which hot solid, liquid and gaseous materials are thrown out from the mantle of the earth onto the surface of the earth, is called volcanic eruption.

Identify and name the internal movements.

Question 1.
Dust, smoke and mud with some lava coming out of Barren Island.
Answer:
Sudden Movement

Distinguish between:

Question 1.
Seismic Focus and Epicentre
Answer:

Seismic Focus	Epicenter
(i) The point below the surface where energy is released during an earthquake is called the seismic focus of the earthquake.	(i) The place on the surface which is directly above the focus and closest to it is called the epicenter.
(ii) From the seismic focus, an energy wave radiates in all directions.	(ii) Seismic waves reach the epicenter first and foremost and so its intensity is the maximum at this point.

Question 2.
Central Type Volcano and Fissure Type Volcano
Answer:

Central Type Volcano		Fissure Type Volcano
(i)	Lava is released through a pipe-like vent, hence it is called central type volcano.	(i)	Lava is released through a number of fissures or cracks, hence it is called fissure type volcano.
(ii)	The ejected material gets settled near the mouth of the central vent, giving rise to conical hills.	(ii)	The ejected material spreads on either side of the fissures and forms volcanic plateaus.
(iii)	e.g. Mt. Fujiyama of Japan, Mt. Kilimanjaro in Tanzania.	(iii)	e.g. the Deccan plateau of India

Question 3.
Orogenic Movements and Epeirogenic Movements
Answer:

Orogenic Movements	Epeirogemic Movements
(i) The movements that give rise to mountains are called Orogenic Movements.	(i) The movements that give rise to continents are called Epeirogenic Movements.
(ii) They lead to the formation of Fold mountains, Block mountains and Rift valleys.	(ii) They lead to the formation of continents and extensive plateaus.

Question 4.
Slow Internal Movements and Sudden Internal Movements
Answer:

Slow Internal Movements	Sudden Internal Movements
(i) The movements in the interior of the earth that are caused by continuous and slow release of energy are called slow internal movements	(i) The movements in the interior of the earth that are caused by the sudden release of energy on a large scale are called sudden internal movements.
(ii) Slow internal movements give rise to mountains and continents.	(ii) Sudden internal movements lead to earthquakes and volcanic eruptions.

Make friends with Maps!

Answer the following questions:

Question 1.
Examine the plate boundaries in the given map and write the names of the plates.
Answer:
North American Plate, South American Plate, Indo-Australian Plate, African Plate, Eurasian Plate, Pacific Plate, Antarctic Plate, Arabian Plate, Nazca Plate, Cocos Plate, Caribbean Plate, Scotia Plate, Arabian Plate and Somali Plate.

Question 2.
On which side of the continents of North and South America are the earthquake-prone zones located? Which mountains are located there?
Answer:
The earthquake-prone zone is located on the western side of North and South America. Rockies and Andes mountain ranges are located there.

Question 3.
In which mountainous zone in Asia does the earthquake-prone zone lie?
Answer:
The Himalayan mountainous zone of Asia is an earthquake-prone zone.

Question 4.
In which region are the volcanoes concentrated in Africa? What could be the reason?
Answer:
Volcanoes are concentrated in the eastern part of Africa along the Rift Valley region as this region is located on plate boundaries.

Question 5.
Correlate earthquake regions, distribution of volcanoes and plate boundaries.
Answer:
Plate boundaries are directly related to areas of earthquakes and volcanoes. Most of the volcanoes are located on the plate boundaries. Similarly, the earthquake zones are also seen in the border areas.

Give geographical reasons:

Question 1.
The secondary earthquake waves are very destructive.
Answer:

• Due to secondary earthquake waves, the grains in the rocks move up and down, that is, perpendicular to the direction of the movement of the waves.
• Therefore, secondary waves are very destructive.

Answer in brief:

Question 1.
Explain the types of volcanoes on the basis of their type of eruption, with examples.
Answer:
On the basis of the type of eruption, volcanoes can be divided into two types.
(i) Central-type or conical volcano:

• During eruption, the molten magma comes out through a pipe-like vent from inside the Earth’s surface. The lava spreads around the mouth of this vent, when it comes out.
•  Asa result, cone-shaped mountains start forming and conical volcanic mountains are formed.
• Mt. Fujiyama in Japan and Mt. Kilimanjaro in Tanzania are examples of central-type volcanoes and conical mountains.

(ii) Fissure-type volcano:

• During eruption, when the magma comes out not from a single vent, but from many cracks (fissures), it is called fissure-type volcanic eruption.
• The molten material coming out with the eruption spreads on both the sides of the fissure. ;
• As a result, volcanic plateaus are formed.
• The Deccan Plateau of India has also been formed due to such a type of volcanic eruption.

Question 2.
Describe the changes that take place on the surface of the Earth, due to the movements taking place in the interior of the Earth.
Answer:
The changes taking place on the surface of the Earth, due to the internal movements of the Earth are as follows:

1. The soft rocks are subjected to pressure due to the energy released in the interior of the Earth. This leads to the development of folds.
2. If the pressure is very high, large scale folds are formed, and their complexity increases. As a result, the surface of the Earth gets uplifted and fold mountains are formed.
3. When the energy waves move away from each other, tension in the rock is developed. In hard rocks, the tension leads to faulting, when a portion between two parallel faults is raised up, block mountains are created.
4. Sometimes, when the portion between two parallel faults subsides, a rift valley is created.
5. Sometimes, an extensive portion is raised to form a continent or an extensive plateau.

Question 3.
How are continents and extensive plateaus formed?
Answer:

• The epeirogenic movements are responsible for the formation of continents.
• Slow movements occur towards the centre or from the Earth’s centre towards the Earth’s crust.
• Because of these movements, a vast part of the Earth’s crust is uplifted or gets subsided.
• When the part of the Earth’s crust is uplifted above the sea mean level, continents are formed.
• Therefore, these movements are called continent-building movements.
• Extensive plateaus can also be formed because of such movements.

Question 4.
What are the effects of volcanoes?
Answer:
The following are the effects of volcanoes:

• Loss of life and property.
• Sometimes tsunamis get generated due to volcanic eruptions occurring below ocean floors.
• Dust, smoke, ash, gases, water vapour, etc. remain in the atmosphere for a long time.
• This may create an imbalance in the environment.
• Land may become fertile due to volcanic ash.
• Many minerals are found near the earth’s surface because of lava.
• New land is formed due to volcanic eruption or at times, an island may even disappear.
• Lakes are formed at the mouth of the craters of dead volcanoes when rainwater accumulates in them.

Question 5.
Explain the process of the formation of Block mountains.
Answer:

• Because of internal movements, horizontal waves moving away from each other are formed.
• This causes tension on the layers of rocks leading to the formation of fractures in the rocks called as faults.
• Similarly, waves coming towards each other in hard rocks also form faults due to compression.
• When a part of the earth’s crust in between two parallel faults is lifted, it looks like a block. Such a landform is called as a Block mountain.
  

Question 6.
Explain the process of formation of Rift valley.
Answer:

• When horizontal movements on the earth’s surface act in opposite direction, it causes tension on the rocks in the earth’s crust.
• When tension increases, fractures develop in the rocks leading to the formation of faults.
• Consequently, rocks on both the ends slide and the continuity in the layers of rocks is not found.
• Sometimes, two fractures develop side-by-side in the earth’s crust and land in between the two fractures subsides. This subsided deep part is called the rift valley.
  

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 9 Geography Solutions Chapter 6 Properties of Sea Water Notes, Textbook Exercise Important Questions and Answers.

Properties of Sea Water Class 9 Questions And Answers Maharashtra Board

Class 9 Geography Chapter 6 Properties of Sea Water Questions And Answers Maharashtra Board

Geography Class 9 Chapter 6 Question Answer Maharashtra Board

1. Tick the correct box according to the salinity of the ocean water ✓

Answer:
(a) Low
(b) Low
(c) High
(d) High
(e) Low
(f) High.

2. Give reasons.

(a) Salinity is low in the land-locked Baltic Sea.
Answer:

• The Baltic Sea lies in the temperate region.
• In temperate regions, the sunrays are slanting and therefore, the temperatures are lower.
• The supply of fresh water is also more, as numerous rivers empty their waters into the Baltic sea.
• Therefore, in spite of being landlocked, due to low rate of evaporation and ample supply of fresh water, the salinity of the Baltic Sea is low.

(b) There is higher salinity in the northern Red Sea while lower in the southern.
Answer:

• The Red Sea is one of the saltiest bodies of water in the world, owing to high evaporation.
• The salinity is 36%o in the southern part because of the effect of the Gulf of Aden.
• It reaches 41 %o in the northern part, owing mainly to the Gulf of Suez and the high evaporation as well as very little precipitation.
• Hence, there is more salinity in the northern Red Sea while lesser in the south.

(c) Oceans located at the same latitude do not have same salinity.
Answer:

• The salinity of the oceans depends on factors like rate of evaporation and supply of fresh water.
• In Oceans where rate of evaporation is more than the supply of fresh water, the salinity is higher.
• In Oceans where supply of freshwater exceeds the rate of evaporation, salinity is low.
• Salinity is not affected much in areas where supply of freshwater and the evaporation of water is low.
• Thus, oceans located on the same latitude do not have the same salinity.

(d) With increasing depth, the temperature of sea water decreases to a certain limit.
Answer:
With increasing depth, the temperature of sea water decreases to a certain limit because –

• While most of the sunrays radiate back from the surface of the sea, some of them penetrate to certain depths in the water.
• As a result, the intensity of sunrays decreases with the increasing depth.
• The temperature decreases up to 2000m depth.
• After 2000m, the temperature of the seawater is uniform everywhere.

(e) There are more salt-pans on the Western coast of India than its eastern coast.
Answer:

• The Arabian Sea lies lying to the west and Bay of Bengal lies to the east of India.
• Many large peninsular rivers drain their waters in the Bay of Bengal and on the contrary, only small seasonal coastal rivers drain in the Arabian Sea.
• Hence, the salinity of the eastern coast is 34%, while it is 35% in the Arabian Sea.
• Thus, there are more salt-pans on the Western coast of India than its Eastern coast.

(f) Salinity increases in the mid-latitudinal zones.
Answer:

• Mid-latitudinal zones lies between 25° to 35° north and south of the equator.
• In this zone, the rainfall is less and the supply of fresh water from rivers is also low.
• This region experiences high-temperature conditions which are marked by the presence of hot deserts of the world. These high-temperature conditions lead to a high rate of evaporation.
• Thus, the salinity of the seas is found to be higher in mid-latitudinal zones.

3. Answer the following questions.

(a) What are the factors affecting the salinity of the sea water?
Answer:

1. The uneven distribution of temperature on earth and uneven supply of freshwater affects the salinity of seawater.
2. In the tropical zone, temperature is higher. Rate of evaporation is also higher and therefore, the salinity is higher.
3. Around 5° N and S of the equator, in the equatorial calm belt, the sky is cloudy for a long period of time and convectional rainfall occurs every day.
4. Large rivers like Congo and Amazon in the equatorial regions meet the sea. Therefore, supply of freshwater is abundant, too. But because of higher temperatures, rate of evaporation is more and therefore, the seas in these areas are more saline.
5. In mid-latitudinal zones (25° to 35° N and S), rainfall is lesser and the supply of freshwater from rivers is also low. This zone has the hot deserts of the world. Thus, the salinity of the seas is found to be higher here.
6. In temperate regions, the sunrays are slanting and therefore, the temperatures are lower. Because of the melting of the snow, the supply of water is also more, and therefore, in this zone, salinity decreases with increasing latitudes.
7. In the polar areas, temperatures are very low. Evaporation is also very less in polar areas. So, salinity is low.
8. Landlocked seas have higher salinity than open seas as the rate of evaporation is more. There is a lack of supply of fresh water from large rivers. Thus, there is a difference in the salinities of open and closed seas.

(b) Explain the distribution of salinity around the Tropic of Cancer and tropic of Capricorn.
Answer:

• The uneven distribution of temperature on earth, and uneven supply of freshwater affects the salinity of sea water.
• Region, between the Tropic of Cancer and Tropic of Capricorn is called as the Tropical zone.
• In the tropical zone, temperature is higher.
• Hence, the rate of evaporation is also higher, and therefore, salinity is higher.

(c) What are the factors affecting the temperature of the sea water?
Answer:

1. Temperature is a major property of the sea water.
2. Sea water upto the depth of 500m is called as surface water. The surface temperature of the sea water is not uniform everywhere. This is dependent on different factors. .
3. Latitudinally, the surface temperature of the seawater decreases from the equatorial areas towards the poles.
4. The average temperature in equatorial areas is around 25° C, while it is about 2° C near the poles.
5. Besides this, cyclones, rainfall, sea waves, ocean currents, salinity, pollution, convectional currents, and seasons also affect the surface temperature.
6. Regions where cold ocean currents flow, the surface temperature of ocean water is less, while the regions where the warm currents move, the temperature increase.

(d) Explain the changes occurring in the temperature of sea water according to the depth.
Answer:

• While most of the sunrays radiate back from the surface of the sea, some of them penetrate to certain depths in the water.
• As a result, the intensity of sunrays decreases with the increasing depth.
• The temperature decreases up to 2000m depth.
• After 2000m, the temperature of the seawater is uniform everywhere.
• It is around 4°C everywhere from the equatorial regions to the polar areas.
• Temperature reduces only up to 4° C according to depth, and therefore, the water at greater depths does not freeze.
• The temperature of the seawater changes rapidly with depth at the equatorial areas. The difference in temperature is lesser in polar areas.
• There is also a difference in open seas and landlocked seas. In low latitudes, because the salinity of the landlocked seas is more, the temperature of the landlocked seas is higher than the open seas.

(e) Name the factors affecting salinity.
Answer:
Due to the sun’s heat, evaporation happens at a faster rate. Evaporated water turns into water vapour and reduces in quantity. But amount of salt remains the same in the remaining water and therefore the salinity of water increases.

• In seas where the rate of evaporation is high than the supply of fresh water, salinity is high.
• In seas where the supply of freshwater exceeds the rate of evaporation, salinity is low.
• Salinity is not affected much in seas where both the supply of freshwater and evaporation of water is low.

4. Explain how temperature affects the following.

(a) the density of sea water
Answer:

• If temperature reduces, density of water increases.
• Hence, cold water is denser than hot water.

(b) the salinity of sea water
Answer:

• If the salinity of water is high, the density of water increases.

Activity:

Complete the table showing the salinity of open and land-locked seas.

Answer:

Class 9 Geography Chapter 6 Properties of Sea Water Intext Questions and Answers

Observe the following Map and answer the questions:

Question 1.
What is the salinity around the tropics?
Answer:
The salinity around the tropics is 36%o.

Question 2.
Which region has the least salinity?
Answer:
The Bay of Bengal has the least salinity of 32%o.

Question 3.
Which ocean has salinity more than 37%o?
Answer:
Atlantic ocean has salinity of more than 37%o.

Question 4.
What are the reasons of differences in salinity on a global level?
Answer:
The uneven distribution of temperature on earth, and uneven supply of freshwater, etc. are the reasons for differences in salinity on a global level.

Observe the Graph and answer the questions:

Question 1.
What is the maximum temperature of seawater in equatorial areas? How much is this temperature at a depth of 500 m?
Answer:
The maximum temperature of sea water in equatorial areas is 18° C. The temperature at the depth of 500 m is 11° C.

Question 2.
What is the temperature of seawater at the sea level in the mid-latitudes?
Answer:
The temperature of seawater at the sea level in the mid-latitudes is 14° C approximately.

Question 3.
How much has this temperature changed at 1500 m depth?
Answer:
The temperature is about 5° C at the depth of 1500 m. Thus the temperature of sea water at mid-latitudes has changed from 14°C at the sea level to about 5°C at the depth of 1500 m i.e. temperature has changed (reduced) by 9°C.

Question 4.
What does the thermal graph for the high latitude say? What is its temperature at 500, 1000 and 1500 m depths?
Answer:
In high latitudes the temperature of sea water at all depths remains constant at 4° C.

Question 5.
After what depth does the seawater temperature remain stable everywhere?
Answer:
After 2000 m, the temperature of the sea water is uniform everywhere.

Question 6.
With increasing depth, what decreases: temperature, salinity or density?
Answer:
Temperature and salinity decreases with increasing depth.

Question 7.
After what depth does the change in these factor become almost zero?
Answer:
After the depth of 1000 m there is no change in all these factors.

Question 8.
Till what depth is the change in these factors higher?
Answer:
The higher change can be seen up to a depth of about 500m.

Question 9.
Explain the correlation between all the three factors.
Answer:
If the temperature is less, density is more. If the salinity is less, then density is also less. However temperature affects the density more as compared to the salinity. If the temperature is less, then the density is more despite less salinity.

Let’s Recall.

Question 1.
Which is the largest water storage of the world?
Answer:
Oceans are the largest water storage of the world.

Question 2.
Why is the seawater salty?
Answer:

• Salt in the ocean comes from rocks on land.
• Rivers carry dissolved salts to the ocean.
• Water evaporates from the oceans to fall again as rain and to feed the rivers, but the salts remain in the ocean.

Question 3.
What are the reasons for high salinity in the oceans?
Answer:
High rate of evaporation and low supply of fresh water leads to high salinity in the oceans:

Question 4.
How can we obtain the salts from the ocean water?
Answer:

• Sea water contains a large amount of common salt and the salts of other metals dissolved in it.
• Near the sea-shore, the sea water is collected in shallow pits (salt pans) and allowed to evaporate in the sunshine.
• In a few days, the water evaporates, leaving behind salt.
• The salt so obtained is collected and transported to factories, where it is purified and packed for consumption.

Question 5.
What is the use of the salts in the oceans to us?
Answer:

• The salts is used in the food we eat.
• It is used for making various chemicals and medicines.
• Salt is also used to preserve things for longer periods. It is also used in ice factories.

Can You Tell?

Question 1.
What is the difference in the temperatures of the land and the sea?
Answer:
During the daytime land is hotter than the sea whereas, during the night time land is cooler than the sea.

Question 2.
What would be the difference in the temperature of the seawater from the equatorial region to the polar areas?
Answer:
Latitudinally, the surface temperature of the seawater decreases from the equatorial areas towards the poles. The average temperature in equatorial areas is around 25° C while it is about 2° C near the poles.

Think about it.

Question 1.
If you think about India there is the Arabian sea to the west and the Bay of Bengal to the east. The salinity of the eastern coast is 34%o while it is 35%o in the Arabian sea. What could be the reason of higher salinity in the western coastal region?
Answer:
Many large peninsular rivers drain their waters in the Bay of Bengal and on the contrary only small seasonal coastal rivers drain in the Arabian sea. Hence the salinity of Arabian sea is more than the Bay of Bengal.

Try this.

Question 1.
In which container has the water increased or decreased?
Answer:

• The water has increased in the container which is in the classroom in which freshwater was added.
• The water has decreased in the container which was kept in the sun outside.

Question 2.
What could be the reasons behind the decrease or increase?
Answer:

• Since freshwater was added to one of the containers in the classroom the water level increased.
• The water has decreased in the container which was kept outside in the sun due to evaporation.

Question 3.
What could be the reason behind the low and high salinity of the water in the container?
Answer:

• In the container which as kept outside in the sun, due to high rate of evaporation, the salinity is high.
• As we kept on adding fresh water to the container kept in the classroom the salinity is low.

Class 9 Geography Chapter 6 Properties of Sea Water Additional Important Questions and Answers

Select the correct option:

Question 1.
The average temperature in equatorial areas is
(a) 25° C
(b) 35° C
(c) 15° C
(d) 5° C
Answer:
(a) 25°C

Question 2.
The average temperature in mid-latitudes is
(a) 25° C
(b) 10° C
(c) 16° C
(d) 5° C
Answer:
(c) 16°C

Question 3.
The average temperature near poles is about
(a) 10° C
(b) 20° C
(c) 15° C
(d) 2° C
Answer:
(d) 2°C

Question 4.
With the increasing depth of sea, the intensity of sunrays
(a) increases
(b) decreases
(c) remains constant
(d) is uneven
Answer:
(b) decreases

Question 5.
Seawater upto the depth of 500m is called
(a) ground water
(b) surface water
(c) deep water
(d) saline water
Answer:
(b) surface water

Question 6.
ocean is the most saline ocean in the world.
(a) Pacific
(b) Arctic
(c) Indian
(d) Atlantic
Answer:
(d) Atlantic

Question 7.
The sea lying on the border of Israel and Jordan has a salinity of %o.
(a) 37
(b) 50
(c) 256
(d) 332
Answer:
(d) 332

Question 8.
The buoyancy of the sea water increases because of its
(a) evaporation
(b) salinity
(c) density
(d) high temperature
Answer:
(b) salinity

Question 9.
has an altitude of – 400m.
(a) Baltic Sea
(b) Arabian Sea
(c) Dead Sea
(d) the Mediterranean Sea
Answer:
(c) Dead sea

Question 10.
act as temperature controllers at a global level.
(a) Ocean currents
(b) Sea breeze
(c) Land breeze
(d) Trade winds
Answer:
(a) Ocean currents

Question 11.
is a major porperty of the sea water.
(a) Temperature
(b) Uniform salinity
(c) Buoyancy
(d) Equal Density
Answer:
(a) Temperature

Question 12.
have higher salinity than open seas.
(a) Equatorial seas
(b) Landlocked seas
(c) Freshwater lakes
(d) Seas in polar regions
Answer:
(b) landlocked seas

Question 13.
Temperature decreases upto depth.
(a) 500 m
(b) 1000 m
(c) 1500 m
(d) 2000 m
Answer:
(d) 2000m

Question 14.
In regions where cold currents flow, the surface temperature of ocean water is
(a) high
(b) less
(c) uniform
(d) uneven
Answer:
(b) less

Question 15.
Temperature of seawater changes rapidly with depth in areas.
(a) equatorial
(b) mid latitudinal
(c) temperate
(d) polar
Answer:
(a) equatorial

Question 16.
In seas where the rate of evaporation is than the supply of fresh water, salinity is high.
(a) less
(b) high
(c) same
(d) low
Answer:
(b) high

Question 17.
The salinity of Bay of Bengal is than that of Arabian sea.
(a) less
(b) more
(c) same
(d) equal
Answer:
(a) less

Question 18.
In areas the salinity of sea water is low.
(a) equatorial
(b) mid-latitudinal
(c) temperate
(d) polar
Answer:
(d) polar

Question 19.
The salinity of Battic sea is %.
(a) 332
(b) 32
(c) 37
(d) 7
Answer:
(d) 7

Match the Column:

Column A	Column B
(1) Equatorial areas (2) Mid-latitudinal areas (3) Temperate regions	(a) Salinity of 332%o (b) Slanting sunrays, melting of snow (c) Cloudy sky and convectional rainfall (d) Hot deserts

Answer:
(1-c),
(2- d),
(3 – b)

Answer in one sentence:

Question 1.
What is the major property of seawater?
Answer:
Temperature is a major property of seawater.

Question 2.
What is the average surface temperature of seawater in equatorial areas, mid-latitudes & poles?
Answer:
The average surface temperature of seawater is equatorial areas is around 25°C in mid-latitude it is around 16°C & 2°C near the poles.

Question 3.
After what depth is the seawater temperature uniform everywhere?
Answer:
After 2000m, the temperature of seawater is uniform everywhere

Question 4.
Name the instruments used to measure salinity?
Answer:
Hydrometer, Refractometer and salinometer are used to measure salinity.

Question 5.
Which is the most saline ocean?
Answer:
The Atlantic ocean is the most saline ocean.

Give geographical reasons:

Question 1.
The climate of the earth gets affected by ocean currents.
Answer:

• The ocean currents are generated because of the difference in the properties of seawater.
• They act as temperature controllers at the global level.
• The distribution of temperature gets controlled due to the ocean currents.
• Thus, the climate of the earth gets affected by ocean currents.

Question 2.
Dead Sea has a salinity of 332%0.
Answer:

• The sea lying on the border of Israel and Jordan has a salinity of 332%0.
• The average salinity of ocean is 35%o.
• Jordan is the only large river meeting this sea.
• Low rainfall, low supply of freshwater and high evaporation is the reason of high salinity.

Question 3.
The surface temperature of the sea is not uniform everywhere.
Answer:

• The surface temperature of sea water is not uniform everywhere and it changes with latitudes.
• The surface temperature of the seawater decreases from the equatorial areas towards the poles.
• The average temperature in equatorial areas is around 25° C, it is 16° C in mid-latitudes while it is about 2° C near the poles.
• Besides this, cyclones, rainfall, sea waves, ocean currents, salinity, pollution, convergence flow, seasons, etc. also affect the surface temperature.
• Thus the surface temperature of the sea is not uniform everywhere.

Question 4.
The seas in equatorial calm belt are more saline.
Answer:

• Around 5° N and S of the equator, in the equatorial calm belt, the sky is cloudy for a long period of time and convectional rainfall occurs every day.
• Large rivers like Congo and Amazon in the equatorial regions meet the sea.
• Therefore, supply of freshwater abundant too.
• But because of higher temperatures, rate of evaporation is more and therefore, the seas in these areas are more saline.

Explain

Question 1.
Factors affecting surface water temperature
Answer:

• Temperature is a major property of the seawater. The surface temperature of the seawater is not uniform everywhere. This is dependent on different factors.
• Latitudinally, the surface temperature of the seawater decreases from the equatorial areas towards the poles.
• Besides this, cyclones, rainfall, sea waves, ocean currents, salinity, pollution, convergence flow and seasons also affect the surface temperature.
• Regions where cold ocean currents flow, the surface temperature of ocean water is less. The regions where the warm currents move, the temperature increase.

Question 2.
Density of sea water
Answer:

• Temperature and salinity are the two properties of sea water that control the density of the sea water.
• If temperature reduces, density of water increases.
• Cold water is denser, and so is saline water.
• As compared to salinity, temperature affects the density more. Hence, sometimes, more saline water has lower temperature at the surface.
• Sea water having higher temperature and low salinity, can have lower density.

Question 3.
Measurement of salinity of sea water.
Answer:

• The weight of all dissolved salts in water in ratio of parts per thousand of water is called the salinity of seawater.
• For example, if the weight of dissolved salts in 1000g (1 kg) of seawater is 40g, then the salinity is 40%o i.e. 40 per thousand parts.
• Hydrometer, refractometer and salinometer are also used to measure salinity.

Question 4.
Factors affecting salinity of sea water.
Answer:

Latitudes	Temperature / Rate of evaporation	Supply of fresh water	Salinity
Tropical Zone 5°N – 5°Sof equator	High	Abundant from (River Congo / Amazon)	High
Mid­latitudes (25° – 35° N and S)	High (hot desert are found here)	low	High
Temperate regions	Temperature is lower due to slanting sunrays	The supply of water is more due to melting snow	low
Polar regions	Very low	low	low

9th Std Geography Questions And Answers:

• Distributional Maps Class 9 Geography Questions And Answers
• Endogenetic Movements Class 9 Geography Questions And Answers
• Exogenetic Movements Part 1 Class 9 Geography Questions And Answers
• Exogenetic Movements Part 2 Class 9 Geography Questions And Answers
• Precipitation Class 9 Geography Questions And Answers
• Properties of Sea Water Class 9 Geography Questions And Answers
• International Date Line Class 9 Geography Questions And Answers
• Introduction to Economics Class 9 Geography Questions And Answers
• Trade Class 9 Geography Questions And Answers
• Urbanisation Human Class 9 Geography Questions And Answers
• Transport and Communication Class 9 Geography Questions And Answers
• Tourism Class 9 Geography Questions And Answers

Balbharti Maharashtra State Board Class 10 English Solutions Unit 4.3 World Heritage Notes, Textbook Exercise Important Questions and Answers.

Class 10 English Chapter 4.3 Question Answer Maharashtra Board

World Heritage Poem 10th Std Question Answer

Question 1.
Pair up with your partner and answer the following questions.
(a) Do you like to travel?
(b) Where have you traveled?
(c) Have you heard about the wonders of the world?
(d) Have you heard about UNESCO?
(e) What does UNESCO stand for?
(f) What is meant by Heritage?
(g) Do you know of any Heritage building in your own city?
Answer:
(a) yes, no, sometimes, etc.
(b) Discuss the places, the mode of travel, the sights, etc.
(c) Yes, I have.
(d) Yes, I have, but not much.
(e) UNESCO stands for United Nations Educational, Scientific and Cultural Organization.
(f) Heritage is something that is valued and preserved because of its historical/cultural/natural importance
(g) Students can find out the heritage buildings in their own towns/cities.

Question 2.
Your teacher will explain the ‘Heritage Cycle’.
→ By understanding (cultural heritage) people value it.
→ By valuing it people want to care for it.
→ By caring for it, it will help people enjoy it.
→ From enjoying it, comes a thirst to understand.
→ By understanding it …………………

Question 3.
Do you know the difference between :
(a) World Heritage
(b) Cultural Heritage
Refer to a dictionary/encyclopedia/reference book/the internet to get the detailed meaning.
Answer:
(a) World heritage means a global heritage that belongs to everyone.
(b) Cultural heritage is the legacy of physical artifacts and intangible attributes of society that are inherited from past generations, maintained in the present and preserved for the benefit of futurft generations. Cultural heritage includes tangible culture (such as buildings, monuments, landscapes, books, works of art, and artifacts), intangible culture (such as folklore, traditions, language, and knowledge), and natural heritage (including culturally significant landscapes, etc.)

Question 4.
With the help of your partner complete the information in the table.

Tourist spot	Favourite	Why?
Park
Mountain
Beach
Sea
Forest
Countryside/Rural site

Question 5.
Heritage Sites – Rank these with your partner. Put the best at the top.

• Great Barrier Reef
• Mount Fuji
• Grand Canyon
• The Pyramids
• Panda Sanctuaries
• Machu Picchu
• Vatican City
• Great Wall of China

World Heritage Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
Answer the following questions.
(a) What do heritage sites in the world include?
Answer:
A World Heritage Site should have significant cultural or natural importance to humanity.

(b) What kind of sites are protected and maintained by the International World Heritage Programme?
Answer:
Sites which have significant cultural or natural importance to humanity are protected and maintained by the International World Heritage Programme. They may include forests, lakes, monuments, buildings and cities. They can also be a combination of cultural and natural areas.

(c) How many world Heritage sites were there around the world?
Answer:
World Heritage Sites include forests, lakes, monuments, buildings and cities. They cari also be a combination of cultural and natural areas.

(d) What is the role of World Heritage Committees?
Answer:
World Heritage Sites are those that are significant culturally and naturally. People are interested in seeing such sites and learning the history behind them; hence they are a major tourist attraction, and they draw tourists to a country, boosting the country’s revenue.

(e) What is the texture of World Heritage Committee?
Answer:
The tenure of the World Heritage Committee is six years.

(f) What are our duties towards preservation/conservation of any historical site?
Answer:
We should see that the historical sites are not in any danger due to pollution, tourism, uncontrolled urbanization, etc. Whenever we visit the site we must maintain the cleanliness and purity of the place. We must obey whatever orders and guidelines are put in place by the authorities. We should motivate others to do so too.

(g) Why should we preserve the World Heritage Sites?
Answer:
World Heritage Sites promote tourism. They are a part of the culture of the world, a part of the past. It is essential to preserve the past in order to learn from it. Natural beauty too should be preserved so that everyone today and in future can enjoy it. Hence, we should preserve World Heritage Sites.

(h) What is the role of World Heritage Sites in developing tourism in any country?
Answer:
World Heritage Sites are those that are significant culturally and naturally. People are interested in seeing such sites and learning the history behind them; hence they are a major tourist attraction, and they draw tourists to a country, boosting the country’s revenue.

Question 2.
Complete the following.

Year	Establishment	Role
1954	…………………………………………………	…………………………………………………
1959	…………………………………………………	…………………………………………………
1965	…………………………………………………	…………………………………………………
1968	…………………………………………………	…………………………………………………
1972	…………………………………………………	…………………………………………………

Answer:

Year	Establishment	Role
1954	Egypt starts plans to build Aswan High Dam	Started the momentum for the protection of cultural and natural heritage sites around the world.
1959	International campaign by UNESCO to protect temples and artifacts likely to be destroyed by Aswan High Dam; a draft convention initiated for the same	Protection of natural and cultural sites around the world
1965	A White House Conference in the US called for a World Heritage Trust’.	To protect not only the historic and cultural sites but also the significant natural and scenic sites around the world.
1968	The International Union for Conservation of Nature	Development of goals similar to those of the White House Conference
1972	Convention concerning the protection of World Cultural and Natural Heritage adopted by UNESCO’s General Conference.	To protect not only Are histone and cultural sites but also the significant natural and scenic sites around the world.

Question 3.
Complete the following by giving reasons why World Heritage Sites are in danger.

Answer:

Question 4.
Choose the correct alternative and complete the given sentences.
(a) Mount Huangshan is situated in …………………………. .
(i) Japan
(ii) China
(iii) Philippines
Answer:
(ii) China

(b) The famous dam situated in Egypt on River Nile is …………………………. .
(i) Buzwaa High Dam
(ii) Rizwa High Dam
(iii) Aswan High Dam
Answer:
(iii) Aswan High Dam

(c) The conference based on Human Environment was held at …………………………. .
(i) Athens, Greece
(ii) Mascow, Russia
(iii) Stockholm, Sweden
Answer:
(iii) Stockholm, Sweden

(d) The highest number of world Heritage Sites are located in …………………………. .
(i) France
(ii) Italy
(iii) Germany
Answer:
(ii) Italy

(e) …………………………. can delete/exclude a site from World Heritage list.
(i) World Heritage Committee
(ii) World Peace Committee
(iii) World Health Committee.
Answer:
(i) World Heritage Committee

(f) The tenure of World Heritage Committee is …………………………. years.
(i) Four
(ii) Five
(iii) Six.
Answer:
(iii) Six.

Question 5.
Match the pairs to define different roles of the World Heritage Sites.

	A		B
(i)	Identify cultural and natural sites	a	green, local based, stable and decent jobs.
(ii)	Identify sites of	b	of outstanding universal value across countries.
(iii)	Identify sites that represent	c	preserve outstanding sites and natural resources.
(iv)	UNESCO seeks to	d	tourism.
(v)	World Heritage Sites should have	e	an asset for economic development and investment.
(vi)	World Heritage Sites should	f	protect these sites.
(vii)	World Heritage Sites serve as	g	best examples of world’s cultural and/or natural heritage.
(viii)	World Heritage Sites should ensure	h	special importance for everyone.
(ix)	It should at large develop	i	relevant development plan policies.

Answer:

‘A’	‘B’
(1) Identify cultural and natural sites	(a) green, local based, stable and decent.
(2) Identify sites of	(b) of outstanding universal values across countries.
(3) Identify sites that represent	(c) preserve outstanding sites and natural resources.
(4) UNESCO seeks to	(d) tourism.
(5) World Heritage Sites should have	(e) an asset for economic development and investment.
(6) World Heritage should	(f) protect these sites.
(7) World Heritage Sites serve as	(g) best examples of world’s cultural and or natural heritage.
(8) World Heritage Site should ensure	(h) special importance for everyone.
(9) It should at large develop	(i) relevant development plan policies.

Question 6.
Look at the words and their meanings. Choose the correct alternative.
(a) determine :
(i) think over
(ii) decide
(iii) ask for
(iv) look over
Answer:
(ii) decide

(b) monument :
(i) statue
(ii) pillar
(iii) memorial
(iv) fort
Answer:
(iii) memorial

(c) significant:
(i) clever
(ii) effective
(iii) systematic
(iv) important
Answer:
(iv) important

(d) disaster:
(i) problem
(ii) incident
(iii) calamity
(iv) accident
Answer:
(iii) calamity

Question 7.
Find from the text minimum 8 words related to cultural heritage and make a word register. Arrange them in alphabetical order.
Cultural heritage: Abu Simbel Temples, artifacts, buildings, cilles, Histqric Center of Vienna, Machu Picchu, monuments, Mount Huangshan, Sydney Opera House.

Question 8.
Complete the following information from the text.

Answer:
(a) Preservation of any historical site (Duties):
(i) International World Heritage Programme
(ii) UNESCO World Heritage Committee.

(b) Preserving World Heritage Sites (Reasons) :
(i) They have significant cultural and natira Importance to humanity.
(ii) They promote tourism.

(C) Promoting tourism (Role) :
(i) They attract tourists.
(ii) They help one to understand the history of a place.

Question 9.
Write a report on any tourist place/historical place/World Heritage Site you recently visited using the points given below.
(i) Title
(ii) Place/Location
(iii) Background/History
(iv) Features/Specialities
(v) Security policies
(vi) Sign boards and discipline
(vii) Overall scenario.
Answer:
Ajanta – A Masterpiece In Rock
– Rani Iyer
Mumbai, 12 February: The Ajanta Caves, situated in the Deccan in Maharashtra and about 110 km from Aurangabad, are a UNESCO World Heritage Site. A visit to the place reveals a large slice of history.

These rock – cut cave temples and monasteries of Buddhists date back to around 2nd century BCE. Since they were in the jungles, cut into a mountainside, the external world did not know about them for a long time. They were discovered only in the 19th century, The caves include paintings and rock – cut sculptures described as among the finest surviving examples of ancient Indian art. The paintings are expressive and present emotion through gesture, pose and form, According to UNESCO, these are masterpieces of Buddhist religious art that influenced the Indian art I that followed.

Two new visitor centers provide extensive information about the heritage site using audiovisual media. Local staff is employed for security purposes. Though photography is allowed at certain places, with fees for the use of a camera, use of tripods and flash is prohibited. Signboards and brochures/leaflets provide information about the care to be taken to preserve this UNESCO protected heritage site. “The caves are now being looked after by a private company under the Indian government’s ‘Adopt a Heritage Site’ program,” said a senior official.

Question 10.
(A) Use ‘not only but also’ in the following sentences.
(a) UNESCO and the International Council on monuments initiated a draft convention to create an international organisation responsible for protecting cultural heritage.
(b) The state parties are responsible for identifying and nominating new sites.
(c) Opera House in Australia and the Historic Center of Vienna in Austria are cultural sites of World Heritage.
(d) World Heritage Sites can also be a combination of both cultural and natural areas.
Answer:
(a) Not only UNESCO but also the International Council on Monuments and Sites initiated a draft convention to create an international organization responsible for protecting cultural heritage.
(b) The State Parties are responsible for not only identifying but also nominating new sites.
(c) Not only the Opera House in Australia but also the Historic Center of Vienna in Austria are cultural sites of World Heritage.
(d) World Heritage Sites can be a combination of not only cultural but also natural areas.

(B) Rewrite the following sentences replacing ‘as soon as’ by ‘No sooner than’
(Note : The phrase, ‘No sooner’ must always be followed by an auxiliary (helping verb).)
For example : As soon as he came, they all gave an applause.
No sooner did he come, than they all gave an applause.

(a) As soon as the Bill is passed, it will become an Act.
(b) As soon as the thief escaped, the family informed the police.
(c) As soon as you have finished, you can submit your answer- papers.
(d) As soon as they can manage, they should change their house.
(e) As soon as the bell rings, the School Assembly will start.
Answer:
(a) No sooner is the Bill passed, than it will become an Act.
(b) No sooner did the thief escape, than the family informed the police.
(c) No sooner do you finish, than you can submit your answer papers.
(d) No sooner can they manage, than they should change their house.
(e) No sooner does the bell ring, than the School Assembly will start.

Question 11.
Identify whether the following sentences are Simple (One Subject + One Predicate or Complex (One Main Clause + One or more Dependent Clauses) or Compound (Combination of 2 or more Independent/ Co-ordinate Clauses).
(1) They vary in type but they include forests, monuments etc.
(2) The mountain is significant because of its characteristics.
(3) To protect the temples and artefacts, UNESCO launched an international campaign.
(4) If the site meets with this criteria, it can be inscribed on the World Heritage List.
(5) There are 890 World Heritage Sites that are located in 148 countries.
(6) The project cost about US $ 80 million and $ 40 million came from 50 different countries.
Answer:
(1) Compound
(2) Simple
(3) Simple
(4) Complex
(5) Complex
(6) Compound

Question 12.
Following are the ways to preserve ‘World Heritage Sites.’ Transfer these points into a small paragraph. Suggest a title.

• Practical conservation of posterity
• Human/animal trespassing to be prohibited
• Monitored/controlled/restricted access
• Threat of local administrative negligence to be removed

Answer:
Ways to Preserve World Heritage Sites
World Heritage Sites need to be preserved for posterity. The future generations must know about their history and culture. For this purpose, steps have to be taken to preserve these sites. First and foremost, trespassing by either humans or animals should be strictly prohibited. Access to these sites for tourists, vendors, officials and the general public should be restricted or monitored carefully. Another important step is to keep a check on the local administration of the site, so that negligence in the performance of the duties at this level is ruled out.

Question 13.
Read the points given in column ‘A’ specifying Dos towards prevention of any historical site. Write Don’ts in column ‘B’ specifying things that should not be done.

	Dos	Don’ts
(i)	Obey rules and regulations.
(ii)	Maintain discipline and order.
(iii)	Maintain cleanliness.
(iv)	Use dustbins and garbage bags.
(v)	Observe silence.
(vi)	Maintain environmental safety.
(vii)	Protect our country’s heritage.

Answer:

Dos	Don’ts
1. Obey rules and regulations.	1. Don’t dirty the surroundings.
2. Maintain discipline and order.	2. Don’t write on the walls/trees.
3. Maintain cleanliness.	3. Don’t pluck flowers/ destroy plants.
4. Use dustbins and garbage bags.	4. Don’t smoke/ drink alcohol.
5. Observe silence.	5. Don’t play loud music or make a loud noise.
6. Maintain environmental safety.	6. Don’t defecate in the open.
7. Protect our country’s heritage.	7. Don’t trespass.

Question 14.
Complete the following flow chart by choosing the option given below to show how any site of any country can become a World Heritage Site.

Options :
1. Inclusion of the name of site from tentative list to the nomination file.
2. Name of the site is inscribed on the World Heritage List after meeting the criteria.
3. Inclusion of the name of site for the nomination in a tentative list after an inventory in country or State.
4. Decision of the World Heritage Committee after review of the nominated file.
5. A review of the included file by the advisory bodies.
Answer:
Step 1 : Inclusion of the name of the site for nomination in a tentative list after inventory in country or state.
Step 2 : Inclusion of the name of site from tentative list to the nomination file.
Step 3 : A review of the included file by the advisory bodies.
Step 4 : Decision of the World Heritage Committee after review of the nominated file.
Step 5 : Name of the site inscribed on the World Heritage List after meeting the criteria.

Question 15.
Projects :
(a) Make a list of sites from our State which are included in the World Heritage Sites. Try to visit one of them. Write the importance of this World Heritage Site. Also write your impression of it in your notebook.

(b) Write a ‘tourism leaflet’ on any one of the following :
(i) Your home town
(ii) A historical place
(iii) A place of natural beauty
(iv) A place of pilgrimage

→ Make use of the following points :
(i) How to reach there?
(ii) Accommodation facilities
(iii) What to see and visit?/Attractions of the place
(iv) Places of interest nearby
(v) Best time to visit
(vi) Shopping Attractions
Add your own points.
Answer:
MATHERAN: ‘UNSPOILT NATURE’
(1) How to get there:
(a) By train: From Mumbai or Pune to Neral Junction.. From Neral to Matheran by narrow – gauge train that depart at fixed times.
(b) By road: Shared taxis or minibuses from Neral to MTDC Holiday Camp. Cars and other vehicles not allowed beyond a certain point.
(2) Accommodation facilities: Plenty of hotels offering full or half board. MTDC Tourist Camp provides dorm – beds at affordable rates. The ‘camp’ is near the Dasturi car park. You can eat at one of the many thali joints along MG Road.
(3) Best Time of the year to visit: All the year round except the rainy season.
(4) What to see: Viewpoints such as Porcupine, Louisa and Echo have the finest views. On a clear day, one can see Mumbai lying afar from ‘Hart Point’; perpendicular cliffs plunge into steep ravines; monkeys and squirrels.
(5) Shopping Attractions: Locally made chappals, home – made chocolates and chikkis, caps and other items for campers; walking sticks.
(6) Special features: Greenery, nature at its best, trekking, horse riding; good for a day’s group picnic.

(c) Vocabulary Extension – Choose several words from the text. Use a dictionary or internet to build up more associations/collocations of each word.
Answer:
(1) Associations:

(2) Collocations:

(d) World Heritage Sites – Make a poster about World Heritage Sites, specifying some details and specialties about each of them.

(e) Letter – Write a letter to an expert on the environment. Ask him/her five questions about your concern/doubts about World Heritage sites. Give him/her three ideas on how to protect them.
Answer:
Amit Awte
102, Riddhi Vihar
R.N. Road
Aurangabad – 431 001,
12th November, 2020

To
Mr. Avinash Ranade
‘Nisarg’
Shastri Marg
Aurangabad – 431 002.
Sub: Protection of World Heritage Sites

Sir
It was with great interest that I read in our local newspaper about your interest in the protection of World Heritage Sites. I would like to ask you a few questions which have haunted me for some time.

They are:
(1) Does India have enough experts to restore the damage done to our sites by nature/visitors etc.?
(2) Is there enough security to protect the sites from vandalism?
(3) Can there be a restriction on the number of visitors to the sites?
(4) Are the funds allocated to the preservation of the sites by the World Heritage Committee sufficient?
(5) Is there enough information about the sites on tourist websites/ Internet?

I would like to give some suggestions. Can we not impose a limit on the number of tourists visiting these places? We can also have sessions on how to maintain cleanliness and prevent vandalism. Stiff fines must be imposed on all those who break the rules.

I hope to receive a reply from you, as I am also very concerned about the preservation of our heritage sites.

Yours faithfully,
Amit Awte

(f) Article – Write an article for a magazine about the World Heritage sites at risk. Include imaginary interviews with people who are trying to save them. Read your article in front of your class.

Question 16.
The project of dismantling and moving the temples in the valley to higher ground cost $80 million.
(i) $40 million
(ii) $50 million
(iii) $80 million.
Answer:
(iii) $80 million.

Question 17.
Complete the following: (The answers are given directly and underlined.)
(1) A World Heritage Site should have significant …………………
(2) World Heritage Sites include ……………………..
(3) They can also be a ……………………..
(4) The convention concerning the protection of  Cultural Natural Herttage was adopted by ……………………
Answer:
(1) cultural or natural importance to humanity.
(2) combination of cultural and natural areas.
(3) forests, lakes, monuments, buildings and cities.
(4) UNESCO’s General Conference on November 16, 1972.

Question 18.
(a) UNESCO launched an international campaign in 1959.
Answer:
In 1954, Egypt started plans to build the Aswan High Dam. The initial plans for the dam’s construction would have flooded the valley containing the Abu Simbel Temples and scores of ancient Egyptian artifacts. To protect the temples and artifacts, UNESCO launched an international campaign in 1959, that called for the dismantling and movement of the temples to higher ground.

(b) A White House Conference in the United States called for a ‘World Heritage Trust’.
Answer:
A White House Conference in the United States called for a World Heritage Trust’ to protect the world’s historic and cultural sites as well as the significant natural and scenic sites.

(c) convention:
(i) typical
(ii) agreement
(iii) old – fashioned
(iv) persuade
Answer:
(d) agreement

Question 19.
Pick out 4 adjectives from the passage ending with the suffix ‘ – al’.
Answer:
1. educational,
2. cultural,
3. natural,
4. historical.

Question 20.
The World Heritage Committee meets once a year.
(i) once a year
(ii) twice a year
(iii) three times a year
Answer:
(i) once a year

Question 21.
A nominated site has to be first included in a Tentative List.
(i) World Heritage List
(ii) Nomination File
(iii) Tentative List
Answer:
(iii) Tentative List

Question 22.
Explain what the World Heritage Committee is responsible for.
Answer:
The World Heritage Committee is the main group responsible for establishing which sites will be listed as UNESCO World Heritage Sites.

Question 23.
Who makes recommendations to the World Heritage Committee?
Answer:
The recommendations to the World Heritage Committee are made by two Advisory Bodies, the International Council on Monuments and Sites and the World Conservation Union.

Question 24.
(1) Choose the correct noun forms from those given in the brackets:
(1) inscribed (inscription/inscribtion)
(2) responsible (responsive/responsibility)
(3) nominated (nominative/nomination)
(4) included (inclusion/inclution)
Answer:
(1) inscription
(2) responsibility
(3) nomination
(4) inclusion.

Question 25.
Complete the following by choosing the correct nouns from the box:
Bodies Parties List File
(1) Tentative ……………….
(2) Nomination ……………….
(3) Advisory ……………….
(4) State ……………….
Answer:
(1) Tentative List
(2) Nomination File
(3) Advisory Bodies
(4) State Parties.

Question 26.
World Heritage Committee can delete/exclude a site from the World Heritage List
(a) World Heritage Committee
(b) World Peace Committee
(c) World Health Committee
Answer:
(a) World Heritage Committee

Question 27.
There are 890 World Heritage Sites around the World.
(a) 689
(b) 890
(c) 36
Answer:
(b) 890

Question 28.
36 – sites have been included from India.
(a) 176
(b) 44
(c) 36
Answer:
(c) 36

Question 29.
Match the places with the countries:

‘A’	‘B’
(1) Sydney Opera House	(a) Vienna
(2) Historic Center	(b) Peru
(3) Grand Canyon National Park	(c) Australia
(4) Machu Pichhu	(d) United States

Answer:

‘A’	‘B’
(1) Sydney Opera House	(c) Australia
(2) Historic Center	(a) Vienna
(3) Grand Canyon National Park	(d) United States
(4) Machu Pichhu	(b) Peru

Question 30.
Complete the following:
(1) Peru’s Machu Picchu is an example of a ………………….
(2) The World Heritage Committee can choose to delete a site from the list if ……………….
Answer:
(1) mixed site, both cultural as well as natural.
(2) the site loses the characteristics which allowed for it to originally be included on the World Heritage List.

Question 31.
Explain the role of the World Heritage Committee.
Answer:
The World Heritage Committee allocates resources from the World Heritage Fund to a World Heritage Site which is in danger due to any reason or in need of protection or restoration. If a site loses the characteristics which allowed for it to originally be included on the World Heritage List, the World Heritage Committee can choose to delete the site from the list.

Question 32.
Choose the correct meanings:
(a) allocate:
(i) allow
(ii) distribute
(iii) catch
(iv) understand
Answer:
(b) distribute

Question 33.
Fill in the blanks with the correct words from the passage: (The answers are given directly and underlined.)
(a) Many small towns of the previous century have become crowded cities now due to rapid ………………..
(b) We should be well – prepared for …………….. problems like global warming.
Answer:
(a) urbanization.
(b) environmental

Question 34.
(1) Pick out a gerund from the lesson and use – it in your own sentence.
(2) Find out five hidden words from the given word: international
(3) Use the following phrase in your own sentence: a corhbination of
(4) Spot the error/errors and rewrite the correct sentence: The State Parties is then responsible for identifying and nominating new sites.
(5) Identify the type of sentence: Get out of my way.
(6) Punctuate: if however a site loses the characteristics which allowed for it to be originally included on the world heritage list the world heritage committee can choose to delete the site from the list.
(7) From the following verbs, pick out the verb which forms its present and past participle by doubling the last letter. run, lose, trip, quit
(8) Arrange the following words in alphabetical order: Sydney, Vienna, Austria, Peru, Australia, Egypt, China
Answer:
(1) protecting: We should think of various ways of protecting our environment.
(2) internatIonal : natIonal, nation, train, trail, trial.
(3) The rainbow is a combination of seven colours.
(4) The State Parties are then responsible for identifying and nominating new sites.
(5) Imperative sentence.
(6) If however, a site loses the characteristics which allowed for it to be originally included on the World Heritage List, the World Heritage Committee can choose to delete the site from the list.
(7) trip : tripped, trIpping.
(8) Australia, Austria, China, Egypt, Peru, Sydney, Vienna

Question 35.
(1) Use the following word and its homophone in two separate sentences : rain
(2) UNESCO launched an International campaign In 1959. (Rewrite beginning ‘An lnternattonal…..)
(3) DIfferent plans are put Into place. (Rewrite using the future perfect tense of the verb.)
Answer:
(1) (i) There was light rain yesterday evening near my house.
(ii) In the past, a cõuntry progressed dutlng the reign of good kings.
(2) An international campaign was launched by UNESCO in 1959.
(3) Different plans will have been put into place.

Question 36.
(1) Italy has the highest number of World Heritage Sites. (Rewrite using the comparative form.)
(2) The World Heritage Committee meets once a year to review these recommendations. (Rewrite as a compound sentence.)
Answer:
(1) Italy has a higher number of World Heritage Sites than any other country.
(2) The World Heritage Committee meets once a year and (it) reviews these recommendations.

Read More:

• A Thing of Beauty is a Joy For Ever Question Answers
• The Luncheon Question Answers
• World Heritage Question Answers
• The Height of the Ridiculous Question Answers
• The Old Man and The Sea Book Review Question Answers
• The Gift of the Magi Question Answers

Balbharti Maharashtra State Board Class 10 English Solutions Unit 1.4 All the World’s a Stage Notes, Textbook Exercise Important Questions and Answers.

Class 10 English Chapter 1.4 Question Answer Maharashtra Board

All the World’s a Stage Poem 10th Std Question Answer

Question 1.
Pair work

• Talk to your friend about all the things related to ‘Seven.’
  For example Seven wonders of the world.
• Pair up with your partner and name those given below all of the under :

(a) The seven wonders of the world
………………………………………………………
(b) The seven continents
………………………………………………………
(c) The seven colours of the rainbow
………………………………………………………
(d) The seven notes of the music
………………………………………………………
(e) The seven seas of the world
………………………………………………………
Answer:
(a) The Seven wonders of the world : The Great Wall of China, Christ the Redeemer Statue, Machu Picchu, Chichen Itza, The Roman Colosseum, The Taj Mahal and Petra.
(b) The Seven continents : Asia, Europe, Australia, Africa, North America, South America, Antarctica.
(c) The Seven colours of the rainbow : violet, indigo, blue, green, yellow, orange, red
(d) The Seven notes of the musical scale : sa-re-ga-ma-pa-da-ni./doh-re-me-fa-so-la-ti
(e) The Seven seas of the world : Arctic Ocean, Antarctic Ocean, North Atlantic Ocean, South Atlantic Ocean, Indian Ocean, North Pacific Ocean, South Pacific Ocean.

Question 2.
Life is often compared to many things. Write down 7 things that life can be compared to and justify the comparison. For example,
(a) Life is a keyboard, because if you press the right keys you have typed a good destiny.
(b) ………………………………………………………
(c) ………………………………………………………
(d) ………………………………………………………
(e) ………………………………………………………
(f) ………………………………………………………
(g) ………………………………………………………
Answer:
(a) Life is a keyboard; if you press the right keys, you have typed out a good destiny.
(b) Life is a river-always flowing.
(c) Life is like a seed; it will never grow unless planted, nourished and nurtured.
(d) Life is like an elevator, with lots of ups and downs. ‘
(e) Life is like an onion. You peel off layer after layer. Sometimes it makes you weep.
(f) Life is like a jigsaw puzzle. You have all the pieces, but you have to put them together correctly.
(g) Life is like a jack-in-the-box. You never know : when you are going to get a box on your chin.

Question 3.
Match the approximate ages with the stages.

No.	Age-group			Stages
1	Birth to 2 years		a	teenage/adolescence
2	3 years to 12 years		b	old age/second childhood
3	13 years to 17 years		c	middle-age
4	18 years to about 44 years		d	babyhood/infancy
5	About 45 years to 60 years		e	senior citizen/elderly person
6	65 years up to 75 to 80 years		f	adulthood
7	Above 80 years		g	childhood

Answer:

No.	Age-group	Stages
(1)	Birth to 2 years	(d) babyhood/infancy
(2)	3 years to 12 years	(g) childhood
(3)	13 years to 17 years	(a) teenage/adolescence
(4)	18 years to about 44 years	(f) adulthood
(5)	About 45 years to 60 years	(c) middle-age
(6)	65 years up to 75 to 80 years	(e) senior citizen/ elderly person
(7)	Above 80 years	(b) old age/second childhood

Maharashtra Board Class 10 English Kumarbharati Unit 1.4 Questions and Answers

Question 1.
Read the words in given clouds. Match them with what they signify.

Answer:
(1) Stage – Life
(2) Characters – Roles played by human beings
(3) Script – Story of life
(4) Dialogues – Conversation
(5) Entry – Birth
(6) Exit – Death

Question 2.
Read the poem carefully and complete the following table.

Ages of Man	Role	Qualities/Actions
1		1. 2.
2		1. 2.
3		1. 2.
4		1. 2.
5		1. 2.
6		1. 2.
7		1. 2.

Answer:

First	infant	(1)   frightened (2)   crying, puking
Second	schoolboy	(1)   unhappy (2)   whining, creeping unwillingly to school
Third	lover	(1)   woeful (2)   sighing, singing sad ballads
Fourth	soldier	(1)  jealous in honor, ambitious (2)   quarreling, facing danger

Question 3.
Write down in your own words the differences between the following stages of a man’s life.
2nd stage and 4th stage …………………………………
……………………………………………………………………
……………………………………………………………………

3rd stage and 5th stage …………………………………
……………………………………………………………………
……………………………………………………………………

1 st stage and 7th (last) stage …………………………………
……………………………………………………………………
……………………………………………………………………
Answer:
2nd stage and 4th stage:
The second stage is that of a school boy, complaining and crying. He goes to school early in the morning, with a well-scrubbed, shining face. He carries his school bag and creeps slowly, like a snail, unwillingly to school.

‘Full of strange oaths and bearded like the pard, Jealous in honour, sudden and quick in quarrel.’

3rd stage and 5th stage:
The third stage is that of a lover, who is’ breathless and sighing with passion. He sings sad Songs dedicated to the beauty of his lover.

The fifth stage is that of , a mature middle-aged man with a round belly. He is stern and formal and full of wisdom. He is full of wise sayings and gives modern examples.

1 st stage and 7th (last) stage:
The first stage is that of an infant, crying weakly and throwing up in his nurse’s arms. He is unaware of what is happening around him.The baby, at this stage, is without teeth, without vision, without taste and without anything.

The last stage of all, which ends one’s eventful life, is when man becomes senile and enters his second childhood. He is again unaware of what is happening around him. This final stage is when he is once more without teeth, without vision, without taste and without anything.

Question 4.
Pick out lines that contain Imagery (a picture created in the mind by using words) of the following people.
(a) School boy …………………………………
(2nd stage) …………………………………
(b) Soldier …………………………………
(4th stage) …………………………………
(c) Judge …………………………………
(5th stage) …………………………………
(d) Senior citizen …………………………………
(6th stage) …………………………………
Answer:
(a) a snail
‘The whining schoolboy, with his satchel and shining morning face, creeping like a snail unwillingly to school.’

(b) acts like the pard
‘Full of strange oaths and bearded like the pard, Jealous in honour, sudden and quick in quarrel.’

(c) In fair round belly with good capon lined
With eyes “severe and beard of formal cut

(d) His youthful hose, well-saved, a world too wide
For his shrunk shank

Question 5.
You will notice that there is no Rhyme-scheme in the poem. It appears similar to the poem 1.1 ‘Where the Mind is Without Fear by Tagore.

However Tagore’s poem has no steady rhythm/meter either it is called Free Verse. Shakespeare uses lines with a steady rhythm of 5 beats in each. It is termed as Blank Verse. (No rhyme-scheme but uniformity in rhythm) Copy the lines from “Ánd all the men and women merely players” to “sudden and quick in quarrel”. Put a stress mark on each of the syllables stressed in the lines as for example, And all the men and women merely players;
Answer:
The poem is written in free verse without any rhyme scheme or consistent metre. There are many figures of speech e.g. Repetition. Metaphor, Alliteration, etc. An Important figure of speech is Personification. ‘Where tireless striving stretches its arms towards perfection’. Here, we can actually visualize ‘tireless striv1ng stretching Its arms to reach its goal.

The poem is a prayer to God. Tagore addresses God as ‘my Father’ and asks Him to awaken his country Into a heaven of freedom, where there is total freedom of good thoughts, good words and good actions. He wishes for a country where people would be free from fear, where knowledge would be free to all individuals and people from all castes and religions would be united.

Question 6.
Think and write on your own.
(a) What is the theme/central idea of this poem?
(b) Which two stages of man, described by Shakespeare sound humorous? Say why.
(c) The last (7th) stage of life sounds very sad and miserable. How can you make old age also cheerful and happy?
Answer:
(a) The theme of this poem is the cycle of life.
It tells us how one starts out an infant, helpless and unaware of the surroundings, and ends the same way, i without being aware of what is happening around one.

(b) The second and third stages are humorous. One can just imagine the school boy, complaining and whining, creeping to school slowly with a well-scrubbed and shining face. The third stage, where the lover sighs loudly and sings sad poems and songs, is also humorous.

(c) We can make the last stage joyful by preparing for it beforehand. We know that most of us will reach this stage before our final exit. Hence, we must maintain good health, and keep good relations with our family and the people around us. We must save enough money to get us through this stage without any stress on ourselves or others.

Question 7.
(A) The poem is entirely metaphorical. Pick out the comparisons from the poem.
(a) world …………………………………
(b) actors …………………………………
(c) birth and death …………………………………
(d) school boy …………………………………
(e) the lover’s sigh …………………………………
(f) spotted leopard …………………………………
(g) last stage (old age) …………………………………
Answer:
(a) stage
(b) –
(c) entrances and exits
(d) a snail
(e) a furnace
(f) bearded soldier

(B) Pick out from the poem two examples of each.
(a) Simile
(1) …………………………………
(2) …………………………………
Answer:
Simile. Two dissimilar objects are compared using the word ‘like’.

(b) Onomatopoeia
(1) …………………………………
(2) …………………………………

(c) Alliteration
(1) …………………………………
(2) …………………………………

(d) Metaphor
(1) …………………………………
(2) …………………………………

(e) Inversion
(1) …………………………………
(2) …………………………………

(f) Transferred Epithet
(1) …………………………………
(2) …………………………………
Answer:

(a) Simile	(1)   Creeping like a snail (2)   Soldier bearded like the pard
(b) Onomatopoeia	(1)   And then the whining schoolboy (2)   Sighing like a furnace
(c) Alliteration	(1) They have -their exits and their entrances (2) His youthful hose, well- saved, a world too wide
(d) Metaphor	(1)   They have their exits and their entrances (2)   men and women merely players
(e) Inversion	(1)   His acts being seven ages. (2)   With eyes severe and beard of formal cut
(f) Transferred Epithet	(1)   with a woeful ballad (2)   Into the lean and slippered pantaloon

Question 8.
Read the summary of the play ‘As You Like It’ by William Shakespeare using the Internet. Find out which character has narrated the above poem and on what occasion. Also, make a list of all the characters of the play.
Answer:
The character who has narrated the above poem in the play ‘As You Like It’ by William Shakespeare is Jacques. He narrates it in Act II, Scene VII.

Some of the other characters in the play are Celia, Rosalind, Orlando, Oliver, Duke Senior, Duke Frederick, Touchstone, etc.

Question 9.
Read the poem again and write an appreciation of the poem in a paragraph format. (Refer to page no. 5)
Answer:
Point Format
(for understanding)
The title of the poem : All the World’s a Stage’
The poet : WIlliam Shakespeare
Rhyme scheme : blank verse I.e. no rhyme scheme, but there is a steady rhythm of five beats In each line.
Figures of speech : Metaphor, Simile, Alliteration, Repetition. etc.
Theme/Central idea : The theme of the poem Is the cycle of life.

Paragraph Format
The poem ‘All the World’s a Stage’ is by William Shakespeare. It is taken from Shakespeare’s play ‘As you like It’. It is a monologue by one of the characters in the play.

The poem is written in blank verse i.e. there is no rhyme scheme, but there Is a steady rhythm of five beats i.e. iambic pentameter in each line. There are many figures of speech, like Simile. Alliteration and Repetition. but the one that stands out Is Metaphor. In the lines ‘All the world’s a stage, And all men and women are merely players’, there is an implied comparison between two different things.

In this poem, Shakespeare compares life to a stage. He has divided life Into seven stages. each having its own varied qualities and features. The theme of the poem is the cycle of life. It tells us how one starts out as an Infant, helpless. without understanding. and ends the same way, without being aware of what Is happening around one.

Question 10.
Complete the following diagram:
Answer:

Question 11.
Match the following :

A	B
(1) Infant	(a) acts like the pard
(2) School boy	(b) mewling and puking
(3) Lover	(c) whining,
(4) Soldier ‘	(d) sighing like furnace

Answer:

(1) Infant	(b) mewling arjd puking
(2) School boy	(c) whining
(3) Lover	(d) sighing like furnace
(4) Soldier	(a) acts like the pard

Question 12.
Complete the following : (The answers are given directly and underlined.)
Answer:
(1) ‘Exits’ and ‘entrances’ refer to deaths and births.
(2) Reputation is like a bubble because one does useless things for one’s reputation, which can burst like a bubble in one instant.

Question 13.
Name and explain the poetic devices used in the following lines:
(a) Soldier bearded like the pard
Answer:
Simile. Two dissimilar objects are compared using the word ‘like’,

(b) Sighing like a furnace
Answer:
Simile. Two dissimilar objects are compared using the word ‘like’.

(c) men and women merely players
Answer:
Metaphor. Implicit comparison between two different things.

(d) They have their exits and their entrances
Answer:
Alliteration. Repetition of the sound of ‘t’ and ‘e’.
Metaphor. Implicit comparison between two different things.

(f) With a woeful ballad
Answer:
Alliteration. Repetition of the sound of ‘w’.
Transferred Epithet. It is not the ballad that is woeful but the lover.

Question 14.
Complete the following diagram :
Answer:

Question 15.
Write if the following statements are True or False :
Answer:

• Man in the fifth stage of life is full of wisdom. (True)
• Man in the sixth stage has a fair, round belly. (False)
• The last few lines are full of melancholy. (True)
• In the last stage, man is unaware of his surroundings. (True)

Question 16.
Write down in your own words the differences between the following stages of a man’s life :
(a) 5th and 6th stage :
Answer:
The fifth stage is that of a mature middle-aged man with a round belly. He is stern and formal and full of wisdom. He is full of wise sayings and gives modern examples.

In the sixth stage, man has become old, with thin legs in slippers and loose pants. He has spectacles on his nose and a pouch by his side. The close-fitting stockings, which he had saved from his younger days, are now too big for his thin legs, which have shrunk with age. His loud voice, which was once manly, has now become childish and shrill. There are whistling sounds when he talks.

Question 17.
Complete the following table based on the extract. (The answers are given directly.)
Answer:

Stages of Man	Role	qualities/Actions
Fifth	adult man	(1)   fat, serious and wise (2)   giving advice
Sixth	middle-aged man	(1)   thin and shrunken (2)   talking in a shrill-voice
Seventh	very old man	(1)   senile, child-like (2)   oblivious to his surroundings

Question 18.
The poem is entirely metaphorical. Pick out the comparison from the extract: last stage (old age)
Answer:
last scene

Question 19.
Name and explain the figures of speech used in the following lines :
(a) His youthful hose, well-saved, a world too wide
Answer:
Alliteration. Repetition of the sound of ‘w’.

(b) For his shrunk shank
Answer:
Alliteration. Repetition of the sound of ‘s’.

(c) Turning again towards childish treble
Answer:
Alliteration. Repetition of the sound of ‘t’.

(d) Sans teeth, sans eyes, sans taste, sans everything.
Answer:
Repetition. The word ‘sans’ is repeated for emphasis.

Read More:

• Where the mind is Without fear Question Answers
• The Thief’s Story Question Answers
• On Wings of Courage Question Answers
• All the World’s a Stage Question Answers
• Joan of Arc Question Answers
• The Alchemy of Nature Question Answers

Balbharti Maharashtra State Board Class 10 English Solutions Unit 3.6 The Concert  Notes, Textbook Exercise Important Questions and Answers.

Class 10 English Chapter 3.6 Question Answer Maharashtra Board

The Concert Poem 10th Std Question Answer

Question 1.
Pair up with your partner and ask and answer the following questions.
(a) Do you like music?
(b) What does a concert mean?
(c) Have you ever attended any live concert?
(d) Have you seen a concert on Television?
(e) Whose concert would you love to attend?
Answer:
(a) Yes, I do.
(b) A concert is a musical programme where musicians and classical singers come together to play different pieces of music.
(c) Yes, I have.
(d) Yes, I have.
(e) I would love to attend the concert of A. R. Rahman.

Question 2.
Look at the web diagram given below and study the traits of a good concert organizer.

Answer:

The Concert Class 10 English Workshop Questions and Answers Maharashtra Board

Question 1.
Who said to whom?
(a) “We mustn’t miss the chance.”
(b) “This is not the last time they are going to play.”
(c) “A walk in the park might make you feel better.”
(d) “Tomorrow morning we perform for the boy- Yes?”
Answer:

Statement	Who	To Whom
(a) “We mustn’t miss the chance.’’	The boy	To his sister and mother
(b) “This is not the last time they are going to play.”	the mother	to anant
(c) “A walk in the park will make you feel better.”	Aunt Sushila	to smita
(d) “Tomorrow morning we perform for the boy- Yes?”	Ustad Sahib	to Pandit Ravi Shankar.

Question 2.
Read the following sentences and write which emotions are revealed from these sentences.
(a) Pandit Ravi Shankar is playing tomorrow at the Shanmukhananda auditorium.
(b) It’s the chance of a lifetime.
(c) Will you come to Aunt Sushila’s house and play for him?
(d) Did you…did you hear him?
(e) Is it…It’s not possible?
Answer:
(a) excitement
(b) anticipation, joy, excitement
(c) This sentence expresses the emotion of a sincere plea or entreaty. Smita is practically begging Pandit Ravi Shankar to consider her request.
(d) This sentence expresses the boy’s innermost curiosity, and his desire to confirm if his sister had indeed heard the performances of the musicians whom he so longed to hear.
(e) This sentence expresses the emotion of complete surprise and disbelief. Something the neighbours had thought absolutely impossible was indeed a reality.

Question 3.
Read the text carefully, you will find some words describing a particular specialty of the individuals/personalities in the text. Explain the meaning of the following words given in the table with reference to the particular personality mentioned in the text.

Speciality	Personality	Explanation
Maestro Pandit Ustad Moustachioed	………………….. Ravi Shankar ………………….. …………………..	………………….. ………………….. ………………….. a person having a large or bushy mustache.

Answer:

Specialty	Personality	Explanation
Ustad	Allah Rakha	title for an expert tabla player
Moustachioed	Name unknown	someone who sports ’ a prominent bushy mustache
Maestro	Pandit Ravi Shankar	a distinguished performer of classical music
Pandit	Ravi Shankar	a talented musician (used as a respectful title or form of address)

Question 4.
Describe the condition of Smita when she was going towards the stage. Read the text again and complete the boxes given below. One is done for you.

Answer:

Question 5.
The whole story revolves around Anant. Write a short paragraph on Anant. Take help of the following points to develop the paragraph.
1. Health
2. Disease
3. Early interests
4. Intense desire/wish
5. Fulfillment of desire/wish.
Answer:
Anant was a fifteen-year-old boy, living in a village named Gaganpur with his sister and parents. Very active in his school days, he was a good athlete, the best table-tennis player, could play the sitar very well and had even been composing his own tunes. Suddenly, he was struck with cancer and came to Mumbai for treatment. Then one day, his sister read in the newspaper that Pandit Ravi Shankar would be performing at the Shanmukhananda auditorium.

It was his earnest desire to watch the performance, but due to his sickness, his mother forbade him. Finally, his sister, in a very daring move, went to the concert and after the concert had ended, went backstage and requested Pandit Ravi Shankar to come to their home and play for her brother. The great generous maestro along with Ustad Allah Rakha agreed and did exactly that. As the beautiful soulful music wafted around the room where Anant lay, Anant breathed his last.

Question 6.
The story has three important characters- Anant, Smita and Aunt Sushila. Go through the story again and complete the following table that highlights their special traits of character. You can put X mark if that trait is not mentioned in the text.

Special traits	Smita	Anant	Aunt Sushila
Strength Weaknesses Dreams Motivation

Answer:

Special traits	Smita	Anant	Aunt Sushila
Strength	daring	courage	concern, generosity
Weakness	given to emotion	physical health	X
Dreams	that her brother would get cured	that he would hear Pandit Ravi Shankar play	X
Motivation	love for her brother	love for music	love for the children

Question 7.
The two contradictory pictures are depicted in the story. Discuss in pairs and describe them in your words in front of the class.
Answer:
The brother and sister seem excited about Pandit Ravi Shankar’s upcoming performance. The girl expresses excitement and the boy’s eyes are shining. The mother, however, is more worried about the physical condition of her son, who is on oxygen and apparently out of breath. The mother’s voice breaks when she speaks and her lips utter unbidden prayers. These are the contradictory images presented in this passage.

Question 8.
The text has a big collection of Indian words in it. Using words from another language in a write up is called Code-mixing. Make a list of all the Indian words in table A and their meanings in table B. One is done for you.

‘A’ Indian word	‘B’ Meaning
1. Raga	(a) piece of Indian classical music based on one of the six basic musical modes.
2.	(b)
3.	(c)
4.	(d)
5.	(e)
6.	(f)

Answer:

‘A’ (Indian word)	‘B’ (Meaning)
1. Raga	(a) piece of Indian classical music based on one of the six basic musical modes.
2. Pandit	(b) a talented musician (used’as a respectful title or form of address)
3. sitar	(c) a large, long-necked Indian lute with movable frets, played with a wire pick
4. Ustad	(d) a highly skilled musician
5. Pandit	(e) address for a talented classical musician
6. divan	(f) a long low sofa without a back or arms

Question 9.
(A) Choose the appropriate Adverb or Adjective form to fill in the gaps.
(1) She spoke in an …………………….. tone. (excited / excitedly)
(2) Smita accepted the suggestion …………………….. (grateful / gratefully)
(3) They gave him whatever made him …………………….. (happy/ happily)
(4) He ran very …………………….. (fast / fastly)
(5) He would become a …………………….. sitarist some day. (great / greatly)
(6) Life went out of him …………………….. (gentle / gently)
Answer:
(1) excited
(2) softly
(3) happy
(4) fast
(5) great
(6) gently

(B) Rewrite in Indirect speech
1. “Please”, she begged him, “Please come”.
……………………………………………………………………

2. He said, “What shall we do, Ustad Sahib?”
……………………………………………………………………

3. Her brother said, “Enjoy yourself”. He added, “Lucky you!”
……………………………………………………………………

4. ‘Yes’ Panditji replied. “It’s settled then. Tomorrow morning we shall perform, for the boy.”
……………………………………………………………………
Answer:
(1) She begged him repeatedly to come.
(2) He asked the Ustad Sahib what they should do.
(3) Her brother told her to enjoy herself and then added that she was indeed lucky.
(4) The Panditji replied in the affirmative and added that the matter was then settled. He further added that they would perform for the boy the following morning.

Question 10.
The text mentions names of stalwarts like Pandit Ravi Shankar and Ustad Allah Rakha. Both have earned world wide name and fame for their outstanding contribution to the field of music. Form groups of 5 students each and write a brief note on other stalwarts in this (music) field. You can take help of your school library or search the relevant information on the internet.
Take help of the following points.
1. Name :
2. Field : Music
3. Specialisation : Tabla/Sitar/Violin etc.
4. Guru :
5. Early life :
6. Education :
7. Early success :
8. Contribution to the field and world :
9. Awards:
10. Any special incident that has occurred in his/her life :
Answer:
Pandit Hariprasad Chaurasia
Hariprasad Chaurasia is an Indian classical flutist. He plays the bansuri, an Indian bamboo flute in the Hindustani classical tradition.

His Guru was Bholanath Prasanna of Varanasi. He studied with him for eight years. In 1957, he joined the All India Radio, Cuttack, Odisha. He worked as composer and performer. Much later, he received guidance from the reclusive Annapurna Devi, daughter of Baba Allaudin Khan. Legend has it that she agreed to teach him only if he played with the left hand. True or not, up till today, Hariprasad plays the bansuri with the left hand.

Apart from classical music, Hariprasad has collaborated with Shivkumar Sharma, the santoor exponent forming an association called Shiv-Hari. He has collaborated with world musicians, including the fusion group Shakti, in experimental cross-cultural performances.

He is at present the artistic director of the World Music Department at the Rotterdam Music Conservatory in the Netherlands. In 2006, he founded the Vrindavan Gurukul in Mumbai and in 2010, the Vrindavan Gurukul in Bhubaneshwar. Both of these institutes are schools dedicated to training students in bansuri in the Guru-shishya tradition.

He has collaborated with several western musicians, including John McLaughlin, Jan Garbarek, and Ken Lauber, and has composed music for Indian films.

Chaurasia also played on The Beatles’ 1968 B-side ‘The Inner Light’, which was written by George Harrison.

Question 11.
Imagine you are the monitor of your class. You are assigned the task to invite a classical singer as a chief guest for the Annual Day Programme. Write a letter of invitation to a famous classical singer. Take help of the following points.
Write in short –
1. About your school.
2. About the Annual Day Programme
3. Interest and love of students for music.
4. Motivation.
Answer:
Dilip Rane
Sulochana Devi High School
Mahatma Phule Chowk
Dhule – 424 001,
Date: 20 November, 2020

Shri Gangadin Murkathe
Govardhan Society
Videhi Nagar
Dhule – 424 003.

Subject: Invitation as Chief Guest for the Sulochana Devi High School Annual Function

Dear Sir,
As monitor of Std. X A, Sulochana Devi High School, it is my privilege to invite you to our School Annual Day Function on 15th January, 2021 as Chief Guest.

It will be an evening filled with song and dance, and the first person we thought of was you, as you are an eminent classical singer in your own right. Most of us know about you and have heard your songs either on DVD or on FM.

Our students are highly interested in the classical genre and many are under training at various local i classes. Your presence will serve as motivation for our budding talent and give us pointers as to future careers in music.

Please confirm your presence; for us it will be an honour.

Yours truly,
Dilip Rane,
Monitor (Std. X A)

Question 12.
Write who said to whom:
Answer:

statements	Who	To whom
(a) You’ll wake him up.	The mother	To her daughter
(a) “The chance of a lifetime.”	Anant	to his mother
(c) “Your father will take you.”	Smita’s mother	to Smita

Question 13.
Complete the following web:
Answer:

Question 14.
Why was Smita excited?
Answer:
Smita was excited because she read in the newspaper that Pandit Ravi Shankar was to play the next day at the Shanmukhananda auditorium.

Question 15.
What was the chance of a lifetime for Anant?
Answer:
To be able to hear and see Pandit Ravi Shankar perform was the chance of a lifetime for Anant.

Question 16.
Give reasons: Smita became nervous.
Answer:
Smita became nervous because she remembered that her brother was very ill and that the doctors had given up hope. The truth that Anant was going to die frightened her.

Question 17.
Write from the passage antonyms for the following words:
(a) bored
(b) forget
(c) worse
(d) worst
Answer:
(a) bored x excited
(b) forgot x remembered
(c) worse X better
(d) worst X best

Question 18.
(1) Choose the appropriate Adverb or Adjective form to fill in the gaps:
(b) I wished the noise would stop. It seemed to go on ……………, (endless, endlessly)
Answer:
(b) endlessly

Question 19.
Add question tags:
(a) You know he needs all the sleep and rest he can get.
(b) You’ll wake him up.
(c) His eyes were shining.
(d) We mustn’t miss the chance.
Answer:
(a) You know he needs all the sleep and rest he can get, don’t you?
(b) You’ll wake him up, won’t you?
(c) His eyes were shining, weren’t they?
(d) We mustn’t miss the chance, must we?

Question 20.
The boy on the bed was not asleep: (Rewrite without ‘not’.)
Answer:
The boy on the bed was awake.

Question 21.
How would you feel and react if you came to know that someone closely known to you was suffering from cancer?
Answer:
If I came to know that someone closely known to me was suffering from cancer, I would feel very bad. I would visit the person, spend time, make the person happy in every way possible and most of all pray to God, to relieve the person from suffering.

Question 22.
Say whether the following are True or False: (The answers are given directly and underlined.)
Answer:
(a) In Bombay, the family stayed with their aunt.
(b) The doctors told the family directly that Anant did not have many days to live.
(c) The family voiced their fears to Anant.
(d) Anant was well enough to take part in the forthcoming table tennis tournament.
Answer:
True
False
False
False

Question 23.
Why was everyone from the family trying to keep Anant happy?
Answer:
Everyone from the family was trying to keep Anant happy because they knew he did not have many days to live. They did not wish to voice their fears but rather wanted him to be surrounded by whatever made him happy.

Question 24.
Why was Smita not ready to go for the concert?
Answer:
Smita was not ready to go for the concert because she and her brother, Anant, had always done things together.

Question 25.
Write from the passage phrases that mean:
(a) participate
(b) feeling that something good will happen
(c) express their worries
(d) a rare opportunity
Answer:
(a) take part In
(b) high hopes
(c) voice their fears
(d) a chance of a
(e) lifetime.

Question 26.
Match the columns:

A	B
(a) choked (b) roasted (c) Yogic (d) daring	(i) exercises (ii) thought (iii) gram (iv) voice

Answer:

A	B
(a) choked (b) roasted (c) Yogic (d) daring	(iv) voice (iii) gram (i) exercises (ii) thought

Question 27.
Complete the sentence with proper option: Smita accepted the suggestion (grateful/gratefully)
Answer:
Smita accepted the suggestion gratefully.

Question 28.
Frame Yes-No questions to get the sentences as the answer:
(a) There’s no harm in trying it.
(b) It would be nice to go to the concert.
Answer:
(a) Is there any harm in trying it?
(b) Wouldn’t it be nice to go to the concert?

Question 29.
*Two contradictory pictures are depicted in the story.
Answer:
On the one hand, the family is aware that Anant does not have many days to live. They are worried. They have fears but they suppress them. Instead they laugh and smile and talk. They surround Anant with whatever makes him happy. They fulfil his every need and give him whatever he asks for.

Question 30.
(1) Complete the following flow-chart:
Answer:

Question 31.
Write whether the following statements are True or False:
(a) Smita dreamt that she was at the concert.
(b) Anant had said, ‘The chance of a lifetime’ the previous evening.
(c) At the end of the concert, the artistes stood and clapped for the audience.
(d) A man with a long moustache was one of the artistes.
Answer:
(a) False
(b) True
(c) False
(d) False

Question 32.
(1) Arrange the following sentences chronologically according to their occurrence in the passage:
(a) The first notes came over the air.
(b) The audience gave the artistes a standing ovation.
(c) The audience gave the great master a thundering welcome.
(d) The ragas unfolded.
Answer:
(c) The audience gave the great master a thundering welcome.
(a) The first notes came over the air.
(d) The ragas unfolded.
(b) The audience gave the artistes a standing ovation.

Question 33.
How did Smita enjoy the concert?
Answer:
Smita felt as if the gates of a land of enchantment and wonder were opening. She listened spellbound to the unfolding ragas.

Question 34.
Give one example of code-mixing (Indian word) from the passage and explain its meaning.
Answer:
raga – a musical mode in Indian classical music

Question 35.
Pick the odd man out from the following based on the passage and give reasons:
(a) sitting, thundering, unfolding, twinkling
(b) slow, boring, plaintive, twinkling
Answer:
(a) sitting (verb – all the others are adjectives)
(b) boring (describes the noun ‘speech’ – all the others describe the ‘ragas’)

Question 36.
Underline the adverbs:
(a) The curtain came down.
(b) The plan remained firmly in her mind.
(c) The plan she had decided on the evening before remained firmly in her mind.
Answer:
(a) The curtain came down.
(b) The plan remained firmly in her mind.
(c) The plan she had decided on the evening before remained firmly in her mind.

Question 37.
Have you ever attended any concert? How was your experience there?
Answer:
Yes, I have attended a concert in which A. R. Rahman was the main performer. When I heard the first few notes being sung, I was thrilled. Never before had I heard such music or singing. I felt as if I were transported to a wonderland where only music reigned. Every beat, every note filled me with delight. I began wondering if I were in heaven!

Question 38.
Who said this to whom?
“Tomorrow morning we perform for the boy – Yes?”
Answer:
Ustad Sahib said this to Pandit Ravi Shankar.

Question 39.
Write whether the following statements are True or False:
(1) When Smita returned home, Anant was awake.
(2) Both Ravi Shankar and Ustad Allah Rakha came to Aunt Sushila’s house.
(3) Anant’s room was on the ground floor.
(4) Anant survived the sickness.
Answer:
(1) True
(2) True
(3) False
(4) False

Question 40.
What was Smita’s plan?
Answer:
It was Smita’s plan to plead with Pandit Ravi Shankar to come to her aunt’s house and play the sitar for her brother, Anant, who was suffering from cancer.

Question 41.
Why were the neighbours surprised?
Answer:
The neighbours were surprised to see the two great musicians Pandit Ravi Shankar and Ustad Allah Rakha, getting out of a taxi which pulled up outside their block.

Question 42.
Give one word for each of the following:
(a) a soft compressed lump – …………………..
(b) twist or turn the body with quick – …………………..
(c) an expert at music – …………………..
(d) unseen backstage area on the sides of a stage – …………………..
Answer:
(a) wad
(b) wriggle movements
(c) wizard
(d) wings

Question 43.
(1) State the tense of the underlined verbs in the sentences:
(a) A small crowd had gathered
(b) Her knees felt weak.
(c) “Will you come to Aunt Sushila’s house?”
(d) “Its settled then.”
Answer:
(a) Past Perfect
(b) Simple Past
(c) Simple Future
(d) Simple Present.

Question 44.
Choose the appropriate Adverb or Adjective form to fill in the gaps.
(a) Smita spoke ………………. to Anant. (excited/excitedly)
Answer:
(a) excitedly

Question 45.
Music can calm the mind. Share your views.
Answer:
This is very true. Music has the profound effect of calming the mind, filling the soul of the listener with peace and transporting the devotee to a state of mind that is almost heaven.

Question 46.
(1) Pick out the gerund and use it in a sentence: She had been so excited at seeing the announcement.
(2) Arrange the words in alphabetical order: wooden, word, would, wonder
(3) Make a meaningful sentence by using the phrase: catch the attention of
(4) Write two smaller words hidden in the given word: table-tennis
(5) Identify the kind of sentence: Lucky you!
(6) Spot the errors and correct the sentence: Her knees were felt weak and her tongue being dry.
(7) Write the past participle forms of the given verbs: (1) die (2) stay
(8) Punctuate the sentence: did you hear him he whispered
Answer:
(1) Gerund: seeing Sentence: Seeing is believing.
(2) wonder, wooden, word, would
(3) Sentence: One of the girls in the dance caught the attention of the chief guest.
(4) tablet, table (tennis, able)
(5) Exclamatory Sentence
(6) Her knees felt weak and her tongue was dry.
(7) (1) died (2) stayed
(8) “Did you hear him?” he whispered.

Question 47.
(a) Write sentences using the word ‘rest’ with two different meanings.
(b) Rewrite the sentences beginning with the underlined word: The audience gave the artistes a standing ovation.
(c) Write a word register of 8 words for the word ‘concert’.
Answer:
(a) (1) Those who have finished may leave. The rest will please stay back, (the remaining ones)
(2) You may rest in the afternoon, (stop work in order to relax, sleep or gather strength)
(b) The artistes were given a standing ovation (by the audience).
(c) concert: programme, stage, audience, music, dance, box office, venue, band, (performance, recital, show, gig)

Question 48.
(1) State the kind of sentence and pick out the clause, if any: They knew then that the boy had not many days to live.
(2) Use the two given words in one meaningful sentence: cured, sitar
Answer:
(1) Kind of sentence: Complex Clause: that the boy had not many days to live – Noun clause
(2) The doctor told him that after he was cured he could play the sitar.

Read More:

• Night of the Scorpion Question Answers
• The Night I Met Einstein Question Answers
• Stephen Hawking Question Answers
• The Will to Win Question Answers
• Unbeatable Super Mom-Mary Kom Question Answers
• The Concert Question Answers