Prasanna

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 3 Applied History Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 3 Question Answer Applied History Maharashtra Board

Class 10 History Chapter 3 Applied History Question Answer Maharashtra Board

History Class 10 Chapter 3 Question Answer Maharashtra Board

Question 1.
(a) Choose the correct option from the given options and complete the statement.
(1) The earliest museum in the world was discovered in the excavations at the city of ……………..………. .
(a) Delhi
(b) Harappa
(c) Ur
(d) Kolkata
Answer:
(c) Ur

(2) The National Archives of India is in ……………..………. .
(a) New Delhi
(b) Kolkata
(c) Mumbai
(d) Chennai
Answer:
(a) New Delhi

(b) Identify and write the wrong pair in the following set.
(1) Kootiyattam- Sanskrit theatre, Kerala
(2) Ramman- Dance form in West Bengal
(3) Ramlila- Traditional Performance of the Ramayana in Uttar Pradesh
(4) Kalbelia- Folk songs and dances of Rajasthan.
Answer:
(2) Wrong pair: Ramman – Dance form in West Bengal

Question 2.
Explain the following concepts :
(1) Applied History
Answer:

•  When one subject is applied to different fields and conclusions are derived, it is known as application of that subject.
• When objectives of History are applied to other subjects; new conclusions are obtained.
• This is known as ‘Applied History’. It is also known as Public History.
• We get insights of the events that took place in the past through history.
• Applied History is concerned with application of knowledge of history to provide guidance in finding solutions.
• Contemporary social issues and include them in social planning.
• Thus Applied History’ is a field of study concerned with the application of history for the benefit of people in contemporary and future times.

(2) Archives
Answer:

•  A place where historical documents are preserved is called an ‘Archive’.
• Many old documents, official records, old films, records of treaties are kept at this place.
• We get references of original documents because of Archives.
• A study of historical events of a particular period is possible.
• We come to know about language, script used in a particular period/era.
• The National Archives of India is in Delhi. It is the largest Archive in Asia.
• Every state in India maintains its archives independently.

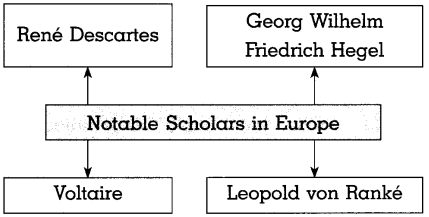
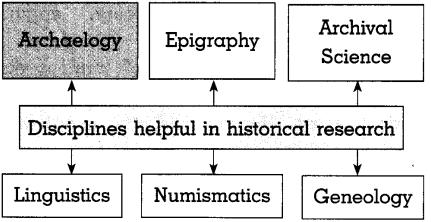
Question 3.
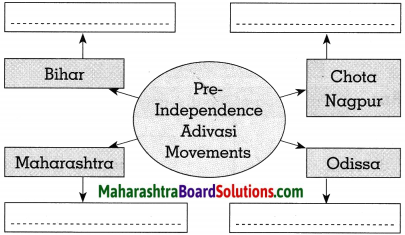
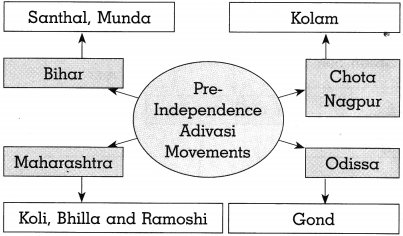
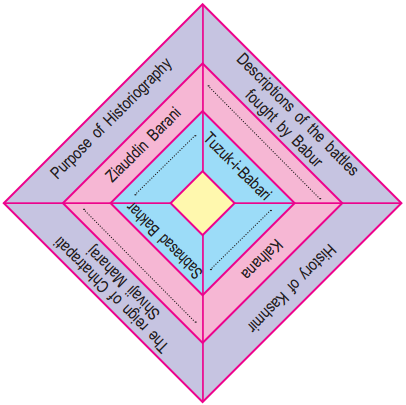
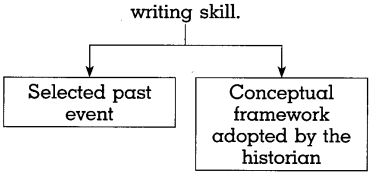
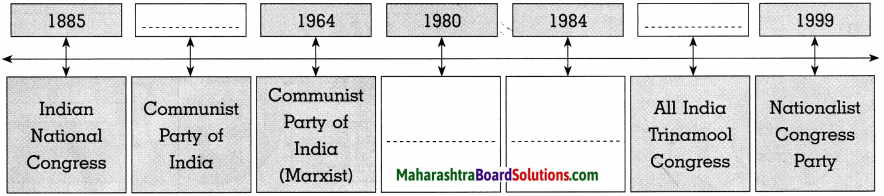
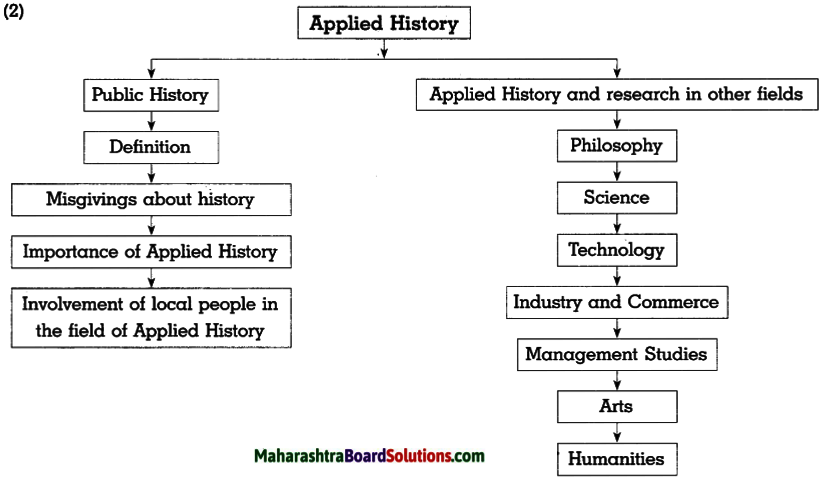
Complete the following concept chart.

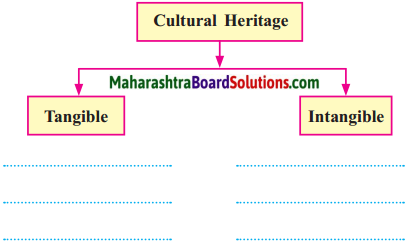
Answer:

Question 4.
Explain the following statements with reasons.
(1) It is essential to study the history of technology.
Answer:

• Man acquired different skills at various stages in his evolution process.
• From mxking stone tools to developing new techniques of agriculture production, he learnt many skills and entered in the age of science.
• Agricultural production, commodity production, architecture, engineering, etc.
• underwent several changes. Production increased manifold bcause of technology.
• Hence, it is necessary to know the history of technology in order to understand the development in mechanisation and mutual dependence between science and technology.

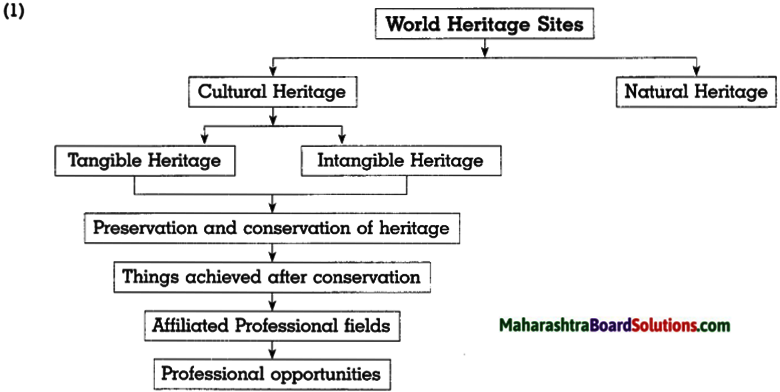
(2) The list of world Heritage Sites is announced by UNESCO.
Answer:

• Cultural heritage is a form of human creation. It is a cultural treasure that has been inherited from our ancestors.
• We feel connected to it and hence preserve and conserve it.
• This heritage is our asset that binds us to our past and hence we should preserve it for the benefit of future generations.
• In order to save this heritage, UNESCO has announced some directives.
• On the basis of those directives, list of sites, and traditions are declared as ‘World Heritage’.
• It has helped us in promoting these sites as tourist places.

Question 5.
Write elaborate answers
(1) How is the method of history useful in the research of
(a) Science
(b) Arts
(c) Management Studies
Answer:
Each field has its own history of building’ knowledge. The direction of development in every field is dependent on the stcrte of available knowledge in that field. The method of history has proved valuable in the research of various fields.

(a) Science: Scientific discoveries /invenfions take place because of humdn efforts to satisfy needs and curiosity. These efforts are based on scientific knowledge that already existed. Knowledge of the history of science helps in understanding the reasons, chronology and factors that facilitated a scientific invention/discovery. Knowledge of history of science helps in every field.

(b) Art: Development of any style of art lies in their expression through intellectual, emotional and cultural traditions. While studying any art form we have to understand the history of its traditions, the key to the expressions in it, and emotional temperament of the artist. Prevalent art style in the given period can be understood with the help of cultural history.

(c) Management Studies: All components like means of production, human resources, processes of production, the chain of market and sales, etc. are interrelated and require management.

Different social and economic institutions are involved in these industrial and commercial processes. Knowledge of similar functional systems of the past is essential to bring about changes, improvements and make the management smooth and efficient. It becomes necessary to know its history.

(2) How can we correlate applied history with our present?
Answer:
History gives us knowledge about the events that happened in past. Applied history helps us in understanding how the knowledge can be put to use for our benefit as well as for the benefit of future generations. Applied history is correlated with our present in the following ways:

(1) Knowledge of our past helps us in deciding our course of action in present. The.heritage of our ancestors exists in tangible and intangible- form. We have the curiosity to know more about our part because they represent the creative thoughts and traditions of that period.

(2) With the help of applied history we can not only come to know about the heritage but also conserve and preserve it.

(3) We can be better equipped to face social challenges in the present because the knowledge of history can provide guidance in finding solutions to contemporary social issues and incorporate them in the ’social planning.

(4) The direction of future development is S decided when we rightly analyse our present with our knowledge of the past acquired through applied history.

(3) Suggest at least 10 solutions for the preservation of the sources of history.
Answer:
There are three types of sources which are used to study history. They are written, oral and material sources. These sources are preserved in different ways. According to me, the following measures should be taken to preserve the sources:

1. A regular repair and maintenance work of forts, memorials and palaces should be carried out. Timely action should be taken to avoid vandalisation of historic and public places.
2. Historical coins, weapons should be handled with precaution and utmost care. They should be kept in a safe place to avoid the possibility of theft.
3. Social awareness regarding the conservation and preservation of our cultural and natural heritage should be created. People will develop affinity towards the heritage and feel connected.
4. Variations in environment and climatic conditions pose a threat to monumental structures. Humidity, dampness, moulds and pollution cause irrevocable damage to manuscripts, rare artefacts, statues, coins, etc.
5. To protect them, special arrangements have to be made like rooms with controlled temperature or sanitising and detoxing the rooms.
6. Oral literature like owis, folk songs should be compiled and written down.
7. Public training programmes should be conducted for understanding the importance of history.
8. Experts from different fields should be involved in preservation and conservation projects. S Stringent laws should be enacted to protect the monuments.
9. Above all, people’s participation in conservation and preservation process is paramount.

(4) What objectives can be fulfilled through the heritage projects.
Answer:
The following objectives can be fulfilled through the heritage projects:

• Preservation, conservation and development of heritage sites can be done without any change in its original state/ structure.
• The local social structure and psychology of the local people, challenges they face in the present situations and their expectations can be surveyed.
• In the process of completing the project of conservation, preservation and development of a heritage site due precaution should be taken to avoid hurting the sentiments of the local people.
• Participation of the local people in the proposed project can be facilitated.
• In order to engage and employ the local skills in a creative way and create better opportunities of livelihood, it becomes easier to design systematic plans.

Project
Show the Indian heritage sites on the map of India.
Answer:

Memory Map

Question 6.
Complete the sentences by choosing the correct option:
(a) ……………………… Institute of Art, Design and Technology at Bengaluru has an independent department named ‘Centre for Public History’.
(a) Pitch
(b) INTACH
(c) Shrushti
(d) AIMS
Answer:
(c) Shrushti

(b) ……………………… is the mother of science and all other branches of knowledge.
(a) Philosophy
(b) History
(c) Technology
(d) Mythology
Answer:
(a) Philosophy

(c) In order to preserve and conserve cultural and natural heritage for the benefit of future generations ……………………… has given directives.
(a) UNICEF
(b) UN
(c) UNESCO
(d) INTACH
Answer:
(c) UNESCO

(d) The ……………………… in the Satara District of the Western Ghats is included in the list of World Natural Heritage.
(a) Balaghat Mountain
(b) Melghat
(c) Masai Plateau
(d) Kas Plateau
Answer:
(d) Kas Plateau

(e) The main office of the National Film Archives of India is situated at ……………………… .
(a) Delhi
(b) Mumbai
(c) Pune
(d) Nagpur
Answer:
(c) Pune

(f) Excavations at the city of ‘Ur’ in Mesopotamia were conducted by ……………………… .
(a) Nathaniel Wallick
(b) Ennigaldi
(c) Leonard Wolley
(d) Sir John Marshall
Answer:
(c) Leonard Wolley.

Question 7.
Identify the wrong pair in the following, and write it:

Answer:
Wrong pair: Ramman – Dance form in West Bengal

(2)

Answer:
Wrong pair: Red Fort – Udaipur

Question 8.
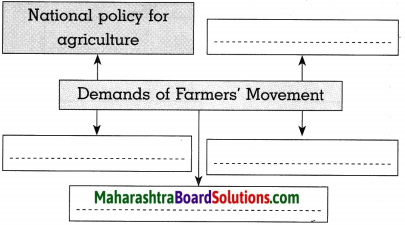
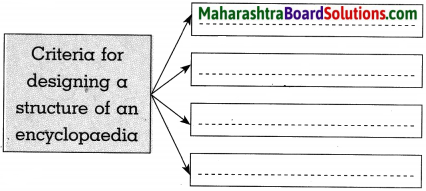
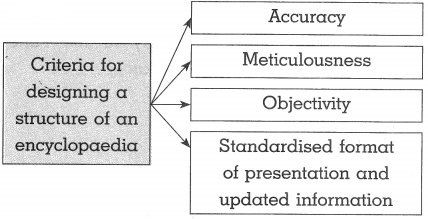
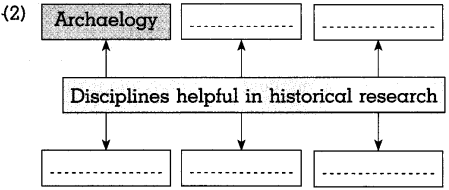
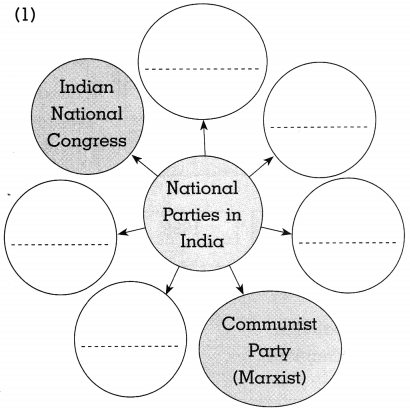
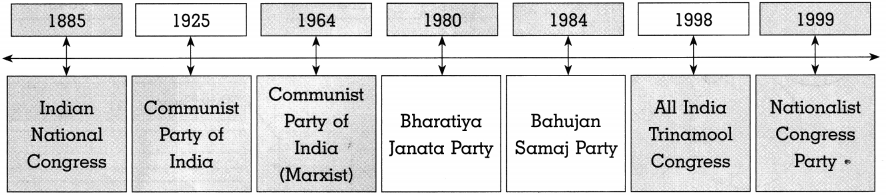
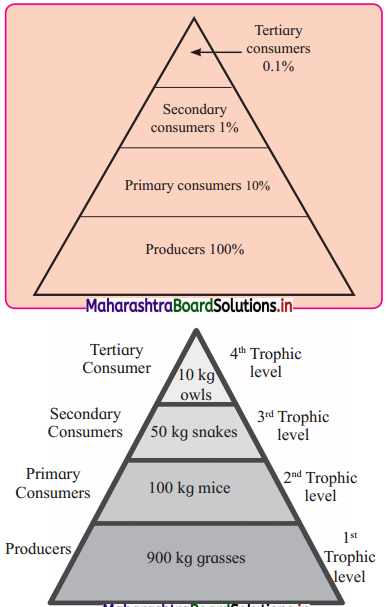
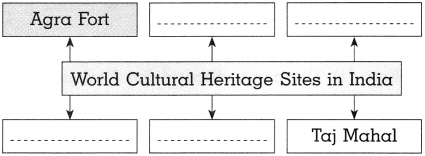
Complete the graphical presentation:
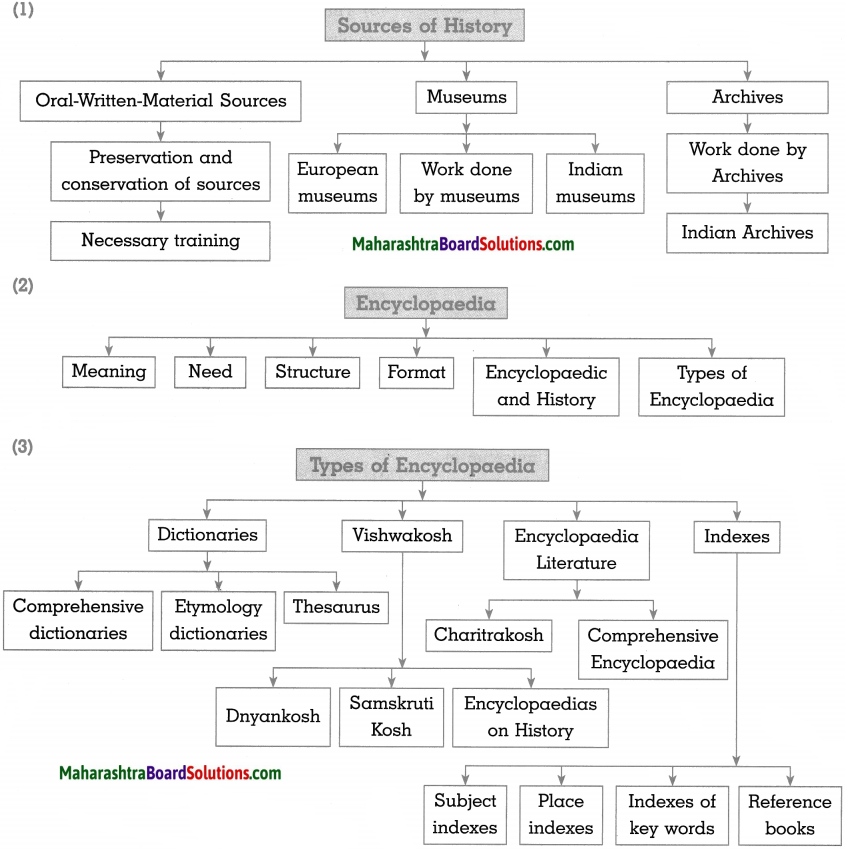
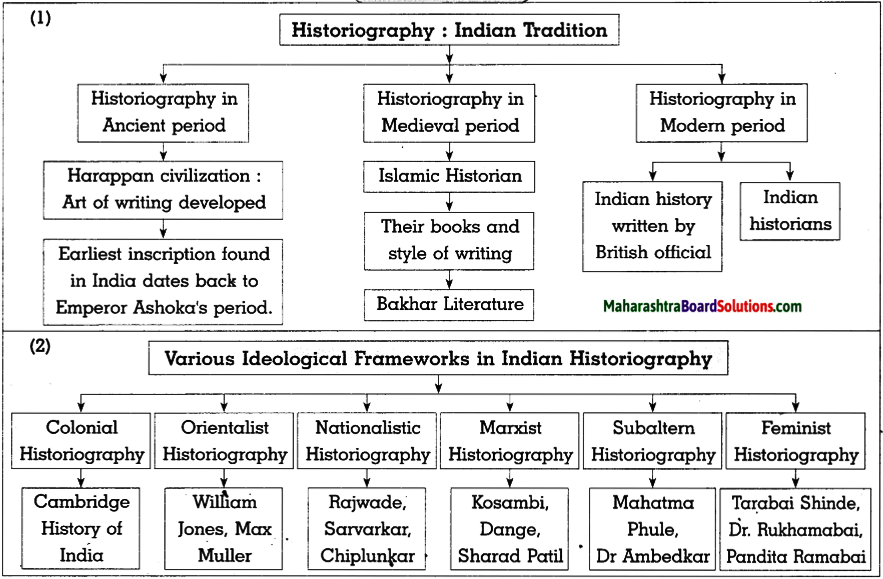
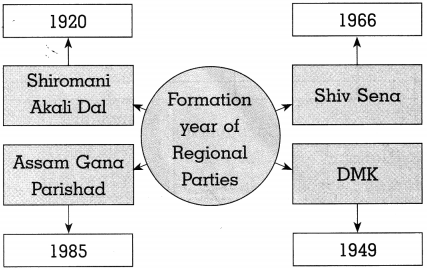
(1)

Answer:

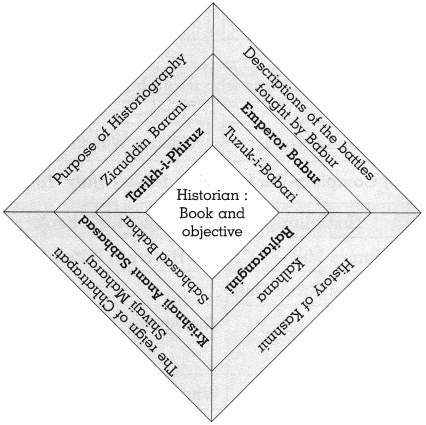
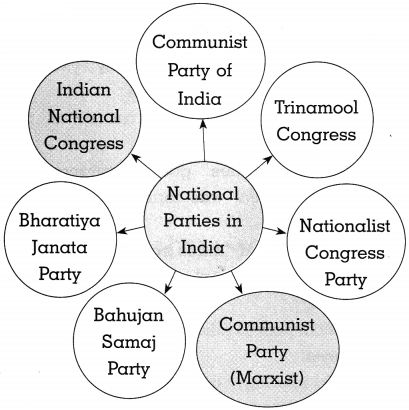
(2)

Answer:

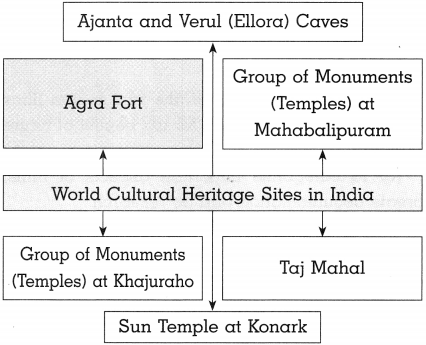
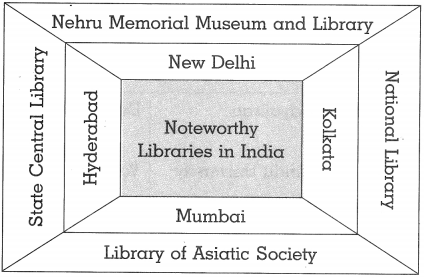
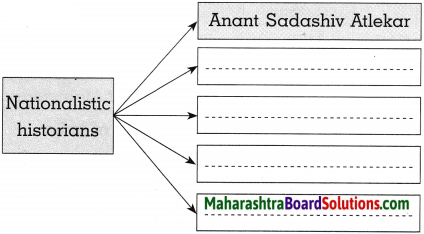
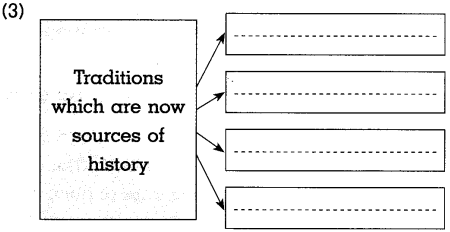
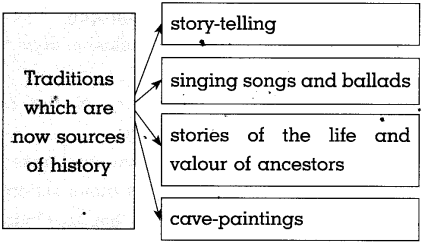
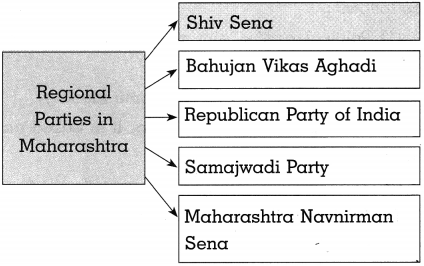
(3)

Answer:

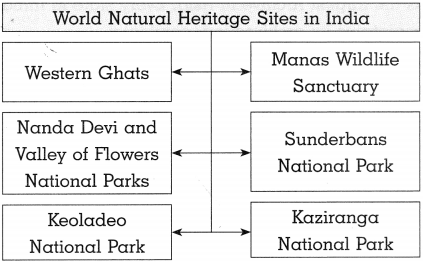
Question 9.
Explain the following concept:
(a) Natural Heritage:
Answer:

• In Cultural heritage what we inherit is man-made but Natural heritage is bestowed upon us by Nature.
• The concept of natural heritage gives importance to the thought of biodiversity.
• The following things are included in natural heritage:
  • Fauna
  • Flora
  • Ecology required for sustaining animal and plant life, flora and fauna of a particular region.
  • Geomorphic characteristics, sanctuaries, mountain ranges, river valleys, lakes and dams are all part of natural heritage.

Question 10.
Write short notes:
(a) Importance of Applied History:
Answer:

• Applied History is a field of study which helps us understand our ancient heritage.
• We realise the importance of preserving our heritage.
• The process of preservation and conservation of tangible and intangible heritage sites generate employment opportunities.
• The study of Applied History help us to get a better understanding of the present and can provide guidance for the future.

(b) Preservation of cultural heritage of India:
Answer:
Conservation and preservation of India’s cultural heritage is done at different levels:

1. Archaeological Survey of India (ASI) is an important body of Indian government which mainly does the work of conservation and preservation along with State Departments of Archaeology.
2. INTACH (Indiqn National Trust for Art and Cultural Heritage) is actively working in this field.
3. Local self-government bodies, social institutions all over India, people who have love for history are seen involved in the work of preservation of our heritage.
4. The work of conservation and preservation of cultural and natural heritage requires participation of experts from various fields as well as local people.

(c) Indian Museum:
Answer:

• The Indian Museum at Kolkata is the oldest museum and one of the important heritage sites of India.
• Nathaniel Wallich, a Danish botanist, founded the museum in 1814 C.E. He was also its first curator.
• The museum has three main departments Arts, Archaeology and Anthropology.
• Other affiliated departments are conservation, publication, photography, exhibition- presentation, model-making, training, library and security.

(d) National Film Archives:
Answer:

• The main office of the National Rim Archives of India is located at Pune and was established in 1964.
• It functions as the Media Unit of the Ministry of Information and Broadcasting of the Indian Government.
• It was established with the view of three objectives. They are:
  • To search and obtain the rare Indian films and preserve our heritage for the benefit of future generations.
  • To categorise important aspects of films, create documentation and do research.
  • To establish a centre for dissemination of ‘films culture’.

Question 11.
Explain the following statements giving reasons:
(a) It is essential to study the history of philosophy.
Answer:

• With the passage of time, many schools of thought came into existence with different ideologies.
• These ideologies had their effect on people and society as a whole.
• What led to the origin of various ideologies, the intellectual tradition giving rise to those ideologies and their historical development needs to be researched.
• To know about the progress of those ideologies, their development and expansion or downfall we need to have knowledge of the history of philosophy.

(b) It is important to know the history of Industry and Commerce.
Answer:

• With the growth of industry and trade, the field of mutual social transactions also expand.
• It promoted development of the network of cultural interactions.
• As the nature of market and commerce changed sp did the nature of human relationships and the social organisation.
• This series of changes is influenced by prevalent culture, social structure and economic system.
• All this is an integral part of the industrial and commercial management.

Therefore, it becomes important to know the history of Industry and Commerce.

(c) It is necessary to preserve and conserve our natural and cultural heritage.
Answer:

• The visible and invisible relics of the past exist in the present.
• They represent the thought and traditions of our ancestors.
• We nurture some kind of curiosity and attraction towards them.
• The history of our heritage links us with our origin.

Therefore, it becomes necessary to preserve and conserve for our future benefit as well as for the benefit of future generations.

Question 12.
Answer the following in 25-30 words:
(a) Explain the concept of ‘Public History’.
Answer:

• Public History also known as ‘Applied History’ is a field of study concerned with the application of history for the benefit of people in the contemporary and future life.
• It provides solutions to the contemporary social issues and incorporate them in social planning.
• It helps to overcome misgivings about history and makes history meaningful in everyday life connecting people to history.

(b) What is the role of UNESCO in the context of heritage sites?
Answer:
The role of UNESCO, the global agency of United Nations, is as follows:

• For preservation and conservation of natural and cultural heritage which is in a ruined state because of years of neglect, UNESCO has announced some directive principles.
• The organisation announces list which includes the names of sites and traditions which meet the criteria.
• On the basis of those directives it declares a list of site and traditions of world heritage.

(c) Find out the cultural heritage sites located in Maharashtra and write their names.
Answer:
The following places in Maharashtra are included in the list of cultural heritage sites declared by UNESCO:

• Ajanta Caves
• Verul (Ellora) Caves and Kailas Temple
• Elephanta Caves
• Chhatrapati Shivaji Maharaj Terminus, Mumbai.

Many forts like the Raigad, Devgiri, Janjira and Sindhudurg are part of the cultural heritage Of Maharashtra though they are not included in the list.

(d) What are the misgivings about history among the people?
Answer:
There are many misgivings about history among the people:

• History is a subject only for historians and students who pursue higher studies in history.
• It has no relevance or applicability in our day-to-day life.
• History is nothing but piece of information about the battles fought by kings and politics.
• History cannot be connected to an economically productive field.

(e) Where can we trace the roots of philosophy?
Answer:

• Ancient people all over the world tried to speculate the relationship between the universe and human existence.
• This gave rise to various myths about origin of this world, universal order, human life.
• Imagination about gods and goddesses, rituals to please them and philosophical explanation of rituals.
• Thus, the roots of philosophy can be traced in these speculations and ponderings of mythological stories.

(f) What are the opportunities created by affiliated professional fields of Applied History?
Answer:
Affiliated fields of Applied History which include museums, archives, tourism ‘and hospitality, entertainment, mass media, etc. needs the following professionals:

• Experts like Historians, Archaeologists, Sociologists, legal experts, etc. are assigned new projects.
• Officers like Managers, Secretaries and Directors are taken into service.
• Technicians like engineers, architects, skilled photographers, laboratory assistants, archive management professionals are hired.
• Tourist guides, boarding and lodging, food services, entertainment and related business get a wide scope for flourishing.

(g) What are the main objectives of ‘National Film Archives’?
Answer:
The main objectives of ‘National Rim Archives’ are as follows:

• To research and obtain the rare Indian films.
• To preserve such films for the benefit of future generations.
• To categorise the important aspects of films to create documentation, catalogue them -and carry out research in the field.
• To establish a centre for dissemination of films culture.

(h) How can we increase people’s participation in the field of applied history?
Answer:

• The field of applied history includes museums, archives, collection and maintenance of artefacts.
• Tourism creates interest in history.
• Awareness is created among people to preserve ancient monuments and sites in their vicinity.
• This realisation increases people’s participation in the field of applied history.

(i) Write information on World Heritage sites in Maharashtra.
Answer:
Maharashtra is endowed with many natural and historical sites. Among them the prominent ones are Ajanta caves, Verul caves, Gharapuri/Elephanta caves and Chhatrapati Shivaji Maharaj Terminus Railway Station at Mumbai.

Chhatrapati Shivaji Maharaj Terminus is finest example of Indo-Gothic architecture emerged in India during British rule. It stands witness to the British empire, freedom struggle and transformation of our country into a modern nation. It needs conservation as it a architectural marvel which stood the test of times recently when there was a terror attack on Mumbai city.

(j) What is the role of Applied History?
Answer:
The role of Applied History is as follows:

• In public training programmes for understanding the importance of history.
• Using knowledge of history, to create awareness regarding the conservation and preservation of our cultural and natural heritage.
• To facilitate participation of people in various projects and programmes related to applied history even in their capacity as tourists.
• To enhance professional skills of people and to develop industrial commercial field.
• To carry out preparatory work and plan for effective implementation of heritage projects.

Question 13.
Read the given passage carefully and answer the questions given below:
(a) Who built this museum?
Answer:
This museum was built by Ennigaldi, the princess of Mesopotamia.

(b) Where was the earliest museum in the world discovered? Who discovered it?
Answer:
The earliest museum in the world was discovered in the city of ‘Ur’ in Mesopotamia. It was discovered by Leonard Woolley.

(c) What is a noteworthy feature of this museum?
Answer:
A noteworthy feature of this museum is the clay tablets inscribed with the descriptions of exhibited artefacts.

Question 14.
Write elaborate answers: OR Answer in detail:
(a) Who does the work of conservation and preservation of the cultural heritage of Indian?
Answer:
The preservation and conservation of Indian cultural heritage is done at various stages:

• The work of preservation and conservation primarily falls under jurisdiction of the Archaeological Survey of India.
• In addition, INTACH (Indian National Trust for Art and Cultural Heritage) is also actively working .in this field.
• Experts from various fields and local people too participate in the work of conservation and preservation of natural and cultural heritage.

Question 15.
Observe the picture and write information about it:

Answer:

• This picture is of the largest Indian rock-cut ancient Hindu temple located in the Ellora cave.
• This famous rock-cut Shiva temple was constructed during the reign of Rashtrakuta king Krishna I.
• It is regarded as a marvel of architecture.
• It bears an eloquent testimony to the high level skill attained by India in the arts of sculpture and architecture under the Rashtrakuta patronage.
• A sculpture of an elephant and a pillar can be seen in the picture.
• The famous rock cut temple in Maharashtra was declared as a world heritage site by UNESCO in 1983.

Brain Teaser

Hints:
Across:
(1) Queen’s stepwell at Patan
(2) Dancing, singing, drumming ritual of Manipur
(3) Religious festival and ritual theatre of Garhwal
(4) Archaeological site of Nalanda University
(5) World famous monument at Agra
(6) Famous city built by emperor Akbar marking his victory
(7) Sanskrit Theatre: Kerala

Down:
(1) The traditional performance of Ramayan in Uttar Pradesh
(2) Ellora caves also known as caves
(3) Observatory at Jaipur, Rajasthan
(4) Group of monuments at (place) in Karnataka
(5) Archaeological park at Pavagadh
(6) Folk songs and dances of Rajasthan
(7) A ritual theatre of Kerala

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Balbharti Maharashtra State Board Class 10 Political Science Solutions Chapter 4 Social and Political Movements Notes, Textbook Exercise Important Questions and Answers.

Std 10 Political Science Chapter 4 Question Answer Social and Political Movements Maharashtra Board

Maharashtra State Board Class 10 Political Science Solutions Chapter 4 Social and Political Movements

Political Science Class 10 Chapter 4 Question Answer Maharashtra Board

Question 1.
Choose the correct option from the given options and complete the sentences.
(1) ………………………….. is the main demand of farmers movement.
(a) Right to cultivate on the forest land
(b) To get the right price for agricultural product
(c) Protection of consumers
(d) Building of dams
Answer:
(b) To get the right price for agricultural products

(2) To increase agricultural production and become self-sufficient with regard to food grains ………………………….. was initiated.
(a) Water revolution
(b) Green revolution
(c) Industrial revolution
(d) White revolution
Answer:
(b) Green revolution

Question 2.
Explain the concepts.
(1) Tribal movement
Answer:

• Tribal community was always dependent on forest wealth for their living.
• The British had prohibited the tribals from making use of forest wealth to earn their livelihõod
• Kolam, Gond, Santhal, Koli, Bhilla, Munda Tribals of different parts of India revolted against the British.
• Even after independence their problem to earn a livelihood is not solved. Their right on the forest land, to gather forest products and to cultivate on forest land is not yet recognised.

Therefore, for these demands, Tribal Movement is active in many parts.

(2) Labour movement
Answer:

• Industries in public and private sector like textile mills, railway companies started in India in the latter part of the nineteenth century.
• Due to industrialisction, a large number’ of labour force came into existence.
• Thiš led to lot of labour issues. In 1920, All India Trade Union. Congress was established to solve their problems.
• Many unions were formed after independence. The Trade Union Movement was very effective from 1960 tifi 1980s.
• After 1980s trade union movement lost its momentum and slowly disintegrated. Globalization gave a final blow to the movement.

Question 3.
Answer the following questions in brief.
(1) Explain the activities/role/functions of environmental movement.
Answer:
(i) Role : The environment movement rias played a key role in –

• Creating public awareness about the importance of balance in environment through television, newspapers, and other mediums.
• Opposing developmental projects with environmental concerns.

(ii) Functions : The function of the environment movement is to make efforts silently or rigorously to protect natural areas through afforestation, recycling or pollution control. Forest department and the pollution board are actively involved and extend support by making stringent laws to book the culprits.

(iii) Activities : Different activities are conducted to promote the environment movement:

• Environmental degradation has become a serious issue not only in India but also in the world.
• The issues of degradation was discussed at. Rio-de-Janeiro, Paris and Kyoto Conferences.
• Even in India many movements are active for conservation of the environment like the Chipko movement, Appiko movement ana Vanmahatsov.

(2) Explain the nature of farmers movement in India.
Answer:

1. The Indian farmers organised themselves in pre-independence era to fight against the anti-agricultural policies of the colonial British rulers.
2. The farmers were inspired by the thoughts of Mahatma Phule, Justice Ranade and Mahatma Gandhi. They organised satyagraha against revenue collection in Bardoli and Champaranya.
3. Farmers’ movement slowed down because of tenancy laws under land reforms. Green revolution failed to improve conditions of the poor farmers.
4. Farmers’ movement gained momentum with demands like, appropriate price for agricultural products, debt relief and debt cancellation after recommendations from Swaminathan Commission.

(3) For which reforms were the women’s movement in the pre-independence period fighting?
Answer:
In the pre-independence period women’s movement were working for the following reforms :

• Eliminating injustice against women.
• To put an end to the exploitation of women and help them lead a respectful and dignified life.
• They should be able to participate actively in social life.
• To end the practices like Sati, child marriage, polygamy and bring about reforms such as widow remarriage and women’s education.

Question 4.
State wheather the following statements are true or false. Give reasons for your answer.
(1) Movements are important in a democracy.
Answer:
The above statement is True.

• People organise themselves and start a movement to solve social issues.
• Leaders and activists provide all the information regarding those issues to the government.
• The government takes, notice of the problems because of the movement.
• Some movements aim at opposing some policies of the government and certain decisions. This is the most recognised method of protest in democracy.

Hence, movements have great importance in democracy

(2) Movements do not need a strong leadership.
Answer:
The above statement is False.

• The success of any movement depends on leadership. The movement remains active because of the strong leader.
• The decisions regarding the objective of the movement, programme of action, strategy of agitation are decided and taken by the leader.
• Firm leadership has a wide reach. They can get public support making the movement very effective. So, the need of a strong leadership is utmost essential.

(3) Consumer movement came into existence.
Answer:
The above statement is True.

• The consumers faced different problems because of changing economy and social system.
• Adulteration increased the cost of products and faulty weights and measures are some of the problems faced by the consumers.
• To protect the consumers from such frauds the Consumer Protection Act was passed in 1986.
• The Consumer Protection movement was started to create awareness among the consumers about their rights and their safety.

Project
(1) Collect the news in the newspapers about various activities of social movements.
(2) Write a report on movements in your area which are working to resolve general problems.
(3) Prepare a format of a complaint you will submit under consumer protection act if you are cheated in purchase of vegetables or grains
Answer:

Memory Map

Question 5.
Choose the correct option from the given options and complete the sentences :
(a) In …………………., movements have more importance.
(a) socialist rule
(b) dictatorship
(c) democracy
(d) communist rule
Answer:
(c) democracy

(b) In democracy, Right to …………………. is considered an important right.
(a) rehabilitate
(b) pursue questions
(c) behave with control and responsibility
(d) protest
Answer:
(d) protest

(c) is the objective of Green Revolution.
(a) To stop degradation of environment
(b) Protection of the forests
(c) Increase in agricultural output
(d) To stop the felling of trees.
Answer:
(c) Increase in agricultural output.

(d) The trade union movement in India has background of ………………… .
(a) freedom struggle
(b) globalisation
(c) prestigious past
(d) industrialisation
Answer:
(d) industrialisation

(e) In 1899, …………………. workers called for a strike.
(a) railway
(b) mill
(c) handloom
(d) rice mill
Answer:
(a) railway

(f) Dr. Rajendrasinh Rana had brought about …………………. in Rajasthan.
(a) White Revolution
(b) Water Revolution
(c) Green Revolution
(d) Consumer Revolution
Answer:
(b) Water Revolution

(g) Dr. Rajendrasinh Rana is known as the …………………. of India.
(a) Farmer man
(b) environment affectionate
(c) Man of the Millennium
(d) Waterman
Answer:
(d) Waterman

(h) Tribals in Bihar revolted against the British under the leadership of ………………… .
(a) Rajendrasinh Rana
(b) Birsa Munda
(c) Umaji Naik
(d) Kajarsingh
Answer:
(b) Birsa Munda.

(i) Swadeshi movement is an important …………………. movement.
(a) political
(b) social
(c) economic
(d) cultural
Answer:
(c) economic

(j) …………………. is one of the problems faced by consumers.
(a) Cancellation
(b) Malnutrition
(c) Adulteration
(d) Transportation
Answer:
(c) Adulteration

(k) The main demand of the farmer’s movement was to accept suggestions of the …………………. Commission.
(a) Sunderlal Bahuguna
(b) Verghese Kurien
(c) Swaminathan
(d) Kothari
Answer:
(c) Swaminathan

(l) In 1986, …………………. Act came into force.
(a) Consumer Protection
(b) Women Empowerment
(c) Child Marriage
(d) Environment Protection
Answer:
(a) Consumer Protection

(m) The post-1980 movements are called ………………… .
(a) New
(b) Neo-social
(c) Broad
(d) Globalisation
Answer:
(b) Neo-social

(n) …………………. was established in 1920.
(a) Farmer’s Organization
(b) Bhartiya Kisan Union
(c) All India Trade Union Congress
(d) All India Kisan Sabha
Answer:
(d) All India Trade Union Congress.

Question 6.
Explain the following statements by giving reasons :
(a) Political parties can concentrate on one particular issue.
Answer:
The above statement is False.

• Political parties contest elections to solve problems of common people.
• Parties have to take into consideration all matters from public cleanliness to roads to space research. They have to have a national perspective and take decisions.
• Political parties should have programmes for the development of all the sections of society like youth, senior citizens, businessmen, women, farmers and labourers.
• This – means that political parties cannot concentrate on just one particular issue.

(b) People’s active participation is expected in the movement.
Answer:
The above statement is True.

• A. movement is started to solve issues of public interest.
• People offer support to the movements which are related to their cause or a particular issue.
• Deciding upon the issues of the people a programme is decided and a group is formed.

(c) Dr. Rajendrasinh Rana is called the Waterman of India.
Answer:
The above statement is True.

• Dr. Rajendrashinh Rana built thousands of ‘Johads’ in Rajasthan.
• He revived many rivers in the desert region of Rajasthan.
• He formed an organisation – “Tarun Bharat Sangh” which built eleven thousand Johads to harvest water. .
• He started a campaign for Water conservation, revival of rivers, forest conservation and wildlife conservation.
• He worked continuously for this cause for 31 years building 11 thousand johads bringing about water revolution in Rajasthan. Therefore, is called the Waterman of India.

Question 7.
Explain the concept :
(a) Movement:
Answer:

1. When people organise themselves to resolve a certain issue it is called a movement.
2. Movements increase the participation of people in social life.
3. Movements are for public welfare and to solve issues. The aim of any movement is not only to pressurize the government but also to oppose its decision or policies.
4. A movement is started for different reasons like religious, social, cúltural, protection of the environment, ill practices and traditions.

(b) Public Interest Litigation:
Answer:

1. A litigation is filed if an individual or group feels that fundamental rights which are enshrined in the Constitution are undermined by the government.
2. To safeguard human rights, citizens can file a litigation in High Court or Supreme Court. Such a litigation is known as Public Interest Litigation.
3. Public Interest Litigation is filed for problems such as pollution, government avoiding public works and for social problems such as violence, discrimination and ostracising someone.
4. It is the most effective way of seeking justice.

(c) Environment Movement :
Answer:

• Different activities are conducted to promote the environment movement in India.
• Environment degradation has become a serious issue not only in India but also all over the world.
• The issues of degradation were discussed at Rio-de-Janeiro, Paris and Kyoto Conferences.
• Even in India many movements are active for conservation of the environment like the Chipko movement, Appika movement and Vanmahatsov.

Question 8.
(A) Complete the graphical representation :

(1)

Answer:

(2)

Answer:

(3)

Answer:

(4)

Answer:

(B) Explain the events in Trade Union Movement:

Answer:

Question 9.
Answer the following questions in brief:
(a) Explain the features of a movement.
Answer:

• A movement is a collective action which has active participation or support of the people.
• People take up a particular issue and organise themselves.
• A movement requires strong leadership. A strong leader makes the movement effective.
• If people feel connected to the issue, then they extend their support to the movement.

(b) What are the demands of Trade Union Movement?
Answer:
The Trade Uniin Movement makes demands regarding following issues :

• Contract labour and unstable employment..
• financial insecurity and unfavourable conditions at workplace.
• Unlimited working hours and health hazards.
• No protection of labour laws.

(c) How did the objectives of women’s movement change after independence?
Answer:

1. In the pre-independence era the aim of the women’s movement was to put an end to the unjust practices against women and end their exploitation.
2. After independence, the aim of their movement changed because they realised that though the Constitution had given equal rights both to men and women in practice they were never considered equal.
3. The objective of the women’s movement was to achieve freedom in real sense, i.e. they should be treated as human beings and should get equal rights and to live a dignified life.

(d) Which issues were taken up by the women’s movement after independence?
Answer:
Many issues were taken up by the women’s movement for welfare of the women after independence. Some are:

• Health and education of women
• financial independence
• Social security
• To be treated as human beings and have a status and prestige.

(e) Which issues are handled through movements?
Answer:
Movements arise out of public issues, which could be social, political, economic and religious.

1. To protect the rights of the citizens like voting, freedom and for similar issues, political movements are organised.
2. financial security, minimum wages, employment, insistence on an indigenous product are the reasons for economic movement.
3. Social and religious movements are organized to eliminate ill practices like untouchability, entry of women in temples,’ discrimination and social issues.
4. Movements are organised to raise voice against injustice done to a particular region, language and for issues like cleanliness, environment and movements for development like Green revolution and White resolution.

(f) Which movements started in India are actively working for rehabilitation of the displaced and to secure their livelihood?
Answer:
People who got displaced started this movement for different reasons. Some movements lasted for short time while some lasted long.

• “Narmada Bachao Andolan” was a popular movement.
• People living in Maharashtra and Gujarat continued it for 28 years.
• People in the Sindhudurg district who got displaced due to the Talamba dam started movement for rehabilitation. It lasted for 32 years.
• Farmers who got displaced because of Pune-Nagpur highway or for the planned Purandar airport launched movements on a large scale. Such movements are going on all over India.

(g) Name the policies started by the government for the welfare of farmers and landless labourers?
Answer:
The government has started the following policies for the welfare of the farmers and landless labourers :

• National agriculture policy
• Crop insurance scheme (FASAL Bima Yojana)
• Jalyukt Shivar
• Indira Gandhi Niradhar (old), landless, destitute women farm labour scheme.
• Neem Coated Urea.
• Name the policies started by the government for the welfare of farmers and landless labourers.

(h) Name the movements started by Mahatma Gandhi, Mahatma Phule, Sant Gadge Maharaj and Dr. Babasaheb Ambedkar.
Answer:

• Mahatma Phule laid the foundation of the movement for education of women and social equality.
• To stop the practice of widow tonsure he called for a strike of barbers in Mumbai.
• Mahatma Gandhi adopted the technique of satyagraha and started the movement for farmers in Champaranya and Kheda.
• He also started the Non-cooperation Movement and Civil Disobedience Movement..
• Sant Gadge Maharaj started the cleanliness campaign.
• Dr. Babashaeb Ambedkar launched satyagraha to allow untouchables to use water from a public tank in Mahad..
• He also led the movement in Nashik for Dalits so that they could get entry into the Kalaram temple.

(i) All movements have ideologies. (Discuss : Textbook page 92)
Answer:

• Even though movements are launched for social welfare there is always an ideology behind every movement.
• The scope of movements against child marriage or dowry prohibition is not limited to oppose the social evil practice but have wider aim of social reformation.
• The movements started against female foeticide ‘Beti Bachao Beti Padhav’, violence against women and to empower women had objectives to achieve equal social status for women and their protection.
• Movements like cleanliness campaign, Chipko Andolan, Save Trees aim not only at environment protection but also aim at saving humanity.
• These movements have faith in democratic values like equality and brotherhood and humanity. This shows all movements have ideologies.
• Generally the movements are devoted to one particular issue but have an ideology behind them.
• For example movements against child marriage, dowry believe in values of democracy, women empowerment and social equality.
• Sometimes some movements gradually get transformed into political parties.

Question 10.
Give your opinion :
(a) Do you think, if all the movements co-ordinate with each other, the result will be more effective?
Answer:

• Our society has witnessed many movements from pre-independence times.
• If all these movements co-ordinate with each other they will be definitely, effective.
• With each other’s cooperation they can work together to find the root cause of the problem and also find a solution.
• The manpower will not get divided. The work will get divided and that would save time and energy to a great extent.
• The movement will be more effective.

(a) On which issues does the ‘Sons of the Soil’ movement in India insist? (Discuss : Textbook page 93)
Answer:
People migrate for various reasons within the country. They create lot of problems in their newly adopted homeland which give rise to the ‘Sons of the Soil’ movement. The main reasons for the movement are :

• Sons of the Soil, i.e. local people lose out on employment opportunities.
• They are deprived of their jobs.
• Their land is confiscated.
• Housing becomes expensive.
• The migrants pose a threat to the language and culture of local people.
• Sons of the Soil lose economic monopoly as well as political influence.

10th Std Political Science Questions And Answers:

• Chapter 1 Working of the Constitution Class 10 Political Science Questions And Answers
• Chapter 2 The Electoral Process Class 10 Political Science Questions And Answers
• Chapter 3 Political Parties Class 10 Political Science Questions And Answers
• Chapter 4 Social and Political Movements Class 10 Political Science Questions And Answers
• Chapter 5 Challenges faced by Indian Democracy Class 10 Political Science Questions And Answers

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 9 Heritage Management Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 9 Question Answer Heritage Management Maharashtra Board

Class 10 History Chapter 9 Heritage Management Question Answer Maharashtra Board

History Class 10 Chapter 9 Question Answer Maharashtra Board

Question 1.
(A) Choose the correct option from the given options and complete the statement.
(1) Lovre Museum has in its collection the much-acclaimed painting of …………..…….. by Leonardo da Vinci.
(a) Napoleon
(b) Mona Lisa
(c) Hans Sloan
(d) George II
Answer:
(b) Mona Lisa

(2) …………..…….. at Kolkata is the first museum in India.
(a) Government Museum
(b) National Museum
(c) Chhatrapati Shivaji Maharaj Vastusangrahalay
(d) Indian Museum
Answer:
(d) Indian Museum

(B) Identify and write the wrong pair in the following set.
(1) Maharaja Sayajirao University – Delhi
(2) Banaras Hindu University – Varanasi
(3) Aligarh Muslim University – Aligarh
(4) Jivaji University – Gwalior
Answer:
(1) Wrong Pair: Maharaja Sayajirao University – Delhi

Question 2.
Explain the following statements with reasons.
(1) Archives and libraries publish research journals, informative pamphlets, leaflets, posters, etc.
Answer:

• Libraries preserve and conserve old’ books and artefacts discovered during excavation.
• If these documents and artefacts are not exhibited then they are kept in archives.
• All the historical sources are our assets and they should reach the people.
• Libraries not only preserve these documents but also carry out research, to know the authenticity.

In order to make the historical events, personalities, and historical research known to the people, archives and libraries publish research journals, informative pamphlets and leaflets.

(2) Only trained persons, who are duly qualified can take up the tasks involved in the work of conservation and preservation.
Answer:

1. While conducting historical research, one has to do the different tasks carefully like collecting sources, preserving, exhibiting, etc.
2. The skill required for every task is different. The procedure followed for each task is different as well as the preliminary preparations.
3. It is essential to know about precautions to be taken.
4. Hence only trained persons who are duly qualified can take up the tasks involved in the work of conservation and preservation.

Question 3.
Write notes:
(1) Sthalakosh
Answer:

• History does not shape itself in oblivion. It takes place at some place.
• Geographic information is essential to study history.
• Chakradhar Swami, of Mahanubav sect, visited many villages and details of those villages were noted by Muni Vyas.
• Siddheshwarshastri Chitrav wrote Prachin Bharatiya Sthalkosh. It gives us information on various places mentioned in Vedic literature, Kautiliya’s Arthashastra, Panini’s Grammar, Ramayana.
• Mahabharata and also in Buddhist Jain Greek, Chinese and Persian literature.
• Sthalakosh gives us information on ancient cities and history of those cities. It serves as an important written source of history.

(2) Vishwakosh
Answer:

• The first Chief Minister of Maharashtra, Shri Yashwantrao Chavan, established the ‘Maharashtra Rajya Sahitya Samskruti Mandal.
• The objective of making Vishwakosh was to develop and enhance Marathi language and literature.
• Tarkteerth Lakshmanshastri Joshi was appointed as the chief editor. 20 volumes of Vishwakosh are published till date.
• Marathi Vishwakosh contains knowledge about all possible subjects which exist in the world. It has important entries about history.

(3) Samdnya Kosh
Answer:

1. While studying any subject we come across many new words. If their exact meaning is not understood, it can create a lot of confusion.
2. Terms in history like colonialism, imperialism, liberalisation, globalisation, socialism, communism need explanation and clarity. In order to avoid such confusions, this kosh is prepared.
3. In Samdnya Kosh, all subject related concepts are collected and explained. Information on what led to the development of concepts is provided.
4. Samdnya Kosh is very helpful for research students, teachers of history as well as common people.

(4) Saraswati Mahal Granthalay
Answer:

• The Saraswati Mahal Granthalay was built in 16-17th century in Tanjavur, Tamil Nadu during the reign of Nayak Dynasty.
• In 1675, Maharaj Vyankojiraje Bhosale conquered ‘ Thanjavur and established his independent rule. He and his successors contributed to the expansion of this library. ‘
• Sarfojiraje Bhosale contributed the most in expanding and enriching the library. Because of his contribution, to honour him, the library was renamed as ‘The Thanjavur Maharaj Sarfoji’s Saraswati Mahal Library’.

Question 4.
Give elaborate answers to the following.
(1) Why is library management important?
Answer:
Library is not just about a collection of books but managing it is equally important.

• Readers can easily get the books they want if the library is properly organised.
• The location of the book should be easily traced. It saves the time and efforts of readers as well as the librarian.
• Preservation and conservation of books is done effectively with proper management. It prolongs life of books and causes less damage.
• If the management is well acquainted, they will have good collection that will make available good quality books to reader.
• Instead of collecting books on one subject there should be variety in the collection so as to cater of different readers who are very selective in their choices.
• Facilities like proper catalogues, indexes, computerised systems and modern facilities are provided by effective management of library.
• If the management is creative it will organise exhibitions, advertise, have seasonal offers for vacations, conduct competitions to increase membership.

(2) Which tasks are important in archives management?
Answer:
The following tasks are important in archives’ management:

• Important documents to be preserved and care should be taken that document with important contents are preserved in their original condition. Confidentiality of important papers should be maintained.
• To classify the documents by preparing indexes and to create accurate systems of retrieval of documents.
• Documents from the archives are supposed to be very reliable.
• Therefore, it is important to safeguard the papers from humidity, fungus and other environmental factors.
• It is important to remain updated with latest technology in archive management.
• Computerise/Digitalse all systems. To make use of information technology in managing libraries and archives.
• To establish regional and local archives*.
• To preserve national, cultural and historical heritage.
• To create a hasslefree system.

Question 5.
Complete the following Concept chart.

Answer:

Project
Obtain information about the important libraries in Maharashtra. Visit the library in your vicinity and learn about its functioning.

Question 6.
Complete the sentences by choosing the correct option:
(a) Documents and artefacts which are not exhibited are kept in …………………… .
(a) Museum
(b) Library
(c) Archives
(d) Government office
Answer:
(c) Archives

(b) ……………………. was the 16th century artist who worked under the patronage of French King Francis I.
(a) Leonardo-da-Vinci
(b) Michaelangelo
(c) Raphael
(d) Dante
Answer:
(a) Leonardo-da-Vinci

(c) The collection in ……………………. increased to a great extent because of the antiquities brought by Napoleon Bonaparte.
(a) National Museum of Natural History
(b) British Museum
(c) Louvre Museum
(d) The Calico Museum
Answer:
(c) Louvre Museum.

(d) ……………………., a natural scientist handed over about 71 thousand objects in his collection to the British Museum.
(a) Sir Hans Sloan
(b) King George II
(c) Napoleon Bonaparte
(d) King Francis I
Answer:
(a) Sir Hans Sloan

(e) The Museum of Natural History which 8 houses more than 12 crore specimens of fossils is in ……………………. .
(a) England
(b) France
(c) Switzerland
(d) USA.
Answer:
(d) USA

(f) Chhatrapati Shivaji Maharaj Vastu-sangrahalay was built to commemorate the visit of ……………………. .
(a) King George I
(b) Queen Elizabeth
(c) Prince Charles
(d) Prince of Wales
Answer:
(c) Prince of Wales

(g) The building of Chhatrapati Shivaji Maharaj Vastusangrahalay is built in ……………………. style.
(a) Mughal
(b) Indo-Greek
(c) Indo-Gothic
(d) Indo-Persian
Answer:
(c) Indo-Gothic

(h) ……………………. is given status of Grade I heritage building in Mumbai.
(a) Chhatrapati Shivaji Maharaj Railway Terminus
(b) Chhatrapati Shivaji Maharaj Vastusangrahalay
(c) Reserve Bank of India
(d) Jehangir Art Gallery
Answer:
(b) Chhatrapati Shivaji Maharaj Vastusangrahalay.

(i) The Royal Library of Ashurbanipal, the ……………………….. Emperor in Mesopotamia is one of the earliest libraries in the world.
(a) Hispanic
(b) Assyrian
(c) Mongol
(d) Akkadian
Answer:
(b) Assyrian

(j) The ……………………….. in Thanjavur, Tamil Nadu was built in 16th-17th century during the times of Nayak dynasty.
(a) Vyankojiraje Bhosale
(b) Sarfojiraje Bhosale
(c) Saraswati Mahal Granthalay
(d) Vidya Niketan
Answer:
(c) Saraswati Mahal Granthalay

(k) The first official archives of India, the ……………………….. was established in 1891 C.E. in Kolkata.
(a) National Archive
(b) Federal Record of Nation
(c) Archive National
(d) Imperial Record Department
Answer:
(d) Imperial Record Department

(l) There are about five crore Modi documents related to Maratha history in the Pune branch which are referred as ………………………. .
(a) Peshwa Daftar
(b) Bhosale Daftar
(c) British Daftar
(d) Maratha Daftar
Answer:
(a) Peshwa Daftar

(m) ……………………….. prepared during the reign of Chhatrapati Shivaji Maharaj is considered as an important encyclopaedia.
(a) Bharatiya Vyavahar Kosh
(b) Rajavyavaharkosh
(c) Vyavaharik Kosh
(d) Bharatiya Prachin Charitrakosh
Answer:
(b) Rajavyavaharkosh.

Question 7.
Identify the wrong pair in the following and write it:
(1)

Answer:
Wrong Pair: Maharaj Sayajirao University – Delhi.

(2)

Answer:
Wrong Pair: Bharatvarshiya Prachin Aitihasik Kosh – Shridhar Vyankatesh Ketkar

(3)

Answer:
Wrong Pair: Marathi Vishwakosh – Raghunath Bhaskar Godbole

(4)

Answer:
Wrong Pair: First Encyclopaedia of Natural History – Denis Diderot

Question 8.
Complete the following concept chart:
(1)

Answer:

(2)

Answer:

(3)

Answer:

Question 9.
Explain the concept :

(a) Archives:
Answer:

1. An archive is a place where documents with important content in their original conditions are preserved in a scientific manner.
2. Artefacts and documents which are not exhibited in museums or libraries but have historical importance are kept in archives.
3. Archives provide documents to the § government, research students and local public when required. Technically, the management of archives is akin to library management.
4. The documents in the archives are preserved in their original condition and hence no changes can be made to it. Documents from archives are very reliable.

(b) Encyclopaedia:
Answer:

1. Encyclopaedia can be defined as a systematic compilation of words with meaning, information or knowledge on various topics.
2. A specific method is adopted to compile the information or to organise the available knowledge. g
3. Accuracy, meticulousness, objectivity, standardised format of presentation and updated information are the special features of good encyclopaedia.
4. The objective of making an encyclopaedia is to make the available knowledge easily accessible to the readers.

(c) Dictionaries:
Answer:

• A type of encyclopaedia giving word meaning arranged in alphabetical order is a Dictionary.
• Dictionaries help the readers to know meaning of the words and enrich their vocabulary.
• Dictionaries have word meanings, synonyms and etymology.
• Dictionaries are of various type like comprehensive dictionaries, dictionaries of terminology, etymology, thesaurus and dictionaries of idioms and proverbs.

(d) Comprehensive Encyclopaedia (Vishwakosh):
Answer:

• Comprehensive Encyclopaedia (Vishwakosh) means a book which has information on all subjects known, i.e. all subjects under the sun.
• Vishwakosh is an important medium” of documenting and disseminating information.
• The information is included in encyclopaedia after thorough research and study.
• (a) There are two types of encydopaedias – one that includes all subjects like ‘Encyclopaedia Britannica’, Maharashtriya Dnyankosh, Marathi Vishvakosh.
  (b) The other type of encyclopaedia includes comprehensive information on one chosen subject, e.g. Bharatiya Samskruti Kosh, ‘Vyayam Dnyankosh1.

(e) Index:
Answer:

• Index means a list.
• Index is at the end of a book which includes alphabetical lists of individuals, subjects, key words, reference books, etc.
• As the list is in alphabetical order, the reader finds it easy to access required information.
• The index of Marathi periodicals prepared by S. G. Date and index of ‘Marathyancha Itihasachi Sadhane1 is well-known.

(f) Charitrakosh (Encyclopaedia of Biographies):
Answer:

1. Charitrakosh contained biographies of individuals who lived in a particular period and their work which inspired and motivated all the people in the society.
2. Charitrakosh enables the researcher and scholars to know about the historic period, with regard to social structure and social life.
3. Bharatvarshiya Prachin Aitihasik Kosh written by Raghunath Bhaskar Godbole is the earliest encyclopaedia of this kind.

(g) Bharatiya Samskruti Kosh:
Answer:

• It contains the description of Indian history, geography, religions, sects, culture, traditions, beliefs, ethnic and lingual groups residing in our country.
• Bharatiya Samskruti Kosh throws light on, people living in a particular region, festivals and their culture.
• Mahadevshastri Joshi edited and published 10 volumes of this Kosh.
• Chakradhar Swami, of Mahanubav sect, visited many villages and details of those villages were noted by Muni Vyas.

Question 10.
Write short notes:
(a) Louvre Museum:
Answer:

• The Louvre Museum in Paris was established in the 18th century.
• It has antiquities collected by the royal family of France.
• The world famous painting of Mona Lisa by Leonardo-Da-Vinci is kept in this museum.
• The antiquities brought back by Napoleon Bonaparte on his return from conquests are exhibited in this museum.
• Presently, the museum has more than 3 lakh and 80 thousand artefacts.

(b) British Museum:
Answer:

• The British Museum was established in the 18th century in London.
• It has a collection of 71 thousand objects given by natural scientist Sir Hans Sloan to King George. II.
• Several books, pictures, specimens of preserved plants are included in it.
• The ancient objects and artefacts which the Britishers have collected from their colonies are exhibited in this museum.
• At present, it has about 80 lakh objects in its collection.

(c) National Museum of Natural History:
Answer:

• The National Museum of Natural History was established in Washington DC in 1846.
• The Smithsonian Institute managed the museum from its inception. This is a museum of natural history.
• Remains of animals, plants, organisms and thousands of specimens of fossils are kept in it.
• It also has human fossils, minerals, rocks, shells, artefacts. All together it has a collection of more than 12 crore (120 million).

(d) Chhatrapati Shivaji Maharaj Vastusangrahalay:
Answer:

1. Chhatrapati Shivaji Maharaj Vastusangrahalay was built to commemorate the visit of Prince of Wales to India. Some influential residents in Mumbai decided to establish a museum in 1904.
2. The foundation of the building was laid on 2nd November 1905 and the construction was completed in 1922. The museum was named as ‘Prince of Wales of Western India’. In 1998 C.E. it was renamed as ‘Chhatrapati Shivaji Maharaj Vastusangrahalay.’
3. The museum building is constructed in Indo-Gothic style and has been awarded the status of Grade I heritage building.
4. The museum has about 50 thousand antiquities which are divided into three categories, viz.. Arts, Archaeology and Natural History.

(e) Bharatvarshiya Prachin Aitihasik Kosh:
Answer:

• Raghunath Bhaskar Godbole wrote Bharatvarshiya Prachin Aitihasik Kosh.
• It is the first dictionary of Biography in Indian regional language.
• We get information on Manu and many ancient personalities from Mahabharat.
• We come to know about legendary people who lived in Bharatvarsha and were renowned.
• Information about their women, their sons, religions, lands, capitals, mountains and rivers.
• Which flowed in their land their entire history is given in this encyclopaedia.

(f) Bharatiya Samskruti Kosh:
Answer:

• Pandit Mahadevshastri Joshi edited and published 10 volumes of Bharatiya Samskruti Kosh.
• He wrote about Indian history, geography, about people speaking different languages and how they created history.
• Detailed information on culture of India and festivals, geography, traditions, ideas, is taken into consideration.

Therefore these koshs are useful for readers and research scholars.

Question 11.
Explain the following statements with reasons:

(a) Encyclopaedias should be created in as many languages as possible.
Answer:
Encyclopaedias symbolise the richness and vast gamut of words a language has.

• It fulfils the curiosity of readers and solves the confusion of a layman.
• Encyclopaedias inspire to carry out more research as one gets information, knowledge and references.
• Encyclopaedias provide complete information and knowledge to researchers and students which enriches their previous knowledge.
• Encyclopaedias represent intellectual and cultural development of a society.
• Many languages in India and the world are rich and resourceful and hence encyclopaedias should be created in as many languages as possible to raise intellectual level of society.

(b) Encyclopaedia and history are related.
Answer:

• Encyclopaedias contain information about personalities, events and ancient cultures.
• In order to gather information it is essential to take the help of history,
• The common factors between an encyclopaedia and history are objectivity and authenticity.
• Research scholars of history need to refer to encyclopaedias to find information on events, personalities, concept, places, etc. as encyclopaedias are created with the help of history. Hence encyclopaedia and history are related.

(c) Improved versions of Encyclopaedia or supplements to original editions need to be published.
Answer:

1. Encyclopaedia is a systematic compilation of information or knowledge on various topics ranging from people, places and events to concepts, word meanings, etc.
2. With the passage of time the spectrum of knowledge has widened.
3. With the advent of new technology new words are added. Latest or updated information, knowledge, concepts enrich the language.
4. The references of the past events change in context of the new research. If all these changes are not incorporated in the encyclopaedias, they will become outdated.

Therefore, encyclopaedia or supplements to original editions need to be published.

Question 12.
Answer the following questions in 25-30 words:
(a) What are the ways to preserve and conserve oral resources?
Answer:

• Folk songs ancl folk tales are collected and compiled.
• Collected material is classified. It is interpreted and analysed after compilation.
• The result of research conducted is then published.

(b) What steps are taken to preserve written sources?
Answer:
Written sources have great importance in the writing of history. To preserve written sources we need –

• To collect old books, historical books, pictures, photographs, copper plates, manuscripts and official records and edit them.
• To decide upon the historical values of collected documents.
• To exhibit the selected documents.
• To publish edited documents and research reports.
• To complete necessary chemical and mechanical process of cleaning for conserving and preserving the documents.

(c) What methods should be followed while studying material source?
Answer:
The following methods should be followed by research scholars while studying material source:

• To collect the artefacts and classify them according to their historical date and type and prepare indexes.
• To arrange exhibitions of selected artefacts or their replicas.
• To write and publish research articles about artefacts.
• To complete required mechanical and chemical processes of cleaning for conservation and preservation of the collected documents.

(d) Write about the earliest libraries in the world.
Answer:
Libraries were established in different parts of the world in ancient times:

• The Royal Library of Ashurbanipal is the earliest library dating back to the 7th century B.C.E. in Mesopotamia. The library was owned by the Assyrian emperor.
• A library was discovered at Alexandria in Egypt which was built in 4th century C.E.
• The library at Takshashila university in 5th century B.C.E. – 5th century C.E. as it was a noted centre of learning.

(e) Write about format of Encyclopaedias.
Answer:
Format of Encyclopaedias:

• Encyclopaedias are made according to selected subjects; therefore encyclopaedias are classified according to the subjects.
• Encyclopaedias are framed according to alphabetical order or as per the order of topics.
• They provide the exact meaning of words and give information on concepts.
• The type of order is kept according to the convenience of the readers. An index is provided at the end of the encyclopaedia for this purpose.

(f) Write about Encyclopaedic Literature.
Answer:

• It appears similar to an encyclopaedia but differs in composition.
• Information and scholarly articles on all possible aspects of a subject is covered.
• Experts are called to write on different topics which are compiled to create encyclopaedia
• ‘Maharashtra Jeevan’ Volume I and II; ‘Shahar Pune’ Volume I and II; Yearbook like Manorama, etc. are the examples of Encyclpaedic Literature.

(g) Give information on early encyclopaedias made in the west.
Answer:

• The process of making encyclopaedias started in before 1st century C.E. in the west. Pliny wrote the first encyclopaedia on natural history between 23 C.E.-79 C.E.
• In the 8th and 9th century, encyclopaedias were written in England, France and in Arab countries.
• French Philosopher Denis Diderot wrote Encyclopaedia in the 18th century C.E.
• The important milestone in this process was ‘Encyclopaedia Britannica’ published in 1767 C.E.
• Wikipedia is considered equivalent to encyclopaedia. The information given in this encyclopaedia is highly reliable and updated.

(h) Write about ancient Indian encyclopaedias.
Answer:

• In the 7th century C.E., Nighantu, a dictionary (information on ancient medicine) in Sanskrit language was written. Dictionaries like Dhatupath were written.
• In tjie medieval times, encyclopaedic text was composed by Mahanubhav sect.
• Amarsimha wrote a thesaurus in Sanskrit ‘Amarkosha’.
• Raghunath Pandit prepared Rajavyavaharkosh as directed by Chhatrapati Shivaji Maharaj.

Question 13.
Read the following passage and answer the following questions:
(a) Which factors influence Encyclopaedia?
Answer:
The influence of national policies, ethical values and ideals, philosophy and traditions is seen in an encyclopaedia.

(b) What is the common factor between history and encyclopaedia?
Answer:
History and encyclopaedia both are objective.

(c) Explain the statement: Encyclopaedias are looked upon as outstanding achievements of a society.
Answer:

• The knowledge in all the spheres of society is made accessible to everyone is the major reason behind making an encyclopaedia.
• What inspires people to create encyclopaedias is the instinct to gain knowledge and spread it.
• Encyclopaedias reflect the collective intellect and creativity of society.
• One develops a sense of pride after knowing about nation’s progress through it.

Hence encyclopaedias are looked upon as outstanding achievements of a society.

Question 14.
Give elaborate answers to the following: (3 marks each)

(a) What kind of training is required to study written sources?
Answer:
While studying and handling written sources the following training is required:

• The students should have knowledge of scripts like Brahmi, Modi, Persian and their development.
• They should know ways to obtain information about the social organisations and traditions.
• They should know about the literature and writing style in past societies.
• They should have basic knowledge about administrative systems, dynasties and cultures of the past.
• They should study prevalent schools of painting and sculpture.
• They should be able to collect information on types of paper, know about ink and colour of ancient document and ways to handle.
• They should be well acquainted with properties of stones and metals used for inscriptions.
• Articles published earlier on case study should be read.
• They should know the chemicals and equipment used in various processes of cleaning and preserving the documents.
• Modern know-how of approaches of managing exhibitions in museums, galleries and information technology.

(b) What kind of training is required to study material sources?
Answer:
Student should have following knowledge to study material resource:

• They should have basic knowledge of archaeological method and theory.
• They should be acquainted with the history of ancient civilisations.
• They should have knowledge of various techniques of excavation.
• Stones, minerals and clay used to make artefacts and their characteristics to be studied.
• They should be well-acquainted with the sources of the material used and their chemical properties.
• They should also know about various styles of making artefacts and development in their making process.
• They should have the knowledge and skills of making replicas of artefacts and fossils.
• They should read research papers previously published on his case study.
• They should acquire information about the approaches of arranging exhibitions and administrations.
• They should know about the equipment and chemicals necessary for the cleaning of artefacts.
• They should be able to write research reports and articles.

(c) Write information about museums in India.
Answer:

• ‘Indian Museum’ established by the Asiatic Society of Bengal in Kolkata was the first museum in India in 1814.
• The ‘Government Museum’ established in Chennai in 1851 C.E. was the second museum in India. The National Museum was established in Delhi in 1949.
• The foundation of the Prince of Wales Museum was laid in Mumbai in 1905. Its construction was completed in 1922. It was renamed as Chhatrapati Shivaji Maharaj Vastusangrahalay in 1998 C.E.
• At present, there are many museums in various states of India.
• Many museums are connected to libraries and archives. Some are connected to Universities.
• Such museums offer courses in Museology also.

(d) Give information on “National Archives of India.
Answer:

• The first official archive of India was established m Kolkata in 1891 C.E. as the ‘Imperial Record Department’.
• It was moved to Delhi in 1911 C.E.
• In 1998 C.E. it was made accessible to the public by the then President of India K.R. Narayanan.
• It was renamed as ‘National Archive’ (National Archive of India). Archives come under the Ministry of Culture of the Indian Government.
• This archive has papers, maps, books and micro films preserved in chronological order since 1748.
• Records in English, Arabic, Hindi, Persian, Sanskrit, Devanagari and Modi languages are preserved.
• Papers kept in archives are classified into public, oriental, manuscripts and private papers.
• The National Archives of India is the largest in Asia and technologically advanced.

(e) Explain the statement: A nation should have museums and libraries.
Answer:
Museums and libraries mirror the history of the country and that is the reason they are very valuable for a nation.

• Museums and Libraries make it easy for the research scholar to write history.
• Historical events and life stories of important people reach the masses.
• People get an idea about past social, political and cultural conditions.
• A visit to museums increases one’s interest.
• A change in a prejudiced view about history is seen.
• Information on animals, microorganisms, birds and elements of nature.
• Museums contribute to the process of gaining and dissemination of knowledge.
• Ancient historical sources are preserved.
• Tourism is promoted.
• It creates opportunities for employment.

Hence it can be said that it is important for a nation to have museums and libraries as they both are symbols of nation’s progress and glory.

Memory Map

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 2 Historiography Indian Tradition Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 2 Question Answer Historiography Indian Tradition Maharashtra Board

Class 10 History Chapter 2 Historiography Indian Tradition Question Answer Maharashtra Board

History Class 10 Chapter 2 Question Answer Maharashtra Board

Question 1.
(A) Choose the correct option from the given options and complete the statement.
(1) …………………..…….. was the first Director-General of the Archaeological Survey of India.
(a) Alexander Cunningham
(b) William Jones
(c) John Marshall
(d) Friedrich Max Muller
Answer:
(a) Sir Alexander Cunningham

(2) …………………..…….. translated the Sanskrit text of ‘Hitopadesh’ in the German language.
(a) James Mill
(b) Friedrich Max Muller
(c) Mountstuart Elphinstone
(d) Sir John Marshall
Answer:
(b) Friedrich Max Muller

(B) Identify and write the wrong pair in the following set.
(1) ‘Who were the Shudras’ – subaltern History
(2) ‘Stri-Purush Tulana’ – Feminist writing
(3) ‘The Indian War of Independence 1857’ – Marxist History
(4) Grant Duff – Colonial History.
Answer:
(1) Right Pair: ‘Who were the Shudras’ – subaltern History
(2) Right Pair: ‘Stri-Purush Tulana’ – Feminist writing
(3) Wrong Pair: ‘The Indian War of Independence 1857’ – Marxist History
(4) Right Pair: Grant Duff – Colonial History.

Question 2.
Explain the following with its reason.
(1) Writing of the regional history received a momentum.
Answer:

• Indian historians trained in the British educational system showed an inclination to restore the self-esteem of Indians They started writing Nationalistic historiography.
• Historians from the different regions of India criticised the prejudiced history of India written by the British officers.
• Their attention was drawn towards geographic conditions and history of different regions of India.
• The nationalistic historiography helped in triggering the independence movement.
• It provided a momentum to the writing of regional histories for e.g.
• Nationalistic writings in Maharashtra were inspired by Vishnu Shastri Chiplunkar.

Hence, writing of the regional history received momentum.

(2) Bakhar is an important type of historical documents.
Answer:

• Bakhars are important source of history like coins, inscriptions, texts, copper plates and travelogues.
• Bakhars contain eulogies of the heroes, historic events, stories of lives of great men and description of battles.
• It portrays a picture of prevalent society, religions and economic life.
• Bakhars are of various types which contain biographies of kings, dynastic history, description of events, sects, autobiographies, mythologies, administration of kings, etc.
• These descriptions are helpful for writing historiography.
• Among well-known Marathi. Bakhars ‘Sabhasad Bakhar’ written by Krishnaji Anant Sabhasad requires a special mention Bhausahebanchi Bakhar and Panipatachi Bakhar describe the ‘Battle of Panipat’.

Hence, Bakhars are important type of historical document.

Question 3.
Write detailed Answers the following questions in detail.
(1) What is Marxist History?
Answer:

1. In the post-independence era, new trends emerged in writing Indian historiography. Marxist historiography is prominent among them.
2. Historiography which is based on ideas of Karl Marx is known as Marxist Historiography. In Marxist Historiography, more importance was given to class struggles.
3. Marxist Historiography reflects concerns for means and modes of production as well as the industrial relations. These became centre of writings of the Marxist historians.
4. How every social event affects the life of people was analysed and it became the theme of Marxist historians Marxist historians studied the transitions that took place in the caste system.
5. Notable Indian historians who adopted Marxist ideologies were Damodar Kosambi, Comrade Shripad Dange, Sharad Patil and Ram Sharan Sharma.
6. Their writings reflected Marxist ideology. Comrade Dange was the founder member of the Indian Communist Party

(2) What is the contribution of Itihasacharya V.K. Rajwade to historiography?
Answer:

1. V.K. Rajwade is well-known for his writings in Marathi on subjects like history, linguistics, etymology and grammar. His contributions are as follows:
2. He compiled and edited 22 volumes of Marathyanchya Itihasachi Sadhane.
3. He stated that history is the all-inclusive image of the past societies.
4. V. K. Rajwade was of the view that history does not include only the stories of political images, conspiracies and Wars for seizing power.
5. He was of the firm opinion that we should write our own history and insisted that history . should be written only using the authentic sources.
6. He was of the opinion that description of any human event in historiography should have balanced combination of three factors namely – Time, Space and Personalities.

Question 4.
(a) Complete the following chart.

Answer:

(b) Complete the following concept chart.

Answer:

Question 5.
Explain the following concepts.
(1) Orientalist historiography.
Answer:

1. In the later part of the eighteenth century many European scholars felt curious to know about civilisations and countries of the East.
2. These scholars who studied the Indian Civilization had respect and admiration for it. They were known as ‘Orientalists’.
3. They studied similarities between Sanskrit and some of the European languages, focussing more on Vedic traditions and Sanskrit literature.
4. It resulted in the notion that an ancient language could be the mother of all Indo-European languages.
5. Notable Orientalist scholars are Friedrich Max Muller and William Jones.

(2) Nationalistic historiography.
Answer:

1. English education started in India in the nineteenth century. The Indian historians who were trained in English education system realised the glory of their past.
2. They showed an inclination to restore the pride in the ancient glory of India and the self-esteem of the Indian readers.
3. They laid the foundation of Nationalistic writing. Nationalistic writings in Maharashtra were inspired by ‘Vishnushastri Chiplunkar’.
4. Nationalistic historians opposed the prejudiced history written by the British officers.
5. Mahadev Govind Ranade, Vinayak Damodar Savarkar, Ramesh Chandra Majumdar are renowned Nationalistic historians.
6. Nationalistic historiography inspired freedom struggle against the Britishers and gave momentum to write about regional history. While glorifying the past, at times they are blamed for ignoring to critically analyse the truth.

(3) Subaltern history.
Answer:

• History of deprived classes or communities who were deprived of all rights is known as subaltern history.
• The seeds of subaltern history can be traced in the Marxist history. Italian historian Antonio Gramsci has special importance in writing the subaltern history.
• He presented the idea that history should be written starting from the bottommost ranks of people in the society.
• Ranjit Guha, an Indian historian, has given prominence to subaltern history and played a major role in establishing it as an important academic school of historiography.
• Similar thoughts were expressed by Mahatma Phule and Dr. Babasaheb Ambedkar which can be found in their writings.

Project
Prepare an illustrated manuscript with the help of the internet giving more information about the historians mentioned in this lesson.
Answer:

Memory Map

Question 6.
Complete the sentences by choosing a correct option:
(a) The first written document found in India was inscribed during the rule of Emperor ……………….. .
(a) Akbar
(b) Harshavardhan
(c) Ashoka Maurya
(d) Aurangzeb
Answer:
(c) Ashoka Maurya

(b) Banabhatta wrote King Harsha’s biography titled ………………… in the 7th century CE.
(a) Meghdoot
(b) Rajtarangini
(c) Rasratnakar
(d) Harshacharit
Answer:
(d) Harshacharit

(c) In the 12th century C.E., ………………… wrote a book ‘Rajtarangini’ about history of Kashmir.
(a) Banabhatta
(b) Kalhana
(c) Ziquddin Barani
(d) Patanjali
Answer:
(b) Kalhana.

(d) The historians in the courts of Muslim rulers were influenced by ………………… historiography.
(a) Greek and Roman
(b) Arabic and Persian
(c) English and French
(d) Arabic and Urdu
Answer:
(b) Arabic and Persian

(e) We get information about the rule of Chhatrapati Shivaji Maharaj from ……………….. .
(a) Bhausahebanchi Bakhar
(b) Panipatachi Bakhar
(c) Sabhasad Bakhar
(d) Holkaranchi Bakhar
Answer:
(c) Sabhasad Bakhar

(f) ‘Bhausahebanchi Bakhar’ describes Battle of ……………….. .
(a) Raigad
(b) Panipat
(c) Plassey
(d) Vasai
Answer:
(b) Panipat

(g) The first book written by a British historian on Indian history is ……………….. .
(a) The History of India
(b) The History of Maharaj
(c) The History of British India
(d) The Sacred Books of the East
Answer:
(c) The History of British India

(h) Nilkanth Janardan Kirtane and V.K. Rajwade exposed the limitations in writings of ……………….. .
(a) Friedrich Max Muller
(b) Colonel Todd
(c) Grant Duff
(d) William Wilson Hunter
Answer:
(c) Grant Duff

(i) …………………, an Indian historian played a major role in establishing subaltern history as an important academic school of historiography.
(a) Comrade Sharad Patil
(b) Ranjit Guha
(c) Dharmanand Kosambi
(d) Ram Sharan Sharma
Answer:
(b) Ranjit Guha.

(j) The writings of British officials on India display strong influence of ……………….. .
(a) Marxism
(b) Colonalism
(c) Feminism
(d) Capitalism
Answer:
(b) Colonalism

(k) The Nationalistic Historiography in Maharashtra was inspired by works of ……………….. .
(a) Vinayak Damotfar Savarkar
(b) Ramkrishna Gopal Bhandarkar
(c) Vishnushastri Chiplunkar
(d) Justice Mahadev Govind Ranade
Answer:
(c) Vishnushastri Chiplunkar

(l) The two volumes written by ……………….. on Indian history show impartial treatment of the subject.
(a) Colonel Todd
(b) William Wilson Hunter
(c) Grant Duff
(d) James Mill
Answer:
(b) William Wilson Hunter

(m) ‘Primitive Communism to Slavery’, represents ……………….. the historiography.
(a) Colonial
(b) Orientalist
(c) Nationalistic
(d) Marxist
Answer:
(d) Marxist

(n) ‘Stripurush Tulana’ was written by ……………….. is acknowledged as first feminist book in India.
(a) Meera Kosambi
(b) Dr. Sharmila Rege
(c) Tarabai Shinde
(d) Pandita Ramabai
Answer:
(c) Tarabai Shinde.

Question 7.
Identify the wrong pair and write it:
(1)

Answer:
Wrong pair: The Indian War of Independence – Marxist History.

(2)

Answer:
Wrong pair: Marathyanchya Itihasachi Sadhane- Vishnushastri Chiplunkar.

(3)

Answer:
Wrong pair: Discovery of Harappan CIvilization – James Mill.

(4)

Answer:
Wrong pair: Subaltern Historiography – Bamchandra Guha.

Question 8.
Do as directed:
(1)

Answer:

(2)

Answer:

(3) Prepare a flow chart on Literary work of Max Muller:
Answer:

Question 9.
Explain the concepts:
(a) Colonial Historiography:
Answer:

• The history written by British officers and Christian missionaries in support of British rule and colonialism is known as Colonial historiography.
• It reflected their prejudiced mindset about Indian culture. They ridiculed the Indian culture as being primitive.
• Their writings justified the colonial British rule.
• The distinct example of colonial historiography is ‘Cambridge History of India’ in five volumes published during 1922-1937.

Question 10.
Write short notes:
(a) Alexander Cunningham:
Answer:

• British rulers started archaeological exploration and research in India in the 20th century.
• They established the Archaeological Survey of India and appointed Sir Alexander Cunningham as its first Director General.
• He mainly chose the sites mentioned in the Buddhist texts for excavations.
• Many other ancient sites were excavated under his supervision.

(b) James Mill:
Answer:

• James Mill, a‘British historian, had written the monumental book ‘The History of British India’. He published it in three volumes in 1817.
• The book is important as it was the first book written by a British officer on Indian history.
• The book: lacks objective perspective and is prejudiced about various aspects of the Indian culture.

(c) Grant Duff:
Answer:

• Grant Duff, a British officer, wrote the book ‘A History of Mahrattas’, in three volumes.
• His name stands out among the British officers who wrote about Maratha history.
• The tendency of the British historians to condemn Indian culture and history is found in Grant Duff’s writing.
• Historians Nilkanth Janardan Kirtane and Vishwanath Kashinath Rajwade exposed the limitations of Grant Duff’s writings.

(d) Indian Feminist Historiography:
Answer:

1. Tarabai Shinde, Pandita Ramabai and Dr. Rukhamabai were feminist historians before independence.
2. They wrote about employment of women, their right to political equality, treatment meted out to women at their workplace and gender discrimination.
3. A lot of literature is available unfolding the viewpoint of Dalit women on problems like social class, caste, etc. In the post-independence era.
4. Dr. Sharmila Rege included her essays on the autobiographies of Dalit women in her book, ‘Writing Caste, Writing Gender: Reading Dalit Women’s Testimonies.’
5. Meera Kosambi’s book, ‘Crossing Thresholds: Feminist Essays in Social History’ contains essays on the life stories of women like Pandita Ramabai and Dr. Rukhamabai, the first practising lady Doctor of India.

Question 11.
Explain the following with reasons:
(a) The history of Indian civilization dates back to 3rd millennium BCE.
Answer:

• Indian civilisation is among the various ancient civilisations in the world.
• Excavations at Harappa took place in 1920 under the supervision of Sir John Marshall, then Director General of Archaeological Survey of India (ASI). This led to the discovery of Harappan Civilization.
• This discovery prqved helpful to trace the antiquity of Indian history which dates back 3rd millennium BCE or earlier.

(b) It became necessary to rethink of women’s position in history.
Answer:

• For a considerable period of time, mainly male scholars were involved in the writing of Indian history.
• It was obvious that the perspective was male-dominated.
• The work of the women historians was neglected for long. So it became important to highlight this fact.
• It was a huge challenge in front of the women: historians to compile the work and do research which would prove to be a medium to put forth their status in society.

Hence, it became necessary to rethink about the position of women in history.

(c) Govind Sakharam Sardesai was addressed as ‘Riyasatkar’.
Answer:

• Govind Sakharam Sardesai had a momentous achievement to his credit by publishing ‘Maratha Riyasat’.
• He published several volumes of Maratha history.
• His work became so popular that people began to address him as ‘Riyasatkar’.

Question 12.
Answer the following in 25-30 words:
(a) Which things are included in the description by Emperor Babur in bis autobiography?
Answer:
Babur, the founder of the Mughal empire, in his autobiography entitled Tuzuk-i-Babari describes:

• The battles fought by him.
• Recordings of minute observations of various regions and cities visited by him noting minute observations.
• Observation of the local customs, economy, fauna and flora of the region travelled by him.

(b) What is the contribution of Swatantryaveer Savarkar to nationalistic historiography?
Answer:

1. The writings of Swatantryaveer Savarkar were infused with nationalistic ideas. He looked at the revolt of 1857 as the First War of Independence and wrote the ‘book ‘The Indian War of Independence, 1857’.
2. His book gave inspiration to Nationalistic historiography which helped in triggering independence movement of the Indian people against the British. Even the writing of regional history got momentum.
3. The attention of historians was drawn towards the history and geographic conditions and variations in the South Indian region.

(c) Write about the contribution of Banabhatta in writing historiographies.
Answer:

• It was considered an important step in the Indian historiography to write biographies of kings and dynastic histories.
• Banabhatta wrote Harshacharit, King Harsha’s biography, in the 7th century C.E.
• It portrays a realistic picture of the social, economic, political, religious and cultural life during the period when King Harsha ruled.

(d) Write information on ‘Rajtarangini’.
Answer:

• Rajtarangini was written by Kalhana in the 12th century C.E. It traces the history of Kashmir.
• These eight books contain records of dynasties which ruled Kashmir, local traditions, coins, remains of monuments and inscriptions. Kalhana wrote the text after critically examining the various sources.
• The book is a good example to show how scientific technique is applied in writing history.

(e) Write about historiography in the post-independence period.
Answer:

• In the post-independence period, along with dynastic history, cultural, social and economic histories were also written.
• New schools of thought like Marxist, Subaltern and Feminist History were included in historiography.
• The scholars in this era began to feel the need of writing histories of various communities, sciences, economic systems, political ideologies, cultural aspects, etc.
• They presented the new schools of ideologies. These changes increased the scope of writing historiography.

(f) What are the objectives of writing history according to Ziauddin Barani?
Answer:

• Ziauddin Barani explained the ’ objectives of historiography. According to him, the duty of a historian does not end with recording the ruler’s valour and welfare policies.
• He should also write about the ruler’s failings and incorrect policies.
• He further adds that a historian should also take into account the impact of the teachings of the wise, the learned and the saints on the cultural life of people.

Thus, Ziauddin Barani holds important place as he expanded the scope of historiography.

(g) What are the salient features of writings of historians in the courts of Mughal emperors?
Answer:
The salient features of writings of historians in the courts of Mughal emperors are:

• Historians praised the Mughal emperors in their writings.
• Their loyalty towards the rulers is exhibited.
• The custom of adding suitable poetic quotes was introduced. The historians started to include beautiful pictures as well.

(h) Write about the importance of Tarabai Shinde in writing feminist historiography. *
Answer:

• Tarabai Shinde has a prominent place among the feminist historians who wrote about women in the nineteenth century, i.e. pre-independence era.
• She wrote a book Stripurush Tulana which was published in 1882. It is acknowledged as the first feminist book published in India.
• Her writings attacked the male-dominated social system and the caste system.

Question 13.
Read the given passage and answer the questions given below:
(a) Complete the graphical presentation:

Answer:

(b) What was considered more important by the historians in the Mughal Court?
Answer:
Praising the Mughal emperor and exhibition of loyalty was considered more 8 important by the historians in the Mughal Court.

(c) Why is Abbul Fazl’s writing considered realistic?
Answer:

• Abul Fazl’s Akbarnama reflects his critical viewpoint.
• He collected authentic historical documents for this book.
• He scrutinized these documents to affirm their reliability. Therefore, his method is looked upon as devoid of bias and hence realistic.

Question 14.
Write detailed answers to the following questions:
(a) Write information about historiography in the ancient period of India.
Answer:

• In the ancient period, stories of great deeds of ancestors, mythological lore, memories of social transitions were preserved through oral traditions.
• The art of writing was mastered by Indians as early as 3rd millennium B.C.E. But Harappan script is not deciphered yet.
• The earliest written documents found in India were in the form of inscriptions that are as old as 3rd century B.C.E. during the period of Emperor Ashok. His edicts are inscribed on natural rocks and stone pillars.
• Inscriptions started to occur on coins, metal images and sculptures and also on copper plates from the 1st century B.C.E.
• Epics like Ramayana, Mahabharat, Puranas, Jain and Buddhist texts are important sources of ancient Indian literature.
• Historical accounts by Indian authors and travelogues by foreign travellers are also important sources of history.

(b) Explain the works of Dr. Babasaheb Ambedkar and Mahatma Phule in Subaltern History.
Answer:

• History of the deprived classes expressed in folklore was known as ‘Subaltern History’.
• Similar thoughts were expressed by Mahatma Jotirao Phule and Dr. Babasaheb Ambedkar.
• Mahatma Phule unfolded the history of the Shudratishudra communities in his book ‘Gulamgiri’.
• He drew attention to show how women, Shudras and Atishudras were exploited under the name of religion.
• Dr. Ambedkar focused on the idea that in spite of having a significant role in shaping the cultural and political aspects of India, the role of Dalits was not duly acknowledged in colonial and nationalistic historiography.
• Injustice done to the Dalits was mostly written by him. ‘Who Were the Shudras’ and ‘The Untouchables’ are his books which can be cited as examples of subaltern history.

Question 15.
Observe the given picture and answer the question given below:

(a) Write a short note on Copper-plate inscriptions.

Answer:

• The copper-plate shown in the picture was found at Sohagaura in Gorakhpur district in Uttar Pradesh.
• It is supposed to be from the Mauryan period and the inscription on it is in Brahmi script.
• Many symbols are inscribed on it ‘Tree-in-railing’ and ‘Mountain’ at the beginning of inscription occur on punch marked coins.
• A structure created on four pillars is indicative of a granary.
• The inscriptions have a record of royal order that the grains stored in the granary should be distributed carefully.
• This order is suggestive of precautionary measures taken during famine.

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Balbharti Maharashtra State Board Class 10 History Solutions Chapter 1 Historiography Development in the West Notes, Textbook Exercise Important Questions and Answers.

Std 10 History Chapter 1 Question Answer Historiography Development In The West Maharashtra Board

Class 10 History Chapter 1 Historiography Development In The West Question Answer Maharashtra Board

History Class 10 Chapter 1 Question Answer Maharashtra Board

Question 1.
(A) Choose the correct option from the given options and complete the statement.
(1) It may be said that …….. was the founder of modern historiography.
(a) Voltaire
(b) Rene Descartes
(c) Leopold Ranke
(d) Karl Marx
Answer:
(a) Voltaire

(2) ………… wrote the book entitled ‘Archaeology of Knowledge’.
(a) Karl Marx
(b) Michel Foucault
(c) Lucien Febvre
(d) Voltaire
Answer:
(b) Michel Foucault

(B) Identify and write the wrong pair in the following set.
(1) Georg Wilhelm Friedrich Hegel – ‘Reason in History’
(2) Leopold von Ranké – ‘The theory and Practice of History’
(3) Herodotus – ‘The Histories’
(4) Karl Marx – ‘Discourse on the Method’
Answer:
(1) Right pair: Georg Wilhelm Friedrich Hegel – ‘Reason in History’
(2) Right pair: Leopold von Ranké – ‘The theory and Practice of History’
(3) Right pair: Herodotus – ‘The Histories’
(4) Wrong pair: Karl Marx – Discourse on the Method.

Question 2.
Explain the following concepts.
(1) Dialectics
Answer:

• In order to understand the true nature of an event, one needs to know its opposite for e.g. True — False, Good — Bad, etc.
• A German philosopher, Georg Wilhelm Friedrich Hegel had put forward this method of analysis of history.
• A theory called ‘Thesis’ is proposed at the beginning. It is followed by another theory called Antithesis’ which is, contrary to ‘Thesis’.
• After a thorough logical discussion of both new thesis is proposed having gist of both (Thesis and Antithesis).
• This process of orriving at a new thesis is called Synthesis.
• This method of analysis of history which is based on opposites is known as ‘Dialectics’.

(2) Annales School
Answer:

• At the dawn of the twentieth century, the writing ¿f history got a new direction.
• Along with political events, kings, great leaders, the study of climate, local people, agriculture, trade, technology, means of communication, social divisions and their collective psychology of a group was also considered important in the study of history.
• This new school of thought is known as Annales School. Annales School was started by French historians.

Question 3.
Explain the following with its reason.
(1) Historical research was driven to focus in depth on various aspects of women’s life.
Answer:

• Initially, there was a lot of dominance of male perspective on historical writing. Simone de Beauvoir, a French scholar, insisted on inclusion of women perspective in historiography.
• She emphasised on the inclusion of women in the process of writing history.
• She insisted on rethinking of the male dominated perspective of history.
• Because of her efforts historical research was driven to focus in depth on various aspects of women’s lives their employment, their role in trade unions, institution working for their cause, and their family life.

(2) Foucault called his method, ‘the archaeology of knowledge’.
Answer:

• According to Michel Foucault, the prevailing method of arranging historical events in a chronological order was not right.
• He threw light on the fact that archaeology does not strive to reach the ultimate historical truth.
• It attempts to explain various transitions in the past.
• Foucault gave more importance for explaining the transitions in history. Hence, his method is called ‘the archaeology of knowledge’.

Question 4.
Complete the concept chart.

Answer:

Question 5.
Answer the following in detail.
(1) Explain Karl Marx’s ‘Class Theory’.

Answer:
In the latter part of nineteenth century, German thinker, Karl Marx put forward ‘Class Theory’ in his book ‘Das Kapital’.

According to him:

1. History i not about abstract ideas but living people. The fullillment of basic needs of people depends on the nature of prevalent means of production and the ownership.
2. All the different strata of the society do not get equal access to these means of production which causes the division of the society into classes. It rešults into class struggle.
3. The class which owns means of production $ economically exploits the rest of the classes. Human history, according to him, is the history of class struggle.

(2) What are the four characteristics of modern historiography?
Answer:
The following are the four characteristics of modern historiography:

1. Its method is based on scientific principles and begins with formation of relevant questions.
2. These questions are anthropocentric i.e. they are about ancient human societies and their deeds in that period of time. No interrelation between the divine and human needs is suggested.
3. Answers to these questions are supported by reliable evidence and they are presented in a logical order.
4. History presents a graph of man’s progress with the help of his deeds in the past.

(3) What is feminist historiography?
Answer:

• Feminist historiography means writing history with women perspective. There was a lot of dominance of male perspective on historical writing.
• Simone de Beauvoir, a French scholar, insisted on rethinking on the male dominated perspective and including the women’s perspective in historiography.
• The idea of feminist historiography was accepted.
• Because of her efforts various aspects of women’s lives like their employment, their role in trade unions and their family life became part of historiography.

(4) Explain Leopold von Ranké’s perspective of history?
Answer:
Leopold’s view on ways to write history throws light on his perspective of history:

1. He spoke about the critical method of historical research. He gave importance to information gathered through original documents.
2. He also stated that all types of original documents related to the historical event should be examined in detail and with great care.
3. He believed that with this method it was possible to reach the historical truth. He was critical of imagination in narration of history.

Historiography : Development In The West Questions And Answers Pdf Project
Obtain detailed information on your favourite subject and write its history. For example :
– History of Pen
– History of Printing technology
– History of Computers
Answer:

Memory Map

Question 6.
Choose the correct option from the given options and complete the sentences:

(a) A scholar who writes critical historical narratives is known as ………………………… .
(a) an archaeologist
(b) a historian
(c) a social scientist
(d) a language expert
Answer:
(b) a historian

(b) The earliest inscription in the world is displayed at Louvre museum in ………………………… .
(a) England
(b) France
(c) Germany
(d) Portugal
Answer:
(b) France

(c) The tradition of recording historical events can be traced back to ………………………… civilization in Mesopotamia.
(a) Sumer
(b) Egyptian
(c) Arab
(d) Mohenjodaro
Answer:
(a) Sumer

(d) The tradition of modern historiography has its roots in the writings of ………………….. historiAnswer:
(a) Roman
(b) Greek
(c) German
(d) French
Answer:
(b) Greek

(e) ………………….., a Greek historian of the fifth century B.C.E., had used the term ‘History’ for the first time for his book entitled, ‘The Histories’.
(a) Leopold Ranke
(b) Georg Hegel
(c) Michel Foucault
(d) Herodotus
Answer:
(d) Herodotus

(f) In 1737 C.E., the ………………….. university in Germany had an independent department for history.
(a) Oxford
(b) Cambridge
(c) Gottingen
(d) Stanford
Answer:
(c) Gottingen

(g) Historiography of the nineteenth century was greatly influenced by the thoughts of …………………..
(a) Karl Marx
(b) Voltaire
(c) Georg Hegel
(d) Leopold von Ranke
Answer:
(d) Leopold von Ranke

(h) A new school of historiography arose in France known as ………………….. school.
(a) Translation
(b) Annales
(c) Nationalism
(d) Communist
Answer:
(b) Annales

(i) The method of analysis which is based on opposites is known as …………………. .
(a) Numismatics
(b) Arithmetic
(c) Polynomial
(d) Dialectics
Answer:
(d) Dialectics

(j) ………………….. considered subjects like psychological disorders, science of medicine, prison administration for historical analysis.
(a) Michel Foucault
(b) Leopold Ranke
(c) Karl Marx
(d) Voltaire
Answer:
(a) Michel Foucault

(k) After 1990, ………………….. were considered as an independent social class.
(a) labourers
(b) women
(c) men
(d) farmers
Answer:
(b) women

(l) According to ………………….., historical realities should be presented in a logical manner.
(a) Georg Hegel
(b) Voltaire
(c) Simone de Beauvoir
(d) Herodotus
Answer:
(a) Georg Hegel

(m) According to ………………….., one should never accept anything as the truth till all the doubts are solved.
(a) Rene Descartes
(b) Karl Marx
(c) Voltaire
(d) Herodotus
Answer:
(a) Rene Descartes.

Question 7.
Identify the wrong pair in the following and write it:
(1)

Answer:
Wrong pair: Karl Marx – Discourse on the Method.

(2)

Answer:
Wrong pair: Simone de Beauvoir Germany.

(3)

Answer:
Wrong pair: History is not about abstract ideas but about living people – René Descartes.

Question 8.
Complete the concept chart

Answer:

Answer:

Question 9.
Prepare a flow chart on the given topic:
Stages of historiography
Answer:

Question 10.
Write short notes:
(1) Georg Wilhelm Friedrich Hegel:
Answer:

• Georg Hegel was a German philosopher.
• He was of the view that the historical realities should be presented in a logical manner. According to him, Timelme was indicative of progress.
• He believed that presentation of history is bound to change as time passes because new evidence surfaces.
• His philosophy convinced many scholars that historical methods were not of lesser quality, though they differed from the scientific method.
• His lectures and articles are published in a book called ‘Encyclopaedia of Philosophical Sciences’.
• His book ‘Reason in History’ is well known. He devised a method of analysis based on opposites known as Dialectics’.

(2) Karl Marx:
Answer:

1. Karl Marx was a German thinker in the nineteenth century. He wrote the world famous treatise Das Kapital’. According to him, history was not about abstract ideas but about living people.
2. He believed that human relationships are shaped by the fundamental needs of people and the ownership of prevalent ineczns of production to meet those needs.
3. He stated that unequal accessibility to the means of production creates à division in socièty leading to class struggle. His theory of class struggle is considered significant all over the world.
4. According to Marx, human history is the history of class struggle because the class which owns the means of production economically exploits the rest of the classes.

(3) Michel Foucault:
Answer:

• Michel Foucault was a twentieth century historian from France.
• He wrote the book ‘Archaeology of Knowledge’.
• In this book, he insisted that the prevailing practice of arranging historical events in a chronological order is not right.
• He gave importance to explaining the transitions that took place in history.
• He acknowledged the role of subjects such as science of medicine, psychological disorders, prison.
• Administration in historical analysis. This was not acknowledged by earlier historiAnswer:

(4) Leopold von Ranke:
Answer:

1. Leopold von Ranke, a German philosopher, laid emphasis on utmost importance of information gathered through original documents.
2. In order to reach historical truth, it was necessary to examine all documents related to historical event. He critcised the imaginative narration of history.
3. Collection of his articles are published in two books, entitled ‘The Theory and Practice of History’ and ‘The Secret of World History’.
4. Ranke had great influence on historiography of nineteenth century.

Question 11.
Give reasons:
(a) In historical research, it may not be possible to use the method of experiments and observation.
Answer:

1. In physical and natural sciences, experiment and observation method is used to establish laws that remain true irrespective of the time and space.
2. These laws can be tested and proved again and again.
3. In historical research, the events had already taken place in the past and we were not present in the historical time and space.
4. Moreover, these events cannot be recreated in the present time and space. Hence, experiment and observation method may not be used in historical research.

(b) Historiography in the 18th century gave importance to objectivity in history.
Answer:

• A remarkable progress was achieved in the fields of Philosophy and Science till the eighteenth century in Europe.
• It was believed that by applying scientific methods it was possible to study social and historical truths.
• In the later period, history and historiography witnessed a lot of philosophical discussion.
• This eliminated the imaginative and divine context in history and gave importance to objectivity.

Question 12.
Answer the following in 25-30 words:
(a) What is Historiography?
Answer:

1. The writing of critical historical narrative is called Historiography. A person who writes it is known as ‘Historian’. The following steps are helpful in writing historical narrative:
2. Information related to history is collected and analyzed.
3. The various sources are critically examined to understand the references regarding time and space in the given information as well as the conceptual framework used.
4. After examining the references of historical information, relevant questions related to these historical references are framed and hypotheseis are formulated.
5. In short, writing of critical historical narrative by following this method is known as historiography.

(b) What did Rene Descartes insist upon?
Answer:
French Philosopher Rene Descartes insisted on the following in writing historiography:

1. ‘Never to accept anything as true till all grounds of doubt are excluded’.
2. Hence, the reliability of a source like historical documents should be verified by critically examining them while writing history.

(c) Why is Voltaire said to be the founder of modern historiography?
Answer:
Voltaire, a french scholar, opined that it was important to consider the following aspects while writing history:

1. objective truth and chronology of events;
2. prevalent social traditions, agriculture, trade and economic system. It was because of his view that all aspects of human life was considered for history writing. Therefore, he is said to be the founder of modern historiography.

(d) What are the objectives of writing history?
Answer:
History is researched and written down with following objectives:

• To analyse the events in the past.
• To verify information about the historical events and their interconnections.
• To study in detail and remove imaginative element and bring forth the truth.
• To put the past events in chronological order.

(e) What progress was achieved in historiography in the eighteenth century?
Answer:
The following progress was achieved in historiography in the eighteenth century:

• Scientific methods were applied to study social and historical truths.
• Philosophical discourses revolving around divine phenomena were given less importance.
• Philosophical discussions focused more on the objectivity in history and historiography.
• Since the universities got an independent department of history, they became centres of historical studies.

Question 13.
Head the given passage carefully and answer the questions given below:
(a) Who is called a Historian?
Answer:
A scholar who writes critical historical narratives is called a Historian.

(b) Complete the concept chart.
Factors which determined historian’s

Answer:
Factors which determined historian’s

(c) How did the people in ancient societies preserve the events in the past?
Answer:
The ancient people preserved the events in the past so that they can pass them to the next generation. They used various means to do this:

• Narrating the stories of valour of ancestors to the next generation.
• Stories of their life preserved through cave paintings.
• Adopting story telling technique.
• Singing songs and ballads to impress events upon the minds of the new generation.

Question 14.
Answer the following questions in detail:
(a) Which experts do we need in order to prove the reliability of historical documents?
Answer:
The following experts are required to prove the reliability of historical documents:

• Language expert who can decipher the language and meaning of the document or the script on the inscription.
• One who can recognise the type of paper used and the period in which it was used.
• One who can understand the lettering style and the writing style of the author.
• Expert who has knowledge of different seals, i.e. stamps of authority used by the rulers.
• Historian who can interpret and do a comparative study of the references given in the document.

(b) Write Hegel’s view on history.
Answer:

• Georg Wilhelm Friedrich Hegel was a German philosopher.
• He was of the view that the historical realities should be presented in a logical manner.
• He believed that presentation of history is bound to change as time passes because new evidence surfaces.
• He proposed a method of analysis based on opposites known as ‘Dialectics’.
• Hegel’s philosophy convinced many scholars that historical methods were not of lesser quality, though they differed from scientific methods.
• His lectures and articles are published in a book called ‘Encyclopaedia of Philosophical Sciences’. His book ‘Reason in History’ is well known.

Question 15.
Observe the inscription in the picture and write information it:

Answer:

1. A fragment of the earliest inscription is shown in the above picture. It dates back to 4500 BCE.
2. It is displayed at the Louvre museum in France.
3. The inscriptions have names of Sumerian kings and stories of battles fought by them.
4. It shows a forward marching file of soldiers holding shields and spears. The General is in the front.
   Brain Teaser
   Hints:
   Down:
   • He used the word ‘History’ for the first time
   • He wrote the book ‘Discourse on the Method’
   • Presented Theory of ‘Dialectics’
   • He called his method ‘Archaeology of Knowledge’

Across:

• founder of modern historiography
• Criticised imaginative narration of history. Articles published in ‘The Secret of World History’
• Her writings helped in establishing the fundamentals of feminism
• He wrote ‘Das Kapital’
  

10th Std History Questions And Answers:

• Historiography Development in the West Class 10 History Questions And Answers
• Historiography Indian Tradition Class 10 History Questions And Answers
• Applied History Class 10 History Questions And Answers
• History of Indian Arts Class 10 History Questions And Answers
• Mass Media and History Class 10 History Questions And Answers
• Entertainment and History Class 10 History Questions And Answers
• Sports and History Class 10 History Questions And Answers
• Tourism and History Class 10 History Questions And Answers
• Heritage Management Class 10 History Questions And Answers

Balbharti Maharashtra State Board Class 10 Political Science Solutions Chapter 3 Political Parties Notes, Textbook Exercise Important Questions and Answers.

Std 10 Political Science Chapter 3 Question Answer Political Parties Maharashtra Board

Class 10 Political Science Chapter 3 Political Parties Question Answer Maharashtra Board

Political Science Class 10 Chapter 3 Question Answer Maharashtra Board

Question 1.
Choose the correct option from the given options and complete the sentences.
(1) When people come together and participate in electoral process, to acquire political power, such organisations are called ………………………….. .
(a) Government
(b) Society
(c) Political parties
(d) Social organisations
Answer:
(c) Political parties

(2) National Conference is a party in ………………………….. this region.
(a) Odisha
(b) Assam
(c) Bihar
(d) Jammu and Kashmir
Answer:
(d) Jammu and Kashmir

(3) Justice Party- a non-Brahmin movement was transformed into ………………………….. Political Party.
(a) Assam Gan Parishad
(b) Shivsena
(c) Dravid Munnetra Kazhagam
(d) Jammu and Kashmir National Conference
Answer:
(c) Dravid Munnetra Kazhagam

Question 2.
State whether the following statements are true or false. Give reasons for your answer.
(1) Political parties act as a link between government and people.
Answer:
The above statement is True.

• The political parties convey the demands and complaints of the people to the government.
• Information about various government policies and schemes are conveyed to the people by the political parties.
• People’s reaction to the policies and their expectations are conveyed to the government too by the parties. In this way, political parties act as a link between government and the people.

(2) Political parties are social organisations.
Answer:
The above statement is True.

• People who have similar views come together voluntarily and form a party, so it can be said that political parties are an integral part of our society.
• The political parties try to solve the problems of the people.
• Some political parties represent the role of a particular community in society, its ideology and work to achieve it. Hence it can be said that political parties are social organizations.

(3) Coalition politics leads to instability.
Answer:
The above statement is False.

• As no single party got majority after the elections held in 1989, coalition government came to power at the centre and many states.
• Parties had to set aside their policies and programmes and concentrate on a common agenda to run the government.
• Both Congress Party and the Bharatiya Janata Party made an experiment of establishing a coalition government.
• The National Democratic Alliance formed by BJP and its partners and the Democratic Front government formed by Congress and its partners ruled at the centre and state level effectively.

Therefore, the belief that the coalition government brings instability was proved wrong.

(4) Shiromani Akali Dal is a national party.
Answer:
The above statement is False.
The Election Commission of India recognises a political party as National or Regional party on the basis of specific criteria namely:

• The number of seats secured in Parliament and Legislative Assembly or percentage of votes secured.
• Shiromani Akali Dal does not meet the criteria listed above.
• As its influence is limited to the state of Punjab and not in any other state.
• The Election Commission has given recognition to it as regional party.

Question 3.
Explain the following concepts.
(1) Regionalism
Answer:

• India is a vast country with great physical diversity. People belonging to different regions have their own language, culture and traditions.
• Along with the physical diversity, we find diversity in literature, education, history and movements.
• Each one feels an affinity for his language, traditions and history of social reforms. This gives rise to linguistic identity.
• This affinity towards all the above-mentioned aspects develops into identity consciousness and gives rise to excessive regional pride.
• People start giving preference only to the development of their language and region.
• This is known as Regionalism.

(2) National Parties
Answer:
A party which functions at the national level is known as National Party.

1. The Election Commission has laid certain criteria for a party to get recognised as a Political party. The political party should secure at least f 6% valid votes in four or more states in the earlier Lok Sabha. OR
2. State Assembly elections and minimum four members should be elected in the Lok Sabha from any state or states in the earlier elections. OR
3. The candidates of a party should be elected from a minimum three states or should be elected from a minimum 2% constituencies of the total Lok Sabha constituencies. OR
4. It is important to get recognition as a state party in at least four states.

Question 4.
Answer the following questions in brief.
(1) What are the major characteristics of political parties?
Answer:
The main features of political parties are as follows:

• Political parties aim at securing power by contesting elections.
• Every political party has some ideology.
• Every party has an agenda. It is based on the party’s ideology.
• The party that gets majority seats in election forms the government and the one that does not secure the majority act as opposition parties.
• Political parties are a link between the people and the government and work to gain the support of the people.

(2) What changes have taken place in the nature of political parties in India?
Answer:
The following changes were seen in the party system in India:

• Indian- National Congress was the only dominant party in states and at the centre after independence.
• All other parties came together and formed a coalition in 1977 and defeated the Congress.
• For the first time in history, the two-party system got importance over one-party system.
• The one-party system came to an end after the 1989 elections.
• Regional parties got importance and the coalition government was formed at the centre and in the states.

Project
(1) In a map of Maharashtra, point out the Loksabha constituency that includes the names of your parents.
(2) In a map of India, point out the places where national political parties have their influence.
Answer:

Memory Map

Question 5.
Choose the correct option from the given options and complete the sentences:
(a) The party which fails to secure majority is known as ………………………. party.
(a) Ruling
(b) Opposition
(c) Independent
(c) Coalition
Answer:
(b) Opposition

(b) ‘Bharatiya Janata Party’ which was formed in 1980 after a split with ………………………. a component of Janata Party.
(a) Jan Sangh
(b) Lok Dal
(c) Independent party
(b) Janata Dal
Answer:
(a) Jan Sangh.

(c) Social support received by a political party is called ………………………. .
(a) Democracy
(b) People’s rule
(c) Mass base
(d) Public relation
Answer:
(c) Mass base

(d) Promotion of the Marathi language is the objective of the ………………………. .
(a) Dravida Munnetra Kazhagam
(b) Shiromani Akali Dal
(c) Shiv Sena
(d) Assam Gana Parishad
Answer:
(c) Shiv Sena

(e) There are ………………………. recognised parties in India.
(a) five
(b) seven
(c) nine
(d) six
Answer:
(b) seven

(f) The main objective of the political party is to capture ………………………. and retain it.
(a) publicity
(b) victory
(c) power
(d) information
Answer:
(c) power

(g) The ideology of the Communist Party of India is based on ………………………. Philosophy.
(a) Capitalist
(b) Marxist
(c) Democracy
(d) Imperialist
Answer:
(b) Marxist

(h) Shiromani Akali Dal is a prominent regional party in ………………………. state.
(a) Odisha
(b) Assam
(c) Punjab
(d) Jammu and Kashmir
Answer:
(c) Punjab

Question 6.
State whether the following statements are true or false. Give reasons for your answer:

(a) Political parties do not need support of the people.
Answer:
The above statement is False.

• To secure power is the main aim of political parties.
• Political parties have to implement various policies and programmes for the welfare of people and to gain the support of the people.
• The party which solves the issues related to the welfare of the people get support.
• Without the support of the people they can never get a mandate.

Hence, all political parties require support of the people.

(b) The Communist Party of India was split.
Answer:
The above statement is True.

• The Communist Party of- India was established in 1925. The Communist Parties follow Marxist ideology.
• In 1962, due to differences in the leadership a rift was created in the party.
• The main reason for the split was about which political line to follow.

(c) Sometimes the sentiments of regionalism gets strengthened in the country.
Answer:
The above statement is True.

1. A country like India has diversity of government language, region and culture. This diversity creates affinity towards a region.
2. This affinity gives rise to excessive regional S pride and initiating movements to save it. The significance of such movements is claimed to be for preserving culture.
3. Asserting to be rightful claimant of material resources, job opportunities and development of the region these movements strengthen the regional pride.
4. Thus, this excessive regional pride turns morbid taking the form of regionalism.

(d) Regional parties have no influence on National Politics.
Answer:
The above statement is False.

• No single party got majority in the elections to Lok Sabha held in 1989.
• The national parties formed coalition government at the centre taking help of regional parties.
• As regional parties share power at the centre they have influence on national politics.

Question 7.
Explain the concept:
(a) Regional Parties:
Answer:

1. The groups having a proud feeling about the different identity of their region and who compete to capture power to bring about regional development are ‘Regional Parties’.
2. The influence of such parties are limited to their region. They give importance to regional problems. Development of one’s own region is the prime objective of these parties.
3. Sometimes they demand for independent state or autonomy. They influence the national politics because of their dominance in the region.
4. They have passed through various phases, from separatism to autonomy and have then merged with mainstream national politics.

(b) Political Party:
Answer:

1. A Political Party is a kind of social organisation of like-minded people. The main aim of any political party is to contest election and secure power.
2. The stand taken by various political parties on issues becomes their political ideology.
3. In democracy, political parties are at the centre of all political activities. They are a link that connects common people, democracy, representation and elections.
4. The party that secures a majority becomes the ruling party and the rest are known as the. opposition.

Question 8.
Write short note:
(a) Party System:
Answer:

1. If one party remains in power in a country for a long period and no other party has any kind of influence the party system it is called ‘One- Party System’.
2. When there are two equally strong parties which alternatively come to power. It is called ‘Two-Party System’.
3. In a country where many political parties exist and compete with each other to capture power and have more or less influence in different states is called ‘Multi-Party System’.
4. Democracy develops in Multi-Party System.

(b) Indian National Congress:
Answer:

• The Indian National Congress was established in 1885.
• The party represented the hopes and aspirations of Indians and led the freedom struggle.
• Groups having diverse ideologies became part of the Congress to fight for freedom.
• It believes in democratic socialism, social equality and international peace.
• After independence, the Congress Party was a dominant party for almost four decades and ruled at the centre and in the states.

(c) Communist Party of India:
Answer:

• The Communist Party of India was established in 1925. The Communist Party follows the Marxist ideology.
• The party aims at working to protect the interests of workers and labourers.
• The main objective of this party is to oppose capitalism and protect the interests of workers.
• The party split due to ideological differences in 1964. Those who walked out of the party formed Communist Party (Marxist).

(d) Nationalist Congress Party:
Answer:

• Nationalist Congress Party (NCP) is the splinter or breakaway party from the Congress Party.
• It considers the values like democracy, equality and secularism important.
• It became part of United Progressive Alliance (UPA) and came to power in Maharashtra.
• It was in power in Maharashtra from 1999 to 2014 and at the centre from 2004 to 2014.

(e) Trinamool Congress:
Answer:

• All India Trinamool Congress was established in 1998.
• The Election Commission of India gave it recognition in 2016.
• Democracy, Secularism and protection of the weaker sections of the society are some of the policies of the party.
• Presently (April 2019), this party is in power in the state of West Bengal.

(f) Shiv Sena:
Answer:

1. The Shiv Sena was founded in 1966.
2. The main objective of the party was to fight for the cause of Marathi-speaking people and preservation of Marathi language.
3. They resisted the people from other regions.
4. In 1995, it became the ruling party with BJP in Maharashtra and its strategic tie-up with BJP helped it to enter national politics.
5. It was in power at the centre with BJP from 1998 to 2004. Again it has shared power with the BJP at the centre and state since 2014.

(g) Shiromani Akali Dal:
Answer:

• Shiromani Akali Dal was formed in 1920.
• It is a dominating party in Punjab.
• It gives preference to nurture religious and for the regional pride.
• The party has retained power in Punjab for many years.

(h) Dravid Munnetra Kazhagam:
Answer:

• Justice party, a non-Brahmin movement, started in 1920. In 1944, it transformed into a political party called Dravid Kazhagam.
• In 1949, a group within the party got split and formed Dravid Munnetra Kazhagam (DMK).
• The party works for the protection of Tamil identity.
• This party implemented many policies for welfare of the people and therefore has support from all the sections of society.
• Another group separated from it in 1972 and formed All India Dravid Munnetra Kazhagham.
• It remained in power for a long time in Tamil Nadu and for sometime at the centre.

Question 9.
Do as directed
(a) Complete the concept map:

Answer:

Answer:

(3)

Answer:

(b) Complete the Time-line writing the name of the party or the year of establishment:

Answer:

Question 10.
Answer the following questions in brief:

(a) What is called “mass base”?
Answer:

• Every political party is formed with some ideology.
• Political parties take a certain stand towards public issues.
• Their ideology and their stand towards public issues are conveyed to the people through various programmes.
• If the people agree with their role and ideology, they get the support of the people.
• Such social support received by a political – party is called ‘mass base’.

(b) Write about the policies of Indian National Congress.
Answer:
The policies of the Indian National: Congress are as follows:

• Equal rights for the minorities and weaker sections of society.
• Secularism, all-round development and social welfare are its objectives.
• Introduction of socialist democracy.
• Belief in values like international peace and social equality.

(c) Explain the role of Bharatiya Janata Party.
Answer:
Bharatiya Janata Party was formed in 1980 with the following objectives:

• To preserve Indian culture and traditions.
• To create a strong and rich India.
• To give importance to economic reforms for development of India.

(d) Write about the policies of Communist Party of India (Marxist).
Answer:
Communist Party of India (Marxist) was formed in 1964 with the following objectives:

• The party advocates socialism, secularism and democracy.
• The main policy of the party is to work for the welfare of farmers, landless labourers and workers.
• The party opposes imperialism.

(e) Why was Bahujan Samaj Party formed?
Answer:
The Bahujan Samaj Party was formed in 1984 to achieve the following objectives:

• To bring socialist ideology into practice.
• To secure power for ‘majority’ comprising of scheduled castes, scheduled tribes and other backward classes.
• To give power in the hands of ‘majority’.

(f) What do the regional parties give preference for?
Answer:
The regional parties give preference to the following issues:

• Importance should be given to regional issues and bring about development.
• Regional issues should be handled* at regional level.
• The power rests in the hands of regional people. ‘
• People living in that region should get preference in administration and jobs. .

(g) What changes are seen in the nature and role of regional parties?
Answer:
The role of regional parties changed over period of time. The changes are as follows:

• After independence, regional identity gave rise to separatists movements and demands were put up by regional parties for separate state.
• They wanted to break away from the Indian union and form a separate state.
• The demands of the regional parties changed gradually and these parties started asking for autonomy.
• In the later period, for the development of their region and people the parties demanded representation of their people in the state and central government.
• Regional parties in the north eastern region also started demanding more autonomy after split up.
• The journey of the regional parties began with a split up and then a demand for autonomy going on to share power in federation and then entry into mainstream national politics.

(h) What are the objectives of Assam Gana Parishad?
Answer:
Assam Gana Parishad was formed in 1985 with the following objectives:

• To preserve the uniqueness of Assam’s culture, language and social identity.
• To make efforts for economical development of Assam.
• To resolve problems of displaced people.

(i) What are the criteria for a regional party to get recognition?
Answer:

• In the last general .elections to the State Assembly, the party should not secure less than 6% of the total number of valid votes polled.
• At least 2 members to be elected to the Legislative Assembly (Vidhan Sabha).
• 3% seats of the total seats of Legislative Assembly or at least 3 seats in Legislative Assembly.

(j) What work is done by political parties?
Answer:
The following work is done by political parties:

• To propagate policies and programmes of the party and contest elections.
• They implement various policies when they come to power.
• If they fail to secure power, they act as opposition party and try to gain support of the people.
• They communicate the demands and complaints of the people to the government and the policies and programmes of the government to the people.

Question 11.
Give your opinion:

(a) Imagine you are opposition party leader and you have observed that the ruling party has not done good work in the field of health. What will you do as a leader of opposition?
Answer:
As opposition leader, I will do the following to make the government realise its negligence in the health field:

• I will question the government in Parliament and point out their shortcomings and ask about the prolonged projects.
• I will create awareness among the people by writing articles in newspapers.
• I will give interviews,on radio and television and criticize the government.
• I will organise rallies and meetings to sensitize among the people.

(b) Think and write
What has to be done to bring partyless democracy in modern times?
Answer:

• The recognition of all the parties should be cancelled. ‘
• People should be given the right to make decisions.
• In order to improve the decision-making power, people should be educated on political issues.
• To improve the moral character of the people who want to take the leadership.
• To initiate direct democracy and prepare the people for the same.
• Stress should be given for decentralization.
• Mahatma Gandhi, Vinoba Bhave and Jayprakash Narayan put forth the idea of partyless democracy.
• What has to be done to bring such democracy in modern times?

Question 12.
What do you understand by the following news in newspapers? Explain in brief.

(a) Opposition parties held a meeting in Mumbai to resist the Ruling party. Will take up the issue of farmers?
Answer:

• The ruling party did not undertake any work for the welfare of farmers. Therefore all the opposition parties decided to trap the government on this issue.
• The opposition parties have kept aside their differences and come together for this cause.
• It is the duty of the opposition party to question the negligence of the government.
• This news makes us aware of the line of action taken by the opposition.
• Opposition parties held a meeting in Mumbai to resist the Ruling party. Will take up the issue of farmers?
• Ruling party organised ‘Samvad Yatra’ in rural areas.

(b) Ruling party has organised ‘Samvad Yatra’ in rural areas.
Answer:

• Political parties adopt different ways to popularise their party and influence the people.
• As the means of communication are limited in rural areas they organise the Yatra.
• It shows the efforts of the government to understand problems of people in rural areas.
• It is essential to have dialogue with people to know their problems and opinions.
• As the initiative is taken by the government, people will develop faith in government.
• The news conveys to us that the ruling party is carrying out its duties properly.
• The faith in government becomes profound when people feel that government is sensitive towards them.

10th Std Political Science Questions And Answers:

• Chapter 1 Working of the Constitution Class 10 Political Science Questions And Answers
• Chapter 2 The Electoral Process Class 10 Political Science Questions And Answers
• Chapter 3 Political Parties Class 10 Political Science Questions And Answers
• Chapter 4 Social and Political Movements Class 10 Political Science Questions And Answers
• Chapter 5 Challenges faced by Indian Democracy Class 10 Political Science Questions And Answers