Balbharti Maharashtra State Board Class 10 Marathi Solutions Aksharbharati Chapter 10 रंग साहित्याचे Notes, Textbook Exercise Important Questions and Answers.
Class 10th Marathi Aksharbharati Chapter 10 रंग साहित्याचे Question Answer Maharashtra Board
Std 10 Marathi Chapter 10 Question Answer
Marathi Aksharbharati Std 10 Digest Chapter 10 रंग साहित्याचे Textbook Questions and Answers
प्रश्न 1.
प्रस्तुत पाठात आलेल्या साहित्य प्रकारांची नावे लिहा.

उत्तर:
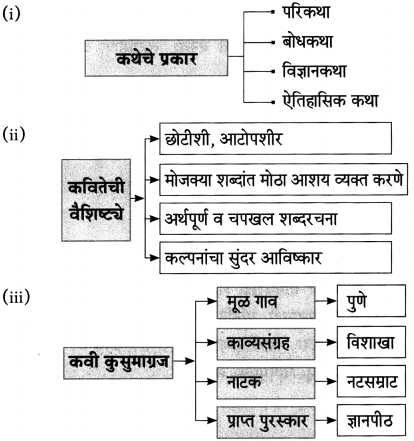
(i) कथा
(ii) कादंबरी
(iii) कविता
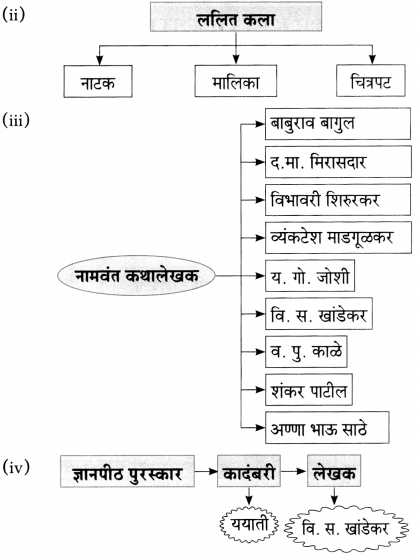
(iv) नाटक
(v) चरित्र
(vi) आत्मचरित्र
(vii) प्रवासवर्णन
प्रश्न 2.
आकृतिबंध पूर्ण करा.
उत्तर:
![]()
प्रश्न 3.
फरक स्पष्ट करा.

उत्तर:
प्रश्न 4.
खाली दिलेल्या अनेकवचनी नामांचे एकवचनी रूप लिहून त्यांचा वापर करून प्रत्येकी एक वाक्य तयार करा.
(i) रस्ते
(ii) वेळा
(iii) भिंती
(iv) विहिरी
(v) घड्याळे
(vi) माणसे
उत्तर:
(i) रस्ते – रस्ता – हा रस्ता रूंद व डांबरी आहे.
(ii) वेळा – वेळ – सकाळची वेळ अभ्यासासाठी चांगली असते.
(iii) भिंती – भिंत – चीनची भिंत खूप उंच व लांब आहे.
(iv) विहिरी – विहीर – गावाकडची विहीर पाण्याने भरली आहे.
(v) घड्याळे – घड्याळ – भिंतीवरचे घड्याळ सुशोभित दिसते.
(vi) माणसे – माणूस – कष्टाळू व इमानदार माणूस बक्षिसपात्र असतो.
![]()
प्रश्न 5.
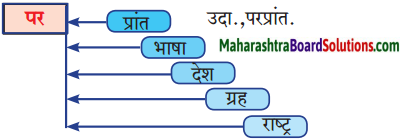
खालील शब्दांना ‘पर’ हा एकच शब्द जोडून नवीन अर्थपूर्ण शब्द तयार होतात. ते बनवा. मराठी भाषेतील अशा विपुल शब्दसंपत्तीचा अभ्यास करा. त्याप्रमाणे वेगवेगळे शब्द तयार करा.
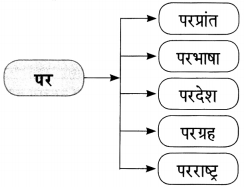
उत्तर:
प्रश्न 6.
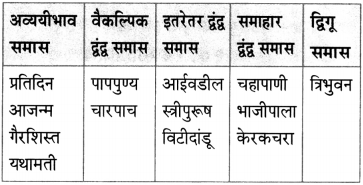
खालील सामासिक शब्दांचा समास ओळखून तक्ता पूर्ण करा.
यथामती, प्रतिदिन, आईवडील, चारपाच, त्रिभुवन, केरकचरा, भाजीपाला, चहापाणी, आजन्म, गैरशिस्त, विटीदांडू, पापपुण्य, स्त्रीपुरुष

उत्तर:
प्रश्न 7.
स्वमत.
(अ) पुस्तकाशी मैत्री करण्याचे फायदे लिहा.
उत्तरः
पुस्तकांशी मैत्री म्हणजे निर्भेळ आनंदच. पुस्तके आपल्याशी बोलतात, त्यांचे विचार प्रगट करतात. ज्ञान देतात. चांगल्या कामासाठी प्रेरणा देतात. कठीण संकल्पना सोप्या करून सांगतात. चित्रांद्वारे, शब्दांतून मनमोकळ्या गप्पा मारतात. शब्दसंग्रह वाढवितात. प्रसंगी विविध स्थळांना भेटी दिल्याचा आनंद देतात. पुस्तके आपल्यावर कधीही रागावत नाहीत. रूसत नाहीत. भांडत नाहीत. काही अपेक्षा ठेवत नाहीत. म्हणून त्यांच्याशी मैत्री करून आपणही त्यांची काळजी घेणे तितकेच गरजेचे आहे.
![]()
(आ) तुम्हाला आवडलेल्या कोणत्याही एका साहित्यप्रकाराची वैशिष्ट्ये तुमच्या शब्दांत लिहा.
उत्तरः
मला आवडलेला साहित्यप्रकार म्हणजे कादंबरी. कादंबरी म्हणजे मोठी कथाच. विविध पात्रांनी, प्रसंगांनी नटलेली, सजलेली. कादंबरी जर खुमासदार असेल तर, ती हातातून सोडवत नाही. पुढे काय होणार याची उत्कंठा लागते. त्यातील पात्रांचा परिचय होतो व ती पात्रे आपल्याला आपल्यातीलच वाटू लागतात. कादंबरीत मन रममाण होते. सुखाच्या प्रसंगात भान हरपते. दु:खी प्रसंगाने अतिशय वाईटही वाटते, इतके तादात्म्य कादंबरीशी साधता येते. ‘ययाति’, ‘स्वामी’, या कादंबऱ्या माझ्या आवडत्या आहेत.
(इ) ‘उत्तम लेखक होण्यासाठी उत्तम वाचक होणे आवश्यक असते’, याबाबत तुमचे विचार स्पष्ट करा.
उत्तरः
‘वाचाल तर वाचाल’ या उक्तीप्रमाणे वाचनाने आपणांस अनेक लाभ होतात. वाचनाने शब्द संपत्ती वाढते. नवनवीन संकल्पना कळतात. विचार प्रगल्भ होतात, लेखक होण्यासाठी या सर्वांचा उपयोग होतो. समाजातील चालीरिती, संस्कृती, नवीन शोध, पर्यटन, शैक्षणिक स्तर यांची माहिती वाचनाने मिळते. विचारांची बैठक पक्की होते. काळाचे भान येते. नव्या जुन्या गोष्टी कळतात. उत्तम विचार समर्थ लेखणीद्वारे प्रगट होतात.
(ई) तुम्हाला आवडलेल्या पुस्तकाबाबत खालील मुद्द्यांचा विचार करून माहिती लिहा.
(१) पुस्तकाचे नाव
(२) लेखक
(३) साहित्यप्रकार
(४) वर्ण्य विषय
(५) मध्यवर्ती कल्पना
(६) पुस्तकातून मिळणारा संदेश
(७) मूल्य
(८) सामाजिक महत्त्व
(९) आवडण्याची कारणे
उत्तरः
मला ‘पांडुरंग सदाशिव साने’ लिखित ‘श्यामची आई’ हे पुस्तक आवडते. हा ‘कादंबरी’ साहित्यप्रकार असून प्रस्तुत कादंबरीत श्याम हे मुख्य पात्र आहे. बालपणी त्यावर झालेले संस्कार, आईने लावलेले वळण, घरची गरीबी पण संस्कारांची श्रीमंती अशा मिश्रणातून घडलेला श्याम म्हणजे स्वतः लेखक पांडुरंग सदाशिव साने, अर्थात साने गुरूजी. मोठेपणी स्वातंत्र्य लढ्यात सहभागी झाले.
गांधीवादाचा पुरस्कार केला. कारागृहात रोज रात्री आपल्या इतर कैदी मित्रांसोबत लहानपणीच्या सर्व आठवणींना उजाळा दिला. रोज एक कथा सांगण्याचा परिपाठ झाला व त्यातून ‘श्यामची आई’ पुस्तक साकारले. धारिष्ट्य, खरेपणा, स्वाभिमान, निखळप्रेम, सहिष्णूता या गोष्टींचा अंतर्भाव या कादंबरीत ओतप्रोत भरला आहे.
आजच्या तंत्रज्ञानाच्या युगात बुद्ध्यांक जरी वाढला तरी भावनांक कमी झाला आहे. ही कादंबरी वाचून समानता, आदरभाव, स्वाभिमान, सच्चेपणा या मुल्यांची सजवणूक समाजात होईल, आईविषयीचे नितांत प्रेम, आईचे ही खरे मार्गदर्शन अशा वात्सल्यतेची अपूर्व कहाणी ‘श्यामची आई’ मध्ये असल्याने ही कादंबरी आवडते.
![]()
Marathi Akshar Bharati Class 10 Textbook Solutions Chapter 10 रंग साहित्याचे Additional Important Questions and Answers
प्रश्न १. खालील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा.
कृती १ : आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः
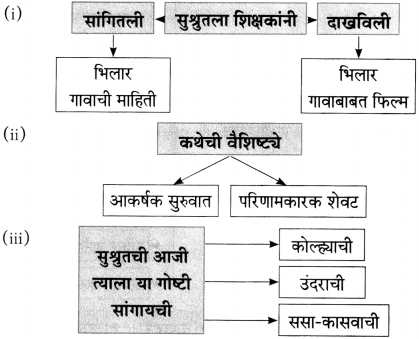
प्रश्न 2.
चौकटीत उत्तरे लिहा.
उत्तरः
(i) सुश्रुतची सहल या गावी नेण्याचे ठरले – [भिलार]
(ii) मुलामुलींचा वेश करून आले – [पुस्तके]
(ii) कथेचे दुसरे नाव – [गोष्ट]
![]()
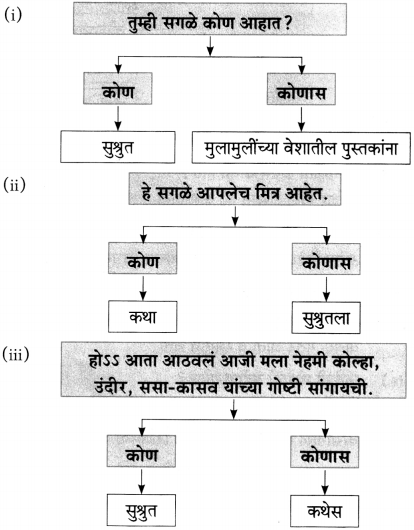
प्रश्न 3.
कोण कोणास म्हणाले?
उत्तरः
कृती २ : आकलन कृती
प्रश्न 1.
खालील शब्द उत्तर येईल असे प्रश्न तयार करा,
(i) हातात हात घालून
(ii) लहानपणापासूनच.
उत्तर:
(i) काही पुस्तके कशी नाचत होती?
(ii) कथेची ओळख सुश्रुतला केव्हापासून आहे?
प्रश्न 2.
सहसंबंध लिहा.
(i) सूचना : वर्ग : : सहल : ……………………………..
उत्तर:
भिलार
![]()
प्रश्न 3.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा,
(i) सुश्रुतच्या वर्गाची …………………………….. गावाला सहल नेण्याचे ठरले. (किल्लारी, भिलार, पुणे, ठाणे)
(ii) काही पुस्तके मुला – मुलींचा वेश करून आणि हातात हात घालून …………………………….. गाणी गात आहेत. (नाचत, बागडत, आनंदाने, उत्साहाने)
उत्तर:
(i) भिलार
(ii) आनंदाने
प्रश्न 4.
खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.
(i) सुश्रुतला कथा आपले दुसरे नाव काय सांगते?
उत्तर:
सुश्रुतला कथा आपले दुसरे नाव ‘गोष्ट’ असे सांगते.
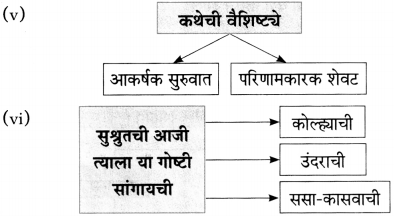
(ii) सुश्रुतची आजी त्याला कोणत्या गोष्टी सांगायची?
उत्तर:
सुश्रुतची आजी त्याला कोल्हा, उंदीर, ससा-कासव यांच्या गोष्टी सांगायची.
(iii) अरे आम्ही सर्व तुला भेटायला आलो आहोत, असे सुश्रुतला कोण म्हणाले?
उत्तर:
अरे आम्ही सर्व तुला भेटायाला आलो आहोत, असे सुश्रुतला पुस्तकाच्या वेशातील मुले म्हणाली.
प्रश्न २. खालील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा.
कृती १ : आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः
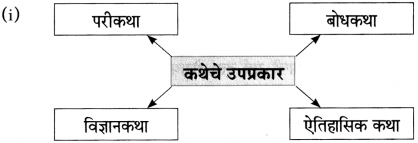
![]()
प्रश्न 2.
खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.
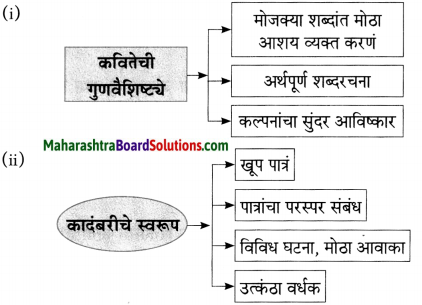
(i) कलाकृती उत्तम केव्हा होते?
उत्तरः
दर्जेदार कथा असली की कलाकृती उत्तम होते.
(ii) कथेच्या यशाचे रहस्य काय?
उत्तर:
उत्तम निवेदनतंत्राचा वापर हे कथेच्या यशाचे रहस्य आहे.
(iii) कादंबरी वाचताना वाचक कशात रममाण होतो?
उत्तरः
कथानकात पुढे काय होईल याच्या विचारात कादंबरी वाचताना वाचक गुंतून जातो व रममाण होतो.
(iv) कथेची थोरली बहीण कोण?
उत्तर:
कथेची थोरली बहीण कादंबरी होय.
प्रश्न 3.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.
(i) …………………………… म्हणजे खरं तर मोठी कथाच; पण माझा आवाका कथेपेक्षा पार मोठा! (कथा, निबंध, कादंबरी, संवाद)
(ii) साहित्य क्षेत्रातील सर्वोच्च मानाचा …………………………… पुरस्कार वि. स. खांडेकर यांच्या ययाति या कादंबरीला मिळाला. (अर्जुन, ज्ञानपीठ, साहित्य)
(iii) कवितेची शब्दरचना अर्थपूर्ण व …………………………… असते. (चपखल, लयबद्ध, वैशिष्ट्यपूर्ण, आशययुक्त)
(iv) उत्तम …………………………… तंत्रामुळे मी खुलत जाते, रंगत जाते किंबहुना उत्तम निवेदनतंत्राचा वापर हे माझ्या यशाचं रहस्य. (भाषण, कथन, निवेदन, अनुवादन)
उत्तर:
(i) कादंबरी
(ii) ज्ञानपीठ
(iii) चपखल
(iv) निवेदन
![]()
कृती २ : आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः
प्रश्न 2.
सकारण लिहा.
(i) कवितांची व आपली फार पूर्वीपासून चांगलीच ओळख आहे.
उत्तर:
शालेय जीवनात पाठ्यपुस्तकातील सगळ्या कविता तालासुरांत म्हटल्या जातात.
(ii) मराठी माणसांचा ऊर अभिमानानं भरून आला.
उत्तरः
साहित्य क्षेत्रातील सर्वोच्च मानाचा ‘ज्ञानपीठ’ पुरस्कार वि. स. खांडेकर यांच्या ‘ययाति’ या कादंबरीला मिळाला.
प्रश्न 3.
चूक की बरोबर ते लिहा.
(i) ‘ही आवडते मज मनापासुनी शाळा’ आणि ‘श्रावणमासी हर्ष मानसी’ या सुश्रुतच्या नावडत्या कविता होत्या.
(ii) कादंबरी म्हणजे खरं तर मोठी कथाच.
उत्तर:
(i) चूक
(ii) बरोबर
कृती ३ : स्वमत
प्रश्न 1.
तुम्ही दूरदर्शनवर किंवा प्रत्यक्षात पाहिलेल्या काव्य संमेलनाविषयी तुमचे मत लिहा.
उत्तर:
होळीच्या निमित्ताने भरलेल्या काव्यसंमेलनास मला प्रत्यक्ष उपस्थित राहण्याचा योग आला. मोठ्या व्यासपीठावर अनेक कवी, कवयित्री विराजमान होते. प्रत्येक जण आपली कविता विशिष्ट हावभावांसहित, चालीत म्हणून दाखवीत होते. कवितांची रचना अर्थपूर्ण व चपखल होती. कल्पनांचा सुंदर आविष्कार होता. काही कविता सामाजिक होत्या तर काही कविता हास्यरसपूर्ण होत्या. श्रोते मनापासून कवितांना दाद देत होते. कवीच्या आवाजातील चढउतार, त्यांचे हावभाव कौतुकास्पद होते. काही कवितांमध्ये अनुप्रासामुळे गोडवा होता. उत्प्रेक्षा, उपमा, रूपक अलंकारांनी सजलेल्या या कविता मनाला मोहून गेल्या. काव्यसंमेलन कधी संपले ते कळले नाही. कविता गुणगुणतच आम्ही बाहेर पडलो.
![]()
प्रश्न ३. खालील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा.
कृती १ : आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः
प्रश्न 2.
खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.
(i) सामान्य लोकांची मते कशी बदलतात?
उत्तर:
चरित्र वाचनाने सामान्य लोकांची मते बदलतात,
(ii) चरित्र कसे असते?
उत्तर:
चरित्र संघर्षमय, कर्तृत्ववान, संधीचे सुवर्णसंधीत रूपांतर करणारे असते.
(iii) चरित्र कसे जन्माला येते?
उत्तर:
एखादया थोर व्यक्तिमत्त्वाच्या आयुष्याची गाथा लिहिण्याची प्रेरणा लेखकाला मिळते व चरित्र जन्माला येते.
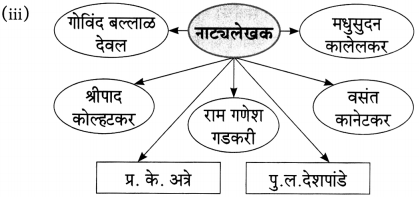
(iv) नाटककाराची कोणती अपेक्षा असते?
उत्तरः
नाटक वाचनीय आणि प्रेक्षणीय व्हावं अशी नाटककाराची अपेक्षा असते.
![]()
प्रश्न 3.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.
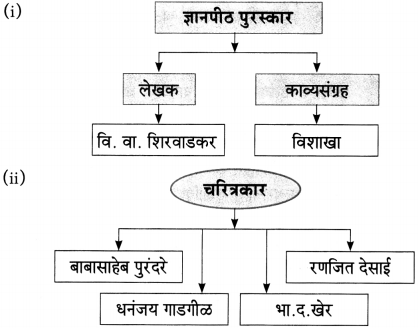
(i) …………………………. नाटकाचे लेखक वि. वा. शिरवाडकर म्हणजेच कवीवर्य कुसुमाग्रज. (‘नटसम्राट’, ‘विठ्ठल तो आला’, ‘गिधाड’, ‘कुलांगार’)
(ii) माझं रंगमंचावर सादरीकरण होणार याचे भान ठेवूनच …………………………. माझी मांडणी करतो. (कादंबरीकार, कथाकार, कविताकार, नाटककार)
उत्तर:
(i) ‘नटसम्राट’
(ii) नाटककार
कृती २ : आकलन कृती
प्रश्न 1.
कारणे शोधा.
(i) नाटक मराठी माणसाच्या हृदयात अढळ स्थान प्राप्त करते कारण . . .
उत्तरः
पात्ररचना, चुरचुरीत संवाद आणि नाट्यमय घटना प्रसंग यांमुळे नाटक मराठी माणसाच्या हृदयात अढळ स्थान प्राप्त करते.
(ii) २७ फेब्रुवारीला मराठी दिन साजरा करतात कारण . . .
उत्तर:
२७ फेब्रुवारी हा ‘ज्ञानपीठ’ पुरस्काराचे मानकरी कविवर्य कुसुमाग्रज म्हणजे वि.वा.शिरवाडकर यांचा जन्मदिन आहे. त्यांच्या साहित्य सेवेमुळेच त्यांचा जन्मदिवस मराठी दिन म्हणून साजरा करतात.
प्रश्न 2.
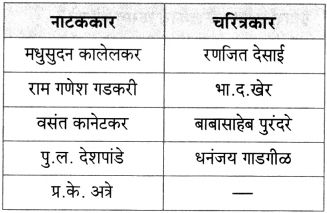
वर्गीकरण करा.
वसंत कानेटकर, रणजित देसाई, पु.ल. देशपांडे, धनंजय गाडगीळ, प्र.के. अत्रे, भा.द.खेर, राम गणेश गडकरी, मधुसुदन कालेलकर, बाबासाहेब पुरंदरे
उत्तरः
![]()
प्रश्न 3.
योग्य पर्याय निवडून विधान पूर्ण करा.
(i) संतकाव्यापासून पंतकाव्य, मध्ययुगीन काव्य, शाहिरी काव्य अशी वळणे घेत आधुनिक काळात मी …
(अ) मुक्त छंदाचे रूप धारण केले आहे.
(आ) करूण रसाचे रूप धारण केले आहे.
(इ) अभंग छंदाचे रूप धारण केले आहे.
(ई) मुक्त छंदाचे रूप स्वीकारले आहे
उत्तर:
संतकाव्यापासून पंतकाव्य, मध्ययुगीन काव्य, शाहिरी काव्य अशी वळणे घेत आधुनिक काळात मी मुक्त छंदाचे रूप धारण केले आहे.
प्रश्न 4.
चूक की बरोबर लिहा.
(i) ‘नटसम्राट’ नाटकाचे लेखक कुसुमाग्रज म्हणजेच वि. वा. शिरवाडकर.
(ii) थोरांची चरित्रे सामान्यांना धोका देतात.
उत्तर:
(i) बरोबर
(ii) चूक
कृती ३ : स्वमत
प्रश्न 1.
‘नाटक कलाकाराला घडवते’ याचे समर्थन करणारे विचार तुमच्या शब्दांत मांडा.
उत्तरः
साहित्यप्रकारातील ‘नाटक’ हा भाग म्हणजे विलक्षण आव्हानात्मक, नाट्यसंहिता लिहिण्यापासून ते थेट रंगमंचापर्यंतचा नाटकाचा प्रवास हा विविधांगी असतो. उत्कृष्ट लेखन, उत्कृष्ट दिग्दर्शन व उत्कृष्ट अभिनय यावर नाटकाचे यश अवलंबून असते, नाटकात काम करणारे कलाकार शब्दांना मूर्तरूप देतात. प्रेक्षकांच्या मनावर पकड करतात. संवादफेक, शब्दांचे उच्चार, आवाजातील चढ-उतार, नाटकाचा आशय व त्यातून समाजाला मिळणारा संदेश याची जबाबदारी कलाकारावर असते. कलाकार त्या भूमिकेत मनापासून शिरल्याखेरीज ती भूमिका प्रभावी होत नाही. नाटक कलाकाराच्या रोमारोमांत भिनलेले असते. म्हणून नाटक कलाकाराची सर्वांगीण प्रगती करते व त्याला घडवते.
प्रश्न ४. खालील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा.
कृती १ : आकलन कृती
प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः
![]()
प्रश्न 2.
मी कोण ते लिहा.
उत्तरः
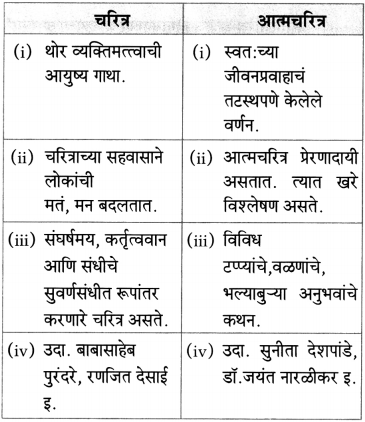
(i) एखादया व्यक्तिच्या आयुष्याचे वर्णन – [चरित्र]
(ii) स्वत:च्या जीवनप्रवासाचे तटस्थपणे केलेले वर्णन – [आत्मचरित्र]
प्रश्न 3.
खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.
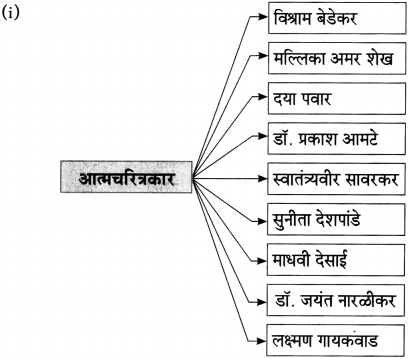
(i) आत्मचरित्रात तटस्थपणे कशाचे कथन आढळते?
उत्तरः
आत्मचरित्रात आयुष्यात आलेल्या विविध टप्प्यांचे, वळणांचे, भल्याबुऱ्या अनुभवांचे तटस्थपणे केलेले कथन आढळते.
(ii) घरी बसून दूरच्या गावी नेणारे कोण असते?
उत्तरः
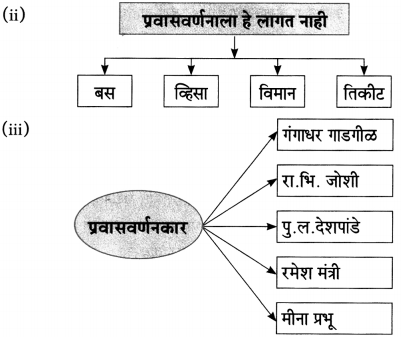
घरी बसून दूरच्या गावी नेणारे प्रवासवर्णन असते.
(iii) प्रवासवर्णनात लेखकाचे कसब कोणते?
उत्तरः
माहिती रटाळ, कंटाळवाणी न होऊ देता रंजक पद्धतीने मनोवेधक भाषेत मांडणं हे लेखकाचं कसब असतं.
(iv) सर्व साहित्य मित्रांमुळे सुश्रुतला काय फायदा होणार आहे ?
उत्तरः
सर्व साहित्य मित्रांमुळे मनोरंजन होऊन ज्ञानही वाढेल व लेखनही सुधारेल.
कृती २: आकलन
प्रश्न 1.
आकृती पूर्ण करा.
उत्तरः
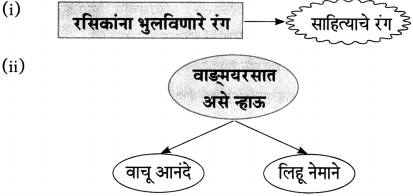
प्रश्न 2.
सकारण लिहा.
प्रवासवर्णन रंजक होते –
उत्तरः
लेखक त्या ठिकाणच्या माहितीबरोबर स्वत:चे अनुभव, भावना, निसर्गसौंदर्य, व्यक्तिविशेष यांची सुरेख मांडणी करतो.
प्रश्न 3.
योग्य पर्याय निवडा.
(i) सुश्रुतला साहित्य मित्रांशी मैत्री करायला आवडेल कारण . . .
(अ) ते सुश्रुतला बक्षिस देतील.
(ब) ते सुश्रुतला कधीच सोडून जाणार नाही.
(क) ते सप्तरंगी इंद्रधनुष्यासारखे आहेत.
(ड) ते सुश्रुतशी खेळतील.
उत्तरः
सुश्रुतला साहित्य मित्रांशी मैत्री करायला आवडेल कारण ते सुश्रुतला कधीच सोडून जाणार नाही.
![]()
(ii) मी प्रेक्षणीय ठिकाणांची माहिती वाचकांपर्यंत पोहोचवतो –
(अ) लेखक
(ब) कवी
(क) चित्रकार
(ड) प्रवासवर्णन
उत्तरः
मी प्रेक्षणीय ठिकाणांची माहिती वाचकांपर्यंत पोहोचवतो प्रवासवर्णन.
प्रश्न 4.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.
(i) …………………………….. रंग विविध हे, भुलविती साऱ्या रसिकजना. (विषयाचे, साहित्याचे, कथेचे, निबंधाचे)
(ii) धन्य आमुची …………………………….. मराठी, धन्य साहित्यसंपदा. (माय, मातृ, श्रेष्ठ, कनिष्ठ)
उत्तर:
(i) साहित्याचे
(ii) माय
कृती ३ : स्वमत
प्रश्न 1.
‘आत्मचरित्र म्हणजे लेखकाच्या जीवनाचा आरसा’ हे विधान स्पष्ट करा.
उत्तरः
आत्मचरित्र म्हणजे लेखकाने स्वत:च्या जीवनप्रवासाचे तटस्थपणे केलेले वर्णन. विविध वळणांचे, आयुष्यातील भल्या-बुऱ्या घटनांचे लेखक तटस्थपणे वर्णन करून शब्दात मांडतो. त्यात खोटेपणाला वाव नसतो. जे घडले ते जसेच्या तसे मांडण्याचा त्याचा प्रामाणिक प्रयत्न असतो.
जसा आरसा जे आहे तसेच दाखवतो तसेच आत्मचरित्र ही घडलेल्या घटना अतिरंजीत न करता जशाच्या तशा दाखवते. त्यात लेखकाचा संघर्ष असू शकतो, त्याचे कर्तृत्व, त्याचा मान-अपमान व त्याची गुणवैशिष्ट्ये आत्मचरित्रातून दिसतात. अनेक आत्मचरित्रे बोधप्रद असतात. त्यातून जिद्द, चिकाटी, सच्चेपणा हे गुण शिकता येतात. मी स्वातंत्र्यवीर सावरकर व गांधीजीचे चरित्र वाचले आहे. खरोखरच आत्मचरित्र म्हणजे लेखकाच्या जीवनाचा आरसा असतो हे तेव्हा उमगले.
स्वाध्याय कृती
(७) स्वमत
(i) पुस्तकाशी मैत्री करण्याचे फायदे.
उत्तरः
पुस्तकांशी मैत्री म्हणजे निर्भेळ आनंदच. पुस्तके आपल्याशी बोलतात, त्यांचे विचार प्रगट करतात. ज्ञान देतात. चांगल्या कामासाठी प्रेरणा देतात. कठीण संकल्पना सोप्या करून सांगतात. चित्रांद्वारे, शब्दांतून मनमोकळ्या गप्पा मारतात. शब्दसंग्रह वाढवितात. प्रसंगी विविध स्थळांना भेटी दिल्याचा आनंद देतात. पुस्तके आपल्यावर कधीही रागावत नाहीत. रूसत नाहीत. भांडत नाहीत. काही अपेक्षा ठेवत नाहीत. म्हणून त्यांच्याशी मैत्री करून आपणही त्यांची काळजी घेणे तितकेच गरजेचे आहे.
(ii) तुम्हांला आवडलेल्या कोणत्याही साहित्यप्रकाराची वैशिष्ट्ये तुमच्या शब्दात लिहा.
उत्तरः
मला आवडलेला साहित्यप्रकार म्हणजे कादंबरी. कादंबरी म्हणजे मोठी कथाच. विविध पात्रांनी, प्रसंगांनी नटलेली, सजलेली. कादंबरी जर खुमासदार असेल तर, ती हातातून सोडवत नाही. पुढे काय होणार याची उत्कंठा लागते. त्यातील पात्रांचा परिचय होतो व ती पात्रे आपल्याला आपल्यातीलच वाटू लागतात. कादंबरीत मन रममाण होते. सुखाच्या प्रसंगात भान हरपते. दु:खी प्रसंगाने अतिशय वाईटही वाटते, इतके तादात्म्य कादंबरीशी साधता येते. ‘ययाति’, ‘स्वामी’, या कादंबऱ्या माझ्या आवडत्या आहेत.
![]()
(iii) ‘उत्तम लेखक होण्यासाठी उत्तम वाचक होणे आवश्यक असते’ यावर तुमचे विचार स्पष्ट करा.
उत्तरः
‘वाचाल तर वाचाल’ या उक्तीप्रमाणे वाचनाने आपणांस अनेक लाभ होतात. वाचनाने शब्द संपत्ती वाढते. नवनवीन संकल्पना कळतात. विचार प्रगल्भ होतात, लेखक होण्यासाठी या सर्वांचा उपयोग होतो. समाजातील चालीरिती, संस्कृती, नवीन शोध, पर्यटन, शैक्षणिक स्तर यांची माहिती वाचनाने मिळते. विचारांची बैठक पक्की होते. काळाचे भान येते. नव्या जुन्या गोष्टी कळतात. उत्तम विचार समर्थ लेखणीद्वारे प्रगट होतात.
रंग साहित्याचे Summary in Marathi
रंग साहित्याचे पाठपरिचय
प्रत्येक भाषा विविध साहित्यप्रकारांनी नटलेली असते. असे साहित्यप्रकार मानवी रूप घेऊन या पाठातून स्वपरिचय करून देत आहेत, भाषासमृद्धीकरणासाठी साहित्यप्रकारांचा, त्यांच्यातील वैशिष्ट्यांचा उपयोग होतो. या साहित्यप्रकारांशी मैत्री केली, तर मनोरंजनाबरोबर आपले ज्ञानही वाढेल असा संदेशही पाठातून दिला आहे. नाट्यस्वरूपातील हा पाठ साहित्यातील विविध कलाकृतींचा परिचय करून देणारा आहे.

रंग साहित्याचे Summary in English
Every language is enhanced by a body of literature. When different types of literature take human form and introduce themselves, they add to the beauty of language. The various characteristics of literature help in this process. If we get acquainted with these literary types, we not only get entertained but also acquire a fair amount of knowledge. This message is conveyed through this lesson. This animated lesson introduces us to various types of literary divisions.
रंग साहित्याचे शब्दार्थ
- सहल – यात्रा – (picnic)
- वेश – पोशाख – (costume)
- सूचना – बातमी – (notice)
- ओळख – परिचय – (introduction)
- कथा – गोष्ट – (story)
- आकर्षक – लक्षवेधी – (attractive)
- परिणामकारक – प्रभावी – (effective)
- शेवट – समारोप – (ending)
- साहसकथा – शौर्यकथा – (adventurous)
- परीकथा – पऱ्यांच्या गोष्टी – (fairly tales)
- बोधकथा – नीतीकथा – (moral stories)
- नाटक – नाटिका – (drama, play)
- मालिका – संलग्नकथा – (episodes)
- चित्रपट – सिनेमा – (movies)
- दर्जेदार – गुणवत्तापूर्ण – (qualitative)
- उत्तम – सुरेख – (excellent)
- निवेदन – कथन – (statement)
- तंत्र – पद्धत – (technique)
- यश – सफलता – (success)
- रहस्य – गुपीत – (mystery)
- तृप्त – समाधान – (satisfaction)
- कादंबरी – अखंड मोठी कथा – (novel)
- आवाका – पसारा – (volume)
- पात्र कलाकार – (characters)
- परस्पर एकमेकांशी – (inter related)
- उत्कंठा – उत्सुकता – (eagerness)
- सर्वोच्च – अत्यंत मोठा – (highest)
- पुरस्कार – बक्षिस – (award)
- आटोपशीर – नेमके – (handily)
- आशय – हेतू – (purpose)
- वैशिष्ट्य – विशिष्टता – (peculiarity)
- यमक – एक शब्दालंकार – (homonym)
- अनुप्रास – एक शब्दालंकार – (alliteration)
- उपमा – एक अर्थालंकार – (example)
- रूपक – एक अर्थालंकार – (metaphor)
- चपखल – तंतोतंत – (precise)
- आविष्कार – प्रगटीकरण – (manifestation)
- रूपांतर – परिवर्तन – (transfiguration)
- निरीक्षण – बारकाईने पहाणे – (observation)
- अर्थालंकार – एक अलंकाराचा प्रकार (figure of speech)
- अर्थपूर्ण – उद्देशपूर्ण – (meaningful)
- कल्पना – कल्पित (imagination)
- संवाद – संभाषण – (dialogue)
Marathi Akshar Bharati Class 10th Digest भाग-३