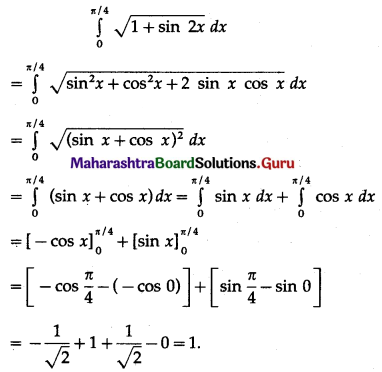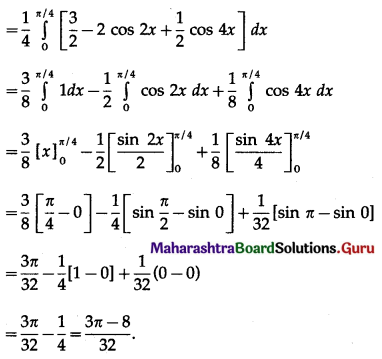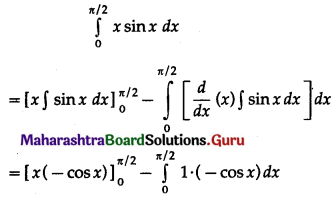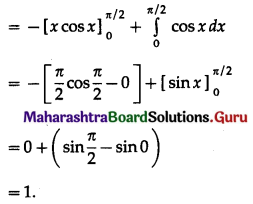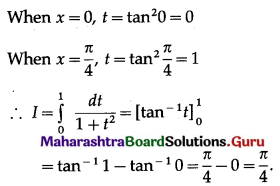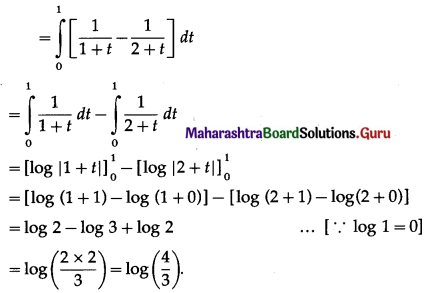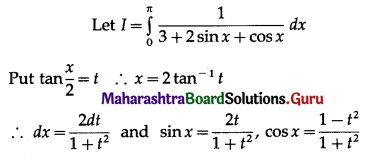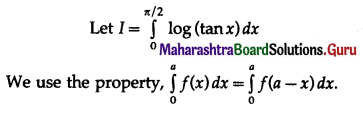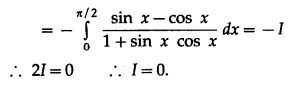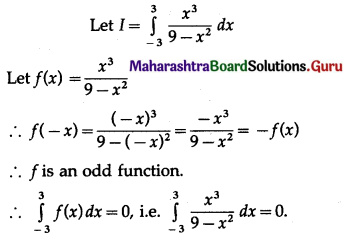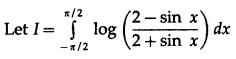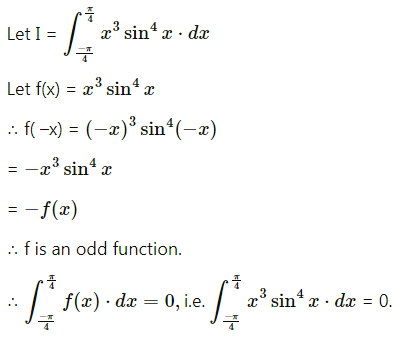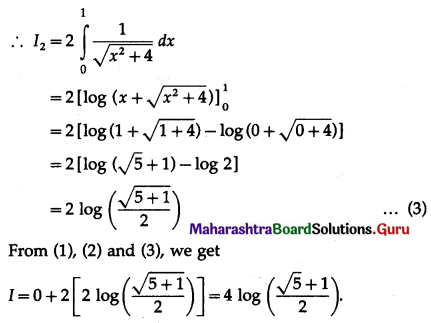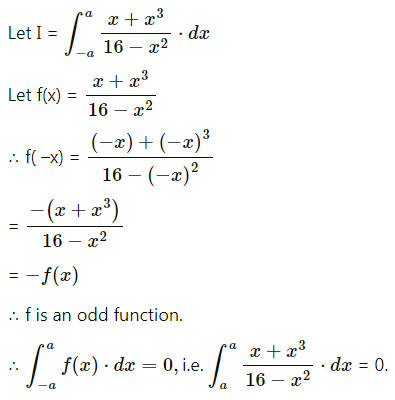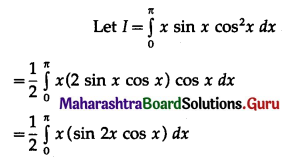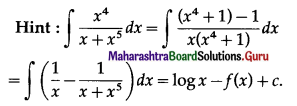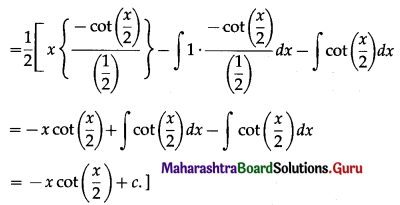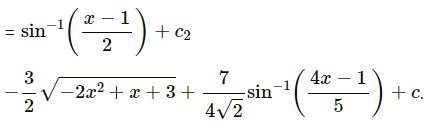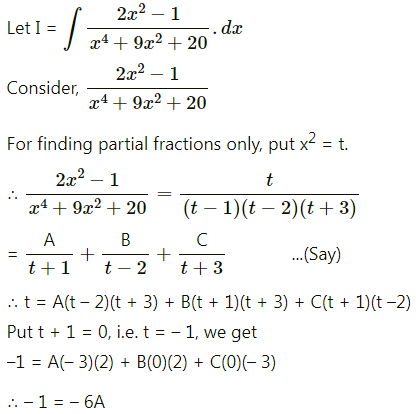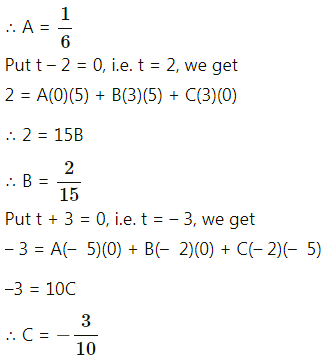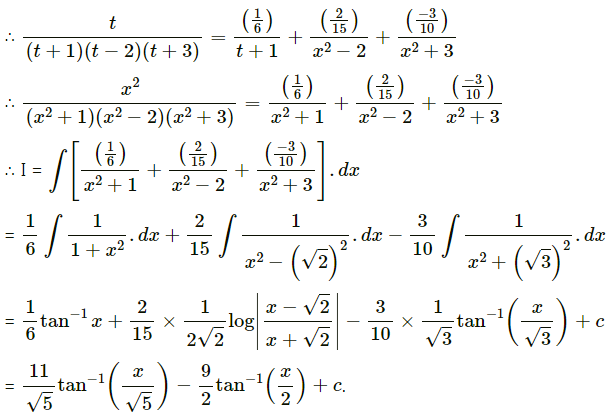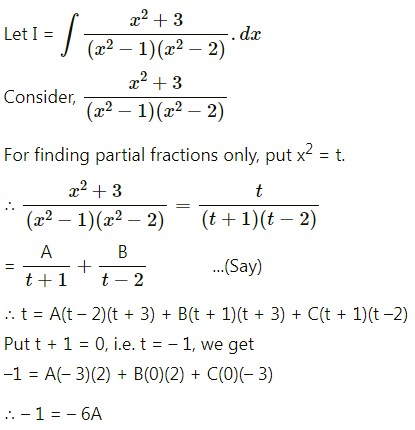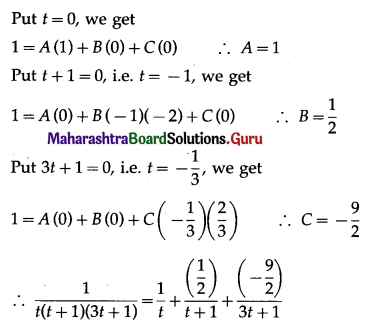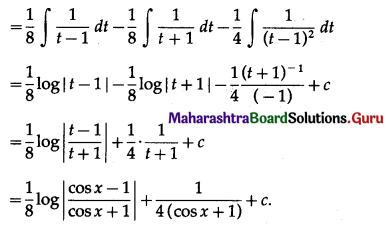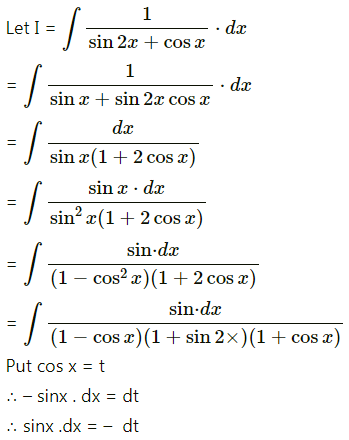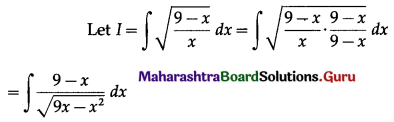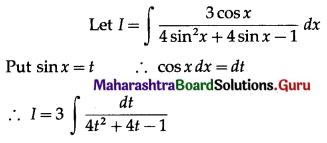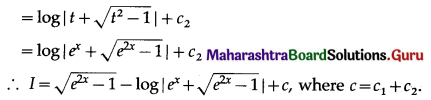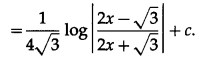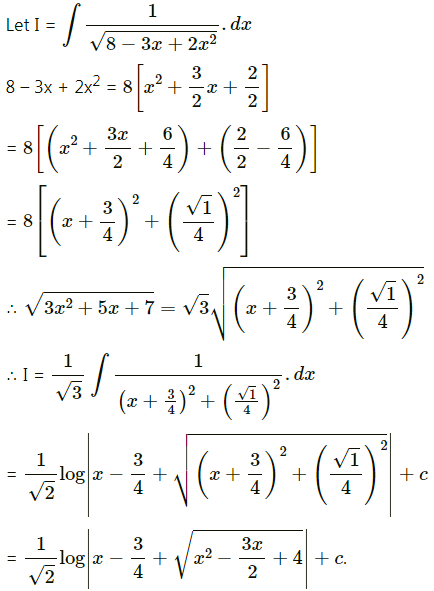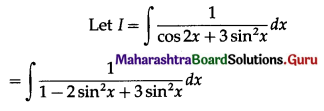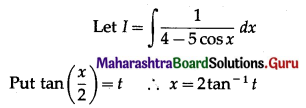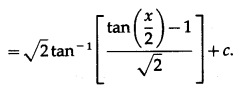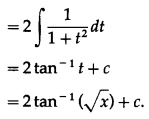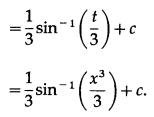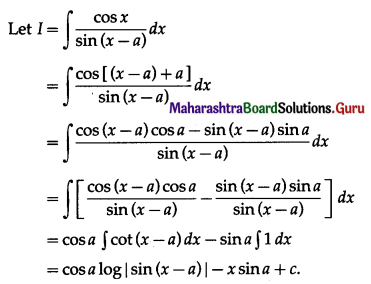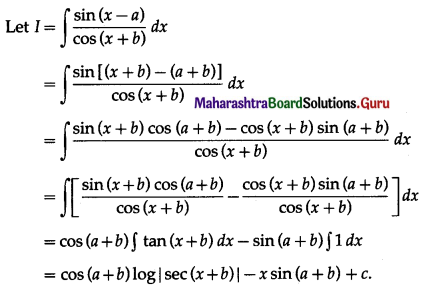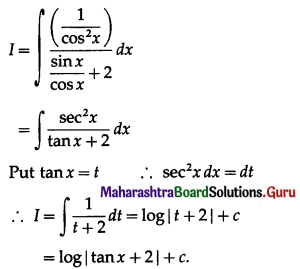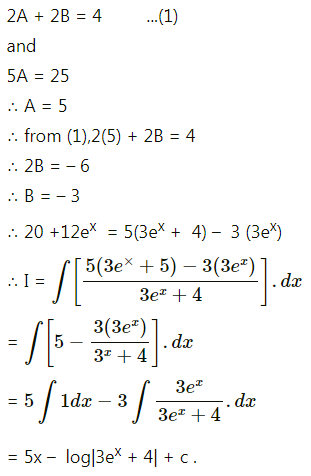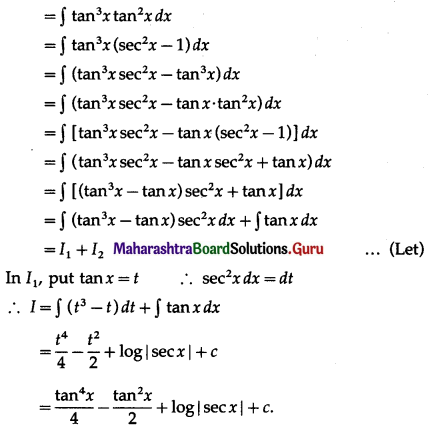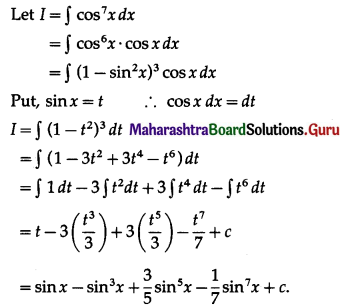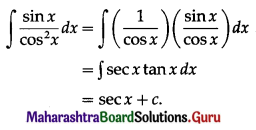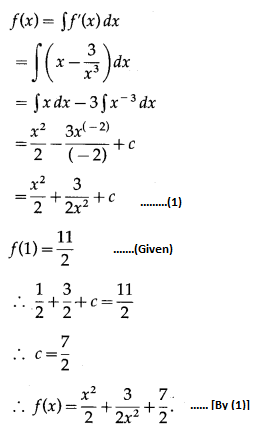Bhagya

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Definite Integration Miscellaneous Exercise 4 Questions and Answers.

12th Maths Part 2 Definite Integration Miscellaneous Exercise 4 Questions And Answers Maharashtra Board

I. Choose the correct option from the given alternatives:

Question 1.
\(\int_{2}^{3} \frac{d x}{x\left(x^{3}-1\right)}=\)
(a) \(\frac{1}{3} \log \left(\frac{208}{189}\right)\)
(b) \(\frac{1}{3} \log \left(\frac{189}{208}\right)\)
(c) \(\log \left(\frac{208}{189}\right)\)
(d) \(\log \left(\frac{189}{208}\right)\)
Answer:
(a) \(\frac{1}{3} \log \left(\frac{208}{189}\right)\)

Question 2.
\(\int_{0}^{\pi / 2} \frac{\sin ^{2} x \cdot d x}{(1+\cos x)^{2}}=\)
(a) \(\frac{4-\pi}{2}\)
(b) \(\frac{\pi-4}{2}\)
(c) 4 – \(\frac{\pi}{2}\)
(d) \(\frac{4+\pi}{2}\)
Answer:
(a) \(\frac{4-\pi}{2}\)

Question 3.
\(\int_{0}^{\log 5} \frac{e^{x} \sqrt{e^{x}-1}}{e^{x}+3} \cdot d x=\)
(a) 3 + 2π
(b) 4 – π
(c) 2 + π
(d) 4 + π
Answer:
(b) 4 – π

Question 4.
\(\int_{0}^{\pi / 2} \sin ^{6} x \cos ^{2} x \cdot d x=\)
(a) \(\frac{7 \pi}{256}\)
(b) \(\frac{3 \pi}{256}\)
(c) \(\frac{5 \pi}{256}\)
(d) \(\frac{-5 \pi}{256}\)
Answer:
(c) \(\frac{5 \pi}{256}\)

Question 5.
If \(\int_{0}^{1} \frac{d x}{\sqrt{1+x}-\sqrt{X}}=\frac{k}{3}\), then k is equal to
(a) √2(2√2 – 2)
(b) \(\frac{\sqrt{2}}{3}\)(2 – 2√2)
(c) \(\frac{2 \sqrt{2}-2}{3}\)
(d) 4√2
Answer:
(d) 4√2

Question 6.
\(\int_{1}^{2} \frac{1}{x^{2}} e^{\frac{1}{x}} \cdot d x=\)
(a) √e + 1
(b) √e − 1
(c) √e(√e − 1)
(d) \(\frac{\sqrt{e}-1}{e}\)
Answer:
(c) √e(√e − 1)

Question 7.
If \(\int_{2}^{e}\left[\frac{1}{\log x}-\frac{1}{(\log x)^{2}}\right] \cdot d x=a+\frac{b}{\log 2}\), then
(a) a = e, b = -2
(b) a = e, b = 2
(c) a = -e, b = 2
(d) a = -e, b = -2
Answer:
(a) a = e, b = -2

Question 8.
Let \(\mathrm{I}_{1}=\int_{e}^{e^{2}} \frac{d x}{\log x}\) and \(\mathrm{I}_{2}=\int_{1}^{2} \frac{e^{x}}{\boldsymbol{X}} \cdot d x\), then
(a) I₁ = \(\frac{1}{3}\) I₂
(b) I₁ + I₂ = 0
(c) I₁ = 2I₂
(d) I₁ = I₂
Answer:
(d) I₁ = I₂

Question 9.
\(\int_{0}^{9} \frac{\sqrt{X}}{\sqrt{X}+\sqrt{9-X}} \cdot d x=\)
(a) 9
(b) \(\frac{9}{2}\)
(c) 0
(d) 1
Answer:
(b) \(\frac{9}{2}\)

Question 10.
The value of \(\int_{-\pi / 4}^{\pi / 4} \log \left(\frac{2+\sin \theta}{2-\sin \theta}\right) \cdot d \theta\) is
(a) 0
(b) 1
(c) 2
(d) π
Answer:
(a) 0

II. Evaluate the following:

Question 1.
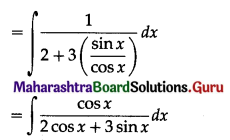
\(\int_{0}^{\pi / 2} \frac{\cos x}{3 \cos x+\sin x} d x\)
Solution:
Let I = \(\int_{0}^{\pi / 2} \frac{\cos x}{3 \cos x+\sin x} d x\)
Put Numerator = A(Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ cos x = A(3 cos x + sin x) + B[\(\frac{d}{d x}\)(3 cos x + sin x)]
= A(3 cos x + sin x) + B(-3 sin x + cos x)
∴ cos x + 0 . sin x = (3A + B) cos x + (A – 3B) sin x
Comparing the coefficients of sinx and cos x on both the sides, we get
3A + B = 1 ………. (1)
A – 3B = 0 ………. (2)
Multiplying equation (1) by 3, we get
9A + 3B = 3 ………(3)
Adding (2) and (3), we get
10A = 3
∴ A = \(\frac{3}{10}\)

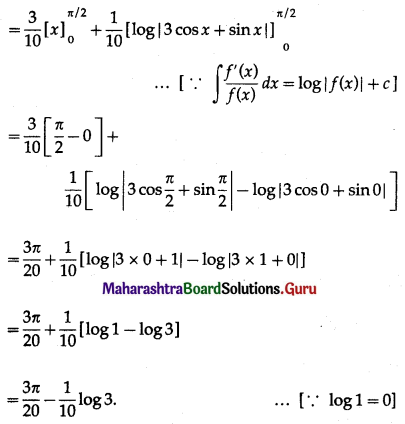
Question 2.
\(\int_{\pi / 4}^{\pi / 2} \frac{\cos \theta}{\left[\cos \frac{\theta}{2}+\sin \frac{\theta}{2}\right]^{3}} d \theta\)
Solution:

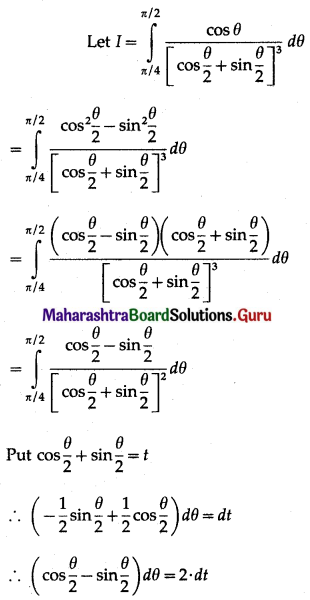
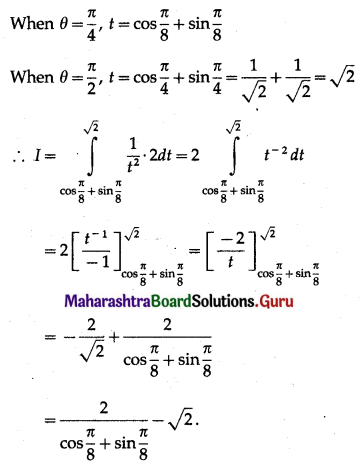
Question 3.
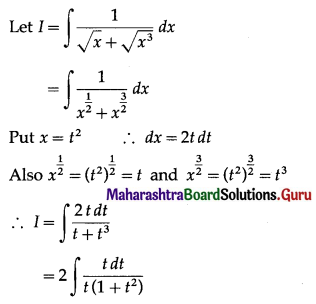
\(\int_{0}^{1} \frac{1}{1+\sqrt{x}} d x\)
Solution:
Let I = \(\int_{0}^{1} \frac{1}{1+\sqrt{x}} d x\)
Put √x = t
∴ x = t² and dx = 2t . dt
When x = 0, t = 0
When x = 1, t = 1

Question 4.
\(\int_{0}^{\pi / 4} \frac{\tan ^{3} x}{1+\cos 2 x} d x\)
Solution:

Question 5.
\(\int_{0}^{1} t^{5} \sqrt{1-t^{2}} d t\)
Solution:

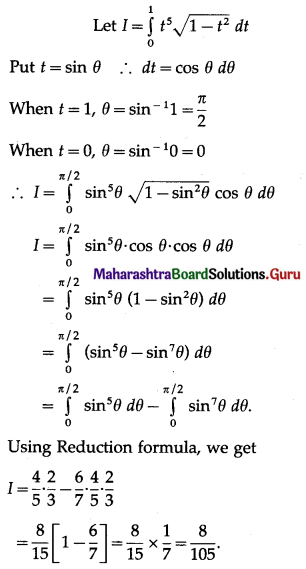
Question 6.
\(\int_{0}^{1}\left(\cos ^{-1} x\right)^{2} d x\)
Solution:

Question 7.
\(\int_{-1}^{1} \frac{1+x^{3}}{9-x^{2}} d x\)
Solution:

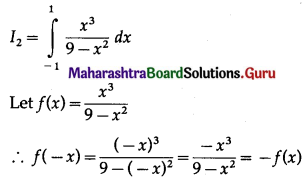
Question 8.
\(\int_{0}^{\pi} x \cdot \sin x \cdot \cos ^{4} x d x\)
Solution:

Question 9.
\(\int_{0}^{\pi} \frac{x}{1+\sin ^{2} x} d x\)
Solution:

Question 10.
\(\int_{1}^{\infty} \frac{1}{\sqrt{x}(1+x)} d x\)
Solution:

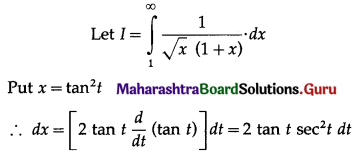
III. Evaluate the following:

Question 1.
\(\int_{0}^{1}\left(\frac{1}{1+x^{2}}\right) \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\)
Solution:

Question 2.
\(\int_{0}^{\pi / 2} \frac{1}{6-\cos x} d x\)
Solution:

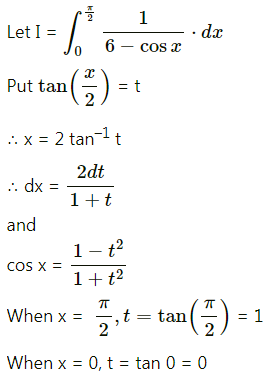
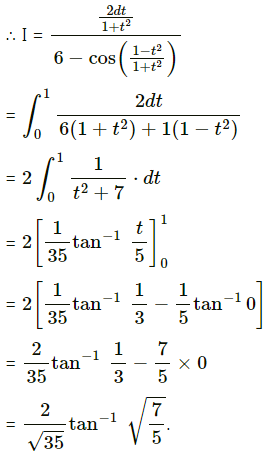
Question 3.
\(\int_{0}^{a} \frac{1}{a^{2}+a x-x^{2}} d x\)
Solution:

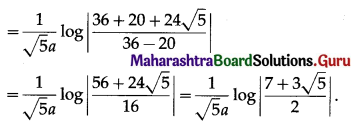
Question 4.
\(\int_{\pi / 5}^{3 \pi / 10} \frac{\sin x}{\sin x+\cos x} d x\)
Solution:

Question 5.
\(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\)
Solution:
Let I = \(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\)

Question 6.
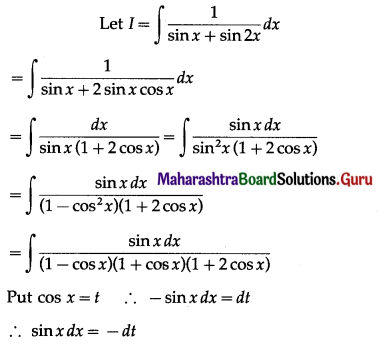
\(\int_{0}^{\pi / 4} \frac{\cos 2 x}{1+\cos 2 x+\sin 2 x} d x\)
Solution:

Question 7.
\(\int_{0}^{\pi / 2}[2 \log (\sin x)-\log (\sin 2 x)] d x\)
Solution:

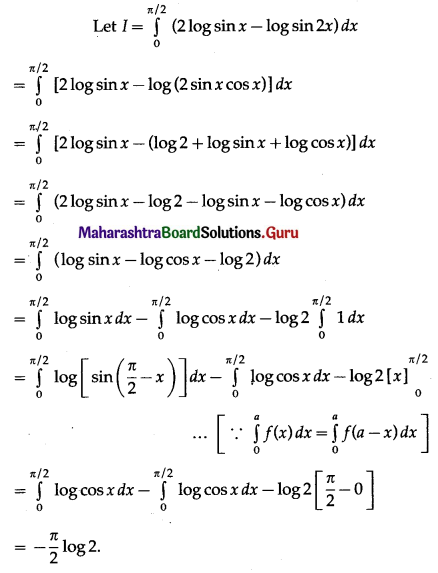
Question 8.
\(\int_{0}^{\pi}\left(\sin ^{-1} x+\cos ^{-1} x\right)^{3} \sin ^{3} x d x\)
Solution:

Question 9.
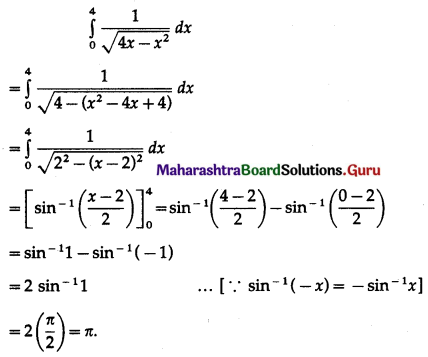
\(\int_{0}^{4}\left[\sqrt{x^{2}+2 x+3}\right]^{-1} d x\)
Solution:

Question 10.
\(\int_{-2}^{3}|x-2| d x\)
Solution:
|x – 2|= 2 – x, if x < 2
= x – 2, if x ≥ 2

IV. Evaluate the following:

Question 1.
If \(\int_{a}^{a} \sqrt{x} d x=2 a \int_{0}^{\pi / 2} \sin ^{3} x d x\), find the value of \(\int_{a}^{a+1} x d x\).
Solution:

Question 2.
If \(\int_{0}^{k} \frac{1}{2+8 x^{2}} \cdot d x=\frac{\pi}{16}\), find k.
Solution:

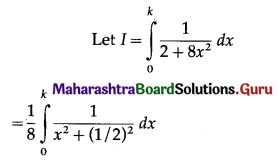
Question 3.
If f(x) = a + bx + cx², show that \(\int_{0}^{1} f(x) d x=\frac{1}{6}\left[f(0)+4 f\left(\frac{1}{2}\right)+f(1)\right]\)
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 4.1 Class 12 Maths 2
• Exercise 4.2 Class 12 Maths 2
• Miscellaneous Exercise 4 Class 12 Maths 2
• Exercise 5.1 Class 12 Maths 2
• Miscellaneous Exercise 5 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Definite Integration Ex 4.2 Questions and Answers.

12th Maths Part 2 Definite Integration Exercise 4.2 Questions And Answers Maharashtra Board

I. Evaluate:

Question 1.
\(\int_{1}^{9} \frac{x+1}{\sqrt{x}} \cdot d x\)
Solution:

Question 2.
\(\int_{2}^{3} \frac{1}{x^{2}+5 x+6} \cdot d x\)
Solution:

Question 3.
\(\int_{0}^{\pi / 4} \cot ^{2} \cdot d x\)
Solution:

The integral does not exist since cot 0 is not defined.

Question 4.
\(\int_{-\pi / 4}^{\pi / 4} \frac{1}{1-\sin x} \cdot d x\)
Solution:

Question 5.
\(\int_{3}^{5} \frac{1}{\sqrt{2 x+3}-\sqrt{2 x-3}} \cdot d x\)
Solution:

Question 6.
\(\int_{0}^{1} \frac{x^{2}-2}{x^{2}+1} \cdot d x\)
Solution:

Question 7.
\(\int_{0}^{\pi / 4} \sin 4 x \sin 3 x \cdot d x\)
Solution:

Question 8.
\(\int_{0}^{\pi / 4} \sqrt{1+\sin 2 x} \cdot d x\)
Solution:

Question 9.
\(\int_{0}^{\pi / 4} \sin ^{4} x \cdot d x\)
Solution:

Question 10.
\(\int_{-4}^{2} \frac{1}{x^{2}+4 x+13} \cdot d x\)
Solution:

Question 11.
\(\int_{0}^{4} \frac{1}{\sqrt{4 x-x^{2}}} \cdot d x\)
Solution:

Question 12.
\(\int_{0}^{1} \frac{1}{\sqrt{3+2 x-x^{2}}} \cdot d x\)
Solution:

Question 13.
\(\int_{0}^{\pi / 2} x \cdot \sin x \cdot d x\)
Solution:

Question 14.
\(\int_{0}^{1} x \cdot \tan ^{-1} x \cdot d x\)
Solution:

Question 15.
\(\int_{0}^{\infty} x \cdot e^{-x} \cdot d x\)
Solution:

II. Evaluate:

Question 1.
\(\int_{0}^{\frac{1}{\sqrt{2}}} \frac{\sin ^{-1} x}{\left(1-x^{2}\right)^{\frac{3}{2}}} \cdot d x\)
Solution:

Question 2.
\(\int_{0}^{\pi / 4} \frac{\sec ^{2} x}{3 \tan ^{2} x+4 \tan x+1} \cdot d x\)
Solution:

Question 3.
\(\int_{0}^{4 \pi} \frac{\sin 2 x}{\sin ^{4} x+\cos ^{4} x} \cdot d x\)
Solution:

Question 4.
\(\int_{0}^{2 \pi} \sqrt{\cos x} \cdot \sin ^{3} x \cdot d x\)
Solution:

Question 5.
\(\int_{0}^{\pi / 2} \frac{1}{5+4 \cos x} \cdot d x\)
Solution:

Question 6.
\(\int_{0}^{\pi / 4} \frac{\cos x}{4-\sin ^{2} x} \cdot d x\)
Solution:

Question 7.
\(\int_{0}^{\pi / 2} \frac{\cos X}{(1+\sin x)(2+\sin x)} \cdot d x\)
Solution:

Question 8.
\(\int_{-1}^{1} \frac{1}{a^{2} e^{x}+b^{2} e^{-x}} \cdot d x\)
Solution:

Question 9.
\(\int_{0}^{\pi} \frac{1}{3+2 \sin x+\cos x} \cdot d x\)
Solution:

Question 10.
\(\int_{0}^{\pi / 4} \sec ^{4} x \cdot d x\)
Solution:

Question 11.
\(\int_{0}^{1} \sqrt{\frac{1-x}{1+x}} \cdot d x\)
Solution:

Question 12.
\(\int_{0}^{\pi} \sin ^{3} x(1+2 \cos x)(1+\cos x)^{2} \cdot d x\)
Solution:

Question 13.
\(\int_{0}^{\pi / 2} \sin 2 x \cdot \tan ^{-1}(\sin x) \cdot d x\)
Solution:

Question 14.
\(\int_{\frac{1}{\sqrt{2}}}^{1} \frac{\left(e^{\cos ^{-1} x}\right)\left(\sin ^{-1} x\right)}{\sqrt{1-x^{2}}} \cdot d x\)
Solution:

Question 15.
\(\int_{2}^{3} \frac{\cos (\log x)}{x} \cdot d x\)
Solution:

III. Evaluate:

Question 1.
\(\int_{0}^{a} \frac{1}{x+\sqrt{a^{2}-x^{2}}} \cdot d x\)
Solution:

Question 2.
\(\int_{0}^{\pi / 2} \log \tan x \cdot d x\)
Solution:

Question 3.
\(\int_{0}^{1} \log \left(\frac{1}{x}-1\right) \cdot d x\)
Solution:

Question 4.
\(\int_{0}^{\pi / 2} \frac{\sin x-\cos x}{1+\sin x \cdot \cos x} \cdot d x\)
Solution:

Question 5.
\(\int_{0}^{3} x^{2}(3-x)^{\frac{5}{2}} \cdot d x\)
Solution:

Question 6.
\(\int_{-3}^{3} \frac{x^{3}}{9-x^{2}} \cdot d x\)
Solution:

Question 7.
\(\int_{-\pi / 2}^{\pi / 2} \log \left(\frac{2+\sin x}{2-\sin x}\right) \cdot d x\)
Solution:

Question 8.
\(\int_{-\pi / 4}^{\pi / 4} \frac{x+\frac{\pi}{4}}{2-\cos 2 x} \cdot d x\)
Solution:

Question 9.
\(\int_{-\pi / 4}^{\pi / 4} x^{3} \cdot \sin ^{4} x \cdot d x\)
Solution:

Question 10.
\(\int_{0}^{1} \frac{\log (x+1)}{x^{2}+1} \cdot d x\)
Solution:

Question 11.
\(\int_{-1}^{1} \frac{x^{3}+2}{\sqrt{x^{2}+4}} \cdot d x\)
Solution:

Question 12.
\(\int_{-a}^{a} \frac{x+x^{3}}{16-x^{2}} \cdot d x\)
Solution:

Question 13.
\(\int_{0}^{1} t^{2} \sqrt{1-t} \cdot d t\)
Solution:

Question 14.
\(\int_{0}^{\pi} x \cdot \sin x \cdot \cos ^{2} x \cdot d x\)
Solution:

Question 15.
\(\int_{0}^{1} \frac{\log x}{\sqrt{1-x^{2}}} \cdot d x\)
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 4.1 Class 12 Maths 2
• Exercise 4.2 Class 12 Maths 2
• Miscellaneous Exercise 4 Class 12 Maths 2
• Exercise 5.1 Class 12 Maths 2
• Miscellaneous Exercise 5 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 4 Definite Integration Ex 4.1 Questions and Answers.

12th Maths Part 2 Definite Integration Exercise 4.1 Questions And Answers Maharashtra Board

I. Evaluate the following integrals as a limit of a sum.

Question 1.
\(\int_{1}^{3}(3 x-4) \cdot d x\)
Solution:
Let f(x) = 3x – 4, for 1 ≤ x ≤ 3
Divide the closed interval [1, 3] into n subintervals each of length h at the points
1, 1 + h, 1 + 2h, 1 + rh, ….., 1 + nh = 3
∴ nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here, a = 1
∴ f(a + rh) = f(1 + rh)
= 3(1 + rh) – 4
= 3rh – 1

Question 2.
\(\int_{0}^{4} x^{2} d x\)
Solution:
Let f(x) = x², for 0 ≤ x ≤ 4
Divide the closed interval [0, 4] into n subintervals each of length h at the points
0, 0 + h, 0 + 2h, ….., 0 + rh, ….., 0 + nh = 4
i.e. 0, h, 2h, ….., rh, ….., nh = 4
∴ h = \(\frac{4}{n}\) as n → ∞, h → 0
Here, a = 0

Question 3.
\(\int_{0}^{2} e^{x} d x\)
Solution:
Let f(x) = e^x, for 0 ≤ x ≤ 2
Divide the closed interval [0, 2] into n equal subntervals each of length h at the points
0, 0 + h, 0 + 2h, ….., 0 + rh, ….., 0 + nh = 2
i.e. 0, h, 2h, ….., rh, ….., nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here, a = 0

Question 4.
\(\int_{0}^{2}\left(3 x^{2}-1\right) d x\)
Solution:
Let f(x) = 3x² – 1, for 0 ≤ x ≤ 2
Divide the closed interval [0, 2] into n subintervals each of length h at the points.
0, 0 + h, 0 + 2h, ….., 0 + rh, ……, 0 + nh = 2
i.e. 0, h, 2h, ….., rh, ….., nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here, a = 0
∴ f(a + rh) = f(0 + rh)
= f(rh)
= 3(rh)² – 1
= 3r²h² – 1

Question 5.
\(\int_{1}^{3} x^{3} d x\)
Solution:
Let f(x) = x³, for 1 ≤ x ≤ 3.
Divide the closed interval [1, 3] into n equal su bintervals each of length h at the points
1, 1 + h, 1 + 2h, ……, 1 + rh, ……, 1 + nh = 3
∴ nh = 2
∴ h = \(\frac{2}{n}\) and as n → ∞, h → 0
Here a = 1

Class 12 Maharashtra State Board Maths Solution 

• Exercise 4.1 Class 12 Maths 2
• Exercise 4.2 Class 12 Maths 2
• Miscellaneous Exercise 4 Class 12 Maths 2
• Exercise 5.1 Class 12 Maths 2
• Miscellaneous Exercise 5 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Miscellaneous Exercise 3 Questions and Answers.

12th Maths Part 2 Indefinite Integration Miscellaneous Exercise 3 Questions And Answers Maharashtra Board

I. Choose the correct options from the given alternatives:

Question 1.
\(\int \frac{1+x+\sqrt{x+x^{2}}}{\sqrt{x}+\sqrt{1+x}} \cdot d x=\)
(a) \(\frac{1}{2} \sqrt{x+1}+c\)
(b) \(\frac{2}{3}(x+1)^{\frac{3}{2}}+c\)
(c) \(\sqrt{x+1}+c\)
(d) \(2(x+1)^{\frac{3}{2}}+c\)
Answer:
(b) \(\frac{2}{3}(x+1)^{\frac{3}{2}}+c\)

Question 2.
\(\int \frac{1}{x+x^{5}} \cdot d x\) = f(x) + c, then \(\int \frac{x^{4}}{x+x^{5}} \cdot d x=\)
(a) log x – f(x) + c
(b) f(x) + log x + c
(c) f(x) – log x + c
(d) \(\frac{1}{5}\) x⁵ f(x) + c
Answer:
(a) log x – f(x) + c

Question 3.
\(\int \frac{\log (3 x)}{x \log (9 x)} \cdot d x=\)
(a) log(3x) – log(9x) + c
(b) log(x) – (log 3) . log(log 9x) + c
(c) log 9 – (log x) . log(log 3x) + c
(d) log(x) + log(3) . log(log 9x) + c
Answer:
(b) log(x) – (log 3) . log(log 9x) + c

Question 4.
\(\int \frac{\sin ^{m} X}{\cos ^{m+2} X} \cdot d x=\)
(a) \(\frac{\tan ^{m+1} \boldsymbol{X}}{m+1}+c\)
(b) (m + 2) tan^m+1 x + c
(c) \(\frac{\tan ^{m} \boldsymbol{X}}{m}+c\)
(d) (m + 1) tan^m+1 x + c
Answer:
(a) \(\frac{\tan ^{m+1} \boldsymbol{X}}{m+1}+c\)

Question 5.
∫tan(sin^-1 x) . dx =
(a) \(\left(1-x^{2}\right)^{-\frac{1}{2}}+c\)
(b) \(\left(1-x^{2}\right)^{\frac{1}{2}}+c\)
(c) \(\frac{\tan ^{m} \boldsymbol{X}}{\sqrt{1-x^{2}}}+c\)
(d) \(-\sqrt{1-x^{2}}+c\)
Answer:
(d) \(-\sqrt{1-x^{2}}+c\)

Hint: sin^-1 x = \(\tan ^{-1}\left(\frac{x}{\sqrt{1-x^{2}}}\right)\)

Question 6.
\(\int \frac{x-\sin x}{1-\cos x} \cdot d x=\)
(a) x cot(\(\frac{x}{2}\)) + c
(b) -x cot(\(\frac{x}{2}\)) + c
(c) cot(\(\frac{x}{2}\)) + c
(d) x tan(\(\frac{x}{2}\)) + c
Answer:
(b) -x cot(\(\frac{x}{2}\)) + c

Question 7.
If f(x) = \(\frac{\sin ^{-1} x}{\sqrt{1-x^{2}}}\), g(x) = \(e^{\sin ^{-1} x}\), then ∫f(x) . g(x) . dx =
(a) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} x-1\right)+c\)
(b) \(e^{\sin ^{-1} x} \cdot\left(1-\sin ^{-1} x\right)+c\)
(c) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} x+1\right)+c\)
(d) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} X-1\right)+c\)
Answer:
(a) \(e^{\sin ^{-1} x} \cdot\left(\sin ^{-1} x-1\right)+c\)

Question 8.
If ∫tan³ x . sec³ x . dx = (\(\frac{1}{m}\)) sec^m x – (\(\frac{1}{n}\)) secⁿ x + c, then (m, n) =
(a) (5, 3)
(b) (3, 5)
(c) \(\left(\frac{1}{5}, \frac{1}{3}\right)\)
(d) (4, 4)
Answer:
(a) (5, 3)

Hint: ∫tan³ x . sec³ x dx
= ∫sec² x . tan² x . sec x tan x dx
= ∫sec² x (sec² x – 1) sec x tan x dx
Put sec x = t.

Question 9.
\(\int \frac{1}{\cos x-\cos ^{2} x} \cdot d x=\)
(a) log(cosec x – cot x) + tan(\(\frac{x}{2}\)) + c
(b) sin 2x – cos x + c
(c) log(sec x + tan x) – cot(\(\frac{x}{2}\)) + c
(d) cos 2x – sin x + c
Answer:
(c) log(sec x + tan x) – cot(\(\frac{x}{2}\)) + c

Question 10.
\(\int \frac{\sqrt{\cot x}}{\sin x \cdot \cos x} \cdot d x=\)
(a) \(2 \sqrt{\cot x}+c\)
(b) \(-2 \sqrt{\cot x}+c\)
(c) \(\frac{1}{2} \sqrt{\cot x}+c\)
(d) \(\sqrt{\cot X}+c\)
Answer:
(b) \(-2 \sqrt{\cot x}+c\)

Question 11.
\(\int \frac{e^{x}(x-1)}{x^{2}} \cdot d x=\)
(a) \(\frac{e^{x}}{x}+c\)
(b) \(\frac{e^{x}}{x^{2}}+c\)
(c) \(\left(x-\frac{1}{x}\right) e^{x}+c\)
(d) x e^-x + c
Answer:
(a) \(\frac{e^{x}}{x}+c\)

Question 12.
∫sin(log x) . dx =
(a) \(\frac{x}{2}\) [sin(log x) – cos(log x)] + c
(b) \(\frac{x}{2}\) [sin(log x) + cos(log x)] + c
(c) \(\frac{x}{2}\) [cos(log x) – sin(log x)] + c
(d) \(\frac{x}{4}\) [cos(log x) – sin(log x)] + c
Answer:
(a) \(\frac{x}{2}\) [sin(log x) – cos(log x)] + c

Question 13.
∫x^x (1 + log x) . dx =
(a) \(\frac{1}{2}\) (1 + log x)² + c
(b) x^2x + c
(c) x^x log x + c
(d) x^x + c
Answer:
(d) x^x + c

Hint: \(\frac{d}{d x}\)(xx) = x^x (1 + log x)

Question 14.
\(\int \cos ^{-\frac{3}{7}} x \cdot \sin ^{-\frac{11}{7}} x \cdot d x=\)
(a) \(\log \left(\sin ^{-\frac{4}{7}} x\right)+c\)
(b) \(\frac{4}{7} \tan ^{\frac{4}{7}} x+c\)
(c) \(-\frac{7}{4} \tan ^{-\frac{4}{7}} x+c\)
(d) \(\log \left(\cos ^{\frac{3}{7}} x\right)+c\)
Answer:
(c) \(-\frac{7}{4} \tan ^{-\frac{4}{7}} x+c\)

Hint: \(\int \cos ^{-\frac{3}{7}} x \sin ^{-\frac{11}{7}} x d x\)
= \(\int \frac{\sin ^{-\frac{11}{7}} x}{\cos ^{-\frac{11}{7}} x \cdot \cos ^{2} x} d x\)
= \(\int \tan ^{-\frac{11}{7}} x \sec ^{2} x d x\)
Put tan x = t.

Question 15.
\(2 \int \frac{\cos ^{2} x-\sin ^{2} x}{\cos ^{2} x+\sin ^{2} x} \cdot d x=\)
(a) sin 2x + c
(b) cos 2x + c
(c) tan 2x + c
(d) 2 sin 2x + c
Answer:
(a) sin 2x + c

Question 16.
\(\int \frac{d x}{\cos x \sqrt{\sin ^{2} x-\cos ^{2} x}} \cdot d x=\)
(a) log(tan x – \(\sqrt{\tan ^{2} x-1}\)) + c
(b) sin^-1 (tan x) + c
(c) 1 + sin^-1 (cot x) + c
(d) log(tan x + \(\sqrt{\tan ^{2} x-1}\)) + c
Answer:
(d) log(tan x + \(\sqrt{\tan ^{2} x-1}\)) + c

Question 17.
\(\int \frac{\log x}{(\log e x)^{2}} \cdot d x=\)
(a) \(\frac{x}{1+\log x}+c\)
(b) x(1 + log x) + c
(c) \(\frac{1}{1+\log x}+c\)
(d) \(\frac{1}{1-\log x}+c\)
Answer:
(a) \(\frac{x}{1+\log x}+c\)

Question 18.
∫[sin(log x) + cos(log x)] . dx =
(a) x cos(log x) + c
(b) sin(log x) + c
(c) cos(log x) + c
(d) x sin(log x) + c
Answer:
(d) x sin(log x) + c

Question 19.
\(\int \frac{\cos 2 x-1}{\cos 2 x+1} \cdot d x=\)
(a) tan x – x + c
(b) x + tan x + c
(c) x – tan x + c
(d) -x – cot x + c
Answer:
(c) x – tan x + c

Question 20.
\(\int \frac{e^{2 x}+e^{-2 x}}{e^{x}} \cdot d x=\)
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)
(b) \(e^{x}+\frac{1}{3 e^{3 x}}+c\)
(c) \(e^{-x}+\frac{1}{3 e^{3 x}}+c\)
(d) \(e^{-x}-\frac{1}{3 e^{3 x}}+c\)
Answer:
(a) \(e^{x}-\frac{1}{3 e^{3 x}}+c\)

II. Integrate the following with respect to the respective variable:

Question 1.
(x – 2)² √x
Solution:

Question 2.
\(\frac{x^{7}}{x+1}\)
Solution:

Question 3.
\((6 x+5)^{\frac{3}{2}}\)
Solution:

Question 4.
\(\frac{t^{3}}{(t+1)^{2}}\)
Solution:

Question 5.
\(\frac{3-2 \sin x}{\cos ^{2} x}\)
Solution:

Question 6.
\(\frac{\sin ^{6} \theta+\cos ^{6} \theta}{\sin ^{2} \theta \cdot \cos ^{2} \theta}\)
Solution:

Question 7.
cos 3x cos 2x cos x
Solution:

Question 8.
\(\frac{\cos 7 x-\cos 8 x}{1+2 \cos 5 x}\)
Solution:

Question 9.
\(\cot ^{-1}\left(\frac{1+\sin x}{\cos x}\right)\)
Solution:
Let I = \(\int \cot ^{-1}\left(\frac{1+\sin x}{\cos x}\right) d x\)

III. Integrate the following w.r.t. x:

Question 1.
\(\frac{(1+\log x)^{3}}{x}\)
Solution:

Question 2.
cot^-1 (1 – x + x²)
Solution:

Question 3.
\(\frac{1}{x \sin ^{2}(\log x)}\)
Solution:

Question 4.
\(\sqrt{x} \sec \left(x^{\frac{3}{2}}\right) \tan \left(x^{\frac{3}{2}}\right)\)
Solution:

Question 5.
log(1 + cos x) – x tan(\(\frac{x}{2}\))
Solution:

Question 6.
\(\frac{x^{2}}{\sqrt{1-x^{6}}}\)
Solution:

Question 7.
\(\frac{1}{(1-\cos 4 x)(3-\cot 2 x)}\)
Solution:

Question 8.
log(log x) + (log x)^-2
Solution:

Question 9.
\(\frac{1}{2 \cos x+3 \sin x}\)
Solution:

Question 10.
\(\frac{1}{x^{3} \sqrt{x^{2}-1}}\)
Solution:

Question 11.
\(\frac{3 x+1}{\sqrt{-2 x^{2}+x+3}}\)
Solution:

Question 12.
log(x² + 1)
Solution:

Question 13.
e^2x sin x cos x
Solution:

Question 14.
\(\frac{x^{2}}{(x-1)(3 x-1)(3 x-2)}\)
Solution:

Question 15.
\(\frac{1}{\sin x+\sin 2 x}\)
Solution:

Question 16.
\(\sec ^{2} x \sqrt{7+2 \tan x-\tan ^{2} x}\)
Solution:

Question 17.
\(\frac{x+5}{x^{3}+3 x^{2}-x-3}\)
Solution:

Question 18.
\(\frac{1}{x\left(x^{5}+1\right)}\)
Solution:

Question 19.
\(\frac{\sqrt{\tan x}}{\sin x \cdot \cos x}\)
Solution:

Question 20.
sec⁴ x cosec² x
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.4 Questions and Answers.

12th Maths Part 2 Indefinite Integration Exercise 3.4 Questions And Answers Maharashtra Board

I. Integrate the following w. r. t. x:

Question 1.
\(\frac{x^{2}+2}{(x-1)(x+2)(x+3)}\)
Solution:

Question 2.
\(\frac{x^{2}}{\left(x^{2}+1\right)\left(x^{2}-2\right)\left(x^{2}+3\right)}\)
Solution:

Question 3.
\(\frac{12 x+3}{6 x^{2}+13 x-63}\)
Solution:

Question 4.
\(\frac{2 x}{4-3 x-x^{2}}\)
Solution:

Question 5.
\(\frac{x^{2}+x-1}{x^{2}+x-6}\)
Solution:

Question 6.
\(\frac{6 x^{3}+5 x^{2}-7}{3 x^{2}-2 x-1}\)
Solution:

Question 7.
\(\frac{12 x^{2}-2 x-9}{\left(4 x^{2}-1\right)(x+3)}\)
Solution:

Question 8.
\(\frac{1}{x\left(x^{5}+1\right)}\)
Solution:

Question 9.
\(\frac{2 x^{2}-1}{x^{4}+9 x^{2}+20}\)
Solution:

Question 10.
\(\frac{x^{2}+3}{\left(x^{2}-1\right)\left(x^{2}-2\right)}\)
Solution:

Question 11.
\(\frac{2 x}{\left(2+x^{2}\right)\left(3+x^{2}\right)}\)
Solution:

Question 12.
\(\frac{2^{x}}{4^{x}-3 \cdot 2^{x}-4}\)
Solution:

Question 13.
\(\frac{3 x-2}{(x+1)^{2}(x+3)}\)
Solution:

Question 14.
\(\frac{5 x^{2}+20 x+6}{x^{3}+2 x^{2}+x}\)
Solution:
Let I = ∫\(\frac{5 x^{2}+20 x+6}{x^{3}+2 x^{2}+x}\) dx

Question 15.
\(\frac{1}{x\left(1+4 x^{3}+3 x^{6}\right)}\)
Solution:

Question 16.
\(\frac{1}{x^{3}-1}\)
Solution:

Question 17.
\(\frac{(3 \sin x-2) \cdot \cos x}{5-4 \sin x-\cos ^{2} x}\)
Solution:

Question 18.
\(\frac{1}{\sin x+\sin 2 x}\)
Solution:

Question 19.
\(\frac{1}{2 \sin x+\sin 2 x}\)
Solution:

Question 20.
\(\frac{1}{\sin 2 x+\cos x}\)
Solution:

Question 21.
\(\frac{1}{\sin x \cdot(3+2 \cos x)}\)
Solution:

Question 22.
\(\frac{5 \cdot e^{x}}{\left(e^{x}+1\right)\left(e^{2 x}+9\right)}\)
Solution:

Question 23.
\(\frac{2 \log x+3}{x(3 \log x+2)\left[(\log x)^{2}+1\right]}\)
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.3 Questions and Answers.

12th Maths Part 2 Indefinite Integration Exercise 3.3 Questions And Answers Maharashtra Board

I. Evaluate the following:

Question 1.
∫x² log x dx
Solution:

Question 2.
∫x² sin 3x dx
Solution:

Question 3.
∫x tan^-1 x dx
Solution:

Question 4.
∫x² tan^-1 x dx
Solution:

Question 5.
∫x³ tan^-1 x dx
Solution:
Let I = ∫x³ tan^-1 x dx
= ∫(tan^-1 x) . x³ dx

Question 6.
∫(log x)² dx
Solution:
Let I = ∫(log x)² dx
Put log x = t

Question 7.
∫sec³ x dx
Solution:
Let I = ∫sec³ x dx
= ∫sec x sec² x dx
= sec x ∫sec² x dx – ∫[\(\frac{d}{d x}\)(sec x) ∫sec² x dx] dx
= sec x tan x – ∫(sec x tan x)(tan x) dx
= sec x tan x – ∫sec x tan² x dx
= sec x tan x – ∫sec x (sec² x – 1) dx
= sec x tan x – ∫sec³ x dx + ∫sec x dx
∴ I = sec x tan x – I + log|sec x + tan x|
∴ 2I = sec x tan x + log|sec x + tan x|
∴ I = \(\frac{1}{2}\) [sec x tan x + log|sec x + tan x|] + c.

Question 8.
∫x . sin² x dx
Solution:

Question 9.
∫x³ log x dx
Solution:

Question 10.
∫e^2x cos 3x dx
Solution:

Question 11.
∫x sin^-1 x dx
Solution:

Question 12.
∫x² cos^-1 x dx
Solution:

Question 13.
\(\int \frac{\log (\log x)}{x} d x\)
Solution:

= t(log t – 1) + c
= (log x) . [log(log x) – 1] + c.

Question 14.
\(\int \frac{t \cdot \sin ^{-1} t}{\sqrt{1-t^{2}}} d t\)
Solution:

Question 15.
∫cos√x dx
Solution:
Let I = ∫cos√x dx
Put √x = t
∴ x = t²
∴ dx = 2t dt
∴ I = ∫(cos t) 2t dt
= ∫2t cos t dt
= 2t ∫cos t dt – ∫[\(\frac{d}{d t}\)(2t) ∫cos t dt]dt
= 2t sin t – ∫2 sin t dt
= 2t sin t + 2 cos t + c
= 2[√x sin√x + cos√x] + c.

Question 16.
∫sin θ . log(cos θ) dθ
Solution:
Let I = ∫sin θ . log (cos θ) dθ
= ∫log(cos θ) . sin θ dθ
Put cos θ = t
∴ -sin θ dθ = dt
∴ sin θ dθ = -dt

= -t log t + t + c
= -cos θ . log(cos θ) + cos θ + c
= -cos θ [log(cos θ) – 1] + c.

Question 17.
∫x cos³ x dx
Solution:
cos 3x = 4 cos³ x – 3 cos x
∴ cos³ x + 3 cos x = 4cos3x
∴ cos³ x = \(\frac{1}{4}\) cos 3x + \(\frac{3}{4}\) cos x

Question 18.
\(\int \frac{\sin (\log x)^{2}}{x} \cdot \log x d x\)
Solution:

Question 19.
\(\int \frac{\log x}{x} d x\)
Solution:
Let I = \(\int \frac{\log x}{x} d x\)
Put log x = t
\(\frac{1}{x}\) dx = dt
∴ I = ∫t dt
= \(\frac{1}{2}\) t² + c
= \(\frac{1}{2}\) (log x)² + c

Question 20.
∫x sin 2x cos 5x dx.
Solution:
Let I = ∫x sin 2x cos 5x dx
sin 2x cos 5x = \(\frac{1}{2}\)[2 sin 2x cos 5x]
= \(\frac{1}{2}\) [sin(2x + 5x) + sin(2x – 5x)]
= \(\frac{1}{2}\) [sin 7x – sin 3x]
∴ ∫sin 2x cos 5x dx = \(\frac{1}{2}\) [∫sin 7x dx – ∫sin 3x dx]

Question 21.
\(\int \cos (\sqrt[3]{x}) d x\)
Solution:
Let I = \(\int \cos (\sqrt[3]{x}) d x\)

II. Integrate the following functions w.r.t. x:

Question 1.
e^2x sin 3x
Solution:

Question 2.
e^-x cos 2x
Solution:

Question 3.
sin(log x)
Solution:

Question 4.
\(\sqrt{5 x^{2}+3}\)
Solution:
Let I = \(\sqrt{5 x^{2}+3}\) dx

Question 5.
\(x^{2} \sqrt{a^{2}-x^{6}}\)
Solution:

Question 6.
\(\sqrt{(x-3)(7-x)}\)
Solution:

Question 7.
\(\sqrt{4^{x}\left(4^{x}+4\right)}\)
Solution:

Question 8.
(x + 1) \(\sqrt{2 x^{2}+3}\)
Solution:
Let I = ∫(x + 1) \(\sqrt{2 x^{2}+3}\) dx
Let x + 1 = A[\(\frac{d}{d x}\)(2x² + 3)] + B
= A(4x) + B
= 4Ax + B
Comparing the coefficients of x and constant term on both the sides, we get
4A = 1, B = 1
∴ A = \(\frac{1}{4}\), B = 1

Question 9.
\(x \sqrt{5-4 x-x^{2}}\)
Solution:
Let I = ∫\(x \sqrt{5-4 x-x^{2}}\) dx
Let x = A[\(\frac{d}{d x}\)(5 – 4x – x²)] + B
= A[-4 – 2x] + B
= -2Ax + (B – 4A)
Comparing the coefficients of x and the constant term on both sides, we get
-2A = 1, B – 4A = 0

Question 10.
\(\sec ^{2} x \sqrt{\tan ^{2} x+\tan x-7}\)
Solution:

Question 11.
\(\sqrt{x^{2}+2 x+5}\)
Solution:

Question 12.
\(\sqrt{2 x^{2}+3 x+4}\)
Solution:

III. Integrate the following functions w.r.t. x:

Question 1.
[2 + cot x – cosec² x] e^x
Solution:
Let I = ∫e^x [2 + cot x – cosec² x] dx
Put f(x) = 2 + cot x
∴ f'(x) = \(\frac{d}{d x}\)(2 + cot x)
= \(\frac{d}{d x}\)(2) + \(\frac{d}{d x}\)(cot x)
= 0 – cosec² x
= -cosec² x
∴ I = ∫e^x [f(x) + f'(x)] dx
= e^x f(x) + c
= e^x (2 + cot x) + c.

Question 2.
\(\left(\frac{1+\sin x}{1+\cos x}\right) e^{x}\)
Solution:

Question 3.
\(e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\)
Solution:
Let I = ∫\(e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\)
Let f(x) = \(\frac{1}{x}\), f'(x) = \(-\frac{1}{x^{2}}\)
∴ I = ∫e^x [f(x) + f'(x)] dx
= e^x f(x) + c
= e^x . \(\frac{1}{x}\) + c

Question 4.
\(\left[\frac{x}{(x+1)^{2}}\right] e^{x}\)
Solution:

Question 5.
\(\frac{e^{x}}{x}\) . [x(log x)² + 2 log x]
Solution:

Question 6.
\(e^{5 x}\left[\frac{5 x \log x+1}{x}\right]\)
Solution:
Let I = ∫\(e^{5 x}\left[\frac{5 x \log x+1}{x}\right]\)

Question 7.
\(e^{\sin ^{-1} x}\left[\frac{x+\sqrt{1-x^{2}}}{\sqrt{1-x^{2}}}\right]\)
Solution:

Question 8.
log(1 + x)^(1+x)
Solution :
Let I = ∫log(1 + x)^(1+x) dx

Question 9.
cosec (log x)[1 – cot(log x)]
Solution:
Let I = ∫cosec (log x)[1 – cot(log x)] dx
Put log x = t
x = e^t
dx = e^t dt
I = ∫cosec t (1 – cot t). e^t dt
= ∫e^t [cosec t – cosec t cot t] dt
= ∫e^t [cosec t + \(\frac{d}{d t}\) (cosec t)] dt
= e^t cosec t + c ….. [∵ e^t [f(t) +f'(t) ] dt = e^t f(t) + c ]
= x . cosec(log x) + c.

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.2(C) Questions and Answers.

12th Maths Part 2 Indefinite Integration Exercise 3.2(C) Questions And Answers Maharashtra Board

I. Evaluate:

Question 1.
\(\int \frac{3 x+4}{x^{2}+6 x+5} d x\)
Solution:
Let I = \(\int \frac{3 x+4}{x^{2}+6 x+5} d x\)
Let 3x + 4 = A[\(\frac{d}{d x}\)(x² + 6x + 5)] + B
= A(2x + B) + B
∴ 3x + 4 = 2Ax + (6A + B)
Comparing the coefficient of x and constant on both sides, we get
2A = 3 and 6A + B = 4
∴ A = \(\frac{3}{2}\) and 6(\(\frac{3}{2}\)) + B = 4
∴ B = -5
3x + 4 = \(\frac{3}{2}\) (2x + 6) – 5

Question 2.
\(\int \frac{2 x+1}{x^{2}+4 x-5} d x\)
Solution:
Let I = \(\int \frac{2 x+1}{x^{2}+4 x-5} d x\)
Let 2x + 1 = A[\(\frac{d}{d x}\)(x² + 4x – 5)] + B
2x + 1 = A(2x + 1) + B
∴ 2x + 1 = 2Ax + (4A + B)
Comparing the coefficient of x and constant on both sides, we get
4A = 2 and 4A + B = 4
∴ A = \(\frac{3}{2}\) and 6(\(\frac{3}{2}\)) + B = 4
∴ B = -5
∴ 2x + 1 = \(\frac{3}{2}\)(2x + 1) – 5

Question 3.
\(\int \frac{2 x+3}{2 x^{2}+3 x-1} d x\)
Solution:
Let I = \(\int \frac{2 x+3}{2 x^{2}+3 x-1} d x\)
Let 2x+ 3 = A[\(\frac{d}{d x}\)(2x² + 3x – 1)] + B
2x + 1 = A(4x + 3) + B
∴ 2x + 1 = 4Ax + (3A + B)
Comparing the coefficient of x and constant on both sides, we get
4A = 2 and 3A + B = 3
∴ A = \(\frac{1}{2}\) and 3(\(\frac{1}{2}\)) + B = 3
∴ B = \(\frac{3}{2}\)
∴ 2x + 3 = \(\frac{1}{2}\)(4x + 3) + \(\frac{3}{2}\)

Question 4.
\(\int \frac{3 x+4}{\sqrt{2 x^{2}+2 x+1}} d x\)
Solution:
Let I = \(\int \frac{3 x+4}{\sqrt{2 x^{2}+2 x+1}} d x\)
Let 3x + 4 = A[\(\frac{d}{d x}\)(2x² + 2x + 1)] + B
∴ 3x + 4 = A (4x + 2) + B
∴ 3x + 4 = 4Ax + (2A + B)
Comparing the coefficient of x and the constant on both the sides, we get
4A = 3 and 2A + B = 4
∴ A = \(\frac{3}{4}\) and 2(\(\frac{3}{4}\)) + B = 4
∴ B = \(\frac{5}{2}\)
∴ 3x + 4 = \(\frac{3}{4}\) (4x + 2) + \(\frac{5}{2}\)

Question 5.
\(\int \frac{7 x+3}{\sqrt{3+2 x-x^{2}}} d x\)
Solution:
Let I = \(\int \frac{7 x+3}{\sqrt{3+2 x-x^{2}}} d x\)
Let 7x + 3 = A[\(\frac{d}{d x}\)(3 + 2x – x²)] + B
7x + 3 = A(2 – 2x) + B
∴ 7x + 3 = -2Ax + (2A + B)
Comparing the coefficient of x and constant on both the sides, we get
-2A = 7 and 2A + B = 3

Question 6.
\(\int \sqrt{\frac{x-7}{x-9}} d x\)
Solution:

Comparing the coefficients of x and constant term on both sides, we get

Question 7.
\(\int \sqrt{\frac{9-x}{x}} d x\)
Solution:

Question 8.
\(\int \frac{3 \cos x}{4 \sin ^{2} x+4 \sin x-1} d x\)
Solution:

Question 9.
\(\int \sqrt{\frac{e^{3 x}-e^{2 x}}{e^{x}+1}} d x\)
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.2(B) Questions and Answers.

12th Maths Part 2 Indefinite Integration Exercise 3.2(B) Questions And Answers Maharashtra Board

I. Evaluate the following:

Question 1.
\(\int \frac{1}{4 x^{2}-3} \cdot d x\)
Solution:

Question 2.
\(\int \frac{1}{25-9 x^{2}} \cdot d x\)
Solution:

Question 3.
\(\int \frac{1}{7+2 x^{2}} \cdot d x\)
Solution:

Question 4.
\(\int \frac{1}{\sqrt{3 x^{2}+8}} \cdot d x\)
Solution:

Question 5.
\(\int \frac{1}{\sqrt{11-4 x^{2}}} \cdot d x\)
Solution:

Question 6.
\(\int \frac{1}{\sqrt{2 x^{2}-5}} \cdot d x\)
Solution:

Question 7.
\(\int \sqrt{\frac{9+x}{9-x}} \cdot d x\)
Solution:

Question 8.
\(\int \sqrt{\frac{2+x}{2-x}} \cdot d x\)
Solution:

Question 9.
\(\int \sqrt{\frac{10+x}{10-x}} \cdot d x\)
Solution:

Question 10.
\(\int \frac{1}{x^{2}+8 x+12} \cdot d x\)
Solution:

Question 11.
\(\int \frac{1}{1+x-x^{2}} \cdot d x\)
Solution:

Question 12.
\(\int \frac{1}{4 x^{2}-20 x+17} \cdot d x\)
Solution:

Question 13.
\(\int \frac{1}{5-4 x-3 x^{2}} \cdot d x\)
Solution:

Question 14.
\(\int \frac{1}{\sqrt{3 x^{2}+5 x+7}} \cdot d x\)
Solution:

Question 15.
\(\int \frac{1}{\sqrt{x^{2}+8 x-20}} \cdot d x\)
Solution:

Question 16.
\(\int \frac{1}{\sqrt{8-3 x+2 x^{2}}} \cdot d x\)
Solution:

Question 17.
\(\int \frac{1}{\sqrt{(x-3)(x+2)}} \cdot d x\)
Solution:

Question 18.
\(\int \frac{1}{4+3 \cos ^{2} x} \cdot d x\)
Solution:

Question 19.
\(\int \frac{1}{\cos 2 x+3 \sin ^{2} x} \cdot d x\)
Solution:

Question 20.
\(\int \frac{\sin x}{\sin 3 x} \cdot d x\)
Solution:

II. Integrate the following functions w. r. t. x:

Question 1.
\(\int \frac{1}{3+2 \sin x} \cdot d x\)
Solution:

Question 2.
\(\int \frac{1}{4-5 \cos x} \cdot d x\)
Solution:

Question 3.
\(\int \frac{1}{2+\cos x-\sin x} \cdot d x\)
Solution:

Question 4.
\(\int \frac{1}{3+2 \sin x-\cos x} \cdot d x\)
Solution:

Question 5.
\(\int \frac{1}{3-2 \cos 2 x} \cdot d x\)
Solution:

Question 6.
\(\int \frac{1}{2 \sin 2 x-3} \cdot d x\)
Solution:

Question 7.
\(\int \frac{1}{3+2 \sin 2 x+4 \cos 2 x} \cdot d x\)
Solution:

Question 8.
\(\int \frac{1}{\cos x-\sin x} \cdot d x\)
Solution:

Question 9.
\(\int \frac{1}{\cos x-\sqrt{3} \sin x} \cdot d x\)
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.2(A) Questions and Answers.

12th Maths Part 2 Indefinite Integration Exercise 3.2(A) Questions And Answers Maharashtra Board

I. Integrate the following functions w.r.t. x:

Question 1.
\(\frac{(\log x)^{n}}{x}\)
Solution:

Question 2.
\(\frac{\left(\sin ^{-1} x\right)^{\frac{3}{2}}}{\sqrt{1-x^{2}}}\)
Solution:
Let I = \(\int \frac{\left(\sin ^{-1} x\right)^{\frac{3}{2}}}{\sqrt{1-x^{2}}} d x\)

Question 3.
\(\frac{1+x}{x \cdot \sin (x+\log x)}\)
Solution:

Question 4.
\(\frac{x \cdot \sec ^{2}\left(x^{2}\right)}{\sqrt{\tan ^{3}\left(x^{2}\right)}}\)
Solution:

Question 5.
\(\frac{e^{3 x}}{e^{3 x}+1}\)
Solution:

Question 6.
\(\frac{\left(x^{2}+2\right)}{\left(x^{2}+1\right)} \cdot a^{x+\tan ^{-1} x}\)
Solution:

Question 7.
\(\frac{e^{x} \cdot \log \left(\sin e^{x}\right)}{\tan \left(e^{x}\right)}\)
Solution:

Question 8.
\(\frac{e^{2 x}+1}{e^{2 x}-1}\)
Solution:

Question 9.
sin⁴x . cos³x
Solution:

Question 10.
\(\frac{1}{4 x+5 x^{-11}}\)
Solution:

Question 11.
x⁹ . sec²(x¹⁰)
Solution:

Question 12.
\(e^{3 \log x} \cdot\left(x^{4}+1\right)^{-1}\)
Solution:

Question 13.
\(\frac{\sqrt{\tan x}}{\sin x \cdot \cos x}\)
Solution:
Let I = \(\int \frac{\sqrt{\tan x}}{\sin x \cdot \cos x} d x\)
Dividing numerator and denominator by cos²x, we get

Question 14.
\(\frac{(x-1)^{2}}{\left(x^{2}+1\right)^{2}}\)
Solution:

Question 15.
\(\frac{2 \sin x \cos x}{3 \cos ^{2} x+4 \sin ^{2} x}\)
Solution:

Question 16.
\(\frac{1}{\sqrt{x}+\sqrt{x^{3}}}\)
Solution:

Question 17.
\(\frac{10 x^{9}+10^{x} \cdot \log 10}{10^{x}+x^{10}}\)
Solution:

Question 18.
\(\frac{x^{n-1}}{\sqrt{1+4 x^{n}}}\)
Solution:

Question 19.
(2x + 1) \(\sqrt{x+2}\)
Solution:

Question 20.
\(x^{5} \sqrt{a^{2}+x^{2}}\)
Solution:

Question 21.
\((5-3 x)(2-3 x)^{-\frac{1}{2}}\)
Solution:

Question 22.
\(\frac{7+4 x+5 x^{2}}{(2 x+3)^{\frac{3}{2}}}\)
Solution:

Question 23.
\(\frac{x^{2}}{\sqrt{9-x^{6}}}\)
Solution:

Question 24.
\(\frac{1}{x\left(x^{3}-1\right)}\)
Solution:

Question 25.
\(\frac{1}{x \cdot \log x \cdot \log (\log x)}\)
Solution:

II. Integrate the following functions w.r.t x:

Question 1.
\(\frac{\cos 3 x-\cos 4 x}{\sin 3 x+\sin 4 x}\)
Solution:

Question 2.
\(\frac{\cos x}{\sin (x-a)}\)
Solution:

Question 3.
\(\frac{\sin (x-a)}{\cos (x+b)}\)
Solution:

Question 4.
\(\frac{1}{\sin x \cdot \cos x+2 \cos ^{2} x}\)
Solution:
Let I = \(\int \frac{1}{\sin x \cdot \cos x+2 \cos ^{2} x} d x\)
Dividing numerator and denominator of cos²x, we get

Question 5.
\(\frac{\sin x+2 \cos x}{3 \sin x+4 \cos x}\)
Solution:
Let I = \(\int \frac{\sin x+2 \cos x}{3 \sin x+4 \cos x} d x\)
Put, Numerator = A (Denominator) + B [\(\frac{d}{d x}\) (Denominator)]
∴ sin x+ 2 cos x = A(3 sin x + 4 cos x) + B [\(\frac{d}{d x}\) (3 sin x + 4 cos x)]
= A(3 sin x + 4 cos x) + B (3 cos x – 4 sin x)
∴ sin x + 2 cos x = (3A – 4B) sin x + (4A + 3B) cos x
Equating the coefficients of sin x and cos x on both the sides, we get
3A – 4B = 1 …… (1)
and 4A + 3B = 2 …… (2)
Multiplying equation (1) by 3 and equation (2) by 4, we get
9A – 12B = 3
16A + 12B = 8
On adding, we get

Question 6.
\(\frac{1}{2+3 \tan x}\)
Solution:
Let I = \(\int \frac{1}{2+3 \tan x} d x\)

Numerator = A (Denominator) + B [\(\frac{d}{d x}\) (Denominator)]
∴ cos x = A(2 cos x + 3 sin x) + B [\(\frac{d}{d x}\) (2 cos x + 3 sin x)]
= A (2 cos x + 3 sin x) + B (-2 sin x + 3 cos x)
∴ cos x = (2A + 3B) cos x + (3A – 2B) sin x
Equating the coefficients of cosx and sinx on both the sides, we get
2A + 3B = 1 …… (1)
and 3A – 2B = 0 ……. (2)
Multiplying equation (1) by 2 and equation (2) by 3, we get
4A + 6B = 2
9A – 6B = 0
On adding, we get

Question 7.
\(\frac{4 e^{x}-25}{2 e^{x}-5}\)
Solution:
Let I = \(\int \frac{4 e^{x}-25}{2 e^{x}-5} d x\)
Put, Numerator = A (Denominator) + B [\(\frac{d}{d x}\) (Denominator)]
∴ 4ex – 25 = A(2ex – 5) + B[\(\frac{d}{d x}\) (2ex – 5)]
= A(2ex – 5) + B(2ex – 0)
∴ 4ex – 25 = (2A + 2B) ex – 5A
Equating the coefficient of ex and constant on both sides, we get
2A + 2B = 4 …….(1)
and 5A = 25
∴ A = 5
from (1), 2(5) + 2B = 4
∴ 2B = -6
∴ B = -3

Question 8.
\(\frac{20+12 e^{x}}{3 e^{x}+4}\)
Solution:

Question 9.
\(\frac{3 e^{2 x}+5}{4 e^{2 x}-5}\)
Solution:
Let I = \(\int \frac{3 e^{2 x}+5}{4 e^{2 x}-5} d x\)
Put, Numerator = A (Denominator) + B [\(\frac{d}{d x}\) (Denominator)]
∴ 3e2x + 5 = A(4e2x – 5) + B [\(\frac{d}{d x}\) (4e2x – 5)]
= A(4e2x – 5) + B(4 . e2x × 2 – 0)
∴ 3e2x + 5 = (4A + 8B) e2x – 5A
Equating the coefficient of e2x and constant on both sides, we get
4A + 8B = 3 …….. (1)
and -5A = 5
∴ A = -1
∴ from (1), 4(-1) + 8B = 3
∴ 8B = 7
∴ B = \(\frac{7}{8}\)

Question 10.
cos⁸ x . cot x
Solution:

Question 11.
tan⁵x
Solution:
Let I = ∫ tan⁵x dx

Question 12.
cos⁷x
Solution:

Question 13.
tan 3x tan 2x tan x
Solution:
Let I = ∫ tan 3x tan 2x tan x dx
Consider tan 3x = tan (2x + x) = \(\frac{\tan 2 x+\tan x}{1-\tan 2 x \tan x}\)
tan 3x (1 – tan 2x tan x) = tan 2x + tan x
tan 3x – tan 3x tan 2x tan x = tan 2x + tan x
tan 3x – tan 2x – tan x = tan 3x tan 2x tan x
I = ∫(tan 3x – tan 2x – tan x) dx
= ∫tan3x dx – ∫tan 2x dx – ∫tan x dx
= \(\frac{1}{3}\) log | sec 3x| – \(\frac{1}{2}\) log |sec 2x| – log |sec x| + c.

Question 14.
sin⁵x cos⁸x
Solution:

Question 15.
\(3^{\cos ^{2} x \cdot} \sin 2 x\)
Solution:

Question 16.
\(\frac{\sin 6 x}{\sin 10 x \sin 4 x}\)
Solution:

Question 17.
\(\frac{\sin x \cos ^{3} x}{1+\cos ^{2} x}\)
Solution:

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.1 Questions and Answers.

12th Maths Part 2 Indefinite Integration Exercise 3.1 Questions And Answers Maharashtra Board

I. Integrate the following functions w.r.t. x:

(i) x³ + x² – x + 1
Solution:

(ii) \(x^{2}\left(1-\frac{2}{x}\right)^{2}\)
Solution:

(iii) \(3 \sec ^{2} x-\frac{4}{x}+\frac{1}{x \sqrt{x}}-7\)
Solution:

(iv) \(2 x^{3}-5 x+\frac{3}{x}+\frac{4}{x^{5}}\)
Solution:

(v) \(\frac{3 x^{3}-2 x+5}{x \sqrt{x}}\)
Solution:

II. Evaluate:

(i) ∫tan² x . dx
Solution:

(ii) \(\int \frac{\sin 2 x}{\cos x} \cdot d x\)
Solution:

(iii) \(\int \frac{\sin x}{\cos ^{2} x} \cdot d x\)
Solution:

(iv) \(\int \frac{\cos 2 x}{\sin ^{2} x} \cdot d x\)
Solution:

(v) \(\int \frac{\cos 2 x}{\sin ^{2} x \cdot \cos ^{2} x} \cdot d x\)
Solution:

= -cot x – tan x + c

(vi) \(\int \frac{\sin x}{1+\sin x} \cdot d x\)
Solution:

(vii) \(\int \frac{\tan x}{\sec x+\tan x} \cdot d x\)
Solution:

(viii) \(\int \sqrt{1+\sin 2 x} \cdot d x\)
Solution:

(ix) \(\int \sqrt{1-\cos 2 x} \cdot d x\)
Solution:

(x) ∫sin 4x cos 3x dx
Solution:

III. Evaluate:

(i) \(\int \frac{x}{x+2} \cdot d x\)
Solution:

(ii) \(\int \frac{4 x+3}{2 x+1} \cdot d x\)
Solution:

(iii) \(\int \frac{5 x+2}{3 x-4} \cdot d x\)
Solution:

(iv) \(\int \frac{x-2}{\sqrt{x+5}} \cdot d x\)
Solution:

(v) \(\int \frac{2 x-7}{\sqrt{4 x-1}} \cdot d x\)
Solution:

(vi) \(\int \frac{\sin 4 x}{\cos 2 x} \cdot d x\)
Solution:

(vii) \(\int \sqrt{1+\sin 5 x} \cdot d x\)
Solution:

(viii) ∫cos² x . dx
Solution:

(ix) \(\int \frac{2}{\sqrt{x}-\sqrt{x+3}} \cdot d x\)
Solution:

(x) \(\int \frac{3}{\sqrt{7 x-2}-\sqrt{7 x-5}} \cdot d x\)
Solution:

IV.

Question 1.
If f'(x) = x – \(\frac{3}{x^{3}}\), f(1) = \(\frac{11}{2}\), find f(x).
Solution:
By the definition of integral,

Class 12 Maharashtra State Board Maths Solution 

• Exercise 3.1 Class 12 Maths 2
• Exercise 3.2(A) Class 12 Maths 2
• Exercise 3.2(B) Class 12 Maths 2
• Exercise 3.2(C) Class 12 Maths 2
• Exercise 3.3 Class 12 Maths 2
• Exercise 3.4 Class 12 Maths 2
• Miscellaneous Exercise 3 Class 12 Maths 2