Std 5 Hindi Lesson 16 मी नदी बोलते Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 5 Marathi Solutions Sulabhbharati Chapter 16 मी नदी बोलते Notes, Textbook Exercise Important Questions and Answers.
5th Std Hindi Poem Mi Nadi Bolte Question Answer
5th Standard Marathi Digest Chapter 16 मी नदी बोलते Textbook Questions and Answers
1. खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.
प्रश्न (अ)
नदीचा जन्म कोठे होतो?
उत्तर:
नदीचा जन्म पर्वतावर होतो.
![]()
प्रश्न (आ)
नदी मोठी कशी होते?
उत्तर:
इतर नदया व ओढे नदीच्या प्रवाहात येऊन मिळतात, त्यामुळे नदी मोठी होते.
प्रश्न (इ)
नदीच्या पाण्याचा उपयोग लोक कशाकशासाठी करतात?
प्रश्न (ई)
नदीचा वेग कधी कमी होतो?
उत्तरः
नदी जेव्हा पर्वतउतारावरून सपाट मैदानी प्रदेशात येते, तेव्हा तिचा वेग कमी होतो.
प्रश्न (उ)
नदी आपल्याला कोणता संदेश देते?
उत्तर:
‘थांबला तो संपला’ हा संदेश नदी आपल्याला देते.
प्रश्न (ऊ)
तुमच्या जिल्ह्यात कोणकोणत्या नद्या आहेत?
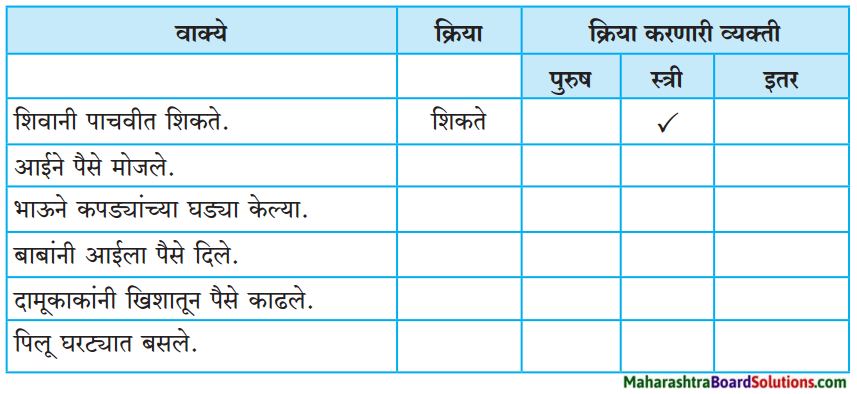
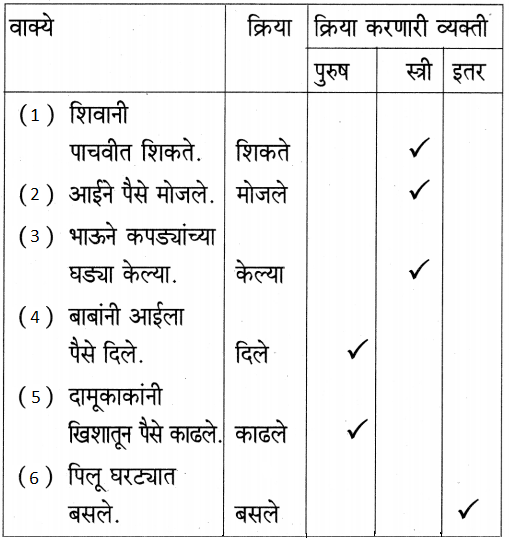
2. पहिल्या दोन उदाहरणांचे निरीक्षण करा. त्यानुसार रिकाम्या जागा भरा.
प्रश्न 1.
पहिल्या दोन उदाहरणांचे निरीक्षण करा. त्यानुसार रिकाम्या जागा भरा.
उत्तरः
| (अ) चालणे | चालतात | चालवतात |
| (आ) पळणे | पळतात | पळवतात |
| (इ) भेटणे | भेटतात | भेटवतात |
| (ई) करणे | करतात | करवतात |
| (उ) मिळणे | मिळतात | मिळवतात |
| (ऊ) थांबणे | थांबतात | थांबवतात |
![]()
3. ‘हिरवेगार’ यासारखे रंगछटा दाखवणारे शब्द सांगा.
प्रश्न 1.
‘हिरवेगार’ यासारखे रंगछटा दाखवणारे शब्द सांगा.
उत्तर:
- पिवळेधमक
- पांढरेशुभ्र
- निळाशार
- लालभडक
- काळेकुट्ट
4. ‘थांबला तो संपला’ यासारखी सुवचने सांगा.
प्रश्न 1.
‘थांबला तो संपला’ यासारखी सुवचने सांगा.
उत्तर:
1. ‘वृक्ष माझा सखा.’
2. ‘थेंबे थेंबे तळे साचे’.
3. ‘मूर्ती लहान पण किर्ती महान’.
5. खालील शब्द वाचा व तसेच लिहा.
प्रश्न 1.
खालील शब्द वाचा व तसेच लिहा.
पर्वत, सर्व, किर, पूर्व, मर्कट, सूर्य, प्रवास, चक्र, चंद्र, क्रमांक, प्रकार, ग्रह.
उपक्रम:
1. परिसर अभ्यासाची पुस्तके, वर्तमानपत्रे, नकाशे यांतून वेगवेगळ्या नद्यांची नावे शोधा. यादी करा.
2. नदीचे प्रदूषण कमी कसे करता येईल ते चर्चा करून सांगा.
3. खालील घोषवाक्ये पाहा. ‘पाणी वाचवणे’ या संदर्भातील आणखी घोषवाक्ये मिळवा व संग्रह करा.
![]()
पाण्याची बचत:
1. पाण्याची टंचाई आहे. पाणी जपून वापरा.


Marathi Sulabhbharati Class 5 Solutions Chapter 16 मी नदी बोलते Additional Important Questions and Answers
प्रश्न 1.
एका शब्दात उत्तरे लिहा.
- माणसे नदीला अडवायला काय बांधतात?
- लोक कचरा, खराब पाणी नदीत सोडून नदीला काय करतात?
- शेवटी नदी कोणाला जाऊन मिळते?
- नदी आपल्या आसपासचा परिसर कसा करते?
- धरणाच्या वाहत्या पाण्यावर काय तयार होते?
- माणसे नदीच्या पाण्यात काय सोडतात?
उत्तरः
- धरण
- प्रदूषित
- सागराला
- हिरवागार
- वीज
- सांडपाणी
![]()
2. खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.
प्रश्न 1.
नदी कोणावर नाराज आहे?
उत्तर:
नदी माणसांवर नाराज आहे.
प्रश्न 2.
नदीकडून आपण काय शिकले पाहिजे?
उत्तर:
नदीकडून आपण ‘दुसऱ्यांना नेहमी देत रहा’, ‘थांबू नका’, ‘पुढे जात रहा’ हे शिकले पाहिजे.
प्रश्न 3.
शेवटी नदीचा प्रवास कुठे संपतो?
उत्तर:
जिथे नदी सागराला जाऊन मिळते, तिथे शेवटी नदीचा प्रवास संपतो.
प्रश्न 4.
नदी कोणत्या रूपाने पर्वतावरून खाली येते?
उत्तर:
नदी धबधब्याच्या रूपाने पर्वतावरून खाली येते.
प्रश्न 5.
तुम्हांला माहीत असलेल्या धरणांची नावे लिहा.
उत्तर:
- कोयना
- बारवी
- खडकवासला
- तानसा.
प्रश्न 6.
रिकाम्या जागा भरा.
- नदीच्या पाण्याने ………………………. तयार करतात.
- पर्वतउतारावरून नदी …………………… मैदानी भागात येते.
- नदी दोन्ही किनाऱ्यावरील परिसर ……………………….. करते.
- नदीच्या प्रवाहात ………………………… सोडतात.
- नदी म्हणून माझा ………………………….. थांबतो.
- ……………………. रूपाने पर्वतावरून खाली येते.
उत्तर:
- वीज
- सपाट
- हिरवागार
- सांडपाणी
- प्रवास
- धबधब्याच्या
प्रश्न 7.
चूक की बरोबर ते लिहा.
- नदीचा जन्म जमिनीवर होतो.
- नदीच्या पाण्याचा वापर पिण्यासाठी करतात.
- नदी पर्वतउतारावरून खोलगट भागात येते.
- माणसांच्या रस्ते, छोटी गांवे, शहरे यांच्याजवळून वाहताना नदी जास्तच प्रदूषित होते.
- नदीचे पाणी खारट असते.
- नदी सर्वांच्या उपयोगी येते.
उत्तर:
- चूक
- बरोबर
- चूक
- बरोबर
- चूक
- बरोबर
![]()
थोडक्यात उत्तरे लिहा.
प्रश्न 1.
नदीला कोणत्या गोष्टींची खंत आहे?
उत्तर:
नदी जेव्हा पर्वतउतारावर सपाट मैदानी भागात येते, तेव्हा तिचा वेग कमी होतो. नदीचा दोन्ही किनाऱ्यांवरील परिसर हिरवागार होतो. शेतकरी शेतात भरपूर धान्य पिकवतात; असे असूनही त्या प्रवाहात सांडपाणी, कचरा टाकून पाण्याला प्रदूषित केले जाते, याची नदीला खंत आहे.
प्रश्न 2.
माणसे नदीच्या पाण्याचा उपयोग कशासाठी करतात?
उत्तर:
माणसे नदीच्या पाण्याचा वापर अनेक कारणांसाठी करतात. नदीच्या पाण्यावर वीज तयार केली जाते, कारखाने, पंप चालवण्यासाठी हीच वीज उपयोगी पडते, पिकांना पाणी देण्यासाठी, पिण्यासाठीही नदीच्या पाण्याचा उपयोग माणसे करतात.
प्रश्न 3.
नदीचे प्रदूषण कमी कसे होईल?
उत्तर:
नदीत कचरा नाही टाकला, गुरे पात्रात न धुता काठावरच धुतली, भांडी काठावरच धुण्यासाठी बादलीत पाणी घेतले, निर्माल्य टाकले नाही, सांडपाणी सोडले नाही, तर नदीचे प्रदूषण कमी होईल.
प्रश्न 4.
नदीचा शेतकऱ्याला काय फायदा होतो?
उत्तर:
नदी ही शेतकऱ्यासाठी जीवनदायीनी आहे. नदीच्या पाण्यामुळे शेतकरी शेतात भरपूर धान्य पिकवतात.
प्रश्न 5.
पाठ्यपुस्तक पृष्ठ क्र. 27 वरील चित्रांचे निरीक्षण करून तुमच्या शब्दांत पाच वाक्ये लिहा.
उत्तरः
- नदीचा जन्म पर्वतावर होतो व इतर नदया, ओढे तिला येऊन मिळतात.
- नदी वेगाने धबधब्याच्या रूपाने पर्वतावरून खाली येते.
- नदयांचे पाणी अडवून त्यांवर धरणे बांधतात.
- नदीच्या पाण्यावर वीज तयार केली जाते.
- नदीच्या पाण्यावर शेतातील पंप चालवतात.
प्रश्न 6.
रिकाम्या जागा भरा.
उत्तरः
| 1. झोपणे | झोपतात | झोपवतात |
| 2. कळणे | कळतात | कळवतात |
| 3. उठणे | उठतात | उठवतात |
| 4. खेळणे | खेळतात | खेळवतात |
| 5. जगणे | जगतात | जगवतात |
| 6. बघणे | बघतात | बघवतात |
![]()
व्याकरण व भाषाभ्यास:
प्रश्न 1.
समानार्थी शब्द लिहा.
- नदी
- पर्वत
- वीज
- पाणी
- वेग
- खंत
- गाव
- शहर
- समुद्र
- भरपूर
- वस्ती
उत्तर:
- सरिता
- मेरू
- विदयुत
- जल
- गती
- दुःख
- ग्राम
- नगर
- सिंधू
- खूप
- वसाहत
प्रश्न 2.
विरुद्धार्थी शब्द लिहा.
- जन्म
- मोठी
- खाली
- भरपूर
- उपयोगी
- गाव
- उंच
- शेवटी
- मला
उत्तर:
- मृत्यू
- लहान
- वर
- कमी
- दुरूपयोगी
- शहर
- ठेंगू
- आरंभी
- तुला
![]()
प्रश्न 3.
वचन बदला.
- नदी
- ओढा
- धरण
- शेत
- उडी
- कडा
- धबधबा
- पर्वत
- मैदान
- किनारा
- गोष्ट
- वस्ती
- गाव
- शहर
- कारखाना
- धान्य
उत्तर:
- नदया
- ओढे
- धरणे
- शेते
- उड्या
- कडे
- धबधबे
- पर्वत
- मैदाने
- किनारे
- गोष्टी
- वस्त्या
- गावे
- शहरे
- कारखाने
- धान्य
प्रश्न 4.
‘पाणी वाचवणे’ या संदर्भात घोषवाक्ये लिहा.
उत्तरः
- संपले पाणी तर संपेल जीवन.
- जीवन म्हणजे पाणी.
- पाणी अडवा पाणी जिरवा.
- पाणी हे अमृत.
- पाण्याला पर्याय नाही.
![]()
पाण्याची बचत
1. पाठ्यपुस्तक पान नं. 29 पाहून खालील प्रश्नांची एका वाक्यात उत्तरे लिहा.
प्रश्न 1.
पाणी जपून का वापरावे?
उत्तर:
पाण्याची टंचाई आहे, म्हणून पाणी जपून वापरावे.
प्रश्न 2.
वॉटरबॅगमधील उरलेल्या पाण्याचे काय करावे?
उत्तर:
वॉटरबॅगमधील उरलेले पाणी वाया न घालवता ते झाडांना घालावे.
प्रश्न 3.
पाणी पिताना कोणती काळजी घ्यावी?
उत्तर:
पाणी पिताना आपल्याला हवे तेवढेच पाणी ग्लासमध्ये घ्यावे.
प्रश्न 4.
भरून ठेवलेले पाणी काय करू नये?
उत्तरः
भरून ठेवलेले पाणी शिळे समजून ओतून देऊ नये.
प्रश्न 5.
वाहने धुताना कोणती काळजी घ्यावी?
उत्तर:
वाहने धुताना पाण्याचा पाइप न वापरता वाहने ओल्या कपड्याने पुसून घ्यावीत.
प्रश्न 6.
नळ गळत असेल तर काय करावे?
उत्तर:
नळ गळत असेल तर तो ताबडतोब दुरूस्त करून घ्यावा.
![]()
प्रश्न 7.
खालील वाक्य योग्य की अयोग्य ते लिहा.
- पाहुण्यांना पिण्यासाठी पाणी देताना तांब्या-पेल्याने पाणी दयावे.
- नळ वाहता ठेवून कपडे, भांडी धुवावीत.
- दात घासताना नळ सुरू ठेवावा.
- शॉवरखाली अंघोळ न करता बादलीत पाणी घेऊन अंघोळ करावी.
- पाण्याचा पाईप गाड्या धुण्यासाठी वापरावा.
उत्तर:
- योग्य
- अयोग्य
- अयोग्य
- योग्य
- अयोग्य
मी नदी बोलते Summary in Marathi
पाठ्यपरिचय:
‘मी नदी बोलते….’ या पाठात लेखकाने नदीच्या उगमापासून ते सागराला जाऊन मिळेपर्यंतच्या प्रवासाचे वर्णन केले आहे.
![]()
शब्दार्थ:
- जन्म – उत्पत्ती (birth)
- पर्वत – मोठा डोंगर (a mountain)
- ओढा – पाण्याचा प्रवाह (stream)
- धरण – बांध, नदीमध्ये पाणी अडवण्यासाठी घातलेला बंधारा (a dam)
- कारखाने – यंत्रशाळा (a factory)
- शेत – धान्य पेरण्याची जागा (a farm)
- पंप – पाणी वर चढण्याचे यंत्र (pump)
- उडी – झेप (leap)
- वेग – गती (speed)
- कोसळणे – जोरात खाली पडणे (to pour in to rents)
- धबधबा – उंचावरून खाली पडणारा पाण्याचा प्रवाह (waterfall)
- सपाट – समतल, उंच सखल नसलेले (flat)
- किनारा – काठ (a shore, a bank)
- परिसर – Taalstel last (surroundings)
- खंत – दुःख (regret)
- सांडपाणी – कपडे, भांडी धुण्यातून तयार झालेले घाण पाणी (dirty and flowing used water)
- कचरा – केर (garbage)
- प्रदूषित – अशुद्ध (polluted)
- वस्ती – वसाहत (colony)
- प्रवास – सफर, भ्रमंती (a journey)
5th Standard Marathi Digest Pdf Download
- नदीचे गाणे Class 5 Marathi Question Answer
- मी नदी बोलते Class 5 Marathi Question Answer
- आमची सहल Class 5 Marathi Question Answer
- पैशांचे व्यवहार Class 5 Marathi Question Answer
- अनुभव-२ Class 5 Marathi Question Answer
- गमतीदार पत्र Class 5 Marathi Question Answer
- छोटेसे बहीणभाऊ Class 5 Marathi Question Answer
- वाचूया लिहूया Class 5 Marathi Question Answer
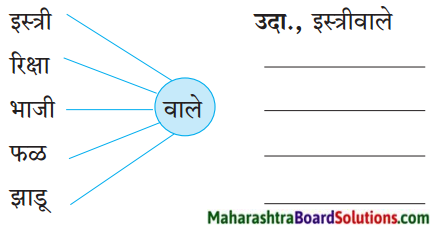
- प्रामाणिक इस्त्रीवाला Class 5 Marathi Question Answer
- ऐका पहा करा Class 5 Marathi Question Answer
- मालतीची चतुराई Class 5 Marathi Question Answer
- पतंग Class 5 Marathi Question Answer
- महर्षी विठ्ठल रामजी शिंदे Class 5 Marathi Question Answer
- फुलपाखरू आणि मधमाशी Class 5 Marathi Question Answer