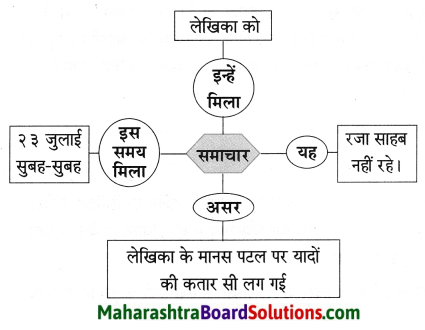
Class 7 Hindi Chapter 2 Phool Aur Kaante Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 7 Hindi Solutions Sulabhbharati Chapter 2 फूल और काँटे Notes, Textbook Exercise Important Questions and Answers.
Std 7 Hindi Chapter 2 Phool Aur Kaante Question Answer Maharashtra Board
Hindi Sulabhbharti Class 7 Solutions Chapter 2 फूल और काँटे Textbook Questions and Answers
स्वयं अध्ययन:
दिए गए चित्रों से संबंधित सुनी हुई कोई कविता सुनाओ।

![]()
बताओ तो सही:
Answer:
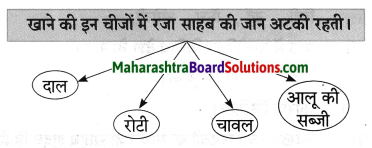
फूल का नाम
गुलाब – गुलाब एक बहुवर्षीय, झाड़ीदार, कंटीला, पुष्पीय पौधा है। जिसमें कई रंग के सुंदर सुगंधित फूल लगते हैं। इसकी १०० से भी अधिक प्रजातियाँ अस्तित्व में हैं। गुलाब की अधिकतर जातियाँ एशियाई मूल की हैं। भारत सरकार ने १२ फरवरी को ‘गुलाब-दिवस’ के रूप में घोषित किया है। गुलाब का फूल अपनी कोमलता, सुंदरता व सुगंध के लिए विशेष प्रसिद्ध है।
गुलाब के उपयोग –
- गुलाब के फूल का उपयोग भगवान के चरणों में चढ़ाने के लिए करते हैं।
- गर्मियों में गुलाब के फूलों का रस चेहरे पर मलने से चेहरे पर ताजगी बनी रहती है।
- आँखों की जलन व खुजली दूर करने के लिए गुलाब के जल का उपयोग किया जाता है।
- गुलाब के घर में महकते रहने से घर का वातावरण पवित्र व शांत बना रहता है।
- गुलाब के फूल से शरबत व गुलकंद बनाई जाती है, जो सेहत के लिए अत्यंत फायदेमंद होती है।
- कान में दर्द होने पर गुलाब की पत्तियों का रस डालने से कान के दर्द से राहत मिलती है।
- गुलाब के फूलों से खुशबूदार इत्र बनाए जाते हैं।
- गुलाब की गंध – गुलाब का फूल खुशबू के लिए भी विशेष प्रसिद्ध है।
- इसकी हलकी, मधुर, भीनी व मोहक गंध सबके मन को आकर्षित करती है।
- भारतवर्ष में ऋतु के अनुसार गुलाब दो प्रकार के माने जाते हैं।
(१) सदागुलाब और (२) चैती गुलाब
सदागुलाब पूरे साल भर फूलता रहता है। चैती गुलाब केवल बसंत ऋतु में ही फूलता है। चैती गुलाब अपनी सुगंध के लिए विशेष प्रसिद्ध होता है। यही फूल अधिकतर इत्र और दवा बनाने के काम में लाया जाता है। ऐसा कहा जाता है कि गुलाब के इस का नूरजहाँ ने १६१२ इ.स. में अपने विवाह के अवसर पर उपयोग किया था। गुलाब का फूल अपनी गंध और औषधीय गुणों के कारण संसार में विशेष रूप से प्रसिद्ध है।
![]()
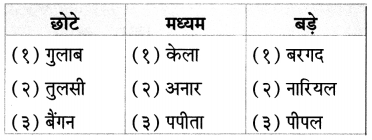
खोजबीन:
अपने आसपास के पेड़-पौधों के नामों का वर्गीकरण कीजिए।
Answer:
वाचन जगत से:
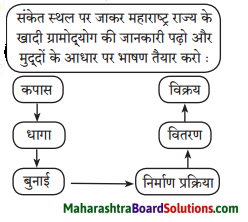
सदैव ध्यान में रखो:
प्रत्येक परिस्थिति का सामना हँसते हुए करना चाहिए।
![]()
कविता के आधार पर रिक्त स्थानों की पूर्ति कीजिए।
Question 1.
रात में उनपर …………..”चाँद भी.
एक ही-सी …………… है डालता।
Answer:
चमकता, चाँदनी
Question 2.
प्यार डूबी तितलियों के …………..” कतर,
भौर का वेध देता ………….” तन।
Answer:
पर, श्याम
Question 3.
……… काँटा किसी की उँगलियाँ,
फाड़ देता है किसी का वर ……….।
Answer:
छेदकर, वसन
Question 4.
निज सुगंध औ’ ……….. रंग से,
है सदा देता ……. जी की खिला।
Answer:
निराले, कली
निम्नलिखित प्रश्नों के उत्तर एक वाक्य में लिखिए।
Question 1.
फूल किनको गोद में लेता है?
Answer:
फूल तितलियों को गोद में लेता है।
Question 2.
बड़प्पन की कसर रह जाने पर क्या काम नहीं देती?
Answer:
बड़प्पन की कसर रह जाने पर कुल की बड़ाई काम नहीं देती।
Question 3.
कौन एक-सा बरसता है?
Answer:
मेह (मेघ) एक-सा बरसता है।
Question 4.
फूल किसको रस पिलाता है?
Answer:
फूल भंवरो को रस पिलाता है।
Question 5.
काँटा किसका तन बेध देता है?
Answer:
काँटा भँवरे का तन बेध देता है।
Question 6.
भौरे का तन किस रंग का है?
Answer:
भँवरे का तन साँवले रंग का है।
![]()
भाषा की ओर
निम्नलिखित वर्षों से समानार्थी और विरुद्धार्थी शब्दों की जोड़ियाँ हूँढ़िए और अपने वाक्यों में प्रयोग कीजिए।
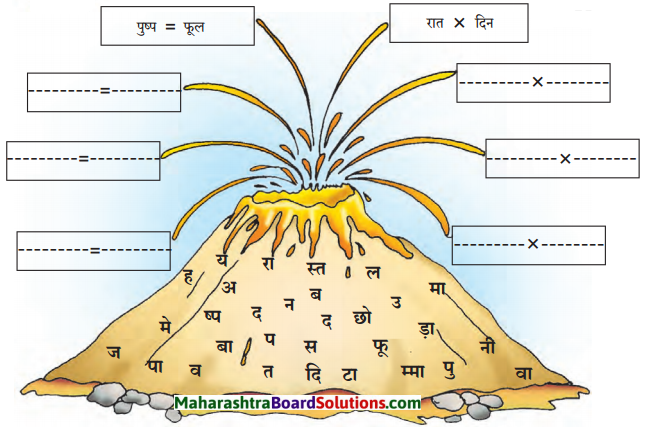
समानार्थी शब्दों का बाक्य में प्रयोग:
- पुष्प – बगीचे में पुष्प खिले हैं।
- फूल – भगवान के चरणों में पड़ा फूल पवित्र होता है।
- तन – सैनिक तन-मन से देश की रक्षा करता है।
- बदन – सैनिक का सारा बदन लहु-लूहान था।
- जल – जल ही जीवन है।
- पानी – पानी के बिना मनुष्य का जीवन सूना है।
- हवा – शाम के समय ठंडी हवा चलती है।
- पवन – चक्रवाती पवन बहुत तीव्र गति की होती है।
![]()
विरुद्धार्थी शब्दों का वाक्य में प्रयोग:
- रात x दिन – मोहन अपने भविष्य के लिए रात-दिन पढ़ाई करता है।
- छोटा x बड़ा- हमारे मन में छोटे-बड़े का भेदभाव नहीं होना चाहिए।
- मान x अपमान – राम मोहन को मान देता है किंतु मोहन ने उसका सबके सामने अपमान कर दिया।
- पावन x अपावन – आज के आधुनिक युग में भी कुछ लोग पावन विचारों के हैं, तो कुछ लोगों के आचरण बिलकुल अपावन हो चुके हैं।
विचार मंथन:
निम्नलिखित विषय पर अपने विचार लिखिए।
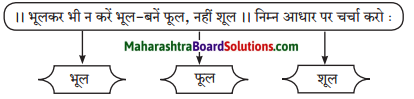
Answer:
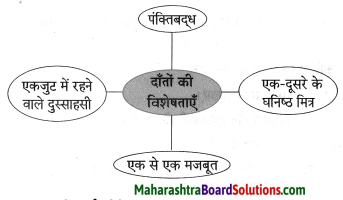
भूल – उपर्युक्त पंक्ति के माध्यम से ‘भूल’ का अर्थ यह है कि मनुष्य को यह नहीं भूलना चाहिए कि उसका जन्म अच्छे कमों के लिए हुआ है, न कि बुरे कर्म करने के लिए। हमें हमेशा दूसरों के बारे में अच्छा सोचना चाहिए व उनकी मदद करनी चाहिए और यह नहीं भूलना चाहिए कि हमारा एक-दूसरे के साथ भाईचारे व मानवता का संबंध है। फूल – उपर्युक्त पंक्ति में ‘फूल’ का अर्थ यह है कि हमें अपने जीवन में अपने व्यवहार से फूल के समान लोगों के जीवन को महकाना चाहिए। दूसरों की मदद करके अपने व समाज के लोगों की जीवनरूपी बगिया को सुंदर बनाने का सतत प्रयास करना चाहिए। शूल – उपर्युक्त पंक्ति में ‘शूल’ का अर्थ यह है कि अपने कार्यों से दूसरों की राह में काँटों के समान रूकावट पैदा नहीं करनी चाहिए। ‘शूल’ यह शब्द शत्रुता व बुरे व्यक्ति के प्रतीक के रूप में इस पंक्ति में प्रयोग किया गया है।
हमें अपने जीवन में ‘फूल’ के समान एक अच्छा मनुष्य बनने का प्रयास करना चाहिए न कि ‘शूल’ के समान बुरा व्यक्ति। सम्मान हमेशा फूल’ को ही मिलता है ‘शूल’ को नहीं।
![]()
Hindi Sulabhbharti Class 7 Solutions Chapter 2 फूल और काँटे Additional Important Questions and Answers
निम्नलिखित शब्दों में से उचित शब्द चनकर रिक्त स्थानों की पूर्ति कीजिए।
(जगह, मेह, ढंग, पर, फूल, आँख)
Question 1.
फूल और काँटे दोनों का ………… भिन्न-भिन्न होता है।
Answer:
ढंग
Question 2.
काँटा तितलियों के . कतर देता है।
Answer:
पर
Question 3.
फूल और काँटे एक ही ……..’ जन्म लेते हैं।
Answer:
जगह
![]()
Question 4.
काँटा सबकी . .. में खटकता है।
Answer:
आँख
Question 5.
…………” उन पर एक समान बरसते हैं।
Answer:
मेह
Question 6.
………… अपनी सुगंध से सबको आकर्षित करता है।
Answer:
फूल
निम्नलिखित प्रश्नों के उत्तर एक शब्द में लिखिए।
Question 1.
रात में पौधों पर क्या चमकता है?
Answer: चाँद
Question 2.
काँटा किसमें छेद कर डालता है?
Answer:
उँगलियों में
Question 3.
निराले रंग किसके हैं?
Answer:
फूल के
![]()
Question 4.
भगवान के सिर पर कौन सजता है?
Answer:
पुष्प, फूल
कविता में आए लयात्मक शब्दों को ढूँडकर लिखिए।
उदाहरण: पिला – खिला
Answer:
- पालता – डालता
- बही – नहीं
- बसन – तन
- पर – कसर
निम्नलिखित बाक्य सही है या गलत लिखिए।
Question 1.
फूल वस्त्र को फाड़ देता है।
Answer:
गलत
Question 2.
फूल और काँटों का स्वभाव एक समान होता है।
Answer:
गलत
Question 3.
फूल की सुगंध से सबका मन प्रसन्न होता है।
Answer:
सही
![]()
Question 4.
फूल काँटों को अनूठा रस पिलाते हैं।
Answer:
गलत
Question 5.
कुल की बड़ाई से मनुष्य महान बनता है।
Answer:
गलत
Question 6.
मनुष्य स्वयं के गलत कार्यों से लोगों की आँखों में खटकता है।
Answer:
सही
निम्नलिखित प्रश्नों के उत्तर दो-तीन वाक्यों में लिखिए।
Question 1.
चाँद रात के समय प्रकृति का कौन-सा कार्य करता है?
Answer:
चाँद रात के समय सभी को ठंडक भरी शीतल छाया देने का कार्य करता है। वह सभी पर समान रूप से चाँदनी बिखेरने का प्राकृतिक कार्य करता है।
![]()
Question 2.
फूल और काँटों पर समान रूप से क्या बहती है?
Answer:
फूल और काँटों पर समान रूप से हवाएँ बहती हैं। हवा किसी भी प्रकार का भेदभाव न करते हुए इन्हें एक-सी हवा देती है।
Question 3.
काँटों द्वारा उँगलियों को छेदने व कपड़े को फाड़ने से काँटों की किस वृत्ति का पता चलता है?
Answer:
काँटों द्वारा उँगलियों को छेदने व कपड़े को फाड़ने से काँटों की दूसरों से घृणा करने, दूसरों का तिरस्कार करने तथा दूसरों को जान-बुझकर तकलीफ देने की वृत्ति का पता चलता है।
Question 4.
‘फूल और काँटे’ कविता के माध्यम से ‘फूल’ हमें क्या संदेश देना चाहता है?
Answer:
‘फूल और काँटे’ कविता के माध्यम से ‘फूल’ हमें यह संदेश देना चाहता है कि हमें दूसरों के साथ प्रेमपूर्वक व्यवहार करना चाहिए तथा अपने अच्छे कर्मों से सबके मन को प्रसन्न व आनंदित रखना चाहिए। हमें अपने कर्मों से श्रेष्ठ बनना चाहिए।
Question 5.
मनुष्य महान कब और कैसे बनता है?
Answer:
मनुष्य महान तब बनता है, जब वह अपना कार्य स्वार्थ हेतु न करते हुए परमार्थ और जगत कल्याण के लिए करता है। वह कुल का बड़प्पन न देखकर स्वयं के बलबूते पर महान बनने का प्रयास करता है। इसलिए कहा गया है ‘कर्मप्रधान विश्व रचि राखा।’ अर्थात परोपकार व योग्य कर्म से मनुष्य को महानता प्राप्त होती है।
![]()
व्याकरण और भाषाभ्यास
निम्नलिखित शब्दों के बहुवचन रूप लिखिए।
- पौधा
- आँख
- भँवरा
- हवा
- तितली
- उँगली
Answer:
- पौधे
- आँखें
- भौरे
- हवाएँ
- तितलियाँ
- उँगलियाँ
![]()
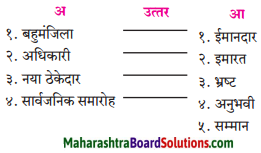
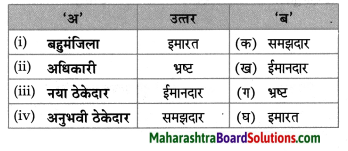
निम्नलिखित संज्ञा शब्दों की उचित विशेषण के साथ जोड़ियाँ मिलाइए।
(१) संज्ञा व सर्वनाम की विशेषता बतानेवाले शब्दों को ‘विशेषण’ कहते हैं। जैसे – सीमा सुंदर है।
विशेषण के मुख्य चार भेद होते हैं : गुणवाचक विशेषण: जो शब्द संज्ञा या सर्वनाम के रंगरूप, गुण-दोष, आकार-प्रकार व स्वभाव का बोध कराते हैं, वे गुणवाचक विशेषण कहलाते हैं। जैसे – गुलाबी चादर,
सुंदर नक्काशी, मीठे बेर आदि।
(२) संख्यावाचक विशेषण: जिस शब्द से संज्ञा या सर्वनाम की निश्चित या अनिश्चित संख्या का बोध होता हो, उन्हें ‘संख्यावाचक विशेषण’ कहते हैं।
(३) परिणामवाचक विशेषणः जिन विशेषण शब्दों से परिणाम की निश्चितता या अनिश्चितता का बोध होता है, वे ‘परिणामवाचक विशेषण’ कहलाते हैं।
(४) सार्वनामिक या संकेतवाचक विशेषण: जो सर्वनाम शब्द संज्ञा शब्द से पहले आकर विशेषण का काम करता है, उसे ‘सार्वनामिक विशेषण’ कहते हैं।
जैसे-

Answer:
(१) – चमकता
(२) – बरसता
(३) – श्याम
(४) – अनूठा
(५) – निराले
(६) – सुरीला
![]()
निम्नलिखित शब्दों में उचित स्थान पर ![]() अनुस्वार व अनुनासिक
अनुस्वार व अनुनासिक ![]() चिह्न का प्रयोग कीजिए।
चिह्न का प्रयोग कीजिए।
- चादनी
- ढग
- हवाए
- सुगध
- भवरा
- तितलिया
- हस
- नदिया
Answer:
- चाँदनी
- ढंग
- हवाएँ
- सुगंध
- भंवरा
- तितलियाँ
- हंस
- नदियाँ
Hindi Sulabhbharti Class 7 Solutions पहली इकाई