Maharashtra Board Class 11 Physics Solutions Chapter 2 Mathematical Methods

Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 2 Mathematical Methods Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Physics Solutions Chapter 2 Mathematical Methods

1. Choose the correct option.

Question 1.
The resultant of two forces 10 N and 15 N acting along + x and – x-axes respectively, is
(A) 25 N along + x-axis
(B) 25 N along – x-axis
(C) 5 N along + x-axis
(D) 5 N along – x-axis
Answer:
(D) 5 N along – x-axis

Question 2.
For two vectors to be equal, they should have the
(A) same magnitude
(B) same direction
(C) same magnitude and direction
(D) same magnitude but opposite direction
Answer:
(C) same magnitude and direction

Question 3.
The magnitude of scalar product of two unit vectors perpendicular to each other is
(A) zero
(B) 1
(C) -1
(D) 2
Answer:
(A) zero

Question 4.
The magnitude of vector product of two unit vectors making an angle of 60° with each other is
(A) 1
(B) 2
(C) \(\frac{3}{2}\)
(D) \(\frac{\sqrt{3}}{2}\)
Answer:
(D) \(\frac{\sqrt{3}}{2}\)

Question 5.
If \(\overrightarrow{\mathrm{A}}\), \(\overrightarrow{\mathrm{B}}\), and \(\overrightarrow{\mathrm{C}}\) are three vectors, then which of the following is not correct?
(A) \(\overrightarrow{\mathrm{A}}\) . (\(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{C}}\)
(B) \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) . \(\overrightarrow{\mathrm{A}}\)
(C) \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{A}}\)
(D) \(\overrightarrow{\mathrm{A}}\) × (\(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{C}}\)
Answer:
(C) \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{B}}\) × \(\overrightarrow{\mathrm{A}}\)

2. Answer the following questions.

Question 1.
Show that \(\overrightarrow{\mathrm{A}}\) = \(\frac{\hat{i}-\hat{j}}{\sqrt{2}}\) is a unit vector.
Solution:

Question 2.
If \(\overrightarrow{\mathbf{v}_{1}}\) = 3\(\hat{i}\) + 4\(\hat{j}\) + \(\hat{k}\) and \(\overrightarrow{\mathbf{v}_{2}}\) = \(\hat{i}\) – \(\hat{j}\) – \(\hat{k}\), determine the magnitude of \(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\).
Solution:
\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\) = (3\(\hat{i}\) + 4\(\hat{j}\) + \(\hat{k}\)) + (\(\hat{i}\) – \(\hat{j}\) – \(\hat{k}\))
= 3\(\hat{i}\) + 3\(\hat{i}\) + 4\(\hat{j}\) – \(\hat{j}\) + \(\hat{k}\) – \(\hat{k}\)
= 4\(\hat{i}\) + 3\(\hat{j}\)
∴ Magnitude of (\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\)),
|\(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\)| = \(\sqrt{4^{2}+3^{2}}\) = \(\sqrt{25}\) = 5 units.
Answer:
Magnitude of \(\overrightarrow{\mathbf{v}_{1}}\) + \(\overrightarrow{\mathbf{v}_{2}}\) = 5 units.

Question 3.
For \(\overline{\mathrm{v}_{1}}\) = 2\(\hat{i}\) – 3\(\hat{j}\) and \(\overline{\mathrm{v}_{2}}\) = -6\(\hat{i}\) + 5\(\hat{j}\), determine the magnitude and direction of \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\).
Answer:
\(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\) = (2\(\hat{i}\) – 3\(\hat{j}\)) + (-6\(\hat{i}\) + 5\(\hat{j}\))
= (2\(\hat{i}\) – 6\(\hat{i}\)) + (-3\(\hat{j}\) + 5\(\hat{j}\))
= -4\(\hat{i}\) + 2\(\hat{j}\)
∴ |\(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\)| = \(\sqrt{(-4)^{2}+2^{2}}\) = \(\sqrt{20}\) = \(\sqrt{4 \times 5}\) = 2\(\sqrt{5}\)
Comparing \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\), with \(\overrightarrow{\mathrm{R}}\) = R_x\(\hat{i}\) + R_y\(\hat{j}\)
⇒ R_x = -4 and R_y = 2
Taking θ to be angle made by \(\overrightarrow{\mathrm{R}}\) with X-axis,

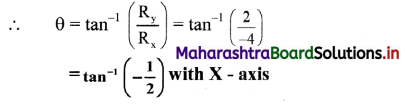
Answer:
Magnitude and direction of \(\overline{\mathrm{v}_{1}}\) + \(\overline{\mathrm{v}_{2}}\), is
respectively 2\(\sqrt{5}\) and and tan^-1\(\left(-\frac{1}{2}\right)\) with X – axis.

Question 4.
Find a vector which is parallel to \(\overrightarrow{\mathrm{v}}\) = \(\hat{i}\) – 2\(\hat{j}\) and has a magnitude 10.
Answer:

Substituting for w_x in (i) using equation (ii),

Using equation (ii),

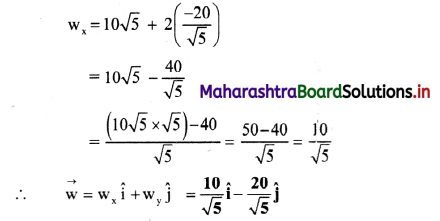
Answer:
Required vector is \(\frac{10}{\sqrt{5}} \hat{\mathbf{i}}\) – \(\frac{20}{\sqrt{5}} \hat{\mathbf{j}}\)

Alternate method:

When two vectors are parallel, one vector is scalar multiple of another,
i.e., if \(\overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{w}}\) are parallel then, \(\overrightarrow{\mathrm{w}}\) = n\(\overrightarrow{\mathrm{v}}\) where, n is scalar.

Question 5.
Show that vectors \(\vec{a}\) = 2\(\hat{\mathbf{i}}\) + 5\(\hat{\mathbf{j}}\) – 6\(\hat{\mathbf{k}}\) and \(\vec{b}\) = \(\hat{\mathbf{i}}\) + \(\frac{5}{2}\)\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\) are parallel.
Answer:
Let angle between two vectors be θ.

⇒ Two vectors are parallel.

Alternate method:

\(\vec{a}\) = 2(\(\hat{\mathbf{i}}\) + \(\frac{5}{2}\)\(\hat{\mathbf{j}}\) + \(\hat{\mathbf{k}}\)) = 2\(\vec{b}\)
Since \(\vec{a}\) is a scalar multiple of \(\vec{b}\), the vectors are parallel.

3. Solve the following problems.

Question 1.
Determine \(\vec{a}\) × \(\vec{b}\), given \(\vec{a}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) and \(\vec{b}\) = 3\(\hat{\mathbf{i}}\) + 5\(\hat{\mathbf{j}}\).
Answer:
Using determinant for vectors in two dimensions,

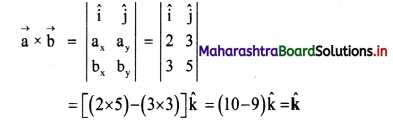
Answer:
\(\vec{a}\) × \(\vec{b}\) gives \(\hat{\mathbf{k}}\)

Question 2.
Show that vectors \(\overrightarrow{\mathbf{a}}\) = 2\(\hat{\mathbf{i}}\) + 3\(\hat{\mathbf{j}}\) + 6\(\hat{\mathbf{k}}\), \(\overrightarrow{\mathbf{b}}\) = 3\(\hat{\mathbf{i}}\) – 6\(\hat{\mathbf{j}}\) + 2\(\hat{\mathbf{k}}\) and \(\overrightarrow{\mathbf{c}}\) = 6\(\hat{\mathbf{i}}\) + 2\(\hat{\mathbf{j}}\) – 3\(\hat{\mathbf{k}}\) are mutually perpendicular.
Solution:
As dot product of two perpendicular vectors is zero. Taking dot product of \(\vec{a}\) and \(\vec{b}\)


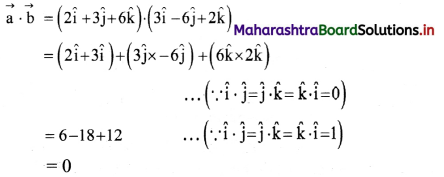
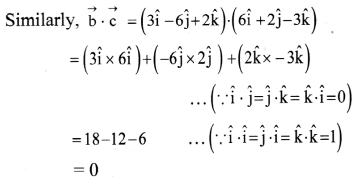
Combining two results, we can say that given three vectors \(\vec{a}\), \(\vec{b}\), and \(\vec{c}\) are mutually perpendicular to each other.

Question 3.
Determine the vector product of \(\overrightarrow{\mathrm{v}_{1}}\) = 2\(\hat{i}\) + 3\(\hat{j}\) – \(\hat{k}\) and \(\overrightarrow{\mathrm{v}_{2}}\) = \(\hat{i}\) + 2\(\hat{j}\) – 3\(\hat{k}\) are perpendicular to each other, determine the value of a.
Solution:

Answer:
Required vector product is -7\(\hat{i}\) + 5\(\hat{j}\) + \(\hat{k}\)

Question 4.
Given \(\bar{v}_{1}\) = 5\(\hat{i}\) + 2\(\hat{j}\) and \(\bar{v}_{2}\) = a\(\hat{i}\) – 6\(\hat{j}\) are perpendicular to each other, determine the value of a.
Solution:
As \(\bar{v}_{1}\) and \(\bar{v}_{2}\) are perpendicular to each other, θ = 90°

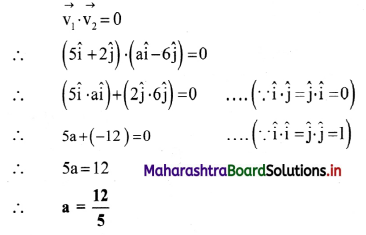
Answer:
Value of a is \(\frac{12}{5}\).

Question 5.
Obtain derivatives of the following functions:
(i) x sin x
(ii) x⁴ + cos x
(iii) x/sin x
Answer:
(i) x sin x
Solution:
\(\frac{d}{d x}\)[f₁(x) × f₂(x)] = f₁(x)\(\frac{\mathrm{df}_{2}(\mathrm{x})}{\mathrm{dx}}\) + \(\frac{\mathrm{df}_{1}(\mathrm{x})}{\mathrm{dx}}\)f₂(x)
For f₁(x) = x and f₂(x) = sin x
\(\frac{d}{d x}\)(x sin x) = x\(\frac{\mathrm{d}(\sin \mathrm{x})}{\mathrm{dx}}\) + \(\frac{d(x)}{d x}\) sin x
= x cos x + 1 × sin x
= sin x + x cos x

(ii) x⁴ + cos x
Solution:

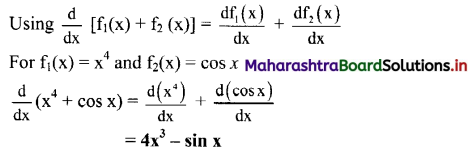
(iii) \(\frac{\mathbf{x}}{\sin x}\)
Solution:

[Note: As derivative of (sin x) is cos x, negative sign that occurs in rule for differentiation for quotient of two functions gets retained in final answer]

Question 6.
Using the rule for differentiation for quotient of two functions, prove that \(\frac{d}{d x}\left(\frac{\sin x}{\cos x}\right)\) = sec²x
Solution:

Question 7.
Evaluate the following integral:
(i) \(\int_{0}^{\pi / 2} \sin x d x\)
(ii) \(\int_{1}^{5} x d x\)
Answer:
(i) \(\int_{0}^{\pi / 2} \sin x d x\)
Solution:

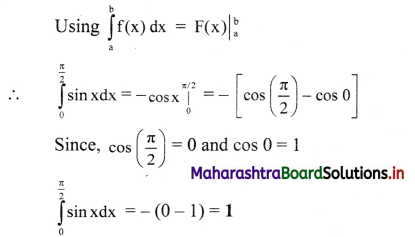
(ii) \(\int_{1}^{5} x d x\)
Solution:

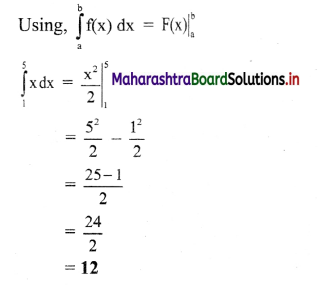
11th Physics Digest Chapter 2 Mathematical Methods Intext Questions and Answers

Can you recall? (Textbook Page No. 16)

Question 1.
Define scalars and vectors.
Answer:

1. Physical quantities which can be completely described b their magnitude (a number and unit) are called scalars.
2. Physical quantities which need magnitude as well as direction for their complete description are called vectors.

Question 2.
Which of the following are scalars or vectors?
Displacements, distance travelled, velocity, speed, force, work done, energy
Answer:

1. Scalars: Distance travelled, speed, work done, energy.
2. Vectors: Displacement, velocity, force.

Question 3.
What is the difference between a scalar and a vector?
Answer:

No.	Scalars	Vectors
i.	It has magnitude only	It has magnitude as well as direction.
ii.	Scalars can be added or subtracted according to the rules of algebra.	Vectors are added or subtracted by geometrical (graphical) method or vector algebra.
iii.	It has no specific representation.	It is represented by symbol (→) arrow.
iv.	The division of a scalar by another scalar is valid.	The division of a vector by another vector is not valid.
	Example: Length, mass, time, volume, etc.	Example: Displacement, velocity, acceleration, force, etc.

Internet my friend (Textbook page no. 28)

1. 1. hyperphysics.phy-astr.gsu.edu/hbase/vect. html#veccon
   2. hyperphysics.phy-astr.gsu.edu/hbase/ hframe.html

Answer:
[Students can use links given above as reference and collect information about mathematical methods]