Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 2 Mechanical Properties of Fluids Textbook Exercise Questions and Answers.
Maharashtra State Board 12th Physics Solutions Chapter 2 Mechanical Properties of Fluids
1) Multiple Choice Questions
i) A hydraulic lift is designed to lift heavy objects of a maximum mass of 2000 kg. The area of cross-section of piston carrying
the load is 2.25 × 10-2 m2. What is the maximum pressure the piston would have to bear?
(A) 0.8711 × 106 N/m2
(B) 0.5862 × 107 N/m2
(C) 0.4869 × 105 N/m2
(D) 0.3271 × 104 N/m2
Answer:
(A) 0.8711 × 106 N/m2
ii) Two capillary tubes of radii 0.3 cm and 0.6 cm are dipped in the same liquid. The ratio of heights through which the liquid will rise in the tubes is
(A) 1:2
(B) 2:1
(C) 1:4
(D) 4:1
Answer:
(B) 2:1
iii) The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly
(A) 0.9 × 10-3 J
(B) 0.4 × 10-3 J
(C) 0.7 × 10-3 J
(D) 0.5 × 10-3 J
Answer:
(A) 0.9 × 10-3 J
iv) Two hail stones with radii in the ratio of 1:4 fall from a great height through the atmosphere. Then the ratio of their terminal velocities is
(A) 1:2
(B) 1:12
(C) 1:16
(D) 1:8
Answer:
(C) 1:16
v) In Bernoulli’s theorem, which of the following is conserved?
(A) linear momentum
(B) angular momentum
(C) mass
(D) energy
Answer:
(D) energy
2) Answer in brief.
i) Why is the surface tension of paints and lubricating oils kept low?
Answer:
For better wettability (surface coverage), the surface tension and angle of contact of paints and lubricating oils must below.
ii) How much amount of work is done in forming a soap bubble of radius r?
Answer:
Let T be the surface tension of a soap solution. The initial surface area of soap bubble = 0
The final surface area of soap bubble = 2 × 4πr2
∴ The increase in surface area = 2 × 4πr2-
The work done in blowing the soap bubble is W = surface tension × increase in surface area = T × 2 × 4πr2 = 8πr2T
iii) What is the basis of the Bernoulli’s principle?
Answer:
Conservation of energy.
iv) Why is a low density liquid used as a manometric liquid in a physics laboratory?
Answer:
An open tube manometer measures the gauge pressure, p — p0 = hpg, where p0 is the pressure being measured, p0 is the atmospheric pressure, h is the difference in height between the manometric liquid of density p in the two arms. For a given pressure p, the product hp is constant. That is, p should be small for h to be large. Therefore, for noticeably large h, laboratory manometer uses a low density liquid.
v) What is an incompressible fluid?
Answer:
An incompressible fluid is one which does not undergo change in volume for a large range of pressures. Thus, its density has a constant value throughout the fluid. In most cases, all liquids are incompressible.
Question 3.
Why two or more mercury drops form a single drop when brought in contact with each other?
Answer:
A spherical shape has the minimum surface area- to-volume ratio of all geometric forms. When two drops of a liquid are brought in contact, the cohesive forces between their molecules coalesces the drops into a single larger drop. This is because, the volume of the liquid remaining the same, the surface area of the resulting single drop is less than the combined surface area of the smaller drops. The resulting decrease in surface energy is released into the environment as heat.
Proof : Let n droplets each of radius r coalesce to form a single drop of radius R. As the volume of the liquid remains constant, volume of the drop = volume of n droplets
∴ \(\frac{4}{3}\)πR3 = n × \(\frac{4}{3}\)πr3
∴ R3 = nr3 ∴ R = \(\sqrt[3]{n}\)r
Surface area of n droplets = n × πR2
Surface area of the drop = 4πR2 = n2/3 × πR2
∴ The change in the surface area = surface area of drop – surface area of n droplets
= πR2(n2/3 – n)
Since the bracketed term is negative, there is a decrease in surface area and a decrease in surface energy.
Question 4.
Why does velocity increase when water flowing in broader pipe enters a narrow pipe?
Answer:
When a tube narrows, the same volume occupies a greater length, as schematically shown in below figure. A1 is the cross section of the broader pipe and that of narrower pipe is A2. By the equation of continuity, V2 = (A1/A2)V1
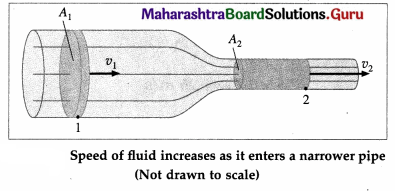
Since A1/A2 > v2 > v1. For the same volume to pass points 1 and 2 in a given time, the speed must be greater at point 2.
The process is exactly reversible. If the fluid flows in the opposite direction, its speed decreases when the tube widens.
Question 5.
Why does the speed of a liquid increase and its pressure decrease when a liquid passes through constriction in a horizontal pipe?
Answer:
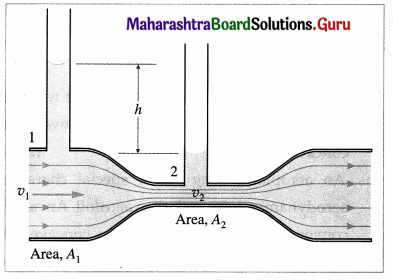
Consider a horizontal constricted tube.
Let A1 and A2 be the cross-sectional areas at points 1 and 2, respectively. Let v1 and v2 be the corresponding flow speeds, ρ is the density of the fluid in the pipeline. By the equation of continuity,
v1A1 = v2A2 …… (1)
∴ \(\frac{v_{2}}{v_{1}}\) = \(\frac{A_{1}}{A_{2}}\) > 1 (∵ A1 > A2)
Therefore, the speed of the liquid increases as it passes through the constriction. Since the meter is assumed to be horizontal, from Bernoulli’s equation we get,
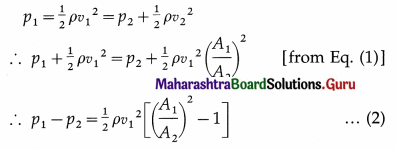
Again, since A1 > A2, the bracketed term is positive so that p1 > p2. Thus, as the fluid passes through the constriction or throat, the higher speed results in lower pressure at the throat.
Question 6.
Derive an expression of excess pressure inside a liquid drop.
Answer:
Consider a small spherical liquid drop with a radius R. It has a convex surface, so that the pressure p on the concave side (inside the liquid) is greater than the pressure p0 on the convex side (outside the liquid). The surface area of the drop is
A = 4πR2 … (1)
Imagine an increase in radius by an infinitesimal amount dR from the equilibrium value R. Then, the differential increase in surface area would be dA = 8πR ∙ dR …(2)
The increase in surface energy would be equal to the work required to increase the surface area :
dW = T∙dA = 8πTRdR …..(3)
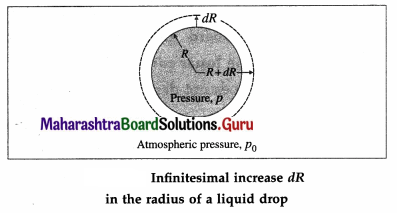
We assume that dR is so small that the pressure inside remains the same, equal to p. All parts of the surface of the drop experience an outward force per unit area equal to ρ — ρ0. Therefore, the work done by this outward pressure-developed force against the surface tension force during the increase in radius dR is
dW = (excess pressure × surface area) ∙ dR
= (ρ – ρ0) × 4πnR2 ∙ dR …..(4)
From Eqs. (3) and (4),
(ρ — ρ0) × 4πR2 ∙ dR = 8πTRdR
∴ ρ – ρ0 = \(\frac{2 T}{R}\) …… (5)
which is called Laplace’s law for a spherical membrane (or Young-Laplace equation in spherical form).
[Notes : (1) The above method is called the principle of virtual work. (2) Equation (5) also applies to a gas bubble within a liquid, and the excess pressure in this case is also called the gauge pressure. An air or gas bubble within a liquid is technically called a cavity because it has only one gas-liquid interface. A bubble, on the other hand, such as a soap bubble, has two gas-liquid interfaces.]
Question 7.
Obtain an expression for conservation of mass starting from the equation of continuity.
Answer:
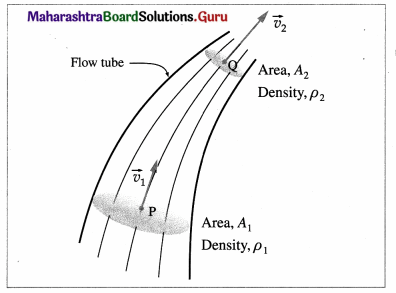
Consider a fluid in steady or streamline flow, that is its density is constant. The velocity of the fluid within a flow tube, while everywhere parallel to the tube, may change its magnitude. Suppose the velocity is \(\vec{v}_{1}\), at point P and \(\vec{v}_{2}\) at point. Q. If A1 and A2 are the cross-sectional areas of the tube at these two points, the volume flux across A1, \(\frac{d}{d t}\)(V2) = A1v1 and that across A2, \(\frac{d}{d t}\)(V2) = A2v2
By the equation of continuity of flow for a fluid, A1v1 = A2V2
i.e., \(\frac{d}{d t}\)(V1) = \(\frac{d}{d t}\)(V2)
If ρ1 and ρ1 are the densities of the fluid at P and Q, respectively, the mass flux across A1, \(\frac{d}{d t}\)(m1) = \(\frac{d}{d t}\)(ρ1 v1) = A1ρ1v1
and that across A2, \(\frac{d}{d t}\)(m2) = \(\frac{d}{d t}\)(ρ2V2) = A2ρ2v2
Since no fluid can enter or leave through the boundary of the tube, the conservation of mass requires the mass fluxes to be equal, i.e.,
\(\frac{d}{d t}\)(m1) = \(\frac{d}{d t}\)(m2)
i.e., A1ρ1v1 = A2ρ2v2
i. e., Apv = constant
which is the required expression.
Question 8.
Explain the capillary action.
Answer:
(1) When a capillary tube is partially immersed in a wetting liquid, there is capillary rise and the liquid meniscus inside the tube is concave, as shown in below figure.
Consider four points A, B, C, D, of which point A is just above the concave meniscus inside the capillary and point B is just below it. Points C and D are just above and below the free liquid surface outside.
Let PA, PB, PC and PD be the pressures at points A, B, C and D, respectively.
Now, PA = PC = atmospheric pressure
The pressure is the same on both sides of the free surface of a liquid, so that
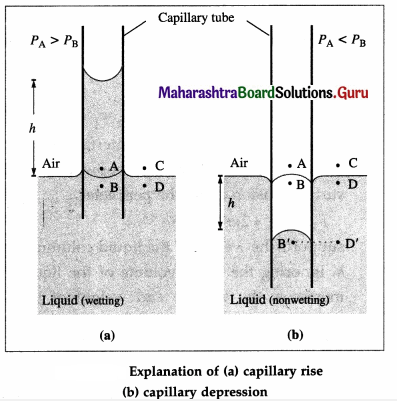
The pressure on the concave side of a meniscus is always greater than that on the convex side, so that
PA > PB
∴ PD > PB (∵ PA = PD)
The excess pressure outside presses the liquid up the capillary until the pressures at B and D (at the same horizontal level) equalize, i.e., PB becomes equal to PD. Thus, there is a capillary rise.
(2) For a non-wetting liquid, there is capillary depression and the liquid meniscus in the capillary tube is convex, as shown in above figure.
Consider again four points A, B, C and D when the meniscus in the capillary tube is at the same level as the free surface of the liquid. Points A and B are just above and below the convex meniscus. Points C and D are just above and below the free liquid surface outside.
The pressure at B (PB) is greater than that at A (PA). The pressure at A is the atmospheric pressure H and at D, PD \(\simeq\) H = PA. Hence, the hydrostatic pressure at the same levels at B and D are not equal, PB > PD. Hence, the liquid flows from B to D and the level of the liquid in the capillary falls. This continues till the pressure at B’ is the same as that D’, that is till the pressures at the same level are equal.
Question 9.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Answer:
Consider a capillary tube of radius r partially immersed into a wetting liquid of density p. Let the capillary rise be h and θ be the angle of contact at the edge of contact of the concave meniscus and glass. If R is the radius of curvature of the meniscus then from the figure, r = R cos θ.
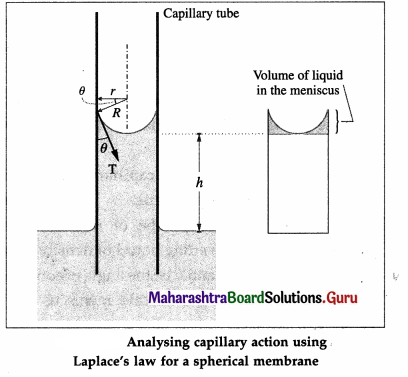
Surface tension T is the tangential force per unit length acting along the contact line. It is directed into the liquid making an angle θ with the capillary wall. We ignore the small volume of the liquid in the meniscus. The gauge pressure within the liquid at a depth h, i.e., at the level of the free liquid surface open to the atmosphere, is
ρ – ρo = ρgh …. (1)
By Laplace’s law for a spherical membrane, this gauge pressure is
ρ – ρo = \(\frac{2 T}{R}\) ….. (2)
∴ hρg = \(\frac{2 T}{R}\) = \(\frac{2 T \cos \theta}{r}\)
∴ h = \(\frac{2 T \cos \theta}{r \rho g}\) …. (3)
Thus, narrower the capillary tube, the greater is the capillary rise.
From Eq. (3),
T = \(\frac{h \rho r g}{2 T \cos \theta}\) … (4)
Equations (3) and (4) are also valid for capillary depression h of a non-wetting liquid. In this case, the meniscus is convex and θ is obtuse. Then, cos θ is negative but so is h, indicating a fall or depression of the liquid in the capillary. T is positive in both cases.
[Note : The capillary rise h is called Jurin height, after James Jurin who studied the effect in 1718. For capillary rise, Eq. (3) is also called the ascent formula.]
Question 10.
Find the pressure 200 m below the surface of the ocean if pressure on the free surface of liquid is one atmosphere. (Density of sea water = 1060 kg/m3) [Ans. 21.789 × 105 N/m2]
Answer:
Data : h = 200 m, p = 1060 kg/m3,
p0 = 1.013 × 105 Pa, g = 9.8 m/s2
Absolute pressure,
p = p0 + hρg
= (1.013 × 103) + (200)(1060)(9.8)
= (1.013 × 105) + (20.776 × 105)
= 21.789 × 105 = 2.1789 MPa
Question 11.
In a hydraulic lift, the input piston had surface area 30 cm2 and the output piston has surface area of 1500 cm2. If a force of 25 N is applied to the input piston, calculate weight on output piston. [Ans. 1250 N]
Answer:
Data : A1 = 30 cm2 = 3 × 10-3 m2,
A2 = 1500 cm2 = 0.15 m2, F1 = 25 N
By Pascal’s law,
\(\frac{F_{1}}{A_{1}}\) = \(\frac{F_{2}}{A_{2}}\)
∴ The force on the output piston,
F2 = F1\(\frac{A_{2}}{A_{1}}\) = (25)\(\frac{0.15}{3 \times 10^{-3}}\) = 25 × 50 = 1250 N
Question 12.
Calculate the viscous force acting on a rain drop of diameter 1 mm, falling with a uniform velocity 2 m/s through air. The coefficient of viscosity of air is 1.8 × 10-5 Ns/m2.
[Ans. 3.393 × 10-7 N]
Answer:
Data : d = 1 mm, v0 = 2 m / s,
η = 1.8 × 10-5 N.s/m2
r = \(\frac{d}{2}\) = 0.5 mm = 5 × 10-4 m
By Stokes’ law, the viscous force on the raindrop is f = 6πηrv0
= 6 × 3.142 (1.8 × 10-5 N.s/m2 × 5 × 10-4 m)(2 m/s)
= 3.394 × 10-7 N
Question 13.
A horizontal force of 1 N is required to move a metal plate of area 10-2 m2 with a velocity of 2 × 10-2 m/s, when it rests on a layer of oil 1.5 × 10-3 m thick. Find the coefficient of viscosity of oil. [Ans. 7.5 Ns/m2]
Answer:
Data : F = 1 N, A = 10-2m2, v0 = 2 × 10-2 y = 1.5 × 10-3 m
Velocity gradient, \(\frac{d v}{d y}\) = \(\frac{2 \times 10^{-2}}{1.5 \times 10^{-3}}\) = \(\frac{40}{3}\)s-1
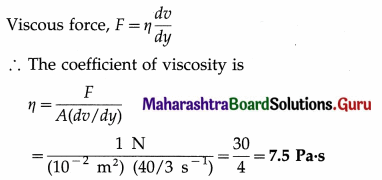
Question 14.
With what terminal velocity will an air bubble 0.4 mm in diameter rise in a liquid of viscosity 0.1 Ns/m2 and specific gravity 0.9? Density of air is 1.29 kg/m3. [Ans. – 0.782 × 10-3 m/s, The negative sign indicates that the bubble rises up]
Answer:
Data : d = 0.4 mm, η = 0.1 Pa.s, ρL = 0.9 × 103 kg/m3 = 900 kg/m3, ρair = 1.29 kg/m3, g = 9.8 m/s2.
Since the density of air is less than that of oil, the air bubble will rise up through the liquid. Hence, the viscous force is downward. At terminal velocity, this downward viscous force is equal in magnitude to the net upward force.
Viscous force = buoyant force – gravitational force
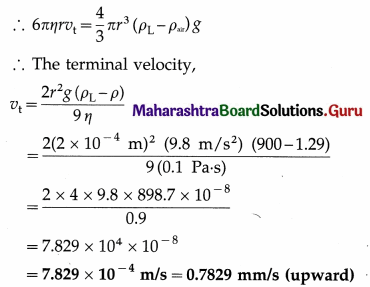
Question 15.
The speed of water is 2m/s through a pipe of internal diameter 10 cm. What should be the internal diameter of nozzle of the pipe if the speed of water at nozzle is 4 m/s?
[Ans. 7.07 × 10-2m]
Answer:
Data : d1 = 10 cm = 0.1 m, v1 = 2 m/s, v2 = 4 m/s
By the equation of continuity, the ratio of the speed is
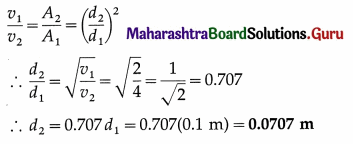
Question 16.
With what velocity does water flow out of an orifice in a tank with gauge pressure 4 × 105 N/m2 before the flow starts? Density of water = 1000 kg/m3. [Ans. 28.28 m/s]
Answer:
Data : ρ — ρ0 = 4 × 105 Pa, ρ = 103 kg/m3
If the orifice is at a depth h from the water surface in a tank, the gauge pressure there is
ρ – ρ0 = hρg … (1)
By Toricelli’s law of efflux, the velocity of efflux,
v = \(\sqrt{2 g h}\) …(2)
Substituting for h from Eq. (1),
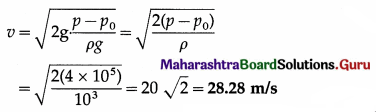
Question 17.
The pressure of water inside the closed pipe is 3 × 105 N/m2. This pressure reduces to 2 × 105 N/m2 on opening the value of the pipe. Calculate the speed of water flowing through the pipe. (Density of water = 1000 kg/m3). [Ans. 14.14 m/s]
Answer:
Data : p1 = 3 × 105 Pa, v1 = 0, p2 = 2 × 105 Pa, ρ = 103 kg/m3
Assuming the potential head to be zero, i.e., the pipe to be horizontal, the Bernoulli equation is
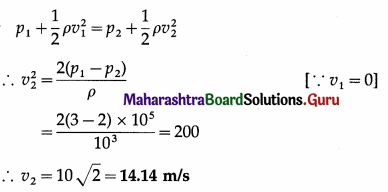
Question 18.
Calculate the rise of water inside a clean glass capillary tube of radius 0.1 mm, when immersed in water of surface tension 7 × 10-2 N/m. The angle of contact between water and glass is zero, density of water = 1000 kg/m3, g = 9.8 m/s2.
[Ans. 0.1429 m]
Answer:
Data : r = 0.1 mm = 1 × 10-4m, θ = 0°,
T = 7 × 10-2 N/m, r = 103 kg/m3, g = 9.8 m/s2
cos θ = cos 0° = 1
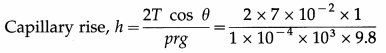
= 0.143 m
Question 19.
An air bubble of radius 0.2 mm is situated just below the water surface. Calculate the gauge pressure. Surface tension of water = 7.2 × 10-2 N/m.
[Ans. 720 N/m2]
Answer:
Data : R = 2 × 10-4m, T = 7.2 × 10-2N/m, p = 103 kg/m3
The gauge pressure inside the bubble = \(\frac{2 T}{R}\)
= \(\frac{2\left(7.2 \times 10^{-2}\right)}{2 \times 10^{-4}}\) = 7.2 × 102 = 720 Pa
Question 20.
Twenty seven droplets of water, each of radius 0.1 mm coalesce into a single drop. Find the change in surface energy. Surface tension of water is 0.072 N/m. [Ans. 1.628 × 10-7 J = 1.628 erg]
Answer:
Data : r = 1 mm = 1 × 10-3 m, T = 0.472 J/m2
Let R be the radius of the single drop formed due to the coalescence of 8 droplets of mercury.
Volume of 8 droplets = volume of the single drop as the volume of the liquid remains constant.
∴ 8 × \(\frac{4}{3}\)πr3 = \(\frac{4}{3}\)πR3
∴ 8r3 = R3
∴ 2r = R
Surface area of 8 droplets = 8 × 4πr2
Surface area of single drop = 4πR2
∴ Decrease in surface area = 8 × 4πr2 – 4πR2
= 4π(8r2 – R2)
= 4π[8r2 – (2r)2]
= 4π × 4r2
∴ The energy released = surface tension × decrease in surface area = T × 4π × 4r2
= 0.472 × 4 × 3.142 × 4 × (1 × 10-3)2
= 2.373 × 10-5 J
The decrease in surface energy = 0.072 × 4 × 3.142 × 18 × (1 × 10-4)2
= 1.628 × 10-7 J
Question 21.
A drop of mercury of radius 0.2 cm is broken into 8 identical droplets. Find the work done if the surface tension of mercury is 435.5 dyne/cm. [Ans. 2.189 × 10-5J]
Answer:
Let R be the radius of the drop and r be the radius of each droplet.
Data : R = 0.2 cm, n = 8, T = 435.5 dyn/cm
As the volume of the liquid remains constant, volume of n droplets = volume of the drop
∴ n × \(\frac{4}{3}\)πr3 = \(\frac{4}{3}\)πR3
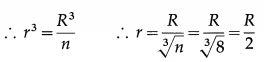
Surface area of the drop = 4πR2
Surface area of n droplets = n × 4πR2
∴ The increase in the surface area = surface area of n droplets-surface area of drop
= 4π(nr2 – R2) = 4π(8 × \(\frac{R^{2}}{4}\) – R2)
= 4π(2 — 1)R2 = 4πR2
∴ The work done
= surface tension × increase in surface area
= T × 4πR2 = 435.5 × 4 × 3.142 × (0.2)2
= 2.19 × 102 ergs = 2.19 × 10-5 J
Question 22.
How much work is required to form a bubble of 2 cm radius from the soap solution having surface tension 0.07 N/m.
[Ans. 0.7038 × 10-3 J]
Answer:
Data : r = 4 cm = 4 × 10-2 m, T = 25 × 10-3 N/m
Initial surface area of soap bubble = 0
Final surface area of soap bubble = 2 × 4πr2
∴ Increase in surface area = 2 × 4πr2
The work done
= surface tension × increase in surface area
= T × 2 × 4πr2
= 25 × 10-3 × 2 × 4 × 3.142 × (4 × 10-2)2
= 1.005 × 10-3 J
The work done = 0.07 × 8 × 3.142 × (2 × 10-2)2
= 7.038 × 10-4 J
Question 23.
A rectangular wire frame of size 2 cm × 2 cm, is dipped in a soap solution and taken out. A soap film is formed, if the size of the film is changed to 3 cm × 3 cm, calculate the work done in the process. The surface tension of soap film is 3 × 10-2 N/m. [Ans. 3 × 10-5 J]
Answer:
Data : A1 = 2 × 2 cm2 = 4 × 10-4 m2,
A2 = 3 × 3 cm2 =9 × 10-4 m2, T = 3 × 10-2 N/m
As the film has two surfaces, the work done is W = 2T(A2 – A1)
= 2(3 × 10-2)(9 × 10-4 × 10-4)
= 3.0 × 10-5 J = 30 µJ
12th Physics Digest Chapter 2 Mechanical Properties of Fluids Intext Questions and Answers
Can you tell? (Textbook Page No. 27)
Question 1.
Why does a knife have a sharp edge or a needle has a sharp tip ?
Answer:
For a given force, the pressure over which the force is exerted depends inversely on the area of contact; smaller the area, greater the pressure. For instance, a force applied to an area of 1 mm2 applies a pressure that is 100 times as great as the same force applied to an area of 1 cm2. The edge of a knife or the tip of a needle has a small area of contact. That is why a sharp needle is able to puncture the skin when a small force is exerted, but applying the same force with a finger does not.
Use your brain power
Question 1.
A student of mass 50 kg is standing on both feet. Estimate the pressure exerted by the student on the Earth. Assume reasonable value to any quantity you need; justify your assumption. You may use g = 10 m/s2, By what factor will it change if the student lies on back ?
Answer:
Assume area of each foot = area of a 6 cm × 25 cm rectangle.
∴ Area of both feet = 0.03 m2
∴ The pressure due to the student’s weight
= \(\frac{m g}{A}\) = \(\frac{50 \times 10}{0.03}\) = 16.7 kPa
According to the most widely used Du Bois formula for body surface area (BSA), the student’s BSA = 1.5 m2, so that the area of his back is less than half his BSA, i.e., < 0.75 m2. When the student lies on his back, his area of contact is much smaller than this. So, estimating the area of contact to be 0.3 m2, i.e., 10 times more than the area of his feet, the pressure will be less by a factor of 10 or more, [Du Bois formula : BSA = 0.2025 × W0.425 × H0.725, where W is weight in kilogram and H is height in metre.]
Can you tell? (Textbook Page No. 30)
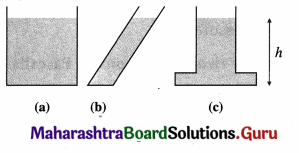
Question 1.
The figures show three containers filled with the same oil. How will the pressures at the reference compare ?
Answer:
Filled to the same level, the pressure is the same at the bottom of each vessel.
Use Your Brain Power (Textbook Page 35)
Question 1.
Prove that equivalent SI unit of surface tension is J/m2.
Answer:
The SI unit of surface tension =
Try This (Textbook Page No. 36)
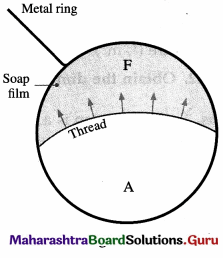
Question 1.
Take a ring of about 5 cm in diameter. Tie a thread slightly loose at two diametrically opposite points on the ring. Dip the ring into a soap solution and take it out. Break the film on any one side of the thread. Discuss what happens.
Answer:
On taking the ring out, there is a soap film stretched over the ring, in which the thread moves about quite freely. Now, if the film is punctured with a pin on one side-side A in below figure-then immediately the thread is pulled taut by the film on the other side as far as it can go. The thread is now part of a perfect circle, because the surface tension on the side F of the film acts everywhere perpendicular to the thread, and minimizes the surface area of the film to as small as possible.
Can You Tell ? (Textbook Page No. 38)
Question 1.
How does a waterproofing agent work ?
Answer:
Wettability of a surface, and thus its propensity for penetration of water, depends upon the affinity between the water and the surface. A liquid wets a surface when its contact angle with the surface is acute. A waterproofing coating has angle of contact obtuse and thus makes the surface hydrophobic.
Brain Teaser (Textbook Page No. 41)
Question 1.
Can you suggest any method to measure the surface tension of a soap solution? Will this method have any commercial application?
Answer:
There are more than 40 methods for determining equilibrium surface tension at the liquid-fluid and solid-fluid boundaries. Measuring the capillary rise (see Unit 2.4.7) is the laboratory method to determine surface tension.
Among the various techniques, equilibrium surface tension is most frequently measured with force tensiometers or optical (or the drop profile analysis) tensiometers in customized measurement setups.
[See https: / / www.biolinscientific.com /measurements /surface-tension]
Question 2.
What happens to surface tension under different gravity (e.g., aboard the International Space Station or on the lunar surface)?
Answer:
Surface tension does not depend on gravity.
[Note : The behaviour of liquids on board an orbiting spacecraft is mainly driven by surface tension phenomena. These make predicting their behaviour more difficult than under normal gravity conditions (i.e., on the Earth’s surface). New challenges appear when handling liquids on board a spacecraft, which are not usually present in terrestrial environments. The reason is that under the weightlessness (or almost weightlessness) conditions in an orbiting spacecraft, the different inertial forces acting on the bulk of the liquid are almost zero, causing the surface tension forces to be the dominant ones.
In this ‘micro-gravity’ environment, the surface tension forms liquid drops into spheres to minimize surface area, causes liquid columns in a capillary rise up to its rim (without over flowing). Also, when a liquid drop impacts on a dry smooth surface on the Earth, a splash can be observed as the drop disintegrates into thousands of droplets. But no splash is observed as the drop hits dry smooth surface on the Moon. The difference is the atmosphere. As the Moon has no atmosphere, and therefore no gas surrounding a falling drop, the drop on the Moon does not splash.
(See http://mafija.fmf.uni-Ij.si/]
Can you tell? (Textbook Page No. 45)
Question 1.
What would happen if two streamlines intersect?
Answer:
The velocity of a fluid molecule is always tangential to the streamline. If two streamlines intersect, the velocity at that point will not be constant or unique.
Activity
Question 1.
Identify some examples of streamline flow and turbulent flow in everyday life. How would you explain them ? When would you prefer a streamline flow?
Answer:
Smoke rising from an incense stick inside a wind-less room, air flow around a car or aeroplane in motion are some examples of streamline flow, Fish, dolphins, and even massive whales are streamlined in shape to reduce drag. Migratory birds species that fly long distances often have particular features such as long necks, and flocks of birds fly in the shape of a spearhead as that forms a streamlined pattern.
Turbulence results in wasted energy. Cars and aeroplanes are painstakingly streamlined to reduce fluid friction, and thus the fuel consumption. (See ‘Disadvantages of turbulence’ in the following box.) Turbulence is commonly seen in washing machines and kitchen mixers. Turbulence in these devices is desirable because it causes mixing. (Also see ‘Advantages of turbulence’ in the following box.) Recent developments in high-speed videography and computational tools for modelling is rapidly advancing our understanding of the aerodynamics of bird and insect flights which fascinate both physicists and biologists.
Use your Brain power (Textbook Page No. 46)
Question 1.
The CGS unit of viscosity is the poise. Find the relation between the poise and the SI unit of viscosity.
Answer:
By Newton’s law of viscosity,
\(\frac{F}{A}\) = η\(\frac{d v}{d y}\)
where \(\frac{F}{A}\) is the viscous drag per unit area, \(\frac{d v}{d y}\) is the velocity gradient and η is the coefficient of viscosity of the fluid. Rewriting the above equation as
SI unit : the pascal second (abbreviated Pa.s), 1 Pa.s = 1 N.m-2.s
CGS unit: dyne.cm-2.s, called the poise [symbol P, named after Jean Louis Marie Poiseuille (1799 -1869), French physician].
[Note : Thè most commonly used submultiples are the millipascalsecond (mPa.s) and the centipoise (cP). 1 mPa.s = 1 cP.]
Use your Brain power (Textbook Page No. 49)
Question 1.
A water pipe with a diameter of 5.0 cm is connected to another pipe of diameter 2.5 cm. How would the speeds of the water flow compare ?
Answer:
Water is an incompressible fluid (almost). Then, by the equation of continuity, the ratio of the speeds, is
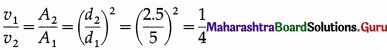
Do you know? (Textbook Page No. 50)
Question 1.
How does an aeroplane take off?
Answer:
A Venturi meter is a horizontal constricted tube that is used to measure the flow speed through a pipeline. The constricted part of the tube is called the throat. Although a Venturi meter can be used for a gas, they are most commonly used for liquids. As the fluid passes through the throat, the higher speed results in lower pressure at point 2 than at point 1. This pressure difference is measured from the difference in height h of the liquid levels in the U-tube manometer containing a liquid of density ρm. The following treatment is limited to an incompressible fluid.
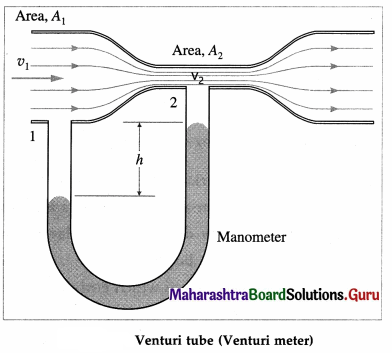
Let A1 and A2 be the cross-sectional areas at points 1 and 2, respectively. Let v1 and v2 be the corresponding flow speeds. ρ is the density of the fluid in the pipeline. By the equation of continuity,
v1A1 = v2A2 … (1)
Since the meter is assumed to be horizontal, from Bernoufli’s equation we get,
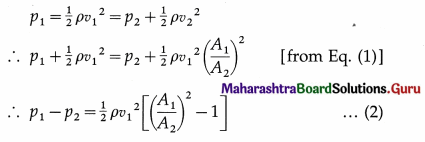
The pressure difference is equal to ρmgh, where h is the differences in liquid levels in the manometer.
Then,
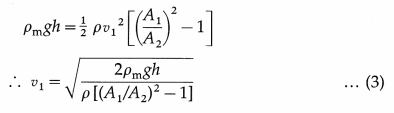
Equation (3) gives the flow speed of an incompressible fluid in the pipeline. The flow rates of practical interest are the mass and volume flow rates through the meter.
Volume flow rate =A1v1 and mass flow rate = density × volume flow
rate = ρA1v1
[Note When a Venturi meter is used in a liquid pipeline, the pressure difference is measured from the difference in height h of the levels of the same liquid in the two vertical tubes, as shown in the figure. Then, the pressure difference is equal to ρgh.
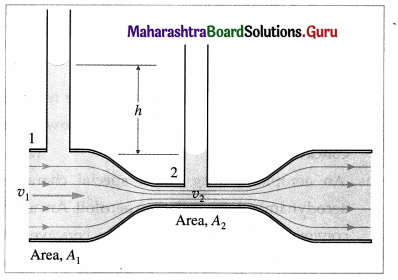
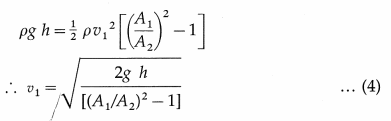
The flow meter is named after Giovanni Battista Venturi (1746—1822), Italian physicist.]
Question 2.
Why do racer cars and birds have typical shape ?
Answer:
The streamline shape of cars and birds reduce drag.
Question 3.
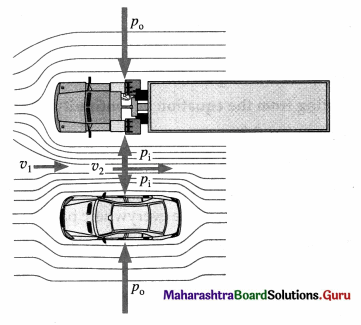
Have you experienced a sideways jerk while driving a two wheeler when a heavy vehicle overtakes you ?
Answer:
Suppose a truck passes a two-wheeler or car on a highway. Air passing between the vehicles flows in a narrower channel and must increase its speed according to Bernoulli’s principle causing the pressure between them to drop. Due to greater pressure on the outside, the two-wheeler or car veers towards the truck.
When two ships sail parallel side-by-side within a distance considerably less than their lengths, since ships are widest toward their middle, water moves faster in the narrow gap between them. As water velocity increases, the pressure in between the ships decreases due to the Bernoulli effect and draws the ships together. Several ships have collided and suffered damage in the early twentieth century. Ships performing At-sea refueling or cargo transfers performed by ships is very risky for the same reason.
Question 4.
Why does dust get deposited only on one side of the blades of a fan ?
Answer:
Blades of a ceiling/table fan have uniform thickness (unlike that of an aerofoil) but are angled (cambered) at 8° to 12° (optimally, 10°) from their plane. When they are set rotating, this camber causes the streamlines above/behind a fan blade to detach away from the surface of the blade creating a very low pressure on that side. The lower/front streamlines however follow the blade surface. Dust particles stick to a blade when it is at rest as well as when in motion both by intermolecular force of adhesion and due to static charges. However, they are not dislodged from the top/behind surface because of complete detachment of the streamlines.
The lower/front surface retains some of the dust because during motion, a thin layer of air remains stationary relative to the blade.
Question 5.
Why helmets have specific shape?
Answer:
Air drag plays a large role in slowing bike riders (especially, bicycle) down. Hence, a helmet is aerodynamically shaped so that it does not cause too much drag.
Use your Brainpower (Textbook Page No. 52)
Question 1.
Does Bernoulli’s equation change when the fluid is at rest? How?
Answer:
Bernoulli’s principle is for fluids in motion. Hence, it is pointless to apply it to a fluid at rest. Nevertheless, for a fluid is at rest, the Bernoulli equation gives the pressure difference due to a liquid column.
For a static fluid, v1 = v2 = 0. Bernoulli’s equation in that case is p1 + ρgh1 = ρ2 + ρgh2
Further, taking h2 as the reference height of zero, i.e., by setting h2 = 0, we get p2 = p1 + ρgh1
This equation tells us that in static fluids, pressure increases with depth. As we go from point 1 to point 2 in the fluid, the depth increases by h1 and consequently, p2 is greater than p1 by an amount ρgh1.
In the case, p1 = p0, the atmospheric pressure at the top of the fluid, we get the familiar gauge pressure at a depth h1 = ρgh1. Thus, Bernoulli’s equation confirms the fact that the pressure change due to the weight of a fluid column of length h is ρgh.