Balbharti Maharashtra State Board Class 11 History Solutions Chapter 5 Janapadas and Republics Textbook Exercise Questions and Answers.
Std 11 History Chapter 5 Question Answer Janapadas and Republics Maharashtra Board
Class 11 History Chapter 5 Janapadas and Republics Question Answer Maharashtra Board
History Class 11 Chapter 5 Question Answer Maharashtra Board
1A. Choose the correct alternative and write the complete sentences.
Question 1.
A region occupied by the ‘janas’ was called as __________
(a) Ganarajya
(b) Janapada
(c) Mahajanapada
(d) Gotra
Answer:
(b) Janapada
Question 2.
The principal functionary of a Ganasangha was known as __________
(a) Senapati
(b) Bhandagarika
(c) Raja
(d) Uparaja
Answer:
(c) Raja
![]()
Question 3.
The author of the ‘Ashtadhyayi’ which mentions ‘Janapadin’ was __________
(a) Kautilya
(b) Panini
(c) Chanakya
(d) Vyas
Answer:
(b) Panini
Question 4.
The sense of territoriality and the ensuing awareness __________ were the main factors responsible for the formation of ancient Janapadas in India.
(a) of unity
(b) of authority
(c) of autonomy
(d) of public authority
Answer:
(c) of autonomy
1B. Find the incorrect pairs from set ‘B’ and write the correct ones.
Question 1.
| Set ‘A’ | Set ‘B’ |
| (a) Praachya | of the east |
| (b) Praatichya | of the west |
| (c) Udichya | of the north |
| (d) Aparanta | the region to the north of Vindhya ranges |
Answer:
(d) Aparanta – the region to the south of Vindhya ranges
2. Choose the correct reason and complete the sentence.
Question 1.
The Ganasangha of the Youdhey, Malav, Kshudraka were mentioned as Ayudhajivi. Because-
(a) it was in the northeast region of the Indian Subcontinent.
(b) these people were skilled warriors and warfare was the means of their livelihood.
(c) they were skilled in trade and commerce.
(d) these were the ganasanghas dependent on agriculture and animal husbandry.
Answer:
(b) these people were skilled warriors and warfare was the means of their livelihood.
![]()
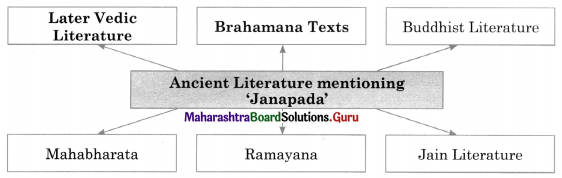
3. Complete the concept map.
Question 1.

Answer:
4. Explain the concepts with examples.
Question 1.
Ganarajya and Sangharajya
Answer:
- ‘Gana’ means the ruling class comprising members of equal social status.
- Similarly, ‘sangha’ means a state formed by many kulas or janapadas by coming together.
- By the 6th century B.C.E. many sangharajyas had come into existence.
- There were three main types of the ancient federation of states in India:
- Ganarajya of the members of the same kula. For example, Malava and Shibi.
- Ganarajya was created by more than one kulas coming together. For example, Vajji Ganasangha. It included eight kulas. Vajji, Lichchhavi, Dnyatruk, and Videha were the important ganas among them.
- More than one ganrajyas coming together to create a sangharajya. For example, Yaudheya- Kshudrak Sangh.
Question 2.
Vartashastarpajivi Ganasnagh
Answer:
- Ancient Indian literature mentions two more types of ganasanghas.
- ‘Ayudhjivi’ sangh and ‘Varta-Shastropajivi’ sangh.
- ‘Varta’ means trade and commerce.
- The people in the Varta-Shastropajivi ganasanghas lived by trade and commerce, agriculture and animal husbandry, as well as their skills in warfare.
- People in the Kamboj and Saurashtra ganasanghas earned their livelihood by these means.
Question 3.
‘Jana’ and ‘Janapada’
Answer:
- Vedic people used the term Jana to designate a group of people, united under a common bond of singular kinship structure.
- Their settlement was known as ‘Grama’.
- A cluster of gramas consisting of the same Jana was known by the name of that particular Jana.
- A region occupied by a Janas was called Janapada.
- Gradually the Janapadas had more formal administrative structures transforming them into independent states.
- These were the first well-established states of ancient India.
- However, this does not necessarily mean that every Janapada evolved into an independent state.
![]()
5. Answer the following questions in detail.
Question 1.
Describe the democratic and oligarchic states in ancient India.
Answer:
Democratic States:
- Some of the ganasanghas were divided into regional zones called ‘Khanda’.
- They functioned through a group of elected individuals, who were found capable.
- Each of the elected members represented his respective khanda.
- These elected members were installed with collective authority for the smooth running of the ganasangha.
- This was a democratic system. Ganasanghas which functioned in this democratic way existed in Punjab and Sindh at the time of Alexander’s invasion.
- Each elective representative of the respective regional zone was designated as ‘Ganamukhya’.
- Every ganamukhya was a member of the assembly known as ‘ganaparishada’.
- The decisions made by the ganaparishada were implemented by designated functionaries of various cadres.
- He was known as the ‘Adhyaksha’ or ‘Raja’.
Oligarchic States:
- In this type the elite class in the society held all the powers of decision-making and administration,
- Panini and Kautilya mention them as ‘Rajshabdopajivi’ Sangh.
- Panini includes Vajji, Andhaka, Vrishni, Yaudheya in the Rajashabdopjivi type.
- Kautilya includes the Vrijji or Vajji, Madrak, Kuru, Panchala, etc. in this type.
- This type of ganasanghas was more prevalent in the eastern region of Uttar Pradesh and Bihar.
![]()
Activity
Present an act in the class based on the simulation of the administrative system of an oligarchic state.
Answer:
Students have to make the presentation in class.
11th Std History Questions And Answers:
- First Farmers Class 11 History Questions And Answers
- First Cities of India Class 11 History Questions And Answers
- Chalcolithic Villages in India Class 11 History Questions And Answers
- Vedic Period Class 11 History Questions And Answers
- Janapadas and Republics Class 11 History Questions And Answers
- Second Urbanisation in India Class 11 History Questions And Answers
- India and Iran (Persia) Class 11 History Questions And Answers
- India During Mauryan Period Class 11 History Questions And Answers
- Post Mauryan India Class 11 History Questions And Answers
- Changing Times Class 11 History Questions And Answers
- Kingdoms in South India Class 11 History Questions And Answers
- India, Nations in the Northwest of the Indian Subcontinent and China Class 11 History Questions And Answers
- India, Sri Lanka and Southeast Asia Class 11 History Questions And Answers
- Delhi Sultanate, Vijayanagar and Bahamani Kingdom Class 11 History Questions And Answers
- India During Mughal Period Class 11 History Questions And Answers
- Swarajya to Empire (Maratha Period) Class 11 History Questions And Answers