Maharashtra Board 12th Maths Solutions Chapter 6 Line and Plane Ex 6.2

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Line and Plane Ex 6.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 6 Line and Plane Ex 6.2

Question 1.
Find the length of the perpendicular from (2, -3, 1) to the line \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z+1}{-1}\)
Solution:
Let PM be the perpendicular drawn from the point P (2, -3, 1) to the line \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z+1}{-1}\) = λ …(Say)
The coordinates of any point on the line are given by x = -1 + 2λ, y = 3 + 3λ, z = -1 – λ
Let the coordinates of M be
(-1 + 2λ, 3 + 3λ, -1 – λ) … (1)
The direction ratios of PM are
-1 + 2λ – 2, 3 + 3λ + 3, -1 – λ – 1
i.e. 2λ – 3, 3λ + 6, -λ – 2
The direction ratios of the given line are 2, 3, -1.
Since PM is perpendicular to the given line, we get
2(2λ – 3) + 3(3λ + 6) – 1(-λ – 2) = 0
∴ 4λ – 6 + 9λ + 18 + λ + 2 = 0
∴ 14λ + 14 = 0 ∴ λ = -1.
Put λ = -1 in (1), the coordinats of M are
(-1 – 2, 3 – 3, -1 + 1) i.e. (-3, 0,0).
∴ length of perpendicular from P to the given line

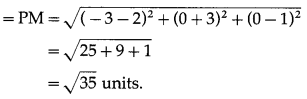
Alternative Method:
We know that the perpendicular distance from the point P\(|\bar{\alpha}|\) to the line \(\bar{r}=\bar{a}+\lambda \vec{b}\) is given by

Substituting these values in (1), we get
length of perpendicular from P to given line

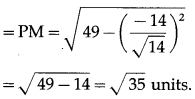
Question 2.
Find the co-ordinates of the foot of the perpendicular drawn from the point \(2 \hat{i}-\hat{j}+5 \hat{k}\) to the line \(\bar{r}=(11 \hat{i}-2 \hat{j}-8 \hat{k})+\lambda(10 \hat{i}-4 \hat{j}-11 \hat{k})\). Also find the length of the perpendicular.
Solution:
Let M be the foot of perpendicular drawn from the point P (\(2 \hat{i}-\hat{j}+5 \hat{k}\)) on the line
\(\bar{r}=(11 \hat{i}-2 \hat{j}-8 \hat{k})+\lambda(10 \hat{i}-4 \hat{j}-11 \hat{k})\).
Let the position vector of the point M be

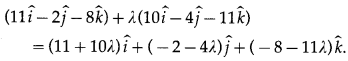
Then \(\overline{\mathrm{PM}}\) = Position vector of M – Position vector of P
= [(11 + 10λ)\(\hat{i}\) + (-2 – 4λ)\(\hat{j}\) + -8 – 11λ) \(\hat{k}\)] – (2\(\hat{i}\) – \(\hat{j}\) + 5\(\hat{k}\))
= (9 + 10λ)\(\hat{i}\) + (-1 – 4λ)\(\hat{j}\) + (-13 – 11λ)\(\hat{k}\)
Since PM is perpendicular to the given line which is parallel to \(\bar{b}=10 \hat{i}-4 \hat{j}-11 \hat{k}\),
\(\overline{\mathrm{PM}}\) ⊥^r\(\bar{b}\) ∴ \(\overline{\mathrm{PM}} \cdot \bar{b}\) = 0
∴ [(9 + 10λ)\(\hat{i}\) + ( – 1 – 4λ)\(\hat{j}\) + (-13 – 11λ)\(\hat{k}\)]-(10\(\hat{i}\) – 4\(\hat{j}\) – 11\(\hat{k}\)) = 0
∴ 10(9 +10λ) – 4( -1 – 4λ) – 11( -13 – 11λ) = 0
∴ 90 + 100λ + 4 + 16λ + 143 +121λ = 0
∴ 237λ + 237 = 0
∴ λ = -1
Putting this value of λ, we get the position vector of M as \(\hat{i}+2 \hat{j}+3 \hat{k}\).
∴ coordinates of the foot of perpendicular M are (1, 2, 3).

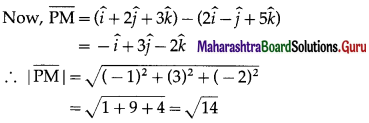
Hence, the coordinates of the foot of perpendicular are (1,2, 3) and length of perpendicular = \(\sqrt {14}\) units.

Question 3.
Find the shortest distance between the lines \(\bar{r}=(4 \hat{i}-\hat{j})+\lambda(\hat{i}+2 \hat{j}-3 \hat{k})\) and \(\bar{r}=(\hat{i}-\hat{j}+2 \hat{k})+\mu(\hat{i}+4 \hat{j}-5 \hat{k})\)
Solution:
We know that the shortest distance between the skew lines \(\bar{r}=\overline{a_{1}}+\lambda \overline{b_{1}}\) and \(\bar{r}=\overline{a_{2}}+\mu \overline{b_{2}}\) is given by

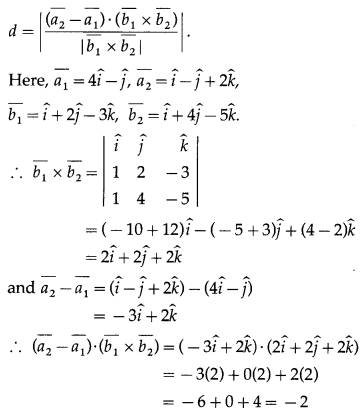
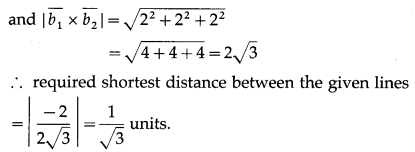
Question 4.
Find the shortest distance between the lines \(\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}\) and \(\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}\)
Solution:
The shortest distance between the lines

= 4(-6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64 = -116
and (m₁n₂ – m₂n₁)² + (l₂n₁ – l₁n₂)² + (l₁m₂ – l₂m₁)²
= (-6 + 2)² + (1 – 7)² + (-14 + 6)²
= 16 + 36 + 64 = 116
Hence, the required shortest distance between the given lines = \(\left|\frac{-116}{\sqrt{116}}\right|\) = \(\sqrt{116}\) = \(2 \sqrt{29}\) units

Question 5.
Find the perpendicular distance of the point (1, 0, 0) from the line \(\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8}\) Also find the co-ordinates of the foot of the perpendicular.
Solution:
Let PM be the perpendicular drawn from the point (1, 0, 0) to the line \(\frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+10}{8}\) = λ …(Say)
The coordinates of any point on the line are given by x = -1 + 2λ, y = 3 + 2λ, z = 8 – λ
Let the coordinates of M be
(-1 + 2λ, 3 + 3λ, -1 – λ) …..(1)
The direction ratios of PM are
-1 + 2λ – 2, 3 + 3λ + 3, -1 – λ – 1
i.e. 2λ – 3, 3λ = 6, -λ – 2
The direction ratios of the given line are 2, 3, 8.
Since PM is perpendicular to the given line, we get
2(2λ – 3) + 3(3λ + 6) – 1(-λ – 2) = O
∴ 4λ – 6 + 9λ + 18 + λ + 2 = 0
∴ 14λ + 14 = 0
∴ λ = -1
Put λ in (1), the coordinates of M are
(-1 – 2, 3 – 3, -1 + 1) i.e. (-3, 0, 0).
∴ length of perpendicular from P to the given line
= PM
= \(\sqrt{(-3-2)^{2}+(0+3)^{2}+(0-1)^{2}}\)
= \(\sqrt{(25 + 9 + 1)}\)
= \(\sqrt{35}\)units.
Alternative Method :
We know that the perpendicular distance from the point

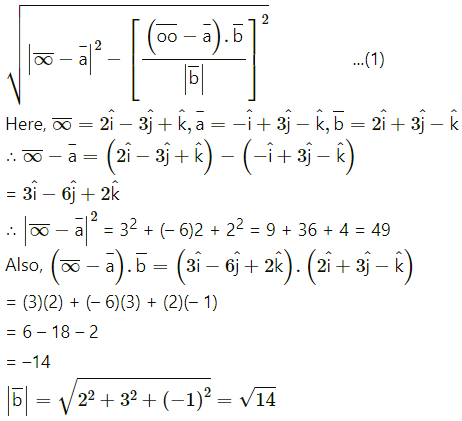
Substitutng tese values in (1), w get
length of perpendicular from P to given line
= PM

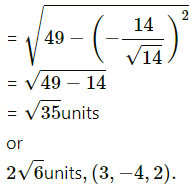
Question 6.
A(1, 0, 4), B(0, -11, 13), C(2, -3, 1) are three points and D is the foot of the perpendicular from A to BC. Find the co-ordinates of D.
Solution:
Equation of the line passing through the points (x₁, y₁, z₁) and (x₂, y₂, z₂) is

AD is the perpendicular from the point A (1, 0, 4) to the line BC.
The coordinates of any point on the line BC are given by x = 2λ, y = -11 + 8λ, z = 13 – 12λ
Let the coordinates of D be (2λ, -11 + 8λ, 13 – 12λ) … (1)
∴ the direction ratios of AD are
2λ – 1, -1λ + 8λ – 0, 13 – 12λ – 4 i.e.
2λ – 1, -11 + 8λ, 9 – 12λ
The direction ratios of the line BC are 2, 8, -12.
Since AD is perpendicular to BC, we get
2(2λ – 1) + 8(-11 + 8λ) – 12(9 – 12λ) = 0
∴ 42λ – 2 – 88 + 64λ – 108 + 144λ = 0
∴ 212λ – 198 = 0

Question 7.
By computing the shortest distance, determine whether following lines intersect each other.
(i) \(\bar{r}=(\hat{i}-\hat{j})+\lambda(2 \hat{i}+\hat{k})\) and \(\bar{r}=(2 \hat{i}-\hat{j})+\mu(\hat{i}+\hat{j}-\hat{k})\)
Solution:
The shortest distance between the lines


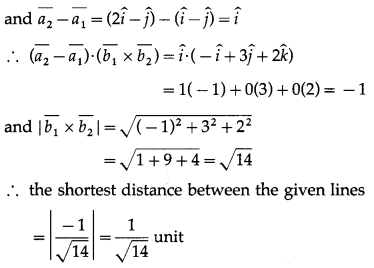
Hence, the given lines do not intersect.

(ii) \(\frac{x-5}{4}=\frac{y-7}{-5}=\frac{z+3}{-5}\) and \(\frac{x-8}{7}=\frac{y-7}{1}=\frac{z-5}{3}\)
Solution:
The shortest distance between the lines

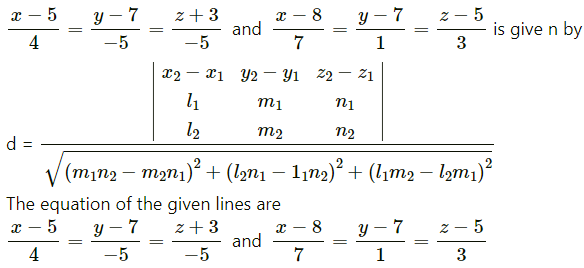
∴ x₁ = -1, y₁ = -1, z₁ = -1, x₂ = 3, y₂ = 5, z₂ = 7,
l₁ = 7, m₁ = -6, n₁ = 1, l₂ = 1, m₂ = -2, n₂ = 1
\(\left|\begin{array}{ccc}
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
l_{1} & m_{1} & n_{1} \\
l_{2} & m_{2} & n_{2}
\end{array}\right|\) = \(\left|\begin{array}{ccc}
4 & 6 & 8 \\
4 & -5 & -5 \\
7 & 1 & 3
\end{array}\right|\)
= 4(- 6 + 2) – 6(7 – 1) + 8(-14 + 6)
= -16 – 36 – 64
= -116
and
(m₁n₂ – m₂n₁)² + (l₂n₁ – l₁n₂)² + (l₁m₂ – l₂m₁)²
= (-6 + 2)² + (1 – 7)² + (-14 + 6)²
= 16 + 36 + 64
= 116
Hence, the required shortest distance between the given lines
= \(\left|\frac{-116}{\sqrt{116}}\right|\)
= \(\sqrt{116}\)
=\(2 \sqrt{29}\) units
or
The shortest distance between the lines
= \(\frac{282}{\sqrt{3830}}\)units
Hence, the gives lines do not intersect.

Question 8.
If lines \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\) and \(\frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}\) intersect each other then find k.
Solution:
The lines

∴ x₁ = 1, y₁ = -1, z₁ = 1, x₂ = 3, y₂ = k, z₂ = 0,
l₁ = 2, m₁ = 3, n₁ = 4, l₂ = 1, m₂ = 2, n₂ = 1.
Since these lines intersect, we get
\(\left|\begin{array}{ccc}
2 & k+1 & -1 \\
2 & 3 & 4 \\
1 & 2 & 1
\end{array}\right|\) = 0
∴ 2 (3 – 8) – (k + 1)(2 – 4) – 1 (4 – 3) = 0
∴ -10 + 2(k + 1) – 1 = 0
∴ 2(k + 1) = 11
∴ k + 1 = \(\frac{11}{2}\)
∴ k = \(\frac{9}{2}\)