Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Line and Plane Ex 6.1 Questions and Answers.
12th Maths Part 1 Line and Plane Exercise 6.1 Questions And Answers Maharashtra Board
Question 1.
Find the vector equation of the line passing through the point having position vector \(-2 \hat{i}+\hat{j}+\hat{k}\) and parallel to vector \(4 \hat{i}-\hat{j}+2 \hat{k}\).
Solution:
The vector equation of the line passing through A (\(\bar{a}\)) and parallel to the vector \(\bar{b}\) is \(\bar{r}\) = \(\bar{a}\) + λ\(\bar{b}\), where λ is a scalar.
∴ the vector equation of the line passing through the point having position vector \(-2 \hat{i}+\hat{j}+\hat{k}\) and parallel to the vector \(4 \hat{i}-\hat{j}+2 \hat{k}\) is
\(\bar{r}=(-2 \hat{i}+\hat{j}+\hat{k})+\lambda(4 \hat{i}-\hat{j}+2 \hat{k})\).
Question 2.
Find the vector equation of the line passing through points having position vectors \(3 \hat{i}+4 \hat{j}-7 \hat{k}\) and \(6 \hat{i}-\hat{j}+\hat{k}\).
Solution:
The vector equation of the line passing through the A (\(\bar{a}\)) and B(\(\bar{b}\)) is \(\bar{r}=\bar{a}+\lambda(\bar{b}-\bar{a})\), λ is a scalar
∴ the vector equation of the line passing through the points having position vectors \(3 \hat{i}+4 \hat{j}-7 \hat{k}\) and \(6 \hat{i}-\hat{j}+\hat{k}\) is
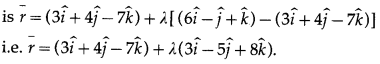
Question 3.
Find the vector equation of line passing through the point having position vector \(5 \hat{i}+4 \hat{j}+3 \hat{k}\) and having direction ratios -3, 4, 2.
Solution:
Let A be the point whose position vector is \(\bar{a}=5 \hat{i}+4 \hat{j}+3 \hat{k}\).
Let \(\bar{b}\) be the vector parallel to the line having direction ratios -3, 4, 2
Then, \(\bar{b}\) = \(-3 \hat{i}+4 \hat{j}+2 \hat{k}\)
The vector equation of the line passing through A (\(\bar{a}\)) and parallel to \(\bar{b}\) is \(\bar{r}=\bar{a}+\lambda \bar{b}\), where λ is a scalar.
∴ the required vector equation of the line is
\(\bar{r}=5 \hat{i}+4 \hat{j}+3 \hat{k}+\lambda(-3 \hat{i}+4 \hat{j}+2 \hat{k})\).
![]()
Question 4.
Find the vector equation of the line passing through the point having position vector \(\hat{i}+2 \hat{j}+3 \hat{k}\) and perpendicular to vectors \(\hat{i}+\hat{j}+\hat{k}\) and \(2 \hat{i}-\hat{j}+\hat{k}\).
Solution:

Since the line is perpendicular to the vector \(\bar{b}\) and \(\bar{c}\), it is parallel to \(\bar{b} \times \bar{c}\). The vector equation of the line passing through A (\(\bar{a}\)) and parallel to \(\bar{b} \times \bar{c}\) is
\(\bar{r}=\bar{a}+\lambda(\bar{b} \times \bar{c})\), where λ is a scalar.
Here, \(\bar{a}\) = \(\hat{i}+2 \hat{j}+3 \hat{k}\)
Hence, the vector equation of the required line is
\(\bar{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(2 \hat{i}+\hat{j}-3 \hat{k})\)
Question 5.
Find the vector equation of the line passing through the point having position vector \(-\hat{i}-\hat{j}+2 \hat{k}\) and parallel to the line \(\bar{r}=(\hat{i}+2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}+2 \hat{j}+\hat{k})\).
Solution:
Let A be point having position vector \(\bar{a}\) = \(-\hat{i}-\hat{j}+2 \hat{k}\)
The required line is parallel to the line

The vector equation of the line passing through A(\(\bar{a}\)) and parallel to \(\bar{b}\) is \(\bar{r}\) = \(\bar{a}\) + λ\(\bar{b}\) where λ is a scalar.
∴ the required vector equation of the line is
\(\overline{\mathrm{r}}=(-\hat{i}-\hat{j}+2 \hat{k})+\lambda(3 \hat{i}+2 \hat{j}+\hat{k})\).
![]()
Question 6.
Find the Cartesian equations of the line passing through A(-1, 2, 1) and having direction ratios 2, 3, 1.
Solution:
The cartesian equations of the line passing through (x1, y1, z1) and having direction ratios a, b, c are
![]()
∴ the cartesian equations of the line passing through the point (-1, 2, 1) and having direction ratios 2, 3, 1 are
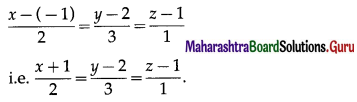
Question 7.
Find the Cartesian equations of the line passing through A(2, 2, 1) and B(1, 3, 0).
Solution:
The cartesian equations of the line passing through the points (x1, y1, z1) and (x2, y2, z2) are
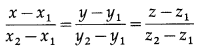
Here, (x1, y1, z1) = (2, 2, 1) and (x2, y2, z2) = (1, 3, 0)
∴ the required cartesian equations are
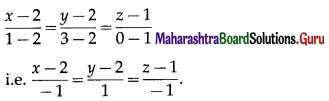
![]()
Question 8.
A(-2, 3, 4), B(1, 1, 2) and C(4, -1, 0) are three points. Find the Cartesian equations of the line AB and show that points A, B, C are collinear.
Solution:
We find the cartesian equations of the line AB. The cartesian equations of the line passing through the points (x1, y1, z1) and (x2, y2, z2) are
\(\frac{x-x_{1}}{x_{2}-x_{1}}\) = \(\frac{y-y_{1}}{y_{2}-y_{1}}\) = \(\frac{z-z_{1}}{z_{2}-z_{1}}\)
Here, (x1, y1, z1) = (-2, 3, 4) and (x2, y2, z2) = (4, -1, 0)
∴ the required cartesian equations of the line AB are
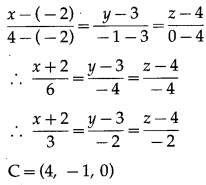
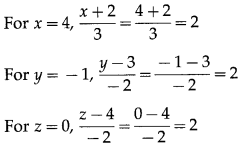
∴ coordinates of C satisfy the equations of the line AB.
∴ C lies on the line passing through A and B.
Hence, A, B, C are collinear.
Question 9.
Show that lines \(\frac{x+1}{-10}=\frac{y+3}{-1}=\frac{z-4}{1}\) and \(\frac{x+10}{-1}=\frac{y+1}{-3}=\frac{z-1}{4}\) intersect each other. Find the co-ordinates of their point of intersection.
Solution:
The equations of the lines are
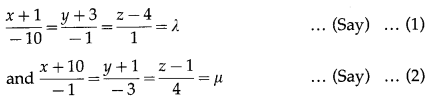
From (1), x = -1 -10λ, y = -3 – 2, z = 4 + λ
∴ the coordinates of any point on the line (1) are
(-1 – 10λ, – 3 – λ, 4 + λ)
From (2), x = -10 – u, y = -1 – 3u, z = 1 + 4u
∴ the coordinates of any point on the line (2) are
(-10 – u, -1 – 3u, 1 + 4u)
Lines (1) and (2) intersect, if
(- 1 – 10λ, – 3 – λ, 4 + 2) = (- 10 – u, -1 – 3u, 1 + 4u)
∴ the equations -1 – 10λ = -10 – u, -3 – 2= – 1 – 3u
and 4 + λ = 1 + 4u are simultaneously true.
Solving the first two equations, we get, λ = 1 and u = 1. These values of λ and u satisfy the third equation also.
∴ the lines intersect.
Putting λ = 1 in (-1 – 10λ, -3 – 2, 4 + 2) or u = 1 in (-10 – u, -1 – 3u, 1 + 4u), we get
the point of intersection (-11, -4, 5).
![]()
Question 10.
A line passes through (3, -1, 2) and is perpendicular to lines \(\bar{r}=(\hat{i}+\hat{j}-\hat{k})+\lambda(2 \hat{i}-2 \hat{j}+\hat{k})\) and \(\bar{r}=(2 \hat{i}+\hat{j}-3 \hat{k})+\mu(\hat{i}-2 \hat{j}+2 \hat{k})\). Find its equation.
Solution:
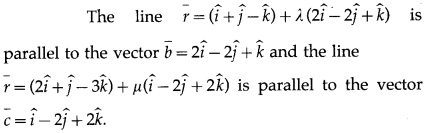
The vector perpendicular to the vectors \(\bar{b}\) and \(\bar{c}\) is given by
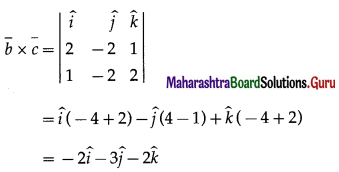
Since the required line is perpendicular to the given lines, it is perpendicular to both \(\bar{b}\) and \(\bar{c}\).
∴ it is parallel to \(\bar{b} \times \bar{c}\)
The equation of the line passing through A(\(\bar{a}\)) and parallel to \(\bar{b} \times \bar{c}\) is
\(\bar{r}=\bar{a}+\lambda(\bar{b} \times \bar{c})\), where λ is a scalar.
Here, \(\bar{a}\) = \(3 \hat{i}-\hat{j}+2 \hat{k}\)
∴ the equation of the required line is
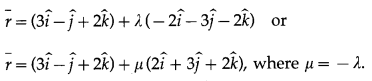
Question 11.
Show that the line \(\frac{x-2}{1}=\frac{y-4}{2}=\frac{z+4}{-2}\) passes through the origin.
Solution:
The equation of the line is
\(\frac{x-2}{1}=\frac{y-4}{2}=\frac{z+4}{-2}\)
The coordinates of the origin O are (0, 0, 0)
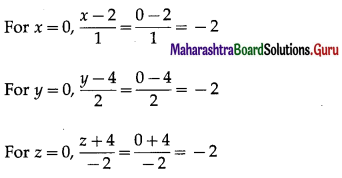
∴ coordinates of the origin O satisfy the equation of the line.
Hence, the line passes through the origin.
Class 12 Maharashtra State Board Maths Solution