Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Miscellaneous Exercise 2 Questions and Answers.
12th Maths Part 2 Applications of Derivatives Miscellaneous Exercise 2 Questions And Answers Maharashtra Board
I. Choose the correct option from the given alternatives:
Question 1.
If the function f(x) = ax3 + bx2 + 11x – 6 satisfies conditions of Rolle’s theorem in [1, 3] and f'(2 + \(\frac{1}{\sqrt{3}}\)) = 0, then values of a and b are respectively.
(a) 1, -6
(b) -2, 1
(c) -1, -6
(d) -1, 6
Answer:
(a) 1, -6
Hint: f(x) = ax3 + bx2 + 11x – 6 satisfies the conditions of Rolle’s theorem in [1, 3]
∴ f(1) = f(3)
a(1)3 + b(1)2 + 11(1) – 6 = a(3)3 + b(3)2 + 11(3) – 6
a + b + 11 = 27a + 9b + 33
26a + 8b = -22
13a + 4b = -11
Only a = 1, b = -6 satisfy this equation.
Question 2.
If f(x) = \(\frac{x^{2}-1}{x^{2}+1}\), for every real x, then the minimum value of f is
(a) 1
(b) 0
(c) -1
(d) 2
Answer:
(c) -1
![]()
Question 3.
A ladder 5 m in length is resting against a vertical wall. The bottom of the ladder is pulled along the ground away from the wall at the rate of 1.5 m/sec. The length of the higher point of the ladder when the foot of the ladder is 4.0 m away from the wall decreases at the rate of
(a) 1
(b) 2
(c) 2.5
(d) 3
Answer:
(b) 2
Question 4.
Let f(x) and g(x) be differentiable for 0 < x < 1 such that f(0) = 0, g(0) = 0, f(1) = 6. Let there exist a real number c in (0, 1) such that f'(c) = 2g'(c), then the value of g(1) must be
(a) 1
(b) 3
(c) 2.5
(d) -1
Answer:
(b) 3
Hint: f(x) and g(x) both satisfies the conditions of LMVT in (0, 1).
∴ f'(c) = \(\frac{f(1)-f(0)}{1-0}=\frac{6-0}{1}=6\)
and g'(c) = \(\frac{g(1)-g(0)}{1-0}=\frac{g(1)-0}{1}\) = g(1)
But f'(c) = 2g'(c)
6 = 2g(1)
∴ g(1) = 3
Question 5.
Let f(x) = x3 – 6x2 + 9x + 18, then f(x) is strictly decreasing in
(a) (-∞, 1)
(b) [3, ∞)
(c) (-∞, 1] ∪ [3, ∞)
(d) (1, 3)
Answer:
(d) (1, 3)
Question 6.
If x = -1 and x = 2 are the extreme points of y = α log x + βx2 + x, then
(a) α = -6, β = \(\frac{1}{2}\)
(b) α = -6, β = \(\frac{-1}{2}\)
(c) α = 2, β = \(\frac{-1}{2}\)
(d) α = 2, β = \(\frac{1}{2}\)
Answer:
(c) α = 2, β = \(\frac{-1}{2}\)
Hint: y = α log x + βx2 + x
∴ \(\frac{d y}{d x}=\frac{\alpha}{x}+\beta \times 2 x+1=\frac{\alpha}{x}+2 \beta x+1\)
f(x) has extreme values at x = -1 and x = 2
∴ f'(-1) = 0 and f(2) = 0
α + 2β = 1
and \(\frac{\alpha}{2}\) + 4β = -1
By solving these two equations, we get
α = 2, β = \(\frac{-1}{2}\)
![]()
Question 7.
The normal to the curve x2 + 2xy – 3y2 = 0 at (1, 1)
(a) meets the curve again in the second quadrant
(b) does not meet the curve again
(c) meets the curve again in the third quadrant
(d) meets the curve again in the fourth quadrant
Answer:
(d) meets the curve again in fourth quadrant
Hint: x2 + 2xy – 3y2 = 0
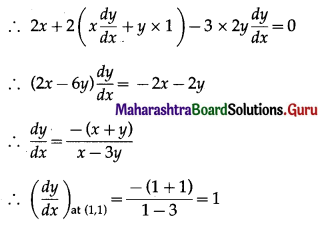
= slope of the tangent at (1, 1)
∴ equation of the tangent at (1, 1) is -1
∴ equation of the normal is
y – 1= -1 (x – 1) = -x + 1
∴ x + y = 2
∴ y = 2 – x
Substituting y = 2 – x in x2 + 2xy – 3y2 = 0, we get
x2 + 2x(2 – x) – 3 (2 – x)2 = 0
⇒ x2 + 4x – 2x2 – 3(4 – 4x + x2) = 0
⇒ x2 – 4x + 3 = 0
⇒ (x – 1)(x – 3) = 0
⇒ x = 1, x = 3
When x = 1, y = 2 – 1 = 1
When x = 3, y = 2 – 3 = -1
∴ the normal at (1, 1) meets the curve at (3, -1) which is in the fourth quadrant.
Question 8.
The equation of the tangent to the curve y = 1 – \(e^{\frac{x}{2}}\) at the point of intersection with Y-axis is
(a) x + 2y = 0
(b) 2x + y = 0
(c) x – y = 2
(d) x + y = 2
Answer:
(a) x + 2y = 0
Hint: The point of intersection of the curve with the Y-axis is the origin (0, 0).
Question 9.
If the tangent at (1, 1) on y2 = x(2 – x)2 meets the curve again at P, then P is
(a) (4, 4)
(b) (-1, 2)
(c) (3, 6)
(d) \(\left(\frac{9}{4}, \frac{3}{8}\right)\)
Answer:
(d) \(\left(\frac{9}{4}, \frac{3}{8}\right)\)
Hint: y2 = x(2 – x)2
= x(4 – 4x + x2)
= x3 – 4x2 + 4x
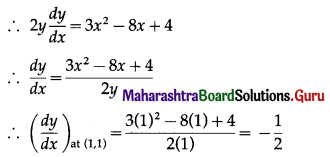
= slope of the tangent at (1, 1)
∴ equation of the tangent at (1, 1) is
y – 1 = –\(\frac{1}{2}\) (x – 1)
∴ 2y – 2 = -x + 1
∴ x + 2y = 3
Only the coordinates \(\left(\frac{9}{4}, \frac{3}{8}\right)\) satisfy both the equations y2 = x(2 – x)2 and x + 2y = 3
∴ P is \(\left(\frac{9}{4}, \frac{3}{8}\right)\)
![]()
Question 10.
The approximate value of tan (44° 30′), given that 1° = 0.0175, is
(a) 0.8952
(b) 0.9528
(c) 0.9285
(d) 0.9825
Answer:
(d) 0.9825
II. Solve the following:
Question 1.
If the curves ax2 + by2 = 1 and a’x2 + b’y2 = 1, intersect orthogonally, then prove that \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a^{\prime}}-\frac{1}{b^{\prime}}\)
Solution:
Let P(x1, y1) be the point of intersection of the curves.


Question 2.
Determine the area of the triangle formed by the tangent to the graph of the function y = 3 – x2 drawn at the point (1, 2) and the coordinate axes.
Solution:
y = 3 – x2

= slope of the tangent at (1, 2)
∴ equation of the tangent at (1, 2) is
y – 2= -2(x – 1)
⇒ y – 2= -2x + 2
⇒ 2x + y = 4
Let this tangent cuts the coordinate axes at A(a, 0) and B(0, b).
∴ 2a + 0 = 4 and 2(0) + b = 4
∴ a = 2 and b = 4
∴ area of required triangle = \(\frac{1}{2}\) × l(OA) × l(OB)
= \(\frac{1}{2}\) ab
= \(\frac{1}{2}\) (2)(4)
= 4 sq units.
![]()
Question 3.
Find the equation of the tangent and normal drawn to the curve y4 – 4x4 – 6xy = 0 at the point M (1, 2).
Solution:
y4 – 4x4 – 6xy = 0
Differentiating both sides w.r.t. x, we get

= slope of the tangent at (1, 2)
∴ the equation of normal at M (1, 2) is
y – 2 = \(\frac{14}{13}\) (x – 1)
∴ 13y – 26 = 14x – 14
∴ 14x – 13y + 12 = 0
The slope of normal at (1, 2)
\(=\frac{-1}{\left(\frac{d y}{d x}\right)_{\mathrm{at}(1,2)}}=\frac{-1}{\left(\frac{14}{13}\right)}=-\frac{13}{14}\)
∴ the equation of normal at M (1, 2) is
y – 2 = \(\frac{-13}{14}\) (x – 1)
14y – 28 = -13x + 13
13x + 14y – 41 = 0
Hence, the equations of tangent and normal are 14x – 13y + 12 = 0 and 13x + 14y – 41 = 0 respectively.
Question 4.
A water tank in the form of an inverted cone is being emptied at the rate of 2 cubic feet per second. The height of the cone is 8 feet and the radius is 4 feet. Find the rate of change of the water level when the depth is 6 feet.
Solution:
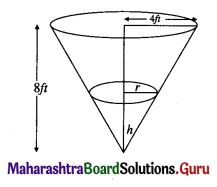
Let r be the radius of the base, h be the height and V be the volume of the water level at any time t.
Since, the height of the cone is 8 feet and the radius is 4 feet,
\(\frac{r}{h}=\frac{4}{8}=\frac{1}{2}\)
r = \(\frac{h}{2}\) ……..(1)

Hence, the rate of change of water level is \(\left(\frac{2}{9 \pi}\right)\) ft/sec.
![]()
Question 5.
Find all points on the ellipse 9x2 + 16y2 = 400, at which the y-coordinate is decreasing and the x-coordinate is increasing at the same rate.
Solution:
Let P(x1, y1) be the point on the ellipse 9x2 + 16y2 = 400 whose y-coordinate decreasing x-coordinate is increasing at the same rate.


Question 6.
Verify Rolle’s theorem for the function f(x) = \(\frac{2}{e^{x}+e^{-x}}\) on [-1, 1].
Solution:
The functions ex, e-x, and 2 are continuous and differentiable in their respective domains.
∴ f(x) = \(\frac{2}{e^{x}+e^{-x}}\) is continuous on [-1, 1] and differentiable on (-1, 1), because ex + e-x ≠ 0 for all x ∈ [-1, 1].
Now, f(-1) = \(\frac{2}{e^{-1}+e}=\frac{2}{e+e^{-1}}\) and f(1) = \(\frac{2}{e+e^{-1}}\)
∴ f(-1) = f(1)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
∴ there exist c ∈ (-1, 1) such that f'(c) = 0
Now, f(x) = \(\frac{2}{e^{x}+e^{-x}}\)

Hence, Rolle’s theorem is verified.
Question 7.
The position of a particle is given by the function s(t) = 2t2 + 3t – 4. Find the time t = c in the interval 0 ≤ f ≤ 4 when the instantaneous velocity of the particle is equal to its average velocity in this interval.
Solution:
s(t) = 2t2 + 3t – 4
∴ s(0) = 2(0)2 + 3(0) – 4 = -4
and s(4) = 2(4)2 + 3(4) – 4 = 32 + 12 – 4 = 40
∴ average velocity = \(\frac{s(4)-s(0)}{4-0}\)
= \(\frac{40-(-4)}{4}\)
= 11
Also, instantaneous velocity = \(\frac{d s}{d t}\)
= \(\frac{d}{d t}\) (2t2 + 3t – 4)
= 2 × 2t + 3 × 1 – 0
= 4t + 3
∴ instantaneous velocity at t = c is \(\left(\frac{d s}{d t}\right)_{t=c}\) = 4c + 3
When instantaneous velocity at t = c equal to its average velocity, we get
4c + 3 = 11
4c = 8
∴ c = 2 ∈ [0, 4]
Hence, t = c = 2.
![]()
Question 8.
Find the approximate value of the function f(x) = \(\sqrt{x^{2}+3 x}\) at x = 1.02.
Solution:
f(x) = \(\sqrt{x^{2}+3 x}\)

Question 9.
Find the approximate value of cos-1(0.51), given π = 3.1416, \(\frac{2}{\sqrt{3}}\) = 1.1547.
Solution:
Let f(x) = cos-1 x

The formula for approximation is f(a + h)= f(a) + h . f'(a)
∴ cos-1 (0.51) = f(0.51)
= f(0.5 + 0.01)
= f(0.5) + (0.01) f'(0.5)
= \(\frac{\pi}{3}\) + 0.01 × (-1.1547)
= \(\frac{3.1416}{3}\) – 0.011547
= 1.0472 – 0.011547
= 1.035653
∴ cos-1 (0.51) = 1.035653.
Question 10.
Find the intervals on which the function y = xx, (x > 0) is increasing and decreasing.
Solution:
y = xx
∴ log y = log xx = x log x
Differentiating both sides w.r.t. x, we get
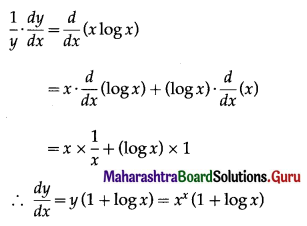
y is increasing if \(\frac{d y}{d x}\) ≥ 0
i.e. if xx (1 + log x) ≥ 0
i.e. if 1 + log x ≥ 0 ……[∵ x > 0]
i.e. if log x ≥ -1
i.e. if log x ≥ -log e …….[∵ log e = 1]
i.e. if logx ≥ log \(\frac{1}{e}\)
i.e. if x ≥ \(\frac{1}{e}\)
∴ y is increasing in \(\left[\frac{1}{e^{\prime}}, \infty\right)\)
y is decreasing if \(\frac{d y}{d x}\) ≤ 0
i.e. if xx (1 + log x) ≤ 0
i.e. if 1 + log x ≤ 0 ……[∵ x > 0]
i.e. if log x ≤ -1
i.e. if log x ≤ -log e
i.e. if log x ≤ log \(\frac{1}{e}\)
i.e. if x ≤ \(\frac{1}{e}\) where x > 0
∴ y is decreasing is \(\left(0, \frac{1}{e}\right]\)
Hence, the given function is increasing in \(\left[\frac{1}{e^{\prime}}, \infty\right)\) and decreasing in \(\left(0, \frac{1}{e}\right]\)
![]()
Question 11.
Find the intervals on which the function f(x) = \(\frac{x}{\log x}\) is increasing and decreasing.
Solution:
f(x) = \(\frac{x}{\log x}\)
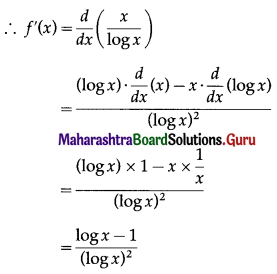
f is increasing if f'(x) ≥ 0
i.e. if \(\frac{\log x-1}{(\log x)^{2}}\) ≥ 0
i.e. if log x – 1 ≥ 0 ……..[∵ (log x)2 > 0]
i.e. if log x ≥ 1
i.e. if log x ≥ log e ………[∵ log e = 1]
i.e. if x ≥ e
∴ f is increasing on [e, ∞)
f is decreasing if f'(x) ≤ 0
i.e. if \(\frac{\log x-1}{(\log x)^{2}}\) ≤ 0
i.e. if log x – 1 ≤ 0 ……..[∵ (log x)2 > 0]
i.e. if log x ≤ 1
i.e. if log x ≤ log e
i.e. if x ≤ e
Also, x > 0 and x ≠ 1 because f(x) = \(\frac{x}{\log x}\) is not defined at x = 1.
∴ f is decreasing in (0, e] – {1}
Hence, f is increasing in [e, ∞) and decreasing in (0, e] – {1}.
Question 12.
An open box with a square base is to be made out of the given quantity of sheet of area a2. Show that the maximum volume of the box is \(\frac{a^{3}}{6 \sqrt{3}}\).
Solution:
Let x be the side of square base and h be the height of the box.
Then x2 + 4xh = a2
∴ h = \(\frac{a^{2}-x^{2}}{4 x}\) …….(1)
Let V be the volume of the box.
Then V = x2h
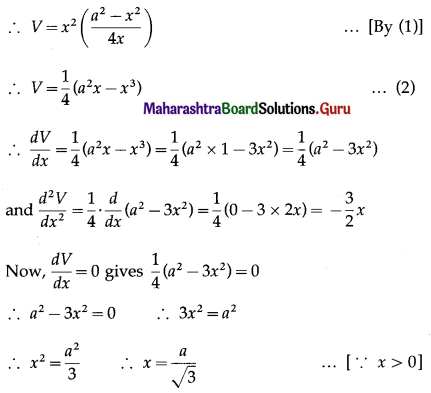
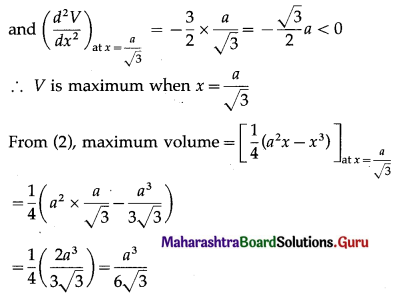
Hence, the maximum volume of the box is \(\frac{a^{3}}{6 \sqrt{3}}\) cu units.
![]()
Question 13.
Show that of all rectangles inscribed in a given circle, the square has the maximum area.
Solution:
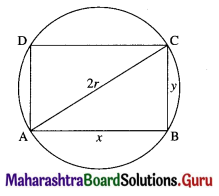
Let ABCD be a rectangle inscribed in a circle of radius r.
Let AB = x and BC = y.
Then x2 + y2 = 4r2 …….(1)
Area of rectangle = xy
= \(x \sqrt{4 r^{2}-x^{2}}\) ……[By (1)]
Let f(x) = x2(4r2 – x2)
= 4r2x2 – x4
∴ f'(x) = \(\frac{d}{d x}\) (4r2x2 – x4)
= 4r2 × 2x – 4x3
= 8r2x – 4x3
and f”(x) = \(\frac{d}{d x}\) (8r2x – 4x3)
= 8r2 × 1 – 4 × 3x2
= 8r2 – 12x2
For maximum area, f'(x) = 0
⇒ 8r2x – 4x3 = 0
⇒ 4x3 = 8r2x
⇒ x2 = 2r2 ……..[∵ x ≠ 0]
⇒ x = √2r …..[x > 0]
and f”(√2r) = 8r2 – 12(√2r)2 = -16r2 < 0
∴ f(x) is maximum when x = √2r
If x = √2r, then from (1),
(√2r)2 + y2 = 4r2
⇒ y2 = 4r2 – 2r2 = 2r2
⇒ y = √2r ……[∵ y > 0]
⇒ x = y
∴ rectangle is a square.
Hence, amongst all rectangles inscribed in a circle, the square has maximum area.
Question 14.
Show that a closed right circular cylinder of a given surface area has maximum volume if its height equals the diameter of its base.
Solution:
Let r be the radius of the base, h be the height and V be the volume of the closed right circular cylinder, whose surface area is a2 sq units (which is given).
2πrh + 2πr2 = a2
⇒ 2πr(h + r) = a2
⇒ h = \(\frac{a^{2}}{2 \pi r}\) – r ……(1)


Hence, the volume of the cylinder is maximum if its height is equal to the diameter of the base.
![]()
Question 15.
A window is in the form of a rectangle surmounted by a semicircle. If the perimeter is 30 m, find the dimensions so that the greatest possible amount of light may be admitted.
Solution:
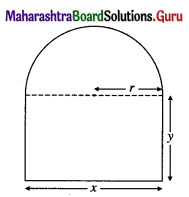
Let x be the length, y be the breadth of the rectangle and r be the radius of the semicircle.
Then perimeter of the window = x + 2y + πr, where x = 2r
This is given to be 30 m
⇒ 2r + 2y + πr = 30
⇒ 2y = 30 – (π + 2)r
⇒ y = 15 – \(\frac{(\pi+2) r}{2}\) ……..(1)
The greatest possible amount of light may be admitted if the area of the window is maximized.
Let A be the area of the window.


Hence, the required dimensions of the window are as follows:
Length of rectangle = \(\left(\frac{60}{\pi+4}\right)\) metres
breadth of rectangle = \(\left(\frac{30}{\pi+4}\right)\) metres
radius of the semicircle = \(\left(\frac{30}{\pi+4}\right)\) metres
Question 16.
Show that the height of a right circular cylinder of greatest volume that can be inscribed in a right circular cone is one-third of that of the cone.
Solution:
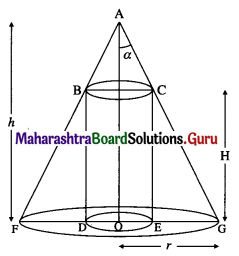
Given the right circular cone of fixed height h and semi-vertical angle a.
Let R be the radius of the base and H be the height of the right circular cylinder that can be inscribed in the right circular cone.
In the figure, ∠GAO = α, OG = r, OA = h, OE = R, CE = H.
We have, \(\frac{r}{h}\) = tan α
∴ r = h tan α ……(1)
Since ∆AOG and ∆CEG are similar.



Hence, the height of the right circular cylinder is one-third of that of the cone.
![]()
Question 17.
A wire of length l is cut into two parts. One part is bent into a circle and the other into a square. Show that the sum of the areas of the circle and the square is the least if the radius of the circle is half of the side of the square.
Solution:
Let r be the radius of the circle and x be the length of the side of the square. Then
(circumference of the circle) + (perimeter of the square) = l
∴ 2πr + 4x = l
∴ r = \(\frac{l-4 x}{2 \pi}\)
A = (area of the circle) + (area of the square)
= πr2 + x2

This shows that the sum of the areas of circle and square is least when the radius of the circle = (\(\frac{1}{2}\)) side of the square.
Question 18.
A rectangular sheet of paper of fixed perimeter with the sides having their lengths in the ratio 8 : 15 converted into an open rectangular box by folding after removing the squares of the equal area from all comers. If the total area of the removed squares is 100, the resulting box has maximum volume. Find the lengths of the rectangular sheet of paper.
Solution:
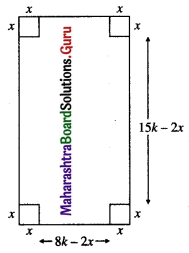
The sides of the rectangular sheet of paper are in the ratio 8 : 15.
Let the sides of the rectangular sheet of paper be 8k and 15k respectively.
Let x be the side of the square which is removed from the comers of the sheet of paper.
The total area of removed squares is 4x2, which is given to be 100.
4x2 = 100
⇒ x2 = 25
⇒x = 5 ……[x > 0]
Now, the length, breadth, and height of the rectangular box are 15k – 2x, 8k – 2x, and x respectively.
Let V be the volume of the box.
Then V = (15k – 2x) (8k – 2x) . x
⇒ V = (120k2 – 16kx – 30kx + 4x2) . x
⇒ V = 4x3 – 46kx2 + 120k2x
\(\frac{d V}{d x}=\frac{d}{d x}\) (4x3 – 46kx2 + 120k2x)
= 4 × 3x2 – 46k × 2x + 120k2 × 1
= 12x2 – 92kx + 120k2
Since, volume is maximum when the square of side x = 5 is removed from the corners,
\(\left(\frac{d V}{d x}\right)_{\text {at } x=5}=0\)
⇒ 12(5)2 – 92k(5) + 120k2 = 0
⇒ 60 – 92k + 24k2 = 0
⇒ 6k2 – 23k + 15 = 0
⇒ 6k2 – 18k – 5k + 15 = 0
⇒ 6k(k – 3) – 5 (k – 3) = 0
⇒ (k – 3)(6k – 5) = 0
⇒ k = 3 or k = \(\frac{5}{6}\)
If k = \(\frac{5}{6}\), then
8k – 2x = 8k – 10 < 0
∴ k ≠ \(\frac{5}{6}\)
∴ k = 3
∴ 8k = 8 × 3 = 24 and 15k = 15 × 3 = 45
Hence, the lengths of the rectangular sheet are 24 and 45.
![]()
Question 19.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \(\frac{4 r}{3}\).
Solution:
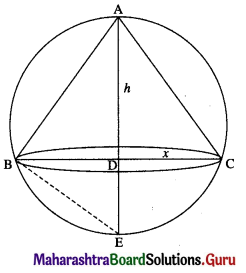
Let x be the radius of the base and h be the height of the cone which is inscribed in a sphere of radius r.
In the figure, AD = h and CD = x = BD
Since, ΔABD and ΔBDE are similar,
\(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{BD}}{\mathrm{DE}}\)
BD2 = AD . DE = AD (AE – AD)
x2 = h(2r – h) …… (1)
Let V be the volume of the cone.


∴ V is maximum when h = \(\frac{4 r}{3}\)
Hence, the altitude (i.e. height) of the right circular cone of maximum volume = \(\frac{4 r}{3}\).
Question 20.
Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \(\frac{2 R}{\sqrt{3}}\). Also, find the maximum Volume.
Solution:
Let R be the radius and h be the height of the cylinder which is inscribed in a sphere of radius r cm.
Then from the figure,
\(R^{2}+\left(\frac{h}{2}\right)^{2}=r^{2}\)
∴ R2 = r2 – \(\frac{h^{2}}{4}\) ………(1)
Let V be the volume of the cylinder.
Then V = πR2h
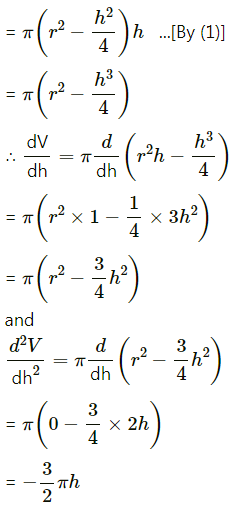
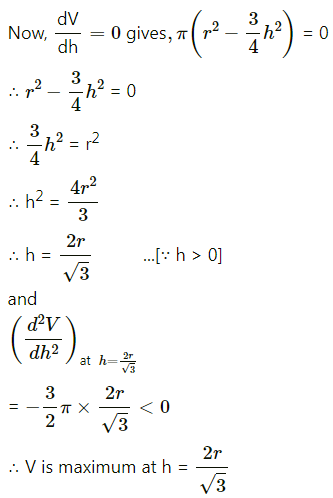
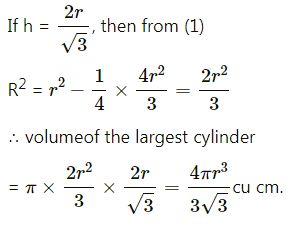
Hence, the volume of the largest cylinder inscribed in a sphere of radius ‘r’ cm = \(\frac{4 R^{3}}{3 \sqrt{3}}\) cu cm.
![]()
Question 21.
Find the maximum and minimum values of the function f(x) = cos2x + sin x.
Solution:
f(x) = cos2x + sin x
∴ f'(x) = \(\frac{d}{d x}\) (cos2x + sin x)
= 2 cos x . \(\frac{d}{d x}\) (cos x) + cos x
= 2 cos x(-sin x) + cos x
= -sin 2x + cos x
and f”(x) = \(\frac{d}{d x}\) (-sin 2x + cos x)
= -cos 2x . \(\frac{d}{d x}\) (2x) – sin x
= -cos 2x × 2 – sin x
= -2 cos 2x – sin x
For extreme values of f(x), f'(x) = 0
-sin 2x + cos x = 0
-2 sin x cos x + cos x = 0
cos x (-2 sin x + 1) = 0
cos x = 0 or -2 sin x + 1 = 0
cos x = cos \(\frac{\pi}{2}\) or sin x = \(\frac{1}{2}\) = sin \(\frac{\pi}{6}\)
∴ x = \(\frac{\pi}{2}\) or x = \(\frac{\pi}{6}\)
(i) f”(\(\frac{\pi}{2}\)) = -2 cos π – sin \(\frac{\pi}{2}\)
= -2(-1) – 1
= 1 > 0
∴ by the second derivative test, f is minimum at x = \(\frac{\pi}{2}\) and minimum value of f at x = \(\frac{\pi}{2}\)
= f(\(\frac{\pi}{2}\))
= \(\cos ^{2} \frac{\pi}{2}+\sin \frac{\pi}{2}\)
= 0 + 1
= 1
![]()
(ii) f”(\(\frac{\pi}{6}\)) = \(-2 \cos \frac{\pi}{3}-\sin \frac{\pi}{6}\)
= \(-2\left(\frac{1}{2}\right)-\frac{1}{2}\)
= \(-\frac{3}{2}\) < 0
∴ by the second derivative test, f is maximum at x = \(\frac{\pi}{6}\) and maximum value of f at x = \(\frac{\pi}{6}\)
= f(\(\frac{\pi}{6}\))
= \(\cos ^{2} \frac{\pi}{6}+\sin \frac{\pi}{6}\)
= \(\left(\frac{\sqrt{3}}{2}\right)^{2}+\frac{1}{2}\)
= \(\frac{5}{4}\)
Hence, the maximum and minimum values of the function f(x) are \(\frac{5}{4}\) and 1 respectively.
Class 12 Maharashtra State Board Maths Solution