Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Ex 2.3 Questions and Answers.
12th Maths Part 2 Applications of Derivatives Exercise 2.3 Questions And Answers Maharashtra Board
Question 1.
Check the validity of the Rolle’s theorem for the following functions.
(i) f(x) = x2 – 4x + 3, x ∈ [1, 3]
Solution:
The function f given as f(x) = x2 – 4x + 3 is polynomial function.
Hence, it is continuous on [1, 3] and differentiable on (1, 3).
Now, f(1) = 12 – 4(1) + 3 = 1 – 4 + 3 = 0
and f(3) = 32 – 4(3) + 3 = 9 – 12 + 3 = 0
∴ f(1) = f(3)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
(ii) f(x) = e-x sin x, x ∈ [0, π].
Solution:
The functions e-x and sin x are continuous and differentiable on their domains.
∴ f(x) = e-x sin x is continuous on [0, π] and differentiable on (0, π).
Now, f(0) = e0 sin 0 = 1 × 0 = 0
and f(π) = e-π sin π = e-π × 0 = 0
∴ f(0) = f(π)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
![]()
(iii) f(x) = 2x2 – 5x + 3, x ∈ [1, 3].
Solution:
The function f given as f(x) = 2x2 – 5x + 3 is a polynomial function.
Hence, it is continuous on [1, 3] and differentiable on (1, 3).
Now, f(1) = 2(1)2 – 5(1) + 3 = 2 – 5 + 3 = 0
and f(3) = 2(3)2 – 5(3) + 3 = 18 – 15 + 3 = 6
∴ f(1) ≠ f(3)
Hence, the conditions of Rolle’s theorem are not satisfied.
(iv) f(x) = sin x – cos x + 3, x ∈ [0, 2π].
Solution:
The functions sin x, cos x and 3 are continuous and differentiable on their domains.
∴ f(x) = sin x – cos x + 3 is continuous on [0, 2π] and differentiable on (0, 2π).
Now, f(0) = sin 0 – cos 0 + 3 = 0 – 1 + 3 = 2
and f(2π) = sin 2π – cos 2π + 3 = 0 – 1 + 3 = 2
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
(v) f(x) = x2, if 0 ≤ x ≤ 2
= 6 – x, if 2 < x ≤ 6.
Solution:
f(x) = x2, if 0 ≤ x ≤ 2
= 6 – x, if 2 < x ≤ 6
∴ f(x) = \(\frac{d}{d x}\left(x^{2}\right)\) = 2x, if 0 ≤ x ≤ 2
= \(\frac{d}{d x}(6-x)\) = -1, if 2 < x ≤ 6
∴ Lf'(2) = 2(2) = 4 and Rf'(2) = -1
∴ Lf'(2) ≠ Rf'(2)
∴ f is not differentiable at x = 2 and 2 ∈ (0, 6).
∴ f is not differentiable at all the points on (0, 6).
Hence, the conditions of Rolle’s theorem are not satisfied.
(vi) f(x) = \(x^{\frac{2}{3}}\), x ∈ [-1, 1].
Solution:
f(x) = \(x^{\frac{2}{3}}\)
∴ \(f^{\prime}(x)=\frac{d}{d x}\left(x^{\frac{2}{3}}\right)=\frac{2}{3} x^{-\frac{1}{3}}\) = \(\frac{2}{3 \sqrt[3]{x}}\)
This does not exist at x = 0 and 0 ∈ (-1, 1)
∴ f is not differentiable on the interval (-1, 1).
Hence, the conditions of Rolle’s theorem are not satisfied.
![]()
Question 2.
Given an interval [a, b] that satisfies hypothesis of Rolle’s theorem for the function f(x) = x4 + x2 – 2. It is known that a = -1. Find the value of b.
Solution:
f(x) = x4 + x2 – 2
Since the hypothesis of Rolle’s theorem are satisfied by f in the interval [a, b], we have
f(a) = f(b), where a = -1
Now, f(a) = f(-1) = (-1)4 + (-1)2 – 2 = 1 + 1 – 2 = 0
and f(b) = b4 + b2 – 2
∴ f(a) = f(b) gives
0 = b4 + b2 – 2 i.e. b4 + b2 – 2 = 0.
Since, b = 1 satisfies this equation, b = 1 is one of the roots of this equation.
Hence, b = 1.
Question 3.
Verify Rolle’s theorem for the following functions.
(i) f(x) = sin x + cos x + 7, x ∈ [0, 2π]
Solution:
The functions sin x, cos x and 7 are continuous and differentiable on their domains.
∴ f(x) = sin x + cos x + 7 is continuous on [0, 2π] and differentiable on (0, 2π)
Now, f(0) = sin 0 + cos 0 + 7 = 0 + 1 + 7 = 8
and f(2π) = sin 2π + cos 2π + 7 = 0 + 1 + 7 = 8
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
∴ there exists c ∈ (0, 2π) such that f'(c) = 0.
Now, f(x) = sin x + cos x + 7
∴ f'(x) = \(\frac{d}{d x}\) (sin x + cos x + 7)
= cos x – sin x + 0
= cos x – sin x
∴ f'(c) = cos c – sin c
∴ f'(c) = 0 gives, cos c – sin c = 0
∴ cos c = sin c
∴ c = \(\frac{\pi}{4}, \frac{5 \pi}{4}, \frac{9 \pi}{4}, \ldots\)
But \(\frac{\pi}{4}, \frac{5 \pi}{4}\) ∈ (0, 2π)
∴ c = \(\frac{\pi}{4} \text { or } \frac{5 \pi}{4}\)
Hence, the Rolle’s theorem is verified.
![]()
(ii) f(x) = sin(\(\frac{x}{2}\)), x ∈ [0, 2π]
Solution:
The function f(x) = sin(\(\frac{x}{2}\)) is continuous on [0, 2π] and differentiable on (0, 2π).
Now, f(0) = sin 0 = 0
and f(2π) = sin π = 0
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
∴ there exists c ∈ (0, 2π) such that f'(c) = 0.


Hence, Rolle’s theorem is verified.
(iii) f(x) = x2 – 5x + 9, x ∈ [1, 4].
Solution:
The function f given as f(x) = x2 – 5x + 9 is a polynomial function.
Hence it is continuous on [1, 4] and differentiable on (1, 4).
Now, f(1) = 12 – 5(1) + 9 = 1 – 5 + 9 = 5
and f(4) = 42 – 5(4) + 9 = 16 – 20+ 9 = 5
∴ f(1) = f(4)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
∴ there exists c ∈ (1, 4) such that f'(c) = 0.
Now, f(x) = x2 – 5x + 9
∴ f'(x) = \(\frac{d}{d x}\) (x2 – 5x + 9)
= 2x – 5 × 1 + 0
= 2x – 5
∴ f'(c) = 2c – 5
∴ f'(c) = 0 gives, 2c – 5 = 0
∴ c = 5/2 ∈ (1, 4)
Hence, the Rolle’s theorem is verified.
Question 4.
If Rolle’s theorem holds for the function f(x) = x3 + px2 + qx + 5, x ∈ [1, 3] with c = 2 + \(\frac{1}{\sqrt{3}}\), find the values of p and q.
Solution:
The Rolle’s theorem holds for the function f(x) = x3 + px2 + qx + 5, x ∈ [1, 3]
∴ f(1) = f(3)
∴ 13 + p(1)2 + q(1) + 5 = 33 + p (3)2 + q(3) + 5
∴ 1 + p + q + 5 = 27 + 9p + 3q + 5
∴ 8p + 2q = -26
∴ 4p + q = -13 ….. (1)
Also, there exists at least one point c ∈ (1, 3) such that f'(c) = 0.
Now, f'(x) = \(\frac{d}{d x}\) (x3 + px2 + qx + 5)
= 3x2 + p × 2x + q × 1 + 0
= 3x2 + 2px + q

But f'(c) = 0
∴ \(4 p+\frac{2 p}{\sqrt{3}}+q+13+\frac{12}{\sqrt{3}}=0\)
∴ (4√3 + 2)p + √3q + (13√3 + 12) = 0
∴ (4√3 + 2)p + √3q = -13√3 – 12 ……. (2)
Multiplying equation (1) by √3, we get
4√3p + √3q= -13√3
Subtracting this equation from (2), we get
2p = -12 ⇒ p= -6
∴ from (1), 4(-6) + q = -13 ⇒ q = 11
Hence, p = -6 and q = 11.
![]()
Question 5.
If Rolle’s theorem holds for the function f(x) = (x – 2) log x, x ∈ [1, 2], show that the equation x log x = 2 – x is satisfied by at least one value of x in (1, 2).
Solution:
The Rolle’s theorem holds for the function f(x) = (x – 2) log x, x ∈ [1, 2].
∴ there exists at least one real number c ∈ (1, 2) such that f'(c) = 0.
Now, f(x) = (x – 2) log x
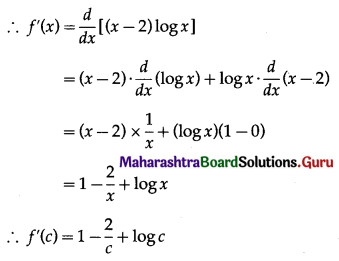
∴ f'(c) = 0 gives 1 – \(\frac{2}{c}\) + log c = 0
∴ c – 2 + c log c = 0
∴ c log c = 2 – c, where c ∈ (1, 2)
∴ c satisfies the equation x log x = 2 – x, c ∈ (1, 2).
Hence, the equation x log x = 2 – x is satisfied by at least one value of x in (1, 2).
Question 6.
The function f(x) = \(x(x+3) e^{-\frac{x}{2}}\) satisfies all the conditions of Rolle’s theorem on [-3, 0]. Find the value of c such that f'(c) = 0.
Solution:
The function f(x) satisfies all the conditions of Rolle’s theorem, therefore there exist c ∈ (-3, 0) such that f'(c) = 0.
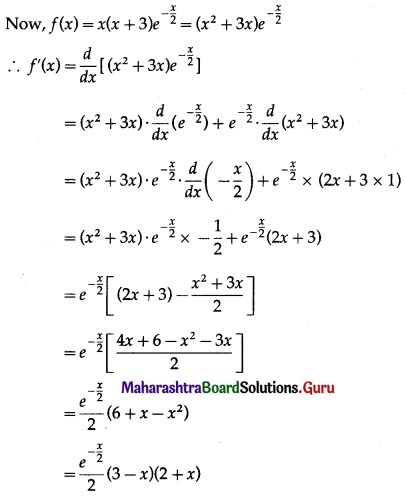

Question 7.
Verify Lagrange’s mean value theorem for the following functions:
(i) f(x) = log x on [1, e].
Solution:
The function f given as f(x) = log x is a logarithmic function that is continuous for all positive real numbers.
Hence, it is continuous on [1, e] and differentiable on (1, e).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (1, e) such that
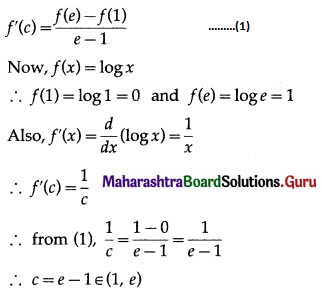
Hence, Lagrange’s mean value theorem is verified.
![]()
(ii) f(x) = (x – 1)(x – 2)(x – 3) on [0, 4].
Solution:
The function f given as
f(x) = (x – 1)(x – 2)(x – 3)
= (x – 1)(x2 – 5x + 6)
= x3 – 5x2 + 6x – x2 + 5x – 6
= x3 – 6x2 + 11x – 6 is a polynomial function.
Hence, it is continuous on [0, 4] and differentiable on (0, 4).
Thus, the function f satisfies the conditions of Lagrange’s, mean value theorem.
∴ there exists c ∈ (0, 4) such that


Hence, Lagrange’s mean value theorem is verified.
(iii) f(x) = x2 – 3x – 1, x ∈ \(\left[\frac{-11}{7}, \frac{13}{7}\right]\)
Solution:
The function f given as f(x) = x2 – 3x – 1 is a polynomial function.
Hence, it is continuous on \(\left[\frac{-11}{7}, \frac{13}{7}\right]\) and differentiable on \(\left(\frac{-11}{7}, \frac{13}{7}\right)\).
Thus, the function f satisfies the conditions of LMVT.
∴ there exists c ∈ \(\left(\frac{-11}{7}, \frac{13}{7}\right)\) such that
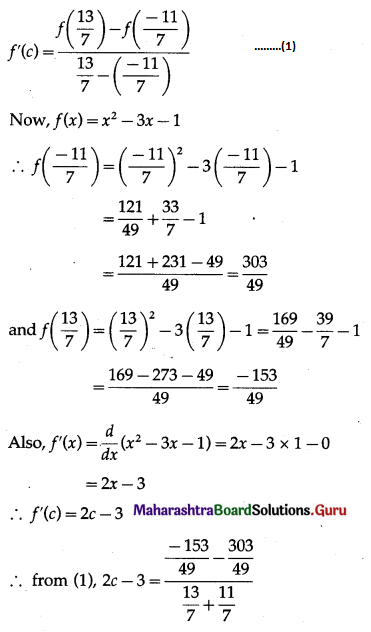
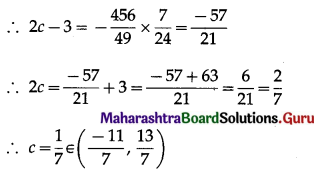
Hence, Lagrange’s mean value theorem is verified.
![]()
(iv) f(x) = 2x – x2, x ∈ [0, 1].
Solution:
The function f given as f(x) = 2x – x2 is a polynomial function.
Hence, it is continuous on [0, 1] and differentiable on (0, 1).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (0, 1) such that

Hence, Lagrange’s mean value theorem is verified.
(v) f(x) = \(\frac{x-1}{x-3}\) on [4, 5].
Solution:
The function f given as
f(x) = \(\frac{x-1}{x-3}\) is a rational function which is continuous except at x = 3.
But 3 ∉ [4, 5]
Hence, it is continuous on [4, 5] and differentiable on (4, 5).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (4, 5) such that
f'(c) = \(\frac{f(5)-f(4)}{5-4}\) ……..(1)

Hence, Lagrange’s mean value theorem is verified.
Class 12 Maharashtra State Board Maths Solution