Linear Regression Class 12 Commerce Maths 2 Chapter 3 Exercise 3.1 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Ex 3.1 Questions and Answers.
Std 12 Maths 2 Exercise 3.1 Solutions Commerce Maths
Question 1.
The HRD manager of the company wants to find a measure which he can use to fix the monthly income of persons applying for the job in the production department. As an experimental project. He collected data of 7 persons from that department referring to years of service and their monthly incomes.
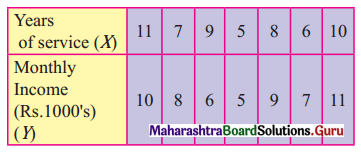
(i) Find the regression equation of income on years of service.
(ii) What initial start would you recommend for a person applying for the job after having served in a similar capacity in another company for 13 years?
Solution:
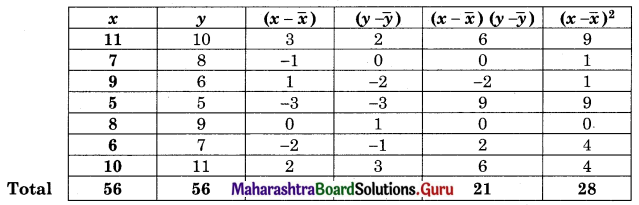
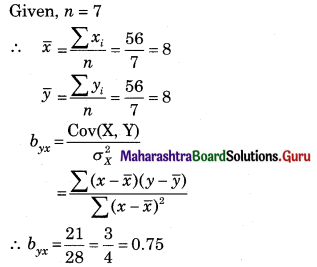
(i) Regression equation of Y on X is (Y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
(Y – 8) = 0.75(x – \(\bar{x}\))
Y = 0.75x + 2
(ii) When x = 13
Y = 0.75(13) + 2 = 11.75
Recommended income for the person is ₹ 11750.
![]()
Question 2.
Calculate the regression equations of X on Y and Y on X from the following date:
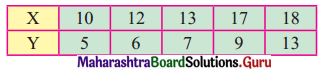
Solution:
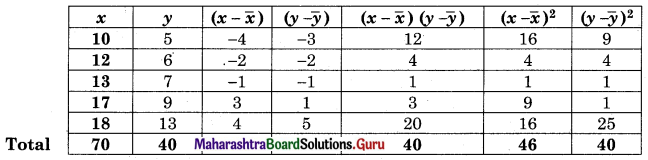

Regression equation of X on Y is (X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 14) = 1(Y – 8)
X – 14 = Y – 8
X = Y + 6
Regression equation Y on X is (Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 8) = 0.87(X – 14)
Y – 8 = 0.87X – 12.18
Y = 0.87X – 4.18
Question 3.
For a certain bivariate data on 5 pairs of observations given
Σx = 20, Σy = 20, Σx2 = 90, Σy2 = 90, Σxy = 76
Calculate (i) cov(x, y), (ii) byx and bxy, (iii) r
Solution:


Sine byx and bxy are negative, r = -0.4
![]()
Question 4.
From the following data estimate y when x = 125

Solution:
Let u = x – 122, v = y – 14

Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 13.5) = -0.21(x – 121.5)
Y – 13.5 = -0.21x + 25.52
Y = -0.21x + 39.02
When x = 125
Y = -0.21(125) + 39.02
= -26.25 + 39.02
= 12.77
Question 5.
The following table gives the aptitude test scores and productivity indices of 10 works selected at workers selected randomly.
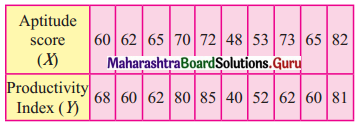
Obtain the two regression equation and estimate
(i) The productivity index of a worker whose test score is 95.
(ii) The test score when productivity index is 75.
Solution:
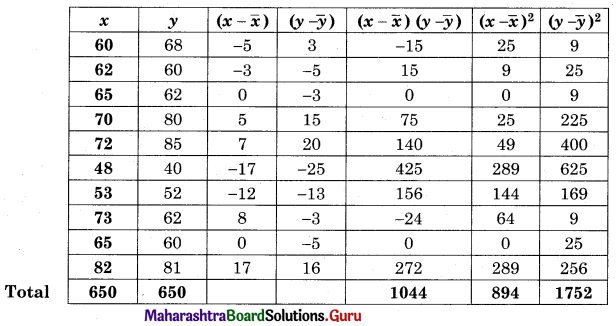

Regression equation of Y on X,
(Y – \(\bar{y}\)) = byx (X – \(\bar{y}\))
(Y – 65) = 1.16 (x – 65)
Y – 65 = 1.16x – 75.4
Y = 1.16x – 10.4
(i) When x = 95
Y = 1.16(95) – 10.4
= 110.2 – 10.4
= 99.8
Regression equation of X on Y,
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 65) = 0.59(y – 65)
(X – 65) = 0.59y – 38.35
X = 0.59y + 26.65
(ii) When y = 75
x = 0.59(75) + 26.65
= 44.25 + 26.65
= 70.9
![]()
Question 6.
Compute the appropriate regression equation for the following data.
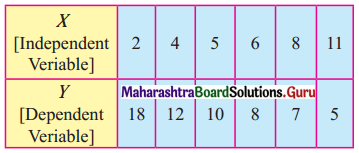
Solution:
Since x is the independent variable, and y is the dependent variable,
we need to find regression equation of y on x
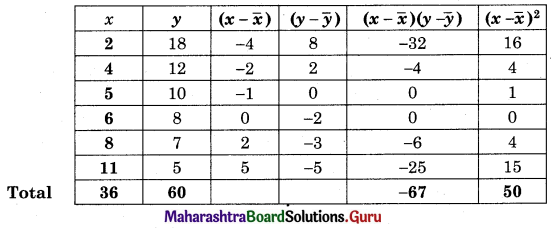
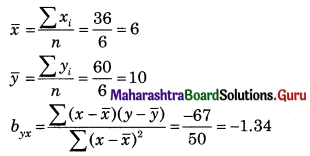
Regression equation of y on x is (y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
(y – 10) = -13.4(x – 6)
y – 10 = -1.34x + 8.04
y = -1.34x + 18.04
Question 7.
The following are the marks obtained by the students in Economic (X) and Mathematics (Y)
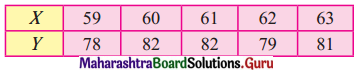
Find the regression equation of Y and X.
Solution:
Let u = x – 61, v = y – 80

Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 80.4) = 0.3(x – 61)
Y – 80.4 = 0.3x – 18.3
Y = 0.3x + 62.1
![]()
Question 8.
For the following bivariate data obtain the equation of two regressions lines:

Solution:
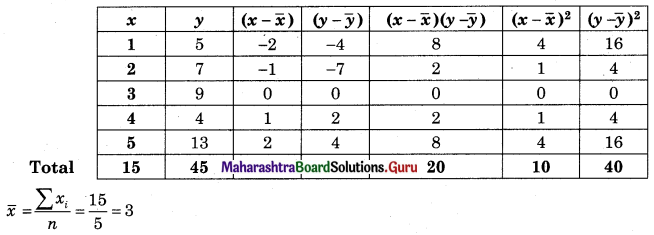

Regression equation of Y on X
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 9) = 2(x – 3)
Y – 9 = 2x – 6
Y = 2x + 3
Regression equation of X on Y
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 3) = 0.5(y – 9)
(X – 3) = 0.5y – 4.5
X = 0.5y – 1.5
Question 9.
Find the following data obtain the equation of two regression lines:

Solution:
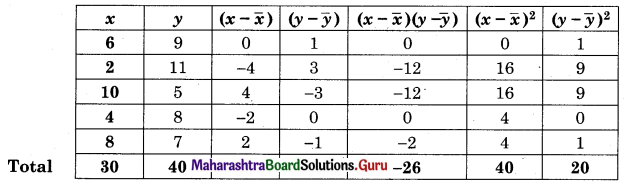

Regression of Y on X,
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 8) = 0.65(x – 6)
Y – 8 = -0.65x + 3.9
Y = -0.65x + 11.9
Regression of X on Y
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 6) = -1.3(y – 8)
(X – 6) = -1.3y + 10.4
X = -1.3y + 16.4
![]()
Question 10.
For the following data, find the regression line of Y on X
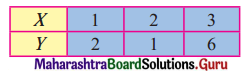
Hence find the most likely value of y when x = 4
Solution:

(Y – 3) = 2(x – 2)
Y – 3 = 2x – 4
Y = 2x – 1
When x = 4
Y = 2(4) – 1
= 8 – 1
= 7
Question 11.
Find the following data, find the regression equation of Y on X, and estimate Y when X = 10.
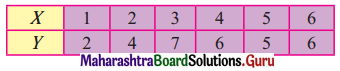
Solution:

Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 5) = (0.63)(x – 3.5)
Y – 5 = 0.63x – 2.2
Y = 0.63x + 2.8
When x = 10
Y = 0.63(10) + 2.8
= 6.3 + 2.8
= 9.1
![]()
Question 12.
The following sample gave the number of hours of study (X) per day for an examination and marks (Y) obtained by 12 students.
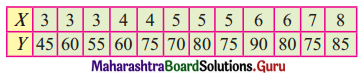
Obtain the line of regression of marks on hours of study.
Solution:
Let u = x – 5, v = y – 70
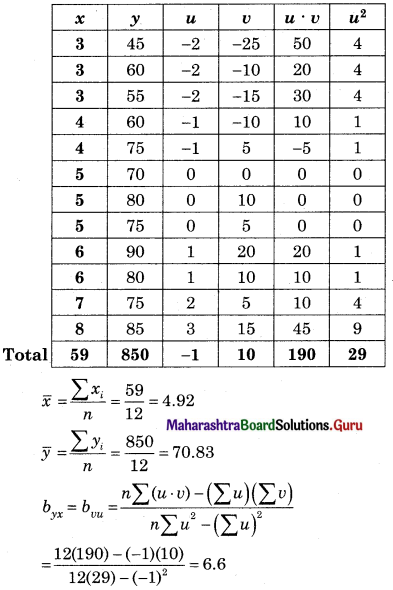
∴ Equation of marks on hours of study is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 70.83) = 6.6(x – 4.92)
Y – 70.83 = 6.6x – 32.47
∴ Y = 6.6x + 38.36
12th Commerce Maths Digest Pdf