Maharashtra Board 11th Maths Solutions Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(B)

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(B) Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Miscellaneous Exercise 4(B)

(I) Select the correct option from the given alternatives.

Question 1.
Given A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 2
\end{array}\right]\), I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) if A – λI is a singular matrix, then ___________
(a) λ = 0
(b) λ² – 3λ – 4 = 0
(c) λ² + 3λ – 4 = 0
(d) λ² – 3λ – 6 = 0
Answer:
(b) λ² – 3λ – 4 = 0
Hint:

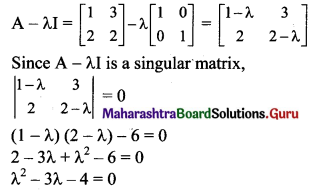
Question 2.
Consider the matrices A = \(\left[\begin{array}{ccc}
4 & 6 & -1 \\
3 & 0 & 2 \\
1 & -2 & 5
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 4 \\
0 & 1 \\
-1 & 2
\end{array}\right]\), C = \(\left[\begin{array}{l}
3 \\
1 \\
2
\end{array}\right]\). Out of the given matrix products, ___________
(i) (AB)^TC
(ii) C^TC(AB)^T
(iii) C^TAB
(iv) A^TABB^TC
(a) Exactly one is defined
(b) Exactly two are defined
(c) Exactly three are defined
(d) all four are defined
Answer:
(c) Exactly three are defined
Hint:
A is of order 3 × 3, B is of order 3 × 2 and C is of order 3 × 1.
(AB)^TC is of order 2 × 1.
C^TC and (AB)^T are of different orders.
C^TC (AB)^T is not defined.
C^TAB is of order 1 × 2.
A^TABB^TC is of order 3 × 1.

Question 3.
If A and B are square matrices of equal order, then which one is correct among the following?
(a) A + B = B + A
(b) A + B = A – B
(c) A – B = B – A
(d) AB = BA
Answer:
(a) A + B = B + A
Hint:
Matrix addition is commutative.
∴ A + B = B + A

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
a & 2 & b
\end{array}\right]\) is a matrix satisfying the equation AA^T = 9I, where I is the identity matrix of order 3, then the ordered pair (a, b) is equal to ___________
(a) (2, -1)
(b) (-2, 1)
(c) (2, 1)
(d) (-2, -1)
Answer:
(d) (-2, -1)

Question 5.
If A = \(\left[\begin{array}{ll}
\alpha & 2 \\
2 & \alpha
\end{array}\right]\) and |A³| = 125, then α = ___________
(a) ±3
(b) ±2
(c) ±5
(d) 0
Answer:
(a) ±3
Hint:
|A³| = 125
|A|³ = 53 …….[∵ |Aⁿ| = |A|ⁿ, n ∈ N]
∴ |A| = 5
\(\left|\begin{array}{ll}
\alpha & 2 \\
2 & \alpha
\end{array}\right|=5\)
α² – 4 = 5
α² = 9
∴ α = ± 3

Question 6.
If \(\left[\begin{array}{ll}
5 & 7 \\
x & 1 \\
2 & 6
\end{array}\right]-\left[\begin{array}{cc}
1 & 2 \\
-3 & 5 \\
2 & y
\end{array}\right]=\left[\begin{array}{cc}
4 & 5 \\
4 & -4 \\
0 & 4
\end{array}\right]\), then ___________
(a) x = 1, y = -2
(b) x = -1, y = 2
(c) x = 1, y = 2
(d) x = -1, y = -2
Answer:
(c) x = 1, y = 2

Question 7.
If A + B = \(\left[\begin{array}{ll}
7 & 4 \\
8 & 9
\end{array}\right]\) and A – B = \(\left[\begin{array}{ll}
1 & 2 \\
0 & 3
\end{array}\right]\), then the value of A is ___________
(a) \(\left[\begin{array}{ll}
3 & 1 \\
4 & 3
\end{array}\right]\)
(b) \(\left[\begin{array}{ll}
4 & 3 \\
4 & 6
\end{array}\right]\)
(c) \(\left[\begin{array}{ll}
6 & 2 \\
8 & 6
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
7 & 6 \\
8 & 12
\end{array}\right]\)
Answer:
(b) \(\left[\begin{array}{ll}
4 & 3 \\
4 & 6
\end{array}\right]\)

Question 8.
If \(\left[\begin{array}{cc}
x & 3 x-y \\
z x+z & 3 y-w
\end{array}\right]=\left[\begin{array}{ll}
3 & 2 \\
4 & 7
\end{array}\right]\), then ___________
(a) x = 3, y = 7, z = 1, w = 14
(b) x = 3, y = -5, z = -1, w = -4
(c) x = 3, y = 6, z = 2, w = 7
(d) x = -3, y = -7, z = -1, w = -14
Answer:
(a) x = 3, y = 7, z = 1, w = 14

Question 9.
For suitable matrices A, B, the false statement is ___________
(a) (AB)^T = A^TB^T
(B) (A^T)^T = A
(C) (A – B)^T = A^T – B^T
(D) (A + B)^T = A^T + B^T
Answer:
(a) (AB)^T = A^TB^T
Hint:
(AB)^T = B^TA^T

Question 10.
If A = \(\left[\begin{array}{cc}
-2 & 1 \\
0 & 3
\end{array}\right]\) and f(x) = 2x² – 3x, then f(A) = ___________
(a) \(\left[\begin{array}{cc}
14 & 1 \\
0 & -9
\end{array}\right]\)
(b) \(\left[\begin{array}{cc}
-14 & 1 \\
0 & 9
\end{array}\right]\)
(c) \(\left[\begin{array}{cc}
14 & -1 \\
0 & 9
\end{array}\right]\)
(d) \(\left[\begin{array}{cc}
-14 & -1 \\
0 & -9
\end{array}\right]\)
Answer:
(c) \(\left[\begin{array}{cc}
14 & -1 \\
0 & 9
\end{array}\right]\)
Hint:

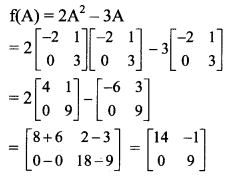
(II) Answer the following questions.

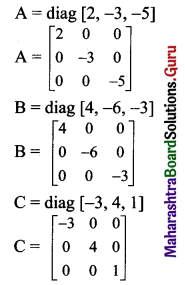
Question 1.
If A = diag[2, -3, -5], B = diag[4, -6, -3] and C = diag [-3, 4, 1], then find
i. B + C – A
ii. 2A + B – 5C.
Solution:

Question 2.
If f(α) = A = \(\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\), find
i. f(-α)
ii. f(-α) + f(α)
Solution:

Question 3.
Find matrices A and B, where
(i) 2A – B = \(\left[\begin{array}{cc}
1 & -1 \\
0 & 1
\end{array}\right]\) and A + 3B = \(\left[\begin{array}{cc}
1 & -1 \\
0 & 1
\end{array}\right]\)
(ii) 3A – B = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 0 & 5
\end{array}\right]\) and A + 5B = \(\left[\begin{array}{ccc}
0 & 0 & 1 \\
-1 & 0 & 0
\end{array}\right]\)
Solution:
i. Given equations are
2A – B = \(\left[\begin{array}{cc}
1 & -1 \\
0 & 1
\end{array}\right]\) …….(i)

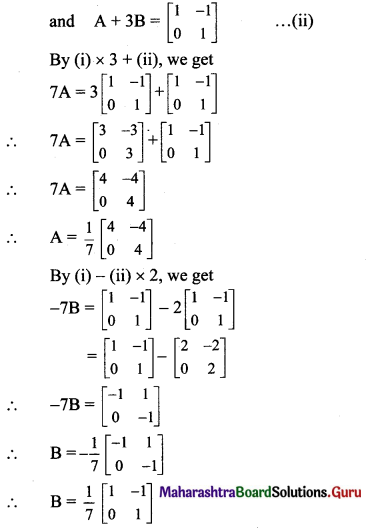
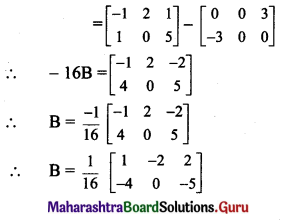
Question 4.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & -2 \\
-1 & 4
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
-3 & 4 & 1 \\
2 & -1 & -3
\end{array}\right]\), verify
i. (A + 2B^T)^T = A^T + 2B
ii. (3A – 5B^T)^T = 3A^T – 5B.
Solution:

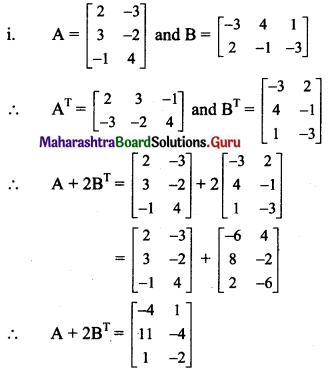
Question 5.
If A = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) and A + A^T = I, where I is a unit matrix of order 2 × 2, then find the value of α.
Solution:

Question 6.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & 2 \\
-1 & 0
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
1 & 3 & 2 \\
4 & -1 & -3
\end{array}\right]\), show that AB is singular.
Solution:

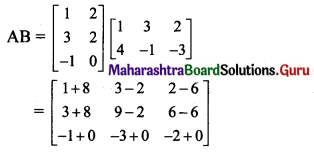
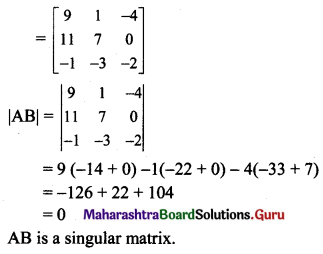
Question 7.
If A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
2 & 4 & 6 \\
1 & 2 & 3
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
-3 & 2 & -1 \\
-2 & 1 & 0
\end{array}\right]\), show that AB and BA are both singular matrices.
Solution:

Question 8.
If A = \(\left[\begin{array}{ccc}
1 & -1 & 0 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
2 & 2 & -4 \\
-4 & 2 & -4 \\
2 & -1 & 5
\end{array}\right]\), show that BA = 6I.
Solution:

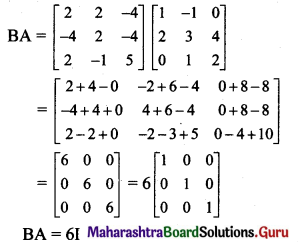
Question 9.
If A = \(\left[\begin{array}{ll}
2 & 1 \\
0 & 3
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -2
\end{array}\right]\), verify that |AB| = |A|.|B|.
Solution:

Question 10.
If Aα = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that Aα . Aβ = Aα+β
Solution:

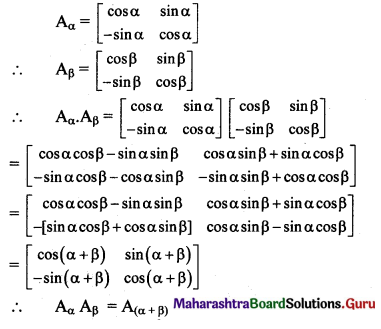
Question 11.
If A = \(\left[\begin{array}{cc}
1 & \omega \\
\omega^{2} & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
\omega^{2} & 1 \\
1 & \omega
\end{array}\right]\), where ω is a complex cube root of unity, then show that AB + BA + A – 2B is a null matrix.
Solution:
ω is the complex cube root of unity.
ω³ = 1
ω³ – 1 = 0
(ω – 1) (ω² + ω + 1) = 0
ω = 1 or ω² + ω + 1 = 0
But, ω is a complex number.
1 + ω + ω² = 0 …….(i)
AB + BA + A – 2B

which is a null matrix.

Question 12.
If A = \(\left[\begin{array}{lrr}
2 & -2 & -4 \\
-1 & 3 & 4 \\
1 & -2 & -3
\end{array}\right]\), show that A² = A.
Solution:

Question 13.
If A = \(\left[\begin{array}{ccc}
4 & -1 & -4 \\
3 & 0 & -4 \\
3 & -1 & -3
\end{array}\right]\), show that A² = I.
Solution:

Question 14.
If A = \(\left[\begin{array}{cc}
3 & -5 \\
-4 & 2
\end{array}\right]\), show that A² – 5A – 14I = 0.
Solution:

Question 15.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
-1 & 2
\end{array}\right]\), show that A – 4A + 3I = 0.
Solution:

Question 16.
If A = \(\left[\begin{array}{cc}
-3 & 2 \\
2 & -4
\end{array}\right]\), B = \(\left[\begin{array}{ll}
1 & x \\
y & 0
\end{array}\right]\) and (A + B)(A – B) = A² – B², find x and y.
Solution:
(A + B)(A – B) = A² – B²
A² – AB + BA – B² = A² – B²
-AB + BA = 0
AB = BA

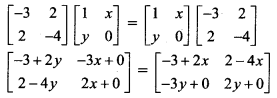
By equality of matrices, we get
2 – 4x = -3x
∴ x = 2 and 2y = 2x
y = x
∴ y = 2
∴ x = 2, y = 2

Question 17.
If A = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\), show that (A + B)(A – B) ≠ A² – B².
Solution:
We have to prove that
(A + B) . (A – B) ≠ A² – B²
i.e., to prove that A(A – B) + B(A – B) ≠ A² – B²
i.e., to prove that A² – AB + BA – B² ≠ A² – B²
i.e., to prove that AB ≠ BA.

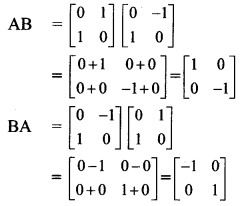
∴ AB ≠ BA

Question 18.
If A = \(\left[\begin{array}{ll}
2 & -1 \\
3 & -2
\end{array}\right]\), find A³.
Solution:

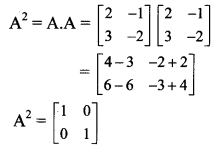
∴ A² = I
Multiplying throughout by A, we get
A³ = A . I
∴ A³ = A

Question 19.
Find x, y if,

Solution:

Question 20.
Find x, y, z if

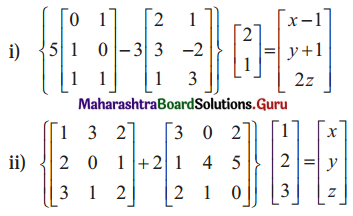
Solution:

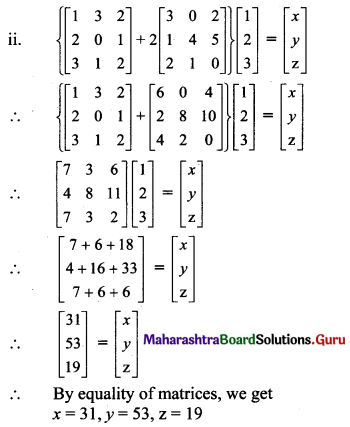
Question 21.
If A = \(\left[\begin{array}{ccc}
2 & 1 & -3 \\
0 & 2 & 6
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & 0 & -2 \\
3 & -1 & 4
\end{array}\right]\), find AB^T and A^TB.
Solution:

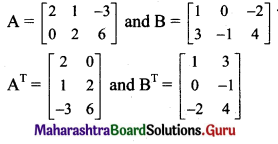
Question 22.
If A = \(\left[\begin{array}{cc}
2 & -4 \\
3 & -2 \\
0 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 1 & 0
\end{array}\right]\), show that (AB)^T = B^TA^T.
Solution:

Question 23.
If A = \(\left[\begin{array}{ll}
3 & -4 \\
1 & -1
\end{array}\right]\), prove that Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), for all n ∈ N.
Solution:

Question 24.
If A = \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\), prove that Aⁿ = \(\left[\begin{array}{cc}
\cos n \theta & \sin n \theta \\
-\sin n \theta & \cos n \theta
\end{array}\right]\), for all n ∈ N.
Solution:

Question 25.
Two farmers Shantaram and Kantaram cultivate three crops rice, wheat, and groundnut. The sale (in Rupees) of these crops by both the farmers for the month of April and may 2008 is given below,

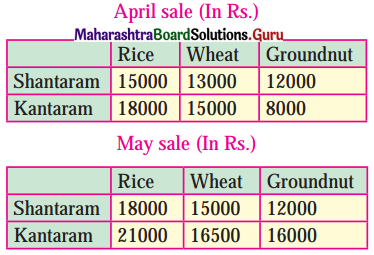
Find
(i) the total sale in rupees for two months of each farmer for each crop.
(ii) the increase in sales from April to May for every crop of each farmer.
Solution:
(i) Total sale for Shantaram:
For rice = 15000 + 18000 = ₹ 33000.
For wheat = 13000 + 15000 = ₹ 28000.
For groundnut = 12000 + 12000 = ₹ 24000.
Total sale for Kantaram:
For rice = 18000 + 21000 = ₹ 39000
For wheat = 15000 + 16500 = ₹ 31500
For groundnut = 8000 + 16000 = ₹ 24000

Alternate method:
Matrix form

∴ The total sale of April and May of Shantaram in ₹ is ₹ 33000 (rice), ₹ 28000 (wheat), ₹ 24000 (groundnut), and that of Kantaram in ₹ is ₹ 39000(rice), ₹ 31500(wheat), and ₹ 24000 (groundnut).

(ii) Increase in sale from April to May for Shantaram:
For rice = 18000 – 15000 = ₹ 3000
For wheat = 15000 – 13000 = ₹ 2000
For groundnut = 12000 – 12000 = ₹ 0
Increase in sale from April to May for Kantaram:
For rice = 21000 – 18000 = ₹ 3000
For wheat = 16500 – 15000 = ₹ 1500
For groundnut = 16000 – 8000 = ₹ 8000

Alternate method:
Matrix form

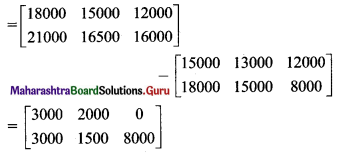
∴ The increase in sales for Shantaram from April to May in each crop is ₹ 3000 (rice), ₹ 2000(wheat), 0 (groundnut), and that for Kantaram is ₹ 3000 (rice), ₹ 1500 (wheat), and ₹ 8000 (groundnut).