Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.7 Questions and Answers.
11th Maths Part 1 Determinants and Matrices Exercise 4.7 Questions And Answers Maharashtra Board
Question 1.
Find AT, if
i. A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
ii. A = \(\left[\begin{array}{ccc}
2 & -6 & 1 \\
-4 & 0 & 5
\end{array}\right]\)
Solution:
i. A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
∴ AT = \(\left[\begin{array}{rr}
1 & -4 \\
3 & 5
\end{array}\right]\)
![]()
ii. A = \(\left[\begin{array}{ccc}
-4 & 0 & 5
2 & -6 & 1 \\
\end{array}\right]\)
∴ AT = \(\left[\begin{array}{cc}
2 & -4 \\
-6 & 0 \\
1 & 5
\end{array}\right]\)
[Note: Answer given in the textbook is AT = \(\left[\begin{array}{cc}
2 & -4 \\
6 & 0 \\
1 & 5
\end{array}\right]\). However, as per our calculation it is AT = \(\left[\begin{array}{cc}
2 & -4 \\
-6 & 0 \\
1 & 5
\end{array}\right]\). ]
Question 2.
If [aij]3×3 where aij = 2(i – j), find A and
AT. State whether A and AT are symmetric or skew-symmetric matrices?
Solution:
A = [aij]3×3 = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
Given aij = 2 (i — j)
∴ a11 = 2(1-1) = 0,
a12 = 2(1-2) = -2,
a13 = 2(1-3) = -4,
a21 = 2(2-1) = 2,
a22 = 2(2-2) = 0,
a23=2(2-3) = -2,
a31 = 2(3-1) = 4,
a32 = 2(3-2) = 2,
a33=2(3-3) = 0
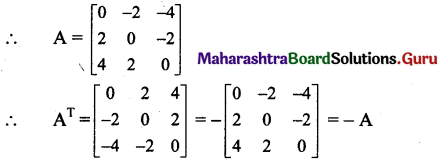
∴ AT = -A and A = -AT
∴ A and AT both are skew-symmetric matrices.
Questionn 3.
If A = \(\left[\begin{array}{cc}
5 & -3 \\
4 & -3 \\
-2 & 1
\end{array}\right]\), prove that (2A)T = 2AT.
Solution:
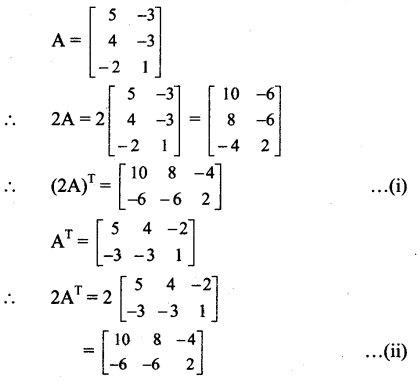
From (i) and (ii), we get
(2A)T = 2AT
![]()
Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\), prove that (3A)T = 3AT.
Solution:

From (i) and (ii), we get
(3A)T = 3AT
Question 5.
If A = \(\left[\begin{array}{ccc}
0 & 1+2 i & 1-2 \\
-1-2 i & 0 & -7 \\
2-i & 7 & 0
\end{array}\right]\),
where i = \(\sqrt{-1}\), prove that AT = – A.
Solution:
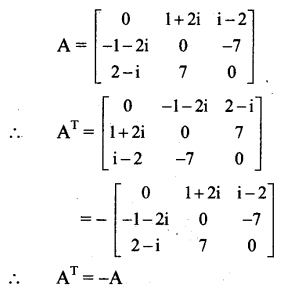
Question 6.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\) , B = \(\left[\begin{array}{cc}
2 & 1 \\
4 & -1 \\
-3 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 4 \\
-2 & 3
\end{array}\right]\) then show that
i. (A + B)T = AT + BT
ii. (A – C)T = AT – CT
Solution:
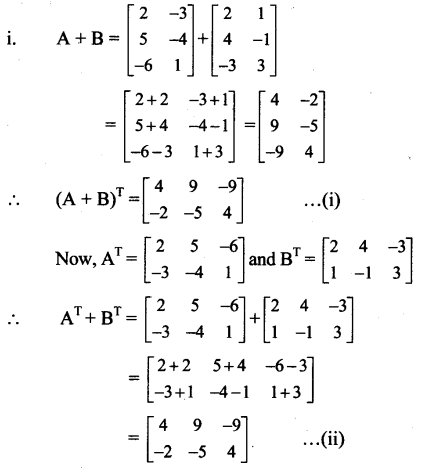
From (i) and (ii), we get
(A + B)T = AT + BT
[Note: The question has been modified.]

From (i) and (ii), we get
(A – C)T = AT – CT</sup
![]()
Question 7.
If A = \(\left[\begin{array}{cc}
5 & 4 \\
-2 & 3
\end{array}\right]\) and \(\left[\begin{array}{cc}
-1 & 3 \\
4 & -1
\end{array}\right]\) then find CT, such that 3A – 2B + C = I, where I is the unit matrix of order 2.
Solution:
3A – 2B + C = I
∴ C = I + 2B – 3A
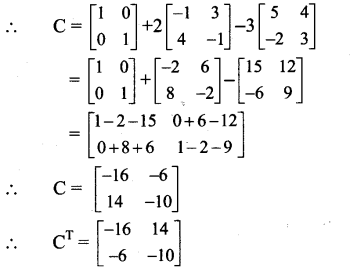
Question 8.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 0 \\
0 & 4 & -2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
0 & -2 & 3 \\
2 & 1 & -4
\end{array}\right]\), then find
i. AT + 4BT
ii. 5AT – 5BT
Solution:
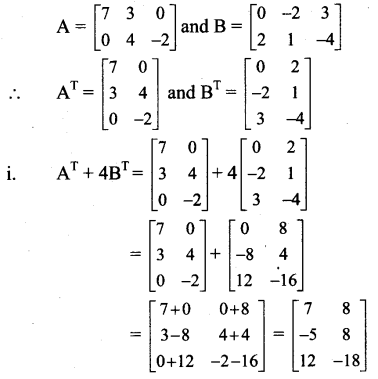
ii. ii. 5AT – 5BT = 5(AT – BT)
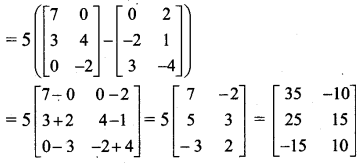
Question 9.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{rrr}
2 & 1 & -4 \\
3 & 5 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
0 & 2 & 3 \\
-1 & -1 & 0
\end{array}\right]\), verify that (A + 2B + 3C)T = AT + 2BT + 3CT.
Solution:
A + 2B + 3C

∴ AT + 2BT + 3CT = \(\left[\begin{array}{cc}
5 & 6 \\
8 & 8 \\
2 & -2
\end{array}\right]\)
From (i) and (ii), we get
(A + 2B + 3C)T = AT + 2BT + 3CT
![]()
Question 10.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
-3 & 2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-3 & 2 \\
-1 & 3
\end{array}\right]\), prove that (A + BT)T = AT + B.
prove that (A + BT)T = AT + B
Solution:
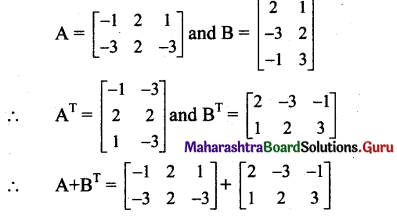
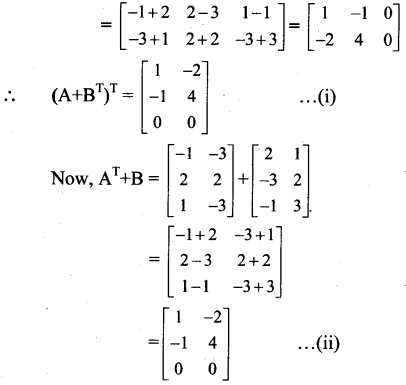
From (i) and (ii), we get
(A + BT)T = AT + B
Question 11.
Prove that A + AT is a symmetric and A – AT is a skew symmetric matrix, where
i. A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 2 & 1 \\
-2 & -3 & 2
\end{array}\right]\)
ii. A = \(\left[\begin{array}{ccc}
5 & 2 & -4 \\
3 & -7 & 2 \\
4 & -5 & -3
\end{array}\right]\)
Solution:

∴ (A + AT)T = A + AT, i.e., A + AT = (A + AT)T
∴ A + AT is a symmetric matrix.
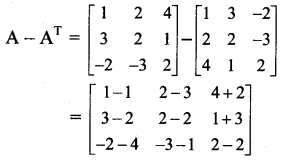
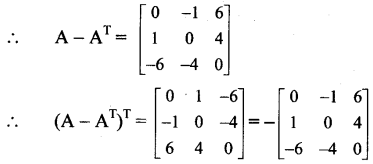
∴ (A – AT)T = – (A – AT),
i.e., A – AT = -(A – AT)T
∴ A – AT is skew symmetric matrix.
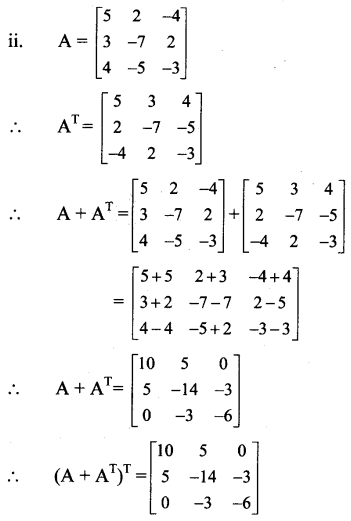
∴ (A + AT)T = A + AT, i.e., A + AT = (A + AT)T
∴ A + AT is a symmetric matrix.
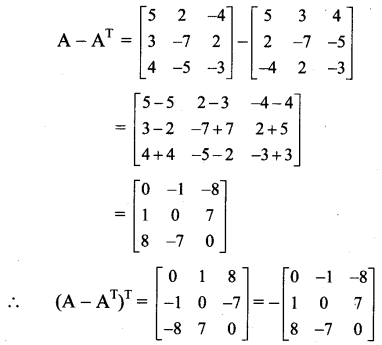
∴ (A – AT)T = – (A – AT),
i.e., A – AT = -(A – AT)T
∴ A – AT is skew symmetric matrix.
![]()
Question 12.
Express the following matrices as the sum of a symmetric and a skew symmetric matrix.
i. \(\left[\begin{array}{cc}
4 & -2 \\
3 & -5
\end{array}\right]\)
ii. \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
Solution:
A square matrix A can be expressed as the sum of a symmetric and a skew symmetric matrix as
A = \(\frac{1}{2}\) (A + AT) + \(\frac{1}{2}\) (A – AT)

P is symmetric matrix …[∵ aij = aji]
and Q is a skew symmetric matrix [∵ -aij = -aji]
A = P + Q
A = \(\left[\begin{array}{cc}
4 & \frac{1}{2} \\
\frac{1}{2} & -5
\end{array}\right]+\left[\begin{array}{ll}
0 & \frac{-5}{2} \\
\frac{5}{2} & 0
\end{array}\right]\)


∴ P is symmetric matrix …[∵ aij = aji]
and Q is a skew symmetric matrix [∵ -aij = -aji]
∴ A = P + Q
∴ A = \(\left[\begin{array}{cc}
4 & \frac{1}{2} \\
\frac{1}{2} & -5
\end{array}\right]+\left[\begin{array}{ll}
0 & \frac{-5}{2} \\
\frac{5}{2} & 0
\end{array}\right]\)
Question 13.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
3 & -2 \\
4 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
0 & 3 & -4 \\
2 & -1 & 1
\end{array}\right]\), verify that
i. (AB)T = BTAT
ii. (BA)T = ATBT
Solution:


From (i) and (ii), we get
(AB)T = BTAT

From (i) and (ii) we get
(BA)T = ATBT
![]()
Question 14.
If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), show that ATA = I, where I is the unit matrix of order 2.
Solution:
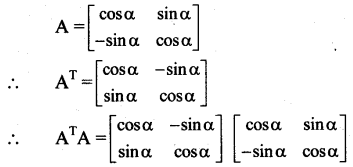

∴ ATA = I, where I is the unit matrix of order 2.
Class 11 Maharashtra State Board Maths Solution