Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.4 Questions and Answers.
11th Maths Part 1 Determinants and Matrices Exercise 4.4 Questions And Answers Maharashtra Board
Question 1.
Construct a matrix A = [aij]3 x 2 whose elements ay are given by
i. aij = \(\frac{(\mathbf{i}-\mathbf{j})^{2}}{5-\mathbf{i}}\)
ii. aij = i – 3j
iii. aij \(\frac{(i+j)^{3}}{5}\)
Solution:

[Note: Answer given in the textbook is A = \(\left[\begin{array}{ll}
0 & \frac{1}{4} \\
\frac{1}{2} & 0 \\
2 & \frac{1}{2}
\end{array}\right]\)
However, as per our calculation it is \(\left[\begin{array}{ll}
0 & \frac{1}{4} \\
\frac{1}{3} & 0 \\
2 & \frac{1}{2}
\end{array}\right]\) ].
![]()
ii. aij = i – 3j
∴ a11 = 1 – 3(1) = 1 – 3 = -2,
a12= 1 – 3(2) = 1 – 6 = -5,
a21 = 2 – 3(1) = 2 – 3 =-1,
a22 = 2 – 3(2) = 2 – 6 = – 4
a31 = 3 – 3(1) = 3-3 = 0,
a32 = 3 – 3(2) = 3 – 6 = -3
∴ A = \(\left[\begin{array}{cc}
-2 & -5 \\
-1 & -4 \\
0 & -3
\end{array}\right]\)
iii. aij = \(\frac{(i+j)^{3}}{5}\)

Question 2.
Classify the following matrices as a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew- symmetric matrix.
i. \(\left[\begin{array}{ccc}
3 & -2 & 4 \\
0 & 0 & -5 \\
0 & 0 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
3 & -2 & 4 \\
0 & 0 & -5 \\
0 & 0 & 0
\end{array}\right]\)
As every element below the diagonal is zero in matrix A.
∴ A is an upper triangular matrix.
ii. \(\left[\begin{array}{ccc}
0 & 4 & 7 \\
-4 & 0 & -3 \\
-7 & 3 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
0 & 4 & 7 \\
-4 & 0 & -3 \\
-7 & 3 & 0
\end{array}\right]\)
∴ AT = \(\left[\begin{array}{ccc}
0 & -4 & -7 \\
4 & 0 & 3 \\
7 & -3 & 0
\end{array}\right]\)
∴ AT = \(-\left[\begin{array}{ccc}
0 & 4 & 7 \\
-4 & 0 & -3 \\
-7 & 3 & 0
\end{array}\right]\)
∴ AT = -A, i.e., A = -AT
∴ A is a skew-symmetric matrix.
![]()
iii. \(\left[\begin{array}{c}
5 \\
4 \\
-3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{c}
5 \\
4 \\
-3
\end{array}\right]\)
∴ As matrix A has only one column.
∴ A is a column matrix.
iv. \(\left[\begin{array}{lll}
9 & \sqrt{2} & -3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
9 & \sqrt{2} & -3
\end{array}\right]\)
As matrix A has only one row.
∴ A is a row matrix.
v. \(\left[\begin{array}{ll}
6 & 0 \\
0 & 6
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
6 & 0 \\
0 & 6
\end{array}\right]\)
As matrix A has all its non-diagonal elements zero and diagonal elements same.
∴ A is a scalar matrix.
vi. \(\left[\begin{array}{ccc}
2 & 0 & 0 \\
3 & -1 & 0 \\
-7 & 3 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
2 & 0 & 0 \\
3 & -1 & 0 \\
-7 & 3 & 1
\end{array}\right]\)
As every element above the diagonal is zero in matrix A.
∴ A is a lower triangular matrix.
vii. \(\left[\begin{array}{ccc}
3 & 0 & 0 \\
0 & 5 & 0 \\
0 & 0 & \frac{1}{3}
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
3 & 0 & 0 \\
0 & 5 & 0 \\
0 & 0 & \frac{1}{3}
\end{array}\right]\)
As matrix A has all its non-diagonal elements zero.
∴ A is a diagonal matrix.
![]()
viii. \(\left[\begin{array}{ccc}
10 & -15 & 27 \\
-15 & 0 & \sqrt{34} \\
27 & \sqrt{34} & \frac{5}{3}
\end{array}\right]\)
Solution:
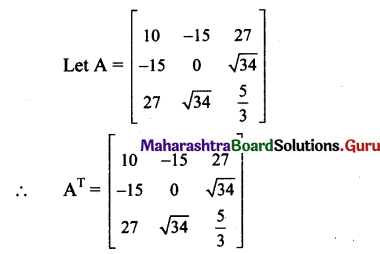
∴ AT = A, i/e., A = AT
∴ A is a symmetric matrix.
ix. \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
Solution:
A = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
In matrix A, all the non-diagonal elements are zero and diagonal elements are one.
∴ A is a unit (identity) matrix.
x. \(\left[\begin{array}{lll}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{array}\right]\)
∴ AT = A, i/e., A = AT
∴ A is a symmetric matrix.
∴ A is a symmetric matrix.
Question 3.
Which of the following matrices are singular or non-singular?
i. \(\left[\begin{array}{ccc}
\mathbf{a} & \mathbf{b} & \mathbf{c} \\
\mathbf{p} & \mathbf{q} & \mathbf{r} \\
\mathbf{2 a}-\mathbf{p} & \mathbf{2 b}-\mathbf{q} & \mathbf{2 c}-\mathbf{r}
\end{array}\right]\)
ii. \(\left[\begin{array}{ccc}
5 & 0 & 5 \\
1 & 99 & 100 \\
6 & 99 & 105
\end{array}\right]\)
iii. \(\left[\begin{array}{ccc}
3 & 5 & 7 \\
-2 & 1 & 4 \\
3 & 2 & 5
\end{array}\right]\)
iv. \(\left[\begin{array}{cc}
7 & 5 \\
-4 & 7
\end{array}\right]\)
Solution:

![]()
ii. Let A = \(\left[\begin{array}{ccc}
5 & 0 & 5 \\
1 & 99 & 100 \\
6 & 99 & 105
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ccc}
5 & 0 & 5 \\
1 & 99 & 100 \\
6 & 99 & 105
\end{array}\right|\)
Applying C2 → C2 + C1
|A| = \(\left|\begin{array}{ccc}
5 & 5 & 5 \\
1 & 100 & 100 \\
6 & 105 & 105
\end{array}\right|\)
= 0 … [∵ C2 and C3 are identical]
∴ A is a singular matrix.
iii. Let A = \(\left[\begin{array}{ccc}
3 & 5 & 7 \\
-2 & 1 & 4 \\
3 & 2 & 5
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ccc}
3 & 5 & 7 \\
-2 & 1 & 4 \\
3 & 2 & 5
\end{array}\right| \)
= 3(5 – 8) – 5(-10 – 12) + 7(-4 – 3)
= -9 + 110 – 49 = 52 ≠ 0
∴ A is a non-singular matrix.
iv. Let A = \(\left[\begin{array}{cc}
7 & 5 \\
-4 & 7
\end{array}\right]\)
∴ |A| = \(\left[\begin{array}{cc}
7 & 5 \\
-4 & 7
\end{array}\right]\) = 49 + 20 = 69 ≠ 0
Question 4.
Find k, if the following matrices are singular.
i. \(\left[\begin{array}{cc}
7 & 3 \\
-2 & k
\end{array}\right]\)
ii. \(\left[\begin{array}{ccc}
4 & 3 & 1 \\
7 & k & 1 \\
10 & 9 & 1
\end{array}\right]\)
iii. \(\left[\begin{array}{ccc}
k-1 & 2 & 3 \\
3 & 1 & 2 \\
1 & -2 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
7 & 3 \\
-2 & k
\end{array}\right]\)
Since A is a singular matrix,
|A|=0
∴ \(\left|\begin{array}{cc}
7 & 3 \\
-2 & \mathrm{k}
\end{array}\right|\) = o
∴ 7k + 6 = 0
∴ 7k = -6
k = -6/7
ii. Let A = \(\left[\begin{array}{ccc}
4 & 3 & 1 \\
7 & k & 1 \\
10 & 9 & 1
\end{array}\right]\)
Since A is a singular matrix,
|A|= 0
∴ \(\left|\begin{array}{ccc}
4 & 3 & 1 \\
7 & \mathrm{k} & 1 \\
10 & 9 & 1
\end{array}\right|\) = 0
∴ 4(k – 9) – 3(7 – 10) + 1(63 – 10k) = 0
∴ 4k – 36 + 9 + 63 – 10k = 0
∴ -6k + 36 = 0
∴ 6k = 36
∴ k = 6
iii. Let A = \(\left[\begin{array}{ccc}
\mathbf{k}-1 & 2 & 3 \\
3 & 1 & 2 \\
1 & -2 & 4
\end{array}\right]\)
Since A is a singular matrix
|A| = 0
∴ \(\left|\begin{array}{ccc}
k-1 & 2 & 3 \\
3 & 1 & 2 \\
1 & -2 & 4
\end{array}\right|\)
∴ (k – 1)(4 + 4) – 2(12 – 2) + 3 (-6 – 1) = 0
∴ 8k-8-20-21 =0
∴ 8k = 49
∴ k = 49/8
![]()
Question 5.
If A = \(\left[\begin{array}{lll}
5 & 1 & -1 \\
3 & 2 & 0
\end{array}\right]\), find (AT)T.
Solution:
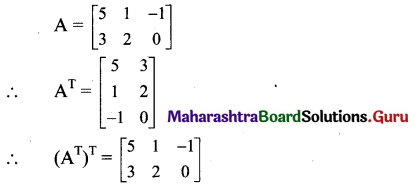
Question 6.
If A = \(\), find (AT)T.
Solution:
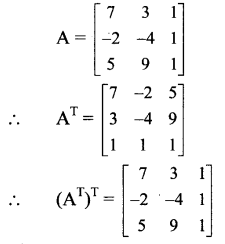
Question 7.
Find a, b, c, if \(\left[\begin{array}{ccc}
1 & \frac{3}{5} & a \\
b & -5 & -7 \\
-4 & c & 0
\end{array}\right]\) is a symmetric matrix.
Solution:

Question 8.
Find x, y, z, if \(\) is a symmetric matrix.
Solution:
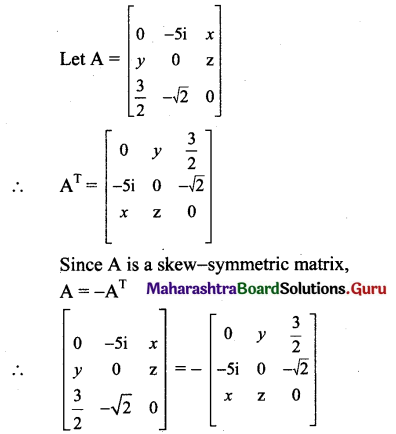
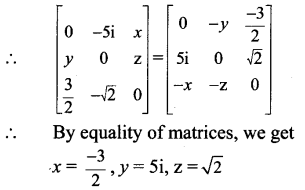
Question 9.
For each of the following matrices, using its transpose, state whether it is symmetric, skew-symmetric or neither.
i. \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\)
ii. \(\left[\begin{array}{ccc}
2 & 5 & 1 \\
-5 & 4 & 6 \\
-1 & -6 & 3
\end{array}\right]\)
iii. \(\left[\begin{array}{ccc}
0 & 1+2 \mathbf{i} & \mathbf{i}-2 \\
-1-2 \mathbf{i} & 0 & -7 \\
2-\mathbf{i} & 7 & 0
\end{array}\right]\)
Solution:
i. Let A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\)
∴ AT =\(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\)
∴ AT = A, i.e., A = AT
∴ A is a symmetric matrix.
ii.
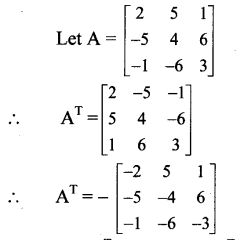
∴ A ≠ AT, i.e., A ≠ -AT
∴ A is neither a symmetric nor skew-symmetric matrix.
![]()
iii.
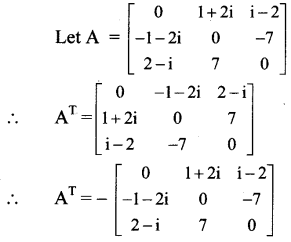
∴ AT = -A, i.e., A = -AT
∴ A is a skew-symmetric matrix.
Question 10.
Construct the matrix A = [aij]3 x 3, where aij = i – j. State whether A is symmetric or skew-symmetric.
Solution:
A = [aij]3 x 3
∴ A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\)
Given, aij = i – j
a11 = 1-1 = 0, a12 = 1-2 = – 1, a13 = 1 – 3 = – 2,
a21 – 2 – 1 = 1, a22 = 2 – 2 = 0, a23 =2 – 3 = – 1,
a31 = 3 – 1 = 2, a32 = 3 – 2 = 1, a33 = 3 – 3 = 0
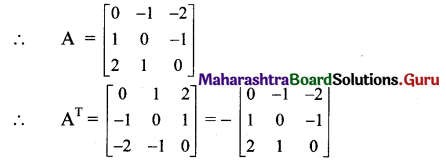
∴ AT = -A, i.e., A = -AT
∴ A is a skew-symmetric matrix.
Class 11 Maharashtra State Board Maths Solution