Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.4 Questions and Answers.
11th Maths Part 2 Methods of Induction and Binomial Theorem Exercise 4.4 Questions And Answers Maharashtra Board
Question 1.
State, by writing the first four terms, the expansion of the following, where |x| < 1.
(i) (1 + x)-4
Solution:

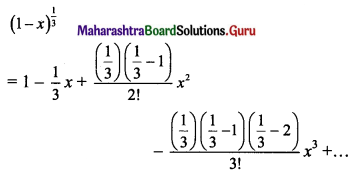
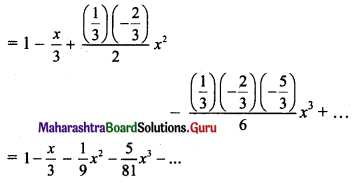
(ii) (1 – x)1/3
Solution:
(iii) (1 – x2)-3
Solution:

(iv) (1 + x)-1/5
Solution:

(v) (1 + x2)-1
Solution:

![]()
Question 2.
State by writing first four terms, the expansion of the following, where |b| < |a|.
(i) (a – b)-3
Solution:
(a – b)-3 = \(\left[a\left(1-\frac{b}{a}\right)\right]^{-3}\)
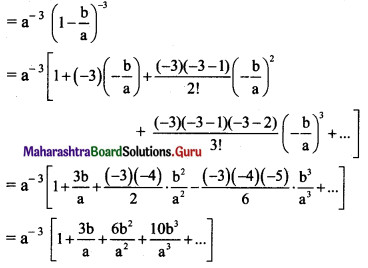
(ii) (a + b)-4
Solution:

(iii) (a + b)1/4
Solution:

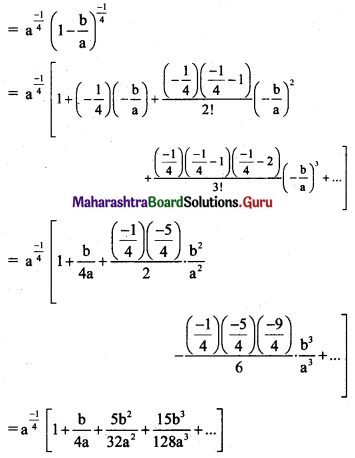
(iv) (a – b)-1/4
Solution:
(a – b)-1/4 = \(\left[a\left(1-\frac{b}{a}\right)\right]^{\frac{-1}{4}}\)
(v) (a + b)-1/3
Solution:

![]()
Question 3.
Simplify the first three terms in the expansion of the following:
(i) (1 + 2x)-4
Solution:

(ii) (1 + 3x)-1/2
Solution:

(iii) (2 – 3x)1/3
Solution:

(iv) (5 + 4x)-1/2
Solution:
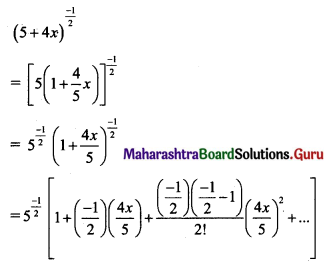
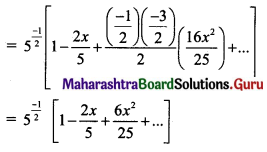
(v) (5 – 3x)-1/3
Solution:

![]()
Question 4.
Use the binomial theorem to evaluate the following upto four places of decimals.
(i) √99
Solution:

= 10 [1 – 0.005 – 0.0000125 – ……]
= 10(0.9949875)
= 9.94987 5
= 9.9499
(ii) \(\sqrt[3]{126}\)
Solution:

(iii) \(\sqrt[4]{16.08}\)
Solution:

(iv) (1.02)-5
Solution:

(v) (0.98)-3
Solution:

Class 11 Maharashtra State Board Maths Solution