Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 1 Angle and its Measurement Miscellaneous Exercise 1 Questions and Answers.
11th Maths Part 1 Angle and its Measurement Miscellaneous Exercise 1 Questions And Answers Maharashtra Board
I. Select the correct option from the given alternatives.
Question 1.
\(\left(\frac{22 \pi}{15}\right)^{c}x\) is equal to
(A) 246°
(B) 264°
(C) 224°
(D) 426°
Answer:
(B) 264°
![]()
Question 2.
156° is equal to

Answer:
(B)
Question 3.
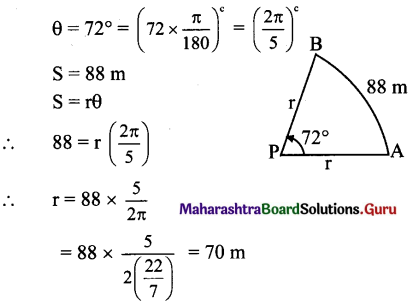
A horse is tied to a post by a rope. If the horse moves along a circular path, always keeping the rope tight and describes 88 metres when it traces the angle of 12° at the centre, then the length of the rope is
(A) 70 m
(B) 55 m
(C) 40 m
(D) 35 m
Answer:
(A) 70 m
Question 4.
A pendulum 14 cm long oscillates through an angle of 12°, then the angle of the path described by its extremities is
![]()
![]()
Answer:
(D)
![]()
Question 5.
Angle between hands of a clock when it shows the time 9 :45 is
(A) (7.5)°
(B) (12.5)°
(C) (17.5)°
(D) (22.5)°
Answer:
(D) (22.5)°
Question 6.
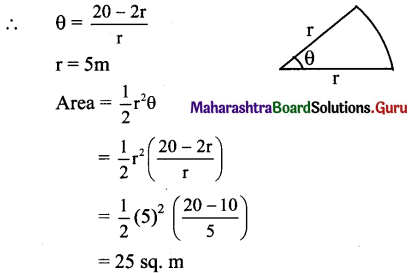
20 metres of wire is available for fencing off a flower-bed in the form of a circular sector of radius 5 metres, then .the maximum area (in sq. m.) of the flower-bed is
(A) 15
(B) 20
(C) 25
(D) 30
Answer:
(C) 25
r + r + rθ = 20m
2r + rθ = 20

Question 7.
If the angles of a triangle are in the ratio 1:2:3, then the smallest angle in radian is
(A) \(\frac{\pi}{3}\)
(B) \(\frac{\pi}{6}\)
(C) \(\frac{\pi}{2}\)
(D) \(\frac{\pi}{9}\)
Answer:
(B) \(\frac{\pi}{6}\)
Question 8.
A semicircle is divided into two sectors whose angles are in the ratio 4:5. Find the ratio of their areas?
(A) 5:1
(B) 4:5
(C) 5:4
(D) 3:4
Answer:
(B) 4:5
![]()
Question 9.
Find the measure of the angle between hour- hand and the minute hand of a clock at twenty minutes past two.
(A) 50°
(B) 60°
(C) 54°
(D) 65°
Answer:
(A) 50°
Question 10.
The central angle of a sector of circle of area 9π sq.cm is 60°, the perimeter of the sector is
(A) π
(B) 3 + π
(C) 6 + π
(D) 6
Answer:
(C) 6 + π
II. Answer the following.
Question 1.
Find the number of sides of a regular polygon, if each of its interior angles is \(\frac{3 \pi^{c}}{4}\).
Solution:
Each interior angle of a regular polygon
= \(\frac{3 \pi}{4}=\left(\frac{3 \pi}{4} \times \frac{180}{\pi}\right)^{\circ}\) = 135°
Interior angle + Exterior angle = 180°
∴ Exterior angle = 180° – 135° = 45°
Let the number of sides of the regular polygon be n.
But in a regular polygon, exterior angle = \(\frac{360^{\circ}}{\text { no.of sides }}\)
∴ 45° = \(\frac{360^{\circ}}{\mathrm{n}}\)
∴ n = \(\frac{360^{\circ}}{45^{\circ}}\) = 8
∴ Number of sides of a regular polygon = 8.
Question 2.
Two circles each of radius 7 cm, intersect each other. The distance between their centres is 7√2 cm. Find the area common to both the circles.
Solution:
Let O and O1 be the centres of two circles intersecting each other at A and B.
Then OA = OB = O1A = O1B = 7 cm
and OO1 = 7√2 cm
OO12 = 98 ………………(i)
Since OA2 + O1A2 = 72
= 98
= OO12 …..[ from (i)]
m∠OAO1 = 90°
□ OAO1B is a square.
m∠AOB = m∠AO1B = 90°
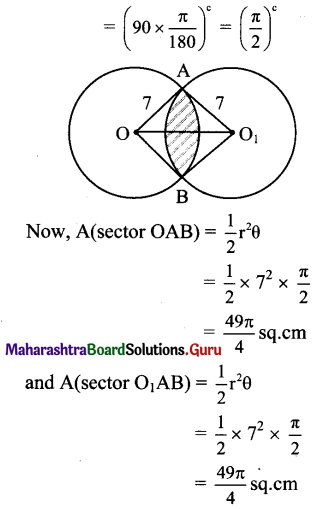
A(□ OAO1B) = (side)2 = (7)2 = 49 sq.cm
∴ Required area = area of shaded portion = A(sector OAB) + A(sector O1AB)) – A(□ OAO1B)
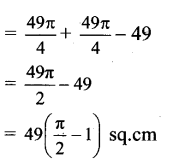
![]()
Question 3.
∆PQR is an equilateral triangle with side 18 cm. A circle is drawn on segment QR as diameter. Find the length of the arc of this circle within the triangle.
Solution:
Let ‘O’ be the centre of the circle drawn on QR as a diameter.
Let the circle intersect seg PQ and seg PR at points M and N respectively.
Since l(OQ) = l(OM),
m∠OM Q = m∠OQM = 60°
m∠MOQ = 60°
Similarly, m∠NOR = 60°
Given, QR =18 cm.
r = 9 cm
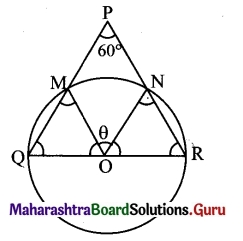
θ = 60° = (60 x \(\frac{\pi}{180}\))c
= \(\left(\frac{\pi}{3}\right)^{c}\)
∴ l(arc MN) = S = rθ = 9 x \(\frac{\pi}{3}\) = 3π cm.
Question 4.
Find the radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm.
Solution:
Let S be the length of the arc and r be the radius of the circle.
θ = 60° = \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
S = 37.4 cm
Since S = rθ,
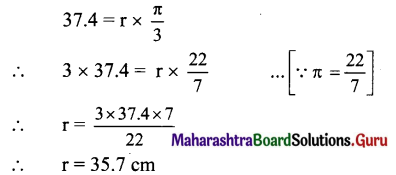
Question 5.
A wire of length 10 cm is bent so as to form an arc of a circle of radius 4 cm. What is the angle subtended at the centre in degrees?
Solution:
S = 10 cm and r = 4 cm
Since S = rθ,
10 = 4 x θ
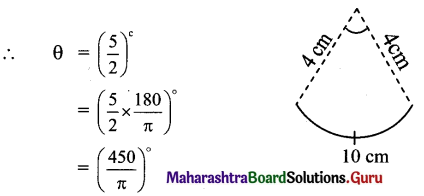
![]()
Question 6.
If two arcs of the same length in two circles subtend angles 65° and 110° at the centre. Find the ratio of their radii.
Solution:
Let r1 and r2 be the radii of the two circles and let their arcs of same length S subtend angles of 65° and 110° at their centres.
Angle subtended at the centre of the first circle,
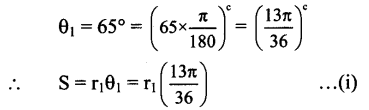
Angle subtended at the centre of the second circle,
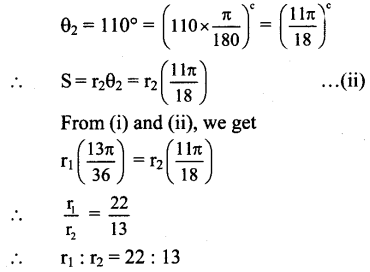
![]()
Question 7.
The area of a circle is 81TH sq.cm. Find the length of the arc subtending an angle of 300° at the centre and also the area of corresponding sector.
Solution:
Area of circle = πr2
But area is given to be 81 n sq.cm
∴ πr2 = 81π
∴ r2 = 81
∴ r = 9 cm
θ = 300° = \(=\left(300 \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(\frac{5 \pi}{3}\right)^{\mathrm{c}}\)
Since S = rθ
S = 9 x \(\frac{5 \pi}{3}\) = 15π cm
Area of sector = \(\frac{1}{2}\) x r x S
= \(\frac{1}{2}\) x 9 x 15π = \(\frac{135 \pi}{2}\) sq.cm
Question 8.
Show that minute-hand of a clock gains 5° 30′ on the hour-hand in one minute.
Solution:
Angle made by hour-hand in one minute
\(=\frac{360^{\circ}}{12 \times 60}=\left(\frac{1}{2}\right)^{\circ}\)
Angle made by minute-hand in one minute = \(\frac{360^{\circ}}{60}\) = 6°
∴ Gain by minute-hand on the hour-hand in one minute
= \(6^{\circ}-\left(\frac{1}{2}\right)^{\circ}=\left(5 \frac{1}{2}\right)^{\circ}\) = 5°30′
[Note: The question has been modified.]
Question 9.
A train is running on a circular track of radius 1 km at the rate of 36 km per hour. Find the angle to the nearest minute, through which it will turn in 30 seconds.
Solution:
r = 1km = 1000m
l(Arc covered by train in 30 seconds)
= 30 x \(\frac{36000}{60 \times 60}\)m
∴ S = 300 m
Since S = rθ,
300 = 1000 x θ
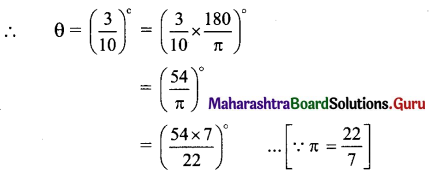
= (17.18)°
= 17° +(0.18)°
= 17° + (0.18 x 60)’ = 17° + (10.8)’
∴ θ = 17°11′(approx.)
![]()
Question 10.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Solution:
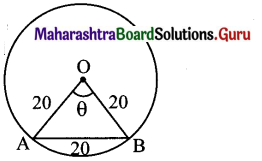
Let ‘O’ be the centre of the circle and AB be the chord of the circle.
Here, d = 40 cm
∴ r = \(\frac{40}{2}\) = 20 cm
Since OA = OB = AB,
∆OAB is an equilateral triangle.
The angle subtended at the centre by the minor
arc AOB is θ = 60° = \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
= l(minor arc of chord AB) = rθ = 20 x \(\frac{\pi}{3}\)
= \(\frac{20 \pi}{3}\) cm
Question 11.
The angles of a quadrilateral are in A.P. and the greatest angle is double the least. Find angles of the quadrilateral in radians.
Solution:
Let the measures of the angles of the quadrilateral in degrees be a – 3d, a – d, a + d, a + 3d, where a > d > 0
∴ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 360°
… [Sum of the angles of a quadrilateral is 360°]
∴ 4a = 360°
∴ a = 90°
According to the given condition, the greatest angle is double the least,
∴ a + 3d = 2.(a – 3d)
∴ 90° + 3d = 2.(90° – 3d)
∴ 90° + 3d = 180° – 6d 9d = 90°
∴ d = 10°
∴ The measures of the angles in degrees are
a – 3d = 90° – 3(10°) = 90° – 30° = 60°,
a – d = 90° – 10° = 80°,
a + d = 90°+ 10°= 100°,
a + 3d = 90° + 3(10°) = 90° + 30° = 120°

Class 11 Maharashtra State Board Maths Solution