Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 1 Angle and its Measurement Ex 1.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 1 Angle and its Measurement Ex 1.2
Question 1.
Find the length of an arc of a circle which subtends an angle of 108° at the centre, if the radius of the circle is 15 cm.
Solution:
Here, r = 15cm and
θ = 108° = \(\left(108 \times \frac{\pi}{180}\right)^{\mathrm{c}}=\left(\frac{3 \pi}{5}\right)^{\mathrm{c}}\)
Since S = r.θ
S = 15 x \(\frac{3 \pi}{5}\)
= 9π cm.
![]()
Question 2.
The radius of a circle is 9 cm. Find the length of an arc of this circle which cuts off a chord of length equal to length of radius.
Solution:
Here, r = 9cm
Let the arc AB cut off a chord equal to the radius of the circle.
Since OA = OB = AB,
ΔOAB is an equilateral triangle.
m∠AOB = 60°
θ = 60°
= \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
Since S = r.θ,
S = 9 x \(\frac{\pi}{3}\) = 3π cm.
Question 3.
Find the angle in degree subtended at the centre of a circle by an arc whose length is 15 cm, if the radius of the circle is 25 cm.
Solution:
Here, r = 25 cm and S = 15 cm
Since S = r.θ,
15 = 25 x θ

∴ The required angle in degree is \(\left(\frac{108}{\pi}\right)^{0}\) or (34.40)°(approx.).
Question 4.
A pendulum of length 14 cm oscillates through an angle of 18°. Find the length of its path.
Solution:
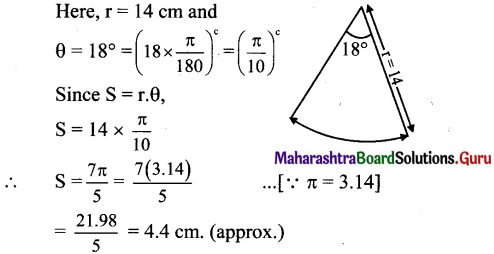
Question 5.
Two arcs of the same length subtend angles of 60° and 75° at the centres of the two circles. What is the ratio of radii of two circles?
Solution:
Let r1, and r2 be the radii of the two circles and let their arcs of same length S subtend angles of 60° and 75° at their centres.
Angle subtended at the centre of the first circle,
θ1 = 60° = \(\left(60 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{3}\right)^{c}\)
∴ S = r1θ1 = r1(\(\left(\frac{\pi}{3}\right)\))
Angle subtended at the centre of the second circle,

![]()
Question 6.
The area of the circle is 2571 sq.cm. Find the length of its arc subtending an angle of 144° at the centre. Also find the area of the corresponding sector.
Solution:
Area of circle = πr2
But area is given to be 25 π sq.cm
∴ 25π = πr2
∴ r2 = 25
∴ r = 5 cm
θ = 144° = \(=\left(144 \times \frac{\pi}{180}\right)^{c}=\left(\frac{4 \pi}{5}\right)^{\mathrm{c}}\)
Since s = rθ
S = 5(\(\frac{4 \pi}{5}\)) = 4π
Also, A(sector) = \(\frac{1}{2}\) x r x S = \(\frac{1}{2}\) x 5 x 4π
= 10π sq. cm
Question 7.
OAB is a sector of the circle having centre at O and radius 12 cm. If m∠AOB = 45°, find the difference between the area of sector OAB and ΔAOB.
Solution:
Here, r = 12 cm
\(\theta=45^{\circ}=\left(45 \times \frac{\pi}{180}\right)^{c}=\left(\frac{\pi}{4}\right)^{c}\)
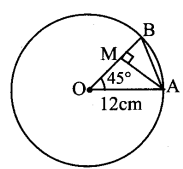
Draw AM ⊥ OB
In ΔOAM,

[Note: The question has been modified.]
Question 8.
OPQ is the sector of a circle having centre at O and radius 15 cm. If m∠POQ = 30°, find the area enclosed by arc PQ and chord PQ.
Solution:
Here, r = 15 cm
m∠POQ = 30°
\(\left(30 \times \frac{\pi}{180}\right)^{c}[/larex]
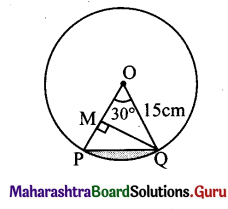
∴ θ = [latex]\left(\frac{\pi}{6}\right)^{c}\)
Draw QM ⊥ OP
In ΔOQM,
sin 30° = \(\frac{\text { QM }}{15}\)
QM= 15 x \(\frac{1}{2}=\frac{15}{2}\)
Shaded portion indicates the area enclosed by arc PQ and chord PQ.
∴ A(shaded portion)
= A(sector OPQ) – A(ΔOPQ)
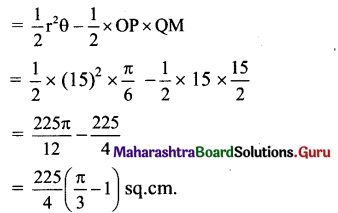
![]()
Question 9.
The perimeter of a sector of the circle of area 25π sq.cm is 20 cm. Find the area of sector.
Solution:
Area of circle = πr2
But area is given to be 25π sq.cm.
∴ 25π = πr2
∴ r2 = 25
∴ r = 5 cm
Perimeter of sector = 2r + S
But perimeter is given to be 20 cm.
∴ 20 = 2(5) + S
∴ 20 = 10 + S
∴ S = 10 cm
Area of sector = \(\frac{1}{2}\) x r x S
= \(\frac{1}{2}\) x 5 x 10
= 25sq.cm.
Question 10.
The perimeter of a sector of the circle of area 64 7i sq.cm is 56 cm. Find the area of the sector.
Solution:
Area of circle = πr2
But area is given to be 25π sq.cm.
∴ 64π = πr2
∴ r2 = 64
∴ r = 8 cm
Perimeter of sector = 2r + S
But perimeter is given to be 20 cm.
∴ 56 = 2(5) + S
∴ 56 = 16 + S
∴ S = 40 cm
Area of sector = \(\frac{1}{2}\) x r x S
= \(\frac{1}{2}\) x 8 x 40
= 160sq.cm.