Practice Set 4.1 Geometry 9th Standard Maths Part 2 Chapter 4 Constructions of Triangles Solutions Maharashtra Board

by

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 4 Constructions of Triangles.

9th Standard Maths 2 Practice Set 4.1 Chapter 4 Constructions of Triangles Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 4.1 Chapter 4 Constructions of Triangles Questions With Answers Maharashtra Board

Question 1.
Construct APQR, in which QR = 4.2 cm, m∠Q = 40° and PQ + PR = 8.5 cm.
Solution:
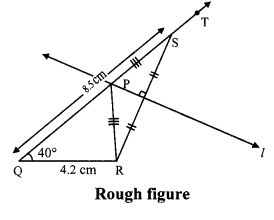
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 1
As shown in the rough figure draw seg QR = 4.2 cm
Draw a ray QT making an angle of 40° with QR
Take a point S on ray QT, such that QS = 8.5 cm
Now, QP + PS = QS [Q-P-S]
∴ QP + PS = 8.5 cm …….(i)
Also, PQ + PR = 8.5 cm ……(ii) [Given]
∴ QP + PS = PQ + PR [From (i) and (ii)]
∴ PS = PR
∴ Point P is on the perpendicular bisector of seg SR
∴ The point of intersection of ray QT and perpendicular bisector of seg SR is point P.

Steps of construction:
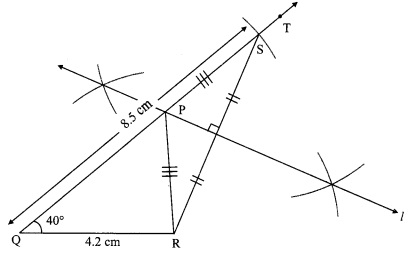
i. Draw seg QR of length 4.2 cm.
ii. Djraw ray QT, such that ∠RQT = 40°.
iii. Mark point S on ray QT such that l(QS) = 8.5 cm.
iv. Join points R and S.
v. Draw perpendicular bisector of seg RS intersecting ray QT.
Name the point as P.
vi. Join the points P and R.
Hence, ∆PQR is the required triangle.
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 2

Question 2.
Construct ∆XYZ, in which YZ = 6 cm, XY + XZ = 9 cm, ∠XYZ = 50°.
Solution:
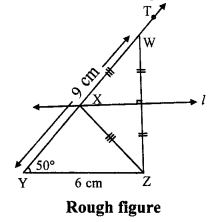
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 3
As shown in the rough figure draw seg YZ = 6 cm
Draw a ray YT making an angle of 50° with YZ
Take a point W on ray YT, such that YW = 9 cm
Now, YX + XW = YW [Y-X-W]
∴ YX + XW = 9 cm ….(i)
Also, XY + XZ = 9 cm ….(ii) [Given]
∴ YX + XW = XY + XZ [From (i) and (ii) ]
∴ XW = XZ
∴ Point X is on the perpendicular bisector of seg WZ
∴ The point of intersection of ray YT and perpendicular bisector of seg WZ is j point X.

Steps of construction:
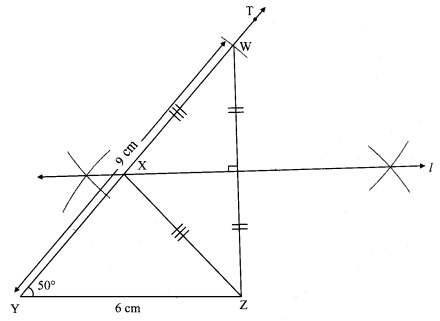
i. Draw seg YZ of length 6 cm.
ii. Draw ray YT, such that ∠ZYT = 50°.
iii. Mark point W on ray YT such that l(YW) = 9 cm.
iv. Join points W and Z.
v. Draw perpendicular bisector of seg WZ intersecting ray YT. Name the point as X.
vi. Join the points X and Z.
Hence, ∆XYZ is the required triangle.
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 4

Question 3.
Construct ∆ABC, in which BC = 6.2 cm, ∠ACB = 50°, AB + AC = 9.8 cm.
Solution:
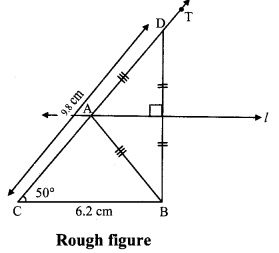
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 5
As shown in the rough figure draw seg CB = 6.2 cm
Draw a ray CT making an angle of 50° with CB
Take a point D on ray CT, such that
CD = 9.8 cm
Now, CA + AD = CD [C-A-D]
∴ CA + AD = 9.8 cm …….(i)
Also, AB + AC = 9.8 cm ……(ii) [Given]
∴ CA + AD = AB + AC [From (i) and (ii)]
∴ AD = AB
∴ Point A is on the perpendicular bisector of seg DB
∴ The point of intersection of ray CT and perpendicular bisector of seg DB is point A.

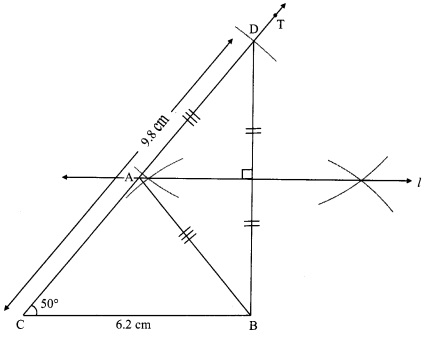
Steps of construction:
i. Draw seg BC of length 6.2 cm.
ii. Draw ray CT, such that ∠BCT = 50°.
iii. Mark point D on ray CT such that l(CD) = 9.8 cm.
iv. Join points D and B.
v. Draw perpendicular bisector of seg DB intersecting ray CT. Name the point as A.
vi. Join the points A and B.
Hence, ∆ABC is the required triangle.
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 6

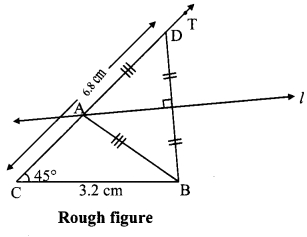
Question 4.
Construct ∆ABC, in which BC = 3.2 cm, ∠ACB = 45° Solution:and perimeter of AABC is 10 cm.
Solution:
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 7
Perimeter of ∆ABC = AB + BC + AC
∴ 10 = AB + 3.2 + AC
∴ AB + AC = 10 – 3.2
∴ AB + AC = 6.8 cm
Now, In ∆ABC
BC = 3.2 cm, ∠ACB = 45° and AB + AC = 6.8 cm ….(i)
As shown in the rough figure draw j seg BC = 3.2 cm
Draw a ray CT making an angle of 45° with CB
Take a point D on ray CT, such that
CD = 6.8 cm
Now, CA + AD = CD [C-A-D]
∴ CA + AD = 6.8 cm …(ii)
Also, AB + AC = 6.8 cm ….(iii) [From (i)]
∴ CA + AD = AB + AC [From (ii) and (iii)]
∴ AD = AB
∴ Point A is on the perpendicular bisector of seg DB
∴ The point of intersection of ray CT and perpendicular bisector of seg DB is point A.

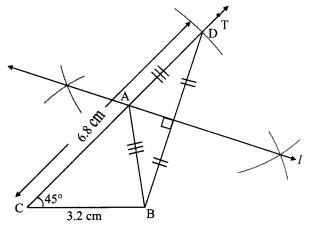
Steps of construction:
i. Draw seg BC of length 3.2 cm.
ii. Draw ray CT, such that ∠BCT = 45°.
iii. Mark point D on ray CT such l(CD) = 6.8 cm. that
iv. Join points D and B.
V. Draw perpendicular bisector of seg DB intersecting ray CT. Name the point as A.
vi. Join the points A and B.
Hence, ∆ABC is the required triangle.
Maharashtra Board Class 9 Maths Solutions Chapter 4 Constructions of Triangles Practice Set 4.1 8

Class 9 Maths Digest