Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.6 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.
10th Standard Maths 1 Practice Set 2.6 Chapter 2 Quadratic Equations Textbook Answers Maharashtra Board
Class 10 Maths Part 1 Practice Set 2.6 Chapter 2 Quadratic Equations Questions With Answers Maharashtra Board
Question 1.
Product of Pragati’s age 2 years ago and years hence is 84. Find her present age.
Solution:
Let the present age of Pragati be x years.
∴ 2 years ago,
Age of Pragati = (x – 2) years
After 3 years,
Age of Pragati = (x + 3) years
According to the given condition,
(x – 2) (x + 3) = 84
∴ x(x + 3) – 2(x + 3) = 84
∴ x2 + 3x – 2x – 6 = 84
∴ x2 + x – 6 – 84 = 0
∴ x2 + x – 90 = 0
x2 + 10x – 9x – 90 = 0
∴ x(x + 10) – 9(x + 10) = 0
∴ (x + 10)(x – 9) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 10 = 0 or x – 9 = 0
∴ x = -10 or x = 9
But, age cannot be negative.
∴ x = 9
∴ Present age of Pragati is 9 years.
Question 2.
The sum of squares of two consecutive even natural numbers is 244; find the numbers.
Solution:
Let the first even natural number be x.
∴ the next consecutive even natural number will be (x + 2).
According to the given condition,
x2 + (x + 2)2 = 244
∴ x2 + x2 + 4x + 4 = 244
∴ 2x2 + 4x + 4 – 244 = 0
∴ 2x2 + 4x – 240 = 0
∴ x2 + 2x – 120 = 0 …[Dividing both sides by 2]
∴ x2 + 12x – 10x – 120 = 0
∴ x(x + 12) – 10 (x + 12) = 0
∴ (x + 12) (x – 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 12 = 0 or x – 10 = 0
∴ x = -12 or x = 10
But, natural number cannot be negative.
∴ x = 10 and x + 2 = 10 + 2 = 12
∴ The two consecutive even natural numbers are 10 and 12.
Question 3.
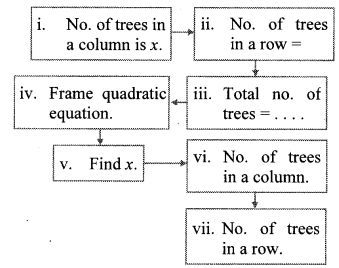
In the orange garden of Mr. Madhusudan there are 150 orange trees. The number of trees in each row is 5 more than that in each column. Find the number of trees in each row and each column with the help of following flow chart.
Solution:
i. Number of trees in a column is x.
ii. Number of trees in a row = x + 5
iii. Total number of trees = x x (x + 5)
iv. According to the given condition,
x(x + 5) = 150
∴ x2 + 5x = 150
∴ x2 + 5x – 150 = 0
v. x2 + 15x – 10x – 150 = 0
∴ x(x+ 15) – 10(x + 15) = 0
∴ (x + 15)(x – 10) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 15 = 0 or x – 10 = 0
∴ x = -15 or x = 10
But, number of trees cannot be negative.
∴ x = 10
vi. Number of trees in a column is 10.
vii. Number of trees in a row = x + 5 = 10 + 5 = 15
∴ Number of trees in a row is 15.
Question 4.
Vivek is older than Kishor by 5 years. The Find their present ages is \(\frac { 1 }{ 6 } \) Find their Present ages
Solution:
Let the present age of Kishor be x.
∴ Present age of Vivek = (x + 5) years
According to the given condition,
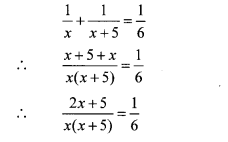
∴ 6(2x + 5) = x(x + 5)
∴ 12x + 30 = x2 + 5x
∴ x2 + 5x – 12x – 30 = 0
∴ x2 – 7x – 30 = 0
∴ x2 – 10x + 3x – 30 = 0
∴ x(x – 10) + 3(x – 10) = 0
∴ (x – 10)(x + 3) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 10 = 0 or x + 3 = 0
∴ x = 10 or x = – 3
But, age cannot be negative.
∴ x = 10 andx + 5 = 10 + 5 = 15
∴ Present ages of Kishor and Vivek are 10 years and 15 years respectively.
Question 5.
Suyash scored 10 marks more in second test than that in the first. 5 times the score of the second test is the same as square of the score in the first test. Find his score in the first test.
Solution:
Let the score of Suyash in the first test be x.
∴ Score in the second test = x + 10 According to the given condition,
5(x + 10) = x2
∴ 5x + 50 = x2
∴ x2 – 5x – 50 = 0
∴ x2 – 10x + 5x – 50 = 0
∴ x(x – 10) + 5(x – 10) = 0
∴ (x – 10) (x + 5) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 10 = 0 or x + 5 = 0
∴ x = 10 or x = – 5
But, score cannot be negative.
∴ x = 10
∴ The score of Suyash in the first test is 10.
Question 6.
‘Mr. Kasam runs a small business of making earthen pots. He makes certain number of pots on daily basis. Production cost of each pot is ₹ 40 more than 10 times total number of pots, he makes in one day. If production cost of all pots per day is ₹ 600, find production cost of one pot and number of pots he makes per day.
Solution:
Let Mr. Kasam make x number of pots on daily basis.
Production cost of each pot = ₹ (10x + 40)
According to the given condition,
x(10x + 40) = 600
∴ 10x2 + 40x = 600
∴ 10x2 + 40x- 600 = 0
∴ x2 + 4x – 60 = 0 …[Dividing both sides by 10]
∴ x2 + 10x – 6x – 60 = 0
∴ x(x + 10) – 6(x + 10) = 0
∴ (x + 10) (x – 6) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 10 = 0 or x – 6 = 0
∴ x = – 10 or x = 6
But, number of pots cannot be negative.
∴ x = 6
∴ Production cost of each pot = 7(10 x + 40)
= ₹ [(10×6)+ 40]
= ₹(60 + 40) = ₹ 100
Production cost of one pot is ₹ 100 and the number of pots Mr. Kasam makes per day is 6.
Question 7.
Pratik takes 8 hours to travel 36 km downstream and return to the same spot. The speed of boat in still water is 12 km. per hour. Find the speed of water current.
Solution:
Let the speed of water current be x km/hr. Speed of boat is 12 km/hr. (x < 12)
In upstream, speed of the water current decreases the speed of the boat and it is the opposite in downstream.
∴ speed of the boat in upstream = (12 – x) km/hr and speed of the boat in downstream = (12 + x) km/hr.

∴ The speed of water current is 6 km/hr.
Question 8.
Pintu takes 6 days more than those of Nishu to complete certain work. If they work together they finish it in 4 days. How many days would it take to complete the work if they work alone.
Solution:
Let Nishu take x days to complete the work alone.
∴ Total work done by Nishu in 1 day = \(\frac { 1 }{ x } \)
Also, Pintu takes (x + 6) days to complete the work alone.
∴ Total work done by Pintu in 1 day = \(\frac { 1 }{ x+6 } \)
∴ Total work done by both in 1 day = (\(\frac { 1 }{ x } \) + \(\frac { 1 }{ x+6 } \))
But, both take 4 days to complete the work together.
∴ Total work done by both in 1 day = \(\frac { 1 }{ 4 } \)
According to the given condition,
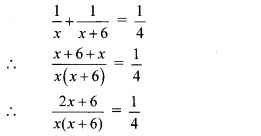
∴ 4(2x + 6) = x(x + 6)
∴ 8x + 24 = x2 + 6x
∴ x2 + 6x – 8x – 24 = 0
∴ x2 – 2x – 24 = 0
∴ x2 – 6x + 4x – 24 = 0
∴ x(x – 6)+ 4(x – 6) = 0
∴ (x – 6) (x + 4) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 6 = 0 or x + 4 = 0
∴ x = 6 or x = -4
But, number of days cannot be negative,
∴ x = 6 and x + 6 = 6 + 6 = 12
∴ Number of days taken by Nishu and Pintu to complete the work alone is 6 days and 12 days respectively.
Question 9.
If 460 is divided by a natural number, quotient is 6 more than five times the divisor and remainder is 1. Find quotient and divisor.
Solution:
Let the natural number be x.
∴ Divisor = x, Quotient = 5x + 6
Also, Dividend = 460 and Remainder = 1
Dividend = Divisor × Quotient + Remainder
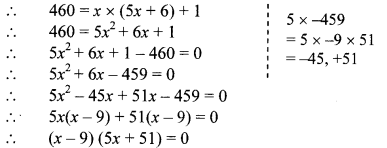
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 9 = 0 or 5x + 51 = 0
∴ x = 9 or x = \(\frac { -51 }{ 5 } \)
But, natural number cannot be negative,
∴ x = 9
∴ Quotient = 5x + 6 = 5(9) + 6 = 45 + 6 = 51
∴ Quotient is 51 and Divisor is 9.
Question 10.
In the given fig. []ABCD is a trapezium, AB || CD and its area is 33 cm2. From the information given in the figure find the lengths of all sides of the []ABCD. Fill in the empty boxes to get the solution.
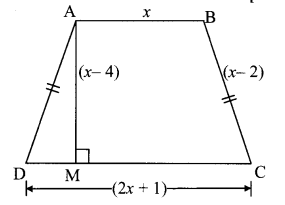
Solution:

By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
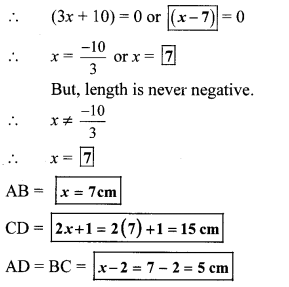
Class 10 Maths Digest