Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.4 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.
10th Standard Maths 1 Practice Set 2.4 Chapter 2 Quadratic Equations Textbook Answers Maharashtra Board
Class 10 Maths Part 1 Practice Set 2.4 Chapter 2 Quadratic Equations Questions With Answers Maharashtra Board
Question 1.
Compare the given quadratic equations to the general form and write values of a, b, c.
i. x2 – 7x + 5 = 0
ii. 2m2 = 5m – 5
iii. y2 = 7y
Solution:
i. x2 – 7x + 5 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = -7, c = 5
ii. 2m2 = 5m – 5
∴ 2m2 – 5m + 5 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 2, b = -5, c = 5
iii. y2 = 7y
∴ y2 – 7y + 0 = 0
Comparing the above equation with
ay2 + by + c = 0, we get
a = 1, b = -7, c = 0
Question 2.
Solve using formula.
i. x2 + 6x + 5 = 0
ii. x2 – 3x – 2 = 0
iii. 3m2 + 2m – 7 = 0
iv. 5m2 – 4m – 2 = 0
v. y2 + \(\frac { 1 }{ 3 } \) y = 2
vi. 5x2 + 13x + 8 = 0
Solution:
i. x2 + 6x + 5 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = 6, c = 5
∴ b2 – 4ac = (6)2 – 4 × 1 × 5
= 36 – 20 = 16
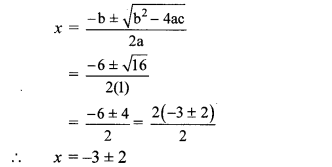
∴ x = -3 + 2 or x = -3 -2
∴ x = -1 or x = -5
∴ The roots of the given quadratic equation are -1 and -5.
ii. x2 – 3x – 2 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = -3, c = -2
∴ b2 – 4ac = (-3)2 – 4 × 1 × (-2)
= 9 + 8 = 17
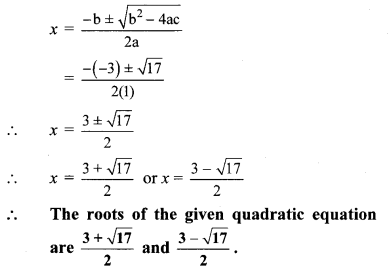
iii. 3m2 + 2m – 7 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 3, b = 2, c = -7
∴ b2 – 4ac = (2)2 – 4 × 3 × ( -7)
= 4 + 84 = 88
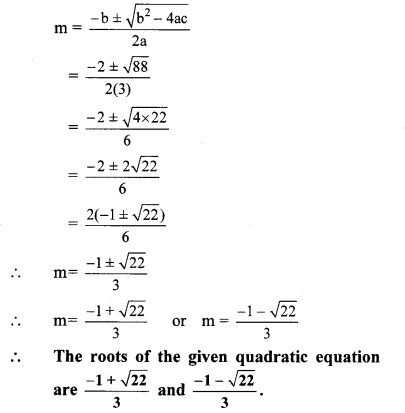
iv. 5m2 – 4m – 2 = 0
Comparing the above equation with
am2 + bm + c = 0, we get
a = 5, b = -4, c = -2
∴ b2 – 4ac = (-4)2 – 4 × 5 × (-2)
= 16 + 40 = 56

v. y2 + \(\frac { 1 }{ 3 } \)y = 2
∴ 3y2 + y = 6 …(Multiplying both sides by 3]
∴ 3y2 + y – 6 = 0
Comparing the above equation with
ay2 + by + c = 0, we get
a = 3, b = 1, c = -6
∴ b2 – 4ac = (1)2 – 4 × 3 × (-6)
= 1 + 72 = 73
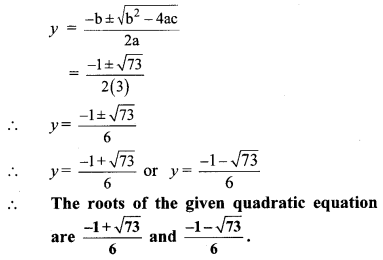
vi. 5x2 + 13x + 8 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 5, b = 13, c = 8
∴ b2 – 4ac = (13)2 – 4 × 5 × 8
= 169 – 160 = 9
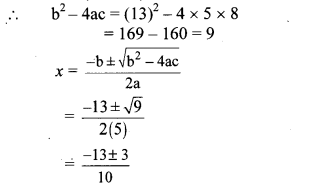
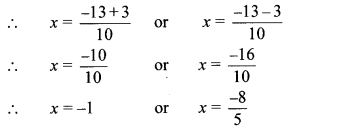
The roots of the given quadratic equation are -1 and \(\frac { -8 }{ 5 } \).
Question 3.
With the help of the flow chart given below solve the equation x2 + 2√3 x + 3 = 0 using the formula.
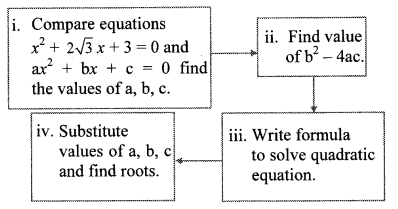
Solution:
i. x2 + 2√3 x + 3 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 1, b = 2√3 ,c = 3
ii. b2 – 4ac = (2√3)2 -4 × 1 × 3
= 12 – 12
= 0
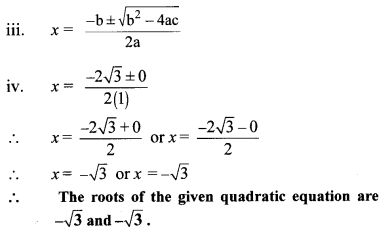
Question 1.
Solve the equation 2x2 + 13x + 15 = 0 by factorisation method, by completing the square method and by using the formula. Verify that you will get the same roots every time. (Textbook pg. no. 43)
Solution:
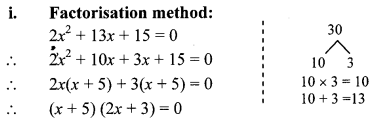
By using the property, if the product of two numbers is zero, then at least zero, we get
∴ x + 5 = 0 or 2x + 3 = 0
∴ x + -5 = 0 or 2x = -3 = 0
∴ x + -5 = or x = \(\frac { -3 }{ 2 } \)
∴ The roots of the given quadratic equation are \(\frac { -3 }{ 2 } \) and -5.
ii. Completing the square method:
2x² + 13x + 15 = 0


∴ The roots of the given quadratic equation are \(\frac { -3 }{ 2 } \) and -5.
iii. Formula method:
2x2 + 13x + 15 = 0
Comparing the above equation with
ax2 + bx + c = 0, we get
a = 2, b = 13, c = 15
∴ b2 – 4ac = (13)2 – 4 × 2 × 15
= 169 – 120 = 49
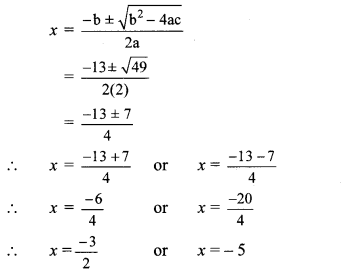
∴ The roots of the given quadratic equation are \(\frac { -3 }{ 2 } \) and -5.
∴ By all the above three methods, we get the same roots of the given quadratic equation.
Class 10 Maths Digest