Std 9 Hindi Chapter 11 Swatantrata Gaan Question Answer Maharashtra Board
Balbharti Maharashtra State Board Class 9 Hindi Solutions Lokbharti Chapter 11 स्वतंत्रता गान Notes, Textbook Exercise Important Questions and Answers.
Hindi Lokbharti 9th Digest Chapter 11 स्वतंत्रता गान Questions And Answers
Hindi Lokbharti 9th Std Digest Chapter 11 स्वतंत्रता गान Textbook Questions and Answers
संभाषणीय:
प्रश्न 1.
‘भारतीय स्वतंत्रता संग्राम’ संबंधी पढ़ी या सुनी हुई घटना या प्रसंग पर चची कीजिए।
उत्तर:
- अध्यापक – राहुल जी, क्या आप मुझे 1857 के विद्रोह व भारतीय स्वतंत्रता संग्राम के बारे में कुछ जानकारी देंगे।
- राहुल – जी हाँ, सर। सन 1857 में राष्ट्रीय बगावत शुरू हुई थी। भारत के राजा-महाराजाओं ने अंग्रेजों के खिलाफ बगावत कर दी थी।
- विद्या – जैसे कि महारानी लक्ष्मीबाई, तात्या टोपे, पेशवा आदि ने अंग्रेजों के खिलाफ बगावत का शंखनाद बजा दिया था।
- अनिल – भारतीय स्वतंत्रता संग्राम से संबंधित मुझे एक घटना याद है। मंगल पांडे अंग्रेजों की बैरकपुर की छावनी में सिपाही थे। मंगल पांडे उस चर्बीयुक्त हथियारों पर रोक लगाना चाहते थे। उन्होंने एक अंग्रेज अधिकारी पर हमला बोल दिया। इसलिए उन्हें फाँसी की सजा हो गई थी।
- अध्यापक – अब आप मुझे बताइए कि स्वतंत्रता सेनानियों से आपको कौन-सी प्रेरणा मिलती है?
- विजय – हमें अपने देश की स्वतंत्रता का सम्मान करना चाहिए।
- अजय – हमें अपने देश की रक्षा के लिए सदैव तत्पर रहना चाहिए।
- नंदन – हमें स्वतंत्रता के दीपक प्रज्वलित रखना चाहिए।
![]()
श्रवणीय:
प्रश्न (क)
राष्ट्रभक्ति पर आधारित कोई कविता सुनिए।
प्रश्न (ख)
अपने देश की विविधताएँ सुनिए।
लेखनीय:
प्रश्न 1.
समूह बनाकर भारत की विशेषता बताने वाले संवाद का लेखन कीजिए तथा समारोह में उसकी प्रस्तुति कीजिए।
पठनीय:
प्रश्न 1.
भारत के अंतरिक्ष अनुसंधान क्षेत्र संबंधी जानकारी पढ़िए और छोटी-सी टिपण्णी तैयार कीजिए।
पाठ से आगे:
प्रश्न 1.
अंतरजाल/ग्रंथालय से ‘दक्षिण एशियाई क्षेत्रीय सहयोग संगठन’ (सार्क) में भारत की भूमिका की जानकारी प्राप्त करके टिप्पणी लिखिए।
कल्पना पल्लवन:
प्रश्न 1.
‘विश्व स्तर पर भारत की पहचान निराली है।’ स्पष्ट कीजिए।
उत्तर:
भारत हमको जान से प्यारा है।
सबसे न्यारा गुलिस्ता हमारा है।
सचमुच विश्व में भारत एक ऐसा राष्ट्र है, जहाँ संस्कृति, विज्ञान व तकनीकी का समन्वय दिखाई देता है। भिन्न-भिन्न धर्म व जाति वर्ग के लोगों के बीच भारत देश ने पारंपरिक संस्कृति, सभ्यता एवं सर्वधर्म सहिष्णुता की भावना के कारण विश्व में अपना महत्त्वपूर्ण स्थान बना रखा है।
विश्व स्तर पर भारत की पहचान अनोखी व निराली है। क्रीड़ा के क्षेत्र में भारतीय खिलाड़ी विश्व स्तर पर अपनी अनोखी पहचान बनाए हुए हैं। सचिन तेंदुलकर को तो ‘क्रिकेट का भगवान’ कहा जाता है। साहित्य के क्षेत्र में भी भारतीय लेखक कवियों का साहित्य कई विदेशी भाषाओं में अनूदित हुआ है।
उद्योग जगत में रिलायन्स, टाटा, बिरला आदि कंपनियों ने विश्व स्तर पर भारत की सशक्त आर्थिक क्षमता का सबूत प्रस्थापित कर दिया है। संगीत की दुनिया में भारत ने समूचे विश्व को मोहित कर दिया है। लता दीदी, आशा भोसले, ए.आर. रहमान आदि गायक-गायिकाओं के गानों ने विदेशों में धूम मचा दी हैं। भारतीय शास्त्रीय संगीत के तो कई विदेशी कायल हैं।
विज्ञान एवं तकनीकी के क्षेत्र में भारत देश ने एक नया आयाम स्थापित कर दिया है। भारत में अनुसंधान कार्यों को बढ़ावा दिया जा रहा है। भारत के डॉक्टर एवं अभियंताओं को विदेशों में काफी महत्त्व प्राप्त हो रहा है। इसीलिए मैं बड़े गर्व के साथ कहता हूँ कि भारत ने विश्व स्तर पर अपनी एक अनोखी पहचान बनाई है। कहा भी गया है –
सारे जहाँ से अच्छा हिंदोस्ता हमारा
हम बुलबुलें हैं इसकी यह गुलिस्ताँ हमारा।
![]()
पाठ के आँगन में …
प्रश्न 1.
‘यह स्वतंत्र भावना का स्वतंत्र गान है।’ इस पंक्ति में आई कवि की भावना स्पष्ट कीजिए।
उत्तरः
कृति (घ) का स्वमत अभिव्यक्ति देखिए।
प्रश्न 2.
उचित जोड़ियाँ मिलाइए।
उत्तरः
| (अ) | (ब) |
| 1. अतीत | (क) प्रार्थना |
| 2. पुनीत | (ख) साधना |
| 3. अनंत | (ग) भावना |
| 4. विनीत | (घ) कल्पना |
| (ङ) अशांति |
उत्तर:
| (अ) | (ब) |
| 1. अतीत | (घ) कल्पना |
| 2. पुनीत | (ग) भावना |
| 3. अनंत | (ख) साधना |
| 4. विनीत | (क) प्रार्थना |
व्याकरण विभाग:
1 & 2.

3.

4. शुद्धीकरण- वाक्यों, शब्दों को शुद्ध रूप में लिखना।
![]()
5. मुहावरों का प्रयोग/चयन करना
6. शब्द संपदा- व्याकरण 5 वीं से 8 वीं तक शब्दों के लिंग, वचन, विलोमार्थक, समानार्थी, पर्यायवाची, शब्दयुग्म, अनेक शब्दों के लिए एक शब्द, भिन्नार्थक शब्द, कठिन शब्दों के अर्थ, विरामचिह्न, उपसर्ग-प्रत्यय पहचानना/अलग करना, लय-ताल युक्त शब्द ।
7.

8.

रचना विभाग:
- पत्रलेखन (व्यावसायिक /कार्यालयीन)
- प्रसंग वर्णन / वृत्तांत लेखन
- कहानी लेखन
- विज्ञापन
- गद्य आकलन
- निबंध
![]()
पत्रलेखन:
कार्यालयीन पत्र
कार्यालयीन पत्राचार के विविध क्षेत्र:
बैंक, डाकविभाग, विद्युत विभाग, दूरसंचार, दूरदर्शन आदि से संबंधित पत्र
महानगर निगम के अन्यान्य / विभिन्न विभागों में भेजे जाने वाले पत्र
माध्यमिक तथा उच्च माध्यमिक शिक्षण मंडल से संबंधित पत्र ।
अभिनंदन/प्रशंसा (किसी अच्छे कार्य से प्रभावित होकर) पत्र लेखन करना।
सरकारी संस्था द्वारा प्राप्त देयक (बिल आदि) से संबंधित शिकायती पत्र
व्यावसायिक पत्र
व्यावसायिक पत्राचार के विविध क्षेत्र:
किसी वस्तु/सामग्री/पुस्तकें आदि की माँग करना।
शिकायती पत्र – दोषपूर्ण सामग्री/ चीजें/ पुस्तकें/ पत्रिका आदि प्राप्त होने के कारण पत्रलेखन
आरक्षण करने हेतु (यात्रा के लिए)।
आवेदन पत्र – प्रवेश, नौकरी आदि के लिए।

कहानी लेखन:
1. मुद्दों के आधार पर कहानी लेखन करना।
2. शब्दों के आधार पर कहानी लेखन करना।
3. किसी कहावत, सुवचन, मुहावरे, लोकोक्ति पर आधारित कहानी लेखन करना।
मुहावरे, कहावतें, सुवचन, लोकोक्तियाँ
मुहावरे:
- आँखों पर परदा पड़ना ।
- एड़ी-चोटी का जोर लगाना ।
- रुपया पानी की तरह बहाना ।
- पहाड़ से टक्कर लेना।
- जान हथेली पर धरना (रखना)।
- लकीर का फकीर होना ।
- पगड़ी संभालना।
- काला अक्षर भैंस बराबर ।
- घाट-घाट का पानी पीना ।
- अकल के घोड़े दौड़ाना।
- पत्थर की लकीर होना।
- भंडाफोड़ करना।
- रंगा सियार होना।
- हाँ में हाँ मिलाना
![]()
लोकोक्तियाँ तथा कहावतें:
- अंधों में काना राजा।
- ओखली में सिर दिया तो मूसलों का क्या डर।
- चमड़ी जाए पर दमड़ी न जाए ।
- जहाँ न पहुंचे रवि, वहाँ पहुँचे कवि ।
- अंधा बाँटे रेवड़ी अपने कुल को देव ।
- अंधेर नगरी चौपट राजा।
- आँख और कान में चार अंगुल का अंतर है।
- अब पछताए होत क्या जब चिड़िया चुग गई खेत ।
- हाथ कंगन को आरसी क्या ?
- चोर की दाढ़ी में तिनका ।
- कोयले की दलाली में हाथ काला ।
- अधजल गगरी छलकत जाए ।
- निंदक नियरे राखिए।
- ढाक के तीन पात ।
सुवचन:
- वसुधैव कुटुंबकम् ।
- सत्यमेव जयते।
- पेड़ लगाओ, पृथ्वी बचाओ।
- जल ही जीवन है।
- पढ़ेगी बेटी तो सुखी रहेगा परिवार ।
- अनुभव महान गुरु है।
- बेटी बचाओ, बेटी पढ़ाओ।
- अतिथि देवो भवः।
- राष्ट्र ही धन है।
- जीवदया ही सर्वश्रेष्ठ है।
- असफलता सफलता की सीढ़ी है।
- श्रम ही देवता है।
- राखौ मेलि कपूर में, हींग न होत सुगंध ।
- करत-करत अभ्यास के जड़मति होत सुजान ।
![]()
निम्नलिखित मुद्दों के आधार पर कहानी लिखिए तथा उसे उचित शीर्षक देकर उससे प्राप्त होने वाली सीख भी लिखिए:
1. एक लड़की __________ विद्यालय में देरी से पहुंचना __________ शिक्षक द्वारा डाँटना _________ लड़की का मौन रहना __________ दूसरे दिन समाचार पढ़ना __________ लड़की को गौरवान्वित करना ।
2. मोबाइल ___________ लड़का _________ गाँव ___________ सफर __________
1. प्रश्न निर्मिति के लिए निम्नलिखित प्रश्नचार्ट उपयुक्त हो सकता है।
प्रश्नचार्ट:

गद्य आकलन (प्रश्न तैयार करना)
निम्नलिखित गद्यांश पर ऐसे पाँच प्रश्न तैयार कीजिए जिनके उत्तर एक-एक वाक्य में हो।
किसी भी देश की संपत्ति उस देश के आदर्श विद्यार्थी ही होते हैं । विद्यार्थियों का चरित्र ही राष्ट्र की संपत्ति होता है । वह समय का मूल्यांकन करना जानता है । वह बैटिंग, सिनेमा, मोबाइल एवं अन्य मनोरंजनों में आवश्यकता से अधिक लिप्त नहीं होता है। उसके सामने सदा मंजिल रहती है और उसे ज्ञात है कि इन प्रलोभनों के वश में न होकर परिश्रम, तप, त्याग और साधना के कटंकाकीर्ण पथ पर चलकर ही वह कुछ बन सकता है । परिवार के लिए, समाज के लिए, राष्ट्र के लिए एवं समूचे विश्व के लिए वह तभी कुछ करने की क्षमता प्राप्त कर सकता है जब वह अपनी सर्वांगीण उन्नति करने का सामर्थ्य रखता हो ।
वह विद्यारूपी समुद्र का मंथन करके ऐसे मोती प्राप्त कर सकता है जो आज तक अनबिद्घ रहे हों।
प्रश्न:
- किसी भी देश की संपत्ति कौन होते हैं?
- विद्यार्थी क्या करना जानता है?
- विद्यार्थी किसके लिए कुछ क्षमता प्राप्त कर सकता है?
- विद्यार्थी किस प्रकार के मोती प्राप्त कर सकता है?
- आप इस गढ्यांश को कौन-सा शीर्षक देना उचित समझेंगे?
![]()
वृत्तांत लेखन:
अपनी पाठशाला में मनाए गए ‘वाचन प्रेरणा दिवस/हिंदी दिवस/विज्ञान दिवस/राजभाषा दिवस/ शिक्षक दिवस/ वसुंधरा दिवस/ क्रीड़ा दिवस आदि का वृत्तांत रोचक भाषा में लिखिए । (लगभग 60 से 70 शब्दों में)।
प्रसंग वर्णन:
निम्नलिखित जानकारी पढ़कर उससे संबंधित प्रसंग लगभग 60 से 70 शब्दों में लिखिए।
1. कूड़ेदान से कूड़ा-कचरा आसपास फैला हुआ है, उसी में कुछ आवारा कुत्ते तथा अन्य जानबर घूम रहे हैं साथ ही कुछ ___ गाए प्लास्टिक की थैलियों को चबा-चबा कर खा रही हैं।…
विज्ञापन:
निम्न विषयों पर विज्ञापन तैयार किए जा सकते हैं।
1. वस्तुओं की उपलब्धि: नवनिर्मित (किसी भी वस्तु संबंधी)
जैसे- किताबें, कपड़े, घरेलू आवश्यक वस्तुएँ, उपकरण, फर्नीचर, स्टेशनरी, शालोपयोगी वस्तुएँ तथा उपकरण आदि ….
2. शैक्षिक: शिक्षा में संबंधित योगासन तथा स्वास्थ्य शिविर, स्वच्छ, सुंदर शुद्ध लिखावट, चित्रकला, इंटरनेट तथा विविध ऐप्स आदि कलाओं से संबंधित अभ्यास वर्ग, व्यक्तित्व विकास शिविर आदि –
3. आवश्यकता: वाहक-चालक, सेवक, चपरासी, द्वारपाल, सुरक्षा रक्षक, व्यवस्थापक, लिपिक, अध्यापक, संगणक अभियंता, आदि ……
4. व्यापार विषयक: दूकान, विविध वाहन, उपकरण, मकान, मशीन, गोदाम, टी. बी., संगणक, भूखंड, रेफ्रीजरेटर आदि
5. मनोरंजन तथा ज्ञानवर्धन: व्याख्यानमाला, परिसंवाद, नाटक वार्षिकोत्सव, विविध विशेष दिनों के उपलक्ष्य में आयोजित कार्यक्रम समारोह आदि……
6. पर्यटन संबंधी: यात्रा विषयक, आरक्षण आदि
7. वैयक्तिक :- श्रद्धांजली, शोकसंदेश, जयंती, पुण्यतिथि, गृहप्रवेश, बधाई आदि
![]()
निबंध लेखन:

Hindi Lokbharti 9th Answers Chapter 11 स्वतंत्रता गान Additional Important Questions and Answers
(क) पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।
कृति (1) आकलन कृति
प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तर:

कृति (2) आकलन कृति
प्रश्न 1.
समझकर लिखिए।
उत्तर:

![]()
प्रश्न 2.
निम्नलिखित विधान सत्य है या असत्य लिखिए।
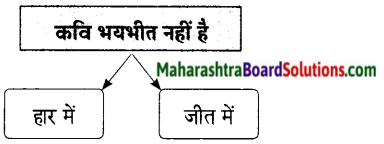
1. प्रतिकूल परिस्थितियों में भी व्यक्ति स्वतंत्रता की भावना को बरकरार रखें।
2. स्वतंत्रता का दीपक शक्ति व भक्ति से परिपूर्ण नहीं हैं।
उत्तर:
1. सत्य
2. असत्य
कृति (3) भावार्थ (1) निम्नलिखित पद्यांश का भावार्थ लिखिए।
प्रश्न 1.
घोर अंधकार हो …………….. ला रहा विहान है।
भावार्थ:
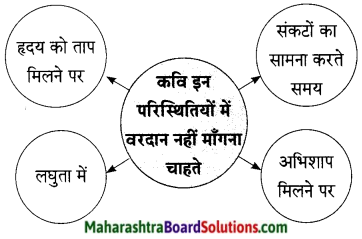
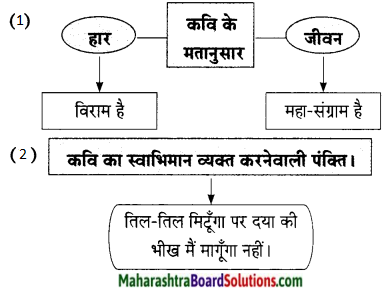
किसी भी कीमत पर स्वतंत्रता का मोल नहीं किया जा सकता। स्वतंत्रता की कीमत हमेशा अधिक होती है। इसीलिए कवि नेपाली कहते हैं, “भले ही चारों ओर घोर अंधकार छाया हुआ हो या फिर हवा तेजी से बह रही हो, फिर भी प्रत्येक भारतीय के हृदय द्वार पर जलता हुआ यह स्वतंत्रता का दीया बुझना नहीं चाहिए। प्रतिकूल परिस्थितियों में भी व्यक्ति स्वतंत्रता की भावना को बरकरार रखें। स्वतंत्रता का यह दीपक रात का दीया है यानी अंधकारूपी परतंत्रता से इस दीपक ने सभी के जीवन में स्वतंत्रता रूपी विहान भर दिया है।”
(ख) पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।
कृति (1) आकलन कृति
1. एक शब्द में उत्तर लिखिए।
प्रश्न 1.
देश और समाज पर किसका वितान है?
उत्तर:
ज्योति का
प्रश्न 2.
तीर और कछार पर किसका दीया बुझना नहीं चाहिए?
उत्तरः
स्वतंत्रता का
![]()
2. संजाल पूर्ण कीजिए।
प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तरः

कृति (2) आकलन कृति.
प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
समझकर लिखिए।
उत्तरः

कृति (3) भावार्थ
1. निम्नलिखित पद्यांश का भावार्थ लिखिए।
प्रश्न 1.
यह अतीत कल्पना …………….. ज्योति का वितान
भावार्थः
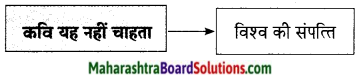
कवि नेपाली कहते हैं, स्वतंत्रता का दीपक हमारे लिए अतीत की कल्पना की भाँति है। यानी हमारे पुरखों ने इसे प्रज्वलित रखने के लिए अपने प्राण अर्पण कर दिए थे। इसीलिए हम इस दीए के समक्ष विनम्र प्रार्थना करते हैं। यह दिया हमारे लिए पवित्र भावना है। स्वतंत्रता के इस दीए को हमने अपनी अनंत साधना के बाद प्राप्त किया है। अतः जीवन में निर्माण होने वाली हर स्थिति यानी कि शांति में या अशांति में, युद्ध की स्थिति हो या संधि की या फिर देश में क्रांति हो, फिर भी तीर पर या नदी के किनारे पर हम इस दीए को बुझने नहीं देंगे। हमारे जीवन में यह स्वतंत्रता का दीपक ज्योति का वितान लेकर आया है।
![]()
(ग) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।
कृति (1) आकलन कृति
प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तरः

कृति (1) आकलन कृति
प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
समझकर लिखिए।
उत्तरः

कृति (3) भावार्थ
प्रश्न 1.
निम्नलिखित पद्यांश का भावार्थ लिखिए।
तीन चार फूल ………………. पुण्य प्राण दान है।
भावार्थ:
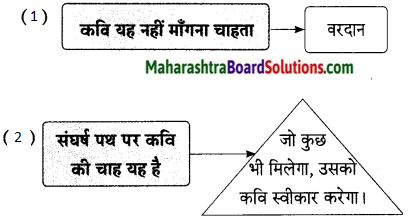
कवि नेपाली कहते हैं, स्वतंत्रता के इस दीपक के प्रति हम भारतीयों में निष्ठा एवं श्रद्धा है। इस दीए के आस-पास तीन-चार फूल है। चारों ओर धूल भी है। बास और बबूल के पेड़ भी हैं। घास के दुपट्टे हैं। हवा की लहर उसे आकर स्पर्श भी करती है। फिर भी किसी शहीद की कब्र पर या किसी स्वतंत्रता सेनानी की समाधि पर हम इस दौए को बुझने नहीं देंगे। स्वतंत्रता का यह दीपक हमारे लिए किसी शहीद का पुण्य प्राण दान है। इसी से प्रेरणा लेकर हम भारतीय अपनी आजादी को बरकरार रखने का प्रयास करेंगे।
![]()
(घ) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।
कृति (1) आकलन कृति
प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तरः

कृति (2) आकलन
प्रश्न 1.
उचित जोड़ियाँ मिलाइए।
| (अ) | (ब) |
| 1. स्वतंत्र | (क) बदलियाँ |
| 2. चूम-चूम | (ख) बिजलियाँ |
| 3. झूम-झूम | (ग) जीत हार |
| 4. क्षुद्र | (घ) भावन |
उत्तरः
| (अ) | (ब) |
| 1. स्वतंत्र | (घ) भावन |
| 2. चूम-चूम | (ख) बिजलियाँ |
| 3. झूम-झूम | (क) बदलियाँ |
| 4. क्षुद्र | (ग) जीत हार |
कृति (3) भावार्थ
प्रश्न 1.
निम्नलिखित पद्यांश का भावार्थ लिखिए ।
झूम-झूम बदलियाँ ………………. स्वतंत्र गान है।
भावार्थ:
कवि नेपाली कहते हैं, आसमान में तूफानी बादल मँडरा रहे हों; बिजलियाँ कड़क रही हों; आँधी निर्माण हो गई हो और उसने हलचलें मचाना शुरू कर दिया हो। भले ही देश के अंतर्गत दंगे फसाद हो रहे हों; व्यथा, वेदना एवं यातना का साम्राज्य निर्माण हुआ हो; फिर भी किसी की भी क्षुद्र जीत-हार पर यह दीया बुझना नहीं चाहिए। आखिर यह दिया हमारे लिए स्वतंत्र भावना का स्वतंत्र गान है। यह हमारी स्वतंत्रता का प्रतीक है। यह हमारी अस्मिता की पहचान है।
![]()
पद्य-विश्लेषण:
कविता का नाम – स्वतंत्रता गान
कविता की विधा – प्रेरणा गीत
पसंदीदा पंक्ति – कब्र पर, मजार पर, यह दीया बुझे नहीं, यह किसी शहीद का पुण्य प्राण दान है।
पसंदीदा होने का कारण – उपर्युक्त पंक्ति मुझे बेहद पसंद है क्योंकि उसमें शहीदों की कब्र या मजार पर स्वतंत्रता के दीपक को ना बुझने देने की बात कही गई है। कविता से प्राप्त संदेश या प्रेरणा – प्रस्तुत कविता से प्रेरणा मिलती हैं कि भारतीयों को स्वतंत्रता के दीपक को सदैव प्रज्वलित रखना चाहिए। स्वतंत्रता के दीपक से व्यक्ति को सीख लेनी चाहिए कि उसे प्रतिकूल परिस्थितियों में भी देश की रक्षा करने के लिए तत्पर रहना चाहिए। व्यक्ति के पास देशभक्ति की भावना होनी चाहिए। त्याग व बलिदान आदि गुणों को अपने जीवन में उतारना चाहिए।
स्वतंत्रता गान Summary in Hindi
कवि-परिचय:
जीवन-परिचय: उत्तर छायावाद के जिन कवियों ने कविता और गीत को जनता का कंठहार बनाया था, गोपाल सिंह नेपाली उनमें अहम थे। गोपाल जी प्रकृति प्रेमी कवि हैं। इनकी कविताएँ देश प्रेम, प्रकृति प्रेम एवं मानवीय भावनाओं का वर्णन करने में प्रमुख भूमिका निभाती हैं। ये प्रबुद्ध पत्रकार भी थे। इन्होंने हिंदी फिल्मों के लिए भी गीत लिखे हैं।
प्रमुख कृतियाँ: काव्य संग्रह – ‘उमंग’, ‘पंछी’, ‘रागिनी’, ‘नीलिमा’, ‘पंचमी’, ‘रिमझिम’ आदि; पत्रिकाएँ – रतलाम टाइम्स’, ‘चित्रपट’,
‘सुधा एवं योगी’।
पद्य-परिचय:
प्रेरणा गीत: जिन गीतों को सुनकर व्यक्ति को कार्य करने की प्रेरणा मिलती है ऐसे गीतों को प्रेरणा गीत कहते हैं। प्रेरणा गीत व्यक्ति
के दिल में सकारात्मक बीज बोने की बात करते हैं। प्रेरणा गीत व्यक्ति को अपने दिल की बात सुनकर जीवन में आगे बढ़ने की प्रेरणा देते हैं।
प्रस्तावना: प्रस्तुत कविता के माध्यम से कवि ने प्रेरणा दी है कि प्रत्येक व्यक्ति को स्वतंत्रता के दीपक को हर परिस्थिति में प्रज्वलित रखने के लिए प्रयास करते रहना चाहिए।
सारांश:
प्रस्तुत कविता एक प्रेरणा गीत है। इस गीत के माध्यम से कवि ने भारतीयों को राष्ट्रप्रेम, देशाभिमान, त्याग व बलिदान की भावना को बरकरार रखने के लिए प्रेरित किया है। इसीलिए कवि ने स्वतंत्रता के दीपक सदैव प्रज्वलित रखने के लिए कहा है। स्वतंत्रता का दीपक हमारी अस्मिता एवं आजादी का प्रतीक है। इस दीपक के प्रति प्रत्येक भारतीय के मन में सम्मान एवं निष्ठा की भावना होनी चाहिए। इस दीपक से प्रेरणा लेकर भारतवासी अपने देश की रक्षा हेतु अग्रसर हो जाए। ऐसा कवि ने संदेश दिया है।
![]()
भावार्थ:
1. घोर अंधकार हो —————— प्राण के समान है।
किसी भी कीमत पर स्वतंत्रता का मोल नहीं किया जा सकता। स्वतंत्रता की कीमत हमेशा अधिक होती है। इसीलिए कवि नेपाली कहते हैं, भले ही चारों ओर घोर अंधकार छाया हुआ हो या फिर हवा तेजी से बह रही हो, फिर भी प्रत्येक भारतीय के हृदय द्वार पर जलता हुआ यह स्वतंत्रता का दीया बुझना नहीं चाहिए। प्रतिकूल परिस्थितियों में भी व्यक्ति स्वतंत्रता की भावना को बरकरार रखें। स्वतंत्रता का यह दीप रात का दीया है यानी अंधकाररूपी परतंत्रता से इस दीपक ने सभी के जीवन में स्वतंत्रता रूपी विहान भर दिया है।
स्वतंत्रता का यह दीपक शक्ति से परिपूर्ण है। स्वयं शक्ति ने ही इसे हमें प्रदान किया हुआ है। अत: इस दीए को हम शक्ति को ही अर्पित करेंगे। इस दीए के प्रति हम सब भारतीयों की भक्ति समाहित हुई है। मानो भक्ति ने ही हमें इसे प्रदान किया हो। इस प्रकार स्वतंत्रता के इस दीए में शक्ति व भक्ति दोनों का समन्वय है। भले ही नाव पानी में तेजी से चल रही हो और पानी का बहाव भी वेगवान हो, फिर भी गंगा नदी के जल में इस दीए को हम बुझने नहीं देंगे क्योंकि यह हमारे स्वदेश का दीया है जो हमें अपने प्राणों के समान प्रिय है।
2. यह अतीत कल्पना ——————- ज्योति का वितान है।
कवि नेपाली कहते है, स्वतंत्रता का दीपक हमारे लिए अतीत की कल्पना की भाँति है। यानी हमारे पुरखों ने इसे प्रज्वलित रखने के लिए अपने प्राण अर्पण कर दिए थे। इसीलिए हम इस दीए के समक्ष विनम्र प्रार्थना करते हैं। यह दिया हमारे लिए पवित्र भावना है। स्वतंत्रता के इस दीए को हमने अपनी अनंत साधना के बाद प्राप्त किया है। अत: जीवन में निर्माण होने वाली हर स्थिति यानी कि शांति में या अशांति में, युद्ध की स्थिति हो या संधि की या फिर देश में क्रांति हो, फिर भी तीर पर या नदी के किनारे पर हम इस दीए को बुझने नहीं देंगे। हमारे जीवन में यह स्वतंत्रता का दीपक ज्योति का वितान लेकर आया है।
3. तीन चार फूल हैं ——————— पुण्य प्राण दान है।
कवि नेपाली कहते हैं, स्वतंत्रता के इस दीपक के प्रति हम भारतीयों में निष्ठा एवं श्रद्धा है। इस दीए के आस-पास तीन-चार फूल हैं। चारों ओर धूल भी है। बास और बबूल के पेड़ भी हैं। घास के दुपट्टे हैं। हवा की लहर उसे आकर स्पर्श भी करती है। फिर भी किसी शहीद की कब्र पर या किसी स्वतंत्रता सेनानी की समाधि पर हम इस दीए को बुझने नहीं देंगे। स्वतंत्रता का यह दीपक हमारे लिए किसी शहीद का पुण्य प्राण दान है। इससे प्रेरणा लेकर हम भारतीय अपनी आजादी को बरकरार रखने का प्रयास करेंगे।
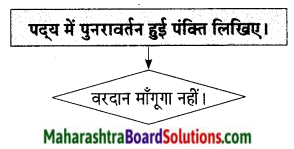
4. झूम-झूम बदलियाँ ———————– स्वतंत्र गान है।
कवि नेपाली कहते हैं, आसमान में तूफानी बादल मँडरा रहे हों। बिजलियाँ कड़क रही हों। आँधी निर्माण हो गई हो और उसने हलचलें मचाना शुरू कर दिया हो। भले ही देश के अंतर्गत दंगे फसाद हो रहे हों व्यथा, वेदना एवं यातना का साम्राज्य निर्माण हुआ हो। फिर भी किसी की क्षुद्र जीत-हार पर यह दीया बुझना नहीं चाहिए। आखिर यह दिया हमारे लिए स्वतंत्र भावना का स्वतंत्र गान है। यह हमारी स्वतंत्रता का प्रतीक है। यह हमारी अस्मिता की पहचान है।
![]()
शब्दार्थ:
- बयार – हवा
- निशीथ – निशा, रात
- विहान – सवेरा
- कछार – किनारा
- वितान – आकाश, गगन
- दुकुल – दुपट्टा
- हिलोर – लहर
Hindi Lokbharti 9th Std Digest दूसरी इकाई
- कह कविराय Question Answer
- जंगल (पूरक पठन) Question Answer
- इनाम Question Answer
- सिंधु का जल Question Answer
- अतीत के पत्र Question Answer
- निसर्ग वैभव (पूरक पठन) Question Answer
- शिष्टाचार Question Answer
- उड़ान Question Answer
- मेरे पिता जी (पूरक पठन) Question Answer
- अपराजेय Question Answer
- स्वतंत्रता गान Question Answer



































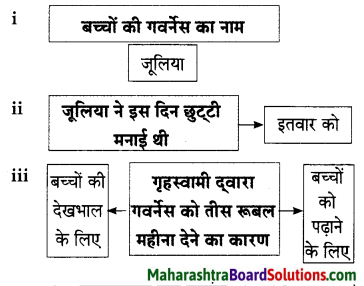
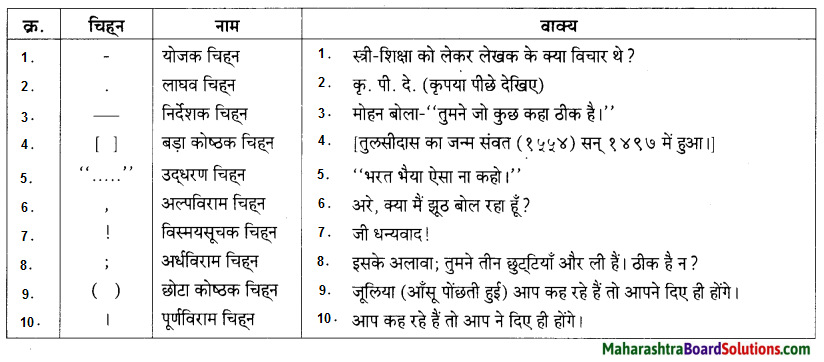 Hindi Lokbharti 9th Answers Chapter 5 जूलिया Additional Important Questions and Answers
Hindi Lokbharti 9th Answers Chapter 5 जूलिया Additional Important Questions and Answers