Balbharti Maharashtra State Board Class 9 Hindi Solutions Hindi Lokvani Chapter 4 मान जा मेरे मन Notes, Textbook Exercise Important Questions and Answers.
Std 9 Hindi Chapter 4 Maan Ja Mere Man Question Answer Maharashtra Board
Hindi Lokvani 9th Digest Chapter 4 मान जा मेरे मन Questions And Answers
1. भाषा बिंदु:
प्रश्न 1.
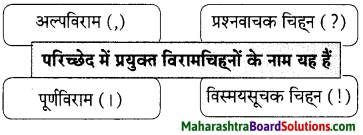
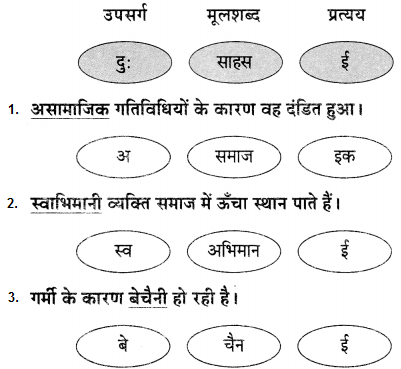
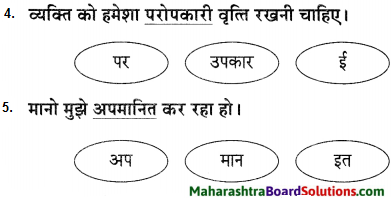
रेखांकित शब्द से उपसर्ग और प्रत्यय अलग करके भाषा बिंद लिखिए।
उत्तर:
उदा. मन बड़ा दुस्साहसी था।
2. संभाषणीय :
प्रश्न 1.
‘मानवीय भावनाएँ मन से जुड़ी होती हैं,’ इस पर गुट में चर्चा कीजिए।
उत्तर:
मन से ही भावनाओं की उत्पत्ति होती है। मनुष्य का मन जैसा होता है, उसकी भावनाएँ भी वैसी ही होती हैं। मन से ही अच्छी तथा बुरी भावनाएँ जुड़ी होती हैं। जिनका मन अच्छा होता है, उनकी भावनाएँ अच्छी होती हैं। जिनका मन बुरा होता है, उनकी भावनाएँ बुरी होती हैं। मन बड़ा ही चंचल होता है, जो प्रति पल बदलता रहता है। परंतु मन को अपनी बुद्धि से नियंत्रित किया जा सकता है। मन घोड़े के भाँति भागता है, तो बुद्धि उसे लगाम की तरह नियंत्रित करती है।
जब मनुष्य अपनी बुद्धि से अपने मन को वश में करता है और अच्छे कार्यों में लगाता है, तो उसकी भावनाएँ और विचार दोनों अच्छे हो जाते हैं, पर जब वह अपने मन को अनियंत्रित छोड़ देता है, तो उसका मन बुरे कार्यों में डूब जाता है। मनुष्य की भावना अच्छी है तो उसे चारों तरफ अच्छाई दिखती है और भावना बुरी है उसे चारों तरफ बुराई ही बुराई दिखाई पड़ती है। क्योंकि उसका मन ही बुराइयों से भरा होता है।
![]()
3. लेखनीय :
प्रश्न 1.
मन और लेखक के बीच हुए किसी एक संवाद को संक्षिप्त में लिखिए।
उत्तर :
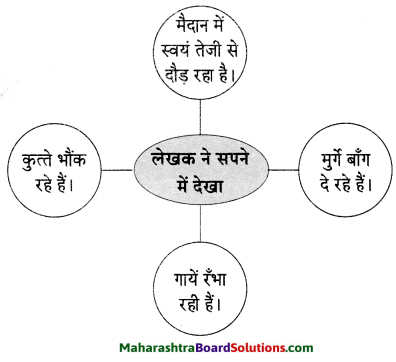
मन को अपनी बुद्धि के द्वारा नियंत्रित करना चाहिए। मन को मनमाना छोड़ देने से अपना बड़ा नुकसान होता है। फिर वह किसी अच्छी बात को मानने के बजाय हजारों तर्क देता है। एक दिन की बात है। आधी रात का वक़्त था। लेखक चारपाई पर उदास बैठा अपने मन को समझाने का प्रयास कर रहा था। उसका मन रूठा-सा कमरे में इधर-उधर घूम रहा था। लेखक ने कहा-‘मन भाई, डॉक्टर कह रहा था कि तुम्हारा वजन बहुत अधिक बढ़ गया है। मैं स्टेशनवाली मशीन पर अपने को वन करने चढ़ा तो उसने भी मना कर दिया। फिर बाज़ार गया तो वहाँ की मशीन ने मेरा वजन बताया। सोचो, जब मेरे वजन से मशीन को इतना कष्ट हो रहा है तो….
मन ने बात काटते हुए उदाहरण देकर समझाया, तुमने बचपन में बाइस्कोप में एक भारी-भरकम महिला देखा था, उससे तुम अभी काफी दुबले पतले हो। लेखक ने कहा, “मेरी तकलीफ पर गौर करो। रिक्शेवाले मुझे रिक्शे पर नहीं बिठाते। दर्जी अकेले मुझे नाप नहीं सकता।” ये सारी घटना शाम को ही घट चुकी थी।
व्यक्तिगत आक्षेप सुनकर लेखक चिढ़कर अपने मन से बोला ‘इतने वर्षों से तुम्हें पालता रहा, यही गलती की। विद्वानों ने कहा है कि ‘मन को मारना चाहिए’, यह सुनकर लेखक का मन अप्रत्याशित ढंग से चिंतित होने लगा और वह बोला- ‘इतने दिनों की सेवाओं का यही फल ! मैं जानता हूँ, तुम डॉक्टर और दुबले आदमियों के साथ मिलकर मेरे खिलाफ षड्यंत्र कर रहे हो। तुम विश्वासघाती हो, मैं तुमसे बोलूंगा नहीं। व्यक्ति को हमेशा उपकारी वृत्ति रखनी चाहिए। लेखक का मन मुँह मोड़कर सिसकने लगा। बहुत तरह से मनाने पर लेखक का मन नहीं माना तो संगीत सुनाकर किसी तरह उन्होंने अपने मन को मनाया।
![]()
4. रचनात्मकता की ओर मौलिक सृजन
प्रश्न 1.
‘मन चंगा तो कठौती में गंगा’ इस उक्ति पर कविता / विचार लिखिए।
उत्तर:
‘मन चंगा तो कठौती में गंगा’ यह उक्ति संत कवि रैदास जी के लिए प्रचालित है। जिसका अर्थ है यदि अपना मन पवित्र है तो घर की कठौती (काठ का बना पात्र) में रखा पानी भी अपने लिए गंगाजल के समान पवित्र है। आप को उस जल में स्नान करने से ही गंगा स्नान का पुण्य मिल जाएगा। आपका मन ही गंदा है तो आप कितने ही बार गंगा स्नान क्यूँ न कर लें आप के पाप धुलने वाले नहीं हैं। मंदिर के अंदर जाकर लाखों रूपए चढ़ाते हैं, मिठाइयाँ और दूध चढ़ाते हैं। इससे पुण्य नहीं मिलेगा। आप भूखे को भोजन, नंगे को कपड़ा और लाचार को सहारा दो और मंदिर में जाकर उनके कल्याण के लिए प्रार्थना करो तो पुण्य मिलेगा। हमेशा अपने मन को पवित्र रखो, लोगों का उपकार करो, बुराइयों से बचो, तो सारे तीर्थ आपके घर में होंगे। ईश्वर आपके हृदय में निवास करेंगे और आपको पुण्य मिलेगा।
5. पाठ के आँगन में :
प्रश्न 1.
‘मन की एकाग्रता’ के लिए आप क्या करते हैं, बताइए।
उत्तरः
मन इतना चंचल है कि इसको वश में रखना वास्तविक रूप से बहुत कठिन है। हमें खुद को भी यह ज्ञान नहीं होता कि मन कितनी जल्दी भटक जाता है। जब तक हम अपनी इंद्रियों को वश में नहीं करते तब तक हम अपने मन को स्थिर नहीं कर सकते। मैं अपने मन की एकाग्रता के लिए अपनी दिनचर्या का विशेष ध्यान देता हूँ। हर कार्य को समय पर करता हूँ। योगा भी नियमित रूप से करता हूँ। विषय-वासना से दूर रहता हूँ। किसी चौज के लिए अपने मन को विचलित नहीं होने देता। अपने चारों तरफ बिछे हुए मायाजाल से मैं अपने आप को बचाता हूँ।
![]()
प्रश्न 2.
‘मान जा मेरे मन’ निबंध का आशय अपने शब्दों में प्रस्तुत कीजिए।
उत्तर:
‘मान जा मेरे मन’ निबंध के माध्यम से लेखक रामेश्वर सिंह कश्यप ने मन पर नियंत्रण रखने की बात बताई हैं। इस निबंध के माध्यम से यह स्पष्ट किया गया है कि आज मन पर नियंत्रण न रख पाना प्रत्येक की कमजोरी बन गई है। मन की चपलता, चंचलता मन को नियंत्रित करने में बाधक होती है। किंतु हमें बुरी चीजों से दूर रहने के लिए मन पर नियंत्रण करना ही चाहिए।
प्रश्न 3.
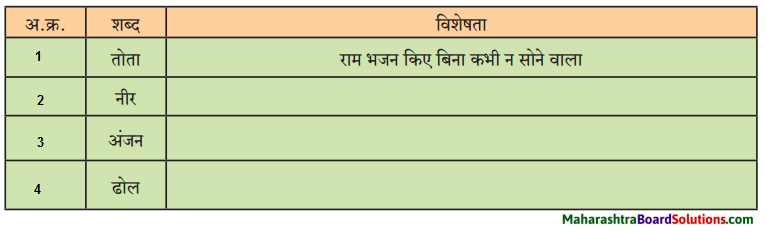
सूची तैयार कीजिए।
उत्तर:
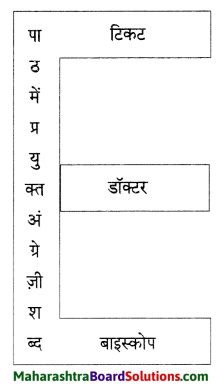
प्रश्न 4.
सूची तैयार कीजिए।
उत्तर:
Hindi Lokvani 9th Std Textbook Solutions Chapter 4 मान जा मेरे मन Additional Important Questions and Answers
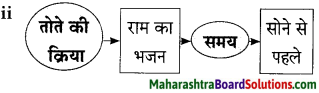
(क) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।
कृति क (1) : आकलन कृति
प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर :
प्रश्न 2.
समझकर लिखिए।
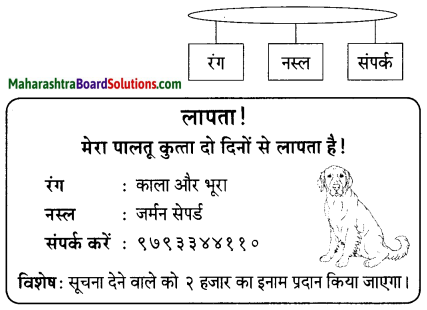
i. सुने कमरे में यह चहलकदमी कर रहा था –
उत्तर :
लेखक का मन ।
![]()
प्रश्न 3.
रिक्त स्थानों की पूर्ति कीजिए।
- मामला बड़ा ………………… था।
- आप ……………… हैं लेकिन गलत दिशा में।
- आदमी का …………. तीन मन से ज्यादा नहीं होता।
उत्तर:
- संगीन
- प्रगतिशील
- वजन
कृति क (2) : शब्द संपदा
प्रश्न 1.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द गद्यांश से ढूँड़कर लिखिए।
i. मौत ………
ii. कम ………..
उत्तर :
i. जिंदगी
ii. ज्यादा
प्रश्न 2.
लिंग पहचानकर लिखिए।
i. आदमी
i. महिला
उत्तर :
i. पुल्लिंग
ii. स्त्रीलिंग
![]()
प्रश्न 3.
उचित शब्द तैयार कीजिए।

उत्तर:
- स्वयंचलित
- संगीन
- प्रगतिशील
कृति क (3) : स्वमत अभिव्यक्ति
प्रश्न 1.
‘मन पर नियंत्रण रखना आवश्यक है।’ इस पर अपने विचार व्यक्त कीजिए।
उत्तर :
मन पर नियंत्रण रखना आवश्यक है। यदि मन को छूट दे देते हैं तो वह बेलगाम घोड़े की तरह दौड़ने लगता है। फिर इस पर काबू पाना कठिन हो जाता है। मनुष्य के मन की शक्ति उसके उन्नति के लिए अनेक द्वार खोलती है। किसी वस्तु को पाने की प्रबल इच्छा हो और उसे प्राप्त करने का प्रयत्न पूरे मन से किया जाए तो उस वस्तु को हासिल करना असंभव नहीं हैं। मन को सदैव स्थिर रखना चाहिए क्योंकि चंचल मन कभी-भी संतुष्ट नहीं होता। जिसने अपने मन को जीत लिया, सफलता उसी के कदम चूमती है।
![]()
(ख) गद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।
कृति ख (1) : आकलन कृति
प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर :
प्रश्न 2.
सत्य या असत्य पहचानकर लिखिए।
i. व्यक्तिगत आक्षेप सुनकर लेखक तिलमिला उठा।
ii. लेखक के पास कसरत का सब सामान तो है ही नहीं।
उत्तर :
i. सत्य
ii. असत्य
![]()
कृति ख (2) : शब्द संपदा
प्रश्न 1.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. जिसकी आशा न की गई हो –
ii. विश्वास घात करने वाला –
उत्तर:
i. अप्रत्याशित
ii. विश्वासघाती
प्रश्न 2.
निम्नलिखित शब्दों के विरुद्धार्थी शब्द लिखिए ।
i. अपकारी
ii. सफल
उत्तर :
i. उपकारी
ii. विफल
![]()
कृति ख (3) : स्वमत अभिव्यक्ति
प्रश्न 1.
‘मन और भावनाएँ एक ही सिक्के के दो पहलू’, इस पर अपने विचार व्यक्त कीजिए।
उत्तर:
मन और भावनाएँ एक ही सिक्के के दो पहलू हैं। मनुष्य का मन जैसा होगा वैसे ही विचार उसके मन में आएंगे। मन के द्वारा ही भावनाओं का संचालन होता है। सुख और दुख दोनों ही मन के भावनाओं की अभिव्यक्ति है। इसी विषय पर महाकवि तुलसीदास जी ने लिखा है, ‘जाकी रही भावना जैसी, प्रभु मूरत देखी तिन तैसी’ अर्थात जिसके मन में जैसी भावना होती है ईश्वर उसे उसी रूप में दिखाई देते हैं। भावनाएँ सकारात्मक और नकारात्मक दोनों प्रकार की होती हैं।
सकारात्मक भावनाएँ मनुष्य को विकास के रास्ते पर ले जाती हैं और नकारात्मक भावनाएँ उसे विनाश के गर्त में पहुँचा देती हैं। दोनों ही प्रकार की भावनाओं का संचालन हमारे मन द्वारा ही होता है। विद्वानों का मत है कि सकारात्मक भावनाएँ हमें मोक्ष की ओर आगे बढ़ाती है इसलिए मन को ऐसा रखना चाहिए कि वह हमेशा सकारात्मक विचार करे और नकारात्मकता को अपने पास फटकने न दे।
![]()
(ग) गद्यांश पड़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।
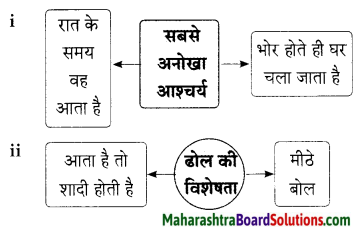
कृति ग (1) : आकलन कृति
प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर:
प्रश्न 2.
उचित पर्याय चुनकर लिखिए।
i. ओस से भीगा मैदान दौड़ता हुआ मैं…
(क) डूबता हुआ सूरज।
(ख) उगता हुआ सूरज।
(ग) प्रकृति का दृश्य।
उत्तर:
(ख) उगता हुआ सूरज।
![]()
ii. व्यायाम करने वालों के लिए……
(क) गहरी नींद जरूरी है।
(ख) जगे रहना जरूरी है।
(ग) दौड़ना और चलना जरूरी है।
उत्तर:
(क) गहरी नींद जरूरी है।।
प्रश्न 3.
निम्नलिखित कथन सत्य है या असत्व लिखिए।
- दोपहर को उठकर सभी को दौड़ना चाहिए।
- व्यायाम करनेवालों के लिए गहरी नींद बहुत जरूरी है।
- मन बड़ा साहसी था।
उत्तर:
- असत्य
- सत्य
- असत्य
![]()
कृति ग (2) : शब्द संपदा
प्रश्न 1.
शुद्ध शब्द पहचानकर लिखिए।
- भुक्खड़ों / भुक्वड़ों / भुख्खड़ों
- व्यायम / व्यायाम / ब्यायाम
- दुस्ससी / दुसाहसी / दुस्साहसी
- चिड़ियाँ / चौड़िया / चिड़ीयाँ
उत्तर :
- भुक्खड़ों
- व्यायाम
- दुस्साहसी
- चिड़ियाँ
प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।
- दिनकर
- चिंता
- विदेशी
उत्तर:
- सूरज
- फिक्र
- विलायती
![]()
कृति ग (3) : स्वमत अभिव्यक्ति
प्रश्न 1.
‘व्यायाम करने से मन की एकाग्रता बढ़ती है। इस पर अपने विचार व्यक्त कीजिए।
उत्तर:
स्वस्थ शरीर में ही स्वस्थ मन का निवास होता है। इसलिए व्यायाम हमारे लिए बहुत आवश्यक है। यह शरीर के साथ-साथ मन को भी स्वस्थ रखता है। स्वस्थ मस्तिष्क में ही किसी कार्य को करने की एकाग्रता बढ़ती है। आधुनिक युग में जब इंसान तनावभरी जिंदगी जीता है और वह अपने मन को एकाग्र करने में असमर्थ होता है; उस समय व्यायाम द्वारा ही वह मन को एकान कर पाता है। इसके द्वारा इंसान तनाव मुक्त हो जाता है और उसका मन शांत हो जाता है तथा शांत मन ही उसे सही दिशा में संचालित करता है और वह सही निर्णय लेने में सक्षम हो पाता है। व्यायाम शरीर तथा मस्तिष्क दोनों को स्फूर्ति तथा ताजगी प्रदान करता है। अत: यह कथन सही है कि व्यायाम करने से मन के एकाग्रता में वृद्धि होती है।
![]()
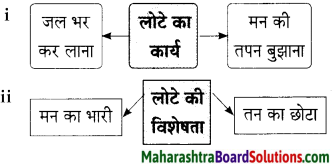
(घ) गद्यांश पड़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।
कृति घ (1) : आकलन कृति
प्रश्न 1.
समझकर लिखिए।
i. लेखक ने यह संकल्प किया –
ii. लेखक रिक्शे पर यहाँ जा रहा था –
उत्तर :
i. जिस तरह ऋषि सिर्फ हवा-पानी से रहते हैं उसी तरह लेखक भी रहेंगे।
ii. बाजार
प्रश्न 2.
आकृति पूर्ण कीजिए।
उत्तर :
कृति घ (2) : शब्द संपदा
प्रश्न 1.
गद्यांश से शब्द-युग्म छाँटकर लिखिए।
उत्तर:
i. हवा – पानी
ii. चलने – फिरने
![]()
प्रश्न 2.
निम्नलिखित शब्दों के समानार्थी शब्द लिखिए।
- अनाकृष्ट
- सम्मानित
- निराशा
- अनिच्छा
उत्तर:
- आकृष्ट
- अपमानित
- आशा
- इच्छा
![]()
कृति ग (3) : स्वमत अभिव्यक्ति
प्रश्न 1.
‘दृढ निश्चय हो, तो सफलता अवश्य मिलेगी’, इस पर अपने विचार व्यक्त कीजिए।
उत्तर :
जीवन में सफलता पाने का मूलमंत्र है दृढ़संकल्प और एकनिष्ठ प्रयास। जिस व्यक्ति की इच्छा शक्ति प्रबल होती है, सफलता उसी के कदम चूमती है। संसार में ऐसे बहुत से मनुष्य हुए जिनमें बहुत सारी दुर्बलताएँ थीं, लेकिन अपनी अटूट इच्छाशक्ति से उन्होंने उन दुर्बलताओं पर विजय प्राप्त की और सफलता के शिखर पर आरुढ़ हुए। यह सत्य है कि हम जिस वस्तु की इच्छा अपने मन से करते हैं उसे पाने के लिए हमारी शारीरिक तथा मानसिक शक्तियाँ लग जाती हैं और अपनी इच्छाशक्ति की बदौलत हम उस वस्तु को हासिल भी कर लेते हैं।
इतिहास गवाह है कि जितने भी व्यक्ति सफल हुए और दुनिया में अपना नाम कमाया, उन सारे व्यक्तियों ने अपने इच्छाशक्ती और कठिन परिश्रम से दुर्बलताओं पर विजय प्राप्त की और अपने प्रतिभा की अमिट छाप छोड़ी। इसलिए दृढ़ संकल्प तथा अटूट इच्छाशक्ति हो तो सफलता अवश्य मिलती है।
मान जा मेरे मन Summary in Hindi
लेखक-परिचय :
जीवन-परिचय : रामेश्वर सिंह कश्यप का जन्म बिहार के रोहतास जिले के सेमरा गाँव में हुआ था। सन 1950 में पटना के बीषन कालेज से उन्होंने एम.ए. किया तथा उसी साल ये पटना विश्वविद्यालय में हिंदी के व्याख्याता पद पर नियुक्त हुए। बाद में एस.पी.जैन कालेज सासाराम के प्राचार्य हुए। रामेश्वर सिंह कश्यप का रेडियो नाटक ‘लोझ सिंह’ भोजपुरी का पहला सोप ओपेरा है।
प्रमुख कृतियाँ : नाटक – ‘रोबोट’, ‘किराए का मकान’, ‘पंचर’, ‘आखिरी रात’, ‘लोहा सिंह’ आदि।
![]()
गद्य-परिचय :
हास्य-व्यंग्यात्मक निबंध : कल्पना व विज्ञान इन दोनों का समन्वय कर पाठकों के मन में जिज्ञासा निर्माण करने का कार्य साहित्य की जो विधा करती है, उसे “विज्ञान कथा’ कहते हैं। इसमें जीवन की किसी घटना का रोचक और प्रवाही वर्णन किया जाता है।
प्रस्तावना : प्रस्ततु निबंध में लेखक ने मन पर नियंत्रण न रख पाने की कमजोरी पर करारा व्यंग्य किया है तथा वास्तविकता की पहचान कराई है। लेखक ने इस निबंध के माध्यम से हमें संदेश भी दिया है कि मन पर नियंत्रण रखना आवश्यक होता है।
सारांश :
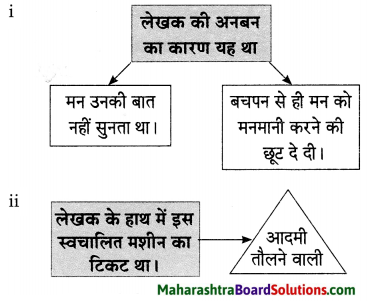
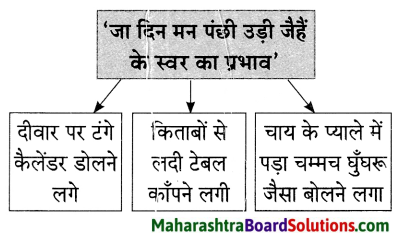
प्रस्तुत निबंध में लेखक ने मन पर नियंत्रण न रख पाने की कमजोरी पर हास्य व्यंग्य किया है। लेखक बताते हैं कि उनका मन कभी उनकी बात नहीं सुनता था जिसके कारण लेखक और उनके मन में अनबन रहती थी। अनबन का मूल कारण यह था कि पूरे जीवन लेखक ने मन को छूट दे रखी थी जिसके कारण वह बुढ़ापे में उनकी बात सुनता ही नहें था। लेखक ने अपने मन को बहुत समझाया पर मन ने उनकी एक बात नहीं सुनी। लेखक चाहता था कि उसका मोटापा दूर हो जिसके लिए उसने व्यायाम करने की योजना बनाई। उसने मन को समझाया कि वह रोज सुबह उठकर दौड़ने जाएगा तथा खाना भी कम खाएगा और व्यायाम करेगा।
यह सब सोचकर वह सो गया और सपने में भी वही दृश्य देखने लगा। अचानक उसने अपने पैरों को जोर से झटका दिया, जिससे उसकी आँख खुल गई तो पता चला कि वह टेबल के नीचे दबा पड़ा है और घर के सदस्य उसे खींचकर निकाल रहे हैं। किसी तरह वह लंगडाता हुआ चारपाई पर गया। मन ने उसे समझाया, तुम्हें चोट काफी आ गई है। सो जाओ और वह सो गया।
सुबह साढ़े नौ बजे नींद खुलने पर उसने नाश्ता करते समय कहा कि पैर की चोट समाप्त होते ही वह फिर व्यायाम करना शुरू कर देगा तो उसकी पत्नी ने कहा कि तब तक खूब खा लो। अंततः पूरी कोशिश करने के बाद भी लेखक का मन उसकी बात नहीं सुना और वह मोटापे के रोग से ग्रसित ही रहा। इसलिए लेखक बताना चाहता है कि हमें अपने मन पर नियंत्रण अवश्य रखना चाहिए जिससे की हम बुरी चीजों से दूर रहें।
![]()
शब्दार्थ :
- लापता – गायब, जिसका पता न लगे
- अनबन – मन-मुटाव
- मनमानी – अपने मन की करना
- देहरी – दहलीज
- बेलगाम – जिस पर नियंत्रण न हो
- संगीन – गंभीर
- चहल-कदमी – टहलना
- लिहाज – आदर, शर्म, लज्जा
- दृष्टांत – उदाहरण
- बाइस्कोप – फ़िल्म, चलचित्र
- विफल – व्यर्थ, असफल
- आक्षेप – आरोप
- बिसूरना – चिंतित होना
- मुग्दर – कसरत का एक साधन
- षडयंत्र – साजिश
- काट – तरह
- रुआँसा – रोते हुए
- भुक्खड़ – हमेशा खानेवाला
- विलायती – विदेशी
- ऐलान किया – घोषणा करना
- संकल्प – प्रतिज्ञा
- ऋषि – साधु
- आकृष्ट – आकर्षित
- राहगीर – आने-जाने वाले
![]()
मुहावरे :
- कन्नी काटना – बचकर निकलना।
- गौर करना – ध्यान देना।
- नाक-भौं सिकौड़ना – अप्रसन्नता प्रकट करना।
- तिलमिला उठना – क्रोधित होना।
- लेने के देने पड़ना – लाभ के बदले हानि होना।
- सुर्थी कूटना टीस उठना – अपना महत्त्व बढ़ाना।
- टीसी उठना – दर्द का अनुभव होना।
कहावतें :
- आस्तीन के साँप – अपनों में छिपा शत्रु
- एक मछली पूरे तालाब को गंदा कर देती है – एक दुर्गुणी व्यक्ति पूरे वातावरण को दूषित करता है
Hindi Lokvani 9th Std Digest पहली इकाई