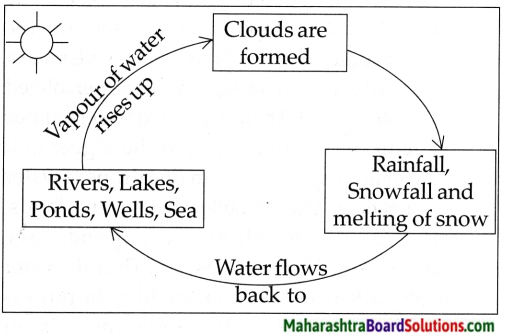
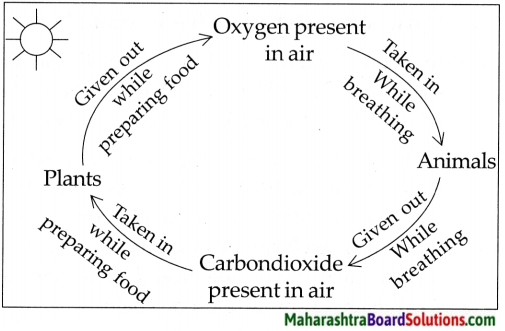
Balbharti Maharashtra State Board Class 5 Environmental Studies Solutions Chapter 2 Motions of the Earth Notes, Textbook Exercise Important Questions and Answers.
5th Standard EVS 1 Lesson Number 2 Question Answer Motions of the Earth System Maharashtra Board
Std 5 EVS 1 Chapter 2 Question Answer
1. What is the Solution?
Question 1.
What is the Solution?
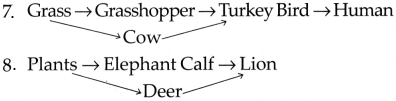
Amit wants to take his granny to Australia which is in the southern hemisphere. But she cannot bear very cold weather. When should they make this trip?
Answer:
They should take their trip between March and September because the southern hemisphere has its summer season then.
![]()
2. Use your brainpower!
Question (a)
How many rotations does the earth complete during one revolution around the sun?
Answer:
Earth makes 365 complete rotations and one quarter rotation.
Question (b)
It is sunrise at Itanagar in Arunachal Pradesh. Write the names of the following cities in the order in which the sun will rise there : Mumbai (Maharashtra), Kolkata (West Bengal), Bhopal (Madhya Pradesh), Nagpur (Maharashtra).
Answer:
Kolkata (West Bengal), Bhopal (Madhya Pradesh), Nagpur (Maharashtra), Mumbai (Maharashtra)
3. Fill in the blanks:
Question 1.
The motion of the earth around itself is called …………………… .
(a) revolution
(b) rotation
(c) dual motion
Answer:
(b) rotation
Question 2.
The motion of the earth around the sun is called ………………….. .
(a) revolution
(b) rotation
(c) dual motion
Answer:
(a) revolution
![]()
Question 3.
The rotation of the earth gives rise to …………………… .
(a) seasons
(b) day and night
(c) year
Answer:
(b) day and night
4. What is meant by each of the following terms:
Question (a)
Full moon
Answer:
At night, when we are able to see the entire illuminated part of the moon, it is called full moon.
Question (b)
New moon.
Answer:
At night, when we are not able to see the entire moon as it does not receive the sun’s light, it is called new moon.
Question (c)
Lunar month
Answer:
The period from one new moon to the next which is of 28 – 30 days is called a lunar month.
Question (d)
Tithi
Answer:
Each day of the lunar month is called a tithi.
5. Answer the following questions.
Question (a)
What is an equator?
Answer:
1. The imaginary4 circle exactly in between the north and south pole is called the equator.
2. The equator divides the earth into two equal parts.
![]()
Question (b)
What are the two parts of the earth made by the equator?
Answer:
The two equal parts of the earth made by the equator are called northern hemisphere and southern hemisphere respectively.
Environmental Studies Part 1 Standard 5th Solutions Chapter 2 Motions of the Earth Additional Important Questions and Answers
Fill in the blanks with the correct answers from the options given below:
Question 1.
The imaginary line around which the earth rotates is called its …………………….. .
(a) axis of rotation
(b) sphere of rotation
(c) line of rotation
Answer:
(a) axis of rotation
Question 2.
The earth rotates from …………………….. .
(a) east to north
(b) west to east
(c) west to south
Answer:
(b) west to east
Question 3.
We divide the whole day into ………………….. parts.
(a) 365
(b) 7
(c) 24
Answer:
(c) 24
Question 4.
The earth’s ………………….. is inclined.
(a) equator
(b) axis
(c) north pole
Answer:
(b) axis
![]()
Question 5.
The imaginary line that divides the earth into two equal parts is called the …………………… .
(a) axis
(b) rotation
(c) equator
Answer:
(c) equator
Question 6.
The earth completes one ………………….., it makes one complete turn around itself.
(a) rotation
(b) revolution
(c) season
Answer:
(a) rotation
Question 7.
The period of time that the earth takes to complete one rotation is called a …………………… .
(a) day
(b) night
(c) fortnight
Answer:
(a) day
Question 8.
A day has two parts, day and ………….. .
(a) day
(b) night
(c) fortnight
Answer:
(b) night
Question 9.
We divide the whole day into 24 parts, each of which is called an …………………… .
(a) day
(b) second
(c) hour
Answer:
(c) hour
Question 10.
There are about ………………. days and 6 hours in a year.
(a) 365
(b) 563
(c) 356
Answer:
(a) 365
![]()
Question 11.
A leap year has ………………. days.
(a) 365
(b) 366
(c) 367
Answer:
(b) 366
Question 12.
Many of our festivals are connected with the
(a) songs
(b) games
(c) seasons
Answer:
(c) seasons
Question 13.
The ……………….. revolves around the earth and the earth revolves around the sun.
(a) earth
(b) moon
(c) sun
Answer:
(b) moon
Question 14.
From the earth we see only ……………. side of the moon.
(a) three
(b) two
(c) one
Answer:
(c) one
Question 15.
The moon has no ………………… of its own.
(a) light
(b) moonlight
(c) daylight
Answer:
(a) light
Question 16.
We can see the moon because of the ………………. light which falls on it.
(a) space
(b) earth’s
(c) sun’s
Answer:
(c) sun’s
Question 17.
On a full moon night, we see the entire …………………. of the moon that faces the earth.
(a) light
(b) side
(c) night
Answer:
(b) side
Question 18.
It takes ………………. days from the new moon to the full moon.
(a) 10 or 12
(b) 14 or 15
(c) 8 or 9
Answer:
(b) 14 or 15
Question 19.
The fortnight from new moon to full moon is called ………………….. of the moon.
(a) waning
(b) waxing
(c) lunar
Answer:
(b) waxing
Question 20.
The fortnight from the full moon to the new moon is called the ………………. of the moon.
(a) waning
(b) waxing
(c) lunar
Answer:
(a) waning
Question 21.
The period from one new moon to the next is called the ……………………… month.
(a) waning
(b) waxing
(c) lunar
Answer:
(c) lunar
Question 22.
Every day of the lunar month is called a …………………….. .
(a) cycle
(b) tithi
(c) season
Answer:
(b) tithi
![]()
Question 23.
The revolution of the earth and the inclination of its axis give rise to the cycle of ………………….. .
(a) seasons
(b) festivals
(c) songs
Answer:
(a) seasons
Name the following:
Question 1.
The period of time that the earth takes to complete one rotation.
Answer:
A day
Question 2.
The period of time the earth takes to complete one revolution.
Answer:
One year
Question 3.
Number of days in a leap year.
Answer:
366
Question 4.
Three main seasons in India.
Answer:
Summer, rainy and winter
Question 5.
The cycle of six seasons.
Answer:
Rituchakra
Question 6.
Every day of the lunar month.
Answer:
A tithi
Question 7.
Two parts of a day.
Answer:
Day time and night time
Question 3.
Match the following:
| ’A’ | ‘B’ |
| (1) The Waxing moon | (a) Krishna Paksha |
| (2) The Waning moon | (b) 22 March to 23 September |
| (3) Summer in northern hemisphere | (c) Shukla Paksha |
| (4) Winter in northern hemisphere | (d) 23 September to 22 March |
Answer:
| ’A’ | ‘B’ |
| (1) The Waxing moon | (c) Shukla Paksha |
| (2) The Waning moon | (a) Krishna Paksha |
| (3) Summer in northern hemisphere | (b) 22 March to 23 September |
| (4) Winter in northern hemisphere | (d) 23 September to 22 March |
Answer the following in one sentence:
Question 1.
What is the name given to the changing shapes of the moon that we see?
Answer:
The different shapes of the moon that we see are called the phases of the moon.
Question 2.
What are the names of the days on which we see a round moon and on which day we see no moon at all?
Answer:
The day we see a round moon is called Full Moon Day and the day we see no moon is called New Moon Day.
![]()
Question 3.
What is a day?
Answer:
The period of time that the earth takes to complete one rotation is called a day, that is 24 hours.
Question 4.
What is the duration of a year?
Answer:
There are about 365 days and 6 hours in a year.
Question 5.
What causes the cycle of seasons?
Answer:
The revolution of the earth and the inclination of its axis give rise to the cycle of seasons.
Question 6.
What is the rotation of the earth?
Answer:
The movement of the earth around itself is called ‘rotation of the earth’.
Question 7.
What is ‘axis of rotation’?
Answer:
The imaginary line around which the earth rotates is called its ‘axis of rotation’. It is an imaginery line between the north pole and south pole.
Question 8.
What is the ‘equator of the earth’?
Answer:
The imaginary line that divides the earth into two equal parts i.e. the northern hemisphere and southern hemisphere is called the equator of the earth.
![]()
Question 9.
In which direction does the earth rotate?
Answer:
The earth rotates from west to east.
Question 10.
Into how many parts is the day divided?
Answer:
The day is divided into two parts i.e. day and night.
Question 11.
Into how many hours is the ‘day’ divided?
Answer:
The day is divided into 24 hours.
Question 12.
What is the revolution of the earth?
Answer:
The movement of the earth around the sun in one year is called the revolution of the earth.
Question 13.
Around whom does the moon revolve?
Answer:
The moon revolves around the earth.
Question 14.
What is waxing of the moon?
Answer:
The moon takes a fortnight to move from new moon to full moon. This period of time is known as waxing of the moon.
Question 15.
What is ‘waning of the moon’?
Answer:
The moon takes a fortnight to move from a full moon to new moon. This period of time is known as waning of the moon.
Question 16.
What is a lunar month?
Answer:
The period from one new moon to the next is of 28 to 30 days. It is called the lunar month.
Question 17.
What is’tithi’?
Answer:
Every day of the Lunar month is called a ‘tithi’.
![]()
Give geographical reasons:
Question 1.
The length of day and night is not always equal.
Answer:
The length of day and night is not always equal because:
1. Of the earth’s inclined axis.
2. Its revolution around the sun.
Question 2.
From 22 March to 23 September, northern hemisphere, experiences summer and southern hemisphere experiences winter.
Answer:
1. From 22 March to 23 September the days are longer than the night in the northern hemisphere.
2. It is warmer here.
3. So, it is summer.
4. However, at this time southern hemisphere nights are longer than the days.
5. So it receives less heat.
6. Therefore, Southern hemisphere experiences winter.
Question 3.
The sun, the moon and the earth are not always along a straight line.
Answer:
1. The moon revolves around the earth.
2. The earth revolves around the sun.
3. These two orbits intersect.
4. Hence the sun, the moon and the earth are not always along a straight line.
Question 4.
We see phases of the moon.
Answer:
1. From the full moon to the new moon the illuminated part of the moon seen from the earth becomes smaller and smaller.
2. From new moon to full moon it again grows bigger and bigger.
3. Therefore we see phases of the moon.
Question 5.
Waxing moon
Answer:
The fortnight from new moon to full moon which is 14 to 15 days is called waxing moon. Here the moon seems to become bigger and bigger, i.e. it waxes.
![]()
Question 6.
Waning moon
Answer:
The fortnight from full moon to new moon which takes 14 to 15 days is called the waning moon. Here the moon seems to become smaller and smaller, i.e. it wanes.
Answer briefly:
Question 1.
Explain ‘Phases of the moon’.
Answer:
1. From the full moon to the new moon the illuminated5 part of the moon seen from the earth becomes smaller and smaller.
2. From new moon to full moon, the illuminated part of the moon grows bigger and bigger.
3. These different shapes of the moon that we see are called the ‘phases of the moon’.
Question 2.
What are the effects of the rotation and revolution of the earth?
Answer:
1. The rotation of the earth gives rise to day and night.
2. The revolution of the earth and the inclination6 of its axis give rise to the cycle of seasons.
Write short notes on:
Question 1.
Leap year.
Answer:
- In the Gregorian calendar, the year has 365 days.
- It counts 6 hours less every year.
- That makes 24 hours or one day in every four years.
- This extra day is added in the fourth year in the month of February.
- That year will have 366 days.
- That year is called a leap year.
Question 2.
Complete the following:
Answer:

3. The fortnight of the waxing moon + the fortnight of the waning moon – A lunar month
![]()
Glossary:
- waning – decreasing
- waxing – increasing.
- orbits – regularly repeated elliptical course of a celestial object.
- imaginary – existing only in the imagination
- illuminated – lit up
- inclination – a degree of sloping.
Class 5 Environmental Studies Questions and Answers:
- Our Earth and Our Solar System Class 5 Questions And Answers
- Motions of the Earth Class 5 Questions And Answers
- The Earth and its Living World Class 5 Questions And Answers
- Environmental Balance Class 5 Questions And Answers
- Family Values Class 5 Questions And Answers
- Rules Are for Everyone Class 5 Questions And Answers
- Let us Solve Our own Problems Class 5 Questions And Answers
- Public Facilities and My School Class 5 Questions And Answers
- Maps – Our Companions Class 5 Questions And Answers
- Getting to Know India Class 5 Questions And Answers
- Our Home and Environment Class 5 Questions And Answers
- Food for All Class 5 Questions And Answers