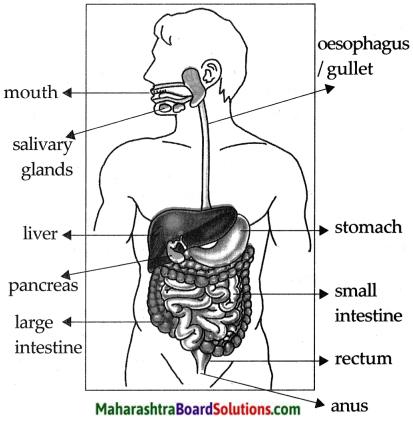
Balbharti Maharashtra State Board Class 5 Environmental Studies Solutions Chapter 18 The Environment and Us Notes, Textbook Exercise Important Questions and Answers.
5th Standard EVS 1 Lesson Number 18 Question Answer The Environment and Us Maharashtra Board
Std 5 EVS 1 Chapter 18 Question Answer
1. What’s the solution?
Question 1.
Rivers and lakes are filled with water hyacinth.
Answer:
Water hyacinth are formed in rivers and lakes due to pollution. That is mainly due to mixture of detergents in the water. To control it the water hyacinth should be removed and waste water from households or washing clothes in water should be banned.
![]()
2. Use your brain power!
Question 1.
What would happen if no kites (birds) are left in a particular region? Which living things would increase in number? Which would decrease?
Answer:
If no kites are left in a particular region the number of birds, amphibian, small mammals and earthworms would increase.
3. Answer the following questions.
Question (a)
What is meant by migration?
Answer:
Movement from one place to another for a short period of time or permanently is called migration.
Question (b)
Describe the life cycle of birds.
Answer:
Birds lay eggs. The eggs are hatched and after a few days, the small birds come out. They grow up in the nest. After three-four weeks they become an adult bird and start laying eggs.
Question (c)
Give two causes of air pollution.
Answer:
The two causes of air pollution are as follows:
1. Fuels are burnt in vehicles, give out certain poisonous gas and smoke.
2. Industries let out some poisonous gases into the air.
Question (d)
For what purpose do we use land obtained by clearing forests?
Answer:
We use land for agriculture, housing, industry and for building roads and railways by clearing forest.
![]()
4. Give reasons:
Question (a)
It is important to conserve the living components of the environment.
Answer:
It is important to conserve the living components of the environment because:
- Due to human intervention in nature the non living components are getting polluted.
- So the living things are threatened.
- Several living things have already become extinct.
- If one factor of the environment is damaged, it disturbs environmental balance.
- The process of extinction is increasingly fast.
- This will be a threat to the whole living world.
Question (b)
The numbers of wild animals are falling day by day.
Answer:
- Forests have been cut down to make place for various reasons of man’s need.
- Forest provide shelter and food to the wild animals.
- If the plants on the earth are destroyed the number of animals also fall day by day.
- Because of hunting, the population of wild animals is falling.
5. True or False:
Question (a)
Dead plants and animals are a biotic components.
Answer:
False
Question (b)
It is necessary to conserve biodiversity.
Answer:
True
![]()
6. Classify the following as natural or man-made:
Question 1.
Classify the following as natural or man-made:
Soil, horse, stone, water hyacinth, book, sunlight, dolphin, pen, chair, water, cottonwool, table, trees, brick.
Answer:
Natural – horse, water hyacinth, sunlight, dolphin, water, trees, cottonwool.
Manmade – soil, stone, book, pen, chair, table, brick.
Environmental Studies Part 1 Standard 5th Solutions Chapter 18 The Environment and Us Additional Important Questions and Answers
Fill in the blanks with the correct answers from the options given below:
Question 1.
The population of the world is now close to hundred crore.
(a) four
(b) five
(c) six
Answer:
(c) six
Question 2.
Tremendous quantities of ………………… enter the air due to burning of fuels.
(a) oxygen
(b) nitrogen
(c) carban dioxide
Answer:
(c) carban dioxide
Question 3.
The ………………….. sanctuary is known for bisons.
(a) Radhanagari
(b) Tadoba
(c) Kaziranga
Answer:
(a) Radhanagari
Question 4.
…………………… state has declared the Nannaj area a sanctuary for the Great Indian Bustard.
(a) Maharashtra
(b) Madhya Pradesh
(c) Meghalaya
Answer:
(a) Maharashtra
![]()
Question 5.
In Madhya Pradesh, Devrais are known as ………….. .
(a) Devran
(b) Sharanvan
(c) Sharanrais
Answer:
(b) Sharanvan
Question 6.
Masrhy or low-lying areas are filled to …………….. the land.
(a) rebuild
(b) reclaim
(c) restore
Answer:
(b) reclaim
Question 7.
There are many types of ……………….. in forests.
(a) plants
(b) rivers
(c) dams
Answer:
(a) plants
Question 8.
Birds build their nests in ………………. .
(a) shrubs
(b) bushes
(c) trees
Answer:
(c) trees
Question 9.
Water sources get ……………… if waste water is let into them without processing.
(a) polluted
(b) clogged
(c) depleted
Answer:
(a) polluted
Question 10.
……………… water is also given out from factories into their surroundings.
(a) Waste
(b) Running
(c) Stagnant
Answer:
(a) Waste
Question 11.
If water from such polluted sources keeps soaking into the soil, it becomes ……………….. .
(a) fertile
(b) infertile
(c) marshy
Answer:
(b) infertile
Question 12.
Chemical fertilizers and pesticides are used on a large scale for ………………. .
(a) Horticulture
(b) Vermiculture
(c) Agriculture
Answer:
(c) Agriculture
![]()
Question 13.
…………………. is used in all homes.
(a) Fuel
(b) Coal
(c) Kerosene
Answer:
(a) Fuel
Question 14.
There are big industries and factories in which ……………… is used in great quantities.
(a) water
(b) smoke
(c) fuel
Answer:
(c) fuel
Question 15.
When the proportion of carbon dioxide in the air rises, it leads to rise in ………………….. .
(a) rain
(b) temperature
(c) pollution
Answer:
(b) temperature
Question 16.
When fuels are burnt in vehicles, they give out certain ……………… gases as well as smoke.
(a) poisonous
(b) polluted
(c) natural
Answer:
(a) poisonous
Question 17.
Industries also let out some ……………….. gases into the air.
(a) poisonous
(b) polluted
(c) natural
Answer:
(a) poisonous
Question 18.
Due to human ……………………. in nature, large scale changes are taking place in air, water and land.
(a) interval
(b) intervention
(c) invention
Answer:
(b) intervention
Question 19.
From time to time, some of the living things on the earth become ………………. .
(a) strong
(b) weak
(c) extinct
Answer:
(c) extinct
![]()
Question 20.
Food, water and clothes are the …………….. of all people.
(a) basics
(b) needs
(c) pollution
Answer:
(b) needs
Question 21.
We need to take steps to prevent the …………………. of the environment.
(a) degradation
(b) pollution
(c) conservation
Answer:
(a) degradation
Question 22.
Let us all ensure that no action on our part will cause ……………….. or cause harm to living things.
(a) conservation
(b) intervention
(c) pollution
Answer:
(c) pollution
Question 23.
Let us make all possible efforts for the …………………. of the living world.
(a) conservation
(b) degradation
(c) confrontation
Answer:
(a) conservation
Question 24.
Several projects are being implemented at the international level to …………………. the balance of nature.
(a) mountain
(b) maintain
(c) destroy
Answer:
(b) maintain
Question 25.
It is important to raise the awareness of people all over the world about the …………………. to environmental balance.
(a) threat
(b) reservation
(c) treat
Answer:
(a) threat
Question 26.
In ‘biodiversity park’, biodiversity is both preserved and ……………….. .
(a) memorized
(b) studied
(c) destroyed
Answer:
(b) studied
Question 27.
People visiting ‘biodiversity park’, enjoy being close to ……………….. .
(a) parks
(b) grass
(c) nature
Answer:
(c) nature
Question 28.
Some areas which are important for the protection and conservation of wild life are …………… for them.
(a) revered
(b) reserved
(c) protected
Answer:
(b) reserved
![]()
Question 29.
If the plants on the earth are destroyed the numbers of …………………….. also fall.
(a) humans
(b) trees
(c) animals
Answer:
(c) animals
Question 30.
If deforestation is stopped, and instead tree plantation is stepped up, animals that depend on plants will get protection and ……………………. .
(a) thrive
(b) threat
(c) deplete
Answer:
(a) thrive
Question 31.
………………… lake has formed due to a dam built on the Chand river in Satara district.
(a) Victoria
(b) Mayani
(c) Tulsi
Answer:
(b) Mayani
Question 32.
………………….. from the Siberia region in northern Asia migrate to this lake.
(a) Deer
(b) Bison
(c) Flamingos
Answer:
(c) Flamingos
Question 33.
Mayani lake has been declared a ………………… for birds.
(a) sanctuary
(b) conservatory
(c) threat
Answer:
(a) sanctuary
Question 34.
People believe that a Devrai is really a jungle reserved for ………………. .
(a) us
(b) god
(c) people
Answer:
(b) god
Question 35.
Devrais give ………………. not only to the plants but also to the animals that live there.
(a) shelter
(b) food
(c) clothing
Answer:
(a) shelter
Question 2.
State whether the following statements are True or False:
- Pollution of water is a threat to aquatic plants and animals.
- Nature provides enough for every man’s greed, but not for every man’s need.
- The Maldhok is also called the Great Indian Bustard.
- Marshy or low lying areas are filled to reclaim the land.
- Man is also a part of nature.
Answer:
- True
- False
- True
- True
- False
![]()
Name the following:
Question 1.
Two National Parks.
Answer:
Kaziranga National Park and Tadoba National Park.
Question 2.
Lake built on the Chand river in Satara.
Answer:
Mayani.
Question 3.
Birds which migrate to Asia from Siberia.
Answer:
Flamingo.
Question 4.
The biggest Maldhok sanctuary in Asia.
Answer:
Nannaj in Solapur district
Question 5.
State known for Devrais.
Answer:
Maharashtra
Question 6.
Village famous for peacock population
Answer:
Morachi Chincholi
Answer in one sentence:
Question 1.
What is a biodiversity park?
Answer:
An area which is reserved for the purpose of protecting and conserving the biodiversity of a region is called a biodiversity park.
![]()
Question 2.
What are national parks?
Answer:
Some areas reserved for the protection and conservation of wildlife are called national parks.
Question 3.
What is a sanctuary?
Answer:
Certain forest areas are reserved for the protection and conservation of a particular animal or plant. It is called a sanctuary.
Question 4.
What are Devrai?
Answer:
In Indian culture, people believe that a jungle is reserved for god which is known as Devrai.
Question 5.
Which trees are commonly looked after for birds in Morachi Chincholi?
Answer:
Tamarind trees are commonly looked after for birds in Morachi Chincholi.
Question 6.
What is the population of the world?
Answer:
The population of the world is now close to six hundred crore.
Question 7.
Why is man using up more and more land and water resources?
Answer:
Man is developing new technology to meet the needs of all the people, so man is using more and more land and water resources.
Question 8.
What happens if forests are reduced?
Answer:
If forests are reduced, biodiversity is also depleted.
Question 9.
How do water sources get polluted?
Answer:
Water sources get polluted if waste water is let into them without processing.
![]()
Question 10.
What happen when water from polluted sources keep soaking into the soil?
Answer:
If water from polluted sources keep soaking into the soil, the soil become infertile.
Question 11.
What happens when the proportion of carbon dioxide in the air rises?
Answer:
When the proportion of carbon dioxide in the air rises, it leads to rise in temperature.
Question 12.
How is the environmental balance disturbed?
Answer:
If one factor of the environment is damaged, its relationships with other factors also get affected. Thus the environmental balance is disturbed.
Question 13.
What steps can be taken to prevent the degradation of the environment?
Answer:
We must use our means frugally and recycle used articles, if every person practices this sincerely then we can prevent degradation of the environment.
Question 14.
What happens when deforestation is stopped and tree plantation is stepped up?
Answer:
If deforestation is stopped and instead tree plantation is stepped up, animals that depend on plants will get protection and thrive.
Question 15.
How is the Mayani lake helpful to migratory birds?
Answer:
Mayani lake homes flamingos from Siberia who migrate to this lake. Here they build nests, lay eggs and when the baby bird grows big enough they return with them to Siberia.
Question 16.
What steps has the Maharashtra State government taken to protect the Great Indian Bustard?
Answer:
Maharashtra State has declared the Nannaj area a sanctuary for Great Indian Bustard thus helping them from extinction.
![]()
Question 17.
The environment is being degraded rapidly.
Answer:
(a) Man fulfil his needs by using materials from environment.
(b) All the people in the world have similar needs and desires.
(c) So, the environment is being degraded rapidly.
Question 18.
Flamingos have stopped coming to Mayani Lake.
Answer:
1. Flamingos used to migrate from Silbeia to Mayani lake to build their nests and lay eggs.
2. In the recent past, the water level in the dam has fallen.
3. Therefore, the flamingos have stopped coming to Mayani lake.
Question 19.
The Indian Bustard are the farmers’ friend.
Answer:
- The Indian Bustard live in open grasslands.
- They feed on insects thus giving protection to crops in fields.
- Therefore, they are the farmers’ friend.
Answer briefly:
Question 1.
Give two causes of water pollution.
Answer:
The two causes of water pollution are as follows:
1. Waste water given out from factories are let into water bodies without processing.
2. Chemical fertilizers and pesticides are used in agriculture which seep into the soil and finally flow into rivers with rainwater.
![]()
Can you tell?
(A) With the help of the questions below, explain what would happen if forests are cleared on a large scale.
Question 1.
Will water and food sources for living things grow or dwindle? Why?
Answer:
If forests are cleared the amount of rain will become less and the amount of food required will dwindle.
Question 2.
Will the living things look for shelters elsewhere or stay on? Why?
Answer:
The living things will look for shelter elsewhere if forest is cleared because forest is their home.
Question 3.
Will the space occupied by the plants and animals increase or decrease? Why?
Answer:
The space occupied by the plants and animals will decrease because forest that is cleared will be used for other purpose.
Question 4.
Will the number of living things increase or decrease? Why?
Answer:
The number of living things will decrease because forest provides food, shelter and water.
![]()
(B)
Question 1.
What could be the reasons of air pollution?
Answer:
The reasons of air pollution are increasing use of vehicles and growth of industries.
Question 2.
What are the different purposes for which fuels such as petrol, diesel, kerosene, natural gas, coal and wood are used?
Answer:
Petrol and diesel are used in vehicles. Kerosene is used in stoves. Natural gas is used for cooking. Coal and wood are used for burning.
Question (C)
You see a food chain in the picture above. One of the links is missing. What effect will it have on the grasshopper? On the bird? What picture should there be in the blank space? If this living thing really died out, what would be the threat to the entire living worlds? Discuss your answers in the class.
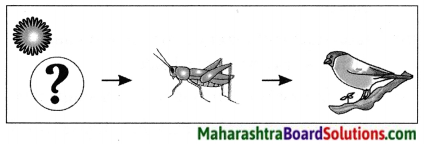
Answer:
Grass is missing. If grass is not there then the number of grasshoppers will become less or even become extinct. Birds will not get enough food and become less or may even extinct.
![]()
Glossary:
- biodiversity -variety of plant and animal life in a particular habitat
- deforestation – clearing/cutting of forests or trees.
- depleted – reduced
- frugally – sparingly
- degradation – breaking down.
- components – parts
- intervention – interference
- extinction – non-existence.
- dwindle diminish gradually.
Class 5 Environmental Studies Questions and Answers:
- Methods of Preserving Food Class 5 Questions And Answers
- Transport Class 5 Questions And Answers
- Communication and Mass Media Class 5 Questions And Answers
- Water Class 5 Questions And Answers
- Clothes – Our Necessity Class 5 Questions And Answers
- The Environment and Us Class 5 Questions And Answers
- Constituents of Food Class 5 Questions And Answers
- Our Emotional World Class 5 Questions And Answers
- Busy at Work – Our Internal Organs Class 5 Questions And Answers
- Growth and Personality Development Class 5 Questions And Answers
- Infectious Diseases and how to Prevent them Class 5 Questions And Answers
- Substances, Objects and Energy Class 5 Questions And Answers
- Community Health and Hygiene Class 5 Questions And Answers