Class 12

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.8 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.8 Questions and Answers.

Std 12 Maths 1 Exercise 1.8 Solutions Commerce Maths

Question 1.
Write the negation of each of the following statements:
(i) All the stars are shining if it is night.
Solution:
The given statement can be written as:
If it is night, then all the stars are shining.
Let p : It is night.
q : All the stars are shining.
Then the symbolic form of the given statement is p → q
Since, ~(p → q) ≡ p ∧ ~q,
the negation of the given statement is ‘It is night and all the stars are not shining.’

(ii) ∀ n ∈ N, n + 1 > 0.
Solution:
The negation of the given statement is
‘∃ n ∈ N, such that n + 1 ≤ 0.’

(iii) ∃ n ∈ N, such that (n² + 2) is odd number.
Solution:
The negation of the given statement is
‘∀ n ∈ N, n² + 2 is not an odd number.’

(iv) Some continuous functions are differentiable.
Solution:
The negation of a given statement is ‘All continuous functions are not differentiable.’

Question 2.
Using the rules of negation, write the negations of the following:
(i) (p → r) ∧ q
Solution:
The negation of (p → r) ∧ q is
~[(p → r) ∧ q] ≡ ~(p → r) ∨ (~q) …..[Negation of conjunction]
≡ (p ∧ ~r) ∨ (~q) ……[Negation of implication]

(ii) ~(p ∨ q) → r
Solution:
The negation of ~(p ∨ q) → r is
~[~(p ∨ q) → r] ≡ ~(p ∨ q) ∧ (~r) …..[Negation of implication]
≡ (~p ∧ ~q) ∧ (~r) ……[Negation of disjunction]

(iii) (~p ∧ q) ∧ (~q ∨ ~r)
Solution:
The negation of (~p ∧ q) ∧ (~q ∨ ~r) is
~[(~p ∧ q) ∧ (~q ∨ ~ r)] ≡ ~(~p ∧ q) ∨ ~(~q ∨ ~r) ……[Negation of conjunction]
≡ [~(~p) ∨ ~q] ∨ [~(~q) ∧ ~(~r)] … [Negation of conjunction and disjunction]
≡ (p ∨ ~q) ∨ (q ∧ r) …..[Negation of negation]

Question 3.
Write the converse, inverse, and contrapositive of the following statements:
(i) If it snows, then they do not drive the car.
Solution:
Let p : It snows.
q : They do not drive the car.
Then the symbolic form of the given statement is p → q.
Converse: q → p is the converse of p → q.
i.e. If they do not drive the car, then it snows.
Inverse: ~p → ~q is the inverse of p → q.
i.e. If it does not snow, then they drive the car.
Contrapositive: ~q → ~p is the contrapositive of p → q.
i.e. If they drive the car, then it does not snow.

(ii) If he studies, then he will go to college.
Solution:
Let p : He studies.
q : He will go to college.
Then two symbolic form of the given statement is p → q.
Converse: q → p is the converse of p → q.
i.e. If he will go to college, then he studies.
Inverse: ~p → ~q is the inverse of p → q.
i.e. If he does not study, then he will not go to college.
Contrapositive: ~q → ~p is the contrapositive of p → q.
i.e. If he will not go to college, then he does not study.

Question 4.
With proper justification, state the negation of each of the following:
(i) (p → q) ∨ (p → r)
Solution:
The negation of (p → q) ∨ (p → r) is
~[(p → q) ∨ (p → r)] ≡ ~(p → q) ∧ ~(p → r) …..[Negation of disjunction]
≡ (p ∧ ~q) ∧ (p ∧ ~r) …[Negation of implication]

(ii) (p ↔ q) ∨ (~q → ~r)
Solution:
The negation of (p ↔ q) ∨ (~q → ~r) is
~[(p ↔ q) ∨ (~q → ~r)] ≡ ~(p ↔ q) ∧ ~(~q → ~r) …..[Negation of disjunction]
≡ [(p ∧ ~q) ∨ (q ∧ ~p)] ∧ [~q ∧ ~(~r)] ……[Negation of biconditional and implication]
≡ [(p ∧ ~q) ∨ (q ∧ ~p)] ∧ (~q ∧ r) ……[Negation of negation]

(iii) (p → q) ∧ r
Solution:
The negation of (p → q) ∧ r is
~[(p → q) ∧ r] ≡ ~(p → q) ∨ (~r) …..[Negation of conjunction]
≡ (p ∧ ~q) ∨ (~r) …..[Negation of implication]

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.7 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.7 Questions and Answers.

Std 12 Maths 1 Exercise 1.7 Solutions Commerce Maths

Question 1.
Write the dual of each of the following:
(i) (p ∨ q) ∨ r
Solution:
(p ∧ q) ∧ r

(ii) ~(p ∨ q) ∧ [p ∨ ~(q ∧ ~r)]
Solution:
~(p ∧ q) ∨ [p ∧ ~(q ∨ ~r)]

(iii) p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r
Solution:
p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r

(iv) ~(p ∧ q) ≡ ~p ∨ ~q
Solution:
~(p ∨ q) ≡ ~p ∧ ~q

Question 2.
Write the dual statement of each of the following compound statements:
(i) 13 is prime number and India is a democratic country.
Solution:
13 is prime number or India is a democratic country.

(ii) Karina is very good or everybody likes her.
Solution:
Karina is very good and everybody likes her.

(iii) Radha and Sushmita can not read Urdu.
Solution:
Radha or Sushmita can not read Urdu.

(iv) A number is real number and the square of the number is non-negative.
Solution:
A number is real number or the square of the number is non-negative.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.6 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.6 Questions and Answers.

Std 12 Maths 1 Exercise 1.6 Solutions Commerce Maths

Question 1.
Prepare the truth tables for the following statement patterns:
(i) p → (~p ∨ q)
Solution:
Here are two statements and three connectives.
∴ there are 2 × 2 = 4 rows and 2 + 3 = 5 columns in the truth table.

(ii) (~p ∨ q) ∧ (~p ∨ ~q)
Solution:

(iii) (p ∧ r) → (p ∨ ~q)
Solution:
Here are three statements and 4 connectives.
∴ there are 2 × 2 × 2 = 8 rows and 3 + 4 = 7 columns in the truth table.

(iv) (p ∧ q) ∨ ~r
Solution:

Question 2.
Examine, whether each of the following statement patterns is a tautology or a contradiction or a contingency:
(i) q ∨ [~(p ∧ q)]
Solution:

All the entries in the last column of the above truth table are T.
∴ q ∨ [~(p ∧ q)] is a tautology.

(ii) (~q ∧ p) ∧ (p ∧ ~p)
Solution:

All the entries in the last column of the above truth table are F.
∴ (~q ∧ p) ∧ (p ∧ ~p) is a contradiction.

(iii) (p ∧ ~q) → (~p ∧ ~q)
Solution:

The entries in the last column are neither all T nor all F.
∴ (p ∧ ~q) → (~p ∧ ~q) is a contingency.

(iv) ~p → (p → ~q)
Solution:

All the entries in the last column of the truth table are T.
∴ p → (p → ~q) is a tautology.

Question 3.
Prove that each of the following statement pattern is a tautology:
(i) (p ∧ q) → q
Solution:

All the entries in the last column of the above truth table are T.
∴ (p ∧ q) → q is a tautology.

(ii) (p → q) ↔ (~q → ~p)
Solution:

All the entries in the last column of the above truth table are T.
∴ (p → q) ↔ (~q → ~p) is a tautology.

(iii) (~p ∧ ~q) → (p → q)
Solution:

All the entries in the last column of the above truth table are T.
∴ (~p ∧ ~q) → (p → q) is a tautology.

(iv) (~p ∨ ~q) ↔ ~(p ∧ q)
Solution:

All the entries in the last column of the above truth table are T.
∴ (~p ∨ ~q) ↔ ~(p ∧ q) is a tautology.

Question 4.
Prove that each of the following statement pattern is a contradiction:
(i) (p ∨ q) ∧ (~p ∧ ~q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p ∨ q) ∧ (~p ∧ ~q) is a contradiction.

(ii) (p ∧ q) ∧ ~p
Solution:

All the entries in the last column of the above truth table are T.
∴ (p ∧ q) ∧ ~p is a contradiction.

(iii) (p ∧ q) ∧ (~p ∨ ~q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p ∧ q) ∧ (~p ∨ ~q) is a contradiction.

(iv) (p → q) ∧ (p ∧ ~q)
Solution:

All the entries in the last column of the above truth table are F.
∴ (p → q) ∧ (p ∧ ~q) is a contradiction.

Question 5.
Show that each of the following statement pattern is a contingency:
(i) (p ∧ ~q) → (~p ∧ ~q)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (p ∧ ~q) → (~p ∧ ~q) is a contingency.

(ii) (p → q) ↔ (~p ∧ q)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (p → q) ↔ (~p ∧ q) is a contingency.

(iii) p ∧ [(p → ~q) → q]
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ p ∧ [(p → ~q) → q] is a contingency.

(iv) (p → q) ∧ (p → r)
Solution:

The entries in the last column of the above truth table are neither all T nor all F.
∴ (p → q) ∧ (p → r) is a contingency.

Question 6.
Using the truth table, verify:
(i) p ∨ (q ∧ r) = (p ∨ q) ∧ (p ∨ r)
Solution:

The entries in columns 5 and 8 are identical.
∴ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r).

(ii) p → (p → q) ≡ ~q → (p → q)
Solution:

The entries in columns 5 and 6 are identical.
∴ p → (p → q) ≡ ~q → (p → q)

(iii) ~(p → ~q) ≡ p ∧ ~(~q) ≡ p ∧ q
Solution:

The entries in columns 5, 7 and 8 are identical.
∴ ~(p → ~q) ≡ p ∧ ~(~q) ≡ p ∧ q.

(iv) ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p
Solution:

The entries in columns 3 and 7 are identical.
∴ ~(p ∨ q) ∨ (~p ∧ q) ≡ ~p.

Question 7.
Prove that the following pairs of statement patterns are equivalent:
(i) p ∨ (q ∧ r) and (p ∨ q) ∧ (p ∨ r)
Solution:

The entries in columns 5 and 8 are identical.
∴ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

(ii) p ↔ q and (p → q) ∧ (q → p)
Solution:

The entries in columns 3 and 6 are identical.
∴ p ↔ q ≡ (p → q) ∧ (q → p)

(iii) p → q and ~q → ~p and ~p ∨ q
Solution:

The entries in columns 5, 6 and 7 are identical.
∴ p → q ≡ ~q → ~p ≡ ~p ∨ q.

(iv) ~(p ∧ q) and ~p ∨ ~q
Solution:

The entries in columns 6 and 7 are identical.
∴ ~(p ∧ q) ≡ ~p ∨ ~q.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.5 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.5 Questions and Answers.

Std 12 Maths 1 Exercise 1.5 Solutions Commerce Maths

Question 1.
Use qualifiers to convert each of the following open sentences defined on N, into a true statement:
(i) x² + 3x – 10 = 0
Solution:
∃ x ∈ N, such that x² + 3x – 10 = 0 is a true statement
(x = 2 ∈ N satisfy x² + 3x – 10 = 0)

(ii) 3x – 4 < 9
Solution:
∃ x ∈ N, such that 3x – 4 < 9 is a true statement.
(x = 1, 2, 3, 4 ∈ N satisfy 3x – 4 < 9)

(iii) n² ≥ 1
Solution:
∀ n ∈ N, n² ≥ 1 is a true statement.
(All n ∈ N satisfy n² ≥ 1)

(iv) 2n – 1 = 5
Solution:
∃ x ∈ N, such that 2n – 1 = 5 is a true statement.
(n = 3 ∈ N satisfy 2n – 1 = 5)

(v) y + 4 > 6
Solution:
∃ y ∈ N, such that y + 4 > 6 is a true statement.
(y = 3, 4, 5, … ∈ N satisfy y + 4 > 6

(vi) 3y – 2 ≤ 9
Solution:
∃ y ∈ N, such that 2y ≤ 9 is a true statement.
(y = 1, 2, 3 ∈ N satisfy 3y – 2 ≤ 9).

Question 2.
If B = {2, 3, 5, 6, 7}, determine the truth value of each of the following:
(i) ∀ x ∈ B, x is a prime number.
Solution:
(i) x = 6 ∈ B does not satisfy x is a prime number.
So, the given statement is false, hence its truth value is F.

(ii) ∃ n ∈ B, such that n + 6 > 12.
Solution:
Clearly n = 7 ∈ B satisfies n + 6 > 12.
So, the given statement is true, hence its truth value is T.

(iii) ∃ n ∈ B, such that 2n + 2 < 4.
Solution:
No element n ∈ B satisfy 2n + 2 < 4.
So, the given statement is false, hence its truth value is F.

(iv) ∀ y ∈ B, y² is negative.
Solution:
No element y ∈ B satisfy y² is negative.
So, the given statement is false, hence its truth value is F.

(v) ∀ y ∈ B, (y – 5) ∈ N.
Solution:
y = 2 ∈ B, y = 3 ∈ B and y = 5 ∈ B do not satisfy (y – 5) ∈ N.
So, the given statement is false, hence its truth value is F.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.4 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.4 Questions and Answers.

Std 12 Maths 1 Exercise 1.4 Solutions Commerce Maths

Question 1.
Write the following statements in symbolic form:
(i) If the triangle is equilateral, then it is equiangular.
Solution:
Let p : Triangle is equilateral.
q : It is equiangular.
Then the symbolic form of the given statement is p → q.

(ii) It is not true that ‘i’ is a real number.
Solution:
Let p : ‘i’ is a real number.
Then the symbolic form of the given statement is ~p.

(iii) Even though it is not cloudy, it is still raining.
Solution:
Let p : It is cloudy.
q : It is still raining.
Then the symbolic form of the given statement is ~p ∧ q.

(iv) Milk is white if and only if the sky is not blue.
Solution:
Let p : Milk is white.
q : Sky is blue.
Then the symbolic form of the given statement is p ↔ (~q).

(v) Stock prices are high if and only if stocks are rising.
Solution:
Let p : Stock prices are high.
q : stocks are rising.
Then the symbolic form of the given statement is p ↔ q

(vi) If Kutub-Minar is in Delhi, then Taj Mahal is in Agra.
Solution:
Let p : Kutub-Minar is in Delhi.
q : Taj Mahal is in Agra.
Then the symbolic form of the given statement is p → q

Question 2.
Find the truth value of each of the following statements:
(i) It is not true that 3 – 7i is a real number.
Solution:
Let p : 3 – 7i be a real number.
Then the symbolic form of the given statement is ~p.
The truth value of p is F.
∴ the truth value of ~p is T. ….[~F ≡ T]

(ii) If a joint venture is a temporary partnership, then a discount on purchase is credited to the supplier.
Solution:
Let p : Joint venture is a temporary partnership.
q : Discount on purchases is credited to the supplier.
Then the symbolic form of the given statement is p → q.
The truth values of p and q are T and F respectively.
∴ the truth value of p → q is F. …..[T → F ≡ F]

(iii) Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
Solution:
Let p : Every accountant is free to apply his own accounting rules.
q : Machinery is an asset.
Then the symbolic form of the given statement is p ↔ q.
The truth values of p and q are F and T respectively.
∴ the truth value of p ↔ q is F. ….[F ↔ T ≡ F]

(iv) Neither 27 is a prime number nor divisible by 4.
Solution:
Let p : 27 is a prime number.
q : 27 is divisible by 4.
Then the symbolic form of the given statement is ~p ∧ ~q.
The truth values of both p and q are F.
∴ the truth value of ~p ∧ ~q is T. …..[~F ∧ ~F ≡ T ∧ T ≡ T]

(v) 3 is a prime number and an odd number.
Solution:
Let p : 3 be a prime number.
q : 3 is an odd number.
Then the symbolic form of the given statement is p ∧ q
The truth values of both p and q are T.
∴ the truth value of p ∧ q is T. …..[T ∧ T ≡ T]

Question 3.
If p and q are true and r and s are false, find the true value of each of the following statements:
(i) p ∧ (q ∧ r)
Solution:
Truth values of p and q are T and truth values of r and s are F.
p ∧ (q ∧ r) ≡ T ∧ (T ∧ F)
≡ T ∧ F
≡ F
Hence, the truth value of the given statement is false.

(ii) (p → q) ∨ (r ∧ s)
Solution:
(p → q) ∨ (r ∧ s) ≡ (T → T) ∨ (F ∧ F)
≡ T ∨ F
≡ T
Hence, the truth value of the given statement is true.

(iii) ~[(~p ∨ s) ∧ (~q ∧ r)]
Solution:
~[(~p ∨ s) ∧ (~q ∧ r)] ≡ ~[(~ T ∨ F) ∧ (~T ∧ F)]
≡ ~[(F ∨ F) ∧ (F ∧ F)]
≡ ~(F ∧ F)
≡ ~F
≡ T
Hence, the truth value of the given statement is true.

(iv) (p → q) ↔ ~(p ∨ q)
Solution:
(p → q) ↔ ~(p ∨ q) = (T → T) ↔ ~(T ∨ T)
≡ T ↔ ~ (T)
≡ T ↔ F
≡ F
Hence, the truth value of the given statement is false.

(v) [(p ∨ s) → r] ∨ [~(p → q) ∨ s]
Solution:
[(p ∨ s) → r] ∨ ~[~(p → q) ∨ s]
≡ [(T ∨ F) → F] ∨ ~[ ~(T → T) ∨ F]
≡ (T → F) ∨ ~(~T ∨ F)
≡ F ∨ ~ (F ∨ F)
≡ F ∨ ~F
≡ F ∨ T
≡ T
Hence, the truth value of the given statement is true.

(vi) ~[p ∨ (r ∧ s)] ∧ ~[(r ∧ ~s) ∧ q]
Solution:
~[p ∨ (r ∧ s)] ∧ ~[(r ∧ ~s) ∧ q]
≡ ~[T ∨ (F ∧ F)] ∧ ~[(F ∧ ~F) ∧ T]
≡ ~[T ∨ F] ∧ ~[(F ∧ T) ∧ T]
≡ ~T ∧ ~(F ∧ T)
≡ F ∧ ~F
≡ F ∧ T
≡ F
Hence, the truth value of the given statement is false.

Question 4.
Assuming that the following statements are true:
p : Sunday is a holiday.
q : Ram does not study on holiday.
Find the truth values of the following statements:
(i) Sunday is not holiday or Ram studies on holiday.
Solution:
The symbolic form of the statement is ~p ∨ ~q.

∴ the truth value of the given statement is F.

(ii) If Sunday is not a holiday, then Ram studies on holiday.
Solution:
The symbolic form of the given statement is ~p → ~q.

∴ the truth value of the given statement is T.

(iii) Sunday is a holiday and Ram studies on holiday.
Solution:
The symbolic form of the given statement is p ∧ q.

∴ the truth value of the given statement is F.

Question 5.
If p : He swims.
q : Water is warm.
Give the verbal statements for the following symbolic statements:
(i) p ↔ ~q
Solution:
p ↔ ~ q
He swims if and only if the water is not warm.

(ii) ~(p ∨ q)
Solution:
~(p ∨ q)
It is not true that he swims or water is warm.

(iii) q → p
Solution:
q → p
If water is warm, then he swims.

(iv) q ∧ ~p
Solution:
q ∧ ~p
The water is warm and he does not swim.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.3 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.3 Questions and Answers.

Std 12 Maths 1 Exercise 1.3 Solutions Commerce Maths

Question 1.
Write the negation of each of the following statements:
(i) All men are animals.
Solution:
Some men are not animals.

(ii) 3 is a natural number.
Solution:
-3 is not a natural number.

(iii) It is false that Nagpur is the capital of Maharashtra.
Solution:
Nagpur is the capital of Maharashtra.

(iv) 2 + 3 ≠ 5.
Solution:
2 + 3 = 5.

Question 2.
Write the truth value of the negation of each of the following statements:
(i) √5 is an irrational number.
Solution:
Let p : √5 is an irrational number.
The truth value of p is T.
Therefore, the truth value of ~p is F.

(ii) London is in England.
Solution:
Let p : London is in England.
The truth value of p is T.
Therefore, the truth value of ~p is F.

(iii) For every x ∈ N, x + 3 < 8.
Solution:
Let p : For every x ∈ N, x + 3 < 8.
The truth value of p is F.
Therefore, the truth value of ~p is T.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.2 Questions and Answers.

Std 12 Maths 1 Exercise 1.2 Solutions Commerce Maths

Question 1.
Express the following statements in symbolic form:
(i) e is a vowel or 2 + 3 = 5.
Solution:
Let p : e is a vowel.
q: 2 + 3 = 5.
Then the symbolic form of the given statement is p ∨ q.

(ii) Mango is a fruit but potato is a vegetable.
Solution:
Let p : Mango is a fruit.
q : Potato is a vegetable.
Then the symbolic form of the given statement is p ∧ q.

(iii) Milk is white or grass is green.
Solution:
Let p : Milk is white.
q : Grass is green.
Then the symbolic form of the given statement is p ∨ q.

(iv) I like playing but not singing.
Solution:
Let p : I like playing.
q : I am not singing.
Then the symbolic form of the given statement is p ∧ q.

(v) Even though it is cloudy, it is still raining.
Solution:
The given statement is equivalent to:
It is cloudy and it is still raining.
Let p : It is cloudy.
q : It is still raining.
Then the symbolic form of the given statement is p ∧ q.

Question 2.
Write the truth values of the following statements:
(I) Earth is a planet and Moon is a star.
Solution:
Let p : Earth is a planet.
q : Moon is a star.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. …[T ∧ F ≡ F]

(ii) 16 is an even number and 8 is a perfect square.
Solution:
Let p : 16 is an even number.
q : 8 is a perfect square.
Then the symbolic form of the given statement is p ∧ q.
The truth values of p and q are T and F respectively.
∴ the truth value of p ∧ q is F. ….[T ∧ F ≡ F]

(iii) A quadratic equation has two distinct roots or 6 has three prime factors.
Solution:
Let p : A quadratic equation has two distinct roots.
q : 6 has three prime factors.
Then the symbolic form of the given statement is p ∨ q.
The truth values of both p and q are F.
∴ the truth value of p ∨ q is F. …..[F ∨ F ≡ F]

(iv) The Himalayas are the highest mountains but they are part of India in the northeast.
Solution:
Let p : the Himalayas are the highest mountains.
q : They are part of India in the northeast.
Then the symbolic form of the given statement is p ∧ q.
The truth values of both p and q are T.
∴ the truth value of p ∧ q is T. …..[T ∧ T ≡ T]

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Mathematical Logic Class 12 Commerce Maths 1 Chapter 1 Exercise 1.1 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 1 Mathematical Logic Ex 1.1 Questions and Answers.

Std 12 Maths 1 Exercise 1.1 Solutions Commerce Maths

State which of the following sentences are statements. Justify your answer. In case of statements, write down the truth value:

Question (i).
A triangle has ‘ n’ sides.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (ii).
The sum of interior angles of a triangle is 180°.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (iii).
You are amazing!
Solution:
It is an exclamatory sentence, hence it is not a statement.

Question (iv).
Please grant me a loan.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (v).
√-4 is an irrational number.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (vi).
x² – 6x + 8 = 0 implies x = -4 or x = -2.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (vii).
He is an actor.
Solution:
It is an open sentence, hence it is not a statement.

Question (viii).
Did you eat lunch yet?
Solution:
It is an interrogative sentence, hence it is not a statement.

Question (ix).
Have a cup of cappuccino.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (x).
(x + y)² = x² + 2xy + y² for all x, y ∈ R.
Solution:
It is a mathematical identity that is true, hence its truth value is ‘T’.

Question (xi).
Every real number is a complex number.
Solution:
It is a statement that is true, hence its truth value is ‘T.

Question (xii).
1 is a prime number.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (xiii).
With the sunset, the day ends.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xiv).
1! = 0.
Solution:
It is a statement that is false, hence its truth value is

Question (xv).
3 + 5 > 11.
Solution:
It is a statement that is false, hence its truth value is ‘F’.

Question (xvi).
The number π is an irrational number.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xvii).
x² – y² = (x + y)(x – y) for all x, y ∈ R.
Solution:
It is a mathematical identity that is true, hence its truth value is ‘T’.

Question (xviii).
The number 2 is only even a prime number.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xix).
Two coplanar lines are either parallel or intersecting.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xx).
The number of arrangements of 7 girls in a row for a photograph is 7!
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xxi).
Give me a compass box.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (xxii).
Bring the motor car here.
Solution:
It is an imperative sentence, hence it is not a statement.

Question (xxiii).
It may rain today.
Solution:
It is an open sentence, hence it is not a statement.

Question (xxiv).
If a + b < 7, where a ≥ 0 and b ≥ 0, then a < 7 and b < 7.
Solution:
It is a statement that is true, hence its truth value is ‘T’.

Question (xxv).
Can you speak English?
Solution:
It is an interrogative sentence, hence it is not a statement.

12th Commerce Maths Digest Pdf

• 12th Commerce Maths Exercise 1.1 Solutions
• 12th Commerce Maths Exercise 1.2 Solutions
• 12th Commerce Maths Exercise 1.3 Solutions
• 12th Commerce Maths Exercise 1.4 Solutions
• 12th Commerce Maths Exercise 1.5 Solutions
• 12th Commerce Maths Exercise 1.6 Solutions
• 12th Commerce Maths Exercise 1.7 Solutions
• 12th Commerce Maths Exercise 1.8 Solutions
• 12th Commerce Maths Exercise 1.9 Solutions
• 12th Commerce Maths Exercise 1.10 Solutions
• 12th Commerce Maths Exercise Miscellaneous Exercise 1 Solutions

Marketing 12th OCM Chapter 8 Solutions Maharashtra Board

Balbharti Maharashtra State Board Organisation of Commerce and Management 12th Textbook Solutions Chapter 8 Marketing Textbook Exercise Questions and Answers.

Class 12 OCM Chapter 8 Exercise Solutions

1. (A) Select the correct options and rewrite the sentence

Question 1.
The term market is derived from the ………………. word ‘mercatus’.
(a) French
(b) Latin
(c) Italian
Answer:
Latin

Question 2.
In the ………………. concept of market, emphasis is given on ‘buying and selling of goods or services’.
[a) Place
(b) Exchange
(c) Customer
Answer:
Exchange

Question 3.
Perishable goods such as vegetables, fruits, milk products, etc. are sold in ………………. Market
(a) Very Short Period
(b) Short Period
(c) Long Period
Answer:
Very Short Period

Question 4.
Retail market is the market where retailer sells goods directly to the ……………… in small quantities.
(a) producer
(b) wholesaler
(c) consumer
Answer:
consumer

1. (B) Match the pairs

Question 1.

Group A	Group B
(A) Market	(1) Single Seller
(B) Registered brands	(2) Stock Market
(C) Monopoly	(3) Distinct Name
(D) Branding	(4) Mercatus
(E) Digital	(5) Single Buyer
	(6) ISI
	(7) Trademark
	(8) Use of traditional media Marketing
	(9) Multiple seller
	(10) Use of digital media

Answer:

Group A	Group B
(A) Market	(4) Mercatus
(B) Registered brands	(7) Trademark
(C) Monopoly	(1) Single Seller
(D) Branding	(3) Distinct Name
(E) Digital	(10) Use of digital media

1. (C) Give one word/phrase/term for the following statements

Question 1.
The market for the commodities which Eire produced in one country and sold in other countries.
Answer:
International market

Question 2.
Type of market where durable commodities which are generally non-perishable in nature are sold.
Answer:
Long period Market

Question 3.
The market where goods Eire sold to the ultimate consumers or the users of the product.
Answer:
Retail Market

Question 4.
Two sellers, selling either a homogeneous product or a differentiated product.
Answer:
Duopoly

Question 5.
Giving of distinct name to one’s product.
Answer:
Branding

1. (D) State whether following the statements are True or False

Question 1.
The term market is derived from the Latin word ‘mercatus’.
Answer:
True

Question 2.
Market may be defined as aggregate demand by potential buyers for a product or service.
Answer:
True

Question 3.
The market for the commodities which are produced in one country and sold in another countries is known as national market.
Answer:
False

Question 4.
In wholesale market sellers are known as retailers and buyers are known as wholesaler.
Answer:
False

Question 5.
Regulated Market operates according to forces of demand and supply.
Answer:
False

1. (E) Find the odd one

Question 1.
Primary Market, Secondary Market, Retail Market, Terminal Market
Answer:
Retail Market

Question 2.
Stock Exchange, Foreign Exchange, Bullion Market, Manufactured Goods Market
Answer:
Manufactured Goods Market

Question 3.
Price, People, Promotion, Product
Answer:
People

Question 4.
People, Promotion, Physical Environment, Process
Answer:
Promotion

1. (F) Complete the sentences

Question 1.
……………. is the place where transaction of buying and selling of goods and services take place in exchange of money or money’s worth.
Answer:
Market

Question 2.
…………… refers to a market situation when there is a single buyer of a commodity or service.
Answer:
Monopsony

Question 3.
…………….. is a slip which is found on the product and provides all the information regarding the product and its producer.
Answer:
Label

1. (G) Select the correct option and complete the following table

(Mercatus, Industrial goods, Oligopoly, E. Jerome McCarthy, Booms & Bitner)

	Group A	Group B
1.	Commodity Market	————–
2.	————–	A few sellers
3.	——————	To trade merchandise
4.	4 Ps	————–
5.	————–	3 Ps

Answer:

	Group A	Group B
1.	Commodity Market	Industrial goods
2.	Oligopoly	A few sellers
3.	Mercatus	To trade merchandise
4.	4 Ps	E Jerome McCarthy
5.	Booms & Bitner	3 Ps

1. (H) Answer in one sentence

Question 1.
What do you mean by ‘Local Market’?
Answer:
Local Market refers to local geographical area in the region within which goods and services are bought and sold, e.g. purchase of grocery from the grocery shop located near to residential area.

Question 2.
What do you mean by ‘Regulated Market’ ?
Answer:
Market which is governed (regulated) by the statutory or legal provisions of the country is called regulated market, e.g. Stock exchange, Foreign exchange, etc.

Question 3.
Define Market.
Answer:
Market is the place where two or more parties, i.e buyer and seller are involved in buying and selling of goods and services for money or money’s worth.

Question 4.
What do you mean by Standardisation?
Answer:
Standardisation means setting up of standards or fixing certain norms in relation to design, quality, size, process, weight, colour, etc. of the product.

Question 5.
What do you mean by Branding?
Answer:
Branding refers to a process in which separate identity to a product is given through unique brand name to differentiate it from other products.

1. (I) Correct the underlined word and rewrite the sentence

Question 1.
Commodity Market refers to the market for borrowing and lending long term capital required by business.
Answer:
Capital Market refers to the market for borrowing and lending long term capital required by business.

Question 2.
In duopoly there is a single seller.
Answer:
In monopoly there is a single seller.

Question 3.
Pricing bridges the time gap between production and sale of goods.
Answer:
Warehousing bridges the time gap between production and sale of goods.

Question 4.
Branding is the process of classification of products according to similar characteristics and/or quality.
Answer:
Grading is the process of classification of products according to similar characteristics and/or quality.

Question 5.
Grading helps in avoiding breakage, damage and destruction of the product.
Answer:
Packaging helps in avoiding breakage, damage and destruction of the product.

1. (J) Arrange in proper order

Question 1.
Local market, International market, National market.
Answer:
Local market, National market, International market.

Question 2.
Grading, Market Planning, Distribution.
Answer:
Market Planning, Grading, Distribution.

2. Explain the following terms/concepts

Question 1.
Market.
Answer:
(1) The word ‘market’ has originated from the Latin word ‘mercatus’ which means ‘to trade’, ‘to trade merchandise’ or ‘a place where business is transacted’. Thus, market refers to the specific place where buyers, sellers and other middlemen gather and buy and sell commodities for certain price which is predetermined or bargained.

(2) In earlier days, place played a significant role in defining the term ‘market’. However, in modern days of information technology it has got wider meaning. Now the term ‘market’ is no more restricted to specific place or area, but it implies a complex network of dealers linked physically by telephone, computer, internet and many other arrangements and facilities which effect transfer of goods and services at a place.

Question 2.
Place Concept of Market.
Answer:
Place concept of market : The place concept of market is usually taken to mean the place where the goods and services are bought and sold for money or money’s worth. In the place concept of market, emphasis is given on the place where trading takes place. It is referred to a place where buyers, sellers and other intermediaries meet and buy and sell goods and services. In ancient days the term market was defined on the basis of place only. However in recent era of information and technology market has wider meaning and not just a place.

Question 3.
Commodity Concept of Market.
Answer:
Commodity concept of market : In this concept of market more stress (significance) is given on exchange of goods and services. In this concept the process of exchange of goods and services is more important and not the place of exchange. The buyer and seller and commodity bought and sold among them play significant role in this process. Accordingly, commodity concept of market means ‘buying and selling of goods and services’.

Question 4.
Digital Concept of Market.
Answer:
Space or Digital concept of market : Growth and development of information technology gave rise to the new concept of the market known as space or digital concept. Now people can buy and sell any commodity easily and conveniently with the help of new and sophisticated E-commerce portals and mobile applications. The direct contact between buyer (customer) and seller is now possible through the communication media such as telephone, mobile, computer, internet, etc.

Question 5.
Product.
Answer:
Product : An article, goods, commodity, or service that is manufactured and offered to the customers for sale is called product. It has capacity to satisfy desire or need of the customers. The products may be either tangible or intangible. It can be in the form of goods or services. By undertaking extensive market research the business enterprises are required to decide the right type of products to be produced and sold. The product creates impact on the mind of the customers on which success or failure of business firm depends.

Question 6.
Price.
Answer:
Price : The amount of money given or required to buy a product is called price. It is essentially the amount that customer ready to pay for a product. The cost of the product, willingness of the customers to pay for the product, value and utility of the product are the main factors that businessmen have to considered while (determining) deciding the price of a product. Price of the product should be neither too high which affects the demand adversely nor too low which reduces the profitability of the business.

Question 7.
Promotion.
Answer:
Promotion : Promotion is one of the basic elements of marketing because it makes the customers aware of its product, creates brand recognition and sales. Promotion refers to any type of marketing communication used to inform and persuade potential buyers or consumers to buy the products by explaining them the regular merits of products, service, brand, etc. Promotion mix comprises of different tools such as advertising, sales promotion, direct marketing, personal selling, etc. promotional strategies to be used in the business depends on various factors such as budget, target market and the message wants to communicate.

Question 8.
Marketing Mix.
Answer:
(1) The term ‘marketing mix’ is of recent origin and it is often used in modern marketing. Marketing mix refers to the mixture or combination of various marketing variables that the business enterprises intermix and control to get expected result from the target market. In other words, marketing mix means placing the right product, at right price, in right place and at right time. It is considered as one of the important tools of marketing. Every business enterprise must develop appropriate marketing mix to expand turnover and achieve its objectives.

(2) The 4 Ps of marketing mix viz. product, price, place and promotion were introduced by E. Jerome McCarthy in 1960. Then in 1981, 4 Ps were further extended by Booms and Bitner by adding 3 new elements viz. People, Process and Physical Environment. The marketing mix is broadly categorised into two types, viz. Product Marketing Mix (first 4 Ps) and Service Marketing Mix (newly added 3 Ps). In brief, marketing mix implies taking appropriate decisions in the above stated 7 broad areas which are supplementary to one another by the business enterprise.

Question 9.
Packaging.
Answer:
Packaging : The term ‘Pack’ means a collected amount of anything wrapped up or tied together for carrying. Package is a parcel, box or container in which things are packed accordingly, packaging means a process by which a finished product is made ready for storage, delivery or transportation, usually by placing the product in container or providing it with a wrapping. It implies designing the package for the product. The aim of packaging is to protect the goods during transport and storage and to preserve the contents and the quality of the product. It facilitates easy handling of goods in transit and helps to avoid breakage, leakage, damage, spoilage, pilferage and destruction of the product.

Question 10.
Labelling.
Answer:
Labelling : The term, ‘label’ means a piece of paper, card or other material attached to an object. It is a slip affixed on the product which provides all detail information in respect to product and its producers. It also gives details of ingredients and their quantity used in the product. Labelling also gives information about the product i.e. its weight, size, price, date of manufacture and expiry name and address of manufacturer, etc. The slip on which all these information are printed is called label and its process is called labelling. A label may be part of the package or it may be attached as a tag on the product. Labelling serves as an effective tool of marketing the product. Label is used to indicate the brand, grade, quality, etc. of the product. Good labelling adds to products overall attractiveness.

3. Study the following case/situation and express your opinion

Question 1.
Mr X purchases goods from nearest shop. Mr Y purchases mobiles from Tokyo. Mr Z of Nandurbar purchases electronic goods from Delhi.

(i) From which type of market does Mr. X purchase?
(ii) Name the type of market from where Mr. Y deals.
(iii) State the type of market from where Mr. Z purchases goods.
Answer:
(i) Mr. X purchases goods from Local market.
(ii) Mr. Y purchase mobiles from Tokyo (foreign market) and hence he deals in International market.
(iii) Mr. Z of Nandurbar purchases electronic goods from Delhi, i.e. from National market.

Question 2.
Mr. X deals in import and export business so he needs different foreign currencies. For the expansion of his business, he borrows money from bank. He invests his funds in the equity shares.

(i) Name the market from where Mr. X borrows money.
(ii) Name the market where Mr. X invests his funds.
(iii) Which type of currency is required for international market?
Answer:
(i) Mr. X borrows money from capital market.
(ii) Mr. X invests his funds in the regulated market.
(iii) The different foreign currency is required by Mr. X for international market.

4. Answer in brief

Question 1.
Explain in detail the significance of marketing to the society.
Answer:
(1) Increase in standard of living : The main aim of marketing is to supply goods and services to fulfil the customers’ requirements. Marketing finds out the requirements of the customers and accordingly make efforts to supply quality products at cheaper prices. This in turn helps to maintain and raise the standard of living of the customers. In recent era, large scale production of products and services have considerably reduced their prices due to which poor people also attain reasonable level of living.

(2) Provide employment : Modern marketing i undertakes almost all functions of organisation such as buying, selling, financing, transport, warehousing, risk bearing, research and development, etc. which generate and create more job opportunities in different capacities and help to solve the problem of unemployment.

(3) Decreases distribution coats : Effective and proper utilisation of channel of distribution reduces overall cost of the products and services, Thus, marketing activities make the goods and services available to the society at cheaper prices. Due to reduction in the cost, number of potential consumers will also increase. It also gives guarantee of timely availability of the product.

(4) Consumer awareness : Marketing helps the society by educating consumers and by giving information of new products and services available in the requirements of consumers by providing relevant information, goods and services to the people as per their demand and taste. Marketing also includes information to help in making a purchase.

(5) Increase in National income : The scientifically well organised marketing activities facilitates rapid economic development of the nation. Well organised and effective marketing of products and services facilitates industrialisation, increases job opportunities and develop the economy. Effective marketing integrates agriculture and industry which in turn bring rapid development in the country.

(6) Managing consumer expectations : Marketing research enables the business organisations to understand the requirements of the consumers which helps in development of products to satisfy the customers expectation. The business organisations make certain changes in the product by considering customers’ review. Through marketing, business enterprises inform consumers about the major changes such as mergers, transfer in ownership which affect product offerings. Government regulations stop marketers to make false and misleading claims.

Question 2.
Explain 4Ps of product marketing mix.
Answer:
7 Ps of marketing are explained as follows:
(1) Product : An article, goods, commodity, or service that is manufactured and offered to the customers for sale is called product. It has capacity to satisfy desire or need of the customers. The products may be either tangible or intangible. It can be in the form of goods or services. By undertaking extensive market research the business enterprises are required to decide the right type of products to be produced and sold. The product creates impact on the mind of the customers on which success or failure of business firm depends.

(2) Price : The amount of money given or required to buy a product is called price. It is essentially the amount that customer ready to pay for a product. The cost of the product, willingness of the customers to pay for the product, value and utility of the product are the main factors that businessmen have to considered while (determining) deciding the price of a product. Price of the product should be neither too high which affects the demand adversely nor too low which reduces the profitability of the business.

(3) Place : The distribution or placement of product is a significant aspect of the marketing, Place is the element of marketing mix that ensures that right product is distribute and made conveniently available to the potential consumers or buyers at right price, at right location and at right time too. The business enterprises are required to distribute the products at a place easily approachable to the potential consumers or buyers. Place in this respect covers location, distribution and the ways of giving the products in the hand of the customers. The system of distribution decides the coverage of the product in the market.

(4) Promotion : Promotion is one of the basic elements of marketing because it makes the customers aware of its product, creates brand recognition and sales. Promotion refers to any type of marketing communication used to inform and persuade potential buyers or consumers to buy the products by explaining them the regular merits of products, service, brand, etc. Promotion mix comprises of different tools such as advertising, sales promotion, direct marketing, personal selling, etc. promotional strategies to be used in the business depends on various factors such as budget, target market and the message wants to communicate.

Question 3.
Explain 3Ps in marketing of services.
Answer:
1. People : The employees, i.e. people inside the business and consumers/customers, i.e. people outside of the business create direct or indirect impact (influence) on the business. People include all individuals that play key role in offering the product or service to the buyer or customer. People inside the business comprise employees who assist to deliver services to the customers. Right people appointed to work at right place definitely add value to the business. The management or employer of the business enterprises are required to recruit right people, train them, develop their skill and retain them for their success.

2. Process : The steps taken by the business organisation in carrying the products and services from the place of business to the doorsteps of customer are called process. Processes are significant to provide a quality service. Good process ensures same standard of service to the customers, save time and cost by enhancing efficiency. The growth and development of technology enable the business organisations in effective monitoring of the process of business and help to take corrective action if necessary.

3. Physical environment : Marketing environment in which the interaction between customer and firm takes place is called physical environment. While providing (offering) intangible services, the service providers always try to incorporate certain tangible elements into their offering to increase experience of customers. In the service market, physical or tangible evidence is essential to ensure that the service is successfully provided. Physical evidence enables the customers to trace conveniently the brand leaders in the market. The physical evidence comprises of location, layout, packaging, branding, interior design, dress of the employees, their action, waiting area, etc.

Question 4.
Explain types of market on the basis of area covered.
Answer:
On the basis of area covered:
(i) Local market: Local market refers to local geographical area in the region within which goods and services are bought and sold, e.g. purchase of grocery from grocery shop located in a market near to residential place.

(ii) National market : National market refers to the area of a country within which goods and services are bought and sold, e.g. purchase of apples on wholesale from the state of Haryana by a customer staying in Mumbai.

(iii) International market : The market where the goods and services which are manufactured in one country and sold in many other countries is called international market, e.g. purchase of petrol by Government of India from Saudi Arabia.

Question 5.
Explain types of market on the basis of time.
Answer:
On the Basis of time:
(i) Very short period market : The market which is organised and carried on for very short period of time is called very short period market. This market has existence for very short period say few hours or for a day at a particular time and place, e.g. market for perishable goods such as vegetables, milk, fish, milk products, meat, fruits, etc.

(ii) Short period market : The market which is organised and carried out its functions for short period of time is called short period market. This market has existence for a short period, weekly market, festival market, market during fairs, etc. are known as short period market. In this market mostly perishable goods and semi-durable goods are bought and sold.

(iii) Long period market : The market which is organised and continued its functions for long period of time is called long period market. This market has existence for long period of time. In this market usually durable commodities are bought and sold.

5. Justify the following statements

Question 1.
Marketing is significant to the consumers.
Answer:
Importance of marketing to the consumers:
(1) Promotes product awareness : Many companies undertake different marketing activities to promote their products and services. Marketing makes consumers aware about the different products, various brands and features of products and services available in the market. Marketing facilitates the consumers to take right decision on purchases of products. On the basis of marketing information consumers can compare product features, availability, price and other essentials. Marketing also improves the quality of life of the consumers.

(2) Provides quality products : On account of increasing competition in the market, consumers easily get information about the product and services available in the market. Marketing creates moral pressure on the business enterprises to sell quality products and services to the consumers. If business enterprises supply defective products to the consumers, sooner or later, it will create negative image of the business and adversely affect customers’ loyalty towards business and products.

(3) Provides variety of products : Marketing provides information to the consumers about the product and attracts them to purchase the same market segment or marketing plan becoming critical in any business on account of increase in customer population their preferences and availability of competitive options. The business organisation are required to launch product by considering market segment. Business organisations are required to make available variety of goods to fulfil the requirements of different market segments of the consumers. According to price, size and quality of products, variety’ may change.

(4) Helps in selection : In the competitive markets, different variety of products with different brands are available. Marketing enables the consumers to select the best products and services from the different options available.

Question 2.
Promotion plays an important role in marketing.
Answer:
(1) Promotion means any type of marketing communication used by the business enterprises to inform and persuade potential buyers to buy the products or services. In promotion merits of products, services, brand benefits, etc. are explained to the potential buyers to attract them towards the products. Promotion mix comprises of different tools such as advertising, sale, promotion, direct marketing, personal selling, publicity, etc.

(2) Business enterprises make use of combination of all or some of these five methods for promotion of their products and services as per the need of the business. Promotional activities help the organisation to increase brand awareness in the market. In brief promotion is concerned with informing the customers about the products of the firm and persuading them to buy the products.

(3) Promotional strategy to be used in the organisation depends on the various factors such as budget, the message it wants to communicate and target market. Promotion is an important element of marketing that creates brand recognition and ultimately increase sales.

(4) Business enterprises through promotion attract consumers to buy and taste the products. Promotion mix to be used will depend upon the nature of the product, type of customers, stage of demand, degree of competition, etc. Promotion helps business organisations to enhance the sales. Increase in sales, increases profit for the organisation. If the increased profit and income is reinvested in the business, it will earn more and more profits in the future. Promotion helps the organisation to create awareness about existing products, new arrivals and the company selling certain products in the market. It creates brand image among the buyers. Business organisations also use promotion to build customers’ layout base. This in turn expands sales and profits.

Question 3.
Market can be classified on the basis of competition.
Answer:
On the basis of competition:
(i) Perfect market : A type of market in which large numbers of buyers and large numbers of sellers exist to buy and sell homogeneous product at prevailing market price is called perfect market. In this market, all buyers and all sellers have equal access to all information and have perfect knowledge about the market conditions. Neither single buyer nor a single seller can influence price. One uniform single price prevails in the market, This model of perfect market is frequently used in economic analysis.

(ii) Imperfect market : A type of market which has distinct features of market imperfection such as single seller, imperfect knowledge of market conditions on the part of buyers or sellers, failure to make adjustment in demand and supply, etc. is called imperfect market, e.g. monopoly market. Imperfect market is further sub-divided into the following categories:

(a) Monopoly : The word monopoly is the combination of two words, viz. ‘mono’ means one and ‘poly’ means seller. Accordingly, a market structure which is characterised by a single seller selling unique product in the market is called monopoly. In monopoly, seller faces no competition as he is the sole seller of goods with no close substitute. He controls the entire supply and enjoys the power of setting the price for his goods. He is price maker.

(b) Duopoly : A market situation in which two suppliers dominate the entire market for a commodity or service. In this market, there are two sellers, who either sell a homogeneous product or differentiated product. They enjoy a monopoly in the product produced and sold by them.

(c) Oligopoly : Oligopoly is a state of limited competition in which market is shared by a limited number (few) of producers or sellers producing and selling either a homogeneous product or a differentiated product.

(d) Monopsony : Market situation in which there is only one buyer substantially controls the market as major and single purchaser of goods and services offered by many producers or sellers, is called monopsony market, e.g. labour market, a firm is the sole purchaser of a certain kind of labour.

Question 4.
Marketing helps in increasing consumer awareness.
Answer:
(1) Many companies undertake different marketing activities to promote their products and services. Marketing makes consumers aware about the different products, brands, features and usefulness of the products and services available in the market. Marketing facilitates the consumers to take right decisions on the purchases of right products and services.

(2) Marketing helps the society by educating consumers and through giving information of new products and services available in the market and their usefulness. Marketing identifies and satisfies the requirements of consumers by providing relevant information, goods and services to the people as per their demand and preferences. Marketing provides information to consumers to take right decisions.

(3) On the basis of marketing information, consumers can compare products features, availability, price and other essentials and chooses right products at right prices. Marketing also helps to improve the quality of life of the consumers. Marketing helps to create awareness about the existing products, new products entering into the market and the company selling specific products in the market. This in turn helps to raise awareness among the potential and prospective consumers. Marketing also creates brand image among the consumers.

(4) The business organisations use marketing to create awareness among the consumers regarding major changes such as mergers and transfer of ownership that influence products offerings or way to improve quality. Thus, marketing creates awareness among the consumers about the products available in the market and attracts the customers to buy the same.

Question 5.
There is a need of branding to get’ recognition among the consumers.
Answer:
(1) A name, design, term, symbol, sign, numeral or combination of them given to the product to identify the goods or services of the one manufacturer and to differentiate them from those of competitors, is called a brand. Branding, therefore means, giving a distinctive identity to a product. Bata, Surf, Coca-Cola, 501 soap, 50-50, etc. are some of the well-known brands. Registered brand is called trade mark. Trade mark cannot be copied by other firms. Branding is done mostly for manufactured goods.

(2) Brands are very effective for wide publicity. It helps sampling. Effectively established brands increases value of business in the industry. Good brand expands the business and create a positive impact on the business and the customers. The customers attracted towards the products are assured dependability and loyalty by using branded products. Strong branding helps to generate new customers and maintain the existing and regular customers.

(3) Branding helps the products and producers to get recognition among the consumers. Branding facilitates advertising and price control. Branded goods enjoy a wider market as the necessity or personal inspection or sample is avoided. By registering his brand, a businessman can protect his products from imitation.

(4) Branding helps to get new business and increase brand awareness in the market. It creates trust in the mind of consumers, potential consumers and people. The consumers prefer to do business with a company that has professional brand name in the market.

6. Attempt the following

Question 1.
Give classification of market in detail on the basis of ‘Volume of Transaction
Answer:
On the basis of volume of transaction:
(i) Wholesale market : Wholesale market refers to market in which goods purchased and sold in bulk (large) quantity at lower (cheaper) prices. In this market goods are purchased by the wholesalers in large quantity from manufacturers. He then sells these goods in moderate quantity to retailers who then sell these goods to consumers in small quantity. In brief, it is a market for bulk purchases and sales of goods. In this type of market, wholesalers are know as sellers and retailers are known as buyers.

(ii) Retail market : Retail market refers to market in which retailers sell goods directly to the ultimate consumers in small quantity or one to one basis, e.g. General provisional goods shop localised in market.

Question 2.
Give classification of market on the basis of ‘Time’.
Answer:
On the Basis of time:
(i) Very short period market : The market which is organised and carried on for very short period of time is called very short period market. This market has existence for very short period say few hours or for a day at a particular time and place, e.g. market for perishable goods such as vegetables, milk, fish, milk products, meat, fruits, etc.

(ii) Short period market : The market which is organised and carried out its functions for short period of time is called short period market. This market has existence for a short period, weekly market, festival market, market during fairs, etc. are known as short period market. In this market mostly perishable goods and semi-durable goods are bought and sold.

(iii) Long period market : The market which is organised and continued its functions for long period of time is called long period market. This market has existence for long period of time. In this market usually durable commodities are bought and sold.

Question 3.
Explain packaging and labelling.
Answer:
(1) Packaging : The term ‘Pack’ means a collected amount of anything wrapped up or tied together for carrying. Package is a parcel, box or container in which things are packed accordingly, packaging means a process by which a finished product is made ready for storage, delivery or transportation, usually by placing the product in container or providing it with a wrapping. It implies designing the package for the product. The aim of packaging is to protect the goods during transport and storage and to preserve the contents and the quality of the product. It facilitates easy handling of goods in transit and helps to avoid breakage, leakage, damage, spoilage, pilferage and destruction of the product.

Sealed packaging reduces the chances of adulteration or duplication of the products. Materials like bottles, containers, plastic bags, bubble bags, tin, jute bags, wooden boxes, packing foam, etc. are used for packing the product. Packaging decorates and beautifies a product and thereby creates a desire in the minds of the customers to buy the product even through they have no immediate need for it. Good packing increases durability of the product. In brief, packaging is an indispensable technique by which the goods are protected, handled, identified, advertised and sold on large scale. Thus, modern packaging promotes sales.

(2) Labelling : The term, ‘label’ means a piece of paper, card or other material attached to an object. It is a slip affixed on the product which provides all detail information in respect to product and its producers. It also gives details of ingredients and their quantity used in the product. Labelling also gives information about the product i.e. its weight, size, price, date of manufacture and expiry name and address of manufacturer, etc. The slip on which all these information are printed is called label and its process is called labelling. A label may be part of the package or it may be attached as a tag on the product. Labelling serves as an effective tool of marketing the product. Label is used to indicate the brand, grade, quality, etc. of the product. Good labelling adds to products overall attractiveness.

Question 4.
Explain standardisation and grading.
Answer:
(1) Standardisation : The term standard means an object, quality or measure serving as a basis or example to which others should confirm. It is a criterion, rule norm or measurement used for distinguishing one product from another so far its quality is concerned. Accordingly standardisation means fixing or determining certain norms or criteria with regard to the quality of a product. It may be related to process, size, quality, design, weight, colour, etc. of the product. It is a mental process of establishing standard as indicator of certain quality. It facilitates grading. Standardised commodities are easily and quickly sold even at high price in the market due to uniformity in their quality. Standardisation helps to achieve customers’ loyalty towards the product.

(2) Grading : The term ‘grade’ means a class or a category. Accordingly grading means physical sorting or classifying of products into different categories of similar characteristics or quality or set standards. Grading is done on the basis of certain features like size, shape, quality, etc. On the basis of grading, the goods are described as superior, good, better, best, inferior, medium, etc. It is necessary in agriculture, dairy, forest and mineral products. Standardisation and grading are interrelated process because without standardisation grading cannot take place and standardisation has no scope without grading.

Question 5.
Explain importance of marketing to the firm.
Answer:
The importance of marketing to the firm is explained as follows:
(1) Increases awareness : Marketing provides information and creates understanding among the consumers about the existing products, new arrivals and the company selling a particular product in the market. This in turn increases awareness among the potential consumers and creates brand image among the consumers.

(2) Increases sales : After providing information successfully about the products or services among the consumers, marketing attracts them to buy the products or services. Successful marketing campaign enables the business organisations to enhance the sales of the organisation. Expansion in sales increases profit for the organisation which is in turn reinvested in the business to earn more and more profits in the future. In recent era, survival of the business organisations depends on the effective and efficient marketing function.

(3) Create trust : The consumers usually prefer to buy required goods and services from those business enterprises which have trustworthy reputation in the market. To create trust among the customers longer time is required. Trustworthy business enterprises earn loyal customers. This trust worthiness creates customers loyalty. Satisfied customers enhance the brand image of the organisation in the market. Efficient and effective marketing plays significant role in creating good relationship between the customers and the organisation. Efficient pricing policy and appropriate after sales service improve image of the business enterprises. Majority of marketing activities move towards building brand equity of the business.

(4) Basis of making decisions : Every business organisation is required to take several decisions before delivering the final products or services to the consumers. The business organisation is required to considered or face many problems such as what to produce, how to produce, when to produce, and for whom to produce? When business expands, the decision making process becomes more complex. Effective marketing facilitates organisation to take right decisions at right time.

(5) Source of new ideas : Marketing enables the business organisations to know the requirements of the consumers. Feedbacks received from the consumers helps the manufacturers or producers to make improvement or desired changes in the existing products. Tastes and preferences of the consumers change rapidly. Due to marketing, business enterprises understand these changes and new demand pattern emerges in the market. Accordingly, Research and Development department develops the products. In the field of product development 4 Ps of marketing mix viz. product, price, place and promotion play major role. Inventions and innovations are made by the Research and Development team of the business when the need arises.

(6) Tackling the competition : On account of ; increasing competition among all the sectors of the economy, it is now difficult for any business enterprise to create monopoly for its products or services. Marketing creates brand loyalty in the mind of potential buyers. Marketing facilitates organisations to communicate the salient features and advantages of products and services to consumers and induce them to buy the same. Efficient marketing strategies depict better image of the business than competitors. The efficient management always uses modern technology for effective marketing.

7. Answer the following

Question 1.
Define Marketing and explain in detail the concepts of marketing.
Answer:
[A] Definition : The concept of ‘marketing’ has originated from the term ‘market’. The term ‘market’ implies any arrangement by which the buyers and sellers come into contact directly or indirectly to exchange goods and services at a price. Accordingly, marketing means an action or business of promoting and selling products including market research and advertising. It includes all the activities responsible for the flow of goods and services from the centre of production to ultimate consumers.

In brief, the sum total of all the activities involved in the promotion, distribution and selling of product or service from the producer or seller to the consumer or buyer is called marketing. According to Philip Kotler, “Marketing is a social process by which individuals and groups obtain what they need and want through creating, offering and freely exchanging products and services of value with others’’. Marketing is consumer-oriented. It creates customers for the goods produced in advance.

[B] Concept of marketing : The different concepts of marketing are explained below:
(1) Place concept of market : The place concept of market is usually taken to mean the place where the goods and services are bought and sold for money or money’s worth. In the place concept of market, emphasis is given on the place where trading takes place. It is referred to a place where buyers, sellers and other intermediaries meet and buy and sell goods and services. In ancient days the term market was defined on the basis of place only. However in recent era of information and technology market has wider meaning and not just a place.

(2) Commodity concept of market : In this concept of market more stress (significance) is given on exchange of goods and services. In this concept the process of exchange of goods and services is more important and not the place of exchange. The buyer and seller and commodity bought and sold among them play significant role in this process. Accordingly, commodity concept of market means ‘buying and selling of goods and services’.

(3) Exchange concept of market : Exchange concept of market has given stress on the selling and buying of goods and services between buyers and seller with free consent and mutual trust. During the buying and selling any coercion, undue influence or fraud should not be applied by either party to the transaction. The process between buyer and seller should be voluntary.

(4) Area concept of market: Area concept of market associated with exchange concept. This concept gives more stress on free association between buyers and seller to determine the price of goods to be bought and sold. To fix price it is not essential for buyer and seller to meet each other personally. With the help of different modern communication media, buyers and sellers can fix the price and complete the transaction of exchange of goods or services.

(5) Demand or customer concept of market : According to this concept, customer being the king of the market, so important side of the market is to assess (measure) then needs or demand of the customers. As per this concept market can be studied from the total size of demand or customers. This concept states that the aggregate (total) demand of prospective (potential) buyers for any product is a market.

(6) Space or Digital concept of market : Growth and development of information technology gave rise to the new concept of the market known as space or digital concept. Now people can buy and sell any commodity easily and conveniently with the help of new and sophisticated E-commerce portals and mobile applications. The direct contact between buyer (customer) and seller is now possible through the communication media such as telephone, mobile, computer, internet, etc.

Now it is easy for the customers to get information of quality, features, price, terms and conditions etc. of any products of any company. In brief, Digital market may be defined as, “market which uses Information Technology for buying and selling of the products or services and facilitate communication of quality, features, price, terms of exchange among them.

Question 2.
Explain different types of market in detail.
Answer:

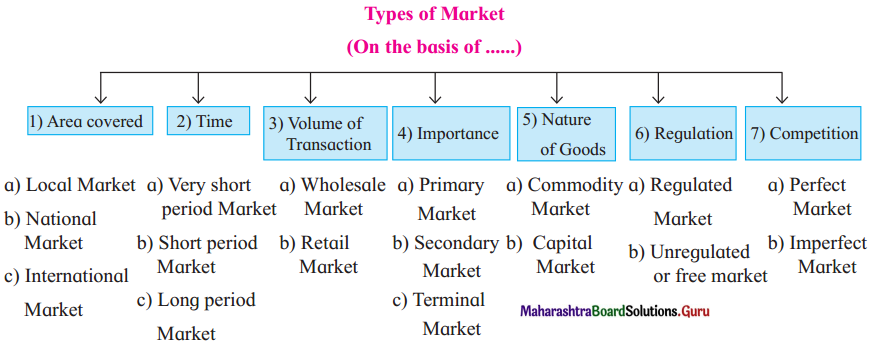
(1) On the basis of area covered:
(i) Local market: Local market refers to local geographical area in the region within which goods and services are bought and sold, e.g. purchase of grocery from grocery shop located in a market near to residential place.

(ii) National market : National market refers to the area of a country within which goods and services are bought and sold, e.g. purchase of apples on wholesale from the state of Haryana by a customer staying in Mumbai.

(iii) International market : The market where the goods and services which are manufactured in one country and sold in many other countries is called international market, e.g. purchase of petrol by Government of India from Saudi Arabia.

(2) On the Basis of time:
(i) Very short period market : The market which is organised and carried on for very short period of time is called very short period market. This market has existence for very short period say few hours or for a day at a particular time and place, e.g. market for perishable goods such as vegetables, milk, fish, milk products, meat, fruits, etc.

(ii) Short period market : The market which is organised and carried out its functions for short period of time is called short period market. This market has existence for a short period, weekly market, festival market, market during fairs, etc. are known as short period market. In this market mostly perishable goods and semi-durable goods are bought and sold.

(iii) Long period market : The market which is organised and continued its functions for long period of time is called long period market. This market has existence for long period of time. In this market usually durable commodities are bought and sold.

(3) On the basis of volume of transaction:
(i) Wholesale market : Wholesale market refers to market in which goods purchased and sold in bulk (large) quantity at lower (cheaper) prices. In this market goods are purchased by the wholesalers in large quantity from manufacturers. He then sells these goods in moderate quantity to retailers who then sell these goods to consumers in small quantity. In brief, it is a market for bulk purchases and sales of goods. In this type of market, wholesalers are know as sellers and retailers are known as buyers.

(ii) Retail market : Retail market refers to market in which retailers sell goods directly to the ultimate consumers in small quantity or one to one basis, e.g. General provisional goods shop localised in market.

(4) On the basis of importance:
(i) Primary market : The market for primary products like agricultural and forest products are called primary market, e.g. market for food grains, vegetables, fruits, etc.

(ii) Secondary market : The market for semi-manufactured goods and semi-processed goods is called secondary market, e.g. iron ore market, yarn market.

(iii) Terminal market : The market where finished goods are bought and then sold to the ultimate consumers or the users of the product.

(5) On the basis of nature of goods:
(i) Commodity market : The market for goods, material or produce is called commodity market, e.g. market for consumer goods, industrial goods, etc.

(ii) Capital market : A market place where long term funds required by business enterprises are borrowed and lent is called capital market, The financial assets which are bought and sold in the capital market have long or indefinite maturity period. It deals in both debt and equity with maturity ranging from 1 year to 10 years.

(6) On the basis of regulation:
(i) Regulated market : Markets which are governed (regulated) and controlled by the statutory or legal provisions of the country are called regulated market, e.g. stock exchanges, foreign exchanges, commodity exchanges, etc.

(ii) Unregulated or free market : The markets which are usually regulated and operated according to the forces of demand and supply and not controlled by any statutory provisions are called unregulated or free market, e.g. market for various S commodities and services.

(7) On the basis of competition:
(i) Perfect market : A type of market in which large numbers of buyers and large numbers of sellers exist to buy and sell homogeneous product at prevailing market price is called perfect market. In this market, all buyers and all sellers have equal access to all information and have perfect knowledge about the market conditions. Neither single buyer nor a single seller can influence price. One uniform single price prevails in the market, This model of perfect market is frequently used in economic analysis.

(ii) Imperfect market : A type of market which has distinct features of market imperfection such as single seller, imperfect knowledge of market conditions on the part of buyers or sellers, failure to make adjustment in demand and supply, etc. is called imperfect market, e.g. monopoly market. Imperfect market is further sub-divided into the following categories:

(a) Monopoly : The word monopoly is the combination of two words, viz. ‘mono’ means one and ‘poly’ means seller. Accordingly, a market structure which is characterised by a single seller selling unique product in the market is called monopoly. In monopoly, seller faces no competition as he is the sole seller of goods with no close substitute. He controls the entire supply and enjoys the power of setting the price for his goods. He is price maker.

(b) Duopoly : A market situation in which two suppliers dominate the entire market for a commodity or service. In this market, there are two sellers, who either sell a homogeneous product or differentiated product. They enjoy a monopoly in the product produced and sold by them.

(c) Oligopoly : Oligopoly is a state of limited competition in which market is shared by a limited number (few) of producers or sellers producing and selling either a homogeneous product or a differentiated product.

(d) Monopsony : Market situation in which there is only one buyer substantially controls the market as major and single purchaser of goods and services offered by many producers or sellers, is called monopsony market, e.g. labour market, a firm is the sole purchaser of a certain kind of labour.

Question 3.
Explain in detail 7Ps of Marketing.
Answer:
7 Ps of marketing are explained as follows:
(1) Product : An article, goods, commodity, or service that is manufactured and offered to the customers for sale is called product. It has capacity to satisfy desire or need of the customers. The products may be either tangible or intangible. It can be in the form of goods or services. By undertaking extensive market research the business enterprises are required to decide the right type of products to be produced and sold. The product creates impact on the mind of the customers on which success or failure of business firm depends.

(2) Price : The amount of money given or required to buy a product is called price. It is essentially the amount that customer ready to pay for a product. The cost of the product, willingness of the customers to pay for the product, value and utility of the product are the main factors that businessmen have to considered while (determining) deciding the price of a product. Price of the product should be neither too high which affects the demand adversely nor too low which reduces the profitability of the business.

(3) Place : The distribution or placement of product is a significant aspect of the marketing, Place is the element of marketing mix that ensures that right product is distribute and made conveniently available to the potential consumers or buyers at right price, at right location and at right time too. The business enterprises are required to distribute the products at a place easily approachable to the potential consumers or buyers. Place in this respect covers location, distribution and the ways of giving the products in the hand of the customers. The system of distribution decides the coverage of the product in the market.

(4) Promotion : Promotion is one of the basic elements of marketing because it makes the customers aware of its product, creates brand recognition and sales. Promotion refers to any type of marketing communication used to inform and persuade potential buyers or consumers to buy the products by explaining them the regular merits of products, service, brand, etc. Promotion mix comprises of different tools such as advertising, sales promotion, direct marketing, personal selling, etc. promotional strategies to be used in the business depends on various factors such as budget, target market and the message wants to communicate.

(5) People : The employees, i.e. people inside the business and consumers/customers, i.e. people outside of the business create direct or indirect impact (influence) on the business. People include all individuals that play key role in offering the product or service to the buyer or customer. People inside the business comprise employees who assist to deliver services to the customers. Right people appointed to work at right place definitely add value to the business. The management or employer of the business enterprises are required to recruit right people, train them, develop their skill and retain them for their success.

(6) Process : The steps taken by the business organisation in carrying the products and services from the place of business to the doorsteps of customer are called process. Processes are significant to provide a quality service. Good process ensures same standard of service to the customers, save time and cost by enhancing efficiency. The growth and development of technology enable the business organisations in effective monitoring of the process of business and help to take corrective action if necessary.

(7) Physical environment : Marketing environment in which the interaction between customer and firm takes place is called physical environment. While providing (offering) intangible services, the service providers always try to incorporate certain tangible elements into their offering to increase experience of customers. In the service market, physical or tangible evidence is essential to ensure that the service is successfully provided. Physical evidence enables the customers to trace conveniently the brand leaders in the market. The physical evidence comprises of location, layout, packaging, branding, interior design, dress of the employees, their action, waiting area, etc.

Question 4.
Explain the functions of marketing in detail.
Answer:
The functions of marketing are explained as follows:
(1) Marketing research : The process of identifying the need and want of the customers, gathering information from the consumers, analysing and interpreting that information is called marketing research. Marketing research helps to assess the need in the market, requirements of consumers, time of purchases, quantity of purchases and prices at which products are bought and sold, etc. Marketing Research helps the business organisations to take various decisions on the marketing of products.

(2) Buying and assembling : Buying and assembling involve buying and bringing raw materials at one place for production purpose. This marketing functions is more important because quality and price of raw materials determine (fix) cost and quality of the final product.

(3) Market planning : After estimating the need of marketing the business enterprises are required to outiine the marketing plan and strategies to accomplish the predetermined aims and objectives. Marketing planning refers to the process of defining, determining and organising the marketing aims and objectives of the business and preparing strategies to accomplish those aims and objectives. In brief, market planning is nothing but a comprehensive blueprint that outlines overall marketing efforts of the business enterprises.

(4) Product development : In recent years, product development and design become an important function of marketing. It plays significant role in marketing (selling) the products. Every business organisation is required to develop its products to suit the needs of the consumers. Product design implies decisions in the areas of quality, colour, standards, shape, design, packing, etc. of the product. Most of the consumers always buy better and attractively designed products. Good and attractive design of the product also provides competitive benefits to the business by increasing its turnover. Product development is ongoing process because the needs of the consumers change as time passes.

(5) Standardisation and grading : Standardisation means setting up of standards or fixing certain norms in relation to design, quality, size, process, weight, colour, etc. of the product. Standardisation ensures uniformity in quality of products and helps to gain customers’ loyalty towards the product. Grading means physical sorting and classifying of the products according to standards set up, i.e. similar characteristics or features. Grading is completed on the basis of some features such as size, shape, quality, etc. Usually grading is done in the case of agricultural commodities like rice, wheat, potatoes, sugar, cotton, etc.

(6) Packing and labelling : Attractive package and label make the product successful and create long lasting impression on the consumers about the product. Designing the package for the product in attractive manner is called packaging, Packaging protects the product from breakage, leakage, damage, and destruction. Botties, plastic bags, wooden boxes, bubble bags, containers, tins, jute bags, packing foams, etc. are used for packing the products. A slip providing information of product and its producer pasted or affixed on the product container is called label. It gives protection to the product and serves as an effective tool of marketing.

(7) Branding : Branding means giving a name, symbol, mark or numeral to a product for the purpose of giving a distinct identity to that product is called branding. A brand which is registered is called Trademark. No one can copy trademark in marketing field. Branding gives the product a separate identity and recognition among the consumers which helps to expand business and increase brand awareness in the market.

(8) Customer support service : As the customer is regarded as centre point or the king of the market, business organisation must take required steps to satisfy the customers. The business organisations are also required to take every possible steps to render support services to the customers. Regular support services given to the customers increase their loyalty towards the business organisation. The support services like pre-sales services, after-sales services, consumer helpline, technical assistance, product demonstration, etc. are usually provided to the customers by the businessmen. Customer support services facilitate the business organisations to get, retain and increase the customers.

(9) Pricing of product : Pricing of product is an important and challenging functions of marketing and plays significant role in the market having cut-throat competition. Many times success or failure of products depend on the price charged for the product. While fixing the price of the product the business organisation is required to considered several factor such as cost, desired profit, price of the competitions product, market condition, demand for the product, etc. As per the requirement of market, the businessmen are required to change the prices of the products. The price fixed should neither be too high which may lose customers nor too low which may compel business to incur loss. Hence for deciding the right price, extensive market research should be undertaken.

(10) Promotional channels : The process of convening the consumers information of the products, their features, prices, uses, etc. and inducing them to buy the products is called promotion. Important tools of promotion include personal selling, advertisement, publicity and sales promotion. The businessmen can use some of the tools or combination of some tools for promotion of their products. Promotional activities increase brand awareness in the market.

(11) Distribution: The activities which are related to movement of finished products from the place of business to the doorsteps of consumers are called distribution. The distribution comprises of transportation, material handling, order processing, packaging, warehousing, inventory control, market forecasting, plant and warehousing location and customer service. The business organisation is required to spend major part of marketing budget of the business or the distribution. The significance of physical distribution for business organisation mostly depends on the type of product and level of customer satisfaction.

(12) Transportation : Physical movement of finished products as well as raw material from the s place of origin or production to the doorsteps of consumers is called transportation. Transportation is necessary because production, sale and consumption cannot take place at one place. By carrying the products from the place of plenty to place of scarcity the transport creates place utility into the products. The factors such as geographical boundaries, nature of products, cost, target ; market, speed, reliability, frequency, safety, etc. help to decide the mode of transport to be used. The modes of transport used by the business are categorised as road, air, water, railways, pipeline transport.

(13) Warehousing : Warehousing means storing of goods in a godown to held them in stock from the time of production or purchase till the time of their sale. Warehousing enables the business organisation to keep and maintain a smooth flow of goods by maintaining balance between supply and demand of the products warehousing helps to stabilizes the prices in the market. This marketing function is carried out by manufacturers, wholesalers and retailers. By holding the stock of products over certain period, warehousing creates time utility in the products.

Question 5.
Explain importance of marketing to the society and consumers.
Answer:
[A] Importance of marketing to the society:
(1) Increase in standard of living : The main aim of marketing is to supply goods and services to fulfil the customers’ requirements. Marketing finds out the requirements of the customers and accordingly make efforts to supply quality products at cheaper prices. This in turn helps to maintain and raise the standard of living of the customers. In recent era, large scale production of products and services have considerably reduced their prices due to which poor people also attain reasonable level of living.

(2) Provide employment : Modern marketing i undertakes almost all functions of organisation such as buying, selling, financing, transport, warehousing, risk bearing, research and development, etc. which generate and create more job opportunities in different capacities and help to solve the problem of unemployment.

(3) Decreases distribution coats : Effective and proper utilisation of channel of distribution reduces overall cost of the products and services, Thus, marketing activities make the goods and services available to the society at cheaper prices. Due to reduction in the cost, number of potential consumers will also increase. It also gives guarantee of timely availability of the product.

(4) Consumer awareness : Marketing helps the society by educating consumers and by giving information of new products and services available in the requirements of consumers by providing relevant information, goods and services to the people as per their demand and taste. Marketing also includes information to help in making a purchase.

(5) Increase in National income : The scientifically well organised marketing activities facilitates rapid economic development of the nation. Well organised and effective marketing of products and services facilitates industrialisation, increases job opportunities and develop the economy. Effective marketing integrates agriculture and industry which in turn bring rapid development in the country.

(6) Managing consumer expectations : Marketing research enables the business organisations to understand the requirements of the consumers which helps in development of products to satisfy the customers expectation. The business organisations make certain changes in the product by considering customers’ review. Through marketing, business enterprises inform consumers about the major changes such as mergers, transfer in ownership which affect product offerings. Government regulations stop marketers to make false and misleading claims.

[B] Importance of marketing to the consumers:
(1) Promotes product awareness : Many companies undertake different marketing activities to promote their products and services. Marketing makes consumers aware about the different products, various brands and features of products and services available in the market. Marketing facilitates the consumers to take right decision on purchases of products. On the basis of marketing information consumers can compare product features, availability, price and other essentials. Marketing also improves the quality of life of the consumers.

(2) Provides quality products : On account of increasing competition in the market, consumers easily get information about the product and services available in the market. Marketing creates moral pressure on the business enterprises to sell quality products and services to the consumers. If business enterprises supply defective products to the consumers, sooner or later, it will create negative image of the business and adversely affect customers’ loyalty towards business and products.

(3) Provides variety of products : Marketing provides information to the consumers about the product and attracts them to purchase the same market segment or marketing plan becoming critical in any business on account of increase in customer population their preferences and availability of competitive options. The business organisation are required to launch product by considering market segment. The business organisations are required to make available variety of goods to fulfil the requirements of different market segments of the consumers. According to price, size and quality of products, variety’ may change.

(4) Helps in selection : In the competitive markets, different variety of products with different brands are available. Marketing enables the consumers to select the best products and services from the different options available.

(5) Consumer satisfaction : The main and primary aim of marketing policy is to advertise and give assurance of good quality product to the consumer. When the expectations and requirements of customers are fulfilled, the customers become more comfortable and get satisfied. Marketing efforts result into customers’ satisfaction by way of honest advertising, assurance of quality products and accessibility of innovative products. In this manner, marketing makes efforts to give satisfaction to the consumers.

(6) Regular supply of goods : Regular supply of goods to the consumers is practicable through effective and efficient distribution channel of marketing. Marketing also helps to keep and maintain the balance between demand and supply. As a result, prices get stabilised.

OCM 12th Commerce Textbook Solutions Digest

• 12th OCM Chapter 1 Practical Problems
• 12th OCM Chapter 2 Practical Problems
• 12th OCM Chapter 3 Practical Problems
• 12th OCM Chapter 4 Practical Problems
• 12th OCM Chapter 5 Practical Problems
• 12th OCM Chapter 6 Practical Problems
• 12th OCM Chapter 7 Practical Problems
• 12th OCM Chapter 8 Practical Problems

Consumer Protection 12th OCM Chapter 7 Solutions Maharashtra Board

Balbharti Maharashtra State Board Organisation of Commerce and Management 12th Textbook Solutions Chapter 7 Consumer Protection Textbook Exercise Questions and Answers.

Class 12 OCM Chapter 7 Exercise Solutions

1. (A) Select the correct options and rewrite the sentence

Question 1.
In India, the Consumer Protection Act was initiated in the year ………………
(a) 1947
(b) 1989
(c) 1986
Answer:
(c) 1986

Question 2.
The President of District Commission is a ………………..
(a) District Judge
(b) High Court Judge
(c) Supreme Court Judge
Answer:
(a) District Judge

Question 3.
The main objective of the consumer organization is to protect the interest of the …………………
(a) consumer
(b) trader
(c) producer
Answer:
(a) consumer

Question 4.
……………… is the highest authority to settle the consumer dispute under Act.
(a) State Commission
(b) National Commission
(c) District Commission
Answer:
(b) National Commission

Question 5.
The Government has established ……………… to settle the consumer disputes by compromise.
(a) District Commission
(b) Lok Adalat
(c) Consumer organisation
Answer:
(b) Lok Adalat

Question 6.
National Commission has ……………… members.
(a) 2
(b) 3
(c) 4
Answer:
(c) 4

Question 7.
District Commission entertains complaints of consumer for compensation which is less than ………………..
(a) one crore
(b) ten lacs
(c) ten crore
Answer:
(a) one crore

Question 8.
…………………. is celebrated as World Consumer Day.
(a) 24th December
(b) 26th January
(c) 15th March
Answer:
(c) 15th March

Question 9.
In modern competitive market, consumer is regarded as the ………………
(a) King
(b) Agency
(c) Owner
Answer:
(a) King

1. (B) Match the pairs

Question 1.

Group A	Group B
(A) King of the market	(1) 1930
(B) National Commission	(2) Socialist
(C) Mumbai Grahak Panchayat	(3) Exceeds Rs ten crore
(D) Sale of Goods Act	(4) Non-Government Organisation
(E) Consumer Right	(5) Consumer
	(6) Legislative Measures
	(7) Exceeds Rs one crore but does not exceed Rs ten crore.
	(8) 1956
	(9) Consumer Protection Act
	(10) Right to Information

Answer:

Group A	Group B
(A) King of the market	(5) Consumer
(B) National Commission	(3) Exceeds Rs ten crore
(C) Mumbai Grahak Panchayat	(4) Non-Government Organisation
(D) Sale of Goods Act	(1) 1930
(E) Consumer Right	(10) Right to Information

1. (C) Give one word/phrase/term for the following statement

Question 1.
The commission which entertains case where the value of the goods or services paid as consideration does not exceed Rs one crore.
Answer:
District Commission

Question 2.
A legal action initiated in a court of law regarding a matter of general public interest.
Answer:
Public Interest Litigation

Question 3.
Organizations which aim at promoting the welfare of the people.
Answer:
Non-Government Organizations

Question 4.
The right of consumer which is about safety and protection to his life and health.
Answer:
Right to Safety

Question 5.
One who consumes or uses any commodity or service.
Answer:
Consumer.

1. (D) State whether the following statements are True or False

Question 1.
The seller has to recognize the rights of Consumer.
Answer:
True

Question 2.
Consumer Protection Act provides protection to the producer.
Answer:
False

Question 3.
Consumer Protection Act is not required in India.
Answer:
False

Question 4.
Lok Adalat cam righty be described as “People’s Court”.
Answer:
True

Question 5.
Consumer, being the king of market, does not have any responsibility.
Answer:
False

1. (E) Find the odd one

Question 1.
District Commission, State Commission, NGO, National Commission.
Answer:
NGO

Question 2.
District Judge, High Court Judge, Commissioner, Supreme Court Judge.
Answer:
Commissioner

1. (F) Complete the sentences

Question 1.
National Commission is to be established by ………………. Government.
Answer:
Centred

Question 2.
Any person who does not agree with the decision of District Commission can appeal to the ……………….
Answer:
State Commission

Question 3.
State commission has ……………….. members.
Answer:
four

Question 4.
The President of National Commission is ………………. judge.
Answer:
Supreme Court

Question 5.
National Commission entertains complaints of consumer for compensation that exceeds Rs ………………
Answer:
ten crore

Question 6.
The Consumer Protection Act established ………………… tier quasi judicial system for consumer protection.
Answer:
three

1. (G) Select the correct option and complete the following table

(High Court Judge, Four, Consumer Organisations, does not exceeds Rs one crore, 2019)

	Group A	Group B
A.	Amount of compensation in District Commission	—————
B.	———————-	State Commission
C.	Consumer Protection Act	——————
D.	———————	Non-profit and non Political organisation
E.	Members of National Commission	——————-

Answer:

	Group A	Group B
A.	Amount of compensation in District Commission	Does not exceed Rs one crore
B.	High Court Judge	State Commission
C.	Consumer Protection Act	2019
D.	Consumer Organisations	Non-profit and non Political organisation
E.	Members of National Commission	4

1. (H) Answer in one sentence

Question 1.
When do we observe a National Consumer Day?
Answer:
On 24th December every year we observe a National Consumer Day.

Question 2.
Who is a consumer?
Answer:
A consumer means any person who buys any goods, hires any service or services for a consideration which has been paid or promised to be paid in future or under any system of deferred payment.

Question 3.
What information should one check before buying a product?
Answer:
Before buying a product the consumer should enquire about the quality, quantity, price, utility of goods and services, etc.

Question 4.
Which forum is set up at the national level for redressal of consumer complaints?
Answer:
National Consumer Disputes Redressal Commission or National Commission is set up at the national level for redressal of consumer complaints.

Question 5.
Who shall be appointed as President of National Commission?
Answer:
A person, who is or has been a Judge of the Supreme Court, shall be appointed by the Central Government as the President of National Commission in consultation with Chief Justice of India.

Question 6.
When do we observe World Consumer’s Rights Day?
Answer:
On 15th March every year we observe World Consumer’s Rights Day.

1. (I) Arrange in proper order

Question 1.
National Commission, District Commission, State Commission.
Answer:
District Commission, State Commission, National Commission.

Question 2.
District Judge, Supreme Court Judge, High Court Judge.
Answer:
District Judge, High Court Judge, Supreme Court Judge.

1. (J) Correct the underlined word and rewrite the sentence

Question 1.
An appeal can be filed against the order of the National Commission to the State forum.
Answer:
Supreme Court

Question 2.
National Commission is established by the State Government.
Answer:
Central Government

Question 3.
District Commission is also referred as People’s Court.
Answer:
Lok Adalat

Question 4.
In India, sellers are widely dispersed and are not united.
Answer:
consumers

Question 5.
National Commission entertains complaints where the value of the goods or services paid as consideration does not exceed Rs one crore.
Answer:
District Commission.

2. Explain the following term/concept:

Question 1.
District Commission.
Answer:
(1) Meaning : A consumer redressal agency established by the State Government in each district to give relief or settle the disputes of consumers who complain against manufacturers or traders, is called District Commission.

(2) Territorial Jurisdiction : District Commission can exercise its jurisdiction within the limits of its district.

(3) Monetary jurisdiction : District Commission has the jurisdiction to entertain complaints where the value of goods and services, including compensation, if any, does not exceed Rs 1 crore.

(4) Appeal : Any person not satisfied with the order of District Commission can appeal against it to the State Commission within 45 days from the date of the order in such form and manner may be prescribed.

Question 2.
National Commission.
Answer:
Meaning : A consumer disputes redressal agency at the national level established by the Central Government by notification is known as National Commission. It is also called as National Consumer Disputes Redressal Commission.

Composition : The National Commission shall consist of:
(a) President: A person who is or has been a Judge of the Supreme Court to be appointed by the Central Government as President of National Commission. Such appointment shall be made after consultation with the Chief Justice of India.

(b) Tenure : Every member of the National Commission shall hold office for a term of 5 years or up to the age prescribed whichever is earlier.

Question 3.
State Commission.
Answer:
Meaning : A consumer disputes redressal agency at state level established by each State Government is known as State Commission.

Composition : Each State Commission shall consist of:
(a) President : A person who is or has been a Judge of a High Court, shall be appointed by the State Government as the president of the State Commission in consultation with the Chief Justice of the High Court.

(b) Members : The number of other members shall not be less than 4 or not more than such number of members as may be prescribed in consultation with the Central Government.

(c) Tenure : Every member of the state commission shall hold office for a term of 5 years or up to the age of 67 years whichever is earlier.

Question 4.
Lok Adalat.
Answer:
Lok Adalat : Lok Adalat, i.e. People’s Court is established by the government to settle the disputes by compromise. It is the effective and economical system for quick redressal of public complaints and grievances. In this system the aggrieved party can directly approach the Lok Adalat with his complaint. In Lok Adalat, issues are discussed immediately and decisions are taken without delay.

The order passed by the Lok Adalat is given statutory recognition. In public sector, some organisations such as Railways, Maharashtra State Electricity Distribution Co. Ltd (MSEDCL). Maharashtra State Road Transport Corporation (MSRTC), Insurance Companies, Banks, etc. regularly hold Lok Adalat to resolve consumer’s problems through compromise.

Question 5.
Janhit Yachika.
Answer:
Public Interest Litigation (Janahit Yachika) : As name indicates it is a legal action initiated in a court of law in regard to a matter of general public interest. Under this, any person can approach a court of law in the interest of the public and ask for justice. It does not involve individual interest but interest of unrepresented groups of the society. After studying and verifying the case, the court gives justice which will benefit the specific group of society or entire society. It can be filed by any party which may not be related to grievance. In some cases Janahit Yachika can be filed in the High Court as well as in Supreme Court directly.

3. Study the following case/situation and express your opinion

Question 1.
Mr. Ashok visited a shop to buy a pair of shoes for Rs 700. The salesman forced him to buy a pair of bigger size shoes of ordinary company by claiming this size would be suitable to him. After reaching home, he discovered that shoes are still too big for him. He complained about the shoes to the shopkeeper. It was denied by the shopkeeper to replace the shoes despite of availability of stock. In above case-
(i) Which right has been violated?
(ii) Comment on the right which has been violated.
(iii) Where can Mr. Ashok file his complaint?
Answer:
(i) In the above case, Right to Choose has been violated.

(ii) In India, the choices are available to consumers to select goods and different services like telecommunications, travel and tourism, banking, electronics, consumer goods, etc. According to right to choose, consumer should be given full liberty j to select an article as per his requirements, liking and purchasing capacity. The seller cannot force or compel the customer to buy specific product or service In this manner monopoly is avoided and j prevented.

(iii) According to the Right to be Heard, Mr. Ashok can lodge complaint to the consumer forum. Mr Ashok can also file online complaint through portal or mobile applications to the trader as well as to the appropriate consumer commission or forum.

Question 2.
Mrs. Meera a resident of Nagpur District bought a washing machine worth Rs 50,000 without cash memo with a warranty period of 2 years. After 1.5 years she noticed some defect and asked the company to repair or replace it. The company did not accept her complaint despite of the defective product.
In the above case,
(i) Suggest suitable redressal machinery to protect her right.
(ii) If she is not satisfied with the decision given by redressal machinery, where should she appeal?
(iii) What was the negligence of Mrs. Meera while buying the washing machine?
Answer:
(i) According to Right to Redressal, Mrs. Meera should file complaint for fair settlement of claim. This right enables Mrs. Meera to demand repair or replacement or compensation for defective product i.e., in above case washing machine supplied. Three tier quasi-judicial consumer dispute redressal machinery is established for the settlement of claim. Mrs. Meera can file complaint in District Commission established in her district as the value of machinery does not exceed Rs 1 crore.

(ii) If Mrs. Meera is not satisfied with the order or judgement given by District Commission, then she can appeal against such order to State Commission within 45 days from the date of such order, in such form and manner as may be prescribed.

(iii) Mrs. Meera did not collect or ask for cash memo and guarantee/warranty card for a period of 2 years as soon as she purchased the washing machine worth Rs 50,000.

4. Distinguish between

Question 1.
District Commission and State Commission
Answer:

	District Commission	State Commission
1. Meaning	A consumer disputes redressal agency at the district level established by the State Government is known as District Commission.	A consumer disputes redressal agency at the state level established by the State Government is known as State Commission.
2. President	A person who is or retired or qualified as a judge of a district court is appointed as president of the. District Commission.	A person who is or retired as a judge of a High Court is appointed as president of State Commission
3. Membership tenure	Every member of District Commission shall hold office for a term of 5 years or up to the age of 65 years whichever is earlier.	Every member of State Commission shall hold office for a term of 5 years or up to the age of 67 years whichever is earlier.
4. Area covered	It has jurisdiction over a particular District.	It has jurisdiction over a particular State.
5. Monetary jurisdiction	It has the jurisdiction to entertain complaints where the value of goods or services, including compensation, if any, does not exceed Rs 1 crore.	It has the jurisdiction to entertain complaints where the value of goods or services, including compensation, if any, exceeds Rs 1 crore but does not exceed Rs 10 crore.
6. Appeal	Any person not satisfied with the order of District Commission can appeal against such order to the State Commission within 30 days of the order.	Any person not satisfied with the order of the State Commission can appeal against such order to the National Commission within 30 days of the order.

Question 2.
State Commission and National Commission
Answer:

	State Commission	National Commission
1. Meaning	A consumer disputes redressal agency at the state level established by each State Government is known as State Commission.	A consumer disputes redressal agency at the national level established by the Centred Government is known as National Commission.
2. President	A person who is or retired or qualified as a judge of a High Court is appointed as president of State Commission.	A person who is or retired as a judge of a Supreme Court is appointed as president of National Commission.
3. Membership Tenure	Every member of District Commission shall hold office for a term of 5 years or up to the age of 65 years whichever is earlier.	Every member of State Commission shall hold office for a term of 5 years or up to the age of 67 years whichever is earlier.
4. Area covered	It has jurisdiction over a particular State.	It has jurisdiction over the entire nation
5. Monetary jurisdiction	It has the jurisdiction to entertain complaints where the value of goods or services, including compensation, if any, exceeds Rs 1 crore, but does not exceed Rs 10 crore	It has the monetary jurisdiction to entertain complaints where the value of goods and services, including compensation, if any, exceeds Rs 10 crore.
6. Appeal	Any person not satisfied with the order of District Forum can appeal against such order to the State Commission within 30 days of the order.	Any person not satisfied with the order of the National Commission may appeal against such order to the Supreme Court within a period of 30 days from the date of the order.

Question 3.
District Commission and National Commission
Answer:

	District Commission	National Commission
1. Meaning	A consumer disputes redressal agency at the district level established by the State Government is known as District Commission.	A consumer disputes redressal agency at the national level established by Central Government is known as National Commission.
2. Nature of complaint	It can entertain only original cases which are within the local limits of district.	It can entertain original cases as well as appeals against the order of State Commission which are within the geographical limits of the entire nation.
3. Membership Tenure	Every member of District Forum shall hold office for a term of 5 years or up to the age of 65 years whichever is earlier	Every member of National Commission shall hold office for a term of 5 years or up to the age prescribed whichever is earlier.
4. Area covered	It has jurisdiction over a particular district.	It has jurisdiction over the entire nation.
5. Monetary jurisdiction	It has the jurisdiction to entertain complaints where the value of goods and services, including compensation, if any, does not exceed Rs 1 crore.	It has the jurisdiction to entertain complaints where the value of goods and services, including compensation, if any, exceeds Rs 10 crore.
6. Appeal	Any person not satisfied with the order of District Commission can appeal against such order to the State Commission within 30 days of the order.	Any person not satisfied with the order of National Commission can appeal against such order to the Supreme Court within a period of 30 days from the date of the order.

5. Answer in brief

Question 1.
Explain any four needs of consumer protection.
Answer:
The need of consumer protection is explained as follows:
(1) Need of participation of consumers : It is noticed that most of the organisations or manufacturing companies take certain decisions which directly or indirectly affect the consumers’ interest without consulting them or their organisations. This leads to consumer exploitation. Only a Strong consumers’ organisation can force business organisations to allow consumers to participate in the decision-making process.

(2) Lack of information : Today consumers live in a dynamic and complex world. Due to vast distance between manufacturer and consumer, it is very difficult to establish direct contact between them. Now market is fully flooded with domestic as well as foreign products due to globalisation and liberalisation. However, it is very difficult for the consumer to get correct and reliable information about the products before they are purchased. He has to rely on trial and error method or on advertisements. In both the cases chances of consumer exploitation cannot be denied.

(3) Ignorance : One of the important causes of consumer exploitation is ignorance of consumers. In India, consumers are mostly ignorant about their rights, market conditions, price levels, product details, etc. Many a time consumers are not aware that they are being cheated by the sellers. An appropriate system is required to protect consumers from business malpractices.

(4) Unorganised consumers : The consumers are widespread and unorganised. Moreover, they are not united. Hence, they are easily exploited by the producers and sellers. Sellers are in better position as compared to unorganised consumers. An individual consumer cannot fight against the powerful manufacturers or sellers.

Question 2.
State any four rights of the consumer.
Answer:
The rights of consumers are explained as follows:
(1) Right to Safety : The right to safety means the right to be protected against products, production processes and services which are hazardous to consumer’s lives or health and property. It includes consumer’s long term interest and immediate requirements. This right demands that consumer must get full safety and protection to his/her life and health in relation to medicines, food, electrical appliances, etc. AGMARK, ISI – Indian Standard Institute, BIS – Bureau of Indian standards, Hallmark, etc. are the safety standards prescribed by the Government of India (GOI).

(2) Right to Information : The consumer has a right to get correct and adequate information of all aspects of goods and services like price, name of manufacturer, contents used, batch number, date of manufacture and expiry date, use manual and safety instructions, etc. This information helps the consumers to make right choice of goods and services. This right is applicable to medicines, food products, spare parts and other consumer products or services.

(3) Right to Choose : According to this right, the consumer has full freedom to select or choose the product or service as per his/her liking, requirement and purchasing capacity. The seller cannot force a consumer to purchase a particular product. This right aims at removing monopoly. The choices available to consumers in India include goods and different services such as telecommunications, travel and tourism, banking, electronics, Fast Moving Consumer Goods (FMCG) etc.

(4) Right to Be Heard : It is the responsibility of every business organisation to listen and solve difficulties, complaints and grievances of the consumers. This right gives an opportunity to the consumers to express and voice their complaints to the consumer forum. The consumers also have rights to give suggestions to the manufacturer as well as to the trader on the quality, quantity, price, packaging, etc. of the products they use. Nowadays consumers can file online complaints through portal or mobile applications.

Question 3.
Explain any four responsibilities of the consumer.
Answer:
The responsibilities of the consumer are explained as follows:
(1) Consumer should use his rights : The consumers have many rights in respect to the goods and services they purchase. They must be aware of their rights while buying the products. They can use their rights if they are misled by advertisement or get faulty or defective articles.

(2) Cautious consumer : The consumers should be alert while dealing with the trader. They should be aware of their responsibilities while buying goods and services. Before buying any product or service, the consumer should make detail enquiry about the quality, quantity available, price, date of manufacture, expiry date, utility of goods and services, etc.

(3) Filing of complaint : If consumer has complaint about the products or services he has purchased, he should immediately approach the officer concerned and lodge complaints about the products or services. A delay in making complaints loses the rights and results in expiry of guarantee or warranty. If consumers ignore the dishonest acts of the traders, it may indirectly amount to encouragement to unethical business practices.

(4) Quality conscious : It is the responsibility of the consumers to buy quality goods. They should never compromise on the quality of goods. They should never buy inferior goods out of greed at lesser prices. For such behaviour of consumers, there is no protection. It is the responsibility of the consumer to ensure about the quality symbols like, ISI, AGMARK, Hallmark, Fruit Products Order (FPO), Food Safety and Standards Authority of India (FSSAI), etc. These are indicative of the good quality of the goods.

Question 4.
State the role of NGO in consumer protection.
Answer:
The role of Non-Government Organisations (NGOs) in consumer protection is explained as follows:
(1) NGOs organise campaigns and various programmes on consumer issues to create social awareness.

(2) They initiate and organise training i programmes for the consumers and make them : aware and conscious of their rights and various modes of redressal of their grievances.

(3) They publish journals and periodicals at regular interval to make the consumers understand and keep them informed about various consumer ) related developments.

(4) They provide legal advice free of charge to the members on the matters of consumer interest and help them to put up grievances before appropriate authority.

(5) NGO’s active members interact (communicate) with the businessmen and Chambers of Commerce and Industry for ensuring better deal for the consumers.

6. Justify the following statements

Question 1.
The Consumer Protection Act was passed in the interest of consumers.
Answer:
(1) The Consumer Protection Act came into force from 1986. Thereafter the Ministry of Law and Justice proposed new act in 2019. The Act has for the first time recognised six rights of the consumer:

• the right to be protected against marketing of hazardous goods
• the right to be informed about the price and features of goods
• the right to make a choice out of a variety of goods
• the right to make a complaint against unsatisfactory goods
• the right to seek redressal against unfair trade practices
• the right to consumer education. All the above rights are in the interest of the consumer and not the seller.

(2) The Act has made provision for the establishment of Consumer Protection Councils at the central and state levels for promoting and protecting these rights.

(3) The Act has created a quasi-judicial machinery consisting of the District Commission, State Commission and National Commission to entertain complaints and to give fair justice to the aggrieved consumers. The Act prescribes punishment of imprisonment not less than one month which may extend to 3 years and a fine which shall not be less than ? 25,000 which may extend to Rs 1 lakh or with both for guilty person.

(4) The strict enforcement of these rights creates a competition among the sellers. Consequently, the consumers get quality goods at fair prices. The government has also adopted various measures for creating public awareness about the rights of consumers. Various programmes are shown on television channels as well as programmes are broadcasted by All India to educate consumers.

Question 2.
Consumers have many responsibilities.
Answer:
The responsibilities of the consumer are explained as follows:
(1) Consumer should use his rights : The consumers have many rights in respect to the goods and services they purchase. They must be aware of their rights while buying the products. They can use their rights if they are misled by advertisement or get faulty or defective articles.

(2) Cautious consumer : The consumers should be alert while dealing with the trader. They should be aware of their responsibilities while buying goods and services. Before buying any product or service, the consumer should make detail enquiry about the quality, quantity available, price, date of manufacture, expiry date, utility of goods and services, etc.

(3) Filing of complaint : If consumer has complaint about the products or services he has purchased, he should immediately approach the officer concerned and lodge complaints about the products or services. A delay in making complaints loses the rights and results in expiry of guarantee or warranty. If consumers ignore the dishonest acts of the traders, it may indirectly amount to encouragement to unethical business practices.

(4) Quality conscious : It is the responsibility of the consumers to buy quality goods. They should never compromise on the quality of goods. They should never buy inferior goods out of greed at lesser prices. For such behaviour of consumers, there is no protection. It is the responsibility of the consumer to ensure about the quality symbols like, ISI, AGMARK, Hallmark, Fruit Products Order (FPO), Food Safety and Standards Authority of India (FSSAI), etc. These are indicative of the good quality of the goods.

(5) Beware from exaggerated advertisement: The sellers always provide various information of the products or services through advertisements to buyers. Many a time they exaggerate the facts in their advertisements. It is the responsibility of the consumers to find out or identify the truth of advertisement and then buy the products, or services.

Question 3.
Aim of consumer organization is to protect the rights of the consumers.
Answer:
The role of Non-Government Organisations (NGOs) in consumer protection is explained as follows:
(1) NGOs organise campaigns and various programmes on consumer issues to create social awareness.

(2) They initiate and organise training i programmes for the consumers and make them : aware and conscious of their rights and various modes of redressal of their grievances.

(3) They publish journals and periodicals at regular interval to make the consumers understand and keep them informed about various consumer ) related developments.

(4) They provide legal advice free of charge to the members on the matters of consumer interest and help them to put up grievances before appropriate authority.

(5) NGO’s active members interact (communicate) with the businessmen and Chambers of Commerce and Industry for ensuring better deal for the consumers.

(6) They file Public Interest Litigation (Janhit Yachika) on important consumer issues like ban on a product or medicine injurious to public health. They also file cases in the court of law to safeguard the rights and protect the interest of general public.

(7) Few examples of NGOs working for the consumers are : Consumer Guidance Society of India (CGSI), Voluntary Organisation in Interest of Consumer Education (VOICE), Consumer Education and Research Centre (CERC), Consumers Association of India (CAI), Mumbai Grahak Panchayat (MGP), Grahak Shakti (GS), etc.

7. Attempt the following

Question 1.
State rights of the consumer.
Answer:
The rights of consumers are explained as follows:
(1) Right to Safety : The right to safety means the right to be protected against products, production processes and services which are hazardous to consumer’s lives or health and property. It includes consumer’s long term interest and immediate requirements. This right demands that consumer must get full safety and protection to his/her life and health in relation to medicines, food, electrical appliances, etc. AGMARK, ISI – Indian Standard Institute, BIS – Bureau of Indian standards, Hallmark, etc. are the safety standards prescribed by the Government of India (GOI).

(2) Right to Information : The consumer has a right to get correct and adequate information of all aspects of goods and services like price, name of manufacturer, contents used, batch number, date of manufacture and expiry date, use manual and safety instructions, etc. This information helps the consumers to make right choice of goods and services. This right is applicable to medicines, food products, spare parts and other consumer products or services.

(3) Right to Choose : According to this right, the consumer has full freedom to select or choose the product or service as per his/her liking, requirement and purchasing capacity. The seller cannot force a consumer to purchase a particular product. This right aims at removing monopoly. The choices available to consumers in India include goods and different services such as telecommunications, travel and tourism, banking, electronics, Fast Moving Consumer Goods (FMCG) etc.

(4) Right to Be Heard : It is the responsibility of every business organisation to listen and solve difficulties, complaints and grievances of the consumers. This right gives an opportunity to the consumers to express and voice their complaints to the consumer forum. The consumers also have rights to give suggestions to the manufacturer as well as to the trader on the quality, quantity, price, packaging, etc. of the products they use. Nowadays consumers can file online complaints through portal or mobile applications.

(5) Right to Consumer Education : The consumers have right to know about consumer rights and solutions to their problems. This is to create awareness among the consumers to make rational choice of goods and services and to protect themselves from the exploitation of unscrupulous (dishonest) businessmen. In this regard, the government, media and various Non-Government Organisations (NGOs) can play an important role to create awareness among the consumers and to educate them, e.g. Jago Grahak Jago campaign.

(6) Right to Represent : The Consumer Protection Act, 2019 gave an opportunity to individual consumer as well as to consumer groups to be represented by a person who is not professional advocate for consumer’s interest or complaint before consumer forum. This provision made in the Act in recognition of consumers’ right to represent.

Question 2.
State responsibilities of the consumer.
Answer:
The responsibilities of the consumer are explained as follows:
(1) Consumer should use his rights : The consumers have many rights in respect to the goods and services they purchase. They must be aware of their rights while buying the products. They can use their rights if they are misled by advertisement or get faulty or defective articles.

(2) Cautious consumer : The consumers should be alert while dealing with the trader. They should be aware of their responsibilities while buying goods and services. Before buying any product or service, the consumer should make detail enquiry about the quality, quantity available, price, date of manufacture, expiry date, utility of goods and services, etc.

(3) Filing of complaint : If consumer has complaint about the products or services he has purchased, he should immediately approach the officer concerned and lodge complaints about the products or services. A delay in making complaints loses the rights and results in expiry of guarantee or warranty. If consumers ignore the dishonest acts of the traders, it may indirectly amount to encouragement to unethical business practices.

(4) Quality conscious : It is the responsibility of the consumers to buy quality goods. They should never compromise on the quality of goods. They should never buy inferior goods out of greed at lesser prices. For such behaviour of consumers, there is no protection. It is the responsibility of the consumer to ensure about the quality symbols like, ISI, AGMARK, Hallmark, Fruit Products Order (FPO), Food Safety and Standards Authority of India (FSSAI), etc. These are indicative of the good quality of the goods.

(5) Beware from exaggerated advertisement: The sellers always provide various information of the products or services through advertisements to buyers. Many a time they exaggerate the facts in their advertisements. It is the responsibility of the consumers to find out or identify the truth of advertisement and then buy the products, or services.

(6) Demand of Invoice and Guarantee, Warranty Card : After purchasing the products, the consumer should ask for cash memo, guarantee or warranty card. The consumer should read and understand the contents of guarantee or warranty card. He should preserve the cash memo and guarantee or warranty card. If the products purchased are of inferior quality or become defective these cards are useful to settle the disputes and claim compensation or replacement of articles.

(7) Pre-planned buying : It is the responsibility of the consumer to make proper planning before buying any product. He should make an estimate of products they want to buy and quantity required, money to spend, etc. He should also decide in advance from which place to buy the products. He should not buy any product in a hurry or without thought.

(8) Organised efforts : The consumer is expected to shoulder the responsibility to promote and protect the interests of his own and other consumers. He should join the group or organisation which is working for the welfare of consumers. It is the responsibility of every consumer to unite for the welfare of all the consumers.

Question 3.
State the need of consumer protection.
Answer:
The need of consumer protection is explained as follows:
(1) Need of participation of consumers : It is noticed that most of the organisations or manufacturing companies take certain decisions which directly or indirectly affect the consumers’ interest without consulting them or their organisations. This leads to consumer exploitation. Only a Strong consumers’ organisation can force business organisations to allow consumers to participate in the decision-making process.

(2) Lack of information : Today consumers live in a dynamic and complex world. Due to vast distance between manufacturer and consumer, it is very difficult to establish direct contact between them. Now market is fully flooded with domestic as well as foreign products due to globalisation and liberalisation. However, it is very difficult for the consumer to get correct and reliable information about the products before they are purchased. He has to rely on trial and error method or on advertisements. In both the cases chances of consumer exploitation cannot be denied.

(3) Ignorance : One of the important causes of consumer exploitation is ignorance of consumers. In India, consumers are mostly ignorant about their rights, market conditions, price levels, product details, etc. Many a time consumers are not aware that they are being cheated by the sellers. An appropriate system is required to protect consumers from business malpractices.

(4) Unorganised consumers : The consumers are widespread and unorganised. Moreover, they are not united. Hence, they are easily exploited by the producers and sellers. Sellers are in better position as compared to unorganised consumers. An individual consumer cannot fight against the powerful manufacturers or sellers.

(5) Spurious Goods : The consumers also face a major problem of duplicate goods. Some traders cheat the consumers by supplying them duplicate or defective goods of the popular brands. It is not possible for the consumers to find difference between genuine and duplicate product. It is therefore necessary to protect the consumers from such exploitation by fixing prescribed norms of quality and safety standards.

(6) Misleading advertising : Sometimes the advertisements of goods and services shown on television, in newspapers and magazines are misleading. They make tall claims about the benefits of the products but do not disclose the drawbacks. Most of the consumers are misled by the misleading advertisement and do not know the real and true quality of advertised products. Appropriate system or mechanism is required to prevent misleading advertisements.

(7) Malpractices of Businessmen : Many businessmen adopt fraudulent, unethical and monopolistic trade practices to earn more money. This leads to exploitation of consumers. Some times consumers get defective, inferior and substandard goods and services. Appropriate measures are necessary to protect the consumers against such malpractices.

(8) Trusteeship : The Gandhian philosophy states that businessmen are the trustees of the society’s wealth. So they should not misuse the society’s wealth for their own benefits. They should use the wealth of the society for the benefit of the people.

Question 4.
State the role of NGOs and consumer protection.
Answer:
The role of Non-Government Organisations (NGOs) in consumer protection is explained as follows:
(1) NGOs organise campaigns and various programmes on consumer issues to create social awareness.

(2) They initiate and organise training i programmes for the consumers and make them : aware and conscious of their rights and various modes of redressal of their grievances.

(3) They publish journals and periodicals at regular interval to make the consumers understand and keep them informed about various consumer ) related developments.

(4) They provide legal advice free of charge to the members on the matters of consumer interest and help them to put up grievances before appropriate authority.

(5) NGO’s active members interact (communicate) with the businessmen and Chambers of Commerce and Industry for ensuring better deal for the consumers.

(6) They file Public Interest Litigation (Janhit Yachika) on important consumer issues like ban on a product or medicine injurious to public health. They also file cases in the court of law to safeguard the rights and protect the interest of general public.

(7) Few examples of NGOs working for the consumers are : Consumer Guidance Society of India (CGSI), Voluntary Organisation in Interest of Consumer Education (VOICE), Consumer Education and Research Centre (CERC), Consumers Association of India (CAI), Mumbai Grahak Panchayat (MGP), Grahak Shakti (GS), etc.

Question 5.
State the composition and monetary jurisdiction of district commission.
Answer:
Composition : Each District Commission shall consist of-

• President : A person who is or has been a .judge of a district court is appointed as president
  of the District Commission.
• Members : The number of other members shall not be less than 2 and not more than such number of members as may be prescribed in consultation with the Central Government.
• Tenure : President and every member of the District Commission shall hold office for a term of 5 years or up to the age of 65 years whichever is earlier.

Monetary jurisdiction : District Commission has the jurisdiction to entertain complaints where the value of goods and services, including compensation, if any, does not exceed Rs 1 crore.

Question 6.
State the composition and monetary jurisdiction of state commission.
Answer:
(2) Composition : Each State Commission shall consist of:

• President : A person who is or has been a Judge of a High Court, shall be appointed by the State Government as the president of the State Commission in consultation with the Chief Justice of the High Court.
• Members : The number of other members shall not be less than 4 or not more than such number of members as may be prescribed in consultation with the Central Government.
• Tenure : Every member of the state commission shall hold office for a term of 5 years or up to the age of 67 years whichever is earlier.

Monetary Jurisdiction : To entertain complaints where the value of the goods or services and compensation exceeds Rs 1 crore but is not more than Rs 10 crore.

Question 7.
State the composition and monetary jurisdiction of national commission.
Answer:
Composition : The National Commission shall consist of:
(a) President: A person who is or has been a Judge of the Supreme Court to be appointed by the Central Government as President of National Commission. Such appointment shall be made after consultation with the Chief Justice of India.
(b) Tenure : Every member of the National Commission shall hold office for a term of 5 years or up to the age prescribed whichever is earlier.

Monetary Jurisdiction : To entertain the complaints where the value of the goods or services and compensation exceeds Rs 10 crore.

8. Answer the following

Question 1.
Who is Consumer? Explain the rights of the consumers.
Answer:
[A] Meaning : The word ‘consumer’ is derived from the Latin word ‘consumere’ which means ‘to eat or drink’. Accordingly consumer is one who consumes or uses any product or service available to him either from nature or through market. In other words, a consumer means any person who buys any product, hires any service or services for certain consideration in exchange of money which has been paid or promised to be paid in future for consumption or use and not for resale. For instance, if a businessman purchases furniture for selling it to the buyers, he is not a consumer. But if he buys a sofa set for his own use in his house, he becomes a consumer. We are all consumers when we use or consume foodgrains or use services like railways, hospitals, banks, etc.

[B] Rights of the Consumers : The rights of the consumers are shown:
Consumer Rights:

1. Right to Safety
2. Right to Information
3. Right to Choose
4. Right to be Heard
5. Right to Consumers Education
6. Right to Represent
7. Right to Redress
8. Right to Healthy
9. Environment
10. Right to Protect from Unfair Business Practices
11. Right against Spurious Goods

The rights of consumers are explained as follows:
1. Right to Safety : The right to safety means the right to be protected against products, production processes and services which are hazardous to consumer’s lives or health and property. It includes consumer’s long term interest and immediate requirements. This right demands that consumer must get full safety and protection to his/her life and health in relation to medicines, food, electrical appliances, etc. AGMARK, ISI – Indian Standard Institute, BIS – Bureau of Indian standards, Hallmark, etc. are the safety standards prescribed by the Government of India (GOI).

2. Right to Information : The consumer has a right to get correct and adequate information of all aspects of goods and services like price, name of manufacturer, contents used, batch number, date of manufacture and expiry date, use manual and safety instructions, etc. This information helps the consumers to make right choice of goods and services. This right is applicable to medicines, food products, spare parts and other consumer products or services.

3. Right to Choose : According to this right, the consumer has full freedom to select or choose the product or service as per his/her liking, requirement and purchasing capacity. The seller cannot force a consumer to purchase a particular product. This right aims at removing monopoly. The choices available to consumers in India include goods and different services such as telecommunications, travel and tourism, banking, electronics, Fast Moving Consumer Goods (FMCG) etc.

4. Right to Be Heard : It is the responsibility of every business organisation to listen and solve difficulties, complaints and grievances of the consumers. This right gives an opportunity to the consumers to express and voice their complaints to the consumer forum. The consumers also have rights to give suggestions to the manufacturer as well as to the trader on the quality, quantity, price, packaging, etc. of the products they use. Nowadays consumers can file online complaints through portal or mobile applications.

5. Right to Consumer Education : The consumers have right to know about consumer rights and solutions to their problems. This is to create awareness among the consumers to make rational choice of goods and services and to protect themselves from the exploitation of unscrupulous (dishonest) businessmen. In this regard, the government, media and various Non-Government Organisations (NGOs) can play an important role to create awareness among the consumers and to educate them, e.g. Jago Grahak Jago campaign.

6. Right to Represent : The Consumer Protection Act, 2019 gave an opportunity to individual consumer as well as to consumer groups to be represented by a person who is not professional advocate for consumer’s interest or complaint before consumer forum. This provision made in the Act in recognition of consumers’ right to represent.

7. Right to Redress : Right to redress implies fair settlement, just and reasonable claims of the consumers. In other words, consumer has the right to receive a fair amount of compensation or get the articles replaced or repaired free of cost for defective products and for poor services received from the manufacturer or trader. It is done through the Consumer Protection Act, 1986 under which District Commission, State Commission and National Commission are established. Thus, consumers are protected from cheating and malpractices.

8. Right to Healthy Environment: A consumer has a right to have a clean and healthy physical environment which is badly affected by pollution of noise, air and water. This is the direct effect of speedy industrialisation. Certain industries like chemicals, fertilisers, etc., add considerably to the pollution. As per this right, consumer can demand actions against such business organi¬sations. Businessmen and companies must take suitable measures to control pollution. All consumers have right to clean and healthy environment in present as well as in the future.

9. Right to Protect against Unfair Business Practices : This right protects the consumers against any kind of unfair business practices. The consumers have right to reuse the voice against the unfair business practices adopted by any trader e.g. using false measurement (weights), hoarding or stocking products to create artificial scarcity, black marketing, profiteering, adulteration, charging exorbitant high prices, selling goods after their expiry dates, etc.

10. Right against Spurious Goods : This right is against the marketing of goods which are health hazards, spurious (false or not genuine) and pose a danger to life itself. This right protects public health and life.

Question 2.
Explain the ways and means of Consumer Protection.
Answer:
The ways and means of consumer protection are stated as follows:

1. Lok Adalat (People’s Court)
2. Public Interest Litigation (Janhit Yachika)
3. Redresssl Forums
4. Awareness Programmes
5. Consumer Organisations
6. Consumer Welfare Fund
7. Legislative Measures

1. Lok Adalat : Lok Adalat, i.e. People’s Court is established by the government to settle the disputes by compromise. It is the effective and economical system for quick redressal of public complaints and grievances. In this system the aggrieved party can directly approach the Lok Adalat with his complaint. In Lok Adalat, issues are discussed immediately and decisions are taken without delay. The order passed by the Lok Adalat is given statutory recognition. In public sector, some organisations such as Railways, Maharashtra State Electricity Distribution Co. Ltd (MSEDCL). Maharashtra State Road Transport Corporation (MSRTC), Insurance Companies, Banks, etc. regularly hold Lok Adalat to resolve consumer’s problems through compromise.

2. Public Interest Litigation (Janahit Yachika) : As name indicates it is a legal action initiated in a court of law in regard to a matter of general public interest. Under this, any person can approach a court of law in the interest of the public and ask for justice. It does not involve individual interest but interest of unrepresented groups of the society. After studying and verifying the case, the court gives justice which will benefit the specific group of society or entire society. It can be filed by any party which may not be related to grievance. In some cases Janahit Yachika can be filed in the High Court as well as in Supreme Court directly.

3. Redressal Forums : Under the Consumer Protection Act, 2019, Consumer Dispute Redressal agencies have been established by the Government to protect the rights of consumers and to offer speedy and inexpensive redressal for their complaints. These agencies are District Commission at district level. State Commission at state level and National Commission at national level. Any aggrieved consumer or association of consumers can file a complaint with respective commission depending on the value of goods and amount of claim for compensation.

4. Awareness Programmes : The Government of India has initiated various publicity measures such as use of journals, brochures, booklets and various posters depicting the rights and responsibilities of consumers redressal machineries, i.e. consumer courts, observation of International (World) Consumer Rights Day on 15th March and National Consumer Day on 24th December every year to create awareness among the consumers about their rights and responsi¬bilities. Various consumer related programmes are also telecast on various TV channels and broadcasted on radio, FM channels and social media to create awareness among the consumers.

5. Consumer Organisations : Many consumer organisations such as Consumer Guidance Society of India, Grahak Panchayat, Grahak Shakti, Consumers’ Association, etc., are active throughout India to fight for consumers’ rights through protest, campaigning, lobbying, etc. Consumer movement is also well active in India and helps individuals to get quick and adequate compensation and justice for their grievances. It is also necessary to strengthen consumer movement throughout India.

6. Consumer Welfare Fund (CWF) : This fund is created by the Department of Consumer Affairs for providing financial help to voluntary consumer movement specially in rural areas. This financial assistance is used for training and research in consumer education, complaint handling, counselling and guidance mechanism, product testing labs, etc.

7. Legislative Measures : The Government of India has passed several acts such as Sale of Goods Act, 1930; Essential Commodities Act, 1955; the Standards of Weights and Measures Act, 1956; Bureau of Indian Standards Act, 1969; Food Safety and Standards Act, 2006; National Food Security Act, 2013, etc. to protect the interest of consumers from unethical practices of businessmen.

However, these laws could not protect the consumers as such and therefore the Government of India has passed a powerful Act known as Consumer Protection Act, 2019 to protect the interest of consumers.

Question 3.
Explain the three tier quasi-judicial machinery under the Act.
Answer:
The Consumer Protection Act, 2019
provides for three-tier quasi-judicial machinery as follows:

1. District Commission
2. State Commission
3. National Commission

1. District Commission :
A. Meaning : A consumer redressal agency established by the State Government in each district to give relief or settle the disputes of consumers who complain against manufacturers or traders, is called District Commission.

B. Composition : Each District Commission shall consist of-

• President : A person who is or has been a .judge of a district court is appointed as president
  of the District Commission.
• Members : The number of other members shall not be less than 2 and not more than such number of members as may be prescribed in consultation with the Central Government.
• Tenure : President and every member of the District Commission shall hold office for a term of 5 years or up to the age of 65 years whichever is earlier.

C. Qualifications : The members of a District Commission shall have the following qualifications :

• Age : The age of each member should not be less than 35 years.
• Education : They should possess a Bachelor’s Degree from a recognised University.
• Experience : Members should have adequate knowledge and experience of at least 10 years in dealing with problems related to economics, law, commerce, accountancy, industries, public affairs or administration.

D. Territorial Jurisdiction : District Commission can exercise its jurisdiction within the limits of its district.

E. Monetary jurisdiction : District Commission has the jurisdiction to entertain complaints where the value of goods and services, including compensation, if any, does not exceed Rs 1 crore.

F. Appeal : Any person not satisfied with the order of District Commission can appeal against it to the State Commission within 45 days from the date of the order in such form and manner may be prescribed.

2. State Commission:
A. Meaning : A consumer disputes redressal agency at state level established by each State Government is known as State Commission.

B. Composition : Each State Commission shall consist of:

• President : A person who is or has been a Judge of a High Court, shall be appointed by the State Government as the president of the State Commission in consultation with the Chief Justice of the High Court.
• Members : The number of other members shall not be less than 4 or not more than such number of members as may be prescribed in consultation with the Central Government.
• Tenure : Every member of the state commission shall hold office for a term of 5 years or up to the age of 67 years whichever is earlier.

C. Qualifications : The members shall have the following qualifications:

• Age : The age of each member should not be less than 35 years.
• Education : They should possess a Bachelor’s Degree from a recognised University.
• Experience : Members should have adequate knowledge and experience of at least 10 years in dealing with problems related to economics, law, commerce, accountancy, industries, public affairs or administration.

D. Territorial Jurisdiction : The State Commission entertains original cases as well as appeals against the order of District Commission within the geographical limits of the state.

E. Monetary Jurisdiction : To entertain complaints where the value of the goods or services and compensation exceeds Rs 1 crore but is not more than Rs 10 crore.

(6) Appeal : Any person aggrieved by an order passed by the State Commission may make an appeal against such order to the National Commission within a period of 30 days from the date of the order in such form and manner as may be prescribed.

3. National Commission
A. Meaning : A consumer disputes redressal agency at the national level established by the Central Government by notification is known as National Commission. It is also called as National Consumer Disputes Redressal Commission.

B. Composition: The National Commission shall consist of:

• President: A person who is or has been a Judge of the Supreme Court to be appointed by the Central Government as President of National Commission. Such appointment shall be made after consultation with the Chief Justice of India.
• Tenure: Every member of the National Commission shall hold office for a term of 5 years or up to the age prescribed whichever is earlier.

C. Qualifications: The members shall have the following qualifications:

• Age: The age of each member should not be less than 35 years.
• Education : They should possess a Bachelor’s Degree from a recognised University.
• Experience : The members should have adequate knowledge and experience of at least 10 years in dealing with problems related to economics, law, commerce, accountancy, industries, public affairs or administration.

D. Territorial Jurisdiction : National Commission entertains original cases as well as appeals against the order passed by the State Commission which are within the geographical limits of the state.

E. Monetary Jurisdiction : To entertain the complaints where the value of the goods or services and compensation exceeds Rs 10 crore.

F. Appeal : Any person who does not agree with the order of the National Commission can appeal to the Supreme Court within 30 days from the date of such order.

OCM 12th Commerce Textbook Solutions Digest

• 12th OCM Chapter 1 Practical Problems
• 12th OCM Chapter 2 Practical Problems
• 12th OCM Chapter 3 Practical Problems
• 12th OCM Chapter 4 Practical Problems
• 12th OCM Chapter 5 Practical Problems
• 12th OCM Chapter 6 Practical Problems
• 12th OCM Chapter 7 Practical Problems
• 12th OCM Chapter 8 Practical Problems