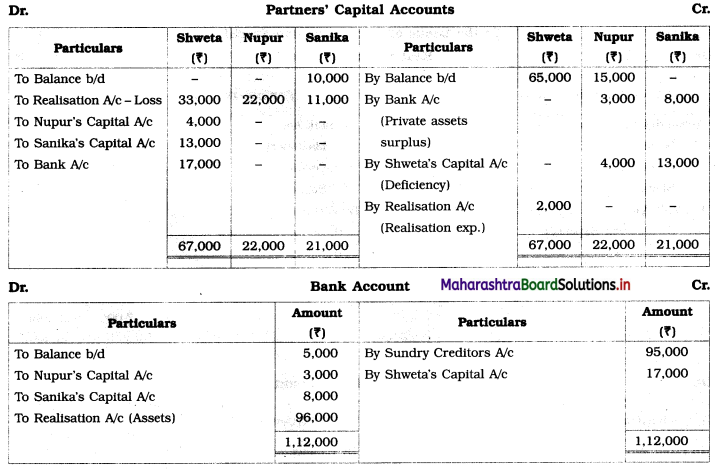
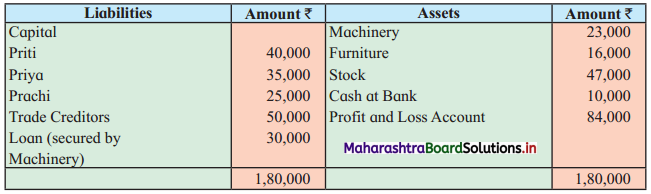
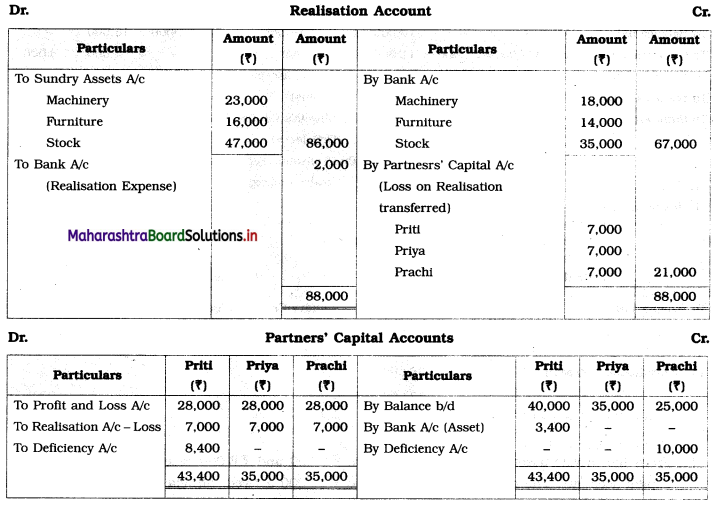
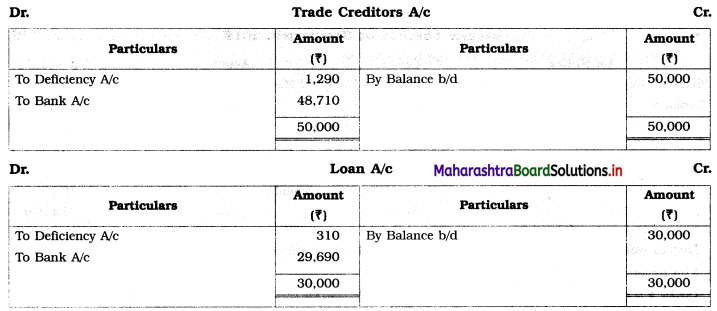
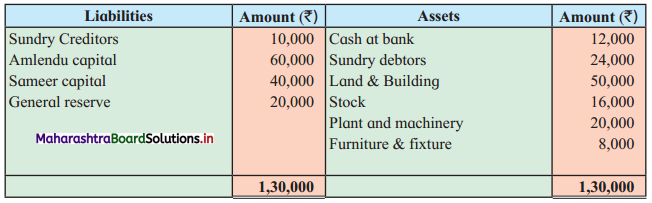
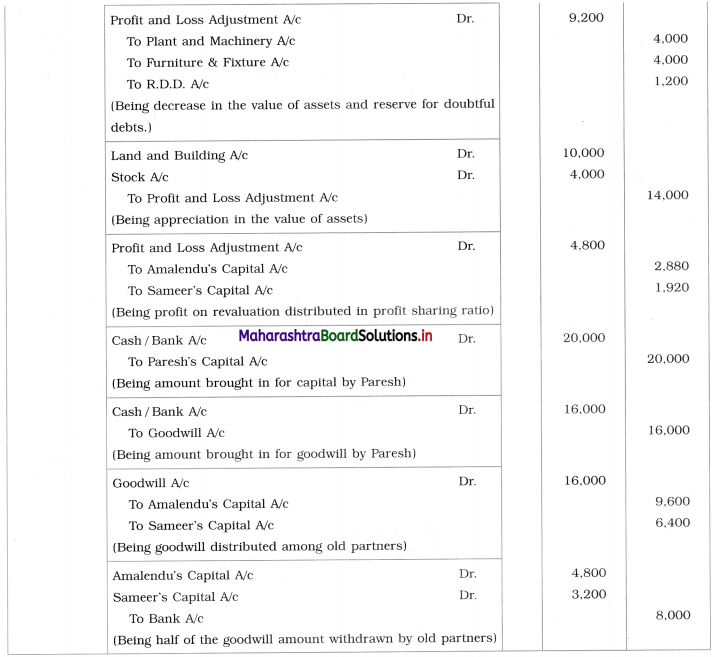
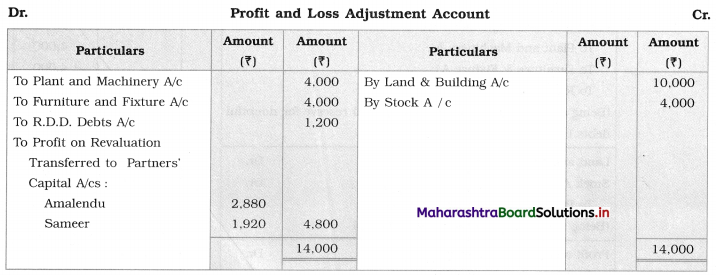
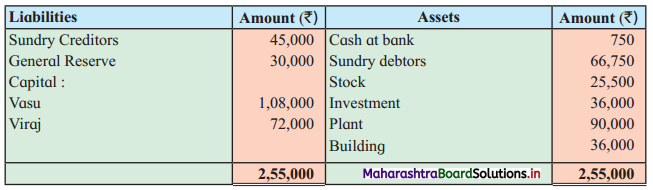
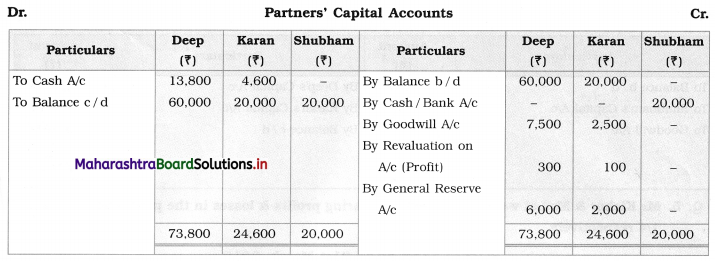
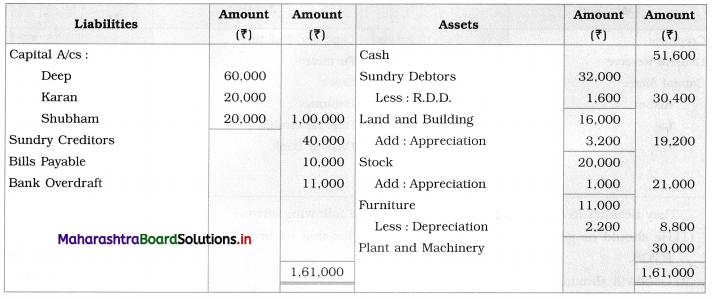
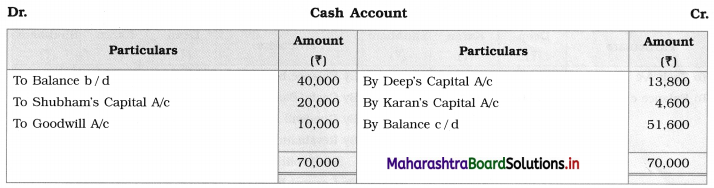
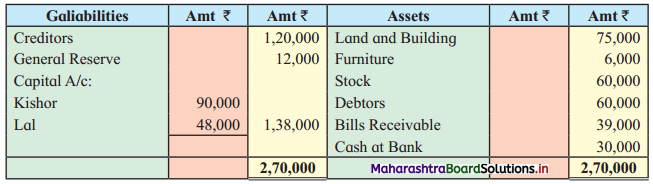
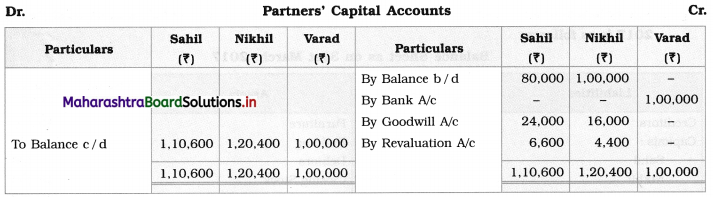
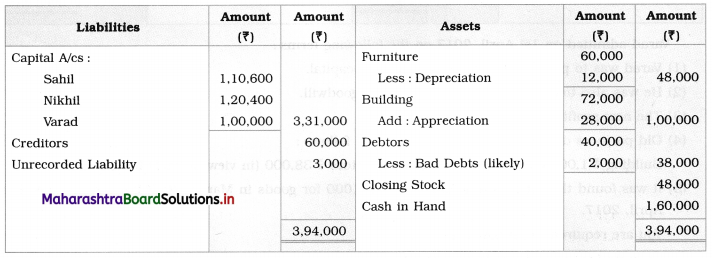
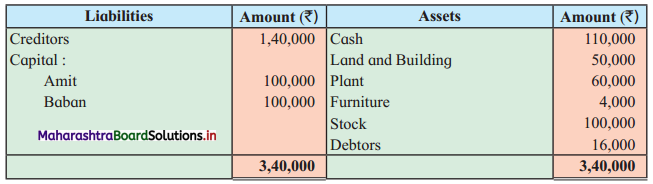
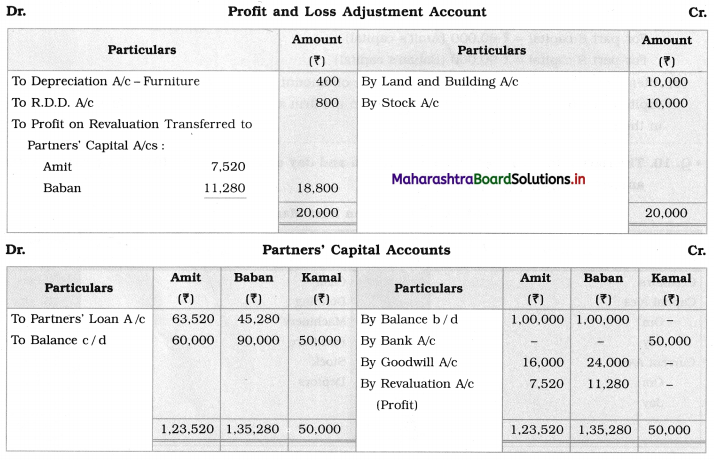
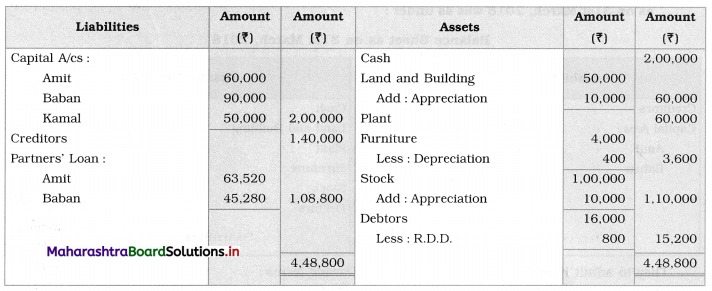
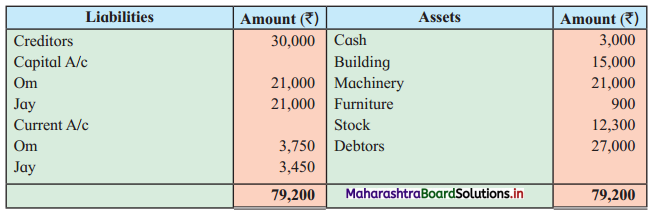
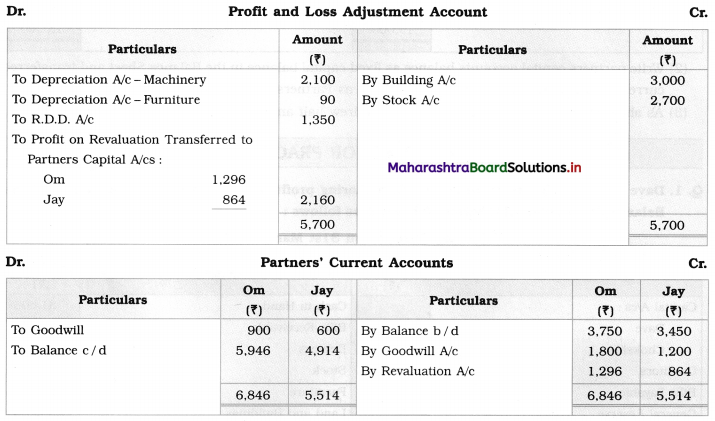
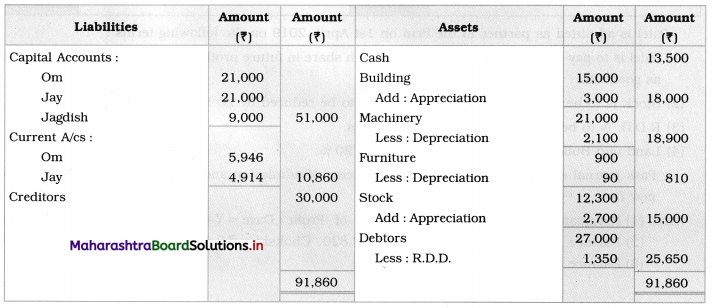
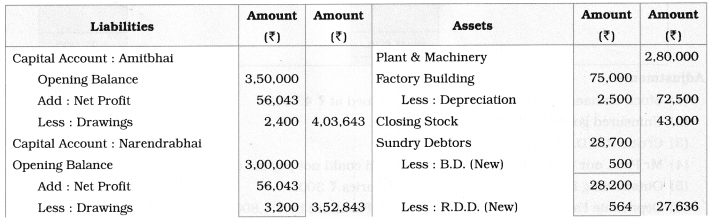
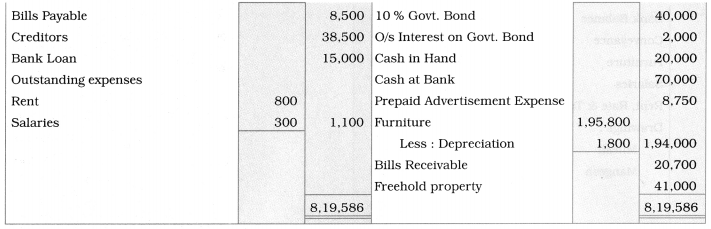
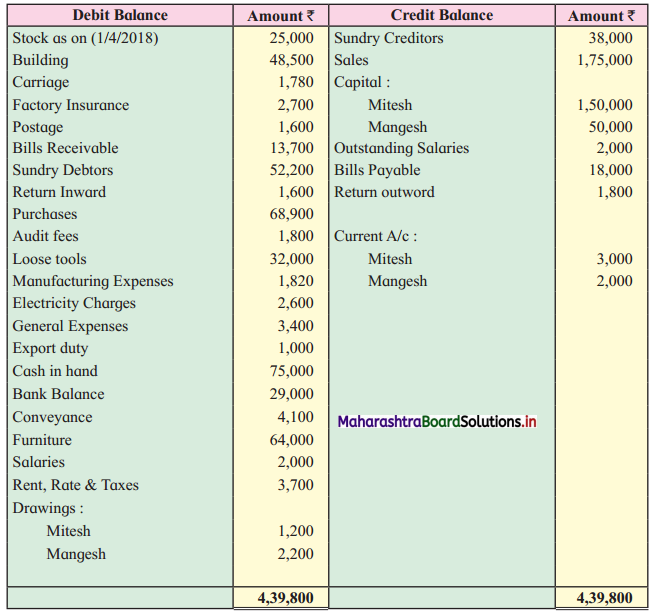
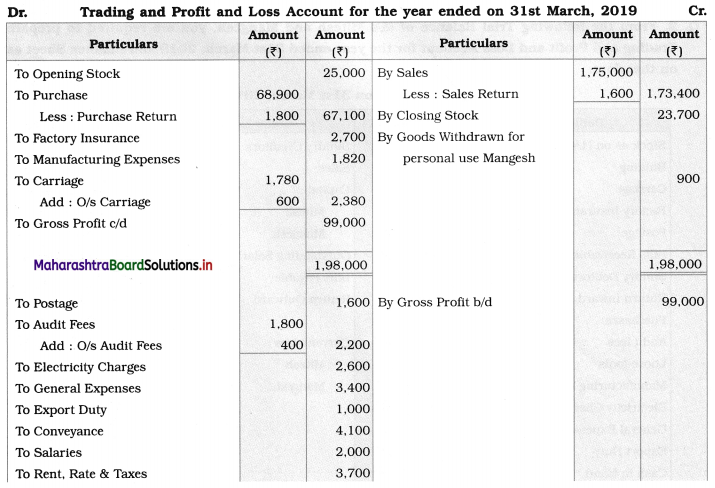
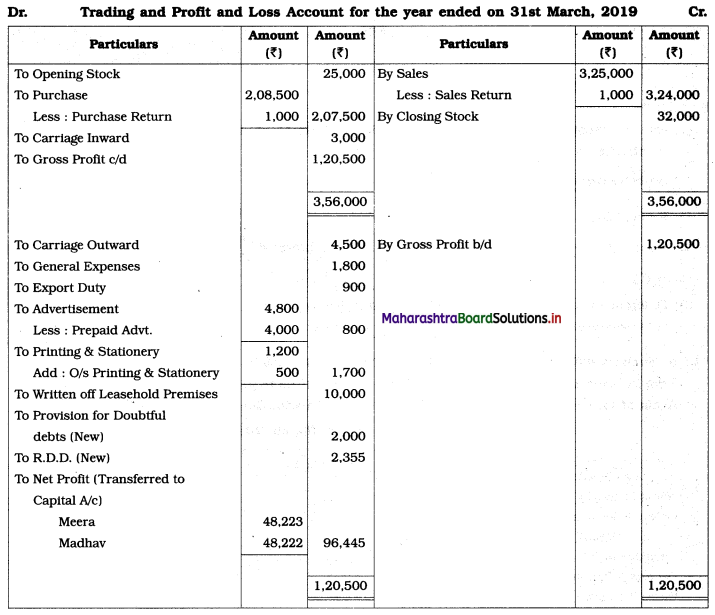
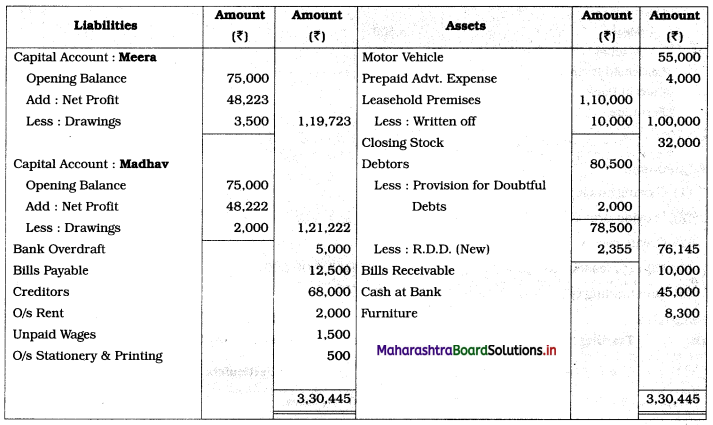
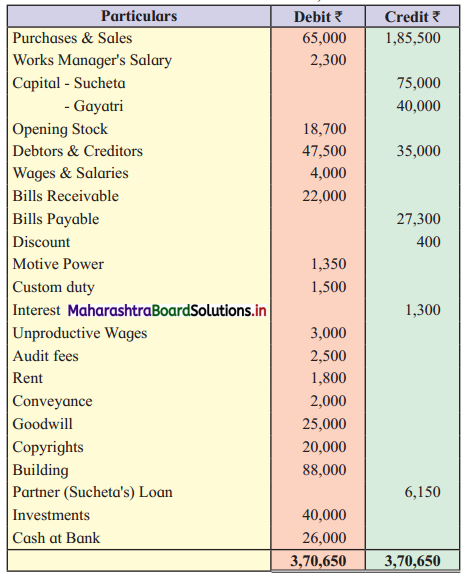
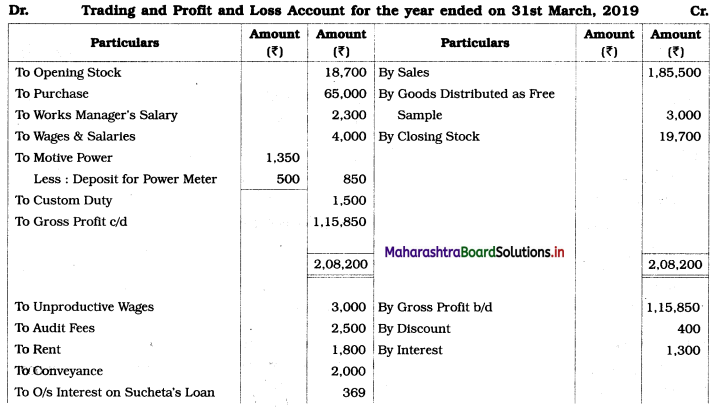
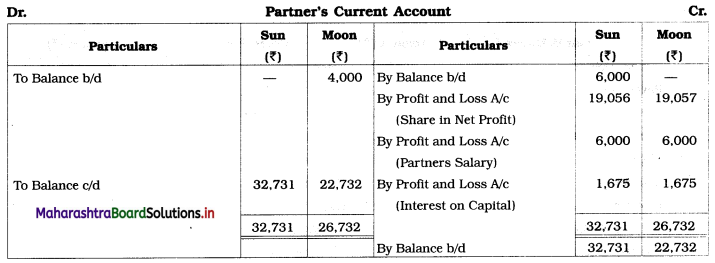
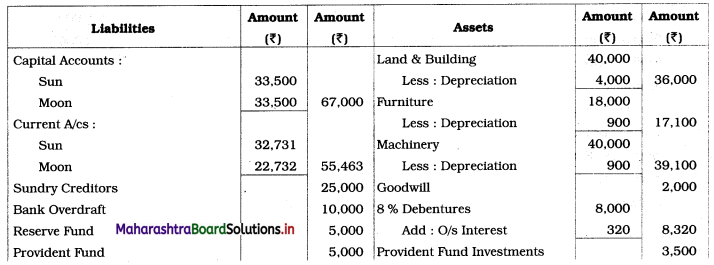
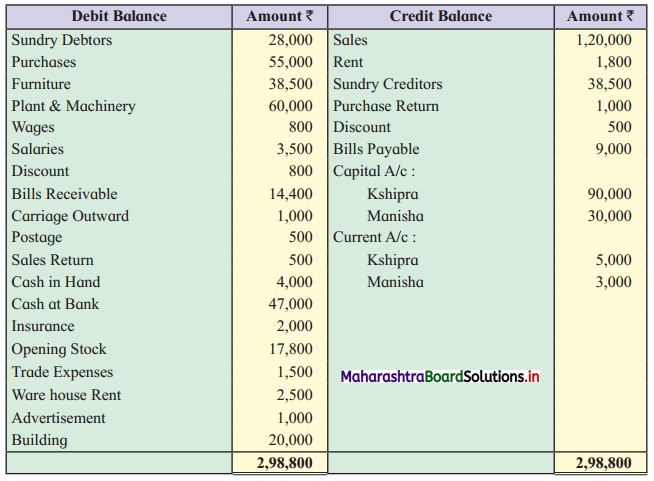
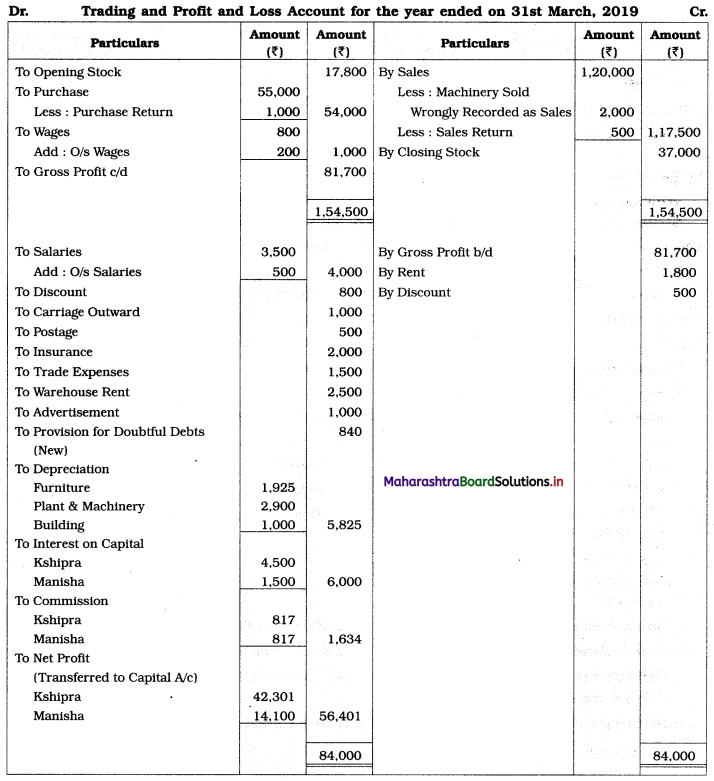
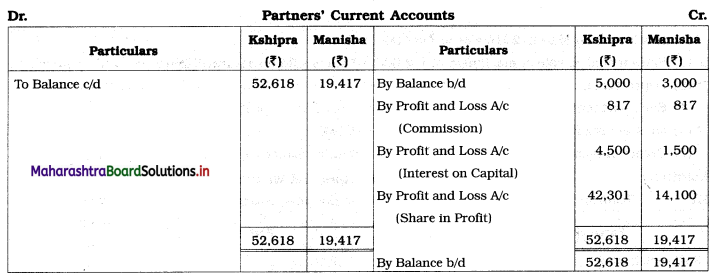
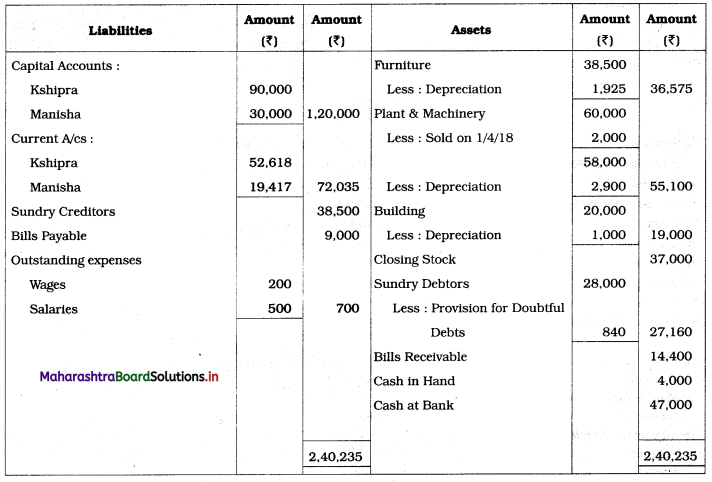
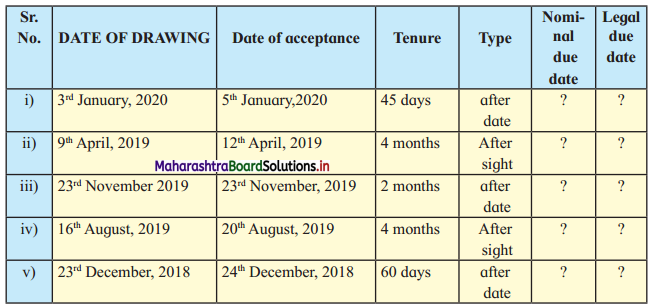
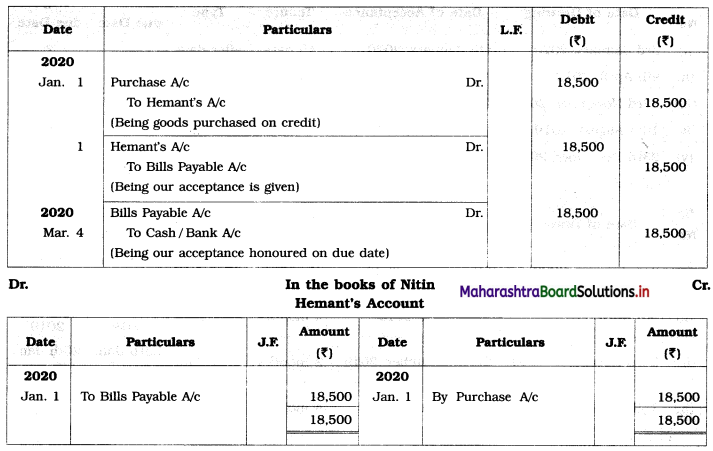
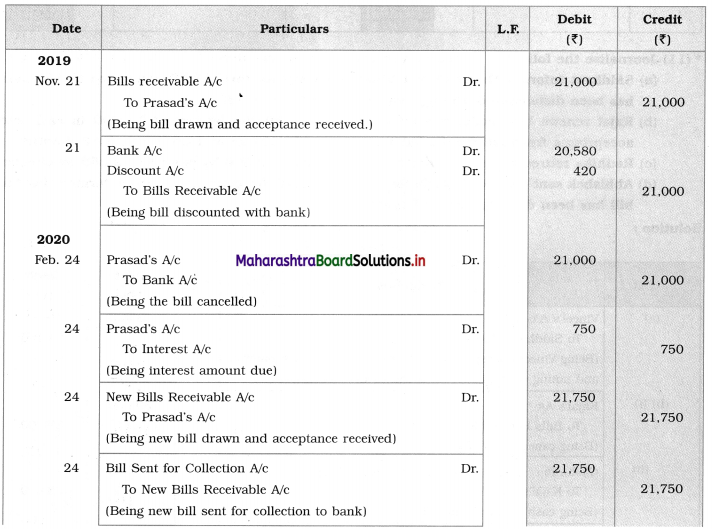
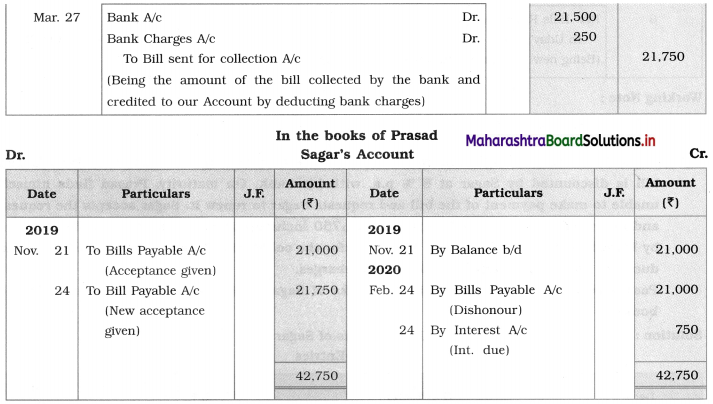
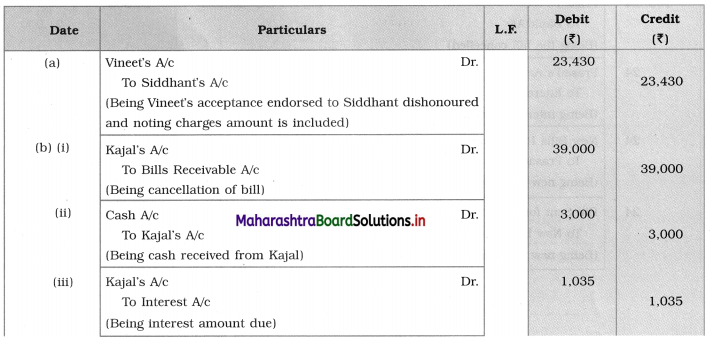
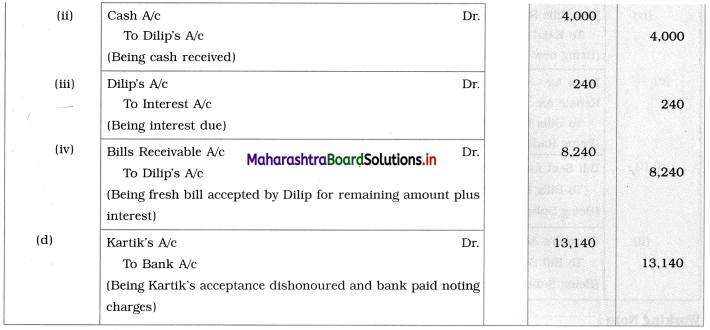
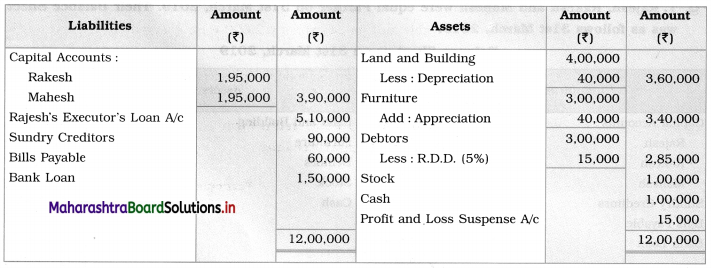
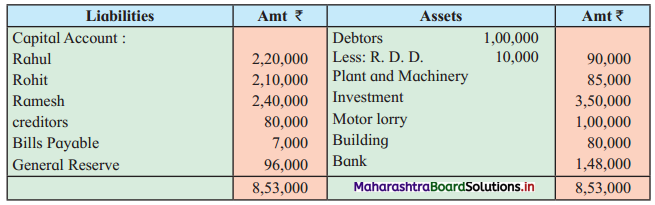
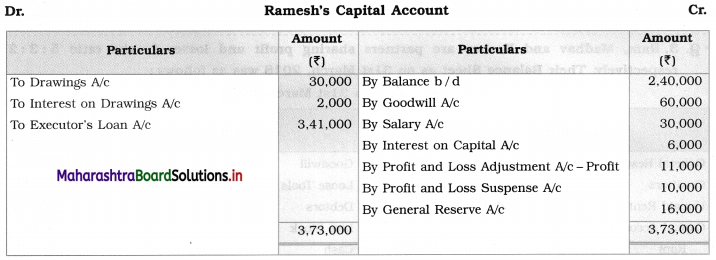
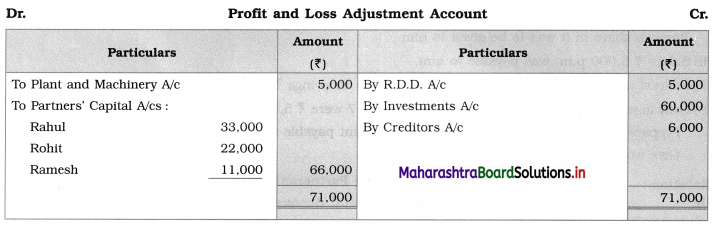
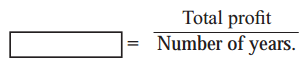Sociology Class 12 Chapter 5 Social Movements in India Question Answers Maharashtra Board
Balbharti Maharashtra State Board Class 12 Sociology Solutions Chapter 5 Social Movements in India Textbook Exercise Questions and Answers.
Social Movements in India Class 12 Sociology Chapter 5 Questions and Answers
1A. Complete the following statements by choosing the correct alternative given in the brackets and rewrite it.
Question 1.
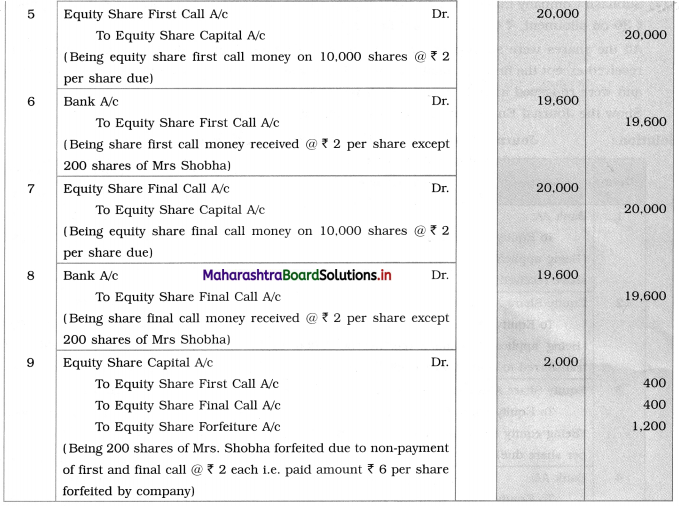
The Chipko Movement is for ____________ (women’s empowerment, labour rights, saving the environment)
Answer:
saving the environment
![]()
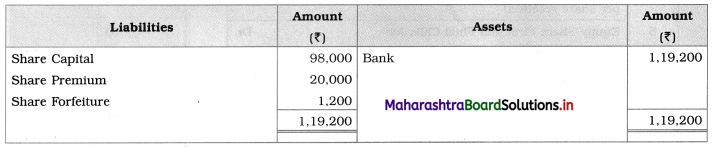
Question 2.
The Bhartiya Lok Dal was started in the year ____________ (1954, 1964, 1974)
Answer:
1974
1B. Correct the incorrect pair and rewrite it.
Question 1.
(a) Women’s Movement – Gender equality
(b) International Decade of Women – From 1991-2001
(c) Towards Equality – Report on the Status of Women in India
(d) Feminist Movements – India after Independence
Answer:
(b) International Decade of Women – 1975-1998
1C. Identify the appropriate term from the given options in the box and rewrite it against the given statement.
S. A. Dange, Sarala Devi, Medha Patkar
Question 1.
Leader of Narmada Bachao Andolan.
Answer:
Medha Patkar
Question 2.
Significant role in the Trade Union Movement.
Answer:
S. A. Dange
1D. Correct underlined words and complete the statement.
Question 1.
The first Kisan Congress held in 1935 led to the establishment of the United Trade Union Congress.
Answer:
The first Kisan Congress held in 1935 led to the establishment of the All India Kisan Sabha.
![]()
Question 2.
The Women’s Indian Association was formed in Bombay.
Answer:
The Women’s Indian Association was formed in Madras.
2. Write short notes.
Question 1.
Farmers’ Movement
Answer:
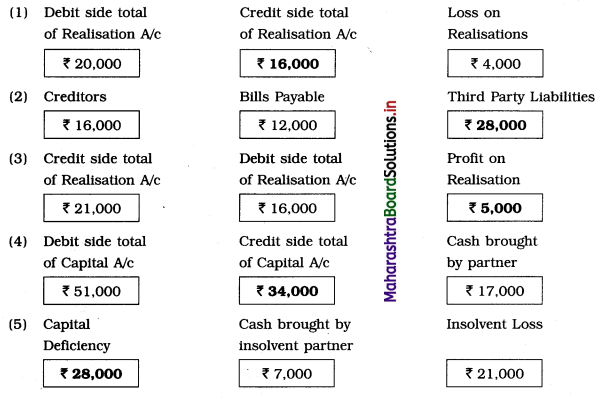
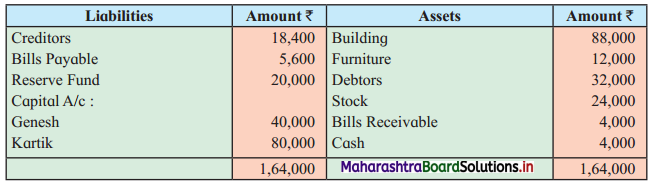
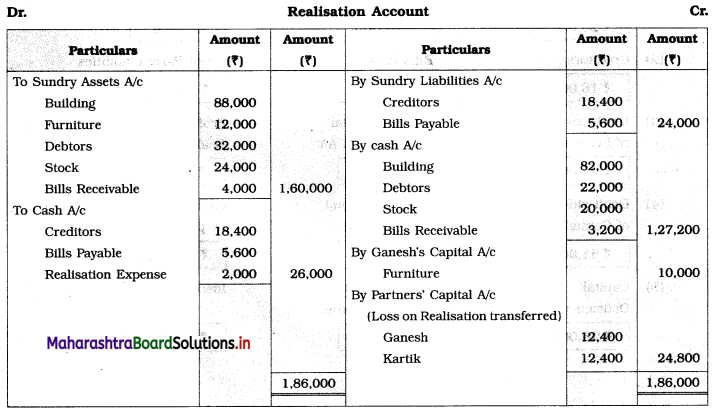
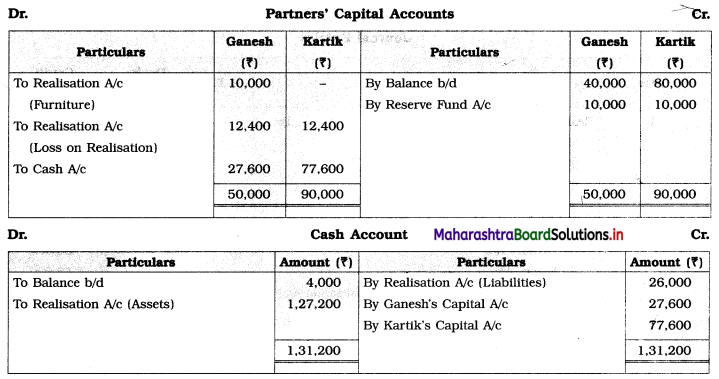
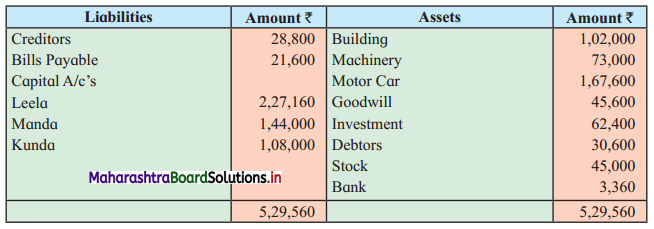
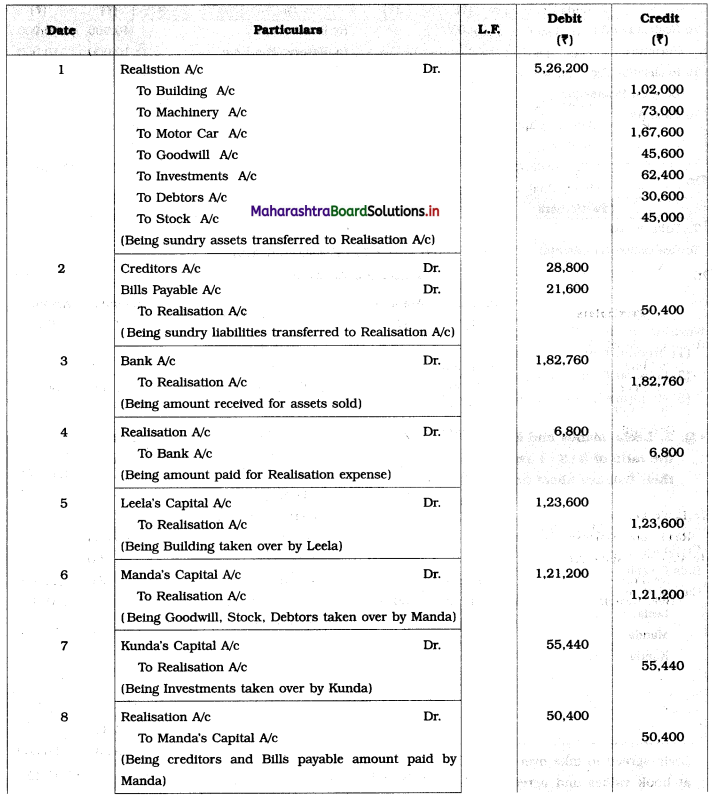
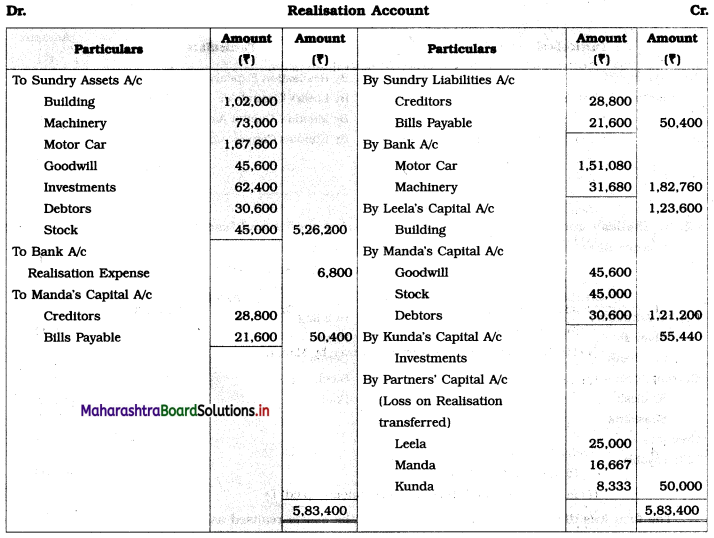
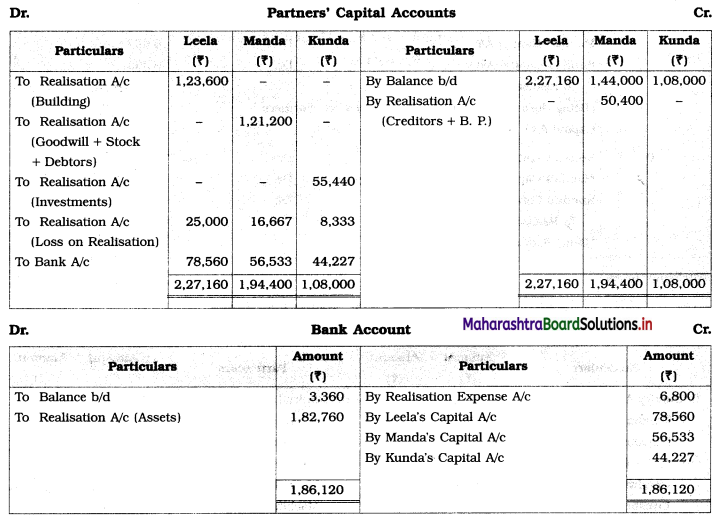
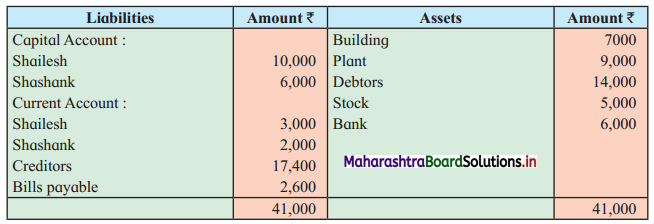
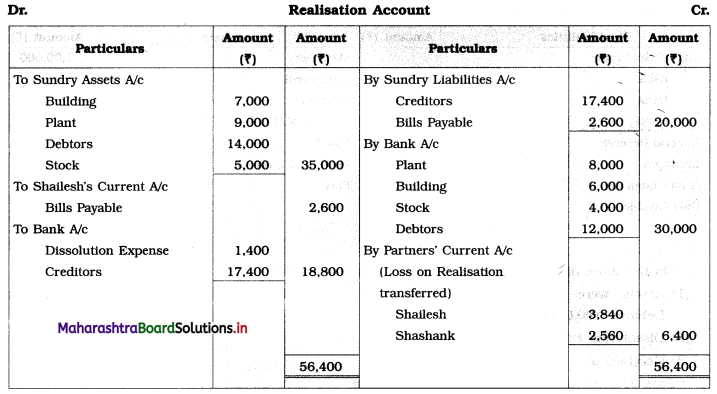
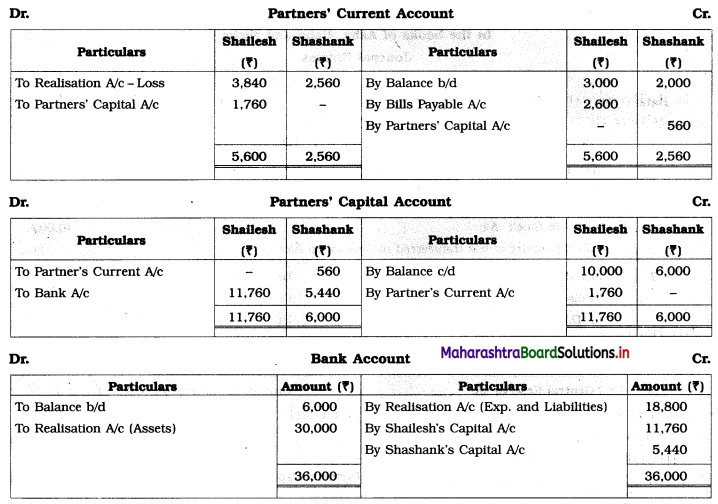
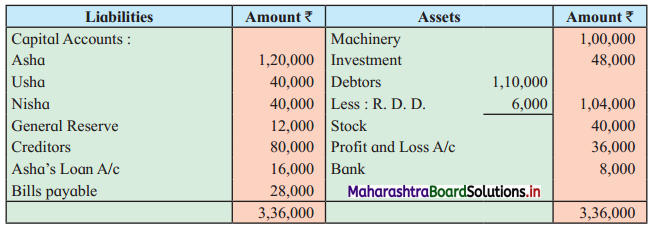
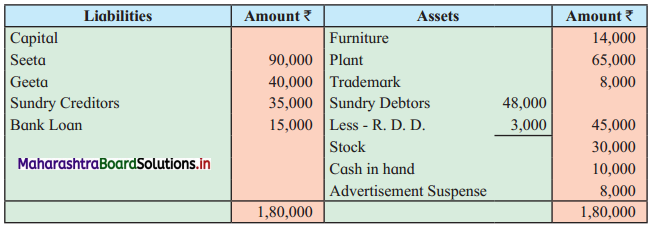
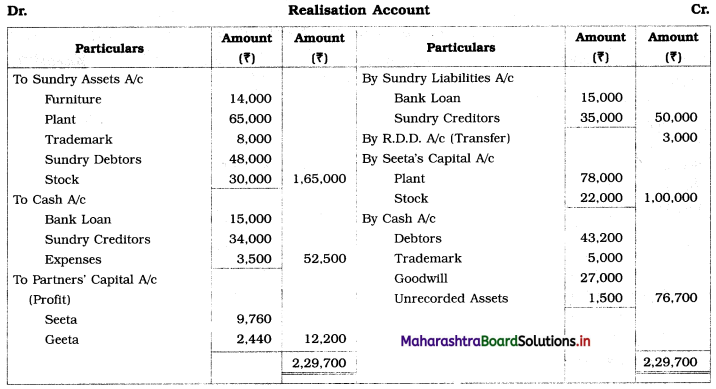
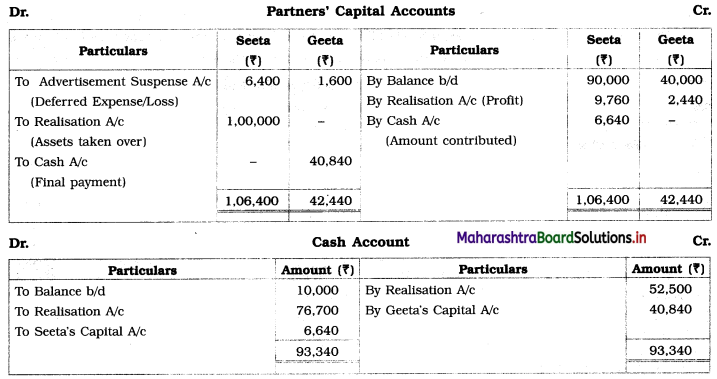
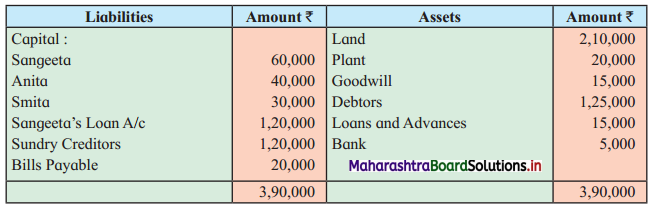
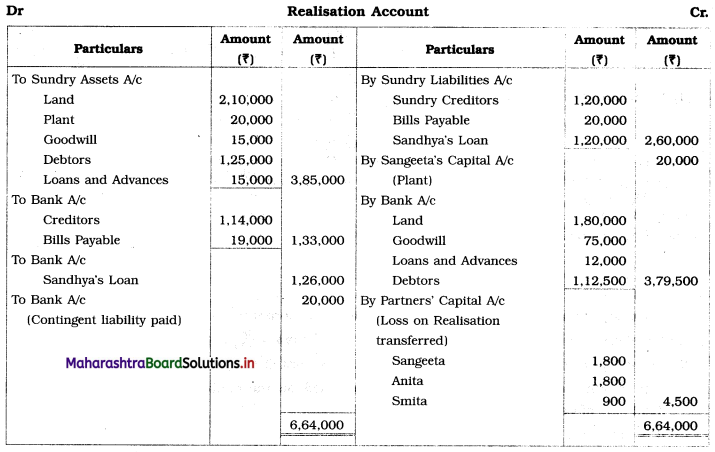
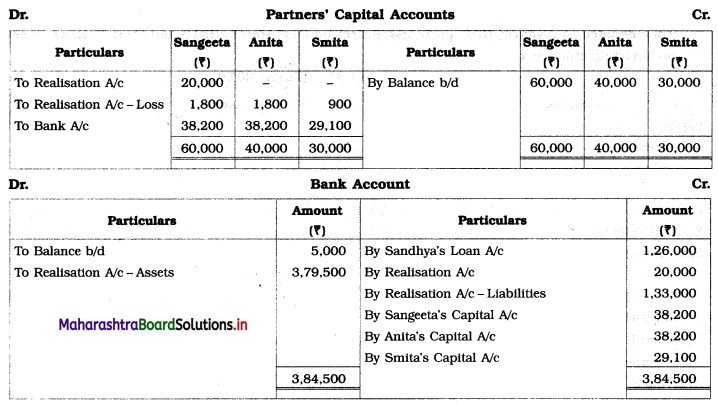
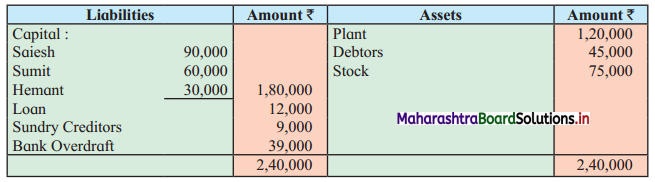
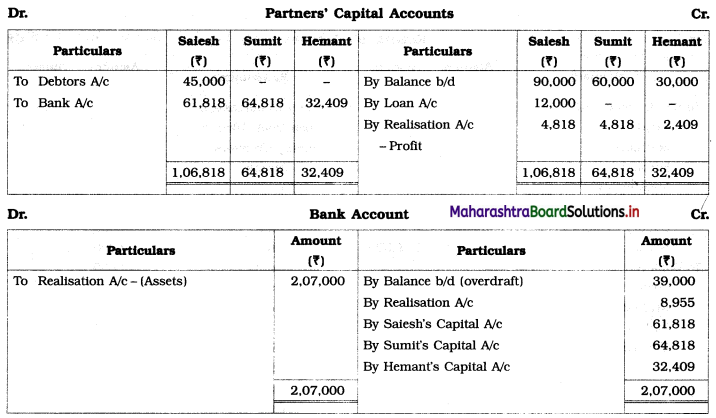
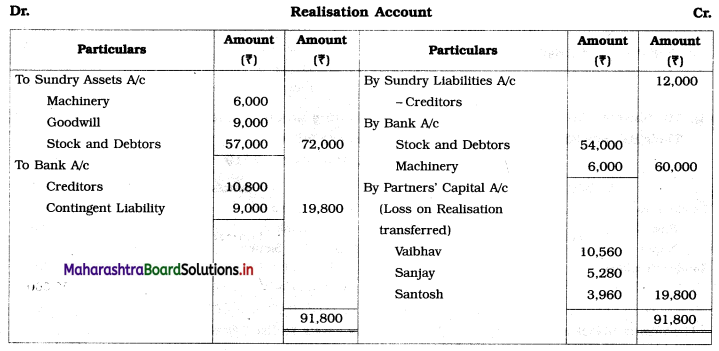
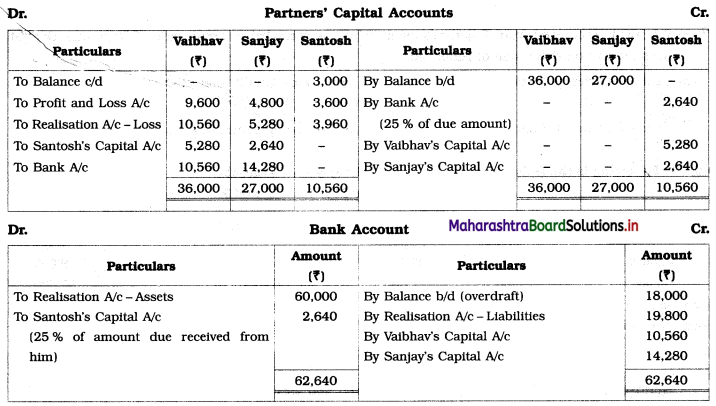
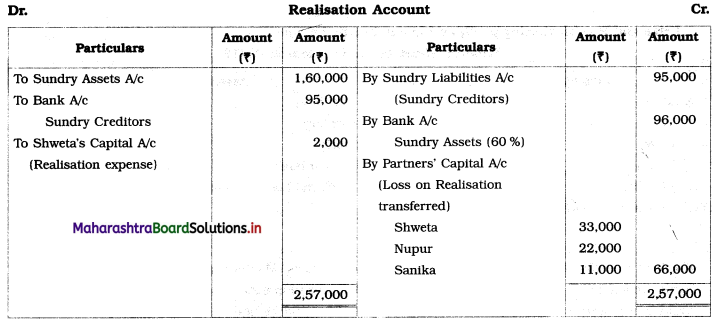
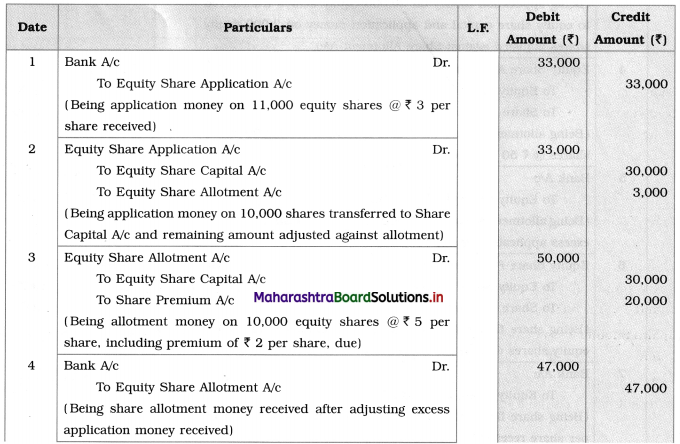
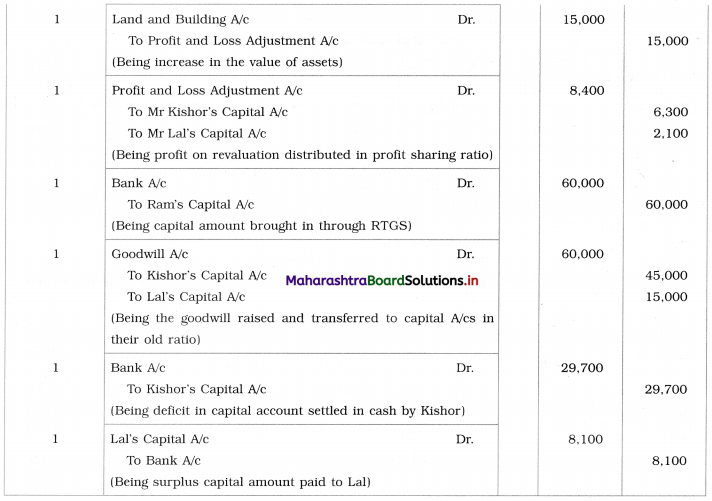
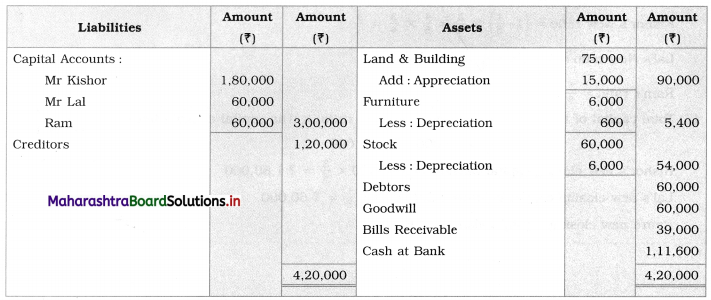
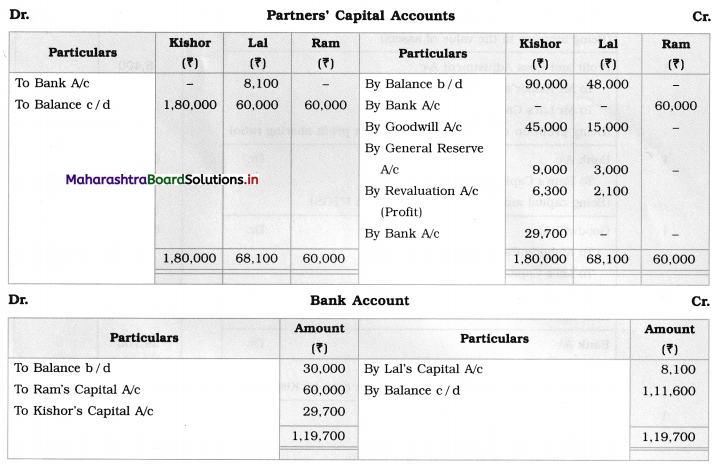
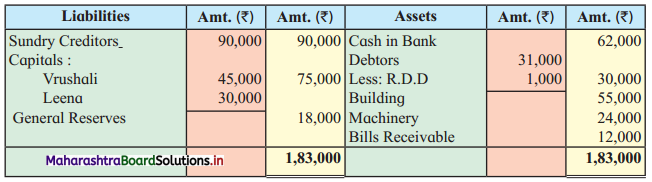
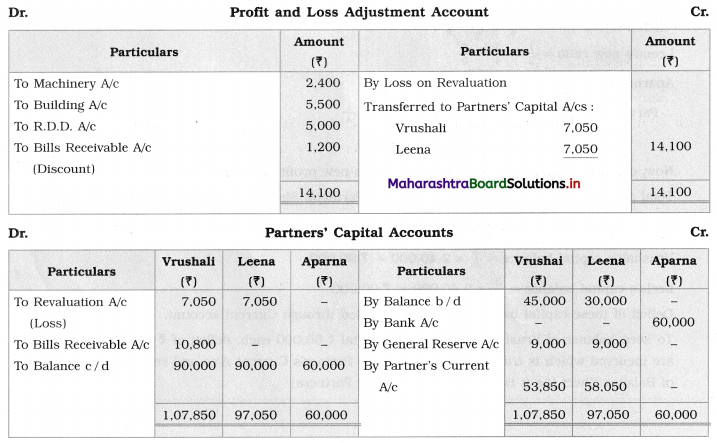
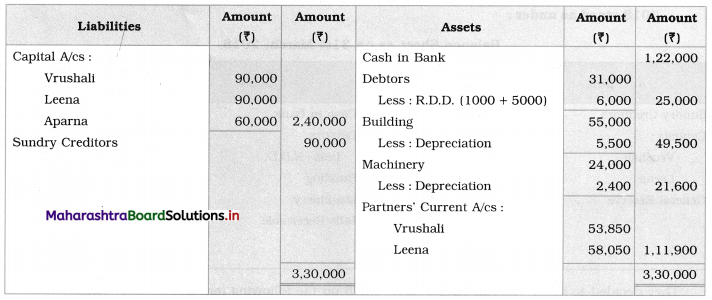
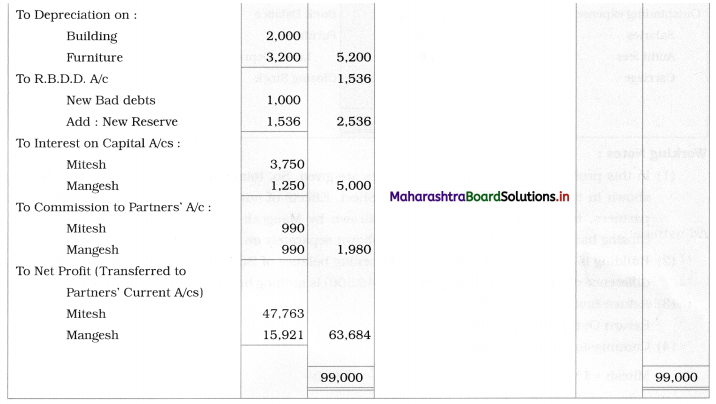
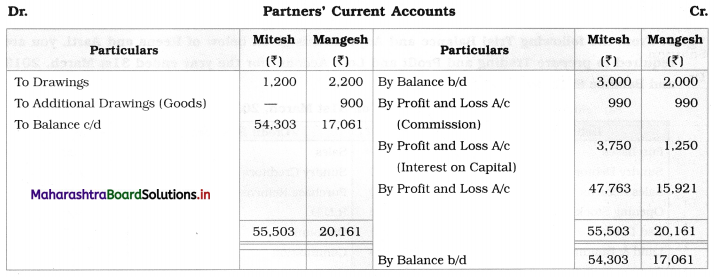
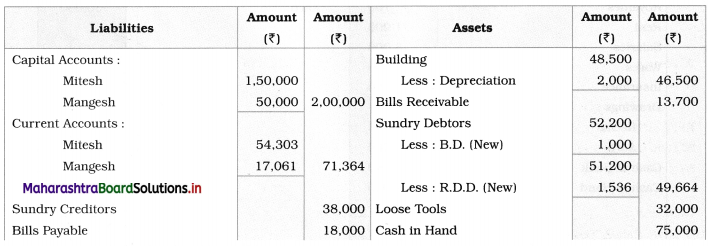
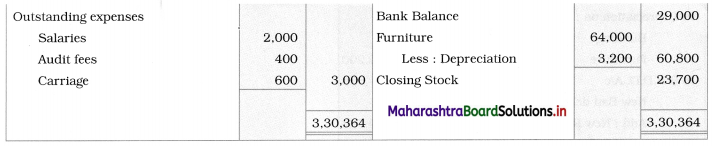
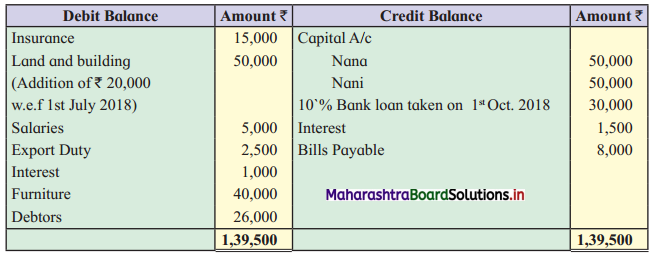
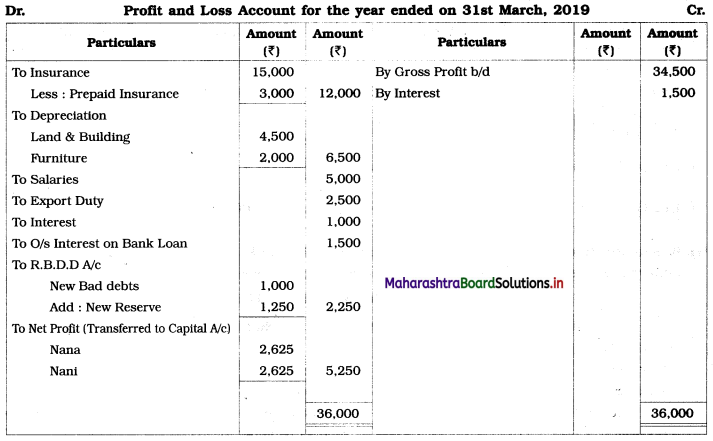
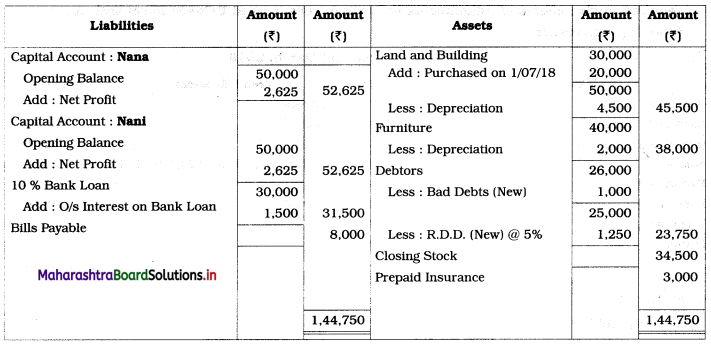
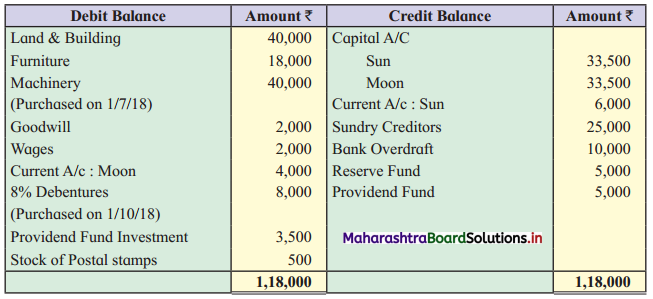
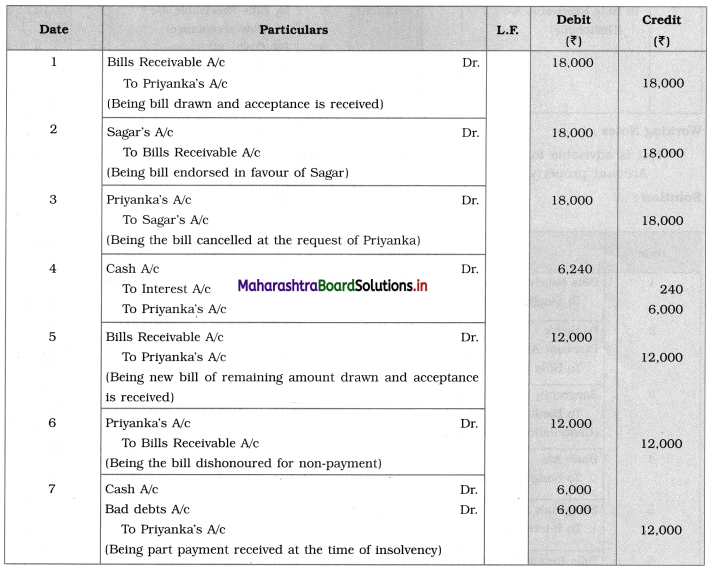
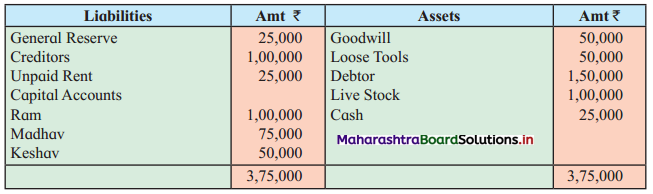
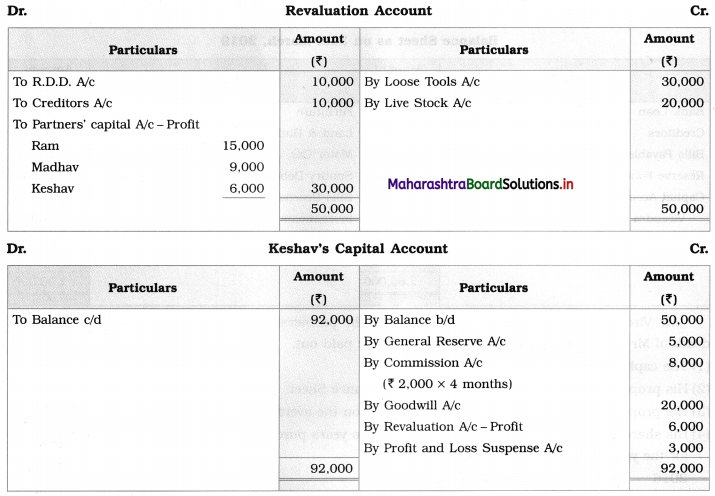
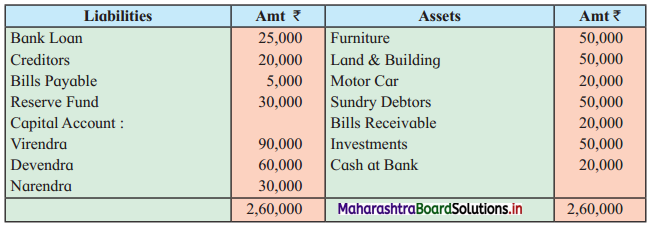
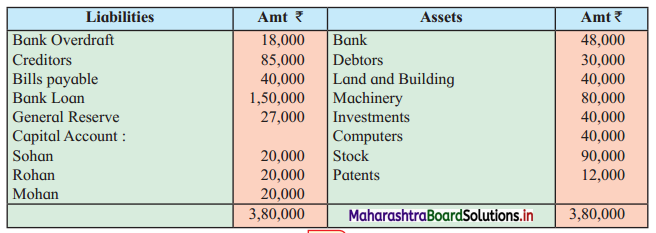
Early Agitations: the early part of British rule was marked by an exploitative revenue system and zamindari system. Many small cultivators lost their rights over their hereditary land and resources. The famines and natural calamities during this period increased Indebtedness and exploitation This led to massive discontent among farmer Several revolts like the Deccan riots against money lenders, the upsurge by Bengal tenants against Zamindari, the Punjab Kisan struggles against money lenders, etc, took place during this period, two peasant struggles led by the National Congress the Champaran Struggle in Bihar against Indigo planters and the Satyagraha movement of the peasants in against collection of land revenue in a situation of crop failure
The emergence of Kisan Sabhas: many Kisan Sabhas were organised in Bengal, Punjab, and Uttar Pradesh to revolt against the initiative taken by the Congress party to support the interests of landlords. The Kisan Sabha movement started in Bihar under the leadership of Swami Sahajanand Saraswati, to oppose zamindari system Two struggles of the peasantry of the Bardoli district (Gujarat) broke out in succession which resulted in the formation of the All India Kisan Sabha (ALKS) at the Lucknow session of the Indian National Congress in April 1936. In Punjab, the farmers’ movement erupted under the leadership of Raja Mahendra Pratap. The Ghadar party played a very important role in mobilising farmers and peasants of Punjab together. In Gujarat, Mahatma Gandhi led the struggle of poor farmers against the British government in Kheda. In the Southern belt, the struggle erupted against the Forest Law. This phase is also characterized by the worsening of peasant position.
Post-Independence period: During this period the unrest was felt in the States were agriculturally, commercially developed States like Punjab, Haryana, Uttar Pradesh, Maharashtra, Gujarat, Karnataka, and Tamil Nadu, the movement became more organised, under Charansingh He opposed heavy mechanisation.the Bharatiya Kranti Dal (BKD) and the Bhartiya Lok Dal (BLD) in 1974. In 1973 a convention of farmers was held in New Delhi, followed by another convention in 1978. Which presented a 20-point charter of demands to the government like representation of farmers on decision-making bodies, bridging the imbalance between agriculture and industry, etc., In 1980, the formation of the Shetkari Sangatana under the leadership of Sharad Joshi and Karnataka Rajya Ryot Sangh under the leadership of M. D. Nanjundaswamy are milestones in the Farmers’ movement in India. With the processes of industrialization and globalisation, conditions have changed rapidly for farmers. In March 2018, thousands of farmers from different parts of Maharashtra got together to march to Azad Maidan (Mumbai), to convey to the government their grievances and frustrations.
![]()
Question 2.
Characteristics of Social Movement
Answer:
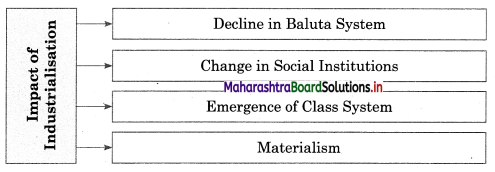
Social movement means when a group of people come together in an organized way, in order to bring change in society. Social Movements are different in nature, features, pace, and operations.
The important characteristics of Social Movements are:
Essentially collective in nature: Social movement is not an individual action. It involves collective action. A group collectively has to be part of the movement. A collective action that creates interest and awakening in a relatively large number of people.
Planned and deliberate action: Social movements have to be preplanned to be executed effectively. Movements are deliberate initiatives and not spontaneous or sudden in nature.
Ideology and objectives: A social movement is backed by an ideology. The ideology guides the course of the movement. There are set objectives and goals to achieve to bring about change in the social system.
Social change: Social movements are oriented towards bringing about a change. It usually demands a change in the already established order or it resists change initiated by the authorities.
Leadership: Collective action must be marked by some degree of organisation. The organisation must include leadership and a structure that defines how members relate to each other, make decisions and how to carry them. Leaders are must for guidance and person who influences others to accomplish the mission.
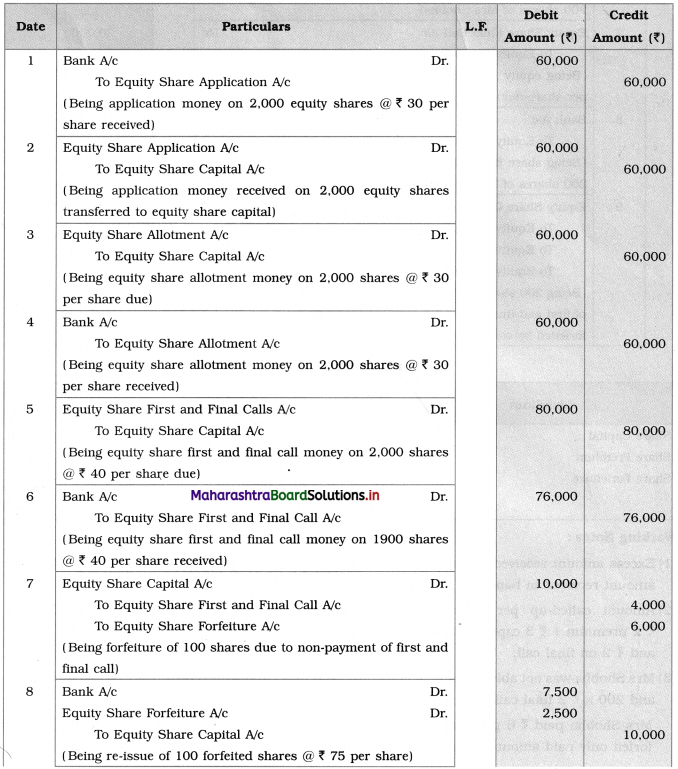
3. Write differences.
Question 1.
Pre-Independence and Post-Independence periods of the Women’s Movement in India.
Answer:
| Pre-Independence period of women’s movement | Post-Independence period of women’s movement |
| (i) Pre-Independence period of the women’s movement overlapped with the Social Reform Movement in many ways. | (i) Post-Independence period of the women’s movement witnessed several issues like tribal unrest, economic crisis, which took away the singular focus of the women’s movement. |
| (ii) Pre-Independence movements challenged the customary practices which were discriminatory and revolted mainly against human rights violations in the form of Sati and ill-treatment of widows. | (ii) Post-Independence movements focused more on violence against women, sex stereotyping, and further legislative demands for equality of women. |
| (iii) Pre-Independence movements were led by social reformers like Raja Rammohan Roy, Jyotiba Phule, Maharshi Karve, and so on. | (iii) Post-Independence movements have mobilised masses in the form of women’s organisation, NGOs, SEWA, etc. |
| (iv) Pre-Independence movement needed the voice of others (social reformers) for the problems to be spoken. | (iv) Post-independence movement women are educated and aware and are ready to speak up for themselves. |
| (v) Pre-Independence movement lacked revolutionary social media. | (v) Social media plays a major role during the Post-Independence movement where these movements can reach across the globe and mobilised the youth on a large scale. |
| (vi) The Pre-Independence movement was more of a socio-religious movement. | (vi) The Post-Independence movement was more progressive in nature. |
4. Explain the following concepts with examples.
Question 1.
Social Movement
Answer:
A social movement is a collective action to change or influence the existing social system by a group. Herbert Blumer has defined the social movement as “Collective enterprises to establish a new order of life.”
A social movement is defined as a collectively acting with some continuity to promote ore resist a change in the society or group of which it is a part. Some movements are directed to modify certain aspects of the existing social order whereas others may aim to change it completely.
A social movement is an organised effort of a large group of people to achieve a particular goal typically a social or political or political one, this may be to carry out resistance or undo a social change.
It is a collective challenge to the authorities organised group of people to come together to establish a new order of life.
Examples
- Environmental movements like the Chipko Movement and Narmada Bachao Andolan organised to protect and preserve our environment.
- Workers movement to protest against the exploit action done on workers like the minimisation of wages, poor working conditions, etc. by the industrialisation factory owners.
- Reform Movements – Arya Samaj, Satyashodhak Samaj, Peasant Movements, Backward Castes Movement, etc.
Question 2.
Environmental Movement
Answer:
Gadgil and Guha have defined Environmental Movement as, “An organised social activity consciously directed towards promoting sustainable use of the natural resource, halting environmental degradation or bringing about environmental restoration.” The terms Green Movement, Conservation Movement are also used alternatively to refer to the Environmental Movement.
Environmental Movement, is centered around a genuine concern for the conservation and improvement of the habitat around us, more specifically the environment and civilization.
Environmental Movement as an organized social activity consciously directed towards promoting sustainable use of natural resources halting Environmental degradation or bringing about Environmental restoration.
Environmental Movement has utilized non-violent ways to fight on issues like sustainable management of natural resources, protection of the Environment many movements are centered on ecology, tribal rights, human rights, ecofeminism, etc.
Environmental Movements are highly organised, its scope is wide ranges from being local to the global level.
The environmental movement surrounds issues related to ecology, health, human rights, tribal rights eco-feminism etc.
Harsh Sethi has presented five prominent categories of struggles associated with environmentalism, namely
- forest and forest resources
- land use
- water
- anti-dam
- against different types of pollution and marine resources.
Examples
The Chipko Movement took place in 1973 in the Chamoli district of Uttarakhand where villagers and women in large numbers hugged the trees where the contractors reached the villages to cut the tree. This was to protest against deforestation and save the forest.
Narmada Bachao Andolan – When it was realised that the building of a dam would deprive local inhabitants of their livelihood and displace them, the need to mobilsed and protest against such a venture was felt. In 1985, the Narmada Bachao Andolan (NBA) emerged as one of the powerful resistance movements under the leadership of Medha Patkar.
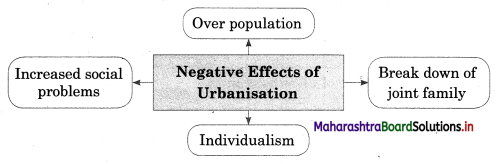
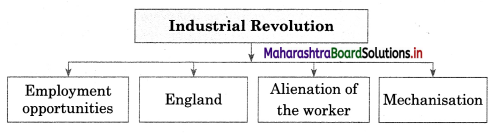
5A. Complete the concept map.
Question 1.
Answer:

6. Give your personal response.
Question 1.
Has the study of Environmental Education had any effect on your behaviour?
Answer:
The study of environmental education has promoted pro-environmental behaviour which plays important role in solving the problem of the environment. It has increased concern about global and local environmental problems and issues.
![]()
Environmental education has created awareness about various environmental issues like how industrialisation and development have led to deforestation and after problems like various pollution, land sliding degradation that endangers our human life and society Above all it has made me release there is need to protect and preserve our environment.
It has helped me to engage in environmental activism like taking shorter showers, reducing private transport, etc. It has taught us how to use the present and future resources optimally to avoid further depletion of the ozone layer, global warming, etc.
Field trips and cleanliness drive camp has taught us to keep our surrounding clean and preserve our natural resources for future. Environmental education has promoted a sense of community involvement in me and has helped me to understand how nature works.
Question 2.
Why is it important to raise social concerns through social movements?
Answer:
- In democratic societies, collective voice on various issues like rights, welfare, and well-being of people has brought changes in society.
- Social movements are collective actions of organised groups who have goals or a demand to change the existing system.
- For instance, during the women’s movement when various issues of consent like equal rights, education, women’s empowerment were raised they demanded a change in the existing system of authority.
- The result of their protest brought various changes. The Constitution of India and Indian law laid down measures for the protection of women’s rights, all these have improved the position of women in present times.
- So, when social concern is raised through social movement, it brings about changes in all aspects of society.
7. Answer the following question in detail. (About 150-200 words)
Question 1.
‘Social movements play an important role in bringing about changes in society. With reference to this statement, choose any two different social movements that you have studied and comment on:
(i) The Issues related to the movement, and
(ii) How the movement has brought about changes in Indian society.
Answer:
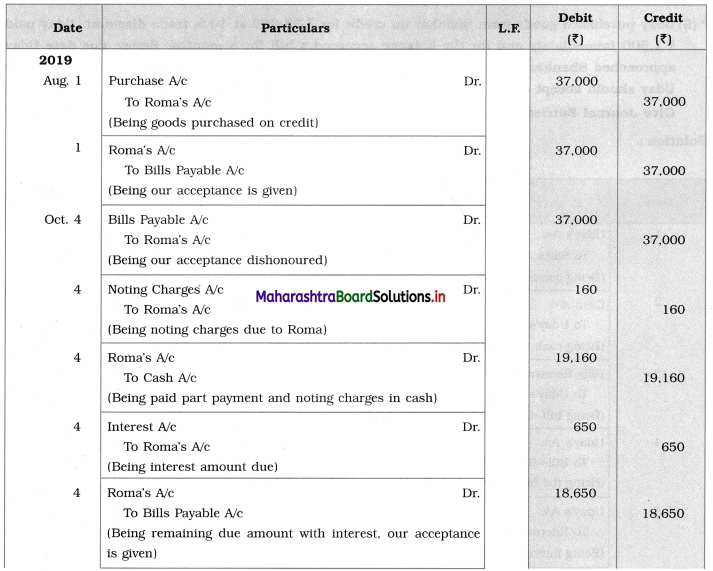
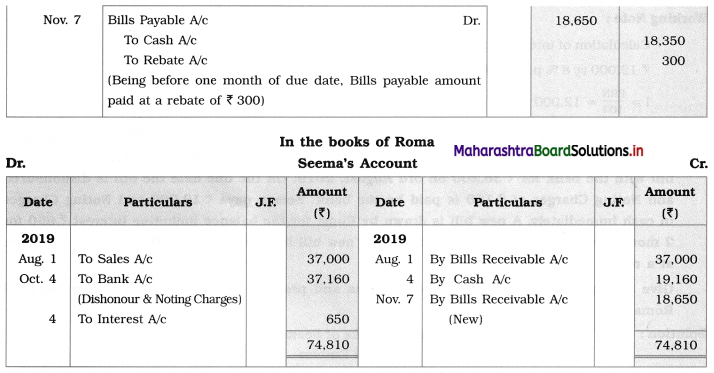
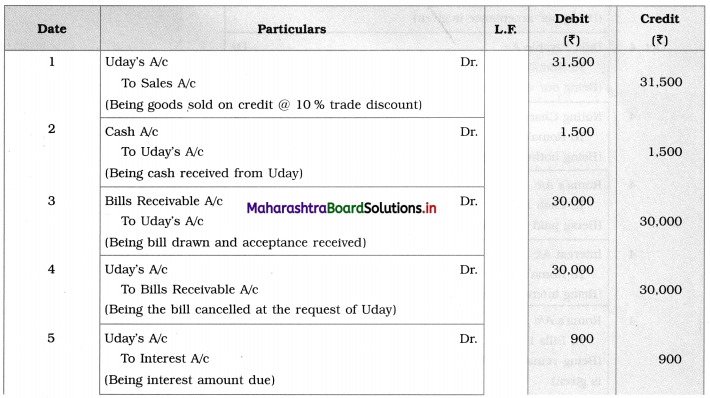
A social movement is an organized effort by a significant number of people to change or resist change. It is a collective action where individuals work tirelessly for months, years, or decades together to change that has mobilised the social structure and social system of the society.
The two movements that had a great impact in changing Indian society are:
(i) Women’s Movement
Women have suffered for countless centuries. The Women’s Movement is divided into three phases they are as follows:
The first phase covers the period of the 19th century where various social reformers like Raja Rammohan Roy, Jyotirao Phule. Justice Govind Ranade and many reformers. Who challenge the unwanted customs like Sati, child marriage, widow remarriage, etc., their efforts and supports of British legislation various laws were enacted like Sati Prohibition Act (1829), The Widow Remarriage Act (1856), The Female Infanticide (Prevention) Act (1870) and so on.
![]()
The second phase of the movement gave a new look to the Women’s Movement, it leads to women participating in the liberation of women and freedom movement till the 20th century.
Feminists like Margaret Cousins formed the Women’s Indian Association, they came up with new ideas about education for women. Participation of women in various national movements like civil disobedience, satyagraha’s, non-cooperation movement, etc., and the influence of Gandhian philosophy inspired women to speak up for themselves.
The third phase of the Women’s Movement shifted towards equality issues of patriarchy, violence against women, crime, dowry deaths, etc. In this phase, various women’s organisations, NGOs, etc. participated to fight for women’s rights and injustice done to them.
In the fourth phase, women from different walks of life joined their hands together in the mission of women’s empowerment in India, summarise women’s movements in India has certain ideologies and objectives like women’s liberation, right to education, struggle for equal rights, violence against women’s and their empowerment. These have changed the position of women in India to a great extent.
(ii) Workers Movement in India
Industrialization not only boomed the Indian economy but brought two classes in society i.e., the industrialist and the working class.
Modern Industry thrives on profit, this brought exploitation of workers. This occurred in terms of extraction of work, minimization of wages, long hours of work, delays in promotion, reduced wages, and poor working conditions.
These issues led to the formation of the Worker’s Movement in India.
The first phase of protest was a group of workers without planning and organization. In 1875 Shapurji Bengalee revolted against bad conditions of labour, his efforts resulted in the enactment of the First Factories Act 1881.
Narayan Meghaji Lokhande known as the father of the Indian workers’ movement set up the first workers’ organization in India i.e., The Bombay Mill hands association 1884, highlighted the problems of workers and passed resolutions to improve the conditions.
The second phase saw the formation of the Trade Union. Strikes became a Powerful Weapon in hands of labour, several strikes were seen from 1918 to 1920.
The Industrial disputes forced to organized Trade Union in India i.e., the establishment of AITUC- All India Trade Union Congress 1926, under the chairmanship of Lala Lajpat Rai, Bombay Textile Labour Union by N. M. Joshi first union to gets its recognition under Act in 1926.
![]()
Trade unions diversified on different ideologies, in order to bring in different coordination’s the National Trade Union Federation (NTUF) was established. Still, there were differences of opinion, in 1947s the Indian National UNION Congress (INUC) was established to safeguard and promote the rights of workers. Various trade unions emerged when Congress came into power, like the Bharatiya Mazdoor Sangh (BMS), United Trade Union Congress (UTUC), and so on.
There were strikes and disputes between management and factory workers meantime came the Industrial Dispute Act of 1947, which used mechanisms like conciliation, arbitration, and adjudication, to resolve the conflicts between management and workers.
The workers’ movement lost its momentum after the 1970s. Textile industries went on strikes, the Great Bombay Textile Strike 1982, under the leadership of Datta Samant. The demands of the workers were a hike in wages, bonuses, scrapping of the Bombay Industrial act of 1947. The strike lasted for a long time and resulted in a negative impact on the industrial relations between labour, industry, and the government.
Further in recent times, the Ministry of Labour gave recognition to central trade union organizations like AITUC, INTUC, AND SEWA.
To sum up, the worker’s movement, began with philanthropists working for the betterment of workers, later on, workers themselves became leaders who started fighting for the workers’ rights, the role of government to solve disputes with globalization the role of the government has altered.
Activity 1 (Textbook Page No. 70)
Small group discussion: Form groups of 5-7 students. Identify various forms of social injustice that you have observed in your village/town/locality. Make a list of the same. Find out names of various organisations that work to remove such injustices or which create awareness about the injustices. (For example, the problems faced by disabled persons, or migrants.)
Answer:
List of social injustice found in Indian society.
The caste system, poverty, child labor, child marriage, low status of women, gender inequality at work, dowry system, the problem faced by women, the problem faced by slum children, migrants, disabled, etc.
(i) Social injustice seen among slum children’s
Form of social injustice we see in our nearby slum area such as lack of proper sanitation, safe drinking water, shortage of space, lack of quality education in municipal schools, high proportion of girls are dropouts to support their family, they work as domestic maids. Though there are legal measures to protect human rights we see child labour is on rampant in slums.
Smile Foundation, beginning in the corridors of education, it has adopted a lifecycle approach with intensive programmes which addresses the needs of less privileged children, their families and the larger community.
![]()
Asha for education projects deal with educational issues from pre-primary schooling to professional education in locations from urban slums to isolated rural areas.
(ii) The problem faced by migrants
Migrants are more vulnerable to discrimination and exploitation as many of them are poor, illiterate, and live in slums and hazardous locations prone to disaster and natural calamities. There is a lack of urban policies and programmes catering to the needs and settlements of migrants.
The National Domestic Workers’ Movement.
(iii) Challenges faced by disability
Disabled face problem of loss of independence, transportation, accessibility issue, loss of independence, education, employment etc.
Narayan Seva Sansthan, established in 1985, is a non-profit charitable organization based in Udaipur, Rajasthan. It is known for providing philanthropic services in the field of treatment and rehabilitation of polio-affected people without discrimination of religion, region, caste, or gender.
Activity 2 (Textbook Page No. 72)
Find out about women’s groups/NGOs in your locality (e.g. anganwadi women teachers, lesbian women, Dalit women’s groups, Muslim women’s organisations). Visit their organisation to find out about the work that they do. You may interview the group members or their volunteers, to find out about the nature of their work or outreach programmes, problems they face etc. Present your findings in class. Initiate a discussion.
Answer:
(i) Self Employed Women’s Association: SEWA is a trade union registered in 1972. It is an organisation of poor, self-employed women workers. These are women who earn a living through their own labour or small businesses. They do not obtain regular salaried employment with welfare benefits like workers in the organised sector. They are the unprotected labour force of our country. Constituting 93% of the labour force, these are workers Of the unorganised sector. Of the female labour force in India, more than 94% are in the unorganised sector. However, their work is not counted and hence remains invisible.
(ii) National Federation of Dalit Women (NFDW): All India Dalit Women Forum and Maharashtra Dalit Mahila Sangasthan etc., address the issues of women empowerment from socially marginalized communities.
Activity 3 (Textbook Page No. 75)
Form groups of 6 students. Identify a workers’ movement in your locality or region. Make a PPT of 12 slides. The content should provide information on how they were established, the significant persons associated with the movement, their major output or successes, the challenges they faced. Make your presentation in class. All group members should discuss a minimum of 2-3 points. The presentation may be followed by a Q&A session.
Answer:
The National Domestic Workers’ Movement [Registered as National Domestic Workers’ Welfare Trust under the Bombay Public Trust Act 1950, Regd. No. E-17253-(Mumbai)] has been at the forefront of championing the rights of domestic workers, children in domestic work and migrant domestic workers, since 1985. It was founded by Dr. (Sr.) Jeanne Devos.
NDWM encourages empowerment of domestic workers through solidarity, participation and leadership training. Together we work for the labour rights of domestic workers, seeking dignity and justice.
![]()
The challenges faced by them are:
- The stigmatisation of domestic workers and their work.
- Total absence of Rights and Legal protection.
- Absence of training, support and bargaining power.
The objectives of the movement are:
- Dignity for domestic work and domestic workers.
- Rights and Legal Protection.
- Support and empowerment.
Activity 4 (Textbook Page No. 77)
Collect newspaper and journal reports on farmer suicides in the past year. Display this information on your class bulletin board.
Answer:
Articles on farmer’s suicide for reference
The geography of farmer suicide
Vishnu Padmanabhan, Pooja Dantewadia | Livemint | Updated : Jan 16, 2020
12 Nashik farmers ended lives in’ 20 so far, 63% drop since last year
Abhilash Botekar | TNN | Times of India | Updated : May 26, 2020
10,349 farmers committed suicide in 2018 : NCRB
PTI | Last Updated Jan 09, 2020 | The Economic Times
Activity 5 (Textbook Page No. 80)
(A) Have you heard of Greta Thunberg? Discuss the effect of her activism.
(B) View the film ‘Lakir ke is Taraf by Shilpa Ballal.
Then have a class discussion.
Answer:
(A) Swedish climate youth activist Greta Thunberg, has received worldwide recognition for her efforts to fight climate change. With the simple message “School strike for climate” handwritten on poster board, she began skipping school on Fridays and protesting outside the Swedish Parliament. Thanks to social media, her actions have spread and influenced millions of young people all over the world to organise and protest.
(B) ‘Lakir ke is taraf a documentary made by Shilpa Ballal, highlights some of the concerns surrounding the Sardar Sarovar Project that led to the beginning of the Narmada Bachao Andolan in 1985. It is 85 minute documentary which enables viewers to understand the situation through the lens of the disadvantaged villagers, who were compelled to leave their ancestral property and witness the submergence of their homes, land and cattle.
Activity 6 (Textbook Page No. 81)
(i) Identify any 5 conservation/environmental initiatives (e.g. Go Green, Save the Forests, Save Aarey, Eco-friendly Ganpati)
(ii) Make group presentations in class about their aims, objectives, and activities.
(iii) This may be followed by a class discussion or home assignment.
Answer:
(i) Swachh Bharat Abhiyaan, is a mass movement launched by Prime Minister Narendra Modi in 2014, develops the responsibility among Indian citizens to keep our surroundings clean and to achieve Mahatma Gandhiji’s aim to clean India.
![]()
(ii) Namami Gange Programme Narendra Modi took over as the Prime Minister of India in 2014. In June that year, recognizing the cultural and environmental importance of the river Ganga, the ‘Namami Gange Programme’ was approved by the Union Government.
(iii) Project Tiger, is a tiger conservation programme launched in April 1973 by the Government of India during Prime Minister Indira Gandhi’s tenure. The project aims at ensuring a viable population of Bengal tigers in their natural habitats, protecting them from extinction, and preserving areas of biological importance as a natural heritage.
Class 12 Sociology Textbook Solutions Digest
- Sociology Class 12 Chapter 1 Question Answers
- Sociology Class 12 Chapter 2 Question Answers
- Sociology Class 12 Chapter 3 Question Answers
- Sociology Class 12 Chapter 4 Question Answers
- Sociology Class 12 Chapter 5 Question Answers
- Sociology Class 12 Chapter 6 Question Answers
- Sociology Class 12 Passages Answers