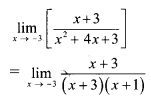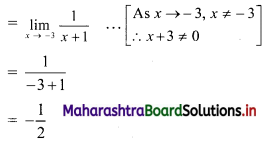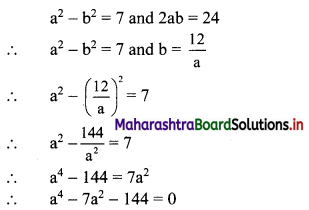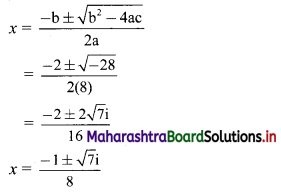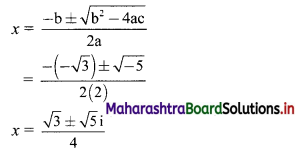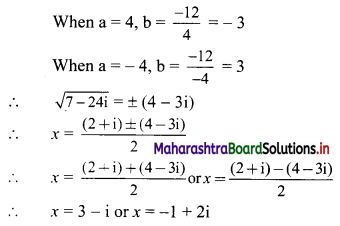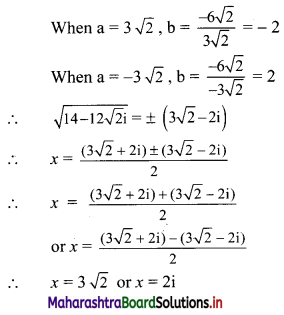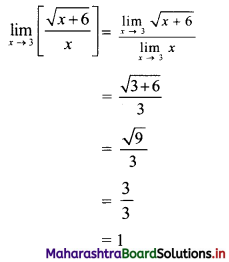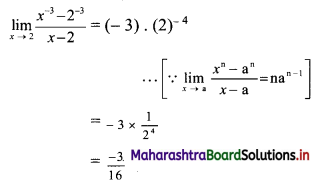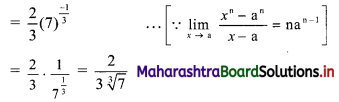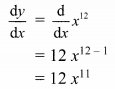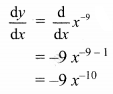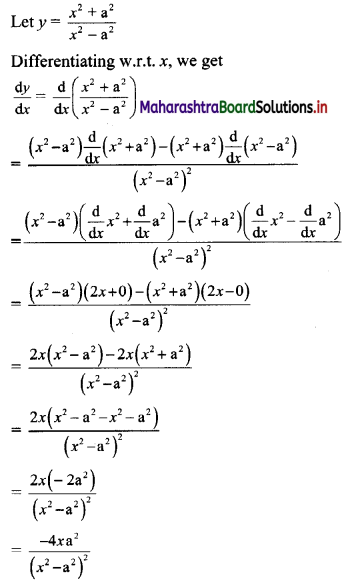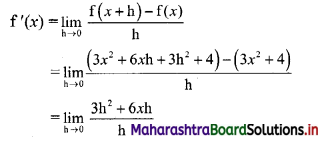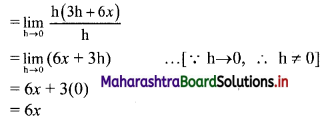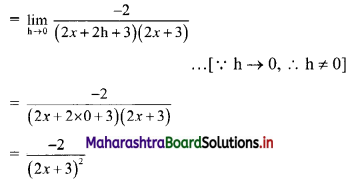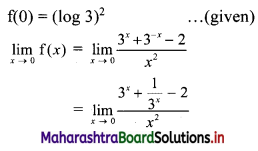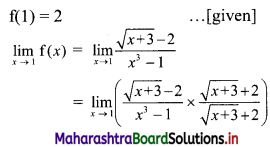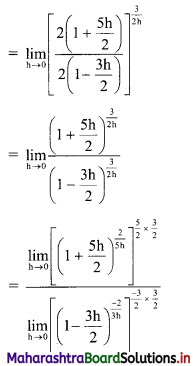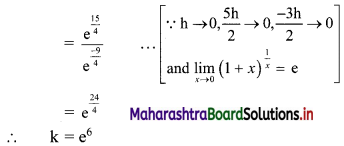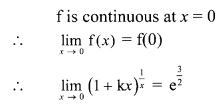Locus and Straight Line Class 11 Commerce Maths 1 Chapter 5 Exercise 5.4 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 5 Locus and Straight Line Ex 5.4 Questions and Answers.
Std 11 Maths 1 Exercise 5.4 Solutions Commerce Maths
Question 1.
Find the slope, x-intercept, y-intercept of each of the following lines.
(a) 2x + 3y – 6 = 0
(b) x + 2y = 0
Solution:
(a) Given equation of the line is 2x + 3y – 6 = 0
Comparing this equation with ax + by + c = 0, we get
a = 2, b = 3, c = -6
∴ Slope of the line = \(\frac{-a}{b}=\frac{-2}{3}\)
x-intercept = \(\frac{-\mathrm{c}}{\mathrm{a}}=\frac{-(-6)}{2}\) = 3
y-intercept = \(\frac{-\mathrm{c}}{\mathrm{b}}=\frac{-(-6)}{3}\) = 2
(b) Given equation of the line is x + 2y = 0
Comparing this equation with ax + by + c = 0, we get
a = 1, b = 2, c = 0
∴ Slope of the line = \(\frac{-a}{b}=\frac{-1}{2}\)
x-intercept = \(\frac{-c}{a}=\frac{-0}{1}\) = 0
y-intercept = \(\frac{-\mathrm{c}}{\mathrm{b}}=\frac{-0}{2}\) = 0
![]()
Question 2.
Write each of the following equations in ax + by + c = 0 form.
(a) y = 2x – 4
(b) y = 4
(c) \(\frac{x}{2}+\frac{y}{4}=1\)
(d) \(\frac{x}{3}=\frac{y}{2}\)
Solution:
(a) y = 2x – 4
∴ 2x – y – 4 = 0 is the equation in ax + by + c = 0 form.
(b) y = 4
∴ 0x + 1y – 4 = 0 is the equation in ax + by + c = 0 form.
(c) \(\frac{x}{2}+\frac{y}{4}=1\)
∴ \(\frac{2 x+y}{4}=1\)
∴ 2x + y = 4
∴ 2x + y – 4 = 0 is the equation in ax + by + c = 0 form.
(d) \(\frac{x}{3}=\frac{y}{2}\)
∴ 2x = 3y
∴ 2x – 3y + 0 = 0 is the equation in ax + by + c = 0 form.
Question 3.
Show that the lines x – 2y – 7 = 0 and 2x – 4y + 5 = 0 are parallel to each other.
Solution:
Let m1 be the slope of the line x – 2y – 7 = 0.
∴ m1 = \(\frac{-1}{-2}=\frac{1}{2}\)
Let m2 be the slope of the line 2x – 4y + 5 = 0.
∴ m2 = \(\frac{-2}{-4}=\frac{1}{2}\)
Since, m1 = m2
∴ The given lines are parallel to each other.
Question 4.
If the line 3x + 4y = p makes a triangle of area 24 square units with the co-ordinate axes, then find the value of p.
Solution:
Let the line 3x + 4y = p cuts the X and Y-axes at points A and B respectively.
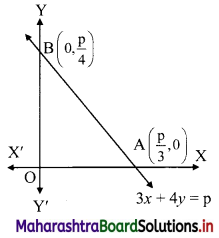
3x + 4y = p
∴ \(\frac{3 x}{\mathrm{p}}+\frac{4 y}{\mathrm{p}}=1\)
∴ \(\frac{x}{\frac{p}{3}}+\frac{y}{\frac{p}{4}}=1\)
The equation is of the form \(\frac{x}{a}+\frac{y}{b}=1\), with a = \(\frac{p}{3}\) and b = \(\frac{p}{4}\)
∴ A = (a, 0) = (\(\frac{p}{3}\), 0) and B = (0, b) = (0, \(\frac{p}{4}\))
∴ OA = \(\frac{p}{3}\) and OB = \(\frac{p}{4}\)
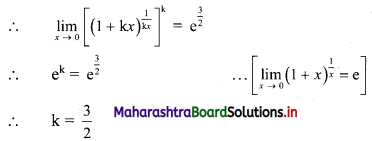
Given, A(∆OAB) = 24 sq. units
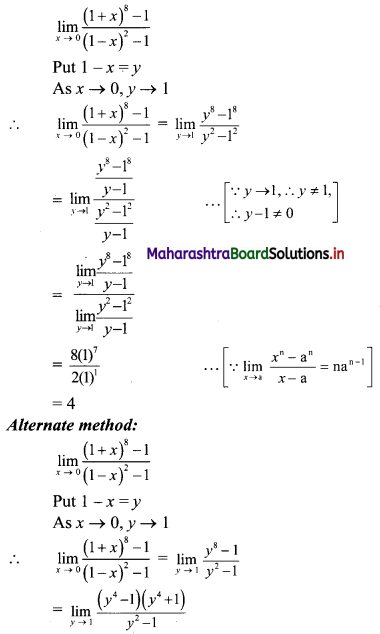
∴ \(\frac{1}{2}\) × OA × OB = 24
∴ \(\frac{1}{2}\) × \(\frac{p}{3}\) × \(\frac{p}{4}\) = 24
∴ p2 = 576
∴ p = ±24
![]()
Question 5.
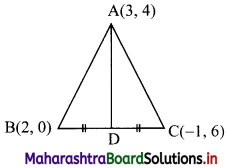
Find the co-ordinates of the circumcentre of the triangle whose vertices are A(-2, 3), B(6, -1), C(4, 3).
Solution:
Here, A(-2, 3), B(6, -1), C(4, 3) are the vertices of ∆ABC.
Let F be the circumcentre of ∆ABC.
Let FD and FE be the perpendicular bisectors of the sides BC and AC respectively.
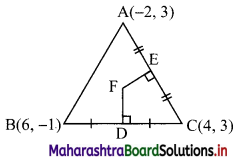
∴ D and E are the midpoints of side BC and AC respectively.
∴ D = \(\left(\frac{6+4}{2}, \frac{-1+3}{2}\right)\) = (5, 1)
and E = \(\left(\frac{-2+4}{2}, \frac{3+3}{2}\right)\) = (1, 3)
Now, slope of BC = \(\frac{-1-3}{6-4}\) = -2
∴ slope of FD = \(\frac{1}{2}\) …..[∵ FD ⊥ BC]
Since, FD passes through (5, 1) and has slope \(\frac{1}{2}\)
∴ Equation of FD is y – 1 = \(\frac{1}{2}\)(x – 5)
∴ 2(y – 1) = x – 5
∴ x – 2y – 3 = 0 ……(i)
Since, both the points A and C have same y co-ordinates i.e. 3
∴ the points A and C lie on the liney = 3.
Since, FE passes through E(1, 3).
∴ the equation of FE is x = 1. …….(ii)
To find co-ordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value of x in (i), we get
1 – 2y – 3 = 0
∴ y = -1
∴ Co-ordinates of circumcentre F = (1, -1).
Question 6.
Find the equation of the line whose x-intercept is 3 and which is perpendicular to the line 3x – y + 23 = 0.
Solution:
Slope of the line 3x – y + 23 = 0 is 3.
∴ slope of the required line which is perpendicular to 3x – y + 23 = 0 is \(\frac{-1}{3}\).
Since, the x-intercept of the required line is 3.
∴ it passes through (3, 0).
∴ the equation of the required line is
y – 0 = \(\frac{-1}{3}\) (x – 3)
∴ 3y = -x – 3
∴ x – 3y = 3
![]()
Question 7.
Find the distance of the point A(-2, 3) from the line 12x – 5y – 13 = 0.
Solution:
Let p be the perpendicular distance of the point A(-2, 3) from the line 12x – 5y – 13 = 0
Here, a = 12, b = -5, c = -13, x1 = -2, y1 = 3
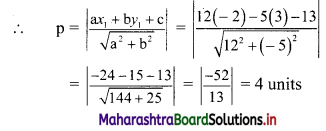
Question 8.
Find the distance between parallel lines 9x + 6y – 1 = 0 and 9x + 6y – 32 = 0.
Solution:
Equations of the given parallel lines are 9x + 6y – 7 = 0 and 9x + 6y – 32 = 0.
Here, a = 9, b = 6, C1 = -7 and C2 = -32
∴ Distance between the parallel lines
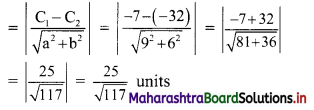
Question 9.
Find the equation of the line passing through the point of intersection of lines x + y – 2 = 0 and 2x – 3y + 4 = 0 and making intercept 3 on the X-axis.
Solution:
Given equations of lines are
x + y – 2 = 0 ……(i)
and 2x – 3y – 4 = 0 ……(ii)
Multiplying equation (i) by 3, we get
3x – 3y – 6 = 0 …..(iii)
Adding equation (ii) and (iii), we get
5x – 2 = 0
∴ x = \(\frac{2}{5}\)
Substituting x = \(\frac{2}{5}\) in equation (i), we get
\(\frac{2}{5}\) + y – 2 = 0
∴ y = 2 – \(\frac{2}{5}\) = \(\frac{8}{5}\)
∴ The required line passes through point (\(\frac{2}{5}\), \(\frac{8}{5}\)).
Also, the line makes intercept of 3 on X-axis
∴ it also passes through point (3, 0).
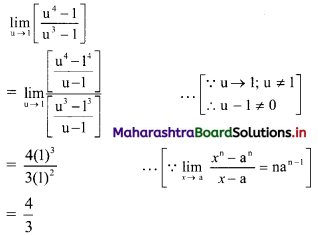
∴ required equation of line passing through points (\(\frac{2}{5}\), \(\frac{8}{5}\)) and (3, 0) is
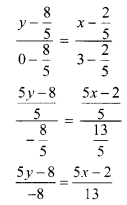
∴ 13(5y – 8) = -8(5x – 2)
∴ 65y – 104 = -40x + 16
∴ 40x + 65y – 120 = 0
∴ 8x + 13y – 24 = 0 which is the equation of the required line.
![]()
Question 10.
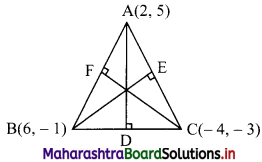
D(-1, 8), E(4, -2), F(-5, -3) are midpoints of sides BC, CA and AB of ∆ABC. Find
(i) equations of sides of ∆ABC.
(ii) co-ordinates of the circumcentre of ∆ABC.
Solution:
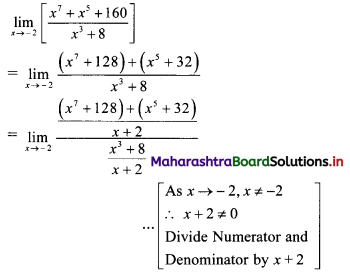
(i) Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of ∆ABC.
Given, points D, E and F are midpoints of sides BC, CA and AB respectively of ∆ABC.

For x-coordinates:
Adding (i), (iii) and (v), we get
2x1 + 2x2 + 2x3 = -4
∴ x1 + x2 + x3 = -2 …..(vii)
Solving (i) and (vii), we get x1 = 0
Solving (iii) and (vii), we get x2 = -10
Solving (v) and (vii), we get x3 = 8
For y-coordinates:
Adding (ii), (iv) and (vi), we get
2y1 + 2y2 + 2y3 = 6
∴ y1 + y2 + y3 = 3 …..(viii)
Solving (ii) and (viii), we get y1 = -13
Solving (iv) and (viii), we get y2 = 7
Solving (vi) and (viii), we get y3 = 9
∴ Vertices of ∆ABC are A(0, -13), B(-10, 7), C(8, 9)

(ii) Here, A(0, -13), B(-10, 7), C(8, 9) are the vertices of ∆ABC.
Let F be the circumcentre of ∆ABC.
Let FD and FE be perpendicular bisectors of the sides BC and AC respectively.
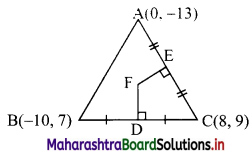
∴ D and E are the midpoints of side BC and AC.
∴ D = \(\left(\frac{-10+8}{2} \cdot \frac{7+9}{2}\right)\) = (-1, 8)
and E = \(\left(\frac{0+8}{2}, \frac{-13+9}{2}\right)\) = (4, -2)
Now, slope of BC = \(\frac{7-9}{-10-8}=\frac{1}{9}\)
∴ slope of FD = -9 ……[∵ FD ⊥ BC]
Since, FD passes through (-1, 8) and has slope -9
∴ Equation of FD is y – 8 = -9(x + 1)
∴ y – 8 = -9x – 9
∴ y = -9x – 1 …..(i)
Also, slope of AC = \(\frac{-13-9}{0-8}=\frac{11}{4}\)
∴ Slope of FE = \(\frac{-4}{11}\) ….[∵ FE ⊥ AC]
Since, FE passes through (4, -2) and has slope \(\frac{-4}{11}\)
∴ Equation of FE is y + 2 = \(\frac{-4}{11}\)(x – 4)
∴ 11(y + 2) = -4(x – 4)
∴ 11y + 22 = -4x + 16
∴ 4x + 11y = -6 ….(ii)
To find co-ordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value of y in (ii), we get
∴ 4x + 11(-9x – 1) = -6
∴ 4x – 99x – 11 = -6
∴ -95x = 5
∴ x = \(\frac{-1}{19}\)
Substituting the value of x in (i), we get
y = -9(\(\frac{-1}{19}\)) – 1 = \(\frac{-10}{19}\)
∴ Co-ordinates of circumcentre F = \(\left(\frac{-1}{19}, \frac{-10}{19}\right)\)
11th Commerce Maths Digest Pdf