Locus and Straight Line Class 11 Commerce Maths 1 Chapter 5 Exercise 5.2 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 5 Locus and Straight Line Ex 5.2 Questions and Answers.
Std 11 Maths 1 Exercise 5.2 Solutions Commerce Maths
Question 1.
Find the slope of each of the following lines which pass through the points:
(a) (2, -1), (4, 3)
(b) (-2, 3), (5, 7)
(c) (2, 3), (2, -1)
(d) (7, 1), (-3, 1)
Solution:
(a) Let A = (x1, y1) = (2, -1) and B = (x2, y2) = (4, 3).
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{3-(-1)}{4-2}\)
= \(\frac{4}{2}\)
= 2
(b) Let C = (x1, y1) = (-2, 3) and D = (x2, y2) = (5, 7)
Slope of line CD = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{7-3}{5-(-2)}\)
= \(\frac{4}{7}\)
![]()
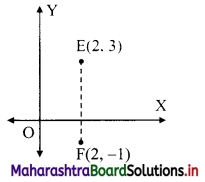
(c) Let E = (2, 3) = (x1, y1) and F = (2, -1) = (x2, y2)
Since x1 = x2 = 2
∴ The slope of EF is not defined. ……[EF || y-axis]
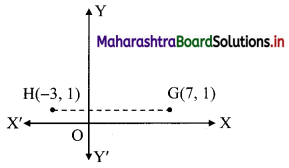
(d) Let G = (7, 1) = (x1, y1) and H = (-3, 1) = (x2, y2) say.
Since y1 = y2
∴ The slope of GH = 0 …..[GH || x-axis]
Question 2.
If the X and Y-intercepts of line L are 2 and 3 respectively, then find the slope of line L.
Solution:
Given, x-intercept of line L is 2 and y-intercept of line L is 3
∴ the line L intersects X-axis at (2, 0) and Y-axis at (0, 3).
i.e. the line L passes through (2, 0) = (x1, y1) and (0, 3) = (x2, y2) say.
Slope of line L = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{3-0}{0-2}\)
= \(\frac{-3}{2}\)
Question 3.
Find the slope of the line whose inclination is 30°.
Solution:
Given, inclination (θ) = 30°
Slope of the line = tan θ = tan 30° = \(\frac{1}{\sqrt{3}}\)
Question 4.
Find the slope of the line whose inclination is 45°.
Solution:
Given, inclination (θ) = 45°
Slope of the line = tan θ = tan 45° = 1
Question 5.
A line makes intercepts 3 and 3 on the co-ordinate axes. Find the slope of the line.
Solution:
Given, x-intercept of line is 3 and y-intercept of line is 3
∴ The line intersects X-axis at (3, 0) and Y-axis at (0, 3).
i.e. the line passes through (3, 0) = (x1, y1) and (0, 3) = (x2, y2) say.
Slope of line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{3-0}{0-3}\)
= -1
![]()
Question 6.
Without using Pythagoras theorem, show that points A(4, 4), B(3, 5) and C(-1, -1) are the vertices of a right-angled triangle.
Solution:
Given, A(4, 4) = (x1, y1), B(3, 5) = (x2, y2), C(-1, -1) = (x3, y3)
Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{5-4}{3-4}=-1\)
Slope of BC = \(\frac{y_{3}-y_{2}}{x_{3}-x_{2}}=\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}\)
Slope of AC = \(\frac{y_{3}-y_{1}}{x_{3}-x_{1}}=\frac{-1-4}{-1-4}=\frac{-5}{-5}=1\)
Slope of AB × slope of AC = -1 × 1 = -1
∴ side AB ⊥ side AC
∴ ΔABC is a right angled triangle, right angled at A.
∴ The given points are the vertices of a right angled triangle.
Question 7.
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured clockwise.
Solution:
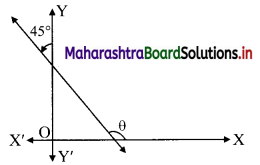
Since, the line makes an angle of 45° with positive direction of Y-axis in anticlockwise direction.
∴ Inclination of the line (θ) = (90° + 45°)
∴ Slope of the line = tan(90° + 45°)
= -cot 45° …….[tan(90 + θ°) = -cot θ]
= -1
Question 8.
Find the value of k for which the points P(k, -1), Q(2, 1) and R(4, 5) are collinear.
Solution:
Given, points P(k, -1), Q(2, 1), and R(4, 5) are collinear.
∴ Slope of PQ = Slope of QR
∴ \(\frac{1-(-1)}{2-k}=\frac{5-1}{4-2}\)
∴ \(\frac{2}{2-k}=\frac{4}{2}\)
∴ 1 = 2 – k
∴ k = 2 – 1 = 1
Check:
For collinear points P, Q, R,
Slope of PQ = Slope of QR = Slop of PR
For k = 1, if the given points are collinear, then our answer is correct.
P(1, -1), Q(2, 1) and R(4, 5)
Slope of PQ = \(\frac{1-(-1)}{2-1}=\frac{2}{1}=2\)
Slope of QR = \(\frac{5-1}{4-2}=\frac{4}{2}=2\)
Slope of PQ = Slope of QR
∴ The given points are collinear.
Thus, our answer is correct.
11th Commerce Maths Digest Pdf